Dynamics of excitable cells: spike-adding phenomena in action

Abstract

We study the dynamics of action potentials of some electrically excitable cells: neurons and cardiac muscle cells. Bursting, following a fast–slow dynamics, is the most characteristic behavior of these dynamical systems, and the number of spikes may change due to spike-adding phenomenon. Using analytical and numerical methods we give, by focusing on the paradigmatic 3D Hindmarsh–Rose neuron model, a review of recent results on the global organization of the parameter space of neuron models with bursting regions occurring between saddle-node and homoclinic bifurcations (fold/hom bursting). We provide a generic overview of the different bursting regimes that appear in the parametric phase space of the model and the bifurcations among them. These techniques are applied in two realistic frameworks: insect movement gait changes and the appearance of Early Afterdepolarizations in cardiac dynamics.

1 Introduction

Cells are covered with a membrane that isolates and protects them from the environment. It also acts as a regulator of ionic concentrations in the cellular plasma of important elements for biological processes, such as Ca, K, etc. As a consequence, the ionic concentration of some elements is different on both sides of the membrane. Since the relative permeability of the cell membrane is also different for those elements, there exists a difference in potential between the inside and outside of the cell, which is called the membrane potential. This is particularly important for the study of electrically excitable cells (muscle cells, secretory cells and neurons), which perform their functions by actively changing their membrane potential and thus generating electrical signals, called action potentials (APs). Therefore, to understand the behavior of an excitable cell we should study the dynamics of their APs. The excitable cells that concern us are neurons and cardiac muscle cells.

Hodgkin and Huxley proposed the first neuron (HH) model [1] describing the action potentials in the neuron membrane. It has given rise to several mathematical models for diverse kinds of neurons in different animals. Among them, some simplified models, like the 3D Hindmarsh–Rose (HR) model, have been developed to help in the study of realistic models based on the HH framework [1]. We consider the HR model [2] for a detailed analysis (a similar study can be carried out to other models) given that, even if it is computationally simple, it reproduces quite well the rich firing patterns exhibited by a biological neuron as well as the main behavior in general. The HR model is the following set of three nonlinear ODEs

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=y-ax^3+bx^2-z+I, \\ {\dot{y}}=c-dx^2-y, \\ {\dot{z}}=\varepsilon [s(x-x_0)-z], \end{array}\right. \end{aligned}$$

(1)

where x, y and z are the membrane potential, the fast and the slow gating variables, respectively. Regarding parameters, $(a,c,d,s,x_0)$ are set to the typical values $(1,1,5,4,-1.6)$, (b, I) take values in specific ranges where the bursting or spiking behavior is exhibited and, along the paper, the value of the small parameter $\varepsilon$ is taken from different intervals in which it has different magnitude to achieve a global analysis of this fast–slow system.

Fig. 1

Left: Fast/slow decomposition that illustrates the bifurcation scenario in which a fold/hom (or square-wave) bursting occurs in the HR model (1). Fixed points occur along the $M_{eq}$ curve (stable when continuous, unstable when discontinuous), and limit cycles occur between both branches of $M_{lc}$. Andronov–Hopf (AH), saddle-node (SN) and primary homoclinic (Hom) bifurcations are shown. Right: Zoom showing a fold/hom bursting orbit in blue. For more details see [7]

Bursting is the main behavior present in neuron models, and follows a fast–slow dynamics [3] (it is also common in laser dynamics and chemical reactions, among other practical applications [4, 5]). The fold/hom (or square-wave) bursting, following the Izhikevich [6] classification, is one of the main bursting regimes. In a fold/hom bursting, the active regime begins in a fold (or saddle-node) bifurcation of equilibria and ends at a homoclinic bifurcation in the fast subsystem. In Fig. 1, the conditions for this type of bursting in the HR model and one orbit are shown. Spike-adding bifurcations are a common set of bifurcations in systems that present fast–slow dynamics. Such special bifurcations give rise to the appearance of extra spikes (turns) in the fast manifold region. They are of interest due to the progressive change that they cause in the spectrum of periodic orbits and the structure of chaotic attractors of the system [8,9,10,11]. In Fig. 2 several bursting orbits and a spike-adding process in the HR model are represented. In the aforementioned type of bursting, this spike-adding phenomenon is associated with the existence of canard explosions and certain codimension-two homoclinic bifurcations (inclination-flip and orbit-flip) [8, 12,13,14].

Fig. 2

Taken from [7] (Figure 6). Left: 3D projections of bursting orbits of the HR model (1) for three different values of parameter b. Right: Waveforms of four bursting orbits (three of them shown on the left) of Hindmarsh–Rose model for a fixed value of I and four distinct values of parameter b. A spike-adding process can be appreciated when going from A to D

Fig. 3

Taken from [19] with modifications (Figures 1 and 4). Top: Spike-counting (SC) diagram on the (b, I) plane, for $\varepsilon =0.05$ and $\varepsilon = 0.01$, classifying the AP as quiescent (0 spikes, i.e. fixed point), spiking (1 spike) or bursting (2 or more spikes). Andronov–Hopf (AH) and primary homoclinic (Hom) bifurcations correspond to curves shown in red and black, respectively. Bottom: The first primary homoclinic bifurcations curves are shown for different values of the small parameter $\varepsilon$. The curves have been computed using the continuation software AUTO [17, 18]

This paper is organized as follows. Section 2 deals with the description of the dynamical properties of the HR model, and is divided into three parts: Sect. 2.1 is devoted to studying slices of the three-parameter space for the HR model, with each slice determined by the values of $\varepsilon$ within a standard range of small values; Sect. 2.2 presents the changes observed when we consider the full three-parameter space and the parameter $\varepsilon$ is allowed to take larger values, and it also shows the geometric bifurcations that can be found in the HR model; Sect. 2.3 shows the limit behavior when the small parameter $\varepsilon \searrow 0$. Section 3 introduces more realistic models of Hodgkin–Huxley type, one used to analyze insect gait movement changes in Sect. 3.1, and the other to study Early Afterdepolarizations in cardiac dynamics in Subsection 3.2. Section 4 gives some conclusions. Finally, Appendix A provides for completion some theoretical aspects of the homoclinic bifurcations used in the paper.

2 Characterization of the HR neuron model

In this section we provide an exhaustive analysis of the dynamical characteristics of the HR model introduced in (1), and in particular we show how they depend on the values of the small parameter $\varepsilon$. Each of the following subsections deals with a different situation regarding this parameter.

2.1 Dynamics at standard values of the small parameter $\varepsilon$

In this section, we study the behavior of the HR model when the small parameter $\varepsilon$ is in a standard range. The main bifurcations of the system are described, thus providing a complete description of the parameter space.

In recent years, the HR model has been thoroughly analyzed (see [7, 8, 15, 16]) applying different techniques, such as the spike-counting (SC) method [7, 16]. This technique, applied to a periodic orbit of a dynamical system, determines the number of spikes that a certain variable shows during a period. In the case of excitable cells, the SC technique allows us to compute the number of spikes of the membrane potential during each activation period of the cell. Figure 3 shows the number of spikes of the membrane potential for stable solutions of the HR model, codified with colors, along the (b, I)-plane. This allows us to distinguish between the regions of chaotic bursting, periodic tonic spiking and regular bursting. Stable spiking is shown as APs with a single spike, while quiescence of neurons occur when a fixed point is reached (in SC terms, the AP shows 0 spikes). Ranging from blue to green, we can see the stripes of a spike-adding cascade that corresponds to bursting that becomes chaotic in a chain of onion-like bulbs colored in brown [8]. In this review paper, we briefly focus on the development of a global study of the complete homoclinic structure that gives rise to the complete phenomena. To that goal, a detailed numerical study with continuation techniques is required (we used the well-known software AUTO [17, 18]) as well as with the SC technique.

Andronov–Hopf (AH) bifurcations, in red, and primary homoclinic (Hom) bifurcations, in black, are superimposed in both representations of Fig. 3. These bifurcations, further characterized in [19], correspond to bifurcations shown in Fig. 1. Also in [19], it was studied how the first primary homoclinic bifurcation curve modifies its geometry when different values of the small parameter $\varepsilon$ are considered and how this phenomenon is related with being in a fast–slow regime or not. At the bottom of Fig. 3, it is shown that the number of “visible” foldings (with respect to parameter b) of the homoclinic curve varies when larger values of $\varepsilon$ are considered [19].

Fig. 4

a Theoretical unfolding of the codimension-two IF and OF homoclinic bifurcations of types $C_{in}$ and $C_{out}$ describing the pencils of period-doubling and fold bifurcations. b Spike-counting diagram on the (b, I) plane for $\varepsilon =0.01$. Superimposed, the bifurcation curves (yellow—fold or saddle-node of periodic orbits, red—period-doubling (PD), black—primary homoclinic bifurcations) and some codimension-two bifurcation points (purple—IF and green—OF) (Color figure online)

A deep use of the SC and continuation techniques also provides a theoretical scheme of the generation of the spike-adding and chaotic regions in fold/hom bursters, related with canard phenomena [20] and codimension-two homoclinic bifurcations [8], respectively. For instance, Fig. 4b shows, for $\varepsilon =0.01$, a two-parameter plot (plane (b, I)) of the HR-model with the SC technique. Superimposed to it, the figure displays the main bifurcation curves for the spike-adding process (yellow—fold or saddle-node of periodic orbits (SN), red—period-doubling (PD), black—primary homoclinic bifurcations) and the codimension-two bifurcation points (purple—inclination-flip (IF) and green—orbit-flip (OF)) where the pencils of period-doubling and fold bifurcations are generated. In Fig. 4a we depict the theoretical unfolding ( [21] and Appendix A) of the “in” and “out” versions of the codimension-two IF and OF homoclinic bifurcations of type C, describing the pencils of period-doubling and fold bifurcations. Although there are more types of IF and OF bifurcations, in HR model only type C is present. See Appendix A for a more detailed mathematical description of homoclinic bifurcations.

Fig. 5

Taken from [22] with modifications (Figure 6). Generic theoretical scenario (for the case of $n>2$) that shows the interlaced bifurcation diagram for the n to $n+1$ spike-adding process when $\varepsilon$ is small. The notation $hom^{(n,n+1)}$ is used for the isola of homoclinic bifurcations for which parameters on one side generate homoclinic orbits with n spikes and on the other side with $n+1$ spikes

Fig. 6

Taken from [22] with modifications (Figure 11). Top: AUTO $L_2$-norm of the orbit for $x_0=-1$, $b=2.7$ and $\varepsilon =0.01$ (several fold and period-doubling bifurcations are represented with black and red points, respectively). Bottom: IBD for the same orbit (Color figure online)

All the above results provide us with some global information of the structure of the parameter space of the HR system, but since in most cases only the first homoclinic bifurcation was used, this information is just partial. In Fig. 5 we display the complete scenario that shows the interlaced bifurcation diagram for the n to $n+1$ spike-adding process when $\varepsilon$ is small. Note that the homoclinic curves contain the codimension-two homoclinic bifurcation points that generate the bifurcations leading to the change from n to $n+1$ spikes, and that they are connected with the other homoclinic curves and with chaotic regions. Moreover, these homoclinic curves are isolas, that is, closed curves in the parameter space. See [22, 23] for a complete description of the theoretical scheme.

The discovery of the relevant role of the homoclinic bifurcations in the fold/hom spike-adding process [8, 12] also allows us to classify the different types of spike-adding processes [14]. See in Fig. 6 how the homoclinic bifurcation acts as a boundary of a continuous case spike-adding involving canard orbits (to the left) and the isola-type one (to the right). The top plot shows the AUTO $L_2$-norm of the periodic orbits, while the bottom plot displays the Interspike Bifurcation Diagram (IBD), giving the time between two consecutive spikes of the periodic orbits. The bottom plot clearly indicates the number of spikes per orbit, while the top plot indicates the type of spike-adding process (see [14] for more details).

2.2 A global three-parameter analysis: case $\varepsilon \nearrow {\mathcal {O}}(1)$

The previous subsection showed the behavior of the parameter planes when the small parameter $\varepsilon$ was taken in a standard range. In this subsection we focus on studying the global parametric phase space. Just to give an idea of the global parametric panorama, Fig. 7 presents a three-parameter plot using the spike-counting technique. As it can be seen from two-parameter plots on the right side of Fig. 7, bifurcation curves of periodic orbits emerge from codimension-two homoclinic bifurcation points, in this case, the HR model exhibits IF, OF and Belyakov bifurcations (see [13] for a complete description). Further details about the bifurcations shown in Fig. 7 will be provided later, but the figure shows us that, by increasing the small parameter $\varepsilon$, some structures change and even disappear. Two-parameter plots show that some color bands and also some codimension-two bifurcation points are present no more when the value of parameter $\varepsilon$ is larger than its standard values. This fact leads us to wonder if there are codimension-three bifurcation points or any other mechanism responsible of the disappearance of the codimension-two bifurcation points.

Fig. 7

Left: Three-parameter (b, I, $\varepsilon$) spike-counting diagram of the HR model. Right: Two-parameter plots showing slices for $\varepsilon = 0.018$, 0.03 and 0.08, with bifurcation lines and points: homoclinic and period-doubling codimension-one curves, IF, OF and Belyakov codimension-two bifurcation points

In most fast–slow systems with explicit small parameters, these parameters play a significant role and drastic changes in the global phase space are exhibited under their variation. As commented before, in the HR model, increasing $\varepsilon$ leads to numerous changes, and in what follows, we want to show how the HR model exhibits geometric bifurcations [24] with respect to $\varepsilon$ that, linked with dynamical bifurcations, explain the observed phenomena. The concept of geometric bifurcations was introduced in [24] to visually classify observed changes in the parameter space when special points “seem” to collide and disappear in points that are not topological bifurcations. These changes are due to the way of observing the dynamics and, although they are not true bifurcations, provide useful insights on the global parametric phase space of the model. Therefore, we add, to the standard codimension of a bifurcation, extra codimensions referred to these geometric bifurcations (see [24] for more details).

We are going to show that codimension–one-plus-one, two-plus-one and one-plus-two geometric bifurcations occur in the HR model. We will see how codimension-one bifurcation surfaces which are unfolded generically from codimension-two bifurcation curves are affected by the existence of codimension–two-plus-one degenerations on these curves.

Fig. 8

Three-parameter plot showing codimension-one homoclinic bifurcation surfaces. In plots a–c the homoclinic surfaces $hom^{(1,2)}$, $hom^{(2,3)}$, $hom^{(6,7)}$ and $hom^{(11,12)}$ are shown together using three points of view to illustrate how close are one to each other and to compare their respective sizes. In plot d it is presented the $hom^{(11,12)}$ homoclinic bifurcation surface with some codimension-two homoclinic bifurcation curves and some geometric bifurcations

From the analysis in [13], it follows that in the HR model there exist many codimension-one homoclinic bifurcation surfaces which are exponentially close to each other, and that their number grows to infinity when the small parameter $\varepsilon$ tends to zero. The intersection of each surface with horizontal planes produces isolas (closed curves) as these homoclinic surfaces are tubular. Moreover, these isolas exhibit a pair of extremely sharp folds and their width is also exponentially small. Folding points determine two different sides in each isola and also in each bifurcation surface. Typically, the number of spikes of the homoclinic orbit for parameter values on one side of a homoclinic bifurcation isola and on the other side differ in 1. The isola for which parameters on one side generate homoclinic orbits with n spikes and on the other side with $n+1$ spikes, with $n=1,2,\ldots$, will be denoted by $hom^{(n,n+1)}$, and so will be the corresponding surface. In Fig. 8 we show three-parameter plots with some codimension-one homoclinic bifurcation surfaces and codimension-two homoclinic bifurcation curves computed using the AUTO continuation software [17, 18]. In plots (a), (b) and (c) the $hom^{(1,2)}$, $hom^{(2,3)}$, $hom^{(6,7)}$ and $hom^{(11,12)}$ surfaces are given. In plot (d) we include Belyakov and IF bifurcation curves. This partial bifurcation diagram allows us to illustrate a collection of geometric bifurcations, some of which are quite evident, while others not so much. First, we observe the existence of some codimension–two-plus-one geometric bifurcations that correspond to folds, with respect to $\varepsilon$, of curves of codimension-two homoclinic bifurcations. Nevertheless, we will distinguish between “visible” and “invisible” folds (see plot (d)) depending on whether the fold is clearly visible or another kind of analysis is needed to ensure its presence (this happens in the very sharp folds of the homoclinic isolas where it is needed a plot of the bifurcation curve showing the AUTO $L_2$-norm of the homoclinic orbit as in Fig. 9). Recall that in all 2D-manifolds of codimension-one homoclinic bifurcations we distinguish two leaves which are exponentially close (in fact the two leaves that form the isolas) and therefore they are indistinguishable in the visualization of our numerical results. They glue together along curves of sharp folding marked with a red line in plot (d) of Fig. 8. If a curve of codimension-two homoclinic bifurcation folds inside one of the leaves, that folding is said a codimension–two-plus-one visible fold. If the fold is along one of the folding curves of the whole surface (that is, going from one leaf to the other), and hence it is hidden for visualization, we refer to the bifurcation as a codimension–two-plus-one invisible fold. In any case, both types of folding are codimension–two-plus-one geometric bifurcations. Note that visible folds appear in pairs, one on each leaf, but invisible folds are unique points. In [24] it is shown that on the surface $hom^{(1,2)}$, both the Belyakov and the IF bifurcation curves exhibit “visible” folds, and that, on the surface $hom^{(2,3)}$, the Belyakov bifurcation curve also undergoes a “visible” fold, but the IF curve presents an “invisible” fold. Note that, as shown in Fig. 8, on the surface $hom^{(11,12)}$, both curves exhibit “invisible” folds.

Fig. 9

Saddle-type codimension–one-plus-one geometric bifurcation located on the homoclinic bifurcation surface $hom^{(2,3)}$. Bottom line: theoretical scheme showing the connection of two folds of two disconnected isolas giving rise to just one isola. Middle-top lines: numerical continuation illustrating the saddle-type bifurcation in parameter space, showing the connection of the isolas and also a continuation in the AUTO $L_2$-norm, to show that really we have two or just one isola

In plots (a), (b) and (c) of Fig. 8 the homoclinic surfaces $hom^{(1,2)}$, $hom^{(2,3)}$, $hom^{(6,7)}$ and $hom^{(11,12)}$ are shown together using three different points of view to show how close they are to each other and to compare their respective sizes. The $hom^{(1,2)}$ homoclinic surface is the biggest one and so over this surface mainly “visible” folds are observed. On the contrary, over the other surfaces, as the size of the homoclinic surface is smaller, and some bifurcations are located in a small region, there are some “invisible” folds because the codimension-one curves reach the fold of the homoclinic isola and go to the other side of the homoclinic surface via an “invisible” fold.

Fig. 10

“Invisible” fold phenomenon giving rise to a codimension-two Belyakov homoclinic bifurcation isola on the surface $hom^{(6,7)}$. a Theoretical scheme of the process. b Projection of the homoclinic surface on the $(b, \, \varepsilon )$ parameter plane and location of the Belyakov isola. c–e Homoclinic orbits on the Belyakov isola on both sides of the curve for the indicated values of I. One side has one extra spike as shown both on the time series (t, x) and (z, x) pictures for three values of the parameter b

Now, looking for codimension–one-plus-one geometric bifurcations, we pay attention to the bifurcation surfaces themselves. In Fig. 8d we see how $hom^{(11,12)}$ splits into two disconnected components and each of them has a maximum (with respect to $\varepsilon$). These two points are isola-type codimension–one-plus-one geometric bifurcations with respect to $\varepsilon$. Also, a saddle-type codimension–one-plus-one geometric bifurcation is detected on the bifurcation surfaces $hom^{(2,3)}$ and $hom^{(6,7)}$ (see Fig. 9). Saddle-type codimension–one-plus-one bifurcations do not appear on $hom^{(1,2)}$ for the studied values of $\varepsilon$, but they are present in $hom^{(n,n+1)}$, when $1<n<n_s$, for certain small $n_s$. Nevertheless, for $n \ge n_s$, the surface $hom^{(n,n+1)}$ splits into two pieces (see Fig. 8d) and hence saddle-type codimension–one-plus-one bifurcations are no longer present. Most likely, isola-type codimension–one-plus-one geometric bifurcations are present in all homoclinic surfaces if the small parameter $\varepsilon$ is large enough. This fact explains why, as the small parameter grows, fewer color bands appear in the 3D graph of Fig. 7 indicating that the bursting orbits have fewer spikes. Note that this structure provides a complete explanation of the maximum number of spikes in models once the parameter $\varepsilon$ is no longer small.

In order to show more clearly a saddle-type codimension–one-plus-one bifurcation we show in Fig. 9 the theoretical scheme of the connection of two folds of two disconnected isolas giving rise to an isola, and therefore giving rise to just one tubular surface from two previous tubular surfaces. On the upper plots, several numerical continuation results permit to illustrate the saddle-type bifurcation in parameter space showing the connection of the isolas. AUTO $L_2$-norm is used to show that really we have isolas of homoclinic bifurcations. Note that the numerical software AUTO stops the continuation process at the dotted areas of the blue curves because of numerical limitations. The magnifications illustrate the very sharp folds of the isolas, only visible with zooms on the AUTO $L_2$-norm plots up to some parameter values due to the numerical precision of the program.

The phenomenon of the “invisible” folds is a direct consequence of the existence of very squashed tubular structures (and therefore isolas when a two-parameter section is considered) where the two leaves are infinitesimally close to each other. Thus, if a codimension-two homoclinic bifurcation curve reaches the homoclinic surface folding curve, then it continues to the other side because the conditions in the phase space that are required to have the codimension-two bifurcation are still satisfied on the other side. So, the bifurcation curve has experimented an “invisible” fold. Figure 10 details a complete process of creation of “invisible” folds on a codimension-two Belyakov homoclinic bifurcation curve on the surface $hom^{(6,7)}$. The plot (a) shows the theoretical scheme of the process and illustrates how one side of the Belyakov isola is on one leaf of the tubular surface and the other side on the other leaf, and so we have “invisible” folds due to the very small distance between the leaves. On the plot (b) the projection of the homoclinic surface on the $(b, \, \varepsilon )$ parameter plane and the location of the Belyakov isola are shown. In order to illustrate that indeed the Belyakov curve forms an isola on both leaves of the homoclinic surface, we present on plots (c), (d) and (e) the time series (t, x) and (z, x) pictures of two homoclinic orbits, one on each side of the surface, for three values of parameter b: $b=2.1597$, 2.1999 and 2.2478, respectively. Note that on one side the homoclinic orbit has one extra spike (7 spikes versus 6 spikes).

Figure 7 shows how some codimension-two points disappear. Now we have enough elements to describe the process and also to explain that a subsidiary effect is the fact that different curves of periodic bifurcations may connect together. We can connect all these phenomena with some geometric bifurcations illustrated in Fig. 8, in particular “visible” or “invisible” folds depending on the size of the homoclinic isolas. As $\varepsilon$ increases, the first geometric bifurcation shown in Fig. 8 that explains what happens in Fig. 7 is a codimension–two-plus-one bifurcation on the IF homoclinic bifurcation curve. For the $hom^{(1,2)}$ case, as the homoclinic surface is big enough, what happens is a maximum of each of the IF curves (one on each leaf of the tubular surface), and so we have a “visible” fold and we observe the geometric “collision” of two pairs of IF points, one pair on each of the leaves of the homoclinic surface (the white points on the figure). On the contrary, for the rest of homoclinic surfaces, the IF bifurcation curves have “invisible” folds, as they are smaller and the surfaces are composed of isolas disconnected for small values of the parameter. Moreover, when n grows enough $hom^{(n,n+1)}$ has only one branch of the IF curve, that is, IF points are only present on one of the two disconnected components of the isolas for a small value of $\varepsilon$. In these cases, the IF point seems to disappear on the limit of a homoclinic curve, and what really happens is that geometrically “collides” with the corresponding point of the another leaf of the surface that we cannot see. The evolution of the Belyakov curve is similar but for higher values of the small parameter $\varepsilon$.

Fig. 11

Left: Fold/hom homoclinic “mille-feuille" organization. Right: Simile of the structure on the left. The behavior of the curves of codimension-two bifurcations is compared to the spine-of-a-book placed on a bookstore that corresponds with the homoclinic surface. The pages of such books consist of surfaces of bifurcations of periodic orbits and secondary homoclinic bifurcations involved in the spike-adding process

Finally, Fig. 11a shows the schematic distribution of the homoclinic bifurcation surfaces giving rise to what we have called fold/hom homoclinic “mille-feuille" organization [13]. On plot (b) we show a simile comparing the structure with a bookstore, where each homoclinic surface is compared with a bookstore shelf, and where each book will take the role of the codimension-two homoclinic bifurcations on the homoclinic surface. They will give rise to the spine-of-a-book structure (plot (c)) with the countable set of bifurcations emanating from the codimension-two points (the “sheets of the book”). Note that this structure provides a complete explanation of the global homoclinic bifurcation in the HR model and in other fold/hom bursters.

2.3 Topological structure of chaotic attractors: limit case $\varepsilon \searrow 0$

In addition to studying the different bifurcations that periodic orbits undergo, we can analyze the topological structure of chaotic attractors and their evolution when the parameter values vary. One of the fundamental tools in such analysis for dissipative three-dimensional dynamical systems are topological templates, which are constructed as a version of the system in the limit case of infinite dissipation. That is, a projection of its flow is made by squeezing it along its stable direction, so that the three-dimensional flow becomes a two-dimensional branched manifold (see Fig. 12). The projection preserves the relative positions of the periodic orbits, so that the crossings between them are neither created nor destroyed in the projection. The template is therefore a useful tool for analyzing the stretching and squeezing processes that shape the chaotic attractor and how the unstable periodic orbits (UPOs) are organized in these processes. To determine the topological template, the intertwining of the low-period periodic orbits must be studied through their topological periods (number of spikes) and linking numbers (number of turns that one orbit makes around another). With that information, the corresponding topological template will be the simplest one that has the characteristics detected in the UPOs.

Fig. 12

Top: Basic elements of topological template analysis. Bottom: Global topological template obtained for HR model, the complete Smale horseshoe template. See [25] for the analysis of the templates and the description of allowed and forbidden symbolic sequences associated to periodic orbits

When the chaotic attractor is hyperbolic, there is a biunivocal correspondence between the periodic orbits of the template and those which foliate the attractor. In the case of the HR system, the attractor is not hyperbolic, which implies that some orbits in the template do not appear in the attractor. However, those that do exist in the attractor have the same internal organization as in the template. This results in the concrete template of the attractor being a subtemplate of the global template in which certain paths of the template are closed (those corresponding to the orbits that are not in the attractor). This gives a Cantor structure in the subtemplate depending on the closed paths and corresponding to the structure of the chaotic attractor, where the “holes” correspond to the periodic orbits laying on those close paths. See [25] for a full analysis of these templates, making use of symbolic dynamics, topological templates and first return maps (FRMs) [26, 27]. In that study, it was found that the topological template of each chaotic attractor corresponds to a subtemplate of the complete Smale horseshoe template where there are paths that are closed, and how they relate with certain forbidden symbolic sequences (Fig. 12).

Fig. 13

Top: Chaotic attractors for different values of b in the line $I=(100-26.5b)/6.91$ (with $\varepsilon =0.01$). Middle-bottom: Two of these chaotic attractors with all their UPOs with multiplicity m from 1 to 4. We can check how, when parameter b decreases, the number of orbits foliated to the attractor increases

Following a line crossing different chaotic regions in the parameter space, we can study how the chaotic attractor changes in the different regions. To do this, we can take, for example, $\varepsilon =0.01$ and $I=(100-26.5b)/6.91$ (see Fig. 4). The upper part of Fig. 13 shows how the shape of these attractors changes along that line. Now, using the symbolic dynamics theory, we get that those chaotic invariants with more foliated periodic orbits have more symbolic chains allowed in their topological template than those with a smaller number of them. That is, depending on the number of periodic orbits that foliate (or not) the chaotic attractor, its generic topological template will have certain open (or closed) paths forming a subtemplate with holes.

Fig. 14

Spike-counting in the bursting attractor along the line $I=14.4-4b$ for $\varepsilon \in [10^{-4},10^{-2}]$ (in logarithmic scale to show exponential increment in the number of spikes) and $b\in [2.9, 3.25]$. The time series for three particular examples are shown too

According to the classification of the different types of spike-adding processes provided in [14], we have a chaos-induced discontinuous spike-adding (Terman [11]) case. This case is generated by a type C OF homoclinic bifurcation (see Sect. 2.1). This codimension-two point generates a countable set of saddle-node and period-doubling bifurcation pencils. Moreover, in [25] it was seen that a symbolic-flip bifurcation occurs before each period-doubling bifurcation. This bifurcation does not change the stability of the periodic orbit or any of its topological properties, but it does modify the symbolic sequence of the periodic orbit and it allows generating new symbolic chains. That is why, as more spike-adding pencils are traversed, more symbolic chains are allowed. Figure 14 plots the number of spikes reached by the periodic attractor as a function of the values of b and $\varepsilon$. The number of spikes grows exponentially as $\varepsilon$ decreases to zero.

Fig. 15

Theoretical scheme showing how, through infinite spike-adding pencils, the topological template of the chaotic attractors fills more and more gaps and tends (when $\varepsilon$ tends to zero) to the complete Smale template

Thus, we can elaborate the hypothesis represented schematically in Fig. 15. The template of any chaotic attractor in the system is a subtemplate of the complete Smale template with closed paths corresponding to the forbidden symbolic chains in the symbolic dynamics of that chaotic attractor. However, when $\varepsilon$ tends to zero, choosing the right path to go through all the different spike-adding pencils as they occur indefinitely, the subtemplate is being filled in and the Smale horseshoe template is completed as the limit case.

3 Realistic models applications

In this section we illustrate how spike-adding phenomena are involved in several real processes, such as changes in movement gaits and the creation of Early Afterdepolarizations in cardiac dynamics.

3.1 Insect gait movement changes

The generation of rhythmic or coordinated behaviors in different organisms, such as heartbeat, respiration, swimming or walking, is an important research topic in neuroscience with applications to other fields like biological-inspired robotics.

Many animals, including humans, present Central Pattern Generators (CPGs) to produce the basics of such rhythms (see [28] and the references therein). A CPG is a small biological neuron circuit, a small network of interconnected neurons, that produces a rhythmic output without needing a rhythmic input, while also adapting it when an input is present. Hence, the organism can modify the rhythms according to the environment as needed. Its dynamics depends on intracellular, synaptic, and network level phenomena.

Classic examples of CPGs driven rhythmic behavior are direct-reverse flow of circulatory system on leeches [29, 30] and locomotive patterns [31,32,33]. Of special interest, on both insect movement and robotics research, is the case of the movement of hexapods. In Nature, hexapod insects can present different gaits, most common (and idealized) ones are shown in Fig. 16. In the tetrapod gait there are four legs in the ground and the other two are moving, while in tripod gait, usually present when the insect wants to go faster, three legs are moving while the other three are at rest.

Fig. 16

Left and center: Illustration of the tetrapod and tripod insect movement gaits. Each leg is associated to a neuron, whose activation (bursting) sets the leg into motion. Bottom figures show the temporal bursting pattern, from left to right, of each neuron, with shaded regions indicating the activation of the corresponding neuron. Right: Network of neurons used as a model for hexapods, with the corresponding connections. Each connection from neuron j to neuron k has an associated non-symmetric relative inhibitory strength $c_{j,k}$, with the indicated values: $c_{1,2} = \frac{1}{2}$, $c_{2,1} = 1$, and so on

Researchers on both mentioned areas have proposed simplified CPGs to describe those movements, usually including six motoneurons [34,35,36,37,38,39,40]. There are more complex models which include biomechanical information [41,42,43], but those simplified CPGs are rich enough to represent the usual patterns and exhibit some of the changes one may observe in the movement of real insects.

Ghigliazza and Holmes [37, 38] introduced one of those simple models for the movement of cockroaches, and examined it analytically using some reductions, which unfortunately hide some non-symmetric patterns that may occur. In this subsection we want to explore its dynamics numerically without resorting to such reductions.

The dynamics of one isolated neuron is described in terms of a fast nonlinear calcium current $I_{Ca}$, a slow potassium current $I_K$, a very slow potassium current $I_{KS}$ [37], a linear leakage current $I_L$ and an external current $I_{ext}$. The ODEs describing the dynamics of the membrane potential v, the potassium gate variable m, and the slow potassium gating variable w are

$$\begin{aligned} \left\{ \begin{aligned} C{\dot{v}}&= -(I_{Ca}+I_{K}+I_{KS}+I_L)+I_{ext}, \\ {\dot{m}}&= \displaystyle \frac{\epsilon }{\tau _m(v)}[m_\infty (v)-m],\\ {\dot{w}}&= \displaystyle \frac{\delta }{\tau _{w}(v)}[w_\infty (v)-w], \end{aligned} \right. \end{aligned}$$

(2)

with the auxiliary ionic current functions defined by

$$\begin{aligned} \begin{array}{ll} I_{Ca}=g_{Ca}\,n_\infty (v)\,(v-E_{Ca}),&{} \qquad I_K=g_K\, m\, (v-E_{K}),\\ I_L=g_L\, (v-E_L), &{}\qquad I_{KS}=g_{KS}\, w\, (v-E_K), \end{array} \end{aligned}$$

and where the different time scales and steady state gating variables are

$$\begin{aligned} \begin{array}{ll} \tau _m(v)=\textrm{sech}\big (k_{0_{K}}\,(v-v^{th}_{K})/2\big ),&{} \qquad \tau _w(v)=\textrm{sech}\big (k_{0_{KS}}\,(v-v^{th}_{KS})/2\big ),\\ m_\infty (v)=\big (1+e^{-2k_{0_{K}}\,(v-v^{th}_{K})}\big )^{-1}, &{}\qquad w_\infty (v)=\big (1+e^{-2k_{0_{KS}}\,(v-v^{th}_{KS})}\big )^{-1},\\ n_\infty (v)=\big (1+e^{-2k_{0_{Ca}}\,(v-v^{th}_{Ca})}\big )^{-1}. &{} \end{array} \end{aligned}$$

The parameters C, $\epsilon$ and $\delta$ determine the time scales of v, m and w, $E_X$ are the Nernst potentials, $g_X$ are maximal conductances, $k_{0_X}$ is the steepness of the transition happening at threshold potential $v^{th}_X$, where X denotes each of the considered ions. See [37, 38, 44] for the parameters and the exact values used in the simulations.

Fig. 17

The spike-counting diagram for an isolated neuron varying the parameters $I_{ext}$ and $v^{th}_{KS}$ of (2). On the right there are three selected membrane potential time series showing the usual behavior in the three different regions [37, 38, 44]

Figure 17 shows the behavior of the membrane potential for the stable periodic orbit when varying parameters $v_{KS}^{th}$ and $I_{ext}$. Within the colorful droplet-shaped region we can observe the characteristic neuronal bursting of the model. Outside of it we have two opposite behaviors: quiescence (an attracting equilibrium) and spiking (a small periodic orbit with one spike). The global picture is similar for any other set of parameters [44].

When the six neurons (each driving the movement of a leg of the hexapod) are coupled, they are arranged in a network shown in the right part of Fig. 16. We assume that the inhibitory coupling is achieved via synapses that produce negative postsynaptic currents (we obtain this by subtraction of positive postsynaptic currents instead of adding negative terms as in the original model). Therefore, the first equation of (2) is modified in each neuron i from 1 to 6 to include the postsynaptic current $I_{s,i}$:

$$\begin{aligned} C{\dot{v}}_i = -(I_{Ca,i}+I_{K,i}+I_{L,i}+I_{KS,i})+I_{ext} - I_{s,i}, \ I_{s,i} = g_{s} (v_i-E_s^{post}) \sum _{j \in N_i} c_{j,i} s_j, \end{aligned}$$

with $N_i$ the set of neighbors of neuron i as indicated in Fig. 16, $c_{j,i}$ the network parameters shown in the same picture, and a new synapse variable $s_i$ associated to each neuron, whose dynamics is described by

$$\begin{aligned} {\dot{s}}_i = \alpha s_{\infty } (v_i)(1-s_i)-\beta s_i, \quad s_{\infty } (v_i) = \frac{T_{max}}{1+e^{-k_s(v_i-E_s^{pre})}}, \end{aligned}$$

where $\alpha$ and $\beta$ are voltage-independent forward and backward rate constants, and $g_{s}$, $T_{max}$, $E_s^{pre}$ and $E_s^{post}$ are parameters describing the synapses (see [44] for details).

Having a roadmap (Fig. 17) for the dynamics of a single neuron allows us to explore the connected case, focusing on the relevant regions of the parameter space. To exemplify this, let us consider the straight line $I_{ext} = 35.5$ in the plane depicted in Fig. 17. We perform a quasi-Monte Carlo sweeping, that is, we sweep for values of $v^{th}_{KS}$ between $-30$ to $-22.5$ and we compute for each parameter set the orbits for 200 initial conditions selected using a low discrepancy sequence to cover nicely the region of reasonable initial conditions (remember that the phase space is 24-dimensional). For each of these orbits we compute the periodic orbit towards which it converges after a large transient of $10^5$ ms and automatically deduce the patterns (as in Fig. 16) it describes. We are not interested in the number of spikes in this case, but only in knowing if a neuron is active (bursting) or not. Figure 18 shows the results of this numerical experiment. At the bottom of the figure, we can see the main obtained patterns.

Fig. 18

The histogram with the percentage of the different gaits corresponding to the parametric line $I_{ext}=35.5$ for variable $v_{KS}^{th}$ using 200 initial conditions for each parametric set. The main patterns are depicted at the bottom. The thick black lines describe the bursting time of each neuron along the periodic orbit; for each pattern, time goes from left to right, and neurons $i=1$ to $i=6$ from top to bottom. See [44] for details

The histogram represents the perceptual amount of initial conditions that converges to a particular pattern. Patterns related by symmetry (interchanging either left and right or front and back neurons) are considered identical. Below the histogram, we have the spike-counting diagram on the line $I_{ext}=35.5$. We can observe that the spike-adding areas affect the smoothness of the transition among patterns, which helps us to locate the regions where most changes are performed. Those changes are related with bifurcations on the system that are explained in [45].

The main observation about our computations is the fact that the tripod gait is ubiquitous: it is a possible movement pattern for any choice of the parameters, although it is unstable for some parameter values. However, when it becomes stable, for $v^{th}_{KS} > -25$, it quickly becomes dominant. This result is general, in the sense that we can observe the same dominance for other sets of parameters. Those results are quite stable under small perturbations [45]. An open problem regarding the different existing gaits and their stability is the interesting question of the dynamic change between them when parameters are varied. While animals are able to change from one gait to another one without tripping, it yet remains to be solved how these smooth transitions can be incorporated in the model.

3.2 Early afterdepolarizations in cardiac dynamics

In previous sections we have centered our study in neurons, either isolated or connected. Now we are going to study other excitable cells, the myocytes (or muscle cells), in particular, heart myocytes. We want to show how the spike-adding phenomenon is relevant in cardiac dynamics, but now with the name of Early Afterdepolarization (EAD).

Although the Hodkin–Huxley model [1] was initially proposed to simulate the behavior of a neuron, this model established a useful mathematical formalism to describe the ionic kinetics of the membrane which has been used as a basis for the development of mathematical models for other excitable cells. In this way, Denis Noble [46] published the first mathematical model of a cardiac cell based on the adaptation of the equations of the Hodkin–Huxley model. After some improvement by McAllister et al. [47], Beeler and Reuter [48] developed the first ventricular myocyte model in 1977, later reformulated by Luo and Rudy in 1991 [49] and 1994 [50, 51].

Fig. 19

In the top panel (a) we can see different APs without (left) with one (middle) and with several (right) EADs depending on the PCL value (taken from Fig. 1 of [52]). In lower panel (b) we show some experimental recordings where for different values of the PCL we detect some APs with one EAD (taken from Fig. 1A of [53]). This is also observed in our numerical simulation (taken from Fig. 1c and d of [54]) for a biophysical realistic model (c) and for a simpler one (d). In all cases, as we increase the PCL, more and more APs show an EAD

In the left plot of Fig. 19a we can see an example of an AP for a cardiomyocyte. It has several phases. The first one, after being stimulated, is an increment in their transmembrane voltage (depolarization or phase 0). This increment is followed by a small partial voltage decrease (transient repolarization or phase 1) and a prolonged phase where voltage remains approximately constant (plateau phase or phase 2). In the final part of the AP, transmembrane voltage decreases (repolarization or phase 3) while returning to the resting potential level, which is maintained until receiving the next stimulus. The time elapsed between two stimuli applied to the cell is called Pacing Cycle Length (PCL). Under some circumstances, transmembrane potential can experience an unexpected rise during AP phase 2 or phase 3, which is termed Early Afterdepolarization (EAD). If EADs at cellular level are of large enough magnitude and occur over a substantial tissue area, they can lead to triggered activity and arrhythmias [55] which makes the study of EADs highly relevant. Recall that, in the mathematical neuroscience notation, the creation of EADs is denoted as a spike-adding process.

For our study we have used two mathematical models, the biophysically realistic Sato model [53] (with 27 variables) and a simpler one (the 3D Luo–Rudy model [49, 56] with just three variables). As we can see in Fig. 19c, d both models show the EADs observed in experimental recordings (as illustrated in Fig. 19b).

The high-dimensional model, updated by Sato et al. [53] to properly reproduce EADs, simulates a rabbit ventricular myocyte. The total ionic current is the sum of nine ionic currents including the L-type Ca$^{2+}$ current, the fast sodium current ($I_{Na}$), five components of the potassium current and two pump currents ($I_{NaK}$ transporting potassium into the cell in exchange for sodium out of the cell and $I_{NaCa}$ transporting sodium in and calcium out of the cell). An additional stimulus current $I_{stim}$ is included, which in this study is delivered at a constant stimulus period defined by the PCL. The complete description of the ionic currents involves 27 ordinary differential equations for the 27 state variables, in which 177 model parameters are used (see [53, 57, 58] for full details and equations).

In Fig. 20 we show some results obtained for the Sato model [59]. In Fig. 20a we show the biparametric bifurcation diagram taking into account the PCL and the $K_{m Nao}$ parameter which is the extracellular sodium dissociation constant used to calculate the $I_{NaCa}$ current and, in turn, update sodium and calcium concentrations. For each configuration we integrate until we find the periodic orbit and we count the number of peaks and the number of APs. The ratio between both quantities indicates the progressive appearance of EADs: a ratio of 1 indicates that no EADs are present, while a ratio of 2 shows that every AP has an EAD; a ratio of 1.5 would thus indicate that an EAD is present in one out of two APs, and so on. This ratio is plotted following a color code. The red bar in the diagram corresponds to the transition region from no EAD to EAD for the standard value of the $K_{m Nao}$. The one-parameter bifurcation diagram varying PCL is plotted in Fig. 20b. The points correspond to the peaks of the AP. On the left (where only the blue line is visible) the ratio is 1 and all APs have a single peak, i.e. present no EADs. On the right (where two red lines are present) the orbit will show two APs: one with EAD and another one without it (both with different AP-peak). Blue points are obtained for increasing PCL values (from left to right) and red points for decreasing PCL values (from right to left). It can be seen that for some PCLs there is coexistence phenomenon, it means that for the same configuration but different initial conditions we obtain different periodic orbits (one with EAD and another one without EADs). Based on our simulations [59] using the 27D Sato model we can conjecture one possible theoretical scheme of the creation of the EAD. First, a torus bifurcation occurs, which allows the creation of alternans and an orbit with different APs. Moving on the bifurcation line, some of the APs of the orbit start to create an EAD and the orbit goes from the configuration without EAD (ratio 1, blue region) towards the configuration with EAD (ratio 1.5, green region). We plot white points and gray lines in Fig. 20b to explain this conjecture. To prove this conjecture we need a simpler model to do a theoretical study.

Fig. 20

Results for the EAD transition region using the high dimensional Sato model. In plot a we show the biparametric bifurcation diagram taking into account the PCL and the $K_{m Nao}$. In b one-parameter bifurcation diagram varying PCL. The points correspond to the transmembrane potential of the AP-peaks. See text for explanation

As with the Hodkin–Huxley model, where a more simplified model was used (the three-dimensional HR model), also for the myocyte we use a more simplified model than Sato, the modified Luo–Rudy 3D model. This model meets, like the HR model, the two basic conditions of being computationally simple but at the same time capable of reproducing the behavior we want to study: the EADs.

The Luo–Rudy 3D model [49, 56] is a simplification of the original Luo–Rudy model [49] following the approach of [56]. This simplified model contains an intermediate time-scale Ca current and a slow K current. The fast Na current was discarded due to its little effects on EAD generation, as it is activated mostly during the AP upstroke but it is practically null during the plateau and repolarization AP phases where the EAD appears. We include, as in Sato model, an additional stimulus current $I_{stim}$ at a constant period defined by the PCL. The three variables of this model correspond to the inactivation gating variable of the Ca current (f), the activation gating variable of the K current (x) and the transmembrane potential (V). After checking that both models experience similar behavior [54], we study the same transition from non-EAD to EAD obtaining the complete families of periodic orbits (stable and unstable ones) using the AUTO continuation software [17, 18].

Fig. 21

Taken from [54] with modifications (Figure 6). The top panel shows the EAD transition region between periodic orbits (PO) without and with EAD using the transmembrane potential of the AP-peaks for the low dimensional Luo–Rudy 3D model. The lower panel shows the above bifurcation diagram, but with the AUTO $L_2$-norm ($\Vert \cdot \Vert _2$) of the periodic orbits. We can also see some time series of the existing attractors for three different values of the PCL. See explanation on the text

We can see the results in Fig. 21. Top panel shows the EAD transition region between periodic orbits without and with EAD for the Luo–Rudy 3D model. This bifurcation diagram has been completed with the unstable branches calculated by the AUTO continuation software. This gives us the opportunity to visualize the complete evolution of the different periodic orbits [54]. The main bifurcations (period-doubling (PD, in red), and fold of limit cycles (in yellow)) that influence the stability of the periodic orbits are marked with dots of different colors. We distinguish between $PD_1$, responsible of the alternans generation, and $PD_2$, responsible of destabilization of the red family and creation of some transient behaviors. In the fold point the periodic orbit family turns generating hysteresis phenomena with different coexistence orbits (with or without bistability). We are also able to detect the EAD generation point (blue dot) which is located in the top plot as the point where a low voltage peak is created in the unstable branch. This point is not visible in the lower panel where we represent the AUTO $L_2$-norm of the periodic orbits but with this representation is more evident the hysteresis phenomena since it can be easily seen how both stable branches connect through an unstable branch that evolves continuously from one to the other as we conjectured with Sato model in Fig. 20. The bistability and coexistence regions have been marked in green and purple, respectively.

This theoretical scheme explains what we observe in the more biophysical realistic model, i.e., a possible mechanism in the generation of the first EAD. This mechanism is not unique, alternans generation can be caused by another type of bifurcations, but it seems that the generation of alternans is a necessary previous step for the subsequent appearance of the first EADs.

In summary, we have observed, in both the Sato model and the Luo–Rudy 3D model, how the periodic orbit without EAD experiences a bifurcation (torus bifurcation or period-doubling bifurcation) that generates the appearance of alternans. Later, the family with alternans evolves and some of them begin to experience EADs. This evolution occurs in the unstable branch, so it can only be detected by continuing that branch, but its effects are evident in the stable branch.

4 Conclusions

Simplified neuron models can be used to better understand more complex models, once we have ensured that they faithfully reproduce the main dynamic patterns of the complex ones. Low-dimensional fold/hom bursting models can be studied in detail using analytical and numerical methods in order to obtain a full portrait of the different dynamical regimes and bifurcations that appear in their parametric phase space. We have exemplified this for the 3D Hindmarsh–Rose neuron model. We have provided an account of recent results about the behavior of this model when its parameters $\varepsilon$, b and I take values along some specific ranges. Our analysis can be reproduced for other models as well.

For fixed values of the small parameter $\varepsilon$, spike-counting methods give snapshots of the different bursting regions into which the (b, I) parameter plane is divided and the bifurcation lines between them. Adding continuation techniques provides a deeper understanding of these snapshots. Homoclinic bifurcations appear as a key element in spike-adding processes that allows to classify them. We have given a complete theoretical scenario of the interlaced bifurcation diagram for the n to $n+1$ spike-adding process.

If we let the parameter $\varepsilon$ vary, new phenomena are observed. For each number of spikes there appears a homoclinic codimension-one bifurcation surface having a spike-adding role (the model has different number of spikes on different sides of the surface). These surfaces are exponentially close to each other, and their number grows as the small parameter $\varepsilon$ tends to zero. Using continuation techniques we have been able to give a detailed description of these surfaces through the concept of geometric bifurcations. Some of these geometric bifurcations are “visible”: they can be easily detected from the plots; but some others (“invisible”) require further analysis in order to be detected.

The topological structure of chaotic attractors changes with the parameters of the system. We have studied these changes using symbolic dynamics and topological templates. The topological templates of the attractors appear as subtemplates of the complete Smale horseshoe template. Moreover, the complete Smale template is obtained as a limit case when the parameter $\varepsilon$ tends to zero.

These types of analysis can be applied to other models and in different realistic situations. We have illustrated this with two examples. Once we have tools for studying the dynamics of a single neuron in the 3D Hindmarsh–Rose neuron model, we have studied the dynamics of sets of neurons that are coupled via synapses having inhibitory effect. In particular, we have studied a network of six neurons modeling a CPG for hexapod insects movement. Different values of the parameters for the neuron model produce different gait movements of the insect, and we have shown that some of the main gait movements observed in Nature (tripod and tetrapod gaits) appear as dominant gaits for some regions of the parameter space. Finally, we have studied a different type of electrically excitable cells: cardiomyocytes (cardiac muscle cells). In this case, spike-adding processes are related with Early Afterdepolarization (EAD), a phenomenon of high clinical interest. Numerical simulations on high-dimensional Sato model of the APs of these cells allowed us to conjecture a theoretical scheme for the creation of EADs. As we did in the neuron case, we have driven a more detailed study on a simplified model (Luo–Rudy 3D model), and this study has proved the conjecture about EAD generation that we stated for the high-dimensional model.

Summarizing, spike-adding phenomena are present in numerous theoretical and realistic excitable cells as key ingredients in important changes of the cells.

Appendix A: Short survey on homoclinic bifurcations

Since this paper deals with homoclinic structures arising in the HR model, we include, for the convenience of the reader, an overview about homoclinic bifurcations, with focus on those detected in the HR model. We mainly follow [21, 60].

Consider a smooth family of vector fields $X_\mu$ on ${\mathbb {R}}^3$ depending on a parameter $\mu \in {\mathbb {R}}^k$ and suppose that there exist $\mu _0\in {\mathbb {R}}^k$ and $p_0\in {\mathbb {R}}^3$ such that $p_0$ is a saddle type hyperbolic equilibrium point of $X_{\mu _0}$. Without loss of generality we can assume $\mu _0=0$ and $p_0=0$. In fact we can assume that $X_\mu (0)=0$ for all $\mu \in {\mathbb {R}}^k$. Because this is the case in the HR model, we only pay attention to saddles with stability index 1 (note that the discussion in the case of stability index equals 2 is identical, but reversing time); hence the vector field has a one-dimensional stable manifold $W^{s}(0)$ and a 2-dimensional unstable manifold $W^u(0)$. Suppose now that $\Gamma _0$ is a homoclinic orbit of $X_0$ asymptotic to 0. We distinguish two cases:

• All eigenvalues of $DX_{0}(0)$ are real.

• Unstable eigenvalues of $DX_{0}(0)$ are complex conjugate.

Moreover, we assume that the connection splits generically when $\mu =0$.

Fig. 22

Unstable manifold, when followed backwards along the homoclinic orbit, can change its orientation

Remark 1

A distance function $\Delta (\mu )$ between $W^{s}(0)$ and $W^{u}(0)$ is well defined (see [21]) and we say that the splitting of the connection is generic when $D_{\mu }\Delta (0)$ does not vanish. Roughly speaking, using Fig. 22 as reference, genericity of the splitting means that $W^{s}(0)$ splits inwards or outwards, that is, to the left or to the right of $W^u$, according to the sign of $\mu$.

1.1 A.1 Codimension-one homoclinic bifurcations

1.1.1 A.1.1 All eigenvalues are real

In this case, $DX_0(0)$ has real eigenvalues $\lambda _s$, $\lambda _u$ and $\lambda _{uu}$ such that $\lambda _s<0<\lambda _u<\lambda _{uu}$ and we define the so called saddle quantity

$$\begin{aligned} \sigma =\lambda _s+\lambda _u. \end{aligned}$$

(3)

A negative (resp. positive) saddle quantity means, geometrically, that the local forward (resp. backward) flow contracts area.

Codimension 1 homoclinic orbits are characterized by the following conditions:

• (H1) $\sigma \ne 0$.

• (H2) $\Gamma _0 \not \subset W^{uu}(0)$.

• (H3) $W^{cs}(0)$ intersects $W^{u}(0)$ transversally along $\Gamma _0$.

Here $W^{uu}(0)$ denotes the one-dimensional strong unstable manifold at 0, whose tangent space at 0 is given by the eigenspace associated with the eigenvalue $\lambda _{uu}$ (the strong unstable direction), and $W^{cs}(0)$ denotes the 2-dimensional center-stable manifold at 0, whose tangent space at 0 is given by the eigenspace associated with eigenvalues $\lambda _{u}$ and $\lambda _{s}$ (see Fig. 22).

Condition (H1) is a non-resonance condition and (H2) means that $\Gamma _0$ is tangent to the weak unstable direction, that is, the direction given by the eigenspace associated with the weak unstable eigenvalue $\lambda _u$. Condition (H3) is a non-inclination property and it requires that the 2-dimensional unstable invariant manifold $W^u(0)$, when followed by the backward flow along $\Gamma$, returns along the strong unstable manifold $W^{uu}$ or, equivalently, a transverse intersection between $W^u(0)$ and $W^{cs}(0)$ along the homoclinic connection.

When $\sigma >0$, a single unstable (repelling) periodic orbit is born from the homoclinic loop when $\mu >0$ and there is no periodic orbit when $\mu \le 0$ (see [60, Theorem 13.6]). For positive saddle quantities (H2) and (H3) play no role. Nevertheless, when $\sigma <0$ those hypotheses are required and moreover one needs to pay attention to orientability (see Fig. 22) of $W^u$ when followed by the backward flow (see [60, Theorem 13.7]). In the orientable (resp. non-orientable) case a saddle periodic orbit with orientable (resp. non-orientable) stable invariant manifold emerges when $\mu <0$ (resp. $\mu >0$).

1.1.2 A.1.2 Complex eigenvalues

In this case the linearization at the equilibrium point has a pair of complex unstable eigenvalues $\rho _u \pm \omega _u \textrm{i}$ and a real stable eigenvalue $\lambda _s$, and we define again the saddle quantity as $\sigma = \rho _u + \lambda _s$. When $\sigma >0$, the result [60], Theorem 13.6] remains valid and we know that there exists an unstable periodic orbit when $\mu >0$. When $\sigma <0$ it follows from [60], Theorem 13.8] the existence of infinitely many saddle periodic orbits in any neighborhood of the homoclinic orbit. In fact, as argued in [61], there exist infinitely many horseshoes in any neighborhood of the homoclinic orbit $\Gamma _0$. When $\mu \ne 0$ and the connection splits, finitely many of the horseshoes persist and hence it follows the existence of an infinite number of periodic solutions for any value of $\mu$ small enough. In fact, each time that a horseshoe is created or destroyed more complex dynamics emerge.

1.2 A.2 Codimension-two homoclinic bifurcations

Attending to the description of codimension-one homoclinic bifurcations contained in the previous section, it follows that there may appear the following codimension-two cases:

• Resonant bifurcation: $\sigma =0$.

• Orbit-flip (OF) bifurcation: $\sigma <0$ and $\Gamma _0 \subset W^{uu}(0)$.

• Inclination flip (IF) bifurcation: $\sigma <0$ and the intersection between $W^{cs}(0)$ and $W^{u}(0)$ is not transversal along $\Gamma _0$.

Since no resonant bifurcation is detected in the HR model, we do not discuss details of its unfolding. Nevertheless, orbit- and inclination-flips do appear and seem to be essential ingredients in the dynamics of the system.

1.2.1 A.2.1 Inclination-flips

The essential feature of an inclination-flip is that the intersection between $W^{cs}(0)$ and $W^{u}(0)$ is not transversal along $\Gamma _0$. As a first consequence, the biparametric unfolding includes a curve of homoclinic bifurcations but the orientation is reversed (see Fig. 22) at the IF point.

Fig. 23

Regions in the $(\alpha ,\beta )$-plane corresponding to different cases of orbit-flip (left) and inclination-flip (right)

We introduce the following ratios between eigenvalues

$$\begin{aligned} \alpha =-\frac{\lambda _{uu}}{\lambda _s}, \qquad \beta =-\frac{\lambda _{u}}{\lambda _s}, \end{aligned}$$

(4)

and note that $\alpha >\beta$. We distinguish the following three cases (see Fig. 23):

• Case A: $\beta >1$.

• Case B: $\alpha >1$ and $\frac{1}{2}<\beta <1$.

• Case C: $\alpha <1$ or $\beta < \frac{1}{2}$.

Each case has its own bifurcation diagram, but we only pay attention to Case C (see Fig. 4).

Hypothesis 1

Type C inclination-flips are codimension-two bifurcations characterized by the following generic assumptions:

• (I1) $\sigma <0$.

• (I2) $\beta \ne \frac{1}{2}\alpha$.

• (I3) If $\beta >\frac{1}{2}\alpha$, the homoclinic orbit does not lie in the unique smooth leading unstable manifold.

• (I4) If $\beta <\frac{1}{2}\alpha$, there is a quadratic tangency between $W^{cs}(0)$ and $W^{u}(0)$ along the homoclinic orbit.

Hypothesis (I3) makes sense in the region $C_1$ depicted in Fig. 23 (right). In this case there exists a unique leading unstable manifold which is smooth. Hypothesis (I4) makes sense in the region $C_2$ depicted in Fig. 23 (right). In this case, when followed by the backward flow, $W^{u}(0)$ strikes out a parabola-shaped curve on the local center-stable (see lower part of Figure 2 in [62]). Moreover, when $\beta <\frac{1}{2}\alpha$, $W^{cs}(0)$ is a ${\mathcal {C}}^2$ manifold and hence a quadratic tangency is feasible and both branches (the two branches separated by the connection) converge to the same branch of the local strong unstable manifold. Note that in the region $C_1$ the tangency is not assumed to be quadratic.

Theorem 2

([21, 60]) Assume Hypothesis 1 is satisfied. Depending on a global condition on the stable and unstable manifolds, the bifurcation diagram is given by one of the two cases shown in Fig. 4a. In particular, infinitely many one-sided curves of N-homoclinics emerge for each $N\ge 2$ from the inclination-flip point at $\mu =0$ on the branch of primary homoclinic orbits.

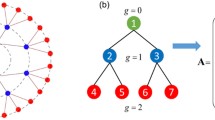
To explain the global condition stated in Theorem 2 we need to consider the Poincaré map around the homoclinic orbit. As before, let $\Gamma _0$ denote the homoclinic orbit and take a cross-section $\Sigma$ transversely intersecting $\Gamma _0$ at a point $p_0$. It is easy to verify that the Poincaré map $\Pi$ is defined on a cusp-shaped domain $D\subset \Sigma$ bounded by curves a, b and c as in Fig. 24 and such that the point $p_0$ is the cusp point but it is not in D. This domain is mapped by $\Pi$ to a region $\Pi (D)$ limited by curves $a'$, $b'$, $c'$, images of a, b, and c, respectively, and a curve $l^{u}=W^u\cap \Sigma$. There are two possibilities, either $a'$ is above $l^{u}$ (left panels in Fig. 24), or $a'$ is below $l^{u}$ (right panels in Fig. 24). The first (resp. second) case is called inward (resp. outward) twist and leads to bifurcation diagrams as that depicted in the left (resp. right) panel of Fig. 4 and labeled as type $C_{in}$ (resp. $C_{out}$).

Let $l^{cs}=W^{cs}\cap \Sigma$ and note that $\Sigma$ is split into two connected components by $l^{cs}$. When $\beta >\frac{1}{2}\alpha$, to assume that, as in hypothesis (I3), the homoclinic orbit does not lie in the unique smooth leading unstable manifold means, geometrically, that D is included in one of such connected components (see top panels in Fig. 24). Note that in these cases the tangency between $l^{u}$ and $l^{cs}$ is not assumed to be quadratic. On the other hand, hypothesis (I4) means that $l^{u}$ and $l^{cs}$ have a quadratic contact at $p_0$ (see bottom panels in Fig. 24).

Fig. 24

Blue colored regions represent the domain D where the Poincaré map $\Pi$ is defined. Red colored regions correspond to $\Pi (D)$. Top (resp. bottom) panels correspond to the case $\beta >\frac{\alpha }{2}$ (resp. $\beta <\frac{\alpha }{2}$). Left (resp. right) panels correspond to the inward (resp. outer) twist

The distinction between regions $C_1$ and $C_2$ corresponds to different ways that a curve which is tangent to the local center stable manifold evolves by local transitions. If $(\alpha ,\beta )\in C_1$ then, by a local transition map, such curve will leave a neighborhood of the equilibrium through a weak unstable direction, otherwise, if $(\alpha ,\beta )\in C_2$, it will do it through a strong unstable direction (see details in [62]). Nonetheless, this local property, which only depends on eigenvalues, does not lead to differences in the bifurcation diagrams. Another distinction, which leads to different unfoldings and does not depend on eigenvalues, has to do with the behavior of a normal vector when followed by the non-local flow in between two local cross-sections along the homoclinic orbit. This leads to the cases $C_{in}$ and $C_{out}$.

It should be noticed that following a homoclinic orbit through a primary homoclinic bifurcation curve, an inclination (or orbit) flip bifurcation point drives a change in the orientation of the unstable manifold (see Fig. 22). In both cases $C_{in}$ and $C_{out}$ a region of parameters corresponding to a horseshoe dynamics exists. For inclination-flips of type $C_{in}$ the closure of such region contains one of the branches of primary homoclinic bifurcations; namely, the branch of orientable homoclinic orbits. This is not the case for inclination-flips of type $C_{out}$; the closure of the region corresponding to shift dynamics does not contain any of the branches of primary homoclinic bifurcations. On the other hand, in both unfoldings a homoclinic doubling cascade appears but, in case $C_{in}$ one of the primary branches of homoclinic orbits separates the cascade from the region of horseshoe dynamics while, in case $C_{out}$, one of such branches is placed at the beginning of the cascade. As shown in Fig. 4 the region of horseshoe dynamics is placed in between a homoclinic doubling cascade, as already mentioned, and a complicated structure of period-doubling cascades and saddle-node bifurcations of periodic orbits.

1.2.2 A.2.2 Orbit-flips

Bifurcation diagrams at orbit-flips closely resemble those at inclination-flips. The essential feature of an orbit-flip is that the homoclinic orbit approaches the equilibrium along the strong unstable manifold as $t\rightarrow -\infty$. With $\alpha$ and $\beta$ as defined in (4), we distinguish the following three cases (see Fig. 23):

• Case A: $\beta >1$.

• Case B: $\beta <1$ and $\alpha >1$.

• Case C: $\alpha <1$.

As we do for inclination-flips, we only pay attention to Case C because none of the others arises in the HR model. Additionally, the following nondegeneracy conditions are required:

• (O1) $\sigma <0$.

• (O2) $W^{cs}(0)$ intersects $W^{u}(0)$ transversally along $\Gamma _0$.

Theorem 3

([21, 60]) Assume that the nondegeneracy conditions (O1) and (O2) are satisfied. Depending on a global condition on the stable and unstable manifolds, the bifurcation diagram is given by one of the two cases shown in Fig. 4a. In particular, infinitely many one-sided curves of N-homoclinics emerge for each $N\ge 2$ from the orbit-flip point at $\mu =0$ on the branch of primary homoclinic orbits.

1.2.3 A.2.3 Belyakov points

The last codimension-two homoclinic bifurcation that we need for our purposes is the Belyakov bifurcation. Original analysis is due to Belyakov [63] but we follow [64] and [21].

Main feature of a Belyakov homoclinic bifurcation is that $DX_0(0)$ has a simple negative real eigenvalue $\lambda _s$ and a double positive real eigenvalue $\lambda _u$ with geometric multiplicity one.

We recall that the imaginary part of the unstable eigenvalues at 0 is nonzero if the discriminant $\Delta (\mu )$ of $DX_\mu (0)$ restricted to the unstable generalized eigenspace is negative. Considering $\mu =(\mu _1,\mu _2)$ we can assume, without loss of generality, that ${\partial \Delta }/{\partial \mu _1}(0)\ne 0$.

We assume that $\lambda _u<-\lambda _s$. Otherwise, the bifurcation set is simple, a unique unstable cycle bifurcates from the homoclinic orbit for $\mu _2>0$. In both cases, crossing the line $\mu _2=0$ when $\mu _1<0$ results in the appearance of a single limit cycle.

As in the previous configurations, the splitting of the homoclinic connections is supposed to be generic, and hence the two-parameter unfolding includes a curve of homoclinic bifurcation through $\mu =0$ and crossing transversely the line $\mu _1=0$.

We also assume conditions which play the role of non orbit-flip and non inclination-flip properties. We assume that the homoclinic orbit does not belong to the strong unstable manifold, that is, $\Vert h(t)\Vert \approx Kte^{\lambda _u t}$ as $t\rightarrow -\infty$, where h(t) denotes the homoclinic orbit. Moreover following the unstable manifold backwards along the homoclinic orbit, the manifold tends toward the strong unstable direction.

Hence we have the following result:

Theorem 4

([21, 60]) We may assume that the primary homoclinic orbit exists for $\mu _2=0$. Hence the homoclinic orbits are of saddle-focus type for $\mu _1>0$ and of saddle-node type for $\mu _2<0$. There are then infinitely many one-sided curves of 2-homoclinic orbits in the half plane $\mu _1>0$ that emerge from $\mu =0$, they are tangent to $\mu _2=0$ at $\mu =(0,0)$ and accumulate onto $\mu _2=0$ from one side. Furthermore, there are infinitely many one-sided curves of saddle-node and period-doubling bifurcation of periodic orbits in $\mu _2>0$ that emerge from $\mu =0$. They are tangent to $\mu _2=0$ at $\mu =(0,0)$, and accumulate onto $\mu _2=0$ from both sides.

Bifurcation diagrams are similar to those in Fig. 4a (right panel) but saddle-node and period-doubling bifurcations curves arise at both sides of the homoclinic bifurcation curve.

Remark 2

It can also be proved that N-homoclinic orbits bifurcate for each $N \ge 2$.