1 Introduction

Mathematical modeling is a critical tool for understanding the dynamics of infectious diseases and making predictions about future scenarios. Especially in the fight against the COVID-19 pandemic, the value of mathematical modeling is increasingly recognized. Various mathematical models have been developed to comprehend the intricate dynamics of the COVID-19, and the findings obtained from these models play a significant role. By assessing the disease transmission rate, infection rates, and intervention strategies, these models shed light for healthcare professionals and decision-makers.

In mathematical epidemiology, models depend on an incidence rate which represents the number of individuals who become infected per unit of time, and plays a crucial role in ensuring that the models accurately capture the qualitative dynamics of disease transmission. Bilinear incidence \(\beta SI\) and standard incidence \(\frac{\beta SI}{N}\) have been commonly employed in mathematical models (see [1,2,3,4,5,6]). Here, S, I, R and N denote the susceptible, infected, recovered individuals and total population size, respectively. Various alternative incidence rates have been used in literature to enhance the representation of infection dynamics. These include saturated incidence rates \(\frac{\beta SI}{1+\alpha _1S}\) and \(\frac{\beta SI}{1+\alpha _2 I},\) along with the Beddington–DeAngelis type incidence rate \(\frac{\beta SI}{1+\alpha _1 S+\alpha _2 I},\) as well as the Crowley–Martin incidence rate \(\frac{\beta SI}{(1+\alpha _1 S)(1+\alpha _2 I)},\) among other formulations (see [7,8,9,10]). Here, \(\alpha _1\) represents measures like preventive actions taken by susceptible individuals, and \(\alpha _2\) denotes factors such as treatment concerning infected individuals. Choosing the appropriate incidence rate is one of the crucial steps in mathematically modeling an infectious disease.

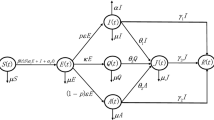
Various mathematical models have been developed to understand the control and spread dynamics of COVID-19 [4,5,6, 11, 12]. Very recently, Ghosh et al. in [12], proposed and studied an SITR model to employ a real data set to analyze the dynamics of the COVID-19 pandemic. The population is divided into four non-intersecting compartments, including susceptible individuals (S),  infected individuals without any treatment who can spread the disease (I),  infected individuals in an isolation ward for treatment who are not spreading the disease (T),  and recovered individuals (R). Model equations are given by

$$\begin{aligned} S^\prime (t) & {} = \Lambda -\frac{\alpha SI}{1+\delta T}-(\gamma _1+d_1)S,\nonumber \\ I^\prime (t)& {} = \frac{\alpha SI}{1+\delta T}-(\beta +d_1)I, \nonumber \\ T^\prime (t)& {} = \beta I-(\gamma _2+d_1+d_2)T, \nonumber \\ R^\prime (t)& {} = \gamma _1S+\gamma _2T-d_1R. \end{aligned}$$
(1.1)

Here, the parameters \(\Lambda ,\alpha ,d_1,d_2\) represent the rate at which newborn individuals are introduced into the susceptible population per unit of time, the disease transmission coefficient, the natural death rate, and the death rate caused by COVID-19. \(\gamma _1\) is the rate at which the secure zone population increases due to factors such as fear and lockdown and \(\gamma _2\) is the rate at which infected individuals in isolation wards recover from the disease. \(\delta\) is a controlling parameter. Here, all parameters are assumed to be positive and initial conditions are

$$\begin{aligned} S(0)>0, \quad I(0)\ge 0, \quad T(0)\ge 0, \quad R(0)>0, \end{aligned}$$

where N(t) denotes the total population size at time t,  and \(N(t)=S(t)+I(t)+T(t)+R(t).\) The authors have discretized model (1.1) using the Euler forward method:

$$\begin{aligned} S_{n+1}& {} = S_n+h\left[ \Lambda -\frac{\alpha S_nI_n}{1+\delta T_n}-(\gamma _1+d_1)S_n \right] , \nonumber \\ I_{n+1}& {} = I_n+h\left[ \frac{\alpha S_nI_n}{1+\delta T_n}-(\beta +d_1)I_n \right] , \nonumber \\ T_{n+1}& {} = T_n+h\left[ \beta I_n-(\gamma _2+d_1+d_2)T_n \right] ,\nonumber \\ R_{n+1}& {} = R_n+h\left[ \gamma _1S_n+\gamma _2T_n-d_1R_n\right] . \end{aligned}$$
(1.2)

Here, \(S_n,I_n,T_n\) and \(R_n\) denote the sub-population sizes at the discrete-time points \(t=nh,\) \(n=0,1,\ldots .\) The value h represents the time-step size. Since the first three equations in model 1.2 are independent of the value \(R_n,\) the authors studied the dynamics of the reduced model given as follows:

$$\begin{aligned} S_{n+1}& {} = S_n+h\left[ \Lambda -\frac{\alpha S_nI_n}{1+\delta T_n}-(\gamma _1+d_1)S_n \right] , \nonumber \\ I_{n+1}& {} = I_n+h\left[ \frac{\alpha S_nI_n}{1+\delta T_n}-(\beta +d_1)I_n \right] , \nonumber \\ T_{n+1}& {} = T_n+h\left[ \beta I_n-(\gamma _2+d_1+d_2)T_n \right] . \end{aligned}$$
(1.3)

In [12], the authors investigated the dynamical properties of the model (1.3) and obtained several important results about disease spreading. However, it has been noticed that some of these results are mathematically incomplete. The purpose of this paper is to clarify some results in [12] and study the qualitative analysis of a discrete-time COVID-19 epidemic model with a saturated incidence rate. Thus, this paper improves the related results presented in [12].

2 Main result

In [12], the authors have obtained two equilibrium points for the model (1.3), namely a COVID-19-free equilibrium (CFE) point \(P_1=(S_0,I_0,T_0)=\left( \frac{\Lambda }{\gamma _1+d_1},0,0 \right)\) and an endemic equilibrium (EE) point \(P_2=(S^*,I^*,T^*),\) where

$$\begin{aligned} S^*& {} = \frac{\Lambda -(\beta +d_1)I^*}{\gamma _1+d_1}, \\ T^*& {} = \frac{(\gamma _2+d_1+d_2)I^*}{\beta }, \\ I^*& {} = \frac{\beta [\alpha \Lambda -(\beta +d_1)(\gamma _1+d_1)]}{(\beta +d_1) [\alpha \beta +\delta (\gamma _1+d_1)(\gamma _2+d_1+d_2)]}. \end{aligned}$$

The correct endemic equilibrium point for the model (1.3) is given in the following result.

Remark 2.1

The endemic equilibrium point of the model (1.3) is as follows:

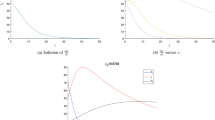
$$\begin{aligned} S^*& {} = \frac{\Lambda -(\beta +d_1)I^*}{\gamma _1+d_1}, \\ T^*& {} = \frac{\beta I^*}{\gamma _2+d_1+d_2}, \\ I^*& {} = \frac{(\gamma _2+d_1+d_2)[\alpha \Lambda -(\beta +d_1)(\gamma _1+d_1)]}{(\beta +d_1)[\delta \beta (\gamma _1+d_1)+\alpha (\gamma _2+d_1+d_2)]}. \end{aligned}$$

For Fig. 3, \(\Lambda =400{,}000\) and other parameters are taken as the values used in Table 1. The phase space of the model to the endemic equilibrium point is shown as \({\mathcal {R}}_0>1\) and \(h=10.\) Here, the endemic equilibrium point obtained in [12] is shown in red and the equilibrium point we obtained is shown in black. It can also be seen here that the endemic equilibrium point obtained here is asymptotically stable.

In [12], the authors used the approach given in [13] to calculate the basic reproduction number \({\mathcal {R}}_0.\) They have obtained the sub-matrices

$$\begin{aligned}{} & {} F=\left[ \begin{array}{cc} h\alpha S_0 &\quad {} 0 \\ 0 &\quad {} 0 \end{array}\right] ,\quad H=\left[ \begin{array}{cc} -h(\beta +d_1)+1 &\quad {} 0 \\ h\beta &\quad {} -h(\gamma _2+d_1+d_2)+1 \end{array}\right] , \end{aligned}$$

and determined \({\mathcal {R}}_0\) by using these matrices, through the next-generation matrix.

The correct method for obtaining the basic reproduction number for the model (1.3) is presented in the following result.

Remark 2.2

To apply the approach in the study [13], the matrices F and H must be non-negative, and the matrix \(F+H\) must be irreducible. However, for sufficiently large values of h,  specifically for

$$\begin{aligned} h>\frac{1}{\beta +d_1} \quad \text{ or } \quad h>\frac{1}{\gamma _2+d_1+d_2}, \end{aligned}$$

the value of h prevents the non-negativity of matrix H. On the other hand, it is obvious that the matrix

$$\begin{aligned} F+H=\left[ \begin{array}{cc} h\alpha S_0-h(\beta +d_1)+1 &\quad {} 0 \\ h\beta &\quad {} -h(\gamma _2+d_1+d_2)+1 \end{array}\right] \end{aligned}$$

is reducible. Therefore, the approach given in the study [13] has not been correctly applied. However, despite this, the basic reproduction number has been calculated correctly:

$$\begin{aligned} {\mathcal {R}}_0=\frac{\alpha \Lambda }{(\gamma _1+d_1)(\beta +d_1)}. \end{aligned}$$

In [12, Theorem 3], the authors have determined the Jacobian matrix at CFE point \(P_1\) as

$$\begin{aligned} J(P_1)=\left( \begin{array}{ccc} 1-h(\gamma _1+d_1) &\quad {} -\frac{h\alpha \Lambda }{(\gamma _1+d_1)} &\quad {} 0 \\ 0 &\quad {} 1+h\left[ \frac{\alpha \Lambda }{(\gamma _1+d_1)}-(\beta +d_1)\right] &\quad {} 0 \\ 0 &{} h\beta &\quad {} 1-h(\gamma _2+d_1+d_2) \end{array}\right) . \end{aligned}$$
(2.1)

They indicated that the CFE point is locally asymptotically stable for \({\mathcal {R}}_0<1,\) and unstable for \({\mathcal {R}}_0>1.\) We observe that, for the locally asymptotically stability of the CFE point, it is not sufficient for only \({\mathcal {R}}_0<1\) to hold. Therefore, we will give the following theorem for stability.

Theorem 2.3

The CFE point of the model (1.3) is locally asymptotically stable if \({\mathcal {R}}_0<1\) and

$$\begin{aligned} h<\min \left\{ \frac{2}{\gamma _1+d_1},\frac{2}{(\beta +d_1)(1-{\mathcal {R}}_0)},\frac{2}{\gamma _2+d_1+d_2} \right\} \end{aligned}$$
(2.2)

holds, and is unstable if \({\mathcal {R}}_0>1\) or

$$\begin{aligned} h>\min \left\{ \frac{2}{\gamma _1+d_1},\frac{2}{(\beta +d_1)(1-{\mathcal {R}}_0)}, \frac{2}{\gamma _2+d_1+d_2} \right\} . \end{aligned}$$
(2.3)

Proof

The eigenvalues of the matrix (2.1) calculated at the CFE point as

$$\begin{aligned} w_1& {} = 1-h(\gamma _1+d_1)<1,\\ w_2& {} = 1+h\left[ \frac{\alpha \Lambda }{\gamma _1+d_1}-(\beta +d_1) \right] \\& {} = 1+h(\beta +d_1)({\mathcal {R}}_0-1), \\ w_3& {} = 1-h(\gamma _2+d_1+d_2)<1. \end{aligned}$$

A necessary and sufficient condition for locally asymptotically stability of the CFE point is \(|w_i|<1,\) \(i=1,2,3\) (see [14]). Then, we have the following inequalities:

$$\begin{aligned} |w_1|<1\Leftrightarrow & {} h<\frac{2}{\gamma _1+d_1}, \\ |w_2|<1\Leftrightarrow & {} h<\frac{2}{(\beta +d_1)(1-{\mathcal {R}}_0)} \quad \text{ and } \quad {\mathcal {R}}_0<1, \\ |w_3|<1\Leftrightarrow & {} h<\frac{2}{\gamma _2+d_1+d_2}. \end{aligned}$$

Note that \(h>0.\) Clearly, if \({\mathcal {R}}_0<1\) and the condition (2.2) is satisfied, then \(|w_i|<1\) holds for \(i=1,2,3.\) On the other hand, if \({\mathcal {R}}_0>1,\) then \(w_2>1.\) Also if the condition (2.3) is satisfied, then one of the eigenvalues of the matrix (2.1) will be less than \(-1.\) Hence, the proof is completed. \(\hfill \square\)

3 A counterexample and its simulations

In this section, some numerical simulations will be provided to verify the theoretical results obtained. The parameter values given in Table 1, used in the study by [12], will be employed. All simulations were made by using MATLAB software.

Table 1 Parameters used for simulations [12]
Full size table

Example 3.1

According to the parameters given in Table 1,

$$\begin{aligned} {\mathcal {R}}_0=0.56900316796<1 \quad \text{ and }\quad P_1=(76923076.9231,0,0). \end{aligned}$$

With initial conditions given in [12], that \(S(0)=8\times 10^8,\) \(I(0)=1400,\) \(T(0)=256,\) the inequality for the time-step size

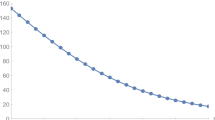
$$\begin{aligned} h<39.9840063974 \end{aligned}$$

must be satisfied for the stability of the equilibrium \(P_1.\) In Fig. 1, the stability behavior of the CFE point \(P_1\) is simulated for sufficiently small h values. On the other hand, as seen in Fig. 2, for sufficiently large h values, the number of individuals in classes I and T oscillates and diverges. These simulations confirm the theoretical results obtained (Fig. 3).

Fig. 1
figure 1

Stability of the CFE point \(P_1\) for sufficiently small various h values

Full size image
Fig. 2
figure 2

Instability of the CFE point \(P_1\) for sufficiently large various h values

Full size image
Fig. 3
figure 3

The asymptotic stability of the endemic equilibrium point for \({\mathcal {R}}_0>1\) and \(h=10\)

Full size image

4 Discussion and conclusions

Differential equation systems are commonly used for the mathematical modeling of biological phenomena. However, for practical purposes, it may be necessary to discretize such models and analyze them in discrete form. Discretization involves partitioning continuous time into discrete time steps to solve the system at specific points in time. The choice of time step size h during the modeling of a biological system is associated with the nature of the system. For instance, smaller time steps may be required for rapidly changing processes, while larger time steps may suffice for slower changing processes. Therefore, selecting the appropriate time step size is of vital importance for accurately reflecting the behavior of the model in the real world. The time step size h used in the Euler discretization is crucial in the dynamical analysis of the model. But, for models discretized using the Euler method, various numerical inconsistencies can occur for sufficiently large h values (see [10, 15]). In this study, attention has been drawn to the significance of the time step size h by correcting certain incomplete results obtained in [12]. The accuracy of theoretical results has been supported by numerical simulations.

On the other hand, during the development of mathematical models for biological systems, it is essential to ensure that the model is biologically well-defined and yields meaningful results. The mathematical tools used in the qualitative analysis of the proposed model should be thoroughly understood and correctly applied. Furthermore, when constructing a mathematical model, attention should be paid to whether the expressions used have direct counterparts in real-life scenarios. What does the incidence function

$$\begin{aligned} \frac{\alpha SI}{1+\delta T} \end{aligned}$$

used in (1.1) explain? What is the meaning of the term \(\frac{1}{1+\delta T}\) here? What is the impact of individuals in the isolated class T on the transition of susceptible individuals to the infected class? It is evident that the theoretical inconsistency in calculating the basic reproduction number originates from here.

For the interested authors, we anticipate that by selecting an incidence function in the form of

$$\begin{aligned} \frac{\alpha SI}{1+a S} \end{aligned}$$

better results can be obtained for this model. Here, the parameter a represents a measure of the inhibition effect taken by susceptible individuals, such as wearing masks. Furthermore, the development of non-standard finite difference schemes could enable more flexible behavior in the selection of the time step size value h.