K isomers in atomic nuclei

Abstract

The properties of K isomers are reviewed. Energies and decay hindrance factors are considered in detail for selected isomers in the $A \approx$ 160–190 region, focusing on pairing effects and the key K-mixing mechanisms that influence $\gamma$-ray decay rates. The $\beta$-decay of K isomers is studied, indicating that, far from the valley of $\beta$ stability, high-K $\beta$-decaying isomers will populate high-K states in the daughter nuclei. The challenges of revealing predicted, but as-yet undiscovered, long-lived isomers in the neutron-rich $N \approx 116$ prolate–oblate shape transition region are highlighted, and the occurrence of oblate high-K isomers is discussed. The 2015 multi-quasiparticle K-isomer table of Kondev, Dracoulis, and Kibédi is updated.

1 Introduction

Nuclear isomers are long-lived excited states of atomic nuclei, with half-lives ranging from less than a nanosecond up to many years. They are principally associated with the rearrangement of individual nucleon orbits. One of the main types of isomer, the K isomer, depends on the orientation of the angular momentum (spin) vector arising from unpaired nucleons. To specify the orientation, the nucleus must have a deformed, i.e., non-spherical, shape. It is K isomers in deformed nuclei that are the subject of this article.

Many deformed nuclei have an axis of symmetry (at least approximately) and the K quantum number represents the projection of the total nuclear angular momentum on that axis. The K value comes mainly from nucleon excitations, which are called quasiparticles, i.e., particle states that are modified by the pairing interaction. For two unpaired nucleons, the angular momentum coupling scheme is illustrated in Fig. 1. Individual nucleons have angular momentum, j, with projection $\Omega$ on the symmetry axis, and K is the sum of these $\Omega$ values. The collective rotational angular momentum, R, is perpendicular to the symmetry axis.

Fig. 1

Schematic representation of the angular momentum coupling scheme for two unpaired nucleons orbiting an axially symmetric, prolate deformed core, reproduced from Ref. [6]

K isomers arise when the electromagnetic decay of a quasiparticle excited state can only proceed if there is a large change in the orientation of the total spin vector, I. Even though the change in the magnitude of the spin vector may itself be small, such as one unit ($\lambda = 1$ $\hbar$), if the change in K value exceeds this, $\Delta K > \lambda$, then the transition is called K-forbidden, and a long half-life can result. The degree of forbiddenness is defined as $\nu = \Delta K - \lambda .$

The observation that K-forbidden electromagnetic transitions do indeed take place shows that the K quantum number is not strictly conserved, i.e., there can be K mixing. The basic physics of $\gamma$-decaying K isomers therefore reduces to two principal aspects: understanding the energetics of quasiparticle states; and understanding the mechanisms of K mixing. In addition, some K isomers are known to $\beta$ decay, which is discussed later, and some may $\alpha$ decay or fission, decay modes which are discussed elsewhere in this Special Topics volume.

A K isomer typically forms the bandhead of a rotational band, and, in accordance with the rotational model, the K value is taken to be equal to the total spin, I, of the bandhead. The basic requirement for a $\gamma$-decaying isomer to be called a K isomer is that the isomer undergoes K-forbidden decay (defined above) and that the Weisskopf hindrance factor, $F_W = T_{1/2}^\gamma /T_{1/2}^W$, for that decay is $F_W \gg 1$, where $T_{1/2}^\gamma$ is the partial $\gamma$-ray half-life and $T_{1/2}^W$ is the corresponding Weisskopf single-particle estimate [1]. Further discussion of this limiting requirement, $F_W \gg 1$, is given in Sect. 4.

For previous reviews of isomers in general, and K isomers in particular, see Refs. [2,3,4,5,6,7,8,9,10,11]. The present work benefits from these reviews. As well as addressing K-isomer energetics and $\gamma$-ray decay rates, special features of the present review include the provision of up-to-date references for recently discovered multi-quasiparticle high-K isomers; a focus on $\beta$-decaying high-K isomers; a discussion of high-K isomers in the neutron-rich $A \approx 190$ region, in connection with a prolate–oblate shape change; and consideration of the occurrence of oblate K isomers. First, however, some of the historical developments associated with K isomers are discussed.

2 Historical developments

The first example of an isomer pair, where there are two long-lived states in a given nuclide, was discovered in $^{234}$Pa by Hahn in 1921 [12], but several additional experimental cases were needed before the existence of isomers became accepted. Isomers were eventually understood by von Weizsäcker in 1936 [13] as spin traps: the possible electromagnetic decay branches from the higher-energy state have to involve large changes in spin, resulting in long half-lives. Nevertheless, it was not until 1955 that Alaga et al. [14] specified the K quantum number in deformed nuclei, leading to the possibility of K-forbidden decays also having long half-lives.

One of the first K isomers to be discovered was a 16-min half-life isomer in odd–odd $^{182}$Ta, identified in 1947 by neutron capture on $^{181}$Ta [15]. However, it was only some years later that the isomer’s electromagnetic decay was characterized. In 1961, Sunyar and Axel [16] were able to argue that the inhibition of the E3 isomeric decay in $^{182}$Ta was due to its K-forbidden character, even though the absolute spins were still not known. It can now be seen that the $K^\pi = 10^-$ isomer decays to the $I^\pi = 7^+$ member of a $K^\pi = 5^+$ rotational band, as shown in Fig. 2. With a K change of five units, the $\lambda = 3$ decay is two-fold K forbidden, which nicely explains its $F_W = 5 \times 10^4$ inhibition compared to the Weisskopf single-particle estimate for an E3 transition, corresponding to a hindrance of $f_\nu = 220$ per degree of K forbiddenness (where $f_\nu = F_W^{1/\nu }$). In addition, there is a low-intensity M4 decay branch from the isomer which is less forbidden ($\nu = 1$), with $F_W \approx 60$ [16], i.e., it is significantly less hindered than the $\nu = 2$, E3 decay. One can ask if this is a K isomer or a spin-trap isomer, but really it is both: the high multipole ($\lambda = 3$) of its strongest decay branch makes it long-lived (a spin isomer) and the significant K forbiddenness ($\nu = 2$) makes it a K isomer. Note that $f_\nu$ is often referred to as the “reduced hindrance”, closely following terminology introduced in 1967 by Borggreen et al. [18], who used “$f_W$” and called it the “reduced retardation factor”.

Fig. 2

Energy levels and $\gamma$-ray transitions associated with the $T_{1/2} = 16$-min isomer of $^{182}$Ta and its decay [17]. $I^\pi$ assignments are given at the left end of each level. The bold arrows indicate the principal decay path

Despite the pre-1955 difficulties with interpreting the isomers themselves, early discoveries of K isomers in the even-even nuclides $^{190}$Os [19, 20] and $^{180}$Hf [21, 22] had important outcomes—they revealed rotational bands built on the corresponding ground state, with excitation energies $E \propto I(I+1)$. In this way, the developing understanding of isomers as based on individual-nucleon excitations and the shell model, went hand-in-hand with the developing understanding of rotational motion and the collective model. The isomer in $^{180}$Hf, now known to have $K^\pi = 8^-$, is also interesting because its seven-fold K-forbidden ($\nu = 7$) E1 decay to the $I^\pi = 8^+$ member of the $K = 0$ ground-state band has the largest Weisskopf hindrance factor of all electromagnetic transitions in nuclei, with $F_W = 3 \times 10^{16}$ [5]. This huge hindrance is testament to the degree of integrity of the K quantum number—but, as will be discussed, this is not always the case.

One of the next key steps in the understanding of nuclear structure was the development of the theory of metallic superconductivity by Bardeen, Cooper and Schrieffer in 1957 [23], and the adaption in 1959 of the same “BCS” concept to superfluidity in atomic nuclei by Belyaev [24]. In the BCS approximation applied to nuclei, the quasiparticle energies, $E_{QP}$, can be obtained [25, 26] from the Nilsson model single-particle energies, $E_{SP}$,

$$\begin{aligned} E_{QP} = \sqrt{(E_{SP}-E_F)^2 + \Delta ^2}, \end{aligned}$$

(1)

where $E_F$ is the Fermi energy (chemical potential) and $\Delta$ is the pairing energy. Multi-quasiparticle energies come from the addition of the individual single-quasiparticle energies. While this gives a good first estimate of K-isomer excitation energies, and their quasiparticle structure, more sophisticated approaches are needed to account for the blocking of pairing correlations and residual interactions between quasiparticles [27,28,29].

Fig. 3

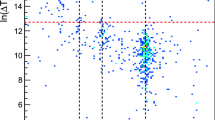
Isomer half-lives for four-or-more-quasiparticle states in the $A \approx 180$ region ($60\le Z\le 76$, $96\le N\le 116$). For a given nuclide with more than one such isomer, the longest half-life is illustrated. The data are from Kondev et al. [5], except for the lowest-mass example, $^{160}$Sm [30]. Stable nuclides are shown as squares in the N–Z plane. The figure is from Walker and Podolyàk [8]

With these developments, it is possible to understand the formation of K isomers and their energies, based on unpaired nucleons in a deformed potential, using, for example, the Nilsson model. The energy gap between the fully paired ground state of an even-even nucleus and its lowest-lying broken pair, two-quasiparticle states is approximately $2\Delta$, or $\approx 1.3$ MeV in the deformed $A \approx 180$ region. Four-quasiparticle excitations begin at $\approx 2.6$ MeV, and so on for higher quasiparticle numbers. Their half-lives depend sensitively on their spin values and excitation energies, leading to rapid half-life variations as a function of N and Z, as the Fermi level moves through the available single-particle configurations. This sensitivity is illustrated in Fig. 3, which shows half-lives in the $A \approx 180$ deformed region, for excited states with at least four unpaired nucleons. Across the whole nuclear chart, the only other established examples of this kind (K isomers with at least four unpaired nucleons) are in $^{254}$No [5] and, possibly, also in $^{254}$Rf [31], making it clear that the $A \approx 180$ nuclides constitute by far the most prolific region of high-K multi-quasiparticle isomers. (As will be discussed, two-quasiparticle K isomers are more widely distributed in N and Z.)

The illustration (Fig. 3) covers 18 orders of magnitude in half-life, with the longest-lived isomer being the 31-year ($\approx 10^9$ s) $K^\pi = 16^+$, 2.4 MeV isomer in $^{178}$Hf [5], discovered in 1968 by Helmer and Reich [32]. Although it is not discernible in the figure, note also that the highest number of quasiparticles for an individual K isomer is nine, which is found in $^{175}$Hf, with $K^\pi = 57/2^+$, a half-life of 22 ns, and an excitation energy 7.5 MeV [5]. This isomer was discovered in 1990 by Gjørup et al. [33].

3 K-isomer energetics

While the basic features of K-isomer excitation energies can be understood from individual nucleons in a deformed mean field (as in the Nilsson model) with pairing, empirical comparison between isotopes and isotones can reveal more subtle features. To illustrate the energy variations, the emphasis here is on the $K^\pi = 8^-$ two-quasiparticle excitations with $A\approx 180$, specifically those in the $Z=72$ hafnium isotopes, based on the two-proton $\{ \pi 7/2^+[404]\otimes \pi 9/2^-[514]\}$ Nilsson configuration, and in the $N = 106$ isotones, based on the two-neutron $\{ \nu 7/2^-[514]\otimes \nu 9/2^+[624]\}$ configuration. With their high $\Omega$ values of 7/2 and 9/2, these are key orbitals for the formation of high-K isomers.

The $K^\pi = 8^-$ excitation energies are illustrated in Fig. 4, including comparison with the proton and neutron pairing energies according to the three-point formula:

$$\begin{aligned} \Delta _\pi = B(N,Z) - 0.5\times [B(N,Z+1) + B(N,Z-1)], \end{aligned}$$

(2)

for protons, and similarly for neutrons, where B(N, Z) is the experimental binding energy obtained from nuclear masses [36]. The steep decline in proton pairing in the hafnium isotopes, with increasing neutron number, has been discussed by Litvinov et al. [37] in connection with the predictions of a range of mass models, which show distinct differences in their abilities to reproduce the data. The focus here, in the left panel of Fig. 4, is on the striking correlation between 2$\Delta _\pi$ and the hafnium $K^\pi = 8^-$ energies, suggesting that pairing is a leading effect in the isomer energy variation. Even over a small mass range, changes in pariring can evidently have a large effect on quasiparticle energies. (This was shown previously [38], but at a time when only limited mass data were available for comparison.) In a similar way, the right panel of Fig. 4 shows that the two-quasineutron $K^\pi = 8^-$ energies for $N=106$ isotones increase considerably between $^{176}_{\ 70}$Yb and $^{182}_{\ 76}$Os, closely following the change in the three-point neutron pairing energy. For higher proton numbers, there are substantial shape changes as the $Z = 82$ closed shell is approached, invalidating any simple comparison. Nevertheless, the Woods-Saxon-Strutinsky calculations [28, 34, 39], which include shape variations, show good quantitative agreement with the experimental energies.

Fig. 4

Energies of $K^\pi = 8^-$ excitations for $Z = 72$ hafnium isotopes (left, two-quasiprotons) and $N = 106$ isotones (right, two-quasineutrons). The filled triangles are for even–even nuclides, relative to the corresponding ground state. Calculated (unperturbed) energies are used for $^{178}$Hf [34] (see text). The small diamonds are for three-quasiparticle states in odd-N hafnium isotopes, where the energy is relative to the appropriate one-quasineutron state. The data are from Refs. [5, 35]. The open circles are from configuration-constrained Woods–Saxon–Strutinsky calculations [34, 39]. The upper curves with error bars represent pairing energies ($2\Delta _\pi$ left panel, $2\Delta _\nu$ right panel) obtained from experimental binding energies [36] with the three-point formula (Eq. 2)

In Fig. 4 the differences between the $2\Delta$ energies and the two-quasiparticle energies can be attributed in part to the pair-blocking effect and in part to the like-nucleon (proton–proton or neutron–neutron) residual interactions. Furthermore, the smaller difference (in the left panel) of about 120 keV between the $K^\pi = 8^-$ two-quasiproton excitation energies in odd-N hafnium isotopes and the average of their even–even neighbors (see also Ref. [38]) must be due to unlike-nucleon residual interactions. However, it is difficult to extract quantitative estimates of the pairing strength from the experimental multi-quasiparticle energies. In contrast, detailed pairing and blocking information can be obtained from theoretical calculations. Using the Lipkin–Nogami approach [28, 40] to avoid the premature collapse of pairing associated with the BCS approximation, neutron pairing energies are shown in Fig. 5 for states in $^{178}$W, taken from Ref. [29]. Note that, for a given number of quasiparticles, the pairing tends to increase as the energy increases. This is because the effect of blocking is reduced for particle orbits that are further from the Fermi surface. While each additional broken pair reduces $\Delta$, it does not go to zero. In a separate study, analysis of high-K rotational bands [29, 41] shows that, after allowing for rotation-alignment effects, moments of inertia tend to 70–80% of the rigid-body value with increasing numbers of quasiparticles, giving a broadly consistent picture of the gradual decline of pairing effects.

Note that the observed $K^\pi = 8^-$ isomer in $^{178}$Hf ($N=106$) has a mixed neutron–proton configuration, 64% two-quasineutron and 36% two-quasiproton [34]. The orthogonal $K^\pi = 8^-$ state is also known, though it is not isomeric. The “unperturbed” two-quasiparticle energies have been used in Fig. 4, as given by Dracoulis et al. [34]. It is remarkable that there is simultaneous minimisation of the energies of both proton and neutron configurations at $Z = 72$, $N = 106$, i.e., for $^{178}$Hf, enabling that nuclide to form an exceptionally low-lying, $K^\pi = 16^+$, four-quasiparticle isomer, with a half-life of 31 years—the maximum shown in Fig. 3.

Fig. 5

Calculated neutron pairing energies for intrinsic states with different numbers of neutron quasiparticles in $^{178}$W. The figure is from Dracoulis et al. [29]

Another prominent feature of Fig. 3 is the appearance of three long-lived isomers in the neutron-rich region, corresponding to $^{184}$Hf ($T_{1/2} \approx 12$ min), $^{186}$W (2 s) and $^{187}$Ta ($\ge$5 min) [5]. These nuclides are difficult to access experimentally, and there are predictions for additional long-lived isomers in this neutron-rich region [42], related to the favorable $K^\pi = 10^-$, $\{ \nu 9/2^-[505]\otimes \nu 11/2^+[615]\}$ configuration which will have low excitation energy for $N=$114–116. This is just where there is also predicted to be a prolate–oblate shape transition in the ground state [44,45,44] (see Sect. 6 for more details) so the nuclear structure is expected to be complex.

As mentioned above, two-quasiparticle K isomers in even-even nuclei are more widely distributed through N and Z. The lowest-mass example with clear K isomerism is in $^{94}$Se [45], with $K^\pi = (7^-)$, a half-life of 0.68 $\mu$s, and $F_W = 2.5 \times 10^8$. However, the yet-lower-mass nuclide $^{44}$S has a first-excited $I^\pi = 4^+$ state which has been discussed in terms of K isomerism [46, 47], with $\Delta K = 4$, E2 decay that is slightly hindered: $T_{1/2} \approx 76$ ps and $F_W \approx 1.6$. This stretches the limits of what is usually meant by K isomerism—an aspect that is further considered in Sect. 4. At the high-mass extreme, $\alpha$ decaying two-quasiparticle isomers are known in $^{266}$Hs and $^{270}$Ds [48, 49], and additional high-K isomers are predicted [50,51,52].

4 K-isomer electromagnetic decay

A central task of K-isomer physics is to understand K-isomer decay half-lives. The observation itself of K-forbidden electromagnetic transitions implies that the K quantum number is not strictly conserved, so it is the different mechanisms of K mixing that come under the spotlight.

A basic feature of highly K-forbidden transitions is the change in nuclear orientation. In a high-K state, the total spin is aligned with the symmetry axis of the (typically) prolate spheroidal nuclear shape, whereas, when the state populated is a member of the ground-state band, the spin orientation changes to that of collective rotation, which is perpendicular to the symmetry axis. It is well known that rotational motion induces K mixing, through the operation of the Coriolis force [53, 54], and this kind of K mixing can be viewed as orientation fluctuations. In contrast, shape fluctuations can provide a pathway for K isomer decay by tunneling through the $\gamma$ (shape asymmetry) degree of freedom [55, 56]. Even though both initial and final states may have the same intrinsic shape, a large ($\approx$ $90^\circ$) orientation change relative to the spin vector is still needed. This approach may also be able to account for the effects of triaxiality in the initial or final states, where a triaxial shape inevitably involves mixed K values.

Another consideration is the excitation energy of the isomer. If this is high relative to the yrast line (the locus of states with minimum energy as a function of spin), then level-density considerations imply that there may be other states of the same spin and parity lying close in energy, yet having different K values. Such states can mix randomly and introduce statistical K mixing [57]. Finally, there is the situation where a particular excited state with the same spin and parity as a K isomer has, by chance, an energy that is close to that of the isomer. This kind of chance near-degeneracy can be amenable to simple two-level mixing calculations to understand the isomer half-life, with mixing matrix elements as small as a few eV [58, 59] (see also Chen et al. [60]).

While these approaches to K mixing are helpful for gaining a general qualitative understanding of K-isomer decay rates, detailed quantitative descriptions remain elusive. This has much to do with the multiple degrees of freedom, and the overall problem that calculations of rates for “forbidden” transitions are intrinsically difficult. It has therefore proved instructive to explore the dependence of hindrance factors, $F_W$, or, more usually, reduced hindrance factors, $f_\nu$, on a range of variables [2,3,4,5,6,7,8,9,10, 61,62,63], with different degrees of success. Whichever variable is chosen, it is clear that reduced hindrances vary enormously, from values of about two, up to more than two hundred, notwithstanding the fact that these reduced hindrances already account for the transition multipole character, the transition energy, and the degree of K forbiddenness. The wide range of $f_\nu$ values evidently reflects the range of physical conditions, such as Coriolis mixing, shape tunneling, etc.

In the present work, emphasis is given to the variation of reduced hindrance with energy relative to a rigid rotor, as illustrated in Fig. 6. This is for multi-quasiparticle states in even-even and odd-A nuclides in the $A \approx 180$ region, based on four or more quasiparticles, and decaying by $\nu \ge 4$, E1 $(I \rightarrow I-1)$, E2 $(I \rightarrow I-2)$ and E3 $(I \rightarrow I-3)$ transitions. The reference rotor energy, $E_R$, for a given spin is calculated using a moment of inertia that is 85% of the full rigid-body value [4], scaled to 85 $\hbar ^2$MeV$^{-1}$ for $A = 178$. (The precise scaling is not critical, but, with a large range of spin values, some account needs to be taken of the reduction of the reference rotor moment of inertia compared to that of a rigid body.)

Before discussing the physical interpretation of Fig. 6, it is necessary to explain two features of the appearance of the data. First, the blue diamonds represent E1 transitions, for which the Weisskopf hindrance factor, $F_W$, has been divided by 10$^4$ before taking the $\nu ^{th}$ root to obtain $f_\nu$. It is well known that K-allowed E1 transitions are highly hindered, and this needs to be accounted for in the comparison of K-forbidden transitions. The 10$^4$ factor is found to be useful not only when comparing with other radiation multipole orders (here E2 and E3) but also when comparing E1 transitions with different degrees of K-forbiddenness [30, 64]. Second, the circled data points are for transitions which change the number of quasiparticles by four. These transitions have $\nu \ge 10$ and are mostly in even-even nuclides, going directly from four-quasiparticle states to excited members of their respective ground-state bands, bypassing the usual pathway through two-quasiparticle states.

Fig. 6

Reduced hindrance as a function of energy relative to a rotor, for E1 decays (diamonds, effective values—see text) and E2 and E3 decays (squares) with $\nu \ge 4$, from multi-quasiparticle isomers in even–even and odd-A nuclides. For the latter, a pairing-gap energy of 0.9 MeV ($\Delta \approx 12/A^{1/2}$ MeV) has been added. Since a large spin range is covered ($11\rightarrow 57/2$ $\hbar$), it is significant that the reference rotor moment of inertia is reduced to 85% of the rigid-body value [4]. The line through the data represents the expected level-density dependence [57]. The isomer data are from Refs. [5, 30, 65], except that, for $^{177}$W, the isomeric E2 transition is taken to have $\Delta K = 6$, as discussed by Walker and Xu [7]. The circled data points are for $\nu \ge 10$ “bypassing” decays, which are discussed in the text. The figure is updated and adapted from Ref. [64]

In Fig. 6, the line through the data represents the energy dependence of the effect of level density on $f_\nu$, as first proposed by Walker et al. [57] in 1997. Many new data values have since become available and are now included. Even if the circled data points are excluded (discussed later), there is considerable scatter, which could be associated with other degrees of freedom, such as the widely varying quasiparticle configurations that are involved. Indeed, one data point, labeled “Hf-176”, deserves specific comment, since it deviates most strongly from the overall correlation. Here, the $^{176}$Hf six-quasiparticle isomer structure differs from that of the four-quasiparticle populated band simply by the addition of a broken pair of two $i_{13/2}$ neutrons, $\{\nu 7/2^+[633]\otimes \nu 9/2^+[624]\}$ coupled to $K = 8$ [66]. The $i_{13/2}$ neutrons are, in this mass region, the most strongly affected by the Coriolis force [53], and, as discussed by Mukherjee et al. [66], mixing between the six- and four-quasiparticle structures can explain the low $f_\nu$ value. The implied mixing matrix element, $|V| \approx 2$ keV, is intermediate between the values of 10–100 eV for chance mixings between states with large nominal K differences [34], and 10–100 keV for $i_{13/2}^2$ rotational alignments that give rise to the backbending phenomenon [53]. Therefore, there is a reasonable understanding of the deviant $^{176}$Hf data point, where the critical part of the K mixing (additional to the level-density effect) is in the initial state, i.e., in the isomer itself.

The above argumentation leads naturally to discussion of the circled data points, which change the quasiparticle number by four and have $\nu \ge 10$. This means that the transition goes to a rotational band member with at least 10$\hbar$ of collective spin, implying significant Coriolis mixing among the paired $i_{13/2}$ neutrons, and hence significant K mixing in the populated state—which could lead to the lower $f_\nu$ values seen in Fig. 6. The clearest demonstration of such mixing is in the five-quasiparticle isomer decay of $^{179}$W, where the $K^\pi = 35/2^-$ isomer initially appeared to decay directly to a $K^\pi = 7/2^-$ band [67, 68], but detailed spectroscopy revealed that the isomer decays into the bandcrossing region where the $\nu 7/2^-[514]$ band is crossed at spin 31/2 by a three-quasiparticle band based on the $\{ \nu 7/2^-[514]\otimes \nu 7/2^+[633]\otimes \nu 9/2^+[624]\}$, $K^\pi = 23/2^-$ configuration [69], i.e., $\nu 7/2^-[514]$ coupled to two $i_{13/2}$ neutrons. If the principal E2 isomer decay is taken to be from $K = 35/2$ to $K = 7/2$ then $f_\nu = 2$, whereas if the decay is to $K = 23/2$ then $f_\nu = 10$. Taking account of the details of the level mixing at the bandcrossing, $f_\nu = 8$ is obtained [69], which falls right on the curve at the appropriate value of $E_K - E_R = 2029$ keV. For other cases, where the bandcrossing effects are less easy to recognize and account for, the implication is that the estimated $f_\nu$ values (circled in Fig. 6) are, in effect, too low.

If, then, all the circled data points in Fig. 6 are ignored, as well as the $^{176}$Hf data point, a significantly improved correlation is evident. From the preceding discussion, it is seen that particular problems arise in the treatment of the high-K coupling of two $i_{13/2}$ neutrons in the $A \approx 180$ mass region. This high-K coupling is called the t configuration, due to the orientation of the angular momentum being intermediate (or tilted) between the nuclear symmetry axis and the collective-rotation axis [7, 69, 70]. It is interesting to note that structures based on a t configuration are also observed in the $A \approx 130$ region, notably in $^{130}$Ba [71], where a pair of $h_{11/2}$ neutrons couples to $K \approx 8$.

To summarize the implications of Fig. 6, the correlation between $f_\nu$ and $E_K - E_R$ is not very strong, but the largest deviations originate from involvement of the t configuration. The remaining scatter of the data could be due to other configuration effects, or other degrees of freedom that have not yet been accounted for. Further work remains to be done.

Notwithstanding the t-configuration problem, there is a large variation of $f_\nu$ values evident in Fig. 6, and it is appropriate to revisit the question of what determines whether or not an excited state should be called a K isomer. This is topical in the sense that fast-timing LaBr$_3$ scintillation detectors are now in regular use with large $\gamma$-ray detector arrays, and sub-nanosecond half-lives have become accessible in complex decay schemes. For example, $^{178}$W has an $I^\pi = 12^+$ state at 3235 keV with a half-life of 275(65) ps, and it has a relatively low intensity 1571 keV, E2 decay branch with a partial half-life of 4 ns [65]. Its Weisskopf hindrance factor of $F_W = 4000$ seems to qualify the 12$^+$ state to be called a K isomer, but, with $\nu = 10$ for the 1571 keV transition, the reduced hindrance is $f_\nu = 2.3$, which is one of the lowest values in Fig. 6. Arguably, the principal criterion for K isomerism should be the existence of electromagnetic transition pathways with $F_W \gg 1$, as advocated in Sect. 1. Furthermore, in order to avoid ambiguity with shape and seniority isomers [10], there should also be a structure reason for calling the transition K forbidden. With these requirements, the $^{178}$W 12$^+$, 3235 keV, 0.3 ns state indeed qualifies as a K isomer.

At the other half-life extreme is the uniquely stable isomer of $^{180}$Ta, a $K^\pi = 9^-$ state at 76.79(55) keV [72]. The $K^\pi = 1^+$ ground state of $^{180}$Ta has a half-life of 8.1 h, yet the isomer has a half-life of at least $0.29 \times 10^{18}$ y [73]. It is the low energy and high spin of the isomer that leads to the extraordinary half-life. Since there is a 2$^+$ ($K = 1$) collective state that is 40 keV above the ground state, the lowest possible multipole electromagnetic decay of the isomer would have E7 character, with $\Delta K = 8$, hence $\nu = 1$. Evidently, the long half-life is relatively little influenced by the weak K forbiddenness, and the isomer is essentially of the “spin-trap” type, rather than being a “K isomer”. However, as a high-K state, the isomer is commonly referred to as a K isomer.

5 K-isomer $\beta$ decay

Fig. 7

Beta-decay schemes of $^{176}$Lu (left) and $^{178}$Ta (right), based on Refs. [9, 36, 78]

Unlike in electromagnetic decays, experimental information about $\beta$-decaying K isomers is sparse, and, as a consequence, the role of the K quantum number on the $\beta$-decay transition strength (often expressed in log ft units) is still not well quantified [14, 76,77,78,77]. A notable example of a $\beta$-decaying K isomer is the ($K^{\pi },I^{\pi } = 7^{-},7^{-}$) $\{\pi 7/2^+[404] \otimes \nu 7/2^-[514]\}$ ground state of $^{176}$Lu. It has a relatively low $Q_{\beta ^-} = 1194.1(9)$ keV [36] which allows access only to the $I^{\pi }=6^{+}$ and 8$^{+}$ levels of the $K^{\pi }=0^{+}$ ground-state band in the daughter nucleus $^{176}$Hf. The state decays via $\Delta K=7$, first-forbidden ($\Delta I=0,1,\, \Delta \pi =yes$) transitions, as shown in Fig. 7 (left), and it has an extremely long half-life of 37.01(17) Gy [9] resulting in log ft values of 19.2 and 19.9, respectively. In contrast, similar first-forbidden decays from the low-spin ($K^{\pi },I^{\pi }=0^{-},1^{-}$) isomer at 122.9 keV in $^{176}$Lu, arising from the same $\{\pi 7/2^+[404]\otimes \nu 7/2^-[514]\}$ configuration, have $\Delta K=0$ and much smaller log ft = 6.9 ($I^{\pi }=0^{+}$) and 6.5 ($I^{\pi }=2^{+}$). By introducing the K hindrance as $F_{\beta }^{\Delta K}={ ft}^{\Delta K}$/${ ft}^{\Delta K=0}$, one can conclude that the $\beta ^{-}$-decay strength of the $K^{\pi }=7^{-}$ ground state in $^{176}$Lu is hindered by $\sim$10$^{12}$ compared to that for the $K^{\pi }=0^{-}$ isomer.

The situation, however, is quite different in the isotone $^{178}$Ta, where the larger $Q_{EC}=1837$ keV [36] allows access to the two-quasiparticle $K^{\pi }=8^{-}$ states at 1147.4 keV (64% $\{\nu 7/2^-[514]\otimes \nu 9/2^+[624]\}$ and 36% $\{\pi 7/2^+[404]\otimes \pi 9/2^-[514]\}$) and 1479.0 keV (36% $\{ \nu 7/2^-[514]\otimes \nu 9/2^+[624]\}$ and 64% $\{\pi 7/2^+[404]\otimes \pi 9/2^-[514]\}$) in the daughter nucleus $^{178}$Hf, as shown in Fig. 7 (right). As a result, the same ($K^{\pi },I^{\pi }=7^{-},7^{-}$) $\{\pi 7/2^+[404]\otimes \nu 7/2^-[514]\}$ state decays via $\Delta K=1$, allowed ($\Delta I=0, 1,\, \Delta \pi =no$) transitions to the two $K^{\pi } =8^{-}$ states with log ft = 5.1 and 4.8, respectively, which are essentially identical to these observed in the decay of the ($K^{\pi },I^{\pi }=1^{+},1^{+}$) $\{\pi 9/2^-[514]\otimes \nu 7/2^-[514]\}$ ground state.

The existence of $\beta$-decaying, spin(K)-trap isomers is a feature of many deformed odd-odd nuclei. When energetically allowable, the high-K ($\pi \otimes \nu$) $\beta$-decaying states preferentially decay to high-K ($\pi ^{2}$ or $\nu ^{2}$), two-quasiparticle states in the even-even daughter nuclei that are located at excitation energies $E_{f}\ (\sim 2\times \Delta _{\pi (\nu })\ge 1.3$ MeV. Therefore, these decays typically have a reduced effective $Q_{\beta }$ value of $Q_{\beta , eff}=Q_{\beta } - E_{f}$, compared to the low-K ($\pi \otimes \nu$) $\beta$-decaying states whose decays usually proceed via the 0$^{+}$ and 2$^{+}$ levels of the ground-state band, where $Q_{\beta , eff}\approx Q_{\beta }$. Since the $\beta$-decay half-lives depend sensitively on $Q_{\beta }$ ($\tau _{\beta }\propto Q_{\beta , eff}^{-5}$), one may expect that the high-K $\beta$-decaying states will have longer half-lives compared to the low-K ones. For example, in the case of $^{178}$Ta (Fig. 7 (right)) one has $T_{1/2}(K^{\pi }=7^{-})=2.36(8)$ h [9], but $T_{1/2}(K^{\pi }=1^{+})=9.31(3)$ min [9], although both states have identical $\beta$-decay transition strengths.

We have surveyed the nuclear physics databases [9, 78] for K-forbidden $\beta ^{-}$ decays in deformed odd-odd nuclei with $Q_{\beta ^-}<1.5$ MeV and we unambiguously identified only a limited number of first-forbidden transitions that have different $\Delta K$. The deduced K-hindrances as a function of $\Delta K$ are shown in Fig. 8. It can be seen that for each order of $\Delta K$, the $\beta$-decay transition strength is suppressed by $10^{1.9} \approx 80$. While there is a striking correlation of increasing $\beta$-decay hindrance with increasing $\Delta K$, similar to that observed for $\gamma$ decay [5], there is not a correspondingly simple specification of the degree of K-forbiddenness. Nevertheless, the implication for nuclei away from the line of stability, where the decay Q values are large ($Q>4$ MeV), is clear: it would be unlikely to observe $\beta$-decay transitions with large $\Delta K$, unless a specific K-mixing scenario is invoked. For example, even for $\Delta K=2$ forbidden decays, one may expect log ft $\sim 9-10$ and therefore the decays would be expected to proceed via non-K-forbidden transitions, by minimizing $\Delta K=0,\pm$1.

Fig. 8

Hindrance factors as a function of $\Delta K$ for first-forbidden transitions in the $\beta ^{-}$-decay of deformed nuclei: $\Delta I=\pm$1: $^{176}$Lu ($\Delta K=0$ and 7), $^{238}$Np ($\Delta K=2$), and $^{158}$Tb ($\Delta K=3$); $\Delta I=0$: $^{244}$Am ($\Delta K=0$), $^{230}$Pa ($\Delta K=2$), and $^{236}$Np ($\Delta K=6$). The ${ ft}^{\Delta K=0}$ values for $^{244}$Am and $^{176}$Lu were used for normalization of the $\Delta I=0$ and $\Delta I=\pm$1 data, respectively. The solid line is drawn to guide the eye and corresponds to $F_{\beta }^{\Delta K}=10^{(1.9\times \Delta K)}$

6 K isomers in the $N \approx 116$ shape-transition region

Fig. 9

Experimental (squares) and calculated (circles) lowest high-K four-quasiparticle excitation energies from Ref. [42], shown as a function of neutron number for hafnium isotopes. The excitation energies are given relative to rotor energies with 85% of the rigid-body moment of inertia (cf. Fig. 6). The data points are labeled with their $K^\pi$ values

In Sect. 3, it was pointed out that high-K isomers are expected to play a prominent role in the $Z \approx 72$, $N =$114–118 prolate–oblate shape transition region. The shape change has been well studied in higher-Z nuclei, where triaxiality plays an important role [79, 80]. However, for $Z \lesssim 72$ the shape change with increasing neutron number, from prolate to oblate, is predicted to maintain approximate axial symmetry [43], though experimental data are lacking.

Specific multi-quasiparticle, potential energy surface (PES) calculations have been carried out for the neutron-rich, $Z = 72$ hafnium isotopes [42, 81], illustrated for four-quasiparticle K-isomer energies (relative to a rotor) in Fig. 9, with experimental and calculated values from Refs. [5, 42], respectively. According to theory, the hafnium ground-state shape should change from prolate ($\beta _2 \approx +0.2$) to oblate ($\beta _2 \approx -0.2$) between $N = 114$ to 118 [42, 43], while the high-K excitations remain prolate [42]. Perhaps more striking are the low excitation energies of the four-quasiparticle states at $N = 114$ and 116, which are predicted [42] to be even more energetically favored than the 31-y, $K^\pi = 16^+$ isomer of $^{178}$Hf (see Fig. 9). An extra experimental complication is the likelihood of competition from isomeric $\beta$ decay, a mode that has already been identified from the $^{184}$Hf (15$^+$) isomer [82].

The existence of high-spin isomers in the $N \approx 116$ shape-transition region extends to higher-Z values. Relatively long-lived examples are the well-known $K^\pi = 10^-$ isomers [5] in $^{190}$Os$_{114}$ ($T_{1/2} = 10$ min) and $^{192}$Os$_{116}$ (6 s) based on the $\{\nu 9/2^-[514] \otimes \nu 11/2^+[615]\}$ configuration. The same structure is identified in $^{190}$W$_{116}$ (240 $\mu$s) [83], though not in $^{188}$W$_{104}$ [83], and, with the addition of a proton in the $11/2^-[505]$ orbital, it is also found in $^{193}$Ir$_{116}$ (180 $\mu$s) and $^{191}$Ir$_{114}$ (8 s) [84], with triaxiality becoming increasingly important as Z increases. However, when comparing with PES calculations [83,84,85], it is the absence of observed isomers involving the high-K, $12^+$ $\{\nu 11/2^+[615]\otimes \nu 13/2^+[606]\}$ coupling that seems most surprising, especially at $N = 116$. It is possible that the corresponding experimental states are very long-lived and undergo $\beta$ decay, making their identification particularly difficult [6, 84, 85].

Experimental access to high-K isomers in this neutron-rich $N \approx 116$ region is challenging, depending mainly on relativistic projectile-fragmentation reactions [82, 86] and near-barrier multi-nucleon transfer (MNT) reactions [85, 87], in both cases using heavy-ion beams. The recently achieved ability to separate refractory ($Z =$72–78) MNT reaction products in both A and Z, after stopping in a gas cell [88, 89], is opening up further opportunities.

7 Oblate high-K isomers

The vast majority of deformed nuclei have prolate shape, and likewise almost all high-K isomers are prolate. Nevertheless, there is evidence for a number of oblate high-K isomers, most notably in even-even lead ($Z = 82$) and polonium ($Z = 84$) isotopes. Dracoulis et al. [90] discuss and compare the $I^\pi = 11^-$ isomers in $^{188,190,192}$Pb, including the rotational-like bands above them, and it seems reasonable to conclude that these isomers have high-K and oblate shape. In addition to these three cases, other possible 11$^-$ isomers (see also [6, 91]) at similar excitation energies in $^{194,196}$Pb and in $^{192,194,196,198}$Po are now included in Table 1 (see Sect. 8) though further evidence of their high-K oblate shape is needed. Their structure, at least in $^{188,190,192}$Pb, is interpreted [90] to have the $\{\pi 9/2^-[505]\otimes \pi 13/2^+[606]\}$ oblate configuration, coupled to $K^\pi = 11^-$. Note that these nuclides have spherical or weakly deformed ground states, and it is not possible to give a straightforward interpretation of the isomer decay transition rates in terms of inhibition due to the K quantum number.

The recent discovery by Lizarazo et al. [45] of an isomer in $^{94}$Se has opened a new chapter in the investigation of oblate high-K structures. Comparison of the experimental data with theoretical calculations indicates that not only is the proposed $K^\pi = 7^-$, 680 ns isomer oblate, with $\beta _2 \approx -0.25$, but so also is the $K^\pi = 0^+$ ground state. Remarkably, the 6-fold K-forbidden E1 decay hindrance factor, for the $\gamma$-ray transition from the isomer to its respective ground-state band, is $F_W = 2.5 \times 10^8$, and the reduced hindrance is $f_\nu = 25$. These values are similar (though at the lower end of the range) to the values found for comparable $\nu = 6$, E1 transitions in the $A = 160$–190 region. As pointed out in Ref. [45], the $^{94}$Se isomeric decay discovery suggests the possibility to measure the electromagnetic moments, and hence to determine more rigorously the structure of the isomer itself.

8 K-isomer update

In Table 1, details are listed of newly found high-K isomers and their properties, updating the table of Kondev et al. [5]. The list is limited to isomers with configurations of two-or-more quasiparticles in even–even nuclides, three-or-more quasiparticles in odd-A nuclides, and four-or-more quasiparticles in odd–odd nuclides, i.e., there must be at least one broken pair compared to the respective ground state. Candidate oblate high-K isomers in lead and polonium isotopes are newly included (see also Sect. 7). Additional data on previously reported isomers in $^{173}$Ta, $^{256}$Rf and $^{246,248}$Cm have been published by Wood et al. [92], Khuyagbaatar et al. [93] and Shirwadkar et al. [94], respectively.

Table 1 K isomers discovered since the last review [5]

9 Summary and prospects

High-K isomers are known in a wide range of deformed nuclei, with up to 7.5 MeV excitation energy and up to nine unpaired nucleons. The majority of multi-quasiparticle K isomers occur in the $A \approx$ 160–190 region, which is the focus of the present review. Isomer energies give information about nucleon–nucleon pairing and residual interactions, while isomer decay rates reflect the variety of K-mixing mechanisms. The quantitative understanding of K-isomer $\gamma$-ray decay rates remains a particular challenge. Both $\beta$ and $\gamma$ decay rates are discussed. Far from stability, the $\beta$ decays of high-K isomers (where favored) are expected to preferentially populate similarly high-K states in the daughter nuclei. The neutron-rich $N \approx 116$ prolate–oblate shape-transition region is expected to be rich in both $\beta$- and $\gamma$-decaying high-K isomers that remain to be identified. These will shed light on the nature and abruptness of the prolate–oblate shape change. The recent discovery of a $T_{1/2} = 680$ ns, $K^\pi = 7^-$ state in $^{94}$Se opens a new avenue for the study of oblate high-K isomerism.

The 2015 compilation [5] of multi-quasiparticle high-K isomers is augmented with a table of the high-K isomer discoveries since that time.