A study on fractional HBV model through singular and non-singular derivatives

Abstract

The current study’s aim is to evaluate the dynamics of a Hepatitis B virus (HBV) model with the class of asymptomatic carriers using two different numerical algorithms and various values of the fractional-order parameter. We considered the model with two different fractional-order derivatives, namely the Caputo derivative and Atangana–Baleanu derivative in the Caputo sense (ABC). The considered derivatives are the most widely used fractional operators in modeling. We present some mathematical analysis of the fractional ABC model. The fixed-point theory is used to determine the existence and uniqueness of the solutions to the considered fractional model. For numerical results, we show a generalized Adams–Bashforth–Moulton (ABM) method for Caputo derivative and an Adams type predictor-corrector (PC) algorithm for Atangana–Baleanu derivatives. Finally, the models are numerically solved using computational techniques and obtained results graphically illustrated with a wide range of fractional-order values. We compare the numerical results for Caputo and ABC derivatives graphically. In addition, a new variable-order fractional network of the HBV model is proposed. Considering the fact that most communities interact with each other, and the rate of disease spread is affected by this factor, the proposed network can provide more accurate insight for the modeling of the disease.

1 Introduction

Hepatitis B virus is an infectious disease that infects a large number of people globally. The virus causes liver damage as well as other diseases that are harmful to human health. Hepatitis B epidemiology indicates two transmission routes in humans: horizontal and vertical. Horizontal transmission occurs when people share blades, needles, unprotected intercourse, and so on, while vertical transmission occurs when an infected mother passes the virus on to her kid. In 2015, many HBV cases of liver infection and death were registered and still, several countries around the world, including China, are dealing with this problem with many cases and deaths. Acute HBV clinical information is age-specific. HBV infection is normally asymptomatic in newborns, young children (under the age of 10) and immunocompromised adults. Adults and older children with 30–50% infection are symptomatic. Sometimes the hepatitis B-infected person who does not show symptoms for more than 6 months may be prone to liver damage or even death, although some research shows that an HBV-infected individual without having symptoms has the potential to infect another individual and could lose their life [1,2,3].

Many mathematical models have been developed to study HBV and its characteristics by researchers from all over the world. For instance, HBV with control strategies and analysis with different age structures with population of New Zealand presented in Refs. [4, 5], control study of hepatitis B via vaccination [6], vaccination effects on HBV transmission presented in Ref. [7], for HBV disease a multi-group model presented in Ref. [8], HBV model with cost-effective analysis presented in Ref. [9], significance of vaccination on HBV transmission analyzed via a mathematical model in Ref. [10], HBV model with diffusion and delay studied in Ref. [11] and model with time delay studied in Ref. [12], the HBV transmission dynamics and its control via a mathematical model studied in Ref. [13], migration effect on HBV transmission presented in Ref. [14], and an HBV model with three controls discussed in Ref. [15]. The above-described HBV models are in the frame of integer-order derivative. As the models with ordinary order do not provide the memory and the genetic properties involved in the fractional-order models. Therefore, in recent years, researchers have given more attention to fractional-order derivatives for mathematical modeling in mathematical biology because the fractional derivatives reflect memory effects and genetic properties in models.

Fractional Calculus (FC) is developing as a robust tool in applied mathematics to solve real-world issues. The fractional-order (FO) models are very suitable for understanding the memory effect and inherited properties than integer-order models. In addition, the integer-order derivative does not examine the dynamics between two different points in the real-world description. Several non-local FO differentiation concepts have been proposed in the existing article to address the limitations of classical local differentiation. The fractional derivatives such as Caputo [16], Caputo-Fabrizio [17] and Atangana–Baleanu (AB) [18] are receiving much attention from the researchers. Because of its Mittag-Leffler (ML) memory and crossover properties for mean-square displacement, the ABC derivative offers an excellent description. In recent years, the Atangana–Baleanu derivative has been applied to the epidemiological model extensively [19,20,21,22,23,24,25]. Several other recent research on application of fractional derivatives to the non-linear models from different engineering and science fields have been studied in Refs. [26,27,28,29,30,31,32]. A novel coronavirus model is investigated with ABC fractional derivative in Ref. [26]. The transmission of Hookworm infection is studied via the Caputo operator in Ref. [28]. In Ref. [33], COVID-19 model is investigated through Caputo fractional derivative. A pine wilt disease model is examined under the Caputo fractional operator in Ref. [34]. In Ref. [35], the authors studied a combined co-infection model of HIV-COVID-19 through ABC fractional derivative. In Ref. [36], wastewater treatment model is examined with Caputo fractional derivative. Some fractional models regarding HBV can be found in the existing literature. A FO HBV model with optimal control is investigated in Ref. [37], and optimal control on HBV model with vaccination, treatment is discussed in Ref. [38]. Using the ABC operator, the HBV model with hospitalized class is studied in Ref. [39] and HBV model with treatment is studied in Ref. [40]. HBV model with hospitalization using Caputo derivative is studied in Ref. [41]. A FO HBV model with antibody immune response is discussed in Ref. [42]. Recently, an HBV model with asymptomatic carriers was studied using Caputo derivative in Ref. [43].

Thus, inspired by recent studies, we consider a FO HBV model [43] with Caputo and ABC derivatives. We study the dynamics of the proposed model using two different numerical techniques. The proposed work is divided as follows: some basic preliminaries of FC are presented in Sect. 2. The FO HBV model in the frame of Caputo and ABC derivatives along with some mathematical results are presented in Sect. 3. The existence and uniqueness of solutions of FO model are presented in Sect. 4. The numerical schemes and obtained numerical results are shown in Sect. 5. A variable-order fractional network of the HBV model is proposed in Sect. 6, also the numerical simulation is presented for the model. Lastly, the outcomes are discussed in Sect. 7.

2 Basic preliminaries of FC

Here, we present a quick glance of some basic concept of FC [16, 18].

Definition 2.1

The Caputo derivative of a function $\chi (t)$ for order p is given by

$$\begin{aligned} {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\chi (t)=\frac{1}{\Gamma (1-\theta )}\int _{0}^{t}(t-\upsilon )^{-p}\chi '(\upsilon )d\upsilon , \, 0<p<1. \end{aligned}$$

(2.1)

Definition 2.2

The Atangana–Baleanu derivative in Caputo sense of a function $\chi (t)$ is given by

$$\begin{aligned} {}_0^{\mathcal {ABC}}{\mathfrak {D}}_t^p\chi (t)=\frac{{\mathfrak {J}}(p)}{1-p}\int _{0}^{t}{\mathcal {E}}_p\Big [-p\frac{(t-\upsilon )^p}{1-p}\Big ]\chi '(\upsilon )d\upsilon , \end{aligned}$$

(2.2)

where ${\mathfrak {J}}(p)$ is the normalization function satisfying ${\mathfrak {J}}(0)={\mathfrak {J}}(1)=1$, and ${\mathcal {E}}_{p}$ is ML function

$$\begin{aligned} {\mathcal {E}}_p(z)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (pk+1)}, \,\,\,p>0. \end{aligned}$$

(2.3)

The corresponding fractional integral of ABC derivative is given by

$$\begin{aligned} {}_0^{\mathcal {AB}}{\mathcal {I}}_t^p\chi (t)=\frac{1-p}{{\mathfrak {J}}(p)}\chi (t)+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\chi (\upsilon )(t-\upsilon )^{p-1}d\upsilon . \end{aligned}$$

(2.4)

Definition 2.3

The Laplace transform of the AB fractional derivative in the Caputo sense ${}_0^{\mathcal {ABC}}{\mathfrak {D}}_t^p\chi (t)$ has the form

$$\begin{aligned} {\mathcal {L}}\{{}_0^{\mathcal {ABC}}{\mathfrak {D}}_t^p\chi (t)\}(s)=\frac{{\mathfrak {J}}(p)}{1-p}\frac{s^p{\mathcal {L}}\{\chi (t)\}(s)-s^{p-1}\chi (0)}{s^p+\frac{p}{1-p}}. \end{aligned}$$

(2.5)

3 Fractional HBV model

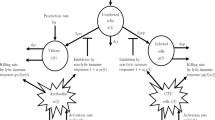
Here, we have considered an HBV model with class of asymptomatic carriers [43]. In the model, total population represented by ${\mathcal {N}}(t)$ divided into six classes, susceptible individuals ($\mathtt {S}(t)$), exposed population ($\mathtt {E}(t)$), acute infected population ($\mathtt {A}(t)$), asymptomatic carrier ($\mathtt {A}_c(t)$), chronic infected individuals ($\mathtt {C}(t)$) and the recovered population ($\mathtt {R}(t))$, so ${\mathcal {N}}(t)=\mathtt {S}(t)+\mathtt {E}(t)+\mathtt {A}(t)+\mathtt {A}_c(t)+\mathtt {C}(t)+\mathtt {R}(t)$. Initially, the HBV model in frame of Caputo derivative is given as follows:

$$\begin{aligned} \begin{aligned} {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\mathtt {S}(t)=&\Lambda _1-\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}-\mu _1\mathtt {S},\\ {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\mathtt {E}(t)=&\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}-(\mu _1+\psi _1)\mathtt {E},\\ {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\mathtt {A}(t)=&\psi _1\theta _1\mathtt {E}-(\mu _1+\gamma _1+\eta _1+\kappa _1)\mathtt {A},\\ {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\mathtt {A}_c(t)=&\psi _1(1-\theta _1)\mathtt {E}-(\mu _1+\tau _1+\nu _1)\mathtt {A}_c,\\ {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\mathtt {C}(t)=&\eta _1\mathtt {A}+\tau _1\mathtt {A}_c-(\mu _1+\varepsilon _1+\sigma _1)\mathtt {C},\\ {}_0^{\mathcal {C}}{\mathfrak {D}}_t^p\mathtt {R}(t)=&\kappa _1\mathtt {A}+\sigma _1\mathtt {C}+\nu _1\mathtt {A}_c-\mu _1\mathtt {R}. \end{aligned} \end{aligned}$$

(3.1)

Further, the HBV model in frame of ABC derivative is given as follows:

$$\begin{aligned} \begin{aligned} {}_0^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {S}(t)=&\Lambda _1-\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}-\mu _1\mathtt {S},\\ {}_0^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {E}(t)=&\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}-(\mu _1+\psi _1)\mathtt {E},\\ {}_0^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {A}(t)=&\psi _1\theta _1\mathtt {E}-(\mu _1+\gamma _1+\eta _1+\kappa _1)\mathtt {A},\\ {}_0^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {A}_c(t)=&\psi _1(1-\theta _1)\mathtt {E}-(\mu _1+\tau _1+\nu _1)\mathtt {A}_c,\\ {}_0^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {C}(t)=&\eta _1\mathtt {A}+\tau _1\mathtt {A}_c-(\mu _1+\varepsilon _1+\sigma _1)\mathtt {C},\\ {}_0^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {R}(t)=&\kappa _1\mathtt {A}+\sigma _1\mathtt {C}+\nu _1\mathtt {A}_c-\mu _1\mathtt {R}, \end{aligned} \end{aligned}$$

(3.2)

where the initial conditions $\mathtt {S}(0)\ge 0,\mathtt {E}(0)\ge 0, \mathtt {A}(0)\ge 0, \mathtt {A}_c(0)\ge 0, \mathtt {C}(0)\ge 0$ and $\mathtt {R}(0)\ge 0,$ and the parameter $\Lambda _1$ is birth rate of the susceptible individuals. The effective contact rate and natural fatality rate are described by the parameters $\beta _1$ and $\mu _1$, respectively. The exposed individuals are infected at the speed $\psi _1(1-\theta _1)$, where the number of individual move to class $\mathtt {A}$ at the rate of $\psi _1\theta _1$ while a portion of $\psi _1(1-\theta _1)$ enters $\mathtt {A}_c$ and become asymptomatically infected. Individuals in acute and asymptomatic classes become carriers at rates of $\eta _1$ and $\tau _1$, respectively. The recovery rate of acute, asymptomatic and the carriers individuals are denoted by $\kappa _1, \nu _1$ and $\sigma _1$, respectively. The death rate because of disease at acute and chronic classes are represented by $\gamma _1$ and $\varepsilon _1$ respectively. The coefficient of asymptomatic and carriers individuals are shown by $\phi _1$ (the infectiousness of asymptomatic relative to acute infections) and $\epsilon _1$ (the infectiousness of carriers relative to acute infections), respectively.

3.1 Invariant region

Lemma 3.1

The closed set

$$\begin{aligned} \Theta =&\Big \{\big (\mathtt {S}(t),\mathtt {E}(t),\mathtt {A}(t),\mathtt {A}_c(t),\mathtt {C}(t),\mathtt {R}(t)\big )\in \mathrm {R}_+^6: \mathtt {S}(t) \nonumber \\&+\mathtt {E}(t)+\mathtt {A}(t)+\mathtt {A}_c(t)+\mathtt {C}(t)+\mathtt {R}(t)\le \frac{\Lambda _1}{\mu _1} \Big \}, \end{aligned}$$

(3.3)

is positively invariant for the ABC fractional model (3.2).

Proof

The dynamics of the total population is obtained by summing all equations of the model (3.2)

$$\begin{aligned}&{}^\mathcal {ABC}{\mathfrak {D}}_t^p{\mathcal {N}}(t)={}^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {S}(t)+{}^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {E}(t) +{}^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {A}(t)\nonumber \\&+{}^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {A}_c(t) +{}^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {C}(t)+{}^\mathcal {ABC}{\mathfrak {D}}_t^p\mathtt {R}(t). \end{aligned}$$

(3.4)

Hence,

$$\begin{aligned} {}^\mathcal {ABC}{\mathfrak {D}}_t^p{\mathcal {N}}(t)= & {} \Lambda _1-\mu _1{\mathcal {N}}(t)\nonumber \\&-\gamma _1\mathtt {A}-\varepsilon _1\mathtt {C}\le \Lambda _1-\mu _1{\mathcal {N}}(t), \end{aligned}$$

(3.5)

employing the Laplace transform on Eq. (3.5), we have

$$\begin{aligned} {\mathcal {L}}[{}^\mathcal {ABC}{\mathfrak {D}}_t^p{\mathcal {N}}(t)+\mu _1{\mathcal {N}}(t)]\le {\mathcal {L}}[\Lambda _1], \end{aligned}$$

after simplification we get

$$\begin{aligned} \begin{aligned} {\mathcal {N}}(t)\le&\Big (\frac{{\mathfrak {J}}(p)}{{\mathfrak {J}}(p)+(1-p)\mu _1}{\mathcal {N}}(0)\\&+\frac{(1-p)\Lambda _1}{{\mathfrak {J}}(p)+(1-p)\mu _1}\Big ){\mathcal {E}}_{p,1}(-\beta ^*t^p)\\&+\frac{p\Lambda _1}{{\mathfrak {J}}(p)+(1-p)\mu _1}{\mathcal {E}}_{p,p+1}(-\beta ^*t^p), \end{aligned} \end{aligned}$$

(3.6)

where $\beta ^*=\frac{p\mu _1}{{\mathfrak {J}}(p)+(1-p)\mu _1}$ and ${\mathcal {E}}_{p,q}$ is two-parameter ML function and describe as

$${\mathcal {E}}_{p,q}(z)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (kp+q)}.$$

Due to asymptotic nature of ML function, we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty }{\mathcal {N}}(t)\le \frac{\Lambda _1}{\mu _1}, \forall \, t>0. \end{aligned}$$

(3.7)

Thus, the entire solutions of the proposed model for the initial conditions belonging to $\Theta$ stay in $\Theta$ for every $t>0$. Hence, $\Theta$ is a positively invariant region and will attract all the solutions in $\mathrm {R}_6^+$. $\square$

3.2 Equilibrium point and basic reproduction number

For the model (3.2), there exist two equilibrium points, disease free equilibrium point (DFE) ${\bar{\xi }}_0$ and the endemic equilibrium (EE) ${\bar{\xi }}_1$. The DFE point is given as

$${\bar{\xi }}_0=(\mathtt {S}_0,\mathtt {E}_0,\mathtt {A}_0,{\mathtt {A}_c}_0, \mathtt {C}_0,\mathtt {R}_0)=\left( \frac{\Lambda _1}{\mu _1},0,0,0,0,0\right) .$$

The basic reproduction number ${\mathfrak {R}}_0$ of the proposed model (3.2) is achieved using next-generation matrix technique [44]. For the reproduction number ${\mathfrak {R}}_0$, we use [44] and obtain the matrices $F$ and $V$ as follows:

$$\begin{aligned} F =&\begin{pmatrix} 0 &{}\frac{\beta _1\Lambda _1}{\mu _1}&{} \,\,\frac{\beta _1\phi _1\Lambda _1}{\mu _1} &{} \,\,\frac{\beta _1\epsilon _1\Lambda _1}{\mu _1}\\ 0 &{} 0 &{}\,\, 0 &{} \,\,\,0\\ 0 &{} 0 &{}\,\, 0 &{} \,\,\,0 \\ 0 &{} 0 &{}\,\, 0 &{} \,\,\,0 \end{pmatrix} ,\nonumber \\ V =&\begin{pmatrix} m_1 &{} \,\,\,0 &{} \,\,\,0 &{}\,\,\, 0\\ -\theta _1\psi _1&{} \,\,\,m_2&{} \,\,\,0 &{} \,\,\,0\\ -(1-\theta _1)\psi _1 &{} \,\,\,0 &{}\,\,\, m_3 &{} \,\,\,0 \\ 0 &{} \,\,\,-\eta _1 &{}\,\,\, -\tau _1 &{} \,\,\,m_4 \end{pmatrix}. \end{aligned}$$

(3.8)

Therefore, using the $\rho ( F V ^{-1})$, we obtained the basic reproduction number for the model (3.2)

$$\begin{aligned} {\mathfrak {R}}_0= & {} \frac{\beta _1\theta _1\Lambda _1\psi _1}{\mu _1 m_1m_2}+\frac{\beta _1(1-\theta _1)\Lambda _1\phi _1\psi _1}{\mu _1 m_1m_3}\nonumber \\&+\frac{\beta _1\eta _1\theta _1\Lambda _1\psi _1\epsilon _1}{\mu _1 m_1m_2m_4}+\frac{\beta _1(1-\theta _1)\Lambda _1\tau _1\psi _1\epsilon _1}{\mu _1 m_1m_3m_4},\nonumber \\ \end{aligned}$$

(3.9)

where $m_1=(\mu _1+\psi _1), m_2=(\mu _1+\gamma _1+\eta _1+\kappa _1), m_3=(\mu _1+\tau _1+\nu _1), m_4=(\mu _1+\varepsilon _1+\sigma _1)$.

3.3 Endemic equilibria

The EE point of the model (3.2) is given by ${\bar{\xi }}_1=(\mathtt {S}^*,\mathtt {E}^*,\mathtt {A}^*,\mathtt {A}_c^*,\mathtt {C}^*,\mathtt {R}^*),$ where

$$\begin{aligned} \begin{aligned} \mathtt {S}^*=&\frac{m_1\mathtt {E}^*}{\beta _1(\mathtt {A}^*+\phi _1\mathtt {A}_c^*+\epsilon _1\mathtt {C}^*)},\\ \mathtt {E}^*=&\frac{m_2\mathtt {A}^*}{\theta _1\psi _1},\\ \mathtt {A}_c^*=&\frac{\mathtt {E}^*(1-\theta _1)\psi _1}{m_3},\\ \mathtt {C}^*=&\frac{\eta _1\mathtt {A}^*+\tau _1\mathtt {A}_c^*}{m_4},\\ \mathtt {R}^*=&\frac{\kappa _1\mathtt {A}^*+\sigma _1\mathtt {C}^*+\nu _1\mathtt {A}_c^*}{\mu _1}, \end{aligned} \end{aligned}$$

using these in first equation of model (3.2), we get

$$a_0\mathtt {A}^*+a_1=0,$$

where

$$\begin{aligned} \begin{aligned} a_0=&\beta _1m_1m_2(\theta _1m_3(m_4+\eta _1\epsilon _1)\\&+(1-\theta _1)m_2(m_4\phi _1+\tau _1\epsilon _1)),\\ a_1=&\mu _1m_1m_2m_3m_4\theta _1(1-{\mathfrak {R}}_0). \end{aligned} \end{aligned}$$

(3.10)

Lemma 3.2

The proposed HBV model (3.2) has a unique positive EE provided ${\mathfrak {R}}_0 > 1.$

4 Existence and uniqueness of the solution

Here, we will examine the existence of unique solution of fractional-order model (3.2). Assume that $H (J)$ is a Banach space containing real-valued continuous functions defined on the interval $J=[0,T]$ with sup norm and ${\mathbb {P}}= H (J)\times H (J)\times H (J)\times H (J)\times H (J)\times H (J)$ with the norm $\Vert (\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\Vert =\Vert \mathtt {S}\Vert +\Vert \mathtt {E}\Vert +\Vert \mathtt {A}\Vert +\Vert \mathtt {A}_c\Vert +\Vert \mathtt {C}\Vert +\Vert \mathtt {R}\Vert$, where $\Vert \mathtt {S}\Vert =\sup _{t\in J}\vert \mathtt {S}(t)\vert , \Vert \mathtt {E}\Vert =\sup _{t\in J}\vert \mathtt {E}(t)\vert ,\Vert \mathtt {A}\Vert =\sup _{t\in J}\vert \mathtt {A}(t)\vert , \Vert \mathtt {A}_c\Vert =\sup _{t\in J}\vert \mathtt {A}_c(t)\vert ,\Vert \mathtt {C}\Vert =\sup _{t\in J}\vert \mathtt {C}(t)\vert , \Vert \mathtt {R}\Vert =\sup _{t\in J}\vert \mathtt {R}(t)\vert$. Employing the AB fractional integral on both-sides of Eq. (3.2), we have

$$\begin{aligned} \begin{aligned}&\mathtt {S}(t)-\mathtt {S}(0)= {}_0^\mathcal {AB}{\mathcal {I}}_t^p\{\Lambda _1-\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}-\mu _1\mathtt {S}\},\\&\mathtt {E}(t)-\mathtt {E}(0)= {}_0^\mathcal {AB}{\mathcal {I}}_t^p\{\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}-(\mu _1+\psi _1)\mathtt {E}\},\\&\mathtt {A}(t)-\mathtt {A}(0)= {}_0^\mathcal {AB}{\mathcal {I}}_t^p\{\psi _1\theta _1\mathtt {E}-(\mu _1+\gamma _1+\eta _1+\kappa _1)\mathtt {A}\},\\&\mathtt {A}_c(t)-\mathtt {A}_c(0)={}_0^\mathcal {AB}{\mathcal {I}}_t^p\{\psi _1(1-\theta _1)\mathtt {E}-(\mu _1+\tau _1+\nu _1)\mathtt {A}_c\},\\&\mathtt {C}(t)-\mathtt {C}(0)={}_0^\mathcal {AB}{\mathcal {I}}_t^p\{\eta _1\mathtt {A}+\tau \mathtt {A}_c-(\mu _1+\varepsilon _1+\sigma _1)\mathtt {C}\},\\&\mathtt {R}(t)-\mathtt {R}(0)={}_0^\mathcal {AB}{\mathcal {I}}_t^p\{\kappa _1\mathtt {A}+\sigma _1\mathtt {C}+\nu _1\mathtt {A}_c-\mu _1\mathtt {R}\}. \end{aligned} \end{aligned}$$

(4.1)

Now, using the definition (2.4) on above equation, we get

$$\begin{aligned} \begin{aligned} \mathtt {S}(t)-\mathtt {S}(0)=&\frac{1-p}{{\mathfrak {J}}(p)}\varXi _1(t,\mathtt {S}(t))\\&\!+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\!(t-\upsilon )^{p-1}\varXi _1(\upsilon ,\mathtt {S}(\upsilon ))d\upsilon ,\\ \mathtt {E}(t)-\mathtt {E}(0)=&\frac{1-p}{{\mathfrak {J}}(p)}\varXi _2(t,\mathtt {E}(t))\\&\!+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\!(t-\upsilon )^{p-1}\varXi _2(\upsilon ,\mathtt {E}(\upsilon ))d\upsilon ,\\ \mathtt {A}(t)-\mathtt {A}(0)=&\frac{1-p}{{\mathfrak {J}}(p)}\varXi _3(t,\mathtt {A}(t))\\&\!+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\!(t-\upsilon )^{p-1}\varXi _3(\upsilon ,\mathtt {A}(\upsilon ))d\upsilon ,\\ \mathtt {A}_c(t)-\mathtt {A}_c(0)=&\frac{1-p}{{\mathfrak {J}}(p)}\varXi _4(t,\mathtt {A}_c(t))\\&\!+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\!(t-\upsilon )^{p-1}\varXi _4(\upsilon ,\mathtt {A}_c(\upsilon ))d\upsilon ,\\ \mathtt {C}(t)-\mathtt {C}(0)=&\frac{1-p}{{\mathfrak {J}}(p)}\varXi _5(t,\mathtt {C}(t))\\&\!+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\!(t-\upsilon )^{p-1}\varXi _5(\upsilon ,\mathtt {C}(\upsilon ))d\upsilon ,\\ \mathtt {R}(t)-\mathtt {R}(0)=&\frac{1-p}{{\mathfrak {J}}(p)}\varXi _6(t,\mathtt {R}(t))\\&\!+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\!(t-\upsilon )^{p-1}\varXi _6(\upsilon ,\mathtt {R}(\upsilon ))d\upsilon , \end{aligned} \end{aligned}$$

(4.2)

where

$$\begin{aligned} \varXi _1(t,\mathtt {S}(t))=\,&\Lambda _1-\beta _1(\mathtt {A}(t)+\phi _1\mathtt {A}_c(t)\nonumber \\ {}&+\epsilon _1\mathtt {C}(t))\mathtt {S}(t)-\mu _1\mathtt {S}(t),\nonumber \\ \varXi _2(t,\mathtt {E}(t))=\,&\beta _1(\mathtt {A}(t)+\phi _1\mathtt {A}_c(t)\nonumber \\&+\epsilon _1\mathtt {C}(t))\mathtt {S}(t)-(\mu _1+\psi _1)\mathtt {E}(t),\nonumber \\ \varXi _3(t,\mathtt {A}(t))=\,&\psi _1\theta _1\mathtt {E}(t)-(\mu _1+\gamma _1+\eta _1+\kappa _1)\mathtt {A}(t),\nonumber \\ \varXi _4(t,\mathtt {A}_c(t))=\,&\psi _1(1-\theta _1)\mathtt {E}(t)-(\mu _1+\tau _1+\nu _1)\mathtt {A}_c(t),\nonumber \\ \varXi _5(t,\mathtt {C}(t))=\,&\eta _1\mathtt {A}(t)+\tau _1\mathtt {A}_c(t)-(\mu _1+\varepsilon _1+\sigma _1)\mathtt {C}(t),\nonumber \\ \varXi _6(t,\mathtt {R}(t))=\,&\kappa _1\mathtt {A}(t)+\sigma _1\mathtt {C}(t)+\nu _1\mathtt {A}_c(t)-\mu _1\mathtt {R}(t). \end{aligned}$$

(4.3)

The expressions $\varXi _1(t,\mathtt {S}(t)),\varXi _2(t,\mathtt {E}(t)),\varXi _3(t,\mathtt {A}(t)),\varXi _4(t,\mathtt {A}_c(t)),\varXi _5(t,\mathtt {C}(t))$ and $\varXi _6(t,\mathtt {R}(t))$ are said to satisfy the Lipschitz condition if and only if $\mathtt {S}(t),\mathtt {E}(t),\mathtt {A}(t),\mathtt {A}_c(t),\mathtt {C}(t)$ and $\mathtt {R}(t)$ have an upper bound. Let $\mathtt {S}(t)$ and $\mathtt {S}_1(t)$ be two functions, then we get

$$\begin{aligned} \begin{aligned}&\Vert \varXi _1(t,\mathtt {S})-\varXi _1(t,\mathtt {S}_{1})\Vert \\&\quad =\Vert -\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})(\mathtt {S}-\mathtt {S}_1)-\mu _1(\mathtt {S}-\mathtt {S}_1)\Vert ,\\&\quad =\Vert -(\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})+\mu _1)(\mathtt {S}-\mathtt {S}_1)\Vert ,\\&\quad \le \Vert -(\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})+\mu _1)\Vert \Vert \mathtt {S}-\mathtt {S}_1\Vert \\&\quad \le \varrho _1\Vert \mathtt {S}-\mathtt {S}_1\Vert , \end{aligned} \end{aligned}$$

(4.4)

where $\varrho _1=\Vert -(\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})+\mu _1)\Vert$. Therefore, we have

$$\begin{aligned} \Vert \varXi _1(t,\mathtt {S})-\varXi _1(t,\mathtt {S}_{1})\Vert \le \varrho _1\Vert \mathtt {S}(t)-\mathtt {S}_{1}(t)\Vert . \end{aligned}$$

(4.5)

In a similar manner, one can obtain

$$\begin{aligned} \begin{aligned} \Vert \varXi _2(t,\mathtt {E})-\varXi _2(t,\mathtt {E}_1)&\Vert \le \varrho _2\Vert \mathtt {E}(t)-\mathtt {E}_1(t)\Vert ,\\ \Vert \varXi _3(t,\mathtt {A})-\varXi _3(t,\mathtt {A}_1)&\Vert \le \varrho _3\Vert \mathtt {A}(t)-\mathrm {A}_1(t)\Vert ,\\ \Vert \varXi _4(t,\mathtt {A}_c)-\varXi _4(t,{\mathtt {A}_c}_1)&\Vert \le \varrho _4\Vert \mathtt {A}_c(t)-{\mathtt {A}_c}_1(t)\Vert ,\\ \Vert \varXi _5(t,\mathtt {C})-\varXi _5(t,\mathtt {C}_1)&\Vert \le \varrho _5\Vert \mathtt {C}(t)-\mathtt {C}_1(t)\Vert ,\\ \Vert \varXi _6(t,\mathtt {R})-\varXi _6(t,\mathtt {R}_1)&\Vert \le \varrho _6\Vert \mathtt {R}(t)-\mathtt {R}_1(t)\Vert . \end{aligned} \end{aligned}$$

(4.6)

Thus, the Lipschitz condition is satisfied for all the six functions $\varXi _1,\varXi _2,\varXi _3,\varXi _4,\varXi _5$ and $\varXi _6$ where $\varrho _1, \varrho _2 , \varrho _3, \varrho _4,\varrho _5$ and $\varrho _6$ are the corresponding Lipschitz constants. Using the recursive principle, the Eq. (4.2) becomes

$$\begin{aligned} \mathtt {S}_{n}(t)= & {} \frac{1-p}{{\mathfrak {J}}(p)}\varXi _1(t,\mathtt {S}_{n-1})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\varXi _1(\upsilon ,\mathtt {S}_{{n-1}})d\upsilon +\mathtt {S}(0),\nonumber \\ \mathtt {E}_{n}(t)= & {} \frac{1-p}{{\mathfrak {J}}(p)}\varXi _2(t,\mathtt {E}_{n-1})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\varXi _2(\upsilon ,\mathtt {E}_{n-1})d\upsilon +\mathtt {E}(0),\nonumber \\ \mathtt {A}_n(t)= & {} \frac{1-p}{{\mathfrak {J}}(p)}\varXi _3(t,\mathtt {A}_{n-1})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\varXi _3(\upsilon ,\mathtt {A}_{{n-1}})d\upsilon +\mathtt {A}(0),\nonumber \\ {\mathtt {A}_c}_n(t)= & {} \frac{1-p}{{\mathfrak {J}}(p)}\varXi _4(t,{\mathtt {A}_c}_{n-1})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\varXi _4(\upsilon ,{\mathtt {A}_c}_{{n-1}})d\upsilon +\mathtt {A}_c(0),\nonumber \\ \mathtt {C}_n(t)G= & {} \frac{1-p}{{\mathfrak {J}}(p)}\varXi _5(t,\mathtt {C}_{n-1})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\varXi _5(\upsilon ,\mathtt {C}_{{n-1}})d\upsilon +\mathtt {C}(0),\nonumber \\ \mathtt {R}_n(t)= & {} \frac{1-p}{{\mathfrak {J}}(p)}\varXi _6(t,\mathtt {R}_{n-1})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\varXi _6(\upsilon ,\mathtt {R}_{{n-1}})d\upsilon +\mathtt {R}(0),\nonumber \\ \end{aligned}$$

(4.7)

where the initial conditions are defined as follows:

$$\begin{aligned}&\mathtt {S}_0(t)=\mathtt {S}(0),\, \mathtt {E}_0(t)=\mathtt {E}(0), \,\mathtt {A}_0(t)=\mathtt {A}(0),\\&\quad \,{\mathtt {A}_c}_0(t)=\mathtt {A}_c(0),\,\mathtt {C}_0(t)=\mathtt {C}(0),\,\mathtt {R}_0(t)=\mathtt {R}(0). \end{aligned}$$

Taking the difference of successive terms, we obtained the following expression:

$$\begin{aligned} \Psi _{\mathtt {S},n}(t)=\,&\mathtt {S}_{n}(t)-\mathtt {S}_{n-1}(t)\nonumber \\&=\frac{1-p}{{\mathfrak {J}}(p)}(\varXi _1(t,\mathtt {S}_{n-1})-\varXi _1(t,\mathtt {S}_{n-2}))\nonumber \\&\quad +\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\nonumber \\&\quad \big (\varXi _1(\upsilon ,\mathtt {S}_{n-1})-\varXi _1(\upsilon ,\mathtt {S}_{n-2})\big )d\upsilon ,\nonumber \\ \Psi _{\mathtt {E},n}(t)=\,&\mathtt {E}_{n}(t)-\mathtt {E}_{n-1}(t)\nonumber \\&=\frac{1-p}{{\mathfrak {J}}(p)}(\varXi _2(t,\mathtt {E}_{n-1})-\varXi _2(t,\mathtt {E}_{n-2}))\nonumber \\&\quad +\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\nonumber \\&\quad \big (\varXi _2(\upsilon ,\mathtt {E}_{n-1})-\varXi _2(\upsilon ,\mathtt {E}_{n-2})\big )d\upsilon ,\nonumber \\ \Psi _{\mathtt {A},n}(t)=\,&\mathtt {A}_n(t)-\mathtt {A}_{n-1}(t)\nonumber \\&=\frac{1-p}{{\mathfrak {J}}(p)}(\varXi _3(t,\mathtt {A}_{n-1})-\varXi _3(t,\mathtt {A}_{n-2}))\nonumber \\&\quad +\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}((t-\upsilon )^{p-1}\nonumber \\&\quad \big (\varXi _3(\upsilon ,\mathtt {A}_{n-1})-\varXi _3(\upsilon ,\mathtt {A}_{n-2})\big )d\upsilon ,\nonumber \\ \Psi _{\mathtt {A}_c,n}(t)=\,&{\mathtt {A}_c}_n(t)-{\mathtt {A}_c}_{n-1}(t)\nonumber \\&=\frac{1-p}{{\mathfrak {J}}(p)}(\varXi _4(t,{\mathtt {A}_c}_{n-1})-\varXi _4(t,{\mathtt {A}_c}_{n-2}))\nonumber \\&\quad +\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\nonumber \\&\quad \big (\varXi _4(\upsilon ,{\mathtt {A}_c}_{n-1})-\varXi _4(\upsilon ,{\mathtt {A}_c}_{n-2})\big )d\upsilon ,\nonumber \\ \Psi _{\mathtt {C},n}(t)=\,&\mathtt {C}_n(t)-\mathtt {C}_{n-1}(t)\nonumber \\&=\frac{1-p}{{\mathfrak {J}}(p)}(\varXi _5(t,\mathtt {C}_{n-1})-\varXi _5(t,\mathtt {C}_{n-2}))\nonumber \\&\quad +\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\nonumber \\&\quad \big (\varXi _5(\upsilon ,\mathtt {C}_{n-1})-\varXi _5(\upsilon ,\mathtt {C}_{n-2})\big )d\upsilon ,\nonumber \\ \Psi _{\mathtt {R},n}(t)=\,&\mathtt {R}_n(t)-\mathtt {R}_{n-1}(t)\nonumber \\&=\frac{1-p}{{\mathfrak {J}}(p)}(\varXi _6(t,\mathtt {R}_{n-1})-\varXi _6(t,\mathtt {R}_{n-2}))\nonumber \\&\quad +\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\nonumber \\&\quad \big (\varXi _6(\upsilon ,\mathtt {R}_{n-1})-\varXi _6(\upsilon ,\mathtt {R}_{n-2})\big )d\upsilon . \end{aligned}$$

(4.8)

It is worth to be notice that $\mathtt {S}_{n}(t)=\sum _{i=0}^{n}{\Psi }_{\mathtt {S},i}(t),\,\mathtt {E}_{n}(t)=\sum _{i=0}^{n}{\Psi }_{\mathtt {E},i}(t),\,\mathtt {A}_{n}(t)=\sum _{i=0}^{n}{\Psi }_{\mathtt {A},i}(t),\,{\mathtt {A}_c}_{n}(t)=\sum _{i=0}^{n}{\Psi }_{\mathtt {A}_c,i}(t),\,\mathtt {C}_{n}(t)=\sum _{i=0}^{n}{\Psi }_{\mathtt {C},i}(t),$ and $\mathtt {R}_{n}(t)=\sum _{i=0}^{n}{\Psi }_{\mathtt {R},i}(t).$ In addition, using Eqs. (4.5)–(4.6) and taking into consideration that $\Psi _{\mathtt {S},n-1}(t)=\mathtt {S}_{n-1}(t)-\mathtt {S}_{n-2}(t),\,\Psi _{\mathtt {E},n-1}(t)=\mathtt {E}_{n-1}(t)-\mathtt {E}_{n-2}(t),\,\Psi _{\mathtt {A},n-1}(t)=\mathtt {A}_{n-1}(t)-\mathtt {A}_{n-2}(t),\Psi _{\mathtt {A}_c,n-1}(t)={\mathtt {A}_c}_{n-1}(t)-{\mathtt {A}_c}_{n-2}(t),\,\Psi _{\mathtt {C},n-1}(t)=\mathtt {C}_{n-1}(t)-\mathtt {C}_{n-2}(t),\,\Psi _{\mathtt {R},n-1}(t)=\mathtt {R}_{n-1}(t)-\mathtt {R}_{n-2}(t),$ we have the following:

$$\begin{aligned} \Vert \Psi _{\mathtt {S},n}(t)\Vert\le & {} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _1\Vert \Psi _{\mathtt {S},n-1}(t)\Vert \nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _1\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\Vert \Psi _{\mathtt {S},n-1}(\upsilon )\Vert d\upsilon ,\nonumber \\ \Vert \Psi _{\mathtt {E},n}(t)\Vert\le & {} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _2\Vert \Psi _{\mathtt {E},n-1}(t)\Vert \nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _2\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\Vert \Psi _{\mathtt {E},n-1}(\upsilon )\Vert d\upsilon ,\nonumber \\ \Vert \Psi _{\mathtt {A},n}(t)\Vert\le & {} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _3\Vert \Psi _{\mathtt {A},n-1}(t)\Vert \nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _3\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\Vert \Psi _{\mathtt {A},n-1}(\upsilon )\Vert d\upsilon ,\nonumber \\ \Vert \Psi _{\mathtt {A}_c,n}(t)\Vert\le & {} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _4\Vert \Psi _{\mathtt {A}_c,n-1}(t)\Vert \nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _4\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\Vert \Psi _{\mathtt {A}_c,n-1}(\upsilon )\Vert d\upsilon ,\nonumber \\ \Vert \Psi _{\mathtt {C},n}(t)\Vert\le & {} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _5\Vert \Psi _{\mathtt {C},n-1}(t)\Vert \nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _5\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\Vert \Psi _{\mathtt {C},n-1}(\upsilon )\Vert d\upsilon ,\nonumber \\ \Vert \Psi _{\mathtt {R},n}(t)\Vert\le & {} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _6\Vert \Psi _{\mathtt {R},n-1}(t)\Vert \nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _6\displaystyle \int _{0}^{t}(t-\upsilon )^{p-1}\Vert \Psi _{\mathtt {R},n-1}(\upsilon )\Vert d\upsilon .\nonumber \\ \end{aligned}$$

(4.9)

Theorem 4.1

The HBV model (3.2) has a unique solution for $t\in [0,T]$, if the following condition holds:

$$\begin{aligned} \frac{1-p}{{\mathfrak {J}}(p)}\varrho _i+\frac{1}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _ib^p< 1, \, i=1,2,\cdots ,6. \end{aligned}$$

(4.10)

Proof

It is evident that $\mathtt {S}(t), \mathtt {E}(t), \mathtt {A}(t), \mathtt {A}_c(t), \mathtt {C}(t)$ and $\mathtt {R}(t)$ are the bounded functions. Furthermore, we can identify from Eqs. (4.5)–(4.6), the expressions $\varXi _1, \varXi _2, \varXi _3, \varXi _4, \varXi _5$ and $\varXi _6$ satisfy the Lipschitz condition. Thus, utilizing Eq. (4.9) along with a recursive formula, we arrive at

$$\begin{aligned}&\Vert \Psi _{\mathtt {S},n}(t)\Vert \le \Vert \mathtt {S}(0)\Vert \Big [\frac{1-p}{{\mathfrak {J}}(p)}\varrho _1+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _1\Big ]^n,\nonumber \\&\Vert \Psi _{\mathtt {E},n}(t)\Vert \le \Vert \mathtt {E}(0)\Vert \Big [\frac{1-\nu }{{\mathfrak {J}}(p)}\varrho _2+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _2\Big ]^n,\nonumber \\&\Vert \Psi _{\mathtt {A},n}(t)\Vert \le \Vert \mathtt {A}(0)\Vert \Big [\frac{1-\nu }{{\mathfrak {J}}(\nu )}\varrho _3+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _3\Big ]^n,\nonumber \\&\Vert \Psi _{\mathtt {A}_c,n}(t)\Vert \le \Vert \mathtt {A}_c(0)\Vert \Big [\frac{1-p}{{\mathfrak {J}}(p)}\varrho _4+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _4\Big ]^n,\nonumber \\&\Vert \Psi _{\mathtt {C},n}(t)\Vert \le \Vert \mathtt {C}(0)\Vert \Big [\frac{1-p}{{\mathfrak {J}}(p)}\varrho _5+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _5\Big ]^n,\nonumber \\&\Vert \Psi _{\mathtt {R},n}(t)\Vert \le \Vert \mathtt {R}(0)\Vert \Big [\frac{1-p}{{\mathfrak {J}}(p)}\varrho _6+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _6\Big ]^n.\nonumber \\ \end{aligned}$$

(4.11)

Therefore, the above specified sequences exist and satisfy $\Vert \Psi _{\mathtt {S},n}(t)\Vert \rightarrow 0,\Vert \Psi _{\mathtt {E},n}(t)\Vert \rightarrow 0,\Vert \Psi _{\mathtt {A},n}(t)\Vert \rightarrow 0,\Vert \Psi _{\mathtt {A}_c,n}(t)\Vert \rightarrow 0,\Vert \Psi _{\mathtt {C},n}(t)\Vert \rightarrow 0,\Vert \Psi _{\mathtt {R},n}(t)\Vert \rightarrow 0,$ as $n\rightarrow \infty$. Moreover, from Eq. (4.11) and using the triangle inequality for any m, we get

$$\begin{aligned}&\Vert \mathtt {S}_{n+m}(t)-\mathtt {S}_n(t)\Vert \le \displaystyle \sum _{j=n+1}^{n+m}{\mathcal {T}}_1^j=\frac{{\mathcal {T}}_1^{n+1}-{\mathcal {T}}_1^{n+m+1}}{1-{\mathcal {T}}_1},\nonumber \\&\Vert \mathtt {E}_{n+m}(t)-\mathtt {E}_n(t)\Vert \le \displaystyle \sum _{j=n+1}^{n+m}{\mathcal {T}}_2^j=\frac{{\mathcal {T}}_2^{n+1}-{\mathcal {T}}_2^{n+m+1}}{1-{\mathcal {T}}_2},\nonumber \\&\Vert \mathtt {A}_{n+m}(t)-\mathtt {A}_n(t)\Vert \le \displaystyle \sum _{j=n+1}^{n+m}{\mathcal {T}}_3^j=\frac{{\mathcal {T}}_3^{n+1}-{\mathcal {T}}_3^{n+m+1}}{1-{\mathcal {T}}_3},\nonumber \\&\Vert {\mathtt {A}_c}_{n+m}(t)-{\mathtt {A}_c}_n(t)\Vert \le \displaystyle \sum _{j=n+1}^{n+m}{\mathcal {T}}_4^j=\frac{{\mathcal {T}}_4^{n+1}-{\mathcal {T}}_4^{n+m+1}}{1-{\mathcal {T}}_4},\nonumber \\&\Vert \mathtt {C}_{n+m}(t)-\mathtt {C}_n(t)\Vert \le \displaystyle \sum _{j=n+1}^{n+m}{\mathcal {T}}_5^j=\frac{{\mathcal {T}}_5^{n+1}-{\mathcal {T}}_5^{n+m+1}}{1-{\mathcal {T}}_5},\nonumber \\&\Vert \mathtt {R}_{n+m}(t)-\mathtt {R}_n(t)\Vert \le \displaystyle \sum _{j=n+1}^{n+m}{\mathcal {T}}_6^j=\frac{{\mathcal {T}}_6^{n+1}-{\mathcal {T}}_6^{n+m+1}}{1-{\mathcal {T}}_6},\nonumber \\ \end{aligned}$$

(4.12)

where ${\mathcal {T}}_i=\frac{1-p}{{\mathfrak {J}}(p)}\varrho _i+\frac{b^p}{{\mathfrak {J}}(p)\Gamma (p)}\varrho _i<1$ by hypothesis. Therefore $\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n, \mathtt {C}_n,\mathtt {R}_n$ are described as Cauchy sequences in the Banach space $H (J)$. Therefore, they are uniformly convergent as mentioned in [45]. Applying the limit theorem on Eq. (4.7) when $n\rightarrow \infty$ indicates that the limit of these sequences is the unique solution of the model (3.2). Finally, the existence of a unique solution for model (3.2) has been achieved under the condition (4.10). $\square$

5 Numerical techniques

It is familiar that biological models are generally non-linear and difficult to solve exactly. Hence, researchers are constantly looking for a suitable numerical approach to solve them. Now, we will present the solution of the mentioned fractional-order HBV model.

5.1 Numerical solution of the Caputo HBV model

Here, we present ABM method (see Diethelm & Ford [46,47,48] for more details on the ABM scheme and its convergence) to the approximate solution of the proposed Caputo HBV model. Following from Refs. [46,47,48], setting $h=\frac{T}{\mathrm {N}},\, t_n=nh,n=0,1,2,\ldots ,\mathrm {N}$, the model solution can be written as follows:

$$\begin{aligned} \mathtt {S}_{n+1}= & {} \mathtt {S}(0)+\dfrac{h^{p}}{\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_1(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{h^p}{\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}{\hat{d}}_{j,n+1}{\mathcal {G}}_1(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {E}_{n+1}= & {} \mathtt {E}(0)+\dfrac{h^{p}}{\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_2(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{h^p}{\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}{\hat{d}}_{j,n+1}{\mathcal {G}}_2(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {A}_{n+1}= & {} \mathtt {A}(0)+\dfrac{h^{p}}{\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_3(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{h^p}{\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}{\hat{d}}_{j,n+1}{\mathcal {G}}_3(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ {\mathtt {A}_c}_{n+1}= & {} \mathtt {A}_c(0)+\dfrac{h^{p}}{\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_4(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{h^p}{\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}{\hat{d}}_{j,n+1}{\mathcal {G}}_4(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {C}_{n+1}= & {} \mathtt {C}(0)+\dfrac{h^{p}}{\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_5(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{h^p}{\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}{\hat{d}}_{j,n+1}{\mathcal {G}}_5(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {R}_{n+1}= & {} \mathtt {R}(0)+\dfrac{h^{p}}{\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_6(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{h^p}{\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}{\hat{d}}_{j,n+1}{\mathcal {G}}_6(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j).\nonumber \\ \end{aligned}$$

(5.1)

where

$$\begin{aligned} \mathtt {S}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {S}(0)+\frac{1}{\Gamma (p)}\sum _{j=0}^{n}{\hat{b}}_{j,n+1}{\mathcal {G}}_1(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {E}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {E}(0)+\frac{1}{\Gamma (p)}\sum _{j=0}^{n}{\hat{b}}_{j,n+1}{\mathcal {G}}_2(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {A}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {A}(0)+\frac{1}{\Gamma (p)}\sum _{j=0}^{n}{\hat{b}}_{j,n+1}{\mathcal {G}}_3(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ {\mathtt {A}_c}_{n+1}^{{\mathcal {P}}}= & {} {\mathtt {A}_c}(0)+\frac{1}{\Gamma (p)}\sum _{j=0}^{n}{\hat{b}}_{j,n+1}{\mathcal {G}}_4(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {C}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {C}(0)+\frac{1}{\Gamma (p)}\sum _{j=0}^{n}{\hat{b}}_{j,n+1}{\mathcal {G}}_5(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {R}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {R}(0)+\frac{1}{\Gamma (p)}\sum _{j=0}^{n}{\hat{b}}_{j,n+1}{\mathcal {G}}_6(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j).\nonumber \\ \end{aligned}$$

(5.2)

and

$$\begin{aligned} {\hat{d}}_{j,n+1} =\left\{ \begin{array}{l@{\quad }l} n^{p+1}-(n-p)(n+1)^p &{} if j=0,\\ (n-j+2)^{p+1}+(n-j)^{p+1} &{} 1\le j\le n,\\ \quad -2(n-j+1)^{p+1}&{}\\ 1 &{} j=n+1. \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} {\hat{b}}_{j,n+1}=\frac{h^p}{p}((n+1-j)^p-(n-j)^p), \qquad 0\le j\le n. \end{aligned}$$

Table 1 CPU time in seconds for $\Delta t=0.01$

Table 2 CPU time in seconds for $\Delta t=0.05$

Fig. 1

Numerical simulation for the HBV model (3.2) for $p=1$, when ${\mathfrak {R}}_0>1$

Fig. 2

Numerical simulation for the HBV model (3.2) for $p=0.9$, when ${\mathfrak {R}}_0>1$

Fig. 3

Numerical simulation for the HBV model (3.2) for $p=0.8$, when ${\mathfrak {R}}_0>1$

Fig. 4

Numerical simulation for the HBV model (3.2) for $p=1$, when ${\mathfrak {R}}_0<1$

Fig. 5

Numerical simulation for the HBV model (3.2) for $p=0.9$, when ${\mathfrak {R}}_0<1$

Fig. 6

Numerical simulation for the HBV model (3.2) for $p=0.8$, when ${\mathfrak {R}}_0<1$

Fig. 7

Comparison of numerical result for the HBV model for $p=1$, when ${\mathfrak {R}}_0>1$

Fig. 8

Comparison of numerical result for the HBV model for $p=0.9$, when ${\mathfrak {R}}_0>1$

Fig. 9

Comparison of numerical result for the HBV model for $p=0.8$, when ${\mathfrak {R}}_0>1$

Fig. 10

Infected class of the HBV model (3.2) for different $\eta _1$ when $p=0.95$

5.2 Numerical solution of the ABC HBV model

Here, we will show a Adams type PC numerical technique [49] with Atangana–Baleanu fractional integral operator for numerical results of the proposed HBV model (3.2). For the sake of simplicity, the model (3.2) is given as

$$\begin{aligned} \begin{array}{rcl} {}_0^\mathcal {ABC}{\mathcal {D}}_t^p\mathtt {S}(t)&{}=&{}{\mathcal {G}}_1(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R}),\\ {}_0^\mathcal {ABC}{\mathcal {D}}_t^p\mathtt {E}(t)&{}=&{}{\mathcal {G}}_2(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R}),\\ {}_0^\mathcal {ABC}{\mathcal {D}}_t^p\mathtt {A}(t)&{}=&{}{\mathcal {G}}_3(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R}),\\ {}_0^\mathcal {ABC}{\mathcal {D}}_t^p\mathtt {A}_c(t)&{}=&{}{\mathcal {G}}_4(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R}),\\ {}_0^\mathcal {ABC}{\mathcal {D}}_t^p\mathtt {C}(t)&{}=&{}{\mathcal {G}}_5(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R}),\\ {}_0^\mathcal {ABC}{\mathcal {D}}_t^p\mathtt {R}(t)&{}=&{}{\mathcal {G}}_6(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R}).\\ \end{array} \end{aligned}$$

(5.3)

Now, we consider the system (5.3) with Atangana–Balenau (AB) integral and get the following:

$$\begin{aligned} \mathtt {S}(t)= & {} \mathtt {S}_0(t)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_1(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}{\mathcal {G}}_1(\upsilon ,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})(t-\upsilon )^{p-1}d\upsilon ,\nonumber \\ \mathtt {E}(t)= & {} \mathtt {E}_0(t)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_2(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}{\mathcal {G}}_2(\upsilon ,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})(t-\upsilon )^{p-1}d\upsilon ,\nonumber \\ \mathtt {A}(t)= & {} \mathtt {A}_0(t)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_3(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}{\mathcal {G}}_3(\upsilon ,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})(t-\upsilon )^{p-1}d\upsilon ,\nonumber \\ \mathtt {A}_c(t)= & {} {\mathtt {A}_c}_0(t)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_4(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}{\mathcal {G}}_4(\upsilon ,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})(t-\upsilon )^{p-1}d\upsilon ,\nonumber \\ \mathtt {C}(t)= & {} \mathtt {C}_0(t)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_5(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}{\mathcal {G}}_5(\upsilon ,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})(t-\upsilon )^{p-1}d\upsilon ,\nonumber \\ \mathtt {R}(t)= & {} \mathtt {R}_0(t)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_6(t,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}{\mathcal {G}}_6(\upsilon ,\mathtt {S},\mathtt {E},\mathtt {A},\mathtt {A}_c,\mathtt {C},\mathtt {R})(t-\upsilon )^{p-1}d\upsilon .\nonumber \\ \end{aligned}$$

(5.4)

We need now a numerical approximation technique for AB fractional integral. For this, we utilize the Adams type PC numerical approach for AB fractional integral. Therefore, we have

$$\begin{aligned} {}_0^{\mathcal {AB}} I _t^p\chi (t )=\frac{1-p}{{\mathfrak {J}}(p)}\chi (t)+\frac{p}{{\mathfrak {J}}(p)\Gamma (p)}\int _{0}^{t}\chi (\upsilon )(t-\upsilon )^{p-1}d\upsilon , \end{aligned}$$

(5.5)

and $h=\frac{T}{\mathrm {N}}, \,\, t_k=h k, (k=0,1,2,\cdots ,\mathrm {N}),$ where T is upper bound of the interval. Then, the corrector formula of integral form of derivative is provided as follows:

$$\begin{aligned} \chi _h(t_{n+1})= & {} \chi _0(t_{n+1})+\frac{(1-p)h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}g(t_{n+1},\chi _h^{{\mathcal {P}}}(t_{n+1}))\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\sum _{j=0}^{n}\varphi _{j,n+1}g(t_j,\chi _h(t_j)), \end{aligned}$$

(5.6)

where

$$\begin{aligned} \varphi _{j,n+1} =\left\{ \begin{array}{ll} n^{p+1}-(n-p)(n+1)^p, &{} if j=0,\\ (n-j+2)^{p+1}+(n-j)^{p+1} &{} 1\le j\le n,\\ \quad -2(n-j+1)^{p+1},&{}\\ 1, &{} j=n+1. \end{array} \right. \end{aligned}$$

The predictor value $\chi _h^{{\mathcal {P}}}(t_{n+1})$ is defined by following:

$$\begin{aligned} \chi _h^{{\mathcal {P}}}(t_{n+1})= & {} \chi _0+\frac{1-p}{{\mathfrak {J}}(p)}g(t_n,\chi _h(t_n))\nonumber \\&+\frac{p}{{\mathfrak {J}}(p)\Gamma ^2(p)}\sum _{j=0}^{n}\delta _{j,n+1}g(t_j,\chi _h(t_j)),\nonumber \\ \end{aligned}$$

(5.7)

where,

$$\begin{aligned} \delta _{j,n+1}=\frac{h^p}{p}((n+1-j)^p-(n-j)^p), \qquad 0\le j\le n. \end{aligned}$$

Operating above Adams type PC technique on the HBV model (3.2), we get the following iterative formula:

$$\begin{aligned} \mathtt {S}_{n+1}= & {} \mathtt {S}(0)+\dfrac{(1-p)h^{p}}{{\mathfrak {J}}(p)\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_1(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}\varphi _{j,n+1}{\mathcal {G}}_1(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {E}_{n+1}= & {} \mathtt {E}(0)+\dfrac{(1-p)h^{p}}{{\mathfrak {J}}(p)\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_2(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}\varphi _{j,n+1}{\mathcal {G}}_2(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {A}_{n+1}= & {} \mathtt {A}(0)+array\dfrac{(1-p)h^{p}}{{\mathfrak {J}}(p)\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_3(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}\varphi _{j,n+1}{\mathcal {G}}_3(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ {\mathtt {A}_c}_{n+1}= & {} \mathtt {A}_c(0)+\dfrac{(1-p)h^{p}}{{\mathfrak {J}}(p)\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_4(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}\varphi _{j,n+1}{\mathcal {G}}_4(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {C}_{n+1}= & {} \mathtt {C}(0)+\dfrac{(1-p)h^{p}}{{\mathfrak {J}}(p)\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_5(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}\varphi _{j,n+1}{\mathcal {G}}_5(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {R}_{n+1}= & {} \mathtt {R}(0)+\dfrac{(1-p)h^{p}}{{\mathfrak {J}}(p)\Gamma (p+2)}\nonumber \\&{\mathcal {G}}_6(t_{n+1},\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}})\nonumber \\&+\frac{p h^p}{{\mathfrak {J}}(p)\Gamma (p+2)}\displaystyle \sum _{j=0}^{n}\varphi _{j,n+1}{\mathcal {G}}_6(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j).\nonumber \\ \end{aligned}$$

(5.8)

The predictor terms $\mathtt {S}_{n+1}^{{\mathcal {P}}},\mathtt {E}_{n+1}^{{\mathcal {P}}},\mathtt {A}_{n+1}^{{\mathcal {P}}},{\mathtt {A}_c}_{n+1}^{{\mathcal {P}}},\mathtt {C}_{n+1}^{{\mathcal {P}}},\mathtt {R}_{n+1}^{{\mathcal {P}}}$ are given as

$$\begin{aligned} \mathtt {S}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {S}(0)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_1(t_n,\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n,\mathtt {C}_n,\mathtt {R}_n)\nonumber \\&+\frac{p}{\Gamma ^2(p){\mathfrak {J}}(p)}\sum _{j=0}^{n}\delta _{j,n+1}{\mathcal {G}}_1(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {E}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {E}(0)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_2(t_n,\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n,\mathtt {C}_n,\mathtt {R}_n)\nonumber \\&+\frac{p}{\Gamma ^2(p){\mathfrak {J}}(p)}\sum _{j=0}^{n}\delta _{j,n+1}{\mathcal {G}}_2(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {A}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {A}(0)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_3(t_n,\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n,\mathtt {C}_n,\mathtt {R}_n)\nonumber \\&+\frac{p}{\Gamma ^2(p){\mathfrak {J}}(p)}\sum _{j=0}^{n}\delta _{j,n+1}{\mathcal {G}}_3(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ {\mathtt {A}_c}_{n+1}^{{\mathcal {P}}}= & {} {\mathtt {A}_c}(0)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_4(t_n,\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n,\mathtt {C}_n,\mathtt {R}_n)\nonumber \\&+\frac{p}{\Gamma ^2(p){\mathfrak {J}}(p)}\sum _{j=0}^{n}\delta _{j,n+1}{\mathcal {G}}_4(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {C}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {C}(0)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_5(t_n,\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n,\mathtt {C}_n,\mathtt {R}_n)\nonumber \\&+\frac{p}{\Gamma ^2(p){\mathfrak {J}}(p)}\sum _{j=0}^{n}\delta _{j,n+1}{\mathcal {G}}_5(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j),\nonumber \\ \mathtt {R}_{n+1}^{{\mathcal {P}}}= & {} \mathtt {R}(0)+\frac{(1-p)}{{\mathfrak {J}}(p)}{\mathcal {G}}_6(t_n,\mathtt {S}_n,\mathtt {E}_n,\mathtt {A}_n,{\mathtt {A}_c}_n,\mathtt {C}_n,\mathtt {R}_n)\nonumber \\&+\frac{p}{\Gamma ^2(p){\mathfrak {J}}(p)}\sum _{j=0}^{n}\delta _{j,n+1}{\mathcal {G}}_6(t_j,\mathtt {S}_j,\mathtt {E}_j,\mathtt {A}_j,{\mathtt {A}_c}_j,\mathtt {C}_j,\mathtt {R}_j).\nonumber \\ \end{aligned}$$

(5.9)

Fig. 11

Numerical simulation for the third neuron of proposed variable-order HBV network

5.3 Numerical solution and discussion

In the present subsection, we have discussed the obtained numerical results for the Caputo model (3.1) and ABC model (3.2) with unit of time per year through the above suggested numerical techniques. The values of model parameter used in the numerical simulations are $\Lambda _1=2,\,\mu _1=1/67.7,\,\beta _1=0.042,\, \phi _1=0.002,\,\epsilon _1=0.002,\, \psi _1=0.004,\,\theta _1=0.6,\,\gamma _1=0.001,\, \eta _1=0.02,\,\kappa _1=0.02,\,\tau _1=0.02,\,\nu _1=0.1,\,\varepsilon _1=0.003,\,\sigma _1=0.2.$ Using the above given parameter values except $\beta _1=0.042,$ we show the numerical simulation for the model (3.2) in Figs. 1, 2, and 3, when ${\mathfrak {R}}_0>1$. From the presented graphics, we observe that the susceptible population decrease while the exposed individuals increase, the infected classes, acute, asymptomatic and chronic population increase, the increase is slower for the smaller values of FO parameter. Making the parameter $\beta _1=0.00042$ too small, we get ${\mathfrak {R}}_0<1$ and the graphical results are shown for this in Figs. 4, 5, and 6. The graphical solutions display that by decreasing the value of the non-integer-order parameter p, the number of individuals in the infected compartment decreases. In Figs. 7, 8, and 9, the comparison of numerical result for Caputo and ABC operators are presented graphically. We observe that ABC provide better results for the smaller fractional order. In Fig. 10, taking distinct values of parameter $\eta _1$ with $p=0.95$, we show the behavior of the infected compartments, acute, asymptomatic and chronic individuals. In addition, we provided the CPU output time in Tables 1 and 2.

6 Variable-order fractional network

In this section, we propose a new mathematical model that considers the interaction of different communities in modeling the disease. Since the relationships and travels between two countries will definitely affect the rate of diseases in both of them, by embedding the interaction between different communities in the modeling of the disease, more realistic results will be obtained.

The mathematical model of the disease is considered as neurons affected by each other in a network. To construct a network of HBV model, using the nearest neighbor method some models are joined. We suppose that the interactions between neurons are through the susceptible as well as asymptomatic carrier components, i.e., the coupling is made on the variable $\mathtt {S}$ and $\mathtt {A}_c$. Consequently, the governing equation of the proposed network is given by

$$\begin{aligned} {}^\mathcal {ABC}{\mathfrak {D}}_t^{p(t)}\mathtt {S}_i(t)= & {} \Lambda _1-\beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}_i\nonumber \\&-\mu _1\mathtt {S}_i+\frac{l}{2q}\displaystyle \sum _{j=i-q}^{i+q}(\mathtt {S}_j-\mathtt {S}_i),\nonumber \\ {}^\mathcal {ABC}{\mathfrak {D}}_t^{p(t)}\mathtt {E}_i(t)= & {} \beta _1(\mathtt {A}+\phi _1\mathtt {A}_c+\epsilon _1\mathtt {C})\mathtt {S}_i-(\mu _1+\psi _1)\mathtt {E}_i,\nonumber \\ {}^\mathcal {ABC}{\mathfrak {D}}_t^{p(t)}\mathtt {A}_i(t)= & {} \psi _1\theta _1\mathtt {E}_i-(\mu _1+\gamma _1+\eta _1+\kappa _1)\mathtt {A}_i,\nonumber \\ {}^\mathcal {ABC}{\mathfrak {D}}_t^{p(t)}\mathtt {A}_{c_i}(t)= & {} \psi _1(1-\theta _1)\mathtt {E}_i-(\mu _1+\tau _1+\nu _1)\mathtt {A}_{c_i}\nonumber \\&+\frac{l}{2q}\displaystyle \sum _{j=i-q}^{i+q}(\mathtt {A}_{c_j}-\mathtt {A}_{c_i}),\nonumber \\ {}^\mathcal {ABC}{\mathfrak {D}}_t^{p(t)}\mathtt {C}_i(t)= & {} \eta _1\mathtt {A}_i+\tau _1\mathtt {A}_{c_i}-(\mu _1+\varepsilon _1+\sigma _1)\mathtt {C}_i,\nonumber \\ {}^\mathcal {ABC}{\mathfrak {D}}_t^{p(t)}\mathtt {R}_i(t)= & {} \kappa _1\mathtt {A}_i+\sigma _1\mathtt {C}_i+\nu _1\mathtt {A}_{c_i}-\mu _1\mathtt {R}_i, \end{aligned}$$

(6.1)

where p(t) stands for the time-varying fractional-order derivative; also, q is the number of nearest neighbors on each side, and l denotes the coupling strength.

Figure 11 demonstrates the numerical results of the third neuron of the proposed network. In this case, the number of communities that are in the network is considered to be $\mathtt {N}_{\mathtt {S}}=4$. In addition, $q=2$ and $l=1$. The fractional-order derivative is considered to be a function of time as $p(t)=0.95+0.01\cos (\frac{t}{20})$. By comparing the results of the HBV model in the network and the case that there is a sole community, it can be found out that the neighborhood communities play important roles in the spread of the disease.

7 Conclusion

In the present work, we explored the dynamics of the HBV model with the asymptomatic carrier-class using two different fractional operators. For the arbitrary order fractional HBV model, we considered the Caputo and ABC fractional derivatives and presented some mathematical analysis for the FO ABC model, such as invariant region and basic reproduction number. Furthermore, with fixed-point results, the existence and uniqueness of system solutions to the arbitrary order HBV model were investigated. The numerical solution was obtained via the presented numerical schemes and the numerical outcomes were explored graphically for different choices of FO parameter. The importance of arbitrarily chosen fractional order can be observed from our presented results. Thus, from the analysis given in this work, we can conclude that the models formulated in FO demonstrate some interesting results and several characteristics that cannot be recognized in integer order. Finally, a network of the HBV model was introduced to consider the effects of different societies on each other. In the proposed model, it is supposed that the value of the fractional derivative is changing with respect to time, and the populations are jointed through the nearest neighbor method. In a future study, we will investigate the control of the proposed variable-order network through an artificial intelligence-based approach. This model can also be studied with other fractional derivatives, such as generalized Caputo and conformable derivatives.