Off-resonance electronic detection and cooling of ions in a Penning trap

Abstract

We present a non-destructive electronic detector for stored charged particles in a Penning trap that uses a symmetric electrode arrangement for signal pickup and a resonator without tap. This system has advantageous off-resonance features which are demonstrated by means of detection and cooling measurements with highly charged ions in a cryogenic Penning trap. In particular, it allows for particle detection across a wide range of frequencies that is not concomitant with cooling and offers a novel way to tune a trap with the help of non-destructive measurements on large particle ensembles.

1 Introduction

The notion of using a resonant electronic circuit to non-destructively detect and cool the motions of charged particles in a Penning trap goes back to Dehmelt et al. [1,2,3,4]. A comprehensive discussion of the interaction of stored particles with such circuits was given by Wineland and Dehmelt [5], including a model for resistive cooling of particle ensembles. These initial developments have been followed by a large number of implementations and variations, for reviews, see [6,7,8,9,10].

Any form of particle detection and cooling with resonant circuits is based on the fact that the motion of charged particles in a Penning trap induces image currents in the conducting electrodes of the trap (Shockley–Ramo theorem [11, 12]). When a suitable electrode is connected to ground via an electronic impedance Z, the induced current I leads to a voltage $U=ZI$ across the impedance that can be amplified and detected. At the same time, this current through the circuit produces Ohmic heat according to $P=ZI^2$ that is dissipated and in turn cools the particle motion. A ’suitable’ electrode is one that effectively picks up the component of the particle motion that is to be cooled: for the axial motion, usually an endcap of the trap is used, while for the radial motion, it is commonly a segment of the radially split ring electrode or one nearby.

For a given trap and particle species, there are two main circuit design choices to make, namely the values of the resonance frequency $\omega _0$ and of the quality factor Q of the circuit, and the choice of electrode(s) the circuit connects to. For an LC circuit [13], the former depend mainly on the achievable values of the inductance L, capacitance C and the series resistance $R_{\textrm{s}}$. Often, these values are fixed prior to the experiment by choice of the components to match the expected oscillation frequency of the particle(s) and the oscillation frequency width due to trap imperfections and other effects. Yet, given dedicated provisions, the resonance frequency $\omega _0$ and its width can also be changed to some degree during runtime [14, 15].

As far as the choice of electrodes is concerned, we focus on the axial particle oscillation, and a common choice is to connect one endcap or one correction electrode to ground via a parallel LC circuit [16, 17]. While for the detection and cooling of a single particle, this choice is largely equivalent to a parallel circuit connected to both endcaps, we show that for experiments with large particle ensembles, the latter configuration has a number of noteworthy advantages. In the following, we present corresponding measurements with bunches of highly charged ions that are produced in an external source and then dynamically captured into the Penning trap of the HILITE experiment.

2 Basics

2.1 Resonant circuits

Non-destructive detection is a well-developed technique, and the concomitant resistive cooling is a very efficient way to cool particles—especially in experiments with single electrons, protons or ions [8,9,10]. For efficient detection and cooling, it is usually desired to work with an electric impedance that represents a large parallel resistance $R_{\textrm{p}}$ but that has a small series resistance $R_{\textrm{s}}$ [5, 16]. This is possible with a parallel LC circuit at its resonance frequency $\omega _0=1/\sqrt{LC}$ [5]. In this case, its complex-valued impedance $Z(\omega )$ becomes a purely real-valued (Ohmic) parallel resistance

$$\begin{aligned} \Re (Z)(\omega _0)=R_{\textrm{p}}=\omega _0LQ , \end{aligned}$$

(1)

where $\Re (Z)(\omega _0)$ is the real part of the impedance at the resonance frequency, and Q is the quality factor that determines the width $\omega _0/Q$ of the resonance [5, 13]. For obtaining large $R_{\textrm{p}}$, the value of Q is desired to be large, which requires L to be large, and C and $R_{\textrm{s}}$ to be small, since $Q=\omega _0L/R_{\textrm{s}}$ [16]. Depending on details of the implementation, Q usually takes values between several $10^1$ and several $10^4$ for a radio-frequency circuit when connected to the trap, with the highest values reached by superconducting LC circuits [14,15,16]. Such circuits can reach parallel resistances $R_{\textrm{p}}$ of several hundreds of M$\Omega$ at series resistances $R_{\textrm{s}}$ below one Ohm [14,15,16].

2.2 Resistive ion cooling

When the axial oscillation of a particle (or likewise the perturbed cyclotron motion) interacts with the LC circuit, the energy of that motion decays like [5, 10]

$$\begin{aligned} E(t)=E(0) \exp (-\gamma t). \end{aligned}$$

(2)

For a single stored particle with mass m and electric charge q, the exponential cooling rate $\gamma$ is equal to $\gamma _1$ given by

$$\begin{aligned} \gamma _1=\frac{q^2\Re (Z)(\omega )}{mD^2}, \end{aligned}$$

(3)

where D is the so-called effective distance between the electrode and the particle [10, 18], and $\Re (Z)(\omega )$ is the real part of the impedance Z at frequency $\omega$. For N identical particles moving in phase, we have [10]

$$\begin{aligned} \gamma =N \gamma _1. \end{aligned}$$

(4)

Equation 2 is true until the induced signal of the initially hot particle comes into equilibrium with the electronic noise of the circuit at its given temperature, often liquid-helium temperature [19] (Fig. 1).

Following Eq. (3), resistive cooling is most efficient if the real part of the impedance is at its maximum. This is the case if the frequency of the particle matches the resonance frequency of the circuit ($\omega _z=\omega _0$), in which case we have $\Re (Z)(\omega _0)=R_{\textrm{p}}$ given by Eq. (1). Generally, however, the impedance Z is given by

$$\begin{aligned} \frac{1}{Z} = i \omega C + \frac{1}{i\omega L + R_{\textrm{s}}}, \end{aligned}$$

(5)

which accounts for the inductive impedance $i\omega L$ in series with $R_{\textrm{s}}$, and together in parallel to the capacitive impedance $(i\omega C)^{-1}$, see also Figs. 2 and 3. From this, the real part $\Re (Z)$ is given by

$$\begin{aligned} \Re (Z)(\omega ) = \frac{R_{\textrm{s}}}{\left( \omega ^2 L C -1 \right) ^2 +\omega ^2 R_{\textrm{s}}^2 C^2}. \end{aligned}$$

(6)

For $\omega = \omega _0 = 1/\sqrt{LC}$, this equation reduces to equation 1.

3 Setup and methods

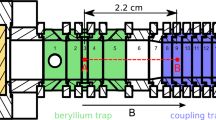
The present detection electronics have been operated at the cryogenic Penning trap of the HILITE experiment; the trap and overall setup have been described previously [18, 20]. In short, bunches of highly charged ions of a single species (presently helium-like neon ions, Ne$^{8+}$) are produced externally [21] and are then dynamically captured [22] into the trap. Once confined, the ions are non-destructively detected and cooled by use of the resonant LC circuit. Figure 1 shows a sectional drawing of the trap and indicates the LC circuit.

Fig. 1

Sectional drawing of the Penning trap. Ion injection is from the left. In the trap centre, stored ions are indicated. The LC circuit connects to the inner correction electrodes. The trap has mirror symmetry with respect to its centre, so only one half is labelled

The endcap electrodes have a separation of 22.4 mm, and the inner diameter of the trap is 15 mm. The endcaps have a central hole with a diameter of 4 mm to allow for loading the trap with externally produced ions.

3.1 The resonant LC circuit

We use a normal-conducting resonant circuit made of high-purity copper wire wound around a toroidal PTFE core (polytetrafluorethylene). The resonator circuit connects to the two inner correction electrodes of the trap, see also Fig. 1. This is in contrast to many implementations where one side connects to ground. We take the signal from one of the junctions between the correction electrode and one end of the resonator and amplify it by a model CX-4 Stahl Electronics low-noise cryogenic amplifier as depicted in Fig. 3.

This setup leads to the following differential equation for the resonator voltage $U_{\textrm{res}}$:

$$\begin{aligned} \ddot{U}_{\textrm{res}} + \frac{R_{\textrm{p}}}{L}\dot{U}_{\textrm{res}} + \omega _0^{2} U_{\textrm{res}} = \omega _0^{2}L\dot{I}+ \omega _0^{2}R_{\textrm{p}}I \end{aligned}$$

(7)

with a resonance frequency $\omega _0$ given by

$$\begin{aligned} \omega _0^{2} = \frac{1}{LC_{\textrm{tot}}} \end{aligned}$$

(8)

and a quality factor of

$$\begin{aligned} Q = \frac{1}{R_{\textrm{s}}}\sqrt{\frac{L}{C_{\textrm{tot}}}}. \end{aligned}$$

(9)

The double-electrode resonator thus behaves like a single-electrode resonator with a capacitance of

$$\begin{aligned} C_{\textrm{tot}}=\frac{C_{T}}{2} + C_{\textrm{res}} + C_{\textrm{amp}} \end{aligned}$$

(10)

and induced current of $I_{\textrm{tot}}=I_{+}-I_{-}$, and a resonance frequency given by (8). Here the capacitance $C_T$ is the capacitance of one electrode, $C_{\textrm{amp}}$ is the input capacitance of the applied amplifier, and $C_{\textrm{res}}$ the capacitance of the resonator coil, its housing and the influence by the surrounding setup. For simplicity, we assume both connected electrodes to have the same capacitance.

3.2 Single-electrode resonators

In most of the existing Penning trap setups, resonant circuits are used to detect and / or cool stored particles inside the trap non-destructively. The resonant circuit is commonly comprised of the trap electrode in question (e.g. one endcap) which contributes to the capacitance, and a wound coil as the inductive element where one end of the coil is connected to the electrode (‘hot end’) and the other one to ground (‘cold end’). The ion signal is tapped by a solder point inside the coil which is placed typically off the middle, thus dividing the coil into two parts of the fraction $\alpha$, where $\alpha =0$ would be a tapping at the cold end and $\alpha =1$ at the hot end. Typically, $\alpha$ is chosen to be between 0.6 and 0.8, and the magnitude of the tapped signal is $U_{\textrm{out}}= \alpha \cdot U_{\textrm{res}}$.

Fig. 2

Schematic of a single-electrode setup. The resonant circuit is driven by the current induced in one electrode. The voltage is tapped across a certain part of the coil. Any coupling capacitances between trap electrode and coil are omitted for better clarity

The voltage $U_{\textrm{res}}$ arises from driving the resonator by the induced current, and its (time-dependent) value can be estimated by Eq. (7). The magnitude is highly frequency-dependent by design and is highest if the ion frequency matches the resonance frequency. The amplification factor in comparison with the non-resonant case is the quality factor Q of the resonant circuit.

3.3 The dual-electrode resonator

Another approach is to connect the resonant circuit with two electrodes that are symmetric with respect to the trap centre, see Fig. 1. Presently, the effective electrode distance for this arrangement is $D=33$ mm. In this configuration, both ends of the resonator are tapped to the electrode and hence the resonator is driven by the induced current in both electrodes as depicted in Fig. 3. Furthermore, the voltage is tapped at one joint of an electrode to the coil. The grounding is ensured via the input resonator of the amplifier which is connected to the electrode $C_T^+$. Hence, this particular joint can be considered as the grounding point of the circuit and the voltage drop is the sum of the voltage in the trapping electrode ($U_{T}^-$) and the voltage at the resonator ($U_{\textrm{res}}$):

$$\begin{aligned} U_{\textrm{out}}= U_{T}^- + U_{\textrm{res}}. \end{aligned}$$

(11)

The voltage at the resonator is again given by Eq. (7). In contrast to the single-electrode setup, the voltage at the resonator contributes fully to the output voltage as one of its ends is connected directly to the amplifier ($\alpha =1$).

Fig. 3

Dual-electrode setup. The resonant circuit is driven by the current induced in both electrodes. The voltage is tapped directly at a node between one pick-up electrode. Any coupling capacitances between trap electrode and coil are omitted for better clarity

The contribution $U_{T}$ is the voltage which is induced directly in the trap electrode and is given by the common relation

$$\begin{aligned} U_T = \frac{Q_{\textrm{ind}}}{C_T}, \end{aligned}$$

(12)

where $Q_{\textrm{ind}}$ is the induced charge of the ion bunch in the electrode as described by the Shockley–Ramo theorem. The magnitude of this contribution is independent of the frequency and can hence been detected also when the ion oscillation frequency is far from the circuit’s resonance.

4 Measurements

With the presented dual-electrode resonator, a number of systematic measurements have been taken with bunches of highly charged ions injected into the Penning trap on its central axis. We first demonstrate detection and measurement of the axial ion frequency outside of the circuit’s resonance, compare measured off-resonance ion cooling rates with expectation from the discussion in Sect. 2.2, and show that one can use detection without concomitant cooling to disentangle ion cooling from ion de-phasing, for which applications to trap tuning are presented.

4.1 Off-resonance detection and frequency measurement

With the described dual-electrode resonant circuit, we are able to detect ions in resonance as well as off resonance. For this measurement, we use a spectrum analyser (model Keysight CXA 9000B) in span mode, where we monitor the axial-frequency distribution of the stored ions. We can detect the ions and determine their axial frequency over a wide range of trap voltages $U_0$. The covered frequency range is shown in Fig. 4. While the resonator marked by the orange region covers a frequency band of less than 200 kHz (from 1270 to 1450 kHz), the measured axial frequencies of the stored ions range from 750 to 1700 kHz. It would be possible to measure over a yet larger range, but the presently possible trap voltages $U_0$ limit us to the frequency window shown in the figure.

Fig. 4

Measured axial oscillation frequency $f_z$ of Ne$^{8+}$ ions as a function of $\sqrt{U_0}$. The resonator bandwidth is indicated by the shaded area, yet we can measure the resonance frequency over the full range shown because of the double-electrode design

4.2 Off-resonance resistive cooling

Measurements of resistive cooling of large ensembles of highly charged ions in resonance with the cooling circuit ($\omega _0=\omega _z$) have been taken previously [18]. In short, one observes a rapid cooling of the axial centre-of-mass (c.m.) motion of the ions upon dynamic capture, with the measured cooling rates $\gamma$ proportional to the number of ions N (typically N being several thousands to several tens of thousands) and in agreement with the theoretical expectation $\gamma =N \cdot \gamma _1$ for such bunches that move with a common phase [18]. In this situation, almost all kinetic particle energy is in the axial centre-of-mass motion. This is due to the bunch being injected on the central trap axis with all particles having the same axial velocity and a common phase. The time scale $1/\gamma$ of the observed resonant cooling is of the order of several ms. To fulfil the resonance condition $\omega _0=\omega _z$, a trap voltage of $U_0={155}$ V is required in the present setup.

Fig. 5

Measured ion signal as a function of time for two different trap voltages—in resonance ($U_0 = {155\,\mathrm{\text {V}}}$, fast cooling) and off-resonance ($U_0 = {135\,\mathrm{\text {V}}}$, slower cooling)

In order to determine the cooling rates, we acquire the time-dependent ion signal directly after ion capture. For this measurement, we run the spectrum analyser in zero-span mode setting the measurement window to a width of 1 kHz. The centre frequency of the captured ions is determined in a separate measurement before each zero-span acquisition.

As an example, Fig. 5 shows two ion signals as a function of time: resonant ion detection (blue signal, $U_0$=155 V) and non-resonant ion detection (purple signal, $U_0$=135 V). Obviously, out of resonance, the detection is connected with slower cooling. The rate of cooling $\gamma$ can be determined from a fit of Eq. (2) to the decay of the signal. Note the logarithmic scale, such that the linear slopes seen in the figure correspond to exponential decays of the energy.

To perform a quantitative study, we have scanned the trap voltage $U_0$ from 127.5 to 185.5 V to cover the entire resonator peak. This corresponds to a frequency range of 1.23 to 1.50 MHz for $f_z=\omega _z/2\pi$. The measured cooling rates $\gamma$ have been scaled by the respective ion number N. This is required to cancel the influence of the slightly varying trap configuration as $U_0$ is changed for each measurement. The result of this scan is shown by the data points in Fig. 6.

Fig. 6

Measured c.m. cooling rates for different axial ion frequencies $f_{z}$. The rate is scaled to avoid the influence of the ion number. The resonator is fixed at a resonance frequency of $f_0={1.37}$ MHz. The orange line in the figure is a fit to Eq. (3)

The line in the figure is a fit of Eq. (4) when we use the frequency-dependent real part of the impedance as given by Eq. (6). Obviously, both the on-resonance and off-resonance values of the cooling rates can be described well by the expected behaviour of the circuit. The fit yields a resonance frequency of $f_0={1.37\,\mathrm{\text {M}\text {Hz}}}$ and a quality factor of $Q=8.5$. This is a comparatively small value, but dedicated to measurements with large numbers of highly charged ion that move in phase, such that the signal detection and cooling can still be efficient. In particular, we require $\gamma \ll \omega _z$ for resistive cooling to work in the conventional way, and it is unclear whether the overall ion-circuit interaction would be predictable otherwise.

4.3 Measurement of axial de-phasing

Previous measurements of on-resonance resistive cooling of ion bunches injected into our trap have shown that the time evolution of the kinetic energies in the different motional degrees of freedom of the ions during cooling is well-described by a relatively simple energy flow model [9, 18]. It considers three different motions—the axial centre-of-mass motion (c.m.), the relative axial motions (ax) and the radial motions (r). Each motion is considered to have a certain amount of energy—$E_{\textrm{cm}}$, $E_{\textrm{ax}}$ and $E_{\textrm{r}}$. Between all motions, energy is transferred according to coupled rate equations that are explained in detail in [9, 18].

Here, we omit the radial part of this picture, since it has proven to contribute only marginally for the present on-axis injection of ions into the trap [18]. Consequently, we consider the following picture of energy transfer:

According to this model, only the axial c.m. motion is directly cooled by the circuit that is kept at a temperature of $T_0$ (which presently is liquid-helium temperature). The individual axial motions relative to the axial centre of mass are converted into c.m. motion at a rate that corresponds to the width of axial frequencies in the ensemble [5]. This contributes to the exchange of axial energy between $E_{\textrm{cm}}$ and $E_{\textrm{ax}}$ at a rate $\gamma _{\textrm{ax}}$ [18].

When used off-resonance, the present dual-electrode resonant setup can detect ions without significant cooling of the c.m. degree of freedom, as becomes obvious from Figs. 5 and 6 when we go even further out of resonance. This allows for ion detection and observation of energy transfer between $E_{\textrm{cm}}$ and $E_{\textrm{ax}}$ at negligible cooling rates $\gamma _{\textrm{cool}} \sim 0$. Consequently, $\gamma _{\textrm{ax}}$ can be separated out. This is not possible in the case of resonant c.m. cooling, since the rate $\gamma _{\textrm{cm}}$ is significantly higher than $\gamma _{\textrm{ax}}$ in all reasonable scenarios. It is hence only resolved in the symmetric off-resonance case where $\gamma _{\textrm{ax}}$ can be observed independently.

To this end, we have chosen a trap potential of $U_0 = {300\,\mathrm{\text {V}}}$, which is far off the resonant voltage $U_0=155$ V. At this trap potential, the real part of the resonator’s impedance $\Re (Z)$ is less than 2% of the value in resonance $R_{\textrm{p}}$. Consequently, the c.m. cooling rate $\gamma _{\textrm{cool}}$ is lowered to the same fraction of the on-resonance value and may hence be neglected in comparison.

4.4 Application to trap tuning

At present, the main mechanism of energy transfer between the relative axial motions and the axial c.m. motion is de-phasing. The ion bunch that enters the trap has a high initial degree of phase correlation, i.e. the by far dominant part of the axial energy is in the axial centre of mass [18]. As shown in [5], the rate of conversion between the two types of motion is given by the width of the axial frequency distribution [23]. This in turn depends on the anharmonicity of the trap potential which can easily be tuned by choice of the voltages applied to both pairs of the correction electrodes.

Fig. 7

Measured signal decay rate as a function of the voltages applied to the inner and outer correction electrodes. The encircled region corresponds to the smallest decay rate and hence to the highest trap harmonicity (optimal tuning)

This opens the possibility for a tuning of the trap by a non-destructive off-resonance measurement with an ensemble of particles. Tuning means to find the optimum tuning ratio, i.e. the combination of voltages that makes the trap potential harmonic and thus makes the axial frequency independent of the axial energy. While in single-ion experiments, it is found by energy-dependent frequency measurements [17], this is not straightforward with ion ensembles due to effects of ion–ion interaction [10]. However, using the present detection scheme off-resonance, we can find the trap tuning that produces the lowest axial de-phasing rate $\gamma _{\textrm{ax}}$ and hence the highest trap harmonicity.

Figure 7 shows the observed rate of signal decay as a function of the voltage combination applied to the inner and outer pair of corrections electrodes. The trap potential $U_0$ has been set to 300 V and the ions’ frequency have been thus far away from resonance and this rate is solely given by the rate $\gamma _{\textrm{ax}}$ of axial de-phasing. The region encircled in green corresponds to the lowest rate of de-phasing and hence to the highest harmonicity of the confining potential. According to the design values published in [18], the optimum voltage pair of the correction electrodes was expected to be 17.7 and 130.2 V for the inner and the outer correction electrode, respectively. This voltage pair lies fairly outside the marked region of the ideal tuning parameters. This behaviour is expected as on the one hand manufacturing errors have a certain influence on the optimum tuning ratio and on the other hand also the space charge of the entire ion cloud will have a measurable influence on the axial frequencies of the involved ions. This effect can hardly be predicted as this requires a deep knowledge of the ion cloud parameters.

Fig. 8

Measured ion signal as a function of time for two different trap tunings. Blue: optimum trap tuning leading to slow axial de-phasing. Red: detuned trap leading to fast axial de-phasing

To illustrate the effect of trap tuning, Fig. 8 compares two signal curves as a function of time that show the signal decay for a tuned trap according to the above procedure (blue curve, slow de-phasing), and a de-tuned trap (red curve, fast de-phasing).

4.5 Ion number dependence of the off-resonance signal

We have taken measurements of the off-resonance ion signal as a function of time for various numbers of ions in a tuned trap. This corresponds to the blue line in Fig. 8, measured for different ion numbers N between 20,000 and 40,000.

Fig. 9

Temporal evolution of the ion signal depending on the number of captured ions. The knee shape is an indicator for an increasing energy-transfer rate from the c.m. motion to the axial motion. Obviously, the higher the number of ions is, the early this effect can be observed

Obviously, the magnitude of the initial ion signal depends on the ion number, as expected. The subsequent decay of the signals initially occurs at similar small rates, in accordance with the lack of c.m. cooling due to the off-resonance situation and the small axial de-phasing due to the optimal trap tuning. At later times, the different de-phasing behaviour becomes more obvious, and the rate of signal decay increases, with the effect being more pronounced for higher ion numbers. We attribute this to stronger ion–ion interaction in the case of higher ion numbers and a broader distribution of axial oscillation frequencies due to the effect of space charge. This leads to an increased energy transfer between the individual axial oscillations and the axial c.m. motion (Fig. 9).

5 Summary and outlook

We have presented the capabilities of a symmetric dual-electrode resonant circuit in measurements with large ensembles of highly charged ions confined in a Penning trap. In this configuration, the motion of confined ensembles of particles can be measured also far outside of the circuit’s resonance frequency. This facilitates non-destructive detection without concomitant cooling and opens up the possibility to measure the exchange of energy between the axial centre of mass and the uncorrelated relative axial motions in the absence of the otherwise dominant centre-of-mass cooling. This has two applications which are of potential interest in trap experiments with injected particle ensembles:

Firstly, it gives insight into the evolution of dynamically captured ion bunches; specifically it allows for a measurement of the rate of motional de-phasing. This is valuable information for any optimisation of the capture process to the end of tailoring the dynamic capture process to individual needs, particularly as a preparation for efficient cooling.

Secondly, it represents a novel way to find the optimal trap tuning by pointing out the trap parameters that lead to the lowest rate of axial de-phasing of the ions. This allows for a tuning of the trap also with large particle ensembles and in the absence of the possibility for frequency measurements at well-defined excitation energies.