Precision Physics in Penning Traps Using the Continuous Stern-Gerlach Effect

Abstract

“A single atomic particle forever floating at rest in free space” (H. Dehmelt) would be the ideal object for precision measurements of atomic properties and for tests of fundamental theories. Such an ideal, of course, can ultimately never be achieved. A very close approximation to this ideal is made possible by ion traps, where electromagnetic forces are used to confine charged particles under well-controlled conditions for practically unlimited time. Concurrently, sensitive detection methods have been developed to allow observation of single stored ions. Various cooling methods can be employed to bring the trapped ion nearly to rest. Among different realisations of ion traps we consider in this chapter the so-called Penning traps which use static electric and magnetic fields for ion confinement. After a brief discussion of Penning-trap properties, we consider various experiments including the application of the “continuous Stern-Gerlach effect”, which have led recently to precise determinations of the masses and magnetic moments of particles and antiparticles. These serve as input for testing fundamental theories and symmetries.

1 Introduction

“A single atomic particle forever floating at rest in free space” (H. Dehmelt) would be the ideal object for precision measurements of atomic properties and for tests of fundamental theories. Such an ideal, of course, can ultimately never be achieved. A very close approximation to this ideal is made possible by ion traps, where electromagnetic forces are used to confine charged particles under well-controlled conditions for practically unlimited time. Concurrently, sensitive detection methods have been developed to allow observation of single stored ions. Various cooling methods can be employed to bring the trapped ion nearly to rest. Among different realisations of ion traps we consider in this chapter the so-called Penning traps which use static electric and magnetic fields for ion confinement. After a brief discussion of Penning-trap properties, we consider various experiments including the application of the “continuous Stern-Gerlach effect”, which have led recently to precise determinations of the masses and magnetic moments of particles and antiparticles. These serve as input for testing fundamental theories and symmetries.

2 Penning-Trap Properties

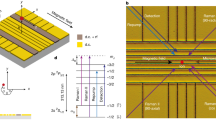
The Penning traps used in the experiments described herein consist of a symmetric stack of cylindrical electrodes as shown in Fig. 1.

Fig. 1

Schematic of our cylindrical Penning trap holding a single highly charged ion stored in this electrode configuration

A static voltage is applied between the connected outer electrodes and the central ring. At a positive polarity at the endcaps a positively charged particle is confined in the axial direction. Escape in the radial direction is precluded by a homogeneous magnetic field directed along the trap’s axis. Additional voltages applied to the so-called correction electrodes, placed between the ring and endcaps, serve to provide an electric potential which depends—at least for small amplitudes of the trapped particle—only on the square of the distance from the trap’s centre. This is a prerequisite for achieving high resolution in the determination of the motional frequencies of the trapped ions. It is further required to avoid perturbation of the confined ion by collisions with background gas molecules. In our case, the trap electrodes and their container box are in thermal contact with a liquid helium bath. The cryopumping results in a residual pressure of less than 10⁻¹⁶ mbar. As a result, not even a single collision of the trapped ion with a neutral molecule was observed during typical trapping times of several months.

The ion’s motion in the trap arrangement described above can be calculated analytically. As a result one obtains a superposition of three harmonic oscillations: An axial one at frequency ν_z, which depends on the ions mass M, the size of the trap, and the voltage, and two radial oscillations with frequencies ν₊ and ν_−. The frequency ν₊ is near the cyclotron frequency ν_c = qB/(2πM) of the free ion with charge q in the magnetic field B, slightly perturbed by the presence of the electric trapping field. The centre of this motion orbits around the trap centre at a low “magnetron frequency” ν₋. Figure 2 shows a sketch of the ion’s motion. An important relation connects the motional frequencies to the free ion’s cyclotron frequency [1]:

Fig. 2

Sketch of the ion’s motion in a Penning trap. For details see text

$$\nu_{ + }^{ 2} + \nu_{ - }^{ 2} + \nu_{\text{z}}^{ 2 } = \nu_{\text{c}}^{ 2} .$$

(1)

Further details on Penning traps can be found in Refs. [2, 3].

3 Single Ion Detection by Induced Image Currents

Achieving high precision in trap experiments requires the use of single trapped particles to avoid perturbations by Coulomb interaction with other ions. The standard way to detect single trapped particles is by observation of laser induced fluorescence. This requires, however, optical transitions in the ions which are in reach of laser wavelengths. This is not the case for highly charged ions or elementary particles such as electrons or protons and their antiparticles. In these cases, detection can be performed by the image current that the oscillating ion induces in the trap’s electrodes [4]. This current is on the order of a few fA and requires very sensitive detection methods. This can be realized by a superconducting high-Q tank circuit, kept at the temperature of the surrounding He-bath and tuned to the resonance frequency of the ion oscillation. Figure 3 shows a scheme of the detection of a radial frequency. The noise power of the circuit can be amplified and Fourier analysed. In case of an ion present in the trap, the Fourier spectrum shows a maximum at the resonance frequency of the ion oscillation, as shown in Fig. 4.

Fig. 3

Scheme for detection of the radial ion oscillation by a superconducting tank circuit attached to segments of the trap’s split ring electrode

Fig. 4

Fourier analysis of the axial detection resonance circuit showing the induced image current of a single trapped ion on top of the Johnson noise of the detection circuit

The ion signal as shown in Fig. 4 indicates that the ion’s kinetic energy is well above the thermal energy of the circuit. In order to reduce the ion’s energy as required for high-precision measurements, the ion is kept in resonance with the circuit. The extra energy which the hot ion transfers into the circuit is then dissipated into the helium bath (resistive cooling) [5]. As consequence the ion adopts the temperature of the environment. The signal is then converted into a minimum in the noise spectrum as shown in Fig. 5. This can be understood based on the fact that the equivalent electronic circuit of the oscillating ion is a series resonance circuit which shortcuts the noise power of the detection circuit at its resonance frequency.

Fig. 5

Signal of a single ion’s axial resonance in thermal equilibrium with the detection system immersed in a liquid He bath

4 The Masses of the Proton and Antiproton

The ion signals such as those shown in Fig. 5 can be used for high-precision mass measurements. As recent examples, we consider the atomic masses of the proton and the antiproton. Their comparison serves as a test of the CPT invariance theorem. Quite general determination of atomic masses requires the comparison with the standard atomic mass, the carbon atom. The comparison is performed through measurements of the cyclotron frequencies of the particle under investigation ν_c(P) = eB/(2πM_P) (e.g. the proton P with mass M_P) and that of a carbon ion of charge state q: ν_c(C^q+) = qB/(2πM ^q+_C ) in the same magnetic field B provided by a superconducting solenoid. In the case of the proton we used C⁶⁺ and correct the measured frequency by the masses of the missing electrons and their respective binding energies:

$$M_{P} = \frac{e}{q}\frac{{\nu_{C} \left( C \right)}}{{\nu_{C} \left( P \right)}}M_{C}$$

(2)

By resolving the central part of the ion detection signal as shown in Fig. 5, we can determine the centre frequency with an uncertainty of a few mHz. In our experiments we measure exclusively the axial frequency. In order to determine the radial frequency as required for the determination of the cyclotron frequencies according to Eq. (1), we couple the radial frequencies to the axial one by an additional r.f. field applied to the trap electrodes at their difference frequency to the axial. This leads to a split of the axial detection signal which allows to determine the radial frequencies with the same uncertainty.

In order to perform the measurements of the respective cyclotron frequencies at the same position of the magnetic field, we extend our Penning trap by a number of additional electrodes. In different potential minima we can store simultaneously a single proton and a single carbon ion. By changing the potentials at the electrodes we can transport one ion into the central part of the trap structure where the homogeneity of the magnetic field is highest, while the other ion is stored in one of the remaining potential minima. Frequent exchange of protons and carbon ions eliminates to a large extent the influence of possible time variations of the magnetic field which is provided by a superconducting magnet. Figure 6 shows the complete setup.

Fig. 6

Setup of the trap configuration for the determination of proton’s atomic mass. The left part serves for the creation of protons and carbon ions by electron bombardment of a target. After ion creation and removal of unwanted species, single ions are transferred to one of the potential minima. Measurements are performed in the so-called measurement trap located at the most homogeneous part of the magnetic field. Shown are the resonance circuits attached to the measurement trap’s electrode tuned to the different axial frequencies for the proton and C⁶⁺. The trap configuration is placed in a hermetically sealed container in thermal contact with a liquid-He bath. The low temperature of the container walls provides a vacuum below 10⁻¹⁶ mbar by cryofreezing. Collisions of the stored particles with background molecules are absent for the period of several months which allows a nearly infinitely long perturbation-free storage time

Our result for the proton’s atomic mass including the statistical and systematic uncertainties is [6]

$$M_{P} = 1.00 7\; 2 7 6\; 4 6 6\; 5 8 3\left( { 1 5} \right)\left( { 2 9} \right)\;{\text{u}}.$$

(3)

i.e. a relative mass uncertainty of 3 × 10⁻¹¹ has been achieved. It improves earlier results by a factor of 3 and determines the proton mass value in the most recent CODATA compilation of fundamental constants [7] (Fig. 7).

Fig. 7

(courtesy F. Heiße)

History of proton mass determinations

A similar experiment as described above using a nearly identical setup has been performed at CERN/Geneva, where single antiprotons have been confined and their cyclotron frequency measured [8]. The main difference was that, for comparison with a reference mass, not a carbon ion could be used since it would require a change of the voltage sign at the trap because of the different charge signs of the particles. This, in turn, could lead to uncontrollable errors. Instead, the CERN experiment used the negative hydrogen ion H⁻. Taking into account the masses of the 2 additional electrons, their binding energies E_a and E_b as well as the polarizability $\alpha_{{pol,H^{ - } }}$ of H⁻, the antiproton’s m_ap mass can be compared to the protons mass through

$$m_{{(H^{ - } )}} = m_{ap} \left( {1 + 2\frac{{m_{e} }}{{m_{p} }} + \frac{{\alpha_{{pol,H^{ - } B_{0}^{2} }} }}{{m_{p} }} - \frac{{E_{b} }}{{m_{p} }} - \frac{{E_{a} }}{{m_{p} }}} \right)$$

(4)

The result of the proton/antiproton mass ratio is

$$\left( {q/m} \right)_{\text{ap}} /\left( {q/m} \right)_{\text{p}} = - 1.000\;000\;000\;00 1\;\left( { 6 9} \right)$$

(5)

at a relative uncertainty level of 7 × 10⁻¹¹. This result represents the most stringent test of the CPT invariance in the baryon sector.

5 The g-Factor of the Bound Electron

The g-factor of the electron is a dimensionless constant which relates the electron’s magnetic moment μ_s to the spin S and the Bohr magnetron μ_B:

$$\mu_{s} = g\mu_{B} S$$

(6)

Dirac’s relativistic treatment of the free electron predicts g = 2. Experimentally a deviation from 2 is found, which among others gave rise to the theory of Quantum Electrodynamics (QED), which describes the interaction of charged particles with electromagnetic fields by the exchange of virtual photons. Evaluation of Feynman diagrams to high orders allows calculating the g-factor of the free electron to extremely high precision [9]:

(g − 2)/2 = 0.001 159 652 181 78 (77). It agrees well with the experimental value [10]: (g − 2)/2 = 0.001 159 652 180 73 (28). The agreement represents the best test of QED in weak external fields.

In contrast to a free electron, an electron bound to an atomic nucleus experiences an extremely strong electric field. The strength of the field for a single electron bound in the 1S-state of a hydrogen-like ion of nuclear charge Z ranges from 10⁹ V/cm in the helium ion (Z = 2) to > 10¹⁵ V/cm in H-like uranium (Z = 92) (Fig. 8). This gives rise to a variety of new effects. The largest change of the bound electron’s g-factor was analytically derived by Breit (1928) from the Dirac equation: $g_{Breit} = \frac{2}{3}\left( {1 + 2\sqrt {1 - \left( {Z\alpha } \right)^{2} } } \right) \approx { 2}\left( { 1- \frac{1}{3}\left( {Z\alpha } \right)^{2} } \right)$ [11], with α ≈ 1/137 the fine structure constant. The extremely high electric fields within atoms also require different methods to be used for calculating the QED contributions to the electron’s magnetic moment. Feynman diagrams have to be calculated using the solution of the Dirac equation as an electron propagator. Contributions of high orders in (Zα) have been calculated by several authors [12]. In addition, nuclear structure and recoil effects must be considered [13]. Figure 9 summarises the different contributions to the electron’s g-factor in the ground state of H-like ions as function of the nuclear charge Z.

Fig. 8

Electric field strength at the 1S- and 2S-states of hydrogen-like ions as function of the nuclear charge Z

Fig. 9

(courtesy Z. Harmann)

Contributions from bound-state QED, nuclear size, structure, and recoil to the g-factor of the electron bound in hydrogen-like ions as function of the nuclear charge Z

6 The Continuous Stern-Gerlach Effect

The determination of the electron’s g-factor requires the measurement of the spin precession (Larmor) frequency ω_L:

$$\omega_{L} = \frac{g}{2}{\kern 1pt} \,\frac{e}{{m_{e} }}\,B$$

(7)

The magnetic field strength B can be derived from the measurement of the three motional frequencies as described in Sect. 4. The spin precession, however, does not influence the ion’s motion in a homogeneous magnetic field and consequently cannot be detected by observation of the axial ion resonance as only observable in our experimental set-up (see Sect. 3). The required coupling of the spin motion to the ion’s oscillation can be provided by an inhomogeneity of the magnetic field. The force of F = μ_SgradB of a B-field inhomogeneity gradB on the magnetic moment μ_S associated with the spin increases or reduces the electric trapping force of the Penning trap depending of the spin’s direction. Consequently, a change in the spin direction leads to a change in the ion’s axial frequency. This method has been first employed by Dehmelt in his experiment on the g-factor of the free electron and termed “continuous Stern-Gerlach effect” [14]. It was later adapted to experiments on highly charged ions [15].

The size of the change in the axial frequency upon a change in the spin direction is given by

$$\Delta \omega_{\text{z}} = \frac{{g\mu_{\text{B}} B_{2} }}{{M\omega_{\text{z}} }}$$

(8)

where M is the ions mass and B₂ is the quadratic part of the series expansion of the magnetic field B_Z = B₀ + B₂ z² + …. The magnetic field inhomogeneity in our experiments is produced by a ferromagnetic central ring electrode (nickel) in the Penning trap assembly. It produces a bottle shaped B-field. Odd terms in the series expansion vanish. The measured value of B₂ in our trap is 10 mT/mm². The calculated change in the axial frequency, e.g., for H-like ²⁸Si¹³⁺ is 240 mHz in a total oscillation frequency of 412 kHz. The detection of such small frequency changes requires high stability of the electric trapping field. Figure 10 shows that changes in the spin direction, induced by a microwave field in the trap, can be unambiguously detected with nearly 100% probability.

Fig. 10

Change in the axial frequency of a single trapped ²⁸Si¹³⁺ when the spin direction is flipped by microwave-induced transitions. For details see text

7 Measurement of g-Factors

Our first application of the continuous Stern-Gerlach effect was the determination of the g-factor of the electron bound in hydrogen-like ions. We monitor induced spin flips as shown in Fig. 10 while varying the microwave field’s frequency. The maximum spin flip probability occurs when the microwave frequency ω coincides with the Larmor precession frequency ω_L. The g-factor can be derived from Eq. (5) when the magnetic field B is known. B is obtained using the single ion detection signals at the ion’s oscillation frequencies as described in Sects. 3 and 4. The g-factor then follows from the measurement of ω_L and ω_c:

$$g = 2\frac{{\omega_{L} }}{{\omega_{c} }}\frac{{q_{ion} }}{{m_{ion} }}\frac{{m_{e} }}{e} = 2\Gamma \frac{{q_{ion} }}{{m_{ion} }}\frac{{m_{e} }}{e}$$

(9)

Γ is the ratio of the applied microwave frequency ω to the measured cyclotron frequency. However, in order to obtain high precision in the g-factor determination we are faced with conflicting requirements: The continuous Stern-Gerlach effect requires a strong inhomogeneity of the B-field at the ions position in order to detect induced spin flips with high probability. High accuracy for B-field determination on the other side requires a very homogeneous field at the ion’s position. In order to resolve this conflict we used a Penning-trap configuration similar to the one shown in Fig. 6 but modified by introducing a nickel ring electrode in one of the storage traps that provides the required B-field inhomogeneity. Step 1 of the measurement procedure is the determination of the ion’s spin direction in the inhomogeneous trap by introduction of a spin flip and observation of the change in the axial oscillation frequency as illustrated in Fig. 10. With a known spin direction, the ion is then transported into the measurement trap where the oscillation frequency ω_c is determined. Simultaneously the ion is irradiated by a microwave field attempting to change the spin direction. Then the ion is transported back into the inhomogeneous trap and, as in step 1, its spin direction is determined again. A successfully induced spin flip in the measurement trap is monitored in the inhomogeneous trap by the corresponding change in the axial frequency. Frequent repetition of this procedure with varying microwave frequencies and monitoring the spin flip probability for different frequencies results in a resonance curve with a maximum at the Larmor precession frequency ω_L. The fact that ω_L and ω_c are measured at the same position as well at the same time eliminates to a large extent the uncertainties due to time fluctuations of the B-field. Figure 11 shows an example of measurements on hydrogen-like ²⁸Si¹³⁺, where the spin flip probability is plotted against the ratio Γ of ω and ω_c.. The maximum is at Γ = ω_L/ω_C..

Fig. 11

Measured spin flip probability of ²⁸Si¹³⁺ as a function of the frequency ratio Γ = ω/ω_C.. The maximum occurs at Γ = ω_L/ω_C. Γ_theo is the theoretical predicted value. Shifts caused by systematic effects are not yet corrected for

The result of the experiment on ²⁸Si¹³⁺ for the g-factor of the single bound electron is g_exp = 1.995 348 958 7 (5)(3)(8) [16]. The numbers in parenthesis correspond respectively to the systematic and statistical uncertainties and the error of the electron mass taken from the CODATA 2012 tables of fundamental constants [17]. The result agrees well with the theoretical value g_theo = 1.995 348 958 0 (17) [18] and represents the most stringent test of QED calculations in strong external fields.

Similar results with comparable precision have been obtained on H-like ¹²C⁵⁺ [19] and ¹⁶O⁷⁺ [20]. Also experiments using lithium-like ions ⁴⁰Ca¹⁷⁺ and ⁴⁸Ca¹⁷⁺ [21], and ²⁸Si¹¹⁺ [22] have been performed. Here the interaction of the additional 2 bound electrons modify slightly the value of the g-factor. The comparisons between theory and experiment test calculations of the inter-electronic interaction. Most recently the g-factor of the boron-like ion ⁴⁰Ar¹³⁺ has been determined with high precision [23]. The experimental result distinguishes between the conflicting predictions of the contribution of the electron-electron interaction.

Analogously to the electronic g-factors, the magnetic moments of the proton and antiproton were obtained. The particular challenge in these experiments had to do with the fact that the magnetic moment of these particles is about 500 times smaller than that of the electron. According to Eq. (6), the corresponding change in the axial frequency is significantly smaller than in the case of hydrogen-like ions. Its observation requires extremely high stability in the trap parameters. A measurable frequency change upon a spin flip was obtained by making the trap diameter about 3 times smaller than in the previous experiments and replacing the Ni-ring by a CoFe-ring and thus obtaining a larger magnetic field inhomogeneity. The result for the proton’s and antiproton’s magnetic moments are μ_p = 2.792 847 344 62(82) μ_N [24] and μ_antip =  −2.792 847 344 1(42) μ_N [25], with μ_N the nuclear magnetron. The agreement of the two values within the error bars represents a test of the CPT invariance theorem.

8 The Electron Mass

As evident from the result of the g-factor determination in ²⁸Si¹³⁺, the largest contribution in the error budget arises from the uncertainty in the electron mass taken from the CODATA 2012 compilation of fundamental constants. The QED contributions to the electronic g-factor of H-like ions scale approximately with the square of the nuclear charge Z. Since in the case of ²⁸Si¹³⁺ with Z = 14 we find an agreement between theory and experiment on the level of 10⁻¹⁰ it can be reasonably assumed that in the case of H-like ¹²C⁵⁺ with Z = 6 the QED contributions to the g-factor have been calculated correctly. We can therefore rewrite Eq. (9) between the g-factor and the electron mass as

$$m_{e} = \frac{g}{2}\frac{e}{q}\frac{{v_{\text{cyc}} }}{{v_{\text{L}} }}m_{\text{ion}} \equiv \frac{g}{2}\frac{e}{q}\frac{1}{\varGamma }m_{\text{ion}}$$

(10)

We take now the g-factor from theory and determine the electron mass. ¹²C⁵⁺ is the natural choice as ion since there is virtually no uncertainty in its mass. In our experiment [26] we obtained as new value for the electron mass m_e = 0.000 548 579 909 067 (14)(9)(2) a.u. The first two errors are the statistical and systematic uncertainties of the measurement, respectively, and the third one represents the uncertainties of the theoretical prediction of the g-factor and the electron binding energies in the carbon ion. The new value surpasses that of the CODATA 2012 literature value by a factor of 13 and represents the basis for the most recent adjustment of fundamental constants [7].

9 What Comes Next?

At the Max-Planck-Institut für Kernphysik in Heidelberg an electron beam ion trap (EBIT) [27] will allow production of hydrogen-like ions of high nuclear charge Z up to ²⁰⁸Pb⁸¹⁺. They can be extracted from the EBIT and injected into an improved Penning-trap arrangement (ALPHATRAP) placed at the center of a superconducting magnet [28]. Here Larmor-to-cyclotron frequency ratio measurements can be performed at the dg/g ≈ 10⁻¹² level of accuracy. This will provide more stringent tests of bound state QED contributions to the electron’s g-factor in an extremely strong electric field as evident from Figs. 8 and 9. In addition a new determination of the fine structure constant α by comparison of theoretical and experimental results seems possible. Figure 12 shows a sketch of the setup.

Fig. 12

Sketch of the ALPHATRAP set-up at MPIK Heidelberg to produce H-like ions of high nuclear charge from an EBIT to be injected into a Penning trap arrangement for g-factor determination [28]. A first experiment on ion ⁴⁰Ar¹³⁺ has been performed successfully [23]

10 Summary

Spectroscopy in Penning traps has reached an amazing level of precision even on exotic systems and has opened up many new fields of research. In this chapter we have summarised the results of recent experiments. They provide, to date, the most accurate values of the atomic masses of the electron, proton, and antiproton, the most accurate magnetic moments of the proton and antiproton, and the most stringent test of bound-state quantum electrodynamic calculations of contributions to the magnetic moment of the electron in strong electric fields through g-factor measurements on various hydrogen- and lithium-like highly charged ions.