Stability and numerical analysis of the generalised time-fractional Cattaneo model for heat conduction in porous media

Abstract

This work investigates the generalised time-fractional Cattaneo model. The homotopy perturbation transform technique is used to get the numerical solution of this model. The stability is analysed using the Lyapunov function, also the error analysis is discussed. Finally, the effectiveness of the proposed technique is illustrated by calculating the $L^{2}$ and $L^{\infty }$ error and comparing it with the existing techniques.

1 Introduction

Fractional Calculus (FC) has become an essential tool to model the phenomena occurring in many physical and engineering processes in the last few years. It is successfully applied in vast areas of science. It is far superior to Integer Calculus for demonstrating the mechanism and physical process in science and nature. The fractional differential equations (FDEs) possess memory because, in the case of FDEs, the system’s current state depends not only on current conditions but also on previous conditions. That is, past events influence the current dynamics. Also, it has various essential aspects and analyses to assist in understanding the actual evidence. In addition, it is pretty helpful in simulating and comprehending natural phenomena due to its inheritance and recall qualities. Many researchers studied and analysed different fractional mathematical models such as the fractional competition model of bank data analysed with CF derivative [1], the fractional Fitzhugh–Nagumo equation is studied in [2] by homotopy perturbation technique, the fractional model of CFWBK equation is studied in [3] by ABC fractional derivative, the fractional multi-dimensional telegraph equation is examined in [4] by Laplace transform, the fractional coupled burger equation is investigated in [5], the nonlinear fractional model of Zakharov–Kuznetsov equation is studied in [6] via Sumudu transform, the fractional model of hearing loss due to Mumps virus is studied in [7] via Caputo–Fabrizio operator, the fractional-order SEIR epidemic of measles is studied in [8] by using Genocchi polynomials, the 2019-nCOV outbreaks are studied in [9] via non-singular derivative, the fractional predator–prey dynamical system is studied in [10], the heat equations arises in diffusion process are studied in [11] using new Yang-Abdel-Aty-Cattani fractional operator.

A class of FDEs that can represent transport dynamics in complicated systems and are therefore widely used in many biological and natural phenomena are used to characterise anomalous diffusion occurrences [12,13,14,15,16,17]. The anomalous diffusion exponent, denoted as $x^{2} \left( t \right) \sim t^{\alpha }$, is known to be a component of anomalous diffusion together with the $\alpha$ anomalous diffusion exponent, the mean square distance of the diffusing species and time $\left( t \right).$ These phenomena lie under the categories of anomalous super-diffusion and sub-diffusion for $1 < \alpha < 2$ and $0 < \alpha < 1$, respectively. However, for $\alpha = 1$ it is called Gaussian diffusion. Many different methods have been applied to characterise anomalous diffusion using the fractional diffusion models [18,19,20].

When there is a temperature difference between two different materials or different regions of the same object, heat transfer occurs naturally as a usual process. Therefore, the scientific community has been interested in predicting heat transport behaviour. Fick’s law is the fundamental theory for explaining Gaussian diffusion, like heat conduction and tracer dispersion [21]. But because this equation suggests an infinite propagation velocity, its validity has been questioned. But because this equation suggests an infinite propagation velocity, its validity has been questioned. This trait is only sometimes evident in terms of its physical meaning. Numerous investigations have examined the heat conduction in the porous medium while taking into account a variety of factors, including (i) the small-scale interactions among various steps, (ii) the quick short-term conduction of heat, (iii) the porous medium's thermal response and (iv) the requirement of local thermal equilibrium. For most applications, the Fourier law-based heat conduction model is adequate. However, the thermal disturbances in this model propagate at an unlimited rate, violating the laws of physics [22,23,24].

Several constitutive models have been proposed to account for the finite propagation speed and explain the anomalous diffusion process. For instance, the fractional-order Fick’s laws, which are described in fractional-order derivatives, are available. This method produces the Cattaneo equation, which is used to describe heat and mass transfer and fractional-order diffusion models [25]. The heat condition law was first put forth by Fourier [26] in 1822. Even though it is a hypothesis law, it enabled the characterisation of heat transport mechanisms and served as a foundation for the subsequent two centuries of research on thermal conduction. By incorporating a term for relaxation time, Cattaneo [27] updated Fourier’s law in 1948. By applying Oldroyd’s upper convected derivative [28] in 2009, Christov [29] generalised Cattaneo’s rule to make it frame differently and produced a model with a single temperature.

The Cattaneo model is frequently employed to represent natural phenomena including extended irreversible thermodynamics [30], cosmological models [31], diffusion theory in crystalline solids [32], computational biology [33, 34], and micro-scale and macro-scale heat conduction [35, 36]. In actuality, the equation depicts the simultaneous generalisation of Fourier’s law and Fick’s law. The Fourier rule, which states that the flow is proportionate to the gradient of the carried quantity, is a phenomenological description, it should be noted. This idea is encountered in several physical contexts and goes by various names. The Fourier law that regulates the concept of conduction of heat and the Fick law that defines the concept of diffusion are equivalent. The one-dimensional fractional-order Cattaneo model is described in terms of $x, t, D, \tau , \frac{{\partial^{n} }}{{\partial {\upzeta }^{n} }}$ and $\xi \left( {x, t} \right).$ Here, $x$ and $t$ are the space and time variable, $D$ is diffusivity coefficient, $\tau$ is relaxation time, $\frac{{\partial^{n} }}{{\partial {\upzeta }^{n} }}$ is the nth derivative w.r.t direction, and $\xi \left( {x, t} \right)$ is the distribution function of heat or temperature. The first law of mass diffusion and the traditional Fourier law for the conduction of heat for the one-dimensional continuous model are typically expressed as follows [21]:

$$I\left( {x,t} \right) = - D\frac{{\partial \xi \left( {x,t} \right)}}{\partial x},$$

(1.1)

$$\frac{{\partial \xi \left( {x,t} \right)}}{\partial t} = - \frac{{\partial I\left( {x,t} \right)}}{\partial x},$$

(1.2)

where $I\left( {x,t} \right)$ is the diffusive flux. From Eqs. (1.1) and (1.2), we get second law of Fick’s as:

$$\frac{{\partial \xi \left( {x,t} \right)}}{\partial t} = D\frac{{\partial^{2} \xi \left( {x,t} \right)}}{{\partial x^{2} }}.$$

(1.3)

Cattaneo constructed a model considering the finite velocity in [27] as:

$$- D\frac{{\partial \xi \left( {x,t} \right)}}{\partial x} = \tau \frac{{\partial I\left( {x,t} \right)}}{\partial t} + I\left( {x,t} \right).$$

(1.4)

An expanded heat conduction law is used to broaden the application of the traditional heat conduction equation. A generalised law for heat conduction, however, enables the traditional heat conduction connection to be expanded even further. Recently, anomalous behaviour has been explained by a constitutive equation with a one-dimensional form that generalises the conventional Cattaneo equation fractionally

$$- D\frac{{\partial \xi \left( {x,t} \right)}}{\partial x} = \tau^{\alpha } \frac{{\partial^{\alpha } I\left( {x,t} \right)}}{{\partial t^{\alpha } }} + I\left( {x,t} \right), 0 < \alpha \le 1,$$

(1.5)

where $\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}$ is the time-fractional derivative.

From Eq. (1.2) and (1.5), the fractional Cattaneo equation can be written as:

$$\frac{{\partial \xi \left( {x,t} \right)}}{\partial t} + \tau \frac{{\partial^{1 + \alpha } \xi \left( {x,t} \right)}}{{\partial t^{1 + \alpha } }} = D\frac{{\partial^{2} \xi \left( {x,t} \right)}}{{\partial x^{2} }}, \quad 0 < \alpha \le 1.$$

(1.6)

The generalised time-fractional Cattaneo model (GTFCM) in the non-dimensional form is considered in [37] as:

$$\frac{{\partial^{\alpha } \xi \left( {{\upzeta },t} \right)}}{{\partial t^{\alpha } }} + \beta \frac{{\partial \xi \left( {{\upzeta },t} \right)}}{\partial t} - \Delta \xi \left( {{\upzeta },t} \right) = S\left( {{\upzeta },t} \right),\left( {{\upzeta },t} \right) \in {\Omega } \times \left( {0,T} \right],\; {\upzeta } = \left( {x,y} \right),\quad 1 < \alpha < 2.$$

(1.7)

In this work, we take into account the following GTFCM in the Caputo sense to deal with non-dimensional thermo-elastic problems of porous media

$${}_{0}^{c} D_{t}^{\alpha } \xi \left( {{\upzeta },t} \right) + \beta \xi_{t} \left( {{\upzeta },t} \right) - \Delta \xi \left( {{\upzeta },t} \right) = S\left( {{\upzeta },t} \right), \;\left( {{\upzeta },t} \right) \in {\Omega } \times \left( {0,T} \right],\quad {\upzeta } = \left( {x,y} \right),$$

(1.8)

with

$$\xi \left( {{\upzeta },0} \right) = g\left( {\upzeta } \right), \frac{{\partial \xi \left( {{\upzeta },0} \right)}}{\partial t} = \varphi \left( {\upzeta } \right), {\upzeta } \in \Omega ,$$

(1.9)

where $\xi \left( {x, t} \right)$ is the distribution function of heat or temperature, $\beta$ is a constant and ${\Omega }$ is bounded domain which is the convex polygon in $R^{2}$ with the boundary $\partial {\Omega }$, $S\left( {{\upzeta },t} \right)$ is the given source term and ${}_{0}^{c} D_{t}^{\alpha }$ is the Caputo derivative of order $\alpha$ with $1 < \alpha < 2,$ and $g\left( {\upzeta } \right)$ and $\varphi \left( {\upzeta } \right)$ are given smooth functions ${\upzeta } = \left( {x,y} \right).$

The study of the mathematical model of fractional order is very important for the betterment of society but sometimes, it is very difficult to solve them. Therefore, there is a need for the development of a numerical technique that can get approximate analytic solutions to these models. Many techniques have been applied to study these fractional models such as the Adomian decomposition technique [38], finite elements technique [3], Adam–Bashforth method [39], homotopy analysis transform technique [40], Shehu transform technique [41], fractional homotopy perturbation transform method [42], collocation method [43], fractional reduced transform method [44], fractional variation iteration method [45], Sumudu transform technique [46], q-HAM [47], Sumudu perturbation transform technique [48] and hybrid numerical technique [49].

In this work, our main objective is to investigate the GTFCM in the Caputo sense in the non-dimensional form for dealing with thermo-elastic problems of the porous media. There are many fractional derivatives available in the literature, but the Caputo derivative [50] is the most reliable because it has power law kernel and it deals with the limitation of the Riemann–Liouville derivative, which gives a nonzero value for the derivative of a constant function. The stability is analysed using the Lyapunov function and the error analysis is discussed. Homotopy perturbation transform technique (HPTT) is used to get the numerical solution of the model $(1.8).$ This technique perfectly combines Laplace transform with the homotopy perturbation method. This model is used to describe various natural phenomena such as macro and micro-scale heat transfer, non-Fickian diffusion, Gaussian diffusion, heat conduction, anomalous super-diffusion, and sub-diffusion.

The novelty of this paper is that it gives a precise forecast about the process of heat conduction for dealing with thermo-elastic problems of the porous media. The combination of the numerical technique, homotopy perturbation technique, with the Laplace transform is proven to be time-saving, and also reduces the computational work to solve nonlinear fractional models, which are applicable in vast areas of engineering and sciences. The main contribution of this work is to provide a high accuracy computational technique to obtain the solution of the GTFCM and can study the process of heat conduction in porous media very precisely. The results achieved in this paper may be of substantial benefit to (but not limited to) material, plasma, extended irreversible thermodynamics, cosmological models, diffusion theory in crystalline solids, computational biology, and micro-scale and macro-scale heat conduction. Also, we simulate three different test examples to show that with the help of proposed technique HPTT, we can study the process of heat conduction very precisely than the other existing techniques.

2 Preliminaries

Definition 2.1.

[52] The fractional Caputo derivative of $y\left( t \right)$ is given as: $D^{\alpha } y\left( t \right) = I^{m - \alpha } D^{m} y\left( t \right) = \frac{1}{{\Gamma \left( {m - \alpha } \right)}}\mathop \int \limits_{0}^{t} \left( {t - f} \right)^{m - \alpha - 1} y^{m} \left( f \right){\text{d}}f,$where $m - 1 < \alpha \le m.$

Definition 2.2.

[51] The fractional Caputo integral of $y\left( t \right)$ is given as:

$${}_{0}^{c} I_{t}^{\alpha } \left\{ {y\left( t \right)} \right\} = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - f} \right)^{\alpha - 1} y\left( f \right){\text{d}}f,$$

where $0 < \alpha \le 1.$

Definition 2.3.

[52] The Laplace transform (LT) of a function $y\left( t \right)$ is given as:

$$L\left[ {y\left( t \right)} \right] = y\left( s \right) = \mathop \int \limits_{0}^{\infty } e^{{ - {\text{st}}}} y\left( t \right){\text{d}}t.$$

Definition 2.4.

[52] The LT of the fractional Caputo derivative is defined as:

$$L\left[ {D_{t}^{\alpha } y\left( t \right)} \right] = s^{\alpha } y\left( s \right) - \mathop \sum \limits_{k = 0}^{m - 1} s^{{\left( {\alpha - k - 1} \right)}} y^{\left( k \right)} \left( 0 \right),\quad m - 1 < \alpha \le m.$$

Definition 2.5.

The fractional Caputo derivative of a constant $a$ is given as:

$${}_{0}^{c} D_{t}^{\alpha } a = 0.$$

Theorem 2.1.

[52] The unique solution of FDE, ${}_{0}^{c} D_{t}^{\alpha } y\left( t \right) = e\left( t \right)$ is given as:

$$y\left( t \right) = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{t} \left( {t - f} \right)^{\alpha - 1} e\left( f \right){\text{d}}f,$$

where $0 < \alpha \le 1.$

3 Stability analysis

In this segment, we analyse the stability of GTFCM by using the Lyapunov function.

We can write $(1.8)$ as:

$${}_{0}^{c} D_{t}^{\alpha } \xi \left( {{\upzeta },t} \right) = \psi \left( {{\upzeta },t,\xi } \right),\, \xi \left( {{\upzeta },0} \right) = g\left( {\upzeta } \right).$$

(3.1)

For investigating the asymptotically stability of Eq. (3.1) we have to show that the solution of the equation given below is $+ ve$ such that $lim \to 0$ as $t \to \infty .$

$${}_{0}^{c} D_{t}^{\alpha } \xi = \delta \xi , \quad \xi \left( 0 \right) = a, \delta < 0,$$

(3.2)

we can convert (3.2) into an integral equation as:

$$\xi = \xi \left( 0 \right) + \delta I_{{0^{ + } }}^{\alpha } \xi , \, \xi \left( 0 \right) = a.$$

(3.3)

For finding the solution of Eq. (3.3) we use Picard’s method. The approximating formula is given by

$$\xi_{n + 1} = \xi_{0} + \delta I_{{0^{ + } }}^{\alpha } \xi_{n} ,\, 0 \le n,$$

(3.4)

where $\xi_{0} = \xi \left( 0 \right) = a,$ we have

$$\begin{array}{*{20}l} {\xi_{1} = \xi_{0} + \delta I_{{0^{ + } }}^{\alpha } \xi_{0} = \xi_{0} + \frac{{\delta \xi_{0} }}{{\Gamma \left( {1 + \alpha } \right)}}t^{\alpha } ,} \hfill \\ {\xi_{2} = \xi_{0} \mathop \sum \limits_{m = 0}^{\infty } \delta^{m} \frac{{t^{m\alpha } }}{{\Gamma \left( {1 + m\alpha } \right)}},} \hfill \\ { \vdots } \hfill \\ {\xi_{m} = \xi_{0} \mathop \sum \limits_{m = 0}^{m} \delta^{m} \frac{{t^{m\alpha } }}{{\Gamma \left( {1 + m\alpha } \right)}}.} \hfill \\ \end{array}$$

(3.5)

So, we obtained the Mittag–Leffler function as:

$$E_{\alpha ,1} \left( {\delta ,1} \right) = \mathop \sum \limits_{m = 0}^{m} \delta^{m} \frac{{t^{m\alpha } }}{{{\Gamma }\left( {1 + m\alpha } \right)}}, \quad 0 < t.$$

(3.6)

The Mittag–Leffler function of one parameter is given as:

$$E_{\alpha } \left( { - t^{\alpha } } \right) = \mathop \sum \limits_{m = 0}^{m} \left( { - 1} \right)^{m} \frac{{t^{m\alpha } }}{{{\Gamma }\left( {1 + m\alpha } \right)}}, \quad 0 < t.$$

(3.7)

The Mittag–Leffler function can be approximated as [53]:

$$E_{\alpha } \left( { - t^{\alpha } } \right)\sim \frac{{t^{ - \alpha } }}{{{\Gamma }\left( {1 - \alpha } \right)}}, t \to \infty .$$

(3.8)

So, we have

$$\mathop {{\text{lim}}}\limits_{t \to \infty } E_{\alpha ,1} \left( {\delta ,t} \right) = 0.$$

(3.9)

In addition, it is evident that $E_{\alpha ,1} \left( {\delta ,t} \right)$ is positive and produces results with identical monotonicity as $E_{\alpha } \left( { - t^{\alpha } } \right)$.

Lemma 3.1.

[53] Let us suppose that ${\upzeta } = 0,$ be an equilibrium point (EP). It is Lyapunov stable if $\forall \epsilon > 0, \exists {\text{a}} \lambda = \lambda \left( {t_{0} ,\epsilon } \right),$ such that if.

$$\left\| {\zeta \left( {t_{0} } \right)} \right\| < \lambda \Rightarrow \left\| {\zeta \left( {t_{0} } \right)} \right\|\left\langle {\varepsilon ,~~\forall t} \right\rangle t_{0} .~$$

Lemma 3.2.

[54] An EP, ${\upzeta } = 0,$ is asymptotically stable if $\forall$ $\epsilon > 0, \exists {\text{a}} \lambda = \lambda \left( {t_{0} } \right) > 0,$ then

$$\left\| {\zeta \left( {t_{0} } \right)} \right\| < \lambda \Rightarrow ~\mathop {\lim }\limits_{{t \to \infty }} \zeta \left( t \right) = 0.$$

Lemma 3.3.

[54] For ${\upzeta }\left( t \right), X\left( t \right) \varepsilon C^{1} \left[ {a,b} \right], {\upzeta }\left( a \right) = X\left( a \right)$, $0 < m,$ such that if.

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }\left( t \right) \le - k{\upzeta }\left( t \right), \quad 0 < \alpha \le 1,$$

(3.10)

and

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\text{X}}\left( t \right) = - k{\text{X}}\left( t \right),$$

(3.11)

then ${\upzeta }\left( t \right) \le X\left( t \right)$ holds $\forall t \varepsilon \left[ {a,b} \right].$

Theorem 3.1.

Let us suppose that ${\upzeta } = 0$ is an EP. If $\exists$ a $+ ve$ definite and declinatory scalar function $V\left( {t,\zeta \left( t \right)} \right), t \in {\mathbb{R}}$, class $- {\rm K}$ function $\beta_{1} , \beta_{2}$ and $\beta_{3}$ such that

$$\beta _{1} \left( {\left\| {\zeta \left( t \right)} \right\|} \right) \le V\left( {t,\zeta \left( t \right)} \right) \le \beta _{2} \left( {\left\| {\zeta \left( t \right)} \right\|} \right),$$

(3.12)

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } V\left( {t,{\upzeta }\left( t \right)} \right) \le - \beta_{3} {\upzeta }\left( t \right),$$

(3.13)

then EP is asymptotically stable.

Proof

From the given Eq. (3.12) and (3.13), we have.

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } V\left( {t,{\upzeta }\left( t \right)} \right) \le - \beta_{3} \left( {\beta_{2}^{ - 1} V\left( {t,{\upzeta }\left( t \right)} \right)} \right),$$

(3.14)

where $\beta_{2}^{ - 1}$ is inverse of $\beta_{2} .$ Now considering the given fractional differential equation.

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } h\left( t \right) \le - \beta_{3} \left( {\beta_{2}^{ - 1} V\left( t \right)} \right),$$

(3.15)

with initial condition $h\left( a \right) = V\left( {a,h\left( a \right)} \right).$ Equation $\left( {3.15} \right)$ has a solution like Mittag–Leffler function $\mathop {\lim }\limits_{t \to \infty } h\left( t \right) = 0.$ Also form lemma $\left( {3.3} \right),$ it is clear that $V\left( {t,{\upzeta }\left( t \right)} \right)$ bounded by $h\left( t \right).$ Which implies that $\mathop {\lim }\limits_{t \to \infty } {\upzeta }\left( t \right) = 0.$ Hence proved.

Lemma 3.4.

[54] If ${}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }\left( t \right) \ge {}_{{a^{ + } }}^{c} D_{t}^{\alpha } X\left( t \right), 1\left\langle {\alpha \le 2, \forall t} \right\rangle a$ and ${\upzeta }\left( a \right) = X\left( a \right)$ then

$${\upzeta }\left( t \right) \ge X\left( t \right).$$

(3.16)

Lemma 3.5.

The following inequality holds.

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }^{2} \left( t \right) \le 2{\upzeta }\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }\left( t \right).$$

(3.17)

Proof

Proceeding like article [55], we have to show that.

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } \zeta^{2} \left( t \right) - 2\zeta \left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } \zeta \left( t \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{\frac{{{\text{d}}\zeta^{2} \left( f \right)}}{ds} - \frac{{2\zeta \left( t \right){\text{d}}\zeta \left( f \right)}}{{{\text{d}}s}}}}{{\left( {t - f} \right)^{\alpha } }} df \le 0.$$

(3.18)

Using definition (2.5) and putting the term $\frac{{d{\upzeta }^{2} \left( t \right)}}{df}$ inside the integral (3.18), so

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } \zeta^{2} \left( t \right) - 2\zeta \left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } \zeta \left( t \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{\frac{{{\text{d}}\zeta^{2} \left( f \right)}}{{{\text{d}}f}} - \frac{2\zeta \left( t \right)d\zeta \left( f \right)}{{{\text{d}}f}} + \frac{{{\text{d}}\zeta^{2} \left( t \right)}}{{{\text{d}}f}} }}{{\left( {t - f} \right)^{\alpha } }} {\text{d}}f.$$

(3.19)

Let $H\left( f \right) = \left( {{\upzeta }\left( f \right) - {\upzeta }\left( t \right)} \right)^{2} ,$ so we get

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }^{2} \left( t \right) - 2{\upzeta }\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }\left( t \right) = \frac{1}{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{H^{\prime}\left( f \right) { }}}{{\left( {t - f} \right)^{\alpha } }} df.$$

(3.20)

Integrating Eq. (3.20), we get

$$\mathop \int \limits_{0}^{t} \frac{{H^{\prime}\left( f \right) { }}}{{\left( {t - f} \right)^{\alpha } }}df = \left. {\frac{G\left( f \right)}{{\left( {t - f} \right)^{\alpha } }}} \right]_{f = a}^{t} - \mathop \int \limits_{0}^{t} \frac{{\alpha H\left( f \right) { }}}{{\left( {t - f} \right)^{\alpha + 1} }}df.$$

(3.21)

Now, we need to find the $\mathop {\lim }\limits_{f \to t} \frac{H\left( f \right)}{{\left( {t - f} \right)^{\alpha } }}$so

$$\begin{aligned} \mathop {\lim }\limits_{f \to t} \frac{H\left( f \right)}{{\left( {t - f} \right)^{\alpha } }} & = \mathop {\lim }\limits_{f \to t} \frac{{\left( {\zeta \left( f \right) - \zeta \left( t \right)} \right)^{2} }}{{\left( {t - f} \right)^{\alpha } }} \\ & = \mathop {\lim }\limits_{f \to t} \frac{{2\left( {\zeta \left( f \right) - \zeta \left( t \right)} \right)\zeta^{\prime}\left( f \right)}}{{\alpha \left( {t - f} \right)^{\alpha - 1} }} = 0, \\ \end{aligned}$$

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }^{2} \left( t \right) - 2{\upzeta }\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }\left( t \right) = \frac{ - 1}{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{H\left( a \right){ }}}{{\left( {t - a} \right)^{\alpha } }} - \frac{\alpha }{{{\Gamma }\left( {1 - \alpha } \right)}} \mathop \int \limits_{0}^{t} \frac{{H\left( f \right){ }}}{{\left( {t - f} \right)^{\alpha + 1} }}{\text{ d}}f.$$

(3.22)

Hence, the required result is established.

Theorem 3.2.

If ${\upzeta } = 0$ is an EP of model (1.8) and ${\upzeta }\left( t \right)\psi \left( {t,{\upzeta }\left( t \right)} \right) < 0,$ then model $\left( {1.8} \right)$ is asymptotically stable.

Proof

Let us suppose that the Lyapunov function is considered as:

$$V = \frac{{{\upzeta }^{2} \left( t \right)}}{2},$$

(3.23)

so, we get

$${}_{{a^{ + } }}^{c} D_{t}^{\alpha } V \le {\upzeta }\left( t \right){}_{{a^{ + } }}^{c} D_{t}^{\alpha } {\upzeta }\left( t \right) = {\upzeta }\left( t \right)\psi \left( {t,{\upzeta }\left( t \right)} \right) < 0.$$

(3.24)

According to theorem (3.1), the GTFCM (1.8) is asymptotically stable.

4 Application of HPTT to the GTFCM for heat conduction in porous media

The GTFCM in Caputo sense is considered in non-dimensional form as:

$${}_{0}^{c} D_{t}^{\alpha } \xi \left( {{\upzeta },t} \right) + \beta \xi_{t} \left( {{\upzeta },t} \right) - \Delta \xi \left( {{\upzeta },t} \right) = S\left( {{\upzeta },t} \right),$$

(4.1)

where $\left( {{\upzeta },t} \right) \in {\Omega } \times \left( {0,T} \right], {\upzeta } = \left( {x,y} \right),\; 1 < \alpha < 2$ and the initial conditions are

$$\xi \left( {{\upzeta },0} \right) = g\left( {\upzeta } \right), \frac{{\partial \xi \left( {{\upzeta },0} \right)}}{\partial t} = \varphi \left( {\upzeta } \right), {\upzeta } \in \Omega .$$

(4.2)

Applying Laplace transform on Eq. (4.1), we get

$${\text{LT}}\left[ {{}_{0}^{c} D_{t}^{\alpha } \xi \left( {{\upzeta },t} \right)} \right] = {\text{LT}}\left[ {\Delta \xi \left( {{\upzeta },t} \right) - \beta \xi_{t} \left( {{\upzeta },t} \right) + S\left( {{\upzeta },t} \right)} \right].$$

From definition (2.4) and Eq. (4.2), we have

$$\begin{aligned} & s^{\alpha } {\text{LT}}\left[ {\xi \left( {\zeta ,t} \right)} \right] - s^{\alpha - 1} \xi \left( {\zeta ,0} \right) - s^{\alpha - 2} \frac{{\partial \xi \left( {\zeta ,0} \right)}}{\partial t} = {\text{LT}}\left[ {\Delta \xi \left( {\zeta ,t} \right) - \beta \xi_{t} \left( {\zeta ,t} \right) + S\left( {\zeta ,t} \right)} \right], \\ & s^{\alpha } {\text{LT}}\left[ {\xi \left( {\zeta ,t} \right)} \right] = s^{\alpha - 1} g\left( \zeta \right) + s^{\alpha - 2} \varphi \left( \zeta \right) + {\text{LT}}\left[ {\Delta \xi \left( {\zeta ,t} \right) - \beta \xi_{t} \left( {\zeta ,t} \right) + S\left( {\zeta ,t} \right)} \right], \\ & {\text{LT}}\left[ {\xi \left( {\zeta ,t} \right)} \right] = \frac{1}{s}g\left( \zeta \right) + \frac{1}{{s^{2} }}\varphi \left( \zeta \right) + \frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi \left( {\zeta ,t} \right) - \beta \xi_{t} \left( {\zeta ,t} \right) + S\left( {\zeta ,t} \right)} \right]. \\ \end{aligned}$$

Applying LT inverse on above equation, we have

$$\xi \left( {{\upzeta },t} \right) = g\left( {\upzeta } \right) + t\varphi \left( {\upzeta } \right) + LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi \left( {{\upzeta },t} \right) - \beta \xi_{t} \left( {{\upzeta },t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\}.$$

(4.3)

Now, we apply homotopy perturbation technique to Eq. (4.3) we put

$$\xi \left( {{\upzeta },t} \right) = \mathop \sum \limits_{n = 0}^{\infty } p^{n} \xi_{n} \left( {{\upzeta },t} \right),$$

so, we get

$$\mathop \sum \limits_{n = 0}^{\infty } p^{n} \xi_{n} \left( {{\upzeta },t} \right) = g\left( {\upzeta } \right) + t\varphi \left( {\upzeta } \right)$$

$$\begin{aligned} \mathop \sum \limits_{n = 0}^{\infty } p^{n} \xi_{n} \left( {{\upzeta },t} \right) & = g\left( {\upzeta } \right) + t\varphi \left( {\upzeta } \right) \\ & \quad + {\text{LT}}^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\mathop \sum \limits_{n = 0}^{\infty } p^{n} \Delta \xi_{n} \left( {{\upzeta },t} \right) - \beta \mathop \sum \limits_{n = 0}^{\infty } p^{n} \left( {\xi_{n} } \right)_{t} \left( {{\upzeta },t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\}. \\ \end{aligned}$$

(4.4)

Now, we compare the like power’s coefficient of $p$ of Eq. (4.4), we have

$$\xi_{0} \left( {{\upzeta },t} \right) = g\left( {\upzeta } \right) + t\varphi \left( {\upzeta } \right),$$

(4.5)

$$\xi_{1} \left( {{\upzeta },t} \right) = LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi_{0} \left( {{\upzeta },t} \right) - \beta \left( {\xi_{0} } \right)_{t} \left( {{\upzeta },t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\},$$

(4.6)

$$\xi_{2} \left( {{\upzeta },t} \right) = {\text{LT}}^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi_{1} \left( {{\upzeta },t} \right) - \beta \left( {\xi_{1} } \right)_{t} \left( {{\upzeta },t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\},$$

(4.7)

$$\vdots$$

$$\xi_{n} \left( {{\upzeta },t} \right) = {\text{LT}}^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi_{n - 1} \left( {{\upzeta },t} \right) - \beta \left( {\xi_{n - 1} } \right)_{t} \left( {{\upzeta },t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\}.$$

(4.8)

The final solution by HPTT is

$$\xi \left( {{\upzeta },t} \right) = \mathop {\lim }\limits_{k \to \infty } \mathop \sum \limits_{n = 0}^{k} \xi_{n} \left( {{\upzeta },t} \right).$$

(4.9)

5 Error analysis

In this segment, we analyse the error of the proposed technique HPTT.

Theorem 5.1.

If there exists a constant $0 < \varepsilon < 1$ such that $~\xi _{{n + 1}} \left( {\zeta ,t} \right) \le \varepsilon ~\xi _{n} \left( {\zeta ,t} \right)$ for each value of $n$. Furthermore, if the truncated series $\mathop \sum \nolimits_{n = 0}^{r} \xi_{n} \left( {{\upzeta },t} \right)$ is employed as a numerical solution $\xi \left( {{\upzeta },t} \right)$, then the maximum absolute truncated error is determined as.

$$\left\| {\xi \left( {\zeta ,t} \right) - \mathop \sum \limits_{{n = 0}}^{r} ~\xi _{n} \left( {\zeta ,t} \right)} \right\| \le \frac{{\varepsilon ^{{r + 1}} }}{{\left( {1 - \varepsilon } \right)}}\left\| {\xi _{0} \left( {\zeta ,t} \right)} \right\|~.$$

Proof

We have

$$\left\| {\xi \left( {{\upzeta },t} \right) - \mathop \sum \limits_{n = 0}^{r} \xi_{n} \left( {{\upzeta },t} \right)} \right\| = \left\| {\mathop \sum \limits_{n = r + 1}^{\infty } \xi_{n} \left( {{\upzeta },t} \right)} \right\|,$$

$$\le \mathop \sum \limits_{n = r + 1}^{\infty } \left\| {\xi_{n} \left( {{\upzeta },t} \right)} \right\|,\quad \le \mathop \sum \limits_{n = r + 1}^{\infty } \varepsilon^{m} \left\| {\xi_{0} \left( {{\upzeta },t} \right)} \right\| ,$$

$$\le \left( \varepsilon \right)^{r + 1} \left[ {1 + \left( \varepsilon \right)^{1} + \left( \varepsilon \right)^{2} + \cdots } \right] \left\| {\xi_{0} \left( {{\upzeta },t} \right)} \right\|,$$

$$\le \frac{{\varepsilon^{r + 1} }}{{\left( {1 - \varepsilon } \right)}} \left\| {\xi_{0} \left( {{\upzeta },t} \right)} \right\|.$$

Hence proved.

6 Numerical simulation

In this segment, we simulate three different test examples of GTFCM to demonstrate the effectiveness of the HPTT by calculating the ${L}^{2}$ and ${L}^{\infty }$ error norm and comparing it with the existing techniques.

${\varvec{L}}^{2}$ and ${\varvec{L}}^{\infty }$ error norm.

The $L^{2}$ and $L^{\infty }$ error norm for the proposed technique HPTT is given as:

$L^{2}$ = $\sqrt {h\mathop \sum \limits_{j = 0}^{N} \left| {\xi_{{{\text{Ex}}}} - \xi_{{\text{N}}} } \right|^{2} }$,

$L^{\infty } = \max_{j} \left| {\xi_{{{\text{Ex}}}} - (\xi_{{\text{N}}} )_{j} } \right|$, where $\xi_{{{\text{Ex}}}}$ is the exact solution and $\xi_{{\text{N}}}$ is the numerical solution obtained by the proposed technique HPTT.

Example 6.1.

Let us consider the GTFCM given below.

$${}_{0}^{c} D_{t}^{\alpha } \xi \left( {{\upzeta },t} \right) + \xi_{t} \left( {{\upzeta },t} \right) - \Delta \xi \left( {{\upzeta },t} \right) = \left( {\frac{{6t^{3 - \alpha } }}{{{\Gamma }\left( {4 - \alpha } \right)}} - 2t^{3} + 3t^{2} } \right)e^{x + y} ,$$

(6.1)

$\left( {{\upzeta },t} \right) \in {\Omega } \times \left( {0,T} \right]$, where ${\upzeta } = \left( {x,y} \right)$ and the analytical solution of Eq. (6.1) at $\alpha = 2$ is $\xi \left( {{\upzeta },t} \right) = t^{3} e^{x + y} .$

Solution

From the analytical solution, let $\xi \left( {{\upzeta },0} \right) = 0$ and $\frac{{\partial \xi \left( {{\upzeta },0} \right)}}{\partial t} = 0$. Here, $\beta = 1$ and $S\left( {{\upzeta },t} \right) = \left( {\frac{{6t^{3 - \alpha } }}{{\Gamma \left( {4 - \alpha } \right)}} - 2t^{3} + 3t^{2} } \right)e^{x + y} .$ Now, we apply HPTT to Eq. (6.1), so we have

$$\xi_{0} \left( {x,y,t} \right) = 0,$$

(6.2)

$$\begin{aligned} \xi_{1} \left( {x,y,t} \right) & = LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}LT\left[ {\Delta \xi_{0} \left( {x,y,t} \right) - \beta \left( {\xi_{0} } \right)_{t} \left( {x,y,t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\} \\ & \quad = e^{x + y} \left[ {6\frac{{t^{3} }}{{{\Gamma }\left( 4 \right)}} - 2\frac{{t^{\alpha + 3} }}{{{\Gamma }\left( {\alpha + 4} \right)}} + 3\frac{{t^{\alpha + 2} }}{{{\Gamma }\left( {\alpha + 3} \right)}}} \right], \\ \vspace*{3pt} \end{aligned}$$

(6.3)

$$\begin{aligned} \xi _{2} \left( {x,y,t} \right) & = {\text{LT}}^{{ - 1}} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi _{1} \left( {x,y,t} \right) - \beta \left( {\xi _{1} } \right)_{t} \left( {x,y,t} \right) + S\left( {\zeta ,t} \right)} \right]} \right\} \\ & = e^{{x + y}} \left[6\frac{{t^{3} }}{{\Gamma \left( 4 \right)}} - \frac{3}{2}\frac{{t^{{\alpha + 3}} }}{{\Gamma \left( {\alpha + 4} \right)}} + \frac{9}{4}\frac{{t^{{\alpha + 2}} }}{{\Gamma \left( {\alpha + 3} \right)}} - 4\frac{{t^{{2\alpha + 3}} }}{{\Gamma \left( {2\alpha + 4} \right)}}\right. \\ & \left.\quad + \frac{{3\left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)}}\frac{{t^{{2\alpha + 1}} }}{{\Gamma \left( {2\alpha + 2} \right)}} + \frac{{\left( {9\alpha + 24} \right)}}{{\left( {\alpha + 3} \right)}}\frac{{t^{{2\alpha + 2}} }}{{\Gamma \left( {2\alpha + 3} \right)}}\right], \\ \vspace*{3pt} \end{aligned}$$

(6.4)

$$\begin{aligned} \xi_{3} \left( {x,y,t} \right) & = LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}LT\left[ {\Delta \xi_{2} \left( {x,y,t} \right) - \beta \left( {\xi_{2} } \right)_{t} \left( {x,y,t} \right) + S\left( {\zeta ,t} \right)} \right]} \right\} \\ & = e^{x + y} \left[ {6\frac{{t^{3} }}{\Gamma \left( 4 \right)} - 42\frac{{t^{\alpha + 3} }}{{\Gamma \left( {\alpha + 4} \right)}} + 6\frac{{t^{\alpha + 2} }}{{\Gamma \left( {\alpha + 3} \right)}} - 3\frac{{t^{2\alpha + 3} }}{{\Gamma \left( {2\alpha + 4} \right)}} - 8\frac{{t^{3\alpha + 3} }}{{\Gamma \left( {3\alpha + 4} \right)}}} + \frac{{\left( {9\alpha + 18} \right)}}{{\left( {4\alpha + 12} \right)}}\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}} \right. \\ & \quad + \frac{{\left( {21\alpha + 15} \right)}}{{\left( {2\alpha + 8} \right)}}\frac{{t^{2\alpha + 2} }}{{\Gamma \left( {2\alpha + 3} \right)}} + \left( {\frac{18\alpha + 48}{{\alpha + 3}}} {\frac{8\alpha + 12}{{2\alpha + 4}}} \right)\frac{{t^{3\alpha + 2} }}{{\Gamma \left( {3\alpha + 3} \right)}} - \frac{{3\left( {2\alpha + 1} \right)\left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)\left( {\alpha + 3} \right)}}\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}} + \left( {\frac{{\left( {6\alpha + 12} \right)}}{{\left( {\alpha + 3} \right)}}} \right. \\ & \left. { \quad \left. { - \frac{{\left( {9\alpha + 24} \right)\left( {2\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\left( {2\alpha + 3} \right)}}} \right)\frac{{t^{3\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}}} \right]. \\ \end{aligned}$$

(6.5)

The final solution is

$$\xi \left( {x,y,t} \right) = \xi_{0} \left( {x,y,t} \right) + \xi_{1} \left( {x,y,t} \right) + \xi_{2} \left( {x,y,t} \right) + \xi_{3} \left( {x,y,t} \right) + \cdots$$

(6.6)

Now, from Eqs. (6.2–6.6), the solution of Eq. (6.1) is given as:

$$\begin{aligned} \xi \left( {x,y,t} \right) & = e^{{x + y}} \left[ {6\frac{{t^{3} }}{{\Gamma \left( 4 \right)}} - 2\frac{{t^{{\alpha + 3}} }}{{\Gamma \left( {\alpha + 4} \right)}} + 3\frac{{t^{{\alpha + 2}} }}{{\Gamma \left( {\alpha + 3} \right)}}} \right] + e^{{x + y}} \left[ {6\frac{{t^{3} }}{{\Gamma \left( 4 \right)}} - \frac{3}{2}\frac{{t^{{\alpha + 3}} }}{{\Gamma \left( {\alpha + 4} \right)}}} \right. \\ & \quad \left. { + \frac{9}{4}\frac{{t^{{\alpha + 2}} }}{{\Gamma \left( {\alpha + 3} \right)}} - 4\frac{{t^{{2\alpha + 3}} }}{{\Gamma \left( {2\alpha + 4} \right)}} + \frac{{3\left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)}}\frac{{t^{{2\alpha + 1}} }}{{\Gamma \left( {2\alpha + 2} \right)}} + \frac{{\left( {9\alpha + 24} \right)}}{{\left( {\alpha + 3} \right)}}\frac{{t^{{2\alpha + 2}} }}{{\Gamma \left( {2\alpha + 3} \right)}}} \right] \\ & \quad + e^{{x + y}} \left[ {6\frac{{t^{3} }}{{\Gamma \left( 4 \right)}} - 42\frac{{t^{{\alpha + 3}} }}{{\Gamma \left( {\alpha + 4} \right)}} + 6\frac{{t^{{\alpha + 2}} }}{{\Gamma \left( {\alpha + 3} \right)}} - 3\frac{{t^{{2\alpha + 3}} }}{{\Gamma \left( {2\alpha + 4} \right)}}} \right. - 8\frac{{t^{{3\alpha + 3}} }}{{\Gamma \left( {3\alpha + 4} \right)}} \\ & \quad + \frac{{\left( {9\alpha + 18} \right)}}{{\left( {4\alpha + 12} \right)}}\frac{{t^{{2\alpha + 1}} }}{{\Gamma \left( {2\alpha + 2} \right)}} + \frac{{\left( {21\alpha + 15} \right)}}{{\left( {2\alpha + 8} \right)}}\frac{{t^{{2\alpha + 2}} }}{{\Gamma \left( {2\alpha + 3} \right)}} - \frac{{3\left( {2\alpha + 1} \right)\left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)\left( {\alpha + 3} \right)}}\frac{{t^{{3\alpha }} }}{{\Gamma \left( {3\alpha + 1} \right)}} \\ & \quad + ~\left( {\frac{{\left( {6\alpha + 12} \right)}}{{\left( {\alpha + 3} \right)}} - \frac{{\left( {9\alpha + 24} \right)\left( {2\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\left( {2\alpha + 3} \right)}}} \right)\frac{{t^{{3\alpha + 1}} }}{{\Gamma \left( {3\alpha + 2} \right)}} + \left( {\frac{{18\alpha + 48}}{{\alpha + 3}}} \right.\left. { + \frac{{8\alpha + 12}}{{2\alpha + 4}}} \right) \left. { \frac{{t^{{3\alpha + 2}} }}{{\Gamma \left( {3\alpha + 3} \right)}}} \right].~~ \\ \end{aligned}$$

(6.7)

Example 6.2.

Let us consider the GTFCM given below

$${}_{0}^{c} D_{t}^{\alpha } \xi \left( {{\upzeta },t} \right) + \xi_{t} \left( {{\upzeta },t} \right) - \Delta \xi \left( {{\upzeta },t} \right) = \left( {\frac{{6t^{2} }}{{{\Gamma }\left( {4 - \alpha } \right)}} + \left( {2 + \alpha } \right)t^{1 + \alpha } + 2\pi^{2} t^{2 + \alpha } } \right)\sin \left( {\pi x} \right)\sin \left( {\pi y} \right),$$

(6.8)

where $\left( {{\upzeta },t} \right) \in {\Omega } \times \left( {0,T} \right]$, ${\upzeta } = \left( {x,y} \right)$ and the analytical solution of (6.8) is $\xi \left( {{\upzeta },t} \right) = \sin \left( {\pi x} \right)\sin \left( {\pi y} \right)t^{\alpha + 2} .$

Solution

From the analytical solution, let $\xi \left( {{\upzeta },0} \right) = 0$ and $\frac{{\partial \xi \left( {{\upzeta },0} \right)}}{\partial t} = 0$. Here, $\beta = 1$ and $S\left( {{\upzeta },t} \right) = \left( {\frac{{6t^{2} }}{{{\Gamma }\left( {4 - \alpha } \right)}} + \left( {2 + \alpha } \right)t^{1 + \alpha } + 2\pi^{2} t^{2 + \alpha } } \right)\sin \left( {\pi x} \right)\sin \left( {\pi y} \right).$ Now, we apply HPTT to Eq. (6.8) so, we have

$$\xi_{0} \left( {x,y,t} \right) = 0,$$

(6.9)

$$\begin{aligned} \xi_{1} \left( {x,y,t} \right) & = LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}LT\left[ {\Delta \xi_{0} \left( {x,y,t} \right) - \beta \left( {\xi_{0} } \right)_{t} \left( {x,y,t} \right) + S\left( {{\upzeta },t} \right)} \right]} \right\} \\ & = \left[ {\frac{12}{{{\Gamma }\left( {4 - \alpha } \right)}}\frac{{t^{\alpha + 2} }}{{{\Gamma }\left( {{\upalpha } + 3} \right)}} + \left( {2 + \alpha } \right){\Gamma }\left( {{\upalpha } + 2} \right)\frac{{t^{2\alpha + 1} }}{{{\Gamma }\left( {2{\upalpha } + 2} \right)}}} \right. \\ & \quad + 2\pi^{2} {\Gamma }\left( {{\upalpha } + 2} \right)\left. {\frac{{t^{2\alpha + 2} }}{{{\Gamma }\left( {2{\upalpha } + 3} \right)}}} \right]\sin \left( {\pi x} \right)\sin \left( {\pi y} \right), \\ \end{aligned}$$

(6.10)

$$\begin{aligned} \xi_{2} \left( {x,y,t} \right) & = LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}LT\left[ {\Delta \xi_{1} \left( {x,y,t} \right) - \beta \left( {\xi_{1} } \right)_{t} \left( {x,y,t} \right) + S\left( {\zeta ,t} \right)} \right]} \right\} \\ & = \left[ {\left( {\frac{ - 24}{{\Gamma \left( {4 - \alpha } \right)}} + 2\pi^{2} \Gamma \left( {\alpha + 3} \right)} \right)\frac{{t^{2\alpha + 2} }}{{\Gamma \left( {2\alpha + 3} \right)}}} \right. - \frac{{\left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)\Gamma \left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)}}\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}} \\ & \quad + \left( {\left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right) - \frac{{12\left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}}} \right)\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}} - 4\pi^{2} \Gamma \left( {\alpha + 3} \right)\frac{{t^{3\alpha + 2} }}{{\Gamma \left( {3\alpha + 3} \right)}} \\ & \quad + \frac{12}{{\Gamma \left( {4 - \alpha } \right)}}\frac{{t^{\alpha + 2} }}{{\Gamma \left( {\alpha + 3} \right)}} + \left( {\frac{{ - 2\pi^{2} \Gamma \left( {2\alpha + 2} \right)\Gamma \left( {\alpha + 3} \right)}}{{\left( {2\alpha + 3} \right)}} - 2\left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right)} \right) \\ & \left. { \quad \times \frac{{t^{3\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}}} \right]\sin \left( {\pi x} \right)\sin \left( {\pi y} \right), \\ \end{aligned}$$

(6.11)

$$\begin{aligned} \xi_{3} \left( {x,y,t} \right) & = LT^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}LT\left[ {\Delta \xi_{2} \left( {x,y,t} \right) - \beta \left( {\xi_{2} } \right)_{t} \left( {x,y,t} \right) + S\left( {\zeta ,t} \right)} \right]} \right\} \\ & = \left[ {\left( {\frac{{ - 2\pi^{2} \left( {2\alpha + 2} \right)\Gamma \left( {\alpha + 3} \right)}}{{\left( {2\alpha + 3} \right)}} - \frac{{24\pi^{2} \left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}} - \frac{{24\left( {2\alpha + 2} \right)}}{{\left( {2\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}}} \right.} \right. \\ & \left. {\quad - 2\pi^{2} \left( {2 + \alpha } \right)\frac{{\Gamma \left( {\alpha + 2} \right)}}{\Gamma \left( 2 \right)}} \right)\frac{{t^{3\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}} + \left( {\frac{ - 24}{{\Gamma \left( {4 - \alpha } \right)}} + 2\pi^{2} \Gamma \left( {\alpha + 3} \right)} \right)\frac{{t^{2\alpha + 2} }}{{\Gamma \left( {2\alpha + 3} \right)}} \\ & \quad + \left( {\frac{{\left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)\Gamma \left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)}} - \frac{{12\left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)\left( {2\alpha + 2} \right)}}} \right)\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}} \\ & \quad + \left( {\frac{{48\pi^{2} }}{{\Gamma \left( {4 - \alpha } \right)}} - 4\pi^{2} \Gamma \left( {\alpha + 3} \right)} \right)\frac{{t^{3\alpha + 2} }}{{\Gamma \left( {3\alpha + 3} \right)}} + \left( {\frac{{2\pi^{2} \left( {2\alpha + 1} \right)\left( {\alpha + 2} \right)\Gamma \left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)}}} \right. \\ & \quad - \frac{{2\pi^{2} \Gamma \left( {\alpha + 3} \right)\left( {2\alpha + 2} \right)\left( {3\alpha + 1} \right)}}{{\left( {3\alpha + 2} \right)\left( {2\alpha + 3} \right)}} - \left. {\frac{{2\Gamma \left( {\alpha + 2} \right)\left( {\alpha + 2} \right)\left( {3\alpha + 1} \right)}}{{\left( {3\alpha + 2} \right)}}} \right)\frac{{t^{4\alpha } }}{{\Gamma \left( {4\alpha + 1} \right)}} \\ & \quad + \left( {\left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right) + \frac{{12\left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}}} \right)\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}} + \frac{12}{{\Gamma \left( {4 - \alpha } \right)}}\frac{{t^{\alpha + 2} }}{{\Gamma \left( {\alpha + 3} \right)}} \\ & \quad + 8\pi^{4} \Gamma \left( {\alpha + 2} \right)\frac{{t^{4\alpha + 2} }}{{\Gamma \left( {4\alpha + 3} \right)}} + \left( {\frac{{ - 4\pi^{4} \left( {2\alpha + 2} \right)\Gamma \left( {\alpha + 3} \right)}}{{\left( {2\alpha + 3} \right)}} - \frac{{4\pi^{2} \Gamma \left( {2\alpha + 3} \right)\left( {3\alpha + 2} \right)}}{{\left( {3\alpha + 3} \right)}}} \right. \\ & \left. {\quad + 4\pi^{2} \left( {2 + \alpha } \right)\frac{{\Gamma \left( {\alpha + 2} \right)}}{\Gamma \left( 2 \right)}} \right)\left. {\frac{{t^{4\alpha + 1} }}{{\Gamma \left( {4\alpha + 2} \right)}}} \right]\sin \left( {\pi x} \right)\sin \left( {\pi y} \right). \\ \end{aligned}$$

(6.12)

The final solution is

$$\xi \left( {x,y,t} \right) = \xi_{0} \left( {x,y,t} \right) + \xi_{1} \left( {x,y,t} \right) + \xi_{2} \left( {x,y,t} \right) + \xi_{3} \left( {x,y,t} \right) + \cdots$$

(6.13)

therefore

$$\begin{aligned} \xi \left( {x,y,t} \right) & = \left[ {\frac{12}{{\Gamma \left( {4 - \alpha } \right)}}\frac{{t^{\alpha + 2} }}{{\Gamma \left( {\alpha + 3} \right)}}} \right. + \left( {\left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right) - \frac{{12\left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}}} \right)\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}} + \left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right)\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}} \\ & \quad+ \left( {\frac{ - 24}{{\Gamma \left( {4 - \alpha } \right)}} + 2\pi^{2} \Gamma \left( {\alpha + 3} \right)} \right)\frac{{t^{2\alpha + 2} }}{{\Gamma \left( {2\alpha + 3} \right)}} + 2\pi^{2} \Gamma \left( {\alpha + 2} \right)\frac{{t^{2\alpha + 2} }}{{\Gamma \left( {2\alpha + 3} \right)}} + \frac{12}{{\Gamma \left( {4 - \alpha } \right)}}\frac{{t^{\alpha + 2} }}{{\Gamma \left( {\alpha + 3} \right)}} \\ & \quad + \left( {\frac{{ - 2\pi^{2} \Gamma \left( {2\alpha + 2} \right)\Gamma \left( {\alpha + 3} \right)}}{{\left( {2\alpha + 3} \right)}}} {\quad - 2\left( {2 + \alpha } \right)\frac{{\Gamma \left( {\alpha + 2} \right)}}{\Gamma \left( 2 \right)}} \right)\frac{{t^{3\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}} + \left( {\frac{ - 24}{{\Gamma \left( {4 - \alpha } \right)}} + 2\pi^{2} \Gamma \left( {\alpha + 3} \right)} \right)\frac{{t^{2\alpha + 2} }}{{\Gamma \left( {2\alpha + 3} \right)}} \\ & \quad + \left( {\frac{{ - 2\pi^{2} \left( {2\alpha + 2} \right)\Gamma \left( {\alpha + 3} \right)}}{{\left( {2\alpha + 3} \right)}} - \frac{{24\pi^{2} \left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}} - \frac{{24\left( {2\alpha + 2} \right)}}{{\left( {2\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}}} \right. \\ & \left. {\quad - 2\pi^{2} \left( {2 + \alpha } \right)\frac{{\Gamma \left( {\alpha + 2} \right)}}{\Gamma \left( 2 \right)}} \right)\frac{{t^{3\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}} - \frac{{3\alpha \Gamma \left( {\alpha + 2} \right)\left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {3\alpha + 1} \right)\left( {2\alpha + 2} \right)}}\frac{{t^{4\alpha - 1} }}{{\Gamma \left( {4\alpha } \right)}} \\ & \quad + \left( {\frac{{48\pi^{2} }}{{\Gamma \left( {4 - \alpha } \right)}} - 4\pi^{2} \Gamma \left( {\alpha + 3} \right)} \right)\frac{{t^{3\alpha + 2} }}{{\Gamma \left( {3\alpha + 3} \right)}} + \left( {\frac{{2\pi^{2} \left( {2\alpha + 1} \right)\left( {\alpha + 2} \right)\Gamma \left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)}}} \right. \\ & \quad - \frac{{2\pi^{2} \Gamma \left( {\alpha + 3} \right)\left( {2\alpha + 2} \right)\left( {3\alpha + 1} \right)}}{{\left( {3\alpha + 2} \right)\left( {2\alpha + 3} \right)}} - \left. {\frac{{2\Gamma \left( {\alpha + 2} \right)\left( {\alpha + 2} \right)\left( {3\alpha + 1} \right)}}{{\left( {3\alpha + 2} \right)}}} \right)\frac{{t^{4\alpha } }}{{\Gamma \left( {4\alpha + 1} \right)}} \\ & \quad + \left( {\left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right) + \frac{{12\left( {\alpha + 2} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)}}} \right)\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}} + \frac{12}{{\Gamma \left( {4 - \alpha } \right)}}\frac{{t^{\alpha + 2} }}{{\Gamma \left( {\alpha + 3} \right)}} \\ & \quad + \left( {\frac{{ - 4\pi^{4} \left( {2\alpha + 2} \right)\Gamma \left( {\alpha + 3} \right)}}{{\left( {2\alpha + 3} \right)}} - \frac{{4\pi^{2} \Gamma \left( {2\alpha + 3} \right)\left( {3\alpha + 2} \right)}}{{\left( {3\alpha + 3} \right)}} + 4\pi^{2} \left( {2 + \alpha } \right)\Gamma \left( {\alpha + 2} \right)} \right) \\ & \quad \times \frac{{t^{4\alpha + 1} }}{{\Gamma \left( {4\alpha + 2} \right)}} + \left( {\frac{{\left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)\Gamma \left( {\alpha + 2} \right)}}{{\left( {2\alpha + 2} \right)}} - \frac{{12\left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {\alpha + 3} \right)\Gamma \left( {4 - \alpha } \right)\left( {2\alpha + 2} \right)}}} \right)\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}} \\ & \left. { \quad + 8\pi^{4} \Gamma \left( {\alpha + 2} \right)\frac{{t^{4\alpha + 2} }}{{\Gamma \left( {4\alpha + 3} \right)}}} \right]\sin \left( {\pi x} \right)\sin \left( {\pi y} \right). \\ \end{aligned}$$

(6.14)

Equation (6.14) gives the by final solution by HPTT.

Example 6.3

Let us consider the GTFCM given below

$${}_{0}^{c} D_{t}^{\alpha } \xi \left( {x,t} \right) + \xi_{t} \left( {x,t} \right) - \Delta \xi \left( {x,t} \right) = \left( {\left( {\alpha + 1} \right)t^{\alpha } + \Gamma \left( {\alpha + 2} \right)t + \pi^{2} t^{1 + \alpha } } \right)\sin \left( {\pi x} \right),$$

(6.15)

where $\left( {x,t} \right) \in {\Omega } \times \left( {0,T} \right]$ and the analytical solution of $\left( {6.15} \right)$ is $\xi \left( {x,t} \right) = \sin \left( {\pi x} \right)t^{\alpha + 1} .$

Solution

From the analytical solution, let $\xi \left( {x,0} \right) = 0$ and $\frac{{\partial \xi \left( {x,0} \right)}}{\partial t} = 0$. Here, $\beta = 1$ and $S\left( {x,t} \right) = \left( {\left( {\alpha + 2} \right)t^{\alpha } + {\Gamma }\left( {\alpha + 2} \right)t + 2\pi^{2} t^{1 + \alpha } } \right)\sin \left( {\pi x} \right).$ Now, we apply HPTT to $\left( {6.15} \right)$, so we have

$$\xi_{0} \left( {x,t} \right) = 0,$$

(6.16)

$$\begin{aligned} \xi _{1} \left( {x,t} \right) & = {\text{LT}}^{{ - 1}} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi _{0} \left( {x,t} \right) - \beta \left( {\xi _{0} } \right)_{t} \left( {x,t} \right) + S\left( {x,t} \right)} \right]} \right\} \\ & = \left( \left( {\alpha + 1} \right)\Gamma \left( {\alpha + 1} \right) \frac{{t^{{2\alpha}} }}{{\Gamma \left( {2\alpha + 1} \right)}} + \Gamma \left( {\alpha + 2} \right) \frac{{t^{{\alpha+1}} }}{{\Gamma \left( {\alpha + 2} \right)}} + {{\pi}^{2}} ({\alpha}+2) \frac{t^{2{\alpha}+1}}{\Gamma(2{\alpha}+2)} \right) {\sin({\pi}x)}, \end{aligned}$$

(6.17)

$$\begin{aligned} \xi_{2} \left( {x,t} \right) & = {\text{LT}}^{ - 1} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi_{1} \left( {x,t} \right) - \beta \left( {\xi_{1} } \right)_{t} \left( {x,t} \right) + S\left( {x,t} \right)} \right]} \right\} \\ & = \Bigg[\Gamma \left( {\alpha + 2} \right)\frac{{t^{\alpha + 1} }}{{\Gamma \left( {\alpha + 2} \right)}} - \pi^{4} \left( {\alpha + 2} \right)\frac{{t^{3\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}} - \frac{{\left( {\alpha + 1} \right)\left( {2\alpha } \right)\Gamma \left( {\alpha + 1} \right)}}{{\left( {2\alpha + 1} \right)}}\frac{{t^{3\alpha - 1} }}{{\Gamma \left( {3\alpha } \right)}} \\ & \quad - \left( {\left( {\alpha + 1} \right)\Gamma \left( {\alpha + 1} \right)\pi^{2} + \frac{{\pi^{2} \left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {2\alpha + 2} \right)}}} \right)\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}}\Bigg]\sin \left( {\pi x} \right), \\ \end{aligned}$$

(6.18)

$$\begin{aligned} \xi _{3} \left( {x,t} \right) & = {\text{LT}}^{{ - 1}} \left\{ {\frac{1}{{s^{\alpha } }}{\text{LT}}\left[ {\Delta \xi _{2} \left( {x,t} \right) - \beta \left( {\xi _{2} } \right)_{t} \left( {x,t} \right) + S\left( {x,t} \right)} \right]} \right\} \\& = \left[ \left( {(\alpha + 1)} {\Gamma{(\alpha+1)}{\pi}^4}+ \frac {{\pi}^4 ({\alpha}+2)(3{\alpha}+1)}{(3{\alpha}+2)}+ \frac {{\pi}^4 ({\alpha}+2)(2{\alpha}+1)}{(2{\alpha}+2)}\right) \right. \\& {\times} \frac {t^{4{\alpha}}} {\Gamma(4{\alpha}+1)}+ \left( \frac {{\pi}^2({\alpha}+1)(2{\alpha})\Gamma({\alpha}+1)}{(2{\alpha}+1)} + \frac {{\pi}^2({\alpha}+1)(3{\alpha})\Gamma({\alpha}+1)}{(3{\alpha}+1)} \right.\\&+ \left. \frac {{\pi}^2({\alpha}+2)(2{\alpha}+1)}{(2{\alpha}+2)(3{\alpha}+1)} \right)\frac {t^{4{\alpha}-1}}{\Gamma(4{\alpha})}+ \frac {2({\alpha}+1)({3 \alpha}-1)\Gamma({\alpha}+1)}{3(2{\alpha}+1)} \frac {t^{4{\alpha}-2}}{\Gamma(4{\alpha}-1)} \\& + \left. {\pi}^6 ({\alpha}+2) \frac {t^{4{\alpha}+1}}{\Gamma(4{\alpha}+2)}+ \Gamma({\alpha}+2)\frac {t^{{\alpha}+1}}{\Gamma({\alpha}+2)} \right] {{\sin}({\pi}{x})}. \end{aligned}$$

(6.19)

The final solution is

$$\xi \left( {x,t} \right) = \xi_{0} \left( {x,t} \right) + \xi_{1} \left( {x,t} \right) + \xi_{2} \left( {x,t} \right) + \xi_{3} \left( {x,t} \right) + \cdots$$

(6.20)

therefore

$$\begin{aligned} \xi \left( {x,t} \right) & = \left[ {\left( {\alpha + 1} \right)\Gamma \left( {\alpha + 1} \right)\frac{{t^{2\alpha } }}{{\Gamma \left( {2\alpha + 1} \right)}} + \Gamma \left( {\alpha + 2} \right)\frac{{t^{\alpha + 1} }}{{\Gamma \left( {\alpha + 2} \right)}} + \pi^{2} \left( {\alpha + 2} \right)\frac{{t^{2\alpha + 1} }}{{\Gamma \left( {2\alpha + 2} \right)}}} \right. \\ & \quad + \Gamma \left( {\alpha + 2} \right)\frac{{t^{\alpha + 1} }}{{\Gamma \left( {\alpha + 2} \right)}} - \pi^{4} \left( {\alpha + 2} \right)\frac{{t3^{\alpha + 1} }}{{\Gamma \left( {3\alpha + 2} \right)}} - \frac{{\left( {\alpha + 1} \right)\left( {2\alpha } \right)\Gamma \left( {\alpha + 1} \right)}}{{\left( {2\alpha + 1} \right)}}\frac{{t^{3\alpha - 1} }}{{\Gamma \left( {3\alpha } \right)}} \\ & \quad - \left( {\left( {\alpha + 1} \right)\Gamma \left( {\alpha + 1} \right)\pi^{2} + \frac{{\pi^{2} \left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {2\alpha + 2} \right)}}} \right)\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}} + \Gamma \left( {\alpha + 2} \right)\frac{{t^{\alpha + 1} }}{{\Gamma \left( {\alpha + 2} \right)}} \\ & \quad + \left( {\frac{{\pi^{2} \left( {\alpha + 1} \right)\left( {2\alpha } \right)\Gamma \left( {\alpha + 1} \right)}}{{\left( {2\alpha + 1} \right)}} + \frac{{\pi^{2} \left( {\alpha + 1} \right)\left( {3\alpha } \right)\Gamma \left( {\alpha + 1} \right)}}{{\left( {3\alpha + 1} \right)}} + \frac{{\pi^{2} \left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {2\alpha + 2} \right)\left( {3\alpha + 1} \right)}}} \right)\frac{{t^{4\alpha - 1} }}{{\Gamma \left( {4\alpha } \right)}} \\ & \quad + \left( {\left( {\alpha + 1} \right)\Gamma \left( {\alpha + 1} \right)\pi^{4} + \frac{{\pi^{4} \left( {\alpha + 2} \right)\left( {3\alpha + 1} \right)}}{{\left( {3\alpha + 2} \right)}} + \frac{{\pi^{4} \left( {\alpha + 2} \right)\left( {2\alpha + 1} \right)}}{{\left( {2\alpha + 2} \right)}}} \right)\frac{{t^{4\alpha } }}{{\Gamma \left( {4\alpha + 1} \right)}} \\ & \quad + \pi ^{6} \left( {\alpha + 2} \right)\frac{{t^{4\alpha + 1} }}{{\Gamma \left( {4\alpha + 2} \right)}} + \frac{{2\left( {\alpha + 1} \right)\left( {3\alpha - 1} \right)\Gamma \left( {\alpha + 1} \right)}}{{3\left( {2\alpha + 1} \right)}}\left. {\frac{{t^{4\alpha - 2} }}{{\Gamma \left( {4\alpha - 1} \right)}}} \right]\sin \left( {\pi x} \right). \\ \end{aligned}$$

(6.21)

7 Simulation result discussion

The proposed technique, HPTT, is applied to solve the GTFCM for heat conduction in porous media. The $L^{2}$ and $L^{\infty }$ error norms are calculated at different values of $\alpha$ and $t$ for Ex. $6.1 -$ Ex. $6.3,$ and the results are illustrated in Tables 1, 2 for Ex. $6.1,$ in Tables 4, 5 for Ex. $6.2,$ and in Tables 7, 8 for Ex. $6.3.$ It can be observed that the both $L^{2}$ and $L^{\infty }$ error norms are very less for HPTT. In Tables 3, 6 and 9, the $L^{\infty }$ error norms of the proposed technique HPTT are compared with the existing techniques RBF-PU and FDM for Ex. $6.1,$ Ex. $6.2$ and Ex. $6.3$, respectively, and we can clearly notice that the HPTT is more accurate than the existing techniques, the $L^{\infty }$ error for proposed technique is lesser than the existing techniques RBF-PU and FDM. Hence from Tables 1, 2, 3, 4, 5, 6, 7, 8 and 9, the supremacy of the proposed technique, HPTT, is validated.

Table 1 ${L}^{2}$ and ${L}^{\infty }$ error norm for $x,y\in [\mathrm{0.01,0.1}]$ and different values of $t$ and $\alpha ,$ for Ex. 6.1

Table 2 ${L}^{2}$ and ${L}^{\infty }$ error norm for $x,y\in [\mathrm{0.01,0.1}]$ and different values of $t$ and $\alpha ,$ for Ex. 6.1

Table 3 Comparison of error for the proposed technique HPTT and RBF-PU method by $L^{\infty }$ error norm on domain consider in [37] and at different values of $t$ and $\alpha$, for Ex. 6.1

Table 4 ${L}^{2}$ and ${L}^{\infty }$ error norm for $x,y\in [\mathrm{0.01,0.1}]$ and different values of $t$ and $\alpha ,$ for Ex. 6.2

Table 5 ${L}^{2}$ and ${L}^{\infty }$ error norm for $x,y\in [\mathrm{0.01,0.1}]$ and different values of $t$ and $\alpha ,$ for Ex. 6.2

Table 6 Comparison of error for the proposed technique HPTT and RBF-PU method by ${L}^{\infty }$ error norm on domain consider in [37] and at different values of $t$ and $\alpha$, for Ex. 6.2

Table 7 ${L}^{2}$ and ${L}^{\infty }$ error norm for $x\in [\mathrm{0.01,0.1}]$ and different values of $t$ and $\alpha ,$ for Ex. 6.3

Table 8 ${L}^{2}$ and ${L}^{\infty }$ error norm for $x\in [\mathrm{0.01,0.1}]$ and different values of $t$ and $\alpha ,$ for Ex. 6.3

Table 9 Comparison of error for the proposed technique HPTT and FDM method by ${L}^{\infty }$ error norm on domain consider in [56] and at different values of $t$ and $\alpha$, for Ex. 6.3

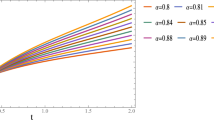
The absolute error for Ex. $6.1,$ Ex.$6.2$ and Ex. $6.3$ at $x = y = 0.1$ and different values of $\alpha$ are illustrated through two-dimensional graphical representation in Figs. 1, 2, 15, 16, 29, 30 respectively. The three-dimensional graphical representation of absolute error at $t = 0.01$ and different values of $\alpha , x$ and $y,$ for Ex.$6.1$, Ex.$6.2$ and Ex. $6.3$ are demonstrated in Figs. 3, 4, 5, 6, 7, 8, 17, 18, 19, 20, 21, 22, 31, 32, 33, 34, 35 and 36, respectively, and it is observed that for smaller values of $t$ the absolute error is lesser than the higher values of $t$, also the absolute error is minimum when we take $\alpha = 2.$ The exact solution and the approximate solution by HPTT at different values of $y, t, \alpha$ and $x = 0.1$ are illustrated through three-dimensional graphs in Figs. 9, 10, 11, 12, 13 and 14, at $y = 0.1$ and different values of $x, t, \alpha$ in Figs. 23, 24, 25, 26, 27 and 28 for Ex. $6.2.$ Figures 37, 38, 39, 40, 41 and 42 represent the three-dimensional graphical representation of the approximate solution and exact solution for Ex. $6.3$, at different values of $x, t$ and $\alpha$. It can be clearly seen in Figs. 13, 14, 27, 28, 41 and 42 that the approximate solution shows exactly the same nature as the exact solution for Ex. $6.1$, Ex. $6.2$ and Ex. $6.3$, respectively. So, from Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, it is observed that the approximate solution by HPTT is very close to the exact solution, and the absolute error is very less.

Fig. 1

Absolute error at distinct value of $\alpha$ and $t,$ for Ex. 6.1

Fig. 2

Absolute error at distinct value of $\alpha$ and $t,$ for Ex. 6.1

Fig. 3

Absolute error at $\alpha =1$ and $t=0.01,$ for Ex. 6.1

Fig. 4

Absolute error at $\alpha =1.25$ and $t=0.01,$ for Ex. 6.1

Fig. 5

Absolute error at $\alpha =1.50$ and $t=0.01,$ for Ex. 6.1

Fig. 6

Absolute error at $\alpha =1.75$ and $t=0.01,$ for Ex. 6.1

Fig. 7

Absolute error at $\alpha =1.90$ and $t=0.01,$ for Ex. 6.1

Fig. 8

Absolute error at $\alpha =2$ and $t=0.01,$ for Ex. 6.1

Fig. 9

HPTT solution $\xi (x,y,t)$ at $x=0.1$ and $\alpha =1$, for Ex. 6.1

Fig. 10

HPTT solution $\xi (x,y,t)$ at $x=0.1$ and $\alpha =1.25$, for Ex. 6.1

Fig. 11

HPTT solution $\xi \left( {x,y,t} \right)$ at $x = 0.1$ and $\alpha = 1.5$, for Ex. 6.1

Fig. 12

HPTT solution $\xi \left( {x,y,t} \right)$ at $x = 0.1$ and $\alpha = 1.75$, for Ex. 6.1

Fig. 13

HPTT solution $\xi \left( {x,y,t} \right)$ at $x = 0.1$ and $\alpha = 2$, for Ex. 6.1

Fig. 14

Exact solution $\xi \left( {x,y,t} \right)$ at $x = 0.1$ and $\alpha = 2$, for Ex. 6.1

Fig. 15

Absolute error at distinct values of $\alpha$ and $t,$ for Ex. 6.2

Fig. 16

Absolute error at distinct values of $\alpha$ and $t,$ for Ex. 6.2

Fig. 17

Absolute error at $\alpha = 1$ and $t = 0.01,$ for Ex. 6.2

Fig. 18

Absolute error at $\alpha = 1.25$ and $t = 0.01,$ for Ex. 6.2

Fig. 19

Absolute error at $\alpha = 1.50$ and $t = 0.01,$ for Ex. 6.2

Fig. 20

Absolute error at $\alpha = 1.75$ and $t = 0.01,$ for Ex. 6.2

Fig. 21

Absolute error at $\alpha = 1.90$ and $t = 0.01,$ for Ex. 6.2

Fig. 22

Absolute error at $\alpha = 2$ and $t = 0.01,$ for Ex. 6.2

Fig. 23

HPTT solution $\xi \left( {x,y,t} \right)$ at $y = 0.1$ and $\alpha = 1,$ for Ex. 6.2

Fig. 24

HPTT solution $\xi \left( {x,y,t} \right)$ at $y = 0.1$ and $\alpha = 1.25$, for Ex. 6.2

Fig. 25

HPTT solution $\xi \left( {x,y,t} \right)$ at $y = 0.1$. and $\alpha = 1.50$, for Ex. 6.2

Fig. 26

HPTT solution $\xi \left( {x,y,t} \right)$ at $y = 0.1$ and $\alpha = 1$.75, for Ex. 6.2

Fig. 27

HPTT solution $\xi \left( {x,y,t} \right)$ at $y = 0.1$ and $\alpha = 2$, for Ex. 6.2

Fig. 28

Exact solution $\xi \left( {x,y,t} \right)$ at $y = 0.1$, for Ex. 6.2

Fig. 29

Absolute error at distinct values of $\alpha$ and $t,$ for Ex. 6.3

Fig. 30

Absolute error at distinct values of $\alpha$ and $t,$ for Ex. 6.3

Fig. 31

Absolute error at $\alpha = 1$, for Ex. 6.3

Fig. 32

Absolute error at $\alpha = 1.25$, for. Ex. 6.3

Fig. 33

Absolute error at $\alpha = 1.50$, for Ex. 6.3

Fig. 34

Absolute error at $\alpha = 1.75$, for Ex. 6.3

Fig. 35

Absolute error at $\alpha = 1.90$, for Ex. 6.3

Fig. 36

Absolute error at $\alpha = 2$, for Ex. 6.3

Fig. 37

HPTT solution $\xi \left( {x,t} \right)$ at $\alpha = 1$, for Ex. 6.3

Fig. 38

HPTT solution $\xi \left( {x,t} \right)$ at $\alpha = 1.25$, for Ex. 6.3

Fig. 39

HPTT solution $\xi \left( {x,t} \right)$ at $\alpha = 1.50$, for Ex. 6.3

Fig. 40

HPTT solution $\xi \left( {x,t} \right)$ at $\alpha = 1.75$, for Ex. 6.3

Fig. 41

HPTT solution $\xi \left( {x,t} \right)$ at $\alpha = 2$, for Ex. 6.3

Fig. 42

Exact solution $\xi \left( {x,t} \right)$ for Ex. 6.3

8 Conclusion

In this work, we examine the HPTT’s potential for investigating GTFCM in the Caputo sense in the non-dimensional form for dealing with thermo-elastic problems of the porous media. The accuracy of HPTT in handling nonlinear fractional models is enhanced by this paper. The asymptotic stability of the given model is proved using the Lyapunov function, and error analysis is discussed. We consider three different examples of GTFCM, and from the numerical results, it has been observed that the proposed technique, HPTT, provides a solution that is more accurate than the existing technique, the ${L}^{2}$ and ${L}^{\infty }$ error is very less for the HPTT as compared to techniques RBF-PU and FDM. This article will be very helpful for understanding the mechanism of heat conduction mathematically and for giving a precise forecast about the process of heat conduction for dealing with thermo-elastic problems of the porous media.

Hence, we can conclude that the proposed technique HPTT, which is a combination of the numerical technique, homotopy perturbation technique, with the Laplace transform is proven to be time-saving, and also reduces the computational work to solve nonlinear fractional models, which are applicable in vast areas of engineering and sciences.