Evolution and invariants of oscillator moments

Abstract

Moments are expectation values over wave functions (or averages over a set of classical particles) of products of powers of position and momentum. For the harmonic oscillator, the evolution in the quantum case is very closely related to that of the classical case. Here we consider the non-relativistic evolution of moments of all orders for the oscillator in one dimension and investigate invariant combinations of the moments. In particular, we find an infinite set of invariants that enable us to express the evolution of any moment in terms of sinusoids. We also find explicit expressions for the inverse of these relations, thus enabling the expression of the evolution of any moment in terms of the initial set of moments. More detailed attention is given to moments of the third and fourth order in terms of the invariant combinations.

1 Introduction

Moments of wave functions or of classical ensembles of particles are used to give a simple measure of average quantities (expectation values). Moments of order n are averages of products of integer powers of position x and momentum p such that the sum of all the powers is n, for example $\langle x^{n-k} p^k\rangle$ with $0\le k\le n$. The first-order moments ($n=1$) are $\langle x\rangle$ and $\langle p\rangle$, which define the centroid of the particle (or ensemble), and the centroid of an oscillator follows a classical evolution. The higher-order moments will always be taken to be relative to the centroid.

The second-order moments ($n=2$) give a measure of the spread in position and momentum; for the oscillator, they can be combined to give the energy. The third-order moments give a measure of the skewness of the distribution (in position or in momentum). Fourth-order moments give a measure of the spread that gives more emphasis to the outer parts of the distribution. Higher-order moments have been used to investigate features of the evolution of small systems [1,2,3] and in cosmology [4]. Invariant combinations of moments in systems with quadratic Hamiltonians have been studied and applied to various physical systems, such as particle beams and paraxial analysis of optical systems (using geometrical, physical or quantum optics). This work has made use of ‘universal invariants’ [5] that are combinations of moments that remain unchanged even if the Hamiltonian has explicit time dependence (and this translates to dependence on the distance along the axis in the paraxial context). For example, a simple application is a paraxial bundle of rays passing through a system of lenses; the universal invariants remain constant as the rays traverse each refracting element of the system. An extensive list of references to this work in a wide range of physical systems can be found in ref. [6].

Here we consider the case of a one-dimensional system (a single quantum particle or an ensemble of classical particles) with a harmonic potential that does not vary with time. This system has time-independent invariants that are not universal invariants. In appendix F we give expressions for the universal invariants in terms of our invariants for $n=2, 3$ and 4. Sections 8 and 9 consider how our invariants can be applied to examine in more detail the evolution of the moments for $n=3$ and 4, with particular attention to the times and values of the extrema and inflections.

The work here is closely related to our study of similar systems free of forces [7]. Some of the development here overlaps that of Brizuela [3].

1.1 Classical and quantum oscillators

Although quantum mechanics deals with wavefunctions and operators acting on wavefunctions while classical mechanics deals with the position of particles and the effect of forces, it has long been observed that there are close connections between the two theories, particularly for quadratic Hamiltonians. In fact, the Wigner function [8] provides a mapping of wavefunctions into a distribution of particles in classical phase space, although this classical distribution is usually unphysical in that the density of particles is negative in some regions. Nevertheless, there is an exact correspondence between the evolution equations of the moments for a wavefunction and those for a classical ensemble with the corresponding quadratic Hamiltonian. This correspondence will be employed to find the evolution and invariants of the symmetrized quantum moments while allowing us to ignore the complications arising because the operators for position and momentum do not commute.

For the oscillator, the Hamiltonian is

$$\begin{aligned} {H} =p^2/2m + \omega ^2 x^2/2. \end{aligned}$$

(1)

In the quantum case, the momentum can be represented by the operator ${\hat{p}}=-\imath \hbar \partial _x$ and there is a natural length scale of $\alpha =(\hbar /m\omega )^{1/2}$. Many of the general results in this work apply to both the classical and the quantum cases, the main difference being that some extra terms (involving $\hbar$) may appear in inequalities. Thus, the range of possible evolutions of the quantum moments may differ from the classical because of these constraints (that restrict the evolution through the initial values of the moments).

2 Moments over a set of classical particles

Consider a set of N identical non-interacting particles, each subject to the same harmonic force, as in Eq. (1). If the $\mu$th particle has position $x_\mu$ and momentum $p_\mu$, then the equations of motion are

$$\begin{aligned} \text {d}_t x_\mu =p_\mu /m \qquad \text {d}_t p_\mu =-m\omega ^2 x_\mu . \end{aligned}$$

(2)

[This analysis could easily be extended to cover an ensemble of particles with unequal masses.] The centroid has position $\bar{x}=N^{-1}\sum _\mu x_\mu$ and momentum ${\bar{p}}=N^{-1}\sum _\mu p_\mu$, and ${\bar{x}}, {\bar{p}}$ satisfy the same equations of motion, Eq. (2). Then the deviations from the centroid $X_\mu =x_\mu -{\bar{x}}$, and $P_\mu =p_\mu -{\bar{p}}$ also satisfy the same equations of motion: $\text {d}_t X_\mu =P_\mu /m$ and $\text {d}_t P_\mu =-m\omega ^2 X_\mu$.

Moments of order n about the centroid then have the form $Y_k=N^{-1}\sum _\mu P_\mu ^kX_\mu ^{n-k}$ and it simply follows that

$$\begin{aligned} \text {d}_tY_k=\omega [(n-k)Y_{k+1}/m\omega -kY_{k-1}m\omega ]. \end{aligned}$$

(3)

This is the evolution equation for classical moments. This analysis can be extended to a continuous distribution $\rho (x, p)$ in phase space. Then the same equations will apply to the evolution of the moments $Y_k=\int \!\!\int \rho (x, p) X^{n-k}P^k \, \text {d} x\,\text {d} p.$

To avoid the frequent occurrences of the factor $m\omega$, we also use the notation $\mathcal {Y}_k=Y_k/(m\omega )^k$. Then

$$\begin{aligned} \text {d}_t\mathcal {Y}_k=\omega [(n-k)\mathcal {Y}_{k+1}-k\mathcal {Y}_{k-1}], \end{aligned}$$

(4)

and all $\mathcal {Y}_k$ of the same order n have the same dimension of [length]$^n$.

To further align the classical and quantum cases, we use angled brackets to denote either an average over all the particles in the ensemble or an expectation value over the wavefunction: For an ensemble, $Y_k=N^{-1}\sum _\mu P_\mu ^kX_\mu ^{n-k}=\langle P^kX^{n-k}\rangle$. Note that the moments $Y_k$ differ for different values of the order n; the index n will often be suppressed.

2.1 Invariant combinations of the classical moments

For each particle of the ensemble, define $a_\mu :=X_\mu +\imath \mathcal {P}_\mu$, with $\mathcal {P}:=P/m\omega$. Then $\text {d}_t a_\mu =-\imath \,\omega \,a_\mu$, and therefore, $e^{\imath \omega t}a_\mu$ is constant. Also $a_\mu ^*a_\mu =X_\mu ^2+\mathcal {P}_\mu ^2$ is constant. All the invariants we use will be built from products of powers of $a_\mu$ and $a_\mu ^*a_\mu$. For each n, we define

$$\begin{aligned} \qquad W_j:=\langle a^{(n+j)/2}(a^*)^{(n-j)/2}\rangle =\langle a^j (a^*a)^{(n-j)/2}\rangle =\langle (X+\imath \mathcal {P})^j(X^2+\mathcal {P}^2)^{(n-j)/2}\rangle , \end{aligned}$$

(5)

where $j=1,3,5,..,n$ if n is odd, and $j=0,2,4,..,n$ if n is even. Then $W_j$ is a sum of moments of order n and $\text {d}_t W_j=-\imath j\omega W_j$. Its evolution is therefore sinusoidal with angular frequency $j\omega$. For each $W_j$, it follows that $e^{\imath j\omega t}W_j$ is constant. Here we use the term invariants to refer to combinations of moments that remain constant due to the equations of motion. Thus, $e^{\imath j\omega t}W_j$ is a time-dependent invariant (unless $j=0$) because the time appears explicitly through $e^{\imath j\omega t}$. Later we will consider time-independent invariants that can be built from the $W_j$.

The combination of moments $W_j$ will be used to examine in detail the evolution of the moments, but before that we consider the quantum equivalent.

3 Symmetrized quantum moments

For any order n, the symmetrized quantum moment $Y_k$ is the expectation value averaged over all products that contain ${\hat{X}}$ exactly $n-k$ times and ${\hat{P}}$ exactly k times. The index k ranges from 0 to n. For example, with $n=3$,

$$\begin{aligned} Y_0= & {} \langle {\hat{X}}^3\rangle , \qquad Y_1 ={\frac{1}{3}}\langle {\hat{X}}^2{\hat{P}}+{\hat{X}}{\hat{P}}{\hat{X}}+{\hat{P}}{\hat{X}}^2\rangle , \end{aligned}$$

(6)

$$\begin{aligned} Y_3= & {} \langle {\hat{P}}^3\rangle , \qquad Y_2 = {\frac{1}{3}}\langle {\hat{P}}^2{\hat{X}}+{\hat{P}}{\hat{X}}{\hat{P}}+{\hat{X}}{\hat{P}}^2\rangle . \end{aligned}$$

(7)

We use the notation $\{f({\hat{x}}, {\hat{p}})\}$ to denote the symmetrized form of the operator $f({\hat{x}}, {\hat{p}})$, and then, $Y_k=\langle \{{\hat{X}}^{n-k}{\hat{P}}^k\}\rangle$. Any moment of order n can be expressed, using $[{\hat{X}}, {\hat{P}}]=\imath \hbar$, in terms of the set of symmetrized moments of order n or less then n.  [9]

Similarly to the classical case in Eq. (5), for the quantum case we define

$$\begin{aligned} W_j:=\langle \{({\hat{X}}+\imath {\hat{P}}/m\omega )^j({\hat{X}}^2+{\hat{P}}^2/(m\omega )^2)^{(n-j)/2}\}\rangle . \end{aligned}$$

(8)

Fortunately, the symmetrized moments have the same evolution equations as the moments of a set of classical particles, and a corresponding set of invariants.

3.1 The Wigner correspondence

The Wigner function W(x, p) [8] is a function in classical phase space that can be generated from the wavefunction. It has the property that the quantum expectation value of a symmetrized operator is equal to the phase-space average using W(x, p) as the density: $\langle \{f({\hat{x}}, {\hat{p}})\}\rangle =\int W (x, p)f (x, p) \, \text {d} x\,\text {d}p.$ Furthermore, the phase-space distribution W(x, p) follows the classical evolution for any quadratic Hamiltonian. More detail on this correspondence is given in [7].

It follows that the quantum moments will have the same evolution Eq. (3) as the classical moments. Therefore, in the quantum context $W_j$ in Eq. (8) also satisfies $\text {d}_t W_j=-\imath j\omega W_j$ and $e^{\imath j\omega t}W_j$ is invariant.

4 Sinusoidal combinations of the moments

To relate these invariants to the moments $Y_k$, we write $W_j=U_j+\imath V_j$ with $U_j$ and $V_j$ real. Then

$$\begin{aligned} \text {d}_t U_j=j\omega V_j, \qquad \text {d}_t V_j=-j\omega U_j. \end{aligned}$$

(9)

It follows that $\text {d}^2_t U_j=-(j\omega )^2 U_j$ and $\text {d}^2_t V_j=-(j\omega )^2 V_j$, so that $U_j$ and $V_j$ oscillate sinusoidally with angular frequency $j\omega$. Since $e^{\imath j\omega t}W_j$ is constant, it equals $u_j+\imath v_j$, where $u_j, v_j$ are the initial values of $U_j, V_j$, and therefore, $U_j+\imath V_j=e^{-\imath j\omega t}(u_j+\imath v_j)$. Thus,

$$\begin{aligned} U_j=u_j \cos j\omega t + v_j \sin j\omega t, \qquad V_j=v_j \cos j\omega t-u_j \sin j\omega t . \end{aligned}$$

(10)

4.1 Expressions for $U_j$ and $V_j$ in terms of the moments

[The analysis here applies equally to the classical context if the hats on ${\hat{X}}$ and ${\hat{P}}$, and the symmetrization, are ignored.] For even order, a simple case is where $j=0$:

$$\begin{aligned} \qquad V_0=0, \qquad U_0=\langle \{({\hat{P}}^2/(m\omega )^2+{\hat{X}}^2)^{n/2}\} \rangle =\sum \nolimits _{k=0, 2, ..}^{n} \big (_{k/2}^{n/2}\big ) \mathcal {Y}_k, \end{aligned}$$

(11)

and $U_0$ is invariant. For low orders, all cases can easily be found. For $n=2$:

$$\begin{aligned} \qquad U_0=\mathcal {Y}_0+\mathcal {Y}_2,\qquad W_2=\langle \{({\hat{X}}+\imath {\hat{P}}/m\omega )^2\}\rangle , \qquad U_2=\mathcal {Y}_0-\mathcal {Y}_2, \;\; V_2=2\mathcal {Y}_1. \end{aligned}$$

(12)

And for $n=3$:

$$\begin{aligned} \;\;W_1= & {} \langle \{({\hat{X}}+\imath {\hat{P}}/m\omega ) ({\hat{X}}^2+({\hat{P}}/m\omega )^2)\}\rangle ,\;\;\;U_1=\mathcal {Y}_0+\mathcal {Y}_2,\;\;\; V_1=\mathcal {Y}_1+\mathcal {Y}_3, \end{aligned}$$

(13)

$$\begin{aligned} \;\;W_3= & {} \langle \{({\hat{X}}+\imath {\hat{P}}/m\omega )^3\}\rangle , \;\;\;U_3=\mathcal {Y}_0-3\mathcal {Y}_2,\;\;\; V_3=3\mathcal {Y}_1-\mathcal {Y}_3. \end{aligned}$$

(14)

[Although $W_3= \langle ({\hat{X}}+\imath {\hat{P}}/m\omega )^3 \rangle , \;W_1 \ne \langle \, ({\hat{X}}+\imath {\hat{P}}/m\omega )({\hat{P}}^2/(m\omega )^2+{\hat{X}}^2) \,\rangle$. Symmetrization is required for $W_1$.]

These relations can be cast in matrix form:

For $n=3$,

$$\begin{aligned} \begin{array}{c}\left[ \begin{array}{c}\! U_1 \!\\ \! U_3 \!\end{array}\right] = \left[ \begin{array}{cr} 1 &{} 1 \\ 1 &{} -3 \end{array}\right] \!\!\left[ \begin{array}{c}\!\mathcal {Y}_0\! \\ \!\mathcal {Y}_2\! \end{array}\right] \!,\, \qquad \left[ \begin{array}{c}\! V_1 \!\\ \! V_3 \!\end{array}\right] = \left[ \begin{array}{cr} 1 &{} 1 \\ 3 &{} -1 \end{array}\right] \!\!\left[ \begin{array}{c}\!\mathcal {Y}_1\! \\ \!\mathcal {Y}_3\! \end{array}\right] \!, \end{array} \end{aligned}$$

(15)

while for $n=4$

$$\begin{aligned} \begin{array}{c} \left[ \!\begin{array}{c}U_0 \\ U_2\\ U_4\end{array}\!\right] = \left[ \begin{array}{crr}\!1 &{} 2 &{} 1 \\ \!1 &{} 0 &{} -1\\ \!1 &{} -6 &{} 1 \end{array}\right] \left[ \begin{array}{c}\!\!\,\mathcal {Y}_0\!\!\, \\ \!\!\,\mathcal {Y}_2\,\!\!\\ \!\!\,\mathcal {Y}_4\,\!\! \end{array}\right] \!, \qquad \left[ \begin{array}{c}\! V_2\! \\ \! V_4\! \end{array}\right] = \left[ \begin{array}{cr}\,2 &{} 2 \\ \,4 &{} -4 \end{array} \right] \left[ \begin{array}{c}\! \mathcal {Y}_1\! \\ \! \mathcal {Y}_3 \! \end{array} \right] \end{array} \end{aligned}$$

(16)

An expression that covers every case is given in Appendix A. Alternatively a recurrence relation there gives $U_j$ and $V_j$ in terms of the moments $\mathcal {Y}_k$.

4.2 The amplitudes of the Fourier components are time-independent invariants

The time-dependent invariants $e^{\imath j\omega t}W_j$ that were used to determine the time evolution of the moments also yield the sequence of time-independent invariants

$$\begin{aligned} A_j:=(W^*_j W_j)^{1/2}=(U_j^2+V_j^2)^{1/2}. \end{aligned}$$

(17)

Then $A_j$ is the magnitude of the complex number $W_j$. To determine the phase, we define the times $t_j$ such that $e^{\imath j\omega t}W_j=\exp ( \imath j\omega t_j) A_j$ with $t_j$ real and $0\le t_j<2\pi$. Then $W_j=\exp [- \imath j \omega (t-t_j)] A_j$. For $t=0$, this gives

$$\begin{aligned} A_j^2=u_j^2+v_j^2, \qquad \cos j\omega t_j=u_j /A_j, \qquad \sin j\omega t_j=v_j /A_j. \end{aligned}$$

(18)

These equations enable the calculation of $A_j$ from the initial moments. The ambiguities in trying to obtain $t_j$ from Eq. (18) are resolved using other invariants, as discussed later for $n=3$ and 4.

The complete evolution can be determined from the $A_j$ and $t_j$ through

$$\begin{aligned} U_j= A_j\cos j\omega (t-t_j)\qquad V_j=-A_j \sin j\omega (t-t_j). \end{aligned}$$

(19)

Many quantitative attributes of the evolution do not depend on the initial time and can be expressed in terms of the invariants only. [The $t_j$ are not invariant, but the difference between any two is invariant.] Examples are the magnitudes of extrema of the moments, or the difference between the times of extrema or zeros. Furthermore, the invariants (or combinations of them) may be subject to inequalities that distinguish the quantum behaviour from the classical. Other forms for the invariant combinations of moments are discussed in Appendix D.

4.3 The inverse relations: the moments in terms of U and V

Inverting the previous matrices gives, for $n=3$

$$\begin{aligned} \begin{array}{c} \!\!\!\!\left[ \begin{array}{c}\! \mathcal {Y}_0 \!\\ \! \mathcal {Y}_2 \!\end{array}\right] = \frac{1}{4}\!\left[ \begin{array}{cr} 3 &{} 1 \\ 1 &{} -1 \end{array}\right] \!\!\left[ \begin{array}{c}\!U_1\! \\ \!U_3\! \end{array}\right] \!,\, \qquad \left[ \begin{array}{c}\! \mathcal {Y}_1 \!\\ \! \mathcal {Y}_3 \!\end{array}\right] = \frac{1}{4}\!\left[ \begin{array}{cr} 1 &{} 1 \\ 3 &{} -1 \end{array}\right] \!\!\left[ \begin{array}{c}\!V_1\! \\ \!V_3\! \end{array}\right] \!, \end{array} \end{aligned}$$

(20)

while for $n=4$

$$\begin{aligned} \begin{array}{c} \!\!\left[ \!\begin{array}{c} \mathcal {Y}_0 \\ \mathcal {Y}_2 \\ \mathcal {Y}_4 \end{array}\!\right] \!\!=\!\frac{1}{8}\!\! \left[ \begin{array}{crr} 3 &{} 4 &{} 1 \\ 1 &{} 0 &{} -1\\ 3 &{} -4 &{} 1 \end{array}\right] \!\!\left[ \begin{array}{c}\!\!\,U_0\!\!\, \\ \!\!\,U_2\,\!\!\\ \!\!\,U_4\,\!\! \end{array}\right] \!, \qquad \left[ \begin{array}{c}\! \mathcal {Y}_1 \!\\ \! \mathcal {Y}_3 \!\end{array}\right] = \!\frac{1}{8}\!\left[ \begin{array}{cr} 2 &{} 1 \\ 2 &{} -1 \end{array} \right] \!\!\left[ \! \begin{array}{c} V_2 \\ V_4 \end{array}\!\right] \end{array} \end{aligned}$$

(21)

An explicit expression for the inverses for any n is derived in Appendix B.

4.4 The moments in terms of their initial values

The sinusoids U and V can be expressed in terms of their initial values using Eq. (10), and inserting this result into Eqs. (20) and (21) gives the moments $\mathcal {Y}_k$ in terms of $u_j$ and $v_j$. These initial $u_j$ and $v_j$ are found from the initial moments $y_k$ using Eqs. (15) and (16). In this way, we can write expressions for the moments in terms of their initial values:

For $n=3$, the result is

(22)

where $y_k$ is the initial value of $\mathcal {Y}_k$ and $c_j=\cos \omega jt$, $s_j=\sin \omega jt$. And for $n=4$,

(23)

As $t\rightarrow 0$, all the diagonal elements of these matrices approach unity and all off-diagonal elements approach zero, so that $\mathcal {Y}_k\rightarrow y_k$, as required.

5 Some features of moments of any order

For classical or quantum systems:

Spatially symmetric (or antisymmetric) distributions or wavefunctions will remain symmetric (or antisymmetric) as they evolve and all moments of odd order will be zero. For even order, both $Y_0$ and $Y_n$ will be positive.

For quantum systems:

All symmetrized moments are real. (They can all be expressed as the expectation value of an Hermitian operator.)

There is a generalization of the usual uncertainty relation for $n=2$ that has the form $Y_0\,Y_n\ge \alpha _n\hbar ^n$, where $\alpha _n$ is a positive constant (Eq. 57 of [2]). In particular, $\alpha _2=\frac{1}{4}$ (the Heisenberg uncertainty relation) and $\alpha _4\approx 0.4878$ [10]. This and other related inequalities are discussed in ref. [11].

Initially real wavefunctions are often used in illustrative examples. (We ignore any phase factor that is independent of position—it would not effect the moments.) Any normalizable eigenfunction of an Hermitian Hamiltonian operator can be taken to be initially real. If the initial wavefunction is real, all moments $Y_k$ with odd k will be initially zero (because there is an odd number of momentum operators and each has a factor $\imath$, but the moment must be real).

Some of these features apply also to free particles and more detail is given in [7].

5.1 Evolution of initially real wavefunctions

For a wavefunction that is initially real, all initial moments $y_k$ with k odd will be zero. (The following remarks also apply to classical distributions where all odd initial moments are zero.) It follows from Sect. 4.1 that all $v_j$ are zero, and Eq. (10) gives

$$\begin{aligned} U_j=u_j \cos j\omega t , \qquad V_j=-u_j \sin j\omega t . \end{aligned}$$

(24)

Thus, whereas in general $A_j=(u_j^2+v_j^2)^{1/2}$, for initially real wavefunctions $A_j=\pm u_j$. (Both signs can occur.) From Eq. (18), $\sin j\omega t_j=0$; so $t_j=0$ and $A_j=u_j$ if $u_j>0$ while $t_j=\pi$ and $A_j=-u_j$ if $u_j<0$. For $n=3$ and 4, we will show that the analysis of the evolution for initially real wavefunctions is much simpler than in the general case.

It will be shown in Sects. 8.2.2 and 9.1.1 that this simplification applies more broadly than just to initially real wavefunctions.

6 Evolution, invariants, and inequalities of the second-order moments

The second-order moments relate to the spread in position $\varDelta _x=Y_0^{1/2}$ and in momentum $\varDelta _p=Y_2^{1/2}$. Their evolution (that also involves the correlation $Y_1$) is discussed in most introductory textbooks on quantum mechanics. In terms of the quantities used here, $U_0=\mathcal {Y}_0+ \mathcal {Y}_2$, $U_2=\mathcal {Y}_0- \mathcal {Y}_2$, and $V_2=2Y_1$. The two amplitude invariants are $A_0=U_0$ (related to the energy) and $A_2=(U_2^2+V_2^2)^{1/2}=[(\mathcal {Y}_0- \mathcal {Y}_2)^2+4\mathcal {Y}_1^2]^{1/2}$. The inverse relations, giving the moments in terms of $U_j$, are $\mathcal {Y}_0=\frac{1}{2}(U_0+U_2)$, $\mathcal {Y}_2=\frac{1}{2}(U_0-U_2)$ and $\mathcal {Y}_1=\frac{1}{2} V_2$. From Eqs. 20 and 19, the evolution of the moments can be expressed as

$$\begin{aligned} \mathcal {Y}_0=\frac{1}{2}[A_0 +A_2\cos 2\omega (t-t_2)],\;\;\;\mathcal {Y}_1=-\frac{1}{2}A_2 \sin 2\omega (t-t_2) ,\;\;\;\mathcal {Y}_2=\frac{1}{2}[A_0 -A_2\cos 2\omega (t-t_2)]. \end{aligned}$$

(25)

The invariant amplitudes $A_j$ (and the constant $t_2$) can be calculated from the initial moments through Eq. (18). In terms of the initial moments,

(26)

where $c_2=\cos 2\omega t$ and $s_2=\sin 2\omega t$.

All these equations apply equally to the classical and quantum cases; but there are inequalities that distinguish these cases. The quantal energy is $\epsilon =\frac{1}{2}\langle {\hat{P}}^2/m + m\omega ^2{\hat{X}}^2\rangle =\frac{1}{2}m\omega ^2 U_0$ and, because $[{\hat{P}}, {\hat{X}}]=\hbar /\imath$, it follows that $\epsilon \ge \frac{1}{2}\hbar \omega$ and $A_0=U_0\ge \hbar /m\omega =\alpha ^2$. Also, the combination $K^2\!:=Y_0 Y_2-Y_1^2$ is subject to Schrödinger’s inequality $K\ge \frac{1}{2}\hbar$, which is stronger than the traditional Heisenberg Uncertainty Relation $(Y_0 Y_2)^{1/2}\ge \frac{1}{2}\hbar$. [The stronger inequality was originally proved by Schrödinger in 1930. It is easily derived from Schwarz’s inequality $\langle {\hat{P}}^2\rangle \langle {\hat{X}}^2\rangle \ge |\langle {\hat{P}}{\hat{X}}\rangle |^2$ using ${\hat{P}}{\hat{X}}=\frac{1}{2}({\hat{P}}{\hat{X}}+{\hat{X}}{\hat{P}} -\imath \hbar )$.] Thus, $A_0^2-A_2^2=4(\mathcal {Y}_0 \mathcal {Y}_2-\mathcal {Y}_1^2)=4K^2/(m\omega )^2\ge \ \alpha ^4$, which is stronger than the energy inequality. [For a classical system: $Y_0\ge 0, \,Y_2\ge 0, \,Y_0 Y_2\ge Y_1^2, \,U_0\ge U_2, \,A_0\ge A_2$].

In general, the evolution of the second-order moments is as follows: $\mathcal {Y}_0$ and $\mathcal {Y}_2$ oscillate with an angular frequency of $2\omega$ and amplitude $\frac{1}{2} A_2$ about the value $\frac{1}{2} A_0$. These oscillations are out-of-phase by $\pi$; they are zero at the same time, but each maximum is at the other’s minimum. The other moment $\mathcal {Y}_1$ oscillates about zero with the same frequency and amplitude, but differing in phase by $\pi /2$. In the quantum case, the centre $\frac{1}{2} A_0$ of the oscillations of $\mathcal {Y}_0$ and $\mathcal {Y}_2$ must be greater than or equal to $\frac{1}{2}\alpha ^2$. These moments must be positive, but their minimum can be arbitrarily close to zero. The product of the minimum value $\frac{1}{2}(A_0-A_2)$ and maximum value $\frac{1}{2}(A_0+A_2)$ is $(K/m\omega )^2\ge \frac{1}{4}\alpha ^4$

A simple example is the Gaussian wavefunction $\psi =\exp (-\frac{1}{2}x^2/a^2)$. The second-order initial moments are $y_0=\frac{1}{2}a^2$, $y_1=0$, and $y_2=\frac{1}{2}a^{-2}$. Then $u_0=\frac{1}{2}(a^2+a^{-2})$ and $u_2=\frac{1}{2}(a^2-a^{-2})$. Therefore, $A_0=u_0$, $A_2=u_2$ if $a>1$, and $A_2=-u_2$ if $a<1$. Furthermore, $t_2=0$ and initially $\mathcal {Y}_1$ is zero; also, if $a>1$ then $\mathcal {Y}_0$ is at its maximum and $\mathcal {Y}_2$ is at its minimum. For the Gaussian, Schrödinger’s inequality is saturated ($K=\frac{1}{2}\hbar$) for any value of a. The maxima of $\mathcal {Y}_0$ and $\mathcal {Y}_2$ become infinitely large, and the minima become infinitely small as $a\rightarrow \infty$ or $a\rightarrow 0$. The case $a=1$ is the ground state of the oscillator with $A_2=0$ and no oscillations.

7 Periodicity and symmetry in the time evolution of moments

7.1 For an ensemble of classical particles

The equations of motion for a classical particle can be integrated to give

$$\begin{aligned} \qquad x(t)=x_0 \cos \omega t +(p_0/m\omega ) \sin \omega t, \qquad p(t)=p_0 \cos \omega t -m\omega x_0 \sin \omega t. \end{aligned}$$

(27)

Hence, both x(t) and p(t) have period $T=2\pi /\omega$, and after time T/2 both x(t) and p(t) change sign. After time T/4, $x(T/4)=p(0)/m\omega$ and $p(T/4)=-m\omega x(0)$. For the moments $\mathcal {Y}_k= N^{-1}\sum _\mu (x_\mu -\bar{x})^{n-k}(p_\mu -\bar{p})^k/(m\omega )^k$ where $\bar{x}=N^{-1}\sum _\mu x_\mu$, $\bar{p}=N^{-1}\sum _\mu p_\mu$, it follows that $\mathcal {Y}_k$ has period T and after a half-period $\mathcal {Y}_k(T/2)=(-1)^n\mathcal {Y}_k(0)$. After one quarter-period, $\mathcal {Y}_k(T/4)=(-1)^k\mathcal {Y}_{n-k}(0)$.

7.2 For a wavefunction

After one period of the oscillator, the wavefunction changes sign: [12] $\,\psi (x,T)=-\psi (x,0)$. Therefore, all moments return to their original values: $Y_k(t+T)=Y_k(t)$; the moments have period T.

After half a period ($t=\pi /\omega$), then $\,\psi (x,T/2)=-\imath \,\psi (-x,0)$ and the effect on the moments becomes apparent by changing the sign of the integration variable in $Y_k=\int \psi ^*(x)\{x^{n-k},(-\imath \hbar \partial _x)^k\}\,\psi (x)\, \text {d}x$. Thus, $Y_k(t+T/2)=(-1)^nY_k(t)$. For even n, the moments over the second half-period repeat the first half-period; for n odd, the sign over the second half is reversed.

After a quarter-period, the wavefunction evolves essentially into its Fourier transform (and a phase factor), a result that comes directly from the propagator. [12] At time $t=T/4$, the propagation equation becomes

$$\begin{aligned} \psi (x, T/4)=e^{-\imath \pi /4}\sqrt{m\omega }\,\phi (m\omega x), \end{aligned}$$

(28)

where $\phi (p)=(2\pi \hbar )^{-1/2}\int _{-\infty }^{\infty }{} \exp (-\imath p\,x/\hbar )\,\psi (x, 0)\,\text {d} x$, the initial momentum wavefunction. Inserting $\psi (x, T/4)$ into the integral for $Y_k$ and changing the integration variable x to $p=m\omega x$ give $\mathcal {Y}_k(T/4)=\int _{-\infty }^{\infty }\phi ^*(p)\,p^{n-k}(-\imath \hbar \,\partial _p)^k \phi (p) \text {d}p$.

The canonical transformation from momentum to position ($p\rightarrow x, x\rightarrow -p$) results in [Eq. (3.31) of [13]]

$$\begin{aligned} \int _{-\infty }^{\infty }\phi ^*(p)f(-\imath \partial _p, p)\phi (p)\,\text {d}p = \int _{-\infty }^{\infty }\psi ^*(x)f(x, \imath \partial _x)\psi (x)\,\text {d}x, \end{aligned}$$

(29)

and it follows that $Y_{n-k}(t)=(-1)^kY_k(t+T/4)$. Thus, the evolution of the moment $\mathcal {Y}_k$ is exactly copied (apart from a sign) by that of $Y_{n-k}$ after a time of one quarter of the period T of the oscillator. In Appendix C, an alternative derivation of these periodicities uses the periodic properties of $U_j$ and $V_j$.

8 Particulars of third moments

The four symmetrized third moments are displayed in Eq. (6). The moment $Y_0 =\langle {\hat{X}}^3\rangle$ is a measure of the skewness of the distribution. All third moments can be positive or negative. As shown in Eq. (15), $W_j=U_j+\imath V_j$ with

$$\begin{aligned} U_1= & {} \mathcal {Y}_0+\mathcal {Y}_2,\qquad \;\;\,V_1=\mathcal {Y}_1+\mathcal {Y}_3, \qquad \; U_3 =\mathcal {Y}_0 -3 \mathcal {Y}_2, \qquad \, V_3=3\mathcal {Y}_1-\mathcal {Y}_3, \end{aligned}$$

(30)

$$\begin{aligned} \mathcal {Y}_0= & {} \frac{1}{4}(3U_1+U_3), \;\;\,\mathcal {Y}_2=\frac{1}{4}(U_1-U_3), \;\;\;\mathcal {Y}_1 =\frac{1}{4}(V_1+V_3), \;\;\;\;\,\mathcal {Y}_3=\frac{1}{4}(3V_1-V_3). \end{aligned}$$

(31)

As in Eq. (19), we set $e^{\imath \omega t} W_1=e^{\imath \omega t_1} A_1$ and $e^{\imath 3\omega t} W_3=e^{\imath 3\omega t_3} A_3$ leading to

$$\begin{aligned} \;\;U_1= & {} A_1\cos \omega (t-t_1),\;\;\;\;\;\; V_1=-A_1 \sin \omega (t-t_1), \;\;\;\;\;\, \text {with}\;\;U_1^2+V_1^2=A_1^2, \end{aligned}$$

(32)

$$\begin{aligned} \;\;U_3= & {} A_3\cos 3\omega (t-t_3), \;\;\;\; V_3=-A_3 \sin 3\omega (t-t_3), \;\;\;\; \text {with}\;\;U_3^2+V_3^2=A_3^2. \end{aligned}$$

(33)

From $W_1=e^{\imath \omega t_1}A_1=u_1+\imath v_1$, it follows that $\cos \omega t_1=(y_0+y_2)/A_1$, and $\sin \omega t_1=(y_1+y_3)/A_1$. In a similar way, $\cos 3\omega t_3=(y_0-3y_2)/A_3, \,\sin 3\omega t_3=(3y_1-y_3)/A_3$. The difference $t_3-t_1$ can be found from the invariant $W_1^{*3}W_3=e^{\imath 3\omega (t_3-t_1)}A_1^3A_3$. This shows that $R_3+\imath I_3:=(U_1-\imath V_1)^3(U_3+\imath V_3)$ must be invariant. That is,

$$\begin{aligned} R_3&= \;U_3\,U_1(U_1^2-3V_1^2)+V_3\,V_1(3U_1^2-V_1^2), \end{aligned}$$

(34)

$$\begin{aligned} I_3\,&= V_3\,U_1(U_1^2-3V_1^2)-U_3\,V_1(3U_1^2-V_1^2) \end{aligned}$$

(35)

are invariant, and

$$\begin{aligned} \qquad C_3:=\cos 3\omega (t_3-t_1)=R_3/A_1^3A_3, \qquad S_3:=\sin 3\omega (t_3-t_1)=I_3/A_1^3A_3. \end{aligned}$$

(36)

The invariants $S_3$ and $C_3$ are not independent since $S_3^2+C_3^2=1$. Given either one, however, the sign of the other remains undetermined.

8.1 Evolution in terms of the invariants and $t_1$

To refer the time to $t_1$ only, we use $(t-t_3)=(t-t_1)-(t_3-t_1)$, and $t_3-t_1$ can be expressed in terms of the invariants $C_3, S_3$ in Eq. (36). With $s := \sin \omega (t - t_1)$ and $c:= \cos \omega (t - t_1)$,

$$\begin{aligned} \sin 3\omega (t-t_3)= & {} s (3 - 4 s^2) C_3 - c (1 - 4 s^2) S_3, \end{aligned}$$

(37)

$$\begin{aligned} \cos 3\omega (t-t_3)= & {} c (1 - 4 s^2) C_3 + s (3 - 4 s^2) S_3, \end{aligned}$$

(38)

where we have used $\,\sin 3\theta = 3\sin \theta -4\sin ^3\theta \,$ and $\,\cos 3\theta = -3\cos \theta +4\cos ^3\theta$.

From Eq. (31) and inserting $r :=A_1/A_3$,

$$\begin{aligned} Y_0= & {} \frac{1}{4}A_3[3r c+c (1-4 s^2) C_3 + s (3-4 s^2) S_3], \end{aligned}$$

(39)

$$\begin{aligned} Y_3= & {} \frac{1}{4}A_3[-3r s+s (3-4 s^2) C_3-c (1-4 s^2) S_3], \end{aligned}$$

(40)

$$\begin{aligned} Y_1= & {} \frac{1}{4}A_3[-r s-s (3- 4 s^2) C_3+ c (1- 4 s^2) S_3], \end{aligned}$$

(41)

$$\begin{aligned} Y_2= & {} \frac{1}{4}A_3[r c-c (1- 4 s^2) C_3-s (3-4 s^2) S_3]. \end{aligned}$$

(42)

Then the scale of the evolution is determined by $A_3$ and the shape depends on $r, S_3, C_3$ only. The timing is set by $t_1$.

8.2 Extrema and inflections with $n=3$

The general features of the shape of the evolution follow from the times and values of the moments at their extrema and inflections. As discussed in 6, $\mathcal {Y}_0(t+\pi /2)=\mathcal {Y}_3(t)$ and $\mathcal {Y}_2(t+\pi /2)=\mathcal {Y}_1(t)$; so there are only two independent shapes involved. The conditions required for extrema are easily found:

$$\begin{aligned} \text {d}_t\mathcal {Y}_0= & {} 0\;\;\Rightarrow \;\;\mathcal {Y}_1=0\;\;\Rightarrow \;\;V_1+V_3=0\;\;\Rightarrow \;A_1 \sin \omega (t-t_1)+A_3 \sin 3\omega (t-t_3)=0 \end{aligned}$$

(43)

$$\begin{aligned} \text {d}_t\mathcal {Y}_1= & {} 0\;\;\Rightarrow \;\; 2\mathcal {Y}_2=\mathcal {Y}_0\;\; \Rightarrow \;\; U_1+3U_3=0\;\; \Rightarrow \;\; A_1 \cos \omega (t-t_1)+3A_3 \cos 3\omega (t-t_3)=0. \end{aligned}$$

(44)

It follows that the times of the inflections of $\mathcal {Y}_0$ are the same as the times of the extrema of $\mathcal {Y}_1$, because both require $\text {d}_t\mathcal {Y}_1=0$. Similarly, the inflections of $\mathcal {Y}_3$ are simultaneous with the extrema of $\mathcal {Y}_2$. (But the times of the inflections of $\mathcal {Y}_1$ and $\mathcal {Y}_2$ are not generally the same as the times of any extrema.)

For the extrema of $\mathcal {Y}_0$, Eqs. (43) and (37) lead to the equation

$$\begin{aligned} s\,r + s (3 - 4 s^2) C_3- c (1 - 4 s^2) S_3=0. \end{aligned}$$

(45)

Similarly, the extrema of $\mathcal {Y}_1$ are subject to the equation

$$\begin{aligned} c\,r/3- c(3-4 c^2) C_3 - s (1 - 4 c^2) S_3=0. \end{aligned}$$

(46)

We have not found useful exact solutions of these equations, but in Sect. 8.2.4 we will convert them into cubic polynomial equations that can be efficiently solved numerically. These equations can, however, be exactly solved for the special class of wavefunctions (or classical distributions) that have $S_3=0$. In the quantum case, this includes the class of initially real wavefunctions or any complex linear combination of any two energy eigenstates of the oscillator. An example is discussed in Sect. 8.2.3. In the case with $S_3=0$, the extreme values of the moments will be expressed in terms of the invariants (independent of $t_1$); this has not been achieved in the general case.

8.2.1 Special features of initially real wavefunctions

All odd moments are initially zero: so for $n=3, y_1=y_3=0$ and $u_1=y_0+y_2, \,u_3=y_0-3y_2, v_1=v_3=0$. Here the invariant amplitudes are $A_1=|u_1|, A_3=|u_3|$, and $S_3=0, C_3=\pm 1$. From Eq. (36), the sign of $C_3$ is the same as that of $u_1 u_3$ and the features of the evolution can be obtained from the results in the next section. The basic sinusoids are $U_1=u_1\cos \omega t, V_1=-u_1\sin \omega t$, $U_3=u_3 \cos 3\omega t , V_3=-u_3 \sin 3\omega t$.

8.2.2 Extrema of third moments of distributions with $S_3=0$, which includes any real wavefunctions

Since $S_3=0$, it follows that $C_3=\pm 1$; the sign can be determined from the initial moments using Eq. (34). The value of $t_1$ is determined from $\cos \omega t_1=u_1/A_1$ and $\sin \omega t_1=v_1 /A_1$ with $0\le t_1 <2\pi$. [In the case of a real wavefunction, $v_1=0$ and $A_1=|u_1|$; hence, $t_1=0$ if $u_1\ge 0$ and $t_1=\pi$ if $u_1<0$.]

For the extrema of $\mathcal {Y}_0$, Eq. (45) leads to

$$\begin{aligned} r s + s (3 - 4 s^2) C_3=0. \end{aligned}$$

(47)

One solution is $s=0$ and therefore $\mathcal {Y}_0$ will be extreme at $t=t_1$. At this time, from Eq. (33), $U_1=A_1$, $U_3=C_3A_3$ and $\mathcal {Y}_0$ takes the extreme value $\frac{1}{4}A_3(3r+C_3)$. To determine whether this is a maximum or a minimum, we need the sign of $\text {d}^2_t \mathcal {Y}_0=-\frac{3}{4}\omega ^2(U_1+3U_3)$. Hence $\mathcal {Y}_0$ will take a maximum value at $t=t_1$ if $r +3C_3>0$.

Another possible pair of solutions has $c^2= \frac{1}{4}(1-C_3 r)$, but $0\le c^2\le 1$, and therefore, there are two extra extrema if $r<2-C_3$. The times of this pair of extrema are $t=t_1\pm \omega ^{-1}\arccos \frac{1}{2}(1-C_3r)^{1/2}$, and each extremum has $\mathcal {Y}_0=-\frac{1}{4}C_3A_3(1-C_3r)^{3/2}$.

For the extrema of $\mathcal {Y}_1$, we use $r_1=r/3$. Then Eq. (46) leads to

$$\begin{aligned} r_1 c - c (3 - 4 c^2) C_3=0. \end{aligned}$$

(48)

One solution is $c=0$ and therefore $s=\pm 1$ and $\mathcal {Y}_1$ will be extreme at $t=t_1+s\pi /2\omega$. At this time, from Eq. (33), $V_1=-s A_1$ and $V_3=s\,C_3A_3$; therefore, $\mathcal {Y}_1=\frac{1}{4}(V_1+V_3)$ takes the extreme value $\frac{1}{4}s\, C_3A_3(1-C_3 r)$.

Another possible pair of solutions has $r_1 = (4s^2 - 1) C_3$ or $s=\pm \frac{1}{2}(1+C_3 r_1)$. But $0\le s^2\le 1$, and therefore, if (and only if) $r_1<2+C_3$ there will be two extra extrema with $t= t_1\pm \omega ^{-1}\arcsin \frac{1}{2}(1+C_3r_1)^{1/2}$ and $\mathcal {Y}_1=-\frac{1}{4}C_3A_3(1+C_3r_1)^{3/2}$.

Thus, if $C_3=-1$, both $\mathcal {Y}_0$ and $\mathcal {Y}_1$ have three exrtema in any half-period if $r<3$ and only one otherwise. But if $C_3=1$, then $\mathcal {Y}_0$ will have three extrema if $r<1$ while $\mathcal {Y}_1$ will have three extrema if $r<9$.

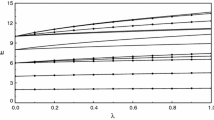
There are some temporal coincidences forced by $S_3=0$. From Eqs. (32, 33, 37), when $c=0$ then $U_1=U_3=0$; hence, $\mathcal {Y}_0=\mathcal {Y}_2=0$ at these times, and both $\mathcal {Y}_1$ and $\mathcal {Y}_3$ take extreme values. Also, when $s=0$ then $V_1=V_3=0$; hence $\mathcal {Y}_1=\mathcal {Y}_3=0$ as well as $\mathcal {Y}_0$ and $\mathcal {Y}_3$ taking extreme values. These features are shown in Fig. 1.

Fig. 1

Evolution of the third moments in a case with $S_3=0$. The wavefunction is a complex superposition of two eigenstates of the oscillator, as in Eq. (49), with $b=2\exp (-2\imath /3)$. Over the second quarter-period, $\mathcal {Y}_2$ is a copy of $\mathcal {Y}_1$ in the first quarter-period, and $\mathcal {Y}_3$ is the negative of $\mathcal {Y}_0$. Over the second half-period, all moments are the negative of the first half-period. The vertical dotted lines join each extremum with either zero or a point of inflection. Where they intersect another curve (without a gap) there is either an inflection or an extremum in the curve

8.2.3 Example of third moments of a wavefunction with $S_3=0$.

To have nonzero third moments, the wavefunction must be neither even nor odd. A simple example is

$$\begin{aligned} \psi (x)=(1+b\,x/a)\exp \left( -\frac{1}{2}x^2/a^2\right) . \end{aligned}$$

(49)

If b is real, then $\psi (x)$ is real, so the odd moments will be initially zero and the results in 8.2.1 will apply, including the result that $S_3=0$.

If b is complex, with $b=\exp (\imath \theta )\,|b|$ and $a=\alpha :=(\hbar /m \omega )^{1/2}$, and then, $\psi (x)$ is a sum of two energy eigenfunctions of the oscillator and the evolution will be $\psi (x,t)=[1+|b|x\exp \imath (\theta -\omega t)]\exp (-\frac{1}{2}\imath \omega t-\frac{1}{2}x^2/a^2)$. At any time t when $|\omega t-\theta |$ is zero or any multiple of $\pi$, then $\psi (x,t)$ will be real apart from the the phase factor $\exp (-\frac{1}{2}\imath \omega t)$ which has no effect on the moments, and $S_3$ must be zero. The time $t_1$ will be one of these times, but one consistent with $\cos \omega t_1 =u_1/A_1$ and $\sin \omega t_1 =v_1/A_1$.

Calculations from the wavefunction give the initial first-order moments as $\langle {\hat{x}}/a \rangle +\imath \langle a{\hat{p}}/\hbar \rangle =b/(1+b^2/2) \exp \imath \theta$. Also $C_3=-1, r=|b|^2/2, A_3=2|b|^3/(1+|b|^2/2)^3$ and a suitable $t_1$ is $\theta +\pi$. From 8.1.2, there is an extremum of $\mathcal {Y}_0$ at $t=t_1$, where $\mathcal {Y}_0=\frac{1}{4} A_3(3r-1)$. If $r>3$ or $|b|^2>6$, this is a maximum and the nearest minima are at $t_1\pm \pi /\omega$. Otherwise, if $r<3$ the extremum of $\mathcal {Y}_0$ at $t=t_1$ is a minimum and there are two maxima at the times $t_1 \pm \omega ^{-1}\arccos \frac{1}{2}(r+1)^{1/2}$, each with the same value $\mathcal {Y}_0=\frac{1}{4}A_3(r+1)^{3/2}$. Thus, the extra extrema are at equal time intervals before and after the single minimum at $t_1$. As $r\rightarrow 0$ the times of the maxima approach $t_1\pm \pi /\omega$, the state approaches the ground state, and the amplitude of the oscillations tends to zero.

There is an extremum of $\mathcal {Y}_1$ at $t_1\pm \pi /2\omega$ with magnitude $\mathcal {Y}_1=\frac{1}{4} A_3(r+1)$. If $r<3$, there is also a pair of extrema at $t=t_1\pm \omega ^{-1}\arcsin \frac{1}{2}(1-r/3)^{1/2}$ with $\mathcal {Y}_1=\frac{1}{4} A_3(1-r/3)^{3/2}$. An example where all moments have three extrema in any half-period is shown in Fig. 1

In the case where $a\ne (\hbar /m \omega )^{1/2}$ and b is complex, it will generally follow that $S_3\ne 0$. Then no useful exact solutions can be found, but the method in the next section can be applied.

8.2.4 The general third-order case: a cubic polynomial equation for the extrema

For the extrema of $\mathcal {Y}_0$, Eq. (45) led to $s\,r + s (3 - 4 s^2) C_3= c (1 - 4 s^2) S_3$. Squaring both sides then gives

$$\begin{aligned} 16 s^6 -8 (3+C_3 r) s^4 + (r^2 + 6 C_3 r + 9) s^2 - S_3^2 = 0. \end{aligned}$$

(50)

The solutions of this cubic equation in $s^2$ yields the times of the extrema of $\mathcal {Y}_0$ as $t=t_1+\arcsin (s)/\omega$. Although the exact solutions of this cubic appear to be too complicated to be useful, the cubic provides the most efficient way to find the numerical values of these times in the general case. The ambiguities due to the arcsin and the sign of the square root of $s^2$ can be resolved by checking that $\mathcal {Y}_1=0$. [If not, then $t=t_1+(\pi -\arcsin s)/\omega$ will work.]

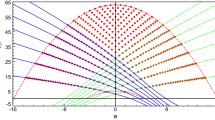
The cubic may have either one or three real roots, corresponding to one or three extrema in any half-period. This number is determined by the discriminant of the cubic. Thus, there will be three extrema if $27 - 18 r^2 - 8 C_3 r^3 - r^4 >0$ and one extremum otherwise. This condition is displayed graphically in Fig. 2.

The equations for the extrema of $\mathcal {Y}_1$ are easily found because Eq. (45) lead to Eq. (46) by substituting $r\rightarrow r_1, s\rightarrow c$, and $C_3\rightarrow -C_3$. Thus, the cubic for the extrema of $\mathcal {Y}_1$ is

$$\begin{aligned} 16 c^6- 8 (3-C_3 r_1) c^4 + (r_1^2 - 6 C_3 r_1 + 9) c^2 - S_3^2 = 0, \end{aligned}$$

(51)

and there will be three extrema if $27 - 18 r_1^2 +8 C_3 r_1^3 - r_1^4 >0$ and one extremum otherwise.

Fig. 2

Regions of r and $C_3$ where the sign of the discriminant of the quartic polynomial in Eq. (66) determines whether there will be two or four extrema of $\mathcal {Y}_0$ in any half-period of the oscillator. This diagram also applies to the extrema of $\mathcal {Y}_1$ if you replace r with $r_1=r/3$ and $C_3$ with $-C_3$

As an example of the general case of the evolution of third-order moments we take the same form of wavefunction, $\psi (x)=(1+b\,x/a)\exp (-\frac{1}{2}x^2/a^2)$, as in Eq. (49); but now we take $a\ne \alpha$, so that $S_3\ne 0$. Again we take $|b|=2$ and $\theta =1$ radian, but now put $a=1.1\,\alpha$. This leads to $r\approx 1.45, C_3\approx -0.51$ and only one extremum of $\mathcal {Y}_0, \mathcal {Y}_3$ in any half-period, but three extrema of $\mathcal {Y}_1, \mathcal {Y}_2$. The results are shown in Fig. 3.

Fig. 3

Evolution of the third moments of the wavefunction in Eq. (49), with $a=1.1$, $b=2\exp \imath \theta$ and $\theta =1$. Over the second quarter-period, $\mathcal {Y}_2$ is a copy of $\mathcal {Y}_1$ over the first, and $\mathcal {Y}_3$ is the negative of $\mathcal {Y}_0$. Over the second half-period, all moments are the negative of the first half-period. The vertical dotted lines join the extrema of $\mathcal {Y}_0, \mathcal {Y}_3$ to the zeros of $\mathcal {Y}_1, \mathcal {Y}_2$, respectively, and the extrema of $\mathcal {Y}_1, \mathcal {Y}_2$ to inflections of $\mathcal {Y}_0, \mathcal {Y}_3$, respectively

9 Particulars of fourth moments

The basic time-independent invariants are $A_0=u_0$, $A_2=(u_2^2+v_2^2)^{1/2}$, $A_4=(u_4^2+v_4^2)^{1/2}$, and invariants related to $t_4-t_2$ that can be expressed as $W_4 W_2^{*2}=e^{4\imath \omega (t_4-t_2)}A_4A_2^2=(U_4+\imath V_4)(U_2-\imath V_2)^2 =: (R_4+\imath I_4)$. Then, with $C_4\!:=\! \cos 4\omega (t_4\!-t_2), \, S_4\!:= \!\sin 4\omega (t_4\!-t_2)$,

$$\begin{aligned} R_4= & {} U_4(U_2^2-V_2^2)+2V_4 U_2 V_2 = A_2^2A_4 C_4, \end{aligned}$$

(52)

$$\begin{aligned} I_4 \,\,= & {} V_4(U_2^2-V_2^2)-2U_4 U_2 V_2 = A_2^2A_4 S_4. \end{aligned}$$

(53)

The invariants $C_4= R_4/A_2^2A_4$, $S_4=I_4/A_2^2A_4$ are are related by $C_4^2+S_4^2=1$, and can be calculated from the initial moments using $R_4$ and $I_4$. The evolution of the moments can be expressed in terms of the invariants $A_0, A_2, A_4, C_4, S_4$ and the reference time $t_2$.

The evolution of $\mathcal {Y}_2$ is especially simple: from Eq. (21), $\mathcal {Y}_2=(U_0-U_4)/8$ and $U_0$ is constant; so $\mathcal {Y}_2$ oscillates with angular frequency $4\omega$ about $A_0/8$ with amplitude $A_4/8$. Classically, $\mathcal {Y}_2\ge 0$, which implies $A_4\le A_0$; for a quantum particle it is possible to have $\mathcal {Y}_2< 0$, but this is a rare and ephemeral possibility. [7] From $\langle \{PX\}^2\rangle =Y_2+\frac{1}{4}\hbar ^2$, it follows that $\mathcal {Y}_2\ge -\frac{1}{4}\alpha ^4$ and that $A_4<A_0+2\alpha ^4$. Both $\mathcal {Y}_0$ and $\mathcal {Y}_4$ will always be positive. Some other inequalities are discussed in Appendix E.

From the discussion of periodicity in Sect. 7 all the fourth moments repeat over the second half-period. Also, after a quarter-period, $\mathcal {Y}_0$ becomes a copy of $\mathcal {Y}_4$ over the first quarter-period, and $\mathcal {Y}_2$ is a copy of $-\mathcal {Y}_3$. And $\mathcal {Y}_2$ repeats each quarter-period.

To refer the time to $t_2$ only, we use $(t-t_4)=(t-t_2)-(t_4-t_2)$. Then

$$\begin{aligned} \;\;\;\sin 4\omega (t-t_4)=2C_4 s c+ S_4(2 s^2 - 1), \;\;\; \cos 4\omega (t-t_4)=2 S_4 s c+C_4 (2 c^2 - 1), \end{aligned}$$

(54)

where $s = \sin 2\omega (t - t_2), c= \cos 2\omega (t - t_2)$ and $t_2$ is determined by $\cos 2\omega t_2=u_2/A_2$, $\sin 2\omega t_2=v_2 /A_2$ with $0\le t_2 <\pi$. Using $r :=A_2/A_4$, the shape of the evolution can be expressed in terms of $r, S_4, C_4$ only, and then the scale of their variation depends on $A_4$, the timing is set by $t_2$, and $A_0$ merely adds a constant to the even moments.

9.1 Extrema and inflections with $n=4$

Similarly to the third-order case, the conditions for extrema are

$$\begin{aligned} \text {d}_t\mathcal {Y}_0= & {} 0 \;\Rightarrow \;\; \mathcal {Y}_1=0 \;\;\Rightarrow 2V_2+V_4=0 \Rightarrow 2A_2 \sin 2\omega (t-t_2)+A_4 \sin 4\omega (t-t_4)=0, \end{aligned}$$

(55)

$$\begin{aligned} \text {d}_t\mathcal {Y}_1= & {} 0 \;\Rightarrow 3\mathcal {Y}_2=\mathcal {Y}_0 \Rightarrow \,U_2+U_4=0 \,\Rightarrow \; A_2 \cos 2\omega (t-t_2)+A_4 \cos 4\omega (t-t_4)=0, \end{aligned}$$

(56)

$$\begin{aligned} \text {d}_t\mathcal {Y}_2= & {} 0 \; \Rightarrow \;\, \mathcal {Y}_3=\mathcal {Y}_1 \Rightarrow \;\;V_4=0 \,\,\Rightarrow \;A_4 \sin 4\omega (t-t_4)=0. \end{aligned}$$

(57)

The times of the inflections of $\mathcal {Y}_0$ are the same as the times of the extrema of $\mathcal {Y}_1$, because both require $\text {d}_t\mathcal {Y}_1=0$, and the inflections of $\mathcal {Y}_4$ are simultaneous with the extrema of $\mathcal {Y}_3$. The times of the inflections of $\mathcal {Y}_1$ and $\mathcal {Y}_3$ are not generally the same as the times of any extrema. Each extremum of each moment $\mathcal {Y}_k$ is simultaneous with one other event:

• $k=0: \,\mathcal {Y}_1=0$,      $k=4: \, \mathcal {Y}_3=0$,            $k=2: \;\mathcal {Y}_1=\mathcal {Y}_3$,      $k=1: \;\mathcal {Y}_0$ inflection,      $k=3: \; \mathcal {Y}_4$ inflection.

These temporal coincidences are shown in Fig. 6.

For the extrema of $\mathcal {Y}_0$, Eq. (55) leads to the equation

$$\begin{aligned} 2r s+ S_4(2 s^2-1)+2C_4s c =0. \end{aligned}$$

(58)

Similarly, the extrema of $\mathcal {Y}_1$ are subject to the equation

$$\begin{aligned} r c+ C_4(2 c^2-1)+2S_4s c =0. \end{aligned}$$

(59)

In sect. 9.1.3, we will convert these equations into quartic polynomial equations that can be efficiently solved numerically for the times of the extrema. For the special class of wavefunctions (or classical distributions) with $S_4=0$, simple exact expressions can be found for these times, and hence for the extreme values in terms of the invariants.

9.1.1 Extrema of fourth moments of distributions with $S_4=0$, which includes any real wavefunctions

For any real wavefunction, all odd moments will be initially zero; for $n=4$ we have $y_1=y_3=0$. From Eq. (16), it follows that $v_1=v_3=0$ and therefore $S_4=0$. There are, however, other wavefunctions in this class, for example any linear combination of two eigenstates of the oscillator. When $S_4=0$, it follows that $C_4=\pm 1$. From Eq. (21), (19), and (54), $\mathcal {Y}_k$ can be expressed in terms of $A_0, A_2, A_4, s, c$ :

$$\begin{aligned} \mathcal {Y}_0= & {} {\frac{1}{8}}[3A_0+4A_2c+C_4A_4(2c^2-1)], \end{aligned}$$

(60)

$$\begin{aligned} \mathcal {Y}_4= & {} {\frac{1}{8}}[3A_0-4A_2c+C_4A_4(2c^2-1)], \end{aligned}$$

(61)

$$\begin{aligned} \mathcal {Y}_2= & {} {\frac{1}{8}}[A_0-C_4A_4(2c^2-1)], \end{aligned}$$

(62)

$$\begin{aligned} \mathcal {Y}_1= & {} {\frac{1}{8}}s(A_2+C_4A_4c), \end{aligned}$$

(63)

$$\begin{aligned} \mathcal {Y}_3= & {} {\frac{1}{8}}s(A_2-C_4A_4c). \end{aligned}$$

(64)

For the extrema of $\mathcal {Y}_0$, Eq. (58) gives $r s + C_4 s c=0$ and one solution is $s=0$. Therefore, $\mathcal {Y}_0$ is extreme at $t=t_2$ and at $t=t_2\pm \pi /2\omega$. At $t=t_2$, we have $c= \cos 2\omega (t - t_2)=+1$ and $\mathcal {Y}_0=\frac{1}{8}[3A_0+A_4(C_4+4r)]$. At $t=t_2\pm \pi /2\omega$, $c=-1$ and $\mathcal {Y}_0=\frac{1}{8}[3A_0+A_4(C_4-4r)]$, always less than the extremum at $t_2$.

If $r<1$ there are two more extrema with $c=-C_4 r$ and times $t=t_2\pm \frac{1}{2\,\omega } \arccos r$, and each has the same magnitude with $\mathcal {Y}_0=\frac{1}{8}[3A_0-C_4A_4(2r^2+1)]$.

For $r>1$, there are only two extrema in any half-period and the one at $t_2$ is a maximum while the one at $t_2\pm \pi /2$ is a minimum. For $r<1$ and $C_4=+1$, the extra pair of extrema has magnitudes less than those at $t=t_2\pm \pi /2$ and is minima equally spaced about the local maximum at $t=t_2\pm \pi /2$. For $r<1$ and $C_4=-1$, the extra pair of extrema has magnitudes greater than those at $t=t_2$ and is maxima equally spaced about the local minimum at $t=t_2$.

For the extrema of $\mathcal {Y}_1$, Eq. (59) gives $r c+ C_4(2 c^2-1) =0$ and $c=-\frac{1}{2}C_4[r_2\pm (r_2^2+2)^{1/2}]$, where $r_2=r/2$. There will be extrema of $\mathcal {Y}_1$ when $t=t_2\pm \frac{1}{2\,\omega }\arccos c$, but the lower sign in the expression for c gives $|c|\le 1$ for any r, and there will be just one pair of extrema; the upper sign gives an extra pair if $r<1$. The extreme values of $\mathcal {Y}_1$ can be calculated as $\frac{1}{4}A_4 s(r+C_4 c)$ with $s=(1-c^2)^{1/2}$.

The moment $\mathcal {Y}_2$ is a simple sinusoid, centred on $A_0/8$, with period T/4. Its extrema require $\sin 4\omega (t-t_4)=0$ and therefore $s c=0$. From Eq. (60), $s=0$ leads to $\mathcal {Y}_2=\frac{1}{8}[A_0-C_4A_4]$. Also $s=0$ at $t=t_2$ and it follows that $\mathcal {Y}_2$ will be a minimum at $t_2$ if $C_4=+1$ and a maximum there if $C_4=-1$.

Thus, both $\mathcal {Y}_0$ and $\mathcal {Y}_1$ have four extrema in any half-period if $r<1$ and only two otherwise, while $\mathcal {Y}_2$ always has four. There are some temporal coincidences forced by $S_4=0$. At $t=t_2$ or $t=t_2\pm \pi /2\omega$, we have $s=0$, and hence, $V_2=V_4=0$ which gives $\mathcal {Y}_1=\mathcal {Y}_3=0$ as well as $\mathcal {Y}_0, \mathcal {Y}_2, \mathcal {Y}_4$ taking extreme values. Furthermore, at $t=t_2\pm \pi /4\omega$ or $t=t_2\pm 3\pi /4\omega$ we have $c=0$ and hence $U_2=0$; therefore, $\mathcal {Y}_0=\mathcal {Y}_4$ and $\mathcal {Y}_4$ takes an extreme value. Also $V_4=0$ which gives $\mathcal {Y}_1=\mathcal {Y}_3$. These features are shown in Fig. 4.

Fig. 4

Evolution of the fourth moments for a sum of the lowest two energy eigenstates of the oscillator, as in Eq. (49) with $b=2\exp \imath \theta$ with $\theta =1$ radian. The vertical axis is broken into three pieces because the oscillations are small compared to $\mathcal {Y}_0$. Over the second quarter-period, $\mathcal {Y}_4$ is a copy of $\mathcal {Y}_0$ over the first, and $\mathcal {Y}_3$ is the negative of $\mathcal {Y}_1$. Over the second half-period, all moments copy the first half-period. The vertical dotted lines join the extrema to inflections, intersections or to zero. Where a vertical dotted line crosses a curve other than at another extremum, there is no special attribute of the curve at that point

9.1.2 Example of fourth moments of a complex wavefunction with $S_4=0$

We take $\psi (x)=(1+\beta \,x/a)\exp (-\frac{1}{2}x^2/a^2)$ with $\beta =b\exp \imath \theta$ and $a=(\hbar /m \omega )^{1/2}$. This is a sum of the lowest two eigenstates of the oscillator as in Eq. (49). Calculations give the first moments as $\langle {\hat{x}}/a+\imath {\hat{p}}\,a/\hbar \rangle =2e^{\imath \theta }b/(2+b^2)^{2}$. Also $C_4=-1$ and, with $B = 2 /(2 + b^2)^4$,

$$\begin{aligned} A_0 = B (16 + 32 b^2 + 48 b^4 + 40 b^6 + 5 b^8),\;\;\; A_2 = 6 B b^2 |b^4 - 4 b^2 - 4|,\;\;\; A_4 = 24 B b^4. \end{aligned}$$

(65)

In Fig. 4, $b=2, \theta =1$, a case where all moments have four extrema in any half-period.

In the case where $a\ne (\hbar /m \omega )^{1/2}$ and b is complex, it will generally follow that $S_4\ne 0$. Then no useful exact solutions can be found, but the method in the next section can be applied.

9.1.3 The general fourth-order case: quartic polynomial equations for the extrema

For $\mathcal {Y}_0$, Eq. (55) and (54) give $2 A_2 s + A_4 S_4 (2 s^2 - 1) =- 2A_4 C_4 s c$, where $s= \sin 2\omega (t-t_2)$, $c= \cos 2\omega (t-t_2)$. Squaring both sides of this equation gives, with $r=A_2/A_4$,

$$\begin{aligned} s^4 + 2S_4 r s^3 + (r^2-1) s^2 - S_4 r s + \frac{1}{4}S_4^2 = 0. \end{aligned}$$

(66)

Numerical solutions of this quartic equation can be directly obtained by standard packages. The values of $S_4$ are best calculated from $I_4$ in Eq. (53), because of the ambiguities in calculating $t_2$ and $t_4$ from Eq. (18).

For $\mathcal {Y}_1$, $U_2+U_4=0$ gives $2r_2 c+ C_4(2 c^2-1)=-2S_4s c$, with $r_2=r/2$. Squaring both sides then leads to

$$\begin{aligned} c^4 +2C_4r_2 c^3 +(r_2^2-1) c^2 -C_4 r_2 c + \frac{1}{4}C_4^2=0. \end{aligned}$$

(67)

The discriminant D of the quartic polynomials gives the number of extrema: If $D>0$, there will be four distinct extrema, while if $D<0$ there will be two. The quartic for $\mathcal {Y}_0$ in Eq. (66) has a discriminant with the same sign as $4 (1-r^2 )^3 - 27 r^2 S_4^2$. Hence, there are four extrema in any half-period if $r<\frac{1}{2}$ and two if $r>1$. For $\frac{1}{2}<r< 1$, the dividing curve is shown in Fig. 5. Similarly, the discriminant of the quartic for $\mathcal {Y}_1$ in Eq. (67) has the same sign as $4 (1-r_2^2)^3 - 27 r_2^2 C_4^2$, also displayed in Fig. 5.

Fig. 5

Regions of r and $S_4$ where the sign of the discriminant of the quartic polynomial in Eq. (66) determines whether there will be two or four extrema of $\mathcal {Y}_0$ in any half-period of the oscillator. This diagram also applies to the extrema of $\mathcal {Y}_1$ if you replace r with $r_2$ and $S_4$ with $C_4$

Fig. 6

Evolution of the fourth moments for the wavefunction in Eq. (49) and $S_4\ne 0$. This is the same wavefunction as used in Fig. 4, with the same parameters $\beta =2\exp \imath \theta$ with $\theta =1$ radian, except that now we take $a=1.005$. The vertical dotted lines show the temporal coincidences in the same way. There are now no coincidences between the extrema of $\mathcal {Y}_2$ and those of $\mathcal {Y}_0$, but the extrema of $\mathcal {Y}_2$ still occur at the intersections of $\mathcal {Y}_1$ and $\mathcal {Y}_3$

9.1.4 Example of the general case

As an example where we use the solutions of the quartic equations (66, 67) to find the times of the extrema, we take the same wavefunction as used in sect. 9.1.2, except that now we take $a\ne 1$ so that the wavefunction is no longer a sum of energy eigenstates and $S_4$ is nonzero.

Figure 6 illustrates the case with $\beta =2\exp \imath \theta$ with $\theta =1$, as in Sect. 9.1.2, and $a=1.005$. This case gives four extrema for both $\mathcal {Y}_0, \mathcal {Y}_4$ and $\mathcal {Y}_1, \mathcal {Y}_3$, but the oscillations are relatively small. [$A_0\approx 8.41, A_2\approx 0.163, A_4\approx 0.405]$. Other values of b may give just two extrema for each pair.

10 Conclusion

Similarly to the case of free particles, the analysis of the evolution of moments for the oscillator is enhanced by the use of invariant combinations of the moments. These lead directly to the Fourier components of the evolution, and the general features of the evolution are more simply expressed in terms of the invariants. The evolution of the moments for a quantum oscillator closely matches that of an ensemble of classical particles where each particle is subject only to the same fixed oscillator force. The evolution equations are the same; but a large number of inequalities constrain the evolution, and in the quantum case these usually have extra terms involving Planck’s constant that imply a different range of possible initial values of the moments and therefore a different range of possible evolutions.

Appendices

General expression for $U_j$ and $V_j$ in terms of the moments $Y_k$

To express $W_j$ in terms of the $Y_k$ we use the expansion of the classical form of $W_j=\langle (X+\imath \mathcal {P})^j(X^2+\mathcal {P}^2)^{(n-j)/2}\rangle$ in terms of $\mathcal {P}^k X^{n-k}$ (where $\mathcal {P}=P/m\omega$). Thus

$$\begin{aligned} (X+\imath \mathcal {P})^j= & {} \sum \nolimits _{r=0}^{\,j}(_r^j)\,(\imath \mathcal {P})^r X^{j-r}, \end{aligned}$$

(68)

$$\begin{aligned} (\mathcal {P}^2+X^2)^{(n-j)/2}= & {} \sum \nolimits _{\,s=0}^{(n-j)/2}(_{\;\;\;\;s}^{(n-j)/2})\,\mathcal {P}^{2s} X^{n-j-2s}. \end{aligned}$$

(69)

Changing the summation variable r to $k=r+2s$ in the product leads to

$$\begin{aligned} W_j=\sum \nolimits _{k=0}^n\sum \nolimits _{r=0}^{k}\imath ^{r}\,(^{j}_{r})\,(_{(k-r)/2}^{(n-j)/2})\,\mathcal {Y}_k, \end{aligned}$$

(70)

where j is restricted to have $n-j$ even, and r is restricted to have $k-r$ even.

Separating the real and imaginary parts, with $W_j=\sum _k ({\mathfrak {u}}_{j,k}+\imath \,{\mathfrak {v}}_{j,k}){\mathcal {Y}}_k$, gives:

$$\begin{aligned} {\mathfrak {u}}_{j,k}=\sum \nolimits _{r=0, 2... }^k (-1)^{r/2}\,(^{j}_{r})\,(_{(k-r)/2}^{(n-j)/2}),\qquad {\mathfrak {v}}_{j,k}=\sum \nolimits _{r=1, 3...}^k(-1)^{(r-1)/2}\,(^{j}_{r})\,(_{(k-r)/2}^{(n-j)/2}), \end{aligned}$$

(71)

where k and r range over even integers for ${\mathfrak {u}}_{j,k}$ and over odd integers for ${\mathfrak {v}}_{j,k}$.

Alternatively ${\mathfrak {u}}, {\mathfrak {v}}$ can be found from the following recurrence relation.

Recurrence relation for $W_j$ in terms of $\mathcal {Y}_k$

Applying $\text {d}_t W_j=-\imath j\omega W_j$ and $\text {d}_t\mathcal {Y}_k$ from Eq. (4) to put $W_j=\sum _k {\mathfrak {w}}_{j,k}\mathcal {Y}_k$, and then equating each coefficient of $\mathcal {Y}_k$ gives

$$\begin{aligned} (n-k+1){\mathfrak {w}}_{j,k-1}+\imath j {\mathfrak {w}}_{j,k}-(k+1){\mathfrak {w}}_{j,k+1}=0. \end{aligned}$$

(72)

This can be used for each j, starting with ${\mathfrak {w}}_{j,0}=1$ and ${\mathfrak {w}}_{j,1}=\imath j$ to sequentially calculate all the ${\mathfrak {w}}_{j,k}$ (and only integer values arise). The next few cases are, with ${\mathfrak {w}}_{i,j}={\mathfrak {u}}_{j, k}+\imath \, {\mathfrak {v}}_{j, k}$,

$$\begin{aligned} {\mathfrak {w}}_{j, 2}= & {} \;{\mathfrak {u}}_{j, 2} \;= \;\;(n - j^2)/2, \end{aligned}$$

(73)

$$\begin{aligned} {\mathfrak {w}}_{j, 3}= & {} \imath \,{\mathfrak {v}}_{j, 3} = \imath \, j [(3 n-2) - j^2)]/6, \end{aligned}$$

(74)

$$\begin{aligned} {\mathfrak {w}}_{j, 4}= & {} \; {\mathfrak {u}}_{j, 3} \,= \;\;[3 n (n - 2) - 2j^2 (3 n - 4)+j^4]/24. \end{aligned}$$

(75)

Solutions of such three-term recurrence relations are usually difficult to find [14], but Eq. (70) is a solution of Eq. (72).

Moments in terms of the sinusoidal combinations U and V

Having found the matrices ${\mathfrak {u}}$ with $U_j=\sum _k {\mathfrak {u}}_{j,k}\mathcal {Y}_k$ for even k, and ${\mathfrak {v}}$ with $V_j=\sum _k {\mathfrak {v}}_{j,k}\mathcal {Y}_k$ for odd k, we need to invert these matrices to give ${\tilde{\mathfrak {u}}}, {\tilde{\mathfrak {v}}}$ such that $\mathcal {Y}_k=\sum _j{\tilde{\mathfrak {u}}}_{kj}U_j$ for even k and $\mathcal {Y}_k=\sum _j{\tilde{\mathfrak {v}}}_{kj}V_j$ for odd k. It suffices to calculate the inverse classically. We need to express $\mathcal {Y}_k=\langle \mathcal {P}^k X^{n-k}\rangle$ in terms of the $W_j= \langle (X+\imath \mathcal {P})^j(\mathcal {P}^2+X^2)^{(n-j)/2}\rangle =\langle a^{(n+j)/2}{\bar{a}}^{(n-j)/2}\rangle$, where $a=X+\imath \mathcal {P}$, $\bar{a}=X-\imath \mathcal {P}$, $X=(a+{\bar{a}})/2$,  $\mathcal {P}=(a-{\bar{a}})/2\imath$, and $W_{-j}$ is the complex-conjugate of $W_{j}$. Expanding $\mathcal {P}^k$ and $X^{n-k}$ as power series in a and ${\bar{a}}$, using $\mathcal {P}^k =(-\imath /2)^k \sum \nolimits _{q=0}^{k}\big (^{k}_{q}\big )a^q(-\bar{a})^{\,k-q}$ and $X^{n-k}= 2^{-(n-k)}\sum \nolimits _{s=0}^{n-k}\big (^{n-k}_{\,\;s}\big )a^s\, {\bar{a}}^{\,n-k-s}$, leads to

$$\begin{aligned} \mathcal {Y}_k= & {} (-\imath )^k 2^{-n} \sum \limits _{q=0}^{k}\sum \limits _{s=0}^{n-k}(-1)^{k-q}\big (^{k}_{q}\big ) \big (^{n-k}_{\;s}\big )\langle a^{q+s}{\bar{a}}^{\,n-q-s}\rangle \nonumber \\= & {} (-\imath )^k 2^{-n} \sum \limits _{\ell =0}^{n}\sum \limits _{s=0}^{\ell }(-1)^{k-\ell +s}\big (^{k}_{\ell -s}\big ) \big (^{n-k}_{\,\;s}\big )W(2\ell -n), \end{aligned}$$

(76)

where $q+s$ has been replaced by $\ell$. Put $j=2\ell -n$, and then $j\ge 0$ requires $\ell \ge n/2$. But $W_j+W_{-j}=2U_j$ and $W_j-W_{-j}=2\imath V_j$, so we define $\varLambda _{k,j}$ by

$$\begin{aligned} \varLambda _{k,j}=(-1)^{k-\frac{1}{2}(n-j)}\sum \limits _{s=0}^{(n-j)/2} (-1)^s\big (^{\;\;\;\;\;\;k}_{\frac{1}{2}(n-j)-s}\big ) \big (^{n-k}_{\;\;s}\big ). \end{aligned}$$

(77)

Then it follows that $\mathcal {Y}_k=\sum _j{\tilde{\mathfrak {u}}}_{k,j}U_j$ for even k and $\mathcal {Y}_k=\sum _j{\tilde{\mathfrak {v}}}_{k,j}V_j$ for odd k, where the matrices ${\tilde{\mathfrak {u}}}_{k,j}, {\tilde{\mathfrak {u}}}_{k,j}$ are the inverse of ${\mathfrak {u}}_{j,k}, {\mathfrak {v}}_{j,k}$ in Eq. ( 71), and with $\epsilon _j=(1-\frac{1}{2} \delta _{j, 0})$,

$$\begin{aligned} \text {for even}\,k: \qquad {\tilde{\mathfrak {u}}}_{k,j}= & {} (-1)^{k/2}2^{-(n-1)}\epsilon _j \varLambda _{k, j}, \qquad \;\;\; k=0, 2,...n, \nonumber \\ \text {for odd}\,k: \qquad \; {\tilde{\mathfrak {v}}}_{k,j}= & {} (-1)^{(k+1)/2}2^{-(n-1)}\varLambda _{k,j}, \qquad k=1, 3,...n-1, \end{aligned}$$

(78)

where $j=0, 2,..., n$ for even n, and $j=1, 3,..., n-1$ for odd n.

1.1 Recurrence relation for $\mathcal {Y}_k$ in terms of $W_j$

Since $W_j=\langle a^{(n+j)/2} \bar{a}^{(n-j)/2}\rangle$ has $W_{-j}= W_j^*$, we can put $\mathcal {Y}_k=\sum _{j=-n}^{\;n} {\mathfrak {y}}_{k,j}W_j$ with j increasing in steps of 2. Then applying $\text {d}_t\mathcal {Y}_k$ from Eq. (4) and $\text {d}_t W_j=-\imath j\omega W_j$ leads to

$$\begin{aligned} (n-k)\,{\mathfrak {y}}_{k+1,j}+\imath j\,{\mathfrak {y}}_{k,j,}-k\,{\mathfrak {y}}_{k-1,j}=0, \qquad {\mathfrak {y}}_{k,j}={\mathfrak {u}}_{k,j}+\imath {\mathfrak {v}}_{k,j}. \end{aligned}$$

(79)

Also $Y_0=\langle X^n\rangle =2^{-n}\langle (a+\bar{a})^n\rangle =2^{-n}\sum _{s=0}^n \big (^n_s\big )\langle a^s\bar{a}^{n-s}\rangle =2^{-n}\sum _j \big (^{\;\;\;\;n}_{(n+j)/2}\big )W_j$. Thus ${\mathfrak {y}}_{0,j}=2^{-n}\sum _j \big (^{\;\;\;\;n}_{(n+j)/2}\big )$ and this can be used to sequentially calculate all ${\mathfrak {y}}_{k,j}$. To obtain a sequence for ${\tilde{\mathfrak {u}}}, {\tilde{\mathfrak {v}}}$ rather than W, use Eq. (79) with ${\mathfrak {y}}_{0,j}=2^{-(n-1)}\epsilon _j\sum _j \big (^{\;\;\;\;n}_{(n+j)/2}\big )$.

Evolution of the moments over any quarter-period

The symmetries of the moments over any quarter-period were described in sect. 7, where they were derived directly for a classical ensemble, but using the Fourier transform of the initial wavefunction in the quantum case. Here we outline an alternative derivation (that applies to both the quantum and the classical cases).

Evolution of U and V over half- and quarter-periods

Half period: $W_j(t+T/2)=(-1)^j W_j(t)$ follows from $e^{\imath j\omega t}W_j(t)=e^{\imath j(\omega t+\pi )}W_j(t+T/2)$, and therefore

$$\begin{aligned} U_j(t+T/2)=(-1)^jU_j(t),\qquad V_j(t+T/2)=(-1)^jV_j(t). \end{aligned}$$

(80)

Quarter-period: $W_j(t+T/4)=\imath ^{-j}W_j(t)$ follows from $e^{\imath j \omega t}W_j(t)=e^{\imath j(\omega t+\pi /2)}W_j(t+T/4)$ and therefore

$$\begin{aligned} \text {if } j \text { even:}\qquad U_j(t+T/4)= & {} (-1)^{j/2}U_j(t),\qquad \;\;\;V_j(t+T/4)=\,(-1)^{j/2}V_j(t),\nonumber \\ \text {if } j \text { odd:}\;\qquad U_j(t+T/4)= & {} (-1)^{(j-1)/2}V_j(t),\;\;\;\;\; V_j(t+T/4)=-(-1)^{(j-1)/2}U_j(t). \end{aligned}$$

(81)

Evolution of the moments over a quarter-period

From Eq. (77), $\varLambda _{k,j}=(-1)^{(n+j)/2}\varLambda _{n-k,j}$. Combining this result and Eq. (81) with the expressions for $Y_k$ in terms of $U_j, V_j$ in Eq. (78) leads to the result that, for any n,

$$\begin{aligned} Y_k(t+T/4)=(-1)^k Y_{n-k}(t). \end{aligned}$$

(82)

Other forms for the invariant combinations of moments

There are some simple invariant quadratic combinations of the moments that can be expressed as linear combinations of the invariants $A_k^2$. Two examples are

$$\begin{aligned} \sigma _n:=\sum \nolimits _{k=0}^n(_k^n)\mathcal {Y}_k^2, \qquad \kappa _n:=\frac{1}{2}\sum \nolimits _{k=0}^n(-1)^k(_k^n)\mathcal {Y}_k \mathcal {Y}_{n-k}, \end{aligned}$$

(83)

but $\kappa _n$ is zero for odd n (as seen by changing k to $n-k$). For $n=2$, $\kappa _2$ is subject to Schrödinger’s inequality, $\kappa _2\ge \frac{1}{4}\alpha ^4$, as in 6, and a similar inequality for $\kappa _4$ is found in Appendix E. Another sequence of invariant combinations of the moments is

$$\begin{aligned} \rho _n:=\sum \nolimits _{k=1}^{n-1}(_{k-1}^{n-2})(\mathcal {Y}_{k-1} \mathcal {Y}_{k+1}-\mathcal {Y}_k^2). \end{aligned}$$

(84)

Since $\rho _2=\kappa _2$, $\rho _n$ is distinct for $n\ge 3$. All these invariants are linear combinations of the $A_k^2$; with $n=2$, $2\sigma _2=A_0^2+A_2^2$ and $4\kappa _2=A_0^2-A_2^2$.

Proof that $\sigma _n$, $\kappa _n$ and $\rho _n$ are invariant, using $\text {d}_t \mathcal {Y}_k=(n-k)\mathcal {Y}_{k+1}-k\mathcal {Y}_{k-1}$.

For $\sigma _n$: $\text {d}_t\sigma _n=2\sum \nolimits _{k=0}^n(_k^n)\big ( (n-k)\mathcal {Y}_k\mathcal {Y}_{k+1}- k\mathcal {Y}_{k-1}\mathcal {Y}_k\big )$ and replacing k with $k+1$ in the second term shows that it cancels the first term because $(n-k)(_k^n)=(k+1)(_{k+1}^{\;\,n})$.

For $\kappa _n\!=\!\frac{1}{2}\sum \nolimits _{k=0}^n(-1)^k(_k^n)\mathcal {Y}_k \mathcal {Y}_{n-k}$: If $Z_k\!:=\!k(_k^n)(\mathcal {Y}_k\mathcal {Y}_{n-k+1}-\mathcal {Y}_{k-1}\mathcal {Y}_{n-k})$, then $Z_0\!=\!Z_{n+1}\!=\!0$ and $(_k^n)\text {d}_t (\mathcal {Y}_k\mathcal {Y}_{n-k})=Z_k+Z_{k+1}$. Therefore $\text {d}_t\kappa _n=\frac{1}{2}\sum \nolimits _{k=0}^n(-1)^k(Z_k+Z_{k+1})=0$.

For $\rho _n\!=\!\sum \nolimits _{k=1}^{n-1}(_{k-1}^{n-2})(\mathcal {Y}_{k-1} \mathcal {Y}_{k+1}-\mathcal {Y}_k^2)$: If $R_k:=(k-1)(_{k-1}^{n-2}) (\mathcal {Y}_{k-1}\mathcal {Y}_k-\mathcal {Y}_{k-2}\mathcal {Y}_{k+1})$, then $(_{k-1}^{n-2})\text {d}(\mathcal {Y}_{k-1} \mathcal {Y}_{k+1}-\mathcal {Y}_k^2)\!=\!R_k-R_{k+1}$ and $R_0=0$. Therefore $\text {d}_t\rho _n=\sum \nolimits _{k=1}^{n-1}(R_k-R_{k+1})=0$.

There is a family of invariant linear combinations of products of two moments that includes the above $\sigma , \rho$ and $\kappa$ and more. For all integers m with $0\le m\le n/2$, define

$$\begin{aligned} \varOmega _{m}:=\sum \nolimits _{k=m}^{n-m}\,(_{\,k-m}^{n-2m})\sum \nolimits _{\ell =0}^{m}(-1)^{m-\ell }\epsilon _{\ell }\,(_{m-\ell }^{\,\,2m})\mathcal {Y}_{k-\ell }\mathcal {\mathcal {Y}}_{k+\ell }, \end{aligned}$$

(85)

where $\epsilon _\ell =\frac{1}{2}$ if $\ell =0$, and $\epsilon _\ell =1$ if .$\ell \ne 0$. The simplest cases are: $\;\; \varOmega _{0}=\frac{1}{2}\sum \nolimits _{k=0}^{n}(_{k}^{n})\mathcal {Y}_{k}^2=\frac{1}{2}\sigma _n$,

$\varOmega _{1}=\sum \nolimits _{k=1}^{n-1}(_{k-1}^{n-2})(\mathcal {Y}_{k-1}\mathcal {Y}_{k+1}-\mathcal {Y}_{k}^2)=\rho _n,$ and $\varOmega _{n/2}=\frac{1}{2}\sum \nolimits _{\ell =0}^{n}(-1)^\ell (_{\ell }^{n})\mathcal {\mathcal {Y}}_{\ell }\mathcal {Y}_{n-\ell }=\kappa _n$ for even n only. For all $m\le n/2$, $\varOmega _m$ can be expressed in terms of the invariant amplitudes $A_k$ as follows:

$$\begin{aligned} \varOmega _m = \sum \nolimits _j {\tilde{\mathfrak {u}}}_{2m,j}A^2_{j}, \end{aligned}$$

(86)

where $j=0, 2, .. n$ if n is even, $j=1, 3, .. n$ if n is odd, and the matrix ${\tilde{\mathfrak {u}}}_{k,j}$ is the inverse of ${\mathfrak {u}}_{j,k}$, with $\mathcal {Y}_k=\sum _j{\tilde{\mathfrak {u}}}_{k,j}U_j$ as in Eq. (78). This result, as yet unproven for all n, has been tested for all $n\le 20$. (It also implies that the $\varOmega _m$ are invariant.) Examples are:

for $n=3, \;4 \sigma _3= 3 A_1^2 + A_3^2, \;\;8 \rho _3 = A_1^2 - A_3^2$,

for $n=4, \;4 \sigma _4= 3 A_0^2 + 4A_2^2+A_4^2,\;\,16 \kappa _4= 3 A_0^2 - 4A_2^2+A_4^2, \;\,16 \rho _4 = A_0^2 - A_4^2.$.

Some inequalities for combinations of fourth-order moments

Inequalities for combinations of moments have usually been found using the Schwarz inequality $\langle {\hat{A}}^2\rangle \langle {\hat{B}}^2\rangle \ge |\langle {\hat{A}}{\hat{B}}\rangle |^2$. With ${\hat{A}}= {\hat{X}}^2$ and ${\hat{B}}= {\hat{P}}^2$, this gives (with $n=4$)

$$\begin{aligned} Y_0 Y_4-Y_2^2\ge 16\hbar ^2 \langle {\hat{P}}{\hat{X}}+ {\hat{X}}{\hat{P}}\rangle ^2\ge 0\;\;\;\;\text {and} \;\;\; \mathcal {Y}_0 \mathcal {Y}_4\ge \mathcal {Y}_2^2. \end{aligned}$$

(87)

Thus the geometric mean of $\mathcal {Y}_0$ and $\mathcal {Y}_4$ is not less than $|\mathcal {Y}_2|$, in agreement with Fig. 6. With ${\hat{A}}=\frac{1}{2}({\hat{P}}{\hat{X}}+{\hat{X}}{\hat{P}})$ and ${\hat{B}}= {\hat{P}}^2$, the result is [7]

$$\begin{aligned} Y_2 Y_4-Y_3^2\ge \hbar ^2\left( \langle {\hat{P}}^2\rangle ^2-\frac{1}{4}\langle {\hat{P}}^4\rangle \right) \;\;\;\; \text {and}\;\;\; \mathcal {Y}_2 \mathcal {Y}_4-\mathcal {Y}_3^2\ge -\frac{1}{4}\alpha ^4\mathcal {Y}_4. \end{aligned}$$

(88)

Similarly with ${\hat{A}}=\frac{1}{2}({\hat{P}}{\hat{X}}+{\hat{X}}{\hat{P}})$ and ${\hat{B}}= {\hat{X}}^2$,

$$\begin{aligned} Y_0 Y_2-Y_1^2\ge \hbar ^2\left( \langle {\hat{X}}^2\rangle ^2-\frac{1}{4}\langle {\hat{X}}^4\rangle \right) \;\;\;\; \text {and}\;\;\; \mathcal {Y}_0 \mathcal {Y}_2-\mathcal {Y}_1^2\ge -\frac{1}{4}\alpha ^4\mathcal {Y}_0. \end{aligned}$$

(89)

Also ${\hat{A}}={\hat{X}}^2-\langle {\hat{X}}^2\rangle$ and ${\hat{B}}= {\hat{X}}^2$ give $\langle {\hat{X}}^4\rangle \ge \langle {\hat{X}}^2\rangle ^2$ and similarly $\langle {\hat{P}}^4\rangle \ge \langle {\hat{P}}^2\rangle ^2$.

This approach is not applicable to $\mathcal {Y}_1 \mathcal {Y}_3-\mathcal {Y}_2^2$, which can be positive or negative; this quantity appears in the invariant $\kappa _4= (\mathcal {Y}_0 \mathcal {Y}_4 - \mathcal {Y}_2^2) - 4 (\mathcal {Y}_1\mathcal {Y}_3 - \mathcal {Y}_2^2)$ in Eq. (83); but a lower bound on $\kappa _4$ can be found using a different method.

A bound on $\kappa _4$. First consider a set of N classical particles with positions $x_i$ and momenta $p_i$. Define $X_i\! :=\!x_i-{\bar{x}}$ and $P_i\! :=\!p_i-{\bar{p}}$, where ${\bar{x}} :=\!N^{-1}\sum _{i=1}^N x_i$ and $\bar{p}:=\!N^{-1}\sum _{i=1}^N p_i$. The equations of motion are $\text {d}_t X_i=\omega \mathcal {P}_i$ and $\text {d}_t \mathcal {P}_i=-\omega X_i$, where $\mathcal {P}_i:=P_i/(\omega m)$. Then $\frac{1}{2}\sum _{i=1}^N \sum _{j=1}^N (X_i \mathcal {P}_j-\mathcal {P}_iX_j)^4=\mathcal {Y}_0\mathcal {Y}_4-4\mathcal {Y}_1\mathcal {Y}_3+3\mathcal {Y}_2^2=\kappa _4\ge 0$. Also $\kappa _4$ is invariant because $\text {d}_t(X_i \mathcal {P}_j-\mathcal {P}_iX_j)=0$.

For the quantum case, we take $\mathcal {K}:=\frac{1}{2}\int \!\!\int \psi ^*(x)\psi ^*(x')({\hat{X}} {\hat{\mathcal {P}}}'-{\hat{\mathcal {P}}}{\hat{X}}')^4 \psi (x)\psi (x')\,\text {d} x\,\text {d} x'$, with ${[}{\hat{X}}, \hat{\mathcal {P}}']=[{\hat{\mathcal {P}}},{\hat{X}}']=[{\hat{X}}, {\hat{X}}']=[{\hat{\mathcal {P}}},{\hat{\mathcal {P}}}']=0$. Then $\mathcal {K}$ is positive and expands to

$$\begin{aligned} \mathcal {K}= & {} \langle {\hat{X}}^4\rangle \langle {\hat{\mathcal {P}}}^4\rangle +\langle {\hat{X}}^2{\hat{\mathcal {P}}}^2\rangle \langle {\hat{\mathcal {P}}}^2{\hat{X}}^2\rangle + \langle {\hat{X}}{\hat{\mathcal {P}}} {\hat{X}}{\hat{\mathcal {P}}}\rangle \langle {\hat{\mathcal {P}}} {\hat{X}} {\hat{\mathcal {P}}} {\hat{X}}\rangle +\langle {\hat{X}}{\hat{\mathcal {P}}}^2{\hat{X}}\rangle \langle {\hat{\mathcal {P}}} {\hat{X}}^2{\hat{\mathcal {P}}}\rangle \nonumber \\&-(\langle {\hat{X}}^3{\hat{\mathcal {P}}}\rangle \langle {\hat{\mathcal {P}}}^3{\hat{X}}\rangle +\langle {\hat{X}}{\hat{\mathcal {P}}}^3\rangle \langle {\hat{\mathcal {P}}} {\hat{X}}^3\rangle +\langle {\hat{X}}^2{\hat{\mathcal {P}}} {\hat{X}}\rangle \langle {\hat{\mathcal {P}}}^2 {\hat{X}}{\hat{\mathcal {P}}}\rangle +\langle {\hat{X}}{\hat{\mathcal {P}}} {\hat{X}}^2\rangle \langle {\hat{\mathcal {P}}} {\hat{X}}{\hat{\mathcal {P}}}^2\rangle ). \end{aligned}$$

(90)

Each of these 16 expectation values can be expressed in terms of the fourth-order and second-order moments using the commutation relation ${\hat{X}} {\hat{\mathcal {P}}}-{\hat{\mathcal {P}}} {\hat{X}}=\imath \,\alpha ^2$. This leads to $\mathcal {K}= \kappa _4-5\alpha ^4\kappa _2+\frac{1}{2}\alpha ^8$, and $\kappa _4\ge 5\alpha ^4\kappa _2-\frac{1}{2}\alpha ^8\ge \frac{3}{4}\alpha ^8$, because $\kappa _2\ge \frac{1}{4}\alpha ^4$. The Gaussian wavefunction $\exp (-\frac{1}{2}x^2/a^2)$ has $\kappa _2=\frac{1}{4}\alpha ^4$ and $\kappa _4= \frac{3}{4}\alpha ^8$, saturating both inequalities.

Some connections with the time-dependent oscillator

The term ‘universal invariants’ [5] was applied to any time-independent invariants of a general quadratic Hamiltonian, and they will be invariants for the oscillator with time-dependent force as well as to our case of an oscillator where the force is constant in time; but the latter case has more time-independent invariants. Here we will give expressions for the universal invariants in terms of our invariants (noting the difference in normalisation between $Y_k$ and $\mathcal {Y}_k)$.

Ref. [15] gives explicit expressions for the universal invariants in one dimension for $n=2, 3, 4$.

For $n=2$ the only universal invariant is $K_2=Y_0 Y_2-Y_1^2$. This has the same form as our $\kappa _2$ as defined in Eq. 83, so that $K_2/\hbar ^2= \kappa _2/\alpha ^4$. It was shown in Sect. 6 that $\kappa _2= \frac{1}{4} (A_0^2-A_2^2)$.

For $n=3$, Eq. (3.34) of ref. [15] gives the invariant $D_3=Y_0^2 Y_3^2 - 3 Y_1^2 Y_2^2 + 4 Y_0 Y_2^3 + 4 Y_1^3 Y_3 - 6 Y_0 Y_1 Y_2 Y_3$ and in terms of our invariants $64 D_3/\hbar ^6=(3 A_1^4 + 6 A_1^2 A_3^2 - A_3^4 - 8 R_3)/\alpha ^{12}$, where $R_3$ was defined in Eq. 34.

For $n=4$, two invariants are given. Equation (3.35) of ref. [15] gives $K_4= Y_0 Y_4 + 3 Y_2^2 - 4 Y_1Y_3$, but this has the same form as our $\kappa _4$ as in Eq. 83 and it was shown in appendix E that $16\kappa _4=3 A_0^2 - 4 A_2^2+ A_4^2$ and that it is subject to the inequality $\kappa _4\ge 5\alpha ^4\kappa _2-h\alpha ^8\ge \frac{3}{4}\alpha ^8$. The other invariant is in Eq.(3.36): $D_4= Y_0 Y_2 Y_4 - Y_0 Y_3^2 - Y_2^3 - Y_1^2 Y_4 + 2 Y_1 Y_2 Y_3$ and in terms of our invariants $64 D_4/\hbar ^6=[A_0 (A_0^2 - 2 A_2^2 - A_4^2) + 2 R_4]/\alpha ^{12}$, where $R_4$ was defined in Eq. 52.