1 Introduction

Cancer is a disease which arises from changes in the genes as a result of DNA damage under the effects of factors such as gender, age, genetics, lifestyle, malnutrition, stress, cigarette and alcohol consumption. This disease, especially in its advanced stages, requires a difficult process to be treated. Because of the fact that people who get cancer or people who die from cancer is increasing day by day it is frequently seen in the research topics of recent days. Among these studies, the interaction between cancer cells and immune system components which consists of tissues and organs, the defense mechanism of the body, has an important place. By the help of its ability to regulate immunity responses, one of the most important parts of the immune system, dendritic cells, reports the presence of cancer cells to CD4+T cells in order for the body to prepare itself to harmful cells and what’s more stimulates IL-12 cytokine. CD4+T cells takes the important steps for the body to protect itself and notifies CD8+T cells and also stimulates IL-2 cytokine production. The purpose of IL-2 is to increase the proliferation of both CD4+T and CD8+T lymphocytes. IL-12 is to increase cytotoxic properties of CD8+T cells which is responsible for killing tumors by attacking them. In this way, immune system components try to protect the body from harm. However, due to the ability of cancers cells to hide from these protective components, this order may not be effective in reducing cancer cells.

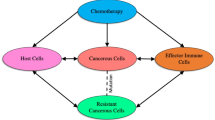
As seen in Fig. 1a cancer cells, as a result of the interaction between PD-1 protein which is expressed (the transformation process of genes to proteins) on the surface of T lymphocytes, and PD-L1 protein which is expressed on cancer cell surfaces, can escape from the immune system and inhibit the activation of T lymphocytes [1, 2].

Recently, anti-PD-L1 inhibitors have been used, in order to increase T cell activation [3] and stop cancer cells escaping from the immune system and to ensure that the immune system can recognize and destroy these cells, as we see Fig. 1b.

Fig. 1
figure 1

Figures about cancer cells can escape from the immune system and the effect of anti-PD-L1

Full size image

Many scientists have studied complex structured tumors, tumor growth and the interaction between the tumor and immune system by using mathematical models. [4,5,6] is among the sources examining the relationship between tumor and immune system cells between mathematical modeling and [7,8,9] is among the sources investigating the interaction between tumor and normal cells. Using mathematical modeling Kirschner and Panetta [10] examine tumor cells, immune system cells and cytokine IL-2 interaction, while Pillis et al. [11,12,13] investigated of tumor growth by using immune system components such as IL-2 concentration, CD8+T cells, natural killer (NK) cells and total circulating lymphocytes. Castiglione-Piccoli [14] study the interaction between CD4+T and CD8+T lymphocytes, cancer cells, dendritic cells, and cytokine IL-2, and [15] examines the model with fractional derivative and gives numerical results.

Recently, [16,17,18] are among the studies examining the cancer-immune system mathematical model, one of the immune system components, especially anti-PD-L1 inhibitors, others lymphocytes, cytokines. By this motivation, IL-12 cytokine due to its ability to increase the number of CD4+T, CD8+T lymphocytes, and the anti-PD-L1 inhibitor due to its help at increasing the effect of CD8+T cells are added Castiglione–Piccoli mathematical model given in [14]. Thus, a new time-dependent ordinary differential system, which is organized as follows, has been obtained.

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}t}= & {} a_{0}+b_{0}DH\left( 1-\frac{H}{f_{0}}\right) +\lambda _{42} \frac{I_{2}}{K_{2}+I_{2}}H\left( 1-\frac{H}{f_{0}}\right) \nonumber \\&\quad +\lambda _{412}\frac{I_{12}}{K_{12}+I_{12}}H\left( 1-\frac{H}{f_{0}}\right) -c_{0}H, \nonumber \\ \frac{\mathrm{d}C}{\mathrm{d}t}= & {} a_{1}+b_{1}\frac{I_{2}}{K_{2}+I_{2}}\left( M+D\right) C\left( 1-\frac{C}{f_{1}}\right) \nonumber \\&\quad +\lambda _{812}\frac{I_{12}}{K_{12}+I_{12}} C\left( 1-\frac{C}{f_{1}}\right) -c_{1}C, \nonumber \\ \frac{\mathrm{d}M}{\mathrm{d}t}= & {} b_{2}M\left( 1-\frac{M}{f_{2}}\right) -d_{2}FMC, \nonumber \\ \frac{\mathrm{d}D}{\mathrm{d}t}= & {} -d_{3}DC, \nonumber \\ \frac{\mathrm{d}I_{2}}{\mathrm{d}t}= & {} b_{4}DH-e_{4}I_{2}C-c_{4}I_{2}, \nonumber \\ \frac{\mathrm{d}I_{12}}{\mathrm{d}t}= & {} \lambda _{D_{I_{12}}}D-d_{I_{12}}I_{12}, \nonumber \\ \frac{\mathrm{d}Z}{\mathrm{d}t}= & {} -\gamma Z \end{aligned}$$
(1)

where

$$\begin{aligned} F=\frac{c_{pd}-1}{\pi }\left( \mathrm{tan}^{-1}\left( \left( Z-1\right) k_{pd}\right) +\frac{\pi }{2}\right) \end{aligned}$$

is given in [18]. The fight of immune system components against cancer cells is modeled with Eq. (1), which is obtained by adding IL-12 and anti-PD-L1 to immune system components. The purpose of adding new variables in Eq. (1) is for the immune system to fight cancer cells more effectively.

In this paper, the modified ordinary differential system, in which H, C, M, D, \(IL-2\), \(IL-12\) and Z symbolize CD4+T and CD8+T lymphocytes, cancer cells, dendritic cells, IL-2 and IL-12 cytokine, anti-PD-L1, respectively, will be examined in the paper using fractional calculus (FC), as the memory and inheritance effect is important in mathematical models used to understand natural phenomenon. Some of the applications related to FC, which have attracted attention in scientific fields such as biology in recent years, is given with [15] and [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. HIV/HCV coinfection model, a new chaotic system, COVID-19 epidemics model, rubella disease model, HIV transmission model, computer virus propagation with kill signals model, tuberculosis model, smoking epidemic model, 2019-nCOV epidemic outbreaks model, cancer treatment model, model of the deathly disease in pregnant women, smoking model, computer worm model, glucose–insulin regulatory system are studied with fractional derivative in [19,20,21,22,23,24,25,26,27,28,29,30,31,32], respectively. [33, 34] emphasize that the solution methods discussed for the problem working on are applicable and practical. [35] set up a new formula for fractional derivative with Mittag-Leffler kernel. This paper is organized as follows; In Sect. 2, the description of the immune system-cancer model obtained, In Sect. 3, some important definitions and theorems to be used in the paper, fractional-order models and stability analysis for model with Caputo derivative, In Sect. 4, existence-uniqueness of the model expressed by considering in term of the Caputo fractional derivative will be examined. In Sect. 5, simulation and interpretations about the new time-dependent ordinary differential and the modified model which is expressed by considering in term of Caputo, CF derivatives, and in Sect. 6, the final part will be given.

2 Description of the immune system-cancer model

In the first equation of Eq. (1), which gives the concentration of CD4+T lymphocytes, the terms \(a_{0}\) and \(-c_{0}H\), symbolize birth and normal death rates, respectively. The term \( b_{0}DH\left( 1-\frac{H}{f_{0}}\right) \) , the term \(\lambda _{42}\frac{I_{2} }{K_{2}+I_{2}}H\left( 1-\frac{H}{f_{0}}\right) \) and the term \(\lambda _{412} \frac{I_{12}}{K_{12}+I_{12}}H\left( 1-\frac{H}{f_{0}}\right) \) refer to CD4+T lymphocyte proliferation under dendritic cell, IL-2 and IL-12 effect, respectively. In the 2nd equation of Eq. (1) discussing CD8+T lymphocytes, the terms \(a_{1}\) and \(-c_{1}C\), stands for birth and normal death rates, respectively . The term \(b_{1}\frac{I_{2}}{K_{2}+I_{2}}\left( M+D\right) C\left( 1-\frac{C}{f_{1}}\right) \) indicates the interaction of CD8+T cells and cancer cells, IL-2 and dendritic cells while the term \( \lambda _{812}\frac{I_{12}}{K_{12}+I_{12}}C\left( 1-\frac{C}{f_{1}}\right) \) models the proliferation of CD8+T lymphocytes under IL-12 effect. In the 3rd equation of Eq. (1), the dynamics of tumor cells are discussed. The term \(b_{2}M\left( 1-\frac{M}{f_{2}}\right) \) symbolizes the growth of tumor cells and the term \(-d_{2}FMC\) symbolizes the decrease in tumor cells under the anti-PD-L1 effect of CD8+T cells. In the fourth equation of Eq. (1 ), the term \(-d_{3}DC\) models the decrease in dendritic cells which is considered to exist in dynamics when CD8+T lymphocytes become active. In the fifth equation of Eq. (1) symbolizing the IL-2 cytokine dynamics, \( b_{4}DH\) and \(-e_{4}I_{2}C\) define IL-2 proliferation under the effect of T (CD4+T and CD8+T) lymphocytes, dendritic cells and the term \(-c_{4}I_{2}\) defines the normal death numbers. In the sixth equation of Eq. (1) symbolizing the dynamics of IL-12 cytokines, \(\lambda _{D_{I_{12}}}D\) defines IL-12 proliferation under the effect of dendritic cells, and the term \(-d_{I_{12}}I_{12}\) defines the normal death numbers. The seventh equation of Eq. (1), the term \(-\gamma Z\) model the amount of reduction of the anti-PD-L1 inhibitor, which is considered to exist in dynamics, while defining the anti-PD-L1 dynamics.

3 Fractional-order cancer-immune model and stability analysis for model with Caputo derivative

In this section, there are some important definitions which using this paper. When we rewrite the new model in Eq. (1), we use Caputo and Caputo–Fabrizio fractional derivative.

Definition 1

[36] Let \(\tau >0\), \(t>0\), and g is a function. The fractional-order integral is

$$\begin{aligned} I^{\tau }g\left( t\right) =\frac{1}{\varGamma \left( \tau \right) }\int _{0}^{t}\left( t-s\right) ^{\tau -1}g\left( s\right) \mathrm{d}s \end{aligned}$$

and the fractional-order derivative \(\tau \in \left( m-1,m\right) \) is

$$\begin{aligned} \frac{d}{dt}g\left( t\right) =I^{m-\tau }D^{m}g\left( t\right) . \end{aligned}$$

Definition 2

[36] The Caputo fractional derivative is given by

$$\begin{aligned} _{0}^{C}D_{t}^{\tau }g\left( t\right) =\frac{1}{\varGamma \left( \tau \right) } \int _{0}^{t}\left( t-s\right) ^{m-\tau -1}f^{\left( m\right) }\left( s\right) \mathrm{d}s, \end{aligned}$$

where \(\tau \in \left( m-1,m\right) ,\tau \in Z^{+}\), g is a time-dependent function.

Definition 3

[37] Let \(a<b\), \(g\in H^{1}\left( a,b\right) \) where \(H^{1}\) is Sobolev space of order 1 in (a, b) and \(\tau \in \left[ 0,1\right] \), the Caputo–Fabrizio derivative is given by

$$\begin{aligned} D_{t}^{\tau }\left[ g\left( t\right) \right] =\frac{M\left( \tau \right) }{ 1-\tau }\int \limits _{a}^{t}g^{\prime }\left( s\right) \exp \left[ -\tau \frac{ t-s}{1-\tau }\right] \mathrm{d}s \end{aligned}$$
(2)

where \(M\left( \tau \right) \) is a normalization function and \( M\left( 0\right) =M\left( 1\right) =1\). If \(g\notin H^{1}\left( a,b\right) \) , this derivative can be written as follow:

$$\begin{aligned} D_{t}^{\tau }\left[ g\left( t\right) \right] =\frac{\tau M\left( \tau \right) }{1-\tau }\int \limits _{a}^{t}\left( g\left( t\right) -g\left( s\right) \right) \exp \left[ -\tau \frac{t-s}{1-\tau }\right] \mathrm{d}s. \end{aligned}$$
(3)

Theorem 1

[38] For Caputo fractional derivative system equilibrium points are found via \(f(x)=0\). If the eigenvalues \(\lambda \) of the Jacobian matrix satisfy \(\left| \mathrm{arg}(\lambda )\right| >\frac{\alpha \pi }{2}\), the eigenvalues are locally asymptotically stable.

The new ordinary systems given in Eq. (1) is rewritten with Caputo fractional derivative as follows:

$$\begin{aligned} {}_{0}^{C}D_{t}^{\tau }\left( H\right)= & {} a_{0}+b_{0}DH\left( 1-\frac{H}{f_{0}} \right) +\lambda _{42}\frac{I_{2}}{K_{2}+I_{2}}H\left( 1-\frac{H}{f_{0}} \right) \nonumber \\&+\lambda _{412}\frac{I_{12}}{K_{12}+I_{12}}H\left( 1-\frac{H}{f_{0}} \right) -c_{0}H, \nonumber \\ {}_{0}^{C}D_{t}^{\tau }\left( C\right)= & {} a_{1}+b_{1}\frac{I_{2}}{K_{2}+I_{2}} \left( M+D\right) C\left( 1-\frac{C}{f_{1}}\right) \nonumber \\&+\lambda _{812}\frac{ I_{12}}{K_{12}+I_{12}}C\left( 1-\frac{C}{f_{1}}\right) -c_{1}C, \nonumber \\ {}_{0}^{C}D_{t}^{\tau }\left( M\right)= & {} b_{2}M\left( 1-\frac{M}{f_{2}} \right) -d_{2}FMC, \nonumber \\ {}_{0}^{C}D_{t}^{\tau }\left( D\right)= & {} -d_{3}DC, \nonumber \\ {}_{0}^{C}D_{t}^{\tau }\left( I_{2}\right)= & {} b_{4}DH-e_{4}I_{2}C-c_{4}I_{2}, \nonumber \\ {}_{0}^{C}D_{t}^{\tau }\left( I_{12}\right)= & {} \lambda _{D_{I_{12}}}D-d_{I_{12}}I_{12}, \nonumber \\ {}_{0}^{C}D_{t}^{\tau }\left( Z\right)= & {} -\gamma Z \end{aligned}$$
(4)

and with Caputo–Fabrizio fractional derivative as follows:

$$\begin{aligned} {}_{0}^{CF}D_{t}^{\tau }\left( H\right)= & {} a_{0}+b_{0}DH\left( 1-\frac{H}{f_{0} }\right) +\lambda _{42}\frac{I_{2}}{K_{2}+I_{2}}H\left( 1-\frac{H}{f_{0}} \right) \nonumber \\&+\lambda _{412}\frac{I_{12}}{K_{12}+I_{12}}H\left( 1-\frac{H}{f_{0}} \right) -c_{0}H, \nonumber \\ {}_{0}^{CF}D_{t}^{\tau }\left( C\right)= & {} a_{1}+b_{1}\frac{I_{2}}{K_{2}+I_{2}} \left( M+D\right) C\left( 1-\frac{C}{f_{1}}\right) \nonumber \\&+\lambda _{812}\frac{ I_{12}}{K_{12}+I_{12}}C\left( 1-\frac{C}{f_{1}}\right) -c_{1}C, \nonumber \\ {}_{0}^{CF}D_{t}^{\tau }\left( M\right)= & {} b_{2}M\left( 1-\frac{M}{f_{2}} \right) -d_{2}FMC, \nonumber \\ {}_{0}^{CF}D_{t}^{\tau }\left( D\right)= & {} -d_{3}DC, \nonumber \\ {}_{0}^{CF}D_{t}^{\tau }\left( I_{2}\right)= & {} b_{4}DH-e_{4}I_{2}C-c_{4}I_{2}, \nonumber \\ {}_{0}^{CF}D_{t}^{\tau }\left( I_{12}\right)= & {} \lambda _{D_{I_{12}}}D-d_{I_{12}}I_{12}, \nonumber \\ {}_{0}^{CF}D_{t}^{\tau }\left( Z\right)= & {} -\gamma Z \end{aligned}$$
(5)

for the initial conditions \(H\left( 0\right) =0\), \(C\left( 0\right) =0\), \( M\left( 0\right) =1\), \(D\left( 0\right) =10\), \(I_{2}\left( 0\right) =0\), \( I_{12}=\left( 0\right) =0\) and \(Z=\left( 0\right) =0.2\) where \(\tau \in \left[ 0,1\right] \). And H, C, M, D, \(I_{2}\), \(I_{12}\), Z represent CD4+T (helper) cells, CD8+T (cytotoxic) cells, myeloid (cancer) cells, dendritic cells, IL-2, IL-12 and anti-PD-L1, respectively.

We study the natural equilibrium points in system (4), as no treatment is considered. To this aim, firstly we assume the system is time independent. Namely,

$$\begin{aligned}&a_{0}+b_{0}DH\left( 1-\frac{H}{f_{0}}\right) +\lambda _{42}\frac{I_{2}}{ K_{2}+I_{2}}H\left( 1-\frac{H}{f_{0}}\right) \\&\quad +\lambda _{412}\frac{I_{12}}{ K_{12}+I_{12}}H\left( 1-\frac{H}{f_{0}}\right) -c_{0}H = 0, \\&a_{1}+b_{1}\frac{I_{2}}{K_{2}+I_{2}}\left( M+D\right) C\left( 1-\frac{C}{ f_{1}}\right) \\&\quad +\lambda _{812}\frac{I_{12}}{K_{12}+I_{12}}C\left( 1-\frac{C}{ f_{1}}\right) -c_{1}C = 0, \\&b_{2}M\left( 1-\frac{M}{f_{2}}\right) -d_{2}FMC = 0, \\&\quad -d_{3}DC = 0, \\&b_{4}DH-e_{4}I_{2}C-c_{4}I_{2} = 0, \\&\lambda _{DI_{12}}D-d_{I_{12}}I_{12} = 0, \\&\quad -\gamma Z = 0. \end{aligned}$$

If we solve the nonlinear system with model parameter, we obtain that

$$\begin{aligned} D=0, I_{12}=0, I_{2}=0, Z=0, H=\frac{a_{0}}{c_{0}}, C=\frac{a_{1}}{c_{1}}. \end{aligned}$$

The tumor growth law to solve

$$\begin{aligned} M\left[ \left( b_{2}-\frac{b_{2}M}{f_{2}}\right) -d_{2}F_{0}C\right] =0 \end{aligned}$$

with when \(Z=0\), \(F_{0}=\frac{c_{pd}-1}{\pi }\left( \mathrm{tan}^{-1}\left( \left( -1\right) k_{pd}\right) +\frac{\pi }{2}\right) +1\).

Hence, obtained by

$$\begin{aligned} M=0\hbox { and }M=-\frac{f_{2}\left( a_{1}d_{2}F_{0}+a_{1}-a_{1}b_{2}\right) }{a_{1}b_{2}}. \end{aligned}$$

The dynamical system has two equilibrium points \(P_{1}=\left( H_{1},C_{1},M_{1},D_{1},{I_{2}}_{1},{I_{12}}_{1},Z_{1}\right) \) and \(P_{2}=\left( H_{2},C_{2},M_{2},D_{2},{I_{2}}_{2},{I_{12}}_{2},Z_{2}\right) \) defined by

$$\begin{aligned}&H_{1,2}=\frac{a_{0}}{c_{0}},C_{1,2}=\frac{a_{1}}{c_{1}}, M_{1}=0\hbox { and }M_{2}=-\frac{f_{2}\left( a_{1}d_{2}F_{0}+a_{1}-a_{1}b_{2}\right) }{a_{1}b_{2}},\\&\quad D_{1,2}=0, I_{{2}_{1,2}}=0, I_{12_{1,2}}=0, Z_{1,2}=0. \end{aligned}$$

By computing the Jacobian matrix J(P) of the system (4), we obtain the eigenvalues of \(J(P_{1})\)

$$\begin{aligned}&\lambda _{1}^{(1)}=-c_{0},\lambda _{2}^{(1)}=-c_{1},\lambda _{3}^{(1)}=\left( b_{2}-d_{2}F_{0}\frac{a_{1}}{c_{1}}\right) , \\&\lambda _{4}^{(1)}=-d_{3}\frac{a_{1}}{c_{1}},\lambda _{5}^{(1)}=-e_{4}\frac{ a_{1}}{c_{1}},\lambda _{6}^{(1)}=-d_{I_{12}},\lambda _{7}^{(1)}=-\gamma , \end{aligned}$$

and \(J(P_{2})\)

$$\begin{aligned}&\lambda _{1}^{(2)}=-c_{0},\lambda _{2}^{(2)}=-c_{1},\lambda _{3}^{(2)}=-\left( b_{2}-d_{2}F_{0}\frac{a_{1}}{c_{1}}\right) , \\&\lambda _{4}^{(2)}=-d_{3}\frac{a_{1}}{c_{1}},\lambda _{5}^{(2)}=-e_{4}\frac{ a_{1}}{c_{1}},\lambda _{6}^{(2)}=-d_{I_{12}},\lambda _{7}^{(2)}=-\gamma . \end{aligned}$$

Using by parameters in Table 1, we say that the eigenvalues are negative except for \(\lambda _{3}^{(1)}\) and \(\lambda _{3}^{(2)}\) because of that all parameters are positive. As can be seen from the equation of \(\lambda _{3}^{(1)}\) and \(\lambda _{3}^{(2)}\), the stability of the equilibrium points depends on the \( -c_{1}b_{2}+d_{2}F_{0}a_{1}\). Namely, if

$$\begin{aligned} \frac{F_{0}a_{1}}{c_{1}}-\frac{b_{2}}{d_{2}}>0, \end{aligned}$$

\(P_{1}\) is unstable and \(P_{2}\) is stable or

$$\begin{aligned} \frac{F_{0}a_{1}}{c_{1}}-\frac{b_{2}}{d_{2}}<0, \end{aligned}$$

\(P_{1}\) is stable and \(P_{2}\) is unstable. To talk biologically, if birth and death rate of CD8+T cells under the effect of anti-PD-L1, \(\frac{ F_{0}a_{1}}{c_{1}}\) is greater than the ratio between tumor growth and tumor killing \(\frac{b_{2}}{d_{2}}\) the immune system can effectively fight tumor cells and kill them. Although both equilibrium points are characterized by CD4+T and CD8+T cells, there is a big difference between tumor density. The first point is unstable with no tumor, but the other is in the stable with tumor because of \(\left| \mathrm{arg}(\lambda _{3}^{(2)})\right| >\frac{ \alpha \pi }{2}\).

4 The existence and uniqueness of the system with Caputo derivative

Let system Eq. (4) with the initial conditions \(H\left( 0\right) \geqslant 0\), \(C\left( 0\right) \geqslant 0\), \(M\left( 0\right) \geqslant 0\) , \(D\left( 0\right) \geqslant 0\), \(I_{2}\left( 0\right) \geqslant 0\), \( I_{12}\left( 0\right) \geqslant 0\), \(Z\left( 0\right) \geqslant 0\) where \( 0<\tau \le 1\) and all parameters are positive. System (4) can be written as follows:

$$\begin{aligned}&D_{\tau }X(t) =A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)+\frac{I_{2}}{K_{2}+I_{2}} A_{4}X(t)+\frac{I_{2}}{K_{2}+I_{2}}A_{5}X(t) \nonumber \\&\quad + H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9} \nonumber \\&\quad \times X(t)\frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2} }MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \nonumber \\&\quad + MA_{12}X(t)+FMA_{13}X(t)+\phi \end{aligned}$$
(6)

where \(t\in \left[ 0,\tau \right] \) and

$$\begin{aligned} {x(t)=}\left( \begin{array}{c} H(t) \\ C(t) \\ M(t) \\ D(t) \\ I_{2}(t) \\ I_{12}(t) \\ Z(t) \end{array} \right) ,x(0)=\left( \begin{array}{c} H(0) \\ C(0) \\ M(0) \\ D(0) \\ I_{2}(0) \\ I_{12}(0) \\ Z(0) \end{array} \right) , \phi =\left( \begin{array}{ccccccc} a_{0} &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad a_{1} &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \end{array} \right) \end{aligned}$$

and for i is row, j is column for

\(i,j\in \{1,2,3,...7\}\) and \(a_{ij}^{m},m\in \{1,2,3,...,13\}\) is the element of \(A_{m}\) matrix, respectively.

\(a_{11}^{1}=-c_{0}\), \(a_{22}^{1}=-c_{1}\), \(a_{33}^{1}=b_{2}\), \( a_{55}^{1}=-c_{4}\), \(a_{66}^{1}=-d_{I_{12}}\), \(a_{77}^{1}=-\gamma \), \( a_{14}^{2}=b_{0}\), \(a_{45}^{2}=b_{4}\), \(a_{44}^{3}=-d_{3}\),

\(a_{55}^{3}=-e_{4}\), \(a_{11}^{4}=\lambda _{42}\), \( a_{11}^{5}=\lambda _{412}\), \(a_{22}^{5}=\lambda _{812}\), \(a_{14}^{6}=-b_{0}\) , \(a_{11}^{7}=-\frac{\lambda _{42}}{f_{0}}\), \(a_{11}^{8}=-\frac{\lambda _{412}}{f_{1}}\), \(a_{13}^{9}=b_{1}\),

\(a_{14}^{9}=b_{1}\), \(a_{16}^{10}=-\frac{\lambda _{812}}{f_{1}}\), \( a_{22}^{11}=-\frac{b_{1}}{f_{1}}\), \(a_{13}^{12}=-\frac{b_{2}}{f_{2}}\), \( a_{12}^{13}=-d_{2}\) and the remaining element of \(A_{m}\) matrix are 0.

We give some definitions about this topic which are given in [39,40,41].

Definition 4

Let \(C^{*}\left[ 0,\tau \right] \) be the class of continuous column vector X(t) whose components H(t), C(t), M(t), \( I_{2}(t)\), \(I_{12}(t)\) , Z(t) and the class of continuous functions on the interval \(\left[ 0,\tau \right] \). The norm of \(X\in C^{*}\left[ 0,\tau \right] \) is shown by a

$$\begin{aligned}&\left\| X\right\| =\underset{t}{\sup }\left| Xe^{-Nt}H(t)\right| +\underset{t}{\sup }\left| Xe^{-Nt}C(t)\right| +\underset{t}{\sup }\left| Xe^{-Nt}M(t)\right| +\underset{t}{\sup }\left| Xe^{-Nt}D(t)\right| \\&\quad +\underset{t}{\sup }\left| Xe^{-Nt}I_{2}(t)\right| +\underset{t}{ \sup }\left| Xe^{-Nt}I_{12}(t)\right| +\underset{t}{\sup }\left| Xe^{-Nt}Z(t)\right| \end{aligned}$$

when \(\ t>\mu \ge 0,\) we write \(C_{\mu }^{*}\left[ 0,\tau \right] \) and \(C^{*}\left[ 0,\tau \right] .\)

Definition 5

\(X\in C^{*}\left[ 0,\tau \right] \) is a solution of the initial value problem in Eq. (6) if

  • \(\left( t,X(t)\right) \in B,t\epsilon \left[ 0,\tau \right] \) where \(B=\left[ 0,\tau \right] \) \(\times \) L,  \(L=\left\{ \left( H,C,M,D,I_{2,}I_{12},Z\right) \in R_{+}^{7}:\right. \)\(\left. \left| H\right| \le h,\right. \) \(\left. \left| C\right| \le c,\left| M\right| \le m,\left| I_{2}\right| \le i_{2},\left| I_{12}\right| \le i_{12},\left| Z\right| \le z\right\} ;\) \(h,c,m,i_{2},i_{12},z\) are positive constants.

  • X(t) satisfy in Eq. (6).

Theorem 2

The initial value problem Eq. (6) has a unique solution \(X\in C^{*}\left[ 0,\tau \right] .\)

Proof

We can write by using properties of fractional calculus and Eq. (6)

$$\begin{aligned} I^{1-\tau }\frac{\mathrm{d}}{\mathrm{d}t}X(t)= & {} A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)+\frac{I_{2}}{ K_{2}+I_{2}}A_{4}X(t)+\frac{I_{2}}{K_{2}+I_{2}}A_{5}X(t) \\&+ H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(t) \\&+ \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \\&+ MA_{12}X(t)+FMA_{13}X(t)+\phi . \end{aligned}$$

We obtain with \(I^{\tau }\)

$$\begin{aligned} X(t)= & {} X(0)+I^{\tau }\left[ A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)+\frac{I_{2}}{ K_{2}+I_{2}}A_{4}X(t)\right. \nonumber \\&+\frac{I_{2}}{K_{2}+I_{2}}A_{5}X(t) \nonumber \\&+ H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(t) \nonumber \\&+ \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \nonumber \\&+ MA_{12}X(t)+FMA_{13}X(t)\left. +\phi \right] . \end{aligned}$$
(7)

Let \(F:C^{*}\left[ 0,\tau \right] \rightarrow C^{*}\left[ 0,\tau \right] \). Hence by using F we obtain

$$\begin{aligned} FX(t)= & {} X(0)+I^{\tau }\left[ A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)+\frac{I_{2}}{ K_{2}+I_{2}}A_{4}X(t)\right. \nonumber \\&+\frac{I_{2}}{K_{2}+I_{2}}A_{5}X(t) \nonumber \\&+ H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(t) \nonumber \\&+ \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \nonumber \\&+ \left. MA_{12}X(t)+FMA_{13}X(t)+\phi \right] . \end{aligned}$$
(8)

Then

$$\begin{aligned} e^{-NT}\left( FX-FY\right)= & {} e^{-Nt}I^{\tau }\left[ A_{1}X(t)+HA_{2}\left( X-Y\right) +CA_{3}\left( X-Y\right) \right. \\&+\frac{I_{2}}{K_{2}+I_{2}}A_{4}\left( X-Y\right) \\&+ \frac{I_{2}}{K_{2}+I_{2}}A_{5}\left( X-Y\right) +H^{2}A_{6}\left( X-Y\right) +\frac{I_{2}}{K_{2}+I_{2}}HA_{7}\left( X-Y\right) \\&+ \frac{I_{12}}{K_{12}+I_{12}}HA_{8}\left( X-Y\right) +\frac{I_{2}}{ K_{2}+I_{2}}CA_{9}\left( X-Y\right) +\frac{I_{12}}{K_{12}+I_{12}}CA_{10} \\&\times \left( X-Y\right) +\frac{I_{2}}{K_{2}+I_{2}}MCA_{11}\left( X-Y\right) +\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}\left( X-Y\right) \\&+ \left. MA_{12}\left( X-Y\right) +FMA_{13}\left( X-Y\right) +\phi \right] \\\le & {} \frac{1}{\varGamma \left( \tau \right) }{\int _{0}^{t}}\left( t-s\right) ^{\tau -1}e^{-N\left( t-s\right) }\left( X(s)-Y(s)\right) \times e^{-Ns}\left( A_{1}+hA_{2}+cA_{3}\right. \\&+ \frac{i_{2}}{K_{2}+i_{2}}A_{4}+\frac{i_{2}}{K_{2}+i_{2}}A_{5}+h^{2}A_{6}+ \frac{i_{2}}{K_{2}+i_{2}}hA_{7}+\frac{i_{12}}{K_{12}+i_{12}}hA_{8} \\&+ \frac{i_{2}}{K_{2}+i_{2}}cA_{9}+\frac{i_{12}}{K_{12}+i_{12}}cA_{10}\frac{ i_{2}}{K_{2}+i_{2}}mcA_{11}+\frac{i_{2}}{K_{2}+i_{2}}dcA_{11}+mA_{12} \\&+ \left. fmA_{13}\right) \mathrm{d}s \\\le & {} \left( A_{1}+hA_{2}+cA_{3}+\frac{i_{2}}{K_{2}+i_{2}}A_{4}+\frac{i_{2} }{K_{2}+i_{2}}A_{5}+h^{2}A_{6}+\frac{i_{2}}{K_{2}+i_{2}}hA_{7}\right. \\&+ \frac{i_{12}}{K_{12}+i_{12}}hA_{8}+\frac{i_{2}}{K_{2}+i_{2}}cA_{9}+\frac{ i_{12}}{K_{12}+i_{12}}cA_{10}+\frac{i_{2}}{K_{2}+i_{2}}mcA_{11} \\&+ \left. \frac{i_{2}}{K_{2}+i_{2}}dcA_{11}+mA_{12}+fmA_{13}\right) \times \frac{1}{N^{\tau }}\left\| X-Y\right\| \frac{1}{\varGamma \left( \tau \right) }{\int _{0}^{t}}s^{\tau -1}\mathrm{d}s. \end{aligned}$$

We see that

$$\begin{aligned} \left\| FX-FY\right\|\le & {} \left( A_{1}+hA_{2}+cA_{3}+\frac{i_{2}}{ K_{2}+i_{2}}A_{4}+\frac{i_{2}}{K_{2}+i_{2}}A_{5}+h^{2}A_{6}+\frac{i_{2}}{ K_{2}+i_{2}}hA_{7}\right. \\&\quad + \frac{i_{12}}{K_{12}i_{12}}hA_{8}\frac{i_{2}}{K_{2}+i_{2}}cA_{9}+\frac{ i_{12}}{K_{12}+i_{12}}cA_{10}+\frac{i_{2}}{K_{2}+i_{2}}mcA_{11}+\frac{i_{2}}{ K_{2}+i_{2}} \\&\quad \times \left. dcA_{11}+mA_{12}+fmA_{13}\right) \times \frac{1}{N^{\tau }} \left\| X-Y\right\| . \end{aligned}$$

If choose N following

$$\begin{aligned} N^{\tau }\ge & {} \left( A_{1}+hA_{2}+cA_{3}+\frac{i_{2}}{K_{2}+i_{2}}A_{4}+ \frac{i_{2}}{K_{2}+i_{2}}A_{5}+h^{2}A_{6}\right. \\&\quad +\frac{i_{2}}{K_{2}+i_{2}}hA_{7}+ \frac{i_{12}}{K_{12}+i_{12}}hA_{8}\\&\quad + \frac{i_{2}}{K_{2}+i_{2}}cA_{9}+\frac{i_{12}}{K_{12}+i_{12}}cA_{10}+\frac{ i_{2}}{K_{2}+i_{2}}mcA_{11}\left. +\frac{i_{2}}{K_{2}+i_{2}} dcA_{11}+mA_{12}+fmA_{13}\right) , \end{aligned}$$

then

$$\begin{aligned} \left\| FX-FY\right\| <\left\| X-Y\right\| . \end{aligned}$$

This is shown the operator F given by Eq. (8) has a fixed point. Therefore, (7) has a unique solution \(X\in C^{*}\left[ 0,\tau \right] .\) We write from Eq. (7) and using \(\frac{d}{dt}X(t)\)

$$\begin{aligned} e^{-Nt}X^{^{\prime }}(t)= & {} e^{-Nt}\left[ \frac{t^{\tau -1}}{\varGamma \left( \tau \right) }\left( A_{1}X(0)+H\left( 0\right) A_{2}X(0)+C\left( 0\right) A_{3}X(0)+\frac{I_{2}\left( 0\right) }{K_{2}+I_{2}\left( 0\right) } A_{4}X(0)\right. \right. \\&+ \frac{I_{2}\left( 0\right) }{K_{2}+I_{2}\left( 0\right) } A_{5}X(0)+H^{2}\left( 0\right) A_{6}X(0)+\frac{I_{2}\left( 0\right) }{ K_{2}+I_{2}\left( 0\right) }H\left( 0\right) A_{7}X(0)+\frac{I_{12}\left( 0\right) }{K_{12}+I_{12}\left( 0\right) } \\&\times H\left( 0\right) A_{8}X(t)+\frac{I_{2}\left( 0\right) }{ K_{2}+I_{2}\left( 0\right) }C\left( 0\right) A_{9}X(0)+\frac{I_{12}\left( 0\right) }{K_{12}+I_{12}\left( 0\right) }C\left( 0\right) A_{10}X(0) \\&+ \frac{I_{2}\left( 0\right) }{K_{2}+I_{2}\left( 0\right) }M\left( 0\right) C\left( 0\right) A_{11}X(0)+\frac{I_{2}\left( 0\right) }{K_{2}+I_{2}\left( 0\right) }D\left( 0\right) C\left( 0\right) A_{11}X(0)+M\left( 0\right) A_{12} \\&\times \left. X(0)+F\left( 0\right) M\left( 0\right) A_{13}X(0)+\phi \right) +I^{\tau }\left( A_{1}X^{^{\prime }}(t)+H^{^{\prime }}\left( t\right) A_{2}X(t)+H\left( t\right) A_{2}X^{^{\prime }}(t)\right. \\&+ C^{^{\prime }}\left( t\right) A_{3}X(t)+C\left( t\right) A_{3}X^{^{\prime }}(t)+\frac{K_{2}}{\left( K_{2}+I_{2}\left( t\right) \right) ^{2}}A_{4}X(t)+ \frac{I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }A_{4}X^{^{\prime }}(t) \\&+ \frac{K_{2}}{\left( K_{2}+I_{2}\left( t\right) \right) ^{2}}A_{5}X(t)+ \frac{I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }A_{5}X^{^{\prime }}(t)+2H\left( t\right) H^{2}\left( t\right) A_{6}X(t)+H^{2}A_{6}X^{^{\prime }}(t) \\&+ \frac{K_{2}}{\left( K_{2}+I_{2}\left( t\right) \right) ^{2}}HA_{7}X(t)+ \frac{I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }H^{^{\prime }}\left( t\right) A_{7}X(t)+\frac{I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }H\left( t\right) A_{7}X^{^{\prime }}(t) \\&+ \frac{K_{2}}{\left( K_{12}+I_{12}\left( t\right) \right) ^{2}}H\left( t\right) A_{8}X(t)+\frac{I_{12}\left( t\right) }{K_{12}+I_{12}\left( t\right) }H^{^{\prime }}\left( t\right) A_{8}X(t)+\frac{I_{12}\left( t\right) }{K_{12}+I_{12}\left( t\right) }H\left( t\right) \\&\times A_{8}X^{^{\prime }}(t)+\frac{K_{2}}{\left( K_{2}+I_{2}\left( t\right) \right) ^{2}}C\left( t\right) A_{9}X(t)+\frac{I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }C^{^{\prime }}\left( t\right) A_{9}X(t)+\frac{ I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) } \\&\times C\left( t\right) A_{9}X^{^{\prime }}(t)+\frac{K_{12}}{\left( K_{12}+I_{12}\left( t\right) \right) ^{2}}C\left( t\right) A_{10}X(t)+\frac{ I_{12}\left( t\right) }{K_{12}+I_{12}\left( t\right) }C^{^{\prime }}\left( t\right) A_{10}X(t) \\&+ \frac{I_{12}\left( t\right) }{K_{12}+I_{12}\left( t\right) }C\left( t\right) A_{10}X^{^{\prime }}(t)+\frac{K_{2}}{\left( K_{2}+I_{2}\left( t\right) \right) ^{2}}M\left( t\right) C\left( t\right) A_{11}X(t)+\frac{ I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) } \\&\times M^{^{\prime }}\left( t\right) C\left( t\right) A_{11}X(t)+\frac{ I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }M\left( t\right) C^{^{\prime }}\left( t\right) A_{11}X(t)+\frac{I_{2}\left( t\right) }{ K_{2}+I_{2}\left( t\right) }M\left( t\right) C\left( t\right) \\&\times A_{11}X^{^{\prime }}(t)+\frac{K_{2}}{\left( K_{2}+I_{2}\left( t\right) \right) ^{2}}D\left( t\right) C\left( t\right) A_{11}X(t)+\frac{ I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }D^{^{\prime }}\left( t\right) C\left( t\right) A_{11}X(t) \\&+ \frac{I_{2}\left( t\right) }{K_{2}+I_{2}\left( t\right) }D\left( t\right) C^{^{\prime }}\left( t\right) A_{11}X(t)+\frac{I_{2}\left( t\right) }{ K_{2}+I_{2}\left( t\right) }D\left( t\right) C\left( t\right) A_{11}X^{^{\prime }}(t)+M^{^{\prime }}\left( t\right) A_{12}X(t) \\&+ \left. \left. M\left( t\right) A_{12}X^{^{\prime }}(t)+F^{^{\prime }}\left( t\right) M\left( t\right) A_{13}X(t)+F\left( t\right) M^{^{\prime }}\left( t\right) A_{13}X(t)+F\left( t\right) M\left( t\right) A_{13}X^{^{\prime }}(t)\right) \right] . \end{aligned}$$

From Eq. (7), we can say that \(X^{\prime }\in C_{\mu }^{*}\left[ 0,\tau \right] .\) Now from Eq. (7), written

$$\begin{aligned}&\frac{dX(t)}{dt} =\frac{d}{dt}I^{\tau }\left[ A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)+\frac{I_{2}}{K_{2}+I_{2}}A_{4}X(t)+\frac{ I_{2}}{K_{2}+I_{2}}A_{5}X(t)\right. \\&\quad + H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(t) \\&\quad + \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \\&\quad + \left. MA_{12}X(t)+FMA_{13}X(t)+\phi \right] , \end{aligned}$$
Fig. 2
figure 2

Figures about ordinary differential system (1) for H, C, M, D, \(I_{2}\), \(I_{12}\), Z, respectively

Full size image
Table 1 Parameter values for \(c=cells\), \(h=hour\)
Full size table
Fig. 3
figure 3

Figures about fractional-order systems (4) for \( \tau =0.99\)

Full size image
Fig. 4
figure 4

Figures about fractional-order systems (4) for \( \tau =0.97\)

Full size image
Fig. 5
figure 5

Figures about fractional-order systems (4) for \( \tau =0.95\)

Full size image

hence,

$$\begin{aligned}&I^{1-\tau }\frac{dX(t)}{dt} =I^{1-\tau }\frac{d}{dt}I^{\tau }\left[ A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)\right. \nonumber \\&\quad +\frac{I_{2}}{K_{2}+I_{2}}A_{4}X(t)+\frac{ I_{2}}{K_{2}+I_{2}}A_{5}X(t) \\&\quad + H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(t) \\&\quad + \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \\&\quad + \left. MA_{12}X(t)+FMA_{13}X(t)+\phi \right] . \end{aligned}$$

So, we get

$$\begin{aligned}&D^{\tau }X(t) = A_{1}X(t)+HA_{2}X(t)+CA_{3}X(t)+\frac{I_{2}}{K_{2}+I_{2}} A_{4}X(t)+\frac{I_{2}}{K_{2}+I_{2}}A_{5}X(t) \\&\quad + H^{2}A_{6}X(t)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(t)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(t)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(t) \\&\quad + \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(t)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(t)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(t) \\&\quad + MA_{12}X(t)+FMA_{13}X(t)+\phi \end{aligned}$$

and

$$\begin{aligned}&X(0) =X_{0}+I^{\tau }\left[ A_{1}X(0)+HA_{2}X(0)+CA_{3}X(0)+\frac{I_{2}}{ K_{2}+I_{2}}A_{4}X\left( 0\right) +\frac{I_{2}}{K_{2}+I_{2}}A_{5}X(0)\right. \\&\quad + H^{2}A_{6}X(0)+\frac{I_{2}}{K_{2}+I_{2}}HA_{7}X(0)+\frac{I_{12}}{ K_{12}+I_{12}}HA_{8}X(0)+\frac{I_{2}}{K_{2}+I_{2}}CA_{9}X(0) \\&\quad + \frac{I_{12}}{K_{12}+I_{12}}CA_{10}X(0)+\frac{I_{2}}{K_{2}+I_{2}} MCA_{11}X(0)+\frac{I_{2}}{K_{2}+I_{2}}DCA_{11}X(0) \\&\quad + \left. MA_{12}X(0)+FMA_{13}X(0)+\phi \right] =X_{0}. \end{aligned}$$

So Eq. (7) is equivalent to the initial value problem Eq. (6). \(\square \)

5 Numerical simulations

5.1 Numerical scheme for ordinary differential immune system-cancer model

Figure 2 is obtained with the Euler method, which is also called the tangent line method for ordinary differential cancer-immune system in Eq. (1) by using parameter of in Table 1. Figure 2c is examined, cancer cells are almost 0 in 5 days and after the 60th day, and cancer cells have grown almost back to the starting point. Conversely, immune system components shown in Fig. 2a, b, e act in the opposite direction with cancer cells in the same time periods. Time-dependent change of dendritic cells and anti-PD-L1, which are presented to the system with \(D(0)=1\), \(Z(0)=0.2\) starting point are observed in Fig. 2d, f, respectively .

5.2 Numerical scheme for Caputo and CF fractional immune system-cancer model

Figures 3, 4, and 5 are obtained with Adams–Bashforth–Moulton predictor–corrector method which is given in [42] for Caputo system in (4) and the scheme given in [43] for the Caputo–Fabrizio system in (5) while for varying \( \tau \) values with the initial values and parameters in Table 1.

In Figs. 3c, 4c, and 5c, it is observed that cancer cells are eliminated in 5 days at first, but they start growing again after about 25 days for Caputo system. Simultaneously, immune system components are almost the peak point in 5 days and are the 25th day bottom point for the order \(\tau \) examined. It is clearly seen that, the order \(\tau \) shrinks, the immune system components are much stronger via IL-12 and anti-PD-L1, whereas cancer cells grow much less at Figs. 3c, 4c, and 5c. It is appeared that brings under control cancer cells much easier and these grow much less under the influence of a stronger immune system components. The other words, cancer cells grow \(45\%\) less in order \(\tau =0.99\) at Fig. 3c, \(60\%\) less in \(\tau =0.97\) at Fig. 4c and \(80\%\) less in \(\tau =0.95\) at Fig. 5c for Caputo system.

For CF system, in Figs. 3, 4, and 5, one can see that cancer cells become almost 0 in 10 days while immune system cells become the strongest by way of IL-12 and anti-PD-L1. Also, it is seen that cancer cells do not grow again after being zero in Figs. 3c, 4c, and 5c. In other words, there are \(100\%\) reduction in cancer cells in considered order \(\tau \).

The main factor in cancer cells being almost zero is that the immune system cells are stronger for CF system. In particular, if the graphs given for the dendritic cell in Figs. 3d, 4d, and 5d are examined the facility the elimination of cancer cells by stimulating the helper cells more, since these type of cells exist longer in CF derivative. If Figs. 2 and 3, 4, and 5 are considered together, it is observed that the equation expressed by fractional derivatives have managed to control cancer cells more in less time because of its memory and hereditary effect.

6 Concluding remarks and future works

In this paper, after briefly giving information about cancer and the immune system, cancer-immune system mathematical model given in [14] is modified by adding IL-12 and anti-PD-L1 variables because they change the number and effectiveness of T lymphocytes. In this way, the immune system’s fight against cancer will be more effective. The ordinary differential new model is considered for the first time by using Caputo and CF fractional derivative. Moreover, after examining the equilibrium points and stability of the fractional-order model with singular kernel, researches on the existence-uniqueness of the model’s numerical solution is included. The model with Caputo derivative is solved Adams–Bashforth–Moulton predictor–corrector method for fractional order, the model with CF derivative is solved numerical solution given in [43] with the help of MATLAB. The immune system plays a major role in the development, growth or destruction of cancer cells. We have added to Eq. (1) the variable anti-PD-L1 inhibitor to catch cells escaping from the immune system and destroy these cells, and the variable IL-12 cytokine to increase the number of CD4+T and CD8+T lymphocytes production. Through Figs. 2, 3, 4 and 5, it is clearly seen that the reason why cancer cells decrease more, is the strengthening of the immune system through newly added variables, as expected. Indeed, the graphs of the model deals with fractional derivative shows that the immune system become stronger as the degree decreases as the application of fractional derivative to natural events is a more accurate approach. And the Table 2, summarizes that using CF derivative for this model yields more effective results due to having a non-singular kernel.

Table 2 The value of cancer cells at \(t=1000\) hours for different order both CF and Caputo fractional derivative
Full size table

In the future, the mathematical model can be updated by considering other cytokines, and the new model obtained can be examined with different types of derivatives.