1 Introduction

Accurately modelling the various processes that take place in ion scattering from molecules is a challenging problem. The simplest example is proton scattering on molecular hydrogen, which remains an active area of research both experimentally and theoretically. One reason for this is the recent emergence of hadron therapy for cancer treatment [1] where the need for accurate stopping cross sections for ion scattering in biologically relevant molecules is of the utmost urgency [2]. In this modern cancer treatment modality, protons (or heavier ions [3]) are used to bombard the tumour site and destroy cancerous cells. This allows for the destruction of harmful tissues while sparing significantly more healthy tissue than traditional X-ray bombardment, resulting in improved effectiveness and reducing patient mortality rates [4]. This is because the majority of energy is deposited in the region of the Bragg peak near the end of the beam path. Consequently, careful planning is required to ensure the beam energy is deposited precisely at the tumour site. Treatment plans for hadron therapy are developed using Monte Carlo simulations, which rely on accurate stopping power cross sections for collisions of the beam ions with biological molecules. The water molecule is used as a reference target in these simulations [1]. Hence, there is an urgent need for accurate stopping power cross sections on proton collisions with \({\hbox {H}_2\hbox {O}}\). The path to developing theories that can accurately calculate cross sections for ion collisions with water starts with the simpler \({\hbox {H}_2}\) molecule target.

While many methods have been developed to address scattering from atomic targets (see Refs. [5, 6] for two most recent reviews of the field of ion-atom collisions), molecular targets are fundamentally more difficult to describe theoretically. The multicentre nature of molecules significantly complicates their description. The obvious starting place for ion-molecule investigations is proton scattering on the \({\hbox {H}_2}\) target. This is the simplest homonuclear molecular target.

Hasan et al. [7] performed a kinematically complete experiment on ionisation of H\(_2\) by 75 keV proton impact. They found large discrepancies between experiment and theory for the fully differential cross section in various kinematic regimes. Furthermore, they found large discrepancies between distorted-wave and a continuum distorted-wave eikonal initial-state calculations. These authors suggested that the reason for these discrepancies could be the absence of strong coupling between the ionisation and capture channels in the aforementioned theoretical approaches. Our ultimate goal is to investigate this problem using the coupled-channel formalism. In this work, we start from the singly differential cross sections.

Experimental investigations of the singly differential cross sections for proton scattering on molecular hydrogen mainly focus on the energy and angular distribution of secondary electrons produced through ionisation. However, Sharma et al. [8] also presented experimental measurements of the angular differential cross section for electron capture at intermediate incident energies of 25 and 75 keV. In this energy region, the velocity of the projectile is comparable to the orbital speed of the target electrons. Additionally, strong coupling between reaction channels has a significant effect on the scattering outcome. As a result, this is the most difficult energy region to describe theoretically.

Angular differential cross sections for single electron capture from \({\hbox {H}_2}\) by proton projectiles were calculated by Igarashi et al. [9] using the continuum distorted wave eikonal initial state (CDW-EIS), and various other eikonal methods, within an effective one-electron model at 25 and 75 keV. Recently, these authors have extended their method to include the effects of vibrational motion within their distorted-wave model, producing differential electron capture cross sections at 25, 75, and 300 keV [10]. Agreement with the experimental data of Sharma et al. [8] is mixed. Their calculated angular differential cross sections for electron capture into the ground state agree well with the experimental data for scattering angles less than 0.5 mrad. However, at larger scattering angles discrepancies are seen between various approaches based on changing the target description. In particular, using a linear combination of atomic orbitals (LCAO) approach, they were able to deduce information about the final vibrational state of the residual ion; however, the angular differential cross sections for electron capture found using this model are very similar to results using a fixed nuclei (FN) approximation. In fact, they find that using the two-effective-centre (TEC) method gives improved agreement with the experimental data despite a less detailed description of the molecular nature of the target. Adivi [11] also used an effective one-electron target description to calculate the differential cross section for electron capture at 300 keV within the first-order Born approximation with correct boundary conditions (B1B). Ghanbari-Adivi and Sattarpour [12] used the four-body eikonal approximation (EA) at 100 and 300 keV. However, perturbative approaches ignore coupling between reaction channels and are only applicable at high impact energies.

The first comprehensive study of the singly differential cross sections (SDCS) for ionisation was performed by Kuyatt and Jorgensen [13]. They measured both the angular and energy distribution of secondary electrons at proton energies of 50, 75, and 100 keV; however, their integrated results were significantly larger than the accepted total ionisation cross section (TICS). Rudd and Jorgensen Jr [14] also measured the singly differential cross section for ionisation in 100 keV proton collisions with \({\hbox {H}_2}\). They extended their work to a wider energy range (up to 300 keV) in Ref. [15]; however, their integrated cross sections also overestimated the TICS. Later, Rudd [16] measured the differential ionisation cross sections at small incident energies from 5 and 100 keV. Gealy et al. [17] used a new apparatus designed to minimise experimental error in measurements of the singly differential cross sections for ionisation in low energy collisions. They measured the SDCS as a function of ejected electron energy and angle at projectile energies of 20, 48, 67, 95, and 114 keV. Additionally, the integrated ionisation cross sections from their SDCSs agreed well with independent measurements of the TICS. An extensive review of experimental studies of the differential ionisation cross sections is given by Rudd et al. [18]. As far as we are aware, there are neither experimental nor theoretical data for the singly differential ionisation cross section as a function of the scattered projectile angle.

Thus far, the majority of theoretical works on ion collisions with molecular hydrogen are limited to negatively charged projectiles, i.e. antiprotons (see, e.g. topical review [19]). One of the major challenges is finding a balance between the accuracy of the target description and complexity of the approach. Abdurakhmanov et al. [20] used a configuration interaction (CI) expansion to generate fully correlated two-electron target states from single-electron orbitals. They found excellent agreement with experiment in antiproton collisions with \({\hbox {H}_2}\); however, this approach is very computationally demanding and cannot be used to evaluate differential cross sections. An alternative approach is to reduce the molecule into an effectively single-electron system. This greatly simplifies the collisional problem, at the cost of detail in the target structure. Modelling scattering of positively charged projectiles brings additional challenges due to electron capture into bound and continuum states of the projectile having significant contributions to the total electron-loss cross section. Separating these processes from direct ionisation requires more elaborate theories such as two-centre expansion approaches. However, this greatly increases computational complexity [21] which makes it less compatible with complex target descriptions. Lühr and Saenz  [22] used an effective one-electron spherically symmetric model potential within the close-coupling framework to calculate the total cross section for electron loss in \({\bar{p}}+{\hbox {H}_2}\) scattering, but their calculations significantly overestimated the low energy ionisation cross section due to the simplified target structure.

There are far fewer theoretical investigations of differential cross sections than calculations of total cross sections for proton scattering on \({\hbox {H}_2}\). Rudd et al. [15] performed calculations of the singly differential ionisation cross section in both ejected electron angle and energy at 100, 200, and 300 keV using the first-order Born approximation (FBA). They also compared the differential cross section in energy to that predicted by the classical Gryziński theory. Both the FBA and Gryziński methods are only applicable at high incident energies, and while agreement with their experimental results was good, the latter deviates from the experimental points at large ejection energies. Lühr and Saenz [22] used their one-centre close-coupling method to calculate the electron-loss cross section differential in ejected-electron energy at 48 keV. Comparison with the experimental results of Gealy et al. [17] shows good agreement except around the region where the ejected electron has a similar velocity to the incident projectile. Here, their theory’s inability to distinguish between pure ionisation and electron capture results in an unphysical peak in their presented cross section. More recently, Schultz et al. [23] used the classical trajectory Monte Carlo (CTMC) method to calculate angular and energy singly differential cross sections for ionisation. At 50 and 75 keV, they obtained a consistently smaller cross section for ionisation as a function of ejection energy than the experimental data of Kuyatt and Jorgensen [13], Rudd et al. [15], and Rudd [16]. At 100 keV, their results agree with the FBA calculations and Gryziński approach for small ejection energies, but deviate further from the experimental points of Refs. [13, 15, 16] than the FBA calculations.

In this work, we use the recently developed effective one-electron wave-packet convergent close-coupling (WP-CCC) approach to proton scattering on molecular hydrogen [24] to calculate singly differential cross sections in \({\hbox {p}}+{\hbox {H}_2}\) collisions. This method is capable of explicitly differentiating between pure ionisation and electron capture by using a two-centre expansion of the total scattering wave function. Previously, the two-centre WP-CCC approach to one-electron scattering systems was used to calculate singly differential cross sections in proton collisions with atomic hydrogen [25]. Plowman et al. [24] extended the method to proton collisions with molecular hydrogen by representing the target as an effective one-electron system following the idea proposed in Ref. [26]. We found that this approach could provide sufficiently accurate total cross sections without the need for a complex multielectron target description. Here we apply this method to calculate angular differential cross sections for elastic scattering, excitation, and electron capture as well as singly differential ionisation cross sections as functions of the ejected electron energy and angle, and the scattering angle of the projectile.

Unless specified otherwise, atomic units (au) are used throughout this manuscript.

2 Two-centre wave-packet convergent close-coupling method

The WP-CCC method was first detailed by Abdurakhmanov et al. [27] and used to calculate differential cross sections for ionisation in antiproton collisions with atomic hydrogen. It was extended to include electron capture channels using a two-centre expansion and applied to proton collisions in Ref. [21]. Singly differential cross sections in \({\hbox {p}}+{\hbox {H}}\) collisions were investigated with the WP-CCC approach by Plowman et al. [25]. The proton-helium differential scatting problem was investigated by Spicer et al. [28, 29]. An effective one-electron approach to ion collisions with multielectron atomic targets has been developed in [30]. Recently, we implemented an effective one-electron description of the molecular hydrogen target in Plowman et al. [24] and calculated total cross sections for all one-electron processes. Here we apply this method to singly differential cross sections. In this section, we give an overview of the relevant aspects of the theory.

2.1 Close-coupling formalism

In the WP-CCC approach to ion collisions with one-electron targets, the Schrödinger equation for the total scattering wave function \(\mathrm{\Psi }^{+}_i \), subject to the outgoing-wave boundary conditions, is written as

$$\begin{aligned} (H-E) \mathrm{\Psi }^{+}_i = 0, \end{aligned}$$
(1)

where H is the full three-body Hamiltonian of the collision system and E is the total energy. Subscript i refers to the initial channel from which the total scattering wave develops. In this work, we assume that in the initial channel the target is in its ground state. The total scattering wave function is expanded in terms of N target-centred (\(\psi ^{\mathrm{T}}_{\alpha }\)) and M projectile-centred (\(\psi ^{\mathrm{P}}_{\beta }\)) pseudostates,

$$\begin{aligned} \Psi ^{+}_i \approx&\sum _{\alpha =1}^{N} F_{\alpha }(t,{\varvec{b}})\psi ^{\mathrm{T}}_{\alpha }({\varvec{r}}_{\mathrm{T}}) \mathrm{e}^{{i}{\varvec{q}}_{\alpha } \cdot {\varvec{\rho }}}\nonumber \\&+\sum _{\beta =1}^{M}G_{\beta }(t,{\varvec{b}}) \psi ^{\mathrm{P}}_{\beta }({\varvec{r}}_{\mathrm{P}})\mathrm{e}^{{i}{\varvec{q}}_{\beta } \cdot {\varvec{\sigma }}}, \end{aligned}$$
(2)

where \(F_\alpha (t,\varvec{b})\) and \(G_\beta (t,\varvec{b})\) are expansion coefficients that depend on time t and impact parameter \(\varvec{b}\). We use two sets of Jacobi coordinates. The first set is made of \(\varvec{r}_{\mathrm{T}}\), the position of the active electron relative to the target nucleus, and \(\varvec{\rho }\), the position of the projectile nucleus relative to the target system. The second set is made of \(\varvec{r}_{\mathrm{P}}\), the position of the active electron relative to the projectile nucleus, and \(\varvec{\sigma }\), the position of the residual target ion relative to the atom formed by the projectile. The momentum of the projectile nucleus relative to the target is denoted as \(\varvec{q}_\alpha \), while \(\varvec{q}_\beta \) denotes the momentum of the residual target ion relative to the projectile atom. The target nucleus is fixed at the origin, and the projectile moves parallel to the z-axis in a straight line with position given by \(\varvec{R}=\varvec{b}+\varvec{v}t\). The impact parameter is defined such that \(\varvec{b}\cdot \varvec{v}=0\). The reason for including both target- and projectile-centred basis states in Eq. (2) is that it allows us to explicitly differentiate between pure ionisation into the continuum of either the residual target ion or projectile atom and electron capture into bound states of the projectile. The number of basis states used in the expansion is increased until the results of interest converge.

The total Hamiltonian in Eq. (1) is given by

$$\begin{aligned} H&=H_0+V, \end{aligned}$$
(3)

where \(H_0\) is the free three-particle Hamiltonian for the projectile, active electron, and target nucleus, and V is the interaction between them. We can write the free Hamiltonian equivalently in terms of either target- or projectile-centred Jacobi coordinates as

$$\begin{aligned} H_0=-\frac{1}{2\mu _{\mathrm{{T}}}}\nabla _{\varvec{\rho }}^2-\frac{1}{2}\nabla _{\varvec{r}_{\mathrm{{T}}}}^2 =-\frac{1}{2\mu _{\mathrm{{P}}}}\nabla _{\varvec{\sigma }}^2-\frac{1}{2}\nabla _{\varvec{r}_{\mathrm{{P}}}}^2, \end{aligned}$$
(4)

where \(\mu _{\mathrm{{T}}}\) is the reduced mass of the \({\hbox {p}}+{\hbox {H}_2}\) system and \(\mu _{\mathrm{{P}}}\) is the reduced mass of the \({\hbox {H}}+{\hbox {H}_2^+}\) system. The total interaction potential is given by the sum of the interaction between the two nuclei and the interaction between the active electron and each of the nuclei,

$$\begin{aligned} V=V_{\mathrm{{mod}}}(R)-V_{\mathrm{{mod}}}(r_{\mathrm{{T}}})-\frac{1}{r_{\mathrm{{P}}}}. \end{aligned}$$
(5)

The interaction of the \({\hbox {H}^+_2}\) ion with the active electron or the projectile is given by the following model effective potential [31]

$$\begin{aligned} V_{\mathrm{{mod}}}(r)=\frac{1}{r} (1+\exp [-\zeta r]). \end{aligned}$$
(6)

The parameter \(\zeta \) is set at 5.4824. This results in a ground-state energy of \(-0.5976\) au, which corresponds to the difference in energy between the ground state of \({\hbox {H}_2}\) at the average internuclear distance of the hydrogen molecule, \(\langle R_{\mathrm{nuc}} \rangle =1.45\) au, and the ground state of \({\hbox {H}^+_2}\) at the same internuclear distance. This effectively represents the hydrogen cation as a spherically symmetric system, so that there is no possibility of the residual ion existing in a vibrationally excited state. Thus, this ground-state energy is analogous to the adiabatic ionisation energy rather than the vertical ionisation energy of the hydrogen molecule. Within this representation, we effectively split the two-electron problem into two equivalent single-electron ones. The resulting probabilities found from solving Eq. (2) are multiplied by a factor of 2 to account for either of the electrons occupying a given final channel.

The target pseudostates are found by solving the Schrödinger equation for the effective \({\hbox {H}^+_2}\) ion core plus electron system using an iterative Numerov approach. This results in a set of negative-energy bound states and a continuum solution. To construct positive-energy pseudostates, we discretise the continuum in momentum space between \(\kappa _{\mathrm{min}}\) and \(\kappa _{\mathrm{max}}\) into \(N_c\) nonoverlapping subintervals, where \(\kappa \) is the momentum of the emitted electron. Then, the wave packets \(\phi ^{\mathrm{WP}}_{n_{\alpha }\ell _\alpha }(r)\) are obtained by integrating the radial part of the continuum wave, \(\varphi _{\kappa \ell _{\alpha }}(r)\), within each subinterval:

$$\begin{aligned} \phi ^{\mathrm{WP}}_{n_{\alpha }\ell _\alpha }(r)=\frac{1}{\sqrt{\kappa _{n_{\alpha }}-\kappa _{n_{\alpha }-1}}} \int _{\kappa _{n_{\alpha }-1}}^{\kappa _{n_\alpha }} d\, \kappa \varphi _{\kappa \ell _{\alpha }}(r). \end{aligned}$$
(7)

We choose \(\kappa _{\mathrm{max}}\) to be sufficiently high that the results of interest converge. The value of \(\kappa _{\mathrm{min}}\) is nominally 0; however, in practice it proves advantageous to exclude a small section of the low-lying continuum to maintain the unitarity of the norm of the total scattering wave function. This is because it is very difficult to construct correctly normalised wave packets for increasingly smaller intervals of the continuum as \(\kappa \rightarrow 0\) since the continuum wave extends much further in the radial dimension before converging to a sinusoid.

Together, the negative- and positive-energy target pseudostates form a square-integrable orthonormal basis that spans both the bound-state and truncated continuum-function space of the model potential,

$$\begin{aligned} \langle \psi ^{\mathrm{T}}_{\alpha '} | \psi ^{\mathrm{T}}_\alpha \rangle =\delta _{\alpha '\alpha }, \quad \langle \psi ^{\mathrm{T}}_{\alpha '} | H_\alpha |\psi ^{\mathrm{T}}_\alpha \rangle =\delta _{\alpha '\alpha } \varepsilon _\alpha , \end{aligned}$$
(8)

where \(\varepsilon _\alpha \) is the energy of the target state described by \(\psi ^{\mathrm{T}}_\alpha \). The bound-state energies are the eigenvalues of the target Schrödinger equation, while the wave-packet energies are found from the midpoints of the continuum bins as

$$\begin{aligned} \varepsilon _n=\frac{\kappa _n^2+\kappa _n\kappa _{n-1}+\kappa _{n-1}^2}{6}. \end{aligned}$$
(9)

For the atom formed by the projectile, we use eigenstates of the hydrogen atom for the negative-energy states and wave packets constructed from the Coulomb wave,

$$\begin{aligned} \phi ^{\mathrm{WP}}_{n_{\beta }\ell _{\beta }}(r)=\frac{1}{\sqrt{\kappa _{n_{\beta }} -\kappa _{n_{\beta }-1}}}\int _{\kappa _{n_{\beta }-1}}^{\kappa _{n_{\beta }}} d\, \kappa U_{\ell _{\beta }}(\kappa ,r), \end{aligned}$$
(10)

for positive-energy states (see Ref. [21] for details), where U is the Coulomb wave function. Combined, these form an orthonormal set spanning a subspace of the projectile eigenstates and continuum,

$$\begin{aligned} \langle \psi ^{\mathrm{P}}_{\beta '} | \psi ^{\mathrm{P}}_\beta \rangle =\delta _{\beta '\beta }, \quad \langle \psi ^{\mathrm{P}}_{\beta '} | H_\beta |\psi ^{\mathrm{P}}_\beta \rangle =\delta _{\beta '\beta }\varepsilon _\beta . \end{aligned}$$
(11)

Here, \(\varepsilon _{\beta }\) is given by the eigenvalues of the hydrogen atom for the bound states and Eq. (9) for the positive-energy pseudostates.

The wave-packet pseudostates must be known to a high precision to prevent ill-conditioning of the scattering equations. Since the continuum wave converges to a plane wave in the limit as \(r\rightarrow \infty \), the wave packets are normalised to the amplitude of the continuum wave at a large distance (up to \(15\,000\) au). Then, a smaller value of \(r_{\mathrm{max}}=300\) au is chosen when solving the scattering equations. This is then systematically increased until the results of interest converge.

Substituting Eq. (2) into Eq. (1) leads to the following set of coupled equations [21]

$$\begin{aligned} \!\!\!\!\! \left\{ \begin{aligned}&i {\dot{F}}_{\alpha ^\prime } + i\sum _{\beta =1}^{M} {\dot{G}}_\beta {\tilde{K}}^{}_{\alpha ^\prime \beta } = \sum _{\alpha =1}^{N} F_\alpha D^{}_{\alpha ^\prime \alpha } +\sum _{\beta =1}^{M} G_\beta {\tilde{Q}}^{}_{\alpha ^\prime \beta },\\&i\sum _{\alpha =1}^{N} {\dot{F}}_\alpha K^{}_{\beta ^\prime \alpha } +i {\dot{G}}_{\beta ^\prime } =\sum _{\alpha =1}^{N} F_\alpha Q^{}_{\beta ^\prime \alpha } +\sum _{\beta =1}^{M} G_\beta {\tilde{D}}^{}_{\beta ^\prime \beta },\\&\alpha ^\prime =1,2, \ldots , N, \quad \beta ^\prime =1,2, \ldots , M. \end{aligned} \right. \nonumber \\ \end{aligned}$$
(12)

that is solved for the unknown time-dependent expansion coefficients \(F_\alpha \) and \(G_\beta \) subject to the boundary condition specified below. Here dots over \(F_\alpha \) and \(G_\beta \) denote time derivatives, \(D^{}_{\alpha ' \alpha }\) are the direct-scattering matrix elements, \(K^{}_{\beta ' \alpha }\), are the overlap integrals, and \(Q^{}_{\beta ' \alpha }\) are the exchange matrix elements. Tildes denote the quantities in the projectile centre. In the limit as \(t \rightarrow +\infty \) the expansion coefficients, \(F_\alpha (t,{\varvec{b}})\) and \(G_\beta (t,{\varvec{b}})\), yield the scattering amplitudes for the final channel \(\alpha \) and \(\beta \), respectively. Conversely, in the limit as \(t\rightarrow -\infty \) they satisfy the initial boundary condition

$$\begin{aligned} \begin{aligned} F_{\alpha }(-\infty ,{\varvec{b}}) =&\delta _{\alpha i},&\alpha =1, 2, \ldots , N, \\ G_{\beta }(-\infty ,{\varvec{b}})=&0,&\beta =1, 2, \ldots , M, \end{aligned} \end{aligned}$$
(13)

i.e. in the initial channel the active electron is in the ground state of the target.

The direct-scattering matrix elements are defined as:

$$\begin{aligned} D^{}_{\alpha ' \alpha } ({\varvec{R}})=&\langle \psi ^{\mathrm{T}}_{\alpha '}| \overline{V}_{\alpha } |\psi ^{\mathrm{T}}_{\alpha }\rangle \exp [i (\varepsilon _{\alpha '}-\varepsilon _{\alpha })t] , \end{aligned}$$
(14)
$$\begin{aligned} {\tilde{D}}^{}_{\beta ' \beta } ({\varvec{R}})=&\langle \psi ^{\mathrm{P}}_{\beta '}| \overline{V}_{\beta } |\psi ^{\mathrm{P}}_{\beta }\rangle \exp [i (\varepsilon _{\beta '}-\varepsilon _{\beta })t], \end{aligned}$$
(15)

where the interaction potentials are

$$\begin{aligned} \overline{V}_{\alpha }=V_{\mathrm{{mod}}}(R)-\frac{1}{|\varvec{r}_{\mathrm{P}}|}, \end{aligned}$$
(16)

and

$$\begin{aligned} \overline{V}_{\beta }=V_{\mathrm{{mod}}}(R)-V_{\mathrm{{mod}}}(|\varvec{r}_{\mathrm{T}}|). \end{aligned}$$
(17)

The overlap matrix elements in Eq. (12) are defined as:

$$\begin{aligned} K^{}_{\beta ' \alpha } ({\varvec{R}})=&\langle \psi ^{\mathrm{P}}_{\beta '}|\exp [-i {\varvec{v}} \cdot {\varvec{r}}_{\mathrm{P}}]|\psi ^{\mathrm{T}}_{\alpha }\rangle \nonumber \\&\times \exp [i v^2 t/2 + i (\varepsilon _{\beta '}-\varepsilon _{\alpha })t], \end{aligned}$$
(18)
$$\begin{aligned} {\tilde{K}}^{}_{\alpha ' \beta } ({\varvec{R}})=&\langle \psi ^{\mathrm{T}}_{\alpha ' }| \exp [i {\varvec{v}} \cdot {\varvec{r}}_{\mathrm{T}}] |\psi ^{\mathrm{P}}_{\beta }\rangle \nonumber \\&\times \exp [-i v^2 t/2 + i (\varepsilon _{\alpha '}-\varepsilon _{\beta })t] , \end{aligned}$$
(19)

and the exchange matrix elements as

$$\begin{aligned} Q^{}_{\beta ' \alpha } ({\varvec{R}})=\,&\langle \psi ^{\mathrm{P}}_{\beta '}| \exp [-i {\varvec{v}} \cdot {\varvec{r}}_{\mathrm{P}}] (H_{\alpha } + \overline{V}_{\alpha } - \varepsilon _{\alpha }) |\psi ^{\mathrm{T}}_{\alpha }\rangle \nonumber \\&\times \exp [i v^2 t/2 + i (\varepsilon _{\beta '}-\varepsilon _{\alpha })t], \end{aligned}$$
(20)
$$\begin{aligned} {\tilde{Q}}^{}_{\alpha ' \beta } ({\varvec{R}})=\,&\langle \psi ^{\mathrm{T}}_{\alpha '}| \exp [i {\varvec{v}} \cdot {\varvec{r}}_{\mathrm{T}}] (H_{\beta } + \overline{V}_{\beta } - \varepsilon _{\beta }) |\psi ^{\mathrm{P}}_{\beta }\rangle \nonumber \\&\times \exp [-i v^2 t/2 + i (\varepsilon _{\alpha '}-\varepsilon _{\beta })t]. \end{aligned}$$
(21)

In Eqs. (20) and (21), \(H_{\alpha }\) and \(H_{\beta }\) are the target and projectile-atom Hamiltonians, respectively. Using the approach outlined in Ref. [32], the overlap and exchange matrix elements are evaluated numerically in spheroidal coordinates. A detailed description of how the scattering matrix elements are evaluated for proton scattering is given in Ref. [24].

2.2 Scattering amplitudes

In general, the post form of the scattering amplitude is given by [33, 34]:

$$\begin{aligned} T_{fi}(\varvec{q}_f,\varvec{q}_i)&=\langle \Phi _f^- | \overleftarrow{H}-E |\Psi _i^+ \rangle , \end{aligned}$$
(22)

where \(\varvec{q}_f\) and \(\varvec{q}_i\) are the relative momenta in the final and initial channels, respectively, and \(\Phi _f^-\) is the asymptotic state corresponding to the final channel. The arrow over the Hamiltonian indicates the direction of its action. The form of \(\Phi _f^-\) depends on the particular final state of the system. For direct scattering (meaning that there is no rearrangement of particles), \(f=\alpha \) and \(\Phi _f^-\) is given by the product of the plane wave \(e^{i\varvec{q}_\alpha \cdot \varvec{\rho }_\alpha }\) representing the motion of the scattered projectile relative to the target and the target wave function \(\psi ^{\mathrm{T}}_\alpha (\varvec{r}_{\mathrm{T}})\). Hence, the direct scattering (DS) amplitude is given by:

$$\begin{aligned} T_{fi}^{\mathrm{DS}}(\varvec{q}_f,\varvec{q}_i)&=\langle \varvec{q}_f\psi ^{\mathrm{T}}_f | \overleftarrow{H}-E |\Psi _i^+ \rangle . \end{aligned}$$
(23)

If the final state corresponds to a negative-energy eigenstate of the target, then this reduces to

$$\begin{aligned} T_{fi}^{\mathrm{DS}}(\varvec{q}_f,\varvec{q}_i)&=\langle \varvec{q}_f\psi ^{\mathrm{T}}_f | \overline{V}_\alpha |\Psi _i^+ \rangle . \end{aligned}$$
(24)

If scattering results in electron capture by the projectile (meaning that there is rearrangement of particles), then \(f=\beta \) and \(\Phi _f^-\) is given by the plane wave \(e^{i\varvec{q}_\beta \cdot \varvec{\rho }_\beta }\) representing the motion of the H atom formed by the projectile (referred to as the projectile atom) relative to the residual target ion and the H-atom wave function \(\psi ^{\mathrm{P}}_\beta (\varvec{r}_{\mathrm{P}})\) in the final state. The electron capture (EC) amplitude is given by:

$$\begin{aligned} T_{fi}^{\mathrm{EC}}(\varvec{q}_f,\varvec{q}_i)&=\langle \varvec{q}_f\psi ^{\mathrm{P}}_f | \overleftarrow{H}-E |\Psi _i^+ \rangle . \end{aligned}$$
(25)

Here again, if the final state is a negative-energy eigenstate of the projectile atom, the EC amplitude reduces to

$$\begin{aligned} T_{fi}^{\mathrm{EC}}(\varvec{q}_f,\varvec{q}_i)&=\langle \varvec{q}_f\psi ^{\mathrm{P}}_f | \overline{V}_\beta |\Psi _i^+ \rangle . \end{aligned}$$
(26)

If scattering results in ionisation, then the final state is given by the three-body asymptotic wave that represents the unbound state of three charged particles in the final channel. Here we use the approach described in Refs. [25, 35] which takes advantage of the fact that our total scattering wave function is expanded in terms of the square-integrable pseudostates to remove the need to know the three-body asymptotic state. Instead, following the idea developed in Ref. [21], we project the continuum wave that describes the final ionised state of the electron onto the total scattering wave function. To do this, we first introduce the following projection operators:

$$\begin{aligned} I=\sum _{\alpha =1}^N\langle \psi ^{\mathrm{T}}_\alpha | \psi ^{\mathrm{T}}_\alpha \rangle ,\ J=\sum _{\beta =1}^M\langle \psi ^{\mathrm{P}}_\beta | \psi ^{\mathrm{P}}_\beta \rangle . \end{aligned}$$
(27)

Now we insert the sum \(I+J\) into Eq. (22) to get

$$\begin{aligned} T_{fi}(\varvec{q}_f,\varvec{q}_i)\approx \,&\langle \Phi _f^-(I+J) | \overleftarrow{H}-E |\Psi _i^+ \rangle \nonumber \\ =\,&\langle \Phi _f^-I | \overleftarrow{H}-E |\Psi _i^+ \rangle +\langle \Phi _f^-J | \overleftarrow{H}-E |\Psi _i^+ \rangle . \end{aligned}$$
(28)

The first term in this expression corresponds to direct ionisation (DI) into the target continuum. We use a short-hand notation \(T^{\mathrm{DI}}_{fi}(\varvec{\kappa },\varvec{q}_f,\varvec{q}_i)\) to denote it, where \(\varvec{\kappa }\) is the electron momentum in the target frame. The second term, denoted hereafter as \(T^{\mathrm{ECC}}_{{fi}}(\pmb {\varkappa },\varvec{q}_f,\varvec{q}_i)\), corresponds to electron capture into the continuum (ECC) of the projectile. Here \({\pmb {\varkappa }}\) is the electron momentum in the projectile frame. We write the amplitude for direct ionisation as

$$\begin{aligned} T_{fi}^{\mathrm{DI}}(\varvec{\kappa },\varvec{q}_f,\varvec{q}_i)&=\sum _{\alpha =1}^N\langle \Phi ^-_f | \psi ^{\mathrm{T}}_\alpha \rangle \langle \psi ^{\mathrm{T}}_\alpha | \overleftarrow{H}-E |\Psi _i^+ \rangle \nonumber \\&=\sum _{\alpha =1}^N\langle \varphi ^{\mathrm{T}}_{\varvec{\kappa }} | \psi ^{\mathrm{T}}_\alpha \rangle \langle \varvec{q}_f \psi ^{\mathrm{T}}_\alpha | \overleftarrow{H}-E |\Psi _i^+ \rangle , \end{aligned}$$
(29)

since I effectively replaces the full set of states (\(L^2\) bound and non-\(L^2\) continuum) of the target Hamiltonian with a complete set of square-integrable pseudostates. For direct ionisation, the only surviving term in Eq. (29) is the one in which \(\psi ^{\mathrm{T}}_\alpha \) corresponds to the continuum bin that contains the energy of the ejected electron. All other pseudostates do not overlap with the true continuum wave, \(\varphi ^{\mathrm{T}}_{\varvec{\kappa }}\), since \(\{\psi ^{\mathrm{T}}_\alpha \}_{N}\) form an orthonormal set. So, we are left with

$$\begin{aligned} T_{fi}^{\mathrm{DI}}(\varvec{\kappa },\varvec{q}_f,\varvec{q}_i)&=\langle \varphi ^{\mathrm{T}}_{\varvec{\kappa }} | \psi ^{\mathrm{T}}_f \rangle T_{fi}^{\mathrm{DS}}(\varvec{q}_f,\varvec{q}_i). \end{aligned}$$
(30)

Thus, we see that the DI amplitude is simply given by the amplitude for excitation into a positive-energy pseudostate of the target atom and the overlap between the corresponding wave packet and true continuum wave.

The amplitude for electron capture into the continuum is written as:

$$\begin{aligned} T_{fi}^\mathrm{ECC}({\pmb {\varkappa }},\varvec{q}_f,\varvec{q}_i)&=\sum _{\beta =1}^M\langle \Phi ^-_f | \psi ^{\mathrm{P}}_\beta \rangle \langle \psi ^{\mathrm{P}}_\beta | \overleftarrow{H}-E |\Psi _i^+ \rangle \nonumber \\&=\sum _{\beta =1}^M\langle \varphi ^{\mathrm{P}}_{\pmb {\varkappa }} | {\psi ^{\mathrm{P}}_\beta } \rangle \langle \varvec{q}_f\psi ^{\mathrm{P}}_\beta | \overleftarrow{H}-E |\Psi _i^+ \rangle , \end{aligned}$$
(31)

since J effectively replaces the full set of states (\(L^2\) bound and non-\(L^2\) continuum) of the projectile Hamiltonian with a complete subset of square-integrable pseudostates. Here we also find that for ionisation into a positive-energy pseudostate of the projectile atom the only surviving term in Eq. (31) is the one in which \(\psi ^{\mathrm{P}}_\beta \) corresponds to the continuum bin that contains the energy of the ejected electron. All other pseudostates do not overlap with the Coulomb wave, \(\varphi ^{\mathrm{P}}_{\pmb {\varkappa }}\), since \(\{\psi ^{\mathrm{P}}_\beta \}_{M}\) form an orthonormal set. Equation (31) becomes

$$\begin{aligned} T_{fi}^{\mathrm{ECC}}(\pmb {\varkappa },\varvec{q}_f,\varvec{q}_i)&=\langle \varphi ^{\mathrm{P}}_{\pmb {\varkappa }} | \psi ^{\mathrm{P}}_f \rangle T_{fi}^{\mathrm{EC}}(\varvec{q}_f,\varvec{q}_i). \end{aligned}$$
(32)

Thus, we see that the ECC amplitude is simply given by the amplitude for excitation into a positive-energy pseudostate of the projectile atom and the overlap between the corresponding wave packet and the true continuum Coulomb wave.

After solving Eq. (12) for the expansion coefficients \(F_{\alpha }\) and \(G_{\beta }\), we must determine the scattering amplitudes in momentum space so that the differential cross section can be calculated. Following the technique outlined in Ref. [25], we write the momentum-space scattering amplitude for direct scattering as:

$$\begin{aligned} T_{fi}^{\mathrm{DS}}(\varvec{q}_f,\varvec{q}_i)&=2\pi i v \mathrm{e}^{im\phi _f}\int _{0}^{\infty }d\,b b [\tilde{F}_f(+\infty ,b)-\delta _{fi}]\nonumber \\&\quad \times J_m(q_\perp b), \end{aligned}$$
(33)

which, depending on the final state f, corresponds to either elastic scattering (\(f=i\)), excitation (\(\varepsilon _f<0\)), or ionisation into a positive-energy pseudostate (\(\varepsilon _f>0\)). The perpendicular component of the momentum transfer \(\varvec{q}=\varvec{q}_i-\varvec{q}_f\) is denoted as \(\varvec{q}_\perp \), \(\tilde{F}_f(t,b)=\mathrm{e}^{im\phi _b}F_f(t,\varvec{b})\), the azimuthal angle of \(\varvec{q}_f\) is \(\phi _f\), the change in magnetic quantum number from the initial to final channel is \(m=m_f-m_i\), and \(J_m\) is the Bessel function of the mth order. Since we take the target to be in the ground state in the initial channel, then m is simply given by the magnetic quantum number of the final state.

Similarly, the momentum-space scattering amplitude for electron capture into either a bound (\(\epsilon _f<0\)) or continuum pseudostate (\(\epsilon _f>0\)) is written as:

$$\begin{aligned} T_{fi}^{\mathrm{EC}}(\varvec{q}_f,\varvec{q}_i)&=2\pi i v \mathrm{e}^{im\phi _f}\int _{0}^{\infty }d\,b b \tilde{G}_f(+\infty ,b)J_m(q_\perp b), \end{aligned}$$
(34)

where \(\tilde{G}_f(t,b)=\mathrm{e}^{im\phi _b}G_f(t,\varvec{b})\). In Eqs. (33) and (34), \(\tilde{F}_f\) and \(\tilde{G}_f\) are simply the expansion coefficients in Eq. (2) except we have taken out the exponential factor, which contains the magnetic quantum number, m. Hence, \(T_{fi}^{\mathrm{DS}}(\varvec{q}_f,\varvec{q}_i)\) and \(T_{fi}^{\mathrm{EC}}(\varvec{q}_f,\varvec{q}_i)\) are defined in terms of \(F_\alpha (t,\varvec{b})\) and \(G_\beta (t,\varvec{b})\).

The integrals in Eqs. (33) and (34) are evaluated using a Gauss–Legendre quadrature rule with 640 impact parameter points ranging from \(b_{\mathrm{min}}=0\) to \(b_{\mathrm{max}}=40\) au for all presented results. However, since \(F_\alpha (t,\varvec{b})\) and \(G_\beta (t,\varvec{b})\) are smooth functions, we use only 64 impact parameter points when solving Eq. (12). Most of the oscillations in the integrands in Eqs. (33) and (34) come from the Bessel function; therefore, we interpolate our solutions for \(F_\alpha (t,\varvec{b})\) and \(G_\beta (t,\varvec{b})\) and use 640 points for integration. This ensures the integration of the oscillatory integrand is accurate without needing to solve the coupled equations for a large number of impact parameters. To check the reliability of our results, we performed calculations with 16, 32, and 64 impact parameter points. We observed no difference between the results obtained using 32 and 64 impact-parameter points.

2.3 Differential cross sections

After calculating the scattering amplitudes in momentum space using Eqs. (33) and (34), the angular differential cross section for excitation or electron capture from initial state i into final channel f is given by:

$$\begin{aligned} \frac{\mathrm{d}\sigma ^\mathrm{DS(EC)}_{fi}}{\mathrm{d}\varOmega _f} =\frac{\mu _{\mathrm{{T}}}\mu _f}{(2\pi )^2}\frac{q_f}{q_i} |T_{fi}^{\mathrm{DS(EC)}}(\varvec{q}_f,\varvec{q}_i)|^2, \end{aligned}$$
(35)

where \(\varOmega _f \) is the solid angle into which scattering takes place. We choose the target to be in its ground state in the initial channel. Therefore, we set \(\varvec{q}_i=\varvec{q}_{\alpha }\) where \(\alpha =1\); however, \(\varvec{q}_f= {\varvec{q}}_{\alpha }\) or \(\varvec{q}_f={\varvec{q}}_{\beta }\) depending on the type of scattering. Accordingly, reduced mass \(\mu _f=\mu _{\mathrm{{T}}}\) for the \({\hbox {p}}+{\hbox {H}_2}\) channel and \(\mu _f=\mu _{\mathrm{{P}}}\) for the \({\hbox {H}}+{\hbox {H}_2^+}\) channel.

The singly differential cross sections for ionisation as a function of ejected electron energy \(\mathrm{d}\sigma ^{\mathrm{ion}}/\mathrm{d}E_e\), ejected electron angle \(\mathrm{d}\sigma ^{\mathrm{ion}}/\mathrm{d}\varOmega _e\), and projectile scattering angle \(\mathrm{d}\sigma ^{\mathrm{ion}}/\mathrm{d}\varOmega _f\) are calculated from the fully differential ionisation cross section by integrating over all other variables.

In the laboratory frame, the ionisation amplitudes are given by the incoherent sum of the direct ionisation and electron capture into continuum components [21]. Accordingly, the fully differential ionisation cross section is given as:

$$\begin{aligned} \frac{\mathrm{d}^{3} \sigma ^{\mathrm{ion}} }{\mathrm{d}E_{\mathrm{e}} \mathrm{d}\varOmega _{\mathrm{e}} \mathrm{d}\varOmega _f}=\,&\frac{\mu ^2_{\mathrm{{T}}}}{(2 \pi )^2} \frac{q_f \kappa }{q_i}\big (\big |T^{\mathrm{DI}}_{fi}(\varvec{\kappa },\varvec{q}_f,\varvec{q}_i) \big |^2\nonumber \\&+\big |T^{\mathrm{ECC}}_{fi}(\varvec{\kappa }-\varvec{v},\varvec{q}_f,\varvec{q}_i)\big |^2\big ). \end{aligned}$$
(36)

Note that the ECC component must be transformed into a common frame of reference with the DI part. We choose the laboratory frame as a common coordinate system. Therefore, the DI amplitude given by Eq. (30) does not need to be transformed since it is defined in the laboratory frame. However, the ECC amplitude given by Eq. (32) is defined in the projectile frame and must, therefore, be converted into the laboratory frame of reference. To do this, we first substitute \((\varvec{q}-\varvec{\kappa })_\perp \) for \(\varvec{q}_\perp \) in Eq. (32) (see also Eq. 34) to obtain (after integration) the amplitudes for charge transfer into the projectile continuum with electron momentum \(\pmb {\varkappa }\). This provides amplitudes for specific electron momenta determined by the distribution of the continuum bins. All other required momenta are obtained using interpolation.

3 Results

In this section, we first present angular differential cross sections for elastic scattering, excitation, and electron capture as functions of scattering angle. Then, we present all three types of the SDCS for ionisation. These are the SDCS as a function of the ejected electron energy, the SDCS as a function of ejected-electron angle, and the SDCS as a function of scattering angle of the projectile. All the presented results are obtained using a symmetric two-centre basis. For each included orbital quantum number \(\ell \), we used \(10-\ell \) bound states and a number of wave packets representing the continuum from \(\kappa _\mathrm{min}=0.01\) up to \(\kappa _{\mathrm{max}}\). At 20 and 25 keV, 20 wave packets with \(\kappa _{\mathrm{max}}=5\) were sufficient; however, we had to increase \(N_c\) and \(\kappa _{\mathrm{max}}\) gradually, reaching \(N_c=25\) and \(\kappa _{\mathrm{max}}=10\) at 300 keV. At the lowest energy, we include pseudostates with orbital angular momentum up to \(\ell _{\mathrm{max}}=5\) to obtain a converged result. However, at the highest energy, \(\ell _{\mathrm{max}}=3\) was sufficient. The z-grid is extended from \(-200\) to \(+200\) au and contained 600 points.

3.1 Angular differential cross sections for elastic scattering, excitation, and electron capture

Fig. 1
figure 1

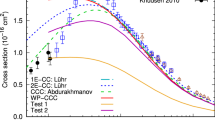
Angular differential cross sections (in the laboratory frame) for elastic scattering, total excitation, and total electron capture in \({\hbox {p}}+{\hbox {H}_2}\) collisions. Experimental data are by Sharma et al. [8]. The theoretical results: the present WP-CCC approach, the distorted-wave-Born methods (DW1, DW2, and DW3) by Igarashi [10], the eikonal approximation by Ghanbari-Adivi and Sattarpour [12], and the first-order Born approximation with correct boundary conditions by Adivi [11]

Full size image

Angular differential cross sections for elastic scattering, excitation into all bound states of the target, and electron capture into all bound states of the projectile atom, calculated using Eq. (35), are shown in Fig. 1. In the first column, we present our results for the angular differential cross section for elastic scattering, excitation into all bound target states included in the basis, and electron capture into all projectile-atom states. In the second column, we compare our results for electron capture to other theories and experimental data where available.

The first column allows us to gauge comparative information about the values of these three cross sections. If we consider scattering into small angles, which practically define the integrated cross section, at 25 keV the dominant process is electron capture. However, as collision energy grows, the excitation cross section grows, while the elastic-scattering and electron-capture cross sections diminish, so that at 75 keV and above, excitation becomes dominant. We can also see that the electron-capture cross section diminishes faster, becoming smaller than the elastic-scattering cross section at 300 keV.

To the authors’ best knowledge, the present results are the first theoretical calculations of the angular differential cross sections for elastic scattering and excitation in this collision system. There are no experimental measurements either. However, there are a number of studies that investigated the angular differential cross section for electron capture. In particular, Sharma et al. [8] reported experimental data at incident energies of 25 and 75 keV. At 25 keV, we find that our results agree well with their measurements up to 0.8 mrad, more closely following the experiment than other calculations. However, at larger scattering angles the WP-CCC method overestimates the experiment and more closely resembles the shape of the DW1 and DW2 models of Igarashi [10]. The DW1 result contains information about the vibrational state of the residual ion, while the DW2 calculation used the FN approximation. At larger angles, the DW3 [9] method shows the best agreement with the experiment, despite describing the molecular target with the simple TEC treatment. This allows us to conclude that neglecting the vibrational motion of the target is not responsible for the discrepancy between our result and the experimental data. At 75 keV, the WP-CCC results generally agree with the experimental data quite well, except they do not suggest any dip around 0.9 mrad. The DW methods of Igarashi et al. [9] and the EA by Adivi [11] also do not show any local minimum. The DW3 method again agrees best with the experimental points. At 100 keV, we compare to the EA calculations of Ghanbari-Adivi and Sattarpour [12] and find that our results fall off less steeply at higher scattering angles where the nucleus–nucleus interaction dominates. There are no experimental data to compare to at this energy.

The highest energy considered for the angular differential cross sections is 300 keV. Here the three distorted-wave methods of Igarashi [10] agree well with one another, while our calculation shows a somewhat different shape. Near the forward direction our cross section is slightly lower than the distorted-wave ones, as it was the case at other projectile energies. Interestingly, we see a secondary peak around 1.2 mrad. While the B1B results from Ref. [11] also show a secondary peak, this is due to the unphysical dip in the B1B cross section resulting from cancellation of the projectile–electron and projectile–residual ion interaction terms in the first-order Born series. This unphysical feature is not present in our theory. The comparison between our results and the EA ones by Ghanbari-Adivi and Sattarpour [12] is similar to the 100-keV case. Both the WP-CCC and DW calculations are larger than the EA and B1B results.

One possible reason for the discrepancy between our calculations and the other models is that our results include electron capture into all projectile-atom states, not only the ground state. Additionally, the WP-CCC method inherently accounts for coupling effects between all the reaction channels.

3.2 Singly differential cross sections for ionisation

Fig. 2
figure 2

Singly differential cross section for ionisation (in the laboratory frame) as a function of the ejected-electron energy. Experimental data are by Gealy et al. [17], Rudd [16], Kuyatt and Jorgensen [13] and Rudd et al. [15]. The theoretical results: the present WP-CCC approach, the effective-one-electron single-centre close-coupling method by Lühr and Saenz [22], the classical trajectory Monte Carlo method by Schultz et al. [23], the first Born approximation and classical Gryziński method by Rudd et al. [15]. The DI and ECC components of the WP-CCC results are also shown

Full size image

Below we present all possible types of the SDCS for ionisation. We emphasise that the integration of each of the three singly differential cross sections reproduces the total ionisation cross section reported by Plowman et al. [24] with the deviation less than 1%. This indicates the consistency of the calculations of the differential cross sections.

In Fig. 2, we present our results for the singly differential cross section for ionisation as a function of ejected electron energy in \({\hbox {p}}+{\hbox {H}_2}\) collisions. There are experimental data at a number of incident projectile energies. The results are shown at 10 typical impact energies from 20 to 300 keV at which there are experimental data from multiple groups. There are also theoretical calculations to compare to at these energies. First of all, we emphasise that at each impact energy our results are given at the ejected electron energies where we have positive-energy wave packets. These points are connected with straight lines to guide the eye.

In general, the obtained results agree very well with the experimental data by Gealy et al. [17]. They also agree with the data by Rudd et al. [15] available at projectile energies within the range 100–300 keV. However, our results slightly underestimate the data from Kuyatt and Jorgensen [13] and Rudd [16] available for 5–100-keV protons. The drop seen in the results of Kuyatt and Jorgensen [13] for low ejection energies at collision energies of 50, 75, and 100 keV was due to the inability of their apparatus to detect all of the low-energy electrons produced in the collision (see Ref. [17] for a detailed discussion of the various experimental results). We find that the WP-CCC calculations appear to better replicate experiment than the CTMC calculations by Schultz et al. [23] available at 50, 75, and 100 keV. At high impact energies, we find good agreement between our calculations and the FBA results by Rudd et al. [15]. The WP-CCC results agree with the experimental results better than the classical Gryziński calculations, especially at high ejected electron energies. Furthermore, our calculations underestimate the experimental data from Rudd et al. [15] at 20 and 50 keV. However, as noted in Ref. [17], the integrated results from Rudd et al. [15] and Kuyatt and Jorgensen [13] both overestimate the total ionisation cross section. Agreement with the data measured by Rudd et al. [15] is excellent at higher energies. Our calculations are checked at each impact energy to ensure that the integrated SDCS gives the same total ionisation cross section as we obtain directly from the impact-parameter amplitudes. (Calculations of TICS are presented in Plowman et al. [24].) Next we provide an in-depth analysis of the WP-CCC results.

At the lowest impact energy considered, 20 keV, our results are slightly lower than the experimental data by both Rudd [16] and Gealy et al. [17], at all ejected-electron energies, except for the last data point at 100 eV. We also see a slight shoulder in our results at small ejection energies. This occurs when the contribution from electron capture into the continuum of the projectile peaks (see Ref. [25] on \({\hbox {p}}+{\hbox {H}}\) collisions for a detailed explanation of this behaviour). Such a shoulder is clearly visible also at higher projectile energies, disappearing only at 95 keV and above. At a projectile energy of 48 keV, we see excellent agreement with the experimental data from Gealy et al. [17] for low emission energies, but our results overestimate the experiment at high ejection energies. At this collision energy, Lühr and Saenz [22] used a one-centre effective-one-electron close-coupling approach to calculate the singly differential ionisation cross section. Their cross section has a peak around 26 eV, the energy that is close to the region where the velocity of the ejected electron matches that of the projectile making electron capture significantly more likely. The single-centre method cannot separate pure ionisation from electron capture leading to the unphysical peak. At 50 keV incident protons, we compare our results to the experimental data by Kuyatt and Jorgensen [13] and Rudd [16]. Similar to the 20-keV case, our calculations underestimate the data from Rudd [16] across the entire ejected-electron energy range considered. The WP-CCC results are systematically smaller than the data measured by Kuyatt and Jorgensen [13] for all but the smallest ejection energies where, as mentioned above, the experimental data are unreliable. Below 10 eV emission energy, our results are very close to the CTMC ones by Schultz et al. [23]. However, as the energy of the ejected electron increases, our results fall less steeply, better replicating the experimental data. At 67 keV, the WP-CCC results agree well with the data from Gealy et al. [17], especially at low emission energies. At 75 keV, our calculations again fall slightly below the data from Kuyatt and Jorgensen [13], except for their unphysical result at small ejection energies. Here we also see that our result falls less steeply than the CTMC calculations by Schultz et al. [23]. As the incident energy increases to 95 keV, we find very good agreement with the experimental results of Gealy et al. [17]. For an incident projectile energy of 100 keV, the WP-CCC results agree well with the experimental data by Rudd et al. [15], Kuyatt and Jorgensen [13], and Rudd [16]. We also see very good agreement with the FBA calculations by Rudd et al. [15]. The classical Gryziński method produces a different shape to the experimental data, dipping slightly around 50–100 eV and then turning sharply down at 300 eV. As at lower impact energies, we find the WP-CCC results to be slightly larger than the CTMC ones by Schultz et al. [23], better agreeing with the experimental data. Our results again agree well with the experimental data by Gealy et al. [17] at 114 keV. At large ejection energies, our cross section overestimates the experiment. At 200 keV, agreement between the WP-CCC results and the data of Rudd et al. [15] is excellent. We also see good agreement with the FBA calculations. The largest impact energy considered is 300 keV. Here again our results agree very well with the experimental data by Rudd et al. [15] across four orders of magnitude from the ionisation threshold up to an ejection energy of 700 eV. The FBA calculations from Rudd et al. [15] also agree well with the experimental data. The Gryziński method slightly underestimates the experiment between 100 and 300 eV and overestimates it above 600 eV.

It appears that, somewhat surprisingly, the simple FBA suffices for the purpose of calculating the SDCS in the emission energy at projectile energy of 100 keV and above. However, as discussed below, this is not the case when the SDCS in the emission angle or the SDCS in the scattered-projectile angle is required.

The direct ionisation and electron capture to continuum components of the WP-CCC results are also shown in Fig. 2. As one can see, the singly differential cross section for ionisation as a function of ejected electron energy is dominated by direct ionisation, while energetic electrons are emitted purely due to electron capture to continuum.

Fig. 3
figure 3

Singly differential cross section for ionisation (in the laboratory frame) as a function of the ejected-electron energy. Experimental data are by Gealy et al. [17], Rudd [16], Kuyatt and Jorgensen [13] and Rudd et al. [15]. The theoretical results: the present WP-CCC approach, the classical trajectory Monte-Carlo method by Schultz et al. [23], and the first Born approximation by Rudd et al. [15]. The DI and ECC components of the WP-CCC results are also shown

Full size image

Figure 3 presents the singly differential cross section for ionisation as a function of the electron emission angle at the same projectile energies as in Fig. 2. Generally, we see very good agreement between the WP-CCC results and available experimental data at all collision energies considered, except for 20 keV. At 20 keV, our SDCS is systematically smaller than the experimental data by Rudd [16] and Gealy et al. [17] though agreeing in shape. This is consistent with our results for the total ionisation cross section where we found that the effective one-electron WP-CCC approach slightly underestimates the TICS for impact energies below about 20 keV [24]. At 48, 67, 95 and 114 keV, our results agree very well with the experimental data from Gealy et al. [17] for the entire range of ejection angles. At 50 keV, our results agree well with the experiments of Kuyatt and Jorgensen [13] and Rudd [16] up to 110 degrees. Above this angle, the WP-CCC method underestimates the experimental data. For an incident energy of 75 keV, our calculations agree well with the measurements from Kuyatt and Jorgensen [13] up to about 110 degrees. Otherwise, the situation is similar to the 50-keV case. At 100, 200 and 300 keV, our results are in excellent agreement with the data from Rudd et al. [15].

The only other theoretical approaches applied to calculate the SDCS in the emission angle are the FBA by Rudd et al. [15] and the CTMC method by Schultz et al. [23]. At 50, 75, and 100 keV, our results agree with the CTMC ones by Schultz et al. [23] reasonably well. As one can see, the FBA results by Rudd et al. [15], available at 100, 200, and 300 keV, fail to reproduce the experiment, significantly underestimating the data below 50 degrees and overestimating at larger angles. Thus, our method provides significant improvement over the FBA.

The direct ionisation and electron capture to continuum components of the WP-CCC results are also shown in Fig. 3. As one can see, at collision energies from 20 to 114 keV, the singly differential cross section for ionisation as a function of ejected electron angle is dominated by electron capture to continuum when electrons are emitted into a cone around the forward direction. Above 200 keV, the situation is opposite. Electrons emitted into large angles are purely due to direct ionisation regardless of the projectile energy.

Fig. 4
figure 4

Singly differential cross section for ionisation (in the laboratory frame) as a function of the projectile scattering angle. The present WP-CCC results are compared with the present FBA ones. The DI and ECC components of the WP-CCC results are also shown

Full size image

In Fig. 4, we present the singly differential cross section for ionisation as a function of the scattering angle of the projectile. There are no experimental data or other theoretical calculations available in the literature to compare to. Therefore, the present WP-CCC results are compared with the present FBA ones. As one can see from the figure, the FBA is expected to fail at all collision energies, even as high as 300 keV. It would be interesting to verify these results using other methods. The direct ionisation and electron capture to continuum components of the WP-CCC results are also shown. At sufficiently low collision energies (50 keV and below), the dominant mechanism of ionisation is ECC if the projectile is scattered into small angles. At 67 and 75 keV, both DI and ECC mechanisms contribute equally. However, starting from 95 keV direct ionisation becomes the dominant channel for electron emission. If the projectile is scattered into large angles, electrons are ejected primarily through direct ionisation.

4 Conclusion

There are a number of theoretical approaches to differential scattering in proton collisions with molecular hydrogen. Some of them can reasonably well describe experiment on the angular differential cross section for electron capture but have not been extended to ionisation. Others can reasonably well describe experiment on the singly differential ionisation cross sections as a function of either ejected-electron energy or ejection angle but fail to provide data on electron capture. For the first time, the angular differential cross sections for elastic scattering, excitation and electron capture, and the singly differential ionisation cross sections as functions of the ejected-electron energy and angle, as well as projectile scattering angle have been calculated using the coupled-channel formalism. To this end, the recently developed two-centre wave-packet convergent close-coupling approach to proton collisions with molecular hydrogen is used. The approach is based on an effective one-electron description of the \({\hbox {H}_2}\) target. Good agreement with available experimental data is obtained for all the processes. In particular, this provides significant improvement over previous theoretical investigations of the various singly differential cross sections for ionisation. Furthermore, we identify specific mechanisms responsible for electron emission in particular kinematic regimes. We demonstrate that the effective one-electron WP-CCC method can provide reasonably accurate results on singly differential cross sections for all interconnected processes taking place in \({\hbox {p}}+{\hbox {H}_2}\) collisions. This paves the way to calculating various doubly differential as well as fully differential cross sections for ion-induced ionisation of molecular hydrogen.