Abstract
Anderson localization is the ubiquitous phenomenon of inhibition of transport of classical and quantum waves in a disordered medium. In dimension one, it is well known that all states are localized, implying that the distribution of an initially narrow wave packet released in a disordered potential will, at long time, decay exponentially on the scale of the localization length. However, the exact shape of the stationary localized distribution differs from a purely exponential profile and has been computed almost fifty years ago by Gogolin. Using the atomic quantum kicked rotor, a paradigmatic quantum simulator of Anderson localization physics, we study this asymptotic distribution by two complementary approaches. First, we discuss the connection of the statistical properties of the system’s localized eigenfunctions and their exponential decay with the localization length of the Gogolin distribution. Next, we make use of our experimental platform, realizing an ideal Floquet disordered system, to measure the long-time probability distribution and highlight the very good agreement with the analytical prediction compared to the purely exponential one over 3 orders of magnitude.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Anderson localization [1, 2], the complete absence of transport due to disorder-induced destructive quantum interference, has been predicted more than 60 years ago and has triggered enormous inspiration on both classical and quantum transport. The main distinctive property of Anderson localization is the exponentially localized form of its wave packet and has been observed in various physical systems ranging from light waves [3, 4], microwaves [5, 6], X-rays [7], sound waves [8], electrons gases [9] and atomic matter waves [10, 11], making it an ubiquitous feature in physics of wave transport in disordered media.
It is well known that in one dimension, all eigenstates of a disordered Hamiltonian decay exponentially [2]. This implies that an initially narrow wave packet will start to expand in the disordered medium until reaching a localized steady-state. This state is characterized by the probability to find a particle at a distance x from its initial position which is given by the so-called Gogolin distribution [12],
This distribution depends only on one parameter, the localization length \(\xi \). In this sense, the shape of the distribution is ‘universal’, whereas the parameter \(\xi \), which describes the localization properties of the system, depends on the microscopic details, such as the disorder strength and energy of the initial state.
While this distribution has first been computed for a strictly one-dimensional system using Berezinskii diagrammatic method [13], it was soon realized that it applies to a much wider class of systems. In particular, it also applies to the asymptotic behavior of a broad class of systems, described by Efetov’s supersymmetric nonlinear sigma model [14], such as quasi-one-dimensional disordered systems [15], random band matrices [16], and the Quantum Kicked Rotor (QKR) [17]. The latter is a paradigmatic model of quantum chaos [18], where a quantum particle is kicked periodically with a sinusoidal potential, and which displays dynamical localization [19]: an initially narrow wave packet in momentum space will reach at long time an exponentially localized momentum distribution. The connection between dynamical localization and Anderson localization has been explicitly realized by mapping the QKR on a disordered tight-binding Hamiltonian, similar to the Anderson model [20]. Thus, the Floquet eigenstates of the evolution operator are exponentially localized, with a similar localization length for all eigenstates.
This makes the experimental realization of the QKR a remarkable quantum simulator of the physics of disordered systems [21]. Indeed, the atomic QKR has allowed the observation of dynamical localization [22, 23], Anderson localization in two dimensions [24], the Anderson transition in three dimensions [11, 25] as well as detailed studies of weak-localization effects [26,27,28,29]
The creation of narrow and monochromatic matter wavepackets is generally very difficult experimentally, and this is expected to hinder a precise observation of the Gogolin density profile. Indeed, the energy dependence of the localization length in ‘usual’ disordered systems makes the asymptotic localized state a superposition of such profiles. The energy-independence of the QKR Floquet states is thus a very important asset in this respect, both numerically and experimentally.
In this paper, we investigate the asymptotic localization properties of Anderson-localized wavepackets in the atomic QKR. Using numerical simulations, we show that the length \(\xi \) that appears in the Gogolin distribution corresponds to the average localization length of the Floquet eigenstates, the distribution of which is shown to be in good agreement with the supersymmetric predictions for the eigenstate statistics. Then, using our experimental realization of the atomic QKR, we show that the long-time momentum distribution is in excellent agreement with the Gogolin distribution (convolved with the initial momentum distribution), while a purely exponential form does not fit the data.
Our manuscript is organized as follows. In Sect. 2, we recall the basic properties of the QKR as well as the relevant theoretical predictions, and present some numerical simulations in very good agreement with the supersymmetric predictions. We present our experimental observation of the Gogolin distribution in Sect. 4, and present our conclusions in Sect. 5.
2 Statistical properties of the QKR eigenstates
The QKR Hamiltonian is defined as
where \(K\cos {{\hat{x}}}\) represents a sinusoidal potential created by a standing wave (formed by counterpropagating lasers of wave number \(k_{L}\)), with length in units of \(\left( 2k_{L}\right) ^{-1}\) and time in units of the kick period \(T_{1}\). Momenta are measured in units such that \({{\hat{x}}}\) and \({\hat{p}}\) obey the canonical commutation relation  , with
, with  the effective Planck constant (for particles of mass M). The kick strength K, as well as
the effective Planck constant (for particles of mass M). The kick strength K, as well as  , can be tuned in the experiment (see below). For an initial state with a well-defined initial momentum, one observes that the kinetic energy of the system initially grows linearly in time, before saturating to a constant value, the hallmark of dynamical localization.
, can be tuned in the experiment (see below). For an initial state with a well-defined initial momentum, one observes that the kinetic energy of the system initially grows linearly in time, before saturating to a constant value, the hallmark of dynamical localization.
Due to the spatial periodicity of the potential, the kicks can only change the particle’s momentum by increments of
 , and writing momenta as
, and writing momenta as
 , with
\(\ell \in {\mathbb {Z}}\) and
\(q\in (-1/2,1/2]\), the quasi-momentum q is a conserved quantity. The evolution operator over one period reads, for a given quasi-momentum q (the dependence on quasi-momentum of all quantities is left implicit from now on):
, with
\(\ell \in {\mathbb {Z}}\) and
\(q\in (-1/2,1/2]\), the quasi-momentum q is a conserved quantity. The evolution operator over one period reads, for a given quasi-momentum q (the dependence on quasi-momentum of all quantities is left implicit from now on):

with \({\hat{\ell }}\left| \ell \right\rangle =\ell \left| \ell \right\rangle \), and the operator splits into a kicking part and a free propagation due to the instantaneous character of the kicks. In practice, it suffices that the kick duration is short enough such that \(p T_1/M\ll 2\pi /k_L\). Dynamical localization can be understood by noting that the Floquet eigenstates \({{\hat{U}}}(1)\left| \phi _{\omega }\right\rangle =\exp (-i\omega )\left| \phi _{\omega }\right\rangle \) are, up to some technicalities, eigenstates of a disordered tight-binding Hamiltonian \({{\hat{H}}}_\textrm{eff}\) displaying Anderson localization [20, 30, 31]. For the QKR, one finds
with on-site energy
 and hopping amplitude
and hopping amplitude
 . The on-site energies are deterministic, but for
. The on-site energies are deterministic, but for
 incommensurate with
\(\pi \), they oscillate strongly enough to play the role of a pseudo-disorder, while each q plays the role of a different disorder realization. Finally, the hopping
\(t_{r}\) has a range of order
incommensurate with
\(\pi \), they oscillate strongly enough to play the role of a pseudo-disorder, while each q plays the role of a different disorder realization. Finally, the hopping
\(t_{r}\) has a range of order
 , and the Hamiltonian is thus similar to a random band matrix in the limit
, and the Hamiltonian is thus similar to a random band matrix in the limit
 .
.
It comes out of the mapping of Ref. [20] that all Floquet eigenstates are eigenvectors of \({{\hat{H}}}_\textrm{eff}\) with zero energy and are thus expected to have the same localization properties (e.g. same localization length). This is in contrast with disordered systems and random band matrices, where the localization properties depend on the position of the states in the spectrum.
The QKR can be described by the same supersymmetric field theory that is used to describe random band matrices and quasi-one-dimensional systems, and as a consequence possesses the same universal features. The characterization of these features can be done by studying the statistical properties of the system’s spectrum and eigenstates, as was initially recognized by Wigner [32], starting the field of Random Matrix Theory [33]. In the present context, the supersymmetric method has allowed for detailed calculation of the statistics of the eigenstates, see [34] for a review. Following [34, 35], we recall here only the relevant results necessary for the discussion.
The exponential decay of an eigenstate \(\vert \phi _\omega \rangle \), \(\vert \phi _\omega (\ell )\vert ^2\propto e^{-\vert \ell \vert /\xi _\omega }\) can be characterized by introducing the quantity \(r_\omega (\ell ,L)=\vert \phi _\omega (\ell )\vert ^2\vert \phi _\omega (\ell +L)\vert ^2\), since
The statistical properties of \(r_\omega \) have been studied in detail [34], as it also describes the Inverse Participation Ratio (IPR) of each eigenstate \(P_\omega =\sum _\ell r_\omega (\ell ,0)\), as well as the asymptotic long-time probability \(\Pi (\ell ,L)\) to find a particle in \(\ell +L\) knowing that it has started at \(\ell \), for a given disorder realization,
where we have used the fact that due to localization the spectrum is discrete and fluctuates, and that therefore the cross-terms in the sum interfere destructively.
Denoting with a bracket the average over disorder realizations, for a narrow energy part of the spectrum, the probability distribution of \(v=-\ln r_\omega \) has been shown to be Gaussian in the limit \(L\gg {\tilde{\xi }}\) [35], with \({\tilde{\xi }}^{-1}=\langle v\rangle /L\) the average inverse localization length of the eigenstates,
Noting that the variance of v is twice its mean, this implies that the distribution of \(1/\xi _\omega \) is sharply peaked as \(L\rightarrow \infty \), and therefore \(\langle \xi _\omega \rangle ={\tilde{\xi }}\).
Using similar supersymmetric methods, one shows that the momentum distribution at long time is given by the Gogolin distribution
with the same localization length as the Floquet eigenstates, i.e. \(\xi ={\tilde{\xi }}\) [15, 35]. The result is independent of the starting position \(\ell \) thanks to translation invariance after averaging over disorder.
Lastly, we point out that, since all the QKR Floquet eigenstates have the same eigenenergy, the energy selection introduced in [35] is no longer required and can be replaced (and used in the following section) by a broader averaging, also denoted with brackets from now on, over both disorder and the whole ensemble of eigenstates.
3 Numerical investigations
We shall now investigate numerically the relation between the typical localization length of the Kicked Rotor’s Floquet eigenstates and the Gogolin distribution (see also [36,37,38] for early numerical studies of the spectral properties of the QKR). In order to realize an accurate investigation, we will make use of an idealized version of the model, the so-called Random Kicked Rotor (RKR) where the kinetic term  is replaced by a purely random, uniformly distributed phase \(\theta _\ell \in [0,2\pi [\). This allows us to suppress the undesired correlation effects that usually complicate the analysis of the QKR [39,40,41]. Recently, it has been shown that a modified and experimentally feasible version of the QKR reproduces the features of this idealized Kicked Rotor [42].
is replaced by a purely random, uniformly distributed phase \(\theta _\ell \in [0,2\pi [\). This allows us to suppress the undesired correlation effects that usually complicate the analysis of the QKR [39,40,41]. Recently, it has been shown that a modified and experimentally feasible version of the QKR reproduces the features of this idealized Kicked Rotor [42].
The Floquet eigenstates \(\phi _\omega (\ell )\) of the RKR can be computed by realizing exact diagonalization of the evolution operator \({\hat{U}}(1)\). The numerical implementation of the Floquet operator implies periodic boundary conditions in momentum space; we therefore choose a cut-off in momentum which is much larger than the localization length of the eigenstates. Figure 1a shows an example of few such eigenstates, obtained for  . In order to compare all the Floquet states, we translate them in momentum by a value \(\ell _0\) that corresponds to their centroid. Doing so we obtain the distribution presented in Fig. 1b illustrating the fact that they all decay exponentially with similar rates.
. In order to compare all the Floquet states, we translate them in momentum by a value \(\ell _0\) that corresponds to their centroid. Doing so we obtain the distribution presented in Fig. 1b illustrating the fact that they all decay exponentially with similar rates.
a Histograms of the probability distribution of \(-\ln (r_\omega )/L\) for various L and  . The circles show the position of the mean, while the vertical dashed line shows the extrapolated mean for \(L\rightarrow \infty \). The inset shows the position of the means as a function of 1/L (symbols), while the line is a fit \(f(L)=f_0 + a_0 / L\), used to extrapolate the data and infer \(\tilde{\xi }=f_0^{-1}\) (\(\tilde{\xi }=35.2\pm 2.1\) in this case). b Evolution of the ratio R between the variance and mean value of \(-\ln {\tilde{r}}_\omega \), as a function of \(y=L/\tilde{\xi }\), for
. The circles show the position of the mean, while the vertical dashed line shows the extrapolated mean for \(L\rightarrow \infty \). The inset shows the position of the means as a function of 1/L (symbols), while the line is a fit \(f(L)=f_0 + a_0 / L\), used to extrapolate the data and infer \(\tilde{\xi }=f_0^{-1}\) (\(\tilde{\xi }=35.2\pm 2.1\) in this case). b Evolution of the ratio R between the variance and mean value of \(-\ln {\tilde{r}}_\omega \), as a function of \(y=L/\tilde{\xi }\), for  . The shaded area represents numerical uncertainty. At large values of y, the ratio tends towards a value close to \(R = 2\) within the numerical uncertainty, compatible with the prediction of Ref. [43]. The inset shows a histogram of the probability distribution of \(- \ln {\tilde{r}}_\omega \), calculated for \(y\simeq 35\), which is well fitted by a Gaussian distribution with \(R\simeq 2\) (dashed red line)
. The shaded area represents numerical uncertainty. At large values of y, the ratio tends towards a value close to \(R = 2\) within the numerical uncertainty, compatible with the prediction of Ref. [43]. The inset shows a histogram of the probability distribution of \(- \ln {\tilde{r}}_\omega \), calculated for \(y\simeq 35\), which is well fitted by a Gaussian distribution with \(R\simeq 2\) (dashed red line)
Without loss of generality, we study the statistical properties of these ‘shifted’ Floquet states, which possess all the same center implying that \(r_\omega (\ell ,L)\) now only depends on L : \(r_\omega (\ell ,L) \mapsto r_{\omega }(L)\). We calculate the histograms of \(-\ln r_\omega (L)/L\) for various L using \(10^5\) Floquet states with  and present the results in Fig. 2a. We see that the distribution gets narrower as L increases. The mean value of each distribution, represented by the circles, slowly converges to \({\tilde{\xi }}^{-1}\), as \(\propto 1/L\), and in practice we can infer the asymptotic value \(\tilde{\xi }=35.2\pm 2.1\) by extrapolating (via a fit) its L-dependence, see the inset of Fig. 2a. For completeness, we plot (dashed line) the distribution corresponding to the obtained average rate \({\tilde{\xi }}^{-1}\) in Fig. 1b.
and present the results in Fig. 2a. We see that the distribution gets narrower as L increases. The mean value of each distribution, represented by the circles, slowly converges to \({\tilde{\xi }}^{-1}\), as \(\propto 1/L\), and in practice we can infer the asymptotic value \(\tilde{\xi }=35.2\pm 2.1\) by extrapolating (via a fit) its L-dependence, see the inset of Fig. 2a. For completeness, we plot (dashed line) the distribution corresponding to the obtained average rate \({\tilde{\xi }}^{-1}\) in Fig. 1b.
To go one step further, we investigate the statistical properties of the dimensionless quantity \({\tilde{r}}_\omega (y) \equiv 4\tilde{\xi }^2 r_\omega (y)\), with \(y\equiv L/\tilde{\xi }\). First, we compute the ratio between the variance and the mean value of \(-\ln {\tilde{r}}_\omega \):
as a function of y. The results are shown in Fig. 2b. At large y (\(L\gg \tilde{\xi }\)), we obtain that the ratio R(y) tends to a constant value, close to the theoretical prediction \(R\rightarrow 2\) of Eq. (7). As shown in the inset, we find that, for \(y\gg 1\), the probability density of \(-\ln {\tilde{r}}_\omega \) is well fitted by a Gaussian satisfying: \(\langle \delta ^2 (\ln {\tilde{r}}_{\omega }) \rangle = -2 \langle \ln {\tilde{r}}_{\omega } \rangle \), in excellent agreement with Ref. [35]. Similar conclusions have been obtained numerically in [44] for the conductance fluctuations in quasi-one-dimensional weakly disordered system. We have also analyzed the IPR probability distribution and found a very good agreement with the corresponding supersymmetric predictions, see Appendix A for details.
These results can be used to analyze the stationary probability distribution of the QKR at long times, deep in the localized regime. This quantity is accessible numerically, as well as in experiments, and is obtained by studying the evolution of a narrow initial momentum distribution after a time much longer than the localization time \(t_\textrm{loc}\). We first focus on numerical aspects.
Numerical simulations of the dynamics of the (random) Kicked Rotor are straightforward [45]. The free evolution between two consecutive kicks is diagonal in momentum representation, while the kick operator is diagonal in position representation. Switching between momentum and position representation is easily done through a Fast Fourier Transform. Such a procedure is equivalent to applying the evolution operator \({\hat{U}}(1)\) once, and thus one can of course repeat the procedure a sufficient number of times until dynamical localization is reached. We truncate the momentum basis ensuring that the final state has a support much smaller than the momentum cut-off. Using this procedure, we compute the evolution of a large number of random phase realizations, and average the resulting momentum distributions.
Time evolution of \(\langle \ell ^2(t)\rangle \) for  . The steady-state value corresponds to \(\langle \ell _\textrm{loc}^2\rangle =12.4 \times 10^3\). The inset shows \(\langle \ell _\textrm{loc}^2\rangle \) vs \(8\zeta (3)\tilde{\xi }^2\), which are expected to be equal, for various values of
. The steady-state value corresponds to \(\langle \ell _\textrm{loc}^2\rangle =12.4 \times 10^3\). The inset shows \(\langle \ell _\textrm{loc}^2\rangle \) vs \(8\zeta (3)\tilde{\xi }^2\), which are expected to be equal, for various values of  . The horizontal error bars correspond to statistical fitting error, the vertical error bars are smaller than the symbol size. The dashed line is a fit with slope 1.05
. The horizontal error bars correspond to statistical fitting error, the vertical error bars are smaller than the symbol size. The dashed line is a fit with slope 1.05
Steady-state momentum distributions at two different times \(t\gg t_\textrm{loc}\), for  , showing an excellent agreement with the Gogolin distribution (dashed line) with parameter \(\xi =35.2=\tilde{\xi }\). The dotted line is the exponential approximation, valid close to \(\ell \simeq 0\), whereas the dash-dotted line is the asymptotic limit for \(\ell \gg \tilde{\xi }\)
, showing an excellent agreement with the Gogolin distribution (dashed line) with parameter \(\xi =35.2=\tilde{\xi }\). The dotted line is the exponential approximation, valid close to \(\ell \simeq 0\), whereas the dash-dotted line is the asymptotic limit for \(\ell \gg \tilde{\xi }\)
We present results for  . At short times, the momentum variance \(\langle \ell ^2(t)\rangle \simeq 2D t\) has a linear growth characterized by a diffusion coefficient D, while at longer time \(\langle \ell ^2(t)\rangle \) saturates to a value \(\langle \ell ^2_\textrm{loc}\rangle \), see Fig. 3. The typical time scale is the so-called localization time \(t_\textrm{loc}\), which is formally defined as \(t_\textrm{loc}=\ell ^2_\textrm{loc}/2D\). Furthermore, the momentum distribution becomes stationary. This can be seen in Fig. 4, which shows the momentum distribution at two different times much larger than \(t_\textrm{loc}\). We find an excellent agreement with the Gogolin distribution given by Eq. (1), if we choose \(\xi = \tilde{\xi }\), with \(\tilde{\xi }\) obtained as described above for the same value of
. At short times, the momentum variance \(\langle \ell ^2(t)\rangle \simeq 2D t\) has a linear growth characterized by a diffusion coefficient D, while at longer time \(\langle \ell ^2(t)\rangle \) saturates to a value \(\langle \ell ^2_\textrm{loc}\rangle \), see Fig. 3. The typical time scale is the so-called localization time \(t_\textrm{loc}\), which is formally defined as \(t_\textrm{loc}=\ell ^2_\textrm{loc}/2D\). Furthermore, the momentum distribution becomes stationary. This can be seen in Fig. 4, which shows the momentum distribution at two different times much larger than \(t_\textrm{loc}\). We find an excellent agreement with the Gogolin distribution given by Eq. (1), if we choose \(\xi = \tilde{\xi }\), with \(\tilde{\xi }\) obtained as described above for the same value of  , see Fig. 4. This proves that the length scale \(\tilde{\xi }\), which characterizes the decay of the Floquet eigenfunctions corresponds exactly to the single-parameter \(\xi \) which characterizes the functional form of the asymptotic probability density. Close to the center of the distribution (\(\ell \approx 0\)), the decay is exponential with a rate \(\tilde{\xi }^{-1}\), whereas the large-momentum wings also decrease exponentially (up to an algebraic factor), with a rate four times lower: \(1/(4\tilde{\xi })\). This difference is attributed to the strong fluctuations of \(\vert \phi _\omega (\ell )\vert ^2\) [31], as it is exemplified in Fig. 1.
, see Fig. 4. This proves that the length scale \(\tilde{\xi }\), which characterizes the decay of the Floquet eigenfunctions corresponds exactly to the single-parameter \(\xi \) which characterizes the functional form of the asymptotic probability density. Close to the center of the distribution (\(\ell \approx 0\)), the decay is exponential with a rate \(\tilde{\xi }^{-1}\), whereas the large-momentum wings also decrease exponentially (up to an algebraic factor), with a rate four times lower: \(1/(4\tilde{\xi })\). This difference is attributed to the strong fluctuations of \(\vert \phi _\omega (\ell )\vert ^2\) [31], as it is exemplified in Fig. 1.
In addition, we checked for different values of  the very good agreement between: (1) the asymptotic momentum distributions obtained numerically; and (2) the Gogolin distribution with \(\xi =\tilde{\xi }\). To be more quantitative, using that \(\int \text {d}\ell \ell ^2 \Pi _G(\ell )=8\zeta (3) \xi ^2\) [12], we assess this agreement by comparing \(\langle \ell _\textrm{loc}^2\rangle \) from our RKR simulations, for a given
the very good agreement between: (1) the asymptotic momentum distributions obtained numerically; and (2) the Gogolin distribution with \(\xi =\tilde{\xi }\). To be more quantitative, using that \(\int \text {d}\ell \ell ^2 \Pi _G(\ell )=8\zeta (3) \xi ^2\) [12], we assess this agreement by comparing \(\langle \ell _\textrm{loc}^2\rangle \) from our RKR simulations, for a given  , to \(8\zeta (3)\tilde{\xi }^2\) for the same parameters, see the inset of Fig. 3. This shows that the two length scales are equal within \(3\%\).
, to \(8\zeta (3)\tilde{\xi }^2\) for the same parameters, see the inset of Fig. 3. This shows that the two length scales are equal within \(3\%\).
Finally, we checked the validity of these results for the ‘standard’ QKR (see Appendix B). It is known that, at low values of  , the QKR is affected by classical correlation effects, which lead to significant discrepancies with respect to a system with uncorrelated disorder [42]. At low
, the QKR is affected by classical correlation effects, which lead to significant discrepancies with respect to a system with uncorrelated disorder [42]. At low  , we found that the classical kick-correlation effects lead to deviations from the predicted Gaussian statistics of Eq. (7). However, the correlation effects disappear at large
, we found that the classical kick-correlation effects lead to deviations from the predicted Gaussian statistics of Eq. (7). However, the correlation effects disappear at large  , where we find an excellent agreement between the QKR and the ideal RKR model.
, where we find an excellent agreement between the QKR and the ideal RKR model.
4 Experimental observation of the asymptotic distribution
The previous section established numerically the relationship between the ‘intrinsic’ localization length \(\tilde{\xi }\), characteristic of the exponential decay of the system’s eigenfunctions, and the long-time probability distribution, obtained when starting from a peaked initial condition. We shall now focus on the experimental investigation of this characteristic asymptotic shape and on its distinction from the commonly-thought exponential shape associated with Anderson localization.
In order to access experimentally the question of the exact form of the momentum distribution at long times, it is necessary to realize experimentally an ideal version of the QKR where the late time dynamics is not plagued by correlation effects for the experimentally accessible low values of the kick strength. This is rendered possible by using a periodically phase shifted version of the QKR [26, 46], described by the Hamiltonian:
For \(a_n = 0\), \(\forall n\), \({{\hat{H}}}(t)\) reduces to the Hamiltonian of the usual QKR. In this work, we will restrict ourselves to a period \(N=3\) phase shift (\(a_{n+N}=a_n\)). We only consider phase shifts such that the Hamiltonian is time-reversal invariant, e.g. \(a_1=-a_3\) and \(a_2=0\), see [27, 42] for details. This insures that our phase-shifted QKR belongs to the same (orthogonal) universality class as the ‘standard’ QKR.
The following experiments are performed by kicking a laser-cooled Cs atomic cloud (temperature \(T\simeq 2 \mu \)K) using a far-detuned, pulsed optical Standing Wave (SW), with a period \(T_1\). The SW is created by two independent laser beams, which allows us to control the amplitude and phase of the potential, using the RF signals driving two different acousto-optic modulators. We can thus shape the phase shift sequence \(a_n\) at will, and generate the Hamiltonian of Eq. (10). The laser parameters are as follows: the detuning \(\Delta = - 2\pi \times 13\) GHz (at the Cs D2 line, wavelength \(\lambda =2\pi /k_L= 852.2\) nm), 1/e radius \(w_0 = 800\,\upmu \)m, and the maximum intensity \(I = 30\,\textrm{W}/\text {cm}^{2}\) for each beam. The pulse duration is \(\tau = 200\) ns, while \(T_1=9.6\,\upmu \textrm{s}\). From these parameters, we get  as well as kick amplitudes
as well as kick amplitudes  up to 6 (where \(I_\textrm{sat}\simeq 2.71\,\mathrm{mW/cm}^{2}\) is the saturation intensity and \(\Gamma =2\pi \times 5.22\) MHz the natural linewidth of the transition). After the desired number of kicks, the cloud expands and the momentum probability density \(\Pi (p)=|\Psi (p)|^2 \) is measured using a time-of-flight technique.
up to 6 (where \(I_\textrm{sat}\simeq 2.71\,\mathrm{mW/cm}^{2}\) is the saturation intensity and \(\Gamma =2\pi \times 5.22\) MHz the natural linewidth of the transition). After the desired number of kicks, the cloud expands and the momentum probability density \(\Pi (p)=|\Psi (p)|^2 \) is measured using a time-of-flight technique.
To realize an accurate analysis of the shape of the final (dynamically-localized) momentum distribution, a careful characterization of the initial state, obtained after the laser cooling stages, is required. Indeed, to perform a meaningful comparison with the theoretical prediction, the initial distribution has to be measured and taken into account through a convolution with the Gogolin distribution. The initial momentum distribution obtained in our experiment is shown in Fig. 5 and is well-approximated with by a Lorentzian shape [47] \(D(p)\simeq \frac{2}{\pi \sigma } (1+p^2/\sigma ^2)^{-2}\), with  (see Appendix C for details).
(see Appendix C for details).
Experimental momentum distribution after 210 kicks (\(K=2.5\),  ) averaged over 100 samplings of triplets \(\{a_0,a_1,a_2\}\), and a Gogolin fit with
) averaged over 100 samplings of triplets \(\{a_0,a_1,a_2\}\), and a Gogolin fit with  ; b exponential fit with inverse decay rate
; b exponential fit with inverse decay rate  . Both fits are performed using the theoretical forms convolved with the initial state. The gray curve is the initial momentum distribution of the system
. Both fits are performed using the theoretical forms convolved with the initial state. The gray curve is the initial momentum distribution of the system
Starting from this initial state, we utilize the Hamiltonian in Eq. (10), with parameters \(K=2.5\) and  , and average over 100 realizations of the periodic phase sequences \(a_n\). The momentum distribution is measured after a time \(t=210\) kicks, and the results are shown in Fig. 5. We have experimentally verified that the distribution has reached a steady-state (see Appendix C, Fig. 8b), which proves that dynamical localization has been attained. In panel a), we fit the experimental distribution with a Gogolin distribution convolved with the initial distribution and find a very good agreement both near the center and in the wings, with
, and average over 100 realizations of the periodic phase sequences \(a_n\). The momentum distribution is measured after a time \(t=210\) kicks, and the results are shown in Fig. 5. We have experimentally verified that the distribution has reached a steady-state (see Appendix C, Fig. 8b), which proves that dynamical localization has been attained. In panel a), we fit the experimental distribution with a Gogolin distribution convolved with the initial distribution and find a very good agreement both near the center and in the wings, with  . The width of the final distribution, given by that of the Gogolin distribution \(\sqrt{8\zeta (3)} \xi \), is about four times larger than that of the initial distribution \(\sigma \). Therefore, the final distribution is dominated by the localization effects and not the initial state. In contrast, panel b) shows a fit of the same final experimental distribution, using an exponential function convolved with the initial state, with an inverse decay rate of
. The width of the final distribution, given by that of the Gogolin distribution \(\sqrt{8\zeta (3)} \xi \), is about four times larger than that of the initial distribution \(\sigma \). Therefore, the final distribution is dominated by the localization effects and not the initial state. In contrast, panel b) shows a fit of the same final experimental distribution, using an exponential function convolved with the initial state, with an inverse decay rate of  . The exponential shape does not describe well neither the center nor the wings of the experimental data. The ratio of the \(\chi ^2\) values corresponding to the two fits presented in Fig. 5 is \(\simeq 0.03\), which clearly proves that the experimental long-time momentum distribution is better described by a Gogolin distribution than by an exponential form.
. The exponential shape does not describe well neither the center nor the wings of the experimental data. The ratio of the \(\chi ^2\) values corresponding to the two fits presented in Fig. 5 is \(\simeq 0.03\), which clearly proves that the experimental long-time momentum distribution is better described by a Gogolin distribution than by an exponential form.
5 Conclusion
In this work, we have investigated the asymptotic properties of a wave packet localized by disorder and their connection to the statistics of the Floquet eigenstates of the QKR. Our numerical simulations were found to be in excellent agreement with the supersymmetric predictions. Using the versatility of the atomic quantum kicked rotor as a quantum simulator of disordered systems, we precisely measured the localized distribution and shown the excellent agreement with the Gogolin prediction.
One important prediction of the supersymmetric formalism is that the Gogolin shape of the localized distribution is preserved in the unitary symmetry class, when time-reversal symmetry is broken, though with a doubling of the localization length. In perspective, this universal feature could in principle be investigated experimentally by using kick sequences breaking time-reversal symmetry [27]. Finally, the detailed description of the dynamics, from weak to strong localization, could also be studied experimentally, though no analytical predictions have been devised yet. We leave these challenging problems for future works.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.]
Change history
06 December 2022
A Correction to this paper has been published: https://doi.org/10.1140/epjd/s10053-022-00564-7
References
P.W. Anderson, Absence of diffusion in certain random lattices. Phys. Rev. 109(5), 1492–1505 (1958). https://doi.org/10.1103/PhysRev.109.1492
E. Abrahams, P.W. Anderson, D.C. Licciardello, T.V. Ramakrishnan, Scaling theory of localization: absence of quantum diffusion in two dimensions. Phys. Rev. Lett. 42(10), 673–676 (1979). https://doi.org/10.1103/PhysRevLett.42.673
D.S. Wiersma, P. Bartolini, A. Lagendijk, R. Righini, Localization of light in a disordered medium. Nature (London) 390, 671–673 (1997). https://doi.org/10.1038/37757
T. Schwartz, G. Bartal, S. Fishman, M. Segev, Transport and Anderson localization in disordered two-dimensional photonic lattices. Nature (London) 446(7131), 52–55 (2015). https://doi.org/10.1038/nature05623
R. Dalichaouch, J.P. Armstrong, S. Schultz, P.M. Platzman, S.L. McCall, Microwave localization by two-dimensional random scattering. Nature 354(6348), 53–55 (1991)
A.A. Chabanov, M. Stoytchev, A.Z. Genack, Statistical signatures of photon localization. Nature 404(6780), 850–853 (2000)
P. van Loevezijn, R. Schlatmann, J. Verhoeven, B.A. van Tiggelen, E.M. Gullikson, Numerical and experimental study of disordered multilayers for broadband X-ray reflection. Appl. Opt. 35(19), 3614–3619 (1996). https://doi.org/10.1364/AO.35.003614
R.L. Weaver, Anderson localization of ultrasound. Wave Motion 12(2), 129–142 (1990). https://doi.org/10.1016/0165-2125(90)90034-2
E. Akkermans, G. Montambaux, Mesoscopic Physics of Electrons and Photons (Cambridge University Press, Cambridge, UK, 2011)
J. Billy, V. Josse, Z. Zuo, A. Bernard, B. Hambrecht, P. Lugan, D. Clément, L. Sanchez-Palencia, P. Bouyer, A. Aspect, Direct observation of Anderson localization of matter-waves in a controlled disorder. Nature (London) 453, 891–894 (2008). https://doi.org/10.1038/nature07000
J. Chabé, G. Lemarié, B. Grémaud, D. Delande, P. Szriftgiser, J.C. Garreau, Experimental observation of the Anderson metal-insulator transition with atomic matter waves. Phys. Rev. Lett. 101(25), 255702 (2008). https://doi.org/10.1103/PhysRevLett.101.255702
A.A. Gogolin, Electron density distribution for localized states in a one-dimensional disordered system. Soviet J. Exper. Theor. Phys. 44, 1003 (1976)
A.A. Gogolin, V.I. Mel’Nikov, É.I. Rashba, Conductivity in a disordered one-dimensional system induced by electron-phonon interaction. Soviet J. Exper. Theor. Phys. 42, 168 (1975)
K. Efetov, Supersymmetry in Disorder and Chaos (Cambridge University Press, Cambridge, UK, 1997)
K. Efetov, A. Larkin, Kinetics of a quantum particle in a long metallic wire. JETP 58(2), 764 (1983)
Y.V. Fyodorov, A.D. Mirlin, Scaling properties of localization in random band matrices: A -model approach. Phys. Rev. Lett. 67, 2405–2409 (1991). https://doi.org/10.1103/PhysRevLett.67.2405
A. Altland, M.R. Zirnbauer, Field theory of the quantum kicked rotor. Phys. Rev. Lett. 77, 4536–4539 (1996). https://doi.org/10.1103/PhysRevLett.77.4536
F.M. Izrailev, Simple models of quantum chaos: spectrum and eigenfunctions. Phys. Rep. 196, 299–392 (1990)
G. Casati, B.V. Chirikov, J. Ford, F.M. Izrailev, In: G. Casati and J. Ford (ed.) Stochastic behavior of a quantum pendulum under a periodic perturbation, vol. 93, pp. 334–352. Springer Berlin Heidelberg, Berlin, Germany (1979). https://doi.org/10.1007/BFb0021757
S. Fishman, D.R. Grempel, R.E. Prange, Chaos, quantum recurrences, and Anderson localization. Phys. Rev. Lett. 49(8), 509–512 (1982). https://doi.org/10.1103/PhysRevLett.49.509
J.-C. Garreau, Quantum simulation of disordered systems with cold atoms. Comptes Rendus Physique 18(1), 31–46 (2017). https://doi.org/10.1016/j.crhy.2016.09.002. Prizes of the French Academy of Sciences 2015 / Prix de l’Acad’emie des sciences 2015
F.L. Moore, J.C. Robinson, C.F. Bharucha, B. Sundaram, M.G. Raizen, Atom optics realization of the quantum \(\delta \)-Kicked rotor. Phys. Rev. Lett. 75(25), 4598–4601 (1995). https://doi.org/10.1103/PhysRevLett.75.4598
F.L. Moore, J.C. Robinson, C. Bharucha, P.E. Williams, M.G. Raizen, Observation of dynamical localization in atomic momentum transfer: a new testing ground for quantum Chaos. Phys. Rev. Lett. 73(22), 2974–2977 (1994). https://doi.org/10.1103/PhysRevLett.73.2974
I. Manai, J.-F. Clément, R. Chicireanu, C. Hainaut, J.C. Garreau, P. Szriftgiser, D. Delande, Experimental observation of two-dimensional Anderson localization with the atomic kicked Rotor. Phys. Rev. Lett. 115(24), 240603 (2015). https://doi.org/10.1103/PhysRevLett.115.240603
M. Lopez, J.-F. Clément, P. Szriftgiser, J.C. Garreau, D. Delande, Experimental test of universality of the Anderson transition. Phys. Rev. Lett. 108(9), 095701 (2012). https://doi.org/10.1103/PhysRevLett.108.095701
C. Hainaut, I. Manai, R. Chicireanu, J-Fmc. Clément, S. Zemmouri, J.C. Garreau, P. Szriftgiser, G. Lemarié, N. Cherroret, D. Delande, Return to the origin as a probe of atomic phase coherence. Phys. Rev. Lett. 118, 184101 (2017). https://doi.org/10.1103/PhysRevLett.118.184101. arXiv:1606.07237
C. Hainaut, I. Manai, J.-F. Clément, J.C. Garreau, P. Szriftgiser, G. Lemarié, N. Cherroret, D. Delande, R. Chicireanu, Controlling symmetry and localization with an artificial gauge field in a disordered quantum system. Nat. Commun. 9(1) (2018)
C. Hainaut, A. Rançon, J.-F. Clément, J.C. Garreau, P. Szriftgiser, R. Chicireanu, D. Delande, Ratchet effect in the quantum kicked rotor and its destruction by dynamical localization. Phys. Rev. A 97, 061601 (2018). https://doi.org/10.1103/PhysRevA.97.061601
C. Hainaut, P. Fang, A. Rançon, J.-F. Clément, P. Szriftgiser, J.-C. Garreau, C. Tian, R. Chicireanu, Experimental observation of a time-driven phase transition in quantum chaos. Phys. Rev. Lett. 121, 134101 (2018). https://doi.org/10.1103/PhysRevLett.121.134101
D.R. Grempel, R.E. Prange, S. Fishman, Quantum dynamics of a nonintegrable system. Phys. Rev. A 29(4), 1639–1647 (1984). https://doi.org/10.1103/PhysRevA.29.1639
D.L. Shepelyansky, Localization of quasienergy eigenfunctions in action space. Phys. Rev. Lett. 56(7), 677–680 (1986). https://doi.org/10.1103/PhysRevLett.56.677
E.P. Wigner, Characteristic vectors of bordered matrices with infinite dimensions. Ann. Math. 62(3), 548–564 (1955)
M.L. Mehta, Random Matrices (Elsevier, Amsterdam, 2004). https://doi.org/10.1016/C2009-0-22297-5
A.D. Mirlin, Statistics of energy levels and eigenfunctions in disordered systems. Phys. Rep. 326(5), 259–382 (2000). https://doi.org/10.1016/S0370-1573(99)00091-5
Y. Fyodorov, A. Mirlin, Distribution of exponential decay rates of localized eigenfunctions in finite quasi-1d disordered systems. Soc. J. Exper. Theor. Phys. Lett. 58, 636 (1993)
G. Casati, I. Guarneri, F. Izrailev, R. Scharf, Scaling behavior of localization in quantum chaos. Phys. Rev. Lett. 64, 5–8 (1990). https://doi.org/10.1103/PhysRevLett.64.5
T. Dittrich, U. Smilansky, Spectral properties of systems with dynamical localization. i. the local spectrum. Nonlinearity 4(1), 59–84 (1991). https://doi.org/10.1088/0951-7715/4/1/006
F.M. Izrailev, Scaling properties of spectra and eigenfunctions for quantum dynamical and disordered systems. Chaos, Solitons & Fractals 5(7), 1219–1234 (1995). https://doi.org/10.1016/0960-0779(94)E0063-U. Quantum Chaos: Present and Future
D.L. Shepelyansky, Localization of diffusive excitation in multi-level systems. Physica D 28(1–2), 103–114 (1987). https://doi.org/10.1016/0167-2789(87)90123-0
A.B. Rechester, M.N. Rosenbluth, R.B. White, Fourier-space paths applied to the calculation of diffusion for the Chirikov–Taylor model. Phys. Rev. A 23(5), 2664–2672 (1981). https://doi.org/10.1103/PhysRevA.23.2664
A.B. Rechester, R.B. White, Calculation of turbulent diffusion for the Chirikov–Taylor model. Phys. Rev. Lett. 44, 1586–1589 (1980). https://doi.org/10.1103/PhysRevLett.44.1586
C. Hainaut, A. Rançon, J.-F. Clément, I. Manai, P. Szriftgiser, D. Delande, J.C. Garreau, R. Chicireanu, Experimental realization of an ideal floquet disordered system. New J. Phys. 21(3), 035008 (2019). https://doi.org/10.1088/1367-2630/ab0a79
Y.V. Fyodorov, A.D. Mirlin, Level-to-level fluctuations of the inverse participation ratio in finite quasi 1d disordered systems. Phys. Rev. Lett. 71, 412–415 (1993). https://doi.org/10.1103/PhysRevLett.71.412
J.-L. Pichard, In: Kramer, B. (ed.) Random Transfer Matrix Theory and Conductance Fluctuations, pp. 369–400. Springer, Boston, MA (1991). https://doi.org/10.1007/978-1-4899-3698-1_24
G. Lemarié, J. Chabé, P. Szriftgiser, J.C. Garreau, B. Grémaud, D. Delande, Observation of the anderson metal-insulator transition with atomic matter waves: Theory and experiment. Phys. Rev. A 80, 043626 (2009). https://doi.org/10.1103/PhysRevA.80.043626
C. Tian, A. Kamenev, A. Larkin, Ehrenfest time in the weak dynamical localization. Phys. Rev. B 72(4), 045108 (2005). https://doi.org/10.1103/PhysRevB.72.045108
Y. Sortais, S. Bize, C. Nicolas, A. Clairon, C. Salomon, C. Williams, Cold collision frequency shifts in a \({}^{87}{\rm Rb}\) atomic fountain. Phys. Rev. Lett. 85, 3117–3120 (2000). https://doi.org/10.1103/PhysRevLett.85.3117
Acknowledgements
The authors thank Dominique Delande, Tony Prat, Nicolas Cherorret and Gabriel Lemarié for fruitful discussions. This work was supported by Agence Nationale de la Recherche (Grants K-BEC No. ANR-13-BS04-0001-01 and QRITiC I-SITE ULNE/ ANR-16-IDEX-0004 ULNE), the Labex CEMPI (Grant No. ANR-11-LABX-0007-01), Programme Investissements d Avenir under the program ANR-11-IDEX-0002-02, reference ANR-10-LABX-0037-NEXT, and the Ministry of Higher Education and Research, Hauts de France Council and European Regional Development Fund (ERDF) through the Contrat de Projets Etat-Region (CPER Photonics for Society, P4S).
Author information
Authors and Affiliations
Contributions
CH performed the experiment, under the supervision of RC, with the help of PS, JFC and JCG. CH and RC analyzed the experimental data. AR and RC performed the numerical simulations and their analysis. CH, RC and AR wrote a first version of the manuscript and all authors have contributed to the final version.
The datasets of this study are available from the corresponding author on reasonable request.
Corresponding author
Additional information
The original online version of this article was revised due to a retrospective Open Access order.
Appendices
Probability distribution of the Inverse Participation Ratio (IPR)
To complement the discussion of Sect. 3, we analyze here the probability distribution of the IPR. It has been thoroughly studied using supersymmetry, see [43]. The IPR of a given Floquet eigenstate \(\vert \phi _\omega \rangle \) (at a given q) is given by
Defining \(z=P_\omega /3\langle P_\omega \rangle \), its probability distribution is given by
The numerical analysis of the distribution of the IPR for the RKR, similar to that described in the main text, gives a very good agreement with the theoretical prediction, as shown in Fig. 6. Furthermore, the mean IPR \(\langle P_\omega \rangle \) is expected to be a function of \({\tilde{\xi }}\) only. This is verified numerically as shown in the inset.
Histogram of the IPR statistics, computed for the RKR with ( ). Red curve: theoretical probability distribution \({\mathcal {P}}(z)\), given by Eq. (12). The inset shows the inverse mean IPR \(\langle P_\omega \rangle ^{-1}\) as a function of \(\tilde{\xi }\) for the RKR (triangles). The line is a fit \(g({\tilde{\xi }})=a{\tilde{\xi }}+b\), with a slope \(a=1.253\) and \(b= 5.14\). The diamond corresponds to the same quantity, computed for the QKR (\(K=44\) and
). Red curve: theoretical probability distribution \({\mathcal {P}}(z)\), given by Eq. (12). The inset shows the inverse mean IPR \(\langle P_\omega \rangle ^{-1}\) as a function of \(\tilde{\xi }\) for the RKR (triangles). The line is a fit \(g({\tilde{\xi }})=a{\tilde{\xi }}+b\), with a slope \(a=1.253\) and \(b= 5.14\). The diamond corresponds to the same quantity, computed for the QKR (\(K=44\) and  ), see Appendix B
), see Appendix B
Statistics of eigenstates of the QKR
In this section, we show that the numerical results obtained in the main text for the RKR are also valid for the standard QKR for large  , i.e. in a regime where the correlations of the disorder are weak enough.
, i.e. in a regime where the correlations of the disorder are weak enough.
Figure 7a shows the statistical properties of the Floquet eigenstates computed for \(K=44\) and  . We observe that the distribution of \(-\ln {\tilde{r}}_\omega \) is well described by a Gaussian distribution. The corresponding ratio between the variance and the mean, obtained with a Gaussian fit (dashed red line), is \(R\simeq 1.94 \pm 0.1\), close to the expected value of 2 predicted by Eq. (7). Following the same procedure as in the RKR case (see Eq. (5)), we obtain an average localization length \({\tilde{\xi }}=39.6 \pm 3\). Furthermore, the long-time momentum distribution is given by the Gogolin distribution with \(\xi ={\tilde{\xi }}\), see Fig. 7b.
. We observe that the distribution of \(-\ln {\tilde{r}}_\omega \) is well described by a Gaussian distribution. The corresponding ratio between the variance and the mean, obtained with a Gaussian fit (dashed red line), is \(R\simeq 1.94 \pm 0.1\), close to the expected value of 2 predicted by Eq. (7). Following the same procedure as in the RKR case (see Eq. (5)), we obtain an average localization length \({\tilde{\xi }}=39.6 \pm 3\). Furthermore, the long-time momentum distribution is given by the Gogolin distribution with \(\xi ={\tilde{\xi }}\), see Fig. 7b.
Finally, the IPR probability distribution of the QKR, shown in Fig. 7c, is in very good agreement with Eq. (12). The relation between the IPR mean value and \({\tilde{\xi }}\) also agrees with the RKR results (see Appendix A, and the diamond data point in the inset of Fig. 6).
a Histogram of the probability distribution of \(- \ln {\tilde{r}}_\omega \), computed for the QKR with \(K=44\) and  , and \(L/{\tilde{\xi }}\simeq 35\). The distribution is well fitted by a Gaussian function (dashed red line). The extrapolation given by Eq. (5) yields \({\tilde{\xi }}=39.6\pm 3\). b Corresponding momentum distributions of the QKR, at long times, compared to the Gogolin distribution with \(\xi =39.6\). c Histogram of the IPR statistics, computed for \(K=44\) and
, and \(L/{\tilde{\xi }}\simeq 35\). The distribution is well fitted by a Gaussian function (dashed red line). The extrapolation given by Eq. (5) yields \({\tilde{\xi }}=39.6\pm 3\). b Corresponding momentum distributions of the QKR, at long times, compared to the Gogolin distribution with \(\xi =39.6\). c Histogram of the IPR statistics, computed for \(K=44\) and  , compared to the analytical prediction of Eq. (12) (red line)
, compared to the analytical prediction of Eq. (12) (red line)
Experimental initial and final momentum distributions
In the experiment, we produce a relatively cold Cs cloud (optical molasses, \(T\simeq 2\,\upmu \textrm{K}\)). As shown in Ref. [47], this implies that the shape of the momentum distribution differs slightly from a usual Gaussian form. Indeed, when operated near the lower end of the temperature range, the optical molasses momentum distribution displays more weight into its tails and can be accurately described by a Lorentzian distribution \(D(p)=p_0 (1+(p-p_1)^2/p_2^2)^{-p_3}\) [47]. We use this functional form, with \(p_0\), \(p_1\), \(p_2\) and \(p_3\) as free parameters, to fit the measured momentum distribution of the molasses. As shown in Fig. 8a, the data are well described by the red dashed-curve corresponding to such distribution. On the other hand, a Gaussian fit (blue dashed curve) clearly shows a significant discrepancy, as it especially underestimates the wings of the initial state distribution.
Figure 8b presents two experimental distributions measured at long times for the parameters mentioned in Sect. 4. The two distributions have barely evolved, showing that the system is indeed deep in the localized regime.
a Comparison between the initial experimental momentum distribution (full line) with two different fit forms. The fit parameters obtained for the form \(D(p)=p_0(1+(p-p_1)^2/p_2^2)^{-p_3}\) are  ,
,  ,
,  and \(p_3=1.946\) (dashed red line). The Gaussian fit gives a standard deviation of
and \(p_3=1.946\) (dashed red line). The Gaussian fit gives a standard deviation of  (dotted-dashed blue line). b Experimental momentum distributions, measured at \(t=150\) (green) and \(t=210\) kicks (red), showing that the asymptotic stationary state has been reached at these times
(dotted-dashed blue line). b Experimental momentum distributions, measured at \(t=150\) (green) and \(t=210\) kicks (red), showing that the asymptotic stationary state has been reached at these times
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hainaut, C., Clément, JF., Szriftgiser, P. et al. Localization properties of the asymptotic density distribution of a one-dimensional disordered system. Eur. Phys. J. D 76, 103 (2022). https://doi.org/10.1140/epjd/s10053-022-00426-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-022-00426-2


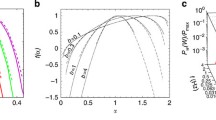


 . b Same distributions as in (a), recentered around
. b Same distributions as in (a), recentered around 





