1 Introduction

The flavor changing neutral current (FCNC) processes involving the quark-level transition \(b \rightarrow s\) are facilitated in the standard model (SM) only via quantum loop effects which are suppressed by the Glashow-Iliopoulos-Maiani mechanism [1]. Theoretical and experimental studies in this regard have thoroughly explored various avenues, such as the rare mesonic decays \(B \rightarrow K^{(*)} \, \ell ^+ \, \ell ^-\), \(B \rightarrow K^{(*)} \, \nu _\ell \, \overline{\nu }_\ell \), \(B_s \rightarrow \mu ^+ \, \mu ^-\), \(B_s \rightarrow \phi \, \ell ^+ \, \ell ^-\) with \(\ell =e,\mu ,\tau \) (for example, see [2] and [3] along with the references therein) as well as the baryonic decay \(\Lambda _b \rightarrow \Lambda \, \mu ^+ \, \mu ^-\) [4, 5]. These studies are focused on finding any deviations from the SM predictions as a way to study different new physics (NP) possibilities, which can contribute either in loops or even at the tree-level [6, 7]. In model-independent analyses these NP contributions are usually parameterized in terms of various effective operators. Experimentally, mesonic decays involving pair of charged leptons (\(\ell ^+ \, \ell ^-\)) in the final state are easier to study. However, these decays also involve contributions due to photon exchange, a feature which breaks factorization and leads to significant hadronic uncertainties beyond form factors. In addition, the presence of intermediate hadronic resonances such as \(J/\psi \), \(\psi (2\,S),\) etc., also affect the study of such processes [8]. However, in the case of \(B \rightarrow K \, \nu \, \overline{\nu }\), the only hadronic uncertainties come from form factors with no extra intermediate resonance effects. The \(B \rightarrow K\) form factors are obtained from studies involving various non-perturbative methods such as lattice QCD and light-cone sum rules (LCSR). In the SM the branching ratio of the decay \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) is predicted to be [9],

$$\begin{aligned} \text {Br}\left( B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\right) _{\text {SM}} = \left( 4.97 \pm 0.37\right) \times 10^{-6}, \end{aligned}$$
(1.1)

from loop contributions alone. For this decay there is a possible tree-level background contribution in the SM arising from the sequential decay \(B^+ \rightarrow \tau ^+ \left( \rightarrow K^+ \, \overline{\nu }_\tau \right) \, \nu _\tau \) [10] which involves doubly-charged-current interaction. According to [9], the branching ratio for this long-distance contribution is,

$$\begin{aligned} & \text {Br}\left( B^+ \rightarrow \tau ^+ \, \nu _\tau \rightarrow K^+ \, \nu _\tau \, \overline{\nu }_\tau \right) _{\text {SM}}\nonumber \\ & \qquad = \left( 0.61 \pm 0.06\right) \times 10^{-6}, \end{aligned}$$
(1.2)

which is roughly ten percent of the SM loop-induced branching ratio. Despite the apparent theoretical advantages in \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\), the presence of a pair of invisible (unreconstructed) neutrinos in the final state offers a formidable experimental challenge to observe this process and distinguish it from various possible background processes.

Notwithstanding the various experimental difficulties, the Belle-II collaboration has recently reported [9] the first evidence for experimental observation of \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) and reported its measured branching ratio to be

$$\begin{aligned} \text {Br}(B^+ \rightarrow K^+ \, \nu \, \overline{\nu })_{\text {Belle-II}} = \left( 2.3 \pm 0.7\right) \times 10^{-5}, \end{aligned}$$
(1.3)

which is \(2.57\sigma \) bigger than the SM expectation from FCNC. The SM allowed tree-level contribution is not large enough to account for this deviation. However, considering the low significance of the reported discrepancy, one can at best consider this as a tentative hint for existence of different NP possibilities [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Nevertheless, we are interested in estimating the contributions from all generic NP possibilities allowed by the current measurement. We conduct a model-independent analysis, starting from the effective Lagrangian, considering vector, scalar, and tensor NP interactions. Moreover, we also study how the new physics contributions vary based on whether the final state neutrinos are Dirac or Majorana. Drawing from the analyses of [34,35,36], we rely on a fundamental aspect of quantum statistics: if the two final state neutrinos are Majorana particles, they are indistinguishable from each other. Consequently, the decay amplitude for Majorana case must be anti-symmetric with respect to the exchange of the two neutrinos, resulting in a different decay width compared to the Dirac case, in presence of NP. Taking one type of NP interaction at a time (scalar, vector or tensor), we put constraints on the relevant NP parameters for both Majorana and Dirac neutrino possibilities, from the experimentally observed value of the \(\text {Br}(B^+ \rightarrow K^+ \, \nu \, \overline{\nu })\).

Before we proceed to our NP analysis in the decay \(B \rightarrow K \nu \overline{\nu }\), we would like to emphasize that our proposed method of using quantum statistics is quite different from proposals that search for signatures of lepton number violation (LNV). A summary review of signatures and tests for Majorana nature of neutrinos using LNV in rare B and K decays can be found in Ref. [37]. It should be noted that Majorana neutrinos can also lead to lepton number conservation just like Dirac neutrinos, and the LNV signals are usually suppressed by powers of neutrino mass. This makes our suggestion of utilizing quantum statistics a useful alternative to the traditional LNV studies.

We would also like to clarify that in principle one might consider neutrino and antineutrino of different flavors in the final state (i.e. consider \(B \rightarrow K \nu _\ell \overline{\nu }_{\ell '}\) with \(\ell \ne \ell '\)). Such lepton flavor violating decays are experimentally impossible to distinguish and isolate from decays having final neutrino and antineutrino of the same flavor (i.e. \(B \rightarrow K \nu _\ell \overline{\nu }_{\ell }\)), since in both cases the neutrino and antineutrino remain undetected in the detector surrounding the place where the decays take place. We assume that the experimentally observed decays are as expected in the SM. In the SM allowed weak interaction lepton flavor is conservedFootnote 1 and is universal. Therefore, in our model-independent analysis we focus on lepton flavor conserving \(B \rightarrow K \nu _\ell \overline{\nu }_{\ell }\) decays, and explore any possible NP effects in this specific context. Considering lepton flavor conservation and lepton flavor universality helps us to write down a minimal set of operators that essentially leads to all possible variations in experimental observables which would be of interest in future experimental studies of the \(B \rightarrow K \nu \overline{\nu }\) decays. Finally we note that sticking to lepton flavor conservation, i.e. working with a neutrino-antineutrino pair of the same flavor in the final state, is required to implement antisymmetrization of the final state for Majorana nature of neutrino when needed. In future when more experimental data get accessible, one can extend our current approach by including lepton flavor violation and lepton flavor non-universality as well.

Our paper is organized as follows. In Sect. 2 we introduce the set of generic new physics operators which can contribute to \(B \rightarrow K \, \nu \, \overline{\nu }\). Then in Sect. 3 we provide a set of very simple analytical expressions which relate the various form factors in \(B \rightarrow K\) transition. Certainly the \(B \rightarrow K\) form factors do play an important role here. In our study, we use the analytical relations among the form factors which fit the \(B \rightarrow K\) lattice QCD results, as mentioned in [38]. Using these analytical relations, we study the signatures of new physics in Sect. 4 more efficiently. Finally we conclude in Sect. 5 highlighting all the important findings of our study.

2 Generic new physics possibilities in effective Lagrangian for \(\varvec{B \rightarrow K \, \nu \, \overline{\nu }}\)

Considering all the new physics possibilities, the full effective Lagrangian facilitating the decay \(B \rightarrow K \, \nu _\ell \, \overline{\nu }_\ell \) is given by,

$$\begin{aligned} {\mathscr {L}}_{\text {NP+SM}}^{b \rightarrow s \nu \overline{\nu }} = \frac{4 \, G_F}{\sqrt{2}} \, \frac{\alpha _{\text {EM}}}{4\pi } \, \lambda _t \, \sum _{\begin{array}{c} {\ell =e,\mu ,\tau }\\ {Y=S,V,T}\\ {X=L,R} \end{array}} \, \left( C_X^Y\right) ^{\ell } \, \left( {\mathcal {O}}_X^Y\right) ^{\ell } + \text {h.c.},\nonumber \\ \end{aligned}$$
(2.1)

where \(G_F\) is the Fermi constant, \(\alpha _{\text {EM}}\) is the electromagnetic fine-structure constant, \(\alpha _{\text {EM}}= e^2/(4\pi )\) with e being the electric charge of electron,

$$\begin{aligned} \lambda _t = V_{tb} \, V_{ts}^* = -0.0398 \pm 0.0008, \end{aligned}$$
(2.2)

with V being the CKM matrix, \(\left( C_X^Y\right) ^{\ell }\) denote the Wilson coefficients and the corresponding operators \(\left( {\mathcal {O}}_X^Y\right) ^{\ell }\) are given by,

$$\begin{aligned} \left( {\mathcal {O}}_L^V \right) ^\ell&= \left( \overline{s} \, \gamma ^\mu \, b \right) \, \left( \overline{\nu }_\ell \, \gamma _\mu \, P_L \, \nu _\ell \right) , \end{aligned}$$
(2.3a)
$$\begin{aligned} \left( {\mathcal {O}}_R^V \right) ^\ell&= \left( \overline{s} \, \gamma ^\mu \, b \right) \, \left( \overline{\nu }_\ell \, \gamma _\mu \, P_R \, \nu _\ell \right) , \end{aligned}$$
(2.3b)
$$\begin{aligned} \left( {\mathcal {O}}_L^S \right) ^\ell&= \left( \overline{s} \, b \right) \, \left( \overline{\nu }_\ell \, P_L \, \nu _\ell \right) , \end{aligned}$$
(2.3c)
$$\begin{aligned} \left( {\mathcal {O}}_R^S \right) ^\ell&= \left( \overline{s} \, b \right) \, \left( \overline{\nu }_\ell \, P_R \, \nu _\ell \right) , \end{aligned}$$
(2.3d)
$$\begin{aligned} \left( {\mathcal {O}}_L^T \right) ^\ell&= \left( \overline{s} \, \sigma ^{\mu \nu } \, b \right) \, \left( \overline{\nu }_\ell \, \sigma _{\mu \nu } \, P_L \, \nu _\ell \right) , \end{aligned}$$
(2.3e)
$$\begin{aligned} \left( {\mathcal {O}}_R^T \right) ^\ell&= \left( \overline{s} \, \sigma ^{\mu \nu } \, b \right) \, \left( \overline{\nu }_\ell \, \sigma _{\mu \nu } \, P_R \, \nu _\ell \right) , \end{aligned}$$
(2.3f)

with \(P_L = \frac{1}{2} \, \left( 1-\gamma ^5 \right) \) and \(P_R = \frac{1}{2} \, \left( 1+\gamma ^5 \right) \) being the left-chiral and right-chiral projection operators, respectively. We have not imposed any constraints for Majorana nature of neutrinos in Eq. (2.1). We will do so later when we compare the effects from Dirac and Majorana nature of neutrinos. It should be noted that in the SM, we have lepton flavor universality and

$$\begin{aligned} \begin{aligned} \left( C_L^V\right) ^e_{\text {SM}}&= \left( C_L^V\right) ^\mu _{\text {SM}} = \left( C_L^V\right) ^\tau _{\text {SM}} = \dfrac{-X_t}{\sin ^2\theta _W},\\ \left( C_R^V\right) ^\ell _{\text {SM}}&= 0, \left( C_X^S\right) ^\ell _{\text {SM}} = \left( C_X^T\right) ^\ell _{\text {SM}} = 0, \end{aligned} \end{aligned}$$
(2.4)

for \(X=L,R\) and \(X_t = 1.469 \pm 0.017 \pm 0.002\) which includes the NLO QCD corrections [39,40,41] as well as 2-loop electroweak contributions [42]. Later when we consider NP effects, we assume that the Wilson coefficients \(\left( C_X^Y\right) ^\ell \) deviate from the SM values by a non-zero but small amount. For simplicity, in this work we assume that NP also respects lepton flavor universality. Then, the Wilson coefficients can be simply denoted without the superscript \(\ell \), i.e.

$$\begin{aligned} \left( C_X^Y\right) ^e = \left( C_X^Y\right) ^\mu = \left( C_X^Y\right) ^\tau \equiv C_X^Y. \end{aligned}$$
(2.5)

Therefore, the lepton or neutrino flavor universal effective Lagrangian is given by,

$$\begin{aligned} {\mathscr {L}}_{\text {NP+SM}}^{b \rightarrow s \nu \overline{\nu }} = \frac{4 \, G_F}{\sqrt{2}} \, \frac{\alpha _{\text {EM}}}{4\pi } \, \lambda _t \, \sum _{\begin{array}{c} {\ell =e,\mu ,\tau }\\ {Y=S,V,T}\\ {X=L,R} \end{array}} \, C_X^Y \, \left( {\mathcal {O}}_X^Y\right) ^{\ell } + \text {h.c.}\,.\nonumber \\ \end{aligned}$$
(2.6)

Note that in writing the operators \(\left( {\mathcal {O}}_X^Y\right) ^{\ell }\) as expressed in Eq. (2.3), we have already taken into consideration the fact that the quark-level currents should preserve parity since both B and K are pseudo-scalar mesons. In this work, we do not consider any specific NP model in particular (e.g. see Refs. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31, 33, 43] and references therein for specific NP model considerations). While going from the quark-level effective Lagrangian of Eq. (2.6) to the decay amplitude at the meson level for \(B \rightarrow K \, \nu _\ell \, \overline{\nu }_\ell \), one usually encounters three different form factors which are evaluated by taking non-perturbative QCD effects into consideration. These form factors are functions of the momentum transfer-squared which is the only available dynamic scalar quantity in this case. We introduce the three form factors as well as analytical relations among them in the following section.

3 The \(\varvec{B \rightarrow K}\) form factors and relations among them

The three dimensionless and real form factors one encounters in the \(B \rightarrow K\) semi-leptonic decays are the scalar form factor \(f_0 (q^2)\), the vector form factor \(f_+ (q^2)\) and the tensor form factor \(f_T (q^2)\), which are defined by the following hadronic matrix elements,

$$\begin{aligned}&\big \langle \overline{K}(p_K) \big |\overline{s} \, b \big |\overline{B}(p_B) \big \rangle = \left( \dfrac{m_B^2 - m_K^2}{m_b - m_s}\right) \, f_0 (q^2), \end{aligned}$$
(3.1a)
$$\begin{aligned}&\big \langle \overline{K}(p_K) \big |\overline{s} \, \gamma ^\mu \, b \big |\overline{B}(p_B) \big \rangle = p^\mu \, f_+ (q^2) \nonumber \\&\quad - \left( \frac{m_B^2 - m_K^2}{q^2}\right) \, q^\mu \, \left( f_+ (q^2) - f_0 (q^2) \right) , \end{aligned}$$
(3.1b)
$$\begin{aligned}&\big \langle \overline{K}(p_K) \big |\overline{s} \, \sigma ^{\mu \nu } \, b \big |\overline{B}(p_B) \big \rangle = i \, \left( \frac{p^\mu \, q^\nu - q^\mu \, p^\nu }{m_B + m_K}\right) \, f_T(q^2), \end{aligned}$$
(3.1c)

where \(p_B\), \(p_K\) denote the 4-momenta of B and K mesons respectively, with \(p = p_B+ p_K\) and \(q= p_B - p_K\) being the two independent 4-momenta combinations, \(m_B\), \(m_K\) denote the masses of B and K mesons, and \(m_b\), \(m_s\) denote the masses of b and s quarks respectively.

Fig. 1
figure 1

The form factor relations of Eqs. (3.2) and (3.3) give excellent numerical fit to the lattice QCD form factors as predicted by HPQCD [10] for \(B \rightarrow K\) transition. The colored bands correspond to \(1\sigma \) errors on the form factor ratios and are estimated by quadrature from HPQCD form factor predictions

Full size image

In the literature there exist various theoretical approaches such as constituent quark model, heavy-quark effective theory, large energy effective theory, light cone sum rules to analyze the form factors and relations among them. The \(B \rightarrow K\) form factors as predicted from lattice QCD by the HPQCD collaboration [10], have excellent numerical agreement (see Fig. 1) with the following form factors relations,

$$\begin{aligned} f_0(q^2) \approx \left( 1-\frac{q^2}{(m_B + m_K)^2}\right) \, f_+(q^2), \end{aligned}$$
(3.2)

and

$$\begin{aligned} f_T(q^2) \approx f_+(q^2). \end{aligned}$$
(3.3)

Such form factor relations can be found in the literature, e.g. in Refs. [44] and [45]. However, a more detailed discussion and comparison of these and other existing form factor relations are given in Ref. [38]. With Eqs. (3.2) and (3.3), one is left with only a single independent form factor instead of three. We choose \(f_+(q^2)\) to be the single independent form factor. This is helpful to formulate signature of NP in a manner where all hadronic uncertainties are encoded into just the single form factor \(f_+(q^2)\) for which the uncertainties are easily available from lattice QCD estimates. Since in this work we do not primarily focus on the form factors, we simply take both Eqs. (3.2) and (3.3) to be ‘empirically’ true as depicted in Fig. 1, and the theoretical considerations that go into analysing form factor relations can be found in Ref. [38]. Before proceeding to the details of the new physics signatures, we wish to point out that we have considered the form factors predicted by HPQCD in [10] which suggest the simple relations Eqs. (3.2) and (3.3). This allows us to do the full analysis using a single form factor. One might as well consider the form factor fits done in Ref. [46], which take into account FNAL/MILC results as well as the HPQCD results for large \(q^2\) region.

4 New physics signatures in missing mass-square distribution of \(\varvec{B \rightarrow K \, \nu \, \overline{\nu }}\)

Before delving into any further details on \(B \rightarrow K \, \nu \, \overline{\nu }\) we reiterate that we consider the final neutrinos to be of the same flavor with non-zero massFootnote 2 (\(m_\nu \ne 0\)) as already experimentally observed. Due to the fact that, by definition, a Majorana neutrino is quantum mechanically indistinguishable from its corresponding antineutrino, the decay amplitude for such a case ought to be anti-symmetric under the exchange of the two final neutrinos. Additionally, due to the fact that both the neutrinos in the final states can not be detected in the detector in the immediate vicinity of the decay event, there are only two final observables in \(B \rightarrow K \, \nu \, \overline{\nu }\): the missing mass-square distribution and the full partial branching ratio for the decay. In this section, we consider both of these observables and study the signatures of new physics in both of them.

4.1 Decay amplitudes

First considering the Dirac neutrino possibility, and assuming the 4-momentum of neutrino and the anti-neutrino to be \(p_1\) and \(p_2\) respectively, the decay amplitude for \(B \rightarrow K \, \nu \, \overline{\nu }\) is given by,

$$\begin{aligned}&{\mathscr {M}}^D = \frac{4 \, G_F}{\sqrt{2}} \, \frac{\alpha _{\text {EM}}}{4\pi } \, \lambda _t \nonumber \\&\quad \times \Bigg ( \left( p^\mu \, f_+ (q^2) - \left( \frac{m_B^2 - m_K^2}{q^2}\right) \, q^\mu \, \left( f_+ (q^2) - f_0 (q^2) \right) \right) \nonumber \\&\quad \times \left( C_L^V \, \left[ \overline{u}(p_1) \, \gamma _\mu \, P_L \, v(p_2)\right] + C_R^V \, \left[ \overline{u}(p_1) \, \gamma _\mu \, P_R \, v(p_2)\right] \right) \nonumber \\&\quad + \left( \left( m_B + m_K\right) \, f_0 (q^2) \, C_L^S - \left( \frac{2 \, \big (p \cdot \left( p_1 - p_2\right) \big )}{m_B + m_K}\right) \, f_T(q^2) \, C_L^T \right) \nonumber \\&\quad \times \left[ \overline{u}(p_1) \, P_L \, v(p_2) \right] \nonumber \\&\quad + \left( \left( m_B + m_K\right) \, f_0 (q^2) \, C_R^S - \left( \frac{2 \, \big (p \cdot \left( p_1 - p_2\right) \big )}{m_B + m_K}\right) \, f_T(q^2) \, C_R^T \right) \nonumber \\&\quad \times \left[ \overline{u}(p_1) \, P_R \, v(p_2) \right] \Bigg ), \end{aligned}$$
(4.1)

where we have made use of Gordon identities to get rid of the tensor and axial-tensor contributions, and have neglected all those terms which came out to be explicitly dependent on \(m_\nu \).

For the case of Majorana neutrinos, as mentioned before [35], the amplitude is anti-symmetric under exchange of the two final neutrinos, and is given by,

$$\begin{aligned}&{\mathscr {M}}^M = \frac{4 \, G_F}{2} \, \frac{\alpha _{\text {EM}}}{4\pi } \, \lambda _t \nonumber \\&\quad \times \Bigg ( \left( p^\mu \, f_+ (q^2) - \left( \frac{m_B^2 - m_K^2}{q^2}\right) \, q^\mu \, \left( f_+ (q^2) - f_0 (q^2) \right) \right) \nonumber \\&\quad \times \Big ( \left( C_L^V - C_R^V\right) \, \left[ \overline{u}(p_1) \, \gamma _\mu \, P_L \, v(p_2)\right] \nonumber \\&\quad + \left( C_R^V - C_L^V\right) \, \left[ \overline{u}(p_1) \, \gamma _\mu \, P_R \, v(p_2)\right] \Big ) \nonumber \\&\quad + 2 \, \left( m_B + m_K\right) \, f_0 (q^2) \, \Big ( C_L^S \, \left[ \overline{u}(p_1) \, P_L \, v(p_2) \right] \nonumber \\&\quad + C_R^S \, \left[ \overline{u}(p_1) \, P_R \, v(p_2) \right] \Big ) \Bigg ), \end{aligned}$$
(4.2)

where we have already introduced a factor \(1/\sqrt{2}\) which takes care of the statistical factor of 1/2 at the stage of decay rate. In Eq. (4.2), the exchange properties of Majorana bilinears have already been used for further simplification [47], which is also the reason for the absence of any contributions from the tensor interactions in Majorana case.

4.2 Missing mass-square distributions

Taking the modulus square of the amplitudes of Eqs. (4.1) and (4.2), neglecting all the terms that are explicitly dependent on \(m_\nu \) and doing the phase space integration, the differential decay rate for \(B \rightarrow K \, \nu \, \overline{\nu }\) in terms of the missing mass-square \(m_{\text {miss}}^2 \equiv q^2\) is given by,

$$\begin{aligned} \frac{\textrm{d}\Gamma ^{D/M}}{\textrm{d}q^2}&= \frac{G_F^2\,\alpha _{\text {EM}}^2 \, \big | \lambda _t \big |^2}{(2\,\pi )^5} \, \frac{\sqrt{\lambda (q^2,m_B^2,m_K^2)}}{64 \, m_B^3} \nonumber \\&\quad \times \left( T_0^{D/M} + \frac{1}{3} \, T_2^{D/M} \right) \, \sqrt{1-\frac{4\,m_\nu ^2}{q^2}}, \end{aligned}$$
(4.3)

where the various terms in the differential decay rate are,

$$\begin{aligned} T_0^D&= q^2 \, \left( m_B+m_K\right) ^2 \, \left( \left( C^S_L\right) ^2 + \left( C^S_R\right) ^2\right) \, f_0^2(q^2) \nonumber \\&\quad + \lambda (q^2,m_B^2,m_K^2) \, \left( \left( C^V_L\right) ^2 + \left( C^V_R\right) ^2\right) \, f_+^2(q^2), \end{aligned}$$
(4.4a)
$$\begin{aligned} T_2^D&= \lambda (q^2,m_B^2,m_K^2) \, \Bigg (\frac{4\,q^2\,\left( \left( C^T_L\right) ^2 + \left( C^T_R\right) ^2\right) \, f_T^2(q^2)}{\left( m_B + m_K\right) ^2} \nonumber \\&\quad - \left( \left( C^V_L\right) ^2 + \left( C^V_R\right) ^2\right) \, f_+^2(q^2) \Bigg ), \end{aligned}$$
(4.4b)
$$\begin{aligned} T_0^M&= 2 \, q^2 \, \left( m_B+m_K\right) ^2\,\left( \left( C^S_L\right) ^2 + \left( C^S_R\right) ^2\right) \, f_0^2(q^2) \nonumber \\&\quad + \lambda (q^2,m_B^2,m_K^2) \, \left( C^V_L - C^V_R\right) ^2 \, f_+^2(q^2), \end{aligned}$$
(4.4c)
$$\begin{aligned} T_2^M&= - \lambda (q^2,m_B^2,m_K^2) \, \left( C^V_L - C^V_R\right) ^2 \, f_+^2(q^2), \end{aligned}$$
(4.4d)

with the Källén function \(\lambda (x,y,z)\) being given by,

$$\begin{aligned} \lambda (x,y,z) = x^2 + y^2 + z^2 - 2\,\big (x\,y+y\,z+z\,x\big ). \end{aligned}$$
(4.5)

From Eq. (4.4) it is easy to infer that the presence of right-chiral vector NP and scalar NP can, in principle, contribute differently to Dirac and Majorana scenarios. As noted before, the tensor current interactions do not affect the Majorana case distribution.

4.2.1 Missing mass-square distribution in the SM

In the SM, we satisfy Eq. (2.4), which upon substitution into Eq. (4.3) clearly shows no observable difference between Dirac and Majorana neutrinos in \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) decay. Therefore, in the SM we have,

$$\begin{aligned} \frac{\textrm{d}\Gamma _\text {SM}}{\textrm{d}q^2}&\equiv \frac{\textrm{d}\Gamma ^{D}_\text {SM}}{\textrm{d}q^2} = \frac{\textrm{d}\Gamma ^{M}_\text {SM}}{\textrm{d}q^2} \nonumber \\&= \frac{G_F^2\,\alpha _{\text {EM}}^2 \, \big | \lambda _t \big |^2}{(2\,\pi )^5} \, \frac{\sqrt{\lambda (q^2,m_B^2,m_K^2)}}{64 \, m_B^3} \nonumber \\&\quad \times \left( \left( T_0\right) _{\text {SM}} + \frac{1}{3} \, \left( T_2\right) _{\text {SM}} \right) \, \sqrt{1-\frac{4\,m_\nu ^2}{q^2}} \, , \end{aligned}$$
(4.6)

where

$$\begin{aligned} \left( T_0\right) _{\text {SM}}&= \lambda (q^2,m_B^2,m_K^2) \, \left( C^V_L\right) _{\text {SM}}^2 \, f_+^2(q^2) \, , \end{aligned}$$
(4.7a)
$$\begin{aligned} \left( T_2\right) _{\text {SM}}&= - \lambda (q^2,m_B^2,m_K^2) \, \left( C^V_L\right) _{\text {SM}}^2 \, f_+^2(q^2) \equiv - \left( T_0\right) _{\text {SM}}. \end{aligned}$$
(4.7b)

Thus, the SM differential decay rate, or the missing mass-square distribution, is dependent on the vector form factor \(f_+(q^2)\) alone,

$$\begin{aligned} \frac{\textrm{d}\Gamma _\text {SM}}{\textrm{d}q^2} = {\textsf{C}} \, \frac{\left( \lambda (q^2,m_B^2,m_K^2)\right) ^{3/2}}{m_B^3} \, \sqrt{1-\frac{4\,m_\nu ^2}{q^2}} \, f_+^2(q^2), \end{aligned}$$
(4.8)

where \({\textsf{C}}\) is the constant factor given by,

$$\begin{aligned} {\textsf{C}} = \frac{G_F^2\,\alpha _{\text {EM}}^2 \, \big | \lambda _t \big |^2}{(2\,\pi )^5} \, \frac{\left( C^V_L\right) _{\text {SM}}^2}{96}. \end{aligned}$$
(4.9)

The \(q^2\) dependence in the SM can be seen from Fig. 2 which plots \(\dfrac{1}{{\textsf{C}}} \, \dfrac{\textrm{d}\Gamma _\text {SM}}{\textrm{d}q^2}\), where the cyan band corresponds to the \(1\sigma \) error in \(f_+(q^2)\) as predicted by the HPQCD collaboration [10].

Fig. 2
figure 2

The trend in the missing mass-square (\(q^2\)) distribution in the SM. The cyan colored band around the central red line corresponds to 1 standard deviation in the form factor \(f_+(q^2)\) taken from the prediction by the HPQCD collaboration [10]

Full size image

4.2.2 Missing mass-square distribution for generic NP possibilities with only one form factor

The Eq. (4.3) is the most general expression for the missing mass-square distribution for generic NP possibilities (i.e. it does not consider a specific UV complete NP model, and thus is model-independent from this perspective). However, as we have noted before we can relate the three form factors using Eqs. (3.2) and (3.3) and express the general missing mass-square distribution in terms of a single form factor, which we choose to be \(f_+(q^2)\), the same form factor which appears in the SM, see Eq. (4.8). Doing this, the expressions for \(T_{0,2}^D\) and \(T_0^M\) get modified to the following form,

$$\begin{aligned} T_0^D&= \Bigg [ \left( \left( C^S_L\right) ^2 + \left( C^S_R\right) ^2\right) \, \frac{q^2 \, \left( (m_B + m_K)^2 - q^2 \right) ^2}{(m_B + m_K)^2} \nonumber \\&\quad + \left( \left( C^V_L\right) ^2 + \left( C^V_R\right) ^2\right) \, \lambda (q^2,m_B^2,m_K^2) \Bigg ] \, f_+^2(q^2), \end{aligned}$$
(4.10a)
$$\begin{aligned} T_2^D&= \lambda (q^2,m_B^2,m_K^2) \, \Bigg (\frac{4\,q^2\,\left( \left( C^T_L\right) ^2 + \left( C^T_R\right) ^2\right) }{\left( m_B + m_K\right) ^2} \nonumber \\&\quad - \left( \left( C^V_L\right) ^2 + \left( C^V_R\right) ^2\right) \Bigg ) \, f_+^2(q^2), \end{aligned}$$
(4.10b)
$$\begin{aligned} T_0^M&= \Bigg [ \left( \left( C^S_L\right) ^2 + \left( C^S_R\right) ^2\right) \, \frac{2 \,q^2 \, \left( (m_B+m_K)^2 - q^2 \right) ^2}{(m_B+m_K)^2} \nonumber \\&\quad + \left( C^V_L - C^V_R\right) ^2 \, \lambda (q^2,m_B^2,m_K^2) \Bigg ] \, f_+^2(q^2), \end{aligned}$$
(4.10c)

The expression for \(T_2^M\) is already proportional to \(f_+^2(q^2)\) in Eq. (4.4d), so it remains unchanged.

Since the missing mass-square distribution for both the generic NP case and the SM case are both dependent on the same single form factor \(f_+(q^2)\), we can parameterize the effects of NP in a manner which does not depend on the hadronic uncertainties inherent in the form factors. Before doing that we introduce the following “effective \(\varepsilon \) parametrization” of NP (similar to the approach in [35]) which are agnostic to Dirac or Majorana nature of neutrino and only parameterize the small deviation from SM Wilson coefficient in terms of \(\left( C_L^V \right) _\text {SM}\), as explained before,

$$\begin{aligned} C^S_{L}&= \varepsilon ^S_{L} \, \left( C^V_L\right) _{\text {SM}}, \end{aligned}$$
(4.11a)
$$\begin{aligned} C^S_R&= \varepsilon ^S_R\, \left( C^V_L\right) _{\text {SM}}, \end{aligned}$$
(4.11b)
$$\begin{aligned} C^V_L&= \left( 1+ \varepsilon ^V_L\right) \, \left( C^V_L\right) _{\text {SM}}, \end{aligned}$$
(4.11c)
$$\begin{aligned} C^V_R&= \varepsilon ^V_R \, \left( C^V_L\right) _{\text {SM}}, \end{aligned}$$
(4.11d)
$$\begin{aligned} C^T_{L}&= \varepsilon ^T_{L} \, \left( C^V_L\right) _{\text {SM}}, \end{aligned}$$
(4.11e)
$$\begin{aligned} C^T_R&= \varepsilon ^T_R \, \left( C^V_L\right) _{\text {SM}}, \end{aligned}$$
(4.11f)

where all the \(\varepsilon _X^Y\)’s (for \(X=L,R\) and \(Y=S,V,T\)) are real but arbitrary constants (i.e. not dependent on \(q^2\) in any manner and arbitrary in absence of a specific UV complete NP model as done in our minimally extended model-independent approach). In terms of these \(\varepsilon \) parameters we can rewrite the generic missing mass-square distribution as follows,

$$\begin{aligned} \dfrac{\textrm{d}\Gamma ^D}{\textrm{d}q^2}&= \dfrac{\textrm{d}\Gamma _\text {SM}}{\textrm{d}q^2} \; \Bigg ( R^D_S(q^2) \, \left( \left( \varepsilon ^S_L\right) ^2 + \left( \varepsilon ^S_R\right) ^2 \right) \nonumber \\*&\quad + R^D_V(q^2) \, \left( \left( 1+\varepsilon ^V_L\right) ^2 + \left( \varepsilon ^V_R\right) ^2 \right) \nonumber \\*&\quad + R^D_T(q^2) \, \left( \left( \varepsilon ^T_L\right) ^2 + \left( \varepsilon ^T_R\right) ^2 \right) \Bigg ), \end{aligned}$$
(4.12a)
$$\begin{aligned} \dfrac{\textrm{d}\Gamma ^M}{\textrm{d}q^2}&= \dfrac{\textrm{d}\Gamma _\text {SM}}{\textrm{d}q^2} \; \Bigg ( R^M_S(q^2) \, \left( \left( \varepsilon ^S_L\right) ^2 + \left( \varepsilon ^S_R\right) ^2 \right) \nonumber \\&\quad + R^D_V(q^2) \, \left( \left( 1+\varepsilon ^V_L - \varepsilon ^V_R\right) ^2 \right) \Bigg ), \end{aligned}$$
(4.12b)

where the “NP weight factors” \(R^{D/M}_Y(q^2)\) are independent of form factor uncertainties (all relevant hadronic uncertainty is present only in \(f_+^2(q^2)\) which appears in the SM differential decay rate, as shown in Eq. (4.8)), and these are given by,

$$\begin{aligned} R^D_S(q^2)&= \frac{3 \, q^2 \, \left( (m_B + m_K)^2 - q^2\right) ^2}{2 \, \lambda (q^2,m_B^2,m_K^2) \, (m_B + m_K)^2} = \frac{1}{2} R^M_S(q^2), \end{aligned}$$
(4.13a)
$$\begin{aligned} R^D_V(q^2)&= 1 = R^M_V(q^2), \end{aligned}$$
(4.13b)
$$\begin{aligned} R^D_T(q^2)&= \frac{2\,q^2}{(m_B + m_K)^2}, \ \end{aligned}$$
(4.13c)
$$\begin{aligned} R^M_T(q^2)&= 0. \end{aligned}$$
(4.13d)
Fig. 3
figure 3

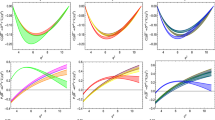
Comparison of \(q^2\) dependence of scalar, vector and tensor NP weight factors \(R_Y^{D/M}(q^2)\) for \(Y=S,V,T\), which appear in Eqs. (4.12a) and (4.12b), and as given in (4.13). Note that \(R_T^M(q^2) = 0\) is simply due to the fact that there is no allowed tensor interaction for our Majorana case

Full size image

Note that the contribution of scalar NP has similar \(q^2\) dependence in both Dirac and Majorana neutrino possibilities, but the effects are two times stronger in Majorana case than the Dirac case, see Eq. (4.13a) and Fig. 3. The scalar NP weight factor has a divergenceFootnote 3 at the kinematic end point as \(\lambda (q^2,m_B^2,m_K^2)\) present in denominator of Eq. (4.13a) vanishes at \(q^2=(m_B-m_K)^2\). The tensor NP contribution only affects the Dirac case, and the effect increases linearly with \(q^2\), see Fig. 3. The different \(q^2\) dependence of the various NP possibilities, suggests that one can distinguish them from one another if one can experimentally study the \(q^2\) distribution. This has been highlighted in Ref. [35], where for simplicity, the \(q^2\) dependencies of the form factors were not taken into consideration. However, our expressions Eqs. (4.12) and (4.13) take into account the form factor relations of Eqs. (3.2) and (3.3) which fit the lattice QCD form factor predictions very well, as shown in Fig. 1. We expect that after the recent observation of the rare decay \(B \rightarrow K \, \nu \, \overline{\nu }\), the experimental study of \(q^2\) distribution in this decay would also be available in future. This would be crucial to study new physics in a more precise manner.

It is also easy to see in Fig. 3 that the NP weight factors \(R_Y^{D/M}(q^2)\) (with \(Y=S,T\)) become greater than the SM weight factor \(R_V^{D/M} = 1\) in some regions of \(q^2\). As mentioned before, the \(\varepsilon \) parameters are constants which are not dependent on \(q^2\). Therefore, in context of our SM allowed decay, if one is interested in NP contributions to be smaller than the SM contribution for any value of \(q^2\), then the \(\varepsilon \) parameters must, in general, satisfy

$$\begin{aligned} -1< \varepsilon _X^Y < 1. \end{aligned}$$
(4.14)

Nonetheless, while comparing experimental measurement or data with the SM prediction to obtain an estimate of NP \(\varepsilon \)’s, one can relax Eq. (4.14). For clarity and convenience, we will use the terminology of “inner region” for \(\varepsilon \)’s satisfying Eq. (4.14) and “outer region” for values of \(\varepsilon \)’s beyond it. We reiterate that the \(\varepsilon \) parameters as defined in Eq. (4.11) are agnostic to the Dirac or Majorana natures of the neutrinos. Hence there are no a priori correlations over the \(\varepsilon \)’s when comparing Dirac and Majorana neutrino possibilities.

We note that, if one considers only vector NP contributions alone, then from Eqs. (4.12a) and (4.12b), it is straightforward to show that

$$\begin{aligned} \dfrac{\textrm{d}\Gamma ^D}{\textrm{d}q^2} - \dfrac{\textrm{d}\Gamma ^M}{\textrm{d}q^2}= & \dfrac{\textrm{d}\Gamma _\text {SM}}{\textrm{d}q^2} \; \left( 2\varepsilon _R^V \, \left( 1+\varepsilon _L^V\right) \right) , \;\nonumber \\ & \left( \text {considering only vector NP possibility}\right) \nonumber \\ \end{aligned}$$
(4.15)

which implies that for \(\varepsilon _R^V >0\) we get \(\dfrac{\textrm{d}\Gamma ^D}{\textrm{d}q^2} > \dfrac{\textrm{d}\Gamma ^M}{\textrm{d}q^2}\) in the whole inner region for \(\varepsilon _L^V\), i.e. \(-1 < \varepsilon _L^V \leqslant 1\). From Eq. (4.15) it is also clear that left-handed vector NP contribution alone would not lead to any difference between the Dirac and Majorana possibilities, one needs non-zero right-handed vector NP contribution for this purpose. In fact, the difference between Dirac and Majorana cases would also exist even if one considers only right-handed vector NP possibility, i.e. \(\varepsilon _R^V \ne 0\) and \(\varepsilon _L^V=0\).

Fig. 4
figure 4

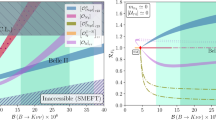
The parameter space of \(\varepsilon _L^V\) and \(\varepsilon _R^V\) constrained by the Belle-II measurement of the branching ratio of \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\). The SM point corresponding to \(\varepsilon _L^V = 0 = \varepsilon _R^V\) is shown by the ‘+’ symbol. The shaded regions correspond to the \(1\sigma \) band for the ratio \(\text {Br}(B^+ \rightarrow K^+ \, \nu \, \overline{\nu })_{\text {Belle~II}}/\text {Br}(B^+ \rightarrow K^+ \, \nu \, \overline{\nu })_{\text {SM}}\), with errors propagated by quadrature. Only for Majorana case the entire \(1\sigma \) region can be found in the inner region of the parameter space which is the interior of the red dashed square

Full size image
Fig. 5
figure 5

The parameter space of \(\varepsilon _L^S\) and \(\varepsilon _R^S\), as well as \(\varepsilon _L^T\) and \(\varepsilon _R^T\), constrained by the Belle II measurement of the branching ratio of \(B^+\rightarrow K^+ \, \nu \, \overline{\nu }\). The SM point corresponding to \(\varepsilon _L^V = 0 = \varepsilon _R^V\) is shown by the ‘+’ symbol. The shaded regions correspond to the \(1\sigma \) band for the ratio \(\text {Br}(B^+ \rightarrow K^+ \, \nu \, \overline{\nu })_{\text {Belle~II}}/\text {Br}(B^+ \rightarrow K^+ \, \nu \, \overline{\nu })_{\text {SM}}\), with errors propagated by quadrature. No tensor NP contribution is possible for Majorana neutrinos. The interior of the red dashed square shows the inner region of the parameter space for which NP contribution is expected to be smaller than the SM contribution

Full size image

As shown in Fig. 3 and as is clear from Eqs. (4.12) and (4.13b), the vector NP contributions do not yield any further \(q^2\) dependence than what is already present in the SM. Therefore, if we were to assume that in addition to SM only vector NP contributes to \(B \rightarrow K \, \nu _\ell \, \overline{\nu }_\ell \) (due to whatever reasons one might have, e.g. in a model with \(Z'\)), it is straightforward to note that,

$$\begin{aligned}&\dfrac{\text {Br}\left( B \rightarrow K \, \nu _\ell \, \overline{\nu }_\ell \right) _{\text {NP}+\text {SM}}}{\text {Br}\left( B \rightarrow K \, \nu _\ell \, \overline{\nu }_\ell \right) _{\text {SM}}} \nonumber \\&\quad = {\left\{ \begin{array}{ll} \left( 1+\varepsilon ^V_L\right) ^2 + \left( \varepsilon ^V_R\right) ^2, & \left( \text {for Dirac neutrinos} \right) \\ \left( 1+\varepsilon ^V_L-\varepsilon ^V_R\right) ^2. & \left( \text {for Majorana neutrinos} \right) \end{array}\right. } \end{aligned}$$
(4.16)

Interestingly, as we noted in introduction in Eqs. (1.1) and (1.3), the Belle-II measurement of the branching ratio of \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) is different from the SM prediction. Therefore, if we consider

$$\begin{aligned} \text {Br}\left( B \!\rightarrow \!K \, \nu _\ell \, \overline{\nu }_\ell \right) _{\text {NP}+\text {SM}} = \text {Br}\left( B \!\rightarrow \!K \, \nu _\ell \, \overline{\nu }_\ell \right) _{\text {Belle~II}}, \end{aligned}$$
(4.17)

and use Eq. (4.16) to estimate the possible contributions from vector NP possibility alone which can accommodate the observed discrepancy. The parameter space of \(\varepsilon ^V_L\) and \(\varepsilon ^V_R\) is scanned in the inner (\(-1 \leqslant \varepsilon ^V_{L,R} \leqslant 1\)) and outer (\(-1 > \varepsilon ^V_{L,R}\) or \(\varepsilon ^V_{L,R} > 1\)) regions in Fig. 4. As shown by the range of the color-bars, the constrained (shaded) regions correspond to the \(1\sigma \) range of the branching ratio as measured by the Belle-II collaboration. Clearly, for the Dirac neutrino hypothesis, no portion of the full \(1\sigma \) band of \(\text {Br}\left( B \rightarrow K \, \nu _\ell \, \overline{\nu }_\ell \right) \) is completely inside inner region, while for Majorana neutrino hypothesis we do find a part of the allowed \(1\sigma \) band to be fully inside the inner region, i.e. \({-}0.2< \varepsilon ^V_{L}< 1, ~ -1< \varepsilon ^V_{R} < 0.2\). At the current level of experimental precision, it might nevertheless be premature to conclude that the Majorana nature is more preferred than the Dirac nature. However, this would be an interesting feature to study in future, when a new improved measurement of the branching ratio of \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) gets reported.

If instead of vector NP contribution, we assume that the scalar or tensor NP contributions alone can account for the Belle-II observed branching ratio in Eq. (1.3), then considering either scalar or tensor NP contributions one at a time, we find that,

$$\begin{aligned} \left( \varepsilon ^S_L\right) ^2 + \left( \varepsilon ^S_R\right) ^2&= {\left\{ \begin{array}{ll} 8.14 \pm 3.25, & \text {(for Dirac neutrinos)}\\ 4.07 \pm 1.63, & \text {(for Majorana neutrinos)} \end{array}\right. } \end{aligned}$$
(4.18a)
$$\begin{aligned} \left( \varepsilon ^T_L\right) ^2 + \left( \varepsilon ^T_R\right) ^2&= 11.45 \pm 4.58 \quad \text {(only for Dirac neutrinos)}. \end{aligned}$$
(4.18b)

The allowed regions inside the parameter space of \(\varepsilon _L^S\) and \(\varepsilon _R^S\), as well as \(\varepsilon _L^T\) and \(\varepsilon _R^T\), are found to be fully in the outer region (i.e. \(-1 \leqslant \varepsilon ^{S,T}_{L,R} \leqslant 1\)), see Fig. 5. These suggest that one would require that the contributions from either scalar or tensor type NP interactions be necessarily larger than the SM contribution to account for the present branching ratio reported by the Belle II collaboration. It would be exciting for specific model-dependent NP searches, if any future measurements of the branching ratio of \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) show preference for scalar and/or tensor NP contributions. Rather than the branching ratio measurements, it is the missing mass-square (\(q^2\)) distribution which would be able to distinguish among the scalar, vector and tensor NP possibilities, as they have different \(q^2\) dependencies. Before we conclude, we would like to reiterate that our model-independent analysis and the results discussed above are strictly in context of both lepton flavor conservation and lepton flavor universality.

5 Conclusion

We have studied the prospects of generically probing NP in the \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) decay in light of the recent measurement of the branching ratio of this process by the Belle-II collaboration. We consider NP interactions involving generic scalar, vector and tensor type of interactions. The scalar form factor \(f_0(q^2)\), vector form factor \(f_+(q^2)\) and tensor form factor \(f_T(q^2)\) play very significant roles in calculating the decay width, since the hadronic uncertainties are majorly contributed by these, although other intermediate resonance effects might also be non-avoidable such as the effect of \(J/\psi \) in case of \(B \rightarrow K \, \ell ^+ \, \ell ^-\). We have utilized a set of simple analytical expressions which relate the \(B \rightarrow K\) form factors and these relations are highly in agreement with the predictions from the fully relativistic lattice QCD calculations reported by the HPQCD collaboration.

Using these form factor relations to our advantage we proceed to do a careful study of generic NP possibilities in the decay \(B \rightarrow K \, \nu \, \overline{\nu }\) in which no intermediate resonances such as \(J/\psi \) play any adverse role. We study the NP signatures for both the Dirac and Majorana neutrino hypotheses. Interestingly, if only vector NP contribution is assumed to be contributing to \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) (due to whatever fundamental reasons one might have in one’s favorite UV complete NP model, such as say a model with a \(Z'\)), then the recently reported measurement of branching ratio of \(B^+ \rightarrow K^+ \, \nu \, \overline{\nu }\) by the Belle-II collaboration shows that the Majorana neutrino can fully account for the entire \(1\sigma \) range of the experimental observation within the ‘inner region’, a generic domain of the NP parameters for which SM contribution is larger than the NP contribution. The Dirac neutrino hypothesis does not fully account for the observed branching ratio in the this inner region of parameter space. However, it remains to be seen if in future more precise branching ratio measurements would ever rule out the Dirac neutrino hypothesis. If one assumes the NP interactions to be either scalar or tensor type in nature, very large values of NP parameters are required to reconcile with the Belle-II measurement, for both Dirac and Majorana cases. More precise future measurements of branching ratio as well as missing-mass square distribution of \(B \rightarrow K \, \nu \, \overline{\nu }\) decay would help in exploration of various new physics possibilities in the context of Dirac or Majorana nature of the neutrinos.