Properties of the ground and excited states of triply heavy spin-1/2 baryons

Abstract

We study the triply heavy spin-1/2 baryons with quark contents ccb and bbc, and calculate their mass and residue using QCD sum rules. In the calculations, we consider the ground (1 S), first orbitally excited (1P) and first radially excited (2 S) states. Aiming to achieve higher accuracies in the results, we perform the computations by taking into account the non-perturbative operators up to eight mass dimensions. We compare our results with the predictions of other theoretical studies existing in the literature. The obtained results may help experimental groups in their search for these yet unseen, but previously predicted by the quark model, interesting particles.

1 Introduction

The investigation of baryons consist of heavy quarks has been one of the important directions of research in non-perturbative quantum chromodynamics (QCD). The prosperous quark model predicts the existence of three types of heavy baryons comprising single, double, or triple heavy quarks. The accessible literature predominantly focuses on the single heavy baryons. In the last couple of decades, the various experimental groups such as CDF, CLEO, BABAR, BELLE, BESIII and LHCb have discovered many ground and excited states of single heavy baryons like $\Lambda _{b(c)}$, $\Sigma _{b(c)}^{(*)}$, $\Xi _{b(c)}^{(*,\prime )}$ and $\Omega _{b(c)}^{(*)}$ listed in particle data group (PDG) summary tables [1]. The discovery of $\Xi _{cc}$, by the SELEX collaboration [2, 3] and its confirmation by LHCb [4, 5], marked a significant breakthrough in the pursuit of doubly heavy baryons. Thus far, none of the triply heavy baryons representing the last group of standard heavy baryons have been reported experimentally. Though they are in the focus of some experimental groups, compared to the single and doubly heavy baryons, there is less consideration dedicated to the identification of these states. Motivated by the opportunity of detecting triply heavy baryons in the experiment on the horizon, the various theoretical approaches are carried out on the properties of triply heavy baryons such as non-relativistic quark model [6,7,8,9,10,11,12], relativistic quark model [13,14,15,16], lattice QCD [17,18,19,20,21,22,23], the QCD sum rules [24,25,26,27,28], Bag model [29, 30], the Regge trajectories [31,32,33,34,35], Fadeev equation [36,37,38,39], Hyperspherical Harmonics method [40], various potential models [41,42,43,44,45,46,47,48], etc. Taking into consideration all the theoretical approaches that have been pointed so far, the QCD sum rule method is considered as one of the most powerful and predictive non-perturbative analytical tools in predicting the properties of heavy hadrons [49,50,51,52,53], and associated predictions are confirmed with the worldwide accelerator experiments for many of hadrons. So far, the theoretical analysis has desired to concentrate on the masses and residues of the ground state triply heavy baryons more than the excited states. On the other hand, the predicted masses have been mainly reported with higher uncertainties giving large mass range for each member. Consequently, more comparisons of theoretical predictions are required in the mass and residue spectra of triply heavy baryons, which stimulates us to calculate them not only in the ground but also in the orbitally and radially exited states; and both in pole and $\overline{MS}$ schemes for heavy quarks. With the aim of achieving higher accuracies in the calculations, we consider the non-perturbative operators up to eight mass dimensions. In light of this, the present manuscript is organized as follows: in Sect. 2, the formulation of the QCD sum rules was utilized to determine the masses and residues of the triply heavy 1 S, 1P and 2 S baryons. Section 3, is dedicated to our numerical analysis, along with a comparison to other theoretical predictions in the literature, and Sect. 4, pertains to a review and our conclusions. We move some lengthy expressions obtained from the calculations to the Appendix.

Table 1 The members of the triply heavy spin-1/2 baryons

2 Spectroscopic parameters of the triply heavy spin-1/2 baryons

The spectroscopic parameters, mass and residue, can be elicited via the QCD sum rule method [54,55,56]. To achieve these quantities, one must utilize an appropriate correlation function. In this regard, we use the following two-point correlation function:

$$\begin{aligned} \Pi (q)=i\int d^{4}xe^{iqx}\langle 0|\mathcal {T}\{\eta (x)\bar{\eta }(0)\}|0\rangle , \end{aligned}$$

(1)

where $\eta (x)$ is the interpolating current for the baryons subjected to evaluations, which is the mathematical demonstration of particles. The symbol $\mathcal {T}$ denotes the time ordering of two $\eta (x)$ and $\bar{\eta }(0)$ interpolating currents and q is the four-momentum of the relating triply heavy baryons. In the present work, the most general form of the interpolation current is considered:

$$\begin{aligned} \eta (x)= & {} 2\varepsilon ^{abc}\Big \{\Big (Q^{aT}(x)CQ^{'b}(x)\Big )\gamma _{5}Q^c(x)\nonumber \\{} & {} + \beta \Big (Q^{aT}(x)C\gamma _{5}Q^{'b}(x)\Big )Q^c (x)\Big \}, \end{aligned}$$

(2)

where Q and $Q^{'}$ illustrate the heavy quark b or c ($Q\ne Q^{'}$ for the triply heavy spin-1/2 baryons), a, b and c are color indices, C is the charge conjugation operator and $\beta$ is an arbitrary auxiliary parameter which for the Ioffe current is expressed as $\beta = -1$. We will fix the working region of $\beta$ when performing numerical analyses. The members of triply heavy spin-1/2 baryons anticipated by the quark model are seen in Table 1.

In the QCD sum rule approach, one initially has to determine the above correlation function in two distinctive sides: i) hadronic side, which is calculated by including the hadronic parameters in the time-like region. The obtained results of this procedure include the mass and residue of the states under investigation. ii) QCD side, which is calculated by including the quark and gluon degrees of freedom in the space-like region. Extracted results of this side contain the gluon condensates of various dimensions representing the interaction of gluons with QCD vacuum, QCD coupling constant, the masses of the quarks and other corresponding parameters. By relating the results of these two representations, via dispersion integrals and by using the quark-hadron duality assumption, one can calculate the masses and residues in terms of other parameters. We apply Borel transformation and continuum subtraction techniques to suppress the contributions of the higher states and continuum. The QCD sum rules for the physical quantities are obtained by matching the coefficients of the Lorentz structures entering the calculations.

The initial point to obtain the correlation function in terms of hadronic parameters is to insert relevant complete sets, which have the same quantum numbers as the interpolating current into the adequate locations. As we aim to consider first three resonances, we use the” ground state $+$ orbitally excited state $+$ radially excited state $+$ continuum” scheme. After fulfilling this duty and performing the integrals over four-x, we can write the hadronic or phenomenological representation of the correlation function as:

$$\begin{aligned} \Pi ^{\textrm{Had}}(q)= & {} \frac{\langle 0|\eta (0)|B_{QQQ^{'}}(q,s)\rangle \langle B_{QQQ^{'}}(q,s)|\bar{\eta }(0)|0\rangle }{m^2-q^2} \nonumber \\{} & {} +\frac{\langle 0|\eta (0)|\tilde{B}_{QQQ^{'}}(q,s)\rangle \langle \tilde{B}_{QQQ{'}}(q,s)|\bar{\eta }(0)|0\rangle }{\tilde{m}^2-q^2}\nonumber \\{} & {} +\frac{\langle 0|\eta (0)|B_{QQQ{'}}'(q,s)\rangle \langle B_{QQQ{'}}'(q,s)|\bar{\eta }(0)|0\rangle }{m'{}^2-q^2}\nonumber \\ {}{} & {} +\cdots . \end{aligned}$$

(3)

The $|B_{QQQ^{'}}(q,s)\rangle$, $|\tilde{B}_{QQQ^{'}}(q,s)\rangle$ and $|B_{QQQ^{'}}'(q,s)\rangle$ states are utilized to represent the various baryonic one-particle states: The ground (1S), the first orbital excitation (1P) and the first radial excitation (2S), respectively. Here, symbols m, $\tilde{m}$ and $m'$ are the corresponding masses and dots indicate an abbreviation of the contribution of the higher states and continuum. The matrix elements of the interpolating current between the vacuum and the baryonic states under study in Eq. (3) are determined as follows:

$$\begin{aligned} \langle 0|\eta (0)|B_{QQQ^{'}}(q,s)\rangle= & {} \lambda u(q,s),\nonumber \\ \langle 0|\eta (0)|\tilde{B}_{QQQ^{'}}(q,s)\rangle= & {} \tilde{\lambda }\gamma _5 \tilde{u}(q,s),\nonumber \\ \langle 0|\eta (0)|B_{QQQ^{'}}'(q,s)\rangle= & {} \lambda ' u'(q,s), \end{aligned}$$

(4)

where $\lambda$, $\tilde{\lambda }$ and $\lambda '$ are residues of the considered states; and u(q, s), $\tilde{u}(q,s)$ and $u'(q,s)$ represent the corresponding Dirac spinors with spin s, satisfying the following identity:

$$\begin{aligned} \sum _{s}u(q,s)\bar{u}(q,s)=(\not \!q+m). \end{aligned}$$

(5)

By inserting Eq. (4) into Eq. (3) and performing summations over the spins of $B_{QQQ^{'}}$, the hadronic representation of the correlation function in momentum-space is found:

$$\begin{aligned} \Pi ^{\textrm{Had}}(q){} & {} =\frac{\lambda ^2(\not \!q+m)}{m^2-q^2}+\frac{\tilde{\lambda }^2(\not \!q-\tilde{m})}{\tilde{m}^2-q^2}+\frac{\lambda '^2(\not \!q+m')}{m'{}^2-q^2}\nonumber \\ {}{} & {} +\cdots . \end{aligned}$$

(6)

Eventually, in order to unveil the final configuration of the hadronic correlation function, one uses the Borel transformation to elevate the contribution of the three first resonances and suppress the contributions of higher states and continuum. To this end, we apply

$$\begin{aligned} \Pi ^{\textrm{Had}}(M^2)=\lim _{{\mathop {Q^2/n=M^2}\limits ^{Q^2,n \rightarrow \infty }}} \frac{(-q^2)^{n}}{(n-1)!}\left( \frac{d}{dq^2}\right) ^{n-1} \Pi ^{\textrm{Had}}(q), \end{aligned}$$

(7)

where $M^2$ is the Borel parameter and $Q^2=-q^2$. This leads to

$$\begin{aligned} \Pi ^{\textrm{Had}}(M^2)= & {} \lambda ^2(\not \!q+m)e^{-\frac{m^2}{M^2}}+\tilde{\lambda }^2(\not \!q-\tilde{m})e^{-\frac{\tilde{m}^2}{M^2}}\nonumber \\ {}{} & {} +\lambda '^2(\not \!q+m')e^{-\frac{m'{}^2}{M^2}}+\cdots . \end{aligned}$$

(8)

Due to the presence of the exponential function in the above equation, the higher the value of the mass of the resonance, the lower is its contribution. We will also apply the continuum subtraction procedure supplied by the quark-hadron duality assumption in next steps that further suppresses the contributions of the higher resonances and continuum. Hence, we keep only the first three resonances and, in the numerical analyses, we will show that the main contribution in the correlation function belongs to these first three resonances. As is seen, we have only two independent Lorentz structures: $\not \!q$ and the unit matrix I, which are used to calculate the masses and residues of the relevant states.

Fig. 1

Sample diagrams considered in the present study

After obtaining the hadronic correlation function in the time-like region, the subsequent phase is to evaluate the QCD side of the correlation function in the deep Euclidean space-like region, where $q^2 \rightarrow -\infty$, by applying the operator product expansion (OPE). For this purpose, one must insert the foregoing interpolating current of $\Omega _{QQQ^{'}}$ given in Eq. (2) within Eq. (1) and carry out all the possible contractions of the heavy quark–antiquark fields via the Wick theorem. Accordingly, one can find a perspicuous expression consisting of heavy quark propagators:

$$\begin{aligned}{} & {} \Pi (q) \nonumber \\{} & {} \quad =4i\epsilon ^{abc}\epsilon ^{a^{'}b^{'}c^{'}}\int d^4x e^{i q x} \Big \{-\gamma _{5} S^{c'b}_{Q}(x)S'^{b'a}_{Q'}(x)S^{a'c}_{Q}(x)\gamma _{5}\nonumber \\{} & {} \quad \quad + \gamma _{5}S^{c'c}_{Q}(x)\gamma _{5}Tr\Big [S^{a'b}_{Q}(x)S'^{b'a}_{Q'}(x)\Big ]\nonumber \\{} & {} \quad \quad + \beta \Big ( -\gamma _{5}S^{c'b}_{Q}(x)\gamma _{5}S'^{b'a}_{Q'}(x)S^{a'c}_{Q}(x)\nonumber \\{} & {} \quad \quad -S^{c'b}_{Q}(x)S'^{b'a}_{Q'}(x)\gamma _{5}S^{a'c}_{Q}(x)\gamma _{5} +\gamma _{5}S^{c'c}_{Q}(x)Tr\nonumber \\{} & {} \quad \quad \times \Big [S^{a'b}_{Q}(x)\gamma _{5}S'^{b'a}_{Q'}(x)\Big ]\nonumber \\{} & {} \quad \quad + S^{c'c}_{Q}(x) \gamma _{5}Tr\Big [S^{a'b}_{Q}(x)S'^{b'a}_{Q'}(x)\gamma _{5}\Big ]\Big )\nonumber \\{} & {} \quad \quad {+} \beta ^2\Big ( {-}S^{c'b}_{Q}(x)\gamma _{5}S'^{b'a}_{Q'}(x)\gamma _{5}S^{a'c}_{Q}(x){+}S^{c'c}_{Q}(x) Tr\nonumber \\{} & {} \quad \quad {\times } \Big [S^{b'a}_{Q'}(x)\gamma _{5}S'^{a'b}_{Q}(x)\gamma _{5}\Big ] \Big ) \Big \}, \end{aligned}$$

(9)

where S is the full heavy quark propagator and $S'=CS^TC$. For the heavy quark propagator, the following explicit formula is utilized in coordinate space [57]:

(10)

where k is the four-momentum of the heavy quark and $m_Q$ is its mass. In Eq. (10) we have:

$$\begin{aligned} G_{ab}^{\mu \nu }= & {} G_{A}^{\mu \nu }\lambda _{ab}^{A}/2,\,\,~~G^{2}=G_{\mu \nu }^{A}G_{A }^{\mu \nu },\nonumber \\ G^{3}= & {} f^{ABC}G^{\mu \nu }_{A}G^{\nu \delta }_{B}G^{\delta \mu }_{C}, \end{aligned}$$

(11)

where $f^{ABC}$ denote the structure constants of the color group $SU_c(3)$; $A,B,C=1,\,2\,\ldots 8$; $\lambda ^{A}$ are the Gell-Mann matrices; and $\mu$, $\nu$ and $\delta$ represent the Lorentz indices. The first term in Eq. (10) represents the perturbative contribution (free heavy propagator) and the others are non-perturbative contributions (the gluonic terms) which include emission of one gluon, and two and three gluon condensates. Placing the heavy quark propagator, Eq. (10), into the QCD side of the correlation function, Eq. (9), results in various terms representing different contributions that are equivalent to some Feynman diagrams corresponding to both the perturbative and non-perturbative contributions. In the current study, the calculation of the QCD correlation function involves non-perturbative terms up to the eight mass dimensions. As depicted in Fig. 1, the diagram 1a represents the perturbative contribution and the sample diagrams (1a–g) stand for gluon condensates of different dimensions. For the two-gluon condensate, $\langle 0 |G^n_{\alpha \beta }(x)G^m_{\alpha ' \beta '}(0)|0 \rangle$, which leads to the four dimension non-perturbative contribution (diagrams 1b, c), we consider the first term of the Taylor expansion for the gluon field at $x=0$. We utilize [58]:

$$\begin{aligned} \langle 0 |G^A_{\alpha \beta }(0)G^B_{\alpha ' \beta '}(0)|0 \rangle = \frac{\langle G^2\rangle }{96}\delta ^{AB} [g_{\alpha \alpha '} g_{\beta \beta '} -g_{\alpha \beta '} g_{\alpha '\beta }],\nonumber \\ \end{aligned}$$

(12)

and

$$\begin{aligned} \begin{aligned} \mathrm t^{a b} \mathrm t^{a'b'}=\frac{1}{2}\left( \delta ^{ab'}\delta ^{a'b}-\frac{1}{3}\delta ^{ab}\delta ^{a'b'}\right) , \end{aligned} \end{aligned}$$

(13)

where $t=\lambda ^A/2$. The six mass dimension non-perturbative contribution is calculated through the three-gluon condensate (diagrams 1d, e). We decompose $\langle 0 |G^A_{\alpha \beta }G^B_{\alpha ' \beta '}G^C_{\alpha '' \beta ''}|0 \rangle$ in terms of three-gluon condensate, $\langle G^3 \rangle$, and other parameters as:

$$\begin{aligned}{} & {} \langle 0 |G^A_{\alpha \beta }G^B_{\alpha ' \beta '}G^C_{\alpha '' \beta ''}|0 \rangle \nonumber \\{} & {} \quad = \frac{\langle G^3\rangle }{576}f^{ABC} \bigg [g_{\alpha ' \beta } g_{\alpha '' \beta '} g_{\beta '' \alpha } -g_{\beta '' \alpha } g_{\beta \beta ' }g_{\alpha ' \alpha ''} \nonumber \\{} & {} \qquad -g_{\alpha \alpha ''} g_{\alpha ' \beta }g_{\beta ' \beta ''} +g_{\alpha \alpha ''} g_{\beta \beta ' }g_{\alpha ' \beta ''}\nonumber \\{} & {} \quad \quad +g_{\alpha \alpha '} g_{\beta \alpha '' }g_{\beta ' \beta ''} -g_{\alpha \alpha '} g_{\beta \beta '' }g_{\alpha '' \beta '} -g_{\alpha \beta '} g_{\beta \alpha '' }g_{\beta '' \alpha } \nonumber \\{} & {} \quad \quad +g_{\alpha \beta '} g_{\beta \beta '' }g_{\alpha ' \alpha ''}\bigg ]. \end{aligned}$$

(14)

We also find:

$$\begin{aligned}{} & {} f^{ABC}\mathrm t_{A}^{a\,b} \mathrm t_{B}^{a^{\prime }\,b^{\prime }}\mathrm t_{C}^{a^{\prime \prime }\,b^{\prime \prime }}\nonumber \\{} & {} \quad =\frac{18}{56}i\bigg [\delta ^{ba'}\delta ^{b'a''}\delta ^{b''a}{-}\frac{1}{3}\Big (\delta ^{ba'}\delta ^{ab'}\delta ^{a''b''} + \delta ^{a'b''}\delta ^{b'a''}\delta ^{ab} \nonumber \\{} & {} \qquad {+}\delta ^{ab''}\delta ^{ba''}\delta ^{a'b'}\Big ) + \frac{2}{9}\delta ^{ab}\delta ^{a'b'}\delta ^{a''b''}\bigg ]. \end{aligned}$$

(15)

The eight dimension diagrams 1f and g are written in terms of two-gluon condensate, $\langle G^2 \rangle ^2$. Such contributions are obtained by multiplication of the third term in Eq. (10 ) for two propagators with the perturbative part of the third quark propagator. For all mass dimensions in the non-perturbative part of the correlation function, all possible permutations have been taken into account.

After insertion of the expression of the heavy quark propagator in x-space into Eq. (9), we perform the resultant Fourier integrals. In the calculations, various types of integrals appear. For instance, integrals of the following types arise in the perturbative part, the diagram 1a:

$$\begin{aligned} \begin{aligned}&\int d^4k_1\,\int d^4k_2\,\int d^4k_3 \, \int d^4x\,e^{i(q-k_1-k_2-k_3)x}\\&\quad \times \frac{f(k_1,\,k_2,\,k_3)}{(k_1^2-m^2_Q)^{n_1}(k_2^2-m^2_{Q'})^{n_2}(k_3^2-m^2_Q)^{n_3}}, \end{aligned} \end{aligned}$$

(16)

where $n_1$, $n_2$ and $n_3$ are the natural numbers. In the first step, we perform the Fourier integrals over four-x:

$$\begin{aligned} \int d^4x e^{i(q-k_1-k_2-k_3)x}=(2\pi )^4\delta ^4(q-k_1-k_2-k_3).\nonumber \\ \end{aligned}$$

(17)

The presence of Dirac’s delta function facilitates the four-integration over $k_3$. The remaining four-integrals over $k_2$ and $k_1$ are performed using the Feynman parametrization:

$$\begin{aligned}{} & {} \frac{1}{A_1^{n_1}A_2^{n_2}A_3^{n_3}}=\frac{\Gamma (n_1+n_2+n_3)}{\Gamma ({n_1})\Gamma ({n_2})\Gamma ({n_3})}\int _0^1\int _0^{1-r}dzdr\nonumber \\{} & {} \quad \times \frac{r^{n_1-1} \ z^{n_2-1}(1-r-z)^{n_3-1}}{[rA_1 \ +zA_2 \ +(1-r-z)A_3]^{n_1+n_2+n_3}}. \end{aligned}$$

(18)

To perform the four-integrals over $k_2$ and $k_1$, we utilize [59]:

$$\begin{aligned} \int d^4 \ell \frac{(\ell ^2)^m}{(\ell ^2{+}\Delta )^n}{=}\frac{i\pi ^2 (-1)^{m-n} \Gamma [m{+}2]\Gamma [n{-}m{-}2]}{\Gamma [2]\Gamma [n] ({-}\Delta )^{n-m-2}},\nonumber \\ \end{aligned}$$

(19)

where $\Delta$ is a function of quark masses, Feynman parameters and other related parameters, but does not depend on four-$\ell$. By using the following relation, we extract the imaginary parts of obtained results:

$$\begin{aligned} \Gamma \Big [\frac{D}{2}-n\Big ]\Big (-\frac{1}{\Delta }\Big )^{D/2-n}=\frac{(-1)^{n-1}}{(n-2)!}(-\Delta )^{n-2}ln[-\Delta ]. \end{aligned}$$

(20)

This procedure is applied also to calculate the two-gluon condensate contributions, diagrams 1b and c. To calculate the contributions of higher dimensional non-perturbative operators, we follow the standard procedures of method and find their contributions in momentum-space. Eventually, by applying the Borel transformation as well as continuum subtraction, the final form of the QCD correlation function is:

$$\begin{aligned} \Pi _i^{\textrm{QCD}}(s_0,M^2){} & {} =\int _{(2m_Q+m_{Q'})^2}^{s_0}ds\,e^{-\frac{s}{M^2}}\rho _i(s)+\Gamma _i(M^2),\nonumber \\ {}{} & {} i= \not \!q~\text{ or }~I. \end{aligned}$$

(21)

Here $s_0$ represents the continuum threshold, $\rho _i(s)=\frac{1}{\pi }\textrm{Im}[\Pi _i^{\textrm{QCD}}]$ are spectral densities that include a perturbative and four-dimensional non-perturbative contributions. $\Gamma _i(M^2)$ denote the results of the non-perturbative operators for the mass dimensions six and eight in the Borel scheme. The explicit mathematical expressions for $\rho _i(s)$ and parts of $\Gamma _i(M^2)$ are provided in the Appendix. As mentioned earlier, both the QCD and hadronic sides are comprised of two independent Lorentz structures, labeled as $\not \!q$ and the unit matrix I. By matching the coefficients of these Lorentz structures from both the QCD and hadronic sides, the desired sum rules are obtained:

$$\begin{aligned} \lambda ^2 e^{-\frac{m^2}{M^2}}+\tilde{\lambda }^2e^{-\frac{\tilde{m}^2}{M^2}}+\lambda '^2e^{-\frac{m'{}^2}{M^2}}=\Pi ^{\textrm{QCD}}_{\not \!q}(s_0,M^2), \end{aligned}$$

(22)

and

$$\begin{aligned} \lambda ^2 m e^{-\frac{m^2}{M^2}}-\tilde{\lambda }^2\tilde{m}e^{-\frac{\tilde{m}^2}{M^2}}+\lambda '^2m'e^{-\frac{m'{}^2}{M^2}}=\Pi ^{\textrm{QCD}}_{I}(s_0,M^2).\nonumber \\ \end{aligned}$$

(23)

These sum rules contain six unknowns (three masses and three residues). To solve them, we need five more equations for each structure, which would be found by applying successive derivatives with the respect to $-\frac{1}{M^2}$ to both sides of the above sum rules. This may impose higher uncertainties to the results, hence, we follow a three-step procedure to find the physical quantities. First we choose the continuum threshold, $s_0$, such that the sum rules contain only the ground state (first terms in Eqs. (22) and (23)). After some manipulations, the mass and residue for the ground state are found. As an example for the $\not \!q$ structure, we have:

$$\begin{aligned} m^2=\frac{\frac{d}{d(-\frac{1}{M^2})}\Pi ^{\textrm{QCD}}_{\not \!q}(s_0,M^2)}{\Pi ^{\textrm{QCD}}_{\not \!q}(s_0,M^2)}, \end{aligned}$$

(24)

and

$$\begin{aligned} \lambda ^2=e^{\frac{m^2}{M^2}}\Pi ^{\textrm{QCD}}_{\not \!q}(s_0,M^2). \end{aligned}$$

(25)

Having calculated the mass and residue of the ground state, we try to calculate the parameters of the first orbital excitation (1P). To this end, we follow the ground $+$ first orbitally excited state $+$ continuum scheme and by adjusting $s_0$ we put the radial excitation (2 S) inside the continuum. Now, using the ground state parameters, we can calculate $\tilde{m}$ and $\tilde{\lambda }$ as the physical quantities related to 1P state using similar procedure mentioned above. Finally, we increase the continuum threshold, $s_0$, and use 1S state $+$ 1P state $+$ 2 S $+$ continuum scheme to calculate the mass and residue of the 2 S state by considering the parameters of the 1S and 1P states as inputs.

3 Numerical analyses

In this section, in order to perform numerical analyses of the expressions related to the mass and residue for triply heavy spin-1/2 baryons in their ground and first orbital and radial excited states, we need a set of input parameters such as the quark masses in two $\overline{MS}$ and pole schemes, two-gluon and three-gluon condensates which are presented in Table 2.

Table 2 Numerical values utilized in the analyses

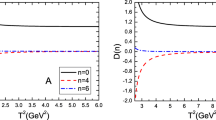
An important task in our calculations is to find working windows for three auxiliary parameters that are entered in the QCD sum rules for the physical quantities, namely Borel parameter $M^2$, threshold parameter $s_0$ and arbitrary mixing factor $\beta$. They are set by analyzing the results using the standard requirements of the method like pole dominance and convergence of the OPE, in such a way that the physical quantities show relatively weak dependence on them. The first auxiliary parameter is $\beta$ to be fixed. As we previously mentioned, this parameter appears in the interpolating currents to help all the possible configurations of the quark fields to be taken into account. Since this parameter can take the values from $- \infty$ to $+\infty$, we introduce a more convenient variable $\theta$ by defining $\beta =\tan \theta$. Then, by examining the dependence of the results on $\cos \theta$ in the range of $[-1,1]$, we can encompass all desired values for $\beta$. In order to find the working regions of $\cos \theta$, as an example, we plot the function $\Pi ^{QCD}_{\not \!q}(s_0,M^2)$ in term of $\cos \theta$ in Fig. 2. The $\beta$ or $\cos \theta$ are mathematical objects, so in principle they should not affect the physical quantities. But in practice, we see some dependencies of the results on these helping parameters. We should select the regions that show relatively small dependence of the physical quantities on these parameters as the working windows. As it is seen from Fig. 2, the following intervals show the slightest variations in terms of $\cos \theta$:

$$\begin{aligned} -1.0 \le \ \cos \theta \le \ -0.5~~~ \textrm{and}~~~0.5 \le \ \cos \theta \le \ 1.0. \end{aligned}$$

(26)

Fig. 2

$\Pi ^{\textrm{QCD}}_{\not \!q}(s_0,M^2)$ (in units of $\textrm{GeV}^{6}$) as a function of $\cos \theta$ at the medial values of $M^2$ and $s_0$

The next auxiliary parameter that needs to be fixed is $M^2$. The upper limit for this parameter is set based on the dominance of the pole contribution over the higher states and continuum. In technique language, we demand

$$\begin{aligned} \frac{\Pi (s_0,M^2,\beta )}{\Pi (\infty ,M^2,\beta )}\ge 0.5. \end{aligned}$$

(27)

Its lower limit is obtained from the convergence of the OPE, implying that the perturbative contribution should exceed the non-perturbative one and the higher dimensional operators have relatively lower contributions. For this, we require that the last non-perturbative operator contribution (eight-mass dimension) does not surpass 0.05 of the total perturbative $+$ non-perturbative contributions. That is

$$\begin{aligned} \frac{\Pi ^{\textrm{Dim8}}(s_0,M^2,\beta )}{\Pi (s_0,M^2,\beta )}\le \ 0.05. \end{aligned}$$

(28)

The obtained intervals for $M^2$ for all the members in all schemes are shown in Table 3. The final auxiliary parameter to be set is the continuum threshold $s_0$. The values of $s_0$ are not entirely arbitrary and depend on the energy of the next excited state and differ for the ground and the first orbital and radial excited states. The selection of thresholds are such that the higher states do not contribute to the calculations for each considered state. The working regions for $s_0$ for all under study channels are also displayed in Table 3. It is instructive to check the pole dominance and OPE convergence by using the determined working intervals of the auxiliary parameters. To this end, we depict Fig. 3, showing the variation of first three resonances’ contribution (FTRC) with respect to $M^2$ at three fixed values of $s_0$ for $\Omega _{ccb}$ channel as an example. From this figure we see that the pole dominance for the considered resonances is nicely satisfied in the working windows of auxiliary parameters. In the average values of all the auxiliary parameters, the higher dimensional term contributes with maximally 1% satisfying the requirements of the method. We shall note that the dimension six operators constitute maximally 5% of the total contribution referring to the nice convergence of OPE.

Table 3 Working windows for the auxiliary parameters and calculated mass and residue results. For the baryons with over-line and baryons without over-line, the $\overline{MS}$ and pole values of the quark masses are used, respectively

The stability diagrams of physical quantities (masses and residues of $\overline{\Omega }_{ccb}$ in the ground and excited states as examples) with respect to the variations of the auxiliary parameters are depicted in Figs. 4, 5, 6 and 7. In Fig. 4a, the mass of $\overline{\Omega }_{ccb}$ in the ground state is drawn with respect to $M^2$ at three fixed values for threshold parameter and at, $\cos \theta =-0.71$. Note that $\cos \theta =-0.71$ corresponds to the Ioffe current, $\beta =-1$. In Fig. 4b, the mass of $\overline{\Omega }_{ccb}$ in the ground state is plotted in terms of $s_0$ at three fixed values for the Borel parameter and at $\cos \theta =-0.71$. In Figs. 5 and 6, the masses of orbital and radial excited states for $\overline{\Omega }_{ccb}$ are shown, respectively. As it is seen from these figures, the masses of ground, first orbitally excited and first radially excited states for $\overline{\Omega }_{ccb}$ show very weak dependence on the parameters $M^2$ and $s_0$. In Fig. 7a the residue of $\overline{\Omega }_{ccb}$ in the ground state is plotted with respect to $M^2$ at three fixed values for threshold parameter and at $\cos \theta =-0.71$. The residues of orbital and radial excited states for $\overline{\Omega }_{ccb}$ are drawn in Fig. 7b and c, respectively. The residual dependence appear as the uncertainties in the obtained results. Such weak dependence of the results on the auxiliary parameters in their working intervals are the case for the masses of $\Omega _{ccb}$, $\overline{\Omega }_{bbc}$ and $\Omega _{bbc}$ as well as all the residues.

Having calculated the working windows for the auxiliary parameters, we proceed to find the numerical values of the pole and $\overline{MS}$ masses and residues for the states under consideration. To this end, we follow a three-step procedure mentioned previously. For calculation of the mass and residue of the ground state, we set $s_0$ such that the first orbital and radial excitations remain inside the continuum. In other words, we choose a ground state $+$ continuum scheme. The obtained results for the ground state masses and residues for all the channels in this step are shown in Table 3. Now, we increase the value of $s_0$ and use the obtained values for the ground state as inputs to calculate the parameters of the first orbital excited states applying the ground state $+$ orbitally excited state $+$ continuum scheme. And finally, for the first radial excitation, we consider the ground state $+$ first orbitally excited state $+$ first radially excited state $+$ continuum, and choose an appropriate threshold parameter to find the values of the physical quantities for the 2 S states. We collect the values obtained for the properties of the 1P and 2 S states in Table 3, as well. The presented uncertainties arise from the errors in the input parameters and uncertainties coming from the calculations of the working regions of the auxiliary parameters. We shall note that the order of uncertainties in the values of the masses are very low compared to those of the residues. This is because of the fact that the mass is obtained from the ratio of two sum rules killing the errors of each other, while the residue is found only from one sum rule as are clear from Eqs. (24) and (25). As is seen from Table  3, the mass difference between the ground and first orbitally exited state (first radially excited state) in structure $\not \!q$ for $\overline{\Omega }_{ccb}$, $\Omega _{ccb}$, $\overline{\Omega }_{bbc}$ and $\Omega _{bbc}$ are 0.15 (0.30) $\textrm{GeV}$, 0.19 (0.39) $\textrm{GeV}$, 0.14 (0.25) $\textrm{GeV}$ and 0.23 (0.42) $\textrm{GeV}$, whereas for structure I, these variances are 0.15 (0.29) $\textrm{GeV}$, 0.18 (0.37) $\textrm{GeV}$, 0.19 (0.23) $\textrm{GeV}$ and 0.20 (0.38) $\textrm{GeV}$, respectively.

Fig. 3

FTRC versus $M^2$ at three fixed values of $s_0$ for $\Omega _{ccb}$ channel

Fig. 4

a The mass of $\overline{\Omega }_{ccb}$ in the ground state with respect to $M^2$ at three fixed values for the $s_0$ and at $\cos \theta =-0.71$. b The mass of $\overline{\Omega }_{ccb}$ in the ground state with respect to $s_0$ at three fixed values for the $M^2$ and at $\cos \theta =-0.71$

Fig. 5

a The mass of $\overline{\Omega }_{ccb}$ in the orbital exited state with respect to $M^2$ at three fixed values for the $s_0$ and at $\cos \theta =-0.71$. b The mass of $\overline{\Omega }_{ccb}$ in the orbital exited state with respect to $s_0$ at three fixed values for the $M^2$ and at $\cos \theta =-0.71$

Fig. 6

a The mass of $\overline{\Omega }_{ccb}$ in the radial exited state with respect to $M^2$ at three fixed values for the $s_0$ and at $\cos \theta =-0.71$. b The mass of $\overline{\Omega }_{ccb}$ in the radial exited state with respect to $s_0$ at three fixed values for the $M^2$ and at $\cos \theta =-0.71$

Fig. 7

a The residue of $\overline{\Omega }_{ccb}$ in the ground state with respect to $M^2$ at three fixed values for the $s_0$ and at $\cos \theta =-0.71$. b The residue of $\overline{\Omega }_{ccb}$ in the orbital exited state with respect to $M^2$ at three fixed values for the $s_0$ and at $\cos \theta =-0.71$. c The residue of $\overline{\Omega }_{ccb}$ in the radial exited state with respect to $M^2$ at three fixed values for the $s_0$ and at $\cos \theta =-0.71$

Table 4 The mass spectra (in units of $\textrm{GeV}$) of the $\overline{\Omega }_{ccb}$ and $\Omega _{ccb}$ baryons compared to other theoretical predictions

Table 5 The mass spectra (in units of $\textrm{GeV}$) of the $\overline{\Omega }_{bbc}$ and $\Omega _{bbc}$ baryons compared to other theoretical predictions

Table 6 The residue spectra (in units of $\mathrm {GeV^3}$) of the $\overline{\Omega }_{ccb}$, $\Omega _{ccb}$, $\overline{\Omega }_{bbc}$ and $\Omega _{bbc}$ baryons compared to other theoretical predictions

Since there is no experimental information available for the triply heavy baryons, Tables 4 and 5 only include comparisons among the predictions of present study and other existing theoretical approaches. As we previously mentioned, with the aim of achieving higher accuracies, we carry out the calculations by considering the non-perturbative operators up to eight mass dimensions and for the first three resonances, while, in the previous study [26], the mass and residue were only computed for the ground state and non-perturbative part up to four mass dimensions. We also include the existing predictions of other studies in Tables 4 and 5. We see that some of them report only the masses of the ground, but others include the parameters of the excited states as well. We shall remark that most of these studies do not present the scheme of the quark masses, hence, we compare them with our values obtained using the $\overline{MS}$ scheme for the quark masses. As shown in Tables 4 and 5, our obtained mass for ground state of $\overline{\Omega }_{ccb}$ aligns well with the predictions of various methods such as the non- relativistic quark [6, 11], the relativistic quark model [15, 16], QCD sum rules [28], the Regge trajectories [35] and effective Hamiltonian [47] within the indicated uncertainties, whiles it is slightly different with predictions of some methods like Faddive equation [38] and QCD sum rules [25, 26], which contain the non-perturbative operators up to dimension four and less numbers of resonances. The small differences with the predictions of Refs. [25, 26] can be attributed to the dimension six and eight operators that are considered in the present study and contribute respectively with 5% and 1% to the total integral as previously mentioned. Our prediction for the mass of ground state of $\overline{\Omega }_{bbc}$ is in good consistency with the various theoretical predictions, including the non- relativistic quark [10], the relativistic quark model [15, 16], QCD sum rules [28], Faddive equation [38] and effective Hamiltonian [47] within the errors and there is small difference with predictions of some approaches, containing the Regge trajectories [35], the non- relativistic quark [6] and QCD sum rules [25, 26]. Our results for 1P and 2 S of $\overline{\Omega }_{ccb}$ are in agreement, within the errors, with the other mentioned theoretical predictions [6, 11, 15, 16, 35, 38, 47]. For 1P of $\overline{\Omega }_{ccb}$, our result is a little bit higher than the predictions of QCD sum rule approach [25]. Within the presented errors of 1P and 2 S, our results of $\overline{\Omega }_{bbc}$, except some predictions [6, 10, 25, 35] which show little differences, exhibit good consistency with the theoretical predictions [15, 16, 38, 47]. Our obtained masses for ground states of $\Omega _{ccb}$ and $\Omega _{bbc}$ are in good agreement with predictions of QCD sum rule method [26] within the errors. Our results for 1 S and 1P of $\Omega _{ccb}$ and $\Omega _{bbc}$ are slightly higher than findings of Ref. [25] using QCD sum rules.

On the other hands, we examine the residues of the ground, first orbitally and first radially excited states of the triply heavy baryons, and depicted our findings in Table 6. As previously mentioned, our residues’ findings include the impacts of non-perturbative operators up to eight mass dimensions as well. So far, there have been few studies conducted on the residues of triply heavy spin-1/2 baryons in the literature. Table 6 summarizes the predictions that are available. In the case of the residues, there are also good agreements, within the uncertainties, presented between existing results of 1 S and 1P in the literature [25, 26] and our findings. The results attained for the residues can be utilized as inputs to analyze various decays of the considered triply heavy spin-1/2 baryons. Our results may help experimental groups in their ongoing search for the triply heavy baryons at different hadron colliders.

4 Conclusion

Calculation of mass and residue is crucial as they are among the most fundamental properties of particles. Their values can be used as inputs in various analyses of the interactions and decays of particles. The mass and residue spectra of the triply heavy spin-1/2 baryons have been calculated using the QCD sum rule approach in the current work. One of the advantages of this approach is its independence of arbitrary parameters, leading to a final result that is not affected by such choices. With the intent of improving accuracy in mass and residue calculations for the ground, the first orbital and the first radial excited states, we extended the non-perturbative contribution to include the operators up to eight mass dimensions. Various predictions for the spectroscopic parameters of these states exist in the literature, but we need more information on the interactions/decays of these particles with/to other known states. Our results obtained with higher accuracies can be used in future related analyses. The obtained results for the parameters of the triply heavy baryons in their ground and excited states can also shed light on the search of different experimental groups for these states at various hadron colliders. Their identification in the experiment will be another impressive success in the colliders and comparison of the future data with theoretical predictions will provide a good insight into the non-perturbative nature of QCD as the successful theory of strong interaction. Such possible progresses will also put the successes of the quark model to the top point as this model has predicted the ground and excited triply heavy baryons decades ago.

Appendix: Some expressions obtained in QCD side of the calculations

Here, we bring forward the explicit forms of different components of the spectral densities $\rho _i(s)$ and parts of $\Gamma _i(M^2)$ attained from calculations for both the structures:

$$\begin{aligned} \rho ^{pert}_{\not \!q}(s)&=\frac{3}{64 \pi ^4} \int ^{1}_{0} dz \int ^{1-z}_{0} dr \ \frac{D\,\Theta (D)}{U_1^4\, U_3^3} \Bigg \{\bigg [2\, m_Q^2\, U_1^2\, U_2\, U_3^2\, z \nonumber \\&\quad + 2 \,m_Q\, m_{Q'}\, U_1^2 \,U_3 \,(U_3 + 4\, z) \,(U_1 + U_2\, z) \nonumber \\&\quad + z \,(10\, s\, U_2\, (U_3 - z) \,z \,(U_1 + U_2\, z)^2 \nonumber \\&\quad - D\, U_1^2\, (U_1\, (U_2 + 14\, U_3 - 14\, z) + 15\, U_2\, (U_3 - z)\, z))\bigg ]\nonumber \\&\quad +2 \beta \bigg [-2\, m_Q^2\, U_1^2\, U_2\, U_3^2 + 2\, s\, U_2 \,(U_3 - z) \,z\, (U_1 + U_2\, z)^2\nonumber \\&\quad + D\, U_1^2\, (3 \,U_2\, z \,(-U_3 + z)\nonumber \\&\quad + U_1\, (U_2 - 4\, U_3 + 4\, z))\bigg ] \nonumber \\&\quad + \beta ^2\bigg [-2\, m_{Q}^{2}\, U_{1}^{2}\, U_{2}\, U_3^2\, z \nonumber \\&\quad + 2\, m_Q \,m_{Q'}\, U_1^2\, U_3\, (U_3 + 4\, z) (U_1 + U_2\, z)\nonumber \\&\quad + z\, (-10\, s\, U_2 (U_3 - z)\, z \,(U_1 + U_2 \,z)^2 \nonumber \\&\quad + D \,U_1^2 (U_1\, (U_2 + 14\, U_3 - 14\, z) \nonumber \\&\quad + 15\, U_2\, (U_3 - z)\, z)) \bigg ] \Bigg \}, \end{aligned}$$

(29)

$$\begin{aligned} \rho _I^{Pert}(s)&=\frac{3}{32 \pi ^4} \int ^{1}_{0} dz \int ^{1-z}_{0} dr \ \frac{D\, \Theta (D)}{U_1^3\, U_3^3} \nonumber \\&\quad \times \Bigg \{\bigg [ -5 \,m_Q^2\, m_{Q'}\, U_1^2\, U_3^2 - m_Q \,s \,U_2 \,U_3\, (5 \,U_3 - 4\, z)\nonumber \\&\quad \times z\, (U_1 + U_2 \,z) - m_{Q'}\, s\, (U_3 - z) \nonumber \\&\quad \times z \,(U_1 + U_2\, z)^2 + D \,U_1^2\, (m_Q \,U_3 \,(5\, U_3 - 4\, z) \nonumber \\&\quad + m_{Q'}\, (U_1 + (U_3 - z)\, z)) \bigg ]\nonumber \\&\quad -2 \beta \,m_{Q'} \bigg [ m_Q^2\, U_1^2 \,U_3^2 - s\, (U_3 - z) \,z\, (U_1 + U_2\, z)^2 \nonumber \\&\quad + D\, U_1^2\, (U_1 + (U_3 - z)\, z)\bigg ]\nonumber \\&\quad + \beta ^2\bigg [-5\, m_Q^2\, m_{Q'}\, U_1^2\, U_3^2 + m_Q \,s\, U_2\, U_3\, \nonumber \\&\quad \times (5\, U_3 - 4\, z)\, z \,(U_1 + U_2\, z)\nonumber \\&\quad - m_{Q'}\, s\, (U_3 - z) \,z\, (U_1 + U_2\, z)^2 \nonumber \\&\quad +D\, U_1^2\, (m_Q\, U_3\, (-5\, U_3 + 4\, z)\nonumber \\&\quad + m_{Q'} (U_1 + (U_3 - z)\, z))\bigg ] \Bigg \}, \end{aligned}$$

(30)

$$\begin{aligned}&\rho ^{dim-4}_{\not \!q}(s) \nonumber \\&\quad = \frac{1}{192 \pi ^2} \int ^{1}_{0} dz \int ^{1-z}_{0} dr \Big \langle \frac{\alpha _{s}GG}{\pi }\Big \rangle \ \frac{\Theta (D)}{U_1^4\, U_3}\nonumber \\&\qquad \times \Bigg \{\bigg [8\,z\Big (-9 \,r^2\, (U_3 - z)\, (U_1 + U_2 \,z) \nonumber \\&\qquad + 3\, U_4\, z\, (3\, U_2\, z\, (-U_3 + z) \nonumber \\&\qquad + U_1 \,(U_2 - 2\, U_3 + 2 \,z)) + r \,(U_1\, U_3\, (9 + 68 \,z) \nonumber \\&\qquad - U_1 \,z\, (9 + 9 \,U_2 + 68\, z) + U_2\, (U_3 - z) \,z \,(9 + 77\, z))\Big )\bigg ] \nonumber \\&\qquad +2\, \beta \bigg [3\,z\Big (U_4 \,z\, (27\, U_1\, U_2 + 50\, U_1\, (-U_3 + z) \nonumber \\&\qquad + 77 \,U_2\, z\, (-U_3 + z)) + 11\, r^2 \,(7\, U_2\, z\, (-U_3 + z)\nonumber \\&\qquad + U_1\, (U_2 - 6\, U_3 + 6\, z)) + r\, (-11\, U_1\, U_2 \nonumber \\&\qquad + 6\, U_1\, (U_3 - z) (11 + 12\, z) \nonumber \\&\qquad + U_2\, (U_3 - z)\, z \,(77 + 72\, z))\Big )\bigg ] \nonumber \\&\qquad + \beta ^2\bigg [8\,z\Big (-9\, r^2\, (U_3 - z)\, (U_1 + U_2\, z) \nonumber \\&\qquad + 3\, U_4 \,z\, (3\, U_2\, z\, (-U_3 + z) + U_1 \,(U_2 - 2\, U_3 + 2\, z)) \nonumber \\&\qquad + r\, (U_1 \,U_3\, (9 + 68\, z) - U_1\, z\, (9 + 9\, U_2 + 68 \,z) \nonumber \\&\qquad + U_2\, (U_3 - z)\, z \,(9 + 77\, z))\Big ) \bigg ] \Bigg \}, \end{aligned}$$

(31)

$$\begin{aligned}&\rho ^{dim-4}_I(s) \nonumber \\&\quad =\frac{1}{192 \pi ^2} \int ^{1}_{0} dz \int ^{1-z}_{0} dr \Big \langle \frac{\alpha _{s}GG}{\pi }\Big \rangle \ \frac{\Theta (D)}{U_1^4\, U_3} \nonumber \\&\qquad \times \Bigg \{\bigg [m_Q \Big (6\, (U_3 - z)\, z^2\, (-3\, U_3^3 \nonumber \\&\qquad + 9\, U_3^2\, z - (9 - 9\, r + U_3)\, z^2 + 4\, z^3)\nonumber \\&\qquad + U_1\, (-3\, U_3^3 \,(r + 4\, U_3) + U_3^2\, (3 - 31\, r + 54\, U_3)\, z \nonumber \\&\qquad + (-36 + 64\, r - 57\, U_3)\, U_3\, z^2 + 68\, U_3\, z^3 - 24 \,z^4)\Big )\nonumber \\&\qquad + m_{Q'}\Big (-3\, r^2\, U_1 (U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad - 3 \,U_1\, U_4\, z\, (U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad + 3\, r\, U_1 \,(1 + z) \,(U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad + 2\, r^3\, U_3\, (2\, U_1 + 3\, z\, (-U_3 + z))\Big )\bigg ]\nonumber \\&\qquad +2\, \beta \bigg [m_{Q'}\,\Big (-3\, r^2\, U_1\, (U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad - 3\, U_1\, U_4\, z\, (U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad + 3\, r\, U_1 (1 + z) (U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad + 2\, r^3 \,U_3\, (2\, U_1 + 3 \,z (-U_3 + z))\Big )\bigg ]\nonumber \\&\qquad + \beta ^2\bigg [m_Q\,\Big (6\, (U_3 - z) \,z^2\, (5\, U_3^3 - 15\, U_3^2\, z \nonumber \\&\qquad + (15 - 15\, r + U_3)\, z^2 - 6 \,z^3) \nonumber \\&\qquad + U_1\, (-3\, (-1 + r)\, r\, U_3^2 + 20\, U_3^4\nonumber \\&\qquad + U_3^2\, (31\, r - 3\, (30\, U_3 + U_4))\, z + 2\, U_3\, (30 - 44\, r \nonumber \\&\qquad + 45\, U_3)\, z^2 - 112 \,U_3\, z^3 + 36\, z^4)\Big )\nonumber \\&\qquad + m_{Q'}\, \Big (-3 \,r^2 \,U_1\, (U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad - 3\, U_1\, U_4\, z \,(U_1 + z\, (-U_3 + z)) \nonumber \\&\qquad + 3 \,r\, U_1 (1 + z)\, (U_1 + z (-U_3 + z))\nonumber \\&\qquad + 2 \,r^3\, U_3 \,(2\, U_1 + 3\, z\, (-U_3 + z))\Big ) \bigg ] \Bigg \}. \end{aligned}$$

(32)

$\Gamma _i(M^2)$ are displayed in 6 and 8 mass dimensions, as follows:

$$\begin{aligned}&\Gamma _i^{dim-j}(M^2)\nonumber \\&\quad =\Gamma _{i,1}^{dim-j}(M^2)+\,\beta \,\Gamma _{i,2}^{dim-j}(M^2)\nonumber \\&\qquad +\,\beta ^2\,\Gamma _{i,3}^{dim-j}(M^2),~i= \not \!q~\text{ or }~I \,~\text{ and } \,~j= 6~\text{ or }~8. \end{aligned}$$

(33)

Due to the lengthy expression of $\Gamma _i^{dim-j}(M^2)$, we only explicitly write the coefficient of $\Gamma _{\not \!q,2}^{dim-j}(M^2)$

$$\begin{aligned} \Gamma ^{dim-6}_{\not \!q,2}(M^2)= & {} \frac{1}{30720 \, \pi ^4 \, M^6} \int ^{1}_{0} dz \int ^{1-z}_{0} dr \,\nonumber \\{} & {} \times \frac{\langle g_s^3 G^3 \rangle }{U_1^5\, U_2^6 \, U_3^8\,r^7 \,z^3}\, e^{-\frac{K}{M^2}}\Bigg \{2\,M^6\, U_2^3\,r^3\,z^3\,V_1 \nonumber \\{} & {} + 2\,m_Q^2\,M^4\,U_1\,U_2^2\,U_3\,r^2\,z^2\,V_2\nonumber \\{} & {} + 2\,m_{Q'}^2\,M^4\, U_1\,U_2^2\,r^3\,z^2\,V_3\nonumber \\{} & {} + m_{Q}^4\,M^2\, U_1^2\, U_2\, U_3^2\,r\, z\,V_4\nonumber \\{} & {} +2\,m_{Q'}^2\,m_Q^2\,M^2\,U_1^2\,U_2\,U_3\,r^2\,z\,V_5\nonumber \\{} & {} +m_{Q'}^4\,M^2\, U_1^2\,U_2\,r^3\,z\,V_6+m_Q^6\,U_1^3 U_3^3\,V_7 \nonumber \\{} & {} +m_{Q'}^2\,m_Q^4\, U_1^3 \,U_2\, U_3^2\,r\,V_8+m_{Q'}^4\,m_{Q}^2\,U_1^3\,U_3\,r^2\,V_9 \nonumber \\{} & {} + m_{Q'}^6 \, U_1^3\,r^3\,V_{10}\Bigg \}, \end{aligned}$$

(34)

$$\begin{aligned} \Gamma ^{dim-8}_{\not \!q,2}(M^2)= & {} \frac{1}{55296 \, M^8} \int ^{1}_{0} dz \int ^{1-z}_{0} dr \,\nonumber \\{} & {} \times \frac{\langle \frac{\alpha _s}{\pi } G^2 \rangle \,^2}{U_1^2\, U_2^6 \, U_3^4\,r^6 \,z^4}\, e^{-\frac{K}{M^2}}\Bigg \{ m_Q^2\,M^4\,U_2^2\,r\,z^3\,S_1\nonumber \\{} & {} + 3\,m_{Q'}^2\,M^4\, U_1\,U_2^4\,U_3^2\,r^5\,z^3\,S_2\nonumber \\{} & {} - m_{Q}^4\,M^2\, U_1\, U_2\, U_3\, z^2\,S_3\nonumber \\{} & {} -\,m_{Q'}^2\,m_Q^2\,M^2\,U_1\,r\,z\,S_4\nonumber \\{} & {} -57\,m_{Q'}^4\,M^2\, U_1^2\,U_2^4\,U_3^4\,r^7\,z^2\nonumber \\{} & {} -32\,m_Q^6\,U_1^2\,U_2^3\, U_3^5\,r^2\,z^3\,S_5 \nonumber \\{} & {} +32\,m_{Q'}^2\,m_Q^4\, U_1^2 \, U_3^4\,r^3\,S_6\nonumber \\{} & {} +32\,m_{Q'}^4\,m_{Q}^2\,U_1^2\,U_3^4\,r^4\,S_7 \Bigg \}, \end{aligned}$$

(35)

and we need to define

$$\begin{aligned} V_1 =&6\, r^2\, U_1\, (r^5 + U_1^2 - r \,U_1^2)\, U_2^2\, (U_1 + 5\, r\, U_2)\, U_3^6\nonumber \\&+ 2\, r\, U_2\, U_3^5\, \bigg [-3\, r^6\, U_1^2\, U_2 + 4\, U_1^5 \,U_3 \nonumber \\&{} - r\, U_1^2\, \big [4\, (-1 + r)\, r^4 + 8\, U_1^2\, U_2 + 81\, r\, U_1\, U_2^2\big ]\, U_3\nonumber \\&+ 5\, r^6\, U2\, (4 \,U_1 + 3\, r\, U_2)\, U_3^2 \nonumber \\ {}&+ 3 \,r\, U_1^2\, U_2\, (2 \,U_1 + 3\, r\, U_2) \,U_3^3\bigg ]\, z\nonumber \\&- r\, U_3^5\, \bigg [U_1^5\, (43\, U_2 + 3\, U_3) + 2\, U_1^4\, U_2\, (7\, r\, U_2 - 16\, U_3^2) \nonumber \\&+ 5\, r^5\, U_1 \,U_2 \,U_3\, (16\, r \,U_2 - 5\, U_3^2)\nonumber \\&+ 30\, r^6 \,U_2^2\, U_3\, (r\, U_2 - U_3^2) \nonumber \\ {}&+ 3\, r \,U_1^2 \,U_3\, (r^3 + 2\, U_2^2 \,U_3)\, (8\, r\, U_2 - U_3^2)\nonumber \\&+ 12\, r\, U_1^3\, U_2^2\, (-29\, r\, U_2 + U_3^2)\bigg ]\, z^2\nonumber \\&+ U_3^4\, \bigg [4 \,r\, U_1^3\, U_2\, (25 \,U_1^2 + 23\, r \,U_1\, U_2 - 93\, r^2\, U_2^2) \nonumber \\&+ U_1\, (15\, U_1^4 + 24\, r^6\, U_1\, U_2 + 40\, r^7\, U_2^2)\, U_3\nonumber \\&- 21\, r\, U_1^2\, U_2\, (9\, U_1^2 + 8\, r \,U_1 \,U_2 + 2\, r^2\, U_2^2) \,U_3^2 \nonumber \\&- 5\, r^5\, (3\, U_1^2 + 20\, r\, U_1\, U_2 + 18\, r^2\, U_2^2)\, U_3^3\nonumber \\&+ 12\, r\, U_1\, U_2\, (4\, U_1^2 + 3\, r\, U_1\, U_2 \nonumber \\&+ 4\, r^2\, U_2^2)\, U_3^4 + 3\, r^5\, (2 \,U_1 + 5\, r \,U_2) \,U_3^5\bigg ] \,z^3\nonumber \\&+ U_3^3\, \bigg [2\, r \,U_1^3 \,U_2 \,(-61\, U_1^2 - 51 \,r \,U_1\, U_2 + 93\, r^2\, U_2^2) \nonumber \\&+ 30\, (-3 + 2\, r) \,U_1^5 \,U_3- 8\, r\nonumber \\&\times \Big (-4 + 5\, r\, \big [2 + (-2 + r)\, r\big ]^2\Big )\, U_1^2\, U_2\, U_3 \nonumber \\&+ r\, U_1^2\, U_2\, (497\, U_1^2 + 612\, r\, U_1\, U_2 + 276\, r^2\, U_2^2)\, U_3^2\nonumber \\&+ 30\, r^5\, (U_1^2 + 5\, r \,U_1\, U_2 + 3\, r^2\, U_2^2)\, U_3^3 - 3\, U_1\nonumber \\&\times (-15 \,U_1^3 + 98\, r\, U_1^2\, U_2 + 118\, r^2\, U_1\, U_2^2 \nonumber \\&+ 86 \,r^3\, U_2^3) \,U_3^4 - 3\, r^5\, (12\, U_1 + 25\, r\, U_2)\, U_3^5 \nonumber \\&+ 32\, r^2 \,U_1 \,U_2^2\, U_3^6 + 3 \,r^5\, U_3^7\bigg ] \,z^4+ U_3^2\nonumber \\&\times \bigg [2 \,r U_1^4 \,U_2\, (38\, U_1 + 17\, r\, U_2) + 15\, (15 - 13 \,r)\, U_1^5\, U_3 \nonumber \\&{} - 6 \,r\, U_1^2\, U_2\, (123\, U_1^2 + 146\, r \,U_1 \,U_2 + 51\, r^2\, U_2^2)\, U_3^2\nonumber \\&- 2\, r\, \bigg (15\, r^4 \,U_1^2 + 2\, \Big [-2 + r\, \Big (10 + r\, \big [-20 \nonumber \\&+ r\,\big (20 + r\, (-10 + 27\, r)\big )\big ]\Big )\Big ]\, U_1\, U_2 + 15\, r^6\, U_2^2\bigg )\, U_3^3\nonumber \\&+ 3\, U_1\, (-105\, U_1^3 + 268 \,r\, U_1^2\, U_2 + 366\, r^2 \,U_1\, U_2^2 \nonumber \\&+ 200\, r^3\, U2^3)\, U_3^4 + 30\, r^5\, (3 \,U_1 + 5\, r\, U_2)\, U_3^5\nonumber \\&+ 2\, (30 \,U_1^3 - 89\, r\, U_1^2\, U_2 - 88\, r^2\, U_1\, U_2^2 \nonumber \\&+ 15\, r^3\, U_2^3)\, U_3^6 - 21\, r^5\, U_3^7\bigg ]\, z^5 \nonumber \\&+ U_3\, \bigg [-19\, r\, U_1^5\, U_2 + 15\, (-20 + 19\, r) \,U_1^5\, U_3 \nonumber \\&+ 6\, r\, U_1^2\, U_2\, (107\, U_1^2 + 96\, r\, U_1\, U_2 + 17\, r^2\, U_2^2)\, U_3^2\nonumber \\&+ 5\, U_1\, \bigg (\Big [9 - 3\, r\,\Big (15 + r\, \big [-30 + r\, \big (30 + r\, (-15 \nonumber \\&+ 2\, r)\big )\big ]\Big )\Big ]\, U_1 + r\, \Big [-3 + r\, \Big (15 + r\, \big [-30 + r \,\big (30 \nonumber \\&+ r\, (-15 + 8\, r)\big )\big ]\Big )\Big ]\, U_2\bigg )\, U_3^3\nonumber \\&- 3 U_1\, (-315\, U_1^3 + 430 \,r\, U_1^2\, U_2 + 592\, r^2\, U_1\, U_2^2 \nonumber \\&+ 244\, r^3\, U_2^3) \,U_3^4 - 30\, r^5\, (4\, U_1 + 5\, r \,U_2)\, U_3^5\nonumber \\&+ 2\, (-240 \,U_1^3 + 191\, r\, U_1^2\, U_2 + 208\, r^2\, U_1\, U_2^2 \nonumber \\&- 75\, r^3\, U_2^3) \,U_3^6 + 63\, r^5 \,U_3^7 + 30\, r^2\, U_2^2\, U_3^8\bigg ]\, z^6 + U_3\nonumber \\&\times \bigg [3\, (75 - 74\, r) \,U_1^5 - r\, U_1^3\, U_2\, (305\, U_1 + 144\, r\, U_2)\, U_3\nonumber \\&+ 3\, \Big [-135 +r\, \Big (675 + r\, \big [-1350 \nonumber \\&+ r\, \big (1350 + r\, (-675 + 134\, r)\big )\big ]\Big )\Big ]\, U_1^2 \,U_3^2 \nonumber \\&+ 3 \,U_1\, (-525\, U_1^3 + 440\, r\, U_1^2\, U_2 + 538 \,r^2 \,U_1\,U_2^2 \nonumber \\&+ 152\, r^3\, U_2^3)\, U_3^3 + 3\, \Big [1 + r\,\Big ( -5 + r\nonumber \\&\times \big [10 + r\, \big (-10 + r\, (5 + 4\, r)\big )\big ]\Big )\Big ] (6\, U_1 + 5\, r\, U_2) \,U_3^4\nonumber \\&+ 2 \,(840 \,U_1^3 - 173\, r\, U_1^2\, U_2 - 280\, r^2\, U_1\, U_2^2 + 150 \,r^3\, U_2^3) \nonumber \\&\times U_3^5 - 105\, r^5\, U_3^6 - 10\, r\, U_2\, (16\, U_1 + 21\, r\, U_2)\, U_3^7\bigg ]\, z^7 \nonumber \\&+ U3 \,\bigg [U_1^4\, (-90\, U_1 + 61\, r \,U_2) - 3\, U_1\, (-525\, U_1^3 \nonumber \\&+ 286\, r\, U_1^2\, U_2 + 260\, r^2\, U_1\, U_2^2 + 38\, r^3\, U_2^3)\, U_3^2 \nonumber \\&+ 3 \,\bigg (12\, \Big [-5 + r\, \big (5 + (-5 + r)\, r\big )\,\big (5 + r\, (-5 + 4\, r)\big )\Big ]\nonumber \\&\times U_1+ 5\, r\,\Big [-9 + r\, \Big (45 + r\, \big [-90 + r\, \nonumber \\&\times \big (90 + r\, (-45 + 8\, r)\big )\big ]\Big )\Big ]\, U_2\bigg ) \,U_3^3\nonumber \\&- 10 \,(336\, U_1^3 + r \,U_1^2 \,U_2 - 48\, r^2 \,U_1 \,U_2^2 \nonumber \\&+ 30\, r^3\, U_2^3) \,U_3^4 + 3\,\Big [1 + r\, \Big (-5 + r\, \big [10 \nonumber \\&+ r\, \big (-10 + r\, (5 + 34\, r)\big )\big ]\Big )\Big ]\, U_3^5 \nonumber \\&+ 2\, (810\, U_1^2 + 434\, r\, U_1\, U_2 + 315\, r^2\, U_2^2)\, U_3^6\bigg ]\, z^8\nonumber \\&+ \bigg [-33 + 15\, r^9 + 30\, r^10 + r^7\, (3330 - 6462 \,U_1) \nonumber \\&+ r^8\, (-855 + 804\, U_1) - 9\, r^6\, (735 - 2518\, U_1 + 420\, U_1^2)\nonumber \\&+ 3\, r^5 \,(2751 + 2 \,U_1\, (-7559 + 3780\, U_1)) \nonumber \\&+ 210 \,r^4\, \Big (-33 + 10 \,U_1\, \big [27 + U_1 \,(-27 + 2\, U_1)\big ]\Big )\nonumber \\&+ 15\, U_1 \,|big(54 + U_1\, \big [-252 + U_1\nonumber \\&\times (280 + (-63 + U_1)\, U_1)\big ]\Big )\nonumber \\&- 30\, r^3\, \Big (-132 + 56 \,U_1\, \big [27 + 5 \,U_1\, (-9 + 2\, U_1)\big ]\nonumber \\&- 5\, U_2^3\, U_3^4\Big ) - r^2 \,\Big [45 \,\Big (33 + 7 \,U_1\, \big [-72 + U_1\, \nonumber \\&\times \big (180 + U_1\, (-80 + 3\, U_1)\big )\big ]\Big )\nonumber \\&- 156 \,U_1^2\, U_2^2 \,U_3^2 + 272\, U_1\, U_2^2\, U_3^4 + 1050\, U_2^2\, U_3^6\Big ]\nonumber \\&+ 2\, r\, \big [165 + 945 \,U_1^4 + 270\, U_2 \,U3^8 \nonumber \\&+ 6\, U_1^3\, (-1400 + 27\, U_2\, U_3^2)\nonumber \\&+ U_1^2 \,(11340 + 149\, U_2\, U3^4) - 72\, U_1\,\nonumber \\&\times (45 + 14\, U_2\, U_3^6)\big ]\bigg ] \,z^9 + U_3\, \bigg [9 \,U_1^3 \,(35\, U_1 \nonumber \\&- 6\, r\, U_2) - 2\, (1680\, U_1^3 + 131\, r\, U_1^2 \,U_2 \nonumber \\&- 48\, r^2\, U_1\, U_2^2 + 15\, r^3\, U_2^3)\, U_3^2 - 3 \,\Big [-55 + r\, \Big (275 \nonumber \\&+ r\, \big [-550 + r\, \big (550 + r\, (-275 + 48\, r)\big )\big ]\Big )\Big ]\, U_3^3 \nonumber \\&+ 14\, 405\, U_1^2 + 193\, r\, U_1\, U_2 + 75\, r^2 \,U_2^2\, U_3^4\nonumber \\&- 180\, (12 \,U_1 + 7\, r\, U_2)\, U_3^6\bigg ]\, z^{10} \nonumber \\&+ \bigg [-45\, U_1^4 + 2\, U_1 \,(840\, U_1^2 + 49\, r\, U_1\, U2 - 8 \,r^2\, U_2^2)\, U_3^2\nonumber \\&+ 3\, \Big [-165 + r\, \Big (825 + r\, \big [-1650 \nonumber \\&+ r\, \big (1650 + r\, (-825 + 164\, r)\big )\big ]\Big )\Big ]\, U_3^3\nonumber \\&- 70\, (81\, U_1^2 + 32 \,r \,U_1\, U_2 + 9\, r^2 \,U_2^2) \,U_3^4 \nonumber \\&+ 1890\, (2\, U_1 + r\, U_2)\, U_3^6\bigg ] \,z^{11} \nonumber \\&+ 2\, U\,3 \bigg [-U_1^2\, (240\, U_1 + 7\, r\, U_2) \nonumber \\&+ 15 \,(126\, U_1^2 + 38 \,r \,U_1\, U_2 + 7\, r^2\, U_2^2)\, U_3^2\nonumber \\&- 189\, (12\, U_1 + 5 \,r\, U_2)\, U_3^4 + 495\, U_3^6\bigg ]\, z^{12}\nonumber \\&+ 2\, \bigg [30\, U_1^3 - (810\, U_1^2 + 164\, r\, U_1\, U_2 + 15 \,r^2\, U_2^2)\, U_3^2\nonumber \\&+ 630 \,(3\, U_1 + r\, U_2) \,U_3^4 - 693\, U_3^6\bigg ] \,z^{13}\nonumber \\&+ U3\, \bigg [U_1\, (405 \,U_1 + 41\, r\, U_2) - 540\, (4\, U_1 + r\, U_2)\, U_3^2\nonumber \\&+ 1386\, U_3^4\bigg ] \,z^{14} - 45\, \bigg [U_1^2 - 3\, (6 \,U_1 + r\, U_2)\, U_3^2 \nonumber \\&+ 22\, U_3^4\bigg ]\, z^{15} - 15\, U_3\, \bigg [12\, U_1 + r\, U_2 - 33\, U_3^2\bigg ] \,z^{16}\nonumber \\&+ 3\, \bigg [6 U_1 - 55\, U_3^2\bigg ]\, z^{17} + 33\, U_3\, z^{18} - 3\, z^{19}, \end{aligned}$$

(36)

$$\begin{aligned} V_2 =&9\, r^{15}\, z^4 + 9 U_4^7\, z^4 \,(U_1 + z - z^2) \,(10\, U_1^3 \nonumber \\&+ 10\, U_1^2\, U_4\, z + 5\, U_1\, U_4^2 \,z^2 + U_4^3\, z^3)\nonumber \\&+ r\, U_4^4\, z^2\, \bigg [-6\, U_1^4\, U_2\, U_3 \nonumber \\&{} - 12\, U_1^3 \,U_4\, \big [U_2\, (U_3 - 11\, U_1\, U_3) + 3\, U_1\, U_4\big ]\, z\nonumber \\&- 2\, U_1^2\, \big [4\, U_2\, U_3 + 9\, U_1\, (35\, U_1 - 18\, U_2\, U_3)\big ]\, U_4^2\, z^2 \nonumber \\&{} - 2\, U_1\, (720\, U_1^2 + U_2\, U_3 - 158\, U_1\, U_2\, U_3)\, U_4^3\, z^3\nonumber \\&+ U_1\, (-1215 \,U_1 + 154\, U_2 \,U_3)\, U_4^4\, z^4 \nonumber \\&+ 30\, (-18\, U_1 + U_2\, U_3) \,U_4^5\, z^5 - 99 \,U_4^6 \,z^6\bigg ]\nonumber \\&+ 3\, r^{14}\, z^3\, \bigg [-6\, U_1 + 10\, U_2\, U_3 + 3\, z\, (-10 + 7 \,z)\bigg ] \nonumber \\&+ r^{13}\, z^2\, \bigg [9\, U_1^2 + 30\, U_2^2\, U_3^2 + 30\, U_2 \,U_3 \,z (-8 + 5\, z)\nonumber \\&+ U_1\, (-53\, U_2\, U_3 + 54\, (3 - 2\, z)\, z) \nonumber \\&+ 27 \,z^2\, (15 + 7\, (-3 + z)\, z)\bigg ]\nonumber \\&+ r^2\, U_4\, \bigg [15\, U_4^6 \,z^6\, (2\, U_2^2\, U_3^2 - 18\, U_2\, U_3\, U_4 \,z + 33\, U_4^2\, z^2)\nonumber \\&+ 2\, U_1\, U_4^4\, z^4\, \big [1215\, U_4^3\, z^3 + 8 \,U_2^2\, U_3^2 (-1 + 11 \,U_4\, z) \nonumber \\&+ U_2\, U_3\, U_4\, z\, (9 - 618\, z + 616\, z^2)\big ]\nonumber \\&+ U_1^4\, \big [-2\, U_2^2\, U_3^2\, (-1 + 5\, U_4\, z)\, (-6 + 13\, U_4\, z) \nonumber \\&+ 9\, U_4^4 \,z^2\, (1 + 28 \,z + 206 \,z^2)\nonumber \\&+ 2\, U_2\, U_3 \,U_4^2 \,z\, (1 + z - 319\, z^2 + 330\, z^3)\big ] \nonumber \\&+ 12\, U_1^3\, U_4 \,z\, \Big (420\, U_4^4\, z^4 \nonumber \\&+ U_2\, U_3\, U_4^2\, z^2\, \big [7 + 2\, z\, (-82 + 81\, z)\big ]\nonumber \\&+ U_2^2\, U_3^2\, \big [-2 + U_4\, z\, (13 - 12\, U_4\, z)\big ]\Big ) \nonumber \\&+ 2\, U_1^2\, U_4^2\, z^2\, \Big (2430\, U_4^4 \,z^4 + 2\, U_2\, U_3 \,U_4^2\, z^2 \nonumber \\&\times \big [16 + z \,(-557 + 553\, z)\big ]\nonumber \\&+ 3 \,U_2^2\, U_3^2\, \big [-2 + U_4\, z\, (9 + 22\, U_4\, z)\big ]\Big )\bigg ] \nonumber \\&+ r^{12}\, z\, \bigg [U_1^2\, \big [16\, U_2\, U_3 + 9\, z\, (-8 + 5\, z)\big ] \nonumber \\&- U_1\, \big [48\, U_2^2\, U_3^2 + 53\, U_2\, U_3\, z\, (-7 + 4 \,z) \nonumber \\&+ 54\, (-2 + z) \,z^2 \,(-6 + 5\,z)\big ]\nonumber \\&+ 3\, z\,\Big (30\, U_2^2\, U_3^2 \,(-2 + z) \nonumber \\&+ 10\, U_2\, U_3\, z\, \big [28 + 5\, z\, (-7 + 2 \,z)\big ] \nonumber \\&+ 3\, z^2 \,\big [-120 + 7\, z\, \big (36 + z\, (-24 + 5\, z)\big )\big ]\Big )\bigg ]\nonumber \\&+ r^{10}\, \bigg [3\, U_1^2\, \Big (2 \,U_2^2 \,U_3^2 \,(-4 + z) \nonumber \\&+ 16\, U_2\, U_3\, z\, \big [5 +\, (-5 + z)\, z\big ] + 3\, z^2\, \nonumber \\&\times \big [-56 + 5 \,z \,(21 + 2\, (-6 + z) \,z)\big ]\Big )\nonumber \\&+ U_1\, \Big [18\, U_2^3\, U_3^3 - 48\,U_2^2\, U_3^2\, z\, \big [10 + (-8 + z)\, z\big ] \nonumber \\&{} - 5\, U_2\, U_3\, z^2\,\Big (-371 + 6\, z\, \big [106 + z\, (-53 + 7\, z)\big ]\Big )\nonumber \\&- 54\, z^3\, \Big (42 + z\, \big [-112 \nonumber \\&+ z\, \big (105 + 4\, (-10 + z)\, z\big )\big ]\Big )\Big ] + 3\, z^2\, \nonumber \\&\times (10\, U_2^2\, U_3^2\, (-2 + z)\, (10 + (-10 + z)\, z)\nonumber \\&+ 10\, U_2\, U_3\, z\, (70 + z\, (-175 + 2\, (-5 + z)\, z\, (-15 + 2\, z)))\nonumber \\&- 3\, U_4\, z^2\, (252 + z\, (-630 + z\, (546 + z\, (-189 + 10 \,z)))))\bigg ]\nonumber \\&+ r^5\, \bigg [2\, U_1\, U_4\, z^3\, \Big (9\, U_4^4\, (U_4 - 756\, z^4)\nonumber \\&+ 40\, U_2^2\, U_3^2\, U_4\, z \,\big [7 + 5\, z\, (-10 + 9\, z)\big ]\nonumber \\&{} - 18\, U_2^3\, U_3^3\, \big [10 + z\, (-32 + 25\, z)\big ]\nonumber \\&- 7\, U_2\, U_3\, U_4^2\, z^2\, \big [18 + z\, (-786 + 773\, z)\big ]\Big ) \nonumber \\&+ U_1^4\, \Big [-45\, U4^2 \,z^2\, \big [7 + z\, (22 + 27\, z)\big ]\nonumber \\&+ 2\, U_2^2\, U_3^2\, \big [60 + z\, (-196 + 151\, z)\big ] \nonumber \\&+ 2\, U_2\, U_3\, z\, \Big (-20 + z\, \big [155 + (106 - 245\, z) \,z\big ]\Big )\Big ]\nonumber \\&+ 6\, U_1^3\, \Big [-1680\, U_4^3\, z^5 - 9\, U_2^3\, U_3^3\, \big [3 + z\, (-9 + 7\, z)\big ]\nonumber \\&{} - 10\, U_2\, U_3\, U_4\, z^3\, \big [7 + z\, (-89 + 83\, z)\big ]\nonumber \\&+ 2\, U_2^2\, U_3^2 \,z\, \Big (40 + z\, \big [-170 + (212 - 87\, z)\, z\big ]\Big )\Big ]\nonumber \\&+ 3\, U_4^4\, z^4\, \Big (3 - z\, \big [9 + z \,\big (350\, U_2^2\, U_3^2 - 1260\, U_2\, U_3\, U_4\, z \nonumber \\&+ 3\,(-3 + z + 462\, U_4^2 \,z^2)\big )\big ]\Big )\nonumber \\&+ U_1^2\, z \,\Big (9\, U_4^4\, z \,(U_4 - 1890\, z^4)\nonumber \\&{} - 20\, U_2\, U_3\, U_4^2\, z^3\, \big [28 + z\, (-581 + 559\, z)\big ] + 18\, U_2^3\, U_3^3\nonumber \\&\times \big (-15 + z\, \big [57 + 8\, z\, (-9 + 4\, z)\big ]\Big ) - 12\, U_2^2\, U_3^2 \,z\, \nonumber \\&\times \Big [-35 + 2\, z\, \big (75 + 2 \,z\, \big [-25 + z\, (-27 + 23 \,z)\big ]\big )\Big ]\Big )\bigg ] \nonumber \\&+ 3\, r^{11}\, \bigg [U_1^2\, \Big (2\, U_2^2\, U_3^2\, + 16\, U_2\, U_3 (-2 + z)\, z \nonumber \\&+ 3\, z^2\, \big [28 + 5\, z\, (-7 + 2\, z)\big ]\Big )\nonumber \\&+ U_1\, \Big (-2 \,U_2^3\, U_3^3 + 16\, U_2^2\, U_3^2\, (5 - 2\, z)\, z \nonumber \\&- 53\, U_2\, U_3 \,z^2\, \big [7 + 2\, (-4 + z)\, z\big ]1 \nonumber \\&+ 6\, z^3\, \big [84 + z \,(-168 + 5\, (21 - 4\, z)\, z)\big ]\Big )\nonumber \\&+ z^2\, \Big (30\, U_2^2 \,U_3^2\, \big [5 + (-5 + z) \,z\big ] \nonumber \\&+ 10\, U_2 \,U_3\, z\, \big [-56 + 5\, z\, (21 + 2\, (-6 + z)\, z)\big ]\nonumber \\&+ 3\, z^2\, \Big [210 + z\,\big (-588 + z\, \big [588 + z\, (-245 + 34\, z)\big ]\big )\Big ]\Big )\bigg ]\nonumber \\&+ r^9\, \bigg [-9 \,U_1^4 \,z^2 + U_1^2\, \Big [6\, U_2^2\, U_3^2\, \big [6 + z\, (-3 + 2\, z)\big ]\nonumber \\&+ 8\, U_2 \,U_3\, z\, \big [-40 + z \,(60 + (-24 + z)\, z)\big ] - 45\, z^2\, \nonumber \\&\times \Big (-14 + z\, \big [35 + 2 \,z\, \big (-15 + z\, (5 + z)\big )\big ]\Big )\Big ] \nonumber \\&+ U_1\, \Big [-18\, U_2^3\, U_3^3 + 16 U_2^2 U_3^2 z \big [30 + (-3 + z) z (12 + z)\big ]\nonumber \\&{} - 54\, U_4\, z^3\, \Big (-42 + z\, \big [98 + z\, \big (-77 + z\, (23 + 8\, z)\big )\big ]\Big ) \nonumber \\&+ 5\, U_2\, U_3\, z^2\, \Big (-371 + z\, \big [848 + z\nonumber \\&\times \big (-636 + z\, (166 + 23\, z)\big )\big ]\Big )\Big ]\nonumber \\&+ 3\, z^2\, \Big (-10\, U_2^2\, U_3^2\, \Big (-15 + z\, \nonumber \\&\times \big [30 + (-3 + z)\, z\, (6 + z)\big ]\Big )\nonumber \\&+ 10\, U_2\, U_3\, U4\, z\, \Big (-56 + z\, \big [119 + z \,\nonumber \\&\times \big (-81 + z\, (19 + 8 \,z)\big )\big ]\Big )\nonumber \\&{}- 3\, U_4^2\, z^2\, \big [-210 + z\, \big (462 + z \,\nonumber \\&\times \big [-336 + z\, (91 + 48\, z)\big ]\big )\big ]\Big )\bigg ] \nonumber \\&+ r^3\, \bigg [-15\, U_4^6 z^6\, (14 U_2^2 U_3^2 - 72 U_2 U_3 U_4 z + 99\, U_4^2\, z^2) \nonumber \\&+ 2\, U_1\, U4^3\, z^3\, \Big (-18\, U_2^3\, U_3^3 \,(1 - 2 z)^2 - 3240\, U_4^4\, z^4\nonumber \\&+ 8\, U_2^2\, U_3^2\, U4\, z\, (7 - 68 \,z + 66\, z^2) \nonumber \\&- 3\, U_2\, U_3\, U_4^2\, z^2 \,\big [12 + z \,(-724 + 719\, z)\big ]\Big ) + 3\, U_1^3\nonumber \\&\times \Big [-3360 \,U_4^5\, z^5 + 9 \,U_2^3 \,U_3^3\, (1 - 2 z)^2\, (-1 + 2 \,U_4\, z)\nonumber \\&{}- 4\, U_2\, U_3\, U_4^3\, z^3\, \big [21 + z\, (-417 + 406 \,z)\big ]\nonumber \\&+ 4\, U_2^2\, U_3^2\, U_4\, z\, \Big (12 + z\, \big [-73 + z\, \nonumber \\&\times \big (139 + 2 \,z \,(-61 + 24\, z)\big )\big ]\Big )\Big ] + U_1^2\, U_4\, z\nonumber \\&\times \Big [-11340 U_4^5 z^5 + 9 U_2^3 U_3^3 (1 - 2 z)^2(-3 + 4 U4\, z)\nonumber \\&- 4\, U_2\, U_3\, U_4^3\, z^3 \,\big [56 + z\, (-1687 + 1661\, z)\big ] \nonumber \\&- 12\, U_2^2\, U_3^2\, U_4\, z\, \Big (-7 + z\, \big [31 + z\, \nonumber \\&\times \big (19 + z\, (-101 + 55 \,z)\big )\big ]\Big )\Big ]\nonumber \\&+ U_1^4\, \Big (-9 \,U_4^4\, z^2\, (7 + 82\, z + 326 \,z^2) \nonumber \\&+ 2\, U_2\, U_3\, U_4^2 \,z\, \big [-6 + z\, (43 + 588\, z - 646\, z^2)\big ]\nonumber \\&+ 2 \,U_2^2\, U_3^2\, \Big [30 + z\, \big (-196 + z\, \nonumber \\&\times \big [453 + z\, (-476 + 195\, z)\big ]\big )\Big ]\Big )\bigg ]\nonumber \\&+ r^4\, \bigg [90\, U_4^5\, z^6\, (7\, U_2^2\, U_3^2 - 28\, U_2\, U_3 \,U_4\, z + 33\, U_4^2\, z^2)\nonumber \\&+ 2\, U_1\, U_4^2\, z^3\, \Big (5670 U_4^4\, z^4 + 18\, U_2^3\, U_3^3 \,(-1 + 2 \,z)\,\nonumber \\&\times (-5 + 8\, z) - 8\, U_2^2 \,U_3^2\, U_4 \,z\, \big [21 + z\, (-177 + 166\, z)\big ]\nonumber \\&+ 7 \,U_2\, U3 \,U_4^2 \,z^2 \,\big [12 + z\, (-624 + 617\, z)\big ]\Big ) \nonumber \\&+ U_1^4\, \Big (9\, U_4^3\, z^2\, \big [21 + z\, (128 + 291\, z)\big ]\nonumber \\&- 2\, U_2\, U_3\, U_4\, z\, \big [-15 + U_4\, z\, (125 + 604\, z)\big ] \nonumber \\&+ 2\, U_2^2\, U_3^2\, \big [-60 + z\,\big (294 + z\, (-453 + 238\, z)\big )\big ]\Big )\nonumber \\&+ 6\, U_1^3\, \Big [2100\, U_4^4\, z^5 - 9\, U_2^3\, U_3^3\,\nonumber \\&\times (-1 + 2 \,z)\, \big [2 + z\, (-5 + 4\, z)\big ] \nonumber \\&+ 10\, U_2\, U_3\, U_4^2\, z^3\, \big [7 + z\, (-114 + 109\, z)\big ]\nonumber \\&{} - 2\, U_2^2\, U_3^2\, z\,\Big (30 + z\, \big [-170 + z\,\nonumber \\&\times \big (318 + z\, (-261 + 85\, z)\big )\big ]\Big )\Big ]\nonumber \\&+ U_1^2\, z\, \Big (17010 \,U_4^5\, z^5 + 4\, U_2\, U_3\, U_4^3\, z^3\, \nonumber \\&\times \big [112 + z\, (-2849 + 2777\, z)\big ] + 9\, U_2^3\, U_3^3\, (-1 + 2 \,z)\nonumber \\&\times \Big (-15 + 2\, z\, \big [23 + 2\, z\, (-13 + 6\, z)\big ]\Big ) \nonumber \\&+ 6\, U_2^2\, U_3^2\, U_4\, z\, \big [-42 + z\, \big (183 + z \,\big [-17 \nonumber \\&+ z \,(-341 + 211 \,z)\big ]\big )\Big ]\Big )\bigg ] + r^7\, \bigg [-3 \,U_1^3\, \big [9\, U_2^3\, U_3^3 \nonumber \\&+ 4\, U_2\, U_3\, (7 - 32\, z)\, z^3 + 480\, U_4\, z^5 \nonumber \\&+ 4\, U_2^2\, U_3^2\, z\, (-12 + 17\, z)\big ] + U_1^4\, \big [12\, U_2^2\, U_3^2 \nonumber \\&+ 2\, U_2\, U_3\, z\, (-6 + 17\, z) + 9\, z^2\, (-21 + 2\, z + 4\,z^2)\big ] \nonumber \\&+ 3\, U_4^2\, z^2\, \Big [10\, U_2^2\, U_3^2\, (U_4 - 21\, z^4)\nonumber \\&+ 10\, U_2\, U_3\, U_4\, z\, \big [-8 + z\, (11 - 3\, z + 84\, z^3)\big ] \nonumber \\&{} - 9\, U_4^2\, z^2\, \Big (-15 + z \,\big [24 + z\, (-10 + z + 110\, z^2)\big ]\Big )\Big ]\nonumber \\&+ U_1\, z\, \Big [36\, U_2^3\, U_3^3\, z^2\, (-5 + 7 \,z)\nonumber \\&{} - 54\, U_4^3\, z^2\,\Big (-12 + z\, \big [20 + z\, (-9 + z + 120\, z^2)\big ]\Big )\nonumber \\&+ 16\, U_2^2\, U_3^2\, \Big (3 + z\, \big [-6 + z\,\big (3 + z\, (21 - 96\, z + 76\, z^2)\big )\big ]\Big )\nonumber \\&- U_2\, U_3\, U_4\, z\, \Big (371 + z \,\big [-901 + z\, \big (689 + z\, [9 + 14 z\,\nonumber \\&(-324 + 313\, z)]\big )\big ]\Big )\Big ]\nonumber \\&+ U_1^2\, \Big (9 \,U_2^3\, U_3^3 \,z\, (-15 + 19\, z) + 6\, U_2^2\, U_3^2\, \big [1 \nonumber \\&+ z\, (-1 + 2 z)\, (1 + 10\, (-4 + z)\, z)\big ]\nonumber \\&- 9\, U_4^2\, z^2\, \Big (-28 + z\, \big [49 + 3\, z\, (-8 + z + 180\, z^2)\big ]\Big )\nonumber \\&- 4\, U_2\,U_3\, z\, \Big [24 + z\, \big (-60 + z\, \big [48 \nonumber \\&+ z\, (44 + z\, (-637 + 583\, z))\big ]\big )\Big ]\Big )\bigg ] \nonumber \\&+ r^8\, \bigg [U_1^4\, z\, \big [2\, U_2 \,U_3 - 9\, (-7 + z)\, z\big ] \nonumber \\&+ 12\, U_1^3\, z\, (-2\, U_2^2\, U_3^2 + U_2\, U_3\, z^2 + 15\, z^4)\nonumber \\&+ U_1^2\, \Big [27\, U_2^3\, U_3^3 \,z - 6\, U_2^2 \,U_3^2\, U_4\, (4 + z + 15 \,z^2) \nonumber \\&+ 4\, U_2\, U_3\, z\, \Big (60 + z \,\big [-120 + z \,(72 + (4 - 91 \,z) \,z)\big ]\Big )\nonumber \\&+ 9 U_4 z^2 \Big (-56 + z \big [119 + z \big (-81 + z (19 + 134 z)\big )\big ]\Big )\Big ] \nonumber \\&+ 3\, U_4\, z^2\, \Big [10\, U_2^2\, U_3^2\, \big [-6 + z\, (9 - 3\, z + 7\, z^3)\big ]\nonumber \\&- 10\, U_2\, U_3\, U_4\, z\,\Big (-28 + z\, \big [49 + 3\, z\, (-8 + z + 12\, z^2)\big ]\Big )\nonumber \\&+ 3\, U_4^2\, z^2\, \Big (-120 + z\,\big [228 + z\,\big (-132 \nonumber \\&+ z (25 + 164\, z)\big )\big ]\Big )\Big ] + U_1\, \Big (6\, U_2^3\, U_3^3\, (1 + 6\, z^3)\nonumber \\&- 16\, U_2^2\, U_3^2\, z\, \Big (15 + z\, \big [-24 + U_4\, z\, (9 + 16\, z)\big ]\Big )\nonumber \\&+ 18\, U_4^2\, z^3\, \Big [-84 + z \,\Big (168 + z\, \big [-105 \nonumber \\&+ 2\, z\, (11 + 67\, z)\big ]\Big )\Big ]+ U_2\, U_3\, z^2\, \Big [1113 + z\, \big (-3180 \nonumber \\&+ z \,\big [3180 + z\, (-1200 + z\, (-1185 + 1274\, z))\big ]\big )\Big ]\Big )\bigg ] \nonumber \\&+ r^6\, \bigg [U_1^4\, \Big (2\, U_2^2\, U_3^2\, (-30 + 49\, z) + 9\, U_4 \,z^2\, \nonumber \\&\times \big [35 + 4\, z\, (11 + 5\, z)\big ]{}- 2\, U_2\, U_3\, z\, \big [-15 + z\, (82 + 7 \,z)\big ]\Big )\nonumber \\&- 6\, U_1^3\, \Big (-840\, U_4^2\, z^5 + 9\, U_2^3\, U_3^3\, (-2 + 3\, z) \nonumber \\&- 2\, U_2\, U_3\, z^3\, \big [21 + 4\, z\, (-48 + 43\, z)\big ]\nonumber \\&+ 2 \,U_2^2\, U_3^2\, z\, \big [30 + z\, (-85 + 53\, z)\big ]\Big ) \nonumber \\&+ 3\, U_4^3\, z^3\, \Big (350\, U_2^2\, U_3^2\, z^3 \nonumber \\&+ 10\, U_2\, U_3\, U_4 \,(U_4 - 126\, z^4) \nonumber \\&+ 3\, U_4^2\, z\, \big [-10 + z \,(13 - 3\, z + 462\, z^3)\big ]\Big ) \nonumber \\&+ U_1\, z^2\, \Big [36\, U2^3\, U3^3\, z \,\big [10 + z\, (-28 + 19\, z)\big ]\nonumber \\&- 80\, U_2^2\, U_3^2\, U_4\, z^2\, \big [7 + z\, (-41 + 35\, z)\big ] \nonumber \\&+ 54\, U_4^4\, z\, \big [-3 + z\, (4 - z + 210\, z^3)\big ]\nonumber \\&+ U_2\, U_3\, U_4^2\, \Big (53 + z\, \big [-106 + z \,\big (53 + 42 \,z \nonumber \\&\times (6 + z\, (-212 + 207\, z))\big )\big ]\Big )\Big ]\nonumber \\&+ U_1^2\, z\,\Big (18\, U_2^3\, U_3^3\, (-3 + 4 \,z)\, (-5 + 6\, z) \nonumber \\&+ 9\, U_4^3\, z\, \big [-8 + z\, (11 - 3 \,z + 1260\, z^3)\big ] - 6\, U_2^2\, U_3^2 \,z\, \nonumber \\&\times \Big (70 + z\, \big [-225 + 2\, z\, (50 + 27\, z)\big ]\Big )\nonumber \\&+ 4\, U_2\, U_3\, U_4\, \Big [4 + z\,\big (-8 + z\,\nonumber \\&\times \big [4 + z\, (112 + z\, (-1799 + 1699\, z))\big ]\big )\Big ]\Big )\bigg ], \end{aligned}$$

(37)

$$\begin{aligned} V_3 =&3\, r^2\, U_1^2\, U_2^2\, U_3^5\, \bigg [-6\, r^4 \,U_1 + 2\, U_1^2\, U_3^2 \nonumber \\&+ r^5\, (-15\, U_2 + 2\, U_3)\bigg ] + 2\, r^2\, U_1\, U_2 \,U_3^4\nonumber \\&\times \bigg [-8 \,U_1^3\, U_3^2\, (U_2 + U_3) + 2\, r^5\, U_2\, U_3^2\, (-9\, U_2 + 10\, U_3)\nonumber \\&+ r^4\, U_1\, U_3\, \big [(-39 + 36\, r)\, U_2 + 8\, U_3^2\big ] \nonumber \\&+ 3\, U_1^2\, \Big (\Big [2 + r\, \big (-8 + r \,\big [12 + r\, (-8 + 5 r)\big ]\big )\Big ]\, U_2 \nonumber \\&- 3\, r^3\, U_3^2\Big )\bigg ]\, z + r\, U_3^5\, \bigg [2\, r \,U_1\, U_2\,\nonumber \\&\times \Big (27\, r^3\, U_1^2 + \Big [8\, r^4\, (-3 + r + 2\, r^2) \nonumber \\&+ 3\, \Big (1 + r\, \big [-4 + r\, \big (6 + r\, (-4 + 27\, r)\big )\big ]\Big )\,\nonumber \\&\times U_1 - 7 \,U_1^3\Big ] \,U_2 + 18\, r^5\, U_2^2\Big )\nonumber \\&+ 2 \,U_1^2\, \big [-6\, r^4\, (3 + r) + (24 + 19\, r) \,U_1^2\big ]\, U_2\, U_3 \nonumber \\&+ 3\, r\, U_1^3\, (3\, U_1 - 4\, U_2^2)\, U_3^2\nonumber \\&+ r^4\, (9 \,U_1^2 + 50\, r \,U_1\, U_2 + 30\, r^2\, U_2^2) \,U_3^3\bigg ] \,z^2 \nonumber \\&{} - r\, U_3^4\, \bigg [2\, U_1^2 \,U_2 \Big (-3 \,\big [4 + (-8 + r)\, r\big ]\, \nonumber \\&\times \big [4 + r\, (-8 + 7\, r)\big ]\, U_1 + 3 \,r\, \Big [-6 + r\, \nonumber \\&\times \big (24 + r\, \big [-36 + r \,(24 + 7\, r)\big ]\big )\Big ]\, U2 - 46\, r \,U_1^2\, U_2\Big ) \nonumber \\&+ 4\, U_1\, U_2\, \big [-36\, r^4\, U_1 + 69\, U_1^3 - 19 \,r \,U_1^3\nonumber \\&+ 12\, r^5\, (2\, U_1 - 3\, U_2) + 26\, r^6\, U_2\big ] \,U_3 \nonumber \\&+ 3\, U_1^3\, \big [3 \,(4 + r)\, U_1 + 56\, r \,U_2^2\big ]\, U_3^2 \nonumber \\&+ r^4 \,\big [45\, U_1^2 + 2\, (9 + 91\, r) \,U_1\, U_2 + 90\, r^2\, U_2^2\big ]\, U_3^3 - 6\, \nonumber \\&r^4\, (3\, U_1 + 5\, r\, U_2)\, U_3^5\bigg ] \,z^3+ U_3^3\, \bigg [-6\, r\, U_1^3\, U_2\, \big [98 + r\nonumber \\&\times (-392 + r \,(588 + r\, (-392 + 95\, r)) + 17\, U_1\, U_2)\big ]\nonumber \\&+ 4\, r\, U_1^2 \,\big [16 + 177\, U_1^2 + 2\, r\, (-40 + r\, (80 + r\, \nonumber \\&\times (-80 + r\, (13 + 17\, r)))- 58\, U_1^2)\big ]\, U_2\, U_3\nonumber \\&+ 2\, U_1\, \Big [45\, U_1^3 + 2\, r^2\, \Big (8 - 4 \,r\, \big [8 + r \nonumber \\&\times (2 + r) \,(-6 + 7\, r)\big ] + 153\, U_1^2\Big )\, U_2^2\Big ] \,U_3^2 \nonumber \\&+ 6\, r \,\big [6\, U_1^4 + 35\, r^5\, U_1\, U_2 + 15 \,r^6\, U_2^2 \nonumber \\&+ 15\, r^4\, U_1 \,(U_1 + U_2)\big ] U_3^3 - 354\, r^2\, U_1^2\, U_2^2\, U_3^4\nonumber \\&- 6\, r^5\, (18\, U_1 + 25\, r\, U_2)\, U_3^5 + 9 \,r^5\, U_3^7\bigg ]\, z^4\nonumber \\&- U_3^2\, \bigg [-34\, r^2\, U_1^4 \,U_2^2 + 8\, (129 - 110\, r) \,r\, U_1^4 \,U_2\, U_3 \nonumber \\&+ 2\, U_1\, \bigg (45 \,\big [7 + 2\, (-4 + r)\, r\big ]\, U_1^3 \nonumber \\&+ 2 \,r \,\Big (89 + r\, \big [-356 + r \,\big (534 + r\, (-356 + 53\, r)\big )\big ]\Big )\nonumber \\&\times U_1\, U_2 + 2\, r^2\, \Big [44 + 8\, r\, \big (-22 + r\, (33 - 22\, r + 4\, r^2)\big ) \nonumber \\&+ 219\, U_1^2\Big ]\, U_2^2\bigg )\, U_3^2+ 2\, r\, \Big [45\, r^4\, U_1^2 + 2 \,\Big (-4 + r \nonumber \\&\times \big [20 + r\, \big (-40 + r\, [40 + r\, (25 + 9\, r)]\big )\big ]\Big )\, U_1\, U_2 \nonumber \\&+ 15\, r^6\, U_2^2\big ]\, U_3^3 \nonumber \\&- 6\, r\, U_1^2 \,U_2\, (268\, U_1 + 183\, r\, U_2)\, U_3^4 - 30 \,r^5\, (9 \,U_1\nonumber \\&+ 10\, r \,U_2)\, U_3^5 - 180\, U_1^3\, U_3^6 + 63\, r^5\, U_3^7\bigg ]\, z^5 \nonumber \\&+ U_3^2\, \bigg [2\, (444 - 425\, r) \,r\, U_1^4\, U_2 \nonumber \\&+ U_1^2\, \Big [45\, \big [42 + r\, (-68 + 27\, r)\big ]\, U_1^2\nonumber \\&+ 4\, r\, \Big (191 + 2\, r\, \big [-382 + r\, \big (573 \nonumber \\&+ r\, (-382 + 91\, r)\big )\big ]\Big )\, U_2 + 576\, r^2\, U_1\, U_2^2\big ]\, U_3 \nonumber \\&- 5\, U_1\, \Big [9\, \Big (-3 + r\, \big [15 + r\, \big (-30 \nonumber \\&+ r\, [30 + r \,(-15 + 2\, r)]\big )\big ]\Big )\, U_1\nonumber \\&+ 2\, r\, \Big (3 + r \,\Big [-15 + r \,\big (30 + r\, \big [-30 \nonumber \\&+ r\, (-3 + 10\, r)\big ]\big )\Big ]\Big )\, U_2\Big ]\, U_3^2\nonumber \\&- 12\, r\, U_1^2\, U_2\, (215 \,U_1 + 148\, r\, U_2)\, U_3^3\nonumber \\&- 60\, r^5 \,(6 \,U_1 + 5 \,r \,U_2)\, U_3^4\nonumber \\&+ 32\, U_1\, (-45\, U_1^2 + 13 \,r^2\, U_2^2)\, U_3^5 + 189 \,r^5\, U_3^6 \nonumber \\&+ 30\, r^2\, U_2^2\, U_3^7\bigg ]\, z^6 \nonumber \\&+ U_3^2\, \bigg [-3 \,U_1^3\, \Big (48 \,r^2\, U_2^2 \nonumber \\&+ U_1\, \big [1050 + 873\, r^2 + 20\, r\, (-96 + 7\, U_2)\big ]\Big ) + 9\, \nonumber \\&\times \Big (-135 + r\, \Big [675 \nonumber \\&+ r\, \big (-1350 + r\, \big [1350 + r\, (-675 + 134\, r)\big ]\big )\Big ]\Big )\, U_1^2\, U_3 \nonumber \\&+ 2 \,r\, U_1\, U_2\, \Big [40 (-4 + 33\, U_1^2) + r\, \Big (640 - 5\, r\nonumber \\&\times \big [192 + r \,(-128 + 41 \,r)\big ] + 807\, U_1\, U_2\Big )\Big ]\, U_3^2 \nonumber \\&+ 6 \,\Big [1 + r \,\Big (-5 + r\, \big [10 + r\, \big (-10 \nonumber \\&+ r\, (5 + 4\, r)\big )\big ]\Big )\Big ]\, (9 \,U_1 + 5\, r\, U_2)\, U_3^3\nonumber \\&+ 4\, U_1\, (1260\, U_1^2 - 173\, r\, U_1\, U2 - 140\, r^2\, U_2^2) \,U_3^4 \nonumber \\&- 315\, r^5\, U_3^5 - 210\, r^2\, U_2^2\, U_3^6\bigg ]\, z^7 \nonumber \\&+ U_3\, \bigg [84\, r\, U_1^4\, U_2 + 18\, (175 - 163\, r)\, U_1^4\, U_3 \nonumber \\&+ 2\, r\, U_1\, U_2\, \Big (868 - 858\, U_1^2 \nonumber \\&+ r\, \big [-3472 + r\, \big (5208 + r\, (-3472 + 877\, r)\big )\nonumber \\&- 390\, U_1\, U_2\big ]\Big )\, U_3^2 + 6\, \Big [18\, \Big (-5 + r \,\big [5 + (-5 + r)\, r\big ]\, \nonumber \\&\times \big [5 + r\, (-5 + 4\, r)\big ]\Big ) \,U_1 + 5\, r\, \Big (-9 + r\, \big [45 + r\nonumber \\&\times \big (-90 + r \,[90 + r\, (-45 + 8 \,r)]\big )\big ]\Big )\, U_2\big ]\, U_3^3 \nonumber \\&- 20 \,U_1 \,(504\, U_1^2 + r\, U_1\, U_2 - 24 \,r^2\, U_2^2)\, U_3^4\nonumber \\&+ 9\, \Big (1 + r \,\big [-5 + r\, \big (10 + r \,[-10 + r (5 + 34\, r)]\big )\big ]\Big )\, U_3^5 \nonumber \\&+ 90 \,(54\, U_1^2 + 7\, r^2\, U_2^2)\, U_3^6\bigg ]\, z^8 + U_3\, \bigg [18\, (-105 + 103\, r)\, \nonumber \\&\times U_1^4 + 12\, r\, U_1^2\, U_2\, (54\, U_1 + 13\, r\, U_2)\, U_3\nonumber \\&- 18\, \Big (-135 + r \,\big [675 \nonumber \\&+ r\, \big (-1350 + r\, [1350 + r\, (-675 + 134\, r)]\big )\big ]\Big )\, U_1\, U_3^2 \nonumber \\&+ 4\, U_1\, (3150\, U_1^2 + 149\, r\, U_1\, U_2 - 68\, r^2\, U_2^2)\nonumber \\&\times U_3^3 - 9 \,\Big (11 + 5\, r\, \big [-11 + r \,\big (22 + r\, [-22 + r\nonumber \\&\times (11 + 2 r)]\big )\big ]\Big ) U_3^4 - 42 \,(270 \,U_1^2 + 96 \,r \,U_1\, U_2 \nonumber \\&+ 25\, r^2\, U_2^2)\, U_3^5 + 1080\, r\, U_2\, U_3^7\bigg ] \,z^9 \nonumber \\&+ U_3\, \bigg [18\, U_1^3\, (35\, U_1 - 6\, r\, U_2)\nonumber \\&- 4\, U_1\, (40\, U_1 - 3 \,r\, U_2) \,(63\, U_1 + 8\, r\, U_2)\, U_3^2\nonumber \\&- 9\, \Big (-55 + r\, \big [275 \nonumber \\&+ r\, \big (-550 + r\, [550 + r\, (-275 + 48\, r)]\big )\big ]\Big )\, U_3^3 \nonumber \\&+ 14\, (1215\, U_1^2 + 386\, r\, U_1\, U_2 + 75\, r^2\, U_2^2)\, U_3^4 \nonumber \\&- 360\, (18\, U_1 + 7\, r\, U_2)\, U_3^6\bigg ]\, z^{10} + \bigg [-90\, U_1^4 \nonumber \\&+ 4\, U_1\, (1260\, U_1^2 + 49 \,r\, U_1\, U_2 - 4\, r^2\, U_2^2)\, U_3^2\nonumber \\&+ 9\, \Big (-165 + r\, \big [825 + r \,\big (-1650 + r\, [1650 \nonumber \\&+ r\, (-825 + 164\, r)]\big )\big ]\Big )\, U_3^3 - 70\, (243 \,U_1^2 + 64 \,r\, U_1 \,U_2 \nonumber \\&+ 9\, r^2 \,U_2^2)\, U_3^4 + 3780\, (3\, U_1 + r\, U_2) \,U_3^6\bigg ] \,z^{11} \nonumber \\&+ 2\, U_3\, \bigg [-2\, U_1^2\, (360\, U_1 + 7\, r \,U_2) \nonumber \\&+ 15\, (378\, U_1^2 + 76\, r\, U_1\, U_2 + 7\, r^2\, U_2^2)\, U_3^2\nonumber \\&- 378\, (18\, U_1 + 5\, r\, U2)\, U_3^4 + 1485\, U_3^6\bigg ]\, z^{12} \nonumber \\&+ 2\, \bigg [90\, U_1^3 - (2430\, U_1^2 + 328\, r\, U_1\, U_2 + 15\, r^2\, U_2^2)\, U_3^2\nonumber \\&+ 630\, (9\, U_1 + 2\, r\, U_2)\, U_3^4 - 2079\, U_3^6\bigg ]\, z^{13} \nonumber \\&+ U_3\, \bigg [U_1\, (1215\, U_1 + 82\, r\, U_2) - 1080 (6\, U_1 \nonumber \\&+ r \,U_2)\, U_3^2 + 4158\, U_3^4\bigg ] \,z^{14}\nonumber \\&- 135\, \bigg [U_1^2 - 2 \,(9\, U_1 + r \,U_2)\, U_3^2 + 22\, U_3^4\bigg ] \,z^{15} \nonumber \\&+ 15\, U_3\, \bigg [-36\, U_1 - 2\, r\, U_2 + 99\, U_3^2\bigg ]\, z^{16} \nonumber \\&+ 9 \,\bigg [6\, U_1 - 55\, U_3^2\bigg ]\, z^{17} + 99\, U_3\, z^{18} - 9\, z^{19}, \end{aligned}$$

(38)

$$\begin{aligned} V_4 =&3\, r^3\, U_1^3\, U_2^2\, U_3^7 \,(-9\, U_2 + 13\, U_3) \nonumber \\&+ r^2\, U_1\, U_2\, U_3^6\, \bigg [8\, r^4\, U_1\, U_3 + 8\, r^5\, U_2\, U_3 \nonumber \\&- 39\, U_1^2 \,U_2\, U_3 + r\, U_1\, (139\, U_1 \,U_2^2 - 213\, U_1\, U_2\, U_3 \nonumber \\&- 7\, (4\, U_1 + 3 \,U_2^2) \,U_3^2)\bigg ]\, z \nonumber \\&+ r^2 \,U_1\, U_3^5\, \bigg [-16\, r^5\, U_2^2\, U_3 + 9 \,r^3\, U_1\, U_3^3 \nonumber \\&+ r^4 \,U_2 \,U_3\, (-24\, U_1 + 31\, U_3^2)\nonumber \\&+ r\, U_1\, \big [-286\, U_1\, U_2^3 + 420 \,U_1\, U_2^2\, U_3 \nonumber \\&+ 3\, U_2\, (51\, U_1 + 46\, U_2^2)\, U_3^2 - 9\, U_1\, U_3^3\big ]\nonumber \\&+ U_1\, U_2 \,U_3\, (243\, U_1\, U_2 + 56\, U_1\, U_3 - 39\, U_2\, U_3^3)\bigg ]\, z^2 \nonumber \\&+ r\, U_3^4\, \bigg [294\, r^2\, U_1^3\, U_2^3\nonumber \\&+ r\, U_1\, U_2\, (24 \,r^4\, U_1 + 8\, r^5 \,U_2 - 579\, U_1^2\, U_2 \nonumber \\&- 345\, r U_1^2\, U_2)\, U_3\nonumber \\&- U_1^2\, U_2\, \Big (\big [84 + r\, (321 + 179\, r)\big ]\, \nonumber \\&U_1 + 375\, r^2\, U_2^2\Big ) \,U_3^2 \nonumber \\&+ r\, U_1\, \big [9\, U_1\, (-5\, r^3 + 3 \,U_1 + 2\, r\, U_1) - 124\, r^4 \,U_2\big ] \,U_3^3 \nonumber \\&+ 234\, r \,U_1^2\, U_2^2\, U_3^4 + 3\, r^4\, (6\, U_1 + 5\, r U_2)\, U_3^5\bigg ]\, z^3\nonumber \\&+ r\, U_3^3\, \bigg [-147\, r^2\, U_1^3\, U_2^3 + U_1^2\, U_2\, \Big (-112 + 8\, r \,\big [70 \nonumber \\&+ r\, \big (-140 + r\, [140 + r\, (-70 + 13\, r)]\big )\big ]\nonumber \\&+ 9\, r\, (75 + 4 \,r)\, U1\, U_2\Big )\, U_3 \nonumber \\&+ U_1^2\, U_2\, \Big (\big [840 - r \,(19 + 43 \,r)\big ]\, U_1 + 540 \,r^2\, U_2^2\Big )\, U_3^2\nonumber \\&+ 186\, r^5\, U_1\, U_2\, U_3^3 - 438\, r\, U_1^2\, U_2^2 \,U_3^4 - 75\, r^5\, U_2\, U_3^5 \nonumber \\&- 48\, r \,U_1\, U_2^2\, U_3^6 + 9\, U_3^3\, \Big (10\, r^4 \,U_1^2\nonumber \\&+ 2\, \big [-3 + (-3 + r)\, r\big ]\, U_1^3 - 12\, r^4\, U_1\, U_3^2 + r^4\, U_3^4\Big )\bigg ]\, z^4 \nonumber \\&+ U_3^3\, \bigg [3\, r^2\, (-145 + 66\, r) \,U_1^3\, U_2^2 \nonumber \\&- r\, U_1^2 \,U_2 \,\big [(3360 - 3846\, r + 986\, r^2) \nonumber \\&\,U_1 + 423\, r^2\, U_2^2\big ]\, U_3\nonumber \\&- 2\, U_1\, \big [45\, (r^5 - U_1) \,U_1 + \big ] 2\, r\, \Big (7 + r\, \big [-35 + r\, \big (70 \nonumber \\&+ r \,[-70 + r\, (35 + 24\, r)]\big )\big ]\Big ) \,U_2\Big ] \,U_3^2\nonumber \\&+ 3\, r\, U_1^2\, \big [9\, (4 + r)\, U1 + 2\, r\, U_2^2\big ]\, U_3^3 \nonumber \\&+ 30\, r^5 \,(9\, U_1 + 5\, r\, U_2)\, U_3^4 \nonumber \\&+ 2\, r\, U_1\, U_2\, (631\, U_1 + 216\, r \,U_2)\, U_3^5 - 63\, r^5\, U_3^6\bigg ]\, z^5\nonumber \\&+ U_3^3\, \bigg [r \,U_1^2 \,U_2\,\Big (141\, r^2\, U_2^2 + U1\, \big [7140 \nonumber \\&+ r\, (-11574 + 4559\, r + 180 \,U_2)\big ]\Big )\nonumber \\&+ r\, \Big (381 - 5\, r\, \big [381 + r\, \big (-762 + r\, [762 \nonumber \\&+ r \,(-381 + 70\, r)]\big )\big ]\Big )\, U_1\, U_2\, U_3\nonumber \\&+ 1002\, r^2\, U1^2\, U_2^2\, U_3^2 - 150\, r^6\, U_2\, U_3^3- 2\, r \,U_1\, U_2\,\nonumber \\&\times (2905\, U_1 + 816\, r\, U_2)\, U_3^4 + 9 \,U_3\, \Big (-5\, \Big [-3 + r\, \nonumber \\&\times \big (15 + r\, \big [-30 + r \,\big (30 + r \,(-15 + 2 r)\big )\big ]\big )\big ]\, U_1^2\nonumber \\&+ \Big (-80 + 3\, r\, \big [38 + r\, (-16 + 3 \,r)\big ]\Big ) \,U_1^3 - 40\, r^5\, U_1\, U_3^2 \nonumber \\&+ 21\, r^5\, U_3^4\Big )\bigg ]\, z^6 + U_3^2\, \bigg [-45\, r^2 \,U_1^3\, U_2^2 + U_1^2 \nonumber \\&\times \Big (45\, (-27 + 56\, U_1) + 9\, r\, \big [675 - 630\, U_1 \nonumber \\&+ r\, \big (r\, (1350 + r \,(-675 + 134\, r) - 114 \,U_1)\nonumber \\&+ 15\, (-90 + 31\, U_1)\big )\big ] + 5\, r\, (-1764 + 1499\, r) \,U_1\, U_2\Big )\, U_3 \nonumber \\&- 1353\, r^2\, U_1^2 \,U_2^2\, U_3^2 \nonumber \\&+ 3\, \Big (1 + r\, \big [-5 + r\, \big (10 + r\, [-10 + r \,(5 + 4\, r])\big )\big ]\Big )\nonumber \\&\times (18\, U_1 + 5\, r\, U_2)\, U_3^3 + 70\, r\, U_1\, U_2\, (209\, U_1 \nonumber \\&+ 48\, r\, U_2)\, U_3^4 - 315\, r^5\, U3^5 - 2068\, r\, U_1\, U_2\, U_3^6\bigg ] \,z^7\nonumber \\&+ U_3^2\, \bigg [(6384 - 6119\, r)\, r \,U_1^3\, U_2 \nonumber \\&+ 3\, U_1^2\, \Big (-6 \,\big [280 + r\, (-455 + 184\,r)\big ] \nonumber \\&\times U_1 + 245\, r^2\, U_2^2\Big )\, U_3 + 3\, \Big [36\, \Big (-5 + r\, \big [5 + (-5 + r)\, r\big ]\,\nonumber \\&\times \big [5 + r \,(-5 + 4\, r)\big ]\Big )\, U_1 + 5\, r\, \Big (-9 + r\, \big [45 + r\nonumber \\&\times \big (-90 + r\, [90 + r\, (-45 + 8\, r)]\big )\big ]\big )\, U_2\Big ]\, U_3^2 \nonumber \\&- 10\, r\, U_1\, U_2\, (2233\, U_1 + 408\, r\, U_2) \,U_3^3\nonumber \\&+ 9\, \Big (1 + r\, \big [-5 + r\, \big (10 + r\, [-10 + r\, (5 + 34\, r)]\big )\big ]\Big )\, U_3^4 \nonumber \\&+ 20\, U_1\, (243\, U_1 + 308\, r\, U_2) \,U_3^5\bigg ]\, z^8\nonumber \\&+ U_3^2\, \bigg [3\, U_1^2\, \Big (-49 \,r^2\, U_2^2 + 3\, U_1 \,\big [700 \nonumber \\&+ 577\, r^2 - 14\, r \,(91 + 20\, U_2)\big ]\Big )\nonumber \\&- 18\, \Big (-135 + r \,\big [675 + r\, \big (-1350 \nonumber \\&+ r\, [1350 + r\, (-675 + 134\, r)]\big )\big ]\Big )\, U_1\, U_3 \nonumber \\&+ 2 \,r\, U_1\, U_2\, (10661\, U_1 + 1464\, r\, U_2)\, U_3^2\nonumber \\&- 9\, \Big (11 + 5\, r\, \big [-11 + r\, \big (22 + r \,[-22 + r \,(11 + 2\, r)]\big )\big ]\Big )\nonumber \\&\times U_3^3 - 11340\, U_1\, (U_1 + r\, U_2) \,U_3^4 + 540 \,r\, U_2\, U_3^6\bigg ]\, z^9 + U_3\nonumber \\&\times \bigg [420\, r\, U_1^3\, U_2 + 126\, (-40 + 37\, r)\, U_1^3\, U_3 - 2\, r\, U_1\, U_2\,\nonumber \\&\times (6251\, U_1 + 576\, r\, U_2) \,U_3^2 - 9\, \Big (-55 + r\, \big [275 + r\nonumber \\&\times \big (-550 + r\, [550 + r\, (-275 + 48\, r)]\big )\big ]\Big )\, U_3^3 \nonumber \\&+ 14\, U_1\, (1215 \,U_1 + 967\, r \,U_2)\, U_3^4 \nonumber \\&- 180\, (36 \,U_1 + 7\, r \,U_2)\, U_3^6\bigg ]\, z^{10}\nonumber \\&+ U3 \,\bigg [18 (140 - 137\, r)\, U_1^3 \nonumber \\&+ 2\, r \,U_1 \,U_2\, (2065\, U_1\, + 96\, r\, U_2)\, U_3\nonumber \\&+ 9\, \Big (-165 + r\, \big [825 + r\, \big (-1650 \nonumber \\&+ r\, [1650 + r \,(-825 + 164\, r)]\big )\big ]\Big )\, U_3^2\nonumber \\&- 14\, U_1\, (1215 \,U_1 + 754\, r\, U_2) \,U_3^3 \nonumber \\&+ 1890\, (6\, U_1 + r\, U_2)\, U_3^5\bigg ]\, z^{11}\nonumber \\&+ 2\, U_3\, \bigg [-5\, U_1^2\, (72\, U_1 + 59\, r\, U_2) \nonumber \\&+ 42\, U_1\, (135\, U_1 + 62\, r\, U_2)\, U_3^2\nonumber \\&- 189\, (36\, U_1 + 5\, r\, U_2)\, U_3^4 + 1485\, U_3^6\bigg ]\, z^{12} \nonumber \\&+ 2 \,\bigg [45 \,U_1^3 - 10\, U_1\, (243\, U_1 + 74\, r \,U_2)\, U_3^2 \nonumber \\&+ 630 \,(9 \,U_1 + r\, U_2) \,U_3^4 - 2079\, U_3^6\bigg ]\, z^{13}\nonumber \\&+ U3\, \bigg [5 \,U_1\, (243\, U_1 + 37 \,r\, U_2) - 540 \,(12\, U_1 \nonumber \\&+ r\, U_2)\, U_3^2 + 4158\, U_3^4\bigg ]\, z^{14} - 135\, \bigg [22 - 88\, r^3 + 22\, r^4\nonumber \\&+ (-18 + U_1) \,U_1 + r\, (-88 + 36\, U_1 - U_2\, U_3) \nonumber \\&+ r^2\, (132 - 18 \,U_1 + U_2\, U_3)\bigg ]\, z^{15}\nonumber \\&- 15\, U_3\, \bigg [36\, U_1 + r\, U_2 - 99\, U_3^2\bigg ]\, z^{16} + 9\, \nonumber \\&\bigg [6\, U_1 - 55\, U_3^2\bigg ]\, z^{17} + 99\, U_3\, z^{18} - 9 \,z^{19}, \end{aligned}$$

(39)

$$\begin{aligned} V_5=&-9 \,r^3\, U_1^2\, U_2^2\, U_3^5\, \bigg [r^4\, U_2 - (-1 + 2\, r)\, U_1\, (-1 + r \,U_3)\bigg ] \nonumber \\&+ r^2 \,U_1\, U_2\, U_3^4\, \bigg [4\, r^5\, U_2\, U_3^3 + 8\, r^4\, U_1\, U_3^2\, (-6\, U_2 + U_3) \nonumber \\&+ U_1^2\, \Big (3\, \big [-3 + r\, \big (-7 + r\, [39 + r\, (-45 + 19\, r)]\big )\big ]\, U_2\nonumber \\&- 2\, r\, \big [5 + 2\, r\, (-5 + 7\, r)\big ] \,U_3^2\Big )\bigg ]\, z + r^2\, U_1\, U_3^5\, \bigg [U_1\, U_2\, \nonumber \\&\times \Big (\big [20 + r\, \big (23 + r \,(-106 + 117\, r)\big )\big ]\, U_1\nonumber \\&+ 3 \,\big [-3 + r\, \big (12 + r\, [-18 + r\, (12 + 29\, r)]\big )\big ]\, U_2\Big ) \nonumber \\&+ 2\, U_2 \,\big [6\, (-3 + r)\, r^3 U_1 + 4 \,r^4\, (-3 + 2\, r)\, U_2\nonumber \\&+ 3\, (7 + 17\, r)\, U_1^2 \,U_2\big ]\, U_3 + r\, \big [9\, (r^2 - U_1) \,U_1 \nonumber \\&+ 28 \,r^3\, U_2\big ]\, U_3^3\bigg ]\, z^2\nonumber \\&- r \,U_3^4\, \bigg [U_1^2\, U2\, \Big (\big [30 + r\, \nonumber \\&\times \big (81 + r\, [-181 + r\, (-1 + 125\, r)]\big )\big ]\, U_1 \nonumber \\&+ 3\, r\, \big [-3 + r\, (6 + r)\big ]\, \big [3 + r\, (-6 + 7\, r)\big ]\, U_2\Big )\nonumber \\&+ r \,U_1\, U_2 \,\big [24\, r^3\, (-6 + 5\, r)\, U_1 + 4 \,r^4\, (-18 + 17\, r)\, U_2 \nonumber \\&+ 3 \,(11 + 53\, r)\, U_1^2 \,U_2\big ]\, U_3+ r\, U_1\, \big [-9 \,U_1\, (-5\, r^3 \nonumber \\&+ 3\, U_1 + 2\, r \,U_1) + 2\, r^3\, (9 + 47\, r) \,U_2\big ]\, U_3^3 \nonumber \\&- 3\, r^4 \,(6\, U_1 + 5\, r\, U_2) \,U_3^5\bigg ] \,z^3\nonumber \\&+ r\, U_3^3\, \bigg [\Big (354 + r\, \big [-691 + r\, (277 + (103 - 25\, r) \,r)\big ]\Big )\,\nonumber \\&\times U_1^3\, U_2 + 8\, U_1^2\, U_2 \Big (-5 + r\, \big [25 - 15\, U_1\, U_2\nonumber \\&+ r\, (-50 + r\, (50 + r\, (-52 + 31\, r)) + 33 \,U_1\, U_2)\big ]\Big )\, U_3 \nonumber \\&- 24\, r\, (1 - 4\, r + 6\, r^2)\, U_1\, U_2^2\, U_3^2\nonumber \\&+ 6\, U_1 \,\Big (3 \,U_1\, \big [5\, r^4 + \big (-3 + (-3 + r)\, r\big ) \,U_1\big ] + r^4\, (15 \nonumber \\&+ 13\, r)\, U_2 + 16\, r^4\, U_2^2\Big )\, U_3^3 + 117\, r\, U_1^2\, U_2^2\, U_3^4\nonumber \\&- 3\, r^4\, (36\, U_1 + 25\, r\, U_2)\, U_3^5 + 9\, r^4\, U_3^7\bigg ]\, z^4 \nonumber \\&+ U_3^3\, \bigg [24\, (11 - 13\, r)\, r^2 \,U_1^3\, U_2^2\nonumber \\&+ 2 \,r\, U_1\, U_2\, \Big (U_1\, \big [271 - 762\, U_1 + r\, (-1084 + r\, (1626 \nonumber \\&+ r\, (-1084 + 343\, r) - 223\, U_1) + 879\, U_1)\big ]\nonumber \\&+ 12\, r\, \big [9 + 2\, r \,\big (-18 + r\, [27 + r\, (-18 + 5\, r)]\big )\big ]\, U_2\Big )\, U_3 \nonumber \\&+ 2\, U_1\, \Big [45\, U_1 \,(-r^5 + U_1) + r\, \Big (-5 + r\, \big [25 \nonumber \\&+ r\, \big (-50 + r\, [50 + r\, (-115 + 39\, r)]\big )\big ]\Big )\, U_2\Big ] \,U_3^2 \nonumber \\&+ 9 \,r\, U_1^2\, \big [3 \,(4 + r)\, U_1 - 79\, r \,U_2^2\big ]\, U_3^3\nonumber \\&+ 30\, r^5\, (9 \,U_1 + 5\, r\, U_2)\, U_3^4 - 63\, r^5\, U_3^6\bigg ]\, z^5 \nonumber \\&+ U_3^3\, \bigg [r \,U_1^2\, U_2 \,\Big (-2714 + 3360\, U_1 + r\, \big [10856 + 10856\, r^2 \nonumber \\&- 2750\, r^3 + 59\, r \,(-276 + 37\, U_1) \nonumber \\&- 6\, U_1\, (915 + 32\, U_2)\big ]\Big ) + U_1\, \Big [9\, U_1\, \Big (15 - 5\, r \,\big [15 + r\, \nonumber \\&\times \big (-30 + r\, [30 + r\, (-15 + 2\, r)]\big )\big ]\nonumber \\&+ \big [-80 + 3\, r\, \big (38 + r\, (-16 + 3\, r)\big )\big ] \,U_1\Big ) \nonumber \\&+ r \,\Big (183 - 5 \,r \,\big [183 + r\, \big (-366 + r\, [366 \nonumber \\&+ r\, (-219 + 67 \,r)]\big )\big ]\Big )\, U_2\Big ]\, U_3 \nonumber \\&+ 1440\, r^2 \,U_1^2\, U_2^2 \,U_3^2 - 30 \,r^5\, (12\, U_1 + 5\, r \,U_2)\, U_3^3 - 816\, \nonumber \\&r^2\, U_1\, U_2^2\, U_3^4 + 189 \,r^5 \,U_3^5\bigg ] \,z^6 + U_3^2 \,\bigg [48\, r^2\, U_1^3\, U_2^2 \nonumber \\&+ U_1^2\, \Big (45\, (-27 + 56\, U_1) + 9\, r\, \big [675 - 630\, U_1\nonumber \\&+ r\, \big (r \,(1350 + r\, (-675 + 134 \,r) - 114\, U_1) \nonumber \\&+ 15\, (-90 + 31\, U_1)\big )\big ] + 5\, r\, (-846 + 725\, r)\, U_1\, U_2\Big )\nonumber \\&U_3 - 2 \,r\, U_1\, U_2 \,\Big (557 + 2\, r \,\big [-1114 \nonumber \\&+ r\, \big (1671 + r\, (-1114 + 301\, r)\big ) \nonumber \\&+ 360\, U_1\, U_2\big ]\Big ) \,U_3^2 + 3 \Big (1 + r\, \big [-5 + r\, \big (10 \nonumber \\&+ r\, [-10 + r\, (5 + 4\, r)]\big )\big ]\Big ) (18 \,U_1 + 5\, r \,U_2)\, U_3^3\nonumber \\&+ 2\, r \,U_1\, U_2\, (3571\, U_1 + 840\, r\, U_2) \,U_3^4 - 315\, r^5\, U_3^5\bigg ]\, z^7 \nonumber \\&+ U_3^2\, \bigg [(3090 - 2969\, r) \,r\, U_1^3\, U_2\nonumber \\&+ 2\, U_1\, \Big (-9\, \big [280 + r \,(-455 + 184\, r)\big ]\, U_1^2 + r\, \big [1757 \nonumber \\&+ 2\, r\, \big (-3514 + r\, [5271 + r\, (-3514 + 883\, r)]\big )\big ]\, U_2\nonumber \\&+ 360\, r^2\, U_1 \,U_2^2\Big )\, U_3 + 3\, \Big (36\, \big [-5 + r\, \big (5 + (-5 + r)\, r\big )\,\nonumber \\&\times \big (5 + r\, (-5 + 4\, r)\big )\big ]\, U_1+ 5\, r\, \big [-9 + r\, \big (45 \nonumber \\&+ r \,[-90 + r\, (90 + r\, (-45 + 8\, r))]\big )\big ]\, U_2\Big )\, U_3^2 \nonumber \\&- 10\, r\, U_1\, U_2\, (1117\, U_1 + 204\, r\, U_2)\, U_3^3\nonumber \\&+ 9\, \Big (1 + r\, \big [-5 + r\, \big (10 + r\, [-10 + r\, (5 \nonumber \\&+ 34\, r)]\big )\big ]\Big )\, U_3^4 + 4860\, U_1^2\, U_3^5\bigg ]\, z^8\nonumber \\&+ U_3^2\, \bigg [9\, U_1^2\, \Big (-16\, r^2\, U_2^2 + U_1\, \big [700 + 577\, r^2 \nonumber \\&- 2 \,r (637 + 68\, U_2)\big ]\Big )\nonumber \\&- 18\, \Big (-135 + r\, \big [675 + r \,\big (-1350 \nonumber \\&+ r \,[1350 + r\, (-675 + 134 \,r)]\big )\big ]\Big )\, U_1\, U_3\nonumber \\&+ 2\, r \,U_1\, U_2\, (5405\, U_1 + 732 \,r\, U_2)\, U_3^2\nonumber \\&- 9\, \Big (11 + 5\, r\, \big [-11 + r\, \nonumber \\&\times \big (22 + r\, [-22 + r\, (11 + 2\, r)]\big )\big ]\Big )\, U_3^3 \nonumber \\&- 126\, U_1 \,(90\, U_1 + 53\, r\, U_2)\, U_3^4 + 540\, r\, U_2\, U_3^6\bigg ]\, z^9 \nonumber \\&+ U_3\, \bigg [204\, r\, U_1^3\, U_2 + 126\, (-40 + 37\, r)\, U_1^3\, U_3 \nonumber \\&- 2\, r \,U_1\, U_2\, (3191\, U_1 + 288\, r\, U_2) \,U_3^2\nonumber \\&- 9\, \Big (-55 + r\, \big [275 + r\, \big (-550 + r \,[550 + r\, (-275 \nonumber \\&+ 48 \,r)]\big )\big ]\Big ) \,U_3^3 + 70\, U_1\, (243\, U_1 + 116\, r\, U_2) \,U_3^4\nonumber \\&- 180\, (36\, U_1 + 7\, r\, U_2)\, U_3^6\bigg ]\, z^{10} \nonumber \\&+ U_3\, \bigg [18 \,(140 - 137\, r)\, U_1^3 \nonumber \\&+ 2\, r\, U_1\, U_2\, (1057\, U_1 + 48\, r\, U_2)\, U_3\nonumber \\&+ 9 \,\Big (-165 + r \,\big [825 + r\, \big (-1650 + r\, [1650\nonumber \\&+ r\, (-825 + 164\, r)]\big )\big ]\Big )\, U_3^2 \nonumber \\&- 14\, U_1\, (1215\, U_1 + 457 \,r\, U_2)\, U_3^3 \nonumber \\&+ 1890\, (6\, U_1 + r\, U_2)\, U_3^5\bigg ]\, z^{11} \nonumber \\&+ 2\, U_3\, \bigg [-U_1^2\, (360 \,U_1 + 151 \,r\, U_2) \nonumber \\&+ 3\, U_1\, (1890\, U_1 + 529\, r\, U_2) \,U_3^2\nonumber \\&- 189\, (36\, U_1 + 5\, r \,U_2)\, U_3^4 + 1485\, U_3^6\bigg ] z^{12} + 2\, \nonumber \\&\times \bigg [45\, U_1^3 - 2 \,U_1\, (1215\, U_1 + 226\, r\, U_2)\, U_3^2\nonumber \\&+ 630\, (9\, U_1 + r\, U_2)\, U_3^4 - 2079\, U_3^6\bigg ] \,z^{13}\nonumber \\&+ U_3\, \bigg [U_1\, (1215\, U_1 + 113\, r\, U_2) \nonumber \\&- 540\, (12\, U_1 + r\, U_2)\, U_3^2 + 4158\, U_3^4\bigg ]\, z^{14} \nonumber \\&- 135\, \bigg [22 - 88 \,r^3 + 22\, r^4 + (-18 + U_1)\, U1 \nonumber \\&+ r\, (-88 + 36\, U_1 - U_2\, U_3) \nonumber \\&+ r^2\, (132 - 18\, U_1 + U_2 \,U_3)\bigg ]\, z^{15} \nonumber \\&- 15\, U_3\, \bigg [36\, U_1 + r\, U_2 - 99\, U_3^2\bigg ] \,z^{16} + 9\, \nonumber \\&\times \bigg [6 \,U_1 - 55\, U_3^2\bigg ]\, z^{17} + 99\, U_3 \,z^{18} - 9\, z^{19}, \end{aligned}$$

(40)

$$\begin{aligned} V_6 =&r^6\, U_1^3\, U_2^2 U_3^4\, (-35\, U_2 + 3\, U_3) \nonumber \\&+ r^3\, U_1^2\, U_2\, U_3^4\, \bigg [3\, r^2\, (-7 + 6\, r)\, U_1\, U_2 - 21\, r^3\, U2^2\, U_3 \nonumber \\&{} - 2 \,\Big (2\, \big [-2 + r\, (4 + 7\, r)\big ]\, U_1 \nonumber \\&+ 39\, r^3\, U_2\Big )\, U_3^2 + 8\, r^3\, U_3^3\bigg ]\, z\nonumber \\&+ r^2\, U_1\, U_3^4\, \bigg [21\, r^3\, U_1\, U_2^2\, (2\, U_1 + r\, U_2) \nonumber \\&+ U_1\, U_2\, \Big (\big [-16 + r\, \big (5 + r \,(38 + 81\, r)\big )\big ]\, U_1\nonumber \\&+ 3\, r^3\, (-7 + 59\, r)\, U_2\Big )\, U_3 + 24\, r^3\, (-3 + 2\, r)\, U_1\, U_2\, U_3^2 \nonumber \\&{} - 48\, r^4\, U_2^2\, U_3^3 + r\, \big [9\, (r^2 - U_1)\nonumber \\&\,U_1 + 25 \,r^3\, U_2\big ]\, U_3^4\bigg ]\, z^2\nonumber \\&+ r\, U_3^3\, \bigg [-21\, r^4\, U_1^3\, U_2^2 - U_1^2\, U_2\, \Big (\big [-24 \nonumber \\&+ r\, \big (9 + r\, [17 + r\, (35 + 71\, r)]\big )\big ]\, U_1\nonumber \\&+ 3\, r^4\, (-21 + 47\, r)\, U_2\Big ) \,U_3\nonumber \\&+ 24\, (12 - 11\, r)\, r^4 U_1^2\, U_2\, U_3^2 + 144\, r^5\, U_1\, U_2^2\, U_3^3 \nonumber \\&+ r \,U_1\, \big [9\, U_1\, (-5\, r^3 + 3\, U_1 + 2\, r\, U_1)\nonumber \\&- 4\, r^3 \,(9 + 16\, r)\, U_2\big ]\, U_3^4 + 3\, r^4\, (6\, U_1 + 5\, r\, U_2)\, U_3^6\bigg ]\, z^3\nonumber \\&- r\, U_3^3\, \bigg [\Big (132 + r\, \big [-317 + r\, \big (281 \nonumber \\&+ r \,(-139 + 7\, r)\big )\big ]\Big )\, U_1^3\, U2+ U_1^2\, U_2\, \Big [-8 \,\Big (4 \nonumber \\&+ r\, \big [-20 + r\, \big (40 + r \,[-40 + r\, (-34 + 49\, r)]\big )\big ]\Big ) \nonumber \\&+ 63\, r^4\, U_2\Big ]\, U_3 + 144 \,r^5\, U_1\, U_2^2\, U_3^2\nonumber \\&+ 6\, U_1 \,\Big (-3\, U_1\, \big [5\, r^4 + (-3 + (-3 + r)\, r)\, U_1\big ]\nonumber \\&+ 5 \,(-6 + r)\, r^4\, U_2\Big )\, U_3^3 \nonumber \\&+ 3 \,r^4\, (36\, U_1 + 25\, r\, U_2)\, U_3^5 - 9\, r^4\, U_3^7\bigg ]\, z^4\nonumber \\&+ U_3^3\, \bigg [21\, r^5\, U_1^2 \,U_2^2 + 2\, r\, U_1 \,U_2\, \Big (U_1\, \big [-89 + 156\, U_1 \nonumber \\&+ r\, \big (356 - 165\, U_1 + r\, (-534 + r\, (356 + 55\, r) + 47\, U_1)\big )\big ]\nonumber \\&+ 24\, r^5\, U_2\Big )\, U_3 + 2\, U_1 \,\Big [45\, U_1\, (-r^5 + U_1) + 2\, r \,\Big (2 + r\, \nonumber \\&\times \big [-10 + r\, \big (20 + r\, [-20 + r\, (-80 + 63\, r)]\big )\big ]\Big )\, U_2\Big ]\, U_3^2\nonumber \\&+ 27\, r\, (4 + r)\, U_1^3\, U_3^3 + 30\, r^5\nonumber \\&\times (9\, U_1 + 5 \,r\, U_2)\, U_3^4 - 63\, r^5\, U_3^6\bigg ]\, z^5\nonumber \\&+ U_3^3\, \bigg [r \,U_1^2 \,\Big [382 - 420 \,U_1 + r \,\big (-1528 + r\, (2292 \nonumber \\&+ 2\, r\, (-764 + 155 \,r) - 193 \,U_1) + 594\, U_1\big )\Big ]\, U_2\nonumber \\&+ U_1\, \Big [9\, U_1\, \Big (15 - 5\, r\, \big [15 + r \,\big (-30 + r\, [30 \nonumber \\&+ r\, (-15 + 2\, r)]\big )\big ] + (-80 \nonumber \\&+ 3\, r\, (38 + r\, (-16 + 3\, r)))\, U_1\Big )\nonumber \\&{} - 5\, r\, \Big (3 + r\, \big [-15 + r\, \big (30 + r\, [-30 \nonumber \\&+ r\, (-57 + 64\, r)]\big )\big ]\Big )\, U_2\Big ]\, U_3 \nonumber \\&{} - 30\, r^5\, (12\, U_1 + 5\, r\, U_2)\, U_3^3 + 189\, r^5\, U_3^5\bigg ]\, z^6 \nonumber \\&+ U_3^3\, \bigg [U_1^2 \,\Big (45 (-27 + 56\, U_1) + 9\, r\,\nonumber \\&\times \big [675 - 630\, U_1 + r \,\big (r\, (1350 + r \,(-675 + 134\, r) \nonumber \\&{} - 114\, U_1) + 15\, (-90 + 31\, U_1)\big )\big ] \nonumber \\&+ 5\, (72 - 49\, r)\, r\, U_1\, U_2\Big ) - 20\, r\, \Big (8 + r\, \big [-32 \nonumber \\&+ r \,\big (48 + r \,(-32 + 17\, r)\big )\big ]\Big )\, U_1\, U_2\, U_3\nonumber \\&+ 3\, \Big (1 + r\, \big [-5 + r\, \big (10 + r\, [-10 + r\, (5 + 4 \,r)]\big )\big ]\Big )\nonumber \\&\times (18\, U_1 + 5\, r\, U_2)\, U_3^2 - 346\, r\, U_1^2\, U_2\, U_3^3 - 315\, r^5\, U_3^4\bigg ]\, z^7 \nonumber \\&+ U_3^2\, \bigg [r \,(-204 + 181\, r)\, U_1^3\, U_2 \nonumber \\&+ 2\, U_1\, \Big (-9\, \Big [280 + r\, (-455 + 184\, r)\big ]\, U_1^2 \nonumber \\&+ 2 \,r\, \big [217 + 2\, r\,\big (-434 + r\, [651 \nonumber \\&+ r\, (-434 + 113\, r)]\big )\big ] \,U_2\Big )\, U_3 \nonumber \\&+ 3\, \Big [36\, \Big (-5 + r\, \big [5 + (-5 + r)\, r\big ]\, \big [5 + r\, (-5 + 4\, r)\big ]\Big ) \nonumber \\&\times U_1 + 5\, r\, \Big (-9 + r \,\big [45 + r\, \big (-90 \nonumber \\&+ r\, [90 + r\, (-45 + 8\, r)]\big )\big ]\Big ) \,U_2\Big ]\, U_3^2 - 10\, r\, U_1^2\, U_2\, U_3^3\nonumber \\&+ 9\, \Big (1 + r\, \big [-5 + r\, \big (10 + r\, [-10 + r\, (5 + 34\, r)]\big )\big ]\Big )\, U_3^4 \nonumber \\&+ 4860\, U_1^2\, U_3^5\bigg ] \,z^8\nonumber \\&+ U_3^2\, \bigg [9\, U_1^3\, (700 + r\, (-1274 + 577\, r + 8 \,U_2))\nonumber \\&{} - 18\,\Big (-135 + r\, \big [675 \nonumber \\&+ r\, \big (-1350 + r \,[1350 + r \,(-675 + 134 \,r)]\big )\big ]\Big )\, U_1\, U_3 \nonumber \\&+ 298\, r\, U_1^2\, U_2\, U_3^2\nonumber \\&{} - 9\, \Big (11 + 5 \,r \,\big [-11 + r\, \big (22\nonumber \\&+ r\, [-22 + r\, (11 + 2\, r)]\big )\big ]\Big )\, U_3^3 - 252\, \nonumber \\&\times U_1\, (45\, U_1 + 8\, r\, U_2)\, U_3^4 + 540 \,r\, U_2\, U_3^6\bigg ]\, z^9\nonumber \\&{} - U3\, \bigg [12\, r\, U_1^3\, U_2 + 126 \,(40 - 37\, r)\, U_1^3\, U_3 \nonumber \\&+ 262\, r\, U_1^2\, U_2\, U_3^2 \nonumber \\&+ 9\, \Big (-55 + r\, \big [275 \nonumber \\&+ r\, \big (-550 + r\, [550 + r\, (-275 + 48\, r)]\big )\big ]\Big ) \,U_3^3 \nonumber \\&- 14\, U_1\, (1215\, U_1 + 193\, r\,U_2)\, U_3^4 \nonumber \\&+ 180\, (36\, U_1 + 7\, r\, U_2)\, U_3^6\bigg ]\, z^{10} + U_3\, \nonumber \\&\times \bigg [18\, (140 - 137\, r)\, U1^3 + 98\, r\, U_1^2 \,U_2\, U_3\nonumber \\&+ 9\,\Big (-165 + r\, \big [825 + r\, \big (-1650\nonumber \\&+ r\, [1650 + r \,(-825 + 164 \,r)]\big )\big ]\Big )\, U_3^2 \nonumber \\&- 70\, U_1\, (243 \,U_1 + 32\, r \,U_2) \,U_3^3 \nonumber \\&+ 1890\, (6\, U_1 + r\, U_2) \,U_3^5\bigg ]\, z^{11} \nonumber \\&+ 2\, U_3\, \bigg [-U_1^2\, (360\, U_1 + 7\, r\, U_2) + 30\, \nonumber \\&\times U_1\, (189 \,U_1 + 19\, r \,U_2)\, U_3^2\nonumber \\&{} - 189\, (36\, U_1\, + 5\, r\, U_2)\, U_3^4 + 1485\, U_3^6\bigg ] \,z^{12} \nonumber \\&+ 2\, \bigg [45 \,U_1^3 - 2\, U_1\, (1215\, U_1 + 82\, r\, U_2)\,\nonumber \\&\times U_3^2 + 630\, (9\, U_1 + r\, U_2) \,U_3^4 \nonumber \\&{} - 2079\, U_3^6\bigg ]\, z^{13} + U3\, \bigg [U_1\, (1215\, U_1 + 41\, r\, U_2) \nonumber \\&{} - 540\, (12\, U_1 + r\, U_2)\, U3^2 + 4158\, U3^4\bigg ] \,z^{14}\nonumber \\&{} - 135\, \bigg [U_1^2 - (18\, U_1 + r \,U_2)\, U_3^2 + 22\, U_3^4\bigg ]\, z^{15} \nonumber \\&{} - 15\, U_3 \,\bigg [36\, U_1 + r \,U_2 - 99\, U_3^2\bigg ]\, z^{16} \nonumber \\&+ 9\, \bigg [6\, U_1 - 55\, U_3^2\bigg ]\, z^{17} + 99\, U_3\, z^{18} - 9\, z^{19}, \end{aligned}$$

(41)

$$\begin{aligned} V_7 =&-7\, r^4\, U_1^2\, U_2^2\, U_3^2 + 49\, r^5 \,U_1^2\, U_2^2\, U_3^2 \nonumber \\&- 147\, r^6\, U_1^2 \,U_2^2 \,U_3^2 + 245\, r^7\, U_1^2\, U_2^2\, U_3^2 \nonumber \\&- 245\, r^8\, U_1^2\, U_2^2\, U_3^2 + 147\, r^9\, U_1^2\, U_2^2\, U_3^2 \nonumber \\&- 49\, r^{10}\, U_1^2\, U_2^2\, U_3^2\nonumber \\&+ 7\, r^{11}\, U_1^2\, U_2^2\, U_3^2 + 2\, r^4\, U_1^2\, U_2^3\, U_3^3 - 10 \,r^5\, U_1^2\, U_2^3\, U_3^3 \nonumber \\&+ 20\, r^6\, U_1^2\, U_2^3\, U_3^3 - 20\, r^7\, U_1^2\, U_2^3\, U_3^3 \nonumber \\&+ 10\, r^8\, U_1^2\, U_2^3\, U_3^3 - 2\, r^9\, U_1^2\, U_2^3\, U_3^3 + 2\, r^3\, U_1^2\, U_2\, U_3^7\, \nonumber \\&\times \bigg [(1 - 6 r)\, U_2^2 + 23 \,r U_2\, U_3 + 3\, r\, U+3^2\bigg ] \,z \nonumber \\&+ r^3\, U_1\, U_3^6 \,\bigg [4\, (-3 + 8\, r)\, U_1\, U_2^3 - 125\, r \,U_1\, U_2^2\, U3 \nonumber \\&+ \Big (r\, U_1 + \big [r^3 - 6\, (1 + 6\, r)\, U_1\big ]\, U_2\Big )\, U_3^2\bigg ]\, z^2 \nonumber \\&+ r^2\, U_1\, U_3^5\, \bigg [10\, (3 - 5\, r) r \,U_1\, U_2^3 \nonumber \\&+ 180 \,r^2\, U_1\, U_2^2\, U_3 - \Big (r\, (2 + r + 2\, r^2)\, U_1 + 4\, r^4\, U_2\nonumber \\&- 6\, \big [1 + 6\, r\, (1 + 2\, r)\big ]\, U_1 \,U_2\Big )\, U_3^2 + 2\, r^3\, U_3^4\bigg ] \,z^3 \nonumber \\&+ r\, U_3^4\, \bigg [10\, \times r^2\, (-4 + 5\, r)\, U_1^2\, U_2^3 - 141\, r^3\, U_1^2\, U_2^2\, U_3\nonumber \\&+ U_1\,\Big (r\, \big [3 + r\, \big (3 + r \,(-5 + 9 \,r)\big )\big ]\, U_1 \nonumber \\&+ 6\, \big [r^5 - \big (1 + r\, [6 + r\, (11 + 7\, r)]\big )\, U_1\big ]\, U_2\Big )\, U_3^2 \nonumber \\&- 12\, r^4\, U_1\, U_3^4 + r^4 \,U_3^6\bigg ]\, z^4\nonumber \\&+ r \,U_3^4\, \bigg [r^2\, U_1^2\, U_2^2\, (47\, r + 30 \,U_2) + U_1\, \Big (2 \,\big [-3 + r\, \nonumber \\&\times \big (15 + r \,[-30 + r\, (30 + (-15 + r)\, r)]\big )\big ]\, U_2\nonumber \\&+ U_1\, \big [-4 + 60\, U_2 + r\, \big (-5 + 24\, U_2 + r\, \nonumber \\&\times [9 + r\, (3 - 13\, r - 24\, U_2) + 36 \,U_2]\big )\big ]\Big ) \,U_3 \nonumber \\&+ 30 \,r^4\, U_1\, U_3^3 - 7\, r^4\, U_3^5\bigg ]\, z^5\nonumber \\&+ U_3^3\, \bigg [-10\, r^3\, U_1^2\, U_2^3 + U_1\, (5\, U_1 + r\, \Big (66 - 5\, r\, \big [66 + r\, \nonumber \\&\times \big (-132 + r \,[132 + r\, (-66 + 13\, r)]\big )\big ]\nonumber \\&- 258\, U_1 + 6\, r\, \big [59 + 10\, (-3 + r)\, r\big ] \,U_1\Big )\, U_2)\, U_3\nonumber \\&- r \,(-7 + r\, (8 + r\, (15 + 4 \,r))) \,U_1^2\, U_3^2\nonumber \\&- 40\, r^5 \,U_1\, U_3^3 + 21\, r^5\, U_3^5\bigg ] \,z^6 + U_3^3\, \bigg [140\, r^8 - 35\, r^9 \nonumber \\&+ 2\, r^6\, (70 - 9\, U_1) + 3\, (2 - 15\, U_1)\, U_1 \nonumber \\&+ 6 \,r^7\, (-35 + 4\, U_1) + 3\, r^4\, U_1\, (70 - 11\, U_1 + 424\, U_2\, U_3) \nonumber \\&+ r^2\, U_1\, (126 - 107\, U_1 + 1272\, U_2 \,U_3\nonumber \\&- 738\, U_1\, U_2\, U_3) + r\, U_1\, (-42 + 113\, U_1 \nonumber \\&+ 6\, (-53 + 104 \,U+1) \,U_2\, U_3)\nonumber \\&+ 3 \,r^3\, U_1\, \big [-70 - 636\, U_2 \,U_3 + 3 \,U_1\, (7 + 26\, U_2\, U_3)\big ] \nonumber \\&+ r^5\, \big [-35 + 8\, U_1^2 - 6 \,U_1 \,(16 + 53\, U_2\, U_3)\big ]\bigg ]\, z^7\nonumber \\&+ U_3^3\, \bigg [-6 r\, \big [155 + r\, (-249 + 98\, r)\big ]\, U_1^2\, U_2\nonumber \\&+ U_1\,\Big (-60 + 12\, r\, (5 + (-5 + r)\, r) \big [5 + r\, (-5 + 4\, r)\big ]\nonumber \\&+ 180\, U_1 + r \,\big [-316 + (197 - 49\, r) \,r\big ] \,U_1\Big )\, U_3 + \Big (1 + r\, \nonumber \\&\times \big [-5 + r\, \big (10 + r \,[-10 + r\, (5 + 34\, r)]\big )\big ]\Big ) \,U_3^3\nonumber \\&+ 882\, r\, U_1\, U_2\, U_3^4\bigg ]\, z^8 - U_3^3 \,\bigg [U_1^2\, \big [420 + r\, \nonumber \\&\times \big (-980 - 876\, U_2 + r\, (763 - 201\, r + 732 \,U_2)\big )\big ]\nonumber \\&+ \Big (11 + 5\, r\, \big [-11 + r\, \big (22 + r\, [-22 + r\, (11 + 2\, r)]\big )\big ]\Big )\nonumber \\&\times U_3^2 + 2\, U_1\, \Big (-135 + r \,\big [675 + r \,\big (-1350 \nonumber \\&+ r\, [1350 + r\, (-675 + 134 \,r)]\big ) + 777\, U_2\, U_3^3\big ]\Big )\bigg ] \,z^9\nonumber \\&+ U3^2 \,\bigg [6\, r\, (-85 + 81\, r)\, U_1^2 \,U_2 + 7\nonumber \\&\times \big [90 + r\, (-148 + 61\, r)\big ]\, U_1^2\, U_3\nonumber \\&+ \Big (55 + r\, \big [-275 + r\, \big (550 \nonumber \\&+ r\, (-550 + (275 - 48\, r)\, r)\big )\big ]\Big )\, U_3^2 \nonumber \\&+ 1806\, r\, U_1\, U_2\, U_3^3 - 720\, U_1\, U_3^5\bigg ]\, z^{10}\nonumber \\&+ U_3^2\, \bigg [U_1^2 \,\big [-630 - 521\, r^2 + 28\, r\, (41 + 6 \,U_2)\big ]\nonumber \\&+ \Big (-165 + r\, \big [825 + r\, \big (-1650 + r\, \nonumber \\&\times [1650 + r\, (-825 + 164 \,r)]\big )\big ]\Big )\, U_3 \nonumber \\&+ 126\, U_1\, U_3^2\, (-11\, r\, U_2 + 10 \,U_3^2)\bigg ]\, z^{11}\nonumber \\&+ 2\, U_3\, \bigg [3\, U_3\, (70\, U_1^2 - 252\, U_1\, U_3^3 + 55\, U_3^5) \nonumber \\&+ r\, U_1\, \big [339 \,U_2\, U_3^2 - 2 \,U_1\, (6\, U_2 + 97\, U_3)\big ]\bigg ]\, z^{12}\nonumber \\&- 2\, U_3\, \bigg [231 + 1155 \,r^4 - 231 \,r^5 + 210\, r^2\, (11 - 9 \,U_1)\nonumber \\&+ 90 \,(-7 + U1)\, U_1 + 210 \,r^3\, (-11 + 3 \,U_1)\nonumber \\&+ r\, \big [-1155 + 2\, U_1\, (945 - 44 \,U_1 + 48\, U_2\, U_3)\big ]\bigg ]\, z^{13} \nonumber \\&+ 3\, U_3\, \bigg [15 \,U_1^2 + 154 \,U_3^4 + 8\, U_1 \,(r\, U_2 - 30\, U_3^2)\bigg ]\, z^{14} \nonumber \\&- 5\, \bigg [U_1^2 - 54\, U_1\, U_3^2 + 66\, U_3^4\bigg ]\, z^{15} + 15\, U_3\, \bigg [-4\, U_1\nonumber \\&+ 11 \,U_3^2\bigg ]\, z^{16} + \bigg [6\, U_1 - 55\, U_3^2\bigg ] z^{17} + 11 U_3 z^{18} - z^{19}, \end{aligned}$$

(42)

$$\begin{aligned} V_{8} =&-7\, r^4\, U_1^2\, U_2^2 \,U_3^8 +3 \,r^4 \,U_1^2\, U_2\, U_3^5\, \bigg [\big [13 + r\, (-26 + 11\, r)\big ]\, \nonumber \\&\times U_2 + 2 \,\big [2 + r\, (-4 + 3\, r)\big ]\, U_3\bigg ]\, z+ r^3\, U_1\, U_3^4\, \nonumber \\&\times \bigg [-2\, r \,(43 - 86\, r + 40\, r^2) \,U_1 \,U_2^2 - 12\, U_1\, U_2 \,U_3 \nonumber \\&+ 6\, r\, (-6 + 11\, r)\, U_1\, U_2 \,U_3^2 + r\, (3\, U_1 + 2\, r^2\, U_2)\, U_3^3\bigg ] \,z^2 \nonumber \\&+ 2\, r^2\, U_1 \,U_3^4 \,\bigg [3 \Big (2 + r\, \big [6 + r\, \big (-4 + 3\, r\, (-5 + 4\, r)\big )\big ]\Big )\, U_1\, U_2 \nonumber \\&+ 47\, r^2\, U_1\, U_2^2\, U_3 - 3\, r\, (U_1 + r^2\, U_1 + r^2\, U_2)\, U_3^2 \nonumber \\&+ 3\, r^3\, U_3^4\bigg ]\, z^3 - r \,U_3^4\, \bigg [-3\, r^4\, U_3^5 \nonumber \\&+ U_1^2\, \big [U_2\, \big (12 + 6\, r\, [8 + r\, (2 + 3\, (-4 + r)\, r)] + 47 \,r^3\, U_2\big ) \nonumber \\&- 3\, r\, (3 + r - 5\, r^2 + 7\, r^3) \,U_3\big ] \nonumber \\&+ 6\, r^4\, U_1\, U_3\, \big [(-4 + 3\, r)\, U_2 + 5 \,U_3^2\big ]\bigg ] \,z^4 \nonumber \\&- 2 \,r\, U_3^3\, \bigg [U_1 \Big (6 - 54 \,U_1+ r\, \big [-36 + r\,\nonumber \\&\times \big (90 + r\, [r \,(r\, (-71 + 23\, r) - 27\, (-4 + U_1)) \nonumber \\&+ 24 \,(-5 + U_1)] - 6\, U_1\big ) + 60 \,U_1\big ]\Big )\, U_2 \nonumber \\&+ 3\, (2 + r - 5 \,r^2 + r^3 + 3\, r^4)\, U_1^2\, U_3 - 30\, r^4\, U_1\, U_3^3 \nonumber \\&+ 9 \,r^4\, U_3^5\bigg ]\, z^5 + 3\, U_3^3 \,\bigg [-60 \,r^8 + 15\, r^9 + r^7 \nonumber \\&\times (90 - 20\, U_1) + 5\, U_1^2 + 20\, r^6\, (-3 + 2\, U_1) \nonumber \\&+ r^4\, U_1\, (9 \,U_1 - 160\, U_2\, U_3) \nonumber \\&+ r\, U_1 \,\big [3 \,U_1 + 8\, (5 - 17\, U_1)\, U_2\, U_3\big ] \nonumber \\&+ 3\, r^3\, U_1\, \big [U_1 - 8\,(-10 + U_1)\, U_2\, U_3\big ]\nonumber \\&+ r^2\, U_1\, \big [-17\, U_1 + 32\, (-5 + 3 \,U_1)\, U_2\, U_3\big ] \nonumber \\&+ r^5\, \big [15 - 2 \,U_1\, (10 + U_1 - 24\, U_2\, U_3)\big ]\bigg ]\, z^6 \nonumber \\&- 6\, U_3^3\, \bigg [r\, U_1\, \big [86 - 140\, U_1 \nonumber \\&+ r\, \big (-344 + r\, [516 + r\, (-344 + 87\, r) \nonumber \\&- 66\, U_1] + 198\, U_1\big )\big ]\, U_2 - U_1\, \big [3 - 20\, U_1 \nonumber \\&+ r\, \big (-15 + 30\, r - 30 \,r^2 + 15\, r^3 + 2\, r^4 + 3\,\nonumber \\&\times [6 + (-2 + r)\, r] \,U_1\big )\big ]\, U_3 + 10\, r^5\, U_3^3\bigg ]\, z^7 \nonumber \\&+ 3\, U_3^3 \,\bigg [U_1 \,\big [-54 + 140\, U_1 + r\, \big (270 \nonumber \\&- 280 \,U_1 + r\, [-540 + r\, (540 - 270\, r\nonumber \\&+ 52 \,r^2 - 43 \,U_1) + 185 \,U_1] \nonumber \\&+ 20\, (-17 + 13\, r)\, U_1\, U_2\big )\big ] + \Big (1 + r\, \big [-5 \nonumber \\&+ r\, \big (10 + r\, [-10 + r\, (5 + 14\, r)]\big )\big ]\Big )\, U_3^2 \nonumber \\&+ 416 \,r U_1\, U_2\, U_3^3\bigg ]\, z^8 \nonumber \\&+ 6\, U_3^2\, \bigg [2\, (61 - 57\, r)\, r\, U_1^2\, U_2 + \big [-140 \nonumber \\&+ (210 - 79\, r) \,r\big ]\, U_1^2\, U_3 \nonumber \\&+ \big [-5 + r\, \big (25 + r\, [-50 + (-10 + r)\, r (-5 + 2\, r)]\big )\big ]\, U_3^2 \nonumber \\&- 310\, r\, U_1\, U_2\, U_3^3 + 108\, U_1\, U_3^5\bigg ]\, z^9 \nonumber \\&- 3\, U_3^2 \,\bigg [U_1^2 \,\big [-350 + r\, (616 - 269\, r + 96 \,U_2)\big ] \nonumber \\&+ \big [-45 + r\, \big (15 + r \,(-15 + 4 \,r)\big ) \big (15 + r \,(-15 + 11\, r)\big )\big ]\nonumber \\&\times U_3 + 8 \,U_1 \,U_3^2\, (-73\, r\, U_2 + 63\, U_3^2)\bigg ]\, z^{10} \nonumber \\&+ 12\, U_3\, \bigg [-70\, U_1^2\, U_3 + 189\, U_1\, U_3^4 - 30\, U_3^6 \nonumber \\&+ r\, U_1\, (4\, U_1\, U_2 + 63\, U_1\, U_3 - 85\, U_2\, U_3^2)\bigg ]\, z^{11} + 6\, U_3 \nonumber \\&\times \bigg [105 - 525\, r + 525\, r^4 - 105\, r^5 + 42\, r^2\, (25 - 27 \,U_1) \nonumber \\&+ 14\, U_1 \,(-27 + 5\, U_1) + 42 \,r^3 (-25 + 9\, U_1) \nonumber \\&+ 2 \,r\, U_1 \,(567 - 34\, U_1 + 28\, U_2\, U_3)\bigg ]\, z^{12}\nonumber \\&- 12\, U_3\, \bigg [10\, U_1^2 + 4\, r\, U_1\, U_2 - 126\, U_1\, U_3^2 + 63\, U_3^4\bigg ]\, z^{13} \nonumber \\&+ 3\, \bigg [5\, U_1^2 - 216\, U_1\, U_3^2 + 210\, U_3^4\bigg ]\, z^{14} \nonumber \\&+ 18 \,U_3\, \bigg [9\, U_1 - 20\, U_3^2\bigg ]\, z^{15}+ 9\, \bigg [-2\, U_1 \nonumber \\&+ 15\, U_3^2bigg]\, z^{16} - 30\, U_3 \,z^{17} + 3 \,z^{18}, \end{aligned}$$

(43)

$$\begin{aligned} V_9 =&7\, r^7 \,U_1^2\, U_2^2\, (U_2 - U_3) \,U_3^5 \nonumber \\&+ r^4\, U_1^2\, U_2\, U_3^5\, \bigg [r^2\, U2 \,(-6 + 13\, r + 7\, U_2)\nonumber \\&+ 6\, \big [1 + r\, (-2 + 3\, r)\big ] \,U_3^2\bigg ]\, z \nonumber \\&+ r^3\, U_1\, U_3^4 \,\bigg [-7\, r^3\, U_1 \,U_2^3+ 12\, r^3\, U_1\, U_2^2\, U_3 \nonumber \\&- 6\, \big [1 + r\,\big (4 + r\, (-9 + 10\, r)\big )\big ]\, U_1\, U_2\, U_3^2 \nonumber \\&+ r\, (3\, U_1\, + r^2\, U_2) \,U_3^4\bigg ]\, z^2 \nonumber \\&+ r^2\, U_1\, U_3^4\, \bigg [-6\, r^4\, U_1\, U_2^2 + 6\, \big [1 + r\, (4 + r)\big ]\, U_1\, U_2\, U_3 \nonumber \\&- 60\, r^3\, U_1\, U_2\, U_3^2+ r\, \big [-3\, (2 + r\, + 2\, r^2)\, U_1\nonumber \\&+ 4\, r^2\, (-3 + 2\, r)\, U_2\big ]\, U_3^3 + 6\, r^3\, U_3^5\bigg ]\, z^3\nonumber \\&+ 3\, r\, U_3^4\, \bigg [r^4\, U_3^6 - 2\, r^4\, U_1\, U_3^2\, \big [(-10 + 9\, r)\, U_2 + 6\, U_3^2\big ] \nonumber \\&+ U_1^2\, \Big (2\, \big [-1 - 4\, r + 3\, r^3\, (3 + (-3 + r)\, r)\big ]\, U_2\nonumber \\&+ r\, \big [3 + r\, \big (3 + r\, (-5 + 9\, r)\big )\big ]\, U_3^2\Big )\bigg ]\, z^4 \nonumber \\&+ r\, U_3^4 \,\bigg [2 \,\Big (-3 + r\, \big [15 + r\, \big (-30 \nonumber \\&+ r\, [30 + r\, (-75 + 61\, r)]\big )\big ]\Big )\, U_1 \,U_2\, U_3\nonumber \\&+ 90\, r^4\, U_1\, U_3^3 - 21\, r^4\, U_3^5 + 3\, U_1^2\,\nonumber \\&\times \Big (4\, \big [5 + r\, (-3 + r - 5\, r^2 + 6\, r^3)\big ]\, U_2 \nonumber \\&+ \big [-4 + r\, \big (-5 + r\, [9 + (3 - 13\, r)\, r]\big )\big ] \,U_3\Big )\bigg ]\, z^5 \nonumber \\&+ U_3^3\, \bigg [r\, U1\, \Big [66 - 258\, U_1 + r\, \Big (-396 + 5\, r\, \big [198 \nonumber \\&+ r\, \big (-264 + r\, [222 + r\, (-127 + 37\, r)]\big )\big ]\nonumber \\&+ 612\, U_1 - 6\, r\, \big [89 + 4\, r\, (-10 + 3\, r)\big ]\, U_1\Big )\Big ]\, U2 \nonumber \\&+ 15\, U_1^2\, U_3 - 3\, r\, \big [-7 + r\, \big (8 + r\, (15 + 4\, r)\big )\big ] \,U_1^2\, U_3^2 \nonumber \\&- 120\, r^5\, U_1\, U_3^3 + 63\, r^5\, U_3^5\bigg ]\, z^6 - 3\, U_3^3\, \bigg [-140\, r^8 \nonumber \\&+ 35\, r^9 + 6\, r^7\, (35 - 4 \,U_1) + 2 \,r^6\, (-70 + 9\, U_1) + 3\, U_1\, \nonumber \\&\times (-2 + 15\, U_1) + r^4\, U_1\, (-210 + 33\, U_1 - 424 \,U_2\, U_3)\nonumber \\&+ r^2\, U_1\, (-126 + 107\, U1 - 424\, U_2\, U_3 + 246 \,U_1\, U_2 \,U_3) \nonumber \\&+ 3\, r^3 \,U_1\, \big [70 + 212\, U_2 \,U_3 - U_1 \,(21 + 26\, U_2\, U_3)\big ]\nonumber \\&+ r^5\, \big [35 + 2 \,U_1\, (48 - 4\, U_1 + 63\, U_2\, U_3)\big ] \nonumber \\&+ r \,U_1\, \big [42 + 106\, U_2\, U_3 - U_1\, (113 + 208\, U_2\, U_3)\big ]\bigg ]\, z^7\nonumber \\&+ 3\, U_3^3\, \bigg [2\, r\, U_1\, \big [147 - 155\, U_1 + r\, \big (-588 \nonumber \\&+ r\, [r\, (-588 + 149\, r) - 98\, (-9 + U_1)] + 249\, U_1\big )\big ]\, U_2\nonumber \\&+ U_1\, \big [-60 + 12\, r\, \big (5 + (-5 + r)\, r\big )\, \big (5 + r \,(-5 + 4 r)\big ) \nonumber \\&+ 180\, U_1 + r\, \big (-316 + (197 - 49\, r)\, r\big )\, U_1\big ]\, U_3\nonumber \\&+ \Big (1 + r\, \big [-5 + r\, \big (10 + r\, [-10 + r\, (5 + 34\, r)]\big )\big ]\Big )\, U_3^3\bigg ]\, z^8 \nonumber \\&- 3 U_3^3\, \bigg [U_1\, \Big (30\, (-9 + 14 \,U_1)\nonumber \\&+ r \big [1350 - 980\, U_1 + r\,\big (-2700 \nonumber \\&+ r\, [2700 + 2\, r \,(-675 + 134 \,r) \nonumber \\&- 201 U_1] + 763\, U_1\big ) + 4\, (-73 + 61\, r)\, U_1\, U_2\big ]\Big ) \nonumber \\&+\Big (11 + 5\, r\, \big [-11 + r \,\big (22 + r \,[-22 + r \,(11 + 2\, r)]\big )\big ]\Big ) \nonumber \\&\times U_3^2 + 518 \,r \,U_1\, U_2\, U_3^3\bigg ]\, z^9\nonumber \\&- 3\, U_3^2\, \bigg [2 \,(85 - 81 \,r)\, r \,U_1^2\, U_2 - 7 \,\nonumber \\&\times \big [90 + r\, (-148 + 61\, r)\big ] \,U_1^2\, U_3\nonumber \\&+ \Big (-55 + r\, \big [275 + r\, \big (-550 \nonumber \\&+ r\, [550 + r\, (-275 + 48\, r)]\big )\big ]\Big ) U_3^2 \nonumber \\&- 602 \,r \,U_1 \,U_2\, U_3^3 + 720\, U_1\, U_3^5\bigg ]\, z^{10}\nonumber \\&+ 3\, U_3^2\, \bigg [U_1^2 \,\big [-630 + r\, (1148 - 521\, r + 56\, U_2)\big ]\nonumber \\&+ \Big (-165 + r\, \big [825 + r\, \big (-1650 \nonumber \\&+ r\, [1650 + r\, (-825 + 164\, r)]\big )\big ]\Big )\, U_3 \nonumber \\&+ 42\, U_1\, U_3^2\, (-11\, r\, U_2 + 30 \,U_3^2)\bigg ]\, z^{11} \nonumber \\&+ 6\, U_3\, \bigg [3\, U_3\, (70 \,U_1^2 - 252 \,U_1\, U_3^3 + 55\, U_3^5) \nonumber \\&+ r\, U_1\, \big [113 \,U_2\, U_3^2 - 2\, U_1\, (2\, U_2 + 97\, U_3)\big ]\bigg ]\, z^{12}\nonumber \\&- 6\, U_3\, \bigg [231 + 1155\, r^4 - 231\, r^5 + 210\, r^2\, (11 - 9\, U_1) \nonumber \\&+ 90\, (-7 + U_1)\, U_1 + 210\, r^3 \,(-11 + 3\, U_1) \nonumber \\&+ r\, \big [-1155 + 2 \,U_1\, (945 - 44 \,U_1 + 16\, U_2\, U_3)\big ]\bigg ]\, z^{13} \nonumber \\&+ 3\, U_3\, \bigg [45\, U_1^2 + 462\, U_3^4 + 8\, U_1\, (r\, U_2 - 90\, U_3^2)\bigg ]\, z^{14} \nonumber \\&- 15\, \bigg [U_1^2 - 54\, U_1\, U_3^2 + 66\, U_3^4\bigg ]\, z^{15} + 45\, U_3\, \bigg [-4 \,U_1 \nonumber \\&+ 11 \,U_3^2\bigg ]\, z^{16} + 3\, \bigg [6\, U_1 - 55\, U_3^2\bigg ]\, z^{17} + 33\, U_3\, z^{18} - 3\, z^{19}, \end{aligned}$$

(44)

$$\begin{aligned} V_{10} =&-7\, r^7 \,U_1^2\, U_2^2\, U_3^6 \nonumber \\&+ r^6\, U_1^2\, U_2\, U_3^5 \,\bigg [7\, r\, U_2 + 6\, U_3^2\bigg ]\, z + r^4\, U_1^2\, U_3^6\, \nonumber \\&\times \bigg [-6\, r \,(1 + 2\, r)\, U_2 + U_3^2\bigg ]\, z^2 \nonumber \\&- r^3\, U_1\, U_3^5\, \bigg [6\, (-4 + r)\, r^2\, U_1 \,U_2+ (2 + r + 2 \,r^2)\, U_1\, U_3^2 \nonumber \\&+ 6\, r^2\, U_2 \,U_3^3 - 2 \,r^2\, U_3^4\bigg ]\, z^3 + r^2\, U_3^4\, \bigg [6\, r^3\, (-6 + 5\, r) \nonumber \\&\times U_1^2\, U_2 + \big [3 + r\, \big (3 + r\, (-5 + 9\, r)\big )\big ]\,\nonumber \\&\times U_1^2\, U_3^2 + 30\, r^3\, U_1\, U_2\, U3^3\nonumber \\&- 12\, r^3\, U_1 \,U_3^4 + r^3\, U_3^6\bigg ] \,z^4 + r\, U_3^4\, \bigg [24 \,r^4 \,U_1^2\, U_2 \nonumber \\&+ \big [-4 + r\, \big (-5 + r \,(9 + (3 - 13\, r)\, r)\big )\big ]\, U_1^2\, U_3 \nonumber \\&- 60\, r^4\, U_1\, U_2\, U_3^2 + 30\, r^4\, U_1\, U_3^3 - 7\, r^4\, U_3^5\bigg ]\, z^5 \nonumber \\&+ U_3^3\, \bigg [-6\, r^5\, U_1^2\, U_2 + 5\, U_1^2\, U_3 \nonumber \\&+ r\, U_1\, \big [7\, U_1 - r \,\big (8 + r\, (15 + 4\, r)\big )\, U_1 + 60\, r^4\, U_2\big ] \,U_3^2 \nonumber \\&- 40\, r^5\, U_1\, U_3^3 + 21 \,r^5\, U_3^5\bigg ] \,z^6 \nonumber \\&+ U_3^3\, \bigg [\Big (-45 + r\, \big [113 + r \,\big (-107 + r\, [63 \nonumber \\&+ r\, (-33 + 8 \,r)]\big )\big ]\Big )\, U_1^2 - 35\, r^5\, U_3^4 \nonumber \\&+ 6\, U_1\, U_3 \,\Big (-5\, r^5\, U_2 + U_3 + r\, \big [-5 + r\,\nonumber \\&\times \big (10 + r\, [-10 + r\, \nonumber \\&\times (5 + 4 \,r)]\big )\big ]\, U_3\Big )\bigg ]\, z^7 \nonumber \\&+ U_3^3\, \bigg [6\, r^5\, U_1\, U_2 + 12\, \big [-5 + r\, \big (5 + (-5 + r)\, r\big ) \nonumber \\&\times \big (5 + r\, (-5 + 4\, r)\big )\big ]\, U_1\, U_3 \nonumber \\&- \big [-180 + r\, \big (316 + r\, (-197 + 49\, r)\big )\big ]\, U_1^2\, U_3 \nonumber \\&+ \Big (1 + r\, \big [-5 + r\, \big (10 + r \,[-10 + r\, (5 + 34\, r)]\big )\big ]\Big )\, U_3^3\bigg ]\, z^8 \nonumber \\&- U_3^3\, \bigg [ U_1\, \big [30\, (-9 + 14\, U_1) + r \,\big (1350 - 980 \,U_1 \nonumber \\&+ r\, [-2700 + r \,(2700 + 2 \,r \,(-675 + 134\, r) - 201\, U_1) \nonumber \\&+ 763\, U_1]\big )\big ] + 11\, U_3^2 + 5\, r \,\big [-11 + r\, \nonumber \\&\times \big (22 + r\, [-22 + r\, (11 + 2\, r)]\big )\big ] \,U_3^2\bigg ] \,z^9 \nonumber \\&+ U_3^3 \,\bigg [55 - 330 \,r + 825\, r^2 - 1100\, r^3 + 825 \,r^4 \nonumber \\&- 323\, r^5 + 48\, r^6 + 7 \,\big [90 + r \,(-148 + 61\, r)\big ]\,\nonumber \\&\times U_1^2 - 720\, U_1\, U_3^4\bigg ]\, z^{10} \nonumber \\&- U_3^2\, \bigg [165 + 630\, U_1^2 + r\, \Big (r \,\Big [2475 + r\,\nonumber \\&\times \big (-3300 + r\, [2475 + r \,(-989 + 164 \,r)]\big )\nonumber \\&+ 521\, U_1^2\big ] - 2\, (495 + 574\, U_1^2)\Big ) - 1260 \,U_1\, U_3^4\bigg ]\, z^11\nonumber \\&+ 2\, U_3^2\,\bigg [ (210 - 194 \,r) U_1^2 - 756\, U_1\, U_3^3 \nonumber \\&+ 165\, U_3^5\bigg ] \,z^{12} + 2\, U_3\, \bigg [(-90 + 88\, r)\, U_1^2 \nonumber \\&+ 630\, U_1\, U_3^3 - 231\, U_3^5\bigg ]\, z^{13} \nonumber \\&+ 3\, U_3\, \bigg [15 \,U_1^2 - 240\, U_1\, U_3^2 + 154\, U_3^4\bigg ]\, z^{14} \nonumber \\&- 5\,\bigg [U_1^2 - 54\, U_1\, U_3^2 + 66\, U_3^4\bigg ]\, z^{15} \nonumber \\&+ 15\, U_3 \,\bigg [-4\, U_1 + 11\, U_3^2\bigg ]\, z^{16} \nonumber \\&+ \bigg [6\, U_1 - 55\, U_3^2\bigg ]\, z^{17} \nonumber \\&+ 11 \,U_3\, z^{18} - z^{19}, \end{aligned}$$

(45)

$$\begin{aligned} S_1 =&3 r^3\, U_1\, U_2\, U_3^2 \,\bigg [1188\, z^7 + U_2\, U_3\, (U_3 - z)\, z\, (48\, U_3^3 - 240\, \nonumber \\&\times U_3^2\, z + 295\, U_3\, z^2 - 295\, z^3)\nonumber \\&+ U_1 \,U_3 \,\big [16\, (U_2 - 3\, U_3)\, U_3^3 - 80\,\nonumber \\&\times (U_2 - 3 \,U_3)\, U_3^2\, z + (52\, U_2 - 297\, U_3) \,U_3\, z^2 \nonumber \\&- 9\, (4\,U_2 + 15\, U_3) \,z^3 + 834 \,z^4\big ]\bigg ] \nonumber \\&- 96\, r\, U_3\, z^2 \,\bigg [2\, U_2\, (U_3 - z)^5 \,z^3\, (7\, U_3^2 + 15\, z^2) \nonumber \\&+ U_1\, U_2 \,(U_3 - z)^4\, z \,(2 \,U_3^3 \nonumber \\&+ 28\, U_3^2\, z + 15 \,U_3 \,z^2 + 42\, z^3)\nonumber \\&+ U_1^2\, \big [2\, U_2 \,U_3^5 + 8\, (U_2 - U_3)\, U_3^4\, z \nonumber \\&+ U_3^3\, (-33\, U_2 + 16\, U_3)\, z^2 + U_3^2\, (55\, U_2 + 32\, U_3)\, z^3 \nonumber \\&- U_3\, (77\, U2 + 216\, U_3) \,z^4\nonumber \\&+ 3 \,(192 + 23\, U_2)\, U_3 \,z^5 - 12\, (2\, U_2 + 33\, U_3)\, z^6 + 388 \,z^7\big ]\bigg ]\nonumber \\&- 384\, z^4\, \bigg [(U_3 - z)^7 \,z^2\, (U_3^2 + 3\, z^2) \nonumber \\&+ 2\, U1\, (U_3 - z)^6\, z\, (2\, U_3^2 - U_3\, z + 6 \,z^2)\nonumber \\&+ U_1^2\, (3\, U_3^5 - 17 \,U_3^4 \,z + 49\, U_3^3\, z^2 - 9 \,z^7 \nonumber \\&+ 5\, U_3^2\, z^3\, (-19 + 25\, z)+ U_3\, z^5\, (-103 + 47\, z))\bigg ] \nonumber \\&+ r^2\, U_3^2\, z\, \bigg [-384\, U2^2\, (U_3 - z)^3\, z^3\, (U_3^2 + 3\, z^2)\nonumber \\&+ U_1^2\, \Big (-32 \,U_2^2 \,U_3\, (U_3 - z)^2\, (2 \,U_3 + 15\, z)\nonumber \\&+ 3\, U_2\, \big [16\, U_3^4\, (3 + 4\, U_3) - 16 \,U_3^3\, (21 + 16\, U_3)\, z \nonumber \\&+ U_3^2 \,(825 + 1568\, U_3)\, z^2 - 3\, U_3 \,(377 + 1184\, U3)\, z^3 \nonumber \\&+ 4667\, U3\, z^4 - 3337 \,z^5\big ] - 384\, z\, \big [U_3^5 - 3\, U_3^4 \,z + 5\, U_3^3 \,z^2 \nonumber \\&- 7\, U_3^2\, z^3 + 16\, U_3 \,z^4 - 52\, z^5\big ]\Big )\nonumber \\&+ 3 \,U_1\, U_2\, z\, \Big (-32\, U_2\, (U_3 - z)^2\, \nonumber \\&(2\, U_3^3 + 23\, U_3\, z^2 - 18\, z^3)\nonumber \\&+ 3 \,\big [16\, U_3^6 - 128\, U_3^5\, z + 387\, U_3^4\, z^2 - 652\, U_3^3 \,z^3 \nonumber \\&+ 674\, U_3^2\, z^4 + 99\, (-4 + z)\, z^5\big ]\Big )\bigg ], \end{aligned}$$

(46)

$$\begin{aligned} S_2 =&-57\, U_4^2\, z\, (U_1 + z - z^2) + 57\, r^3\, (U_1 + z^2)\nonumber \\&+ r^2 \,\bigg [-114\, U_1 + z \,(55\, U_2 \,U_3 - 171\, U_4\,z)\bigg ] \nonumber \\&+ r \bigg [-20\, U_1\,U_2\, U_3 \nonumber \\&+ U_4\, z\, (-55\, U_2\, U_3 + 171 \,U_4\, z)\nonumber \\&+ 57\, U_1\, (1 + z - 2\, z^2)\bigg ], \end{aligned}$$

(47)

$$\begin{aligned} S_3 =&-3\, r^4\, U_1 \,U_2\, U_3^4\, \bigg [16\, U_3^4 - 96\, U_3^3 \,z \nonumber \\&+ 211\, U_3^2\, z^2 - 262\, U_3\, z^3 + 163\, z^4\bigg ]\nonumber \\&- 64\, r^2\, U_1\, U_3^2\, z^3\, \bigg [U_3^3\, (U_2^2 + 10\, U_2\, U_3 - 4\, U_3^2) \nonumber \\&- 4 \,U_3^2\, (U_2^2 + 7\, U_2 \,U_3 - 2\, U_3^2)\, z \nonumber \\&+ U_3\, (6 \,U_2^2 + 43 \,U_2\, U_3 - 8 \,U_3^2) \,z^2\nonumber \\&+ U_3\, \big [-U_2\, (55 + 4\, U_2) + 32\, U_3\big ]\, z^3 + (U_2^2 - 92\, U_3 \nonumber \\&+ 47\, U_2\, U_3) \,z^4 + 4\, (4\, U_2 + 15\, U_3)\,\nonumber \\&\times z^5 - 128\, z^6\bigg ]\nonumber \\&- 32\, r^3\, U_1 \,U_3^3\, z\, \bigg [-2\, U_2\, U_3^5 \nonumber \\&+ U_3^3\, (5\, U_2^2 + 6\, U_2\, U_3 + 8\, U_3^2) \,z - U_3^2\, (U_2\, (-3 + 17\, U_2) \nonumber \\&+ 45\, U_2\, U_3 + 32\, U_3^2)\, z^2 + U_3\, \big [U_2\, (-6 + 23\, U_2)\nonumber \\&+ 124\, U_2 \,U_3 + 72\, U_3^2\big ] \,z^3 - (17\, U_2^2 + 174\, U_2 \,U_3 \nonumber \\&+ 88\, U_3^2) \,z^4 + 2\, (89\, U_2 + 8\, U_3)\, z^5 + 72\, z^6\bigg ] \nonumber \\&+ 64 \,r\, U_3\, z^4\, \bigg [U_2\, (U_3 - z)^5 \,z\, (7\, U_3^2 + 15\, z^2) + U_1\, U_2\, \nonumber \\&\big [7\, U_3^4 - 22\, U_3^3 \,z + U_3^2\, (27 - 28\, z)\, z^2 \nonumber \\&+ U_3 \,(37 - 30\, z)\, z^4 + 9 \,z^6\big ] - 4\, U_1\, \nonumber \\&\times \big [U_3^5 - 2\, U_3^4\, z - 5\, U_3^3\, z^2 + U_3^2\, (29 - 41\, z)\, z^3 \nonumber \\&+ U_3\, (89 - 51\, z)\, z^5 + 43\, z^7\big ]\bigg ]\nonumber \\&+ 256\, z^5\, \bigg [(U_3 - z)^7 \,z\, (U_3^2 + 3 \,z^2) \nonumber \\&+ U_1 \,\big [U_3^5 - 6 \,U_3^4 \,z + 2\, U_3^3\, (9 - 19\, z)\, z^2 \nonumber \\&+ 6\, U_3^2\, (10 - 11 \,z)\, z^4 + 2\, U_3\, (23 - 9\, z) \,z^6 + 3\, z^8\big ]\bigg ],\nonumber \\ \end{aligned}$$

(48)

$$\begin{aligned} S_4 =&-3\, r^6\, U_1 \,U_2\, U_3^5\, z \,\bigg [35\, U_3^2 - 169\, U_3 \,z + 364 \,z^2\bigg ]\nonumber \\&+ r^5\, U_1\, U_2\, U_3^3\, \nonumber \\&\times \bigg [32\, U_3^5\, (-3\, U_2 + 4\, U_3) + (153 + 416\, U_2 - 768\, U_3)\, U_3^4\, z \nonumber \\&+ 3\, U_3^3\, (-281 - 192\, U_2 + 576\, U_3)\, z^2 \nonumber \\&+ 3\, (671 + 96\, U_2 - 640\, U_3)\, U_3^2\, z^3\nonumber \\&+ 4\, U_3\, (40\, U_2 + 199\, U_3) \,z^4 - 4645 \,U_3\, z^5 - 585\, z^6\bigg ] \nonumber \\&+ 256 \,z^6\, \bigg [(U_3 - z)^8 \,z\, (U_3^2 + 3\, z^2)\nonumber \\&+ U_1\, \big [U_3^6 - 7\, U_3^5 \,z + 24\, U_3^4\, z^2 - 3 \,z^9 \nonumber \\&+ 14\, U_3^3\, z^3\,(-4 + 7 z) + 14\, U_3^2\, z^5\, (-9 + 8\, z) \nonumber \\&+ U_3\, z^7\, (-64 + 21\, z)\big ]\bigg ] - r^4\, U_1\, U_2 \,U_3^3\, z\, \bigg [16 \,U_3^3\,\nonumber \\&\times (-21 + 4\, U_2 - 48\, z) \,z - (873 + 256\, U_2)\, z^5\nonumber \\&+ 16 \,U_3^4\, (3 + 8 \,z) + U_3^2 \,z^2 \,(921 - 192 \,U_2 + 3413\, z) \nonumber \\&+ U_3\, z^3 \,\big [32\, U_2\, (7 + 5\, z) \nonumber \\&+ z\, (-13733 + 10656\, z)\big ]\bigg ]\nonumber \\&+ 32\, r^3 \,U_1\, U_3^3\, z^2\, \bigg [-8 \,z\, \nonumber \\&(U_3^6 - 5 \,U_3^5\, z + 13\, U_3^4\, z^2 - 20\, U_3^3\, z^3 \nonumber \\&+ 13\, U_3^2\, z^4 + 7 \,U_3\, z^5 - 24\, z^6) \nonumber \\&+ U_2\, \big [2 \,U_3^4 - 12\, U_3^3\, z + 108\, U_3^2\, z^2 \nonumber \\&+ U_3\, z^3\, (-338 + 483\, z - 372\, z^2) \nonumber \\&+ 3\, z^4\, (-3 + 92\, z^2)\big ]\bigg ]\nonumber \\&- 64 \,r^2\, U_1 \,U_3^2\, z^4\, \nonumber \\&\times \bigg [-4\, \big [U_3^6 - 3\, U_3^5\, z + 4\, U_3^4\, z^2 - 10 \,U_3^3\, z^3 \nonumber \\&+ 31\, U_3^2\, z^4 - 83\, z^7 + U_3\, z^5 \,(-79 + 47\, z)\big ]\nonumber \\&+ U_2\, \Big (10 \,U_3^3 + U_3\, (74 - 31\, z)\, z^4 - 46\, z^6 \nonumber \\&- 2\, U_3^2\, z\, \big [12 + 7\, z\, (-3 + 7 \,z)\big ]\Big )\bigg ]\nonumber \\&+ 64\, r\, U_3\, z^5\, \bigg [U_2\, (U_3 - z)^6\, z\,\nonumber \\&\times (7 \,U_3^2 + 15\, z^2) - 4\, U_1\, \big [U_3^6 - 3\, U_3^5\, z\nonumber \\&- 3\, U_3^4\, z^2 + 34\, U_3^3\, z^3 - 61\, z^8\nonumber \\&+ 2\, U_3\, z^6\, (-103 + 47\, z)\nonumber \\&+ 2\, U_3^2 \,z^4 \,(-54 + 65\, z)\big ] + U_1\, U_2\, \Big (-9\, z^7 \nonumber \\&+ 5 \,U_3^2\, z^3\, (-11 + 13\, z) + U_3\, z^5 (-67 + 39\, z)\nonumber \\&+ U_3^3\, \big [7 + z\, (-29 + 49\, z)\big ]\Big )\bigg ], \end{aligned}$$

(49)

$$\begin{aligned} S_5 =&r\, U_3^2\, \bigg [-U_2 + U_3\bigg ] \nonumber \\&- U_3 \,\bigg [U_2 - 2\, r\, U_2 + 2\, r\, U_3\bigg ]\, z + \bigg [-2 + (7 - 5\, r)\, r \nonumber \\&+ 2\, U_2\, U_3\bigg ]\, z^2 - \bigg [U_2 - 2\, U_3\bigg ]\, z^3, \end{aligned}$$

(50)

$$\begin{aligned} S_6 =&r^3 \,U2\, U3^6 + \bigg [1 - 6\, r\bigg ]\, r^2\, U2 \,U3^5\, z\nonumber \\&+ 2\, r^2\, \bigg [-3 + 7\, r\bigg ]\, U2\, U3^4 \,z^2 + r\, U3^3\, \bigg [U2 \nonumber \\&+ (11 - 16\, r)\, r\, U2 - 2\, U3^3\bigg ]\, z^3 \nonumber \\&+ U3 \,\bigg [(1 + r \,(-7 + r + 3 \,r^2))\, U2\, U3 + 10\, r\, U3^4\bigg ]\, z^4 \nonumber \\&+ U3^3\, \bigg [(-5 + 13\, r)\, U2 + 4\, (1 - 7\, r) \,U3\bigg ]\, z^5\nonumber \\&- 2\, \bigg [(-5 + 2\, (7 - 5\, r)\, r)\, U2\, U3 + 8\, (1 - 3\, r)\, U3^3\bigg ]\, z^6 \nonumber \\&+ U3\, \bigg [(-10 + 13\, r)\, U2 + (24 - 46\, r) \,U3\bigg ] \,z^7\nonumber \\&+ \bigg [-16 + 38\, r - 22\, r^2 + 5\, U2\, U3\bigg ]\, z^8 \nonumber \\&- \bigg [U2 - 4\, U3\bigg ]\, z^9, \end{aligned}$$

(51)

$$\begin{aligned} S_7 =&r^3\, U_2\, U_3^5 + \bigg [1 - 6\, r\bigg ]\, r^2\, U_2\, U_3^4\, z \nonumber \\&+ 2\, r^2\, \bigg [-3 + 7\, r\bigg ]\, U_2\, U_3^3\, z^2 \nonumber \\&- r\, U_3^2 \,\bigg [r \,(-13 + 17\, r) \,U_2 + U_3^3\bigg ]\, z^3\nonumber \\&+ r\, U_3\, \bigg [2\, r\, (-5 + 4\, r)\, U_2 + 5\, U_3^3\bigg ]\, z^4 \nonumber \\&+ 2\, U_3^2\, \bigg [r\, (U_2 - 7 \,U_3) + U_3\bigg ]\, z^5 \nonumber \\&+ 2 \,\bigg [r\, (-2 + 3\, r)\, U_2 + 4 \,(-1 + 3\, r)\, U_3^2\bigg ]\, z^6 \nonumber \\&+ \bigg [2\, r\, U_2 + 12\, U_3 - 23\, r\, U_3\bigg ]\, z^7 \nonumber \\&+ \bigg [-8 + 11\, r\bigg ]\, z^8 + 2\, z^9. \end{aligned}$$

(52)

Here, we have utilized the following short-hand symbolizations:

$$\begin{aligned} K= & {} \frac{U_1}{U_3\,r\,z} \Big ((m_{Q}^2 \, U_3 + m_{Q'}^2 \, r \Big ),\nonumber \\ D= & {} \frac{U_3}{U_1^2} \Big ((m_{Q}^2 \, U_3 + m_{Q'}^2 \, r)\,U_1 + s \,r\,z\,U_3 \Big ),\nonumber \\ U_1= & {} r^2 + r\, (-1 + z) + (-1 + z) \, z,\nonumber \\ U_2= & {} 1 -r - z,\nonumber \\ U_3= & {} 1 -r,\nonumber \\ U_4= & {} 1 -z. \end{aligned}$$

(53)