1 Introduction

Gravitational lensing, which involves the bending of light in curved space as predicted by general relativity [1,2,3], is an intriguing and fundamental phenomenon with significant importance in astrophysics and cosmology. Over the past decades, extensive research has been dedicated to studying gravitational lensing, contributing significantly to addressing crucial topics, including the distribution of structures [4,5,6], dark matter [7,8,9], dark energy [10,11,12,13], quasars [14,15,16,17] and gravitational waves [18,19,20]. In the context of an idealized lens model featuring a distant source and a Schwarzschild black hole, the slight deflection of light in a weak gravitational field results in the observation of primary and secondary images. Moreover, strong gravitational lensing near the photon sphere gives rise to an infinite sequence of higher-order images, referred to as relativistic images, on both sides of the optic axis [21]. Notably, relativistic images exhibit minimal sensitivity to the characteristics of the astronomical source, making them valuable tools for exploring the nature of black hole spacetime.

The Event Horizon Telescope collaboration has recently achieved high angular resolution [22,23,24,25,26,27,28,29,30,31,32,33,34,35], allowing for the study of gravitational lensing in the strong gravity regime and reigniting interest in the shadow of black hole images and the associated phenomenon of strong gravitational lensing [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76]. This research has shown a close relationship between strong gravitational lensing and bound photon orbits, which lead to the existence of photon spheres in spherically symmetric black holes. Interestingly, horizonless ultra-compact objects have been discovered to possess photon spheres, effectively mimicking black holes in various observational simulations [75, 77,78,79,80,81,82,83,84,85,86]. Future observations may offer the opportunity to test observable effects characteristic of specific spacetimes, thus enabling a precise distinction between black hole mimickers.

Among black hole mimickers, naked singularities have attracted considerable attention. Although the cosmic censorship conjecture prohibits the formation of naked singularities, they can arise through the gravitational collapse of massive objects under specific initial conditions [87,88,89,90,91,92,93]. Since photon spheres allow naked singularities to mimic the optical appearance of black holes, extensive research has focused on investigating the gravitational lensing phenomena associated with naked singularities [94,95,96,97,98,99,100,101,102]. Specifically, a photon emanating from the singularity might necessitate an infinite coordinate time to reach a distant observer, akin to photons departing from a black hole’s event horizon [103]. This discovery, coupled with the presence of photon spheres, leads to the absence of images of distant sources within the critical curve, casting a shadow in naked singularity images. Nonetheless, in certain spacetimes with naked singularities, photons can reach and escape the singularity in a finite coordinate time [103].

By minimally extending the Einstein field equations to include a massless scalar field, the Janis–Newman–Winicour (JNW) solution naturally emerges as the sole spherically symmetric solution permitted by the theory [104,105,106,107]. Since these solutions are exact and satisfy the weak energy condition, they serve as valuable examples for discussing the Penrose singularity theorem and the weak cosmic censorship conjecture [105, 108, 109]. It is noteworthy that the presence of a non-trivial scalar field differentiates the JNW solution from the Schwarzschild black hole, resulting in a naked singularity. The JNW solution is thus characterized by a single metric parameter representing the scalar charge, encompassing the Schwarzschild black hole as a specific limit. This allows for straightforward comparisons between simulated images of naked singularities and black holes, offering a compelling avenue for differentiating between these objects in future observations. Motivated by this, extensive research has been conducted on the JNW naked singularity’s various observational properties, including gravitational lensing, relativistic images, accretion disk images and shadows [94,95,96, 110,111,112,113,114,115,116,117,118,119,120]. Additionally, other properties of the JNW naked singularity have been explored in further studies [121,122,123]. Nevertheless, it has seldom been explored whether photons can reach and depart from the singularity in a finite coordinate time. If this occurs, how does the singularity’s nature influence the observational signatures of JNW naked singularities?

To tackle these questions, we investigate the behavior of null geodesics around the singularity and the gravitational lensing effects on distant sources for the JNW naked singularity spacetime in this paper. The subsequent sections of this paper are organized as follows: Sect. 2 offers a concise overview of the JNW solution and examines the behavior of photon trajectories near the singularity. In Sect. 3, we proceed with numerically simulating images of a distant light source and a luminous celestial sphere. Following that, Sect. 4 analyzes images produced by a point-like source. Lastly, our conclusions are presented in Sect. 5. Throughout the paper, we adopt the convention \(G=c=1\).

2 Janis–Newman–Winicour spacetime

In this section, we provide a succinct overview of the JNW spacetime and investigate the behavior of null geodesics within it, particularly in proximity to the singularity. Subsequently, we explore light rays in regularized singularity models, wherein the singularity is substituted with a non-zero-sized regular core.

2.1 Metric

The JNW metric presents a static solution in Einstein-massless-scalar-field models, characterized by equations of motion,

$$\begin{aligned}&R_{\mu \nu } -\frac{1}{2}Rg_{\mu \nu }=8\pi T_{\mu \nu },\nonumber \\&T_{\mu \nu } =\nabla _{\mu }\Phi \nabla _{\nu }\Phi -\frac{1}{2}g_{\mu \nu } g^{\rho \sigma }\nabla _{\rho }\Phi \nabla _{\sigma }\Phi ,\nonumber \\&\nabla _{\mu }\nabla ^{\mu }\Phi =0, \end{aligned}$$
(1)

where \(\Phi \) stands for the massless scalar field, and \(T_{\mu \nu }\) is the corresponding energy-momentum tensor. The metric was initially derived by Janis, Newman and Winicour, and is given as [105, 121]

$$\begin{aligned} ds^{2}{=}{-}A\left( r\right) dt^{2}{+}B\left( r\right) dr^{2}{+}C\left( r\right) \left( d\theta ^{2}{+}\sin ^{2}\theta d\varphi ^{2}\right) ,\nonumber \\ \end{aligned}$$
(2)

where the metric functions are

$$\begin{aligned} A\left( r\right) {=}B^{-1}\left( r\right) {=}\left( 1-\frac{r_{g}}{r}\right) ^{\gamma }\text { and }C\left( r\right) {=}\left( 1{-}\frac{r_{g}}{r}\right) ^{1-\gamma }r^{2}.\nonumber \\ \end{aligned}$$
(3)

In addition, the scalar field is expressed as

$$\begin{aligned} \Phi =\frac{q}{r_{g}}\ln \left( 1-\frac{r_{g}}{r}\right) , \end{aligned}$$
(4)

where q is the scalar charge.

Fig. 1
figure 1

Penrose diagram for JNW naked singularity. The red and blue lines denote light rays travelling toward and away from the singularity, respectively

Full size image

The JNW metric is characterized by two parameters, \(\gamma \) and \(r_{g}\), which are related to the ADM mass M and the scalar charge q by [105]

$$\begin{aligned} \gamma =\frac{2M}{r_{g}}\text { and }r_{g}=2\sqrt{M^{2}+q^{2}}. \end{aligned}$$
(5)

When \(\gamma =1\), the JNW metric describes Schwarzschild black holes with no scalar charge. For \(0.5<\gamma <1\), the JNW metric represents weakly naked singularity solutions with a non-trivial scalar field profile. In this case, a naked curvature singularity occurs at \(r=r_{g}\), and a photon sphere is present at \(r_{ps}=r_{g}\left( 1+2\gamma \right) /2\). However, the photon sphere disappears in the JNW metric when \(0\le \gamma <0.5\), leading to distinct light propagations. Since a spacetime with photon spheres can mimic black hole observations, such as black hole shadows, the focus in this paper is on the JNW metric with \(0.5<\gamma <1\). The causal structure of the JNW naked singularity is depicted in the corresponding Penrose diagram shown in Fig. 1. The timelike curvature singularity is located at \(r=r_{g}\).

2.2 Null geodesics

For a photon with 4-momentum vector \(p^{\mu }=(\dot{t},\dot{r},\dot{\theta },\dot{\varphi })\), where dots stand for derivative with respect to some affine parameter \(\lambda \), the null geodesic equations exhibit separability and can be fully characterized by three conserved quantities,

$$\begin{aligned} E= & {} p_{\mu }\partial _{t}^{\mu }=-p_{t},\quad L_{z}=p_{\mu }\partial _{\varphi }^{\mu }=p_{\varphi },\nonumber \\ L^{2}= & {} K^{\mu \nu }p_{\mu }p_{\nu }=p_{\theta }^{2}+L_{z} ^{2}\csc ^{2}\theta , \end{aligned}$$
(6)

where the tensor \(K^{\mu \nu }\) is a symmetric Killing tensor

$$\begin{aligned} K=C^{2}\left( r\right) \left( d\theta \otimes d\theta +\sin ^{2}\theta d\varphi \otimes d\varphi \right) . \end{aligned}$$
(7)

Here, E, \(L_{z}\) and L denote the total energy, the angular momentum parallel to the axis of symmetry, and the total angular momentum, respectively. Consequently, the 4-momentum \(p=p_{\mu }dx^{\mu }\) can be expressed in terms of E, \(L_{z}\) and L as follows

$$\begin{aligned} p&=-Edt\pm _{r}\sqrt{\mathcal {R}(r)}dr\pm _{\theta }\sqrt{\Theta (\theta )}d\theta +Ld\varphi ,\nonumber \\ \mathcal {R}(r)&=B(r)\left[ \frac{E^{2}}{A(r)}-\frac{L^{2}}{C(r)}\right] \text { and }\Theta (\theta )=L^{2}-L_{z}^{2}\csc ^{2}\theta , \end{aligned}$$
(8)

where the choices of sign \(\pm _{r}\) and \(\pm _{\theta }\) depend on the radial and polar directions of travel, respectively.

Fig. 2
figure 2

Effective potential of photons \(V_{\text {eff}}\left( r\right) \) in the JNW spacetime for values of \(\gamma \) ranging from 0.6 to 1. The location \(r_{g}\) corresponds to the naked singularity for \(\gamma <1\) and the event horizon for \(\gamma =1\), as indicated by the blue dot

Full size image

The null geodesic equations can then be written as

$$\begin{aligned} \dot{t}= & {} \frac{E}{A(r)},~\dot{r}=\pm _{r}L\sqrt{b^{-2}-V_{\text {eff}} (r)},\nonumber \\ \dot{\theta }= & {} \pm _{\theta }\frac{\sqrt{L^{2}-L_{z}^{2}\csc ^{2}\theta }}{C(r)},~\dot{\varphi }=\frac{L_{z}}{C(r)\sin ^{2}\theta }\text {,} \end{aligned}$$
(9)

where \(b\equiv L/E\) is the impact parameter, and the effective potential of photons is defined as

$$\begin{aligned} V_{\text {eff}}(r)=\frac{A\left( r\right) }{C(r)}. \end{aligned}$$
(10)

Figure 2 depicts the effective potential \(V_{\text {eff} }(r)\) for various values of \(\gamma \) within the range \(0.5<\gamma \le 1\). All curves exhibit a peak corresponding to the photon sphere. Additionally, \(V_{\text {eff}}(r)\) approaches zero as r tends towards both spatial infinity and \(r_{g}\). It is important to note that for \(\gamma <1\), a naked singularity forms at \(r=r_{g}\), whereas for \(\gamma =1\), an event horizon appears at \(r=r_{g}\). The vanishing effective potential at \(r=r_{g} \) implies that photons can reach the point where \(r=r_{g}\) without being reflected back upon entering the photon sphere. Moreover, for distant observers, determining whether photons can arrive at this point in a finite time is crucial for imaging the JNW spacetime. This question can be addressed by analyzing the rate of change of the radius r with respect to time t. Particularly, the rate of change of radius r with respect to time t can be expressed as

$$\begin{aligned} \frac{dr}{dt}=\pm A(r)\sqrt{1-b^{2}V_{\text {eff}}(r)}. \end{aligned}$$
(11)

The plus and minus signs in the equation represent motion radially outward and inward towards the naked singularity, respectively. It is crucial to note that null geodesics are only permitted when \(b^{-2}\ge V_{\text {eff}}(r)\). The maximum of \(V_{\text {eff}}(r)\) determines the locations of circular light rays, which constitute the photon sphere. Interestingly, when the impact parameter b is smaller than the critical parameter \(b_{c}\) (representing the impact parameter for photon trajectories on the photon sphere), photons can cross the photon sphere and travel toward the singularity.

To investigate whether a photon can reach and leave the singularity at \(r=r_{g}\) within a finite coordinate time (i.e., the proper time measured by a distant observer), we first consider a radial light ray with \(b=0\), arriving at or departing from the singularity at \(t=0\). For this light ray, Eq. (11) yields

$$\begin{aligned} t\left( r\right) {=}\pm \frac{r_{g}^{\gamma }\left( r{-}r_{g}\right) ^{1{-}\gamma }}{\gamma {-}1}\text { }{}_{2}F_{1}\left( 1{-}\gamma ,{-}\gamma ,2{-}\gamma ,1{-}\frac{r}{r_{g}}\right) ,\nonumber \\ \end{aligned}$$
(12)

where plus and minus signs correspond to the outgoing and ingoing cases, respectively. Here, \(_{2}F_{1}\left( a,b,c;x\right) \) denotes the hypergeometric function. The implication of Eq. (12) is twofold: firstly, photons emitted from distant sources reach the singularity in a finite coordinate time, and secondly, photons leaving the singularity reach distant observers in a finite coordinate time. It is worth mentioning that \(t\left( r\right) \) approaches infinity in the limit of \(\gamma =1\), which is consistent with expectations for Schwarzschild black holes. For general null geodesics, Eq. (11) describes the behavior of photons around the singularity at \(r=r_{g}\), yielding

$$\begin{aligned} \frac{dt}{dr}=\pm r_{g}^{\gamma }\left( r-r_{g}\right) {}^{-\gamma }+\mathcal {O}\left( \left( r-r_{g}\right) ^{1-\gamma }\right) . \end{aligned}$$
(13)

The corresponding asymptotic solution is

$$\begin{aligned} t\left( r\right) \sim \pm \frac{r_{g}^{\gamma }\left( r-r_{g}\right) ^{1-\gamma }}{1-\gamma }, \end{aligned}$$
(14)

which also shows that photons travel through the singularity in a finite coordinate time.

Furthermore, in the vicinity of the singularity, the solutions of the null geodesic equations (9) take the form

$$\begin{aligned} r\left( \lambda \right)&=r_{g}\pm _{r}E\lambda +\mathcal {O}\left( \left| \lambda \right| ^{\frac{1}{2-2\gamma }}{}\right) ,\nonumber \\ t\left( \lambda \right)&=t_{0}\pm _{r}\frac{E^{1-\gamma }{}r_{g}^{\gamma }\left| \lambda \right| ^{1-\gamma }}{1-\gamma }+\mathcal {O}\left( \left| \lambda \right| {}^{1-\gamma }\right) ,\nonumber \\ \theta \left( \lambda \right)&=\theta _{0}\pm _{\theta }\sqrt{L^{2}-L_{z} ^{2}\csc ^{2}\theta _{0}}\frac{E^{\gamma -1}\left| \lambda \right| ^{\gamma }}{\gamma r_{g}^{1+\lambda }}\nonumber \\&\quad +\mathcal {O}\left( \left| \lambda \right| {}^{\gamma }\right) ,\nonumber \\ \varphi \left( \lambda \right)&=\varphi _{0}+\frac{L_{z}E^{\gamma -1} \csc ^{2}\theta _{0}\left| \lambda \right| ^{\gamma }}{\gamma r_{g}^{\gamma +1}}+\mathcal {O}\left( \left| \lambda \right| ^{\gamma }\right) , \end{aligned}$$
(15)

where \(t_{0}\), \(\theta _{0}\) and \(\varphi _{0}\) are the integration constants, and we assume \(r\left( 0\right) =r_{g}\). It shows the existence of two classes of light rays: radially outgoing and ingoing light rays, denoted as \(+_{r}\) and \(-_{r}\), respectively. To simplify, we adopt \(\lambda <0\) for ingoing light rays and \(\lambda >0\) for outgoing ones. As the affine parameter \(\lambda \) approaches 0 from the right and left, respectively, both outgoing and ingoing light rays converge towards the singularity. In Fig. 1, the blue and red lines represent outgoing and ingoing light rays, respectively.

2.3 Regularized naked singularity

Fig. 3
figure 3

Penrose diagram for regularized JNW naked singularity with a wormhole throat (Left) and a regular center (Right)

Full size image

As mentioned earlier, photons with a sufficiently small impact parameter can reach the singularity in a finite coordinate time, prompting inquiry into their fate at the singularity as observed by distant observers. However, the existence of the singularity indicates a breakdown in the applicability of general relativity around it, which has ignited the pursuit of a theory of quantum gravity. Given the lack of a definitive quantum gravity framework, researchers frequently resort to effective models to regularize such singularities, thereby facilitating investigations into the characteristics of null geodesics at these points. These effective models often employ a regularized singularity metric that can describe spacetime like wormholes or non-singular manifolds. An example in the former category is the modified JNW geometry through the application of the Simpson and Visser (SV) method [123]. Specifically, the SV-modified JNW geometry is derived by substituting r with \(\sqrt{r^{2}+\epsilon ^{2}}\), where \(\epsilon \) represents the SV parameter. When two such SV-modified JNW metrics are connected by a thin shell at \(r=r_{g}\), the resulting spacetime forms a traversable wormhole with a throat located at \(r=r_{g}\). The corresponding Penrose diagram is depicted in the left panel of Fig. 3, where the red and blue lines illustrate that light rays moving toward \(r=r_{g}\) will traverse the throat and enter another universe.

Of particular interest, the regularization of singularities can be achieved by incorporating higher-order curvature terms, such as the complete \(\alpha ^{\prime }\) corrections of string theory [124,125,126]. This approach leads to a regularized singularity spacetime that maintains regularity throughout, and \(r=r_{g}\) serves as the center of this well-behaved manifold. Moreover, apart from a vicinity around the center, the singularity spacetime closely approximates the regularized singularity spacetime. Therefore, photons with sufficiently small impact parameters are able to traverse the neighborhood of the center and reach distant observers. The right panel of Fig. 3 shows the corresponding Penrose diagram, where a red line illustrates a light ray passing through the neighborhood of the center. Note that this light ray comprises both radially outgoing and ingoing branches. Typically, a specific formulation of the regularized singularity spacetime is necessary to establish the connection between the ingoing and outgoing branches.

For the sake of simplicity, we construct a regularized singularity spacetime by matching the JNW metric with a regular spacetime, introducing a thin shell centered at \(r=r_{g}\) with a tiny yet non-zero radius \(\epsilon \). The metric of the regular spacetime within this thin shell is described by

$$\begin{aligned} ds_{\text {in}}^{2}= & {} -A_{\text {in}}\left( r\right) dt^{2}+B_{\text {in}}\left( r\right) dr^{2}\nonumber \\{} & {} +C_{\text {in}}\left( r\right) \left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) . \end{aligned}$$
(16)

In the vicinity of \(r=r_{g}\), the metric functions are expanded in the following manner,

$$\begin{aligned} A_{\text {in}}\left( r\right)&=a_{0}+a_{1}\left( r-r_{g}\right) +\cdots ,\nonumber \\ B_{\text {in}}\left( r\right)&=b_{0}+b_{1}\left( r-r_{g}\right) +\cdots ,\nonumber \\ C_{\text {in}}\left( r\right)&=\left( r-r_{g}\right) ^{2}\left[ c_{0}+c_{1}\left( r-r_{g}\right) +\cdots \right] , \end{aligned}$$
(17)

where the equality of \(b_{0}\) and \(c_{0}\) arises from the absence of a conical singularity at \(r=r_{g}\). For a light ray entering the regular core from the JNW spacetime, the corresponding energy \(E_{\text {in}}\) and angular momentum \(L_{\text {in}}\) in the regular core are related to the energy E and angular momentum L in the JNW spacetime as [127, 128],

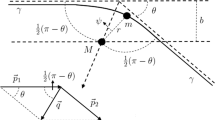
$$\begin{aligned} E_{\text {in}}= & {} \sqrt{\frac{A_{\text {in}}\left( r_{g}+\epsilon \right) }{A\left( r_{g}+\epsilon \right) }}E\text { and }\nonumber \\ L_{\text {in}}= & {} \sqrt{\frac{C_{\text {in}}\left( r_{g}+\epsilon \right) }{C\left( r_{g} +\epsilon \right) }}L. \end{aligned}$$
(18)

Due to the spherical symmetry, we restrict the light ray to the equatorial plane and assume its entry and exit from the thin shell occur at \(\varphi =\varphi _{1}\) and \(\varphi _{2}\), respectively. Beyond the thin shell, in the JNW spacetime, the light ray follows the trajectory given by Eq. (15), encompassing both ingoing and outgoing branches that terminates at \(\varphi =\varphi _{1}\) and departs from \(\varphi =\varphi _{2}\) on the thin shell, respectively. The deflection angle \(\Delta \varphi =\varphi _{2}-\varphi _{1}\), due to the influence of the regular core, is quantified as

$$\begin{aligned} \Delta \varphi =2\int _{b_{\text {in}}}^{r_{g}+\epsilon }\frac{\sqrt{A_{\text {in} }\left( r\right) B_{\text {in}}\left( r\right) }dr}{C_{\text {in}} (r)\sqrt{b_{\text {in}}^{-2}-A_{\text {in}}\left( r\right) /C_{\text {in} }\left( r\right) }}, \end{aligned}$$
(19)

where \(b_{\text {in}}=L_{\text {in}}/E_{\text {in}}\). As \(\epsilon \) approaches zero,

$$\begin{aligned} \Delta \varphi \rightarrow 2\arccos \left( \epsilon ^{\gamma -1/2}r_{g} ^{-\gamma -1/2}b\right) \rightarrow \pi , \end{aligned}$$
(20)

illustrating that the entry and exit points on the thin shell are antipodal opposite. Furthermore, when the singularity is modeled with an infinitesimally small regular core, the portion of the light ray within the thin shell can be safely disregarded. Thus, the light ray is well approximated by the combination of the ingoing and outgoing branches in the JNW metric outside the thin shell. Since these branches intersect with the thin shell at exactly two antipodal points, their connection is given by

$$\begin{aligned} \theta \rightarrow \pi -\theta \text { and }\varphi \rightarrow \varphi +\pi . \end{aligned}$$
(21)

In short, the condition (21) and the conservation of E, \(L_{z}\) and L determine the corresponding outgoing branch for a given ingoing branch.

Given its stronger theoretical motivation and its potential for generating a richer set of observational outcomes, we focus on the case of a regularized JNW singularity with a regular center throughout the remainder of this paper. Moreover, the observations related to the wormhole case can be encompassed within the context of the regular center case, an aspect that we will briefly address in the concluding section.

Fig. 4
figure 4

Images of a luminous object centered at \(x_{\text {s}}^{\mu }=(0,25M,\pi /2,\pi /6)\) as viewed by an observer positioned at \(x_{\text {o}}^{\mu }=(0,10M,\pi /2,\pi )\) in Minkowski spacetime, a Schwarzschild black hole, and a JNW singularity with \(\gamma =2/3\). The critical curve, formed by light rays escaping from the photon sphere, is depicted with dashed white lines, while the JNW singularity is marked by a blue dot. Unlike the Schwarzschild black hole, the JNW singularity displays additional images of the object inside the critical curve, due to the capability of light rays to pass through the singularity. A zoom-in view near the JNW singularity’s critical curve is presented in the bottom panel, showing one higher-order image outside the critical curve and two higher-order images inside it

Full size image

3 Lensing images

This section presents a numerical simulation of gravitational lensing images produced by a distant luminous object and a celestial sphere around JNW naked singularities, aiming to illustrate the gravitational lensing phenomenon. The observer and the center of the luminous object are positioned on the equatorial plane at \(\left( r,\phi \right) =\left( 10M,\pi \right) \) and \(\left( 25M,\pi /6\right) \), respectively, while the luminous celestial sphere is placed at \(r=25M\). Here, M represents the mass of the JNW metric. To generate observational images, we vary the observer’s viewing angle and numerically integrate \(2000\times 2000\) photon trajectories until they intersect with the celestial sphere. For a detailed explanation of the numerical implementation, interested readers can refer to [102].

The strong deflection around the photon sphere causes light rays to produce multiple images of the distant object when they orbit the photon sphere multiple times. We conveniently classify these images based on the number of orbits, denoted by n. Moreover, the positive and negative signs of n indicate whether the orbiting occurs in the counter-clockwise or clockwise directions. As anticipated, light rays can circle around the photon sphere slightly outside of it, generating images similar to the Schwarzschild black hole case. Interestingly, our earlier discussion revealed that light rays, being able to traverse the singularities, can also orbit the photon sphere from inside, resulting in a new set of images. Throughout the remainder of this paper, we use the notations \(n^{>}\) and \(n^{<}\) to refer to the \(\left| n\right| ^{\text {th}}\)-order images produced by light rays orbiting n times outside and inside the photon sphere, respectively.

Figure 4 displays images of the luminous object in three different scenarios: Minkowski spacetime, a Schwarzschild black hole, and a JNW naked singularity with \(\gamma =2/3\). In the figure, the dashed white lines represent the critical curve, which is formed by photons originating from the photon sphere. The images produced by light rays with \(n^{>}\) and \(n^{<}\) lie outside and inside the critical curve, respectively. Outside the critical curve, both the Schwarzschild black hole and the JNW singularity cases exhibit two observable images: \(n=+0^{>}\) and \(-0^{>}\), referred to as the primary and secondary images, respectively. These images can be analyzed using the weak lensing approximation. However, for the Schwarzschild black hole, no images are visible inside the critical curve due to the presence of the event horizon. In contrast, the JNW naked singularity presents an image with \(n=0^{<}\) near the center and two additional images with \(n=\pm 1^{<}\) within the critical curve. The light rays responsible for generating these images are illustrated in the upper panel of Fig. 5. It should be noted that the higher-order images are located so close to the critical curve that they cannot be resolved in the two middle panels of Fig. 4. To provide a closer view of the critical curve region, the bottom panel of Fig. 4 zooms in and displays the \(n=+1^{>}\), \(+3^{<\text { }}\) and \(+2^{<\text { }}\) images from left to right. Furthermore, the light rays responsible for producing these three images are depicted in the lower panel of Fig. 5. It is worth emphasizing that, except for the \(n=0^{<}\) image, all other images are significantly distorted due to the effects of gravitational lensing. In addition, the magnified views of light rays within the photon sphere are presented in the insets of Fig. 5, thereby demonstrating that these light rays are capable of reaching and escaping from the singularity.

Furthermore, Fig. 6 illustrates images of the celestial sphere in both a Schwarzschild black hole and JNW singularities. The celestial sphere is divided into four quadrants, each distinguished by a different color, and a white dot is placed in front of the observer. Moreover, a grid of black lines, with adjacent lines separated by \(\pi /18\), is overlaid to represent constant longitude and latitude. In the images shown in Fig. 6, the dashed circular lines represent the critical curve. Outside the critical curve, the celestial sphere images in JNW singularities bear a resemblance to those observed in the Schwarzschild black hole spacetime. However, while shadows are observed in the black hole image, the celestial sphere images persist within the critical curve for JNW singularities. This unique feature is attributed to the transparency of the singularity, allowing light to traverse through it.

Outside the critical curve, we observe a white Einstein ring generated by the white dot placed on the celestial sphere in both the Schwarzschild black hole and JNW singularity cases. However, in JNW singularities, an additional Einstein ring appears within the critical curve, representing photons that pass through the singularity with angular coordinate changes of \(\Delta \varphi =3\pi \). Furthermore, light rays passing through the singularity and undergoing an angular coordinate change of \(\Delta \varphi =\pi \) result in a white dot positioned at the center of the image.

Fig. 5
figure 5

Upper: light rays responsible for generating the object images in the third panel (located just above the bottom panel) of Fig. 4, where the images with \(n=+0^{>} \), \(+1^{<}\), \(0^{<}\), \(-1^{<}\) and \(-0^{>}\) are presented from left to right. Lower: light rays that produce the object images in the bottom panel of Fig. 4, where the images with \(n=+1^{>}\), \(+3^{<\text { }}\)and \(+2^{<\text { }}\) are displayed from left to right. In n, the number denotes the number of orbits of light rays, while the \(+\) and − signs indicate the counter-clockwise and clockwise directions, respectively. Additionally, the > and < symbols correspond to orbiting outside and inside the photon sphere, respectively. The dashed circular lines represent the photon sphere

Full size image

4 Point-like source

In order to investigate point-source gravitational lensing, we adopt an idealized thin lens model that assumes a high degree of alignment among the source, lens and observer. The lens equation, as presented in [21, 129], is expressed as

$$\begin{aligned} \beta =\vartheta -\frac{D_{LS}}{D_{OS}}\Delta \alpha , \end{aligned}$$
(22)

where \(\beta \) represents the angular separation between the source and the lens, \(\vartheta \) denotes the angular separation between the lens and the image, and \(\Delta \alpha \) represents the offset of the total deflection angle \(\alpha \) after accounting for all the windings experienced by the photon. Here, the distances \(D_{OL}\), \(D_{LS}\) and \(D_{OS}\) correspond to the observer-lens, lens-source and observer-source distances, respectively. Furthermore, we define the magnification \(\mu \) of an image as the ratio of the image’s flux to the flux of the unlensed source. This ratio is determined by the solid angles of the image and the unlensed source measured by the observer, resulting in the following expression [71, 129]

$$\begin{aligned} \mu =\mu ^{r}\mu ^{t}=\frac{\vartheta }{\beta }\frac{d\vartheta }{d\beta }. \end{aligned}$$
(23)

In the above equation, the factors \(\mu ^{r}\equiv \) \(d\vartheta /d\beta \) and \(\mu ^{t}\equiv \) \(\vartheta /\beta \) represent the radial and tangential magnifications of the image, respectively. Additionally, the sign of the magnification factors determines the parity of the image.

Fig. 6
figure 6

Images of a celestial sphere located at \(r=25M\) in the JNW metric with \(\gamma =0.6\) (Left), 0.9 (Middle) and 1 (Right). The observer’s location is \(x_{\text {o}}^{\mu }=(0,10M,\pi /2,\pi )\), and the field of view spans \(2\pi /5\). The dashed lines represent the critical curve. In the case of \(\gamma =1\), the JNW metric corresponds to a Schwarzschild black hole, and thus, the right panel includes the black hole shadow depicted as a gray area. For \(\gamma =0.6\) and 0.9, the image inside the critical curve is formed by light rays passing through the singularity. A central white dot is visible, surrounded by two white Einstein rings

Full size image

By taking advantage of the spherical symmetry, our computations of the deflection angle \(\alpha \) are confined to the equatorial plane. Within the thin-lens approximation, the deflection angle \(\alpha \) is governed by the expression from [21],

$$\begin{aligned} \alpha =I(b)-\pi , \end{aligned}$$
(24)

where I(b) represents the change in \(\varphi \), and b denotes the impact parameter related to \(\vartheta \) through the equation \(b=D_{OL}\vartheta \). When a photon approaches a turning point at \(r=r_{0}\) and then gets deflected towards a distant observer, the integral I(b) is given by

$$\begin{aligned} I(b)=2\int _{r_{0}}^{\infty }\frac{dr}{C(r)\sqrt{b^{-2}-V_{\text {eff}}\left( r\right) }}, \end{aligned}$$
(25)

where \(r_{0}\) is determined by \(V_{\text {eff}}\left( r_{0}\right) =b^{-2}\). On the other hand, if the photon passes through the singularity at \(r=r_{g}\), the azimuthal angle \(\varphi \) increases by \(\pi \), leading to the expression,

$$\begin{aligned} I(b)=2\int _{r_{g}}^{\infty }\frac{dr}{C(r)\sqrt{b^{-2}-V_{\text {eff}}\left( r\right) }}+\pi . \end{aligned}$$
(26)

4.1 Images outside the critical curve

Table 1 The angular position \(\vartheta _{\pm n^{>}}\) and the magnification factor \(\mu _{\pm n^{>}}\) of images outside the critical curve for a point-like source in JNW singularities with varying \(\gamma \). Here, \(\Delta \vartheta _{\pm n^{>}}\equiv \vartheta _{\pm n^{>}}-\vartheta _{\pm \infty }\) represents the angular separation between the \(n^{\text {th}}\)-order relativistic images and the critical curve. The superscript > indicates that the images are produced by light rays with \(b>b_{c}\) and therefore reside outside the critical curve. The values \(M=4.31\times 10^{6}M_{\odot }\), \(D_{OL}=D_{LS}=7.86\) kpc and \(\beta =5\) arcsec are used. All angles are expressed in units of microarcseconds
Full size table

As depicted above, the images located outside the critical curve are produced by light rays reaching a turning point at \(r=r_{0}\), which lies outside the photon sphere. To calculate the angular position \(\vartheta _{\pm 0^{>}}\) and magnification factor \(\mu _{\pm 0^{>}}\) for the primary image with \(n=+0^{>}\) and the secondary one with \(n=-0^{>}\), we employ Eq. (25) to numerically determine I(b) and \(dI\left( b\right) /db\). By utilizing the resulting I(b) and \(dI\left( b\right) /db\), Eqs. (22) and (23) provide the desired \(\vartheta _{\pm 0^{>}}\) and \(\mu _{\pm 0^{>}}\). Additionally, our findings reveal that \(\mu _{\pm 0^{>}}^{t}\sim \beta ^{-1}\) and \(\mu _{\pm 0^{>}}^{r}\sim \mathcal {O}\left( 1\right) \), as expected from weak gravitational lensing. When \(\beta \ll 1\), the magnitude of \(\mu _{\pm 0^{>}}^{t}\) greatly exceeds that of \(\mu _{\pm 0^{>}}^{r}\), resulting in significantly distorted images.

In the case of relativistic images with \(\left| n\right| \ge 1\), their impact parameter b closely approaches the critical impact parameter \(b_{c}\), allowing us to expand I(b) around \(b=b_{c}\). In this strong deflection limit, the total deflection angle \(\alpha \) is expressed as [130, 131]

$$\begin{aligned} \alpha&{=}&{-}\bar{a}^{>}\ln \left( b/b_{c}{-}1\right) {+}\bar{b}^{>}{+}\mathcal {O} \left( \left( b/b_{c}{-}1\right) \ln \left( b/b_{c}{-}1\right) \right) , \nonumber \\ \end{aligned}$$
(27)

where

$$\begin{aligned} \bar{a}^{>}=1\text { and }\bar{b}^{>}=-\pi +I_{R}^{>}+\ln \left[ \frac{2\left( 2\gamma +1\right) }{2\gamma -1}\right] . \end{aligned}$$
(28)

Here, the term \(I_{R}^{>}\) represents a regular integral that can be computed numerically. Using Eqs. (22) and (23), we can solve for the angular position \(\vartheta _{\pm n^{>}}\) and magnification factor \(\mu _{\pm n^{>}}\) of \(n^{\text {th}}\)-order relativistic images. Specifically, the angular position \(\vartheta _{\pm n^{>} }\) is given by [130]

$$\begin{aligned} \vartheta _{\pm n^{>}}=\vartheta _{\pm n^{>}}^{0}+\frac{b_{c}e_{n}^{>}D_{OS} }{\bar{a}^{>}D_{LS}D_{OL}}\left( \beta -\vartheta _{\pm n^{>}}^{0}\right) , \end{aligned}$$
(29)

where \(e_{n}^{>}=e^{\frac{\bar{b}^{>}-2\pi n}{\bar{a}^{>}}}\), and \(\vartheta _{\pm n^{>}}^{0}\), satisfying \(\alpha \left( \vartheta _{\pm n^{>} }^{0}\right) =\pm 2n\pi \), is given by

$$\begin{aligned} \vartheta _{\pm n^{>}}^{0}=\pm \frac{b_{c}}{D_{OL}}\left( 1+e_{n}^{>}\right) . \end{aligned}$$
(30)

The factors \(\mu ^{t}\) and \(\mu ^{r}\) are then expressed as

$$\begin{aligned} \mu _{\pm n^{>}}^{t}=\pm \frac{b_{c}\left( 1+e_{n}^{>}\right) }{\beta D_{OL} }\text { and }\mu _{\pm n^{>}}^{r}=\frac{b_{c}e_{n}^{>}D_{OS}}{\bar{a}^{>} D_{LS}D_{OL}}, \end{aligned}$$
(31)

which gives the magnification factor \(\mu _{\pm n^{>}}=\mu _{\pm n^{>}}^{r} \mu _{\pm n^{>}}^{t}\). As \(\left| \mu _{\pm n^{>}}^{t}\right| \gg \left| \mu _{\pm n^{>}}^{r}\right| \), the relativistic images are significantly stretched along the critical curve.

To numerically estimate \(\vartheta _{\pm n^{>}}\) and \(\mu _{\pm n^{>}}\) in an astrophysical setting, we model the supermassive black hole Sgr A* located at the center of our Galaxy as a JNW singularity. Specifically, we assume a mass of \(M=4.31\times 10^{6}M_{\odot }\) and a lens-source distance of \(D_{OL}=7.86\) kpc. Additionally, a source is positioned at \(D_{LS}=7.86\) kpc with an angular separation of \(\beta =5\) arcsec. Table 1 presents \(\vartheta _{\pm 0^{>}}\) and \(\mu _{\pm 0^{>}}\) for the primary and secondary images, along with \(\Delta \vartheta _{\pm n^{>}}\equiv \vartheta _{\pm n^{>} }-\vartheta _{\pm \infty }\) and \(\mu _{\pm n^{>}}\) for the relativistic images, considering various values of \(\gamma \) in JNW singularities. Here, \(\vartheta _{\pm \infty }=\lim \limits _{n\rightarrow \infty }\vartheta _{\pm n^{>} }^{0}=\pm b_{c}/D_{OL}\) represents the angular position of the critical curve. The results indicate that the angular position \(\vartheta _{\pm n^{>}}\) and magnification factor \(\mu _{\pm n^{>}}\) of the images outside the critical curve show little sensitivity to \(\gamma \).

Previous research has modeled the massive dark object at the Galactic center as both a Schwarzschild black hole and a JNW naked singularity to compute the angular position and magnification factor of \(n=\pm 0^{>}\) images of a point source [94, 95]. These studies found that, for weakly JNW naked singularities, the properties of \(n=\pm 0^{>}\) images closely resemble those observed in Schwarzschild black holes. Specifically, changes in \(\gamma \) have a minimal impact on the angular position \(\vartheta _{\pm 0^{>}}\) and magnification factor \(\mu _{\pm 0^{>}}\) of these images, as evident in Table 1. Additionally, Virbhadra et al. presented values for \(\vartheta _{\pm 0^{>}}\) and \(\mu _{\pm 0^{>}}\) of a point source with \(\beta =5\) arcsec in their Tables I and II [95]. Our findings are largely consistent with these values, with discrepancies attributable to slight variations in the adopted astrophysical parameters. Furthermore, Bozza investigated the strong gravitational lensing properties of JNW naked singularities, presenting the angular position of the critical curve \(\vartheta _{\pm \infty }\) for different M and \(D_{OL}\) values than ours [130]. Since \(\vartheta _{\pm \infty }\propto M D_{OL}^{-1}\), our results for \(\vartheta _{\pm \infty }\) are compatible with theirs once our M and \(D_{OL}\) values are scaled accordingly.

4.2 Images inside the critical curve

Table 2 The angular position \(\vartheta _{\pm n^{<}}\) and the magnification factor \(\mu _{\pm n^{<}}\) of images inside the critical curve for a point-like source in JNW singularities with varying \(\gamma \). The parameters M, \(D_{OL}\), \(D_{LS}\) and \(\beta \) are chosen to be consistent with those presented in Table 1. All angles are expressed in units of microarcseconds
Full size table

When \(b<b_{c}\), photons emitted from the source have the capability to traverse the singularity, resulting in additional images within the critical curve. In this scenario, the deflection angle \(\alpha \) is computed using Eq. (26). For light rays that pass through the singularity without orbiting it, their impact parameter b is often much smaller than \(b_{c}\), leading to

$$\begin{aligned} \alpha \simeq 2b\int _{r_{g}}^{\infty }\frac{dr}{C(r)}=\frac{b}{M}. \end{aligned}$$
(32)

Consequently, the resulting image with \(n=0^{<}\) has

$$\begin{aligned} \vartheta _{0^{<}}\simeq -\frac{D_{OS}M}{D_{LS}D_{OL}}\beta \text { and } \mu _{0^{<}}^{r}=\mu _{0^{<}}^{t}\simeq -\frac{D_{OS}M}{D_{LS}D_{OL}}, \end{aligned}$$
(33)

where we assume \(M\ll D_{LS}D_{OL}/D_{OS}\). Notably, the \(n=0^{<}\) image is barely distorted by gravitational lensing since \(\mu _{0^{<}}^{r}=\mu _{0^{<} }^{t}\).

Relativistic images produced by light rays traversing the singularity have been discussed in a generic spherically symmetric metric using the strong deflection approximation [102]. Applying these calculations to the JNW singularity, we obtain

$$\begin{aligned} \alpha= & {} -\bar{a}^{<}\ln \left( b^{2}/b_{c}^{2}-1\right) +\bar{b} ^{<}\nonumber \\{} & {} +\mathcal {O}\left( \left( b^{2}/b_{c}^{2}-1\right) \ln \left( b^{2}/b_{c}^{2}-1\right) \right) , \end{aligned}$$
(34)

where

$$\begin{aligned} \bar{a}^{<}=2\text { and }\bar{b}^{<}=2\ln \left[ \frac{4\left( 2\gamma +1\right) }{2\gamma -1}\right] +I_{R}^{<}. \end{aligned}$$

As a result, the angular position of the \(n^{\text {th}}\)-order images is given by

$$\begin{aligned} \vartheta _{\pm n^{<}}=\vartheta _{\pm n^{<}}^{0}-\frac{b_{c}e_{n}^{<}D_{OS} }{2\bar{a}^{<}D_{LS}D_{OL}}\frac{\left( \beta -\vartheta _{\pm n^{<}} ^{0}\right) }{\left( 1+e_{n}^{<}\right) {}^{3/2}}, \end{aligned}$$
(35)

where

$$\begin{aligned} \vartheta _{\pm n^{<}}^{0}=\pm \frac{b_{c}}{D_{OL}}\frac{1}{\sqrt{1+e_{n}^{<}} }\text { and }e_{n}^{<}=e^{\frac{\bar{b}^{<}-2\pi n}{\bar{a}^{<}}}. \end{aligned}$$
(36)

The corresponding radial and tangential magnification factors are

$$\begin{aligned} \mu _{\pm n^{<}}^{r}= & {} -\frac{b_{c}e_{n}^{<}D_{OS}}{2\bar{a}^{<}D_{OL}D_{LS} }\left( 1+e_{n}^{<}\right) ^{2/3}\text { and }\nonumber \\ \mu _{\pm n^{<}}^{t}= & {} \pm \frac{b_{c}}{\beta D_{OL}\sqrt{1+e_{n}^{<}}}, \end{aligned}$$
(37)

respectively, showing that the relativistic images are highly stretched along the critical curve.

Similarly, in the aforementioned astrophysical scenario, Table 2 presents the angular position and magnification factor of the images inside the critical curve. For the \(n=0^{<}\) image, its angular position and magnification factor hardly depend on \(\gamma \). It shows that the \(n=0^{<}\) image is almost centered in the image plane, positioned far away from the critical curve. Moreover, compared to the relativistic images listed in the table, the \(n=0^{<}\) image has a smaller magnification factor, mainly due to the very small value of \(\mu _{0^{<}}^{t}\). Notably, the relativistic images inside the critical curve are more widely separated and magnified compared to the images outside the critical curve, resulting from the significant bending of light rays upon entering or exiting the photon sphere. This bending also leads to a noticeable dependence of the angular positions and magnification factors on \(\gamma \). As \(\gamma \) increases, the relativistic images tend to approach the critical curve. Additionally, there is a marked rise (fall) in the magnification factor of the \(n=\pm 1^{<}\) (\(n=\pm 2^{<}\) and \(\pm 3^{<}\)) images with the increase of \(\gamma \).

5 Conclusions

This paper investigated the phenomenon of gravitational lensing by JNW naked singularities, which possess a photon sphere. Similar to Schwarzschild black holes, light rays that orbit the photon sphere outside of it result in multiple images of a distant source beyond the critical curve. However, when photons originating from the source enter the photon sphere, they are observed to approach the singularity in a finite coordinate time. Assuming that the singularity is remedied by a regular core, these photons can traverse the regularized singularity, leading to the emergence of new images inside the critical curve. In particular, the \(n=0^{<}\) image, formed by light rays passing directly through the singularity, remains well-separated from the critical curve and exhibits minimal distortion. Furthermore, we have demonstrated that relativistic images inside the critical curve are more magnified and positioned farther from the critical curve than those outside the critical curve, enhancing the possibility of resolving relativistic images within the critical curve. As a result, these findings present a powerful means of detecting and studying JNW naked singularities through their distinct gravitational lensing signatures.

Although current observational facilities lack the capability to distinguish new images within the critical curve in JNW singularity spacetime, the next-generation Very Long Baseline Interferometry has emerged as a promising tool for this purpose [132,133,134]. Hence, it would be highly intriguing to extend our analysis to encompass more astrophysically realistic models, such as the rotating JNW naked singularity solution and the imaging of accretion disks around JNW singularities.

Lastly, it is important to note that the optical appearances of distant sources within the JNW singularity spacetime are contingent upon the specific regularization method applied to address the singularity. In cases where the singularity is regularized by a wormhole throat instead of a regular core, photons reaching the throat will traverse to another universe. In scenarios where the source and observer inhabit the same universe, the resultant images are solely located outside the critical curve, bearing a close resemblance to the black hole case. In contrast, if the source and the observer reside in different universes, only images situated within the critical curve become observable, thereby presenting observational phenomena distinct from those associated with black holes.