1 Introduction

Vector boson scattering (VBS) processes are a particularly appealing class of reactions for exploring the electroweak (EW) sector of the Standard Model (SM) and possible extensions thereof. In the context of the SM, cross sections for the scattering of the longitudinal modes of an EW gauge boson are unitarised by Higgs-boson exchange contributions. The underlying cancellation mechanism is sensitive to both the Higgs- and the gauge-boson sector with deviations from the SM in particle content or properties immediately affecting the relevant cross sections. This makes VBS one of the most promising classes of processes for the discovery of physics beyond the SM in the EW sector.

In hadronic collisions the scattering of EW gauge bosons can be accessed in VBS processes which involve the scattering of hadronic constituents by EW gauge boson exchange. The experimental signature of such a reaction includes the gauge bosons’ decay products and two distinctive jets resulting from the scattered partons. Because of the colour-singlet nature of the t-channel gauge-boson exchange these so-called tagging jets tend to be located in the far forward and backward regions of the detector with a large separation in rapidity. This feature of VBS reactions helps to identify the signal in the presence of QCD background processes with large production rates but rather different signatures.

VBS processes have received a lot of attention from the particle physics community. Tree-level predictions are available from the dedicated parton-level generator Phantom [1], and the multi-purpose tool Whizard [2]. Next-to-leading-order (NLO) QCD corrections to VBS processes with massive gauge bosons have first been considered in Refs. [3,4,5,6,7] and been implemented in the framework of the VBFNLO parton-level Monte-Carlo program [8]. An alternative option is provided by the multi-purpose program MadGraph5_aMC@NLO [9]. The matching of the NLO-QCD calculations with parton-shower (PS) programs according to the POWHEG formalism [10, 11] has been considered in Refs. [12,13,14,15] and made publicly available in the POWHEG BOX [16] repository. An independent implementation of VBS processes at NLO-QCD accuracy matched with PS in the context of the HERWIG7 Monte Carlo program [17] was presented in Ref. [18]. More recently, in addition to QCD corrections the NLO electroweak corrections have been considered in Refs. [19,20,21,22,23,24,25,26]. For a review of existing work at LO and NLO-QCD accuracy on the representative VBS \(W^+W^+jj\) channel and a comparison of the individual programs’ features we refer the interested reader to Ref. [27]. A LO review of event generators for the VBS \(WZjj\) channel is available from [28].

At the CERN Large Hadron Collider (LHC), the ATLAS collaboration reported the observation of EW \(W^\pm Zjj\) production at a center-of-mass energy of \(\sqrt{s}=13\) TeV in final states with three identified leptons of electron or muon type in 2018 [29]. The CMS collaboration observed the production of \(W^\pm Z\) pairs with leptonic decays in association with two jets at \(\sqrt{s}=13\) TeV in 2020, and also provided constraints on anomalous quartic vector boson interactions [30]. In Refs. [31, 32], semi-leptonic decay modes were considered.

In all of these experimental publications, however, the signal simulation was severely limited in accuracy: Refs. [29, 30, 32] resorted to a leading-order approximation of the signal process. In Ref. [31] NLO-QCD corrections to the on-shell WZjj production process were taken into account, but a factorised ansatz was used to simulate the subsequent decay of the gauge-boson system. This approximation works reasonably well in the resonance region, but fails to provide an accurate description in other regions of phase space, as will be illustrated below.

In this article we specifically consider the VBS-induced \(W^\pm Zjj\) process. Building on an existing implementation of the VBS \(WZjj\) process [15] in the POWHEG BOX [16] that, however, was limited to fully leptonic decays of the gauge bosons, we provide an updated version of the program accounting for leptonic, semi-leptonic, and fully hadronic decay modes of the EW gauge bosons. For each mode, NLO-QCD corrections, off-shell effects, and spin correlations in the decay system are taken into account. Moreover, we provide an option to consider generic extensions of the SM. To illustrate the capabilities of the updated program, phenomenological results are presented for selected scenarios.

In detail, our work builds on previous developments for VBS-induced \({{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) and \(\nu _e e^+\mu ^-\mu ^+jj\) production in the context of the SM. In Ref. [15] the NLO-QCD corrections for these reactions as calculated in [5] have been implemented in the POWHEG BOX. Here, we go beyond this existing implementation by adding semi-leptonic and hadronic decays of the gauge bosons, and considering an extension of the SM using the effective field theory (EFT) approach of Ref. [33] that has already been used in the related \(ZZjj\) VBS process [14]. Effects of dimension-six EFT operators in VBS have also been studied in Refs. [34, 35]. In addition, we investigate the relevance of off-shell effects and spin correlations in the decays by an explicit comparison to approximate treatments of these effects. We would like to point out the existence of a complementary calculation [21] for EW \(W^+Zjj\) calculation in the fully leptonic decay mode which focuses on perturbative corrections and provides results including the full NLO QCD and EW corrections. This calculation has, however, not been matched to a parton shower.

The article is structured as follows: In Sect. 2 we describe the features of the updated implementation of EW \(WZjj\) production in hadronic collisions in the POWHEG BOX. Using this program, we present some representative numerical results of EW \(WZjj\) production at the LHC and a potential future circular hadron collider (FCC) operating at an energy of 100 TeV. We conclude in Sect. 4.

2 Details of the POWHEG BOX implementation

In order to provide a Monte-Carlo program for the simulation of EW \(WZjj\) production in hadronic collisions at NLO+PS accuracy with the option for various leptonic, semi-leptonic, and hadronic final states in the context of the SM and a generic model supporting anomalous interactions in the gauge boson sector we provide appropriate extensions of the public POWHEG BOX implementation of Ref. [15].

We recall that this existing program resorts to tree-level and NLO-QCD matrix elements for the purely EW processes \(pp\rightarrow \nu _e e^+\mu ^-\mu ^+jj\) and \(pp\rightarrow {{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) adapted from the VBFNLO parton-level Monte-Carlo generator [8]. Even though in the following referred to as “EW \(WZjj\) production” for the sake of brevity, it is implicitly understood that all resonant and non-resonant diagrams giving rise to a \(\nu _e e^+\mu ^-\mu ^+jj\) or \({{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) final state system are taken into account within the so-called VBS approximation. The VBS approximation only retains contributions from t-channel and u-channel diagrams, but not their interference, and disregards s-channel contributions. When selection cuts typical for an experimental VBS analysis are applied this approximation has been found [28] to reproduce the full result for the VBS cross section very well. For instance, for a representative setup at LO the authors of [28] report an agreement at the level of 0.6% between calculations based on full matrix elements and predictions of VBFNLO within the VBS approximation. We note, however, that the validity of this approximation deteriorates when more inclusive selection cuts are applied, see e.g. Ref. [27] for a comprehensive study of the VBS approximation. For this reason we only consider analysis setups with tight VBS cuts in Sect. 3. The Cabibbo–Kobayashi–Maskawa matrix is assumed to be diagonal, and contributions from external top or bottom quarks are not taken into account. For the updated POWHEG BOX implementation of the EW \(WZjj\) production process presented here we resort to the same approximations.

As long as fully leptonic decays of the gauge bosons are considered, within the mentioned approximations the structure of the NLO-QCD corrections does not change if new interactions in the EW gauge-boson sector are taken into account. The original SM amplitudes for \(\nu _e e^+\mu ^-\mu ^+jj\) and \({{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) production are structured in a modular way with leptonic tensors for those building blocks of the relevant Feynman diagrams that only contain colour-neutral particles, and hadronic currents accounting for the scattering quarks and, in the real-emission contributions, gluons. The NLO-QCD corrections only affect the hadronic currents. Extensions of the SM in the EW sector thus merely require an appropriate replacement of the leptonic tensors.

We provide such an extension in the framework of the effective field theory (EFT) approach of Ref. [33] accounting for anomalous interactions in the EW gauge boson sector by an extension of the SM Lagrangian with operators of higher mass dimension,

$$\begin{aligned} \mathcal {L}_\textrm{eff} = \mathcal {L}_\textrm{SM} + \sum _{d>4}\sum _i \frac{c_i^{(d)}}{\Lambda ^{d-4}}\mathcal {O}_i^{(d)} . \end{aligned}$$
(1)

Here, d denotes the mass dimension of the operators \(\mathcal {O}_i^{(d)}\), and the \(c_i^{(d)}\) are the expansion coefficients. The sum over d includes contributions of all higher-dimensional operators starting from \(d=6\). The summation index i runs over all non-vanishing operators of a given mass dimension. The parameter \(\Lambda \) denotes the energy scale up to which the EFT is supposed to be valid. We assume \(\Lambda \) to be much larger than the EW scale and thus restrict ourselves to the contribution of operators up to dimension six.

Following Ref. [33] we consider three independent operators that conserve charge (C) and parity (P),

$$\begin{aligned} {\mathcal {O}}_{WWW}&= \textrm{Tr}[{\hat{W}}_{\mu \nu }{\hat{W}}^{\nu \rho }{\hat{W}}_{\rho }^{\mu }], \end{aligned}$$
(2)
$$\begin{aligned} {\mathcal {O}}_{W}&= (D_{\mu }\Phi )^{\dag }{\hat{W}}^{\mu \nu }(D_{\nu }\Phi ), \end{aligned}$$
(3)
$$\begin{aligned} {\mathcal {O}}_B&= (D_{\mu }\Phi )^{\dag }{\hat{B}}^{\mu \nu }(D_{\nu }\Phi ), \end{aligned}$$
(4)

and two C and/or P violating operators,

$$\begin{aligned} {\mathcal {O}}_{{\tilde{W}}WW}&= \textrm{Tr}[{\tilde{W}}_{\mu \nu }{\hat{W}}^{\nu \rho }{\hat{W}}_{\rho }^{\mu }], \end{aligned}$$
(5)
$$\begin{aligned} {\mathcal {O}}_{{\tilde{W}}}&= (D_{\mu }\Phi )^{\dag }{\tilde{W}}^{\mu \nu }(D_{\nu }\Phi ). \end{aligned}$$
(6)

These operators are constructed from the Higgs doublet field \(\Phi \) and the electroweak field strength tensors \(W_{\mu \nu }^{a}\) \((a=1,2,3)\) and \(B_{\mu \nu }\),

$$\begin{aligned} W^{a}_{\mu \nu }&=\partial _{\mu }W^{a}_{\nu }-\partial _{\nu }W^{a}_{\mu }-g\epsilon _{abc}W_{\mu }^{b}W_{\nu }^{c} ,\end{aligned}$$
(7)
$$\begin{aligned} B_{\mu \nu }&=\partial _{\mu }B_{\nu }-\partial _{\nu }B_{\mu }, \end{aligned}$$
(8)

with the U(1) and SU(2) gauge fields \(B_{\mu }\) and \(W^a_{\mu }\) and their respective couplings \(g'\) and g. The \(\sigma ^a\) denote the Pauli matrices. The covariant derivative \(D_\mu \) is given by

$$\begin{aligned} D_{\mu } = \partial _{\mu }+igW_{\mu }^{a}\dfrac{\sigma ^{a}}{2}+\dfrac{1}{2}i g'B_{\mu }, \end{aligned}$$
(9)

and the modified field strength tensors \({\hat{W}}_{\mu \nu }\) and \({\hat{B}}_{\mu \nu }\) are defined by

$$\begin{aligned} {\hat{W}}_{\mu \nu }&= i g \dfrac{\sigma ^{a}}{2} W_{\mu \nu }^{a}, \end{aligned}$$
(10)
$$\begin{aligned} {\hat{B}}_{\mu \nu }&=\dfrac{i}{2}g' B_{\mu \nu }, \end{aligned}$$
(11)
$$\begin{aligned} \left[ D_{\mu },D_{\nu }\right]&={\hat{W}}_{\mu \nu }+{\hat{B}}_{\mu \nu }\,, \end{aligned}$$
(12)

while the modified dual field strength tensor is given by

$$\begin{aligned} {\tilde{W}}_{\mu \nu } = \epsilon _{\alpha \beta \mu \nu }{\hat{W}}^{\alpha \beta }. \end{aligned}$$
(13)

To simplify our notation we denote the coefficients of the operators of Eqs. (2)–(6) that appear in the EFT expansion of Eq. (1) up to dimension six as

$$\begin{aligned} C_i \equiv \dfrac{c_i^{(6)}}{\Lambda ^2}. \end{aligned}$$
(14)

In the following, instead of a numbered index i we use the label of the corresponding operator to identify each operator coefficient. For instance, \(C_{WWW}\) is the properly normalized coefficient of the \({\mathcal {O}}_{WWW}\) operator.

In the actual calculation of scattering cross sections care has to be taken to ensure a consistent EFT expansion up to the desired order in \(1/\Lambda ^2\). Schematically, the operators of different mass dimension enter in the relevant matrix elements squared as

$$\begin{aligned}&\vert {\mathcal {M}}_{SM} + {\mathcal {M}}_{dim-6} +{\mathcal {M}}_{dim-8} + \cdots \vert ^2 \nonumber \\&\quad = \underbrace{\vert {\mathcal {M}}_{SM} \vert ^2}_{\Lambda ^0} + \underbrace{2 Re({\mathcal {M}}_{SM}{\mathcal {M}}_{dim-6}^\star )}_{\Lambda ^{-2}} \nonumber \\&\qquad + \underbrace{\vert {\mathcal {M}}_{dim-6}\vert ^2+2 Re({\mathcal {M}}_{SM}{\mathcal {M}}_{dim-8}^\star )}_{\Lambda ^{-4}}+\cdots \,. \end{aligned}$$
(15)

Thus, if one truncates the EFT expansion at order \(1/\Lambda ^2\), in addition to the pure SM contribution one should only keep the interference term \(2 Re({\mathcal {M}}_{SM}{\mathcal {M}}_{dim6}^\star )\), and disregard the quadratic term \( \vert {\mathcal {M}}_{dim6}\vert ^2\), which is part of the \(\mathcal {O}(1/\Lambda ^4)\) result. However, in the past in many applications this quadratic term was considered as part of the “dimension six” results. Below we therefore consider both options and refer to them as SM+lin and SM+quad.

In addition to the \(\nu _e e^+\mu ^-\mu ^+jj\) and \({{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) final states provided in Ref. [15], in this work we also implemented EW production of a \({{\bar{\nu }}}_e e^-\nu _\mu {{\bar{\nu }}}_\mu \), a \(q{{\bar{q}}}' \mu ^-\mu ^+\), a \({{\bar{\nu }}}_e e^-Q{{\bar{Q}}}\), a \(\nu _e e^+Q{{\bar{Q}}}\), or a \(q{{\bar{q}}}' Q {{\bar{Q}}}\) system, respectively, in association with two tagging jets (here q and Q refer to massless quarks of different types). Representative diagrams for the partonic channel \(u c \rightarrow u s\, \bar{d} u\, \mu ^+\mu ^-\) are shown in Fig. 1.

Fig. 1
figure 1

Representative Feynman diagrams for the VBS-process \( u \,\, c \rightarrow u \,\, s \,\, {\bar{d}} \,\, u \,\, \mu ^{+} \,\, \mu ^{-} \): (a, b) genuine vector-boson scattering diagrams, (c, d) diagrams including gauge-boson emission from a quark line, (e) singly-resonant, and (f) non-resonant diagrams

Full size image

For each channel, not only resonant diagrams related to the leptonic or hadronic decay of a W or Z boson are taken into account, but also non-resonant diagrams resulting in the same final state. For simplicity we will refer to the previously listed processes (including off-resonant contributions) as fully leptonic, leptonic-invisible, semi-leptonic, and fully hadronic decay modes. In the case of semi-leptonic and fully hadronic decay modes we do not take QCD corrections to the decays into account, and we neglect QCD corrections connecting the \(WZjj\) production with the decay part of the considered final state. The latter type of corrections are expected to be negligible. Corrections to the hadronic decays of the Z and W bosons are accounted for by the multi-purpose Monte-Carlo programs matched to our NLO-QCD calculation.

For each final state, at Born level singularities in the production cross section arise from diagrams with the t-channel exchange of a photon of very low virtuality \(Q^2\). Such contributions are entirely negligible after selection cuts on the tagging jets are applied and can thus be removed already at generation level by a cut,

$$\begin{aligned} Q^2_\textrm{min}= 4~\text {GeV}^2. \end{aligned}$$
(16)

To further improve the numerical efficiency of the Monte-Carlo integration additionally a Born-suppression factor of the form

$$\begin{aligned} F(\Phi ) = \left( \frac{p_{T,1}^2}{p_{T,1}^2+\Lambda _\Phi ^2}\right) ^2 \left( \frac{p_{T,2}^2}{p_{T,2}^2+\Lambda _\Phi ^2}\right) ^2. \end{aligned}$$
(17)

can be employed. Here, the \(p_{T,i}\) denote the transverse momenta of the final-state partons of the underlying Born configuration \(\Phi \), and \(\Lambda _\Phi \) is a technical parameter, by default set to 10 GeV.

We remind the reader that contributions with a pair of same-type charged fermions (f) in the final state cannot only stem from decays of the WZ system, but also from diagrams where a photon decays into a fermion pair. An additional type of singularity at Born level arises from diagrams where such a photon exhibits very low virtuality. For analyses that require a fermion pair with an invariant mass close to the mass of the Z boson, such singularities can easily be removed already at generation level by an invariant mass cut on the respective lepton pair. The requirement

$$\begin{aligned} m_{f {{\bar{f}}}}>0.5~\text {GeV} \end{aligned}$$
(18)

suffices to remove any potentially problematic contributions from photons of very low virtuality at generation level.

3 Phenomenological results

In the following we will provide some phenomenological results generated by our implementation in version 2 of the POWHEG BOX. For all of these results we use the following general settings: We set the Fermi constant to \( G_{\mu } = 1.1663787 \cdot 10^{-5} \, \mathrm {GeV^{-2}} \). For the masses and widths of the EW bosons we use: \({m_H = 125.25 \, \textrm{GeV}}\), \({m_W = 80.377 \, \textrm{GeV}}\), \({m_Z = 91.1876 \, \textrm{GeV}}\), \({\Gamma _H = 0.0032 \, \textrm{GeV}}\), \({\Gamma _W = 2.085 \, \textrm{GeV}}\), and \({\Gamma _Z = 2.4952 \, \textrm{GeV}}\). The EW coupling, \(\alpha _{em}\), is calculated therefrom via tree-level EW relations.

In addition to the POWHEG BOX we also use the tool-chain MadGraph5_aMC@NLO [9, 36] including the program MadSpin [37] for comparison to the POWHEG BOX results. To simulate the parton shower we use PYTHIA8, version 8.245, with the Monash2013 tune [38]. Hadronisation, MPI, and QED emissions are turned off in order to isolate the effect of the shower and matching. We note that in realistic simulations non-perturbative effects have to be considered [39]. For reconstructing jets we resort to FastJet [40], version 3.3.4. For all results presented in this section jets are clustered via the anti-\(k_T\) algorithm [41] with a radius-parameter of \(R=0.4\), and the NNPDF31_nlo_as_0118 (ID 303400) set [42] of parton distribution functions (PDFs) is used as provided by version 6.3.0 of the LHAPDF library [43].

3.1 EFT results

In this subsection we explore the impact of SM extensions in the EFT framework introduced in Sect. 2. We individually set the coefficient of each EFT operator defined in Eqs. (2)–(6) to the largest value compatible with the experimental limits of Ref. [44] while setting the coefficients of all other EFT operators to zero. As it turned out that the impact of the \(\mathcal {O}_{WWW}\) operator is most pronounced, below we only display results obtained for non-vanishing values of the \(C_{WWW}\) coefficient. For instance, results obtained with non-vanishing values of the \(C_{W}\) operator coefficient are basically identical to the SM results and will thus not be further discussed here.

For the unitarisation of our EFT predictions we proceeded along the lines of Ref. [45] where unitarity violations are avoided by using appropriate cuts on the invariant mass of the vector bosons produced in a VBS reaction. We calculated the limits beyond which unitarity violations are to be expected for the setups considered in this work using the tool calc-formfactor [46, 47] that is available within the VBFNLO package [48, 49]. We found that unitarity violations would occur only beyond scales relevant for the results shown below.

Throughout this subsection we use a renormalisation scale, \(\mu _{\textrm{R}}=\xi _{\textrm{R}}\mu _0\), and factorisation scale, \(\mu _{\textrm{F}}=\xi _{\textrm{F}}\mu _0\), that is expected to optimally account for the region of high transverse momenta where the effects of the dimension-six operators are expected to have the largest impact (c.f. Ref. [14]). The scale \(\mu _0\) is given by

$$\begin{aligned} \mu _0 = \dfrac{1}{2}\left( E_{T,W}+E_{T,Z}+ \sum _f^{\mathrm {n_{part}}} p_{T,f}\right) , \end{aligned}$$
(19)

where the sum includes the transverse momenta \(p_{T,f}\) of all \(\mathrm {n_{part}}\) final-state partons of a considered Born-type or real-emission configuration. In addition we define

$$\begin{aligned} E_{T,W} = \sqrt{m_W^2+p_{T,W}^2}, \qquad E_{T,Z} = \sqrt{m_Z^2+p_{T,Z}^2}, \end{aligned}$$
(20)

where \(p_{T,Z}\) and \(p_{T,W}\) are the transverse momenta of the muon pair and the positron-neutrino pair of the fixed-order configuration, respectively. The factors \(\xi _{\textrm{R}}\) and \(\xi _{\textrm{F}}\) are varied between 0.5 and 2 with 7-point variation in our NLO+PS simulations and set to one for the fixed-order calculations.

For our representative numerical studies we use settings inspired by the ATLAS analysis described in Ref. [50]. In particular, we construct jets using the anti-\(k_T\) algorithm with \(R=0.4\). In the following we will denote the jets with index \(j_1\) for the hardest jet and \(j_2,j_3,...\) for further jets ordered by their transverse momentum. The two hardest jets are identified as tagging jets and are required to have a transverse momentum, rapidity and invariant mass of

$$\begin{aligned} p_{T,j}^{\textrm{tag}}> 30 \, \textrm{GeV}, \qquad \vert y_j^{\textrm{tag}} \vert < 4.5, \qquad m_{jj}^{\textrm{tag}} > 500 \, \textrm{GeV}. \end{aligned}$$
(21)

Moreover, we only keep events where the tagging jets lie in opposite hemispheres,

$$\begin{aligned} \eta _{j_1}^{\textrm{tag}}\cdot \eta _{j_2}^{\textrm{tag}} < 0, \end{aligned}$$
(22)

and have a large rapidity separation of

$$\begin{aligned} \Delta y_{jj}^{\textrm{tag}} = \vert y_{j_1}^{\textrm{tag}}-y_{j_2}^{\textrm{tag}} \vert \ge 2.5. \end{aligned}$$
(23)

To identify additional non-tagging jets we require them to be located in a rapidity range of

$$\begin{aligned} \vert y_j \vert < 4.5. \end{aligned}$$
(24)

No other cuts are applied on non-tagging jets unless specifically stated otherwise.

Fig. 2
figure 2

NLO+PS predictions for \(pp\rightarrow \nu _e e^+\mu ^-\mu ^+jj\) at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (21)–(29) for the SM+lin (green) and the SM+quad case (orange) with \(C_{WWW} = -4.2 \, \textrm{TeV}^{-2}\), and within the SM (purple). The upper panels show the transverse momentum of the hardest tagging jet (a), the rapidity of the hardest tagging jet (b), the reconstructed transverse momentum of the Z boson (c), and the azimuthal angle separation of the tagging jets (d). The respective lower panels show the ratios of the SM+lin and SM+quad predictions to the pure SM results

Full size image
Fig. 3
figure 3

NLO+PS predictions for \(pp\rightarrow \nu _e e^+\mu ^-\mu ^+jj\) at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (21)–(29) for the SM+lin (green) and the SM+quad case (orange) with \(C_{WWW} = -4.2 \, \textrm{TeV}^{-2}\), and within the SM (purple). The upper panels show the transverse momentum of the 3rd jet (a) and the rapidity of the 3rd jet for a \(p_T\) cut of \(p_{T,j_3} > 10 \, \textrm{GeV}\) (b). The respective lower panels show the ratios of the SM+lin and SM+quad predictions to the pure SM results

Full size image

In our fixed-order results the final state contains two muons, one positron and one neutrino. Within the PYTHIA setup we consider, i.e. in the absence of QED radiation in the parton shower and without hadron decays, the events we simulate at NLO+PS level do not exhibit any additional leptons or neutrinos. For the charged leptons \(\ell \) we demand

$$\begin{aligned} p_{T,\ell } > 15 \, \textrm{GeV}, \qquad \vert y_\ell \vert < 2.5. \end{aligned}$$
(25)

We do not apply any cuts on the neutrino. Furthermore, we require a clear separation of the tagging jets and the charged leptons, i.e. we require a separation in the rapidity-azimuthal angle plane of

$$\begin{aligned} R_{j\ell } > 0.3. \end{aligned}$$
(26)

For the muons which are stemming from the Z decay we additionally demand

$$\begin{aligned} R_{\mu \mu } > 0.3, \end{aligned}$$
(27)

as well as that their reconstructed invariant mass, \(m_\textrm{inv}^Z\), lies in a window around the physical Z-boson mass of

$$\begin{aligned} 66 \, \textrm{GeV}< m_\textrm{inv}^Z < 116 \, \textrm{GeV}. \end{aligned}$$
(28)

Finally, we also require all charged leptons to lie in the rapidity gap between the two tagging jets

$$\begin{aligned} \textrm{min}(y_{j_1}^{\textrm{tag}},y_{j_2}^{\textrm{tag}})< y_\ell < \textrm{max}(y_{j_1}^{\textrm{tag}},y_{j_2}^{\textrm{tag}}). \end{aligned}$$
(29)

Let us now discuss results for the LHC with a center-of-mass energy of \(\sqrt{s}=13 \, \textrm{TeV}\). In Figs. 2 and 3 we compare SM results at NLO+PS accuracy for selected distributions of the tagging jets and the leptons with those obtained in the EFT framework of Sect. 2. In particular, we set the operator coefficient \(C_{WWW}\) to the maximal negative value compatible with current experimental limits, i.e. \(C_{WWW}= -4.2 \, \textrm{TeV}^{-2}\), and consider separately the case where only the linear term of the EFT expansion sketched in Eq. (15) is taken into account (dubbed SM+lin), and the case where additionally the quadratic term is retained (referred to as SM+quad).

For the SM+lin implementation we find only small differences to the SM results for all considered distributions. These effects are best visible for the azimuthal angle separation of the two tagging jets, \(\Phi _{jj}\). In particular for \(\Phi _{jj}\lesssim \pi /2\) the shape is slightly different from the SM case. Larger differences to the SM case are found for the SM+quad implementation. However, we would like to remind the reader that the limits chosen for \(C_{WWW}\) have been derived for the SM+lin implementation and that the SM+quad version is shown only for the purpose of comparison. The SM+lin and SM+quad predictions can barely be distinguished from the respective SM results for the transverse momentum and the rapidity distributions of the hardest tagging jet and the transverse momentum of the Z boson. The latter is reconstructed from the momenta of the muon pair closest in invariant mass to \(m_Z\).

In Figs. 4 and 5 we display the same observables as in Figs. 2 and 3 for a potential future circular collider (FCC) with proton-proton collisions at a center-of-mass energy of \(\sqrt{s}=100~\textrm{TeV}\). For the FCC discussion we use the following setup inspired by Ref. [51]. We use the same renormalisation and factorisation scale as in Eq. (19), but apply stronger cuts on the tagging jets. More precisely, we require

$$\begin{aligned} p_{T,j}^{\textrm{tag}}> 50 \, \textrm{GeV}, \qquad \vert y_j^{\textrm{tag}} \vert < 6, \qquad m_{jj}^{\textrm{tag}} > 2500 \, \textrm{GeV}. \end{aligned}$$
(30)

Additionally, the tagging jets have to fulfill

$$\begin{aligned} \eta _{j_1}^{\textrm{tag}}\cdot \eta _{j_2}^{\textrm{tag}} < 0, \quad \Delta y_{jj}^{\textrm{tag}} = \vert y_{j_1}^{\textrm{tag}}-y_{j_2}^{\textrm{tag}} \vert \ge 5. \end{aligned}$$
(31)

For the charged leptons we require

$$\begin{aligned} p_{T,\ell } > 20 \, \textrm{GeV}, \qquad \vert y_\ell \vert < 5, \end{aligned}$$
(32)

as well as a separation of the tagging jets and the charged leptons in the rapidity-azimuthal angle plane of

$$\begin{aligned} R_{j\ell } > 0.4. \end{aligned}$$
(33)

We keep the requirements of Eqs. (27)–(29).

Fig. 4
figure 4

Same as in Fig. 2, but for the FCC with an energy of \(\sqrt{s}=100\) TeV and with the cuts of Eqs. (27)–(33)

Full size image
Fig. 5
figure 5

Same as in Fig. 3, but for the FCC with an energy of \(\sqrt{s}=100\) TeV and with the cuts of Eqs. (27)–(33)

Full size image

Differences between the SM and the SM+quad implementation are clearly enhanced at this energy for all distributions. However, the azimuthal angle separation of the tagging jets exhibits sensitivity to the effects of the SM+lin implementation.

3.2 Leptonic decays

The objective of this subsection is to explore the relevance of simulating the full leptonic final state of VBS-induced \({{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) production as opposed to approximations where a \(W^+Z\) boson pair is produced on-shell and combined with a simulation for the decays of these bosons into the desired leptonic final state. Such an approximation is used, for instance, in the search for anomalous EW production of vector boson pairs in association with two jets by the CMS collaboration [32] and in the search for EW diboson production in association with a high-mass dijet system in semi-leptonic final states by the ATLAS collaboration [31]. Since QCD corrections do not directly affect the leptonic decays, we conduct this discussion at LO. To that end we compare our POWHEG BOX implementation for \({{\bar{\nu }}}_e e^-\mu ^-\mu ^+jj\) production via VBS with two alternative ones: The first is using MadGraph5_aMC@NLO  where a \(W^+Zjj\) final state is produced on-shell. The decays of the two bosons are afterwards simulated via MadSpin (this simulation is denoted by MG5+MadSpin below). The other implementation is using the LO version of MadGraph5_aMC@NLO and includes off-shell contributions and spin-correlations in the lepton system (this implementation will be denoted by MG5-full in the following). This comparison serves as a consistency check for the correct usage of the two tools. It also shows the equivalence of the POWHEG BOX and the MG5-full implementation after the application of VBS cuts despite more approximations being used in the matrix elements entering the POWHEG BOX than the MG5-full implementation.

For the comparison presented in this subsection we use a fixed factorisation and renormalisation scale of

$$\begin{aligned} \mu _F = \mu _R = m_W/\sqrt{1+(\Gamma _W/m_W)^2}. \end{aligned}$$
(34)

As before, we consider proton collisions at the LHC with \(\sqrt{s}=13\) TeV. For the selection of signal events we proceed along similar lines as in the previous subsection. We impose the cuts of Eqs. (21)–(29) defined above.

Fig. 6
figure 6

LO predictions for \(pp\rightarrow \nu _e e^+\mu ^-\mu ^+jj\) at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (21)–(29) as obtained with the POWHEG-BOX (purple), MG5+MadSpin (green), and with MG5-full (orange). The upper panels show the reconstructed invariant mass of the W boson (a), the reconstructed invariant mass of the Z boson (b), the transverse mass of the WZ system (c), and the reconstructed transverse momentum of the Z boson (d). The respective lower panels show the ratios of the MG5+MadSpin and MG5-full predictions to the POWHEG-BOX results

Full size image

In Fig. 6 we show several distributions related to the decay system of the VBS-induced \(\nu _e e^+\mu ^-\mu ^+jj\) production process. The invariant masses of the W and Z systems, \(m_\textrm{inv}^W\) and \(m_\textrm{inv}^Z\), are reconstructed from the momenta of the \(\nu _e e^+\) and \(\mu ^-\mu ^+\) pairs, respectively. The transverse mass of the WZ system is defined by

$$\begin{aligned} m_T(WZ) = \sqrt{({\tilde{E}}_{T,W}+{\tilde{E}}_{T,Z})^{2} - (p_{T,W}+p_{T,Z})^{2}}, \end{aligned}$$
(35)

where \( p_{T,W} \) and \( p_{T,Z} \) are the transverse momenta of the reconstructed W and Z systems, and the transverse energies \({\tilde{E}}_{T,i} \) (\(i = {W,Z}\)) are given by

$$\begin{aligned} {\tilde{E}}_{T,i}=\sqrt{(m_\textrm{inv}^i)^{2}+p_{T,i}^{2}}. \end{aligned}$$
(36)

We find that, for each considered distribution, the results of the MG5-full and the POWHEG BOX implementations are in very good agreement within their respective statistical uncertainties. In contrast, the results of MG5+MadSpin deviate from the implementations that retain full control on off-shell contributions and spin correlations in the leptonic decay system. While near the W and Z resonances MG5+MadSpin yields satisfactory results, further away from the peaks of the invariant mass distributions, and in particular in the tails of the transverse mass distribution, the on-shell approximation does no longer accurately reproduce the full results. Deviations can reach almost an order of magnitude for \(m_T(WZ) \lesssim 150\) GeV and \(m_T(WZ) \gtrsim 350\) GeV. This should be kept in mind for the simulation of VBS processes when off-shell regions are of interest.

3.3 Semi-leptonic and hadronic decays

While in Ref. [15] an implementation for VBS-induced WZ production with fully leptonic decays was developed and made available in the POWHEG BOX program package, semi-leptonic and fully hadronic final states were not considered before in that framework. We have closed this gap and are now able to simulate all possible decay modes of the WZ system in the VBS mode.

As an example for a semi-leptonic decay mode in this subsection we provide phenomenological results for the VBS process where a \(W^+\) boson decays hadronically into an \(u{{\bar{d}}}\) pair, and the Z boson into a muon pair. All off-shell diagrams giving rise to the same final state are taken into account, see Fig. 1.

The decay quarks of the W boson give rise to jets. For the selection of the VBS signal in the presence of background processes it is important to distinguish these decay jets from the tagging jets of the production process. The representative numerical analysis below is designed to take that into account.

Fig. 7
figure 7

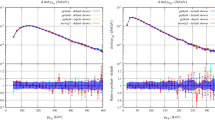
Predictions for VBS-induced \(W^+ Z\) production in the semi-leptonic decay mode at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (37)–(44) at LO (purple), NLO (green) and NLO+PS (orange). The upper panels show the transverse momentum of the hardest tagging jet (a), the rapidity of the hardest tagging jet (b), the transverse momentum of the hardest decay jet (c), the rapidity of the hardest decay jet (d). The respective lower panels show the ratios of the LO and NLO+PS predictions to the NLO results

Full size image

Throughout this subsection we use the dynamical scale of Eq. (19). For the selection of events in the semi-leptonic mode at the LHC with an energy of \(\sqrt{s}=13\) TeV we impose the following cuts: Charged leptons are required to fulfill the basic requirements

$$\begin{aligned} p_{T,\ell } > 20 \, \textrm{GeV}, \qquad \vert y_\ell \vert < 2.47. \end{aligned}$$
(37)

For the hardest lepton we additionally request

$$\begin{aligned} p_{T,\ell }^\textrm{hardest} > 28 \, \textrm{GeV} . \end{aligned}$$
(38)

Furthermore, the invariant mass reconstructed from the muon pair has to fulfill

$$\begin{aligned} 83 \, \textrm{GeV}< m_\textrm{inv}^Z < 99 \, \textrm{GeV}. \end{aligned}$$
(39)

Jets and the leptons have to be separated by

$$\begin{aligned} R_{j\ell } > 0.4 . \end{aligned}$$
(40)

We require all jets to have

$$\begin{aligned} p_{T,j} > 20 \, \textrm{GeV}, \qquad \vert y_j \vert < 4.5. \end{aligned}$$
(41)

The jets in an event are then further classified. The decay jets are identified as those two jets with the invariant mass being closest to the mass of the W boson. These two jets are required to lie within a window around the W mass of

$$\begin{aligned} 64 \, \textrm{GeV}< m_{inv}^\textrm{W} < 106 \, \textrm{GeV}, \end{aligned}$$
(42)

and to fulfill the transverse-momentum requirements

$$\begin{aligned} p_{T,j_1}^\textrm{dec}> 40 \, \textrm{GeV}, \qquad p_{T,j_2}^\textrm{dec} > 30 \, \textrm{GeV}, \end{aligned}$$
(43)

where \(j_1\) and \(j_2\) denote the hardest and second hardest decay jets.

After the selection of the decay jets, the two hardest remaining jets are identified as the tagging jets. For the tagging jets we require

$$\begin{aligned}{} & {} p_{T,j}^{\textrm{tag}}> 30 \, \textrm{GeV}, \quad m_{jj}^{\textrm{tag}}> 400 \, \textrm{GeV}, \quad R_{jj} > 0.4,\nonumber \\{} & {} \eta _{j_1}^{\textrm{tag}}\cdot \eta _{j_2}^{\textrm{tag}} < 0. \end{aligned}$$
(44)
Fig. 8
figure 8

Predictions for VBS-induced \(W^+ Z\) production in the semi-leptonic decay mode at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (37)–(44) at LO (purple), NLO (green) and NLO+PS (orange). The upper panels show the transverse momentum of the hardest lepton (a) and the reconstructed invariant mass of the W-boson system (b). The respective lower panels show the ratios of the LO and NLO+PS predictions to the NLO results

Full size image

Figures 7 and 8 display some representative distributions related to the tagging jets and the decay jets at LO, NLO, and NLO+PS accuracy. As expected, tagging jets and decay jets exhibit entirely different properties. Both, transverse momentum and rapidity distributions look very different for the two types of jets. From the rapidity distributions one can understand that the decay jets are preferentially located a central rapidities, while the tagging jets peak in the forward and backward regions, analogous to the leptonic decay mode. We note that generally the curves for the NLO+PS results lie below the fixed-order predictions, indicating smaller event rates. As can be deduced from the invariant mass distribution in Fig. 8b the shift of momenta beyond LO results in a considerable change of shape in \(m_\textrm{inv}^W\). However this quantity is used as a selection criterion (c.f. Eq. (42)). With \(m_{inv}^\textrm{W}\) shifted to values further away from \(m_W\), at NLO+PS level fewer events pass the selection criterion of Eq. (42) resulting in a smaller value of the associated cross section.

Let us now consider a representative fully hadronic decay mode with the \(W^+\) boson decaying into a \(u{{\bar{d}}}\) pair and the Z boson into a pair of s quarks. The large number of jets emerging from this mode requires a dedicated analysis allowing for a proper classification of tagging and decay jets.

Fig. 9
figure 9

Predictions for VBS-induced \(W^+ Z\) production in the fully hadronic decay mode at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (45)–(48) at LO (purple), NLO (green) and NLO+PS (orange). The upper panels show the transverse momentum of the hardest tagging jet (a), the rapidity of the hardest tagging jet (b), the transverse momentum of the hardest decay jet from the W decay (c), the transverse momentum of the hardest decay jet from the Z decay (d). The respective lower panels show the ratios of the LO and NLO+PS predictions to the NLO results

Full size image
Fig. 10
figure 10

Predictions for VBS-induced \(W^+ Z\) production in the fully hadronic decay mode at the LHC with \(\sqrt{s}=13\) TeV within the cuts of Eqs. (45)–(48) at LO (purple), NLO (green) and NLO+PS (orange). The upper panels show the reconstructed mass of the W boson (a), the reconstructed mass of the Z boson (b). The respective lower panels show the ratios of the LO and NLO+PS predictions to the NLO results

Full size image

We require all jets to have

$$\begin{aligned} p_{T,j} > 10\, \textrm{GeV}, \qquad \vert y_j \vert < 4.5. \end{aligned}$$
(45)

To identify the jets associated with the decay of the W and Z boson we proceed in the following way: In the first step, from all pairs of jets we choose the one with its invariant mass closest to \(m_W\). These two jets are then considered to correspond to the decay of the W boson. In a second step, we proceed analogously for the Z boson (replacing \(m_W\) with \(m_Z\)). In a third step, we check if a jet is contained in both the jet-pair associated with the W boson and the one associated with the Z boson. If this is the case we assign it to the boson with mass closer to the corresponding jet-pair. In a fourth step, we repeat the first or second step for the boson that was not chosen in the third step with the remaining jets not assigned to the other boson. The jets having thus been associated with the W and Z decays have to fulfill the transverse-momentum requirements of

$$\begin{aligned} p_{T,j_1}^\mathrm {W-dec}> 20 \, \textrm{GeV},{} & {} \qquad p_{T,j_2}^\mathrm {W-dec}> 10 \, \textrm{GeV}, \nonumber \\ p_{T,j_1}^\mathrm {Z-dec}> 20 \, \textrm{GeV},{} & {} \qquad p_{T,j_2}^\mathrm {Z-dec} > 10 \, \textrm{GeV}. \end{aligned}$$
(46)

and exhibit invariant masses close to the respective gauge-boson mass,

$$\begin{aligned} 64 \, \textrm{GeV}< m_{jj}^\mathrm {W-dec}< 88 \, \textrm{GeV}, \nonumber \\ 84 \, \textrm{GeV}< m_{jj}^\mathrm {Z-dec} < 106 \, \textrm{GeV}. \end{aligned}$$
(47)

If an event does not pass these cuts, it is discarded.

After the selection of the decay jets, the two hardest remaining jets are identified as the tagging jets. As in the semi-leptonic case, for the tagging jets we additionally require

$$\begin{aligned}{} & {} p_{T,j}^{\textrm{tag}}> 30 \, \textrm{GeV}, \qquad m_{jj}^{\textrm{tag}}> 400 \, \textrm{GeV}, \qquad R_{jj} > 0.4, \nonumber \\{} & {} \qquad \eta _{j_1}^{\textrm{tag}}\cdot \eta _{j_2}^{\textrm{tag}} < 0. \end{aligned}$$
(48)

In Figs. 9 and 10 we show several distributions for the fully hadronic decay mode.

We observe results that are qualitatively similar to the semi-leptonic case discussed above. However, the “smearing effect” in the NLO+PS results is even larger than in the semi-leptonic case, because now window cuts for both the Z and the W system have to be passed for an event to be accepted.

4 Conclusions and outlook

In this article we have presented new features for the implementation of VBS-induced WZjj production in the framework of the POWHEG BOX V2. We are providing semi-leptonic and fully hadronic decays of the intermediate vector bosons that were missing in the previously existing implementation, and account for physics beyond the SM by the inclusion of dimension-six operators of a generic EFT expansion in the EW sector.

To illustrate the capabilities of the updated implementation we considered some selected applications. We explored the sensitivity of typical VBS observables to dimension-six operators in an EFT framework, and found that, when the expansion is performed consistently, predictions with contributions from EFT operators compatible with current experimental limits barely deviate from the SM case at LHC energies. Larger effects are found at higher energies which could be achieved, for instance, at a future FCC.

Using the leptonic decay mode as an example, we investigated the relevance of including off-shell contributions and spin correlations in the simulation. By comparing our results to those obtained with the MadGraph5_aMC@NLO+MadSpin tool that combines a calculation of VBS-induced WZ production with a simulation of the gauge-boson decays we could show that the on-shell approximation is appropriate when all final-state leptons stem from the resonant decay of a gauge boson, but deviates from the full result in regions away from the resonance. This limitation of the approximation should be kept in mind for ensuring its application is restricted to its region of validity.

Finally, we considered semi-leptonic and fully hadronic decay modes. We found that in these cases QCD corrections and PS effects can lead to a reshuffling of momenta such that they pass different selection cuts than the corresponding LO configurations. This kinematic effect results in a reduction of cross section beyond the LO, which becomes particularly pronounced once the NLO result is matched with a PS.

The new features of the VBS \(WZjj\) code have been made available via the POWHEG BOX V2 repository, see https://powhegbox.mib.infn.it/.