1 Introduction

The theory of general relativity (GR) predicts the existence of fascinating objects known as black holes (BHs). The extremely strong gravitational field observed in the universe is thought to have originated from BHs. Furthermore, it is widely accepted that BHs are characterized by powerful magnetic fields and spin. Considering these characteristics, BHs serve as an ideal astrophysical laboratory for investigating the properties of gravity and matter. Based on an extensive examination of observational evidence, recent empirical data has certainly verified the existence of BHs. The first achievement demonstrates the identification of gravitational waves resulting from the collision of two BHs in a binary system, as observed through the collaborative efforts of Ligo and Virgo [1]. The Event Horizon Telescope plays a vital role in utilizing baseline interferometry to capture the first image of the BH shadow of \(M87^{*}\) [2, 3]. Additionally, it has also revealed an image of Sgr \(A^{*}\) [4]. It is widely accepted that cosmic objects, such as BHs, experience mass accumulation through the process known as accretion. Additionally, they could be utilized for the analysis of modified gravity theories. Whenever the fluid velocity is identical to the sound speed, these particles must pass through the critical point. The fluid is projected onto its central mass at supersonic speed. The BH mass needs to be raised as a result of this event [5]. It is fascinating to analyze numerous radii as a consequence of examining the particles geodesic structure near the BH, such as innermost stable circular orbit (ISCO) and marginally bound orbit (\(r_{mb}\)). In the examination of BH accretion discs, the considered radii are the significant factors. The presence of the accretion disk is crucial for the investigation of the accelerated accretion rate associated with these compact objects. As a result of the presence of diffuse matter, the accretion disk evolves into a centrally condensed object that emits energy as it spirals progressively. Accretion refers to the phenomenon in which nearby fluids attract particles towards a compact object, such as BH.

The ISCO corresponds to the inner boundary of the disk. Its radius can be utilized to calculate the energy emission efficiency, which determines the rate at which energy from the rest mass transforms into radiation. The locations of unstable or stable circular orbits are determined by the maximum or minimum value of the effective potential, respectively. According to the principles of Newtonian theory, it is widely accepted that the ISCO cannot have a minimum radius. The ISCO has the ability to determine any radius in which the effective potential has decreased to its minimum value for all feasible angular momentum [6]. The effective potential in GR and the behavior of particles rotating near the Schwarzschild BH exhibit two distinct extremes, corresponding to the minimum and maximum values of angular momentum. In \(r = 3r_{g}\) [6, 7], one can investigate ISCO, where \(r_g\) stands for the Schwarzschild radius. In [8, 9], researchers investigated the effects of ISCO in the surrounding of Kerr BH introduced these characteristics in GR. Thorne and Novikov [10] determined the Kerr and Schwarzschild BH accretion discs efficiency. In [11] Johannsen created the accretion discs around such BHs, while Johannsen and Psaltis [12] presented the Kerr-like metric. The geodesic structure and spherical orbits of charged particles near revolving, weakly magnetic BHs have been identified by Tursunov et al. [13]. Based on the stability of the particles within the accretion disk, it follows that any perturbation will lead to oscillatory behavior in both the radial and vertical dimensions, characterized by a rise of epicyclic frequencies. As a consequence, the formation of accretion discs around BHs depends on comprehending orbital and epicyclic frequencies. Furthermore, the geodesic form and accretion disk have been investigated in the literature for a variety of BHs [14,15,16,17,18,19,20,21,22].

One of the primary concerns in Einstein’s theory of GR relates to the presence of singularities at the beginning of the universe along with BH solutions. Maxwell’s theory of Electrodynamics comprises similar singularities [23]. In order to prevent the occurrence of these singularities, the Maxwell theory of electrodynamics was modified in 1934 by Born–Infeld (BI), which also comprises a relativistic and gauge invariant theory called BI nonlinear electrodynamics (NED) [24]. The self energy of charges is finite in BI NED. Additionally, it is possible to determine the effective action of BI NED on open superstrings occurring at low energy dynamics of D-branes in the absence of any physical singularity [23, 25]. Euler–Heisenberg (EH) NED is another illustration, which happens as a result of vacuum polarization [26]. Both the BI NED and EH NED, which possess SO(2) electric-magnetic duality invariance, demonstrate a reduction to Maxwell electrodynamics under the conditions of a weak field regime due to the presence of fixed energy scale interactions that result in the breaking of conformal invariance. Subsequently, utilizing the Einstein-NED theories as the basis, regular BH solutions using duality rotation freedom have been identified [27,28,29]. The researchers in [30] have developed a ModMax electrodynamics extension of Maxwell electrodynamics that features a low-energy limit of a one-dimensionless parameter refinement of BI, and lapses back to Maxwell equations for \(\gamma = 0\). In ModMax electrodynamics, Flores-Alfonso et al. [31] recently determined the new BH solutions. In [32], the researchers discuss various aspects like shadow, lensing, quasinormal modes, greybody constraints, and neutrino propagation of Dyonic ModMax BHs. Dynamic solutions are obtained through SO(2) invariance for electric and magnetic fields. Actual charges are shielded by the screening factor \(\gamma \) exerted by ModMax electrodynamics on BH spacetimes. Many researchers subsequently examined ModMax electrodynamics [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53].

Based on the above motivation, we are particularly interested to investigate the impacts on particle dynamics and the accretion process in the vicinity of the Dyonic ModMax BH. This is the primary objective of the present article. The paper will be completed according to the following manner. Section 2 explores the fundamental formulation for particle dynamics in the provided subsections, like flux of radiant energy, circular motion, oscillations, and stable circular orbits. Section 4 and its subsections provide the generic formulas for various dynamical parameters, including the critical flow speed, accretion for an isothermal fluid, and the accretion rate. In Sect. 5, we analyzed the solution of the Dyonic ModMax BH by considering the circular geodesic in the equatorial plane. In Sect. 6, we provide the summary of our findings.

2 Dyonic ModMax black hole

In this particular section, we examine the spherically symmetric metric associated with the Dyonic ModMax BH solutions, which has been proposed in [31] as follows

$$\begin{aligned} ds^{2}=+f(r)dt^{2}-f^{-1}(r)dr^{2}-r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2}),\nonumber \\ \end{aligned}$$
(1)

with

$$\begin{aligned} f(r)=1-\frac{2 M}{r}+\frac{Q^2 e^{-\gamma }}{r^2}, \end{aligned}$$
(2)

where \(Q=\sqrt{Q^{2}_{e}+Q^{2}_{m}}\) while \(Q_{e}\) is the electric charge and \(Q_{m}\) is the magnetic charge. In order to analyze the accretion disk surrounding the Dyonic ModMax BH, we determine the BH horizons by considering \(f(r)=0\). So, the horizons of BH are located at \(r_{\pm }=M\pm \sqrt{M^{2}-Q^{2}e^{-\gamma }}\). Also, in Fig. 1, we present the comparison of the metric functions f(r) for the Schwarzschild, RN, and Dyonic ModMax BH. The horizon radius of the Dyonic ModMax BH is greater than that of the RN BH and smaller than that of the Schwarzschild BH. The Dyonic ModMax BH exhibits singularity at the radial coordinate \(r = 0\).

Fig. 1
figure 1

The profile of metric function f(r) along r

Full size image

3 General formulation for the geodesic motion of test particles

This section presents the fundamental expression for the geodesic motion of the particles by analyzing the Dyonic ModMax BH. We assume \(\xi _{t}=\partial _{t}\) and \(\xi _{\phi }=\partial _{\phi }\) as killing vectors that correspond to fundamental constants L and E, which stand for conserved angular momentum and energy, respectively, related to the given trajectory

$$\begin{aligned} E=-g_{\mu \nu } \xi _{t}^{\mu } u^{\nu }\equiv -u_{t}, \end{aligned}$$
(3)

and

$$\begin{aligned} L=g_{\mu \nu } \xi _{\phi }^{\mu }u^{\nu }\equiv u_{\phi }, \end{aligned}$$
(4)

furthermore, the four-velocity vector \(u^{\mu }=\frac{dx^{\mu }}{d\tau }=(u^{t}, u^{r},u^{\theta }, u^{\phi })\) satisfies \(u^{\mu }u_{\mu }=1\) that gives us

$$\begin{aligned}{}[g_{rr}(u^{r})^{2}+g_{\theta \theta }(u^{\theta })^{2}]=[1-g^{tt}(u_t)^{2}-g^{\phi \phi }(u_{\phi })^{2}], \end{aligned}$$
(5)

by using Eqs. (3), (4) and (5), in the equatorial plane (i.e. \(\theta =\frac{\pi }{2}\)), we obtained

$$\begin{aligned} u^t= & {} -\frac{E}{f(r)}, \end{aligned}$$
(6)
$$\begin{aligned} u^\theta= & {} 0, \end{aligned}$$
(7)
$$\begin{aligned} u^\phi= & {} -\frac{L}{r^2}, \end{aligned}$$
(8)
$$\begin{aligned} u^r= & {} \sqrt{-f(r)\left( 1-\frac{E^2}{f(r)}+\frac{L^2}{r^2}\right) }. \end{aligned}$$
(9)

From (9), we attain

$$\begin{aligned} (u^r)^2+V_{eff}=E^2, \end{aligned}$$
(10)

and

$$\begin{aligned} V_{eff}=f(r)\left[ 1+\frac{L^2}{r^2}\right] . \end{aligned}$$
(11)

It is clear that the effective potential is determined by radial distance r, the metric function f(r) and angular momentum L. In the analysis of particle geodesic motion, the effective potential is quite useful because it can be used to determine the location of the ISCO by examining the local extrema of the effective potential.

3.1 Circular motion of test particles

We investigate how test particles move in a circular orbit in the vicinity of the equatorial plane by considering radial component r constant, so \(u^{r}=\dot{u}^{r}=0\). Using Eq. (10), we found that \(V_{eff} =E^2\) and \(\frac{d}{dr}V_{eff}=0\). Also, we determine the angular velocity \(\Omega _{\phi }\), angular momentum l, specific energy E, and specific angular momentum L, which are given by

$$\begin{aligned} \Omega _{\phi }^2= & {} \frac{1}{2r}f'(r), \end{aligned}$$
(12)
$$\begin{aligned} E^2= & {} \frac{2f^2(r)}{2f(r)-r f'(r)}, \end{aligned}$$
(13)
$$\begin{aligned} L^2= & {} \frac{r^3f'(r)}{2f(r)-r f'(r)}, \end{aligned}$$
(14)
$$\begin{aligned} l^2= & {} \frac{r^3f'(r)}{2f^2(r)}. \end{aligned}$$
(15)

The Eqs. (13) and (14) must have real solutions if

$$\begin{aligned} 2f(r)-r f'(r)>0. \end{aligned}$$
(16)

The inequality (16) is necessary for the presence of circular orbits because it is feasible to examine the certain area of the circular orbit. Furthermore, in the case of marginally bound and bound orbits, Eq. (13) must fulfill the given conditions of \(E^{2}=1\) and \(E^{2}<1\), respectively. Furthermore, by utilizing Eq. (13), we achieve

$$\begin{aligned} 2[f(r)-1]f(r)+r f'(r)=0, \end{aligned}$$
(17)

the marginally bound orbit will be identified using Eq. (17). The Eqs. (13) and (14) exhibit divergence if

$$\begin{aligned} -r f'(r)+2f(r)=0. \end{aligned}$$
(18)

Equation (18) can be used to compute the radius of the photon sphere, which is necessary for the investigation of gravitational lensing.

3.2 Radiant energy flux and circular orbits

The existence of stable circular orbits depends on the local minimum of the effective potential, which is found by \(\frac{d^{2} V_{eff}}{dr^{2}}>0\). Furthermore, the Eq. (11), gives us

$$\begin{aligned} \frac{d^2}{dr^2}V_{eff}=\left( 1+\frac{L^2}{r^2}\right) f''(r)-\frac{4L^2}{r^3}f'(r)+\frac{6L^2}{r^4}f(r). \nonumber \\ \end{aligned}$$
(19)

By employing the requirements \(V_{eff} =0\), \(\frac{dV_{eff}}{dr} =0\) and \(\frac{d^{2}V_{eff}}{dr^{2}} =0\) we can calculate ISCO, i.e.,\(r_{isco}\). Furthermore, the process of accretion is possible when \(r<r_{isco}\). When particles transition from a state of rest to an infinite distance and accumulate around compact objects, they emit gravitational energy that is subsequently converted into radiation. The angular speed \(\Omega _{\phi }\), the specific energy E, and the specific angular momentum L are used to describe the radiation energy flux across the accretion disk [54]

$$\begin{aligned} K=-\frac{\dot{M} \Omega _{\phi },_{r}}{{4\pi \sqrt{-g} (E-L \Omega _{\phi })^2}}\int ^{r}_{r_{isco}}(E-L \Omega _{\phi })L,_{r}dr, \nonumber \\ \end{aligned}$$
(20)

the radiant flux is indicated by K, the mass accretion rate can be expressed as \(\dot{M}\), \(\Omega _{\phi },_{r} \equiv \frac{d\Omega _{\phi }}{dr}\), and the determinant of \(g_{\mu \nu }\) is denoted as g we acquired

$$\begin{aligned} g=\det (g_{\mu \nu })=-r^4sin^2\theta . \end{aligned}$$
(21)

To conduct the comprehensive analysis of our results within the \(\theta =\frac{\pi }{2}\), we determine the relationship as \(\sin \theta =\sin \frac{\pi }{2}=1\). By utilizing Eqs. (12-14), we obtain

$$\begin{aligned} K(r)= & {} \frac{-\dot{M}}{4\pi r^4} \sqrt{\frac{r}{2f'(r)}}\nonumber \\{} & {} \times \frac{[r f'(r)-2f(r)][r f''(r)-f'(r)]}{[2f(r)+r f'(r)]^2} \int ^{r}_{r_{isco}} F(r)dr, \nonumber \\ \end{aligned}$$
(22)

where

$$\begin{aligned} F(r)= & {} \sqrt{\frac{r}{2f'(r)}}\nonumber \\{} & {} \times \frac{[r f'(r){+}2f(r)][r f(r)f''(r){-}2r f'^2(r){+}3f(r)f'(r)]}{[2f(r)-r f'(r)]^2}. \nonumber \\ \end{aligned}$$
(23)

The link between energy flux and temperature, represented as \(K(r)=\sigma T^{4}(r)\), is based on the assumption that the accretion disk is in a state of thermal equilibrium. Therefore, it is assumed that the radiation emitted from the disk demonstrates characteristics that are comparable to black body radiation. By taking into consideration the thermal black body radiation, it is possible to calculate the temperature distribution across the accretion disk by employing the provided equation. This will allow us to determine the luminosity of the disk, represented by L(v). The luminosity of the accretion disk is defined by the inclination angle \(\gamma \) of the disk [55]

$$\begin{aligned} L(\nu )=4\pi d^2 I(\nu )=\frac{8}{\pi }(\cos \gamma ) \int ^{r_{f}}_{r_{i}} \int ^{2\pi }_{0} \frac{\nu _{e}^{3} r d\phi dr}{exp(\frac{\nu _{e}}{T})-1}.\nonumber \\ \end{aligned}$$
(24)

Based on the previous outcome, it is evident that the flux energy is represented by \(I(\nu )\). The maximum efficiency, \(\eta ^{*}\), can be achieved by

$$\begin{aligned} \eta ^{*}=1-E_{isco}. \end{aligned}$$
(25)

Here, the particle energy in ISCO is denoted by \(E_{isco}\). When all released photons are capable of escaping into infinity, then the above relation is true. In the plane \(\theta =\frac{\pi }{2}\), the motion of the particles produced by a perturbation in a fluid element corresponds to a circular orbit.

3.3 Oscillations

Throughout the accretion procedures, several kinds of oscillatory motion arise as a consequence of the presence of restoring forces. The significant impact of restoring forces depends on perturbations in the vicinity of accretion disks, which are caused by the oscillation in both the horizontal and vertical directions. The accretion disk produces numerous restoring forces caused by its rotational motion within a vertical gravitational field. The presence of a restoring force in a fluid element allows its return to a state of equilibrium, as the rotational motion of the element counteracts its radial motion. It is noteworthy to mention that the gravitational force acting throughout accretion disks counteracts the centrifugal force generated by central objects. The fluid element is displaced either inward or outward and then restored to its original radius using the epicyclic frequency \(\Omega _{r}\), lies on whether the latter exceeds the former or vice versa. Because the gravitational field pinches the perturbed elements, the fluid element returns to its equilibrium state after experiencing a vertical perturbation in the plane \(\frac{\pi }{2}\). Because of the existence of a restoring force, the element of fluid produces harmonic oscillations in plane \(\frac{\pi }{2}\), which corresponds to a vertical epicyclic frequency \(\Omega _{\theta }\). Three different types of motions, harmonic vertical motion with a vertical frequency, circular motion with an orbital frequency, and radial motion with a radial frequency determine the movement of particles within the accretion disk. In this study, we will focus on the radial and vertical motion near the circular orbits in the equatorial plane.

Motions in the radial and vertical directions can be characterized by \(\frac{1}{2}(\frac{dr}{dt})^2=V_{eff}^{(r)}\), and \(\frac{1}{2}(\frac{d\theta }{dt})^2=V_{eff}^{(\theta )}\), so according to Eq. (5) \(u^{r}=0\), describes radial motion, while \(u^{\theta }=0\), describes vertical motion. By considering \(u^{r}=\frac{dr}{d \tau }=\frac{dr}{dt}u^{t}\) and \(u^{\theta }=\frac{d\theta }{d\tau }=\frac{d\theta }{dt}u^{t}\), we obtained

$$\begin{aligned} \frac{1}{2}\Big (\frac{dr}{dt}\Big )^{2}= & {} -\frac{1}{2}\frac{f^3(r)}{E^2}\Big [1-\frac{E^{2}}{f(r)} +\frac{L^{2}}{r^{2}sin^{2}(\theta )}\Big ]=V_{eff}^{(r)},\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} \frac{1}{2}\Big (\frac{d\theta }{dt}\Big )^2= & {} -\frac{1}{2}\frac{f^2(r)}{E^2 r^2}\Big [1-\frac{E^2}{f(r)}+\frac{L^2}{r^2 sin^2\theta }\Big ]=V_{eff}^{(\theta )}.\nonumber \\ \end{aligned}$$
(27)

We will examine the radial and vertical epicyclic frequencies near circular orbits in the plane \(\frac{\pi }{2}\) by assuming small perturbations indicated by the \(\delta \theta \) and \(\delta r\). From Eqs. (26) and (27), we have

$$\begin{aligned} \frac{d^2 r}{dt^2}=\frac{d V_{eff}^{(r)}}{dr}. \end{aligned}$$
(28)

The resultant expression for a particle with a perturbation in its original radius at \(r = r_{0}\) and a deviation \(\delta r = r - r_{0}\) can be written as

$$\begin{aligned} \frac{d^2}{dt^2} (\delta r)=\frac{d^2 V_{eff}^{(r)}}{dr^2} (\delta r) \Rightarrow (\delta \ddot{r})+\Omega _{r}^2(\delta r)=0, \end{aligned}$$
(29)

where \(\Omega _{r}^2\equiv -\frac{d^2}{d r^2} V_{eff}^{(r)}\) and dots represent time derivative. By assuming a vertical perturbation \(\delta \theta =\theta -\theta _{0}\), we obtain the following outcome using analogous approach

$$\begin{aligned} \frac{d^2 (\delta \theta )}{dt^2}=\frac{{d^2 V_{eff}}^{(\theta )}}{dr^2} (\delta \theta ) \Rightarrow (\delta \ddot{\theta })+\Omega _{\theta }^2(\delta \theta )=0, \end{aligned}$$
(30)

and \(\Omega _{\theta }^2\equiv -\frac{d^2}{d\theta ^2} V_{eff}^{(\theta )}\). Equations (26) and (27), gives following result in the plane \(\frac{\pi }{2}\)

$$\begin{aligned}{} & {} \Omega _{r}^2=\frac{1}{2E^2 r^4} [((r^2+L^2)3f(r)-2 E^2 r^2)r^2 f(r)f''(r)\nonumber \\{} & {} \quad +2r^2((r^2+L^2)3f(r)-E^2 r^2)f'^2(r) \nonumber \\{} & {} \quad -6L^2 f^2(r)(2rf'(r)-f(r))], \end{aligned}$$
(31)

and

$$\begin{aligned} \Omega _{\theta }^2=\frac{f^2(r)L^2}{E^2 r^4}. \end{aligned}$$
(32)

where prime indicates the derivative w.r.t r.

The study of the basic dynamical equations underlying ModMax BH is given in the following section.

4 Basic dynamical equations

In this section,we explored the basic formalism for accretion proposed by Babichev et al. [56, 57] and also investigate the ideal fluid defined by its energy–momentum tensor

$$\begin{aligned} T^{\mu \nu }=(\rho +p)u^{\nu }u^{\mu }-g^{\mu \nu }p, \end{aligned}$$
(33)

where \(\rho \) and p represent the energy density and pressure of the fluid, respectively. The characterization of the four-velocity \(u^{\mu }\) in the plane \(\frac{\pi }{2}\) is given as

$$\begin{aligned} u^{\mu }=\frac{dx^\mu }{d\tau }=(u^t,u^r,0,0), \end{aligned}$$
(34)

here, \(\tau \) represents the proper time. The previous expression along with \(u^{\mu }u_{\mu }=1\), gives us

$$\begin{aligned} u^t=\frac{\sqrt{f(r)+(u^r)^2}}{f(r)}, \end{aligned}$$
(35)

For forward fluid motion and accretion (inward flow) we must have \(u^{t}>0\) and \(u^{r}<0\), respectively. The conservation equations of energy momentum and particle number must be computed in order to examine the accretion process. Energy–momentum tensor conservation is provided by

$$\begin{aligned} T_{;\mu }^{\mu \nu }=0 \Rightarrow T_{;\mu }^{\mu \nu }=\frac{1}{\sqrt{-g}}(\sqrt{-g}T^{\mu \nu })_{,\mu }+ \Gamma _{\alpha \mu }^\nu T^{\alpha \mu }=0,\nonumber \\ \end{aligned}$$
(36)

where \(\sqrt{-g}=r^{2} sin\theta \), \(\Gamma \) represents Christoffel symbol of 2nd kind and (; ) indicates the covariant derivative. By using the BH metric, Eq. (36) becomes

$$\begin{aligned} T_{,r}^{10}+\frac{1}{\sqrt{-g}} T^{10} (\sqrt{-g})_{,r}+2 \Gamma _{01}^{0}T^{10}=0, \end{aligned}$$
(37)

From Eq. (37), we obtain

$$\begin{aligned} \frac{d}{dr}[(\rho +p)u^r r^2 {\sqrt{f(r)+(u^r)^2}}]=0. \end{aligned}$$
(38)

We can obtain the following expression by integrating the previous equation.

$$\begin{aligned} (\rho +p)u^r r^2 {\sqrt{f(r)+(u^r)^2}}=C_{0}, \end{aligned}$$
(39)

where \(C_{0}\) denoted the constant of integration. projecting the energy-momentum conservation law onto the four-velocity, we have

$$\begin{aligned}{} & {} (\rho +p) u_{;\nu }^{\mu } {u_\mu u^\nu }+(\rho +p)_{,\nu } u_{\mu } {u^\mu u^\nu }\nonumber \\{} & {} \quad +(\rho +p) {u_{\mu } u^\mu } u_{;\nu }^\nu +p_{,\nu }g^{\mu \nu } u_\mu +p{u_\mu } g_{;\nu }^{\mu \nu }=0, \end{aligned}$$
(40)

since \(g_{;\nu }^{\mu \nu }=0\), by use of \(u^{\mu }u_{\mu }=1\), we get

$$\begin{aligned} (p+\rho ){u_{;\nu }^\nu }+u^{\nu }{\rho ,_\nu }=0, \end{aligned}$$
(41)

because \(A_{;a}^b=\partial _a A^b+\Gamma _{ac}^b A^c\), Eq. (41) takes the form

$$\begin{aligned}{} & {} u^{r} \rho _{,r}+[\Gamma _{0c}^0u^c+u_{,r}^r+\Gamma _{1c}^{1}u^c+\Gamma _{2c}^{2}u^c+\Gamma _{3c}^{3}u^c]\nonumber \\{} & {} \quad (\rho +p)=0. \end{aligned}$$
(42)

Equation (42), produces the following expression

$$\begin{aligned} \frac{\rho '}{(\rho +p)}+\frac{u'}{u}+\frac{2}{r}=0, \end{aligned}$$
(43)

which, after integrating, gives the following

$$\begin{aligned} r^2 u^r \exp \left( \int {\frac{d\rho }{p+\rho }}\right) =-C_1, \end{aligned}$$
(44)

where \(C_{1}\) represents the integration constant. Considering the \(u^{r}<0\), we compute the resulting expression

$$\begin{aligned} (p+\rho )\sqrt{(u^{r})^2+f(r)}\exp \left( -\int {\frac{d\rho }{p+\rho }}\right) =C_2, \end{aligned}$$
(45)

where \(C_{2}\) is the integration constant.

The expression of flux mass is

$$\begin{aligned} (\rho u^\mu )_{;\mu }\equiv \frac{1}{\sqrt{-g}}(\sqrt{-g} \rho u^{\mu })_{,\mu }=0, \end{aligned}$$
(46)

from Eq. (46), we have

$$\begin{aligned} \frac{1}{\sqrt{-g}}(\sqrt{-g}\rho u^{\mu })_{,r}+\frac{1}{\sqrt{-g}}(\sqrt{-g}\rho u^{\theta })_{,\theta }=0, \end{aligned}$$
(47)

because we are concentrating on the equatorial plane, the second term in Eq. (47) vanishes. Hence the term \(\sqrt{-g}\rho u^{\mu }\) should be constant, that is

$$\begin{aligned} \rho u^r r^2=C_3, \end{aligned}$$
(48)

where \(C_{3}\) is constant of integration.

4.1 Dynamical parameters

In order to proceed further, we will assume an isothermal fluid using the equation of state \(p=k\rho \), where k represents the state parameter. For an isothermal fluid \(p\propto \rho \), it is necessary that the speed of sound remain constant throughout the accretion process. Also, by using Eqs. (44), (45) and (48), we found

$$\begin{aligned} \frac{\rho +p}{\rho } \sqrt{f(r)+(u^{r})^{2}}=C_4, \end{aligned}$$
(49)

while the integration constant is represented by \(C_{4}\). After substituting \(p=k\rho \) into Eq. (49), we obtain

$$\begin{aligned} u=\frac{\sqrt{A_4^2-\frac{(k+1)^2 \left( r (r-2 M)+e^{-\gamma } Q^2\right) }{r^2}}}{k+1} . \end{aligned}$$
(50)
Fig. 2
figure 2

Radial velocity variation along r with the equation of state parameter \(k = 0.5\) a for \(\gamma =0.1\) and numerous values of Q, b for \(Q=0.2\) and various values of \(\gamma \)

Full size image

Figure 2 depicts the radial velocity variation along radial distance r. From Fig. 2a, we can see that the radial velocity increases initially for smaller radii of the BH and attains its largest value at \(Q=0.4\) and decreases with increasing the BH radius. It is important to observe that the radial velocity decreases with the increment in Q. Furthermore, the impact of the BH parameter \(\gamma \) observed in Fig. 2b. We observe that as the value of BH parameter \(\gamma \) increases the radial velocity decreases.

Now, we calculate the density of the fluid from Eq. (48), as

$$\begin{aligned} \rho =\frac{A_3 (k+1)}{r^2 \sqrt{A_4^2-\frac{(k+1)^2 \left( r (r-2 M)+e^{-\gamma } Q^2\right) }{r^2}}}. \end{aligned}$$
(51)
Fig. 3
figure 3

The graph of the fluid density \(\rho \) along r a for \(\gamma =0.1\) with different values of Q, b for \(Q=1\) and different values of \(\gamma \)

Full size image

It is observed in Fig. 3, that fluid density decreases along the radius r. Furthermore, in left panel we can see that as the value of charge Q grows, the density of the fluid also grows. The effect of BH parameter \(\gamma \) on density represented in right panel. It is worthwhile to note that as the value of BH parameter \(\gamma \) increases the density \(\rho \) decreases. Additionally, we may calculate the pressure by using the equation \(p=k\rho \).

4.2 Mass evolution

According to astronomical studies, the mass of BH may change significantly over time as a result of numerous events, including mass accreting around the BH and the emission of Hawking radiation. The following expressions \(ds=\sqrt{-g}d\theta d\phi \) and \(T_{t}^{r}=(p+\rho )u_{t}u^{r}\) are utilized to determine the mass accretion rate around the Dyonic ModMax BH. Consequently, the \(\dot{M}\) accretion rate is obtained by

$$\begin{aligned} \dot{M}=-4\pi r^{2}u(p+\rho ) \sqrt{u^{2}+f(r)} \equiv -4\pi C_{0}. \end{aligned}$$
(52)

By considering \(C_{0}=-C_{1}C_{2}\) and \(C_{2}=(p_{\infty }+\rho _{\infty }) \sqrt{f(r_{\infty })}\), we get

$$\begin{aligned} \dot{M}=4\pi C_{1}(p_{\infty }+\rho _{\infty }) \sqrt{f(r_{\infty })}M^{2}. \end{aligned}$$
(53)

So, it is feasible to determine the time evolution of the BH mass having an initial mass of \(M_{i}\) by integrating Eq. (53), we have

$$\begin{aligned} \frac{d M}{M^{2}}=\mathcal {F}t, \end{aligned}$$
(54)

here \(\mathcal {F}\equiv 4\pi C_{1}(p+\rho ) \sqrt{f(r_{\infty })}\). From Eq. (54), we obtained

$$\begin{aligned} M_{t}=\frac{M_{i}}{1-\mathcal {F} M_{i}t}\equiv \frac{M_{i}}{1-\frac{t}{t_{cr}}}, \end{aligned}$$
(55)

where time accretion \(t_{cr}\) is computed by using the following expression: \(t_{cr}=[4\pi C_{1}(p+\rho )\sqrt{f(r_{\infty })}M_{i}]^{-1}\). From Eq. (55), we can see that the BH mass grows up to infinity within a finite time at \(t=t_{cr}\). Consequently, the BH mass accretion rate obtained by

$$\begin{aligned} \dot{M}=4 \pi C_{1}(p+\rho )M^2. \end{aligned}$$
(56)
Fig. 4
figure 4

The mass accretion rate \(\dot{M}\) represented as a function of r a by assuming \(\gamma =0.1\) and different values of \(Q=1\), b for \(Q=1\) and various values of \(\gamma \)

Full size image

Figure 4 displays the profile of mass accretion rate along the BH radius r. From Fig 4a, it is noticed that when the charge parameter Q varies, the accretion rate initially decreases along the BH radius r to some extent and subsequently increases to its maximum. We also see that the accretion rate \(\dot{M}\) enhanced quickly as the charge parameter Q increased. The effect of parameter \(\gamma \) on mass accretion rate \(\dot{M}\) as shown in Fig 4b. We can observe that the mass accretion rate \(\dot{M}\) decreases as the value of BH parameter \(\gamma \) increases.

4.3 Critical accretion

The fluid experiences inward motion as a consequence of the BH gravitational pull, but it remains static far from the BH. As the fluid moves inward, it passes through the sonic point, so at this point, the fluid velocity must be equivalent to sound speed. From Eqs. (48) and (49), we have

$$\begin{aligned} \frac{\rho '}{\rho }+\frac{u'}{u}+\frac{2}{r}=0, \end{aligned}$$
(57)

and

$$\begin{aligned} \frac{\rho '}{\rho }\left[ \frac{d\ln (p+\rho )}{d\ln \rho }-1\right] +\frac{u u'}{u^{2}+f(r)}+\frac{1}{2} \frac{f'(r)}{u^{2}+f(r)}=0.\nonumber \\ \end{aligned}$$
(58)

Using Eq. (58), we have

$$\begin{aligned} \frac{d\ln u}{d\ln r}=\frac{D_{1}}{D_{2}}, \end{aligned}$$
(59)

where

$$\begin{aligned} D_{1}=\left[ \frac{r f'(r)}{2(u^{2}+f(r))}-2V^{2}\right] , \end{aligned}$$
(60)

and

$$\begin{aligned} D_{2}=\left[ V^{2}-\frac{u^{2}}{u^{2}+f(r)}\right] . \end{aligned}$$
(61)

By utilizing Eqs. (59)–(61), we acquire

$$\begin{aligned} V^{2}=\frac{d\ln (p+\rho )}{d\ln \rho }-1. \end{aligned}$$
(62)

The critical points are found by assuming \(D_{1}=D_{2}=0\), so we can get

$$\begin{aligned} V_{c}^{2}=\frac{r f'(r)}{4f(r)+r f'(r)}, \end{aligned}$$
(63)

and

$$\begin{aligned} u_{c}^{2}=\frac{1}{4} r f'(r), \end{aligned}$$
(64)

where critical point is represented by the index c. The rhs of Eq. (62), must be positive. The subsequent inequality establishes the range of the critical radius

$$\begin{aligned} 4f(r)+r f'(r)>0. \end{aligned}$$
(65)

From Eq. (50), we attain

$$\begin{aligned} c_{s}^{2}=C_{4} \sqrt{[u^{2}+f(r)]^{-1}}-1, \end{aligned}$$
(66)

so, \(c_{s}^{2}=\frac{d p}{d\rho }\) is the necessary expression for the sound speed.

5 Circular equatorial geodesics

The effective potential, which can be determined from Eq. (11), is essential to investigate circular geodesics in the plane \(\theta = \frac{\pi }{2}\)

$$\begin{aligned} V_{eff}=\left( 1-\frac{2 M}{r}+\frac{Q^2 e^{-\gamma }}{r^2}\right) \left( 1+\frac{L^2}{r^2}\right) . \end{aligned}$$
(67)

The condition \(\frac{d^{2}V_{eff}}{dr^{2}}>0\) is necessary for the existence of stable circular orbit and Eq. (18), locate the position of ISCO at

$$\begin{aligned} r_{isco}= & {} \frac{e^{-2 \gamma } \root 3 \of {8 e^{6 \gamma } M^6-9 e^{5 \gamma } M^4 Q^2+2 e^{4 \gamma } M^2 Q^4+\sqrt{5 e^{10 \gamma } M^8 Q^4-9 e^{9 \gamma } M^6 Q^6+4 e^{8 \gamma } M^4 Q^8}}}{M} \nonumber \\{} & {} -\frac{e^{-2 \gamma } \left( 27 e^{3 \gamma } M^2 Q^2-36 e^{4 \gamma } M^4\right) }{9 M \root 3 \of {8 e^{6 \gamma } M^6-9 e^{5 \gamma } M^4 Q^2+2 e^{4 \gamma } M^2 Q^4+\sqrt{5 e^{10 \gamma } M^8 Q^4-9 e^{9 \gamma } M^6 Q^6+4 e^{8 \gamma } M^4 Q^8}}}+2 M, \end{aligned}$$
(68)
Fig. 5
figure 5

The illustration of \(V_{eff}\) is a function of r a for \(\gamma =0.1\), \(Q=0.2\), with different values of L, b for \(\gamma =1\), \(L=10\) and various values of Q, c for \(Q=0.2\), \(L=10\) and different chosen values of \(\gamma \)

Full size image

The profile of effective potential along radius r is represented in Fig. 5. From Fig. 5a, we observe that the first extremum exists at \(L = 5\) and none of the other extrema exist before \(L<5\). Furthermore, we can see that the effective potential rises with the rise of angular momentum L. The position of ISCO is represented by the black dot in Fig. 5a, which lies at \(r=5.94536\). It is important to note that there are two extrema observed for the larger value of L. The stable and unstable circular orbits correspond to the minimum and maximum values of effective potential \(V_{eff}\), respectively. Moreover, in Fig. 5b, we see how the BH charge Q impacts the effective potential \(V_{eff}\) across r. It is evident that the effective potential increases according to the increase in the charge parameter Q. Figure 5c represents that as the value of the BH parameter \(\gamma \) increases, the effective potential decreases. It is worthwhile to note that the ISCO is essential for the examination of accretion processes in the vicinity of the BH. Also, for the completion of this procedure, some other particular radii are essential. As it has been stated before, there exists a circular orbit when \(r>r_{ph}\). Assuming \(r_{ph}<r<r_{isco}\), the particle’s motion will exhibit instability for small perturbations. This connection implies that particles are either pulled into the BH or escape to infinity. The particle moves in stable circular orbits if \(r>r_{isco}\). In addition, the photon sphere \(r_{ph}\) and marginally bound orbit \(r_{mb}\), are obtained as

$$\begin{aligned}{} & {} \,r_{ph}=\frac{1}{2} e^{-\gamma } \left( e^{\gamma /2} \sqrt{9 e^{\gamma } M^2-8 Q^2}+3 e^{\gamma } M\right) , \end{aligned}$$
(69)
$$\begin{aligned}{} & {} \,r_{mb}=\frac{e^{-2 \gamma } \root 3 \of {128 e^{6 \gamma } M^6-144 e^{5 \gamma } M^4 Q^2+27 e^{4 \gamma } M^2 Q^4+3 \sqrt{3} \sqrt{27 e^{8 \gamma } M^4 Q^8-32 e^{9 \gamma } M^6 Q^6}}}{3 \root 3 \of {2} M} \nonumber \\{} & {} \!\quad -\frac{\root 3 \of {2} e^{-2 \gamma } \left( 12 e^{3 \gamma } M^2 Q^2-16 e^{4 \gamma } M^4\right) }{3 M \root 3 \of {128 e^{6 \gamma } M^6-144 e^{5 \gamma } M^4 Q^2+27 e^{4 \gamma } M^2 Q^4+3 \sqrt{3} \sqrt{27 e^{8 \gamma } M^4 Q^8-32 e^{9 \gamma } M^6 Q^6}}}+\frac{4 M}{3}. \end{aligned}$$
(70)

We now compute the specific angular momentum, specific energy, angular velocity, and angular momentum of the motion of particles in circular orbits for the Dyonic ModMax BH. Consequently

$$\begin{aligned} E^{2}= & {} \frac{e^{-\gamma } \left( e^{\gamma } r (r-2 M)+Q^2\right) ^2}{r^2 \left( e^{\gamma } r (r-3 M)+2 Q^2\right) }, \end{aligned}$$
(71)
$$\begin{aligned} L^{2}= & {} \frac{r^2 \left( e^{\gamma } M r-Q^2\right) }{e^{\gamma } r (r-3 M)+2 Q^2}, \end{aligned}$$
(72)
$$\begin{aligned} \Omega _{\phi }^{2}= & {} \frac{M r-e^{-\gamma } Q^2}{r^4}, \end{aligned}$$
(73)
$$\begin{aligned} l^{2}= & {} \frac{e^{\gamma } r^4 \left( e^{\gamma } M r-Q^2\right) }{\left( e^{\gamma } r (r-2 M)+Q^2\right) ^2}. \end{aligned}$$
(74)

For ISCO the above expression are given in Appendix A.

Fig. 6
figure 6

The profile of energy and angular momentum is represented as a function of r. The left plots are drawn for \(\gamma =0.1\) and numerous values of charge Q while right plots are drawn for \(Q=1\) and various values of BH parameter \(\gamma \)

Full size image

The specific energy and specific angular momentum profiles along the radial direction r is illustrated in Fig. 6. Furthermore, the impact of the charge Q and BH parameter \(\gamma \) also observed. From left penal it is clear that specific energy and specific angular momentum decreases with the increment of charge Q while in right penal it is observe that as the value of BH parameter \(\gamma \) grows, the specific energy and specific angular momentum increases.

5.1 Radiant energy flux

We study the flux radiation emitted by the outermost layer of the disk in the plane \(\theta =\frac{\pi }{2}\) utilizing the quantities E, L, and \(\Omega _{\phi }\). The investigation of the flux radiant energy related to the accretion disk can be conducted using Eqs. (22) and (23), which gives us

$$\begin{aligned}&K(r)\nonumber \\&=-\frac{\dot{M} \sqrt{\frac{e^{\gamma } r^4}{e^{\gamma } M r{-}Q^2}} \left( 3 e^{\gamma } M r{-}4 Q^2\right) \left( e^{\gamma } r \left( r^2{-}M (2 r{+}1)\right) {+}Q^2 (r{+}1)\right) }{8 \pi r^5 \left( e^{\gamma } r \left( -2 M r+M+r^2\right) +Q^2 (r-1)\right) ^2}\nonumber \\&\quad \times \int ^{r}_{r_{isco}}F(r)dr, \end{aligned}$$
(75)

where

$$\begin{aligned} F(r)= & {} \left( e^{-\gamma } \sqrt{\frac{e^{\gamma } r^4}{e^{\gamma } M r-Q^2}}(e^{\gamma } r(-2 M r+M+r^2)\right. \nonumber \\{} & {} +Q^2 (r-1))(e^{\gamma } M Q^2 r (r+8)\nonumber \\{} & {} \left. -e^{2 \gamma } M r^2(2 M (r+2)-r^2)-4 Q^4)\right) \nonumber \\{} & {} \times \Big (2 r^3(e^{\gamma } r(r^2-M (2 r+1))+Q^2 (r+1))^2\Big )^{-1}.\nonumber \\ \end{aligned}$$
(76)
Fig. 7
figure 7

The profile of energy flux K along r, for different value of Q and \(\gamma \)

Full size image

To analyze the radiation flux behavior of the accretion disk surrounding the BH for various values of the charge parameter Q, as represented in Fig. 7. In left panel we observe that the increase in BH parameter Q leads to a higher flux energy of the accretion disk while in right penal we can see that as the value of BH parameter \(\gamma \) increases the radiation energy flux decreases.

5.2 Radiant temperature

There is speculation that the accretion disk is in thermal equilibrium, leading to the emission of radiation that follows the principles of black body radiation. The Stefan–Boltzmann law, indicated as \(K(r)=\sigma T^{4}\), establishes a fundamental relationship between energy flux and temperature. In this scenario, the symbol \(\sigma \) denotes the Stefan–Boltzmann constant. The disk temperature is determined by evaluating the BH parameter Q. In Fig. 8, the temperature distribution on a disk is observed for various values of Q, with the parameter \(\gamma =0.1\) fixed. In left penal it has been noticed that the temperature of the disk rises as the parameter Q grows. In right penal we have observed that the temperature of the disk decline as the value of BH parameter increases.

Fig. 8
figure 8

The radiation temperature profile for various values of Q and BH parameter \(\gamma \)

Full size image
Table 1 The numerical results of below mentioned quantities are given by considering \(Q=1\) with various values of BH parameter \(\gamma \)
Full size table

5.3 Radiative efficiency

The gravitational energy radiation is emitted as the material of the disk gradually spirals towards the center. Determining the specific energy in the ISCO radius allows us to calculate the central object’s radiative efficiency, or its capacity to convert rest mass into radiation. Radiative efficiency can be calculated by using the following formula

$$\begin{aligned} \eta ^{*}=1- E_{isco} \end{aligned}$$
(77)

The numerical result of ISCO, \(E^{2}_{isco}\), \(L^{2}_{isco}\), \(\Omega ^{2}_{isco}\),\(l^{2}_{isco}\), maximum energy flux and maximum temperature distribution are provided in the given Table 1.

5.4 Epicyclic frequencies

When perturbations occur within the plane \(\theta =\frac{\pi }{2}\), particles moving along a circular orbit will experience small oscillations in both the vertical and radial directions. The radial and vertical epicyclic frequencies are calculated by using Eqs. (31) and (32), as provided

$$\begin{aligned}&\Omega _{r}^2\nonumber \\&=\Big (e^{-2 \gamma }(2 e^{2 \gamma } Q^6 r^2(-276 M^2-2 Mr(75 r^2+106)\nonumber \\&\quad +3 r^2(7 r^2+24))+2 e^{4 \gamma } Q^2 r^4(-336 M^4+3(19 M^2+1) r^4\nonumber \\&\quad -18(10 M^2+3) M r^3+(237 M^2-2) r^2+6(1-32 M^2) M r)\nonumber \\&\quad +2 e^{3 \gamma } Q^4 r^3(440 M^3+3 M^2 r(83 r^2+107)-6 M r^2\nonumber \\&\quad \times (10 r^2+39){+}29 r^3-2 r){-}e^{5 \gamma } r^5(-192 M^5{+}4(9 M^2+1)\nonumber \\&\quad \times M r^4 +6(26 M^2-1) M r^2+(9-80 M^2) M^2 r+(1-48\nonumber \\&\quad \times (2 M^4+M^2)) r^3)+6 e^{\gamma } Q^8 r(28 M+11 r^3+16r)\nonumber \\&\quad -20 Q^{10})\Big )\Big (2 r^6(e^{\gamma } r (r-2 M)+Q^2)^3\Big )^{-1}, \end{aligned}$$
(78)

and

$$\begin{aligned} \Omega _{\theta }^2=\frac{e^{-\gamma -2} \left( Q^2-e^{\gamma } M r\right) ^2 \left( e^{\gamma } r (r-2 M)+Q^2\right) }{\left( e^{\gamma } r (r-3 M)+2 Q^2\right) ^2}. \end{aligned}$$
(79)
Fig. 9
figure 9

The profile of radial epicyclic frequency \(\Omega _{r}\) along r for different chosen values of Q and \(\gamma \)

Full size image
Fig. 10
figure 10

The vertical epicyclic frequency \(\Omega _{\theta }\) along radial coordinate r for different chosen values of Q and \(\gamma \)

Full size image

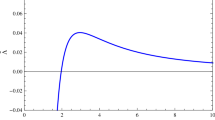
In Fig. 9, the profile of radial epicyclic frequency \( \Omega _{r}\) can be examined along the dimensionless radial coordinate r for numerous values of BH parameter \(\gamma \) and charge Q. In Fig. 9, we observe that initially the radial epicyclic frequency increases to its maximum value for small BH radius and then decreases as BH radius r increases. Also, the effect of the BH parameter \(\gamma \) and charge Q illustrated in Fig. 9. The behavior of the vertical epicyclic frequency \( \Omega _{\theta }\) along radial coordinates r is represented in Fig 10. In left penal we can see that as the value of BH parameter charge Q rises the vertical frequency decreases. Furthermore, the effect of BH parameter \(\gamma \) observed in right penal. It can be easily seen that the vertical epicyclic frequency \( \Omega _{\theta }\) increases with the increment of BH parameter \(\gamma \).

6 Conclusions

The procedures of accretion and particle geodesic motion around the Dyonic ModMax BH in the equatorial plane are investigated. The investigation of the stability and circular geodesics of their orbits has allowed the formation of a fundamental formulation for examining the accretion flow around the BH and analyzing the oscillations that arise from perturbations. The mass accretion rate, emission rate, effective potential, typical radius, specific energy, epicyclic frequency, specific angular momentum, and dynamical properties of the BH are also determined. Some generic solutions for fluid flow around Dyonic ModMax BH have been obtained by considering the equation of state \(p = k\rho \) for the isothermal fluid. Based on our outcomes, it is evident that the influence of the BH parameters Q, \(\gamma \) and the effective potential can be linked to the distinct loci of unstable and stable circular orbits. By increasing the parameter Q, the value of \(V_{eff}\) also rises, enabling the determination of the exact location of the ISCO, as illustrated in Fig. 5a. The location of the radii indicated as \(r_{isco}\), \(r_{ph}\), \(r_{sin}\) within the spacetime deviates considerably from the Schwarzschild solutions. In Fig. 6, one can see the impact of the BH parameters Q and \(\gamma \) on the angular momentum and energy of the BH. Moreover, we noted that as the value of Q rises, the efficiency of the accretion process also rises. It is evident that as the BH parameter \(\gamma \) increases, there is a corresponding increase in the flux of radiation and the radiant temperature.

We studied the isothermal fluid and kept the equation of state parameter \(k=0.5\) to analyze the fluid particle density, radial velocity, and accretion processes. It has been noted that the radial velocity reaches its highest value at small radii for the minimum value of the charge \(Q=0.4\) and gradually decrease by increasing the value of Q. However, the fluid farthest from the BH does not have any radial velocity. Accretion occurs when the fluid crosses the critical points where its velocity is equal to the speed of sound. Before reaching the critical point, the fluid’s flow is characterized by a subsonic regime. However, once the fluid crosses the critical point around the BH, it transform to a supersonic flow due to the intense gravitational field. After analyzing the rate of accretion, we concluded that its behavior is significantly dependent on the fluid nature as well as the parameters Q and \(\gamma \) of the BH. In the scenario of a normal fluid, the increase in mass accretion occurs as a result of the strong gravitational field, reaching its highest value in the vicinity of the BH. Furthermore, the circular orbits, including their properties and epicyclic frequencies are investigated. It is evident that the radial frequency reaches its highest value at a small radius r of the BH. As the value of Q increases, the the vertical epicyclic frequency exhibits a decreasing trend as the radial distance r increases. The influence of the charge Q on the radial frequency is also significant. Additionally, it is observed that the vertical frequency reaches its maximum value at \(Q=3\) and then decreases towards the equilibrium position, while increase in the charge parameter Q leads to a decrease in the vertical frequency.