Holographic entanglement entropy and subregion complexity for s-wave superconductor from massive gravity

Abstract

In this paper, in the framework of massive gravity, the holographic entanglement entropy (HEE) and holographic subregion complexity (HSC) are numerically investigated by means of the RT formula and the subregion CV conjucture for holographic superconductor with backreaction. We find that both the HEE and HSC exhibit discontinuity of slope at critical temperature, hence both of them are able to reflect the information of phase transition in the holographic superconducting system. Different from the previous studies, the HEE and HSC as function of strip-width are not always lower in the superconducting phase than ones in the normal phase, in particular the HSC decreases linearly as the subregion increases for positive coupling parameters. We notice that when the coupling parameters $\alpha$ and $\beta$ are taken as positive values, the HSC behaves in the same way as HEE, but when they are negative, the HSC has many different behaviors from HEE. Furthermore, we also observe that the HEE and HSC in the superconducting phase illustrate a tendency to converge to the same value as the temperature approaches zero, regardless of the coupling parameters of model. It is worth mentioning that in the massless gravity limit (the coupling parameters $\alpha =0$ and $\beta =0$), the results given by us are consistent with the case of holographic superconductor with backreaction from Einstein gravity.

1 Introduction

As we know, the AdS/CFT correspondence provides us a duality between the d-dimensional strongly interacting field theory on the boundary and the $d+1$-dimensional weakly coupled gravity theory in the bulk [1]. One of the widely investigated objects is the application of the AdS/CFT correspondence to quantum information physics. Such as entanglement entropy and computational complexity, as concepts from quantum information, are introduced into quantum field theory on the boundary and reflected through duality by geometric quantities in the bulk. The Ryu–Takayanagi (RT) proposal [2] provides us a method to compute the entanglement entropy of CFT on the boundary by calculating the extremal surfaces in the bulk, which is summarized into the formula called holographic entanglement entropy(HEE)

$$\begin{aligned} S_A=\frac{Area(\gamma _{\mathcal {A}})}{4 G_{d+1}}, \end{aligned}$$

(1)

where $Area(\gamma _{{\mathcal {A}}})$ is the extremal surface that is anchored on the d-dimensional boundary with both ends fixed on $\partial {\mathcal {A}}$ and extends into $d+1$-dimensional bulk, and $G_{d+1}$ is Newton’s constant.

The computational complexity is a measure of difficulty in implementing the target state from a reference state. If we introduce a set of fundamental unitary operators (or called “simple gate” in quantum information), complexity is defined as the minimum number of these unitary operators applied to the reference state required to implement the target state. A well-defined complexity in quantum field theory remains a research worthy of investigation today. Recently there have been some progresses, such as Nielsen’s geometric [3, 4], Fubini-Study metric [5] and Krylov complexity [6, 7] etc. Or we can also utilize AdS/CFT correspondence to seek a geometric quantity in the bulk corresponding to it. Susskind proposes that the complexity is proportional to the size of Einstein–Rosen bridge (ERB) which connects two boundaries of external black hole [8, 9], this proposal is called complexity-volume (CV) duality. And another proposal is called complexity-action (CA) duality which relates complexity to the on-shell action of the Wheeler–De Witt (WdW) patch [10,11,12]. Based on holographic entanglement entropy and CV duality, Alishahiha considers a volume $V(\gamma _{\mathcal {A}})$ enclosed by the subsystem ${\mathcal {A}}$ on the boundary and RT surface to be the holographic subregion complexity(HSC) [13]

$$\begin{aligned} {\mathcal {C}}=\frac{V(\gamma _{{\mathcal {A}}})}{8\pi L G_{d+1}}, \end{aligned}$$

(2)

where L is the AdS radius and $G_{d+1}$ is Newton’s constant. In recent literature, some scholars have connected the holographic subregion complexity with the reduced fidelity susceptibility, referred to as the HSC/RFS duality [14,15,16,17].

On the other hands, due to the property of Weak/Strong coupling duality in the framework of AdS/CFT, the AdS/CFT correspondence has been extensively used to study the strongly coupled quantum many-body system in the past few years. A remarkable progress is the realization of holographic superconductor [18, 19] which is based on previous Gubser’s work [20] in 2008. The physical picture is that some gravity background would become unstable as one tunes some parameter, such as temperature for black hole and chemical potential for AdS soliton, to develop some kind of hair. The emergency of the hair in the bulk corresponds to the condensation of a composite charged operator in the dual field theory. More precisely, the dual operator acquires a non-vanishing vacuum expectation value breaking the U(1) symmetry spontaneously [21]. This simple holograhic setup can yield condensed curve of scalar hair, which has the similar properties with real superconductors. We expect that both HEE and HSC are able to reflect some information such as phase transition in holographic superconductor. Albash et al. [22] uncovered the behavior of the HEE across the metal/superconductor phase transition, and showed a discontinuity of the slope at the phase transition temperature $T_c$. Moreover, it is pointed out that the entanglement entropy in superconducting phase is always less than that in the normal phase, and a kink on the curve of holographic entanglement entropy with respect to strip-width is also observed. They attribute this phenomenon to the sensitivity to a new scale in the theory. In Ref. [23], Chakraborty showes that this kind of multi-valuedness not only appears in the HEE case, but also appears in the HSC for ${\mathcal {O}}_2$ superconductor. However, Zangeneh et al. [24] state that the HSC does not behave in the same way as HEE. With a fixed subregion strip-width, the HSC decreases with the increasing temperature, instead of increasing in HEE case. Moreover, the HSC in superconducting phase is larger than that in normal phase. Similarly, Refs. [25,26,27] indicate the same property of HSC, where it decreases with increasing temperature below the critical temperature. In Ref. [28], the authors claim that the superconducting phase always has the smaller complexity than the unstable normal phase below the critical temperature. It is noticed that this holographic complexity refers to the volume of the wormhole connecting two spacetime regions, rather than the volume enclosed by the extremal surface of entanglement entropy. By comparison, it is easy to find that the holographic correspondence of the field theory quantities for holographic complexity and subregion complexity should have some differences between them.

From a “Bottom-Up” perspective, we are always interested in exploring whether a different effective gravity model from Einstein gravity can lead to interesting properties or give rise to a specific dual quantum field theory in the context of AdS/CFT correspondence. In the Hartnoll’s et al. holographic superconductive model [29], they considered Einstein’s gravity coupling to a complex scalar field. Thus, it is important to explore whether a holographic superconductor model can be built in the framework of massive gravity and how to make it dual to a real condensed matter system. According to the work in Refs. [30, 31], a non-linear massive gravity is constructed by introducing higher order interaction term in the action. We know that the theory of massive gravity would suffer from the instability problem, such as the Boulware–Deser ghost [32], but the ghost field is eliminated satisfactorily [33, 34]. The massive gravity as a holographic framework can describe a class of strongly interacting quantum field theories with broken translational symmetry. In this framework, a charged black brane solution in 4-dimensional spacetime with a negative cosmological constant is constructed in [35], and in this holographic set-up, the conductivity generally exhibits a Drude peak which approaches to a delta function in the massless gravity limit. Soon afterwards, Zeng. et al. [36] constructed a holographic superconductor with momentum relaxation, and they reproduce the Drude scaling and pawer-law scaling in the normal state, while the superconducting part induces a delta function for real part conductivity when $\omega =0$ in the superconducting state. Thus, a natural question is, on the basis of works in [24, 36], we wonder whether there are some new properties about the HEE and HSC within the framework of massive gravity with complex scalar hair in AdS space compared to Einstein gravity, and the HEE and HSC can still reflect the phase transition information, which is just our motivation and aim of this paper. Concretely, we will numerically investigate HEE and HSC by means of the RT formula and subregion CV conjucture for holographic superconductor with backreaction. Our research results show that in the case of negative coupling parameters, the HEE and HSC as function of strip-width behave in a same way, in which the HEE and HSC in the superconducting phase are lower than them in the normal phase, and both of them increase as the strip-width increase. However when we take the positive parameters, the holographic subregion complexity decreases as the subregion increases, and the relation between them in the superconducting phase and in the normal phase has also become more diverse.

This paper is organized as follows: In next section, we will review the massive gravity with a complex scalar hair in AdS bulk which is dual to 3+1-dimensional superconductor system. In Sect. 3, we will briefly look back the related consents to the HEE and HSC, and study them deeply as the function of strip-width and temperature for ${\mathcal {O}}_1$ and ${\mathcal {O}}_2$ superconductor respectively. The discussion and conclusions are given in Sect. 4.

2 Review for holographic superconductors from massive gravity

In this section, we will briefly review a holographic s-wave superconductor in $3+1$-dimensional massive gravity with complex scalar and U(1) gauge field. Let us review the massive gravity first. We consider an action for $n+2$-dimensional massive gravity [37]:

$$\begin{aligned} S= & {} \frac{1}{2 \kappa ^{2}} \int d^{n+2} x \sqrt{-g}\nonumber \\{} & {} \left[ R+\frac{n(n+1)}{L^{2}}+ m_{g}^2 \sum _{i}^{4} c_{i} {\mathcal {U}}_{i}(g, f)\right] \end{aligned}$$

(3)

where f is a fixed symmetric, and usually called reference metric, $c_{i}$ are coupling parameters and $m_{g}$ is the mass of graviton. The coupling parameter should be required to be negative for a self-consistent massive gravity theory with $m_{g}^2 > 0$. However, the theory may exhibit different characteristics in the AdS space. The fluctuations of scalar field with negative mass square could still be stable if the mass square obeys corresponding Breitenlohner–Freedman bounds [37]. And ${\mathcal {U}} _{i}$ are symmetric polynomials of the eigenvalues of the matrix ${\mathcal {K}}^{\mu }{ }_{\nu } \equiv \sqrt{g^{\mu \alpha } f_{\alpha \nu }}$,

$$\begin{aligned} \begin{array}{l} {\mathcal {U}}_{1}=[{\mathcal {K}}], \\ {\mathcal {U}}_{2}=[{\mathcal {K}}]^{2}-\left[ {\mathcal {K}}^{2}\right] ,\\ {\mathcal {U}}_{3}=[{\mathcal {K}}]^{3}-3[{\mathcal {K}}]\left[ {\mathcal {K}}^{2}\right] +2\left[ {\mathcal {K}}^{3}\right] , \\ {\mathcal {U}}_{4}=[{\mathcal {K}}]^{4}-6\left[ {\mathcal {K}}^{2}\right] [{\mathcal {K}}]^{2}+8\left[ {\mathcal {K}}^{3}\right] [{\mathcal {K}}]\\ \qquad \qquad +3\left[ {\mathcal {K}}^{2}\right] ^{2}-6\left[ {\mathcal {K}}^{4}\right] . \end{array} \end{aligned}$$

(4)

the matrix ${\mathcal {K}}^{2}$ is expressed as ${\mathcal {K}}^{2}={\mathcal {K}}^{\mu }_{~\rho } {\mathcal {K}}^{\rho }_{~\nu }=\sqrt{g^{\mu \alpha } f_{\alpha \rho }}\sqrt{g^{\rho \beta } f_{\beta \nu }}$, and $\left[ {\mathcal {K}}\right] \equiv {\mathcal {K}}^{\mu }_{~\mu }$ is the trace of ${\mathcal {K}}^{\mu }_{~\nu }$, and $\left[ {\mathcal {K}}^{2}\right] \equiv \left( {\mathcal {K}}^{2}\right) _{\mu }^{\mu }$. We take the following reference metric as

$$\begin{aligned} f_{\mu \nu }=\textrm{diag}\left( 0,0, c_{0}^{2} h_{i j}\right) . \end{aligned}$$

(5)

In this paper, we are interested in the case of a spatial reference metric [35], i.e., we set $h_{ij}=\delta _{ij}$. According to the subsequent metric ansatz and the spatial reference metric, we have

$$\begin{aligned} \begin{array}{l} {\mathcal {U}}_{1}=n c_{0} z,\\ {\mathcal {U}}_{2}=n(n-1) c_{0}^{2} z^{2}, \\ {\mathcal {U}}_{3}=n(n-1)(n-2) c_{0}^{3} z^{3}, \\ {\mathcal {U}}_{4}=n(n-1)(n-2)(n-3) c_{0}^{4} z^{4}. \end{array} \end{aligned}$$

(6)

We consider a $2+1$-dimensional superconductor system in boundary, which is dual to a 4-dimensional gravity in AdS space. For the case $n=2$, we have ${\mathcal {U}}_{3}=0$ and ${\mathcal {U}}_{4}=0$. Thus, there are only two massive terms. Following the notation used in the reference [36], we set $c_0=1$, and denote $\alpha =c_{1}$, $\beta =c_2$. Therefore, the gravitational massive term becomes $m_{g}^{2}(\alpha {\mathcal {U}}_1 + \beta {\mathcal {U}}_2)$. In massive gravity, the values of $c_0$, $\alpha$, $\beta$ and $m_g$ can affect the existence of a stable solution of the black hole [35]. It is evident from the massive term mentioned above that due to the multiplicative relationship among the parameters, the variations in the parameters $m_g$, $\alpha$ and $\beta$ may yield similar outcomes. Therefore, in this paper, we set the mass of gravity $m_g^2=1$ and focus only on the variations of the coupling parameters $\alpha$ and $\beta$.

In order to build a gravitational system which is dual to the superconducting system, we also introduce a U(1) gauge field and a charged complex scalar field in the bulk, with action

$$\begin{aligned} S_{M}= & {} -\frac{1}{2 \kappa ^{2}} \int d^{4} x \sqrt{-g}\nonumber \\{} & {} \left( \frac{L^{2}}{4} F_{\mu \nu } F^{\mu \nu }+|D \psi |^{2}+\frac{m_{\psi }^{2}}{L^{2}}|\psi |^{2}\right) , \end{aligned}$$

(7)

where $F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }$ and $D_{\mu }=\nabla _{\mu }-iqA_{\mu }$. $m_{\psi }$ is the mass of the complex scalar field $\psi$, and q is not only the charge of $\psi$, but also the backreation parameter, which could determine the strength of the backreaction of matter field on the background metric. According to the document [38], if we rescale $A_\mu$ = ${\tilde{A}}_\mu /q$ and $\psi ={\tilde{\psi }}/q$, then the matter action has a $1/q^2$ in front, so the backreaction of matter field on the metric is suppressed when q is large. The limit $q\rightarrow \infty$ with ${\tilde{A}}_\mu$ and ${\tilde{\psi }}$ fixed is called probe limit, which means ignoring the backreaction of the matter field on the metric. But, in this paper we only focus on the effects of the coupling parameters $\alpha$ and $\beta$ on the HEE and HSC, and fix the backreaction parameter $q=1$ when considering the case of backreaction. For convenience, we will set the AdS radius $L=1$ and the horizon $z_{+}=1$ in the subsequent context, which is allowed because of the scaling symmetry. The total action is the action (3) of massive gravity plus the matter action (7). The ansatz for metric and matter fields is given by

$$\begin{aligned} ds^{2}= & {} \frac{1}{z^{2}}\left( -g(z)e^{-\chi (z)}dt^{2}+\frac{dz^{2}}{g(z)}+dx^{2}+dy^{2}\right) ,\nonumber \\ A= & {} \phi (z)dt,~~~\psi =\psi (z). \end{aligned}$$

(8)

By taking variation of the action with respect to $g^{\mu \nu }$, $\psi$ and $A_{\mu }$, then substituting the ansatz into the equation of motion, we get the following system of ordinary differential equations [36]:

$$\begin{aligned}{} & {} \psi ''+\left( \frac{g'}{g} - \frac{\chi '}{2} - \frac{2}{z}\right) \psi ' +\frac{q^{2}e^{\chi }\phi ^{2}\psi }{g^{2}}-\frac{m_{\psi }^{2}\psi }{z^2g}=0, \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \phi ''+\frac{\chi '\phi '}{2}-\frac{2 q^{2} \psi ^{2}\phi }{z^2g}=0, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \psi '^{2}-\frac{\chi '}{z}+\frac{q^{2}e^{\chi }\phi ^{2}\psi ^{2}}{g^{2}}=0, \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \frac{3}{z^2}-\frac{3}{z^2g}-\frac{\alpha m^2_g}{zg}-\frac{\beta m^2_g }{g}+\frac{m^2_\psi \psi ^2}{2z^2g}+\frac{q^2e^{\chi }\psi ^2\phi ^2}{2g^2}\nonumber \\{} & {} \quad -\frac{g'}{zg}+\frac{e^\chi z^2 \phi '^2}{4g}+\frac{1}{2}\psi '^2=0. \end{aligned}$$

(12)

At the horizon, $g(z)_{z=z_+}=0$. The Hawking temperature of the black hole is

$$\begin{aligned} T= & {} \frac{1}{16 \pi L^{2}}\left( \left( 12+4 \psi _{+}^{2}\right) e^{-\chi +/ 2}-L^{2} E_{+}^{2} e^{\chi _{+} / 2}\right. \nonumber \\{} & {} \left. +4(\alpha +\beta ) e^{-\chi +/ 2}\right) , \end{aligned}$$

(13)

where $\psi _{+}$, $E_{+}$ and $\chi _{+}$ are the value of $\psi (z)$, $\phi '(z)$ and $\chi (z)$ at the horizon.

In order to solve this system of nonlinear ordinary differential equations (9)–(12), we need to know the behavior of various field at the horizon and toward the asymptotical AdS boundary. The fields have an expansion near the horizon:

$$\begin{aligned} \psi _{h}= & {} \psi _{h0}+\psi _{h1}(z-1)+\psi _{h2}(z-1)^2+\cdots , \end{aligned}$$

(14)

$$\begin{aligned} \phi _{h}= & {} \phi _{h0}(z-1)+\phi _{h1}(z-1)^2+\cdots , \end{aligned}$$

(15)

$$\begin{aligned} \chi _{h}= & {} \chi _{h0}+\chi _{h1}(z-1)+\cdots , \end{aligned}$$

(16)

$$\begin{aligned} g_{h}= & {} g_{h0}(z-1)+g_{h1}(z-1)^2+\cdots . \end{aligned}$$

(17)

By substituting Eqs. (14)–(17) into Eqs. (9)–(12), we obtain a system of algebraic equations composed of series coefficients. By solving this system the series coefficients can be expressed in terms of three free parameters $\psi _{h0}$, $\phi _{h0}$ and $\chi _{h0}$. The double-shooting method employed in this work involves fixing $\psi _{h0}$, while adjusting the two parameters $\phi _{h0}$ and $\chi _{h0}$ to make the source term of the scalar operator vanish as well as $\chi \rightarrow 0$ at the UV boundary.

The field has the following expansion towards the AdS boundary $z=0$:

$$\begin{aligned} \psi _{b}\approx \psi _{-} z^{\Delta _{-}} - \psi _{+}z^{\Delta _{+}},\quad \phi _b=\mu - \rho z, \end{aligned}$$

(18)

where $\Delta _{\pm }=\frac{3\pm \sqrt{9+4 m_{\psi }^2}}{2}$, and here we choose the scalar mass $m_{\psi }^2=-2$(i.e. $\Delta _{-}=1$ and $\Delta _{+}=2$) above Breitenlohner-Freedman bound for stability. $\mu$ is the chemical potential and $\rho$ is the charge of density in dual field theory. According to the AdS/CFT dictionary, depending on the choice of boundary conditions, the coefficient $\psi _{+}$ can be regarded as the source of the dual scalar operator and the coefficient $\psi _{-}$ is the expectation value of the scalar operator. Alternatively, $\psi _{-}$ is regarded as the source and $\psi _{+}$ is the expectation. Since we want U(1) symmetry to be broken spontaneously, we should turn off the source, i.e., $\psi _{+}=0$ or $\psi _{-}=0$:

$$\begin{aligned} \psi _{+}=0, \quad and\quad \left\langle {\mathcal {O}}_1 \right\rangle =\sqrt{2}\psi _{-} \end{aligned}$$

(19)

or

$$\begin{aligned} \psi _{-}=0,\quad and\quad \left\langle {\mathcal {O}}_2 \right\rangle =\sqrt{2}\psi _{+}, \end{aligned}$$

(20)

where $\sqrt{2}$ is a normalisation factor.

When the temperature is above the critical temperature, the order parameter of the superconducting system becomes zero. Thus, in Eqs. (9)–(12), we have $\Psi (z)=0$ and $\chi (z)=0$. The massive RN-AdS solution can be obtained in this case.

$$\begin{aligned} \phi (z)= & {} \frac{2Q}{z_{+}}\left( 1-\frac{z}{z_{+}}\right) ,\end{aligned}$$

(21)

$$\begin{aligned} g(z)= & {} 1-(1+Q^2+\frac{\alpha m_{g}^{2}}{2}+\beta m_{g}^{2})z^3+Q^2 z^4\nonumber \\{} & {} +\frac{\alpha m_{g}^{2}}{2} z +\beta m_{g}^2 z^2. \end{aligned}$$

(22)

The temperature, chemical potential and charge density are given by

$$\begin{aligned} T= & {} \frac{1}{4 \pi z_{+}}(3+\alpha m_{g}^{2}+\beta m_{g}^{2}-Q^2),~~~\mu =\frac{1}{\sqrt{16\pi G_{4} }}\frac{2Q}{z_{+}},\nonumber \\ \rho= & {} \frac{1}{\sqrt{16\pi G_{4} }}\frac{2Q}{z_{+}^2}. \end{aligned}$$

(23)

Fig. 1

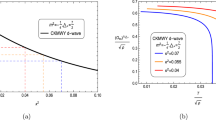
For ${\mathcal {O}}_1$ superconductor, a the first excited state solution of the complex scalar field $\psi (z)$ in superconducting phase at $T/\sqrt{\rho }\approx 0.01$ with $\alpha =-1$ and $\beta =0$; b the ground state solution of the complex scalar field $\psi (z)$ in superconducting phase at $T/\sqrt{\rho }\approx 0.01$ with $\alpha =1$ and $\beta =0$

Then, we depict the condensation phase diagram of ${\mathcal {O}}_1$ and ${\mathcal {O}}_2$. For ${\mathcal {O}}_1$ superconductor, we attempt to gradually decrease the value of $\alpha$ from the case of ground state of $\alpha =0,\beta =0$ (i.e., the massless gravity limit). We notice that it is difficult to obtain a numerical solution of ground state with the shooting method for $\alpha \lesssim -0.0689$, whereas obtaining a solution for the first excited state is comparatively easier. In Fig. 1a, we illustrate the behavior of the solution of complex scalar field $\psi (z)$ for taking $\alpha =-1$, which indicates the presence of one node along the z-axis at the temperature $T/\sqrt{\rho } \approx 0.01$. According to the literature [39], we can infer that the holographic superconducting system is in its first excited state. Here we also exhibit the ground state solution of complex scalar field for $\alpha =1$ at the temperature $T/\sqrt{\rho } \approx 0.01$ in Fig. 1b.

Fig. 2

a, c The ${\mathcal {O}}_1$ condensate as the function of temperature in the superconducting first excited state and ground state respectively; b, d the change of critical temperature with the coupling parameter $\alpha$ for the first excited state and ground state respectively

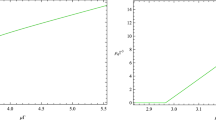
Figure 2a and c present the condensation in the first excited state and ground state of the operator ${\mathcal {O}}_1$ for the different values of coupling parameter $\alpha$. In Fig. 2b and d, we display the critical temperature of the superconducting phase transition as a function of the coupling parameter $\alpha$. It is worth noting that there is an evident decrease of the critical temperature with increasing $\alpha$. It deserves to be mentioned that this result is contrary to the result of the document [40], in which they consider a s-wave holographic superconductor from massive gravity without backreaction. We attribute this difference to whether we consider the backreaction of scalar field. In the massless gravity limit, i.e., taking the values of $\alpha =0$ and $\beta =0$, the system could reduce to the case of Einstein gravity with a complex scalar field and a U(1) gauge field [29].

Fig. 3

a The ${\mathcal {O}}_1$ condensate as a function of temperature, $q=1,\alpha =0$, $\beta =-0.5,1,3,10$ and 50; b the change of critical temperature $T_c$ with the coupling parameter $\beta$, $q=1,\alpha =0$

Below, we continue to discuss the condensation of ${\mathcal {O}}_1$ and the critical temperature as function of the coupling parameter $\beta$, which is shown in Fig. 3. As the same as the case of $\alpha \lesssim -0.0689,\beta =0$, through our numerical investigation, it is also difficult to obtain the ground state solution for $\alpha =0, \beta \lesssim -0.9$ by the shooting method. We find that the numerical results are sensitive to the initial value set by us in shooting method. Therefore, here we consider the situations of $\beta =-0.5,1,3,10$ and 50(see Fig. 3a). Figure 3b describes the critical temperature of the superconducting phase transition as a function of the coupling parameter $\beta$, in which $\beta$ can be taken relatively larger values. We notice that the critical temperature $T_c$ increases as the parameter the $\beta$ increases when $\beta >0$, however, $T_c$ decreases as the parameter $\beta$ increases when $\beta <0$.

Fig. 4

a, c The ${\mathcal {O}}_2$ condensate as the function of temperature with different values of coupling parameter $\alpha$ or $\beta$; b, d the change of critical temperature $T_c/\sqrt{\rho }$ with the coupling parameter $\alpha$ or $\beta$ respectively

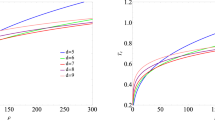
The Fig. 4a depicts the condensation of ${\mathcal {O}}_2$ for the different values of coupling parameters $\alpha$ with $\beta =0$, and Fig. 4b depicts the relation between the critical temperature of the superconducting phase transition and the coupling parameter $\alpha$. It is evident that with an increasing parameter $\alpha$, the critical temperature of the phase transition gradually decreases. When we take $\alpha =0$, the system returns to the ground state solution of holographic superconducting from Einstein gravity. In Fig. 4c, we also exhibit the condensation of ${\mathcal {O}}_2$ superconductor for different values of the coupling parameter $\beta$ when we set $\alpha =0$, and the curves correspond to an increasing values of parameter $\beta$ from top to bottom. The Fig. 4d depicts the relation between the critical temperature $T_c$ and the coupling parameter $\beta$. Notably, when the parameter $\beta$ is positive, the solution could exist in the holographic superconducting system for large values of parameter $\beta$. As observed from Fig. 4d, as $\beta$ gradually increases, the critical temperature dose not increase linearly but approaches a maximum value as the slope gradually becomes less steep.

3 Holographic entanglement entropy and subregion complexity for s-wave superconductors from massive gravity

In this section, we consider a strip subregion ${\mathcal {A}}$ on the boundary with strip-width $l_x$ and length $L_y\rightarrow \infty$. The entanglement entropy between the boundary subsystem and its complement is dual to the extremal surface in the bulk, which extends from the fixed boundaries $\partial {\mathcal {A}}$ of the subsystem ${\mathcal {A}}$. In reference [13], it is suggested that this extremal surface, enclosing the subsystem ${\mathcal {A}}$, corresponds to the volume of the subsystem complexity. We consider a static system at a fixing time slice, where the induced metric of the line element is regarded as

$$\begin{aligned} ds^2_{induced}=\frac{1}{z^2}\left( 1+\frac{1}{g}\left( \frac{dz}{dx}\right) ^2\right) dx^2+\frac{1}{z^2}dy^2. \end{aligned}$$

(24)

Therefore, the area of surface is given by

$$\begin{aligned} Area(\gamma _{{\mathcal {A}}})=L_y\int _{-l_x/2}^{l_x/2} dx \frac{1}{z^2}\root \of { 1+\frac{1}{g} \left( \frac{dz}{dx} \right) ^2 }. \end{aligned}$$

(25)

To find the extremum of this surface area, we can use the variational method by treating the integrand as the Lagrangian. Since it does not explicitly depend on x, the corresponding Hamiltonian

$$\begin{aligned} {\mathcal {H}} = \frac{1}{z^2\sqrt{1+\frac{z'(x)^2}{g(z)}}} = \lambda = \frac{1}{z_*^2} \end{aligned}$$

(26)

is a constant. The point $z_*$ corresponds to the turning point of the surface when $z'(x) = 0$. Therefore, we can deduce the equation for the minimal surface $\gamma _A$ as follows:

$$\begin{aligned} \frac{dz}{dx}=\frac{\sqrt{(z_{*}^4-z^4)g(z)}}{z^2}. \end{aligned}$$

(27)

Integrating above equation, we have the strip-width $l_x$ as function of turning point $z_*$

$$\begin{aligned} \frac{l_x(z_*)}{2}=\int _{0}^{z_*} dz \frac{z^2}{\sqrt{(z_{*}^4-z^4)g(z)}}, \end{aligned}$$

(28)

and substituting Eq. (27) into Eqs. (25) and (1), the holographic entanglement entropy becomes

$$\begin{aligned} S\!=\!\frac{L_y }{2 G_{4}}\int _{\epsilon }^{z_{*}} \!\!dz \frac{z_{*}^2}{z^2}\frac{1}{\sqrt{(z_{*}^4-z^4)g(z)}}\!=\!\frac{L_{y} }{2 G_{4}}\left( s+\frac{1}{\epsilon }\right) , \end{aligned}$$

(29)

where $\epsilon$ is a small cut-off to regularize the area integral, s is the finite part and has dimension of inverse length [22].

The holographic subregion complexity can be computed by finding out the volume enclosed by extremal surface $\gamma _A$ and the boundary subregion ${\mathcal {A}}$

$$\begin{aligned} V(z_{*})=2 L_{y} \int _{z_{*}}^{\epsilon } dz \frac{1}{z^3 \sqrt{g(z)}} x(z), \end{aligned}$$

(30)

where

$$\begin{aligned} x(z)=\int _{z_{*}}^{z} du \frac{u^2}{\sqrt{(z_{*}^4-u^4)g(u)}}. \end{aligned}$$

(31)

Then using Eqs. (2) and (30) the subregion complexity becomes:

$$\begin{aligned} {\mathcal {C}}=\frac{L_y}{4 \pi G_4 }\left( c+\frac{{\mathcal {F}}(z_{*})}{\epsilon ^2}\right) , \end{aligned}$$

(32)

where c represents a physically meaningful finite term, and $\frac{{\mathcal {F}}(z_*)}{\epsilon ^2}$ represents the divergent part. Due to the finite term c being independent of the cutoff, the two distinct UV cutoffs $\epsilon _1$ and $\epsilon _2$ could be chosen, this divergent term $F(z_*)$ in Eq. (32) can be expressed as [24]

$$\begin{aligned} {\mathcal {F}}(z_{*})=\frac{4\pi G_4}{L_{y} } \cdot \frac{\epsilon _1^{2} \epsilon _2^{2}({\mathcal {C}}(\epsilon _1)-{\mathcal {C}}(\epsilon _2))}{ \epsilon _2^{2}-\epsilon _1^{2}}. \end{aligned}$$

(33)

Finally, for the convenience of numerical calculation, we require physical quantities to be independent on scaling scale. It is useful to follow dimensionless quantities to analyze the system of holographic superconductor by scaling symmetry:

$$\begin{aligned} \frac{{\mathcal {O}}_1}{\sqrt{\rho }},~~\frac{{\mathcal {O}}_2}{\rho },~~\frac{T}{\sqrt{\rho }},~~\frac{l_x}{2}\sqrt{\rho },~~\frac{s}{\sqrt{\rho }}~\textrm{and} ~\frac{c}{\sqrt{\rho }}. \end{aligned}$$

(34)

3.1 ${\mathcal {O}}_1$ superconductor

Fig. 5

The HEE and the HSC as functions of the strip-width $l_{x}\sqrt{\rho }$ with a fixed temperature. a, b $T/\sqrt{\rho }=0.01$, $\alpha =-1,-0.5,-0.2$ and $\beta =0$; c, d $T/\sqrt{\rho }=0.015,0.1$, $\alpha =0$ and $\beta =0$, which are the cases of massless gravity limits; e, f $T/\sqrt{\rho }=0.015$, $\alpha =1,2$ and $\beta =0$

We exhibit the variations of HEE and HSC as functions of the strip-width of the boundary subregion for different values of the coupling parameter $\alpha$ in Fig. 5. From Fig. 5a we see that, at the fixed temperature $T/\sqrt{\rho }=0.01$, the corresponding values of HEE in the superconducting phase to $\alpha =-1.0,-0.5$ and $-0.2$ are smaller than ones in the normal phase. Moreover, the HEE linearly grows as strip-width increases for the larger values of $\frac{l_x}{2}\sqrt{\rho }$ whether in the superconducting phase or in the normal phase, but the growth rates corresponding to the different values of $\alpha$ are different for each other. Hence, there is a crossing point among the curves of HEE in both the superconducting phase and normal phase. It is easy to find that, around the crossing point in the normal phase, the value of HEE with $\alpha =-0.5$ is larger than that with $\alpha =-0.2$, when the strip-width is smaller than the corresponding value to the crossing point, vise versa. The same phenomenon also occurs in the superconducting phase, except that the value of HEE with $\alpha =-0.2$ becomes largest when the strip-width is taken as larger than the corresponding value to the crossing point. Obviously, the results mentioned above indicate that, at the fixed temperature of $T/\sqrt{\rho }=0.01$, when taking $\alpha <0$ the curves of HEE as the function of strip-width are evidently influenced by coupling parameter $\alpha$, whether in the normal phase or superconducting phase. It follows that, for the cases of $\alpha < 0$, the variation of the HEE due to the coupling parameter $\alpha$ does not follow a consistent rule at a fixed temperature, and is further influenced by the size of the boundary subregion. In Fig. 5b, as the same as the case of HEE, the HSC in the superconducting phase is smaller than that in the normal phase for the same value of $\alpha$. Moreover, it illustrates linear growth with increasing strip-width. When considering the three different values of $\alpha$ at the fixed temperature $T/\sqrt{\rho }=0.01$, the increase of the parameter $\alpha$ leads to the decrease of HSC for both the superconducting and normal phases. In essence, the increase in $\alpha$ suppresses the values and growth rate of HSC.

Figures 5c, d show the corresponding results to the coupling parameters $\alpha =0$ and $\beta =0$, which is just one in massless gravity limit, and here complex scalar field is chosen in the ground state. We find that for the fixed temperatures of $T/\sqrt{\rho }=0.1$ and $T/\sqrt{\rho }=0.015$, both the HEE and HSC in the superconducting phase are smaller than those in the normal phase. Moreover, we observe a linear decrease of the HSC in the superconducting phase for larger strip-width. The Fig. 5e, f display the cases of parameters $\alpha =1$ and $\alpha =2$. From Fig. 5e we see that, different from the results corresponding to $\alpha <0$ in Fig. 5a, for the fixed positive $\alpha$ such as $\alpha =1$, there is a crossing point between the curves of HEE in the superconducting phase and that in the normal phase, which means when the strip-width is smaller than the corresponding value of this crossing point, the HEE in the superconducting phase is larger than that in the normal phase, vise versa. The similar result has also been mentioned in Xu’s paper [41] about their result of HSC. However, in Fig. 5f the HSC exhibits a significant linear decrease as the strip-width increases, and the HSC in the superconducting phase is larger than that in the normal phase. By numerical analysis, it is observed that this phenomenon arises due to the finite part $\frac{L_y}{4\pi G}\cdot c={\mathcal {C}}(z_*,\epsilon )-\frac{L_y}{4\pi G} \cdot \frac{{\mathcal {F}}(z_*)}{\epsilon ^2}$, although both the ${\mathcal {C}}(z_*,\epsilon )$ and ${\mathcal {F}}(z_*)$ are increasing with strip-width, the divergent term ${\mathcal {F}}(z_*)$ has more rapid increase than ${\mathcal {C}}(z_*,\epsilon )$. Therefore, the finit part of HSC decreases with an increasing strip-width.

Fig. 6

The HEE and HSC as functions of the temperature $T/\sqrt{\rho }$ for the fixed $\frac{l_x}{2}\sqrt{\rho }=1$. The various colors represent different values of coupling parameter $\alpha =-1,-0.5,-0.2,0,1$ and 2 (blue, red, green, black, orange and purple) with $\beta =0$ respectively. The dashed curves represent the normal phase and the solid curves represent superconducting phase

In Fig. 6, we illustrate the HEE and HSC as the function of the temperature for the fixed strip-width $\frac{l_x}{2}\sqrt{\rho }=1$ corresponding to the different values of coupling parameters $\alpha$, such as $\alpha =-1,-0.5,-0.2,0,1$ and 2. From Fig. 6a, we find that when $\alpha \le 0$, the HEE increases as the temperature increases whether the HEE in the superconducting phase or in the normal phase. Moreover, the HEE in the superconducting phase is lower than that in the normal phase below the critical temperature. This is consistent with the expectation that in the superconducting phase the degrees of freedom decrease due to the formation of Cooper pairs [27]. At the point of critical temperature, the values of HEE in superconducting and normal phase are equal, but there is a discontinuity of slope. This indicates that HEE can indeed capture information related to phase transitions. However, the situation is reversed with $\alpha >0$. In this case, the values of HEE both in the superconducting phase and in the normal phase exhibit decrease with increasing temperature. Moreover, below the critical temperature, the HEE in the superconducting phase is larger than that in the normal phase. In other words, the superconducting phase has more degrees of freedom than normal phase with parameter $\alpha \ge 0$.

As the temperature approaches zero, the HEE in the superconducting phase tends to a point. It is noteworthy that the approaching points are different between the two cases of $\alpha < 0$ and $\alpha \ge 0$. This can be trivially explained that when the temperature reaches zero, the gravitational system returns to the AdS vacuum, where the metric g(z) becomes a constant independent of the coupling parameter. As mentioned above, when numerically solving the differential equations for the case of $\alpha <0$ and $\alpha >0$, we respectively select the first excited state solution and the ground state solution for complex scalar field. Therefore, as the temperature approaches zero, they exhibit distinct asymptotic behaviors. In addition, from Fig. 6b, we see that the HSC also exhibits discontinuity of slope at the temperature of phase transition, and the curves for different values of $\alpha$ almost behave in the same way as ones of HEE. Nevertheless, a difference emerges as the temperature approaches zero: the numerical values of HSC converge towards a single point, in stark contrast to the case of HEE, which could distinctly discriminate between the ground state and first excited state. It remains an open question whether HSC inherently lacks the capacity to characterize such information, or within the framework of quantum field theory, the physical quantity of HSC like fidelity inherently possesses invariant numerical values regardless of the system’s specific state. This question deserves further investigation.

Fig. 7

The HEE and HSC as functions of the strip-width $l_{x}\sqrt{\rho }$ with the fixed temperature $T/\sqrt{\rho }=0.1$, $\alpha =0$. a, b $\beta =-0.5,1$ and 3; c, d $\beta =10$ and 50

Figure 7 depicts the variations of the HEE and HSC with the strip-width $\frac{l_x}{2} \sqrt{\rho }$ at the fixed temperature $T/\sqrt{\rho }=0.1$. It is worth noting that when taking $\beta =-0.5,1$ and 3 for the larger strip-width, the HEE in the superconducting phase remains lower than that in the normal phase and exhibits a linear increase. However, as shown in the Fig. 7a, c, when the coupling parameter is taken to be $\beta =3$, there is still a crossing point for small strip-width. When strip-width is smaller than the corresponding value to crossing point, the HEE in the superconducting phase larger than that in the normal phase. When $\beta =10$, the value of strip-width corresponding to this crossing point becomes larger than the value to $\beta =3$. It is worth mentioning that when $\beta =50$, the point at $\frac{l_x}{2}\sqrt{\rho } \approx 0.2$ for the curve of HEE is seemingly a crossing point, actually it is not, which is caused by the less samples for small subregions due to the numerical limitations. For the larger values of strip-width, the curves of HEE exhibit the slow linear increases. When the strip-width is smaller than the corresponding value to the crossing point, the HEE in the superconducting phase is larger than that in the normal phase, while strip-width is larger than the corresponding value to the crossing point, the HEE in the superconducting phase becomes lower than that in the normal phase. From Fig. 7b, d, we find that the HSC both in the normal phase and superconducting phase increases as the strip-width increases for $\beta =-0.5$. However, as the same as the case with the positive parameter $\alpha$, the HSC in the superconducting phase is larger than that in the normal phase for $\beta >0$. Moreover, the HSC for small strip-width increases to the maximum value, and then linearly decrease as the strip-width increases.

Fig. 8

The HEE and HSC as function of the temperature $T/\sqrt{\rho }$ for a fixed strip-width $\frac{l_x}{2}\sqrt{\rho }$. a, b $\frac{l_x}{2}\sqrt{\rho }=2.5$, $\alpha =0$, $\beta =1,3$ and 10; c, d $\frac{l_x}{2} \sqrt{\rho }=1$, $\alpha =0$, $\beta =-0.5,0,1,3,10$ and 50

In Fig. 8, we present the HEE and HSC as the function of temperature for two fixed strip-width values, such as $\frac{l_x}{2}\sqrt{\rho }=2.5$ and $\frac{l_x}{2}\sqrt{\rho }=1$. In Fig. 8a, c, we notice that the HEE in the normal phase presents a decreasing and then increasing trend. Similarly, the HEE in the superconducting phase also slightly decreases to the minimum and then increases. Moreover, when parameter $\beta =1$ and 3 the HEE in the superconducting phase is lower than that in the normal phase below the critical temperature for the strip-width $\frac{l}{2} \sqrt{\rho }=2.5$ and 1. However, in the case of $\beta =10$ at $\frac{l_x}{2}\sqrt{\rho }=2.5$, the curve of HEE in the superconducting phase intersects once with the curve of the normal phase below the critical temperature. This phenomenon has been observed in the curve of HSC in reference [41]. In Fig. 8c, for the cases of $\beta =10$ and 50 at $\frac{l_x}{2}\sqrt{\rho }=1$, the HEE in the superconducting phase is larger than that in the normal phase below the critical temperature. From the curve with different values of coupling parameters $\beta$, we can infer that as $\beta$ increases, the slope of the curves of HEE in the superconducting phase becomes gradually small, and these curves approach those in the normal phase. When the values of parameter $\beta$ larger than a certain parameter value, the two curves intersect twice, until larger than the normal phase completely. Moreover, as mentioned above in the case of $\alpha$, when the temperature approaches zero, all HEE curves in superconducting phase will converge towards a point. Unlike the case of HEE, as shown in Fig. 8b, d, for the cases of $\beta =-0.5$ and massless gravity limit, i.e., $\alpha =0$ and $\beta =0$, they exhibit an increasing trend with increasing temperature. However, the HSC both in the superconducting phase and in the normal phase exhibits a decrease with increasing temperature for $\beta >0$. For the curves of $\beta =1$ in Fig. 8b, d, the two crossing points appear. The HSC in superconducting phase is larger than that in the normal phase for $\beta =3$ and 10. Moreover, the HSC in superconducting phase converges to a point when the temperature approaches zero, and shows a discontinuity of slope at the critical temperature.

3.2 ${\mathcal {O}}_2$ superconductor

Fig. 9

The HEE and the HSC as functions of the strip-width $\frac{l_x}{2}\sqrt{\rho }$ in a fixed temperature. a, b $T/\sqrt{\rho }=0.02$, $\alpha =-1,-0.5$ and $-0.2$; c, d $T/\sqrt{\rho }=0.01$, $\alpha =0$ and 1

Firstly, we only consider the variation of $\alpha$ and set $\beta$ to be zero. In Fig. 9, we present the HEE and HSC as function of the strip-width at the fixed temperature $T/\sqrt{\rho }=0.02$ or $T/\sqrt{\rho }=0.01$ respectively which is below the critical temperature. It can be observed that for parameter $\alpha < 0$, both HEE and HSC demonstrate linear growth at large strip-width. The HEE and HSC in the superconducting phase are lower than those in the normal phase when the parameter $\alpha < 0$. This phenomenon is the same as the case in ${\mathcal {O}}_1$ superconductor. When we take $\alpha =0$, the HEE in the superconducting phase is lower than that in the normal phase, which is just the results in massless gravity limit [24]. However, the HSC in the superconducting phase initially is slightly larger than that in the normal phase at the a small strip-width, but when larger than the corresponding value to the crossing point, the HSC in the superconducting phase becomes lower than that in the normal phase. For the case of $\alpha =1$, due to the critical temperature being approximately $T_c/\sqrt{\rho } \approx 0.022$, the temperature $T/\sqrt{\rho } = 0.01$ far from the critical temperature is chosen to ensure the system remains in the superconducting phase. The Fig. 9c presents characteristic that the HEE in the superconducting phase is slightly larger than that in the normal phase for small strip-width, and when strip-width is larger than the corresponding value to the crossing point, the HEE in the superconducting phase is lower than that in the normal phase. For the case of HSC in Fig. 9d, the HSC in the superconducting phase consistently exhibits larger than that in the normal phase. Furthermore, the HSC linearly decreases with an increasing strip-width after the curve of HSC reaching the maximum in small strip-width.

Fig. 10

The HEE and HSC as function of the temperature for a fixed strip-width $\frac{l_x}{2}\sqrt{\rho }=1$, $\beta =0$, $\alpha =-1,-0.5,-0.2,0$ and 1 respectively

Fig. 11

The HEE and HSC as function of the strip-width $\frac{l_x}{2} \sqrt{\rho }$ with a fixed temperature $T/\sqrt{\rho }=0.02$. a, b $\alpha =0$, $\beta =-2,-1,1$ and 2. c, d $\alpha =0$, $\beta =10$ and 20

Fig. 12

The HEE and HSC as function of temperature with a fixed strip-width. The various colors represent different values of coupling parameter $\beta =-2,-1,0,1,2,10$ and 20 (blue, red, green, orange, purple, black and gray) with $\alpha =0$ respectively. The dashed curves represent the normal phase and the solid curves represent superconducting phase

We also present the HEE and HSC as the function of temperature with a fixed strip-width $\frac{l_x}{2}\sqrt{\rho }=1$ for different values of coupling parameter $\alpha$ in Fig. 10. Both the HEE and HSC in the superconducting phase are lower than those in the normal phase when we take parameters $\alpha <0$ with $\beta =0$. When taking $\alpha =0$, the HEE in the superconducting phase is lower than that in the normal phase, but the HSC in the superconducting phase is larger than that in the normal phase. As mentioned in the ${\mathcal {O}}_1$ superconductor with the case of $\alpha =1$ and 2, both the HEE and HSC in the superconducting phase are larger than those in the normal phase when $\alpha =1$, and both the HEE and HSC can capture information about phase transition, exhibiting a discontinuity of the slope at the critical temperature. Moreover, the curves of both HEE and HSC in the superconducting phase converge to a point when temperature approaches zero.

Next, in Fig. 11 we depict the HEE and HSC as the function of strip-width for the different values of coupling parameter $\beta$ at fixed temperature. We notice that the HEE and HSC in the superconducting phase are larger than those in the normal phase, and grow linearly at larger strip-width when we take the parameter $\beta =-2$ and $-1$, or extensively speaking, with $\beta <0$. For the parameters $\beta =1,2,10$ and 20, the crossing point also appears between the curves of superconducting phase and normal phase. Observing the curves in the figures, we can find that an increasing parameter $\beta$ suppresses the growth of HEE with respect to strip-width. for small strip-width, the HSC in the superconduting phase and the normal phase increases to maximum, then linearly decreases as the strip-width increases. The HSC in the superconducting phase is larger than that in the normal phase for large strip-width.

The Fig. 12 depicts the HEE and HSC as the function of temperature $T/\sqrt{\rho }$ with the fixed strip-width when we take various values of $\beta$. As the same as the characteristic mentioned above, both the HEE and HSC exhibit a discontinuity of slope at the critical temperature, and converge to a point when approaching $T/\sqrt{\rho }=0$. With the parameter $\beta < 0$, the HEE and HSC in the superconducting phase are lower than those in the normal phase and they all increase with increasing temperature. However with $\beta >0$, the HEE and HSC in the superconducting phase are larger than that in the normal phase and present a decreasing function with the temperature.

4 Summary

In summary, we have numerically investigated holographic superconductor condensation in the framework of massive gravity with backreaction. Concretely, by using the obtained numerical solutions, we have further calculated the holographic entanglement entropy and subregion complexity. For condensations of two different operators ${\mathcal {O}}_1$ and ${\mathcal {O}}_2$, we revealed some same and different characters between them. For ${\mathcal {O}}_1$ superconductor, by using shooting method,we find that it is difficult to obtain the ground state solution with the coupling parameter $\alpha \lesssim -0.0689,\beta =0$ or $\alpha =0,\beta \lesssim -0.9$, because of the numerical results being sensitive to initial value. Hence, the results could not indicate there is no ground state solutions for these cases. But it is easy to find the solution of first excited state for the case of $\alpha < 0, \beta = 0$. Whereas, there is not any difficulty mentioned above for the case of ${\mathcal {O}}_2$ superconductor. We studied the HEE and HSC as the function of strip-width with the fixed temperature. From the results of HEE in two different operators, we found that the HEE in the superconducting phase is lower than that in the normal phase for the negative coupling parameter. Moreover the curves of HEE show the linear increases with the increasing strip-width for the large strip-strip, which means that the area law holds in this case. However, when the parameters are positive, the situation becomes slightly more complicated, the HEE in the superconducting phase is not always lower than that in the normal phase. The HSC shows the same behavior as HEE for the negative coupling parameter, but for the positive coupling parameter, the HSC decreases linearly with the increasing strip-width. Meanwhile, the HSC in the superconduting phase is larger than that in the normal phase. From a numerical computation perspective, this phenomenon can be explained by the fact that diverging term increases more rapidly with the increasing strip-width. In terms of the dual field theory, if the HSC/RFS conjecture holds, it is necessary to further investigate whether the reduced fidelity susceptibility(RFS) with a system of dissipative momentum also exhibits the property of decrease with increasing subregion. In addition, we investigated the HEE and HSC as the function of the temperature with the fixed strip-width. For the condensations of ${\mathcal {O}}_1$ and ${\mathcal {O}}_2$, when one of the coupling parameters is negative and the other is set to be zero, both the HEE and HSC increase with increasing temperature, whether in the superconduting phase or in the normal phase. But, when one of the parameter is positive, both the HEE and HSC show the diverse behaviors as mentioned above in this paper. For example, for $\beta =1$ and 3 with fixed $\alpha =0$ in ${\mathcal {O}}_1$ superconductor, the HEE in the superconducting phase is lower than that in normal phase, the HSC in the superconducting phase is larger than that in normal phase. But for $\beta =1,2,10$ and 20 in ${\mathcal {O}}_2$ superconductor, both the HEE and HSC in the superconducting phase are larger than those in the normal phase. We inferred that the presence of the positive coupling parameter in the framework of massive gravity decreases the degree of freedom of the entanglement between the two subsystems with increasing temperature. Also, no matter what we take the values of coupling parameter, the research results show that both the HEE and HSC exhibit a discontinuity of slope at the critical temperature, therefore they can always reflect information about phase transition. Finally, we pointed out that as the temperature approaches zero, the curves of the HEE and HSC in the superconducting phase converge to a point regardless of the coupling parameter values. For ${\mathcal {O}}_1$ superconductor with varying coupling parameter $\alpha$, it is exception that the curves of HEE corresponding to the first excited state and the ground state approach the two different points. However, the HSC does not reflect this information in this case. At low temperature the different characters of HSC and HEE in the two different states above deserve further investigation in future work. Certainly, it is worth mentioning that in the massless gravity limit, the results given by us are consistent with the case of holographic superconductor with backreaction from Einstein gravity.