1 Introduction

Particle production by extended structures in motion is a well-studied phenomenon, particularly in the presence of an acceleration or an acceleration-like gravitational field. It has been analytically understood in a number of situations, including as Hawking radiation [1] around black holes and as the Unruh effect [2] for an accelerating detector (or equivalently, in terms of the radiation from moving mirrors [3]). Particle production can be viewed as transitions between the quantum vacuum and Fock states containing one or more excitations. The transitions induced by moving structures in quantum field theory are actually analogous to situations that occur in nonrelativistic quantum mechanics, when transitions between different states can occur even when a system is moving with constant velocity, as shown in Refs. [4, 5]. Indeed, the problem of how quanta may be created (or annihilated) by moving boundaries or structures is very rich one, with ties to problems in a number of topics in fundamental physics; besides Hawking–Unruh radiation, there are also natural connections to the Casimir effect [6].

In many cases of interest, the motion of the relevant boundary structures is quite slow compared to the characteristic transit times of any real or virtual particles that may be produced. When an eigenstate \(\psi _{n}\) with energy \(E_{n}\) is evolving under a time-dependent Hamiltonian H(t), there are two important time scales. One of them is the time scale describing the rate at which the Hamiltonian is varying. The other is \(\sim 2\pi /|E_{n}-E_{m}|\), which is the time scale at which the phase difference between the state \(\psi _{n}\) and the nearest other accessible eigenstate \(\psi _{m}\) accumulates; in a state that is a superposition of \(\psi _{n}\) and \(\psi _{m}\), this is the period over which the observables of the system oscillate. If the first time scale is much larger than the second, the time evolution process is called “adiabatic”; there are effectively no state transitions, as the state of the system tracks the instantaneous energy eigenstate in which it began, and the sole effect on \(\psi _{n}\) due to a cyclic change in the Hamiltonian, \(H(t_{1})=H(t_{0})\), will be a geometric phase which depends on the path the Hamiltonian has taken between \(t_{0}\) and \(t_{1}\) and which can be described by the Berry curvature [7]. Using superpositions, this kind of phase is observable; a striking example is actually the well-known Aharonov–Bohm effect [8], where introduction of a magnetic field in a region inaccessible to the particle beam leads to a change in the pattern in an electron interference experiment.

In first-order perturbation theory with a time-dependent perturbation Hamiltonian, however, one does find transitions between unperturbed eigenstates \(\psi _{n}\) and \(\psi _{m}\) at a rate proportional to \(\langle m|\dot{H}|n\rangle /(E_{m}-E_{n})\). Such terms are neglected in the adiabatic approximation, meaning that the approximation misses these weak – but potentially interesting – state transitions. An example of this situation is treated in Ref. [5], which describes two plates (represented by infinite, hard-wall potentials) which are moving away from or towards one-another with finite velocity. In such a situation, because of the time dependence of the Hamiltonian, the time-dependent wave functions that satisfy the Schrödinger equation are not energy eigenstates, but they can be expressed in terms of the instantaneous energy eigenstates that exist when the plates are not moving at all. The mixing of the instantaneous eigenstates represents transitions between different states. Intuitively, a particular solution of the Schrödinger equation not being an energy eigenstate tells us that there must be energy exchanged between the plates and the quantum-mechanical particle trapped between them. The hard wall potential is a very special, exactly solvable system, but the argument for transitions into different states is generic in non-adiabatic processes. In Ref. [4] the transition probabilities between different energy levels was computed under a more general set of conditions; the paper considered a system of molecules which could occupy either of two eigenstates – with either polar or nonpolar characteristics depending on their bond lengths. As the molecules move close together and then separate, their energy levels also get closer and then spread apart again. In such a scenario there is a finite probability of transition between the two energy levels – a Landau-Zener transition. To compute the probability involved, it was presumed that the difference in energies varied approximately linearly with time, and thus with the relative velocity of a pair of molecules. In this paper, we shall encounter a similar situation in which the difference between two bound-state energies varies linearly with the relative velocity, although it does not necessarily lead to any state transitions.

We can extend these idea to quantum field theories where the particle number is not conserved and in which there may be transitions between states corresponding to different numbers of quanta. In such a scenario, a Landau–Zener transition would not only excite a quantum particle to a higher energy but could produce transitions between multi-particle states, which may represent either the creation or destruction of quanta. One can try to imagine the quantum-field-theoretic extension of the hard wall potential problem, in which each hard wall may be modeled as a very heavy solitary wave coupled to additional quantum fields, toward which it behaves like a boundary object. If we start from a vacuum state, with no light quanta present, and then move the one or more soliton boundaries with some finite velocities, then there can be a nonzero amplitude for the quantum fields coupled to the solitons to transition to single- or multi-particle states; the soliton’s motion has resulted in the creation of particles. However, particle creation is always going to be suppressed by the differences in energy (and momentum) between the vacuum and states containing quanta. For the creation of even a single unbound propagating particle, the energy required to effect the transition is sizable. However, if the coupling to a solitary wave is strong enough, there may be bound states attached to the soliton, with energies well below the continuum threshold – which may mean that the particle production will be dominated by creation of quanta in these bound states. A specific illustrative model would be that of a bosonic kink or antikink coupled to a fermion field in \(1+1\) dimensions [9]. The coupling between a kink and the fermion field modifies the spectrum of the fermionic states – creating zero-energy modes, possibly other discrete states, and a modified continuum structure for the fermions that can still escape to infinity.

In this paper, we shall be specifically studying theories with fermions quantized in a time-dependent background composed of multiple bosonic kink structures, looking particularly at the behavior of zero-energy and almost-zero-energy fermion states. We can approximate the virtual fermion contributions to the vacuum energy and the pair production thresholds by essentially neglecting the effects of the other states with energies much farther from zero. Moreover, if one or more solitons are moving with finite velocities, it seems that there may be some probability of pair production within the manifold of almost-zero-energy states, due to Landau–Zener-like transitions. However, it turns out there is actually no such effect in a system with only two solitons, as we shall show in Sect. 3. Therefore we introduce a third kink, far away from a close kink-antikink system, and calculate the approximate fermionic energies and wave functions in this background in Sect. 4. As we let the faraway kink move with some finite velocity, we compute the probability transition between different discrete states and interpret the result in Sect. 5. Additional details and subsidiary calculations are presented in four appendices.

2 Fermions in a kink-antikink system

Our system with scalar field solitons coupled to a fermion field in \(1+1\) dimensions is described by the Lagrange density

(1)

This \(\phi ^{4}\) model with a spontaneously broken discrete symmetry has a extensive history as a venue for exploring quantum effects in theories that support classical solitary waves [9,10,11,12,13,14,15,16,17,18,19,20,21,22]. As is commonly done, we shall set the scalar field parameters to be \(\lambda =m^2=2\) for simplicity, so that the Lagrange density becomes . This leaves the Yukawa coupling as the principal free parameter describing the model; specifically, g is twice the ratio between the masses of the continuum fermion and boson excitations. Although we shall derive many results that are nonperturbative in g, we typically assume \(g\ll 1\) to simplify and make more illustrative our analytical computations. (How some of the results in this section generalize to arbitrary g is discussed in Appendix A.)

In the absence of the fermions, the scalar field admits vacuum solutions \(\phi =\pm 1\) (which spontaneously break the discrete symmetry \(\phi \rightarrow -\phi \) and give the continuum fermion states mass), as well as finite-energy kink and antikink solutions that interpolate between the two vacua. The stationary kink solution \(\phi _{K1}=\tanh {(x-x_{K1})}\) has a localized energy density centered at \(x_{1}\), with an integrated total energy \(E=\frac{4}{3}\). If we assume that the fermion interactions are weak enough that they do not destabilize the kink itself, then we can find the energy levels (at one-loop order) for the fermion field \(\Psi \) attached to the kink by solving the Dirac equation simultaneously with the modified scalar field equation itself. This will give us coupled differential equations [13], which modify the energy levels of both the fermion modes and and the nonperturbative kink. However, it turns out that for a zero-energy fermion mode, the modified field equation for the scalar is satisfied identically, and we get an improved approximation with a minimum of additional analytical effort.

Using the representation of the \(2\times 2\) Dirac matrices in which \(\gamma ^{0}= \sigma _{1}\) and \(\gamma ^{1}= i\sigma _{3}\), the single-particle Dirac Hamiltonian is

$$\begin{aligned} H= & {} \alpha p +g\beta \phi \end{aligned}$$
(2)
$$\begin{aligned}= & {} -i\sigma _{2}\partial _{x}+\sigma _{1}g\phi \end{aligned}$$
(3)
$$\begin{aligned}= & {} \left[ \begin{array}{cc} 0 &{} -\partial _{x}+g\phi \\ \partial _{x}+g\phi &{} 0 \end{array} \right] . \end{aligned}$$
(4)

In the background of a kink situated at \(x=x_{K1}\), we can find the zero-energy fermion mode by solving \(H\Psi _{K1}=0\). The normalized solution is

$$\begin{aligned} \Psi _{K1}&= \left[ \frac{g\Gamma \left( g+\frac{1}{2}\right) }{\sqrt{\pi }\,\Gamma (g+1)}\right] ^{1/2}\left[ \begin{array}{c} {{\,\textrm{sech}\,}}^{g}(x-x_{K1}) \\ 0 \end{array} \right] \equiv \left[ \begin{array}{c} \psi _{K1} \\ 0 \end{array} \right] \end{aligned}$$
(5)
$$\begin{aligned}&\approx \sqrt{\frac{g}{4^g}}\left[ \begin{array}{c} {{\,\textrm{sech}\,}}^{g}(x-x_{K1}) \\ 0 \end{array} \right] . \end{aligned}$$
(6)

The approximate form is valid in the \(g\ll 1\) limit that we shall typically be using. Similarly, for an antikink situated at \(x=x_{A}\) the zero-energy fermion mode is given by

$$\begin{aligned} \Psi _{A} \equiv \left[ \begin{array}{c} 0 \\ \psi _{A} \end{array} \right]\approx & {} \sqrt{\frac{g}{4^g}}\left[ \begin{array}{c} 0 \\ {{\,\textrm{sech}\,}}^{g}(x-x_{A}) \end{array} \right] . \end{aligned}$$
(7)

The presence of a zero mode in the spectrum of a quantum system indicates a degeneracy. In the presence of a single kink or antikink, the states with the attached fermion mode filled and empty are identical in energy. This leads to the remarkable phenomenon of fermion fractionalization [9]. To have a vacuum state that is invariant under charge conjugation, the formal vacuum must contain a fractional part of the fermion number for the zero mode; effectively, the mode is split, half and half, between the fermion and antifermion parts of the spectrum. The physical states, with the zero mode either fully occupied or fully unoccupied, have (after the subtraction of the Dirac sea) fermion numbers \(n_{F}=\frac{1}{2}\) and \(n_{F}=-\frac{1}{2}\), respectively.

A natural question would be what happens to the energy levels of the fermion field in presence of both a kink and antikink. While exact classical multiple-kink solutions are known for the closely related sine-Gordon equation, general analytic solutions representing interacting kink-antikink pairs are not available in the \(\phi ^{4}\) model. However, a smooth scalar field profile approximating the presence of a well-separated kink and antikink is

$$\begin{aligned} \phi = \phi _{K1}+\phi _{A}-1= \tanh (x-x_{K1})-\tanh (x-x_{A})-1, \end{aligned}$$
(8)

which centers a kink at \(x_{K1}\) and an antikink at \(x_{A}\), with \(x_{K1}<x_{A}\) (so that \(\phi \) is close to a vacuum value in between the solitons). Using this expression for \(\phi \), we can approximate the fermion wave functions variationally, beginning with a trial wave function of the form \(a\Psi _{K1}+b\Psi _{A}\). These describe superpositions of fermion states that are closely localized around the kink and antikink cores. Since the (first-order, matrix) Dirac equation may be converted into a second-order Schrödinger-like equation for \(E^{2}\), there should be no difficulties with justifying the usual variational approach for finding the ground state of the system (even though we shall not actually work with the second-order formulation). The correct values a and b should minimize the energy of the Dirac Hamiltonian (subject to the usual normalizability condition), and in this approximation, the ground state turns out to be

$$\begin{aligned} \Psi _{-}=\frac{1}{\sqrt{2}}\left[ \begin{array}{c} \psi _{K1} \\ \psi _{A} \end{array} \right] =\sqrt{\frac{g}{2\left( 4^{g}\right) }}\left[ \begin{array}{c} {{\,\textrm{sech}\,}}^{g}({x-x_{K1}}) \\ {{\,\textrm{sech}\,}}^{g}({x-x_{A}}) \end{array} \right] , \end{aligned}$$
(9)

and the corresponding energy (for \(g\ll 1\), in which case the physical widths of the solitons are much smaller than the extent of the fermion zero modes, so it is suitable to approximate \(\phi \) as a sum of step functions) is

$$\begin{aligned} \int dx\,\Psi ^{\dagger }_{-} H \Psi _{-}= - ge^{-g(x_{A}-x_{K1})}\equiv -E_{+}. \end{aligned}$$
(10)

Since this energy is negative, in the vacuum state, this mode is occupied.

The excited mode wave function may be found by the requirement that it must be orthogonal to \(\Psi _{-}\) within the state manifold spanned by \(\Psi _{K1}\) and \(\Psi _{A}\). This gives \(\Psi _{+}=\sigma _{3}\Psi _{-}\), and the energy of this excited state is \(E_{+}= \int dx\,\Psi ^{\dagger }_{+} H \Psi _{+}= ge^{-g(x_{A}-x_{K1})}\). \(2E_{+}\) can be seen as the energy required to create a fermion-antifermion pair, by emptying the \(\Psi _{-}\) state and (to conserve fermion number) filling the \(\Psi _{+}\) state. It is also seen that the energy of the fermion field is zero when there is exactly one fermion or one antifermion particle present. This additive nature of energy levels is characteristic of a (fermionic) harmonic oscillator, and it confirms our idea of a weakly interacting ground state for \(g\ll 1\).

Note that as the separation \(x_{A}-x_{K1}\) grows large, these energies approach zero exponentially. When the kink and antikink are infinitely far apart, there are two separate and degenerate zero-energy modes – precisely what we expect for fermions coupled to two completely isolated solitary waves. The dependence on \(x_{A}-x_{K1}\) represents a spectral flow of the energy eigenvalues away from the degenerate limiting value of \(E_{\pm }=0\) that is taken when the solitary waves are infinitely far apart. A more general variational wave function than \(a\Psi _{K1}+b\Psi _{A}\) would be expected to lead to lead to a larger (and more accurate) approximate value for the splitting between the negative- and positive-energy bound states, and the states would not need to be displaced by exactly equal and opposite amounts away from \(E=0\). In a time-dependent scenario in which the kink and antikink eventually approach and annihilate into radiation, the spectral flow will also include changes in the number of discrete fermion modes attached to the solitary waves. As the solitons coalesce and lose their shapes, the attractive strengths of the effective Schrödinger potential for the upper and lower components will grow weaker, so the additional discrete localized eigenstates that are present when \(g\gtrsim 1\) can flow back into the positive- and negative-energy continua. However, in \(1+1\) dimensions, the discrete states with energies closest to zero will persist as long as the evolving scalar field profile still generates global minima of the effective potentials.

Fig. 1
figure 1

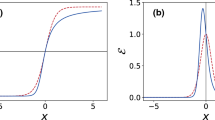
Comparison of the upper and lower components of the variational wave function \(\Psi _{-}\) and a numerical solution of the Dirac equation, all with Yukawa coupling \(g=0.1\) and soliton positions \(x_{K1}=-10\) and \(x_{A}=10\). The upper components are peaked on the left, and the lower components on the right, with the variational expressions shown as lines (black for \(x_{K1}\) and gray for \(x_{A}\)) and the corresponding numerically integrated values lying close by. The most notable differences between the solutions and the variational forms are the salient points in the integrated solutions located at \(x_{A}\) for the upper component and \(x_{K1}\) for the lower

Full size image

Figure 1 shows a comparison of the variational form \(\Psi _{-}\) with the numerically integrated solution of the Dirac equation in the background (8), for \(g=0.1\) and \(g(x_{A}-x_{K1})=2\), showing good agreement between the two, except for some small qualitative features that it is evident cannot be present in the analytical approximation \(\Psi _{-}\). In particular, there are fairly abrupt changes in the slopes of the upper and lower components of the numerical solution at the locations of both solitary waves, \(x_{K1}\) and \(x_{A}\); however, \(\Psi _{-}\) only captures the peak in each fermion component at the soliton about which is primarily localized, missing the smaller feature at the location of the farther-off soliton. Yet that the secondary changes in slope should exist is in fact quite clear from the form of the Dirac equation – or, equivalently, from the relation between the upper and lower components – in the presence of the kink-antikink background (8).

When \(g<1\), each isolated one-soliton system has only a single bound state (the zero mode) [10], so the kink-antikink system we are considering has just the two bound fermion modes. For larger values of g, this approximation gives the energies for the fermion bound states that lie closest to zero energy (the almost-zero-energy modes). More details about these analytic approximations for the discrete fermion states are discussed in Appendix A.

Because of the fermion energies’ dependences on on \(x_{A}-x_{K1}\), the bound states generate contribution to the effective potential between the kink and the antikink. There are also bosonic, Casimir-like quantum forces between them [15, 16]; however, the character of the fermion-induced potential is somewhat different, because it depends on which fermionic states are occupied. In the vacuum, the state \(\Psi _{-}\) is occupied, while \(\Psi _{+}\) is empty. \(E_{-}\) is negative and becomes more negative as \(x_{A}-x_{K1}\) decreases, creating an attraction between pair. Since this effective interaction exists in the absence of any fermion or antifermion excitations, it must be a product of virtual particle effects. If either a single fermion or a single antifermion is present – that is, if both almost-zero-energy fermion modes are either occupied or empty – the total energy vanishes, and there is no fermion contribution to the kink-antikink effective potential at this order of approximation; the presence of a single quantum produces a cancellation of the virtual particle corrections mentioned above. Finally, in the presence of both a fermion and an antifermion (\(\Psi _{+}\) occupied and \(\Psi _{-}\) empty), the kink-antikink potential term becomes repulsive.

However, there are several alternative interpretations that might be assigned to the physics of the two almost-zero-energy fermion states of the kink-antikink system. The ambiguity of the situation was already noted in Ref. [9], and we shall revisit it below when we discuss the almost-zero-energy fermion modes in three-soliton backgrounds. The crux of this issue is as follows. Globally, since there is one such state with an actually slightly positive energy and one with a negative energy, these may be designated according to the usual Dirac procedure, as \(\Psi _{+}\) being a fermion state and \(\Psi _{-}\) being a state in which a hole represents an antifermion; charge conjugation interchanges the corresponding fermion and antifermion states. However, an alternative approximate viewpoint is possible for an observer who is themselves “localized” around just one of the solitary waves. To a very good approximation, the discrete states still look like zero modes. To an observer who makes measurements in the vicinity of \(x_{K1}\), the system appears at short times to be just a single kink with fermion number \(\pm \frac{1}{2}\), depending on whether or not the state \(\Psi _{K1}\) is filled – although this picture needs to be adjusted at sufficiently long times. In fact, if the initial state of the full kink-antikink system is that there is a single fermionic quantum with wave function \(\Psi (t=0)=\Psi _{K1}\), then the fermion state will evolve in time, since \(\Psi _{K1}\) is not an energy eigenstate. Over time, the quantum will tunnel back and forth with frequency \(E_{+}\), between the state \(\Psi _{K1}\) localized around the kink and \(\Psi _{A}\) at the antikink. From the point of the local observer who sees only the kink, the process by which the \(\Psi _{K1}\) mode evolves from occupied to empty could be interpreted entirely in terms of the local degrees of freedom that have half-integer fermion numbers. From this viewpoint, the time evolution looks like having the half-fermion that is initially present tunnel away (effectively disappearing to infinity) and a half-antifermion tunnel in from infinity to replace it. Then, after enough time has elapsed, the two half-quanta will switch places again – and so on. This is certainly a peculiar description of what is happening, but it appears to accord with what the local observer, looking only at the kink region, would see.

It may seem puzzling that the very meaning of the natural eigenstates of the theory may depend qualitatively on the distance between the two solitons – that when the kink and antikink are very, very far apart, it is logical to describe the theory in terms of local states with half-integer numbers of localized fermions; yet when the solitons are closer together, it may be more natural to use the delocalized energy eigenstates with integral fermion numbers. Apparently, the appropriate assignment of states to the fermion and antifermion parts of the spectrum depends on the parameters of the interaction background. However, this is actually a known feature of the Dirac theory; whether particular states represent fermions or the absences of antifermions cannot, in general, be disentangled from the background bosonic fields with which the fermion field is interacting [23].

3 In the moving kink-antikink system

Since kink-antikink pairs interact (according to the classical field equations, augmented by quantum corrections), it makes sense to ask what happens to the fermion states when the two solitons are in relative motion. When the solitons are in motion relative to one-another, we can always Lorentz boost to the center of mass frame, in which the kink and antikink are moving towards or away from each other with equal speeds. The rate of tunneling transition in these boosted and unboosted frames will be related by a multiplicative Lorentz factor, and hence calculation done in the center of the mass frame will suffice for our current purposes. The solution \(\Psi '_{K1'}\) for the fermion attached to a kink moving at constant velocity v, centered instantaneously at \(x_{K1'}=x_{K1}+vt\), can be obtained by Lorentz boosting the previous solution for when the kink was at rest. The calculations in this section can be easily done to all orders in the velocity v; however, we will be keeping terms only up to first order in v, so that we can most easily see the differences between different scenarios in which calculation to all orders in v may not be so trivial (such as those we shall encounter in Sect. 5). The wave function for the fermion, boosted with the kink’s rapidity \(\eta \) is

$$\begin{aligned} \Psi '_{K1'}= & {} e^{\frac{\eta }{2}\sigma _{2}}\left[ \begin{array}{c} {{\,\textrm{sech}\,}}^{g}\gamma (x-x_{K1}-vt) \\ 0 \end{array} \right] \end{aligned}$$
(11)
$$\begin{aligned}= & {} \left( 1+\frac{\eta }{2}\sigma _{2}\right) \left[ \begin{array}{c} {{\,\textrm{sech}\,}}^{g}\gamma (x-x_{K1}-vt) \\ 0 \end{array} \right] \end{aligned}$$
(12)
$$\begin{aligned}= & {} \Psi _{K1'}+\frac{v}{2}\sigma _{2}\Psi _{K1'}, \end{aligned}$$
(13)

where we have used the \(v\ll 1\) aproximations \(\eta =\tanh v=v+\mathcal {O}(v^3)\) and \(\gamma =1+\mathcal {O}(v^2)\); and \(\Psi _{K1'}\) is same as \(\Psi _{K1}\) except that it is centered at the moving position \(x_{K1'}\). Similarly, the boosted fermion attached to an antikink moving with velocity \(-v\) is \(\Psi '_{A'}=\Psi _{A'}-\frac{v}{2}\sigma _{2}\Psi _{A'}\). We have assigned the kink and antikink equal and opposite velocities (converging together if \(v>0\)), so that \(\Psi '_{K1'}\) and \(\Psi '_{A'}\) are the wave functions in the kink-antikink center-of-mass frame.

In this framework, the instantaneous variational ground state is modified to

$$\begin{aligned} \Psi '_{-'}= & {} \frac{1}{\sqrt{2}}(\Psi '_{K1'}+\Psi '_{A'}) \end{aligned}$$
(14)
$$\begin{aligned}= & {} \Psi _{-'}+\frac{v}{2}\sigma _{2}\Psi _{+'}, \end{aligned}$$
(15)

where the primed subscripts \(+'\) and \(-'\) again refer to the use of instantaneous coordinates \(x_{K1'}\) and \(x_{A'}=x_{A}-vt\). The orthogonal (to first order in v) excited state must then be \(\Psi '_{+'}=\Psi _{+'}+\frac{v}{2}\sigma _{2}\Psi _{-'}\). This makes the energies of the two states \(E_{\pm '}=\pm (1+2gvt)E_{\pm }\). Although the energy eigenvalues are time dependent, in the adiabatic limit we expect these states not to mix, although there is gradual spectral flow of the eigenvalues as the separation changes.

However, as the solitons move towards each other, the wave functions which satisfy the exact Dirac equation \((H-i\partial _{t})\Psi =0\) will really be composed of a linear combination of basis states which actually includes more than just the moving almost-zero-energy modes – but also both any additional discrete (bound) states that may exist and the continuum scattering states,

$$\begin{aligned} \Psi&=\alpha \Psi '_{+'}+\beta \Psi '_{-'}+\text {higher discrete states}\nonumber \\&\quad +\text {free continuum states}. \end{aligned}$$
(16)

Including all the states gives us various transition probabilities, which could be computed perturbatively. However, at low velocity the dominant contribution should come only from transitions between \(\Psi '_{-'}\) and \(\Psi '_{+'}\), because their energies are exponentially close to zero. Evolution within this manifold of almost-degenerate states should be faster than transitions to other states that are separated by substantial energy gaps. Therefore, ignoring the transitions to other states (in order to get at least a semiquantitative analytic understanding of the behavior), the Dirac equation for the time-dependent almost-zero-modes simplifies to

$$\begin{aligned} -i\dot{\alpha }\Psi '_{+'}-i\dot{\beta }\Psi '_{-'}+\alpha (H-i\partial _{t})\Psi '_{+'}+ \beta (H-i\partial _{t})\Psi '_{-'} =0. \end{aligned}$$
(17)

Note that the image of the operator \((H-i\partial _{t})\) on \(\Psi '_{+'}\) or \(\Psi '_{-'}\) should really include both the almost-zero-energy wave functions and the more distant states. Although we are neglecting these contributions to the evolving wave functions, the decomposition of the image into these different state types does describe the coupling and transitions into higher-energy states – paving a path for numerical or even analytical calculation in the future. Dropping the extra terms in the decomposition for the action on \(\Psi '_{+'}\),

$$\begin{aligned}{} & {} (H-i\partial _{t})\Psi '_{+'}=E_{1}\Psi '_{+'}+E_{12} \Psi '_{-'}\nonumber \\{} & {} \quad +\text {higher discrete}+\text {continuum}, \end{aligned}$$
(18)

the time dependence is controlled by the two parameters \(E_{1}\) and \(E_{12}\).

Besides these approximations, note that we have already neglected the fact that our kink-antikink profile for \(\phi \) is not an exact solution of the scalar field equations, even in the limit in which the solitons are instantaneously stationary. In fact, there is an extensive literature, both analytical and especially computational, on the classical and quantum-mechanical behavior of \(\phi ^{4}\) theory solitary waves – how they interact at long and short distances, including the excitation of perturbative waves that eventually radiate away the energy of a kink-antikink system. See for example, Ref. [24] and references therein for a partial overview of important results. Specifically, it should be kept in mind that the discrete-state fermion energies are not the sole one-loop contributors to the kink-antikink effective potential. Besides contributions from fermion continuum states, there are also corrections coming from virtual (non-topological) excitations of the \(\phi \) field. These again can include both continuum states, as well as discrete excitation modes tied to individual solitary waves. The localized, discrete shape deformation modes (as well as the translational zero mode) of an isolated kink are the bosonic analogues of the fermion bound states attached to a kink background. Excitation of the shape deformation modes can play a key role in interactions both between kinks and continuum scalar modes and between adjacent kinks and antikinks [25,26,27]. For example, for a sufficiently energetic colliding soliton pair, the collision may result in an inelastic rebound – in which one or both of the solitary waves bounce back from the impact with the shape mode excited. The qualitative effects of exciting the discrete bosonic modes in this kind of way may be quite complicated, with the long-term behavior of a colliding kink-antikink pair displaying a “fractal” dependence on the initial soliton velocities [28,29,30]. A variety of approximate methods have been developed to deal with these complexities that already exist in the purely bosonic \(\phi ^{4}\) theory. So although the focus of the present work is on the effects of discrete fermion modes when the bosonic theory is Yukawa coupled to \(\Psi \), it is always important to remember that interactions between multiple solitary waves already have rich virtual interaction structure, even before the introduction of the fermion field.

As one may guess, the parameter \(E_{1}\) is equal to the instantaneous energy eigenvalue for \(\Psi '_{+'}\), \(E_{1}= E_{+'}=(1+2gvt)ge^{-g(x_{A}-x_{K1})}\). This controls the evolution of the phase of the wave function. More interesting is \(E_{12}\), which will determine the rate for a fermion to make a transition from the \(\Psi '_{+'}\) state to \(\Psi '_{-'}\). This can be computed directly by integrating the Eq. (18) after multiplying by \(\Psi '_{-'}\) from the left and ignoring the contributions from the other states – producing, up to \(\mathcal {O}(v)\),

$$\begin{aligned} E_{12}= & {} \int dx\, \Psi '^{\dag }_{-'} (H-i\partial _{t}) \Psi '_{+'} \end{aligned}$$
(19)
$$\begin{aligned}= & {} \int dx\, \Psi ^{\dag }_{-'}(H-i\partial _{t})\Psi _{+'}+ \frac{v}{2}\left[ \int dx\,\Psi ^{\dag }_{-'}H\sigma _{2}\Psi _{-'}\right. \nonumber \\{} & {} \left. + \int dx\, \Psi ^{\dag }_{+'}\sigma _{2}H\Psi _{+'}\right] \end{aligned}$$
(20)
$$\begin{aligned}= & {} \frac{v}{2}\left[ \int dx\,\Psi ^{\dag }_{-'}(-i\partial _{x}+i\sigma _{3}g\phi )\Psi _{-'}\right. \nonumber \\{} & {} \left. + \int dx\, \Psi ^{\dag }_{+'}(-i\partial _{x}-i\sigma _{3}g\phi )\Psi _{+'}\right] \end{aligned}$$
(21)
$$\begin{aligned}= & {} \frac{v}{2}\left[ \int dx\,\frac{-i}{2}\partial _{x}(\mid \Psi _{-'}\mid ^2+\mid \Psi _{+'}\mid ^2)\right. \nonumber \\{} & {} \left. + \int dx\, ig\phi (\Psi _{-'}^{\dag }\Psi _{+'}-\Psi _{+'}^{\dag }\Psi _{-'})\right] \end{aligned}$$
(22)
$$\begin{aligned}= & {} 0. \end{aligned}$$
(23)

A similar computation starting from the state \(\Psi '_{-'}\) also naturally yields a null result for the tunneling parameter which is responsible for producing state transitions. Hence, we actually do not get any fermion-antifermion pair production due to the motion of the soliton background. Moreover, extending the calculation to all orders in v does not change this result. This may point towards the need to include the more distant states that we initially neglected in our decomposition; or, more likely, such transition simply do not occur unless the solitons are not just moving, but accelerating. In retrospect, this might not actually look like a surprising result, because a fermion-antifermion pair is of opposite parity compared with the vacuum; therefore, since the perturbation is parity even, the transition rate should be zero. However, this provides a nice consistency check, showing that this method reproduces the null result anticipated from parity and Lorentz symmetry arguments, and yet a generalization of this calculation will give us non-zero amplitude when we introduce a third kink in the background; we shall discuss this interesting case in Sect. 5.

4 A stationary three-soliton system

Since relative motion of the two-soliton background does not lead to any changes in the occupation number for the almost-zero-energy fermion modes at leading order in the relative velocity, it makes sense to look instead at more elaborate backgrounds – particularly ones that lack the reflection symmetry of the two-soliton system. To this end, suppose we have kink at \(x_{K1}\), then an antikink at \(x_{A}\), and then additionally another kink at \(x_{K2}\), with \(x_{K1}<x_{A}<x_{K2}\) and a separation in distance scales: \((x_{K2}-x_{K1})\gg (x_{A}-x_{K1})\). In our further calculations we shall denote \(x_{K2}-x_{K1}\) and \(x_{A}-x_{K1}\) by \(\Delta _{2}\) and \(\Delta _{1}\), respectively. In the next section, when we shall be dealing with the kink at \(x_{K2}\) moving towards \(x_{A}\), we use \(x_{K2'}=x_{K2}-vt\) (again working only up to first order in velocity) and similarly \(\Delta '_{2}=\Delta _{2}-vt\). It can be seen that there are two separate small parameters, \(e^{-g\Delta _{1}}\) and \(e^{-g\Delta _{2}}\), which are independent of each other. Our calculation will neglect everything beyond first order of these parameters, including terms such as \(e^{-g(\Delta _{1}+\Delta _{2})}\) and \(e^{-2g\Delta _{2}}\). We would like to be able to treat the presence of the kink at \(x_{K2}\) as a perturbation to the tighter system consisting of the kink at \(x_{K1}\) and the antikink at \(x_{A}\).

With the introduction of the third kink, we anticipate there should be three almost-zero-energy states: one each with positive and negative energies and one exact zero-energy fermion state. [The existence of the exact zero mode is guaranteed topologically whenever the limiting values \(\phi (-\infty )\) and \(\phi (+\infty )\) of the scalar background have opposite signs.] The new positive- and negative-energy states should represent perturbed versions of the previous \(\Psi _{+}\) and \(\Psi _{-}\) and states of the two-soliton system. Hence we expect the new ground and upper excited state to be in the forms

$$\begin{aligned} \Psi _{g}= & {} \Psi _{-} + \frac{1}{\sqrt{2}}b_{g}\Psi _{K2}=\frac{1}{\sqrt{2}} \left[ \begin{array}{c}\psi _{K1}+b_{g} \psi _{K2}\\ \psi _{A} \end{array}\right] \end{aligned}$$
(24)
$$\begin{aligned} \Psi _{e}= & {} \Psi _{+} + \frac{1}{\sqrt{2}}b_{e}\Psi _{K2}= \frac{1}{\sqrt{2}}\left[ \begin{array}{c}\psi _{K1}+b_{e} \psi _{K2}\\ -\psi _{A} \end{array}\right] \!; \end{aligned}$$
(25)

and the zero-energy wave function may be computed exactly using the soliton profile \(\phi = \phi _{K1}+\phi _{A}+\phi _{K2}= \tanh (x-x_{K1})-\tanh (x-x_{A})+\tanh (x-x_{K2})\), revealing

$$\begin{aligned} \Psi _{0,\text {exact}}=\left[ \begin{array}{c} \frac{{{\,\textrm{sech}\,}}^{g}(x-x_{K1}){{\,\textrm{sech}\,}}^{g}(x-x_{K2})}{{{\,\textrm{sech}\,}}^{g}(x-x_{A})} \\ 0 \end{array}\right] \!. \end{aligned}$$
(26)

(Note that this wave function is not normalized.)

We can see that the zero-mode wave function is localized mostly around \(x_{K2}\), away from which its amplitude is exponentially damped – although there also is a smaller peak at \(x_{K1}\). This state is therefore mostly composed of \(\Psi _{K2}\), with the other kink and the antikink acting as perturbations. We thus expect to be able to write this zero-energy state as, at least approximately,

$$\begin{aligned} \Psi _{0}=\left[ \begin{array}{c}c_{1}\psi _{K1}+c_{2}\psi _{K2} \\ 0 \end{array}\right] \!. \end{aligned}$$
(27)

To compute these parameters \(c_{1}\) and \(c_{2}\), we should simply equate \(\Psi _{0,\text {exact}}\) and \(\Psi _{0}\) at the peak locations \(x_{K1}\) and \(x_{K2}\). At \(x_{K2}\), equating these two and neglecting the term \(c_{1}\psi _{K1}\), as this is \(\mathcal {O}\left( e^{-2g\Delta _{2}}\right) \) in this vicinity,

$$\begin{aligned} c_{2}= & {} \frac{{{\,\textrm{sech}\,}}^{g}(x_{K2}-x_{K1})}{{{\,\textrm{sech}\,}}^{g}(x_{K2}-x_{A})}+ \mathcal {O}\left( e^{-2g\Delta _{2}}\right) \end{aligned}$$
(28)
$$\begin{aligned}\approx & {} e^{-g(x_{A}-x_{K1})} \end{aligned}$$
(29)
$$\begin{aligned}= & {} e^{-g\Delta _{1}}. \end{aligned}$$
(30)

Similarly, equating the two expressions for the wave function at \(x_{K1}\), we get

$$\begin{aligned} c_{1}= & {} \frac{{{\,\textrm{sech}\,}}^{g}(x_{K1}-x_{K2})}{{{\,\textrm{sech}\,}}^{g}(x_{K1}-x_{A})}+ \mathcal {O}\left( e^{-g(\Delta _{1}+\Delta _{2})}\right) \end{aligned}$$
(31)
$$\begin{aligned}\approx & {} e^{-g(x_{K2}-x_{A})} \end{aligned}$$
(32)
$$\begin{aligned}= & {} e^{-g(\Delta _{2}-\Delta _{1})}. \end{aligned}$$
(33)

Now, we normalize the wave function \(\Psi _{0}\) and the final result, to the necessary order, is

$$\begin{aligned} \Psi _{0}=\left[ \begin{array}{c} c\psi _{K1} +\psi _{K2} \\ 0 \end{array} \right] \!, \end{aligned}$$
(34)

where \(c=c_{1}/c_{2}=e^{-g(\Delta _{2}-2\Delta _{1})}\).

Finally, requiring that the discrete-state wave functions \(\Psi _{g}\), \(\Psi _{e}\), and \(\Psi _{0}\) all be mutually orthogonal fixes the remaining parameters to be \(b_{g}=b_{e}\equiv b = -(c+d)\), where,

$$\begin{aligned} d\equiv \int dx\, \psi _{K1}^{*}\psi _{K2}=(1+g\Delta _{2})e^{-g\Delta _{2}} \approx g\Delta _{2}e^{-g\Delta _{2}}, \end{aligned}$$
(35)

using that the step function approximation for the soliton profiles that we have employed in our calculations entail that we are in the \(g\Delta _{1}\), \(g\Delta _{2}\gg 1\) regime. Without taking the motion of the solitons into account, these are not only orthogonal but also stationary states – since for these eigenfunctions of a time-independent Hamiltonian, we must automatically have \(\int dx\, \Psi _{\xi }^{\dag }H\Psi _{\zeta }= 0\) (where \(\xi \) and \(\zeta \) may be e, g or 0), unless \(\xi =\zeta \). For the diagonal matrix elements (the energy expectation values), we have

$$\begin{aligned} \int dx\, \Psi _{\xi }^{\dag }H\Psi _{\xi }=\left\{ \begin{array}{ll} -ge^{-g\Delta _{1}}, &{} \xi =g \\ 0, &{} \xi =0 \\ ge^{-g\Delta _{1}}, &{} \xi =e \end{array} \right. \!\!. \end{aligned}$$
(36)

Further details of the calculations are given in Appendix B.

Now, circling back to our discussion from the end of Sect. 2, we shall try to understand what a local observer situated near \(x_{K1}\) would witness in this situation as the fermion modes’ time evolution proceeds. To understand this, note that evolution of \(\Psi _{K1}\) is given by

$$\begin{aligned} \Psi _{K1}(t)= \frac{1}{\sqrt{2}}\left( \Psi _{g}e^{iE_{+}t}+\Psi _{e}e^{-iE_{+}t}\right) -b\Psi _{0}. \end{aligned}$$
(37)

It is easy to see that as time passes, there is again the anticorrelated tunneling of a half-fermion and a half-antifermion at \(x_{K1}\), just as discussed at the end of Sect. 2. More importantly, for localized observations around \(x_{K1}\) the additional term \(b\Psi _{0}\) will bring about no significant change – since the wave function \(\Psi _{0}\) appearing in this term term is \(\mathcal {O}(e^{-2g\Delta _{2}})\) at \(x_{K1}\). So locally, the observer still sees tunneling of half-quanta with frequency \(E_{+}\), even after a stationary third soliton is introduced very far away.

5 When the faraway kink is moving

To find a system in which there are nontrivial fermion state transitions, we may let the more distant kink at \(x_{K2}\) now approach (moving with velocity v) the more compactly spaced kink-antikink pair. We will again perform calculations up to first order in this velocity. It is now convenient to define new co-ordinate \(x_{K2'}= x_{K2}-vt\). Our new basis states are \(\Psi _{\mp }\) and \(\Psi '_{0}\), where \(\Psi '_{0}\) is the Lorentz-boosted fermion state given by

$$\begin{aligned} \Psi '_{0}= & {} e^{-\frac{\eta }{2}\sigma _{2}}\Psi _{K2'} \end{aligned}$$
(38)
$$\begin{aligned}\approx & {} \left( 1-\frac{v}{2}\sigma _{2}\right) \Psi _{K2'}. \end{aligned}$$
(39)

We want to identify the approximate states that instantaneously represent the ground, excited, and zero-energy states of the system. For exact zero modes (and when the charge conjugation symmetry C is not broken [31]), we must still have the Jackiw–Rebbi fermion fractionalization; such states may be interpreted as representing a net \(n_{F}=\frac{1}{2}\) fermion present when they are occupied, versus \(n_{F}=-\frac{1}{2}\) when they are unoccupied. This happens as a result of the renormalization subtraction of the infinite number of fermions in the negative-energy Dirac sea. In order to perform this subtraction in a C-invariant fashion, a zero-energy state must be assigned half to the set of negative-energy sea states and half to the set of positive-energy states. As a consequence, whenever an odd number of solitons are present – so that the vacuum configurations at \(x=-\infty \) and \(x=+\infty \) are different – the fermion number eigenvalues will be half-integers.

Now, it is natural to expect that instantaneously the almost-zero-energy states should be represented by modifying the previous stationary states from depending on \(\Psi _{K2}\) to depending on the boosted \((1-\frac{v}{2}\sigma _{2})\Psi _{K2'}\) instead. This intuition is further supported by a calculation of the energies of these modified states, which match exactly with our previous results; the details are given in Appendix C. So our modified states are

$$\begin{aligned} \Psi '_{e}= & {} \Psi _{e}- \frac{b'v}{2\sqrt{2}}\sigma _{2}\Psi _{K2'} \end{aligned}$$
(40)
$$\begin{aligned} \Psi '_{g}= & {} \Psi _{g}- \frac{b'v}{2\sqrt{2}}\sigma _{2}\Psi _{K2'} \end{aligned}$$
(41)
$$\begin{aligned} \Psi '_{0}= & {} \Psi _{0}- \frac{v}{2}\sigma _{2}\Psi _{K2'}. \end{aligned}$$
(42)

It is understood that these depend on revised parameters parameters \(b'\) and \(c'\), each of which depends on the the instantaneous position of the faraway kink \(x_{K2}-vt\) and the instantaneous separation \(\Delta _{2}'=x_{K2'}-x_{K1}\) in the same way that b and c depended on \(\Delta _{2}\). This dependence enters both explicitly in the formulas (40) and (41), as well as implicitly – since the wave functions \(\Psi _{e}\) and \(\Psi _{g}\) include a \(\Psi _{K2}\) part and thus depend upon the instantaneous position of the moving kink. The wave functions \(\Psi '_{e}\) and \(\Psi '_{g}\) are no longer orthogonal to \(\Psi '_{0}\) on their own, and their values are given in the appendix. It might seem that the non-orthogonality might be avoided if one simply got rid of the \(-\frac{v}{2}\sigma _{2}\) term in the boost modification with \(\Psi _{K2'}\), keeping only the change in coordinates \(x_{K2'}= x_{K2}-vt\), which naively seems like a nonrelativistic change, whereas the \(-\frac{v}{2}\sigma _{2}\) term seemingly represents a relativistic effect coming from the boost. However, the only way the \(x_{K2'}\) differs from \(x_{K2}\) is through the effects of its time derivatives, which would always be associated with factors of the inverse speed of light (were that maintained as a dimensional parameter); hence they both represent relativistic corrections of the same order and thus must be included together. We also demonstrate in Appendix C that the occupation numbers of these states evolve in time, with a “tunneling” parameter

$$\begin{aligned} \lambda _{2}\equiv & {} \int dx\, \Psi '_{0}H \Psi '_{e}= \int dx\, \Psi '_{0}H \Psi '_{g}\nonumber \\= & {} -\frac{ig^2v}{\sqrt{2}}(\Delta _{2}'-\Delta _{1})e^{-g(\Delta _{2}'-\Delta _{1})}. \end{aligned}$$
(43)

Now, as the distant kink moves, let \(\Psi \) be a solution of Dirac equation. Resolving this into ground, excited, and zero-energy states,

$$\begin{aligned} \Psi = \alpha \Psi '_{e}+\beta \Psi '_{0}+\gamma \Psi '_{g}, \end{aligned}$$
(44)

the Dirac equation gives

$$\begin{aligned} 0= & {} (H-i\partial _{t})\Psi \end{aligned}$$
(45)
$$\begin{aligned}= & {} -i\dot{\alpha }\Psi '_{e}+\alpha (H-i\partial _{t})\Psi '_{e}-i\dot{\beta }\Psi '_{0}+ \beta (H-i\partial _{t})\Psi '_{0}\nonumber \\{} & {} -i\dot{\gamma }\Psi '_{g}+\gamma (H-i\partial _{t})\Psi '_{g} \end{aligned}$$
(46)
$$\begin{aligned}= & {} (-i\dot{\alpha }+E_{+}\alpha +\tau \beta )\Psi '_{e}+ \left[ -i\dot{\beta }-(\alpha +\gamma )\tau \right] \Psi '_{0}\nonumber \\{} & {} +(-i\dot{\gamma }-E_{+}\gamma +\tau \beta )\Psi '_{g}. \end{aligned}$$
(47)

We have used results from Appendix C to get these final equations. The parameter \(\tau \) is derived in the appendix and has the value \(\tau =-\frac{igv}{\sqrt{2}}e^{-g(\Delta _{2}'-2\Delta _{1})}\). The key fact about \(\tau \) is that it is \(\mathcal {O}(v)\). Keeping terms up to this order, it can be shown that

$$\begin{aligned} -i\dot{\alpha }+E_{+}\alpha +\tau \beta= & {} 0 \end{aligned}$$
(48)
$$\begin{aligned} -i\dot{\beta }-\tau (\alpha +\gamma )= & {} 0 \end{aligned}$$
(49)
$$\begin{aligned} -i\dot{\gamma }-E_{+}\gamma +\tau \beta= & {} 0 \end{aligned}$$
(50)

If we are interested in the problem of a fermionic quantum that begins primarily in the instantaneous zero-mode (largely localized around \(x_{K2}\)), but which may subsequently tunnel into the other states, we may take the the initial value of the zero-mode amplitude \(\beta \) to be a \(\beta _{0}\), compared to which the other initial values \(\alpha _{0}\) and \(\gamma _{0}\) may be small. We can now directly integrate (48–50) to obtain,

$$\begin{aligned} \alpha (t)\approx & {} \alpha _{0}e^{-iE_{+}t}-\frac{\beta _{0}\tau }{E_{+}}\left( 1-e^{-iE_{+}t}\right) \end{aligned}$$
(51)
$$\begin{aligned} \gamma (t)\approx & {} \gamma _{0}e^{iE_{+}t}-\frac{\beta _{0}\tau }{E_{+}}\left( 1-e^{iE_{+}t}\right) . \end{aligned}$$
(52)

(Further details of this calculation are shown in Appendix D.) This solution, given this kind of initial configuration, should be valid so long as \(t\ll e^{g\Delta _{2}'}\). However, if t is too great, then naturally we will need a higher-order calculation.

To see how the quanta move from state to state, consider a configuration in which initially only \(\Psi '_{0}\) is occupied: \(\beta _{0}=1\), \(\alpha _{0}=0\) and \(\gamma _{0}=0\). The total fermion number in this state is \(-\frac{1}{2}\). Under the global interpretation, assigning fermion versus antifermion identity to the delocalized instantaneous energy eigenstates, this fermion content may be interpreted as consisting of one whole antifermion (corresponding to the unoccupied negative-energy mode \(\Psi _{g}'\)) and half a fermion (from the occupied \(\Psi _{0}'\)). It can be seen from (51–52) that the time evolution gives rise to nonzero occupation amplitudes \(\alpha \) and \(\gamma \), indicating a reshuffling of the fermion states. A state in which solely \(\Psi '_{e}\) is occupied also has fermion number \(-\frac{1}{2}\), but it is made up of one fermion (occupied \(\Psi '_{e}\)), a half antifermion (unoccupied \(\Psi '_{0}\)) and one antifermion (the empty \(\Psi '_{g}\)). Finally, when \(\Psi '_{g}\) is occupied, the state is made up of just half an antifermion (since \(\Psi '_{0}\) is unoccupied) and thus possesses the same fermion number \(-\frac{1}{2}\).

The fermion number is necessarily conserved when the single occupying Dirac quantum tunnels between states – from the initial zero-energy state to either the excited or the ground state. However, when it transitions to filling the excited state, this can be interpreted (globally) as the creation of production of a novel pair: a half fermion and a half-antifermion. Likewise, when it transitions to filling the negative-energy ground state, then there is destruction of half-fermion-plus-half-antifermion pair. This is an interesting new structure for particle production through soliton interactions. In the Dirac sector, the excitations produced by the relative motions of the kinks are – according to this interpretation – dominated by creation and annihilation of bound half-particle pairs.

However, it is also interesting to consider whether there is any change in the picture seen by the local observer at \(x_{K1}\) who observed the simultaneous tunneling of a half-fermion and half-antifermion each back and forth between the local kink and the nearby antikink (as discussed at the end of Sects. 2 and 4). To address this, we note that if at \(t=0\) the local observer sees the fermion mode attached to the kink at \(x_{K1}\) filled, this wave function has the decomposition \(\Psi _{K1}=\frac{1}{\sqrt{2}}(\Psi '_{e}+\Psi '_{g})-b\Psi '_{0}\). However, the time dependence of \(\Psi _{K1}\) is now more complicated than (37). The occupation amplitudes evolve according to (51–52), with the initial condition \(\alpha _{0}= \gamma _{0}= \frac{1}{\sqrt{2}}\) and \(\beta _{0}= -b\). Solving this to the order to which we have been working, the coefficient of \(\Psi '_{e}\) becomes \(\alpha =\frac{1}{\sqrt{2}}e^{-iE_{+}t}-\mathcal{O}(e^{-2\,g\Delta _{2}})\approx \frac{1}{\sqrt{2}}e^{-iE_{+}t}\), which is still effectively the same result as in Sects. 2 and 4. So if the single occupying fermion is initially localized around \(x_{K1}\), the local observer sees minimal change to the oscillatory behavior. However, we also note that in this particular case, (51–52) do not show any evidence of transitions between \(\Psi _{K1}\) and \(\Psi _{A}\), hence the unchanged result is perhaps not so surprising. On the other hand, we know that if \(\beta _{0}=1\) and \(\alpha _{0}=\gamma _{0}=0\), then there is a local influx of half-fermion density to \(x_{K1}\) and \(x_{A}\). With these initial conditions, the local observer at \(x_{K1}\) sees that there is some amplitude representing tunneling of a half fermion toward \(x_{K1},\) but it is suppressed by a factor proportional to \(ve^{-g\Delta _{2}}\) and oscillates with a frequency \(E_{+}\). More precisely, the coefficient of \(\Psi _{K1}\) as the time evolves is proportional to \(-\frac{\sqrt{2}\tau }{E_{+}}(1-\cos {E_{+}t})+b\). Note that \(\tau \) is imaginary, whereas b is real. The imaginary contribution may be interpreted as coming from the production of a pair with a half-fermion and half-antifermion. This exotic pair production leads to a (nonzero but exponentially suppressed) tunneling amplitude for the half-fermion over to the vicinity of \(x_{K1}\).

We previously mentioned the potential similarity between this kind of pair production and a Landau–Zener transition. However, the amplitudes we have found cannot be directly connected to the Landau–Zener formula – which says that for two states \(\phi _{1}\) and \(\phi _{2}\), with energies \(E_{1}\) and \(E_{2}\) that approach very close together, the probability of the adiabatic approximation being violated by a transition is \(1-e^{-2\pi \Gamma }\), where \(\Gamma =2\pi H_{12}^2/[\partial _{t}(E_{1}-E_{2})]\), in terms of the off-diagonal matrix element of the Hamiltonian \(H_{12}\). In the limit in which \(H_{12}\) is small, the non-adiabatic transition probability is approximately \(2\pi \Gamma \), which differs in form from the squares of the transition terms in (51–52), which are proportional to \(v^{2}\). Although there is a common exponential suppression of the transition rate (\(\tau \) being an exponentially small function of the system parameters), there are also several reasons apparent for this dissimilarity. The difference in energies is not strongly-enough time dependent to our order of calculation (as shown in Appendix C); thus there is no avoided crossing of two levels that have otherwise stable energies in the \(t\rightarrow \pm \infty \) limits (unless perhaps a kink and an anti-kink actually collide; but that is a situation well outside the limits of our approximation regime). In fact, the Landau–Zener formula assumes that we are effectively studying the evolution of a system from the ultimate past to the ultimate future, which for the present system under consideration would necessitate the inclusion of higher-order terms that we have uniformly neglected. Nevertheless, the system of solitons and attached fermion modes does have all the key elements which come together produce Landau-Zener transitions in other situations. The off-diagonal Hamiltonian terms are present, and the differences in energy levels do vary in time, as shown in Sect. 3. In fact, at intermediate times, the solutions of the coupled differential Eq. [4] for the coefficients \(C_{1}\) and \(C_{2}\) of the two aforementioned states \(\phi _{1}\) and \(\phi _{2}\) can, with a similar choice of initial conditions, look exactly like (51–52). In short, the transition amplitudes we have computed are physically similar to those in the Landau-Zener problem, but integrated only up through an intermediate time scale.

It is also natural to ask what the charge-conjugate analogue of (51–52) would be. To answer this, we shall need to construct wave functions analogous to \(\Psi _{e}\), \(\Psi _{g}\), and \(\Psi _{0}\), but for which the global fermion number is \(n_{F}=+\frac{1}{2}\). These are states for which exactly two of the fermion modes localized around \(x_{K1}\), \(x_{A}\), and \(x_{K2}\) are occupied; they are created by the action of two fermion creation operators upon the vacuum-like state in which all three of the almost-zero-energy modes are empty. We denote these new wave functions by \(\Psi _{Ce}\), \(\Psi _{C0}\), and \(\Psi _{Cg}\). Expressed as antisymmetrized two-particle wave functions for the two fermions that the operators create, they take the forms

$$\begin{aligned} \Psi _{Ce}(x_{1},x_{2})&= \frac{1}{\sqrt{2}}[\Psi _{g}(x_{1})\otimes \Psi _{0}(x_{2}) -\Psi _{0}(x_{1})\otimes \Psi _{g}(x_{2})]\nonumber \\ \Psi _{C0}(x_{1},x_{2})&= \frac{1}{\sqrt{2}}[\Psi _{g}(x_{1})\otimes \Psi _{e}(x_{2}) -\Psi _{e}(x_{1})\otimes \Psi _{g}(x_{2})]\nonumber \\ \Psi _{Cg}(x_{1},x_{2})&= \frac{1}{\sqrt{2}}[\Psi _{0}(x_{1})\otimes \Psi _{e}(x_{2}). -\Psi _{e}(x_{1})\otimes \Psi _{0}(x_{2})]. \end{aligned}$$
(53)

The Hamiltonian anticommutes with charge conjugation, and since \(H\Psi _{e}=E_{+}\Psi _{e}\), the corresponding charge conjugated version of this equation ought to be \(H\Psi _{Ce}=-E_{+}\Psi _{Ce}\). Using the decomposition \(H= H_{1}\otimes I+I\otimes H_{2}\) of the Hamiltonian into single-particle Dirac operators, it can be straightforwardly checked that it is indeed true. When the third kink at \(x_{K2}\) is in motion, then our two-particle wave functions become \(\Psi _{Ce}'\), \(\Psi _{C0}'\), and \(\Psi _{Cg}'\), analogously to the moving wave functions in the \(n_{F}=-\frac{1}{2}\) sector. We let \(\Psi \) be the wave function which solves the two-particle Dirac equation; supposing that only the almost-zero-energy modes are appreciably occupied, \(\Psi \) admits the decomposition,

$$\begin{aligned} \Psi = \alpha _{C}\Psi _{Ce}'+\beta _{C}\Psi _{C0}'+\gamma _{C}\Psi _{Cg}'. \end{aligned}$$
(54)

Acting on this with \((H-i\partial _{t})\Psi =0\) should give us three equations homologous to (48–50). In fact, a little bit of algebra demonstrates that the differential equations for the time evolution of \(\alpha _{C}\), \(\beta _{C}\), and \(\gamma _{C}\) are identical with those for \(\alpha \), \(\beta \), and \(\gamma \), except for the inversion of the Hamiltonian matrix elements, \(E_{+}\rightarrow E_{-}=-E_{+}\) and \(\tau \rightarrow -\tau \), providing a clear demonstration of the C invariance. As the kink at \(x_{K2'}\) approaches the other solitons (in whose vicinity the net number of fermion vanishes), the behavior of the system is essentially the same whether the faraway kink is carrying a half-fermion or a half-antifermion. Either half-quantum may tunnel over to the close kink-antikink region.

6 Conclusions and discussion

We have already stated that for the localized observer in the vicinity of \(x_{K1}\), (51) and (52) predict that with an initial condition of \(\Psi '_{0}\) being occupied (i.e. \(\beta =\beta _{0}\) and \(\alpha _{0}=\gamma _{0}=0\)), there is a tunneling amplitude for a half-fermion to arrive, and the tunneling rate also oscillates with frequency \(E_{+}\). It is fruitful, however, to discuss the different interpretations of this situation in terms of what different observers (operating at different spatiotemporal scales) would see, and to see how all their observations can be reconciled. In that spirit, consider another observer who is making partially localized measurements in the vicinity of the close kink-antikink pair; this observer can see quanta interacting over length scales of \(\mathcal {O}(\Delta _{1})\). In the the aforementioned scenario, what this observer sees does not require an understanding of half-fermion pairs – in contrast to the situation for the previous observer who was completely localized around \(x_{K1}\). The observer monitoring the whole kink-antikink region can describe any transitions in terms of two energy states equally displaced around zero. If this observer were to include the effect of all the other discrete and scattering states that we have neglected so far, then the observer would see a positive tower of states above \(\Psi _{e}\) and negative tower of states below \(\Psi _{g}\), but obviously no zero-energy state. The lack of a strictly-zero-energy mode means that, according to what this observer sees within their regional bailiwick, there should be no need to posit the existence of half-integer fermion numbers. When the zero energy state \(\Psi '_{0}\) is initially occupied, this observer initially sees one antifermion in the observation region (because of the essentilly unoccupied \(\Psi '_{g}\)), and the energy of the fermion field around the close kink-antikink system is consequently zero. There is neither attraction nor repulsion between these solitary waves due to the fermionic fields. If, after some time has passed, \(\Psi '_{e}\) becomes occupied, the kink-antikink observer sees this as one fermion having tunneled in from infinity, bringing with it enough energy to lift the total to from zero to \(E_{+}\). This local observer can furthermore see that now the close kink-antikink pair repel each other. On the other hand if \(\Psi '_{g}\) becomes occupied (which is equally likely) then the local observer sees that the existing antifermion has tunneled away from the region toward spatial infinity, and now the kink-antikink pair attract one-another due to virtual particle effects. In short, this observer either sees tunneling of a whole fermion towards the region, resulting in a fermion-antifermion pair; or the initially antifermion tunneling away, leaving the region in its local vacuum configuration.

In contrast, from the viewpoint of another local observer positioned at \(x_{K2'}\), there is initially a half-fermion present. To this observer, regardless of whether \(\Psi '_{e}\) or \(\Psi '_{g}\) becomes occupied, what is left behind at \(x_{K2'}\) is a half-antifermion. For this local observer, the half-fermion has tunneled away and a half-antifermion has tunneled inwards to replace it.

Finally, we may consider a fully delocalized observer who can see what is happening around all the solitary waves and is capable of observing delocalized states above \(\mathcal {O}(\Delta _{2})\) in size. Since the background scalar field \(\phi \) takes different vacuum expectation values at \(+\infty \) and \(-\infty \), this observer will know of the existence of a single exact zero mode, necessitating the existence of half-integral fermion numbers to describe the relevant physics. If this observer tried to write down a quantum field theory describing the quasiparticles of this theory, then due to the renormalization subtraction of the infinite number of fermions in the negative-energy Dirac sea, the observer would end up positing the existence of half-integral fermion numbers. This broadest observer must be capable of reconciling all the different interpretations seen by all the more localized observers we have talked about so far. For this delocalized observer, the occupation of \(\Psi '_{e}\) will represent tunneling of one full fermion, but the observer must account for the fact that there was only a single half-fermion localised around \(x_{K2'}\) to begin with. Therefore this observer may conclude that there has been creation of a half-fermion-and-half-antifermion pair. The half-antifermion appears at \(x_{K2'}\), while the half-fermion seemingly “merges” with the half-femrion that was initially located at \(x_{K2'}\) to become the full fermion that moves over to the close kink-antikink region. Similarly, when the time evolution leads to \(\Psi '_{g}\) being occupied, the initial antifermion localized around the close kink-antikink pair tunnels to the faraway kink at \(x_{K2'}\), and there half of it “annihilates” the half-fermion present, leaving the same net half-antifermion at \(x_{K2'}\) as in the previous case. In each of these transitions, a quantity of energy of magnitude \(E_{+}\) has been either added to or taken away from the fermion fields, depending precisely on whether the interpretation calls for the creation or destruction of a half-fermion-and-half-antifermion pair! The ultimate source or sink for this energy must be the motion of the solitary wave at \(x_{K2'}\).

We have computed the probability of production or destruction of exotic pairs that may be interpreted as consisting of one half-fermion and one half-antifermion each. Moreover, this kind of qualitative behavior seems like it should be ubiquitous in (\(1+1\))-dimensional systems containing odd numbers of \(\phi ^{4}\) solitons. Yet there is clearly plenty of room for improved understanding of these kinds of processes. For example, our calculations have entirely neglected the quantitative impact of higher-energy fermion and antifermion states, including the infinite collection of continuum states. These kinds of approximation cause problems at longer times. If the initial fermion wave function is a superposition of the ground and excited states, we do not find any creation of fermion-antifermion pairs; however, the total probability is not conserved, because we did not use a complete basis when expanding the image of the operator \((H-i\partial _{t})\) acting on the discrete eigenstates.

This shows that the multi-particle spectrum must be included if we are to understand the time evolution of such states fully. So performing analogous calculation with the inclusion of multi-particle states would be a natural way to extend this work. On the other hand, it would also be interesting to study whether the creation of pairs with full fermions and antifermions might actually take place, by extending our calculations to higher orders or by including additional solitons – while still working entirely within the manifold of almost-zero-energy states. Another issue that we have not yet addressed is related to the fact that that when the soliton at \(x_{K2}\) is set in motion, we have identified \(\Psi '_{\pm '}\) and \(\Psi '_{0}\) as the states with the same matter content as the states \(\Psi _{\pm }\) and \(\Psi _{0}\) of the stationary system. When the solitary waves are very far apart, so that the each individual wave functions do no significantly overlap, this is should be a valid approximation. For perturbative calculations, in which fermionic mode energies can simply be added up to find how the overall energy of the multi-soliton system is affected, this kind of identification makes logical sense. However, it is unclear what kinds of corrections we should expect – or if such identification is at all possible – when the solitary waves approach each other more closely, so that the wave functions overlap significantly, potentially giving rise to nontrivial interaction and exchange energies.

Since fractionalized states may also exist for configurations with fermions coupled to topologically nontrivial bosonic spin-0 and spin-1 fields in 3+1 dimensions (including monopoles [11, 32] and dyons [33]), it may be interesting to expand the kind of analysis performed in this paper to such systems as well. However, with more than one spatial dimension, things obviously become quite a bit more complicated. There are more possibilities for how three (or more) solitons may be positioned in space, and the spin structure of the fermion field adds another complicating factor. The presence of the spin quantum number in 3+1 dimensions introduces additional potential degeneracy; depending on precisely how the solitonic gauge fields are coupled to the Dirac field, it seems that there may or may not be multiple exact zero-energy modes in the presence of two or more solitary wave structures [34]. In fact, there is probably quite a bit of information left to be teased out about these systems, and addressing these various additional questions, whether in \(1+1\) or \(3+1\) dimensions, may provide deeper insights into the dynamics of systems with fermions, spontaneous symmetry breaking, and topologically nontrivial bosonic field configurations more generally.