Fermion-soliton scattering in a modified $\mathbb{C}\mathbb{P}^{1}$ model

Abstract

The scattering of fermions in the background field of a topological soliton of the modified $(2 + 1)$-dimensional $\mathbb{C}\mathbb{P}^{1}$ model is studied here both analytically and numerically. Unlike the original $\mathbb{C}\mathbb{P}^{1}$ model, the Lagrangian of the modified model contains a potential term. Due to this, a dilatation zero mode of the topological soliton disappears, which results in stability of the fermion-soliton system. The symmetry properties of the fermion-soliton system are established, and the asymptotic forms of fermionic radial wave functions are studied. Questions related to the bound states of the fermion-soliton system are then discussed. General formulae describing the scattering of fermions are presented. The amplitudes of the fermion-soliton scattering are obtained in an analytical form within the framework of the Born approximation, and their symmetry properties and asymptotic forms are studied. The energy levels of the fermionic bound states and the partial phase shifts of fermionic scattering are obtained by numerical methods, and the ultrarelativistic limits of the partial phase shifts are found.

1 Introduction

Spatially localised nondissipative solutions with finite energy and nontrivial topology exist in many models of field theory [1,2,3]. Known as topological solitons, these solutions play an important role in field theory, high-energy physics, condensed matter physics, cosmology, and hydrodynamics. Among these, we can distinguish a class of planar topological solitons of $(2 + 1)$-dimensional field models. The vortices of the effective theory of superconductivity [4] and of the $\left( 2 + 1\right)$-dimensional Abelian Higgs model [5] are probably the best known planar topological solitons. The topological soliton of the $(2+1)$-dimensional nonlinear $O\left( 3\right)$ sigma model, called a lump, is another well-known example of a planar topological soliton [6].

Nonlinear sigma models can also be formulated for orthogonal groups O(N) with $N \ge 4$, but unlike the O(3) sigma model, these models have no topological solitons. There is also another family of nonlinear field models whose properties are similar to those of the nonlinear O(N) sigma models in many respects; these are the so-called $\mathbb{C}\mathbb{P}^{N - 1}$ models [7,8,9,10]. For $N = 2$, the $\mathbb{C}\mathbb{P}^{1}$ model is equivalent to the O(3) sigma model, whereas for $N \ge 3$, the $\mathbb{C}\mathbb{P}^{N - 1}$ model is a better generalisation of the O(3) sigma model than the $O(N+1)$ sigma model, as it continues to have topological soliton solutions [11, 12].

Soon after their appearance in the late 1970s, it was realised that two-dimensional $\mathbb{C}\mathbb{P}^{N - 1}$ models could be used to study nonperturbative effects in four-dimensional Yang–Mills models, as these two types of models have many properties in common, such as conformal invariance at the classical level, asymptotic freedom in the ultraviolet region [13], and strong coupling in the infrared region. Furthermore, a topological term and instanton solutions [11, 12] exist for two types of models, resulting in a complex structure of the vacuum at the quantum level. It is clear that the lower dimensionality of the $\mathbb{C}\mathbb{P}^{N - 1}$ models simplifies the analysis of nonperturbative effects in the strong coupling regime compared to the more complex four-dimensional Yang–Mills models.

Two-dimensional $\mathbb{C}\mathbb{P}^{N-1}$ models can be used to describe low-energy dynamics on the world sheet of non-Abelian vortex strings in a class of four-dimensional gauge theories [14,15,16,17,18,19]. In addition, $\mathbb{C}\mathbb{P}^{N - 1}$ models have interesting applications in various fields of condensed matter physics [20], and particularly in relation to ferromagnetism, the Hall effect, and the Kondo effect. They also find application in the study of the fermion number violation realised via a sphaleron transition at high temperature [21].

The static energy functional of the $(2+1)$-dimensional $\mathbb{C}\mathbb{P}^{1}$ model is invariant under scale transformations, meaning that the soliton solutions of the model (lumps) depend on an arbitrary scale parameter that determines the soliton size. At the same time, the energy of a lump does not depend on its spatial size. As a result, in addition to two translational zero modes, the lump also possesses a dilatation zero mode. This is a source of instability of the lump in dynamic processes, since collisions between lumps or interactions between the lump and bosonic and fermionic fields can lead to the radius of the lump tending either to zero or to infinity [22,23,24,25].

There are several ways in which the $\mathbb{C}\mathbb{P}^{1}$ model can be modified to remove the size instability of a lump. One of them, which was proposed in Ref. [26], involves adding a potential term of a certain type to the Lagrangian of the original $\mathbb{C}\mathbb{P}^{1}$ model. This breaks the scale invariance of the original model, leading to the disappearance of the dilatation zero mode. At the same time, it follows from Derrick’s theorem [27] that there can no longer be static lump solutions, since the potential term will cause them to collapse. However, it was shown in Ref. [26] that time-dependent lump solutions can be constructed in this case. These solutions, called Q-lumps due to their similarities with Q-balls [28], have the same form as the original lumps of the $\mathbb{C}\mathbb{P}^{1}$ model, except that their phase changes linearly with time. Due to this, Q-lumps carry a conserved Noether charge, which prevents them from collapsing.

The $\mathbb{C}\mathbb{P}^{N-1}$ models can be extended to include fer- mionic fields, either by a supersymmetric extension of the $\mathbb{C}\mathbb{P}^{N - 1}$ model [7, 12, 29] or by minimal coupling between fermionic fields and a composite gauge field of the $\mathbb{C}\mathbb{P}^{N - 1}$ model [30]. The supersymmetric extension of the $\mathbb{C}\mathbb{P}^{N-1}$ model involves Majorana fermionic fields that satisfy nontrivial constraints, whereas the minimal model deals with unconstrained Dirac fermionic fields. In the present paper, we study, within the background field approximation, a fermion-soliton system of the $\mathbb{C}\mathbb{P}^{1}$ model with a potential term. In this model, Dirac fermionic fields interact minimally with a composite gauge field. The results obtained here can be used to describe the interaction between fermions and two-dimensional or thread-like three-dimensional topological defects in condensed matter physics.

This paper is structured as follows. In Sect. 2, we briefly describe the Lagrangian, symmetries, field equations, and topological solitons of the modified $\mathbb{C}\mathbb{P}^{1}$ model. In Sect. 3, we explore fermion-soliton scattering within the background field approximation. We establish the symmetry properties of the fermion-soliton system, and study the asymptotic forms of fermionic radial wave functions. We also consider some questions concerning fermionic bound states, and present general formulae for fermion-soliton scattering. In Sect. 4, we present an analytical description of fermion scattering within the framework of the Born approximation. In Sect. 5, we present numerical results, based on which we obtain several analytical expressions related to fermion-soliton scattering. In particular, we find expressions for the fermionic partial phase shifts in the ultrarelativistic limit. In the final section, we briefly summarise the results obtained in the present work. In Appendix A, we derive expressions for the fermionic partial phase shifts in the semiclassical approximation.

Throughout the paper, the natural units $c = 1$ and $\hbar = 1$ are used.

2 Lagrangian, field equations and topological solitons of the model

The Lagrangian density of the model considered here has the form

$$\begin{aligned} \mathcal {L}= & {} g^{-1}\left( D_{\mu }n_{a}\right) ^{*}D^{\mu }n_{a}-g^{-1}U\left( \left| n_{1}\right| ,\left| n_{2}\right| \right) \nonumber \\{} & {} +i\bar{\psi }_{a}\gamma ^{\mu }D_{\mu }\psi _{a} - M\bar{\psi } _{a}\psi _{a}, \end{aligned}$$

(1)

where g is a coupling constant, $n_{a}$ is a complex scalar isodoublet, $\psi _{a}$ is the Dirac fermionic isodoublet, and M is the fermionic mass. In Eq. (1), the complex scalar isodoublet is under the constraint $n_{a}^{*}n_{a} = 1$, the quartic potential term

$$\begin{aligned} U\left( \left| n_{1}\right| ,\left| n_{2}\right| \right)= & {} 2^{-2}\alpha ^{2}\left[ 1-\bigl ( \left| n_{1}\right| ^{2}-\left| n_{2}\right| ^{2}\bigr ) ^{2}\right] \nonumber \\= & {} \alpha ^{2}\left| n_{1}\right| ^{2}\left| n_{2}\right| ^{2}, \end{aligned}$$

(2)

where $\alpha$ is a parameter with the dimension of mass, and the covariant derivatives of the fields are defined as

$$\begin{aligned} D_{\mu }n_{a}= & {} \partial _{\mu }n_{a} + i A_{\mu }n_{a} \end{aligned}$$

(3a)

$$\begin{aligned} \text {and}{} & {} \nonumber \\ D_{\mu }\psi _{a}= & {} \partial _{\mu }\psi _{a} + i A_{\mu }\psi _{a}, \end{aligned}$$

(3b)

where $A_{\mu }$ is a vector gauge field. The Lagrangian density in Eq. (1) describes the $\mathbb{C}\mathbb{P}^{1}$ model that possesses the quartic potential $U\left( \left| n_{1}\right| , \left| n_{2}\right| \right)$ and interacts minimally with the fermionic isodoublet $\psi _{a}$. The choice of potential (2) is due to the fact that in this case, all soliton solutions of model (1) can be obtained in analytical form, which facilitates the study of fermion-soliton systems. Note that quartic potential (2) is equivalent to the quadratic potential used in Ref. [26] in the context of the nonlinear O(3) sigma model.

The field equations for model (1) are obtained by varying the action $S = \int \mathcal {L}d^{2}xdt$ in the fields $n_{a}$, $\bar{\psi }_{a}$, and $A_{\mu }$, and taking into account the constraint $n_{a}^{*}n_{a} = 1$ by means of the Lagrange multiplier method:

$$\begin{aligned} D_{\mu }D^{\mu }n_{a}-\left( n_{b}^{*} D_{\mu }D^{\mu }n_{b}\right) n_{a}+ \mathcal {P}_{ab} \partial _{n_{b}^{*}}U= & {} 0, \end{aligned}$$

(4)

$$\begin{aligned} \left( i\gamma ^{\mu }D_{\mu }-M\right) \psi _{a}= & {} 0, \end{aligned}$$

(5)

$$\begin{aligned} A_{\mu }-in_{a}^{*}\partial _{\mu }n_{a}-\frac{g}{2}\bar{\psi } _{a}\gamma _{\mu }\psi _{a}= & {} 0, \end{aligned}$$

(6)

where the projector $\mathcal {P}_{ab} = \mathbb {I}_{ab} - n_{a}n_{b}^{*}$. Equation (6) tells us that that the gauge field $A_{\mu }$ is expressed in terms of the fields $n_{a}$ and $\psi _{a}$, meaning that it is not dynamic but auxiliary.

In the absence of the potential term, the Lagrangian (1) is invariant under transformations of a $SU(2)\times U(1)$ group, where the first (second) factor corresponds to global (local) transformations. The presence of the potential term leads to breaking of the SU(2) global factor to a U(1) subgroup corresponding to the generator $t_{3}=\tau _{3}/2$, whereas the U(1) gauge factor remains unbroken. The Noether currents that correspond to the first and second factors of the symmetry group $U(1)\times U(1)$ are

$$\begin{aligned} j_{3}^{\mu }= & {} - i g^{-1}\text {Tr}\left[ \tau _{3}n\overleftrightarrow {D} ^{\mu }n^{*}\right] +\text {Tr}\left[ \tau _{3}\bar{\psi }\gamma _{\mu }\psi \right] \end{aligned}$$

(7)

$$\begin{aligned} \text {and}{} & {} \nonumber \\ j^{\mu }= & {} -ig^{-1}\text {Tr}\left[ n\overleftrightarrow {D}^{\mu }n^{*}\right] + \text {Tr}\left[ \bar{\psi }\gamma _{\mu }\psi \right] , \end{aligned}$$

(8)

respectively. In Eqs. (7) and (8), the trace is over the indices of the isodoublets n and $\psi$ and the Pauli matrix $\tau _{3}$.

Using the well-known formula $T_{\mu \nu }\!=\!2 \partial \mathcal {L}/\partial \eta ^{\mu \nu }\! - \eta ^{\mu \nu } \mathcal {L}$, we obtain the symmetric energy-momentum tensor for a bosonic field configuration of model (1) as

$$\begin{aligned} T_{\mu \nu }= & {} 2g^{-1}\left( D_{\mu }n_{a}\right) ^{*}D_{\nu }n_{a}-\eta _{\mu \nu }g^{-1} \nonumber \\{} & {} \times \left[ \left( D_{\sigma }n_{a}\right) ^{*}D^{\sigma }n_{a}-U\left( \left| n_{1}\right| ,\left| n_{2}\right| \right) \right] . \end{aligned}$$

(9)

Eq. (9) tells us that for the energy $E = \int T_{00}d^{2}x$ of a field configuration to be finite, the potential U must tend to zero at spatial infinity. It then follows from Eq. (2) that at spatial infinity, we have either $n_{1} = e^{i f_{1}\left( \theta \right) },\, n_{2}=0$ or $n_{1} = 0, \, n_{2} = e^{i f_{2}\left( \theta \right) }$, where $\theta$ is the polar angle and $f_{1,2}(\theta )$ are periodic functions of $\theta$. In any case, each finite energy field configuration of model (1) can be attributed to one of the classes of the homotopy group $\pi _{1}(S^{1}) = \mathbb {Z}$. Hence, the finite energy field configurations of model (1) can be labelled by an integer n, called the winding number, as explicitly given in Ref. [11]:

$$\begin{aligned} n = -\frac{1}{2\pi }\int \limits _{S^{1}}A_{i}dx^{i} = -\frac{1}{2\pi }\int \epsilon _{ij}\partial _{i}A_{j} d^{2}x, \end{aligned}$$

(10)

where $A_{i} = i n_{a}^{*} \partial _{i} n_{a}$ and $\epsilon _{i j}$ is the two-dimensional antisymmetric tensor with $\epsilon _{1 2} = 1$.

It follows from Derrick’s theorem [27] that the presence of the potential term excludes the existence of static soliton solutions in the $(2+1)$-dimensional model (1). At the same time, the presence of the potential term does not prohibit soliton solutions with nontrivial time dependence. Indeed, it can be shown that a rather specific form of the potential in Eq. (2) allows us to rewrite the obvious inequality

$$\begin{aligned}{} & {} \int \left[ \left( D_{i}n_{a}\pm i\epsilon _{ij}D_{j}n_{a}\right) ^{*}\left( D_{i}n_{a}\pm i\epsilon _{ij}D_{j}n_{a}\right) /2 +\right. \nonumber \\{} & {} \left. \left( \partial _{t}n_{a}+i\alpha \left( t_{3}\right) _{ab}n_{b}\right) ^{*}\left( \partial _{t}n_{a} + i \alpha \left( t_{3}\right) _{ab}n_{b}\right) \right] d^{2}x \ge 0\nonumber \\ \end{aligned}$$

(11)

in the form

$$\begin{aligned} E - 2 \pi g^{-1} \left| n\right| -\left| \alpha \right| \left| Q_{3}\right| /2 \ge 0, \end{aligned}$$

(12)

where $E = \int T_{00}d^{2}x$, $n = -(2\pi )^{-1} \int \epsilon _{ij}\partial _{i} A_{j} d^{2}x$, and $Q_{3} = - i g^{-1} \int \text {Tr} \bigl [\tau _{3} n \overleftrightarrow {D}^{\mu } n^{*}\bigr ] d^{2}x$ are the energy, the winding number, and the Noether charge of the field configuration, respectively. It follows from Eq. (11) that the saturation of inequality (12) is only possible for field configurations that satisfy the Bogomolny equations

$$\begin{aligned} \partial _{t}n_{a} + i \alpha \left( t_{3}\right) _{ab}n_{b}= & {} 0, \end{aligned}$$

(13)

$$\begin{aligned} D_{i}n_{a}\pm i\epsilon _{ij}D_{j}n_{a}= & {} 0. \end{aligned}$$

(14)

It can be shown that solutions to Eqs. (13) and (14) also satisfy field equation (4) if we neglect the contribution of the fermionic fields in Eq. (6).

Equation (13) determines the time dependence $n_{a} \left( t,\textbf{x} \right) = \exp \left[ -i \alpha t t_{3}\right] _{a b} n_{b}\left( \textbf{x}\right)$ of the field configurations, and Eq. (14) determines their spatial dependence. All solutions to Eq. (14) are well known [11, 12] and can be obtained in analytical form. In particular, the $\mathbb {Z}_{\left| n \right| }$ symmetric soliton solution with winding number n can be written as

$$\begin{aligned} n_{a}\left( t,\rho ,\theta \right) =\exp \left[ -i\alpha t t_{3} \right] _{ab} \frac{\lambda ^{\left| n\right| }u_{b}+\rho ^{\left| n\right| }e^{in\theta }v_{b}}{\left( \lambda ^{2\left| n\right| }+\rho ^{2\left| n\right| }\right) ^{1/2}}, \end{aligned}$$

(15)

where $\rho$ and $\theta$ are polar coordinates, $u^{T} = \left( 1,0\right)$ and $v^{T}=\left( 0, 1\right)$ are orthonormal isospinors, and $\lambda$ is a parameter that determines the effective size of the soliton.

Having obtained the analytical form in Eq. (15), we can derive analytical expressions for the auxiliary gauge field

$$\begin{aligned} A_{\mu }=n\frac{\rho ^{2\left( \left| n\right| -1\right) }}{\rho ^{2\left| n\right| }+\lambda ^{2\left| n\right| }}\left[ \frac{\alpha }{2n}\frac{\lambda ^{2\left| n\right| }-\rho ^{2\left| n\right| }}{\rho ^{2\left( \left| n\right| -1\right) }},y,-x\right] , \end{aligned}$$

(16)

the Noether charge

$$\begin{aligned} Q_{3}=\int j_{3}^{0}d^{2}x=\frac{4\pi ^{2}\alpha \lambda ^{2}}{gn^{2}\sin \left( \pi /\left| n\right| \right) }, \end{aligned}$$

(17)

and the energy

$$\begin{aligned} E = \int T_{00}d^{2}x = 2 \pi \left| n \right| g^{-1} + \alpha Q_{3}/2 \end{aligned}$$

(18)

of the soliton solution, where we factor out the common factor of the components of the auxiliary gauge field $A_{\mu }$ for brevity. Equations (17) and (18) tell us that $Q_{3}$ and E are infinite when the winding number $n = \pm 1$. Hence, there are no soliton solutions for $\left| n \right| = 1$, and $\left| n \right| = 2$ is the minimum possible value for the magnitude of the winding number. We note that $A_{0}$ does not depend on the sign of n but on the sign of $\alpha$, and that $\text {sign}(Q_{3}) = \text {sign}(\alpha )$, which implies that $\alpha Q_{3} > 0$. We also note that in Eq. (18), the topological part of the energy increases linearly with an increase in $\left| n \right|$, whereas the Noether (kinetic) part of the energy decreases monotonically and tends to zero $\propto \left| n \right| ^{-1}$ as $\left| n \right| \rightarrow \infty$.

From Eq. (18), we find that the derivative

$$\begin{aligned} dE/dQ_{3} = \alpha /2. \end{aligned}$$

(19)

We see that the derivative of the energy of the soliton with respect to its Noether charge is proportional to the phase frequency of rotation of the scalar isodoublet. This behavior is typical for all nontopological solitons, and in particular for the Q-balls [28]. In view of this similarity, the soliton solutions of model (1) are called Q-lumps [26].

It follows from Eq. (18) that in the absence of the potential ($\alpha = 0$), the energy E does not depend on the parameter $\lambda$ that determines the effective size of the soliton. In this case, the parameter $\lambda$ and soliton size are arbitrary, and the soliton solution has a dilatation zero mode. This situation changes in the presence of a potential ($\alpha \ne 0$); in this case, the Noether charge $Q_{3}$ and the energy E depend quadratically on $\lambda$. Since both $Q_{3}$ and E are conserved, the parameter $\lambda$ and the soliton size are fixed, and there is no dilatation zero mode in this case.

Equation (15) tells us that the soliton solution depends on the polar angle $\theta$ only via the combination $\phi = n \theta + \alpha t/2$. We see that a point of constant $\phi$ rotates with angular velocity $\omega = -\alpha /\left( 2 n\right)$. It follows that the soliton solution in Eq. (15) possesses angular momentum

$$\begin{aligned} J = \int J^{012} d^{2}x = \frac{4\pi ^{2}\lambda ^{2}\omega }{g\sin \left( \pi /\left| n\right| \right) }=-\frac{n}{2}Q_{3}, \end{aligned}$$

(20)

where the tensor $J^{\lambda \mu \nu } = x^{\mu } T^{\lambda \nu } - x^{\nu } T^{\lambda \mu }$. Unlike the Noether charge $Q_{3}$, the angular momentum J depends on the sign of the winding number n, and tends to the nonzero limit $-\text {sign}(n) 2\pi g^{-1}\alpha \lambda ^{2}$ as $\left| n \right| \rightarrow \infty$.

3 Fermion-soliton system in the background field approximation

A characteristic property of model (1) is that the auxiliary gauge field $A_{\mu } = i n_{a}^{*} \partial _{\mu } n_{a} + 2^{-1} g \bar{\psi }_{a} \gamma _{\mu } \psi _{a}$ is the sum of quadratic bosonic and fermionic terms. Hence, field equation (4) contains nonlinear terms that are quadratic and quartic in the fermionic fields. These terms describe the fermion backreaction on the bosonic soliton solution. Furthermore, the Dirac equation (5) also contains nonlinear (cubic) terms in the fermionic fields. A consistent description of these nonlinear fermionic terms is possible only within the framework of QFT.

Here, we consider the fermion-soliton system within the background field approximation, i.e., we neglect the fermionic term in $A_{\mu }$ in comparison with the bosonic term. In this case, the auxiliary gauge field $A_{\mu } = in_{a}^{*}\partial _{\mu } n_{a}$, there is no fermion backreaction on the soliton, and the Dirac equation (5) becomes linear in the fermionic field. Estimation of the bosonic and fermionic terms in Eq. (6) shows that neglecting this term is possible under the condition

$$\begin{aligned} g \ll a\varrho _{F}^{-1}, \end{aligned}$$

(21)

where $a = \min \left( \left| n \right| \lambda ^{-1}, \alpha \right)$ and $\varrho _{F}$ is the two-dimensional density of fermions in an incident plane wave. In addition, we can neglect the cubic fermionic terms in the Dirac equation (5) compared to the mass term under the condition

$$\begin{aligned} g \ll M \varrho _{F}^{-1}, \end{aligned}$$

(22)

where M is the fermion mass.

The estimates (21) and (22) were obtained from an analysis of the classical field equations in Eqs. (4)–(6). From the viewpoint of QFT, however, we are talking about the scattering of a fermion of mass M on a $\mathbb{C}\mathbb{P}^{1}$ soliton of mass $M_{\text {s}} = 2 \pi \left| n \right| g^{-1} + \alpha Q_{3}/2$. To enable the recoil of the $\mathbb{C}\mathbb{P}^{1}$ soliton to be neglected, the mass $M_{\text {s}}$ must be much larger than the energy $\varepsilon$ of the incident fermion, which leads to the inequality

$$\begin{aligned} g \ll F\varepsilon ^{-1} < F M^{-1}, \end{aligned}$$

(23)

where $F=2\pi \left| n\right| +2\pi ^{2}\alpha ^{2}\lambda ^{2}n^{-2}\csc \left( \pi /\left| n \right| \right)$ does not depend on g.

The conditions (21), (22), and (23) do not contradict each other, and can always be met if the coupling constant g is sufficiently small. In this case, the Dirac equation (5) is linear in the fermionic fields and can be written in the Hamiltonian form

$$\begin{aligned} i\partial _{t}\psi _{a}=H\psi _{a}, \end{aligned}$$

(24)

where the Hamiltonian

$$\begin{aligned} H = \mathbb {I}A_{0} + \alpha ^{k}\left( -i\partial _{k} + A_{k}\right) + \beta M, \end{aligned}$$

(25)

the Dirac matrices

$$\begin{aligned} \gamma ^{0}= \sigma _{3},\, \gamma ^{1}=-i\sigma _{1},\, \gamma ^{2}=-i\sigma _{2}, \end{aligned}$$

(26)

the matrices $\alpha ^{i} = \gamma ^{0}\gamma ^{i}$ and $\beta = \gamma ^{0}$, and $\mathbb {I}$ is the identity matrix. Equations (24)–(26) tell us that the isodoublet components $\psi _{1}$ and $\psi _{2}$ of the fermionic field interact in the same way with the soliton background field. Hence, we will not consider the isodoublet index of the fermionic field in the following.

The Dirac equation (24) possesses several discrete symmetries. Indeed, it can easily be shown that if $\psi (t,\textbf{x})$ is a solution to this equation, then

$$\begin{aligned} \psi ^{P}\left( t,\textbf{x}\right) =\sigma _{3}\psi \left( t, -\textbf{x}\right) , \end{aligned}$$

(27)

and

$$\begin{aligned} \psi ^{\varPi _{2}T}\left( t,x,y\right) =\psi ^{*}\left( -t,x,-y\right) \end{aligned}$$

(28)

are also solutions to this equation. Furthermore, the transformed spinor field

$$\begin{aligned} \psi ^{C}\left( t,\textbf{x}\right) =\sigma _{1}\psi ^{*}\left( t,\textbf{x}\right) \end{aligned}$$

(29)

is also a solution to the Dirac equation (24) provided that we substitute $A_{\mu }(\textbf{x}) \rightarrow A^{C}_{\mu }(\textbf{x}) = - A_{\mu } (\textbf{x})$ in the Hamiltonian (25). The solutions in Eqs. (27), (28), and (29) are obtained from the original solution $\psi (t, \textbf{x})$ by means of the P, $\varPi _{2}T$, and C transformations, respectively, where in the combined transformation $\varPi _{2}T$, the symbol $\varPi _{2}$ denotes reflection about the $Ox_{1}$ axis.

3.1 Fermionic radial wave functions

In Eq. (16), the time component $A_{0}$ of the auxiliary gauge field tends to the nonzero limit $-\alpha /2$ as $\rho \rightarrow \infty$, which is inconvenient when studying solutions to the Dirac equation (24). We therefore perform the U(1) gauge transformation $A_{\mu }\rightarrow A_{ \mu } - \partial _{\mu } \varLambda ,\, \psi \rightarrow e^{i \varLambda } \psi$, where $\varLambda = -\alpha t/2$. After this transformation, the spatial components $A_{1,2}$ remain unchanged, whereas the time component $A_{0} = \alpha \left( 1 - \rho ^{2\left| n\right| }/\left( \rho ^{2\left| n\right| }+\lambda ^{2\left| n\right| } \right) \right)$ tends to zero as $\rho \rightarrow \infty$. Hereafter, we shall use this gauge.

It is easily shown that the Hamiltonian (25) commutes with the angular momentum operator

$$\begin{aligned} J_{3} = -i\partial _{\theta } + \sigma _{3}/2, \end{aligned}$$

(30)

and that the common eigenfunctions of the operators H and $J_{3}$ have the form

$$\begin{aligned} \psi _{\varepsilon m}=\left( \begin{array}{c} e^{i\left( m - 1/2\right) \theta }f\left( \rho \right) \\ e^{i\left( m + 1/2\right) \theta }g\left( \rho \right) \end{array} \right) e^{-i \varepsilon t}, \end{aligned}$$

(31)

where $\varepsilon$ and m are the eigenvalues of H and $J_{3}$, respectively. Substitution of Eq. (31) into Eq. (24) leads to the following system of differential equations for the radial wave functions:

$$\begin{aligned} f^{\prime }\left( \rho \right)= & {} \rho ^{-1}\left( A_{mn}\left( \rho \right) -1/2\right) f\left( \rho \right) \nonumber \\{} & {} +\left( M+\varepsilon -\alpha B_{\left| n\right| }\left( \rho \right) \right) g\left( \rho \right) , \end{aligned}$$

(32)

$$\begin{aligned} g^{\prime }\left( \rho \right)= & {} \rho ^{-1}\left( -A_{mn}\left( \rho \right) -1/2\right) g\left( \rho \right) \nonumber \\{} & {} +\left( M-\varepsilon +\alpha B_{\left| n\right| }\left( \rho \right) \right) f\left( \rho \right) , \end{aligned}$$

(33)

where the coefficient functions are

$$\begin{aligned} A_{mn}\left( \rho \right)= & {} m-n+\frac{n\lambda ^{2\left| n\right| } }{\lambda ^{2\left| n\right| }+\rho ^{2\left| n\right| }} \end{aligned}$$

(34)

$$\begin{aligned} \text {and}{} & {} \nonumber \\ B_{\left| n\right| }\left( \rho \right)= & {} \frac{\lambda ^{2\left| n\right| }}{\lambda ^{2\left| n\right| }+\rho ^{2\left| n\right| }}. \end{aligned}$$

(35)

It follows from Eqs. (32)–(35) that the radial wave functions $f(\rho )$ and $g(\rho )$ are real modulo a common phase factor, since the coefficient functions $A_{mn}(\rho )$ and $B_{\left| n\right| }(\rho )$ are real.

It is easy to see that the wave function $\psi _{\varepsilon m}$ is an eigenfunction of the operators P and $\varPi _{2} T$:

$$\begin{aligned} \left[ \psi _{\varepsilon m n \alpha }\left( t,\textbf{x} \right) \right] ^{P}= & {} \left( -1\right) ^{m-1/2} \psi _{\varepsilon m n \alpha }\left( t,\textbf{x}\right) , \end{aligned}$$

(36)

$$\begin{aligned} \left[ \psi _{\varepsilon m n \alpha }\left( t,\textbf{x}\right) \right] ^{\varPi _{2}T}= & {} \psi _{\varepsilon m n \alpha }\left( t,\textbf{x}\right) , \end{aligned}$$

(37)

where the parameters n and $\alpha$ of the soliton background field are indicated, and the radial wave functions $f(\rho )$ and $g(\rho )$ are assumed to be real. At the same time, the charge conjugation C transforms the wave function $\psi _{\varepsilon m n \alpha }$ as follows:

$$\begin{aligned} \left[ \psi _{\varepsilon m n \alpha }\left( t,\textbf{x} \right) \right] ^{C} = \psi _{-\varepsilon \,-m\,-n\,-\alpha }\left( t,\textbf{x}\right) , \end{aligned}$$

(38)

where in the C-transformed wave function

$$\begin{aligned} \psi _{-\varepsilon \,-m\,-n\,-\alpha }\left( t, \textbf{x} \right) = \left( \begin{array}{c} e^{i\left( -m-1/2\right) \theta }g\left( \rho \right) \\ e^{i\left( -m+1/2\right) \theta }f\left( \rho \right) \end{array} \right) e^{i\varepsilon t}, \end{aligned}$$

(39)

the real radial wave functions $f(\rho )$ and $g(\rho )$ are permuted compared to Eq. (31).

Equation (38) tells us that the charge conjugation transforms the wave function of a positive energy state $\left| \varepsilon ,m \right\rangle$ into the wave function of a negative energy state $\left| -\varepsilon ,-m \right\rangle$. In addition, the background soliton field with parameters n and $\alpha$ is transformed into one with reversed parameters $-n$ and $-\alpha$. Note that the system of differential equations (32) and (33) is invariant under the replacement $\varepsilon , m, n, \alpha \rightarrow -\varepsilon , -m, -n, -\alpha$ together with the permutation $f \leftrightarrow g$. It follows from Eq. (38) that in the study of the fermion-soliton system, it is sufficient to restrict ourselves to fermionic ($\propto e^{- i \varepsilon t}$) solutions, since the antifermionic ($\propto e^{i \varepsilon t}$) solutions are obtained from the fermionic ones via charge conjugation.

The system of differential equations (32) and (33) can be reduced to a second-order differential equation for the radial wave function $f(\rho )$

$$\begin{aligned} f^{\prime \prime }\left( \rho \right) +P\left( \rho \right) f^{\prime }\left( \rho \right) +Q\left( \rho \right) f\left( \rho \right) = 0, \end{aligned}$$

(40)

where the coefficient functions

$$\begin{aligned} P\left( \rho \right)= & {} \frac{1}{\rho }+\frac{\alpha B_{\left| n\right| }^{\prime }\left( \rho \right) }{M+\varepsilon -\alpha B_{\left| n\right| }\left( \rho \right) }, \end{aligned}$$

(41)

$$\begin{aligned} Q\left( \rho \right)= & {} \left( \varepsilon -\alpha B_{\left| n\right| }\left( \rho \right) \right) ^{2}-M^{2} \nonumber \\{} & {} -\frac{\left( 1/2-A_{mn}\left( \rho \right) \right) ^{2}}{\rho ^{2}}-\frac{ A_{mn}^{\prime }\left( \rho \right) }{\rho } \nonumber \\{} & {} +\alpha \frac{1/2-A_{mn}\left( \rho \right) }{\rho }\frac{B_{\left| n\right| }^{\prime }\left( \rho \right) }{M+\varepsilon -\alpha B_{\left| n\right| }\left( \rho \right) }, \end{aligned}$$

(42)

and we have turned to dimensionless variables according to the substitution rule: $\rho \rightarrow \lambda \rho$, $M\rightarrow \lambda ^{-1}M$, $\varepsilon \rightarrow \lambda ^{-1} \varepsilon$, $\alpha \rightarrow \lambda ^{-1}\alpha$. To obtain the second-order differential equation for the radial wave function $g(\rho )$, we must perform the substitutions $f \rightarrow g,\, \varepsilon \rightarrow -\varepsilon , m \rightarrow -m, n\rightarrow -n, \alpha \rightarrow -\alpha$ in Eqs. (40)–(42).

The analysis shows that for the minimum possible $\left| n \right| = 2$, differential equation (40) has nine regular singular points (one of which is $\rho = 0$), and one irregular singular point at spatial infinity. For $\left| n\right| >2$, the number of regular singular points is even greater. This means that the solution to differential equation (40) cannot be expressed in terms of known special functions [31]. Note, however, that in some field models, the background field approximation allows fermionic wave functions to be found in an analytical form. In particular, it was found in Ref. [32] that for a fermion-soliton system of the original $\mathbb{C}\mathbb{P}^{N-1}$ model, the fermionic wave functions could be expressed in terms of the local confluent Heun functions [33, 34]. In addition, it was shown in Refs. [35, 36] that the fermion scattering on a one-dimensional kink or Q-ball could also be described in terms of local Heun functions [33, 34].

Next, we shall consider the minimal possible case $\left| n \right| =2$. Using standard methods of analysis, we find that for small $\rho$, the radial wave functions have the forms

$$\begin{aligned} f\left( \rho \right)= & {} N\rho ^{\mu }\left( 1+\frac{M^{2}-\left( \varepsilon -\alpha \right) ^{2}}{4(\mu +1)}\rho ^{2}+O\left[ \rho ^{4} \right] \right) , \end{aligned}$$

(43)

$$\begin{aligned} g\left( \rho \right)= & {} N\frac{\alpha -\varepsilon +M}{2\left( \mu +1\right) }\rho ^{\mu +1} \nonumber \\{} & {} \times \left( 1+\frac{M^{2}-\left( \varepsilon -\alpha \right) ^{2}}{4(\mu +2)}\rho ^{2}+O\left[ \rho ^{4}\right] \right) , \end{aligned}$$

(44)

where N is a normalisation factor, $\mu = m - 1/2$, and the angular momentum eigenvalues $m = 1/2, 3/2, 5/2, \ldots$ For $m = -1/2, -3/2, -5/2, \ldots$, the small $\rho$ asymptotics of the radial wave functions is

$$\begin{aligned} f\left( \rho \right)= & {} N\frac{-\alpha +\varepsilon +M}{2\left( \mu +1\right) }\rho ^{\mu +1} \nonumber \\{} & {} \times \left( 1+\frac{M^{2}-\left( \varepsilon -\alpha \right) ^{2}}{4(\mu +2)}\rho ^{2}+O\left[ \rho ^{4}\right] \right) , \end{aligned}$$

(45)

$$\begin{aligned} g\left( \rho \right)= & {} N\rho ^{\mu }\left( 1+\frac{M^{2}-\left( \varepsilon -\alpha \right) ^{2}}{4\left( \mu +1\right) }\rho ^{2}+O\left[ \rho ^{4}\right] \right) , \end{aligned}$$

(46)

where $\mu = -m - 1/2$. We see that in both cases, $\mu = 0, 1, 2, \ldots$, and therefore plays the role of the orbital angular momentum and determines the behaviour of $f\left( \rho \right)$ and $g\left( \rho \right)$ at small distances. Furthermore, we see that in the leading order in $\rho$, the asymptotics of the radial wave functions does not depend on the sign of the soliton winding number $n = \pm 2$. This dependence appears only in terms of the order of $\rho ^{4}$ in the parentheses in Eqs. (43)–(46).

It is also possible to determine the asymptotics of the radial wave functions in the neighbourhood of the irregular singular point at spatial infinity. Following the methods described in Ref. [31], we obtain the following asymptotics for the radial wave functions of the continuous spectrum:

$$\begin{aligned} f_{\pm }\left( \rho \right)\sim & {} N\frac{e^{\pm ik\rho }}{\sqrt{k\rho }} \left( 1\pm \frac{i c_{-1} }{2k\rho }+O\left[ \left( k\rho \right) ^{-2} \right] \right) , \end{aligned}$$

(47)

$$\begin{aligned} g_{\pm }\left( \rho \right)\sim & {} \pm N\frac{ik}{\varepsilon +M}\frac{ e^{\pm ik\rho }}{\sqrt{k\rho }} \nonumber \\{} & {} \times \left( 1\pm \frac{i d_{-1} }{2k\rho }+O\left[ \left( k\rho \right) ^{-2}\right] \right) , \end{aligned}$$

(48)

where $k^{2} = \varepsilon ^{2}-M^{2}$, and the coefficients

$$\begin{aligned} c_{-1}= & {} (m-n)(m-n-1), \end{aligned}$$

(49)

$$\begin{aligned} d_{-1}= & {} (m-n)(m-n+1). \end{aligned}$$

(50)

Similar expressions can also be obtained for the radial wave functions of the discrete spectrum.

It should be noted that the long-range gauge field of the soliton decreases sufficiently fast that there is no need to modify the pre-exponential factor in Eqs. (47) and (48). It remains equal to $\left( k \rho \right) ^{-1/2}$, which is standard for the two-dimensional case and allows us to correctly determine the phase shifts of fermionic scattering. Furthermore, in Eqs. (47) and (48), the leading terms of the asymptotic expansions do not depend on the parameter $\alpha$, which determines the time dependence of the soliton solution in Eq. (15). It can be shown that this dependence appears only in terms of the order $(k \rho )^{-3}$.

3.2 Fermionic bound states

In this subsection, we discuss some issues concerning the fermionic bound states. It is convenient to perform the substitution

$$\begin{aligned} f\left( \rho \right)= & {} \sqrt{\frac{\varepsilon +M-\alpha +\left( \varepsilon +M\right) \rho ^{4}}{\rho \left( 1+\rho ^{4}\right) }}u\left( \rho \right) , \end{aligned}$$

(51)

$$\begin{aligned} g\left( \rho \right)= & {} \sqrt{\frac{\varepsilon -M-\alpha +\left( \varepsilon -M\right) \rho ^{4}}{\rho \left( 1+\rho ^{4}\right) }}v\left( \rho \right) \end{aligned}$$

(52)

and to obtain differential equations for the new radial functions $u\left( \rho \right)$ and $v\left( \rho \right)$ in the normal form

$$\begin{aligned} u^{\prime \prime }\left( \rho \right) -\left[ \varkappa ^{2} + U\left( \rho \right) \right] u\left( \rho \right)= & {} 0, \end{aligned}$$

(53)

$$\begin{aligned} v^{\prime \prime }\left( \rho \right) -\left[ \varkappa ^{2} + V\left( \rho \right) \right] v\left( \rho \right)= & {} 0, \end{aligned}$$

(54)

where the potentials

$$\begin{aligned} U\left( \rho \right)= & {} \left( m-1\right) m\rho ^{-2} +W\left( \rho \right) , \end{aligned}$$

(55)

$$\begin{aligned} V\left( \rho \right)= & {} \left( m+1\right) m\rho ^{-2} +\tilde{W}\left( \rho \right) , \end{aligned}$$

(56)

and the parameter $\varkappa ^{2} = M^{2}-\varepsilon ^{2}$. Both $U\left( \rho \right)$ and $V\left( \rho \right)$ are sums of the centrifugal and interaction potentials. The interaction potentials $W\left( \rho \right)$ and $\tilde{W}\left( \rho \right)$ are rational functions of the radial variable $\rho$ and the parameters m, n, $\alpha$, $\varepsilon$, and M. An explicit form of the potential $W\left( \rho , m, n, \alpha , \varepsilon , M \right)$ is given in Appendix A. The potential $\tilde{W}\left( \rho , m, n, \alpha , \varepsilon , M \right)$ is determined from $W\left( \rho , m, n,\alpha ,\varepsilon ,M\right)$ by the symmetry relation

$$\begin{aligned} \tilde{W}\left( \rho ,m,n,\alpha ,\varepsilon ,M\right) = W\left( \rho ,\!-m,\!-n,\!-\alpha ,\!-\varepsilon ,M\right) . \end{aligned}$$

(57)

We now consider the case $\alpha = 0$ when the time component $A_{0}$ of gauge field (16) vanishes. The potentials $W\left( \rho \right)$ and $\tilde{W}\left( \rho \right)$ then cease to depend on the parameters $\varepsilon$ and M, which simplifies the analysis. In particular, in the limiting case $\varkappa ^{2} = 0$ ($\varepsilon = \pm M$), the solutions to Eqs. (53) and (54) can be expressed in terms of elementary functions. These solutions, however, are not normalised except for the two cases $m = 1/2, n = 2, \varepsilon = M$ and $m = -1/2, n = -2, \varepsilon = -M$. In the first case, the normalised solution is $u_{M\,1/2\,2}=2\pi ^{-1/2}\rho ^{ 1/2}\left( 1+\rho ^{4}\right) ^{-1/2}$, and in the second case, it is $v_{-M\, -1/2\,-2} = 2\pi ^{-1/2}\rho ^{1/2}$ $\times \left( 1+\rho ^{4}\right) ^{-1/2}$. Returning to the initial notation, we obtain two normalised fermionic wave functions

$$\begin{aligned} \psi _{M\frac{1}{2}2}=\frac{\sqrt{2}}{\pi } \begin{pmatrix} \left( 1+\rho ^{4}\right) ^{-1/2} \\ 0 \end{pmatrix} e^{-iMt} \end{aligned}$$

(58)

and

$$\begin{aligned} \psi _{-M-\frac{1}{2}-2}=\frac{\sqrt{2}}{\pi } \begin{pmatrix} 0 \\ \left( 1+\rho ^{4}\right) ^{-1/2} \end{pmatrix} e^{iMt}, \end{aligned}$$

(59)

which correspond to the so-called half-bound fermionic states.

In Eqs. (53) and (54), the potentials U and V have second-order poles at $\rho = 0$, and tend to zero as $\rho \rightarrow \infty$. From the general properties of the Schrödinger equation [40], it follows that for bound states ($\varkappa ^{2} > 0$) to exist, both U and V must take negative values. An analysis shows that for $\alpha = 0$, both U and V have domains of negative values only when $m = 3/2,\, n = 2$ or $m = -3/2,\, n = -2$. In all other cases, at least one of the potentials U and V turns out to be positive for all $\rho \in (0, \infty )$, which makes the existence of bound fermionic states impossible.

Consider one of the possible cases, say $m = 3/2,\, n = 2$. It can be shown that in the limiting case $\varkappa ^{2} = 0$, the solution $u_{M\,3/2\,2} \propto \rho ^{3/2}\left( 1 + \rho ^{4}\right) ^{-1/2} \sim \rho ^{ -1/2}$, and hence it is not normalised. We note that Eq. (53) admits a mechanical analogy, as it describes the one-dimensional motion of a unit mass particle along the u-axis over time $\rho$. The particle starts from the origin with zero initial velocity at time $\rho = 0$, and moves along the u-axis under the action of the time-dependent linear force $F(\rho )=\left( \varkappa ^{2}+U\left( \rho , 3/2, 2\right) \right) u(\rho )$. For the trajectory of the particle to correspond to a normalised solution, the particle must tend to the origin fast enough ($\propto \rho ^{-1/2 + \epsilon }$) as $\rho \rightarrow \infty$.

We have shown above, however, that for $\varkappa ^{2} = 0$, the trajectory of the particle does not correspond to a normalised solution. For bound states, the parameter $\varkappa ^{2} = M^{2} - \varepsilon ^{2}$ is positive, which corresponds to an elastic repulsive force $\varkappa ^{2} u$. However, if the particle does not approach the origin fast enough when $\varkappa ^{2} = 0$, it is slowed further or even change the direction of movement when the additional repulsive force appears. Hence, for $\alpha = 0$, there are no bound fermionic states corresponding to $m = 3/2$, $n = 2$. The case $m = -3/2$, $n = -2$ can be treated similarly, with the same result. Thus, we conclude that there are no bound fermionic states if the parameter $\alpha = 0$.

We now consider the case when the parameter $\alpha \ne 0$. We note that the Hamiltonian (25) describes the minimal interaction of a massive Dirac fermion with gauge field (16). This gauge field, however, is not dynamic, since there is no gauge kinematic term in the Lagrangian (1). If the parameter $\alpha = 0$, the fermion interacts with a purely “magnetic” field with strength $B^{\pm 2} = \pm 8\rho ^{2}\left( 1 + \rho ^{4} \right) ^{-2}$, where the superscript indicates the winding number of the soliton. As shown above, the bound fermionic states are absent in this case. If the parameter $\alpha \ne 0$, then besides the “magnetic” field, the fermion also interacts with an “electric” field with radial strength $E_{\rho }^{\pm 2} = 4 \alpha \rho ^{3}\left( 1 + \rho ^{4}\right) ^{-2}$. When the parameter $\alpha > 0$, the “electric” field is repulsive, and hence there are no bound fermionic states. However, the “electric” field is attractive when $\alpha < 0$; in this case, fermionic bound states are possible, and their existence can be established by numerical methods. The situation is reversed for antifermionic bound states: these states may exist if $\alpha > 0$, and do not exist if $\alpha < 0$.

We have shown above that in the background field of static ($\alpha =0$) $\mathbb{C}\mathbb{P}^{1}$ soliton (15) with winding number $n = \pm 2$, the Hamiltonian (25) has one normalised mode with energy $\varepsilon = \pm M$. More generally, it can be shown that in the background field of static $\mathbb{C}\mathbb{P}^{1}$ soliton (15) with winding number n satisfying the condition $\left| n \right| \ge 2$, the Hamiltonian (25) has $\left| n \right| -1$ normalised modes with energy $\varepsilon = \text {sign}(n) M$. These modes exhaust the discrete spectrum of the Hamiltonian (25) in the static limit $\alpha = 0$. In addition to these normalised discrete modes, the Hamiltonian (25) also has one non-normalised mode of the continuous spectrum with energy $\varepsilon = \text {sign}(n) M$ for all nonzero n. An example of such modes for $n = \pm 1$ can be found in Ref. [32]. There are no other regular solutions to the Dirac equation (24) with energy $\varepsilon = \pm M$.

Following Ref. [37], we associate the Hermitean operator $H_{0} = \alpha ^{k} \left( -i\partial _{k} + A_{k}\right)$ with the Hamiltonian (25). It is easy to see that the above modes of the Hamiltonian (25) with energies $\varepsilon = \pm M$ are zero modes of the operator $H_{0}$. Let us define the index of $H_{0}$ as the difference in the number of its zero modes corresponding to the energies $\varepsilon = M$ and $\varepsilon = -M$ of the Hamiltonian (25). Then it follows from the above that the index of the operator $H_{0}$ is equal to the winding number n of the background soliton field:

$$\begin{aligned} \text {Ind}\left[ H_{0}\right] = n. \end{aligned}$$

(60)

It is known that an interaction between soliton and fermionic fields in general induces a fermion number on the soliton, as is the case for the fermion-kink system [38]. It can be shown that this effect also takes place in our case. Indeed, in the static limit $\alpha = 0$, our fermion-soliton system is essentially equivalent to the fermion-vortex system considered in Ref. [39]. Using this equivalence and the results obtained in Refs. [37, 39], we come to the conclusion that when $\alpha = 0$, the induced fermion number of the soliton

$$\begin{aligned} N = -\text {Ind}\left[ H_{0}\right] /2 = -n/2. \end{aligned}$$

(61)

When $\alpha \ne 0$, new bound (anti)fermionic states appear in the spectrum of the Hamiltonian (25) compared to the case $\alpha = 0$. These states are asymmetric under charge conjugation. In addition, the spectral density of continuum states is also asymmetric under charge conjugation, and this asymmetry depends on $\alpha$. Hence, the induced fermion number of the soliton also depends on $\alpha$. In particular, it will no longer be an integer or half-integer as it is when $\alpha = 0$, but will be a real number. Furthermore, it follows from physical considerations that the induced fermion number N changes the sign when n and $\alpha$ change the signs: $N(-n, -\alpha ) = -N(n,\alpha )$.

3.3 General formulae for fermion-soliton scattering

In this subsection, we present general formulae describing fermion scattering for the two-dimensional case. According to general principles of the theory of scattering [40, 41], for a fermion with initial momentum $\textbf{k} = (k, 0)$, the asymptotic form of the wave function of a fermionic scattering state is

$$\begin{aligned} \varPsi \sim \psi _{\varepsilon ,\textbf{k}\,}+\frac{1}{\sqrt{2\varepsilon }} u_{\varepsilon ,\textbf{k}^{\prime }}f\left( k,\theta \right) \frac{ e^{ik\rho }}{\sqrt{-i\rho }}, \end{aligned}$$

(62)

where

$$\begin{aligned} \psi _{\varepsilon ,\textbf{k}}=\frac{1}{\sqrt{2\varepsilon }} \begin{pmatrix} \sqrt{\varepsilon + M} \\ i\sqrt{\varepsilon - M} \end{pmatrix} e^{-i k x} \end{aligned}$$

(63)

is the wave function of the incoming fermion with momentum $\textbf{k}=(k, 0)$,

$$\begin{aligned} u_{\varepsilon ,\textbf{k}^{\prime }}= \begin{pmatrix} \sqrt{\varepsilon + M} \\ i\sqrt{\varepsilon - M}e^{i\theta } \end{pmatrix} \end{aligned}$$

(64)

is the spinor amplitude of the wave function of the outgoing fermion with momentum $\textbf{k}^{\prime } = (k\cos (\theta ), k\sin (\theta ))$, and $f\left( k, \theta \right)$ is the scattering amplitude. Due to the conserved angular momentum (30), we can expand the scattering amplitude $f\left( k, \theta \right)$ in terms of the partial scattering amplitudes $f_{m}\left( k\right)$ as

$$\begin{aligned} f\left( k,\theta \right) =\sum \limits _{m}f_{m}\left( k\right) e^{i\left( m-1/2\right) \theta }, \end{aligned}$$

(65)

where the summation is taken over the half-integer eigenvalues of the angular momentum.

Similarly to Eq. (65), wave function (62) for a fermionic scattering state can also be expanded into partial waves as $\varPsi = \sum \nolimits _{m}\psi _{m}$. The large $\rho$ asymptotics of the partial waves $\psi _{m}$ is

$$\begin{aligned} \psi _{m} \sim \frac{\left( -1\right) ^{1/4}}{\sqrt{2\pi k\rho }} \begin{pmatrix} -i\sqrt{\frac{\varepsilon + M}{2\varepsilon }}F_{m}\left( k,\rho \right) e^{i\left( m-1/2\right) \theta } \\ \sqrt{\frac{\varepsilon -M}{2\varepsilon }}G_{m}\left( k,\rho \right) e^{i\left( m+1/2\right) \theta } \end{pmatrix}, \end{aligned}$$

(66)

where the radial functions

$$\begin{aligned} F_{m}\left( k,\rho \right)= & {} i\left( -1\right) ^{m-1/2}e^{-i k \rho }+S_{m}\left( k\right) e^{ik\rho }, \end{aligned}$$

(67)

$$\begin{aligned} \text {and}{} & {} \nonumber \\ G_{m}\left( k,\rho \right)= & {} i\left( -1\right) ^{m+1/2}e^{-i k \rho }+S_{m}\left( k\right) e^{ik\rho } \end{aligned}$$

(68)

are expressed in terms of the partial elements of the S-matrix

$$\begin{aligned} S_{m}\left( k\right) = 1 + i\sqrt{2 \pi k}f_{m}\left( k\right) . \end{aligned}$$

(69)

The differential cross-section of the elastic fermion scattering are expressed in terms of the scattering amplitude $f\left( k, \theta \right)$ as

$$\begin{aligned} d\sigma /d\theta =\left| f\left( k, \theta \right) \right| ^{2}. \end{aligned}$$

(70)

Similarly, the partial cross-sections of the elastic fermion scattering are expressed in terms of the partial scattering amplitudes as

$$\begin{aligned} \sigma _{m}=2\pi \left| f_{m}\left( k\right) \right| ^{2}=k^{-1}\left| S_{m}\left( k\right) -1\right| ^{2}. \end{aligned}$$

(71)

Both $d\sigma /d\theta$ and $\sigma _{m}$ have the dimension of length, as it should be in the two-dimensional case [40]. The partial elements of the S-matrix satisfy the unitarity condition $\left| S_{m}\left( k \right) \right| = 1$, which makes it possible to express them in terms of the partial phase shifts $\delta _{m}$ as

$$\begin{aligned} S_{m}\left( k\right) = e^{2 i \delta _{m}\left( k\right) }. \end{aligned}$$

(72)

General formulae for antifermion scattering can be obtained from those presented in this subsection via charge conjugation (29). In particular, the partial phase shifts of antifermion scattering are expressed in terms of those of fermion scattering as

$$\begin{aligned} \bar{\delta }_{m n \alpha }\left( k\right) = \delta _{-m \,-n \,-\alpha }\left( k\right) , \end{aligned}$$

(73)

where the dependence of the phase shifts on the parameters n and $\alpha$ is indicated.

We now consider the question of the symmetry of differential cross-section (70) under the reflection $\theta \rightarrow -\theta$. It is obvious that the symmetry of the cross-section is determined by the symmetry of the scattering amplitude $f\left( k, \theta \right)$. An analysis of Eqs. (65) and (70) shows that the differential cross-section is symmetric (even) under the reflection $\theta \rightarrow -\theta$ if the partial scattering amplitudes satisfy the relation $f_{-mn\alpha }\left( k\right) = f_{m n \alpha }\left( k \right)$, while the other possibility $f_{-m n \alpha }\left( k\right) =-f_{m n \alpha }\left( k \right)$ is incompatible with Eq. (69) and unitarity condition (72).

In our case, the relation $f_{-mn\alpha }\left( k\right) = f_{m n \alpha }\left( k \right)$ is not satisfied, and therefore differential cross-section (70) is asymmetric under the reflection $\theta \rightarrow -\theta$. This asymmetry is due to the fact that the reflection $\theta \rightarrow -\theta$ changes the sign of the winding number n of $\mathbb{C}\mathbb{P}^{1}$ soliton (15), which, in turn, changes the sign of the component $A_{\theta }$ of gauge field (16). At the same time, we can expect that in the ultrarelativistic limit $k \rightarrow \infty$, the leading term of the expansion of differential cross-section (70) in k is symmetric under the reflection $\theta \rightarrow -\theta$.

4 Fermion scattering in the Born approximation

In Sect. (3), we established that the wave functions of the fermionic scattering states (and hence the differential cross-sections) cannot be found in analytical form. In view of this, it is important to study the fermion scattering in the Born approximation, which gives us a chance to obtain an approximate analytical description for fermion-soliton scattering.

It follows from Eqs. (1) and (3) that the interaction of the fermionic isodoublet with the soliton gauge field is described by the term

$$\begin{aligned} V_{\text {int}}=\bar{\psi }_{a}\gamma ^{\mu }A_{\mu }\psi _{a}. \end{aligned}$$

(74)

In the background field approximation, the gauge field $A_{\mu }$ is defined by Eq. (16) and does not depend on the fermion fields $\psi _{a}$. It follows from this and Eq. (74) that the components of the fermionic isodoublet $\left( \psi _{1}, \psi _{2}\right)$ interact with the gauge field of the $\mathbb{C}\mathbb{P}^{1}$ soliton in the same way, and independently of each other.

Using Eq. (74) and free-fermion wave functions in Eqs. (63) and (64), we can write the first-order Born amplitude for fermion-soliton scattering as

$$\begin{aligned} f\left( \textbf{k}^{\prime },\textbf{k}\right) = -\left( 8\pi k\right) ^{-1/2}\bar{u} _{\varepsilon ,\textbf{k}^{\prime }}\mathbb {\gamma }^{\mu }A_{\mu }\left( \textbf{q}\right) u_{\varepsilon ,\textbf{k}}, \end{aligned}$$

(75)

where

$$\begin{aligned} A_{\mu }\left( \textbf{q}\right) = \int A_{\mu }\left( \textbf{x}\right) e^{-i\mathbf {q \cdot x}}d^{2}x \end{aligned}$$

(76)

and $\textbf{q} = \textbf{k}^{\prime } - \textbf{k}$ is the momentum transfer. The Born amplitude in Eq. (75) can be expressed in terms of the Meijer G-functions [42, 43]. In particular, for the minimum possible magnitude of the soliton winding number $\left| n \right| = 2$, the Born amplitude is

$$\begin{aligned} f\left( \textbf{k}^{\prime },\textbf{k}\right)= & {} - \sqrt{\pi } 2^{-5/2} \alpha \lambda ^{2}\sqrt{k}\left[ \sqrt{\frac{\varepsilon + M}{ \varepsilon -M}}\right. \nonumber \\{} & {} \left. +\sqrt{\frac{\varepsilon -M}{\varepsilon +M}}e^{-i\varDelta \vartheta } \right] \! F\left( \lambda q\right) \nonumber \\{} & {} + i \sqrt{\pi } 2^{-3/2} \tau n \lambda \sqrt{k}e^{-i\varDelta \vartheta /2}G\left( \lambda q\right) , \end{aligned}$$

(77)

where the form-factor functions

$$\begin{aligned} F\left( \lambda q\right)= & {} G_{0,4}^{3,0}\left( \left( \lambda q/4\right) ^{4}\left| 0,\frac{1}{2},\frac{1}{2},0\right. \right) , \end{aligned}$$

(78)

$$\begin{aligned} G\left( \lambda q\right)= & {} G_{0,4}^{3,0}\left( \left( \lambda q/4\right) ^{4}\left| -\frac{1}{4},\frac{1}{4},\frac{3}{4},\frac{1}{4}\right. \right) , \end{aligned}$$

(79)

and we use the shorthand notations:

$$\begin{aligned} \varDelta \vartheta&=\vartheta '-\vartheta , \end{aligned}$$

(80a)

$$\begin{aligned} \tau&=\text {sign}\left( \varDelta \vartheta \right) , \end{aligned}$$

(80b)

$$\begin{aligned} q&=2k\sin \left( \left| \varDelta \vartheta \right| /2\right) . \end{aligned}$$

(80c)

The condition of applicability of the Born approximation can be formulated as

$$\begin{aligned} k \lambda \gg 1 \quad \text {and} \quad \alpha \lambda \ll 1. \end{aligned}$$

(81)

Equation (81) tells us that the Born approximation is suitable for the scattering of high-ehergy fermions in the background field of a slowly rotating $\mathbb{C}\mathbb{P}^{1}$ soliton.

From Eq. (77), it follows that

$$\begin{aligned} f\left( \textbf{k}^{\prime },\textbf{k}\right) = f^{*}\left( \textbf{k},\textbf{k}^{\prime }\right) . \end{aligned}$$

(82)

We see that the amplitude $f\left( \textbf{k}^{\prime }, \textbf{k}\right)$ is Hermitian, as it should be in the first Born approximation [40, 41]. Furthermore, it can be shown that the amplitude of antifermion scattering differs only in sign from the amplitude of fermion scattering in Eq. (77). It follows that in the first Born approximation, antifermion-soliton scattering is essentially no different from fermion-soliton scattering. This also implies that the scattering of fermions on a soliton with the parameters $(n, \alpha )$ is equivalent to the scattering of antifermions on a soliton with the opposite parameters $(-n,-\alpha )$, which is in agreement with Eq. (38).

We now study the behaviour of the Born amplitude for large and small values of the momentum transfer q. To do this, we use the known asymptotic forms of the Meijer G-functions [42, 43]. For $\lambda q \gg 1$, and hence $\left| \varDelta \vartheta \right| \gg \left( \lambda k \right) ^{-1}$, we find that the Born amplitude

$$\begin{aligned} f\sim & {} - \pi 2^{-3/2} \left( \alpha \lambda \right) \lambda ^{1/2}e^{-\lambda q/\sqrt{2}}\left( 1+e^{-i\varDelta \vartheta }\right) \nonumber \\{} & {} \times \sin \left( \pi /8+\lambda q/\sqrt{2}\right) \sin \left( \left| \varDelta \vartheta \right| /2\right) ^{-1/2} \nonumber \\{} & {} - i \pi 2^{-1/2} n \tau \lambda ^{1/2}e^{-\lambda q/\sqrt{2}}e^{-i\varDelta \vartheta /2} \nonumber \\{} & {} \times \cos \left( \pi /8-\lambda q/\sqrt{2}\right) \sin \left( \left| \varDelta \vartheta \right| /2\right) ^{-1/2}. \end{aligned}$$

(83)

It follows from Eq. (83) that both the “electric” ($\propto \alpha$) and “magnetic” ($\propto n$) parts of the Born amplitude decrease exponentially with an increase in the momentum transfer q. In addition, both of these parts are oscillating functions of the dimensionless combination $\lambda q$, due to the corresponding trigonometric factors.

Next, we consider the case of low momentum transfer in which $\lambda q \rightarrow 0$, $\lambda k \gg 1$, and hence $\left| \varDelta \vartheta \right| \ll \left( \lambda k\right) ^{-1} \ll 1$. In this case, the asymptotic form of the Born amplitude is

$$\begin{aligned} f \sim -(\pi /2)^{3/2}\alpha \lambda ^{2}k^{1/2} - i \sqrt{2\pi } n \tau k^{1/2}q^{-1}. \end{aligned}$$

(84)

We see that for the low momentum transfer q, the “electric” part of the Born amplitude does not depend on q, whereas the “magnetic” part diverges $\propto q^{-1}$. Furthermore, the magnetic part of amplitude (84) does not depend on the parameters $\alpha$ and $\lambda$ of the soliton solution, but is determined only by the momentum k and the scattering angle $\varDelta \vartheta$ of the fermion.

We now study the partial Born amplitudes $f_{m}\left( k \right) = \left( 2 \pi \right) ^{-1}\int \nolimits _{-\pi }^{\pi } e^{-i\left( m-1/2 \right) \varDelta \vartheta } f\left( k,\varDelta \vartheta \right) d\varDelta \vartheta$, where $f\left( k,\varDelta \vartheta \right)$ is the first-order Born amplitude in Eq. (77). It can be shown that the imaginary part of the integrand diverges as $\varDelta \vartheta \rightarrow -\pi \, \text {or} \, \pi$, and is an odd function of $\varDelta \vartheta$. It follows that the imaginary part of the integral vanishes in the sense of the principal value. In contrast, the real part of the integrand is a finite, even function of $\varDelta \vartheta$, meaning that the real part of the integral exists and is nonzero. Hence, the partial amplitudes of fermion scattering are real in the first Born approximation. Note that this property of the partial Born amplitudes follows from Eqs. (65) and (82).

In general, the partial Born amplitudes cannot be obtained in analytical form; however, it is possible to obtain their asymptotic forms in the parametric domain $1 \lesssim \left| m \right| \ll k \lambda$ as

$$\begin{aligned} f_{m n}\sim 2^{-1}\sqrt{\pi }k^{-1/2}\left[ -\alpha \lambda + n m \left( k \lambda \right) ^{-1}\right] . \end{aligned}$$

(85)

Then, using Eqs. (69) and (85), we can obtain asymptotic forms of the partial elements of the S-matrix as

$$\begin{aligned} S_{m n} \sim 1+i 2^{-1/2}\pi \left[ -\alpha \lambda + m n \left( k \lambda \right) ^{-1}\right] . \end{aligned}$$

(86)

It follows from Eq. (86) that the partaial elements of the S-matrix do not satisfy the unitarity condition in Eq. (72), and this is a characteristic property of the Born approximation [40, 41]. We also see that the imaginary part of Eq. (86) is much less than unity when $\left| m \right| \ll k \lambda$ and condition (81) is satisfied. In this case, we can rewrite Eq. (86) in the approximate unitary form $S_{m n}\approx \exp (2 i \delta _{m n}^{\text {B}})$, where the Born partial phase shifts

$$\begin{aligned} \delta _{m n}^{\text {B}}=2^{-3/2}\pi \left[ -\alpha \lambda + m n \left( k\lambda \right) ^{-1}\right] . \end{aligned}$$

(87)

It is known that the condition for validity of the Born approximation is the smallness of the partial phase shifts [40, 41]. Equation (87) tells us that that this condition will be met provided that $\left| m \right| \ll k \lambda$ and condition (81) holds.

The analytical form (77) of the first-order Born amplitude makes it possible to obtain an expression for the differential cross-section of the fermion scattering in the Born approximation as follows:

$$\begin{aligned} \frac{d\sigma }{d \varDelta \vartheta }= & {} \frac{\pi }{2} k\lambda ^{2}G^{2} - \frac{\pi }{4}\alpha n M\lambda ^{3}\sin \left( \left| \varDelta \vartheta \right| /2\right) F G \nonumber \\{} & {} +\frac{\pi }{8}\alpha ^{2}\lambda ^{4}k^{-1}\left( M^{2}+k^{2}\cos ^{2}\left( \varDelta \vartheta /2\right) \right) F^{2}, \end{aligned}$$

(88)

where the form-factor functions F and G are defined by Eqs. (78) and (79), respectively. The same expression is valid for antifermion scattering. We see that differential cross-section (88) is the sum of the “magnetic” ($\propto G^2$), interference ($\propto F G$), and “electric” ($\propto F^{2}$) terms. It is symmetric under the reflection $\varDelta \vartheta \rightarrow -\varDelta \vartheta$, which is a consequence of the Hermiticity of the Born amplitude (77). Furthermore, differential cross-section (88) is invariant under the replacement $\alpha ,\,n \rightarrow -\alpha ,\,-n$. It follows that in the first Born approximation, scattering of an (anti)fermion on a soliton with parameters $\alpha$ and $n = \pm 2$ does not differ from scattering on a soliton with parameters opposite in sign, $-\alpha$ and $n = \mp 2$.

In the region of small scattering angles $\varDelta \vartheta \ll \left( k \lambda \right) ^{-1}$, the asymptotic form of differential cross-section (88) is

$$\begin{aligned} \frac{d\sigma }{d\varDelta \vartheta }\sim \frac{32\pi \lambda }{\left( k\lambda \right) \left( \varDelta \vartheta \right) ^{2}}-8\pi ^{2}\lambda \left( k\lambda \right) +\frac{\pi ^{3}}{2}\lambda \left( \alpha \lambda \right) ^{2}\left( k\lambda \right) , \end{aligned}$$

(89)

where the large ($k \lambda$) and small ($\varDelta \vartheta$, $\alpha \lambda$) dimensionless parameters are indicated by parentheses. We see that the main contribution to the differential cross-section comes from the “magnetic” term in Eq. (88), and that it diverges quadratically as $\varDelta \vartheta \rightarrow 0$. Hence, the total cross-section $\sigma = \int \nolimits _{-\pi }^{\pi } \left( d\sigma /d\varDelta \vartheta \right) d\varDelta \vartheta$ of the fermion-soliton scattering is infinite. However, the transport cross-section $\sigma _{\text {tr}}=\int \nolimits _{-\pi }^{ \pi }\left( 1 - \cos \left( \varDelta \vartheta \right) \right) \left( d\sigma /d\varDelta \vartheta \right) d\varDelta \vartheta$ remains finite. Using approximate analytical methods, it can be shown that

$$\begin{aligned} \sigma _{\text {tr}}\approx \frac{24.44}{\left( k \lambda \right) ^{2}}\lambda +\frac{2.23}{\left( k \lambda \right) ^{2}}(\alpha \lambda )^{2}\lambda +O\left[ \left( \lambda k\right) ^{-4}\right] . \end{aligned}$$

(90)

We see that the transport cross-section tends to zero $\propto (k \lambda )^{-2}$ as the dimensionless parameter $k \lambda \rightarrow \infty$.

5 Numerical results

In this section, we find the dependence of the energy $\varepsilon _{m n}$ of bound (anti)fermionic states on the parameter $\alpha$. We also find the dependence of the partial phase shifts $\delta _{m n}$ on the fermion momentum. In both cases, we restrict ourselves to the soliton winding number $n = \pm 2$, which corresponds to the minimal allowed magnitude $\left| n\right| =2$. To solve these problems, we use numerical methods implemented in the Mathematica software package [43]. We also use dimensionless variables according to the substitution rule $\rho \rightarrow \lambda \rho , \; M \rightarrow \lambda ^{-1} M, \; \varepsilon \rightarrow \lambda ^{-1} \varepsilon , \;\alpha \rightarrow \lambda ^{-1}\alpha$, where the parameter $\lambda$ determines the effective size of the soliton. In addition, the dimensionless fermionic mass M is taken to be equal to unity.

To determine the energy levels of bound (anti)fer- mionic states for a given value of $\alpha$, we must find the values of the parameter $\varepsilon$ for which the solutions to Eq. (40) satisfy the necessary boundary conditions: f(0) $= 0$ and $f(\infty ) = 0$. Note that unlike the usual eigenvalue problem, in Eq. (40), the differential operator depends on the parameter $\varepsilon$. To solve this generalised eigenvalue problem, we used the shooting method. Some small value of $\rho$ is chosen as the initial point of the shooting method, since $\rho = 0$ is a regular singular point of differential equation (40). Depending on the sign of m, the radial wave function $f(\rho )$ and its first derivative $f'(\rho )$ can be determined at the initial point from Eq. (43) or Eq. (45). Note that the second-order differential equation for the radial wave function $g(\rho )$ can also be used to find the energy of bound (anti)fermionic states.

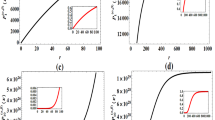
Figures 1, 2, 3 and 4 show the dependence of the energy $\varepsilon _{m n}$ of bound (anti)fermionic states on the parameter $\alpha$. These four figures correspond to the four possible combinations of signs of the quantum numbers m and n. It follows from these figures that bound fermionic states are possible only when the parameter $\alpha < 0$. In contrast, bound antifermionic states are possible only when the parameter $\alpha > 0$. Furthermore, in Figs. 1, 2, 3 and 4, all the curves $\varepsilon _{m n}(\alpha )$ satisfy the symmetry relation

$$\begin{aligned} \varepsilon _{mn}\left( \alpha \right) = -\varepsilon _{-m-n}\left( -\alpha \right) , \end{aligned}$$

(91)

which is a consequence of the symmetry (38) of the Dirac equation (24) with respect to charge conjugation. Equation (91) tells us that it is sufficient to restrict ourselves to negative $\alpha$ (fermionic bound states) to study the behaviour of the $\varepsilon _{m n}\left( \alpha \right)$ curves.

Firstly, we note that in Figs. 1, 2, 3 and 4, the behaviour of all the curves $\varepsilon _{m n} (\alpha )$ fits a common pattern. For each (m, n), the curve $\varepsilon _{m n}(\alpha )$ consists of an infinite sequence of branches $\varepsilon _{m n}^{(i)}(\alpha )$, $i = 1,\ldots , \infty$. For each (m, n) there exists a minimum value of $\left| \alpha \right| =-\alpha$ above which the corresponding bound fermionic state emerges from the positive energy continuum for the first time. The minimum value is positive for all (m, n) except for the fermionic state with $(m, n) = (1/2, 2)$, for which it is equal to zero. This is obviously caused by the presence of half-bound fermionic state (58) with $(m, n) = (1/2, 2)$. It follows from the subplot in Fig. 1, that the first bound state (3/2, 2) emerges at a positive (albeit small) value of $\left| \alpha \right|$. It was found numerically that for $\left| m \right| \gtrsim 9/2$, the first emergence of a bound fermionic state becomes equidistant with respect to $\alpha$.

Fig. 1

Dependence of the energy $\varepsilon _{m n}$ of bound (anti)fermionic states on the parameter $\alpha$. The red, green, blue, and orange solid curves correspond to the fermionic levels $\varepsilon _{1/2\,2}$, $\varepsilon _{3/2\, 2}$, $\varepsilon _{5/2\, 2}$, and $\varepsilon _{7/2\, 2}$, respectively. The red, green, blue, and orange dashed curves correspond to the antifermionic levels $\varepsilon _{-1/2\,-2}$, $\varepsilon _{-3/2\, -2}$, $\varepsilon _{-5/2\, -2}$, and $\varepsilon _{-7/2\, -2}$, respectively

Consider a fermionic curve $\varepsilon _{m n} (\alpha )$. After the emergence of the first branch $\varepsilon _{m n}^{(1)}(\alpha )$ from the positive energy continuum, the energy $\varepsilon _{m n}$ of the bound fermionic state decreases monotonically with an increase in $\left| \alpha \right|$. With further growth of $\left| \alpha \right|$, the first branch $\varepsilon _{m n}^{(1)}(\alpha )$ reaches the lower admissible bound $\varepsilon = -M$ and is interrupted. At the same time, the second branch $\varepsilon _{m n}^{(2)}(\alpha )$ emerges from the positive energy continuum, and its behaviour is similar to that of the first branch as $\left| \alpha \right|$ grows. With further growth in $\left| \alpha \right|$, this pattern is repeated over and over again, resulting in an infinite sequence of branches $\varepsilon _{m n}^{(i)}(\alpha )$ for each (m, n). We find that for the i-th branch $\varepsilon _{m n}^{(i)}(\alpha )$, the radial wave function $f(\rho )$ has exactly $i - 1$ nodes. It follows that for a given (n, m), the branch number i determines the radial quantum number $n_{\rho } = i - 1$. We also find that for a given (m, n) and any fixed $\alpha$, there are at most two bound (anti)fermionic states, and their radial quantum numbers differ by one. The distance between neighboring branches $\varepsilon _{m n}^{(i + 1)}(\alpha )$ and $\varepsilon _{m n}^{(i)}(\alpha )$ is approximately constant, and does not depend on m, n, and i.

It follows from Figs. 1, 2, 3 and 4 that each branch $\varepsilon _{m n}^{(i)}(\alpha )$ crosses the level $\varepsilon = 0$ at some nonzero $\alpha$. This corresponds to the appearance of an (anti)fermionic zero mode in the background field of the $\mathbb{C}\mathbb{P}^{1}$ soliton. In each of Figs. 1, 2, 3 and 4, the fermionic and antifermionic zero modes are arranged symmetrically with respect to the origin, in accordance with Eq. (91). Furthermore, we see that for a given value of $\alpha$, there exists at most one (anti)fermionic zero mode.

Fig. 2

Dependence of the energy $\varepsilon _{m n}$ of bound (anti)fermionic states on the parameter $\alpha$. The red, green, blue, and orange solid curves correspond to the fermionic levels $\varepsilon _{-1/2\,2}$, $\varepsilon _{-3/2\,2}$, $\varepsilon _{-5/2\,2}$, and $\varepsilon _{-7/2\,2}$, respectively. The red, green, blue, and orange dashed curves correspond to the antifermionic levels $\varepsilon _{1/2\, -2}$, $\varepsilon _{3/2\, -2}$, $\varepsilon _{5/2\, -2}$, and $\varepsilon _{7/2\, -2}$, respectively

We now proceed to a study of the phase shifts of fermionic scattering. To find the phase shifts, we need to find a numerical solution to the system of differential equations in Eqs. (32) and (33) on the interval $\left[ \rho _{\min },\rho _{\max } \right]$, where $\rho _{\min } \ll 1$ and $\rho _{\max } \gg 1$. Since $\rho =0$ is a regular singular point of the system, we cannot set $\rho _{ \min }$ equal to zero; instead, we set $\rho _{\min }$ equal to a value on the order of $10^{-2}$, and determine the values of the radial wave functions $f(\rho )$ and $g(\rho )$ at $\rho _{\min }$ using Eqs. (43)–(46). We also set $\rho _{\max }$ equal to a value on the order of $10^{2}$. For such large distances, we neglect the terms in Eqs. (32) and (33) that decrease faster than $\rho ^{-1}$, and obtain an approximate solution in terms of the cylindrical functions

$$\begin{aligned} f\left( \rho \right)\approx & {} A\left( c_{1}J_{n-m+1/2}(k\rho )+c_{2}Y_{n-m+1/2}(k\rho )\right) , \end{aligned}$$

(92)

$$\begin{aligned} g\left( \rho \right)\approx & {} B\left( c_{1}J_{n-m-1/2}(k\rho )+c_{2}Y_{n-m-1/2}(k\rho )\right) , \end{aligned}$$

(93)

where the factors $A = \left( \varepsilon + M \right) ^{1/2}\left( 2 \varepsilon \right) ^{-1/2}$ and $B = \left( \varepsilon -M\right) ^{1/2}\left( 2\varepsilon \right) ^{-1/2}$. To determine the coefficients $c_{1}$ and $c_{2}$, we fit the numerical and approximate solutions at $\rho = \rho _{\max }$. Using known asymptotic expansions of the cylindrical functions and general expressions (67) and (68) for the radial wave functions of a fermionic scattering state, we obtain two independent linear equations that determine one S-matrix partial element $S_{m n}=\exp (2 i \delta _{m n})$. The coincidence of the solutions to these two equations (within a numerical error) was used as a criterion for the correctness of the result.

Fig. 3

Dependence of the energy $\varepsilon _{m n}$ of bound (anti)fermionic states on the parameter $\alpha$. The red, green, blue, and orange solid curves correspond to the fermionic levels $\varepsilon _{1/2\,-2}$, $\varepsilon _{3/2\,-2}$, $\varepsilon _{5/2\,-2}$, and $\varepsilon _{7/2\, -2}$, respectively. The red, green, blue, and orange dashed curves correspond to the antifermionic levels $\varepsilon _{-1/2\, 2}$, $\varepsilon _{-3/2\, 2}$, $\varepsilon _{-5/2\, 2}$, and $\varepsilon _{-7/2\, 2}$, respectively

Equation (A.6) tells us that as the fermion momentum $k\rightarrow \infty$, the phase shift $\delta _{m n} \left( k \right)$ tends to a constant value of $-2^{-3/2}\pi \alpha$ up to a term that is an integer multiple of $\pi$. From the numerical results, we also find that as $k \rightarrow 0$, the fermionic phase shifts

$$\begin{aligned} \delta _{m n} \left( k\right) \sim a_{m n} k^{\tau }, \end{aligned}$$

(94)

where $a_{m n}$ is a constant, the exponent

$$\begin{aligned} \tau = 2 \left| n - m + 1/2\right| , \end{aligned}$$

(95)

and it is assumed that $\tau > 0$. If $(m, n) = (5/2, 2)$ or $(-3/2, -2)$, then the exponent $\tau$ vanishes. We find that in these exceptional cases, the fermionic phase shifts

$$\begin{aligned} \delta _{m n} \left( k\right) \sim \pi /\ln (k^{2}) \end{aligned}$$

(96)

as $k \rightarrow 0$. We see that as $k \rightarrow 0$, the phase shifts tend to zero according to a power law when $\tau > 0$, but only logarithmically when $\tau = 0$. This significant difference in the behaviour of the phase shifts is due to the fact that in Eq. (92), in the limit of small k, the Bessel function of the second kind $Y_{n - m + 1/2}(k\rho )$ diverges $\propto k^{-\tau /2}$ if $\tau > 0$, whereas it diverges only $\propto \ln (k)$ if $\tau = 0$. Note that the other Bessel function of the second kind $Y_{n - m - 1/2}(k\rho )$ included in Eq. (93) does not cause the logarithmic behaviour of any fermionic phase shift as $k \rightarrow 0$, since the factor $B\rightarrow 0$ in this case. Instead, the Bessel function $Y_{n - m - 1/2}(k \rho )$ causes the logarithmic behaviour of the antifermionic phase shifts $\delta _{3/2\,2}(k)$ and $\delta _{ -5/2\,-2}(k)$ in the limit of small k.

We investigated the behaviour of the curves $\delta _{m n}(k)$ for all possible combinations of signs of m and n. In particular, we found the limiting values of the fermionic phase shifts $\delta _{m n}(k)$ as $k \rightarrow \infty$ as

$$\begin{aligned} \delta _{mn}\left( \infty \right) = -2^{-3/2}\pi \alpha - \left( \nu _{mn}\left( \alpha \right) + 1 \right) \pi \end{aligned}$$

(97)

if $m n > 0$, and

$$\begin{aligned} \delta _{mn}\left( \infty \right) =-2^{-3/2}\pi \alpha -\left( \nu _{mn}\left( \alpha \right) -1\right) \pi \end{aligned}$$

(98)

if $m n < 0$. In Eqs. (97) and (98), $\nu _{m n}(\alpha )$ is the total number of branches $\varepsilon _{m n}^{(i)}$, where $i = 1, \ldots , \nu _{m n}(\alpha )$, emerging from the positive energy continuum on the interval $\left[ \alpha , 0 \right]$. Eqs. (97) and (98) are valid for all (m, n) except those equal to $(-1/2,-2)$, (1/2, 2), and (3/2, 2). For these states, the following relations hold:

$$\begin{aligned} \delta _{-1/2\,-2}\left( \infty \right)= & {} -2^{-3/2}\pi \alpha -\nu _{-1/2\,-2}\left( \alpha \right) \pi , \end{aligned}$$

(99)

$$\begin{aligned} \delta _{1/2\,2}\left( \infty \right)= & {} -2^{-3/2}\pi \alpha -\left( \nu _{1/2\,2}\left( \alpha \right) -1\right) \pi , \end{aligned}$$

(100)

$$\begin{aligned} \delta _{3/2\,2}\left( \infty \right)= & {} -2^{-3/2}\pi \alpha -\nu _{3/2\,2}\left( \alpha \right) \pi . \end{aligned}$$

(101)

We note that the exceptional states of Eqs. (99)–(101) form the sequences $(-3/2,-2)$, $(-1/2,-2)$ and (1/2, 2), (3/2, 2), (5/2, 2) with the “logarithmic” states of Eq. (96).

Fig. 4

Dependence of the energy $\varepsilon _{m n}$ of bound (anti)fermionic states on the parameter $\alpha$. The red, green, blue, and orange solid curves correspond to the fermionic levels $\varepsilon _{-1/2\,-2 }$, $\varepsilon _{-3/2\,-2}$, $\varepsilon _{-5/2\,-2}$, and $\varepsilon _{-7/2 \,-2}$, respectively. The red, green, blue, and orange dashed curves correspond to the antifermionic levels $\varepsilon _{1/2\, 2}$, $\varepsilon _{3/2\, 2}$, $\varepsilon _{5/2\, 2}$, and $\varepsilon _{7/2\, 2}$, respectively

It follows from Eqs. (97)–(101) that the dependence of the value of $\delta _{m n}(\infty )$ on the parameter $\alpha$ is the sum of two terms: the first is a regular linear function of $\alpha$, while the second is an irregular stepwise function of $\alpha$. When $\alpha > 0$, the fermionic bound states are absent, the function $\nu _{m n}(\alpha ) = 0$, and $\delta _{m n}(\infty )$ decreases linearly with an increase in $\alpha$. In contrast, for negative $\alpha$, the function $\nu _{m n}(\alpha )$ increases stepwise by $\pi$ with an increase in $\left| \alpha \right|$. We find that the width of the step (the distance between two successive jumps of $\nu _{m n}(\alpha )$) $\varDelta \alpha \approx 2^{3/2} \approx 2.83$, and this is independent on (m, n). This value of $\varDelta \alpha$ results in the fact that for $\alpha < 0$, the linear term $-2^{-3/2} \pi \alpha$ and the term $-\nu _{m n}(\alpha ) \pi$ compensate each other on average, and the dependence of $\delta _{m n}(\infty )$ on $\alpha$ therefore has a sawtooth shape.

Thus $\delta _{mn}(\infty )$ considered as a function of $\alpha$ changes discontinuously by $\pi$ whenever a new bound fermionic state (m, n) emerges from the positive energy continuum. This behaviour can be explained based on the analytical properties of the S-matrix [41]. Any partial element $S_{mn}$ of the S-matrix can be regarded either as a function of the momentum k or as a function of the energy $\varepsilon = [k^{2}+M^{2}]^{1/2}$. In the latter case, the partial element $S_{mn}\left( \varepsilon \right)$ is an analytical function defined on a two-sheeted Riemann surface with two branch cuts, $\left( -\infty , -M \right]$ and $\left[ M, +\infty \right)$. The physical region of fermionic scattering ($k>0$) corresponds to the upper edge of the first (physical) sheet along the branch cut $\left[ M, +\infty \right)$. The bound fermionic states correspond to the poles of $S_{n m}$, which lie on the physical sheet in the interval $\left( -M, M\right)$.

Suppose a new bound fermionic state (m, n) emerges at $\alpha = \alpha _{0}$. In a small neighbourhood of $\alpha _{0}$, the parameter $\alpha$ can be written as the sum of $\alpha _{0}$ and a small term $\tilde{\alpha }$: $\alpha = \alpha _{0} + \tilde{\alpha }$. A small positive $\tilde{\alpha }$ corresponds to the situation preceding the appearance of the bound fermionic state (m, n). The theory of scattering tells us that in this case, $S_{m n}(\varepsilon )$ has a first-order pole on the second (unphysical) sheet at the point

$$\begin{aligned} \varepsilon = M + \tilde{\varepsilon }_{m n} \left( \tilde{\alpha }\right) - i\varGamma _{mn}\left( \tilde{\alpha }\right) /2, \end{aligned}$$

(102)

where both $\tilde{\varepsilon }_{m n} \left( \tilde{\alpha } \right)$ and $\varGamma _{mn}\left( \tilde{\alpha } \right)$ are positive and tend to zero as $\tilde{\alpha } \rightarrow 0$. In addition, $\varGamma _{mn}\left( \tilde{\alpha }\right) \ll \tilde{\varepsilon }_{mn} \left( \tilde{\alpha }\right)$ for small positive $\tilde{\alpha }$. Thus, for small positive $\tilde{\alpha }$, the partial element $S_{m n}$ has a first-order pole on the unphysical sheet under the branch cut $\left[ M, +\infty \right)$ in the small neighbourhood of the point $\varepsilon = M$. This information is sufficient to obtain the Breit–Wigner formula for the partial phase shift in the threshold region

$$\begin{aligned} \sin \left( \delta _{mn} \right) =\frac{\varGamma _{mn}\left( \tilde{\alpha }\right) /2}{\bigl [ \left( \varepsilon -\varepsilon _{mn}^{r}\left( \tilde{\alpha }\right) \right) ^{2}+\left( \varGamma _{mn}\left( \tilde{\alpha }\right) /2\right) ^{2}\bigr ] ^{\frac{1}{2}}}, \end{aligned}$$

(103)

where $\varepsilon _{m n}^{r}\left( \tilde{\alpha }\right) =M + \tilde{\varepsilon } _{m n}\left( \tilde{\alpha }\right)$.

It follows from Eq. (103) that if $\alpha$ is slightly greater than $\alpha _{0}$, the phase shift $\delta _{m n}$ varies from approximately 0 to $\pi$ in a narrow range of energies centered at the resonance point $\varepsilon = \varepsilon _{m n}^{r}\left( \tilde{\alpha }\right)$. However, as soon as $\alpha$ becomes slightly less than $\alpha _{0}$, a new bound fermionic state (m, n) appears, and the pole of $S_{mn}$ moves from the old position located under the branch cut $\left[ M,+\infty \right)$, through the branch point $\varepsilon = M$, to a new position located on the physical sheet in the interval $(-M, M)$. The new position $\varepsilon = M - \epsilon$ of the pole of $S_{m n}$ makes resonant behaviour (103) impossible, and there is no phase jump by $\pi$ in this case. It follows that $\delta _{m n}(\infty )$ decreases discontinuously by $\pi$ as $\alpha$ changes from $\alpha _{0} + \epsilon$ to $\alpha _{0} - \epsilon$, in accordance with Eqs. (97)–(101).

Fig. 5

Dependence of the fermionic phase shifts $\delta _{m 2}$ on the momentum k for the first few positive values of m (the parameter $\alpha = -2$)

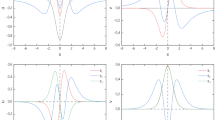
When presenting numerical results for the phase shifts $\delta _{m n}(k)$, we restrict ourselves to the states with $m > 0$ and $n = 2$. For the other combinations of signs of m and n, the behaviour of the phase shifts $\delta _{m n}(k)$ is similar to that for the case considered here, and does not provide any new information. Figure 5 shows the curves $\delta _{m 2}(k)$ for the first few positive values of m. The curves correspond to the parameter $\alpha = -2$. It follows from Fig. 1 that for $\alpha = -2$, there are three bound fermionic states: (1/2, 2), (3/2, 2), and (5/2, 2). Then, Eqs. (100), (101), and (97) tell us that for the fermionic states (1/2, 2), (3/2, 2), and (5/2, 2), the limiting values $\delta _{m 2}(\infty )$ of the phase shifts are $2^{-1/2} \pi \approx 2.22$, $(2^{-1/2} - 1) \pi \approx -0.92$, and $(2^{-1/2} - 2) \pi \approx -4.06$, respectively. This is consistent with the behaviour of the corresponding curves in Fig. 5. Furthermore, it follows from Fig. 1 that for $\alpha = 2$, there are no fermionic bound states (m, 2) with $m > 5/2$. Equation (97) tells us that for these states, $\delta _{m 2}(\infty ) = (2^{-1/2}-1)\pi \approx -0.92$, which is also consistent with Fig. 5.

In Fig. 5, all the curves $\delta _{m 2}(k)$ except for $\delta _{5/2\,2 }(k)$ tend rapidly to zero (according to the power law in Eq. (94)) as $k \rightarrow 0$. In contrast, the curve $\delta _{5/2\,2}(k)$ tends slowly to zero according to the logarithmic law in Eq. (96). We can rewrite partial cross-sections (71) in terms of the phase shifts as $\sigma _{mn}=4k^{-1}\sin \left( \delta _{mn}\left( k \right) \right) ^{2}$. It then follows from Eq. (94) that the partial cross-section

$$\begin{aligned} \sigma _{m n}(k) \propto k^{2\tau - 1} \underset{k \rightarrow 0}{\longrightarrow } 0 \end{aligned}$$

(104)

for all (m, n) except for (5/2, 2) and $(-3/2,-2)$. For these two states, the partial cross-section

$$\begin{aligned} \sigma _{mn}(k)\approx 2\pi ^{2}k^{-1}\ln \left( k\right) ^{-2}, \end{aligned}$$

(105)

and diverges as $k \rightarrow 0$. Hence, the main contribution to the low-energy fermion scattering comes from the “logarithmic” states (5/2, 2) or $(-3/2,-2)$.

Equations  (97)–(101) tell us that in the general case, the phase shift $\delta _{m n}\left( \infty \right) \ne 0 \; \text {mod} \; \pi$. It follows that the partial cross-sections $\sigma _{m n}(k)$ tend to zero $\propto k^{-1}$ as $k \rightarrow \infty$. It also follows from Eqs.  (97)–(101) that for each (m, n), there exists a discrete set of $\alpha _{p} = 2^{3/2} p,\; p \in \mathbb {Z}$ for which the limiting value $\delta _{m n}\left( \infty \right) = 0 \; \text {mod} \;\pi$. From Eq. (A.6), we see that if $\delta _{m n} \left( \infty \right) = 0\; \text {mod}\;\pi$, then the partial cross-sections $\sigma _{m n}(k)$ tend to zero $\propto k^{-3}$ as $k \rightarrow \infty$. Note that although the partial cross-sections tend to zero, the total cross-sections diverge in both cases, which agrees with the results presented in Sect. 4.

Equations (97)–(101) can be considered as a generalisation of Levinson’s theorem [44] for our relativistic case. This theorem relates the difference in the partial phase shifts $\delta _{l} (\infty ) - \delta _{l}(0)$ to the number of corresponding bound states $n_{l}$ in the case of nonrelativistic potential scattering:

$$\begin{aligned} \delta _{l}\left( \infty \right) -\delta _{l}\left( 0\right) =-\pi n_{l}. \end{aligned}$$

(106)

In the derivation of Eq. (106), the nonrelativistic potential is assumed to satisfy certain requirements [41]; in particular, it must decrease faster than $r^{-d}$ as $r \rightarrow \infty$, where d is the spatial dimension.

The main difference between Eqs. (97)–(101) and Eq. (106) is that in our case, the phase shift difference is not equal to $0\!\! \mod \pi$ as in Eq. (106), but is equal to $-2^{-3/2}\pi \alpha \!\! \mod \pi$. It follows that the partial elements $S_{m n}\left( k \right) = \exp \left( 2 i \delta _{m n}\left( k \right) \right)$ tend to the universal limit $\exp (-i 2^{-1/2} \pi \alpha )$ as $k \rightarrow \infty$. This limit is not equal to unity, provided that $\alpha \ne 2^{3/2} p,\; p \in \mathbb {Z}$, and we can therefore say that in the general case, the fermion-soliton interaction does not vanish from the viewpoint of unitarity in the ultrarelativistic limit $k \rightarrow \infty$. The occurrence of the term $-2^{-3/2} \pi \alpha$ is due to the relativistic character of fermionic scattering, and is explained in Appendix A.

Another difference is that in Eq. (106), $n_{l}$ is the number of really existing bound states of angular momentum l for a given nonrelativistic potential. In contrast, in Eqs. (97)–(101), the stepwise function $\nu _{m n}(\alpha )$ is the total number of bound fermionic (m, n) states emerging from the positive energy continuum on the interval $\left[ \alpha , 0 \right]$. From Figs. 1, 2, 3 and 4, we know that for a given value of $\alpha < 0$, some bound fermionic states can reach the lower bound $\varepsilon = -M$ and then disappear. Hence, for a given $\alpha$, the difference $\delta _{m n}\left( \infty \right) - \delta _{m n}\left( 0 \right)$ is determined by both the really existing and disappeared bound fermionic (m, n) states.

6 Conclusion

In this paper, we have studied the scattering of fermions in the background field of a topological soliton of a modified $\mathbb{C}\mathbb{P}^{1}$ model [26], in which a potential term was added to the Lagrangian of the original $\mathbb{C}\mathbb{P}^{1}$ model. This potential term breaks the invariance of the action of the original $\mathbb{C}\mathbb{P}^{1}$ model under the scale transformations $\textbf{x} \rightarrow \lambda \textbf{x}$. As a result, the energy of the soliton of the modified $\mathbb{C}\mathbb{P}^{1}$ model depends on its size, which is fixed by a conserved Noether charge. For this reason, the soliton has no dilatation zero mode, meaning that it does not suffer from the rolling scale instabilities inherent to solitons of the original $\mathbb{C}\mathbb{P}^{1}$ model.

Both the original and modified $\mathbb{C}\mathbb{P}^{1}$ models are invariant under local U(1) transformations, and hence include an Abelian gauge field. This field, however, is not dynamic, since there is no corresponding kinetic term in the Lagrangian (1). The incorporation of fermions into the $\mathbb{C}\mathbb{P}^{1}$ model is realised through their minimal interaction with the Abelian gauge field. As a result, the fermion-soliton interaction looks like an interaction between an electrically charged particle and a two-dimensional object (soliton) with long-range electric and magnetic fields.

The presence of the long-range “electric” field leads to the existence of bound (anti)fermionic states. These bound fermionic (antifermionic) states exist only at negative (positive) values of the parameter $\alpha$ that determines the phase frequency of the $\mathbb{C}\mathbb{P}^{1}$ soliton. As $\left| \alpha \right|$ increases, the fermionic (antifermionic) bound states emerge from the positive (negative) energy continuum of states and then disappear when the negative (positive) energy continuum of states is reached. The invariance of the Lagrangian (1) under charge conjugation leads to a certain symmetry between the fermionic and antifermionic states of the $\mathbb{C}\mathbb{P}^{1}$ solitons whose parameters are opposite in sign. At the same time, the spectrum of bound states and the spectral density of continuum states of the $\mathbb{C}\mathbb{P}^{1}$ soliton with given parameters n and $\alpha$ are not invariant under charge conjugation, which leads to the induction of the fermion number on the $\mathbb{C}\mathbb{P}^{1}$ soliton.

In addition to the bound (anti)fermionic states of the discrete spectrum, there exist scattering (anti)fer- mionic states of the continuous spectrum. We have investigated the (anti)fermion scattering in the framework of the Born and semiclassical approximations, and also by numerical methods. In particular, we have found that due to the long-range character of the Abelian gauge field, the total scattering cross-section diverges, whereas the transport cross-section remains finite.

Fermion scattering can be completely described in terms of partial phase shifts. In view of this, we have investigated the momentum dependence of the partial phase shifts using approximate analytical and numerical methods. In particular, we have established the relations between the difference in the partial phase shifts and the number of corresponding bound fermionic states. These relations are a generalisation of Levinson’s theorem for our relativistic case. The main difference is that in our case, the difference in the partial phase shifts is not equal to $0\mod \pi$ (an integer multiple of $\pi$) as stated by Levinson’s theorem; instead, this difference is equal to $-2^{-3/2}\pi \alpha \, \mod \, \pi$. It follows that as the fermion momentum $k \rightarrow \infty$, the partial elements of the S-matrix tend to the universal limit $\exp (-i 2^{-1/2} \pi \alpha )$, which is different from unity in the general case. Hence, the fermion-soliton interaction does not tend to zero from the viewpoint of unitarity in the ultrarelativistic limit $k \rightarrow \infty$.

The $\mathbb{C}\mathbb{P}^{1}$ Q-lumps discussed in this present paper can be generalised to a whole class of Kähler sigma models with potential terms, provided the target manifold has a Killing vector field with at least one fixed point [45]. In particular, such a generalisation can be done for $\mathbb{C}\mathbb{P}^{N-1}$ models with $N \ge 3$. The results obtained here for the $\mathbb{C}\mathbb{P}^{1}$ model can be easily extended to this general case.

Partial phase shifts in the semiclassical approximation

Besides the Born approximation, we can also study the fermion scattering within the semiclassical approximation [40]. This approximation is applicable when the fermion momentum $k \gg 1$, where we use the dimensionless variables from Sect. 5. In this case, we can use normal form (53) of the second-order differential equation to obtain a semiclassical expression for the partial phase shifts as follows:

$$\begin{aligned} \delta _{mn}\left( k\right)\approx & {} \int \limits _{\rho _{0}}^{\infty }\left\{ \left[ k^{2}-\left( m-1/2\right) ^{2}\rho ^{-2}-W\left( \rho \right) \right] ^{1/2}\right. \nonumber \\{} & {} -\left. \left[ k^{2}-\left( m-1/2\right) ^{2}\rho ^{-2}\right] ^{1/2}\right\} d\rho , \end{aligned}$$

(A.1)

where the lower limit of integration

$$\begin{aligned} \rho _{0}\approx \left| m-1/2\right| /k, \end{aligned}$$

(A.2)

and the semiclassical potential

$$\begin{aligned} W\left( \rho \right)= & {} -\frac{\alpha ^{2}}{\left( 1+\rho ^{4}\right) ^{2}}+\frac{2\alpha \varepsilon }{1+\rho ^{4}} \nonumber \\{} & {} -\frac{2(2m-3)(\varepsilon +M)\rho ^{2}}{\varepsilon - \alpha +M+(\varepsilon +M)\rho ^{4}} \nonumber \\{} & {} -\frac{12(\varepsilon +M)(\varepsilon -\alpha +M)\rho ^{2}}{\left( \varepsilon -\alpha +M+(\varepsilon + M)\rho ^{4}\right) ^{2}} \nonumber \\{} & {} +\frac{2-n}{4}R(\rho ). \end{aligned}$$

(A.3)

In Eq. (A.3), the function $R(\rho )$ is a ratio of two polynomial functions, $R(\rho ) = A(\rho )/B(\rho )$, where

$$\begin{aligned} A(\rho )= & {} 4(2m+3)(\varepsilon - \alpha + M)\rho ^{2}+4(2m-1) \nonumber \\{} & {} \times (\varepsilon + M)\rho ^{6} \end{aligned}$$

(A.4)

and

$$\begin{aligned} B(\rho )=\left( 1+\rho ^{4}\right) \left( \varepsilon -\alpha + M + (\varepsilon + M)\rho ^{4} \right) . \end{aligned}$$

(A.5)

Although the integral in Eq. (A.1) cannot be calculated analytically, in the limit of large k, we can compute the first few terms of its asymptotic expansion using approximate analytical methods as

$$\begin{aligned} \delta _{mn}\left( k\right)\sim & {} -2^{-3/2}\pi \alpha +2^{-5/2}\pi \nonumber \\{} & {} \times \left( 2mn -3\right) k^{-1}+O\left[ k^{-3/2}\right] . \end{aligned}$$

(A.6)

Note that in the theory of scattering, the phase shifts $\delta _{mn}$ are not unique, but are defined only up to an integer multiple of $\pi$. The characteristic feature of phase shifts (A.6) is that $\underset{k \rightarrow \infty }{\lim }\ \delta _{m n} \left( k \right) = -2^{-3/2} \pi \alpha$, and is not equal to $0 \, \text {mod} \,\pi$ in the general case. Note, however, that $\underset{k \rightarrow \infty }{\lim }\delta _{m n} \left( k \right) = 0 \,\text {mod}\,\pi$ if $\alpha =2^{3/2} p$, where $p \in \mathbb {Z}$.

In Eq. (A.6), the limiting term $-2^{-3/2} \pi \alpha$ is due to the term $2 \alpha \varepsilon \left( 1 + \rho ^{4} \right) ^{-1} \sim 2 \alpha k \left( 1 + \rho ^{4}\right) ^{-1}$ in Eq. (A.3), which increases indefinitely with an increase in k. This term, in turn, arises from the square of the time component of covariant derivative (3b) included in the Dirac equation (5). The nonzero (modulo $\pi$) limiting value of $\delta _{m n}\left( k\right)$ tells us that in the general case, the fermion-soliton interaction does not tend to zero from the viewpoint of unitarity, even in the ultrarelativistic limit $k \rightarrow \infty$.

A similar situation is seen for the Coulomb scattering of fermions. In this three-dimensional case, a term proportional to the fermion energy $\varepsilon$ also arises when the Dirac equation is squared, and the partial phase shifts (determined with account of the logarithmically divergent Coulomb phase) tend to nonzero values as $k \rightarrow \infty$.

Finally, we note that the Born phase shifts in Eq. (87) tend to the same limiting value of $-2^{-3/2}\pi \alpha$ as the semiclassical phase shifts in Eq. (A.6). Furthermore, the next-to-leading order terms of Eqs. (87) and (A.6) practically coincide for sufficiently large values of $\left| m \right|$, when the accuracy of the semiclassical approximation improves.