1 Introduction

Scientists and authors have been fascinated by the idea of wormholes for ages. Numerous works of science fiction have drawn inspiration from these improbable spacetime tunnels that connect distant regions of the cosmos. They have also grown to be an exciting topic of study in theoretical physics. The history of wormholes is a testament to humanity’s curiosity and willingness to investigate the universe’s mysteries, even though they are still hypothetical and unproven. A wormhole (WH) is a hypothetical route that theoretically connects faraway regions of the cosmos, cutting down on both travel time and distance.

In terms of history, Flamm [1] first suggested the concept of this hypothetical structure in 1916. After Flamm’s ideas, Einstein and Rosen proposed a bridge [2] that looked like a structure. On the other hand, Misner and Wheeler first used the word “wormhole” in 1957 [3] to describe these entities as spaces having several connected topologies. Without scalar charge, Bronnikov (1973) investigated the scalar-electrovacuum situations [4]. In higher dimensions, a class of traversable wormholes was presented by Clement [5]. The thin-shell wormhole that Visser created in 1989 [6] via the cut-and-paste approach gave rise to a new class of wormholes on its own.

Wormholes, also known as astrophysical compact objects, are unique, non-trivial topological structures that lack singularities and horizons [7]. The structures have been examined using a variety of methods, including applying certain equations of state, constraining fluid parameters, and solving metric elements. These geometric models can be visualized as a means of warp drives, time travel, and swift interstellar travel. Within the context of the general theory of relativity (GR), the static and spherically symmetric Lorentzian wormhole solutions are studied. When examining the characteristics and behavior of traversable WHs, shape functions are crucial. It is a mathematical function that expresses the spatial geometry of the WH, particularly the relationship between the radius of the neck and the radial coordinate [8].

The research of Visser et al. [9] has demonstrated that, with the right wormhole geometry selection, the null energy condition (NEC) violation can be contained to an arbitrarily small region. The presence of an exotic matter component, which causes the EMT to deviate from the NEC, is one of the necessities for developing a WH within the framework of GR. The NEC, which is violated by the flaring-out condition through the Einstein field equations, is necessary for the wormhole spacetime to be traversable in GR, which in turn violates all of the energy conditions [9,10,11,12]. Violating the NEC acts as a source of exotic matter. Now there has recently been a rise in interest among scientists on modified theories of gravity.

Through the work [13] of Xu et al., the \(F(\texttt{Q})\) gravity was expanded to become the \(\texttt{F}(\texttt{Q, T})\) gravity, where \(\texttt{T}\) is the trace of the EMT. This kind of trace gives classical gravity additional contributions from the quantum domain. The validity of cosmological models for \(\texttt{F}(\texttt{Q, T})\) gravity with energy conditions was recently revealed by Arora et al. [14], while according to Tayde et al. [15], the stability of a thin-shell encircling the wormhole and its potential was ascertained by using the Israel junction condition [16].

Further development of \(F(\texttt{R})\) gravity, the \(\texttt{F}(\texttt{R, T})\) theory of gravity takes into account the dependency of the stress-energy tensor trace \(\texttt{T}\) as well as the scalar curvature \(\texttt{R}\) in the gravitational action. The fields of cosmology [17, 18], thermodynamics [19, 20], and astrophysics of compact objects have [21,22,23] examined this \(F(\texttt{R, T})\) gravity. Particularly, \(\texttt{F}(\texttt{R, T})\) gravity-specific examples include \(\texttt{F}(\texttt{R})\) and \(\texttt{F}(\texttt{T})\) theories. \(\texttt{F}(\texttt{R})\) and \(\texttt{F}(\texttt{T})\) gravity are combined in the \(\texttt{F}(\texttt{R, T})\)) gravity theory. Several functional variants of \(\texttt{F}(\texttt{R, T})\) theories have been examined for the impact of cosmic dynamics in multiple contexts [24]. Similar to the \(\texttt{F}(\texttt{R, T})\), the newly formulated \(\texttt{F}(\texttt{Q, T})\) gravity is built [25, 26], but the mathematical component of the action is substituted by the symmetric teleparallel approach.

Wormholes can be tested by many gravity theories such as Einstein–Gauss–Bonnet gravity [27,28,29], Rastall theory of gravity [30, 31], supported by Chaplygin gas with its modified and generalized forms [32,33,34,35], Born-field theory [32, 36], Einstein–Cartan gravity [37,38,39], Braneworld [40,41,42] etc. Mustafa et al. recently looked at the geometry of wormholes in galactic halo regions with changing symmetric teleparallel gravity [43]. In the framework of \(\texttt{F}(\texttt{R})\) gravity, Lobo et al. [44] created traversable wormhole geometries by taking into account a variety of state equations and certain shape functions. Maurya et al. used matter coupling gravity formalism [45] with observational data to look for potential wormhole solutions. Our focus in this work is on \(\texttt{F}(\texttt{Q, T})\) gravity and \(F(\texttt{R, T})\) gravity, which is an extension of \(\texttt{F}(\texttt{Q})\) and \(\texttt{F}(\texttt{R})\) gravity respectively. We also showed that these wormholes are stable with the help of the equilibrium conditions derived from the generalized TOV.

Film scriptwriters and science fiction writers have long utilized the WH as an essential premise. Humans can quickly move from Point A to Point B over great distances in spacetime using these tunnel-like constructions [46]. Although many theorists have speculated about the possibility of these spacetime gateways for decades, no one has until recently been able to offer concrete evidence of their existence.

To examine the wormhole mechanism in the modified theory of gravity, the major objective of this research is to propose a new form function. The following paragraphs provide an overview of the concepts discussed in the present work. Section 2 provides WH’s framework, which includes basic conditions for form function and energy conditions. In Sect. 3 we discussed the field equation of \(\texttt{F}(\texttt{Q, T})\) gravity and \(\texttt{F}(\texttt{R, T})\) gravity. In Sect. 4 we covered graphical and theoretical analysis of energy conditions for wormhole geometry. Further, we evaluate the Equilibrium condition in Sect. 5, the Surface diagram in Sect. 6, and the exoticity parameter in Sect. 7. Our findings are concluded in the final portion 8.

2 Wormhole framework

In this part, we characterize and extract relevant information about the geometry of wormholes using a shape function. For the redshift and shape functions, we search for wormhole solutions taking into account the following constraints [47].

  1. 1.

    The radial coordinate r lies between \(r_{0}\le r <\infty \), where \(r_{0}\) is throat radius.

  2. 2.

    The shape function should follow throat condition at \(r=r_{0}\), \(\texttt{R}_{s} (r_{0})=r_{0}\), \(\texttt{R}_{s} (r)< r \) for \(r > r_{0}\) that is out of throat.

  3. 3.

    For flaring out condition at the throat, \(\texttt{R}_{s} (r)\) has to follow, \(\texttt{R}_{s} ^{\prime }(r_{0})< 1\;\;i.e. \frac{\texttt{R}_{s} (r)-r\texttt{R}_{s} ^{\prime }(r)}{\texttt{R}_{s} ^{2}(r)}>0 \).

  4. 4.

    For Asymptotical flatness: \(\displaystyle {\lim _{r\rightarrow \infty }\frac{\texttt{R}_{s} (r)}{r}=0}\) is fulfilled.

  5. 5.

    All instances of the redshift function \(\epsilon (r)\) should be finite.

In this work, we take a novel shape function [48] for both gravities

$$\begin{aligned} \texttt{R}_{s} (r)=e^{1-\frac{r}{r_{0}}}\cosh \left( \frac{r}{r_{0}}\right) . \end{aligned}$$
(1)
Fig. 1
figure 1

Characteristics of shape function \(\texttt{R}_{s} (r)\) with \(r_{0}=1.55\)

Full size image

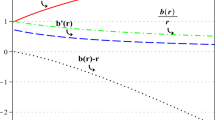
The provided Fig. 1 clarifies that our suggested shape function satisfies all requirements. The results obtained using this shape function are identical to those of a study on traversable wormholes conducted within the framework of modified gravity theories [49,50,51,52,53].

2.1 Energy conditions

Studying these energy conditions is necessary to learn about the characteristics of spacetime and the matter sources that create it. In general relativity, the NEC is seen to be the most important of these criteria for wormhole solutions because of its association with the energy density necessary to keep the wormhole throat open. The presence of exotic material with negative energy density, which is absent from sources of ordinary matter, would be indicated by the NEC occurring at a wormhole’s throat [54]. The energy conditions are

  • To satisfy the NEC, the energy density and pressure must total up to be non-negative in all directions (\(\rho +\mathscr {P}_{j} \ge 0 \) for \(j=r,t\)).

  • The energy density must always be non-negative by the Weak energy condition (WEC), and the total of the energy density and pressure must likewise be non-negative in any direction ( \(\rho \ge 0\) & \(\rho +\mathscr {P}_{j} \ge 0 \) for \(j=r,t\)).

  • For there to be a Dominant energy condition (DEC), There must be no negative energy density and the energy density has to balance all pressures (\(\rho \ge 0\) & \(\rho - |\mathscr {P}_{j}| \ge 0 \) for \(j=r,t\)). The DEC states that the speed of light, which is the fastest that energy can move, is the limit for any flow of energy or matter [55].

  • The energy density and the total of the energy density and pressure in all directions must not be negative to satisfy the strong energy condition (SEC), which is the strongest energy condition (\(\rho +\mathscr {P}_{r}+2\mathscr {P}_{t} \ge 0\)).

3 Background of the field equations in modified gravity theory

3.1 The basic field equations in \(F(\texttt{Q, T})\)-gravity for wormhole geometry

We take into account the symmetric teleparallel gravity action put out by Xu et al. [13]

$$\begin{aligned} \mathtt {S_{\texttt{G}}}=\int \Bigg [\frac{F(\texttt{Q, T})}{16\pi }+\texttt{L}_{m}\Bigg ]\sqrt{-g}d^{4}x. \end{aligned}$$
(2)

In this scenario, \(F(\texttt{Q, T})\) is a function of the non-metricity of \(\texttt{Q}\) and the trace of the EMT is \(\texttt{T}\), g is the metric’s determinant of \(g_{\beta \eta }\), and \(\texttt{L}_{m}\) is the density of the Lagrangian of the matter. The explicit notation for the non-metricity tensor is [56]

$$\texttt{Q}_{\alpha \beta \eta }=\nabla _{\alpha }g_{\beta \eta }.$$

The non-metricity conjugate or superpotential is another important component of this theory. Its form is

$$\begin{aligned} \mathscr {P}^{\tau }\hspace{0.1cm}_{\beta \eta }=\frac{1}{4}\left[ -\texttt{Q}^{\tau }_{\hspace{0.2cm}\beta \eta }+2\texttt{Q}^{\hspace{0.2cm}\tau }_{(\beta \hspace{0.1cm}\eta )}-\texttt{Q}^{\tau }g_{\beta \eta }-\tilde{\texttt{Q}}^{\tau }g_{\beta \eta }-\delta ^{\tau }_{(\beta }\texttt{Q}_{\eta })\right] , \end{aligned}$$

where \(\texttt{Q}_{\tau }=\texttt{Q}_{\tau \hspace{0.2cm}\beta }^{\hspace{0.2cm}\beta }\),    \(\tilde{\texttt{Q}}^{\beta }\hspace{0.1cm}_{\tau \beta }\) are the non-metricity tensor’s traces. By adopting the following contraction from the above formulation, one can get the non-metricity scalar as

$$\begin{aligned} \hspace{0.5cm}\texttt{Q}= & {} -\texttt{Q}_{\tau \beta \eta }\mathscr {P}^{\tau \beta \eta }\end{aligned}$$
(3)
$$\begin{aligned} \hspace{0.9cm}= & {} -g^{\beta \eta }(\texttt{L}^{\xi }_{\tau \beta }\texttt{L}^{\tau }_{\beta \xi }-\texttt{L}^{\xi }{\tau \xi }\texttt{L}^{\tau }_{\beta \eta }) \end{aligned}$$
(4)

the disformation \(\mathtt {L^{\xi }_{\beta \eta }}\) is characterised as

$$ \mathtt {L^{\xi }_{\beta \eta }}=\frac{1}{2}\texttt{Q}^{\xi }_{\beta \eta }-\texttt{Q}^{\hspace{0.3cm}\xi }_{(\beta \hspace{0.2cm}\eta )}. $$

Now, by changing the action concerning the metric tensor \(g_{\beta \eta }\), we can derive the equations of motion for \(F(\texttt{Q, T})\) gravity, which has the following form:

$$\begin{aligned}{} & {} \hspace{-0.5cm} \frac{-2}{\sqrt{-g}}\nabla _{\tau }(\sqrt{-g}F_{\texttt{Q}}\mathscr {P}^{\tau }_{\hspace{0.3cm} \beta \eta })-\frac{1}{2}g_{\beta \eta }F- F_{\texttt{Q}}(\mathscr {P}_{\beta \tau \xi }\texttt{Q}_{\eta }^{\hspace{0.2cm}\tau \xi } \nonumber \\{} & {} \hspace{0.5cm}-2\texttt{Q}^{\tau \xi }_{\beta }\mathscr {P}_{\tau \xi \eta }) = 8\pi T_{\beta \eta }-F_{\texttt{T}}(\texttt{T}_{\beta \eta }+\Theta _{\beta \eta }), \end{aligned}$$
(5)

where \(\texttt{F}_{\texttt{Q}}=\frac{\partial F}{\partial \texttt{Q}}\),  \(F_{\texttt{T}}=\frac{\partial F}{\partial \texttt{T}}\).

As we write for notational simplified \(F_\texttt{Q}=\frac{\partial F}{\partial \texttt{Q}}\) and the tensor of energy–momentum \(\texttt{T}_{\beta \eta }\) is given by

$$\begin{aligned} \texttt{T}_{\beta \eta }=-\frac{2}{\sqrt{-g}}\frac{\partial \sqrt{-g}\texttt{L}_{m}}{\partial g^{\beta \eta }}. \end{aligned}$$
(6)

and

$$\begin{aligned} \Theta _{\beta \eta }=g^{\tau \xi } \frac{\delta \texttt{T}_{\tau \xi }}{\delta g^{\beta \eta }}. \end{aligned}$$
(7)

According to Morris and Thorne’s original study, let’s examine the static and spherically symmetric wormhole metric in Schwarzschild coordinates (\(t, r,\theta , \Phi \)), whose exact form is

$$\begin{aligned} ds^{2}= & {} e^{2 \epsilon (r)}dt^{2}-\left( 1-\frac{\texttt{R}_{s} (r)}{r}\right) ^{-1}dr^{2}\nonumber \\{} & {} -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\Phi ^{2}), \end{aligned}$$
(8)

where, respectively, “\(\texttt{R}_{s} (r)\)” and “\(\epsilon (r)\)” stand for the shape function and red-shift function. Given that we are writing the line element in Schwarzschild form and assuming that the wormhole solutions for \(F(\texttt{Q, T})\) are consistent with Birkhoff’s theorem. Our speculation about the validity of Birkhoff’s theorem is based on the work of Meng and Wang [57] as well as the most current review of Bahamond et al. [58].

We analyze wormhole solutions in this work by assuming an anisotropic EMT, which is provided by [59] and represented by Eq. (9), i.e.

$$\begin{aligned} T_{\beta \eta }=(\rho +\mathscr {P}_{t})u_{\beta }u_{\eta }-\mathscr {P}_{t}\delta ^{\beta }_{\eta }+(\mathscr {P}_{r}-\mathscr {P}_{t})\chi _{\beta }\chi ^{\eta }. \end{aligned}$$
(9)

where, respectively, \(\mathscr {P}_{r}\) and \(\mathscr {P}_{t}\) stand for radial and tangential pressures, and all are functions of the radial coordinate r, where \(\rho \) stands for the energy density. The four vectors of motion and unitary space-like vector are denoted by the symbols \(u_{\beta }\) and \(\chi _{\beta }\).

To examine a two-fluid model in plasma physics, Letelier [60] introduced the anisotropic EMT. Additionally, it has been used in various circumstances for modeling magnetized neutron stars [61]. As can be shown from Eq. (9), the trace of the EMT is such that \(\texttt{T}=\rho +\mathscr {P}_{r}-2\mathscr {P}_{t}\). In this article, we work with the matter lagrangian \(\texttt{L}_{m} =-\mathscr {P}\) [62], where \(\mathscr {P}=\frac{\mathscr {P}_{r}+2\mathscr {P}_{t}}{3}\) Such Lagrangian changes Eq. (6) to

$$\Theta _{\beta \eta }=-g_{\beta \eta }\mathscr {P}-2\texttt{T}_{\beta \eta }.$$

Furthermore, the explicit written non-metricity scalar \(\texttt{Q}\) for the metric (7) is

$$\begin{aligned} \texttt{Q}=-\frac{\texttt{R}_{s} (r)}{r^{2}}\Bigg [\frac{r\texttt{R}_{s}^{\prime } (r)-\texttt{R}_{s} (r)}{r(r-\texttt{R}_{s} (r))}+2\epsilon ^{\prime }(r)\Bigg ]. \end{aligned}$$
(10)

The field equations related to \(\texttt{F}(\texttt{Q}, T)\) gravity are shown below:

$$\begin{aligned} 8\pi \rho (r)= & {} \frac{1}{2r^{2}}\left( 1-\frac{\texttt{R}_{s} }{r}\right) \Bigg [2rF_{\texttt{Q}\texttt{Q}}\texttt{Q}^{\prime }\frac{\texttt{R}_{s} }{r-\texttt{R}_{s} }\nonumber \\{} & {} +F_{\texttt{Q}}\bigg (\frac{\texttt{R}_{s} }{r-\texttt{R}_{s} }(2+2r \epsilon ^{\prime }(r))\nonumber \\{} & {} +\frac{(2r-\texttt{R}_{s} )(\texttt{R}_{s} ^{\prime }r-\texttt{R}_{s} )}{(r-\texttt{R}_{s} )^{2}}\bigg )\nonumber \\{} & {} -\frac{2r^{3}F_{\texttt{T}}(\mathscr {P}+\rho )}{(r-\texttt{R}_{s} )}+F\frac{r^{3}}{r-\texttt{R}_{s} }\Bigg ], \end{aligned}$$
(11)
$$\begin{aligned} 8\pi \mathscr {P}_{r}= & {} -\frac{1}{2r^{2}}\left( 1-\frac{\texttt{R}_{s} }{r}\right) \Bigg [2rF_{\texttt{Q}\texttt{Q}}\texttt{Q}^{\prime }\frac{\texttt{R}_{s} }{r-\texttt{R}_{s} }\nonumber \\{} & {} \quad +F_{\texttt{Q}}\left( \frac{\texttt{R}_{s} }{r-\texttt{R}_{s} }\left( 2+\frac{r\texttt{R}_{s} ^{\prime }-\texttt{R}_{s} }{r-\texttt{R}_{s} }+2r \epsilon ^{\prime }(r)\right) \right. \nonumber \\{} & {} \quad \left. -4r \epsilon ^{\prime }(r)\right) -\frac{2r^{3}F_{\texttt{T}}(\mathscr {P}-\mathscr {P}_{r})}{(r-\texttt{R}_{s} (r))}\nonumber \\{} & {} \quad +F\frac{r^{3}}{r-\texttt{R}_{s} }\Bigg ], \end{aligned}$$
(12)
$$\begin{aligned} 8\pi \mathscr {P}_{t}= & {} -\frac{1}{4r}\left( 1-\frac{\texttt{R}_{s} }{r}\right) \Bigg [-4r \epsilon ^{\prime }(r)F_{\texttt{Q}\texttt{Q}}\texttt{Q}^{\prime }\nonumber \\{} & {} \quad +F_{\texttt{Q}}\left( 4\epsilon ^{\prime }(r)\frac{2\texttt{R}_{s} -r}{r-\texttt{R}_{s} }-4r(\epsilon ^{\prime }(r))^{2}\right. \nonumber \\{} & {} \quad \left. +\frac{r\texttt{R}_{s} ^{\prime }-\texttt{R}_{s} }{r(r-\texttt{R}_{s} )}\left( \frac{2r}{r-\texttt{R}_{s} }+2r \epsilon ^{\prime }(r)\right) -4r \epsilon ^{\prime \prime }(r)\right) \nonumber \\{} & {} \quad -\frac{4r^{2}F_{\texttt{T}}(\mathscr {P}-\mathscr {P}_{t})}{(r-\texttt{R}_{s} )}+2F\frac{r^{2}}{r-\texttt{R}_{s} }\Bigg ] . \end{aligned}$$
(13)

Our three equations Eq. (11) through Eq. (13) contain six unknown functions, including \(\rho \), \(\texttt{R}_{s} (r)\), \(\epsilon (r)\), \(\mathscr {P}_{r}\), \(F(\texttt{Q, T})\) and \(\mathscr {P}_{t}\). For the traversable wormholes to avoid having horizons, the redshift function \(\epsilon (r)\) must be finite everywhere [59]. To derive analytic constraints over the energy conditions, one simple form of \(\epsilon (r)\) that is finite is as follows: \(\epsilon (r)=Constant\) and we take into account the \(F(\texttt{Q, T})\) gravity’s linear functional form, which is given by

$$\begin{aligned} \texttt{F}(\texttt{Q, T})=\vartheta \texttt{Q}+\kappa \texttt{T}, \end{aligned}$$
(14)

where \(\vartheta \) and \(\kappa \) are model parameters. After simplifying these values we obtained these equations

$$\begin{aligned} \rho= & {} \frac{\vartheta (12\pi -\kappa )\texttt{R}_{s}^{\prime } }{3(4\pi -\kappa )(\kappa +8\pi )r^{2}},\end{aligned}$$
(15)
$$\begin{aligned} \mathscr {P}_{r}= & {} -\frac{\vartheta (2\kappa r\texttt{R}_{s} ^{\prime }-3\kappa \texttt{R}_{s} +12\pi \texttt{R}_{s} )}{3(4\pi -\kappa )(\kappa +8\pi )r^{3}},\end{aligned}$$
(16)
$$\begin{aligned} \mathscr {P}_{t}= & {} -\frac{\vartheta ((\kappa +12\pi )r\texttt{R}_{s} ^{\prime }+3\texttt{R}_{s} (\kappa -4\pi ))}{6(4\pi -\kappa )(\kappa +8\pi )r^{3}}. \end{aligned}$$
(17)

3.2 The basic field equations in \(\texttt{F}(\texttt{R,T})\)-gravity under wormhole geometry

The general relativity of Einstein has been modified by Harko et al. [25] by replacing \(F(\texttt{R})\) with an arbitrary function \(F(\texttt{R, T})\), where \(\texttt{T}\) represents the EMT’s trace and the gravitational action is explained as

$$\begin{aligned} \mathtt {S_{\texttt{G}}}=\int \sqrt{-\texttt{g}}\Bigg [\frac{1}{16\pi }F(\texttt{R,T})+\texttt{L}_{m}\Bigg ]d^4 x. \end{aligned}$$
(18)

where \(F(\texttt{R,T})\) is an arbitrary function of the Ricci scalar, \(\texttt{T}\) is the trace of the stress EMT, and \(\texttt{L}_{m}\) is the Lagrangian density of matter of the source. Imperfect fluids may exist in the cosmos, which is what drives the additional material terms in the gravitational force.

The definition of the EMT \(\texttt{T}_{\xi \eta }\) from Lagrangian matter is as follows:

$$\begin{aligned} \texttt{T}_{\xi \eta }=-\frac{2}{\sqrt{-g}}\frac{\partial \sqrt{-g}\texttt{L}_{m}}{\partial g^{\xi \eta }}. \end{aligned}$$
(19)

and trace is given by \(\texttt{T}=g^{\xi \eta }\texttt{T}_{\xi \eta }\)

On taking variation action of Eq. (18) with respect to metric \(g_{\xi \eta }\), field equations are given by

$$\begin{aligned}{} & {} F_{\texttt{R}}(\texttt{R,T})\texttt{R}_{\xi \eta }-\frac{1}{2}F(\texttt{R,T})g_{\xi \eta }\nonumber \\{} & {} \quad +[g_{\xi \eta }\square -\nabla _{\xi }\nabla _{\eta }]F_ {\texttt{R}}(\texttt{R,T})\nonumber \\ {}{} & {} \qquad =8\pi T_{\xi \eta }-F_{\texttt{T}}(\texttt{R,T})\texttt{T}_{\xi \eta }-F_{\texttt{T}}(\texttt{R,T})\Theta _{\xi \eta } \end{aligned}$$
(20)

Here

$$\Theta _{\xi \eta }=-2\texttt{T}_{\xi \eta }+g_{\xi \eta }\texttt{L}_{m}-2g^{\texttt{L}_{m}}\frac{\partial ^2\texttt{L}_{m}}{\partial g^{\xi \eta }\partial g^{\texttt{L}_{m}}},$$

where \(F_{\texttt{R}}(\texttt{R,T})=\frac{\partial F(\texttt{R,T})}{\partial \texttt{R}}\) and \(F_{T}(\texttt{R,T})=\frac{\partial F(\texttt{R,T})}{\partial \texttt{T}}\)    \(\square =\nabla ^{\xi }\nabla _{\eta }\) called D’Alembert Operator and \(\nabla _{\xi },\nabla _{\eta }\) are called covariant derivative.

A source term for the curvature of space-time can be thought of as the EMT. The anisotropic fluid’s EMT in this model is provided as

$$\begin{aligned} T^{\xi }_{\eta }=(\rho +\mathscr {P}_{t})u^{\xi }u_{\eta }-\mathscr {P}_{t}g^{\xi }_{\eta }+(\mathscr {P}_{r}-\mathscr {P}_{t})x^{\xi }x_{\eta }, \end{aligned}$$
(21)

by taking matter Lagrangian as \(\texttt{L}_{m}=-(\frac{\mathscr {P}_{r}+2\mathscr {P}_{t}}{3})\).

Now for \(F (\texttt{R, T} ) =\texttt{R} + 2F(\texttt{T} )\), to \(F(\texttt{T}) = \chi \texttt{T}\), where \(\chi \) is a constant, and the gravitational field equation is obtained as

$$\begin{aligned} \texttt{G}_{\eta }^{\xi }=(8\pi +2\chi )\texttt{T}_{\eta }^{\xi }+\chi (\rho -\mathscr {P}). \end{aligned}$$
(22)

The wormhole’s geometry in spherically symmetric spacetime is as follows

$$\begin{aligned} ds^{2}= & {} -e^{2 \epsilon (r)}dt^{2}+\left( 1-\frac{\texttt{R}_{s} (r)}{r}\right) ^{-1}dr^{2}\nonumber \\ {}{} & {} +r^{2}(d\theta ^{2}+\sin ^{2}\theta d\Phi ^{2}). \end{aligned}$$
(23)

For the metric Eq. (23) with a constant redshift function (i.e. \(\epsilon ^{\prime }(r)= 0\)), the field equations from Eq. (22) are as follows:

$$\begin{aligned} \frac{\texttt{R}_{s} ^\prime }{r^2}= & {} (8\pi +3\chi )\rho -\frac{1}{3}\chi \mathscr {P}_{r}-\frac{2}{3}\chi \mathscr {P}_{t} \end{aligned}$$
(24)
$$\begin{aligned} \frac{\texttt{R}_{s} }{r^3}= & {} -(8\pi +\frac{7}{3}\chi )\mathscr {P}_{r}+\chi \rho -\frac{2}{3}\chi \mathscr {P}_{t} \end{aligned}$$
(25)
$$\begin{aligned} \frac{\texttt{R}_{s} ^\prime r-\texttt{R}_{s} }{2r^3}= & {} -(8\pi +\frac{8}{3}\chi )\mathscr {P}_{t}-\frac{1}{3}\chi \mathscr {P}_{r} +\chi \rho . \end{aligned}$$
(26)

We have three distinct equations for our four unknown quantities. To construct wormhole solutions, a variety of techniques can be applied. Here we use the shape function (Eq. 1) and then after simplifications, we get the stress-energy tensor components:

$$\begin{aligned} \hspace{-0.5cm} \rho= & {} -\frac{e^{1-\frac{2r}{r_{0}}}(12\pi +5\chi )}{12r_{0}r^{2}(4\pi +\chi )(2\pi +\chi )} \end{aligned}$$
(27)
$$\begin{aligned} \hspace{-0.5cm}\mathscr {P}_{r}= & {} \frac{e^{1-\frac{2r}{r_{0}}}(-r\chi +3(1+\frac{2r}{r_{0}})r_{0}(2\pi +\chi ))}{12r_{0}r^{3}(2\pi +\chi )(4\pi +\chi )} \end{aligned}$$
(28)
$$\begin{aligned} \hspace{-0.5cm}\mathscr {P}_{t}= & {} -\frac{e^{1-\frac{2r}{r_{0}}}(3(1+\frac{2r}{r_{0}})r_{0}(2\pi +\chi )+4r(3\pi +2\chi ))}{24r_{0}r^{3}(2\pi +\chi )(4\pi +\chi )} \nonumber \\\end{aligned}$$
(29)
$$\begin{aligned} \hspace{-0.5cm} \rho +\mathscr {P}_{r}= & {} \frac{e^{1-\frac{2r}{r_{0}}}(r_{0}+e^{\frac{2r}{r_{0}}}r_{0}-2r)}{4r_{0}r^{3}(4\pi +\chi )} \end{aligned}$$
(30)
$$\begin{aligned} \hspace{-0.5cm} \rho +\mathscr {P}_{t}= & {} -\frac{e^{1-\frac{2r}{r_{0}}}(r_{0}+e^{\frac{2r}{r_{0}}}r_{0}+6r)}{8r_{0}r^{3}(4\pi +\chi )}. \end{aligned}$$
(31)

Furthermore, the outcomes obtained from utilizing Eqs. (27)–(31) and solving Eqs. (24)–(26) match the physical properties of the wormhole.

4 Physical analysis of wormhole solution in modified gravity theory

Fig. 2
figure 2

Nature of the energy density (\(\rho \)) for WH-I with \(\vartheta =1\), \(r_{0}=1.55\) and \(\kappa \in [-35,-26]\)

Full size image
Fig. 3
figure 3

Nature of the null energy condition (\(\rho +\mathscr {P}_{r}\)) for WH-I with \(\vartheta =1\), \(r_{0}=1.55\) and \(\kappa \in [-35, -26]\)

Full size image
Fig. 4
figure 4

Nature of the null energy condition (\(\rho +\mathscr {P}_{t}\)) for WH-I with \(\vartheta =1\), \(r_{0}=1.55\) and \(\kappa \in [-35, -26]\)

Full size image
Fig. 5
figure 5

Nature of the dominant energy condition (\(\rho -|\mathscr {P}_{r}|\)) for WH-I with \(\vartheta =1\), \(r_{0}=1.55\) and \(\kappa \in [-35, -26]\)

Full size image
Fig. 6
figure 6

Nature of dominant energy condition (\(\rho -|\mathscr {P}_{t}|\)) for WH-I with \(\vartheta =1\), \(r_{0}=1.55\) and \(\kappa \in [-35, -26]\)

Full size image
Fig. 7
figure 7

Nature of strong energy condition (\(\rho +\mathscr {P}_{r}+2\mathscr {P}_{t})\) for WH-I with \(\vartheta =1\), \(r_{0}=1.55\) and \(\kappa \in [-35, -26]\)

Full size image

As we all know, the energy conditions are the best geometrical tool for assessing the stability of cosmological models. So, we put our models to the test using this methodology.

4.1 Analysis of energy conditions in \(\texttt{F}(\texttt{Q, T})\)-gravity for wormhole geometry

In Fig. 2, we clearly show that Energy density (\(\rho \)) is positive when \(r\in (0.5,2.5)\) and \(\kappa \in [-35,-26]\). For other ranges of free parameter \(\kappa \), we also check the behavior of energy density and we obtained that when \(\kappa < -26\) & \(13\le \kappa \le 37\) it behaves positively with decreasing nature, and for the remaining range it behaves negatively. The initial NEC term \(\rho +\mathscr {P}_{r}\) is positive as can be seen in Fig. 3 with decreasing nature if \(r\in (0.5,2.5)\) and \(\kappa \in [-35,-26]\) but it also behaves positively with decreasing nature with respect to(w.r.t) \(\kappa <-35\) and negative for remaining values of \(\kappa \). From Fig. 4, \(\rho +\mathscr {P}_{t}\) is negative with increasing nature for \(r\in (0.5,2.5)\) and \(\kappa \in [-35,-26]\) and also negative whole range of \(\kappa <-35\). Hence we concluded the infractions of NEC which is necessary for the existence of traversable wormholes. Now it’s intriguing to see that the DEC is also violated as it behaves negatively with an increasing nature for the whole range of r and \(\kappa \) (see Figs. 5, 6). The SEC condition (Fig. 7) behaves positively with decreasing nature for \( -35 \le \kappa \le -26\). In brief, we also discuss the nature of energy conditions in Table 1.

4.2 Analysis of energy conditions in \(\texttt{F}(\texttt{R, T})\)-gravity for wormhole geometry

The nature of all energy conditions and energy density over the specified range of \(\chi \in [-35, -26]\) are shown in Figs. 8, 9, 10, 11, 12 and 13, as can be seen. The energy density (Fig. 8) behaves positively with decreasing nature for a given range of \(\chi \in [-35, -26]\) and \(0.5< r < 2.5\) but negative for \(-5 \le \chi \le 5\). It also appears that the null energy requirement is negative with an increasing nature in the case of the radial coordinate for \(0.5< r < 2.5\) and \(\chi \in [-35,-26]\) while in the case of tangential co-ordinate, null energy condition behaves positively with decreasing nature. From this scenario, we concluded that the null energy condition is violated which is required for the existence of exotic matter and traversable WHs (see Figs. 9, 10). From Figs. 11 and 12, we observe that the dominant energy conditions are not satisfied in both cases that is radial coordinate and tangential coordinate. Hence both behave negatively with increasing nature for the whole range of \(\chi \) and r. SEC fulfills the criteria for a given range. It behaves positively with decreasing nature for \( -35 \le \chi \le -26\) but for \(-5 \le \chi \le 5\) sum of all stress-energy tensors behaves negatively with increasing nature for \(0.5<r<2.5\) (see Fig. 13). Table 1 also discusses the general characteristics of energy situations.

Table 1 Summary of the energy conditions
Full size table
Fig. 8
figure 8

Nature of energy density (\(\rho \)) for WH -II with \(r_{0}=1.55\) and \(\chi \in [-35,-26]\)

Full size image
Fig. 9
figure 9

Nature of null energy condition (\(\rho +\mathscr {P}_{r}\)) for WH -II with \(r_{0}=1.55\) and \(\chi \in [-35,-26]\)

Full size image
Fig. 10
figure 10

Nature of null energy condition (\(\rho +\mathscr {P}_{t}\)) for WH -II with \(r_{0}=1.55\) and \(\chi \in [-35,-26]\)

Full size image
Fig. 11
figure 11

Nature of dominant energy condition (\(\rho -|\mathscr {P}_{r}|\)) for WH -II with \(r_{0}=1.55\) and \(\chi \in [-35,-26]\)

Full size image
Fig. 12
figure 12

Nature of dominant energy condition (\(\rho -|\mathscr {P}_{t}|\)) for WH -II with \(r_{0}=1.55\) and \(\chi \in [-35,-26]\)

Full size image
Fig. 13
figure 13

Nature of strong energy condition (\(\rho +\mathscr {P}_{r}+2\mathscr {P}_{t}\)) for WH -II with \(r_{0}=1.55\) and \(\chi \in [-35,-26]\)

Full size image

5 Equilibrium condition

The equilibrium arrangement of WH models is examined in this subsection. One can attain the equilibrium situation for WHs using the resolution of the TOV equations provided by

$$\begin{aligned} \frac{d\mathscr {P}_{r}}{dr}+\frac{\sigma ^{\prime }(\rho +\mathscr {P}_{r})}{2}+\frac{2(\mathscr {P}_{r}-\mathscr {P}_{t})}{r}=0, \end{aligned}$$
(32)

where \(\sigma (r)=2\epsilon (r)\). Taking into consideration the gravitational, hydrostatic, and anisotropic forces (resulting from the anisotropy of matter), this equation establishes the equilibrium state of the configuration. The following relationships characterize these forces:

$$\begin{aligned} \texttt{F}_{gf}= & {} \frac{-\sigma ^{\prime }(\rho +\mathscr {P}_{r})}{2}, \\ \texttt{F}_{af}= & {} \frac{2({\mathscr {P}_{t}}-\mathscr {P}_{r})}{r}, \\ \texttt{F}_{hf}= & {} \frac{-d\mathscr {P}_{r}}{dr}. \end{aligned}$$
Fig. 14
figure 14

Nature of equilibrium condition for WH-I (left panel) with \(\vartheta =1\) and \(r_{0}=1.55\) & for WH -II (right panel) with \(r_{0}=1.55\)

Full size image

Hence \(\texttt{F}_{gf}+\texttt{F}_{af}+\texttt{F}_{hf}=0\) is a necessary condition for the WH solutions to be in equilibrium.

The impact of gravitational forces is zero in our situation due to the constant redshift function. Now The remaining forces of WH-I are provided as

$$\begin{aligned}{} & {} \texttt{F}_{af}=\frac{e^{1-\frac{2r}{r_{0}}}(3(1+e^{\frac{2r}{r_{0}}})r_{0}+2r)}{2r_{0}(\kappa +8\pi )r^{4}}\end{aligned}$$
(33)
$$\begin{aligned}{} & {} \texttt{F}_{hf}\nonumber \\{} & {} {=}\frac{e^{1{-}\frac{2r}{r_{0}}}(12r_{0}\pi (3(1{+}e^{\frac{2r}{r_{0}}})r_{0}+2r){-}\kappa (9(1+e^{\frac{2r}{r_{0}}})r_{0}^{2}{+}14r_{0}r{+}8r^{2}))}{6r_{0}^{2}(\kappa -4\pi )(\kappa {+}8\pi )r^{4}}.\nonumber \\ \end{aligned}$$
(34)

For WH -II, the hydrostatic force and anisotropic forces are given as

$$\begin{aligned}{} & {} \texttt{F}_{af}=-\frac{e^{1-\frac{2r}{r_{0}}}(3(1+e^{\frac{2r}{r_{0}}})r_{0}+2r)}{4r_{0}r^{4}(4\pi +\chi )}\end{aligned}$$
(35)
$$\begin{aligned}{} & {} \texttt{F}_{hf}=-\frac{e^{1{-}\frac{2r}{r_{0}}}(2r^{2}\chi {-}9(1{+}e^{\frac{2r}{r_{0}}})r_{0}^{2}(2\pi +\chi ){-}4r_{0}r(3\pi +\chi ))}{12r_{0}^{2}r^{4}(2\pi +\chi )(4\pi +\chi )}. \end{aligned}$$
(36)

Figure 14 illustrates the stability study of the wormhole solution for WH-I (left panel) and WH -II (right panel). For WH-I, we observed that hydrostatic force behaves positively in nature while anisotropic force behaves negatively in nature. In their structure, the hydrostatic case takes over anisotropic force.

On the other hand, for WH-II, anisotropic force exhibits a positive behavior in nature while hydrostatic force exhibits a negative behavior. Hence the anisotropic case prevails over hydrostatic force in its shape.

These forces reflect the same intensity but are in opposition to one another, for each wormhole as can be shown. It is revealed by this balancing of the forces that our wormholes are stable.

6 Surface diagram

Wormholes can be represented as embedding diagrams, and by using these diagrams, we can learn some important details about the shape function that should be applied. The Morris-Thorne metric’s spatial sector is typically compared to the spatial three-dimensional flat metric written in cylindrical coordinates to generate this diagram [63]. With a rigorous part of time \(t =\) constant, we can take an equatorial slice \(\theta = \frac{\pi }{2}\) due to the spherical symmetry [64]. We make use of these assumptions in the action field.

$$\begin{aligned} ds^{2}=\left( 1-\frac{\texttt{R}_{s} (r)}{r}\right) ^{-1}dr^{2}+r^{2}d\Phi ^{2}. \end{aligned}$$
(37)

Now, using the cylindrical coordinates \((\texttt{r}, z, \phi )\), which can project the previous slice onto its hypersurface. So, we write

$$\begin{aligned}{} & {} ds^{2}=dr^{2}+dz^{2}+r^{2}d\Phi ^{2}. \end{aligned}$$
(38)

Applying axial symmetry, the embedded surface z(r) in three-dimensional space can be expressed using the following formula:

$$\begin{aligned}{} & {} ds^{2}=\left[ 1+\left( \frac{dz}{dr}\right) ^{2}\right] dr^{2}+r^{2}d\Phi ^{2}. \end{aligned}$$
(39)

Through comparing Eqs. (37) and (39)

$$\frac{dz}{dr}=\pm \left( \frac{r}{\texttt{R}_{s} (r)}-1\right) ^{-\frac{1}{2}}$$

We examine that the surface diagram is vertical at the neck, i.e., \(\frac{dz}{dr} \rightarrow \infty \). Additionally, we look at the fact that the space is asymptotically flat far from the throat because \(\frac{dz}{dr}\) goes to 0 as r tends to infinity. The embedded diagram is displayed in Fig. 15. The visualized ideas of WH are very well displayed via the embedding diagrams. Here the chosen shape function, \(\texttt{R}_{s} (r)\), is important.

Fig. 15
figure 15

Visualization of embedding diagrams w.r.t. \(r_{0}=1.55\)

Full size image
Fig. 16
figure 16

Nature of exoticity parameter for WH-I (left panel) with \(\vartheta =1\) and \(r_{0}=1.55\) & for WH -II (right panel) with \(r_{0}=1.55\)

Full size image

7 Exoticity parameter

For wormholes to be capable of being traversed, exotic matter, or something that differs from ordinary matter, must exist. Exotic stuff that does not adhere to the weak or any other energy conditions because it does not adhere to the NEC. By applying the exoticity factor, we investigate the presence of unusual materials close to the neck and its surroundings. The exoticity parameter is defined as [65]

$$\begin{aligned} \xi =-\frac{(\rho -\mathscr {P}_{r})}{|\rho |}. \end{aligned}$$
(40)

Since the non-negativity of \(\xi \) guarantees that the exotic matter is present at the throat or close to the wormhole’s throat and the negative behavior of the exoticity factor shows that the matter distribution is exotic near the throat but normal far from the throat [65,66,67]. We plotted the graph of the exoticity parameter against the radial coordinate for WH-I & WH-II. As can be seen from Fig. 16 (left panel) the exoticity parameter behaves positively for WH-I and negatively for WH-II (Fig. 16, right panel). Hence it verifies the presence of exotic matter near the throat of \(\texttt{F}(\texttt{Q, T})\) gravity wormhole (WH-I) and exotic matter near but normal matter far from the throat in \(\texttt{F}(\texttt{R, T})\) gravity wormhole (WH-II).

8 Conclusion

In the literature, wormholes have received a lot of attention and numerous models have been put forth in this area. The history of wormholes is a tale of fantasy, conjecture and research. With the motivation of creating new wormhole solutions, we have considered two different gravity \(\texttt{F}(\texttt{Q, T})\) and \(\texttt{F}(\texttt{R, T})\) respectively in this work. The following points provide a summary of the findings from the two gravity wormhole models that were presented:

  1. (i)

    First, we have demonstrated in Fig. 1 that the selected shape function 1 for both wormhole models satisfies all necessary criteria with throat radius \(r_{0}=1.55\). We analyze the wormhole solution in \(\texttt{F}(\texttt{Q, T})\) and \(\texttt{F}(\texttt{R, T})\) with taking range of \(r \in (0.5, 2.5) \) and free parameters \(\kappa \) & \(\chi \) lies in \([-35,-26]\).

  2. (ii)

    The idea of non-minimal coupling between the geometry and matter fields has opened up new possibilities for understanding the dynamics of wormholes in the context of \(\texttt{F}(\texttt{Q, T})\) gravity. In the same manner study of wormholes under the effect of \(\texttt{F}(\texttt{R, T})\) gravity has revealed the impact of curvature-matter coupling on the endurance of such structures.

  3. (iii)

    In both cases, we obtained energy density is positive within the given range. NEC in radial pressure case behaves negatively in \(\texttt{F}(\texttt{R, T})\) gravity but positively in \(\texttt{F}(\texttt{Q, T})\) gravity, and in tangential pressure case behaves both in opposite nature. Hence NEC is violated in both cases which is necessary for the existence of wormholes. DEC is violated in both the gravity cases. The sum of all the stress-energy tensors or we can say SEC behaves positively according to the values of \(\kappa \) in both the cases.

  4. (iv)

    The stability of these wormhole solutions has also been examined using a generalized equation called TOV. In \(\texttt{F}(\texttt{Q, T})\) gravity the hydrostatic case is dominating in nature as compared to anisotropic force but in the case of \(\texttt{F}(\texttt{R, T})\) gravity anisotropic force is dominating in nature as compared to hydrostatic case.

  5. (v)

    Furthermore, we used an embedding diagram to demonstrate the geometry of wormhole models. The energy conditions are violated in both cases which becomes a source of exotic matter and the presence of exotic matter is verified by the exoticity factor (\(\xi \)). By using these concepts, we got the presence of exotic matter near the throat in case of \(\texttt{F}(\texttt{Q, T})\) gravity and matter distribution is exotic near the throat but normal matter far from the throat in \(\texttt{F}(\texttt{R, T})\) gravity case.

In summary, the study of wormholes in \(\texttt{F}(\texttt{Q, T})\) gravity and \(\texttt{F}(\texttt{R}, \texttt{T})\) gravity showcases the rich interplay between modified theories of gravity and the theoretical possibility of traversable shortcuts in spacetime. The approach here opens up a new way to derive wormhole solutions in different gravities.