A New Evaluation of the ${}^{11}$B(p,$\alpha )\alpha \alpha$ Reaction Rates

Abstract

Reaction rates of the $^{11}$B(p,$\alpha$)$\alpha \alpha$ process have been evaluated on the basis of a data set spanning incident proton energies $E_p$ from 0.15 to 3.8 MeV. A previously published analysis (Spraker et al. in J Fusion Energy 31(4):357, 2012) of these data provided the number of outgoing $\alpha$-particles in a restricted range of the detected $\alpha$-energy spectrum, making it unsuitable for the evaluation of the reaction rates. The present work takes advantage of a calculation of the $\alpha$-energy spectrum based on a sequential model of the reaction and the assumption that the primary $\alpha$-particles are emitted with $\ell =3$. A full description of this ansatz, which has been shown to reproduce the essential features of the observed $\alpha$-energy spectra, can be found in Stave et al. (Phys Lett B 696:26, 2011). The accuracy of these calculated spectra has made it possible to reliably extrapolate the new data to zero-energy $\alpha$-particles. In the ensuing calculation of the cross section, the total measured $\alpha$-yield is then divided by a fixed factor of three at all incident proton energies. In addition, this technique has enabled a treatment of the $\alpha _0$ channel where the ¹²C nuclei decay to the ground state of ⁸Be via emission of an $\alpha$-particle. This channel contributes at incident proton energies above 2 MeV. The new cross section data have then been used to evaluate the $^{11}$B(p,$\alpha$)$\alpha \alpha$ reaction rates. The new evaluation is $\sim$10–15 % higher than the currently accepted result (Angulo et al. in Nucl Phys A 656(1):3, 1999) at temperatures between 200 and 600 keV (2–7 $\times$ 10$^9$ K). The inclusion of a narrow, low-lying resonance at $E_p=0.162$ MeV in the evaluation is found to have a minimal effect on the reaction rate above 100 keV (1.2 $\times$ 10$^9$ K), and a higher-lying state at $E_p=3.75$ MeV is shown to enhance the reaction rates by only $\sim$15 % above 400 keV (4.6 $\times$ 10$^9$ K).

Introduction

The $^{11}$B(p,$\alpha$)$\alpha \alpha$ reaction at incident proton energies $E_p < 4$ MeV has been studied since the 1930s [4–8]. The reaction proceeds through a two-step process involving emission of a primary $\alpha$-particle followed by two secondary $\alpha$-particles emitted from the decay of $^8$Be. Based on cross section data collected previously at the Triangle Universities Nuclear Laboratory (TUNL) [1] and a model of the reaction mechanism developed to account for the observed $\alpha$-energy spectra [2], the reaction can be described via its behavior at resonances at $E_p=0.675$ and $E_p=2.64$ MeV. At $E_p=0.675$ MeV, the primary $\alpha$-particles produced from the decay of the 2$^{-}$ state in $^{12}$C have $\ell =3$, forming the 2$^{+}$ first-excited state of $^8$Be. This then decays to two $\alpha$-particles with $\ell '=2$. The 3$^{-}$ state in $^{12}$C formed at $E_p=2.64$ MeV has two possible decay modes. Primary $\alpha$-particles can be emitted with either $\ell =1$ to the first-excited state of $^8$Be, or with $\ell =3$ to the 0$^{+}$ ground state. The residual $^8$Be nucleus then decays, emitting two secondary $\alpha$-particles.

Interest in the $^{11}$B(p,$\alpha$)$\alpha \alpha$ reaction is driven by studies in stellar evolution, where relative abundances of $^{11}$B, Li and Be provide insight into stellar processes [9]. This reaction is also being investigated for use in practical nuclear fusion reactors, exploiting the aneutronic nature of this fusion reaction [10]. Total cross sections and reaction rates are key input parameters in the design of such reactors.

The full observed $\alpha$-energy spectra must be integrated over all outgoing energies and the yield divided by 3 to account for the final-state multiplicity in order to extract absolute cross sections. Practically, this cannot be done using only the collected data for two reasons. First, the $\alpha$-energy spectra contain a dominant peak at the nominal beam energy from protons elastically scattered from the target. The other reason is the low-energy truncation of the energy spectra due to hardware thresholds required to reduce background rates which would overwhelm the data acquisition system. Consequently, the analysis presented in [1] calculated yields by integrating over a 2.75 MeV wide window centered on the dominant $\alpha$-particle peak observed in each detector, circumventing the ambiguity in the number of $\alpha$-particles located in the integration region by reporting results in units of Counts/Luminosity ($\equiv X$), defined as

$$\begin{aligned} X = \frac{\text {Counts}}{N_t N_p d\Omega } ({\text{cm}}^2/{\text{sr}}) \end{aligned}$$

(1)

where $N_t$ is the target density, $N_p$ is the number of incident protons, and $d\Omega$ is the detector solid angle. To convert X to a differential cross section, the number of $\alpha$-particles in the energy window used must be divided out. This number varies with proton energy and is difficult to determine.

The present work addresses this complication by utilizing the model described in Ref. [2] to extrapolate the entire $\alpha$-energy spectra. Yields are then obtained from these extrapolations to extract angular distributions and total cross sections, which are then used to evaluate the reaction rate.

Total Cross Sections

The aforementioned model was used to generate simulated $\alpha$-energy spectra at each measurement angle and beam energy over 0.15 MeV $< E_p <$ 3.8 MeV. The reaction was taken to proceed through excitation of the 2$^{-}$ state in $^{12}$C for $E_p \le$ 2.0 MeV, while the 3$^{-}$ state was used for $E_p >$ 2.0 MeV. Each simulated spectrum was normalized to the corresponding measured $\alpha$-energy spectrum using the previously discussed 2.75 MeV wide summing region. The number of counts observed in the data over the integration region was compared to the simulated yield. This ratio defined a scaling factor that was then applied to the total simulated $\alpha$-energy spectrum. The process is illustrated in Fig. 1 at $E_p = 0.65$ MeV at $\theta ^{lab}_{\alpha }=90^{\circ }$. By definition, the scaled simulated $\alpha$-energy spectrum has the same number of counts in the original summing region as the data. The final total yield was then obtained by integrating the scaled simulated $\alpha$-energy spectrum down to 0.

Fig. 1

Comparison of observed and calculated $\alpha$-energy spectra at $\theta ^{lab}_{\alpha }=90^{\circ }$ and $E_p=0.65$ MeV. The total $\alpha$-contribution calculated using the model was normalized to the data over the integration window used in the previous analysis, indicated above. The $\alpha$-energy spectrum was then extended to $E_{\alpha }=0$ by using the normalized model output

As noted in Sect. 1, the two decay modes of the $3^{-}$ state in $^{12}$C can lead to contributions from both the $\alpha _0$ and $\alpha _1$ channels from decays to the ground state or the first excited state of $^8$Be, respectively. For incident proton energies exciting this state, the same procedure was used to obtain the $\alpha _1$ yields as described for the resonance at $E_p=0.675$ MeV, shown in Fig. 2. The same technique was then applied separately to the $\alpha _0$ channel, as demonstrated in Fig. 3. The primary $\alpha _0$ peak is clearly separated from the $\alpha _1$ contribution, providing a convenient reference for normalizing the modeled primary $\alpha _0$ yield. The scaling factor obtained in this way is then applied to the calculated yield of secondary $\alpha _0$ particles, which have an energy distribution lying below the proton elastic scattering peak.

Fig. 2

Comparison of observed and calculated $\alpha$-energy spectra at $\theta ^{lab}_{\alpha }=90^{\circ }$ and $E_p=2.6$ MeV. The total $\alpha _1$-contribution calculated using the model was normalized to the data over the integration window used in the previous analysis, indicated above. The $\alpha$-energy spectrum was then extended to $E_{\alpha }=0$ by using the normalized model output

Fig. 3

The modeled primary and secondary $\alpha _0$-energy distributions at $\theta ^{lab}_{\alpha }=90^{\circ }$ and $E_p=2.6$ MeV, after scaling. The primary $\alpha _0$ peak is free of any $\alpha _1$ contribution and can thus be used to scale the calculated $\alpha _0$ distribution

As in [1], the extrapolated $\alpha _0$ and $\alpha _1$ spectra were then integrated down to $E_{\alpha } = 0$, and the resulting Counts/Luminosity were used to obtain angular distributions which were fit to an expansion in terms of Legendre polynomials

$$\begin{aligned} \frac{d\sigma }{d\Omega } = \sum _{i=0}^{i=i_{max}} A_i P_i(\text {cos}\theta ) \end{aligned}$$

(2)

The data obtained at $E_p<1.4$ MeV were fit with a Legendre expansion up to and including $i= 2$, while for $E_p\ge 1.4$ MeV the expansion included up to $i=4$. Similarly, the $\alpha _0$ angular distributions went up to $i = 4$. More than 95 % of the individual data points were within 3 % of the corresponding fit result. The expansion coefficients are listed in Tables 1, 2 and 3 in the Appendix. The $A_0$ coefficients extracted from the fits were then multiplied by $4\pi /3$ (with the factor of 3 accounting for the total number of final-state $\alpha$-particles) to give total cross sections. The results, which include the $\alpha _0$ channel where applicable, are displayed as a function of $E_p$ in Fig. 4.

Fig. 4

The total cross section of the $^{11}$B(p,$\alpha$)$\alpha \alpha$ as a function of $E_p$. The error bars are smaller than the size of the points

A 2$^+$ state in $^{12}$C with a full width at half maximum of $\Gamma =5$ keV is excited at $E_p=0.162$ MeV with a maximum cross section of 100 mb. Measuring this state experimentally was not possible due to the narrow width relative to the energy resolution of the proton beam. In order to account for the effect of this state on the reaction rates, cross section values were generated using an existing parameterization of the astrophysical factor S(E) based on a fit to experimental data [7, 11]. The cross section as a function of center of mass energy E could then be obtained using

$$\begin{aligned} \sigma (E) = \frac{S(E)}{E}\text {exp}\left( -\sqrt{\frac{E_G}{E}}\right) \end{aligned}$$

(3)

where $E_G=22.589$ MeV is the Gamow energy. Cross section values were calculated using Eq. 3 over the energy range 0.15 MeV $< E_p < 0.22$ MeV and were used in the evaluation of the reaction rates discussed in Sect. 3.

Reaction Rates

Using the total cross section values from Sect. 2, the Maxwellian-averaged reaction rates [3] were computed as a function of temperature using

$$\begin{aligned} \langle \sigma \nu \rangle = \frac{(8/\pi )^{1/2}}{\mu ^{1/2} (k_BT)^{3/2}} \int _{0}^{\infty } \sigma E \text {exp}(-E/k_BT) dE \end{aligned}$$

(4)

where $\mu$ is the reduced mass, $k_B$ is the Boltzmann constant, T is temperature, $\sigma$ is the total cross section, $\nu$ is the relative velocity, and E is the center of mass energy.

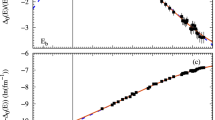
The reaction rate as a function of temperature is shown in Fig. 5. The dot-dashed lines were obtained by varying the total cross section by the combined statistical ($\sim$ 0.1 %) and systematic (3.4 %) uncertainties. Also shown is a previous evaluation of the reaction rate [3].

Fig. 5

The $^{11}$B(p,$\alpha$)$\alpha \alpha$ reaction rate as a function of temperature. The dot-dashed lines indicate the $\pm \sigma _{stat.+sys.}$ limits. The dashed line is a previous result from [3]

The previous result was based on an interpretation of the reaction described in [7] which assumed that primary $\alpha$-particles emitted from the decay of the 2$^{-}$ resonance at $E_p=0.675$ MeV have $\ell =1$ rather than $\ell = 3$. In this ansatz, the simulated kinematics of the secondary $\alpha$-particles indicated that the observed $\alpha _1$ yields should be divided by 2 based on the chosen integration region. This interpretation, adapted in [3] in evaluating the reaction rate displayed in Fig. 5, leads to rates that are 10–15 % lower than the new results over a temperature range of 200-600 keV. As shown in [2], this ansatz does not give an accurate description of the new data set.

Fig. 6

A comparison of the reaction rates with and without inclusion of the narrow low-lying resonance at $E_p=0.162$ MeV. The effect is most pronounced at temperatures near 20 keV and exerts negligible influence on the reaction rates above 100 keV

To determine the importance of including the narrow resonance at $E_p=0.162$ MeV, the reaction rates were evaluated both with and without inclusion of the cross section values calculated with Eq. 3. As the comparison shown in Fig. 6 demonstrates, inclusion of these generated values more than doubles the reaction rates at temperatures near 20 keV. At temperatures greater than 100 keV, the enhancement becomes negligible, as the reaction mechanism is dominated by the much stronger resonances at $E_p=0.675$ and $E_p=2.64$ MeV.

Fig. 7

The $^{11}$B(p,$\alpha$)$\alpha \alpha$ reaction rate evaluated using various upper limits on the cross section data. The minimal effect on the reaction rate suggests the results are relatively insensitive to the higher energy resonances. Note that the y-axis has been zero-suppressed for visual clarity

The current analysis has only considered the resonances occuring at $E_p=0.675$ MeV and $E_p=2.64$ MeV in modeling the energy and angular distributions of the outgoing $\alpha$-particles. The range of incident proton energies extends high enough to excite a higher-lying state in $^{12}$C at $E_p=3.75$ MeV ($\Gamma =480$ keV) with a possible spin assignment of $J^{\pi } = 2^{-}$. The effect on the reaction rate of neglecting the contribution from this state can be assesed by truncating the cross section data set at various values of $E_p$, as shown in Fig. 7. The effect is minimal below 400 keV and and is less than $\sim$15 % at higher temperatures, indicating that the two resonances included in the simulation provide a reasonable description of the data even at higher energies.

Conclusion

A data set built on previously published cross section data of the $^{11}$B(p,$\alpha$)$\alpha \alpha$ reaction [1] and extended with a detailed model of the reaction mechanism [2] has been used to generate new angular distributions and total cross section results. The new results cover the entire $\alpha$-energy spectra and are now reported as true cross sections rather than in terms of Counts/Luminosity. These new results provide the basis for a new evaluation of the reaction rates, which are 10–15 % higher than a previous evaluation [3] at temperatures between 200 and 600 keV (2–7 $\times$ 10$^9$ K). These results will provide useful inputs to astrophysical studies and will have application in the design of novel aneutronic fusion reactors.

Appendix

See Tables 1, 2 and 3.

Table 1 Coefficients from the 2nd order Legendre polynomial fitting of the integrated $\alpha _1$ Counts/$N_t N_p d\Omega$ data covering the incident proton energy range of 0.15–1.3 MeV

Table 2 Coefficients from the 4th order Legendre polynomial fitting of the integrated $\alpha _1$ Counts/$N_t N_p d\Omega$ data covering the incident proton energy range from 1.4 to 3.8 MeV

Table 3 Coefficients from the 4th order Legendre polynomial fitting of the integrated $\alpha _0$ counts/$N_t N_p d\Omega$ data covering the incident proton energy range from 2.1 to 3.8 MeV