Electromagnetic extension of Buchdahl bound in f(R, T) gravity

Abstract

We develop a static charged stellar model in f(R, T) gravity where the modification is assumed to be linear in T which is the trace of the energy momentum tensor. The exterior spacetime of the charged object is described by the Reissner–Nordström metric. The interior solution is obtained by invoking the Buchdahl–Vaidya–Tikekar ansatz, for the metric potential $g_{rr}$, which has a clear geometric interpretation. A detailed physical analysis of the model clearly shows distinct physical features of the resulting stellar configuration under such a modification. We find the maximum compactness bound for such a class of compact stars which is a generalization of the Buchdahl bound for a charged sphere described in f(R, T) gravity. Our result shows physical behaviour that is distinct from general relativity.

1 Introduction

One of the main pillars of modern physics for understanding the present universe is the general theory of relativity (GTR), discovered by Einstein in 1915, which was first experimentally verified by Eddington in 1920, and later by various tests in the solar system. Note that GTR was first modified very soon after its discovery. In 1919, Weyl [1] introduced higher order invariants in the Einstein–Hilbert (EH) action unifying electromagnetism (EM) and gravity. Later, Kaluza and Klein [2, 3] investigated the higher dimensional effects on EM. Although the complexity of EH action had no apparent experimental motivations during that period, around the 1960s, many investigators found virtue in such an approach. Based on Kaluza’s unitary field theory, Brans et al. [4] introduced a scalar-tensor theory from the observation of the solar oblateness and the precession of Mercury’s orbit [5] which was later taken up by Bergmann [6].

The recent shreds of evidence emerging from astrophysics and observational cosmology suggest that the cosmic acceleration of the universe may have occurred in two phases. Preceding radiation domination, the inflationary phase [7] took place, which not only solves the flatness problem [8] in standard cosmology, but also justifies the nearly flat spectrum of temperature anisotropies observed in cosmic microwave background (CMB) [9]. The second phase is the matter-dominated present universe, i.e. the late-time acceleration supposedly originated from dark energy [10]. A supernova search team has experimentally verified the late-time expansion of the universe [11] based on the observational data of 10 new high-redshift Type Ia supernovae as well as through rigorous and detailed experiments [12] considering the brightness of supernovae as an indicator. Subsequently, the existence of a small but non-zero cosmological constant [13] has been justified by the current mass-energy density of the universe. Moreover, when the information coming from anisotropies in CMB is combined with measurements of the light chemical element abundances on a cosmological scale, one concludes that about one-fifth of our universe is composed of non-luminous and non-baryonic material called dark matter [14,15,16,17,18]. Thus, despite remarkable success in predicting many tests of gravitational phenomena including the most recent discovery of gravitational waves, GTR faces many challenges on several fronts - both on small and large scales.

While scientific curiosity on the theoretical front provides ample motivation to contemplate modifying Einstein’s gravity, the above observational evidence strongly justifies such exercises. GTR can be modified by adopting the EH action containing the Lagrangian density $\sqrt{-g}R$, R being the curvature scalar. The initial de-Sitter state of the universe is explained by adding a term proportional to $\sqrt{-g}R^{m}$ ($m > 0$) to the action, known as Starobinsky inflation [7]. However, if $m < 0$, then the acceleration of the universe originates from gravitation as shown by Carroll et al. [19]. The $\varLambda$ cold dark matter ($\varLambda$CDM) model, based on inflationary theory, explains the acceleration of the universe where one adds the cosmological constant $\varLambda$ to the EH action [20], which fits well with several observational data [21], and thereby also offers the possibility for time varying equation of state of dark energy [22]. However, the $\varLambda$CDM model is burdened with magnitude problems. A more radical alternative approach is the modified f(R) gravity, which allows a generalization of the EH action to interpret some of the basic characteristics of the higher order curvature gravity. Before experimental observation, treating both the metric and the affine parameters as independent variables, Palatini [23] formulated a different perspective of f(R) gravity leading to second order field equations free from the instability associated with negative signs of the second order partial derivative of R in the functional f(R). However, Palatini’s formulation turned out to be inconsistent with the late-time cosmic acceleration. Consequently, the formulation demanded a different approach to f(R) theory. To obtain a divergence-free Einstein equation, Lanczos [24] proposed a specific combination of curvature-squared terms offering a modified theory named Einstein–Gauss–Bonnet (EGB) gravitational theory. Different cosmological models have been developed based on EGB gravity [25]. In higher dimensions, the possible existence of a black hole was shown by including a 4D Gauss–Bonnet (GB) term to the EH action [26]. Investigators have also reconciled the early-time inflation with late-time acceleration of the universe in EGB gravity [20, 27,28,29], and the cosmic history has been unified via some cosmological models based on f(R) theories of gravity [30, 31]. Recently, EGB gravity has also received a widespread application in astrophysics. Many researchers have interpreted the physical quantities in five-dimensional framework of EGB gravity assuming different kinds of interior geometries and fluid distributions [32,33,34,35,36]. In addition to EGB gravity, f(R) theory [37,38,39,40](and references therein) explains how the cosmological constant can be bypassed geometrically [41] by adding higher order curvature scalar to the action.

To explain the current expansion of the universe as well as the dark energy scenario, the action in f(R) is further extended by coupling non-minimally the matter field to the geometry (viz. the Ricci scalar R) [42], which leads to f(R, T) theory, T being the trace of stress-energy tensor. Thus, the associated continuity equation takes a different form which justifies the energy exchange between the matter and geometry beyond the curved spaces. This coupled matter part generates an additional force term orthogonal to the four velocities of a massive object connoting a non-geodesic nature of motion. The non-vanishing divergence of the stress tensor violates the equivalence principle which, however, can be controlled by the corresponding coupling parameter. Considering matter as a perturbation to a locally flat spacetime, it can be shown that the extension mentioned above satisfies the equivalence principle [43]. Following this, Harko et al. [44] developed a model for stellar configuration filled with a perfect fluid. Various classes of solutions in f(R, T) gravity have been discussed by Harko et al. [45]. Note that the action in f(R, T) theory is not Lorentz invariant and does not provide a frame-independent gravitational theory. The theory can only be formulated properly in a strong gravity regime by considering a linear functional form of f(R, T) [46] for a spherically symmetric stellar configuration. With the linear functional form of f(R, T), the anisotropic behaviour of a collapsing object [47, 48], effect of charge [49,50,51], and the stability criterion [52,53,54,55] have been studied.

Despite the fact that a power law dependency of T in the modified theories of gravity has been severely challenged [56], the f(R, T) gravity models are being extensively used to analyze astrophysical objects where the coupling is mostly linear in T. In the recent past, many investigators have analyzed the gross physical properties of a stellar configuration by considering different stellar solutions in f(R, T) gravity, viz. Tolman-IV solution [57], embedded class I solution with Karmakar condition [58], Krori–Barua type compact stellar solution [59], and solutions obtained by utilizing Buchdahl’s ansatz [60,61,62]. The effect of the parameter that couples the matter contribution to geometry on the interior structure of a compact object (e.g. neutron star) has been investigated by Pappas et al. [63] for the Tolman-VII solution in linear f(R, T) gravity. The investigation also provided an analysis of the logical extension for the uniform density configuration. The analyses in Ref. [63] also facilitated an examination of the upper bound on the mass to radius ratio in an appropriate parametric regime. In addition, the bound on mass for the compact objects have been analysed in the framework of f(R) gravity [64,65,66,67]. A sharp inequality indicating the upper bound on compactness was developed by Andréasson et al. [69] for a charged infinitely thin shell solution which was shown to satisfy all the required energy conditions. Motivated by the above developments, we felt it worthwhile to obtain an upper bound on the compactness of a charged sphere in f(R, T) gravity analogous to the Buchdahl bound in GTR. Note that a charged generalization of the Buchdahl bound in Einstein’s gravity was provided by Sharma et al. [68]. In this paper, we attempt to analyze the functional dependency of the coupling parameter on the compactness bound for a charged sphere filled with isotropic fluid by obtaining a solution in f(R, T) gravity which is linear in T. The solution is obtained by introducing the Buchdahl–Vaidya–Tikekar ansatz [70, 71] as one of the metric potentials of the spherically symmetric static distribution. By invoking a particular coordinate transformation, we solve the system of equations and fix the constants of the solution by matching the interior solution to the exterior Reissner–Nordström (RN) metric across the boundary which facilitates its physical analysis.

The structure of this paper is as follows: In Sect. 2, the effective field equations are obtained for a charged object with perfect fluid distribution enclosed in a sphere in f(R, T) gravity theory. Section 3 deals with the technique for generating solutions of the field equations. The section is subdivided into two classes: (i) uncharged VT model, which reduces to the Schwarzschild incompressible interior solution for a particular choice of the model parameters; and (ii) charged VT model. The unknown constants are fixed in Sect. 4 by matching the interior solution to the exterior RN metric across the boundary. Gross physical properties are discussed in Sect. 5. Section 6 is devoted to the analysis of the modification on the compactness bound of the charged sphere. Some concluding remarks are made in Sect. 7.

2 Electromagnetic formulation of field equations

To study the stellar configurations of a charged compact star, Einstein’s gravity is modified in conjunction with the trace of the stress-energy tensor T to the existing Ricci scalar term R. Pretel et al. [51] prescribed such a modification in f(R, T) gravity by rewriting the action as

$$\begin{aligned} {S = \int {\Big [\frac{f(R,T)}{16\pi }+{\mathcal {L}}_m +{\mathcal {L}}_e\Big ]\sqrt{-g}d^4 x},} \end{aligned}$$

(1)

${{\mathcal {L}}_m}$ being the Lagrangian matter density and g is the determinant of the metric tensor $g_{ab}$.¹ In (1), ${{\mathcal {L}}_e}$ represents the electromagnetic field Lagrangian density given by

$$\begin{aligned} {{\mathcal {L}}_e = j^{a}A_{a} - \frac{1}{16\pi }F_{ab}F_{cd}g^{ac}g^{bd},} \end{aligned}$$

(2)

where the four-current density is given by $j^{a} = \sigma u^{a}$, with $\sigma$ being the electric charge density and $u^{a}$ is the four-velocity of the fluid satisfying the relations $u_{a}u^{b}=1$ and $u^{a}\nabla _{b}u_{a}=0$. $F_{ab}=\nabla _{a}A_{b}-\nabla _{b}A_{a}$ is the electromagnetic field strength tensor where $A_{a}$ represents the electromagnetic four potential and $\nabla _{a}$ denotes the covariant derivative associated with the Levi-Civita connection of metric tensor $g_{ab}$.

Thus, the total stress-tensor is a sum of two terms, namely the matter part ${({\mathcal {M}}_{ab})}$ and the electromagnetic part ${({\mathcal {E}}_{ab})}$, i.e.

$$\begin{aligned} {T_{ab}={\mathcal {M}}_{ab} + {\mathcal {E}}_{ab}.} \end{aligned}$$

(3)

In this paper, we consider a perfect fluid distribution, which implies

$$\begin{aligned} {{\mathcal {M}}_{ab}=(p+\rho )u_{a}u_{b} + pg_{ab},} \end{aligned}$$

where $\rho$ is the matter density and p is the isotropic pressure, and the electromagnetic field tensor takes the form

$$\begin{aligned} {{\mathcal {E}}_{ab}=\frac{1}{4\pi }\Bigg (F_{ac}F^{c}_{b}-\frac{1}{4}g_{ab}F_{cd}F^{cd}\Bigg ).} \end{aligned}$$

The Lagrangian matter density is related to the energy  - momentum tensor as

$$\begin{aligned} {{\mathcal {M}}_{ab} = - \frac{2}{\sqrt{-g}} \frac{\delta (\sqrt{-g} {\mathcal {L}}_m)}{\delta g^{ab}},} \end{aligned}$$

(4)

where it is assumed that ${\mathcal {L}}_m$ depends only on the metric and not on its derivatives. The above equation on contraction yields

$$\begin{aligned} {{\mathcal {M}}_{ab} = g_{ab} {\mathcal {L}}_m - 2\frac{ \partial {\mathcal {L}}_m}{\partial g^{ab}}.} \end{aligned}$$

(5)

On variation of action (1), with respect to the metric components $g^{ab}$, yields the following relationship

$$\begin{aligned} \delta S= & {} \frac{1}{16 \pi } \int \Bigg [(R_{ab}+g_{ab}\Box -\nabla _{a}\nabla _{b})f_{R}(R,T)\delta g^{ab} \nonumber \\{} & {} +f_{T}(R,T)\frac{\delta (g^{cd}{\mathcal {M}}_{cd})}{\delta g^{ab}}\delta g^{ab} -\frac{1}{2} g_{ab}f(R,T)\delta g^{ab} \nonumber \\{} & {} +16\pi \frac{1}{\sqrt{-g}}\frac{\delta (\sqrt{-g}L_{m})}{\delta g^{ab}}\Bigg ]\sqrt{-g}d^{4}x, \end{aligned}$$

(6)

where $f_{R}(R,T)=\frac{\partial f(R,T)}{\partial R}$, $f_{T}(R,T)=\frac{\partial f(R,T)}{\partial T}$ and $\Box \equiv$

$\frac{1}{\sqrt{-g}}\partial _{a}(\sqrt{-g}g^{ab}\partial _{b})$. As the trace of the electromagnetic energy-momentum tensor vanishes, the variation of the trace of the stress tensor with respect to the metric tensor is given by

$$\begin{aligned} {\frac{\delta (g^{cd}{\mathcal {M}}_{cd})}{\delta g^{ab}}={\mathcal {M}}_{ab}+\varTheta _{ab},} \end{aligned}$$

(7)

where ${\varTheta _{ab}\equiv g^{cd}\frac{\delta {\mathcal {M}}_{cd}}{\delta g^{ab}}}$. On simplification of Eq. (6), and using Eq. (7), one obtains the modified form of Einstein’s field equations in f(R, T) theory as

$$\begin{aligned} \Big (R_{ab}+g_{ab}\Box -\nabla _{a} \nabla _{b}\Big )f_{R}(R,T)-\frac{1}{2}f(R,T)g_{ab} = T_{ab}^{eff}, \end{aligned}$$

(8)

where ${T_{ab}^{eff}\equiv 8\pi T_{ab}-f_{T}(R,T)({\mathcal {M}}_{ab}+\varTheta _{ab})}$.

On account of all the terms contained in the conservation law [55], performing the covariant derivative of the right hand side of Eq. (8), and re-arranging, we obtain

$$\begin{aligned} \nabla ^{a} {\mathcal {M}}_{ab}= & {} \frac{f_{T}(R,T)}{8\pi -f_{T}(R,T)}\Bigg [\left( {\mathcal {M}}_{ab}+ \varTheta _{ab}\right) \nabla ^{a}lnf_{T}(R,T) \nonumber \\{} & {} +\nabla ^{a}\varTheta _{ab}-\frac{1}{2}g_{ab}\nabla ^{a}T-\frac{8\pi }{f_{T}(R,T)}\nabla ^{a}{\mathcal {E}}_{ab}\Bigg ].\nonumber \\ \end{aligned}$$

(9)

The right hand side of the above equation vanishes if $f_{T}(R,T)=0$, i.e. f(R, T) is simply a function of the Ricci scalar R, and hence one can easily retrieve the conservation law in Einstein gravity. The non-vanishing right hand term of Eq. (9) was shown to play a crucial role in explaining the gravitational effects on the solar system beyond GR [45].

Motivated by the growing interest of f(R, T) gravity in the high gravity regime, we would like to develop and study the distinctive features of a charged fluid sphere in f(R, T) gravity. Even though different functional forms of f(R, T) have been explored in the past [45], Cemsinan et al. [46] showed that the only possible and acceptable form of f(R, T) is a linear functional form of T which can provide a plausible relativistic compact star model in f(R, T) gravity. Hence, we write the modification in the form $f(R,T) =R+2\chi T$, where $\chi$ is a dimensionless coupling parameter. Further, by choosing the matter Lagrangian density as ${{\mathcal {L}}_m = p}$ [63] (opposite signature was taken in Ref. [72]), we have ${\varTheta _{ab}=-2 {\mathcal {M}}_{ab}+ p g_{ab}}$ and it’s trace provides ${\varTheta = -2 {\mathcal {M}}+4p}$. Utilizing (8), we eventually obtain

$$\begin{aligned} {G_{ab}= 8\pi T_{ab}+\chi {\mathcal {M}}g_{ab}+2\chi ({\mathcal {M}}_{ab}-pg_{ab}),} \end{aligned}$$

(10)

where $G_{ab}= R_{ab} - \frac{1}{2}R g_{ab}$ is the Einstein tensor. When $\chi$ vanishes, one regains the unmodified form of Einstein’s field equations.

3 Einstein–Maxwell system in f(R, T) gravity

We consider a static charged sphere filled with a perfect fluid in a spherically symmetric static spacetime metric

$$\begin{aligned} ds_{-}^2 = -e^{2\nu (r)} dt^2 + e^{2\mu (r)}dr^2 + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2),\nonumber \\ \end{aligned}$$

(11)

in standard coordinates $x^i = (t, r, \theta , \phi )$. The undetermined functions $\nu (r)$ and $\mu (r)$ can be obtained by solving (10) together with Maxwell’s equations

$$\begin{aligned} F_{[ab,c]} = 0, ~~~~~\left[ e^{-(\nu +\mu )}r^2E\right] ' = {4\pi }\sigma e^{\mu } r^2. \end{aligned}$$

(12)

Spherical symmetry implies that $F_{tr}$ is the only non-vanishing component of the electromagnetic field tensor. Using Eq. (12), we write the electric field intensity as

$$\begin{aligned} E = \frac{e^{(\nu +\mu )}}{r^2}q(r), \end{aligned}$$

(13)

where the total charge q(r) contained within the sphere of radius r is defined as

$$\begin{aligned} q(r) = 4\pi \int _0^r\sigma r^2 e^\mu dr. \end{aligned}$$

(14)

In the natural unit system having $G = c = 1$, using Eq. (14), the Einstein-Maxwell field Eqs. (10) and (12) yield

$$\begin{aligned}{} & {} {8\pi }\left( \rho +\frac{q^2}{8\pi r^4}\right) + \chi (3\rho -p)\nonumber \\{} & {} \quad = -\frac{1}{r^2}+\frac{1}{r^2}\frac{d}{dr}\left( re^{-2\mu }\right) , \end{aligned}$$

(15)

$$\begin{aligned}{} & {} {8\pi }\left( p-\frac{q^2}{8\pi r^4}\right) + \chi (-\rho +3p) \nonumber \\{} & {} \quad = e^{-2\mu } \Bigl (\frac{2\nu '}{r}+\frac{1}{r^2}\Bigr ) -\frac{1}{r^2}, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} {8\pi }\left( p+\frac{q^2}{8\pi r^4}\right) + \chi (-\rho +3p) \nonumber \\{} & {} \quad = e^{-2\mu } \Bigl (\nu ''+\nu '^2-\nu '\mu ' +\frac{\nu '}{r}-\frac{\mu '}{r}\Bigr ), \end{aligned}$$

(17)

$$\begin{aligned}{} & {} 4\pi \sigma =\frac{e^{-\mu }}{r^2}\frac{dq}{dr}. \end{aligned}$$

(18)

The prime ($'$) denotes differentiation with respect to the radial parameter r. Subtracting Eq. (17) from Eq. (16), we obtain

$$\begin{aligned} \frac{2q^2}{r^4} = e^{-2\mu } \left( \nu ''+\nu '^2-\nu '\mu '-\frac{\nu '}{r}-\frac{\mu '}{r}-\frac{1-e^{2\mu }}{r^2}\right) .\nonumber \\ \end{aligned}$$

(19)

It is noted that all the physical quantities like matter density, pressure, and charge density can be evaluated by solving the system of Eqs. (15)–(19). To solve the system, the metric potential $\mu (r)$ is assumed in the most general form of the Buchdahl-VT [70, 71] ansatz

$$\begin{aligned} e^{\mu } = \sqrt{\frac{1+ f(r)}{1 - \frac{r^2}{C^2}}}, \end{aligned}$$

(20)

where C is an arbitrary constant. Setting $f(r)=0$ in (20), it is possible to obtain the Schwarzschid interior solution for an incompressible fluid sphere, as will be shown later.

Equation (19) is a second order differential equation. To obtain a tractable form, at this stage, we make a coordinate transformation $x^2=1-\frac{r^2}{C^2}$ and introduce a new variable as in Ref. [68]

$$\begin{aligned} e^\nu (1+f)^{-\frac{1}{4}} = \psi (x), \end{aligned}$$

(21)

so that Eq. (19) takes the form

$$\begin{aligned}{} & {} \frac{d^2\psi }{dx^2}+\left[ \frac{f_{xx}}{4(1+f)}-\frac{5f^2_x}{16(1+f)^2}+\frac{xf_x}{2(1-x^2)(1+f)}\right. \nonumber \\{} & {} \quad \left. +\frac{f}{(1-x^2)^2}-\frac{2q^2(1+f)}{C^2(1-x^2)^3}\right] \psi = 0, \end{aligned}$$

(22)

where $f_x$ represents the first order derivative with respect to x. The charged analogue of the Schwarzschild solution demands the linearity of $\psi (x)$, i.e. $\frac{d^2\psi }{dx^2}$ must vanish [68] which implies

$$\begin{aligned} q^2(x)= & {} \frac{C^2(1-x^2)^3f_{xx}}{8(1+f)^2}-\frac{5C^2(1-x^2)^3f^2_x}{32(1+f)^3}\nonumber \\{} & {} +\frac{C^2x(1-x^2)^2f_x}{4(1+f)^2}+\frac{C^2(1-x^2)f}{2(1+f)}, \end{aligned}$$

(23)

and hence

$$\begin{aligned} \psi (x) = a -b x, \end{aligned}$$

(24)

where a and b are integration constants. The expression (23) in terms of the radial parameter r takes the form

$$\begin{aligned} q^2(r)= & {} \frac{r^4(C^2-r^2)f''}{8C^2(1+f)^2}-\frac{5r^4(C^2-r^2)f'^2}{32C^2(1+f)^3}\nonumber \\{} & {} -\frac{r^3(3C^2-2r^2)f'}{8C^2(1+f)^2}+\frac{r^2f}{2(1+f)}, \end{aligned}$$

(25)

which ensures that q(r) is well behaved at $r=0$ as well as at all interior points of the star for any particular choice of f(r). Consequently, the spacetime metric of a static and spherically symmetric object in the presence of an electric field is obtained as

$$\begin{aligned} ds_{-}^2= & {} -(1+ f(r))^\frac{1}{2}\left( a -b\sqrt{1- \frac{r^2}{C^2}}\right) ^2 dt^2 + \frac{1+ f(r)}{1 - \frac{r^2}{C^2}} dr^2 \nonumber \\{} & {} + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2). \end{aligned}$$

(26)

The constants (a, b and C) can be determined by matching this solution to the exterior Reissner–Nordström metric at the boundary. A physically viable f(R, T) gravity model can be obtained by choosing f(r) suitably.

3.1 Uncharged case: ($q=0$ which implies $f(r)=0$)

For $f(r)=0$, Eq. (23) shows that the electric field vanishes. Using Eqs. (15) and (16), the density and pressure in this case are obtained as

$$\begin{aligned} \rho= & {} \frac{3(4\pi +\chi )\sqrt{1-r^2/C^2}-8a(3\pi + \chi )}{4C^2(\sqrt{1-r^2/C^2}-2a)(2\pi +\chi )(4\pi +\chi )}, \end{aligned}$$

(27)

$$\begin{aligned} p= & {} \frac{3\chi \sqrt{1-r^2/C^2}-8\pi (-a+3b\sqrt{1-r^2/C^2})}{8C^2\left( b\sqrt{1-r^2/C^2}-a\right) (2\pi +\chi )(4\pi +\chi )}. \end{aligned}$$

(28)

Obviously, for $\chi = 0$, Eqs. (27) and (28) represent the density and pressure in Einstein’s gravity for an uncharged incompressible fluid sphere. At $r=0$, Eq. (28) can be rewritten in the form

$$\begin{aligned} p_c = \frac{(p_{c})_{0} - \frac{3\chi }{8\pi C^2 (a-b)}}{(2 +\chi /\pi )(4\pi +\chi )}, \end{aligned}$$

(29)

where $(p_{c})_{0} = \frac{3b-a}{(a-b)C^2}$ represents the central pressure in Einstein’s gravity ($\chi =0$). It should be stressed that in our construction the modified gravity contribution essentially appears on the right hand side of the field equations which might lead to misleading or unphysical results unless the coupling parameter $\chi$ is fixed appropriately. For example, in Eq. (29), we note that the central pressure becomes negative for arbitrarily high values of $\chi$. The parameter space of $\chi$ over which our model may provide a physically meaningful solution can be evaluated in the following manner.

To find a reasonable bound on $\chi$ from Eq. (29), we note the following:

• (i) The central pressure diverges if (1) $a = b$ or,   (2) $\chi = -2\pi$ or, $-4\pi$;

• (ii) The central pressure vanishes if $\chi = \frac{8\pi }{3}(3b-a)$ which implies that $\chi$ is positive or negative depending on whether $b > a/3$ or $b < a/3$.

• (iii) Depending on whether $\chi$ is positive or negative, either $p_{c} > (p_{c})_{0}$ or $p_{c} < (p_{c})_{0}$, i.e. the respective values of the central pressure is greater or less in f(R, T) gravity than Einstein’s gravity.

• (iv) The bound on the dimensionless parameter $\chi$ is obtained in the form

  $$\begin{aligned} -4\pi ~< \chi ~< ~\frac{8\pi }{3}(3b-a). \end{aligned}$$

  (30)

Now the $p(r=R) = 0$) condition determines the constant $R=C\sqrt{1-\frac{a^2}{9b^2}}$ in Einstein’s gravity which is the radius of the star. For positive pressure, we must also have $b > a/3$. In f(R, T) gravity, the vanishing of pressure condition yields

$$\begin{aligned} \mathbf{b = \frac{\chi }{8\pi }+\frac{a}{3\sqrt{1-R^2/C^2}}}, \end{aligned}$$

(31)

which leads us to an interesting conclusion that $\chi$ must vanish for Schwarzschild’s interior incompressible solution for which the constant takes the value $b=1/2$, provided $\mathbf{a=\frac{3}{2}\sqrt{1-\frac{R^2}{C^2}}}$. This issue will be further taken up in Sect. (5).

Consequently, using Eq. (26), the interior line element for an uncharged compact object in f(R, T) gravity can be written as

$$\begin{aligned} ds_{-}^2= & {} -\left[ \frac{3}{2}\sqrt{1-\frac{R^2}{C^2}}-\frac{1}{2}\left( \frac{\chi }{4\pi }+1\right) \sqrt{1-\frac{r^2}{C^2}}\right] ^2 c^2 dt^2\nonumber \\{} & {} + \left( 1 - \frac{r^2}{C^2}\right) ^{-1} dr^2 + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2), \end{aligned}$$

(32)

where we have substituted $a=\frac{3}{2}\sqrt{1-\frac{R^2}{C^2}}$. It is easy to note that the usual form of the Schwarzschild interior solution for an incompressible fluid sphere can be regained simply by setting $\chi = 0$.

3.2 Charged Buchdahl–Vaidya–Tikekar model in f(R, T) gravity: ($f(r) \ne 0$)

We now consider the Vaidya and Tikekar (VT) [71] ansatz so that $f(r) = k\frac{r^2}{C^2}$. The VT ansatz is motivated by the observation that the $t=$ constant hypersurface of the associated spacetime, when embedded in a 4-Euclidean space, turns out to be spheroidal in which the parameter k denotes the departure from the sphericity of associated 3-space. The 3-hypersurface becomes flat and spherical for $k = -1, 0$, respectively. The associated spacetime is well behaved for $r < C$ and $k > - 1$. The VT ansatz has been widely used over the years to model compact stars and radiating stellar models, and this geometry is relevant in our construction, particularly in the context of a similar approach adopted by Sharma et al. [68].

With the VT ansatz, using Eqs. (15–18), (20), (21) and (24), we obtain the metric potentials, energy-density, pressure and charge-density as

$$\begin{aligned} e^{\nu (r)}= & {} (a-b\sqrt{1-r^2/C^2})(1+kr^2/C^2)^{1/4}, \end{aligned}$$

(33)

$$\begin{aligned} e^{\mu (r)}= & {} \sqrt{\frac{1+\frac{kr^2}{C^2}}{1-\frac{r^2}{C^2}}}, \end{aligned}$$

(34)

$$\begin{aligned} \rho= & {} \frac{1}{D(r,k,\chi )} \times \Bigg [\left\{ b(C^2-r^2)-aC^2\sqrt{1-r^2/C^2}\right\} \nonumber \\{} & {} \times \left\{ 3C^2kr^2\left[ 4\pi (10+11k)+3\chi (2+5k)\right] + 12C^4 \right. \nonumber \\{} & {} \times \left. \left[ 8\pi (1+k)+\chi (2+3k)\right] +k^2 r^4 \bigl [4\pi (1+4k) \bigr .\right. \nonumber \\{} & {} \bigl .\left. \chi (11-4k)\bigr ]\right\} -8aC^2\chi \sqrt{1-r^2/C^2} \nonumber \\{} & {} - (C^2+kr^2)^2\Bigg ], \end{aligned}$$

(35)

$$\begin{aligned} p= & {} \frac{1}{2D(r,k,\chi )} \times \Bigg [\left\{ b(C^2-r^2)-aC^2\sqrt{1-r^2/C^2}\right\} \nonumber \\{} & {} \left\{ 6C^2kr^2\left[ \chi (k-22)-12\pi (k+6)\right] +24C^4 \right. \nonumber \\{} & {} \left. \left[ \chi (k-2)-8\pi \right] -k^2 r^4\bigl [8\pi (4k+25)+2\chi \bigr .\right. \nonumber \\{} & {} \bigl .\left. (4k+37)\bigr ] \right\} -16aC^2\sqrt{1-r^2/C^2}(8\pi +3\chi ) \nonumber \\{} & {} (C^2+kr^2)^2\Bigg ], \end{aligned}$$

(36)

$$\begin{aligned} \sigma= & {} \frac{\sqrt{k(C^2-r^2)}}{8\pi \sqrt{2}(C^2+k r^2)^3\sqrt{C^2(2-k)+k(7+4 k)r^2}} \nonumber \\{} & {} \times \Bigl [3 C^4(2-k)+(4 C^2+k r^2)(7+4 k)k r^2\Bigr ], \end{aligned}$$

(37)

where

$$\begin{aligned} D(r,k,\chi )= & {} 32(C^2+kr^2)^3(2\pi +\chi )(4\pi +\chi )\bigl [b(C^2-r^2)\bigr .\\{} & {} \bigl . -aC^2\sqrt{1-r^2/C^2}\bigr ]. \end{aligned}$$

At the centre $r=0$, Eq. (35 - 37) take the form

$$\begin{aligned} \rho _c= & {} \frac{1}{8(a-b)C^2(2\pi +\chi )(4\pi +\chi )} \times \Bigl [24\pi (a-b)(1+k) \Bigr .\nonumber \\{} & {} \Bigl . +\chi \left\{ a(8+9k)-3b(2+3k)\right\} \Bigr ], \end{aligned}$$

(38)

$$\begin{aligned} p_c= & {} \frac{8\pi (3b - a)+3\chi \left\{ 2b+k(a-b)\right\} }{8(a-b)C^2(2\pi +\chi )(4\pi +\chi )}, \end{aligned}$$

(39)

$$\begin{aligned} \sigma _c= & {} \frac{3}{8\pi C^2}\sqrt{\frac{k(2-k)}{2}}. \end{aligned}$$

(40)

Obviously the central density ($\rho _c$) will be positive if

$$\begin{aligned} k > \frac{2\left[ 3(b-a)(4\pi +\chi )-a\chi \right] }{3(a-b)(8\pi +3\chi )}. \end{aligned}$$

Moreover the positive central pressure ($p_c$) for the above bound on k implies

$$\begin{aligned} \frac{(3b-a)}{8C^2(a-b)} > 0. \end{aligned}$$

(41)

The above bound further suggests that $a> b > a/3$. For a well behaved stellar configuration, k can take values within the range $-1< k <\infty$.

Using Eq. (25), the charge contained within a radial distance r is obtained as

$$\begin{aligned} q^2(r) = \frac{kr^6\left[ C^2(2-k) + k(7 + 4k)r^2\right] }{8(C^2 + kr^2)^3}, \end{aligned}$$

(42)

which clearly vanishes at the centre. It is also interesting to note that the charge is zero for $k=0$.

4 Boundary conditions and fixation of the constants

To evaluate the physical quantities, we need to fix the constants (a, b, C) for given values of $\chi$ and k. The constants can be determined by utilizing the appropriate boundary conditions, as discussed below.

The exterior spacetime of the static charged object is described by the Reissner–Nordström metric

$$\begin{aligned} ds_{+}^2= & {} -\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) dt^2 +\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) ^{-1} dr^2\nonumber \\{} & {} + r^2(d \theta ^2 + \sin ^2 \theta d\phi ^2), \end{aligned}$$

(43)

where M and Q represent the total mass and charge, respectively. The matching conditions at the boundary $r=R$ are the continuity of the metric potentials $e^\nu ,~ e^\mu$ and the vanishing of pressure at the boundary i.e., $p(r=R) = 0$. Noting that $m(R)=M$ and $q(R)=Q$, these conditions imply

$$\begin{aligned} 1-2u +\alpha ^2 u^2= & {} (1+ k n)^\frac{1}{2}(a -b\sqrt{1- n})^2, \end{aligned}$$

(44)

$$\begin{aligned} 1-2u+\alpha ^2 u^2= & {} \frac{1 - n}{1+ k n}, \end{aligned}$$

(45)

$$\begin{aligned} 16\left( 1+nk\right) ^2= & {} \Bigl [\frac{b(1-n)-a\sqrt{1-n}}{8\pi b(1-n)+3\chi a\sqrt{1-n}}\Bigr ] \nonumber \\{} & {} \times \Bigl [\chi \bigl \{24(k-2)+6nk(k-22) \Bigr .\bigr .\nonumber \\{} & {} -2n^2k^2\Bigl .\bigl . (37+4k)\bigr \} -8\pi \bigl \{8+nk(22+9k) \Bigr . \bigr . \nonumber \\{} & {} \Bigl . \bigl . +n^2k^2(9+4k)\bigr \}\Bigr ], \end{aligned}$$

(46)

where we have substituted $n=\frac{R^2}{C^2}$, $u=\frac{M}{R}$ and $\alpha ^2 = \frac{Q^2}{M^2}$ for simplicity. Using Eq. (45), we determine the constant

$$\begin{aligned} C = R\sqrt{\frac{1+ky}{1-y}}, \end{aligned}$$

(47)

where $y = 1-2u +\alpha ^2 u^2$.

Using Eqs. (44) and (46), we evaluate the remaining two constants as

$$\begin{aligned} b= & {} \frac{y}{8\sqrt{1-n}(8\pi +3\chi )(1+kn)^2\sqrt{y\sqrt{1+kn}}} \nonumber \\{} & {} \times \Bigl [(4\pi +\chi ) \left\{ n^2k^2(4k+9)+nk(9k+22)+8\right\} \Bigr . \nonumber \\{} & {} \Bigl . +4\chi (1+nk)(nk-3k-2)\Bigr ], \end{aligned}$$

(48)

$$\begin{aligned} a= & {} b\sqrt{1-n}+\frac{y}{\sqrt{y\sqrt{1+kn}}}. \end{aligned}$$

(49)

Note that all constants thus are given in terms of k, M, R, Q and $\chi$. It is interesting to note that in the uncharged case with $k=0$, the above constants take the form

$$\begin{aligned} a= & {} \frac{3(4\pi +\chi )\sqrt{1-2u}}{(8\pi +3\chi )}, \end{aligned}$$

(50)

$$\begin{aligned} b= & {} \frac{4\pi }{(8\pi +3\chi )}, \end{aligned}$$

(51)

$$\begin{aligned} C= & {} R \sqrt{\frac{1}{2u}}, \end{aligned}$$

(52)

which is exactly the same as in Sect. 3.1 if one sets $\chi =0$.

By setting $q(R) = Q$, we rewrite Eq. (42) in the form

$$\begin{aligned} \alpha ^2 u^2 n =\frac{kn^3[2-k+(7+4k)kn]}{8(1+kn)^3}, \end{aligned}$$

(53)

and substitute the value of n to obtain

$$\begin{aligned} k = \frac{8\alpha ^{2}}{\left( 2-u\alpha ^{2}\right) \left[ \left( 2-u\alpha ^{2}\right) +G(u,\alpha ^{2})-8\alpha ^{2}\right] }, \end{aligned}$$

(54)

where $\displaystyle {G(u,\alpha ^{2})=\sqrt{\left( 2-u\alpha ^{2}\right) \left( 2+39u\alpha ^{2}\right) -24\alpha ^{2}}}$. Thus, to have $\alpha =0$, we must have $k=0$ while the converse is also true as can be seen in Eq. (53).

5 Physical acceptability and analysis of physical quantities

Any physically acceptable stellar interior solution should have the following features: (i) The density and pressure should be positive throughout the interior of the star i.e., $\rho ,~p > 0$; (ii) the pressure p should vanish at some finite radial distance i.e., $p (r = R) = 0$ and (iii) the causality condition should be satisfied throughout the star, which implies that $0 \le \sqrt{\frac{dp}{d\rho }} \le 1$.

To verify whether the above conditions are fulfilled in this model, we consider a hypothetical compact object of a given mass and radius. For this, we take the same set of values as in Ref. [68] i.e., $M = 1.58~M_\odot$ and $R = 9.1~$km. Using Eqs. (47)–(49), we evaluate the constants for different values of k and $\chi$.

Let us first consider the feasibility of an uncharged compact object in f(R, T) gravity. Making use of the data given in Table 1, we plot the radial variation of matter density and pressure, which are shown in Figs. 1 and 2. Clearly, in Fig. 2, we note that the model becomes unphysical for $\chi \ne 0$. In other words, Schwarzschild’s interior solution for an incompressible fluid provides an extreme case which cannot be further modified.

Table 1 Values of the model parameters for an uncharged ($k = 0$) compact star of mass $M = 1.58~M_\odot$ and radius $R = 9.1~$km

Fig. 1

Radial variation of energy density $\rho$ with $\chi$ for an uncharged compact star

Fig. 2

Radial variation of pressure p with $\chi$ for an uncharged compact star. Interestingly, a physically meaningful model is obviously possible only for $\chi = 0$

Table 2 Values of the model parameters for different choices of k and $\chi$ for a hypothetical charged compact star of mass $M = 1.58~M_\odot$ and radius $R = 9.1~$km

Let us now consider the charged case. For a charged (k or $q(r) \ne 0$) compact object with the mass and radius given above, the values of the constants are given in Table 2. In the table, we note that all values of a are less than 3/2, and values of b are greater than a/3 as well as greater than 1/2 [as discussed in Sect. 3.1]. With this set of values, we investigate the behaviour of the matter density and pressure for different choices of k and $\chi$ as shown in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 and 22. The plots indicate that the model parameters are regular and well behaved at all interior points of the compact object. Some features of the model are discussed below:

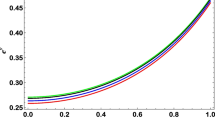
• (i) Figures 3, 5, 7, 9 and 11 show that the radial variation of matter density monotonically decreases as one goes outward.

• (ii) Figures 4, 6, 8, 10 and 12 show that as $\chi$ increases the matter density gradually decreases near the core or the central region. Irrespective of the signature and values of $\chi$, all the density curves cross the constant density line at $r\sim 6~$ km, which imply that any uniform density stellar configuration has the largest value at the boundary.

• (iii) Figures 13, 15, 17, 19 and 21 show that as the charge increases, the central pressure decreases monotonically.

• (iv) Figures 14, 16, 18, 20 and 22 show the radial variation of the isotropic pressure for different values of $\chi$. Figure 14 indicates that the negative values of $\chi ~$ exert more pressure at the core region than positive values. Interestingly, k and negative values of $\chi$ seem to have opposite effects.

Fig. 3

Energy density $\rho$ plotted against the radial distance r with $k = 0.1$

Fig. 4

Energy density $\rho$ plotted against the radial distance r with $\chi = 0$

Fig. 5

Energy density $\rho$ plotted against the radial distance r with $k = 0.5$

Fig. 6

Energy density $\rho$ plotted against the radial distance r with $\chi = -1.0$

Fig. 7

Energy density $\rho$ plotted against the radial distance r with $k = 1.0$

Fig. 8

Energy density $\rho$ plotted against the radial distance r with $\chi = 1.0$

Fig. 9

Energy density $\rho$ plotted against the radial distance r with $k = 1.5$

Fig. 10

Energy density $\rho$ plotted against the radial distance r with $\chi = 3.0$

Fig. 11

Energy density $\rho$ plotted against the radial distance r with $k = 2.0$

Fig. 12

Energy density $\rho$ plotted against the radial distance r with $\chi = 5.0$

Fig. 13

Isotropic pressure p plotted against the radial distance r with $k = 0.1$

Fig. 14

Isotropic pressure p plotted against the radial distance r with $\chi = 0$

Fig. 15

Isotropic pressure p plotted against the radial distance r with $k = 0.5$

Fig. 16

Isotropic pressure p plotted against the radial distance r with $\chi = -1.0$

Fig. 17

Isotropic pressure p plotted against the radial distance r with $k = 1.0$

Fig. 18

Isotropic pressure p plotted against the radial distance r with $\chi = 1.0$

Fig. 19

Isotropic pressure p plotted against the radial distance r with $k = 1.5$

Fig. 20

Isotropic pressure p plotted against the radial distance r with $\chi = 3.0$

Fig. 21

Isotropic pressure p plotted against the radial distance r with $k = 2.0$

Fig. 22

Isotropic pressure p plotted against the radial distance r with $\chi = 5.0$

It should be pointed out here that in the standard approach of stellar modelling, a barotropic equation of state (EOS) is usually assumed i.e., based on our understanding about the micro-physics of the system, the right hand side of the field equations is assumed which subsequently determines the left hand side of the field equations. However, in the present work, we do not prescribe any EOS to solve the system. Rather, by prescribing the geometry, we solve the system of equations and look for parameter values which can provide realistic stellar observables. The energy density and pressure are functions of the radial coordinate r and a parametric plot of these quantities give us some insight into the nature of EOS of the composition. In our formulation the geometric part was provided in the form of Buchdahl–Vaidya–Tikekar [70, 71] metric ansatz. Such an approach turns out to be useful for physical systems where the nature of particle interaction remains inconclusive.

6 Compactness bound in f(R, T) gravity

The mass to radius ratio, i.e compactness (M/R), plays a crucial role in modelling a compact star. The most compact object is a black hole (BH) for which the compactness ratio is $\frac{1}{2}$. For non-BH compact objects, amongst others, the upper bound on M/R in Einstein’s gravity was investigated by Sharma et al. [68] in which it has been shown that a charged non-BH could be overcharged as compared to a charged black hole. In the current investigation, we intend to analyze the impact of the modification made in Einstein’s gravity on the compactness bound. Recently, in the uncharged case, Pappas et al. [63] have extended the Tolman III and VII solutions to f(R, T) gravity and showed that the mass to radius ratio becomes greater than the Buchdahl limit of compactness for positive values of $\chi$. The ratio never exceeds the black hole compactness.

In the charged case, we obtain the bound by demanding that the central pressure must not diverge. From Eq. (39), it is evident that $(a - b) \ge 0$ is the condition for the divergence-free central pressure. Substituting the value of a, as given in Eq. (49) in the above requirement, we obtain

$$\begin{aligned} \frac{y}{\sqrt{y\sqrt{1+kn}}} \ge b\left( 1-\sqrt{1-n}\right) . \end{aligned}$$

(55)

For an uncharged ($k = \alpha = 0$) compact object this condition simplifies to

$$\begin{aligned} \left( 4\pi +\chi \right) \left( 3\sqrt{1-2u} - 1\right) + \chi \ge 0, \end{aligned}$$

(56)

which, on further simplification, gives

$$\begin{aligned} \boxed { \frac{M}{R} \le \frac{1}{2} \left[ 1- \frac{1}{9\left( 1+\frac{\chi }{4\pi }\right) ^2}\right] }. \end{aligned}$$

(57)

One can readily retrieve the Buchdahl bound $\frac{M}{R} \le \frac{4}{9}$ from Eq.(57) for $\chi = 0$. For $\chi \ne 0$ in the uncharged case, Eq. (57) provides the maximum compactness bound which can also be expressed in the form

$$\begin{aligned} u \le \frac{9\chi ^{2}+72\pi \chi +128\pi ^{2}}{18(\chi +4\pi )^2}, \end{aligned}$$

(58)

which is exactly the same as obtained earlier by Pappas et al [Eq. (33) in Ref. [63]].

For a charged star, condition (55) takes the form as

$$\begin{aligned}{} & {} \left( 4\pi +\chi \right) \Bigl [16\left( 1+nk\right) ^2\sqrt{1-n}-\left( 1-\sqrt{1-n}\right) \Bigr .\nonumber \\{} & {} \quad \times \Bigl .\left\{ 8+nk(9k+22)+n^2k^2(4k+9)\right\} \Bigr ]+4\chi \left( 1+nk\right) \nonumber \\{} & {} \quad \times \left[ k(n-1)(3\sqrt{1-n}-1)+2(k+1)\right] \ge 0. \end{aligned}$$

(59)

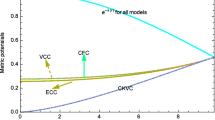
Equations (45) and (54) suggest that the above condition (59) is governed by choice of $\alpha$ and $\chi$. Condition (59) can be utilized numerically to find a bound on compactness as shown in Fig. 23. The black solid line in Fig. 23 corresponds to the uncharged case which is same as in Ref. [63]. It is noteworthy that while the compactness for an uncharged stellar configuration cannot go beyond black hole compactness, it can go beyond the BH compactness when the star is charged. As the values of $\alpha ^{2}$ are increased, the compactness goes beyond the BH compactness limit even for small values of $\chi$.

Fig. 23

Compactness $\frac{M}{R}$ plotted against $\chi$ for different choices of $\alpha ^{2}$

Having understood the dependency of $\chi$ on compactness numerically, let us now explore the possibility of obtaining an analytic expression yielding similar behaviour, which might be considered as the compactness bound for a charged sphere in f(R, T) gravity analogous to the Buchdahl bound. To achieve this goal, let us assume $k = \kappa \epsilon$ and $\chi = X \epsilon$, where $\left| \epsilon \right|<< 1$. This approximation will be valid if the departure from sphericity is small and the modification is moderate. With these assumptions, we have from Eq. (54)

$$\begin{aligned} \alpha ^2= & {} \frac{2\left[ \left( 1-k+3ku\right) -\sqrt{\left( 1-k+3ku\right) ^2 - 5k^2u^2}\right] }{5ku^2} \nonumber \\{} & {} + {\mathcal {O}}(\epsilon ^2). \end{aligned}$$

(60)

Inserting the value of $\alpha ^{2}$ in Eq. (59) and retaining terms upto ${{\mathcal {O}}(\epsilon )}$, we obtain

$$\begin{aligned} \boxed { u = \frac{\frac{32\pi }{9}\left[ \frac{2}{(8\pi - \chi )}-\frac{\chi }{(8\pi -\chi )^2}\right] }{1+\frac{4\pi }{(8\pi -\chi )}\sqrt{\frac{16\alpha ^2}{9}(\frac{3\chi }{8\pi }-2)+(\frac{\chi }{4\pi }-2)^2}}}, \end{aligned}$$

(61)

which for a charged compact object in Einstein’s gravity (i.e. $\chi = 0$) takes the form

$$\begin{aligned} u = \frac{M}{R} = \frac{8/9}{1+\sqrt{1-\frac{8\alpha ^2}{9}}}. \end{aligned}$$

(62)

Thus, as far as compactness is concerned, we notice a distinctive behaviour in f(R, T) gravity. Equation (61) may be considered as a charged generalization of the Buchdahl bound in f(R, T) gravity.

For a small value of $\chi$ (we take $=0.1$), we first evaluate the variation of compactness ($\frac{M}{R}$) with $\alpha ^{2}$ by utilizing the condition (59) which is tabulated in Table 3. Figure 24 utilizes the data obtained in Table 3 to plot the variation of compactness with $\alpha ^2$. The plot is then embedded on a similar plot obtained by utilizing condition (61). The overlapping of the two plots justifies the validity of our approximation method and the result in Eq. (61). It should be mentioned here that the overlapping is good for relatively smaller values of $\chi$ and they seem to diverge for $\chi \ge 1$. This implies that the analytical expression for compactness bound of a charged sphere in f(R, T) gravity obtained by our approximation method remains valid when $\chi$ takes relatively smaller ($\le 1$) values. Thus, the compactness bound Eq. (61) might not be the stringiest bound. Moreover, one can not regain Eq. (57) simply by putting $\alpha ^{2}=0$ in Eq. (61). In fact, for $\alpha ^{2}=0$ Eq. (61) takes the form (Fig. 25)

$$\begin{aligned} u = \frac{16\pi (16\pi -3\chi )}{9(8\pi -\chi )^2}. \end{aligned}$$

(63)

We show this variation separately in Fig. 26. The plot shows that as $\chi$ is increased from a negative value, the maximum compactness steadily increases towards 0.5. On further increase of $\chi$, the compactness decreases.

Table 3 Variation of compactness $\frac{M}{R}$ with $\alpha ^2$ for $\chi = 0.1$

Fig. 24

Compactness ratio $\frac{M}{R}$ plotted against $\alpha ^2$ for $\chi = 0.1$ using Eq. (61) and Eq. (59)

Fig. 25

Compactness ratio $\frac{M}{R}$ plotted against $\alpha ^2$ for different choices of $\chi$

Fig. 26

Compactness ratio $\frac{M}{R}$ plotted against $\chi$ for $\alpha ^2 = 0$

7 Concluding remarks

The Buchdahl bound in modified gravity was studied earlier by Goswami et al. [73] leading to new features in stellar objects. We also expect to obtain interesting features in f(R, T) theory for the Buchdahl limit. This paper provides an analysis of the physical behaviour of a charged compact star in f(R, T) gravity. The electromagnetic extension of the Buchdahl bound obtained in f(R, T) gravity is distinct from the results obtained earlier by Sharma et al. [68] for general relativity. Our study shows that the compactness can be increased by considering a modification in Einstein’s gravity which is further enhanced by the inclusion of charge. While in the absence of charge, the compactness never exceeds the BH compactness 0.5, even a comparatively small amount of charge together with the impact of the trace of the stress-energy tensor T can exceed the compactness bound beyond the BH limit 0.5. Whether this is indicative of a more stringent bound on the coupling term $\chi$ requires further probe.

Another point to note is that in Eq. (61), u will be a positive real quantity if the squared root term in the denominator remains positive. This restricts the charge to mass ratio $\frac{Q^2}{M^2} < \frac{9}{8}\frac{(\chi -8\pi )^2}{4\pi (16\pi -3\chi )}$. Obviously, $\frac{Q^2}{M^2} < 9/8$ for $\chi =0$.

While in the absence of charge, the variation of compactness is same as in Ref. [63], the presence of charge changes the scenario and provides some new insight into the effects f(R, T) gravity on the compactness. Equation (61) is the main result of this investigation which opens up the possibility of studying the most compact stars (other than black holes) such as a Buchdahl star can be seen in Fig. 23. It is evident from our analysis that f(R, T) gravity can accumulate more mass within a volume element leading to a greater compactness. Hence, it will be interesting to explore the mass gap between the GR predicted compactness bound (4/9) and black hole compactness (0.5) in the context of f(R, T) gravity inspired stellar models.

To conclude, the theoretical framework of f(R, T) gravity remains very much an open area which demands an in-depth analysis of its relevance and application in physical world [56]. In the context of its application in astrophysics, fixing the appropriate boundary conditions remains one such problem. Once accomplished, such theories are expected to provide interesting and distinctive features as far as their astrophysical and cosmological implications are concerned.