Study of anomalous $W^-W^+\gamma /Z$ couplings using polarizations and spin correlations in $e^-e^+\rightarrow W^-W^+$ with polarized beams

Abstract

We investigate the anomalous $W^-W^+\gamma /Z$ couplings in $e^-e^+\rightarrow W^-W^+$ followed by semileptonic decay using a complete set of polarization and spin correlation observables of W boson with the longitudinally polarized beam. We consider a complete set of dimension-six operators affecting $W^-W^+\gamma /Z$ vertex, which are $SU(2)\times U(1)$ gauge invariant. Some of the polarization and spin correlation asymmetries average out if the daughter of $W^+$ is not tagged and to overcome this we developed an artificial neural network and boosted decision trees to distinguish down-type jets from up-type jets. We obtain bounds on the anomalous couplings using MCMC analysis at $\sqrt{s} = 250$ GeV with integrated luminosities of $\mathcal {L}\in \{100~\text {fb}^{-1}, 250~\text {fb}^{-1}, 1000~\text {fb}^{-1}, 3000~\text {fb}^{-1}\}$ and different sets of systematic errors. We find that using spin-related observables along with cross section in the presence of initial beam polarization significantly improves the bounds on anomalous couplings compared to previous studies.

1 Introduction

The standard model is dimension-4 local quantum field theory, which has been successfully tested experimentally. With the discovery of a Higgs-like boson at LHC [1, 2], the last missing piece of SM is finally in place. However, despite all these wonderful experimental justifications, many unexplained phenomena suggest SM’s incompleteness. The mass of the Higgs boson (125 GeV) cannot be explained within SM. The higher-order quantum corrections would shift the mass of the Higgs boson to the cut-off scale unless there are perfect cancellations of these corrections. These fine-tuning mechanisms are not present within the framework of SM. SM QCD still has an unexplained problem with the $\theta$ parameter known as the strong-CP problem. Dark matter constitutes approximately $80\%$ of all the matter in our universe [3], yet the structure of dark matter is still a mystery. The recent report on the magnetic moment of muon [4, 5], W bosons mass [6] are some of the additional reasons to cast doubt that the SM is not a complete theory of fundamental particle. Though many theories beyond SM explain deviations with the inclusion of new particles, symmetry, or dimensions, experiments have not seen any signature in favor of any of these explicit models. In this article, we follow a more natural way of extending the SM called the effective field theory (EFT), which provides a suitable framework to parameterize deviations from the SM predictions according to the decoupling theorem [7]. This framework expands the Lagrangian of SM by adding higher dimensional terms. These higher dimensional terms are made out of SM fields, assuming that the new degrees of freedom are too heavy to be observed with currently available energy and are integrated out of the Lagrangian. The effects of new physics are encoded in the Wilson coefficient of these infinite series of higher dimensional operators. Considering the conservation of the lepton-baryon number, the effective Lagrangian is compactly written as [8]

$$\begin{aligned} \mathscr {L}_{eft} = \mathscr {L}_{SM} + \frac{1}{\Lambda ^2}\sum _i \mathcal {C}^{(6)}_i \mathscr {O}^{(6)}_i + \frac{1}{\Lambda ^4}\sum _j\mathcal {C}^{(8)}_j\mathscr {O}^{(8)}_j + .., \end{aligned}$$

(1)

where $c_i$ are the Wilson coefficient and $\mathscr {O}_i$ are higher order operators. Each higher dimensional term is suppressed by the power of $\Lambda ^{(d-4)}$, where $\Lambda$ is a characteristic new physics scale usually taken to be several TeVs. This suggests that the contribution to SM decreases as one moves towards $d>6$. Thus, we can truncate the above Lagrangian at some lowest higher-order terms of one interest. This study focused on the dimension-6 operators which affect $WWV, V\in \{\gamma ,Z\}$ vertex. Considering both CP-even and -odd operators, five relevant dimension-6 operator affects WWV vertex, which in HISZ basis [9, 10] are listed as:

$$\begin{aligned} \begin{aligned} \mathscr {O}_{WWW}&=\text {Tr}[W_{\nu \rho }W^{\mu \nu } W_{\rho }^{\mu }],\\ \mathscr {O}_{W}&=(D_\mu \Phi )^\dagger W^{\mu \nu } (D_\nu \Phi ), \\ \mathscr {O}_B&=(D_\mu \Phi )^\dagger B^{\mu \nu } (D_\nu \Phi ), \\ \mathscr {O}_{\tilde{WWW}}&=\text {Tr}[\widetilde{W}_{\mu \nu } W^{\nu \rho } W^\mu _\rho ], \\ \mathscr {O}_{\tilde{W}}&=(D_\mu \Phi )^\dagger \widetilde{W}^{\mu \nu } (D_\nu \Phi ), \end{aligned} \end{aligned}$$

(2)

where $\Phi = \begin{pmatrix} \phi ^+ \\ \phi ^0 \end{pmatrix}$ is the Higgs doublet and $W^{\mu \nu }, B^{\mu \nu }$ represents the field strengths of W and B gauge Fields. The covariant derivative is defined as $D_\mu = \partial _\mu +\frac{i}{2}g\tau ^i W_\mu ^i + \frac{i}{2}g'B_\mu$. The field tensor are given by $W_{\mu \nu } = \frac{i}{2}g\tau ^i(\partial _\mu W_\nu ^i-\partial _\nu W_\mu ^i + g\epsilon _{ijk}W_\mu ^i W_\nu ^k)$ and $B_{\mu \nu } = \frac{i}{2}g'(\partial _\mu B_\nu - \partial _\nu B_\mu )$. The first three operators in Eq. (2) are CP-even, and the last two are CP-odd. After electroweak symmetry breaking (EWSB), each operator of Eq. (2) generates anomalous WWV vertex along with triple vertex containing Higgs and vector gauge boson. These operators ($c_{WWW}, c_W$ and theirs dual) also generate quartic gauge boson couplings. The general couplings of two charged vector bosons with a neutral vector boson can be parameterized in an effective Lagrangian [9]:

$$\begin{aligned} \mathscr {L}^{eff}_{WWV}= & {} ig_{WWV}\left[ g_1^V(W^+_{\mu \nu }W^{-\mu } - W^{+\mu }W^-_{\mu \nu })V^\nu \right. \nonumber \\{} & {} +\left. k_V W^+_\mu W^-_\nu V^{\mu \nu } +\frac{\lambda _V}{m_W^2}W_\mu ^{\nu +}W_\nu ^{-\rho }V_{\rho }^{\mu } \right. \nonumber \\{} & {} +\left. ig_4^VW_\mu ^+W_\nu ^-(\partial ^\mu V^\nu +\partial ^\nu V^\mu ) \right. \nonumber \\{} & {} \quad -\left. ig_5^V\epsilon ^{\mu \nu \rho \sigma }(W_\mu ^+ \partial _\rho W_\nu ^- - \partial _\rho W_\mu ^+W_\nu ^-)V_\sigma \right. \nonumber \\{} & {} +\left. \tilde{k}_VW_\mu ^+W_\nu ^-\tilde{V}^{\mu \nu } + \frac{\tilde{\lambda }_V}{m_W^2}W_\mu ^{\nu +}W_\nu ^{-\rho }\tilde{V}_\rho ^{\mu }\right] , \end{aligned}$$

(3)

where $W^{\pm }_{\mu \nu } = \partial _\mu W^{\pm }_\nu -\partial _\nu W^\pm _\mu$, $V_{\mu \nu } = \partial _\mu V_\nu -\partial _\nu V_\mu$, $g_{WW\gamma } = -e$ and $g_{WWZ} = -e\cot \theta _W$, where e and $\theta _W$ are the proton charge and weak mixing angle respectively. The dual field is defined as $\tilde{V}^{\mu \nu } = 1/2\epsilon ^{\mu \nu \rho \sigma }V_{\rho \sigma }$, with Levi-Civita tensor $\epsilon ^{\mu \nu \rho \sigma }$ follows a standard convention, $\epsilon ^{0123}=1$. As discussed in Ref. [9], these seven operators exhaust all possible Lorentz structures to define the most general WWV interaction. Within the SM, the couplings are given by $g_1^Z=g_1^\gamma = k_Z = k_\gamma = 1$ and all others are zero. The gauge invariance fixes the value couplings like $g_1^\gamma ,g_4^V,g_5^V$, but in the presence of the effective operators given in Eq. (2), the values of other couplings changes, and are listed below:

$$\begin{aligned} \Delta g_1^Z&=c_W\frac{m^2_Z}{2\Lambda ^2}, \quad \lambda _V = \quad c_{WWW}\frac{3m_W^2g^2}{2\Lambda ^2} \nonumber \\ \Delta k_Z&=\left[ c_W-\sin ^2\theta _W\left( c_B+c_W\right) \right] \frac{m_Z^2}{2\Lambda ^2} \nonumber \\ \Delta k_\gamma&=\left( c_B+c_W\right) \frac{m_Z^2}{2\Lambda ^2},\quad \tilde{\lambda }_V =c_{\widetilde{WWW}}\frac{3m_W^2g^2}{2\Lambda ^2} \nonumber \\ \tilde{k}_Z&=-c_{\tilde{W}}\sin ^2\theta _W \frac{m_Z^2}{\Lambda ^2},\quad \tilde{k}_\gamma =\quad c_{\tilde{W}}\frac{m_W^2}{2\Lambda ^2}. \end{aligned}$$

(4)

Here,

$$\begin{aligned} c_i = \{c_{WWW},c_W,c_B,c_{\widetilde{W}},c_{\widetilde{WWW}}\}, \end{aligned}$$

(5)

are the Wilson coefficient associated with the effective operators listed in Eq. (2). The presence of these anomalous couplings will bring change in the observable that could be measured in the current or future collider, given that the deviation is within the measurable reach of the collider. The BSM matrix element for a given process in the presence of effective operators of Eq. (1) truncated at dimension-6 is given by

$$\begin{aligned} |\mathcal {M}_{BSM}|^2 = |\mathcal {M}_{SM}|^2 + 2\mathcal {R}e\left\{ \mathcal {M}_{SM}\mathcal {M}^*_{d6}\right\} +|M_{d6}|^2. \end{aligned}$$

(6)

The interference, i.e., the second term of Eq. (6) between the SM amplitude and the dim-6 amplitude, induces asymmetries in appropriately constructed CP-odd observable. The direct observation of the non-zero value of observable related to CP-odd operators would be a strong marker for the new physics as their values are predicted to be zero in SM at tree and loop level [11]. The last term, i.e., square term if the dimension-6 operator is of order $\Lambda ^{-4}$, comparable to SM’s interference with dimension-8 operators. However, we have assumed all dimension-8 couplings to be zero while performing the analyses upto order $\Lambda ^{-4}$.

Many theoretical studies on $W^-W^+\gamma /Z$ couplings are done at $e^-e^+$ collider [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] and hadron collider [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] and large hadron electron collider (LHeC) [46,47,48,49,50]. On experimental side, the similar studies was reported by different collaborations like OPAL [51,52,53,54,55,56], ALEPH [57,58,59,60,61], DELPHI [62], CDF [63, 64], D0 [65,66,67], ATLAS [68,69,70,71,72,73,74,75,76,77] and CMS [78,79,80, 80,81,82,83,84,85,86,87,88,89,90]. We list the experimentally measured current tightest limits on anomalous couplings ($c_i$) at $95\%$ confidence level (CL) in Table 1.

Table 1 The list of tightest constraints observed on the anomalous couplings in $SU(2) \times U(1)$ gauge at 95$\%$ confidence level (CL) from various experiments

The limits on the anomalous couplings listed in Table 1 are obtained by varying one parameter at a time and keeping other couplings to zero.

Due to the $SU(2)_L\times U(1)_Y$ gauge structure of SM, the electro-weak interactions are susceptible to the chirality of fermions. Left-handed fermions interact fundamentally differently than their right-chiral counterpart with the weak boson. This fundamental difference in interaction can be used as a tool to probe a deviation from the Standard Model (SM) prediction. Apart from increasing the luminosity, it has been shown [91] that the use of polarized beams can bring down the systematic error on the measurement of the left-right asymmetry ($A_{\text {LF}}$). Reducing systematic error of asymmetries becomes important when observables like polarization and spin correlation asymmetries are used as observables to probe beyond Standard Model (BSM) physics. The polarized positron beams can be used to probe physics models that would allow some unconventional combinations of helicities like in Minimal Sypersymmetric SM (MSSM) where $e^+_{R}e^-_R \rightarrow \tilde{e}^-_R\tilde{\chi }^+\bar{\nu }_e$ and $e^+_{L}e^-_L \rightarrow \tilde{e}^+_L\tilde{\chi }^-\nu _e$ [92]. Also, the ability to adjust the polarization of both beams independently provides unique possibilities for directly probing the properties of the produced particles like quantum numbers, and chiral couplings. The important effects of initial beam polarization are [93]

• $e^-$ and $e^+$ polarization allow obtaining a subset of the sample with higher rates for interesting physics and lower background. It would lead to an overall increase in sensitivities,

• When both beams are polarized, one obtains four distinct data sets instead of the two available if only the $e^-$ beam can be polarized.

• The likely most important effect is the control of systematic error for precision studies in Lepton collider.

The future Lepton collider viz. International Linear Collider (ILC) [94, 95], Compact Linear Collider (CLIC) [96], Future Circular Lepton Collider-ee (FCC-ee) [97] will be equipped with the potential of colliding polarized beams. With such specifications, these colliders will be the ideal place to undertake precision measurements.

In the current article, we use polarized $e^-$ and $e^+$ beams to probe a set of dimension-6 operators listed in Eq. (2) using various observable like cross section, polarization asymmetries, and spin correlation asymmetries. The study is done at the center-of-mass energy ($\sqrt{s})$ of 250 GeV at machine parameters planned for ILC using longitudinal polarized beams. However, the analysis can be easily translated to other colliders. The process we probed is the di-boson production of $W^-W^+$ followed by their semi-leptonic decay,

(7)

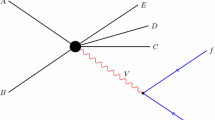
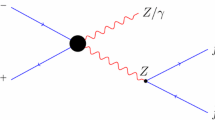
where j are the light quarks and $l^- \in \{ e^-, \mu ^-\}$. The amplitude of the process $e^-e^+ \rightarrow W^-W^+$ results from the t-channel neutrino and s-channel $\gamma$ and Z exchange, see Fig. 1. The current study focus on the leading order (LO) production of $W^-W^+$, and for a comprehensive treatment of $e^-e^+\rightarrow W^-W^+$ production in next-to-leading order, one may refer to [98,99,100,101,102,103,104].

Fig. 1

Leading order Feynman diagrams for the $W^-W^+$ production process in $e^-e^+$ lepton collider. The blob in the diagram in the left panel represents anomalous vertex contribution

In the leading order the s-channel diagrams contain trilinear $\gamma W^-W^+$ and $ZW^-W^+$ gauge boson couplings whose deviations from SM due to the above given dim-6 EFT operators are being probed in this current article.

Some of the asymmetries we use require knowledge about the W boson decay products being up/down fermions. It is straightforward in the leptonic channel but requires us to flavor tag the hadronic decay of $W^+$ into up-type and down-type jets. We use machine learning (ML) models to develop such a tagger. ML has been used to identify the jets originated from the gluon and quarks [105,106,107,108,109,110,111]. The generic ML models have also been developed to classify the jets as originating from light-flavor or heavy-flavor quarks [112,113,114,115,116,117]. In this article, we develop artificial neural network (ANN) and boosted decision tree (BDT) to assist in classifying the jets from the $W^+$ boson as originating from up-type or down-type light quarks.

We describe in Sect. 2 the effect of beam polarization on the observable. We also describe spin-related observables like polarization asymmetries and spin correlation asymmetries and the method to calculate them. In Sect. 3, we describe the machine learning (ML) technique, especially artificial neural networks (ANN) and boosted decision tree (BDT) that will be used for flavor tagging or to reconstruct $W^+$ boson. We also discuss the performance of various models in classifying the jets. Section 4 deals with the parameter estimation to find the limits on various anomalous couplings and discuss the results obtained. We conclude in Sect. 5.

2 Beam polarization and observables

The polarization of resonance W bosons is reconstructed through the angular distribution of its decay products. The full hadronic channel suffers from the significant background contribution from the decay of Z to hadrons. The full leptonic channel is cleaner to detect the polarization but comes with two missing neutrinos, which makes the reconstruction of the rest frame of the W boson non-trivial. Thus, for a $W^-W^+$ final state, the optimal channel to study the polarization and spin correlations is the semi-leptonic channel. The normalized production density matrix of a W boson which is a spin-1 boson can be written as [118]:

$$\begin{aligned} \rho (\lambda ,\lambda ^\prime ) = \frac{1}{3}\left[ I+\frac{3}{2}\vec {P}\cdot \vec {S}+\sqrt{\frac{3}{2}}T_{ij}(S_iS_j+S_jS_i)\right] , \end{aligned}$$

(8)

where $\vec {P} = \{P_x,P_y,P_z\}$ is the vector polarization of W boson, $\vec {S} = \{S_x,S_y,S_z\}$ is the spin basis and $T_{ij}(i,j=x,y,z)$ is the second-rank symmetric traceless tensor and $\lambda ,\lambda ^\prime$ are the helicities of the W boson. Similarly, the normalized decay density matrix of W boson decaying to two fermions with helicities $s_1$ and $s_2$ via an interaction vertex $Wf\bar{f}:$ $\gamma ^\mu (L_fP_L+R_fP_R)$ is given in equation below [118],

$$\begin{aligned} \Gamma _W(s_1,s_2)= \begin{bmatrix} \frac{1+\delta +(1-3\delta )\cos ^2\theta _f+2\alpha \cos \theta _f}{4}&{}\frac{\sin \theta _f(\alpha +(1-3\delta )\cos \theta _f)}{2\sqrt{2}}e^{i\phi _f}&{}(1-3\delta )\frac{(1-\cos ^2\theta _f)}{4}e^{i2\phi _f}\\ \frac{\sin \theta _f(\alpha +(1-3\delta )\cos \theta _f)}{2\sqrt{2}}e^{-i\phi _f}&{}\delta +(1-3\delta )\frac{\sin ^2\theta _f}{2}&{}\frac{\sin \theta _f(\alpha -(1-3\delta )\cos \theta _f)}{2\sqrt{2}}e^{i\phi _f} \\ (1-3\delta )\frac{1-\cos ^2\theta _f}{4}e^{-i2\phi _f}&{}\frac{\sin \theta _f(\alpha -(1-3\delta )\cos \theta _f)}{2\sqrt{2}}e^{-i\phi _f}&{}\frac{1+\delta +(1-3\delta )\cos \theta _f-2\alpha \cos \theta _f}{4} \end{bmatrix}, \end{aligned}$$

(9)

where the parameters $\alpha$ and $\delta$ are given in terms of chiral couplings and the ratio of mass of final fermions and mother resonance, $x_i$ as [118],

$$\begin{aligned}{} & {} \begin{aligned}&\alpha =\frac{2(R_f^2-L_f^2)\sqrt{1+(x_1^2-x_2^2)^2-2(x_1^2+x_2^2)}}{12R_fL_fx_1x_2+(R_f^2+L_f^2)\left[ 2-(x_1^2-x_2^2)^2+(x_1^2+x_2^2)\right] }, \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \begin{aligned}&\delta = \frac{4R_fL_fx_1x_2+(R_f^2+L_f^2)\left[ (x_1^2+x_2^2)-(x_1^2-x_2^2)\right] }{12R_fL_fx_1x_2+(R_f^2-L_f^2)\left[ 2-(x_1^2-x_2^2)^2+(x_1^2+x_2^2)\right] }. \end{aligned}\nonumber \\ \end{aligned}$$

(11)

Assuming narrow width approximation, the production and decay part can be factorized into different terms, and on combining Eqs. (9) and (8), the differential cross-section would be,

$$\begin{aligned} \frac{1}{\sigma }\frac{d\sigma }{d\Omega _f}&= \frac{3}{8\pi }\left[ \left( \frac{2}{3}-(1-3\delta )\frac{T_{zz}}{\sqrt{6}}\right) +\alpha P_z \cos \theta _f \right. \nonumber \\&\quad +\left. \sqrt{\frac{3}{2}}(1-3\delta )T_{zz}\cos ^2\theta _f \right. \nonumber \\&\quad +\left. \left( \alpha P_x + 2\sqrt{\frac{2}{3}}(1-3\delta )T_{xz}\cos \theta _f\right) \sin \theta _f \cos \theta _f \right. \nonumber \\&\quad +\left. \left( \alpha P_y + 2\sqrt{\frac{2}{3}}(1-3\delta )T_{yz}\cos \theta _f\right) \sin \theta _f \sin \theta _f \right. \nonumber \\&\quad +\left. (1-3\delta )\left( \frac{T_{xx}-T_{yy}}{\sqrt{6}}\right) \sin ^2\theta _f\cos (2\phi _f) \right. \nonumber \\&\quad +\left. \sqrt{\frac{2}{3}}(1-3\delta )T_{xy}\sin ^2\theta _f\sin (2\phi _f) \right] \end{aligned}$$

(12)

where $\theta _f,\phi _f$ are the polar and azimuth orientation of the fermion f, in the rest frame of W boson with its would-be momentum along z-axis. The initial beam direction and the $W^-$ momentum in the lab frame define the x–z plane, i.e., $\phi = 0$ plane, in the rest frame of $W^-$. In this case, along with assuming high energy limits, the mass of final state fermions can be zero, then $\alpha = -1$ and $\delta = 0$. The construction of various polarization at the rest frame of W boson requires one to find the single missing neutrino. As the Lepton collider does not involve PDFs, reconstructing four momenta of a single neutrino is straightforward. One can construct several asymmetries to probe various polarization parameters using partial integration of the differential distribution given in Eq. (12) of the final state f. For example, we can get $P_x$ from the left-right asymmetry as:

$$\begin{aligned} P_x = \frac{4}{3\alpha }\left[ \int _{\theta =0}^\pi \int _{\phi =-\frac{\pi }{2}}^{\frac{\pi }{2}} -\int _{\theta =0}^\pi \int _{\phi =\frac{\pi }{2}}^{\frac{3\pi }{2}} \right] \frac{1}{\sigma }\left( \frac{d\sigma }{d\Omega _f}d\Omega _f\right) . \end{aligned}$$

(13)

Finding $P_x$ would be a counting procedure, which can be written in terms of asymmetries in $c_x$,

$$\begin{aligned} P_x= & {} \frac{4}{3\alpha }\frac{\sigma (c_x>0) - \sigma (c_x<0)}{\sigma (c_x>0) + \sigma (c_x<0)},\nonumber \\= & {} \frac{4}{3\alpha }A_x. \end{aligned}$$

(14)

Similarly, the tensorial polarization parameter $T_{xy}$ can be obtained by integrating the differential rate as,

$$\begin{aligned} T_{xy}&= \sqrt{\frac{2}{3}}\frac{\pi }{2}\frac{1}{(1-3\delta )}\left[ \int _{\theta =0}^\pi \int _{\phi =0}^{\frac{\pi }{2}}-\int _{\theta =0}^\pi \int _{\phi =\frac{\pi }{2}}^\pi \right. \nonumber \\&\quad \left. +\int _{\theta =0}^\pi \int _{\phi =\pi }^\frac{3\pi }{2} - \int _{\theta =0}^\pi \int _{\frac{3\pi }{2}}^{2\pi } \right] d\Omega \left( \frac{1}{\sigma }\frac{d\sigma }{d\Omega }\right) ,\nonumber \\&= \sqrt{\frac{2}{3}}\frac{\pi }{2}\frac{1}{(1-3\delta )} \frac{\sigma (c_xc_y> 0) - \sigma (c_xc_y<0)}{\sigma (c_xc_y>0 + \sigma (c_xc_y<0))},\nonumber \\&= \sqrt{\frac{2}{3}}\frac{\pi }{2}\frac{1}{(1-3\delta )} A_{xy}. \end{aligned}$$

(15)

All other polarization parameters can be obtained in a similar fashion using various angular functions listed in Table 2.

Table 2 List of correlators used to construct asymmetries

When a pair of particles is produced as in the process probed in this article, i.e., $e^-e^+\rightarrow W^-W^+$, one can create various observables related to the spin correlations of these two W bosons. Studies [119] show angular correlations between the decay products of two W bosons. W-boson spin correlations are measured by tagging the helicity of the W boson, which decays into hadrons, and measuring the helicity of the W boson, which decays into leptons. Spin correlations of W boson had been used to study the triple gauge boson couplings in Refs. [24, 52, 58]. We construct various spin correlation asymmetries using the angular distribution of the decay products of W bosons using the correlators listed in Table 2. Similar to polarization, the spin correlation can be calculated in terms of asymmetries as,

$$\begin{aligned} A_{ij}^{WW} = \frac{\sigma (c_i^ac_j^b> 0) - \sigma (c_i^ac_j^b< 0)}{\sigma (c_i^ac_j^b > 0) + \sigma (c_i^ac_j^b < 0)}, \end{aligned}$$

(16)

where a and b are the final state leptons and jets coming from the decay of W bosons, and $c's$ are the correlators listed in Table 2. There will be 64 spin correlation asymmetries for a pair of spin-1 particles. Since the polarization and correlation depend strongly on the $\cos \theta$, where $\theta$ is the production angle of $W^-$ boson in the lab frame, we can divide the events in certain bins of $\cos \theta$ to increase the overall sensitivity.

Fig. 2

Total production cross-section of $W^-W^+$ pair with respect to the center-of-mass energy $\sqrt{s}$ in the presence of initial beam polarization and anomalous triple gauge couplings. The left panel represents $(\eta _3,\xi _3) = (+0.8, -0.3),$ and right panel represents flip polarization

Effect of initial beam polarization: The future particle collider like ILC will use polarized beams for both electron and positron [95, 120] to increase its sensitivity to new physics and to improve its measurement accuracy. The presumed design values of the beam polarization are 80$\%$ for the electron and 30$\%$ for the positron beam [94]. Here, we will discuss how various observable changes in the presence of initial beam polarization. The observables like cross section and asymmetries change in the presence of initial beam polarization, and we can show this with the change in the transition amplitude as defined in [121]

$$\begin{aligned} |\mathcal {M}|^2 = \sum _{\lambda 's}\rho _{\lambda _{e^-},\lambda _{e^-}'}\rho _{\lambda _{e^+},\lambda _{e^+}'}F_{\lambda _{e^-},\lambda _{e^+}}F^*_{\lambda _{e^-}'{\lambda _{e^+}'}} \end{aligned}$$

(17)

where $\rho$ are the spin density matrix of $e^-/e^+$ and F are the helicity amplitude.

The cross-section with beam polarization $\eta _3$ and $\xi _3$ for electron and positron, respectively, can be written as:

$$\begin{aligned} \sigma (\eta _3,\xi _3)= & {} \frac{(1+\eta _3)(1+\xi _3)}{4}\sigma _{\text {LR}} \nonumber \\ {}{} & {} \quad + \frac{(1-\eta _3)(1-\xi _3)}{4}\sigma _{\text {RL}}, \end{aligned}$$

(18)

where $\sigma _{\text {LR}}(\sigma _{\text {RL}})$ is the cross-section with 100$\%$ left polarized (right polarized) electron beam and 100$\%$ right polarized  (left polarized) positron beam. The contribution like $\sigma _{\text {LL}}(\sigma _{\text {RR}})$ can be safely dropped as they are negligible. The SM cross section and its modifications due to the anomalous couplings are shown in Fig. 2 for beam polarization ($\eta _3,\xi _3)=(-0.8,+0.3)$ in the left panel and for the flipped polarization in the right panel. The anomalous couplings are chosen to be 20 TeV$^{-2}$ one at a time, keeping others to zero. We see that the flipped polarization has smaller $\sigma$ for SM, and the fractional change due to anomalous couplings is large and increases with the increase in $\sqrt{s}$. We further observe that the contribution from the CP-odd couplings is much smaller than the CP-even couplings due to the interference effect, which will be discussed later.

3 Flavor tagging

As discussed in Sect. 1, constructing some of the polarization asymmetries and spin correlation asymmetries requires identifying the daughter of W boson. From Eq. (12) and Table 2, we note that the correlators of vectorial polarization $\vec {P}\in \{P_x,P_y,P_z\}$ are parity odd and that of tensorial polarization, the correlators are parity even. It suggests that unless the daughter fermion is not tagged, the vectorial polarization and its related spin correlation parameters average out. Since the daughter of $W^-$ boson is a lepton, the identification becomes non-ambiguous in such a topology. Whereas, in the case of $W^+$ decaying hadronically, the identification of the jet initiator (quark) remains fuzzy due to the close behavior of light quarks. In this article, we classify the final jets as initiated by up-type or down-type quarks. We used MadGraph5$\_$aMC@NLO (MG5 henceforth) [122, 123] to generate event sets using a diagonal Cabibbo Kobayashi Maskawa (CKM) matrix for training and testing purposes. The parton-level events were used as an input to the Pythia8 [124] for showering and hadronization of the colored partons. This process will lead to the formation of hadrons which can undergo further decay within a detector given their short lifetime. The final state, colorless particles, are clustered in a region called jets. The final state particles with $p_T\ge 0.3$ GeV and $|\eta | \le 3.0$ are selected for jet clustering using Fastjet [125]. The lepton from the decay of $W^-$ is excluded from jet analyses. The jet clustering is done using anti-$k_T$ [126] algorithm with jet radius $R=0.7$, and the jets thus obtained are re-clustered using $k_T$ [127] algorithm with jet radius $R=1.0$. The two hardest jets account for more than $90\%$ of the parton level momentum of $W^+$ boson, and they are passed through ML models for tagging as up/down-type. These two jets’ truth labeling is done by using the distance $\Delta R_{jq}$ with the initiator quarks. In a case when both the jets become close to a single quark, the hardest jet is selected.

For tagging purposes, apart from the features listed in Ref. [24], additional features are obtained from the jets, which are used as input to ANN and BDT models. For a up/down tagger, a strange tagging can enhance the overall efficiency of classification. In an event where a strange quark is present along with other light quarks, due to a comparatively longer lifetime of strange meson $K_S^0$ with $\tau = \mathcal {O}(10^{-10})$ s can decay within the detector range, one can obtain a secondary vertex resulting to displaced tracks. Similarly, the charmed mesons can provide displaced tracks provided such particles gets a significant $\beta \gamma$ factor. Such displaced tracks act as a good classifier for light quarks. A charged kaons $K^\pm$ with $\tau = \mathcal {O}(10^{-8})$ s are collider-stable particles; hence the multiplicity and momenta of charged kaons are used as features. To use the charged kaons as a feature, it is necessary to distinguish them from charged pions, protons, and vice-versa. Many techniques have been developed to perform particle identification like using mean ionization energy loss, dE/dx [128,129,130,131,132,133,134,135,136], time-of-flight [137, 138]. The higher multiplicity of kaons on strange jets can act as a good classifier of strange vs. other light quark jets. In general, we construct $x_i$ using the information of the jet and the objects contained within a jet. The variables we obtained to use as input to our network can be divided into two classes, discrete and continuous variables, and they are listed below.

• Discrete Variables:

  • Total number (nlep), positive leptons (nl$+$), negative leptons (nl−);

  • Total number of visible particles (nvis);

  • Total number of charged particles (nch), positive charged particles (nch$+$), negative charged particles (nch−);

  • Total number of charged kaons (nK$+$, nK−)$^\star$;

  • Total number of charged pions (npi$+$, npi−)$^\star$;

  • Total number of hadrons (nhad);

  • Total number of charged hadrons (nChad), positively charged hadrons (nChad$+$),

    negative hadrons (nChad−);

  • Displaced tracks satisfying $p_T > 1.0$ GeV are used. They are binned with respect to the lifetime ($\tau$) in mm of their mother particles:

    • c1: $\tau < 3.0$ and $\tau > 0.3$,

    • c2: $\tau < 30.0$ and $\tau > 3.0$,

    • c3: $\tau < 300.0$ and $\tau > 30.0$,

    • c4: $\tau < 1200.0$ and $\tau > 300.0$,

    • c5: $\tau > 1200.0$.

  • Total number of $+$ve (pcl) and −ve (ncl) mother particles are also counted. The particle that decay and produces secondary displaced vertex are considered.

• Continuous variables:

  • Energy of photons (egamma)$^\star$;

  • $P^{\mu \star }_i = \sum _{j \in i}p^\mu _j$, $P_i^\star = \sum _{j \in i}|\vec {p}_j|$, $|(P^\mu _i)_T|^\star$,

    $i \in \{\text {Leptons}, K^+, K^-, \pi ^+, \pi ^-,K^0_L,\text {Hadrons}\}$;

  • Energy of charged hadrons ($E^+_{\text {Had}},E^-_{\text {Had}}$).

The features with ($^\star$) represent the additional features on top of all the features used in Ref. [24]. One can also obtain features related to the jet and use them as input to the classifying network. These variables, in general, provide a significant correlation to the jet class, which translates to increased classification accuracy. Some of the features related to the jet itself are:

• Transverse momentum $p_T$, magnitude of momentum $|\vec {p}|$, transverse mass $m_T$ and mass of Jet;

• Pseudo rapidity $\eta$, azimuth angle $\phi$ of the jets;

• Momentum component ($p_x,p_y,p_z$).

The jet variables like $p_T,\eta ,E$, and the three-momenta have large correlation with the label of jets. These variables depend on the polarization of the mother particle, and since we are using the observable related to polarization to constrain the new physics parameters, using these variables to flavor tag will not be useful. Hence, these jet features are excluded from our inputs to train the ML models. We use the above-listed discrete and continuous variables in a concatenated form for our ANN and BDT models.

BDT: The ML models using BDT are implemented in XGBoost [139]. The parameter of our BDT models is as follows:

• Sub-sample ratio of columns for when constructing each tree: colsample$\_$bytree = 0.6;

• Step size shrinkage used in the update to prevent overfitting: eta = 0.3;

• Minimum loss reduction required to make a further partition on a leaf node of the tree: gamma = 1.5;

• Maximum depth of a tree: max$\_$depth = 6;

• Number of decision tree: n$\_$estimators = 300;

• L2 regularization term on weights: lambda = 1.0.

ANN: The ANN models are implemented using

TensorFlow. The architecture of ANN consists of three hidden layers, each consisting of 160, 80, and 40 nodes, respectively; see Fig. 3. We used Relu as an activation function for each hidden layer, and for the output layer, Sigmoid function is used. The optimization is done using adam algorithm.

Fig. 3

Architecture of ANN used for flavor tagging. It contains three hidden layers (HL). The input layer contains 79 nodes, 1st hidden layer with 160 nodes, 2nd HL with 80, 3rd HL contains 40 nodes, and the output layer has one node

The training datasets ($10^7$ events) and test datasets ($10^6$ events) were generated for three different beam polarization ($\eta _3,\xi _3$) $\in \{(0,0),(+0.8,-0.3),(-0.8,+0.3)\}$. We train ANN and BDT models separately for three polarization datasets and test them on all three test datasets. The final accuracy obtained using different sets of datasets (with different polarization) are listed in Table 3. We estimate the efficiency of our ML models as follows; a random subset with 60$\%$ of the test sample is taken, and we estimate the model accuracy on that subset. This process is repeated 1000 times, and the average accuracy is quoted in Table 3. We note that all the accuracy listed in Table 3 are comparable, i.e., one can use any of the models on any datasets with varying beam polarization (and hence varying W polarization) with comparable efficiency. For the rest of the paper, we choose BDT trained on an unpolarized beam. We want to highlight the fact that using the additional features ($^\star$) increases the accuracy from $\approx 70\%$ in Ref. [24] to $\approx 80\%$, which should improve the constrain on anomalous couplings. In the later section, we describe the tagger’s role in constraining the anomalous couplings.

Table 3 Accuracy on classifying two hard jets as up-type or down-type using different train and test models using artificial neural network (ANN) and boosted decision tree (BDT). The model differs in the initial degree of beam polarization

4 Parameter estimation

In order to constrain the new physics parameters effectively, it is advantageous to utilize a wide range of observables that are sensitive to such phenomena. This article employs cross section, polarization, and spin correlation asymmetries as the observables of interest. With two spin-1 W bosons, there exist 80 spin-related observables, of which 16 are polarization, and the rest 64 are spin correlation asymmetries. To further enhance the sensitivity to new physics, a division of these observables into intervals of $\cos \theta$ is proposed, where $\theta$ is the production angle of $W^-$ boson in the lab frame. It is motivated by the fact that due to the chiral couplings, the polarization and spin correlations depend on $\cos \theta$. By dividing the backward region ($\cos \theta \le 0.0$) into four equal intervals, which corresponds to the region where the new physics contributions are maximal, the statistical error dominance, which could be substantial due to the lower rate in this region, can be mitigated. In contrast, the forward region exhibits a significantly higher rate statistically and, therefore, can be divided into finer bins. However, to maintain uniformity, the forward region is also divided into four equal bins of $\cos \theta$. This binning approach allows for the identification of specific regions that possess greater sensitivity than the case without binning, leading to an overall increase in sensitivity when the contributions from all these bins are combined. A detailed demonstration of the enhanced sensitivity achieved through this binning scheme is provided in Appendix A. With this kind of binning, we would have 648 different observables. The value of these observables in each bin is obtained for a set of couplings. Then those are used for numerical fitting to obtain a semi-analytical expression of all the observables as a function of the couplings. For cross-section, which is a CP-even observable, the following parameterization is used to fit the data,

$$\begin{aligned} \sigma (\{c_i\})= & {} \sigma _0 + \sum _{i=1}^3 c^i\sigma _i + \sum _{i=1}^5 c_i^2\sigma _{ii} \nonumber \\ {}{} & {} + \frac{1}{2}\sum _{i,j(\ne i)=1}^3 c_ic_j\sigma _{ij} + c_4c_5\sigma _{45}. \end{aligned}$$

(19)

For the asymmetries, the denominator is the cross-section, and the numerator $\Delta \sigma \{c_i\} = A\{c_i\}\sigma$ is parameterized separately. For the CP-even asymmetries the parameterization of $\Delta \sigma$ is same as in Eq. (19) and for CP-odd asymmetries it is done as,

$$\begin{aligned} \Delta \sigma (\{c_i\}) = \sum _{i=4}^5 c_i\sigma _i + \sum _{i=1}^3 c_ic_4\sigma _{i4} + \sum _{i=1}^3 c_ic_5\sigma _{i5}. \end{aligned}$$

(20)

Here, $c_i$ denotes the five couplings of the dimension-6 operators $c_i=\{c_{WWW},c_W,c_B,c_{\widetilde{W}},c_{\widetilde{WWW}}\}$. We define $\chi ^2$ distance between the SM and SM plus anomalous point as,

$$\begin{aligned} \chi ^2(\{c_i\}) = \sum _k \sum _l \left( \frac{\mathscr {O}_k^l(\{c_i\}) - \mathscr {O}_k^l(0)}{\delta \mathscr {O}^l_k}\right) ^2, \end{aligned}$$

(21)

where k and l corresponds to observable and bins respectively and $c_i$ denotes some non-zero anomalous couplings. The denominator $\delta \mathscr {O} = \sqrt{(\delta \mathscr {O}_{stat})^2 + (\delta \mathscr {O}_{sys})^2}$ is the estimated error in $\mathscr {O}$. If an observable is asymmetries $A = \frac{N^+-N^-}{N^++N^-}$, the error is given by

$$\begin{aligned} \delta A = \sqrt{\frac{1-A^2}{\mathcal {L}\sigma }+\epsilon _{A}^2}, \end{aligned}$$

(22)

where $N^++N^- = \mathcal {L}\sigma ,$ $\mathcal {L}$ being the integrated luminosity of the collider. The error in the cross-section $\sigma$ is given by

$$\begin{aligned} \delta \sigma = \sqrt{\frac{\sigma }{\mathcal {L}}+(\epsilon _\sigma \sigma )^2}. \end{aligned}$$

(23)

Here, $\epsilon _{A}$ and $\epsilon _{\sigma }$ are the fractional systematic error in asymmetries (A) and cross-section ($\sigma$) respectively. The benchmark systematic errors chosen in our analysis are:

$$\begin{aligned} (\epsilon _A, \epsilon _{\sigma }) \in \{(0,0),(0.25\%,0.5\%),(1\%,2\%)\}. \end{aligned}$$

(24)

We perform our analysis at $\sqrt{s}= 250$ GeV and different values of integrated luminosity,

$$\begin{aligned} \mathcal {L} \in \{100\text { fb}^{-1},250\text { fb}^{-1},1000\text { fb}^{-1},3000\text { fb}^{-1}\}. \end{aligned}$$

(25)

The SM cross sections at the LO obtained using MG5 for the process given in Eq. (7) with initial beam polarizations of (0, 0), $(+0.8,-0.3)$, and $(-0.8,+0.3)$ are 2.347 pb, 0.396 pb, and 5.467 pb, respectively. With these values of cross-sections, the relative statistical error for the chosen set of luminosities is:

$$\begin{aligned} \begin{aligned}&\frac{\delta \sigma _{(0,0)}}{\sigma _{(0,0)}} = \{0.2\%,0.1\%,0.06\%,0.03\%\}, \\&\frac{\delta \sigma _{(+,-)}}{\sigma _{(+,-)}} = \{0.5\%,0.3\%,0.015\%,0.09\%\},\\&\frac{\delta \sigma _{(-,+)}}{\sigma _{(-,+)}} = \{0.1\%,0.08\%,0.04\%,0.02\%\}. \end{aligned} \end{aligned}$$

(26)

Fig. 4

Variation of $\chi ^2$ for a set of observables as a function of one anomalous coupling $c_i$ (TeV$^{-2}$) at a time. The systematic errors are chosen to be zero

For the unpolarized case, the number corresponds to luminosity $\mathcal {L}$ listed in Eq. (26), while the polarized cases stand for luminosity $\mathcal {L}$/2 each. It has been shown in Ref. [13] that combining the two opposite beam polarization at the level of $\chi ^2$ provides tighter constraints on anomalous couplings than combining the observable algebraically. The combined $\chi ^2$ at different set of beam polarization ($\pm \eta _3,\mp \xi _3$), and using different observable $\mathcal {O}$ for a given value of anomalous couplings c is defined as,

$$\begin{aligned}{} & {} \chi ^2(\mathcal {O},c_i,\pm \eta _3,\mp \xi _3) \nonumber \\{} & {} \quad =\sum _{l,k} \left[ \left( \frac{\mathscr {O}_k^l(c_i,+\eta _3,-\xi _3) - \mathscr {O}_k^l(0,+\eta _3,-\xi _3)}{\delta \mathscr {O}^l_k(0,+\eta _3,-\xi _3)}\right) ^2 \right. \nonumber \\{} & {} \qquad \left. + \left( \frac{\mathscr {O}_k^l(c_i,-\eta _3,+\xi _3) - \mathscr {O}_k^l(0,-\eta _3,+\xi _3)}{\delta \mathscr {O}^l_k(0,-\eta _3,+\xi _3)}\right) ^2 \right] , \end{aligned}$$

(27)

where k and l correspond to different observables and bins.

We perform $\chi ^2$ analysis by varying one parameter and two parameters at a time which will be described below. We also perform a set of Markov-Chain-Monte-Carlo (MCMC) analyses with a different set of observable with polarized beams to obtain simultaneous limits on the anomalous couplings.

4.1 One parameter estimation

This section discusses the analysis done by varying one anomalous coupling $c_i$ at a time while others are kept at zero. The analysis are done at the center-of-mass energy, $\sqrt{s} = 250$ GeV, integrated luminosity, $\mathcal {L} = 100$ fb$^{-1}$ with zero systematic errors. The polarized beams are used with a degree of polarization $(+0.8,-0.3)$ and $(-0.8,+0.3)$. Variation of $\chi ^2$ for different sets of observables as a function of one anomalous coupling is shown in Fig. 4. The different sets of observables are: cross section $\sigma$, set of $W^-$ asymmetries Pol($W^-$), set of $W^+$ asymmetries Pol($W^+$), union of $W^-$ and $W^+$ asymmetries Pol($W^-+W^+$), spin correlations Corr($W^-W^+$), union of all asymmetries Pol($W^-+W^+$) $\cup$ Corr($W^-W^+$) and set of all observables. The horizontal line in all panels represents $\chi ^2$ at 95$\%$ confidence level (CL). From the bottom row of Fig. 4, it is evident that the cross section (shown in the red curve) provides the least contribution to $\chi ^2$ in the case of CP-odd couplings, i.e., $c_{\widetilde{W}}$ and $c_{\widetilde{WWW}}$. This behavior can be explained by the fact that in case of cross section or any other CP-even observables, the contribution from CP-odd anomalous couplings comes only in a quadratic form or $1/\Lambda ^4$ term, which naturally becomes tiny. Generally, cross section, in the presence of one anomalous coupling $c_i$, can be parameterized as:

$$\begin{aligned} \sigma (c_i) = \sigma _0 + \sigma _i\times c_i + \sigma _{ii}\times c_i^2. \end{aligned}$$

(28)

Thus, the absence of a linear term in case of CP-odd couplings $c_i~\in ~\{c_{\widetilde{W}},c_{\widetilde{WWW}}\}$ suggests that the significant contribution will only arise when large values of anomalous couplings are taken. Whereas, in the case of CP-even couplings, the cross section provides a reasonable contribution due to linear term, see top row of Fig. 4. The sensitivity of the polarization asymmetries constructed from the $W^-$ boson is comparatively more prominent than that of the $W^+$ boson because the accuracy with which we can tag the daughter lepton of $W^-$ boson is close to $100\%$. While, as discussed in Sect. 3, the machine learning (ML) models achieved an approximate accuracy of $80\%$ in classifying up-type versus down-type jets from $W^+$ boson. In our specific scenario, these jets are initiated by light quarks, resulting in similar overall hadronization and jet contents. Consequently, distinguishing between them becomes challenging for the tagging process, and this would dilute the overall sensitivity of polarization asymmetries related to the $W^+$ boson. For the CP-even parameters, the contribution from the spin correlations is comparable to the $W^-$ polarization for $c_W$ and to the cross section in the case of $c_{WWW}$. On the other hand, for the CP-odd parameters, the spin correlations perform better than polarizations of either W bosons. We list the one parameter limits on all anomalous couplings $c_i$ obtained using all observables in Table 4.

The confidence interval obtained for various anomalous coupling $c_i \in \{c_{W},c_{B},c_{\widetilde{W}}\}$ are significantly tighter than that of the experimental confidence interval listed in Table 1. In contrast, for $c_{WWW}$ and $c_{\widetilde{WWW}}$, the limits remain comparable. Next, we discuss the significance of various observable on constraining the limits of two anomalous couplings at a time.

4.2 Two parameter estimation

Here, we vary two anomalous couplings simultaneously while keeping all others to zero. The systematic error is taken to be zero, and luminosity is set to 100 fb$^{-1}$ with the center-of-mass energy, $\sqrt{s}$ of 250 GeV in the presence of polarized beams.

We study the role of various observables in setting simultaneous limits on different pairs of anomalous couplings. The observables are described in the previous section. To understand the role of these observables, we show two dimensional 95$\%$ CL contours for different pairs of anomalous couplings in Fig. 5. For a case when both the parameters are CP-odd, cross section provides the poorest bounds on both the axis (see left panel top row) due to a tiny contribution from $1/\Lambda ^4$ term. While for a case when both the parameters are CP-even, cross section can be parameterized as,

$$\begin{aligned} \sigma (c_i,c_j)= & {} \sigma _0 + \sigma _i \times c_i +\sigma _j\times c_j + \sigma _{ii}\times c_i^2 \nonumber \\{} & {} +\sigma _{jj}\times c_j^2 + \sigma _{ij}\times c_ic_j. \end{aligned}$$

(29)

The cross section provides tighter limits in the orthogonal direction and extended limits in the second and fourth quadrants. It is due to the cancellation of the linear terms in Eq. (29), i.e., $c_i\sigma _i+c_j\sigma _j = 0$, or $c_i\sim -c_j\sigma _j/\sigma _i$. The polarization of $W^-$ contributes more to $\chi ^2$ than that of $W^+$ boson due to the reconstruction error of $W^+$ boson as seen in the 1-D case. The bounds obtained using spin correlations alone are tighter than that of a combination of polarization of W boson in case of $(c_{WWW},c_{\widetilde{WWW}})$ pair. In the case of the first panel, spin correlation alone provides a maximal contribution to $\chi ^2$ along the y-axis, i.e., $c_{\widetilde{WWW}}$.

Table 4 The list of constraints on five anomalous couplings $c_i$ (TeV$^{-2}$) at $95\%$ confidence level obtained by varying one parameter at a time and keeping the other at zero. The limits are obtained for $\sqrt{s}=250$ GeV, integrated luminosity $\mathcal {L}=100$ fb$^{-1}$ and initial beam polarization of $\eta _3=\pm 0.8$, $\xi _3=\pm 0.3$. The systematic errors are kept to zero

Fig. 5

Two dimensional 95$\%$ CL contours for a set of observables as a function of two anomalous couplings $c_i$ (TeV$^{-2}$) at a time. The legend for all the panels follows the upper row first panel. The contours are shown for $\sqrt{s} = 250$ GeV, $\mathcal {L} = 100$ fb$^{-1}$ and zero systematic errors

Below, we discuss the impact of beam polarization, flavor-dependent asymmetries, and tagger efficiency on determining the limits on anomalous couplings separately.

Fig. 6

Two dimensional $95\%$ CL contours for combining all observables as a function of two anomalous couplings $c_i$ (TeV$^{-2}$) at a different set of beam polarization. The analysis is done with zero systematic errors

Fig. 7

Two dimensional $95\%$ CL contour for combining all flavor-dependent and flavor-independent asymmetries as a function of two anomalous couplings $c_i$ (TeV$^{-2}$). The systematic errors are kept at zero

Role of beam polarization: We choose two sets of beam polarization for electron and positron beams, $(-0.8,+0.3)$ and $(+0.8,-0.3)$. Figure 6 presents the 95$\%$ CL $\chi ^2$ contours for a combination of all observables as a function of two anomalous couplings. The contours correspond to each beam polarization and unpolarized and combined cases. For individual set of beam polarization, $\chi ^2$ is obtained at luminosity $\mathcal {L}=100$ fb$^{-1}$, while for a combined case each contribution is computed at 50 fb$^{-1}$. The contour due to the two sets of opposite beam polarization provides directional limits on anomalous couplings. The intersection of these two contours corresponds to the bounds on the anomalous couplings obtained by combining the two sets of beam polarization (see magenta curve). In case of ($c_{WWW},c_B$) pair, $(-0.8,+0.3)$ provides tighter limits on $c_{W}$ and loose bounds on $c_{WWW}$, while with $(+0.8,-0.3)$ limits on $c_W$ becomes loose and $c_{WWW}$ gets tighter. Moreover, on combining two beam polarization, the overall limits get tighter, which is also seen in $(c_{\widetilde{WWW}},c_{\widetilde{W}})$ pair. The contour without beam polarization is displayed in red and is wider than the one created by adding two sets of beam polarization. It emphasizes the importance of using polarized beams when investigating beyond the SM physics. Next, the contrast between the flavor-dependent and -independent asymmetries is emphasized.

Comparison between flavor dependent and independent observable: As discussed in Sect. 3, some of the asymmetries are flavor-dependent, i.e., the value of those observables averages out unless the daughter of W bosons is tagged. In each bin, there are 45 different flavor-dependent and 35 flavor-independent asymmetries. Here, we compare the role of these two different sets of asymmetries in constraining the anomalous couplings. For this, we show $95\%$ CL contours for all observables as a function of two anomalous couplings in Fig. 7. We choose a pair ($c_W,c_B$) and ($c_{WWW},c_W$) for graphical demonstration. The contours are obtained by combining two sets of beam polarization at $\mathcal {L}=50$ fb$^{-1}$ each. In both panels, the limits set by flavor-dependent (red curve) are tighter along both axes than those obtained by flavor-independent (green curve). The 45 distinct flavor-dependent asymmetries thus make up most of the $\chi ^2$ contribution in the case of spin-related observables. It strongly advises the development of taggers or machine learning models that are incredibly efficient. To better understand the direct impact of taggers on limiting anomalous couplings, we will compare two machine learning models with varying degrees of efficiency.

Role of tagger efficiency: To understand the role of the efficiency of the tagger in constraining the anomalous couplings, we compare two different BDT models with different accuracy. One BDT model is trained using all the features listed in Sect. 3, and another model is trained using features apart from those listed as additional features.

Fig. 8

Two dimensional $\chi ^2$ for a combination of all flavor-dependent observable as a function of two anomalous couplings $c_i$ (TeV$^{-2}$). The systematic errors are kept at zero

The second class of models was used for flavor tagging in Ref. [24] with an accuracy of $\approx 70\%$, while the former model provides an accuracy of $\approx 80\%$. To demonstrate the role of the tagger, we compute $\chi ^2$ for the combination of flavor-dependent asymmetries as a function of two anomalous couplings with two sets of beam polarization. For each set of beam polarization, $\chi ^2$ is calculated at luminosity $\mathcal {L}$ = 50 fb$^{-1}$ and zero systematic errors. It is sufficient to demonstrate the involvement of the tagger with flavor-dependent asymmetries because the contribution from flavor-independent observables will be similar in both cases. In Fig. 8, the resulting $95\%$ CL contours are displayed. According to the figures in both panels, the simultaneous bounds on a pair of anomalous couplings obtained using ML models with $\approx 80\%$ accuracy are tighter than those produced with $70\%$ accuracy.

In conclusion, we need to use two beam polarization combination with as good a flavor tagger as possible to include the flavor-dependent asymmetries in the analysis. With these choices, we do a full five coupling simultaneous analysis below.

4.3 Five parameter analysis

In this section, we comprehensively explain the methodology used to obtain simultaneous limits on anomalous couplings and the impact of systematic errors on those limits. The likelihood function used in this analysis is constructed using the chi-squared distance between the Standard Model (SM) and the SM plus anomalous points, which is expressed in Eq. (27). The likelihood function is then defined as,

$$\begin{aligned} \lambda (\vec {x},c_i) \propto \text {Exp}\left[ -\frac{\chi ^2(\vec {x},c_i)}{2}\right] , \end{aligned}$$

(30)

where $\vec {x} \in \{\mathcal {O},\eta _3,\xi _3\}$ represents observable and the degree of initial beam polarization.

Fig. 9

The graphical visualizations of 95$\%$ BCI limits obtained from MCMC global fits on the anomalous couplings $c_i$ (TeV$^{-2}$) for a different set of systematic error, $(\epsilon _\sigma ,\epsilon _{A})$ = (0,0) in the leftmost panel, ($1\%,0.25\%$) in the middle panel and ($2\%,1\%$) in the right-most panel. The limits are obtained at $\sqrt{s}=250$ GeV and luminosity given in Eq. (25)

The Markov-Chain-Monte-Carlo (MCMC) integration technique is used to obtain the posterior distribution of the anomalous couplings, $c_i$, based on the likelihood function. Specifically, the MCMC algorithm generates a set of samples from the posterior distribution by iteratively sampling the likelihood function and updating the current position in the parameter space. The resulting posterior distribution is then used as an input chain to the GetDist [140] package, which provides the marginalized limits on the couplings.

The analysis is performed for different values of luminosity values and systematic errors. The chi-squared values are calculated separately for each beam polarization and then combined to obtain the overall chi-squared value. Specifically, we combine the two beam polarizations at half the luminosity stated in Eq. (25).

To visualize the variation of limits on anomalous couplings with respect to luminosities, the $95\%$ Bayesian confidence intervals obtained from the MCMC global fits on the anomalous couplings for $\sqrt{s}=250$ GeV and one specific set of systematic errors are illustrated in Fig. 9. The results show that the limits become tighter as the luminosity increases for zero systematic error. However, the saturation of the limits is observed for most of the couplings at particular luminosity values under conservative values of systematic error. Specifically, for the systematic error of ($2\%,1\%$) in the case of $c_{WWW}$, $c_W$, and $c_{\widetilde{WWW}}$, the boundaries of each anomalous coupling saturate at a luminosity value of 250 fb$^{-1}$. However, for $c_{\widetilde{W}}$ and $c_B$, the limits saturate at a luminosity value of 1000 fb$^{-1}$.

The significant influence of systematic errors on the constraints of anomalous $W^-W^+Z/\gamma$ couplings can be elucidated as follows: At the center-of-mass energy $\sqrt{s}=250$ GeV, the cross-section for $W^-W^+$ production approaches its maximum in the Standard Model scenario, thereby leading to lower statistical errors for large luminosities. Consequently, the estimated uncertainty in the measurement is primarily governed by systematic errors. It leads to the observed trend of saturation of limits for conservative levels of systematic errors.

Table 5 The list of posterior $95\%$ BCI of anomalous couplings $c_i$ (TeV$^{-2}$) of effective operators for $\sqrt{s} = 250$ GeV with beam polarization $(\eta _3,\xi _3) = (\pm 0.8,\pm 0.3)$ at systematic error of $(\epsilon _{\sigma }, \epsilon _{A}) = (2\%,1\%)$ from MCMC global fits at the reconstruction level at different values of $\mathcal {L}$. The reconstruction of $W^+$ is done using an artificial neural network

Finally, we list down the 95$\%$ BCI of anomalous couplings $c_i$ (TeV$^{-2}$) of effective operators given in Eq. (2) at the center-of-mass energy of 250 GeV and systematic errors ($\epsilon _\sigma ,\epsilon _{A}$) = (2$\%$,1$\%$) in Table 5. The translation of these bounds to the LEP parameters can be found using Eq. (4). In comparison to [24], the current limits on $c_{B},c_{\widetilde{W}}$ are $\approx$ a factor four and three tighter respectively, and all other couplings are reduced by a factor, k, of $1\le k \le 2$.

The di-boson ($W^-W^+$) production process stands to be a very important platform to test the electroweak sector of SM and thus for a stability of theoretical precision results, a study of higher quantum corrections to the said process become very important. Though the study in this article is limited to the LO, we estimate the effect of initial state radiation (ISR) on the cross-sections and angular distributions. At a center-of-mass energy of $\sqrt{s}=250$ GeV, the cross-section experiences a reduction of approximately $2\%$ and so does the $\cos \theta _W$ distribution. In case of asymmetries, $A_z~(\cos \theta )$ constructed from lepton and jet at the rest frame of the W boson were compared a reduction of $3\%$ and $9\%$, respectively, were observed in presence of ISR. In case of the binned asymmetries, some were enhanced while some were diluted due to ISR. We note that a comprehensive exploration involving higher-order real and virtual electroweak corrections lies beyond the scope of this article.

5 Conclusion

In this article, we examine the impact of dimension-6 operators on the charged triple gauge boson vertex in $e^-e^+$ Collider at $\sqrt{s}=250$ GeV. The notion is that when new physics is present at the top of the energy pyramid, sectors like electroweak are most likely to experience their indirect effects. We used a variety of observables, including asymmetries in cross section, polarization, and spin correlation asymmetries, to restrict a set of anomalous couplings. Since some of these asymmetries requires the daughter of $W^+$ boson to be tagged, we developed machine learning models for flavor tagging. With the features listed in Sect. 3, we were able to classify the jets as up-type and down-type with an efficiency of around $80\%$. Several studies [114,115,116,117] use features like jet energy, transverse momenta of jet for generic flavor tagging, while in our case, we excluded them because these are polarization dependent features. Using these features would increase the efficiency of our ML models above $90\%$ and thus tighten the anomalous couplings better.

Fig. 10

1-D chi-squared plots for cross-section and asymmetries for each bin as a function of one anomalous coupling $c_i$ (TeV$^{-2}$) at a time. The $\chi ^2$ is obtained at $\sqrt{s}=250$ GeV, $\mathcal {L}=100$ fb$^{-1}$ and zero systematic error

The limits on each anomalous coupling are studied under different sets of luminosity, systematic error, and beam polarization. Initial beam polarization provides directional cuts, which results in tighter constraints. Hence a future collider like ILC would be a perfect machine to probe such weak effects of new physics in the electroweak sector. Our five parameter simultaneous limits in Table 5 at 100 fb$^{-1}$ are tighter than the experimental one parameter limits listed in Table 1 for $c_{W}, c_{B}$ and $c_{\widetilde{W}}$, while for $c_{WWW},c_{\widetilde{WWW}}$, the limits obtained by CMS using production rates alone remains better. It is due to the presence of $p^2$ term in case of $c_{WWW}$ and $c_{\widetilde{WWW}}$, which leads to enhanced contribution in machines like LHC running at 13 TeV. While in our case, the limits on these couplings are obtained using asymmetries at smaller momentum. Also, in the presence of beam polarization, the contribution of asymmetries increases significantly over the cross section. There is a cancellation of the cross section due to non-zero values of CP-even couplings in Fig. 5. All these effects would add up, leading to a poorer limit on $c_{WWW}$ and $c_{\widetilde{WWW}}$ in Table 5.

In our study, we found that systematic error is a significant challenge when it comes to constraining anomalous couplings. When we assume a conservative choice of systematic error $(\epsilon _{\sigma },\epsilon _{A}) = (2\%,1\%)$, we found that the limits on certain anomalous couplings like $c_{WWW},c_W$ and $c_{\widetilde{WWW}}$ only improved by a factor of approximately 1.5 when we increased the luminosity from 100 fb$^{-1}$ to 3000 fb$^{-1}$. The improvement on the limits of $c_B$ and $c_{\widetilde{W}}$ saturates to a factor of 2.3 and 3.1, respectively. This is not very encouraging, given the substantial increase in luminosity. Therefore, in significant systematic errors, it may be necessary to look for additional observables from various processes to constrain anomalous couplings more effectively. Our study suggests that a more efficient flavor tagging method could be implemented to reduce the dependence on certain polarization-dependent observables, which could help tighten the limits on anomalous couplings in the future.

Appendix A: Significance of binning

In the earlier section, we discussed that to obtain a more significant number of observables to scan the effect of new physics; each observable is divided into eight bins of $\cos \theta _{W^-}$. Moreover, in finding the final limits of anomalous couplings $c_i$, we combine all 648 observable of eight bins. Here, we tried to quantify the effect of binning, and for that, 1-D chi-squared plots for cross section and asymmetries are shown for each bin along with a combination of all bins in Fig. 10. In the left panel top row, the limit provided by cross section without binning (Full) is looser than some bins in the range $-1.0 \le \cos \theta _{W^-} \le 1.0$. Furthermore, in the case of CP-odd couplings $c_{\widetilde{WWW}}$, the unbinned limit is tighter but remains weaker than the limit provided by combined bins. In the bottom row of Fig. 10, a forward–backward asymmetry exists only in CP-odd case (right panel). For $c_{\widetilde{WWW}}$, the unbinned limit is tighter than that of individual bins obtained using asymmetries but remains poorer than the combined limit of all bins. The tightest limit is obtained in each panel by combining all the bins. It highlights the importance of binning technique to increase observables’ sensitivity to new physics.