1 Introduction

Quantum gravity is one of the most active fields in modern physics. The black hole information paradox, which lasted about half a century, is one of the key signposts to the theory of quantum gravity [1]. In 1974, Hawking calculated that black holes have a temperature and can emit Hawking radiation, which resembles black-body radiation [2]. As the black hole evaporates, information that falls into the black hole is lost along with the evaporation. Therefore, Hawking predicted in 1976 that the evaporation of a black hole would lead to information loss, which is known as the black hole information paradox [1]. This paradox has leads to persistent debates and studies in the field of theoretical physics. On the one hand, according to quantum mechanics, the evolution of physical systems must follow the principle of unitary. On the other hand, Hawking radiation is produced by quantum fluctuations near the event horizon of a black hole, so the information loss violates the unitary. More specifically, a black hole that is formed from a pure state will evolve into a mixed state during the evaporation.

The issue has improved since 1993 – The Page curve [3, 4], which describes the entanglement entropy of Hawking radiation, is explained in detail by the Page theorem [5] under the assumption of unitarity. The black hole information paradox can be solved if the Page curve can be calculated directly from semi-classical gravity without this hypothesis. Although still challenging, the development of the holographic principle provides confidence in this issue [6]. The AdS/CFT duality has been an important and fascinating topic, not only providing a key connection between the theory of gravity in AdS (anti-de Sitter) spacetime and the CFT (conformal field theory) that lives on its boundary, but also opening a window into quantum gravity. Recently, many advances in holographic descriptions of the evaporation of black holes further support the view of information conservation. The Ryu-Takayanagi (RT) formula for calculating the holographic entanglement entropy is undoubtedly one of the best of these works [7, 8]. When one considers higher-order quantum corrections, the RT formula is generalized to the quantum extremal surface (QES) formula of the entropy functional that consists of the contributions of the bulk field and the area term [9]. Once we use the QES formula to calculate the entropy of Hawking radiation based on the semi-classical gravity method, the Page curve is naturally reproduced [10]. In particular, the most critical point is that the contribution of the bulk field includes a disconnected region located in the interior of the black hole, which called the “island” [11]. The idea of reconstructing the Page curve by correctly tracking the radiation outside black holes and the interior of black holes is summarized as the “entanglement wedge reconstruction” [12]. Finally, we can express the formula for calculating the fine-grained entropy of Hawking radiation as the so-called “island formula” [13]:

$$\begin{aligned} S_{\textrm{Rad}}=\text {Min}\big [\text {Ext}(S_{\textrm{gen}})\big ], \end{aligned}$$
(1.1)

where \(S_{\textrm{gen}}\) represents the generalized entropy of radiation, which can be written as

$$\begin{aligned} S_{\textrm{gen}}=\frac{\text {Area}(\partial I)}{4G_N} +S_{\textrm{bulk}} (I \cup R), \end{aligned}$$
(1.2)

where the first term is the area term of islands, in which I refer to the island, \(\partial I\) is denoted the boundary of the island. The second term is the entropy that is contributed by matter fields around the black hole. One should note that besides the radiation region R, the region I inside the black hole is also considered. It also provides a glimpse of insight into the interior of black holes. In brief, the island formula (1.1) gives us a guideline: in the explicit calculation, one first extremizes the generalized entropy (1.2), these saddle points correspond to positions of QES, namely the island. Then, the minimal value of the entropy is our candidate. For the whole process of an evaporating black hole, at early times, the QES is just a trivial (vanishing) surface, so there is no island at early times, which leads to a Hawking curve. However, the minimal condition requests that the QES is a non-trivial (non-vanishing) surface at late times, which provides a decreasing curve for the entropy. Therefore, combining two curves, we finally obtain the Page curve. The island formula (1.1) then can be rewritten as follows:

$$\begin{aligned} S_{\textrm{Rad}}=\text {Min} \big [S_{\textrm{gen}} (\text {without island}), S_{\textrm{gen}} (\text {with island})\big ]. \end{aligned}$$
(1.3)

The first breakthroughs were achieved in the evaporating Jackiw–Teitelboim (JT) black hole in two-dimensional (2D) gravity, where the auxiliary thermal bath is coupled to the asymptotically AdS black hole [10, 14]. However, the applicability of the island paradigm goes far beyond the framework of AdS black holes, one can refer to [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73] for an inexhaustive list of recent studies.

There is no doubt that 2D gravity, despite the simplicity of calculations, is still only a toy model. The more realistic and universal Einstein gravity, in which the Kerr-Newmann family is a typical example of four-dimensional (4D) black holes. They are characterized by the mass, charge, and angular momentum parameters. However, there is a less-known exact solution for a 4D black hole: the “C-metric”, which describes an accelerating black hole [74,75,76]. The “C”-metric was first discovered by Weyl in 1917, which is an axially symmetric soulution to the Einstein–Maxwell equation. In [74], its physical interpretation and causal properties were discussed for the first time. This kind of black hole has some intriguing properties compared to other black holes, such as a conical defect angle along the polar axis of the black hole. It is this defect angle that provides the driving force for the black hole to accelerate. Subsequent studies have shown that the concial singularity can be removed by introducing an external electromagnetic field [77]. Moreover, the asymptotic behavior of this spacetime determined by the C-metric is depends on various parameters, which lead to an accelerating horizon and complicates the structure of spacetime. Ref. [78] indicates that this spacetime is asymptotically flat, but not asymptotically Euclidean. As a result, this type of black hole also attracts more research interest. In particular, the issue of information loss in this spacetime is worth paying attention based on the rich causal results of this spacetime. The study of the island in accelerating black holes is an unexplored field, which deserves to be consider deeply, which is also the motivation and purpose of our current work. On the other hand, the exact solution described by the “C-metric” is ideal. Nevertheless, its applications are widespread beyond the theory of classical general relativity. It can also describe the creation of black hole pairs in electromagnetic fields [79], and the splitting of cosmic strings [80], especially recent work on its thermodynamics [81]. More work in this field can be found in [82,83,84].

Based on these remarkable special properties of the C-metric, in this paper we investigate the information issue in the charged version of the C-metric. To solve the information issue, we explicitly calculate the entanglement entropy of the charged accelerating black hole using the island formula (1.1) and reconstruct the corresponding Page curve. We also discuss the effects of the charge and the acceleration, especially for the neutral black hole, which has the largest Page time. Moreover, the Page time is inversely proportional to the charge in the constant-acceleration case. However, for the constant-charge case, the Page time increases and then decreases with accelerations. Interestingly, it is noted that in the extremal case, due to the vanishing of the temperature, some physical quantities become divergent, which strongly implies that quantum information is closely related to the causal structure of spacetime.

The structure of this paper is as follows. In Sect. 2, we briefly review some properties of the charged C-metric. In Sect. 3, the entanglement entropy of Hawking radiation in the with and without island configuration is calculated by the island paradigm. In Sect. 4, we obtain the Page curve satisfying the unitary and the scrambling time, then discuss the impact of the charge and the acceleration parameters. The summary is given in Sect. 5. In what follows, we will use the nature units where \(c=\hbar =k_B=1\).

2 Review for accelerating black holes

In this section, we give a brief review of accelerating black holes. Physically, the accelerating black holes can be produced by a cosmic string collision with a black hole- to accelerate, the cosmic string at the horizon attaches and pulls the black hole. A cosmic string can be thought of as an ideal quasi-linear object without thickness, whose tension is equal to its energy [85]. They can be generated in field theory of non-simply connected vacuums. However, they does not produce a long-range local curvature under the gravitational interaction, but instead produce a global conical deficit in the cross-section of spatial direction, so that the string is actually a local conical deficit in spacetime. In fact, it is this conical deficit that provides the acceleration for a black hole. The accelerating black hole can be described by the C-metric, which represents a pair of black holes that accelerating away from each other in an opposite direction. For the charged version of the C-metric, it can be regarded simply as a generalization of Reissner–Nordstr\(\ddot{\text {o}}\)m (RN) black holes. Besides the parameters of mass M and electric charge Q, it also includes an extra parameter which associated with the acceleration \(\alpha \). This charged C-metric is actually the solution to the Einstein’s gravity for four dimensions of spacetime with linear and nonlinear electrodynamics fields, which can be written as follows [74, 86]

$$\begin{aligned} ds^2= & {} \frac{1}{\Omega ^2(r)} \bigg [-f(r)dt^2 +\frac{dr^2}{f(r)}\nonumber \\{} & {} +r^2\bigg (\frac{d\theta ^2}{P(\theta )} + P(\theta ) \sin ^2 \theta d\phi ^2 \bigg ) \bigg ], \end{aligned}$$
(2.1)

where

$$\begin{aligned} f(r)&=\big (1-\alpha ^2r^2\big )\bigg (1-\frac{2M}{r} +\frac{Q^2}{r^2} \bigg ), \end{aligned}$$
(2.2a)
$$\begin{aligned} P(\theta )&=1+2\alpha M \cos \theta +\alpha ^2 Q^2 \cos ^2 \theta , \end{aligned}$$
(2.2b)
$$\begin{aligned} \Omega (r)&=1+\alpha r \cos \theta . \end{aligned}$$
(2.2c)

The gauge potential is given by

$$\begin{aligned} F=dA, \qquad A=-\frac{Q}{r}dt. \end{aligned}$$
(2.3)

One can easily finds that this metric is asymptotically flat. In the limit \(\alpha \rightarrow 0\), the charged C-metric approaches the RN black hole. As for the main features of accelerating black holes, one of the key features is that they would be moving through space at a constant acceleration rather than remaining stationary. Further, in the vanishing charge case, one can obtain Schwarzschild black holes. There is an intrinsic singularity at \(r=0\), but there exist three coordinate singularities at the root of the metric function f(r), then we define the following constraints:

$$\begin{aligned} r_{\alpha }&=\frac{1}{\alpha }, \end{aligned}$$
(2.4a)
$$\begin{aligned} r_+&=M+\sqrt{M^2-Q^2}, \end{aligned}$$
(2.4b)
$$\begin{aligned} r_-&=M-\sqrt{M^2-Q^2}, \end{aligned}$$
(2.4c)

which corresponds to the acceleration horizon, the event horizon, and the Cauchy horizon, respectively. In order to avoid the naked singularity, one must insist on the following relation:

$$\begin{aligned} r_- \le r_+ \le r_{\alpha }. \end{aligned}$$
(2.5)

Thus, for non-extremal case, namely \(r_+<r<r_{\alpha }\), the metric function f(r) is always positive in this range, which also imply that the angular function \(P(\theta )\) is also positive for the range \([0,\pi ]\). Different from RN black holes, in addition to become extremal when \(M=Q\), i.e. the event and Cauchy horizons are coincides. The accelerating black hole can also becomes extremal for \(\alpha =\frac{1}{r_+}\), which is called the Nariai limit. In this paper, we mainly consider the non-extremal case for simplicity.

The other interesting property of accelerating black holes is that there are two conical singularities at the axis at \(\theta =0\) and \(\theta =\pi \). Therefore, the ratio of the circumference to the radius there is not to equal to \(2\pi \). For instance, we can consider a circle around the half-axis \(\theta =0\) in a constant t, r slice and restrict the range of angular coordinates \(\phi \) to \( \phi \in [0,2 \pi a]\), where a is a constant. Then, we obtain

$$\begin{aligned} \frac{C_{\textrm{m}}}{\text {R}}=\lim _{\theta \rightarrow 0} \frac{2\pi a P(\theta ) \sin \theta }{\theta }=2\pi a P(0), \end{aligned}$$
(2.6)

where \(C_{\textrm{m}}\) and \(\text {R}\) represents the “circumference” and the “radius”, respectively. Similarity, at \(\theta =\pi \), we have

$$\begin{aligned} \frac{C_{\textrm{m}}}{\text {R}}=\lim _{\theta \rightarrow \pi } \frac{2\pi a P(\theta ) \sin \theta }{\pi - \theta }=2\pi a P(\pi ). \end{aligned}$$
(2.7)

Thus, the Eqs. (2.6) and (2.7) indicate that there are different conical singularities for different conicities. Nevertheless, one can still remove one of two conical singularities by resetting the coordinate \(\phi \). One of the two conical singularities can be eliminated, but not both when we choose a reasonable constant a. For example, if one selects that \(a=P^{-1}(0)\), then the deficit angles at the poles \(\theta =0\) and \(\theta =\pi \) are [86]

$$\begin{aligned} \delta (0)=0, \qquad \delta (\pi )=2\pi \bigg [1-\frac{P(\pi )}{P(0)} \bigg ]. \end{aligned}$$
(2.8)

In this way, we remove the conical singularity at \(\theta =0\) and left a deficit angle at \(\theta =\pi \). Likewise, if we choose \(a=P^{-1}(\pi )\), which leads to a deficit angle at \(\theta =0\) and the regularity at \(\theta =\pi \) is maintained, i.e.

$$\begin{aligned} \delta (\pi )=0, \qquad \delta (0)=2\pi \bigg [1-\frac{P(0)}{P(\pi )} \bigg ]. \end{aligned}$$
(2.9)

Henceforth, we choose \(a=P^{-1}(0)\) and preserve the Eq. (2.8) for simplicity.

Now, we introduce some thermodynamic qualities. For the Hawking temperature, we can use the standard Euclidean method: we analytically continue to the Euclidean signature, namely

$$\begin{aligned} t \rightarrow -i \tau , \qquad \tau \sim \tau +\beta , \end{aligned}$$
(2.10)

with \(\beta \) is the inverse temperature. Then the temperature of black holes is determined by

$$\begin{aligned} T_H=T \big |_{r=r_+}&=\frac{(r_+-r_-) (1-\alpha ^2 r_+^2)}{4 \pi r_+^2} \nonumber \\&=\frac{\sqrt{M^2-Q^2} \bigg (1\!-\! \alpha ^2 \big ( M\!+\! \sqrt{M^2-Q^2} \big )^2 \bigg ) }{2\pi \big (M+ \sqrt{M^2 -Q^2} \big )^2}. \end{aligned}$$
(2.11)

Meanwhile, one can determine the Bekenstein–Hawking entropy, which is a quarter of the horizon area \({\mathcal {A}}\) [81]

$$\begin{aligned}&S_{BH}=\frac{1}{4G_N}\int _{-\pi a}^{\pi a} \int _0^{\pi } \sqrt{g_{\theta \theta } g_{\phi \phi }} \Bigg |_{r=r_+} d \theta d\phi \nonumber \\&=\frac{\pi r_+^2}{G_N} \cdot \frac{1}{(1-\alpha ^2 r_+^2) P(0)} \nonumber \\&=\frac{\pi \big [M+\sqrt{M^2-Q^2} \Big ]^2}{G_N \Big ( 1\!+\!2M\alpha \!+\!\alpha ^2 Q^2 \Big ) \Big [1- \Big (M+\sqrt{M^2-Q^2} \Big )^2\alpha ^2 \Big ]}. \end{aligned}$$
(2.12)

This clearly differs from the RN black hole in which the extremal case corresponds to the finite entropy. This means that entropy is not well-defined in the Nariai limit. However, the entropy is finite in the charged limit. Finally, we perform the Kruskal transformation to obtain the maximum extended spacetime. For the charged C-metric (2.1), we define the tortoise coordinate as

$$\begin{aligned} r_{\star }&=\int \frac{1}{f(r)}dr =\frac{(r_+-r_- + \alpha ^2 r_+^2 r_- -\alpha ^2 r_+ r_-^2) \log \big | \frac{1+\alpha r}{1- \alpha r} \big |}{2\alpha (r_+-r_-)(\alpha ^2 r_+^2 -1)(\alpha ^2 r_-^2 -1)}\nonumber \\&+\frac{2r_-^2 (\alpha ^2 r_+^2-1) \log |r-r_-| - 2r_+^2 (\alpha ^2 r_-^2 -1) \log |r-r_+| - (r_+^2 -r_-^2) \log |1- \alpha ^2 r^2|}{2(r_+-r_-)(\alpha ^2 r_+^2 -1) (\alpha ^2 r_-^2 -1)}. \end{aligned}$$
(2.13)

So the null Kruskal coordinates areFootnote 1

$$\begin{aligned} U(t,r_{\star })&= - e^{-\kappa _+ u} =- e^{-\kappa _+(t-r_{\star })} ,\nonumber \\ V(t,r_{\star })&= + e^{+\kappa _+ v} = + e^{+\kappa _+(t+r_{\star })}, \end{aligned}$$
(2.14)

where \(\kappa _+ =2 \pi T_H\) is the surface gravity on the event horizon. Thus, the metric (2.1) can be recast as

$$\begin{aligned} d{s}^2=-\frac{dU dV}{g^2(r)}+\frac{r^2}{\Omega ^2} \bigg ( \frac{d \theta ^2}{P(\theta )} +P(\theta ) \sin ^2 \theta d\phi ^2 \bigg ), \end{aligned}$$
(2.15)

with the conformal factor

$$\begin{aligned} g^2(r)&=\frac{k_+^2 e^{2 \kappa _+ r_{\star }(r)} \Omega ^2(r) }{f(r)}\nonumber \\&=\frac{(1+\alpha r)^2 (r_+-r_-)^2}{4r_+^4} e^{- \frac{\frac{1}{2} (r_+ -r_-) (1+\alpha ^2 r_+ r_-) \log \big | \frac{1+ \alpha r}{1-\alpha r} \big | }{\alpha r_+^2 (\alpha ^2 r_-^2 -1)}} \nonumber \\&\quad r^2 (r-r_-)^{\frac{r_+^2 +r_-^2 - 2\alpha ^2 r_+^2 r_-^2 }{r_+^2 (\alpha ^2 r_-^2 -1)}} \nonumber \\&\quad \times (\alpha ^2 r_+^2 -1)^2 (1- \alpha ^2 r^2)^{\frac{3r_+^2-r_-^2-2\alpha ^2 r_+^2 r_-^2}{2r_+^2 (\alpha ^2 r_-^2 -1)}}. \end{aligned}$$
(2.16)

Here \(\Omega \) is defined by (2.2c). Such metric form (2.15) will prove to be important to our calculation in the following sections.

3 Island paradigm for black holes

In this section, we investigate the entanglement entropy between the radiation and black holes, together with the inclusion of the island. We start with the no-island case, then consider the effect of islands.

3.1 Early times: without island

The total system is a thermofield double state, or equivalently, the Hartle–Hawking state, since we consider an eternal black hole. We first assume that the black hole is formed by a pure state and then assume that the observer on the cut-off surface is far away from the black hole. For the later assumption, it can allow us to perform the S-wave approximation and ignore angular dependence of bulk fields that coupled the metric (2.15), and only focus on the contribution of the radial direction.Footnote 2 Thus, the metric (2.15) is reduced to a 2D form:

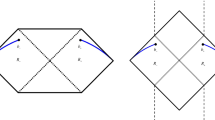
$$\begin{aligned} ds^2=-\frac{1}{g^2(r)} dU dV. \end{aligned}$$
(3.1)

The corresponding Penrose diagram is plotted in Fig. 1. In the absence of island, there is only the radiation part left in the island formula (1.1). For a thermofield double state

$$\begin{aligned} \left| {\text {TFD}}\right\rangle =\frac{1}{\sqrt{Z}} \sum _n e^{\frac{\beta E_n}{2}} \left| {n}\right\rangle _L \otimes \left| {n}\right\rangle _R, \end{aligned}$$
(3.2)
Fig. 1
figure 1

The Penrose diagram for the charged C-metric. The solid lines represents null hypersurfaces. The dashed lines are identity. \({\mathcal {H}}^{\pm }\), \({{\mathcal {H}}}_c^{\pm }\), and \({{\mathcal {H}}}_{a}^{\pm }\) represents the future/past event horizons, acceleration horizons, and Cauchy horizons, respectively. Blue lines are labeled as radiation regions \(R_{\pm }\), where the boundaries are noted by \(b_{\pm }\), whose coordinate is \(b_{\pm }=(\pm t_b,b)\) for the left and right wedge. In fact, these boundaries also represent the anchored cut-off surfaces where an observer collects the Hawking radiation. The singularity is located at \(r=0\)

Full size image

the relation \(\big (H_L -H_R \big ) \left| {\text {TFD}}\right\rangle =0\) is maintained for such a state and these two subsystems are maximally entangled. To sum up, the mutual information between the radiation at the left and the right wedge can be calculated by 2D CFTFootnote 3 [87]

$$\begin{aligned} S_{\textrm{bulk}}(R)=\frac{c}{3} \log d(b_+,b_-), \end{aligned}$$
(3.3)

where c is the central charge, \(d(b_+,b_-)\) is the geodesic distance between the points \(b_+=(+t_b,b)\) and \(b_-=(-t_b,b)\) in the Penrose diagram (Fig. 1). For the metric (3.1), the geodesic distance \(d(b_+,b_-)\) is represented by

$$\begin{aligned} d(b_+,b_-)&=\sqrt{-ds^2}\nonumber \\&=\sqrt{-\frac{[U(b_+)-U(b_-)][V(b_+)-V(b_-)]}{g(b_+)g(b_-)}}. \end{aligned}$$
(3.4)

We substitute the coordinate of \(b_{\pm }\), then obtain the result as

$$\begin{aligned} S_{\textrm{bulk}}&=\frac{c}{6} \log \bigg [\frac{1}{g^2(b)} 2 e^{2 \kappa _+ r_{\star }(b)} [2\cosh (2 \kappa _+ t_b)+1] \bigg ]\nonumber \\&=\frac{c}{6} \log \bigg [ \frac{4(1+\alpha b)^2f(b)}{\kappa _+^2} \cosh ^2 (\kappa _+ t_b) \bigg ] \nonumber \\&=\frac{c}{6} \log \Bigg [ \frac{16r_+^4 (r_+-b)(b-r_-) (\alpha ^2b^2-1)(1\!+\!\alpha b)^2}{(r_+-r_-)^2 b^2 (\alpha ^2 r_+^2-1)^2 } \nonumber \\&\quad \cosh ^2 (\kappa _+ t_b) \Bigg ]. \end{aligned}$$
(3.5)

At late times limit, \(t \gg \kappa _+\), we can use the approximation: \(\cosh (\kappa _+ t_b) \simeq \frac{1}{2} e^{\kappa _+ t_b}\), then

$$\begin{aligned} S_{\textrm{bulk}} (R)&\simeq \frac{c}{3} \log [\cosh (\kappa _+ t_b)] \nonumber \\&\simeq \frac{c}{3} \kappa _+ t_b = \frac{2c}{3} \pi T_H t_b \nonumber \\&=\frac{2c \pi t_b}{3} \frac{\sqrt{M^2-Q^2} \big [1- \alpha ^2 \big ( M\!+\! \sqrt{M^2\!-\!Q^2} \big )^2 \big ]}{2\pi \big (M+ \sqrt{M^2 -Q^2} \big )^2}. \end{aligned}$$
(3.6)

One can obviously see from this result that the entanglement entropy of radiation is proportional to the time \(t_b\) for the observer at infinity and the temperature of black holes. Besides, we also find that increasing acceleration will decrease the rate of growth. Finally, the entanglement entropy behaves divergent at late times. In particular, for an eternal black hole, the amount of radiation is infinite at late times, which leads to the entanglement entropy far exceeding the Bekenstein–Hawking entropy bound [88]. Therefore, there exists an intuitive paradox here: on the one hand, our result provides a linear increase in the entanglement entropy; On the other hand, the fine-grained (entanglement) entropy must be small than the coarse-grained (Bekenstein–Hawking) entropy. We expect to solve this thorny issue through the island paradigm.

Fig. 2
figure 2

The Penrose diagram for charged accelerating black holes with an island. The disconnected island region is labeled as I, its boundary is \(a_{\pm }\). We set their coordinates are \(a_{\pm } = (\pm t_a,a)\). In the same way, the Hawking radiation is emitted from the cut-off surfaces \(b_{\pm }=(\pm t_b,b)\), where the asymptotic observer collects the radiation

Full size image

3.2 Late times: with island

Now we introduce the disconnected island region in our system by following the island paradigm. The Penrose diagram is shown in Fig. 2. At this time, the expression of the von Neuman entropy for these disconnected multi-interval is given by [87]

$$\begin{aligned}{} & {} S_{\textrm{bulk}}(I \cup R)\nonumber \\= & {} \frac{c}{6} \log \Bigg [ \frac{d(a_+,a_-)d(b_+,b_-)d(a_+,b_+)d(a_-,b_-)}{d(a_+,b_-)d(a_-,b_+)} \Bigg ].\nonumber \\ \end{aligned}$$
(3.7)

Here d(x, y) still refers to the geodesic distance (3.4). Similarity, we still assume that the late times and the large distance are allowed [29]. This approximation allows us to rewrite the above equation into a simpler formFootnote 4. In this limit, we have:

$$\begin{aligned}&d(a_+,a_-) \simeq d(b_+,b_-) \simeq d(a_+,b_-) \simeq d(a_-,b_+)\nonumber \\&\quad \gg d(a_+,b_+) \simeq d(a_-,b_-), \end{aligned}$$
(3.8)

and

$$\begin{aligned} S_{\textrm{bulk}}&\simeq \frac{c}{6} \log [d(a_-,b_-) d(a_+,b_+)] \nonumber \\&=\frac{c}{3} \log \Bigg [ \frac{2e^{\kappa _+ (r_{\star }(a) +r_{\star }(b))}}{g(a) g(b)} \nonumber \\&\quad \times \bigg [ \cosh [\kappa _+ (r_{\star }(a) -r_{\star }(b))] \!-\!\cosh [\kappa _+ (t_a\!-\!t_b)] \bigg ] \Bigg ]. \end{aligned}$$
(3.9)

Accordingly, the generalized entropy (1.2) read as

$$\begin{aligned} S_{\textrm{gen}}&=\frac{2\pi a^2}{G_N} \frac{1}{(1-\alpha ^2 a^2 ) \big [ 1+\alpha (r_++r_-) +\alpha ^2 r_+r_- \big ]} \nonumber \\&+\frac{c}{6} \log \Bigg [ \frac{4f(a)f(b)(1+\alpha a) (1+\alpha b)}{\kappa _+^4} \nonumber \\&\quad \times \Big ( \cosh [\kappa _+ (r_{\star }(a) \!-\! r_{\star }(b) )] \!-\!\cosh [\kappa _+ (t_a-t_b)]\Big )^2\Bigg ] . \end{aligned}$$
(3.10)

Extremizing the above expression with respect to \(t_a\) firstly

$$\begin{aligned}{} & {} \frac{S_{\textrm{gen}}}{\partial t_a} \nonumber \\= & {} \frac{c}{3} \frac{- \kappa _+ \sinh [\kappa _+ (t_a-t_b)]}{\cosh \big [\kappa _+ (r^{\star }(a)-r^{\star }(b) \big ] -\cosh [\kappa _+(t_a-t_b)]}=0.\nonumber \\ \end{aligned}$$
(3.11)

Thus, the only solution for the equation is \(t_a=t_b\). Substituting this relation and then extremizing it with respect to a:

$$\begin{aligned} \frac{S_{\textrm{gen}}}{\partial a}&=\frac{4 \pi a}{G_N (1+\alpha r_+) (1+\alpha r_-) (\alpha ^2 a^2 -1)^2}\nonumber \\&\quad +\frac{c \bigg ( f^{\prime }(a) -2 \kappa _+ \frac{e^{\kappa _+ x }+1}{e^{\kappa _+ x }-1} \bigg ) }{6f(a)}=0, \end{aligned}$$
(3.12)

Where \(x \equiv r_{\star }(b) -r_{\star }(a)\), and \(f^{\prime }(r)\) is the derivative of f(r). Now, we make the near horizon limit, where \(a \simeq r_+\). By taking this approximation, the above equation is recast as

$$\begin{aligned}&\frac{S_{\textrm{gen}}}{\partial a} \simeq \frac{4 \pi }{G_N \alpha ^6 a^3 r_+ r_-} + \frac{c}{6} \frac{2e^{\kappa _+ (r_{\star }(b) -r_{\star }(a))}}{(e^{\kappa _+ (r_{\star }(b) - r_{\star }(a))}-1)(a-r_+)}=0.\nonumber \\ \end{aligned}$$
(3.13)

Thus, we finally obtain the location of the quantum extremal island is

$$\begin{aligned} a&\simeq r_+ + \frac{c G_N \alpha ^6 r_+^4 r_- }{12 \pi e^{\kappa _+ r_{\star }(b)} } \nonumber \\&\simeq r_+ + {\mathcal {O}} \Big ( \frac{cG_N}{r_+} \Big ). \end{aligned}$$
(3.14)

Therefore, at late times, the entanglement entropy of Hawking radiation with the island is given by

$$\begin{aligned} S_{\textrm{Rad}}&= \frac{2 \pi r_+^2}{G_N} \frac{1}{(1-\alpha ^2 r_+^2) [1+ \alpha (r_++r_-) + \alpha ^2 r_+r_-]} \!+\! \frac{c}{3} \log \Bigg [ \frac{cG_N r_+^2 (b-r_+) (b-r_-) (r_+-r_-)(\alpha ^2 b^2 -1)(\alpha ^2 r_+^2 -1)}{(r_+-r_-)(\alpha ^2 r_+^2 -1)r_+ b^2} \Bigg ] \nonumber \\&\simeq 2S_{BH}. \end{aligned}$$
(3.15)

Therefore, we find that once we consider the contribution of an island, the fine-grained entropy of radiation approaches a saturated value eventually. This result consist with the expectation of the uniarity and is the opposite of Hawking’s calculation: at late times, the entanglement entropy of radiation stops increasing and tends to be about twice of the Bekenstein–Hawking entropy. This conclusion also respects the principle of unitary. Now the black hole has enough degree of freedom to entangle with the external radiation, since now the fine-grained entropy of black holes is smaller than the coarse-grained/Bekenstein–Hawking entropy. Therefore, we obtain the expression of the fine-grained entropy of Hawking radiation for the whole process of the evaporation

$$\begin{aligned} S_{\textrm{FG}}=\text {Min} \bigg [ \frac{2c \pi }{3} T\cdot t , \ 2S_{\textrm{BH}} \bigg ], \end{aligned}$$
(3.16)

where the effect of charges and acceleration is absorbed in the temperature \(T_H\) and the Bekenstein–Hawking entropy \(S_{BH}\), which we will discuss in detail below.

Fig. 3
figure 3

The Page time by charged accelerating black holes as the function for charges Q, in which the acceleration \(\alpha \) is fixed (in the unit of \(\frac{6 \pi }{c G_N}\) and set \(M=1\)). On the left, it is the non-extremal case with a small amount of charges, while on the right is the near extremal case

Full size image
Fig. 4
figure 4

The Page time by charged accelerating black holes as the function for the acceleration \(\alpha \) (in the unit of \(\frac{6 \pi }{c G_N}\) and set \(M=1\)). On the left is the non-extremal case, while on the right is the near extremal case

Full size image

4 Page curve and scrambling time

At present, we have calculated the behavior of the entanglement entropy of radiation from the discussion of applying the island paradigm in the previous section. Therefore, the natural thing to do in this section is to plot the corresponding Page curve and obtain some by-products, such as the scrambling time of black holes.

At first, we derive the Page time that defined as the moment when the entanglement entropy approaches the peak. In the language of the entanglement island, the entropy without island (3.6) is roughly equal to the entropy with island (3.15) at the Page time. Accordingly, we obtain the Page time is

$$\begin{aligned} t_{\textrm{Page}}&= \frac{3 S_{BH}}{\pi c T_H} = \frac{12 \pi r_+^4}{ cG_N (r_+-r_-) (\alpha r_+ -1)^2 (\alpha r_+ +1)^3 (\alpha r_- +1) } \nonumber \\&=\frac{6 \pi \big (M+ \sqrt{M^2-Q^2} \big )^4 }{cG_N \sqrt{M^2-Q^2} \bigg (1+M \alpha - \alpha \sqrt{M^2-Q^2} \bigg ) \bigg [ (M+\sqrt{M^2 -Q^2}) \alpha -1 \bigg ]^2 \bigg [(M+\sqrt{M^2 -Q^2}) \alpha +1 \bigg ]^3 }. \end{aligned}$$
(4.1)

The corresponding graphs as a function for the charge Q and the acceleration \(\alpha \) are shown in Fig. 3 (\(\alpha \) is fixed) and Fig. 4 (Q is fixed), respectively.

Through these figures, one can easily find that in the \(\alpha \)-fixed case, the Page time decreases first and then increases with the acceleration increasing. But in the \(\alpha \)-fixed case, the Page time decreases as charges increase. In particular, the Page time reaches its maximum for neutral black holes (\(Q=0\)). Note that these conclusions are applied only to non-extremal black holes. However, once the acceleration or charges makes the black hole approaches an extremal black hole, the Page time behaves divergent. Finally, the Page curves for non-extremal charged accelerating black holes are given in Fig. 5.

Fig. 5
figure 5

The Page curve for eternal charged accelerating black holes, where setting \(M=c=G_N=1\). On the left, we fix the acceleration \(\alpha =\frac{1}{2r_+}\). On the right, we fix the charge \(Q=0.5M\)

Full size image

Now we discuss the scrambling time, which is based on the Hayden–Preskill Gedanken experiment: one drops a quantum diary into a black hole after the Page time. He would have to wait for what is so-called the scrambling time to recover this quantum information from Hawking radiation [89]. In the suggestion of the entanglement wedge reconstruction, the scrambling time is determined by how long it takes the information to touch the boundary of the entanglement island. Therefore, the asymptotic observer sends a light signal at the cutoff surface \((r=b)\), then the time when the signal reaches the island \((r=a)\) is

$$\begin{aligned} \text {v}(t_b,b)-\text {v}(t_a,a) =(t_b-t_a) + \big [ r_{\star } (b) -r_{\star }(a) \big ], \end{aligned}$$
(4.2)

where \(\text {v}(t,r)\) is denoted the null Kruskal coordinate (2.14). Thus, the scrambling time is the shortest delivery time

$$\begin{aligned} t_{\textrm{scr}}&\equiv \text {Min} [t_a-t_b]\nonumber \\&=\text {Min} \big \{ [r_{\star }(b) -r_{\star }(a)] - [\text {v}(t_b,b) -\text {v}(t_a,a)] \big \} \nonumber \\&=r_{\star }(b) -r_{\star }(a). \end{aligned}$$
(4.3)
Fig. 6
figure 6

The scrambling time by black holes as functions of charges Q and accelerations \(\alpha \). Here we set the mass \(M=G_N=1\)

Full size image

We obtain the expression of the scrambling time by invoking the location of the island (3.14)

$$\begin{aligned} t_{\textrm{scr}}&=\frac{r_+^2}{2(r_+-r_-) (\alpha ^2 r_+^2 -1) (\alpha ^2 r_-^2 -1) } \nonumber \\&\quad \times \Bigg ( (2\alpha ^2 r_-^2 -2) \log \bigg ( \frac{a-r_+}{b-r_+} \bigg ) \nonumber \\&\quad + (2 \alpha ^2 r_+^2-2) \log \bigg ( \frac{b-r_-}{a-r_-} \bigg ) \nonumber \\&\quad +\alpha (r_+-r_-) (\alpha ^2 r_+ r_- +1)\nonumber \\&\quad \times \bigg ( \log \frac{1+b \alpha }{1-b \alpha } - \log \frac{1+a \alpha }{1- a \alpha } \bigg )\nonumber \\&\quad +(r_+^2 - r_-^2 )\alpha ^2 \log \frac{1-\alpha ^2 a^2}{1-\alpha ^2 b^2} \Bigg ) \nonumber \\&\simeq \frac{r_+^2}{2(r_+-r_-)(1-\alpha ^2 r_+^2 )}\nonumber \\&\quad \times \Bigg ( \log \frac{(b-r_+)(a-r_-)}{(a-r_+)(b-r_-)}\nonumber \\&\quad +\alpha (r_+-r_-) \log \frac{(1+b\alpha )(1-a \alpha )}{(1-b\alpha ) (1+a\alpha )} \Bigg )\nonumber \\&\simeq \frac{2r_+^2}{(r_+-r_-)(1-\alpha ^2 r_+^2)} \log \frac{(b-r_+)(a-r_-)}{(a-r_+)(b-r_-)}\nonumber \\&\simeq \frac{1}{2 \pi T_H} \log \frac{r_+^2}{c G_N} \simeq \frac{1}{2 \pi T_H} \log S_{BH}. \end{aligned}$$
(4.4)

Here, we assume that the acceleration is not large \(( \alpha \ll \frac{1}{r_+} )\). Then all second-order terms associated with \(\alpha \) can be omitted, namely, \(\alpha ^2 r_{\pm }^2 \simeq 0\). In the last line, we assume that b has the order \({\mathcal {O}} (r_+)\) and make a further approximation: \(r_+ \gg r_-\) to omit the term \(\alpha (r_+ - r_-)\). This finally result follows the conclusion of the initial Hayden–Preskill experiment [90, 91]. We emphasize that the results and approximations are only applicable for small accelerations. But these approximation breaks down when the acceleration is large enough. Last, the scrambling time as a function of the acceleration \(\alpha \) and the charge Q is plotted in Fig. 6.

In the same way, the scrambling time decreases when the charge increases, while as the acceleration increases, it decreases and then increases. The neutral black hole also has the greatest scrambling time. However, in the extremal case, the scrambling time is also divergent. This is for the same reason that the Page time diverges in extremal cases. Moreover, Since the results are obtained under small acceleration approximation, the accuracy of the curve needs to be further tested for the large acceleration. We will discuss some remarks in the next section.

5 Conclusion and discussion

In summary, we study the information paradox in the charged “C-metric” that describes an accelerating black hole. Unlike the RN black holes, the existence of acceleration parameters \(\alpha \) results in accelerating black holes existing three horizons. Consequently, the corresponding geometry is richer. Therefore, it is very meaningful to study the Page curve under this background, and to further expand the scope of application of the island paradigm. We explicitly calculate the fine-grained entropy of the Hawking radiation by the island formula (3.16). Accordingly, the Page curve is successfully reproduced by the island paradigm in Fig. 5. In brief, the fine-grained entropy of radiation increases monotonically with time before the Page time. After this moment, it stays at a fixed value that is about twice of the Bekenstein–Hawking entropy. This is also consistent with the finiteness of the entanglement entropy for two-sided eternal black holes or a system at the thermofield double state.

A significant feature of the Page curve for the “C-metric” is the presence of the charge and the acceleration. In the non-extremal case, when they are both small, the decrease in charges will cause the Page time to go up for the fix-\(\alpha \) case (Fig. 3). On the contrary, the increase in acceleration will first move forward and then delay the Page time (Fig. 4). In addition, the dependence of scrambling time on charges and accelerations has similar behavior to the Page time (Fig. 6). We also find that both the Page time and the scrambling time are maximized in neutral black holes. Again, we emphasize that the conclusion about the scrambling time is only valid for small accelerations. Note that, both the Page time and the scrambling time become divergent at the extremal case. A simple view is that the Hawking temperature of extremal black holes is zero, and the expressions of the Page time and the scrambling time are inversely proportional to the temperature. However, one needs to investigate extremal cases more prudently. Some reports suggest that the causal structure of extremal cases manifests different and the corresponding calculations need to be modified [56, 57], while other work suggests the extremal black holes are completely dominated by the superradiance, which can turn a black hole into a neutral black hole, thus avoiding difficulties in extreme cases. In this process, the Page time and the Bekenstein–Hawking entropy both decrease [46]. In brief, the Page curve of the extremal case remains an open question and more investigation is needed.

Another interesting open question involves the transfer of quantum information. The island formula only gives us a prescription on how to calculate the unitary Page curve, but the details of the information escaping from black holes are unknown. What happens when the black hole evaporates to a Planck scale, or does the wormhole appear at the end of the evaporation? Further studies into quantum gravity may be required to reveal these intriguing questions.