1 Introduction

General relativity (GR) is the most successful theory describing gravity and our Universe. In particular, recent observation of gravitational waves generated from binary compact objects [1, 2] and black hole shadows [3, 4] match the predictions of GR and also provide us remarkable chances to test GR in strong field regime, but the uncertainties in the data leave some space for alternative theories of gravity. Moreover, GR also comes across some challenges in the explanation of the accelerated expansion of the Universe, the large scale structure and the understanding of the quantum gravity [5,6,7]. Therefore, from both observational and theoretical perspectives, a more general theory of gravity is eagerly required, thus, plenty of modified gravitational theories have been proposed [8,9,10]. Among them, a remarkable way of modifying the action of GR is to introduce scalar field as an additional field. The advantage mainly stems from three aspects. Firstly, the scalar field may be ubiquitous composite in nature, for example, ultralight axions are indispensable in string theory [11]. Secondly, scalar field is an important candidate for dark matter, dark energy and inflation which are commonly believed to exist but their essences are not clear. Thirdly, the no hair theorem of black hole in classical GR states that black holes are solely characterized by their mass, electric charge and angular momentum [12, 13]. However, there is no hint for the absence of other fundamental quantity describing black holes, and the introducing of scalar field into the action is one of the direct ways to verify the no hair theorem of the black hole and help us further understand gravity.

A minimally coupled scalar field usually does not obey the Gauss-law and thus, a black hole cannot have a non-trivial regular scalar hair in GR [14] so that the no hair theorem holds. However, it can be circumvented by introducing nonminimal couplings between the gravity and scalar field. It was addressed in [15, 16] that an Einstein-conformally coupled scalar theory could lead to a secondary scalar hair around the Bocharova–Bronnikov–Melnikov–Bekenstein (BBMB) black hole, which was considered as the first counterexample to the no hair theorem using scalar field. The uniqueness of BBMB was then discussed in [17, 18] and also numerically reproduced in [19]. Nevertheless, in this sector the scalar field diverges at the horizon and so its physical properties are difficult to interpret. This situation was then improved by introducing a cosmological constant in the solution, dubbed the “Martinez–Troncoso–Zanelli (MTZ)” black hole, which pushes the scalar field singularity behind the event horizon [20, 21]. The MTZ black hole only has a spherical or hyperbolic horizon depending on the sign of the cosmological constant but no planar solution is allowed. Inspired by this, many efforts have been made to construct planar black hole with various matter hair [22,23,24]. In particular, physicists added the Maxwell field and extended the theory into Einstein–Maxwell-conformally coupled scalar theory of which the action is [20]

$$\begin{aligned} S=\frac{1}{2\kappa }\int {d^4x}\sqrt{-g}\Bigg [R-F_{\mu \nu }F^{\mu \nu }-\frac{\kappa }{6}(\varphi ^2 R+6\partial _{\mu }\varphi \partial ^{\mu }\varphi )\Bigg ]\nonumber \\ \end{aligned}$$
(1)

where \(\kappa =8\pi G\). The equations of motion derived from the above action admit the static spherically symmetric solution [25]

$$\begin{aligned}{} & {} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2(d\theta ^2+\text {sin}^2\theta d\phi ^2), \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \textrm{with} ~~~ f(r)=1-\frac{2M}{r}+\frac{q^2}{r^2}+\frac{s}{r^2}, \end{aligned}$$
(3)

and the matter fields are given by

$$\begin{aligned} \varphi =\pm \sqrt{\frac{6}{\kappa }}\sqrt{\frac{s}{q^2+s}}, ~~~A_\mu =-\frac{q}{r}\delta _\mu ^t. \end{aligned}$$
(4)

Here M denotes the mass parameter, q is the electric charge parameter and s characterizes the conformally-coupled scalar hair or scalar charge of solution. The metric (2) could indicate different spacetimes depending on the parameters, and \(f(r)=0\) gives the roots \(r_{c,e}=M\mp \sqrt{M^2-q^2-s}\). Thus, (i) when \(s>M^2-q^2\), the metric describes a naked singularity without horizon. (ii) when \(M^2-q^2\ge s\ge 0\), the metric describes a black hole with Cauchy horizon \(r_c\) and event horizon \(r_e\), and the black hole becomes extreme as \(s=M^2-q^2\). It is noted that in this case the geometry is similar to Reissner–Nordstr\(\ddot{\text {o}}\)m (RN) black hole with a electric charge \(Q^2=q^2+s\). (iii) when \(-q^2<s<0\), it is easy to obtain that the scalar field \(\varphi \) is imaginary, in which case the kinetic part in the action (1) should be written as \(\partial _{\mu }\varphi ^{*}\partial ^{\mu }\varphi \) [26]. The new form of the kinetic term does not matter because it is trivial for constant \(\varphi \), but we will not consider this case in the following study. (iv) when \(s<-q^2\), it could also describe a black hole, but the coefficient of the term \(1/r^2\) is negative differentiating from the RN black hole. So, the black hole in this situation is also dubbed mutated RN black hole. The black hole solution (2) is closely related to the “BBMB black hole” constructed in [15, 16], but instead of non-regular scalar field in the BBMB BH, the scalar field in the current system is regular. Many physical phenomena on this black hole have been extensively studied. For example, the stability of the black hole (2) against perturbations was studied in [15, 26]. The Hawking radiation of charged particles was disclosed in [27]. The significant effect of the conformally-coupled scalar charge on the black hole shadow was recently explored in [28].

The aim of this work is to study the gravitational lensing effects of the hairy black hole solution (2). We shall explore the effect of the conformally coupled scalar hair on the weak and strong gravitational effects, respectively. The gravitational lensing is a phenomenon in which the path of light from a distant object is bent by the gravitational field of a massive object. Depending on the amount of light deflection, the gravitational lensing is usually divided into weak and strong effects. Weak deflection limit occurs when the light ray passes far away from the photon sphere while strong deflection limit occurs when the light ray passes from the vicinity of the photon sphere. The gravitational lensing is one of the powerful astrophysical tools to investigate the features of central gravitational source and even the related theory of gravity. Many approaches have been proposed to investigate the gravitational lensing of black holes in both limits.

Early studies on the weak gravitational field approximation have successfully explained the astronomical observations, please see [29,30,31] for reviews. With a perturbative method, the deflection angle and weak gravitational lensing of RN black hole have been analyzed in [32]. The formula with Taylor expansion was proposed for weak field limit of static and spherically symmetric black hole in [33], which was then generalized in Kerr black hole lensing [34, 35]. Later, the Gibbons–Werner method was proposed in [36], in which the Gauss–Bonnet theorem in the optical geometry was resorted. Specifically, Gibbons and Werner proposed that for a static and spherically symmetric black hole, the deflection angle of light can be calculated by integrating the Gaussian curvature of the optical metric outwards from the light ray, as a consequence of the focusing of light rays emerges as a global topological effect. This method was soon used in stationary and axisymmetric black holes [37]. For a comprehensive review on the applications of the Gauss–Bonnet theorem to gravitational deflection angle of light in the weak field limit, one refers to [38]. On the other hand, the gravitational lensing in the strong gravity regime of black hole has attracted considerable attention since one could get the near horizon properties of black hole from it. The authors of [39] introduced the lens equation for the strong field limit of Schwarzschild black hole with numerical methods, after that Bozza proposed an analytical logarithmic expansion method for strong field lensing [40], which was then extended into general asymptotically flat spacetime [41]. Based on the analytical method, various lensing observables for static and spherically symmetric spacetimes have been proposed in [40, 42] and then extensively studied in [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. Especially, since the achievements of the Event Horizon Telescope [3, 4] provide us with the direct observation to explore the strong gravity regime, so we could expect to understand the properties of black holes from the lensing effect. This is why the gravitational lensing in the strong gravity regime of black holes has attracted more and more attentions, in which the observables may serve as diagnosis to reveal properties of black holes in alternative theories of gravity and compare with their counterparts in GR.

This paper is organized as follows. In Sect. 2, we shall analyze the null geodesic equation in the equatorial plane of charged black holes with conformally coupled scalar hair. With the use of Gauss–Bonnet theorem, we will calculate the light deflection angle in the weak field limit in Sect. 3. In Sect. 4, we focus on the light deflection in the strong field limit and evaluate the lensing observable of the supermassive black holes with conformally coupled scalar hair. The last section contributes to our closing remarks. We shall set \(G=c=1\) unless we restore them for discussion.

Fig. 1
figure 1

The geometrical configuration of gravitational lensing

Full size image

2 Light rays in the equatorial plane of charged black holes with scalar hair

As a preparation, in this section we shall analyze the null geodesic of the hairy black hole (2) and check how the scalar charge affects the light rays. Since the spacetime is spherical symmetric and all \(\theta =const.\) are equivalent, hence we can consider the equatorial plane with \(\theta =\pi /2\) without loss of generality. To this end, it is convenient to rescale all quantities in the units of 2M to be dimensionless. Thus, we rewrite the metric Eq. (2) projected on the equatorial plane as

$$\begin{aligned} ds^2=-A(r)dt^2+B(r)dr^2+C(r)d\phi ^2 \end{aligned}$$
(5)

where the functions are

$$\begin{aligned} A(r)=B(r)^{-1}=1-\frac{1}{r}+\frac{q^2}{r^2}+\frac{s}{r^2} ~~\text {and}~~C(r)=r^2. \end{aligned}$$
(6)

Due to the time-translational and spherical symmetries of the metric, the photon’s motion will have two conserved quantities

$$\begin{aligned} E=A(r){\dot{t}}~~\text {and}~~L=C(r){\dot{\phi }}, \end{aligned}$$
(7)

where the dots denote the derivative respective to the affine parameter. Then, recalling that we have

$$\begin{aligned} A(r){\dot{t}}^2-B(r){\dot{r}}^2-C(r){\dot{\phi }}^2=0 \end{aligned}$$
(8)

for photon, we obtain the orbit equation

$$\begin{aligned} {\dot{r}}^2=E^2-\frac{L^2 A(r)}{C(r)}\equiv V_{\text {eff}}(r). \end{aligned}$$
(9)

Due to the gravitational effect, the light rays exist in the region where \(V_{\text {eff}}(r)\le 0\). According to the orbit equation, a photon incoming from infinity with a impact parameter \(u\equiv L/E\) larger than some minimum value approaches the center object, and then goes far away after reaching the radial minimum distance \(r_0\). Otherwise, the photon falls into the horizon. The turning point of the trajectory, \(r_0\), should satisfy \(V_{\text {eff}}(r)=0\) which gives us the relation

$$\begin{aligned} u\equiv L/E=\sqrt{\frac{C(r_0)}{A(r_0)}}. \end{aligned}$$
(10)

The turning point \(r_0\) has a minimum \(r_m\) which is determined by \(V_{\text {eff}}(r)=V_{\text {eff}}'(r)=0\). For the hairy black hole (2), the light ring with radium \(r_m\) corresponds to the photon sphere due to the spherical symmetry, and the radius of unstable photon sphere \((V_{\text {eff}}''(r)>0)\) is

$$\begin{aligned} r_m=\frac{3}{4}\left( 1+\sqrt{1-\frac{32}{9}(q^2+s)}\right) . \end{aligned}$$
(11)

It is clear that for positive allowed scalar charge, a larger s corresponds to a smaller radius of the light ring or photon sphere, while for \(s<-q^2\), increasing s also suppresses \(r_m\). Subsequently, the critical impact parameter \(u_m\) is defined as

$$\begin{aligned}{} & {} u_m\equiv u(r_m)=\sqrt{\frac{C(r_m)}{A(r_m)}}\nonumber \\{} & {} \quad =\frac{1}{2} \sqrt{\frac{\left( \sqrt{-8q^2-8s+\frac{9}{4}}+\frac{3}{2}\right) ^2}{\frac{4q^2}{\left( \sqrt{-8q^2-8\text {s}+\frac{9}{4}}+\frac{3}{2}\right) ^2}-\frac{2}{\sqrt{-8q^2-8s+\frac{9}{4}}+\frac{3}{2}}+\frac{4s}{\left( \sqrt{-8q^2-8s+\frac{9}{4}}+\frac{3}{2}\right) ^2}+1}}.\nonumber \\ \end{aligned}$$
(12)

In this scenario, the photons with impact parameter \(u<u_m\) will be attracted into the horizon of the black hole; while photons with \(u>u_m\) move towards to the black hole till a minimum distance \(r_0\) and then are scattered into infinity; and photons with \(u=u_m\) circle around the black hole forming a bright photon sphere with radius \(r=r_m\).

Therefore, the light deflection angle \(\alpha _D\) is finite only for \(r_0>r_m\) and becomes infinity at \(r_0=r_m\). A cartoon of geometrical configuration about gravitational lensing is shown in Fig. 1, where \(\beta \) is the angular separation between the source and the black hole, and \(\theta \) is the angular separation between the image and the black hole, \(D_{OL}\) is the distance between the observer and the lens, and \(D_{OS}\) is the distance between the observer and the source, respectively. The calculation of light deflection angle for the black hole lensing is an overlasting topic, but it is still difficult to give a general formula of \(\alpha _D\) for all the possible light rays. Fortunately, in the far limit of the source and the observer, the deflection angle of light can be evaluated from the null geodesic as [62]

$$\begin{aligned} \alpha _D=2\int _{r_0}^{\infty } \frac{dr}{dr/d\phi }-\pi . \end{aligned}$$
(13)

where \(dr/d\phi \) can be obtained from (7) and (9) as

$$\begin{aligned} \frac{dr}{d\phi }=\sqrt{\frac{C(r)}{B(r)} \left( {\frac{C(r)}{A(r)}\frac{1}{u^2}}-1\right) }. \end{aligned}$$
(14)

In general, it is not easy to solve (13) for arbitrary impact parameter, but many effective methods have been proposed to calculate the deflection angle for the light rays in weak field limit, in which the closet approach distance of a light ray to the lens is much larger than its gravitational radius, i.e., \(r_0\gg M\); and in strong field limit (\(r_0\sim M)\). Thus, in next sections, we shall employ the Gauss–Bonnet method [36, 38] to evaluate \(\alpha _D\) in weak field limit and Bozza’s proposal [40, 43] to calculate \(\alpha _D\) in strong field limit for the light rays around the hairy black hole (2) with a conformally coupled scalar field, respectively.

3 Weak gravitational lensing effect

In this section, we shall study the influence of the conformally coupled scalar hair on the deflection angle of light in the weak gravitational lensing effect of black hole. We will use the Gauss–Bonnet theorem in the optical geometry, which was pioneerly proposed by Gibbons and Werner [36]. With this inspiration, the Gauss–Bonnet method has been widely used to calculate the deflection angle of light in various spherically or axisymmetric black holes, see for examples [63,64,65,66,67,68,69,70,71,72,73] and references therein. It is noted that Gibbons and Werner’s approach to gravitational lensing is only valid when the observer and source are both Euclidean (or equivalently they are both in a flat region of spacetime), otherwise there would be contributions to the deflection angle coming from the background geometry of the spacetime. A comprehensive applications of Gauss–Bonnet method to compute the gravitational deflection angle of light in weak field limit has been reviewed in [38]. In that paper, the authors firstly considered the effects of finite distance from a massive object to a light source and a receiver on the gravitational deflection angle of light and then took the infinite-distance limit to obtain the final results which are consistent with the previous works. We will proceed our study following the main steps of this method.

For convenience, we introduce the new coordinate \({\mathfrak {u}}\equiv 1/r\), then we can rewrite the orbital equation of photon (14) as

$$\begin{aligned} \Big (\frac{d{\mathfrak {u}}}{d\phi }\Big )^2=\frac{{\mathfrak {u}}^4 C(r) (C(r) - A(r) u^2)}{B(r) A(r) u^2}. \end{aligned}$$
(15)

Obviously, by inserting the metric functions into (15), we can obtain the orbital equation of photons. However, due to the complexity, we cannot solve the differential equation analytically. Instead, we use the weak field, small charges q and s approximation to obtain the analytical approximation solution. The orbital function of the photon is then obtained as

$$\begin{aligned} {\mathfrak {u}}\simeq&\,\frac{\sin \phi }{u}+\frac{M(1+\cos ^2\phi )}{u^2}\nonumber \\&+\frac{M^2\cos \phi (-3\sin 2\phi +5(3\pi -6\phi +4\tan \phi ))}{8u^3}\nonumber \\&-\frac{q^2\cos \phi (3\pi -6\phi +\sin 2\phi +4\tan \phi )}{8u^3}\nonumber \\&-\frac{s \cos \phi (3\pi -6\phi +\sin 2\phi +4\tan \phi )}{8u^3}\nonumber \\&+{\mathcal {O}}(M^3, q^3, s^2). \end{aligned}$$
(16)

Then by solving the above equation, we get the angle \(\phi \) as

$$\begin{aligned} \begin{aligned} \phi \simeq \left\{ \begin{array}{ll} \arcsin (u{\mathfrak {u}})+\frac{M(u^2 {\mathfrak {u}}^2-2)}{u\sqrt{1-u^2 {\mathfrak {u}}^2}}-\frac{M^2(15u{\mathfrak {u}}-20u^3{\mathfrak {u}}^3+3u^5{\mathfrak {u}}^5+15(1-u^2{\mathfrak {u}}^2)^{\frac{3}{2}}\arccos (u{\mathfrak {u}}))}{4u^2(1-u^2{\mathfrak {u}}^2)^{\frac{3}{2}}}\\ +\frac{q^2(\frac{4u{\mathfrak {u}}}{\sqrt{1-u^2{\mathfrak {u}}^2}}+6\arccos (u{\mathfrak {u}})+\sin (2\arccos (u{\mathfrak {u}})))}{8u^2} +\frac{s(\frac{4u{\mathfrak {u}}}{\sqrt{1-u^2{\mathfrak {u}}^2}}+6\arccos (u{\mathfrak {u}})+\sin (2\arccos (u{\mathfrak {u}})))}{8u^2} &{} \text {for}~~~ |\phi |<\frac{\pi }{2}, \\ \pi -\arcsin (u{\mathfrak {u}})+\frac{M (2-u^2{\mathfrak {u}}^2)}{u\sqrt{1-u^2{\mathfrak {u}}^2}}+\frac{M^2(15u{\mathfrak {u}}-20u^3{\mathfrak {u}}^3+3u^5{\mathfrak {u}}^5+15(1-u^2{\mathfrak {u}}^2)^{\frac{3}{2}}\arccos (u{\mathfrak {u}}))}{4u^2(1-u^2{\mathfrak {u}}^2)^{\frac{3}{2}}}\\ +\frac{q^2(\frac{2u{\mathfrak {u}}(u^2{\mathfrak {u}}^2-3)}{\sqrt{1-u^2{\mathfrak {u}}^2}}-6\arccos (u{\mathfrak {u}}))}{8u^2}+\frac{s(\frac{2u{\mathfrak {u}}(u^2{\mathfrak {u}}^2-3)}{\sqrt{1-u^2{\mathfrak {u}}^2}}-6\arccos (u{\mathfrak {u}}))}{8u^2} &{} \text {for}~~~ |\phi |>\frac{\pi }{2}. \end{array} \right. \end{aligned} \end{aligned}$$

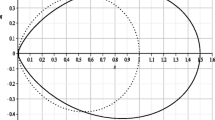
For the weak field limit, we can choose the domain of \(\phi \) to be \(-\pi \le \phi \le \pi \) without the loss of generality. As shown in Fig. 2, the range of angular coordinates value \(\phi _S\) of the source point is \(-\pi /2\le \phi _S\le \pi /2\), and the range of the angular coordinate value \(\phi _O\) of the observer point is \(|\phi _O|>\pi /2\). We assume the infinite distance limit for the source and observer, i.e., \({\mathfrak {u}}_S,{\mathfrak {u}}_O\rightarrow 0\) which corresponds to the angles \(\phi _S\rightarrow 0\) and \(\phi _O\rightarrow \pi \), respectively.

Fig. 2
figure 2

The schematic figure of lensing setup and domain of integration, which is a copy of FIG.2 from Ref. [38]

Full size image

Then, we will calculate the deflection angle of light in the weak-field limit by using the Gauss–Bonnet theorem. For the source and the observer on the equatorial plane, the deflection angle of light is expressed as [38, 64, 74]

$$\begin{aligned} \alpha _D\equiv \Psi _O-\Psi _S+\phi _{OS}. \end{aligned}$$
(17)

Here \(\Psi _S\) and \(\Psi _O\) are the included angles of the connecting line between the source and the lens, and the connecting line between the observer and the lens and the radial direction of the light rays respectively. \(\phi _{OS}\) is the longitude separation angle between source and observer (cf. Fig. 2). For convenience, we define the integral region of the quadrilateral \((O_\infty , O, S, S_\infty )\) as \({\mathcal {D}}\). According to Gauss–Bonnet theorem, the deflection angle of light is then evaluated by [38, 64]

$$\begin{aligned} \alpha _D=-\int \int _{\mathcal {D}}K_o d{\mathcal {S}}-\int ^S_O\kappa _gd\ell . \end{aligned}$$
(18)

Here \(\kappa _g\) and \(K_o\) are the geodesic curvature of light rays and the Gaussian curvature of the integral region \({\mathcal {D}}\) respectively. \(d\ell \) and \(d{\mathcal {S}}\) are the infinitesimal line element along the boundary and the area element of surface respectively. To proceed, we solve out dt from the null condition \(ds^2=0\) for a stationary axisymmetric metric as

$$\begin{aligned} dt=\sqrt{\rho _{ij}dx^idx^j}+\beta _idx^i, \end{aligned}$$
(19)

where i, j run from 1 to 3, the metric \(\rho _{ij}\) defines a three-dimensional Riemannian manifold, and \(\rho _{ij}\) and \(\beta _i\) are

$$\begin{aligned}{} & {} \rho _{ij}dx^idx^j\equiv -\frac{g_{rr}(r,\theta )}{g_{tt}(r,\theta )}dr^2-\frac{g_{\theta \theta }(r,\theta )}{g_{tt}(r,\theta )}d\theta ^2\nonumber \\{} & {} \quad +\frac{g_{t\phi }^2(r,\theta )-g_{tt}(r,\theta )g_{\phi \phi }(r,\theta )}{g_{tt}^2(r,\theta )}d\phi ^2, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \beta _idx^i\equiv -\frac{g_{t\phi }(r,\theta )}{g_{tt}(r,\theta )}d\phi . \end{aligned}$$
(21)

For the metric (2), we have \(\beta _i=0\) and \(\rho _{ij}\) is the optical metric due to the spherical symmetry. Consequently, the geodesic curvature \(\kappa _g\) is zero and the light deflection angle is [38, 75]

$$\begin{aligned} \alpha _D=-\int \int _{\mathcal {D}}K_o d{\mathcal {S}}. \end{aligned}$$
(22)

For the light propagation on the equatorial plane of the current hairy black hole, the Gaussian curvature \(K_o\) can be defined as [38, 64, 74]

$$\begin{aligned} \begin{aligned} K_o&=\frac{^{(2)}R_{r\phi r\phi }}{\text {det} \rho _{ij}^{(2)}}=\frac{1}{\sqrt{\text {det}\rho _{ij}^{(2)}}}\\&\quad \times \left[ \frac{\partial }{\partial \phi }\left( \frac{\sqrt{\text {det}\rho _{ij}^{(2)}}}{\rho _{rr}^{(2)}}{^{(2)}\Gamma _{rr}^\phi }\right) - \frac{\partial }{\partial r}\left( \frac{\sqrt{\text {det}\rho _{ij}^{(2)}}}{\rho _{rr}^{(2)}}{^{(2)}\Gamma _{r\phi }^\phi }\right) \right] , \end{aligned}\nonumber \\ \end{aligned}$$
(23)

where \(^{(2)}R_{r\phi r\phi }\), \(^{(2)}\Gamma _{rr}^\phi \) and \(\text {det}\rho _{ij}^{(2)}\) are defined by the optical metric \(\rho _{ij}\) on the equatorial plane. Therefore, the closed surface integral of Gaussian curvature is [38]

$$\begin{aligned} -\int \int _{\mathcal {D}}K_od{\mathcal {S}}=\int ^{\phi _R}_{\phi _S}\int ^{\infty }_{r_{(\phi )}}K_o\sqrt{\text {det}\rho ^{(2)}}drd\phi , \end{aligned}$$
(24)

where \(r(\phi )\) is the orbit function obtained from (16), and the area element of surface is defined as \(d{\mathcal {S}}=\sqrt{\text {det} \rho ^{(2)}}dr d\phi \). Then recalling the metric factors of (2), we can obtain the Gaussian curvature and the area element of surface

$$\begin{aligned} K_o\simeq & {} -\frac{2M}{r^3}+\frac{3M^2}{r^4}+\frac{3q^2+3s}{r^4},~~~~~d{\mathcal {S}}\nonumber \\= & {} \left( r+3M+\frac{15M^2}{2r}-\frac{3(q^2+s)}{2r}\right) drd\phi , \end{aligned}$$
(25)

such that the surface integral of Gaussian curvature is given as

$$\begin{aligned} -\int \int _{\mathcal {D}}K_od{\mathcal {S}}\simeq \frac{4M}{u}+\frac{15M^2\pi }{4u^2}-\frac{3\pi (q^2+s)}{4u^2}. \end{aligned}$$
(26)

Subsequently, the deflection angle of light ray (18) in weak field limit is evaluated as

$$\begin{aligned} \alpha \simeq \frac{4M}{u}+\frac{15M^2\pi }{4u^2}-\frac{3\pi (q^2+s)}{4u^2}+{\mathcal {O}}\left( \frac{1}{u^3}\right) . \end{aligned}$$
(27)

It is clear that when the scalar hair parameter \(s=0\), the deflection angle reproduces the result for RN black hole [76], and further setting \(q=0\) will recover the deflection angle of light for Schwarzschild black hole [38]. The effect of scalar charge on the deflection angle we can read from (27) is interesting. For the hairy black hole with \(s>0\), the light deflection angle cannot be distinguished from that happens in RN black hole with charge \(Q^2=q^2+s\), and both of them have smaller deflection angle than Schwarzschild black hole. However, for the hairy black hole with \(s<-q^2\), the deflection angle is enhanced by the comformally coupled scalar, which means that the negative scalar charge could make the light bend more, when comparing to Schwarzschild and RN black hole.

4 Strong gravitational lensing effect

In this section, we will move on to the strong lensing limit, in which the closest distance of a light ray to the lens is very close to its gravitational radius \((r_0\sim M)\). Thus, the deflection angle in this case will increase and eventually diverge as \(r_0\) decreases into the radius of photon sphere. We will first calculate the deflection angle in strong field limit, and then combine it with the lens equation to evaluate various lensing observables including the images and the time delay for the supermassive black holes.

Fig. 3
figure 3

The lens coefficients \({\bar{a}}\) and \({\bar{b}}\) in strong filed limit as functions of scalar charged for selected electric charge. Here we fix \(M=1/2\)

Full size image

4.1 Deflection angle

To handle the integral in (13) in the strong deflection limit, we will follow the method proposed in [40, 41], the main strategy of which is to expand the deflection angle near the radius of photon sphere and then give an analytical formula of the deflection angle. To proceed, we introduce the auxiliary variable \(z\equiv \frac{A(r)-A(r_0)}{1-A(r_0)}=\frac{A-A_0}{1-A_0}\), then we can rewrite the integral as

$$\begin{aligned} 2\int _{r_0}^{\infty } \frac{dr}{dr/d\phi }=\int _{0}^{1} R(z,r_0)h(z,r_0)dz, \end{aligned}$$
(28)

where

$$\begin{aligned} R(z,r_0)= & {} \frac{2(1-A_0)}{A'} \frac{\sqrt{B}\left( 2A_0Au\right) }{\sqrt{CA_0}\sqrt{4AC}}, ~~\nonumber \\ h(z,r_0)= & {} \frac{1}{\sqrt{A_0-A\frac{C_0}{C}}}. \end{aligned}$$
(29)

with \(A_0=A(r_0)\) and \(C_0=C(r_0)\). It is easy to check that \(R(z,r_0)\) is regular for all values of z and \(r_0\), while \(h(z,r_0)\) diverges as \(z \rightarrow 0\). To deal with the divergent term, we expand the expression of the square root in \(h(z,r_0)\) to the second order such that

$$\begin{aligned} h(z,r_0)\sim h_0(z,r_0)=\frac{1}{\sqrt{{\bar{m}}(r_0) z + {\bar{n}}(r_0)z^2}}, \end{aligned}$$
(30)

where \({\bar{m}}(r_0)\) and \({\bar{n}}(r_0)\) are the expansion coefficients. Subsequently, according to [40, 43], the deflection angle in the strong field limit for the light ray with impact parameter, \(u (r_0)\), can be given as

$$\begin{aligned} \alpha _D(u)=-{\bar{a}} \log \Big (\frac{u}{u_m}-1\Big )+ {\bar{b}} + {\mathcal {O}}\left( u-u_m\right) \end{aligned}$$
(31)

where \({\bar{a}}\) and \({\bar{b}}\) are the strong deflection coefficients

$$\begin{aligned} {\bar{a}} = \frac{R(0,r_m)}{2\sqrt{{{\bar{n}}}_m}}, ~~~ \text {and}~~~ {\bar{b}} = -\pi +b_D+b_R + {\bar{a}} \log \frac{{\bar{c}} r_m^2 }{u_m},\nonumber \\ \end{aligned}$$
(32)

with \({\bar{c}}\) defined as the coefficient in Taylor expansion of \(u-u_m={\bar{c}}(r_0-r_m)^2\) and

$$\begin{aligned} b_D= & {} 2{\bar{a}}\log \frac{2(1-A_m)}{A'_mr_m},~~~~~ b_R\nonumber \\= & {} \int _{0}^{1} [R(z,r_m)h(z,r_m)-R(0,r_m)h_0(z,r_m)]dz. \end{aligned}$$
(33)

It is noticed that in the above formulas the functions with the subscript m are evaluated at \(r =r_m\).

With the above preparation, we are ready to study the features of the light deflection angle in strong gravitational lensing by the hairy black hole (2), and we focus on the effect of the scalar charge. In Fig. 3 we show the strong field deflection coefficients \({\bar{a}}\) and \({\bar{b}}\), depicted as a function of the scalar hair with selected values of electric charge. We can read off the following features from the plots. (i) Both \({\bar{a}}\) and \({\bar{b}}\) (if real) are enhanced by the electric charge, which means that the coefficients have smallest values for Schwarzschild black hole. (ii) For positive scalar charge, \(s>0\), the coefficients are larger for hairy black hole with stronger s, which is expected because in this case increasing s corresponds to larger effective electric charge of RN black hole. (iii) For negative scalar charge with \(s<-q^2\), stronger scalar hair smoothly suppresses the coefficients. These features of \({\bar{a}}\) and \({\bar{b}}\) have obvious prints on the the deflection angle, \(\alpha _D\), shown in Fig. 4, from which we see that the effects of the electric and scalar charges on the \(\alpha _D\) are similar to those on the coefficients. This similarity can be easily understood from the expression (31).

Fig. 4
figure 4

The light deflection angle in strong filed limit as functions of scalar charged for selected electric charge. Here we fix \(M=1/2\) and set \(u=u_{m}+0.003\)

Full size image

4.2 Observables in strong lensing by supermassive black holes

4.2.1 Various observables in strong lensing

We assume that the observer and source are almost aligned and are located in flat spacetime and the curvature influence the light deflection angle only near the lens [77]. Then, considering that the source is behind the lens, one shall have the lens equation [39, 78]

$$\begin{aligned} \beta =\theta -\frac{D_{LS}}{D_{OS}}\Delta \alpha _{n}, \end{aligned}$$
(34)

where \(\Delta \alpha _{n}=\alpha _D-2n\pi \) is the offset of deflection angle looping over the black hole n times. Then combining the deflection angle (31) and the lensing equation (34), one can approximately obtain the position of the n-th relativistic image as [40]

$$\begin{aligned} \theta _n=\theta ^0_n+\frac{u_{m}e_n(\beta -\theta ^0_n)D_{OS}}{{\bar{a}}D_{LS}D_{OL}}, \end{aligned}$$
(35)

where \(\theta ^0_n\) is the image position corresponding to \(\alpha _D=2n\pi \) and the factor \(e_n\) is

$$\begin{aligned} e_n=\text {exp}\left( {\frac{{\bar{b}}-2n\pi }{{\bar{a}}}}\right) . \end{aligned}$$
(36)

Considering that the gravitational lensing has conservative surface brightness and the magnification is the quotient of the solid angles subtended by the n-th image and the source, the magnification of n-th relativistic image can then be evaluated as [40, 79, 80]

$$\begin{aligned} \mu _n=\left( \frac{\beta }{\theta } \; \;\frac{d\beta }{d\theta } \right) ^{-1}\Bigg |_{\theta _n ^0} = \frac{u^2_me_n(1+e_n)D_{OS}}{{\bar{a}}\beta D_{LS}D^2_{OL}}. \end{aligned}$$
(37)

The above formula implies two features of the magnification. One is that it decreases exponentially with n, so the first relativistic image could be the brightest one. The other is that the magnification is proportional to 1/\(D_{OL}^2\) which is very small and thus the relativistic images are very faint, however, the images can have large brightness if the alignment \(\beta \) is close to zero. Besides, in order to define some more interesting observables, one usually treats only the outermost image \(\theta _1\) as a single image, and packs all the remaining ones together as \(\theta _{\infty }\) which represents the asymptotic position of a set of images in the limit \(n\rightarrow \infty \). Then one can evaluate the following three observables of the relativistic images [40]:

$$\begin{aligned}{} & {} \text {the angular position of the asymptotic relativistic image }\nonumber \\{} & {} \theta _{\infty } = \frac{u_{m}}{D_{OL}}, \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \text {the angular separation between the outermost and} \nonumber \\{} & {} \text {asymptotic relativistic images }\nonumber \\{} & {} S=\theta _\infty ~\text {exp}\left( {\frac{{\bar{b}}}{{\bar{a}}}-\frac{2\pi }{{\bar{a}}}}\right) , \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \text {and the relative magnification of the outermost relativistic}\nonumber \\{} & {} \text {image}\nonumber \\{} & {} r_{\text {mag}} =\frac{\mu _1}{\sum {_{n=2}^\infty }\mu _n }\simeq \frac{5\pi }{{\bar{a}}~\text {log}(10)}, \end{aligned}$$
(40)

respectively. Consequently, with the above formulas, we can theoretically predict various observables of the strong lensing for the hairy black hole (2) once we determine the lensing coefficients \({\bar{a}}\), \({\bar{b}}\) and the critical impact parameter \(u_{m}\). Inversely, if it is successful to measure the above lensing observable from experiment, the results would be helpful for us to identify the nature of the hairy black holes or lens.

In addition, in the aspect of time measurement, if one can distinguish the time signals of the two images from the lens, then he/she can consider another important observable in strong field lensing, i.e. the time delay. Since the deflection angle for the hairy black hole could be more than \(2\pi \) and multiple images of the source could be formed, hence the travel time in different light paths corresponding to different images will be theoretically distinguishable. The time delay between i-th and j-th images could be approximated as [43]

$$\begin{aligned}{} & {} \Delta T^s_{i,j}=2 \pi (i-j)\frac{{\tilde{a}}}{{\overline{a}}}+2 \sqrt{\frac{B_{m}u_{m}}{A_{m}{\bar{c}}}} e^{\frac{{\overline{b}}}{2 {\overline{a}}}} \left( e^{-\frac{2 \pi j\mp \beta }{2 {\overline{a}}}}-e^{-\frac{2 \pi i\mp \beta }{2 {\overline{a}}}}\right) \nonumber \\{} & {} \text {for the images on same side of the lens,} \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \Delta T^o_{i,j}=\left( 2 \pi (i-j)-2 \beta \right) \frac{{\tilde{a}}}{{\overline{a}}}\nonumber \\{} & {} +2 \sqrt{\frac{B_{m}u_{m}}{A_{m}{\bar{c}}}} e^{\frac{{\overline{b}}}{2 {\overline{a}}}} \left( e^{-\frac{2 \pi j - \beta }{2 {\overline{a}}}}-e^{-\frac{2 \pi i + \beta }{2 {\overline{a}}}}\right) \nonumber \\{} & {} \text {for the images on opposite sides of the lens}, \end{aligned}$$
(42)

with \({\bar{a}}, {\bar{b}} \), \({\bar{c}}\) defined in last subsection and \({\tilde{a}}=\frac{{\tilde{R}}(0,r_m)}{2 \sqrt{\beta _m }}\),

$$\begin{aligned} {\tilde{R}}(z,r_0)=\frac{2(1-A_0)}{A'} \frac{\sqrt{C B A_0}}{\sqrt{A C}} \left( 1-\frac{1}{\sqrt{A_0} h(z,r_0)}\right) . \end{aligned}$$
(43)

In both cases, the time delay mainly comes from the first term as the contribution from the second term usually can be negligible, subsequently, the time delay between the first and second relativistic images on same side of the lens is given by [43]

$$\begin{aligned} \Delta T^s_{2,1}=2\pi \theta _{\infty }D_{OL}. \end{aligned}$$
(44)

With those formulas in hands, we can evaluate the values of various lensing observations by presupposing the astrophysical compact objects as the hairy lens.

4.2.2 Evaluating the observables by M87* and SgrA* supermassive black holes

In this subsection, we shall investigate the lensing observations by supposing the supermassive M87* and SgrA* black hole as the lens by the hairy black hole with conformally coupled scalar, and do the comparison with the Schwarzschild and RN cases. To this end, we should apply the realistic mass and distance of the lens, i.e., \(M=6.5\times 10^{9}M_{\odot }\) and \(D_{OL}=16.8\, \textrm{Mpc}\) for M87* [81] while \(M=4.0\times 10^{6}M_\odot \) and \(D_{OL}=8.35 \, \textrm{Kpc}\) for SgrA* [82].

The angular positions of the first and second relativistic images, \(\theta _{1}\) and \(\theta _{2}\) for selected parameters are computed via (34) and listed in Table 1. Here we take \(D_{LS}/D_{OS}=0.5\). For both M87* and SgrA*, when \(s=0\), the results are for RN black hole with the electric charge \(q=1/4\). We see that as the value of the scalar hair increases, both \(\theta _{1}\) and \(\theta _{2}\) decrease, but the position of source \(\beta \) slightly affects the angular positions. This means that comparing to the RN black hole, the supermassive black hole with negative conformally coupled scalar hair corresponds to larger angular positions while the ones with the positive scalar hair has smaller angular positions, which will be hold for higher order relativistic images. Moreover, with the same parameters, both the angular positions of the hairy black hole and their deviations from GR for SgrA* are larger than those for M87*, making it is easier to detect in SgrA*. Next, using (37), we calculate the relative magnification of the first and second order images and tabulated the selected results in Table  2 for M87* and Table 3 for SgrA*. From the tables, we see that the first order image for the current hairy black hole is highly magnified than the second order image, and the effect of the hair is again monotonous. It implies that the images of this hairy black hole can be brighter or darker than those of RN, depending on the sign of the scalar hair. The inverse proportional effect of \(\beta \) on the relative magnifications is also reflected in the tables. Moreover, the relative magnification of the outermost relativistic image, \(r_{mag}\), as a function of the scalar charge for selected electric charge is plotted in Fig. 5, which shows that with the increasing of both charges, \(r_{mag}\) will become smaller. This behavior is expected as it is related with the deflection coefficient \({\bar{a}}\) (shown in Fig. 3) via (40).

Table 1 The angular positions of the first and second relativistic images, \(\theta _{1}\) and \(\theta _{2}\), for supermassive black holes with the selected scalar charge s and the position of the source \(\beta \). Here we fix the electric charge \(q=1/4\). The unit is microarcseconds \((\mu as)\)
Full size table
Table 2 The relative magnification of the first and second order images, \(\mu _1\) and \(\mu _2\), for the supermassive M87* black hole with the selected s and \(\beta \). Again we fix \(q=1/4\)
Full size table
Table 3 The relative magnification of the first and second order images, \(\mu _1\) and \(\mu _2\), for the supermassive SgrA* black hole with the selected s and \(\beta \). Again we fix \(q=1/4\)
Full size table
Fig. 5
figure 5

The behaviors of relative magnification of the outermost relativistic image as a function of the scalar charge with different electric charge. The left panel is for M87* supermassive black hole while the right panel is for SgrA*

Full size image
Fig. 6
figure 6

The behaviors of lensing observables \(s-\theta _{\infty }\) (left), \(s-S\)(right). The upper panel is for M87* supermassive black hole while the bottom panel is for SgrA*

Full size image

Then the characteristic observables including the position of the innermost image \(\theta _{\infty }\) and the separation S defined in (38)-(39), as functions of the scalar charge for supermassive black holes are depicted in Fig. 6. \(\theta _{\infty }\) descends but S grows up with the increasing of the electric charge, similar as the phenomena in RN black hole [83]. In the allowed region of the scalar charge, \(\theta _{\infty }\) decreases and S increases as the value of scalar hair increases, and their deviations from those in GR are both more significant for positive scalar charge. Moreover, by comparing the upper plots and bottom plots, we find that the characteristic observables in the current hairy black hole and their deviation from GR are more profound for the SgrA* than M87*.

Finally, we evaluate the time delay between the first image and the second image for black hole with scalar hair as the M87* and SgrA* supermassive black hole, respectively. The results with selected charges are listed in Tables 4 and 5. In each table, it is clear that comparing to the Schwarzschild black hole, the electric charge shortens the time delay, and the negative scalar charge enhances it while the positive scalar charge suppresses it. In addition, the time delay and its deviation for M87* can be thousands (hundreds) minutes and even more, which is much longer than the several minutes for SgrA*. This is reasonable because M87* is much farther than SgrA* from us.

Table 4 The time delay between the first and the second images \(\Delta T_{2,1}\) (44) for the supermassive M87* black hole with selected charges
Full size table
Table 5 The time delay between the first and the second images \(\Delta T_{2,1}\) (44) for the supermassive SgrA* black hole with selected charges
Full size table

5 Closing remarks

Gravitational lensing has powerful applications in solving important astrophysical problems as well as testing GR and modified theories of gravity. In classical GR, black holes are determined by the mass, electric charge, and spin as the characterized quantities, which is known as no hair theorem for black holes. However, in a modified gravity with introduced scalar field, besides of the three characterized parameters, additional parameters encoding the matters are usually involved to describe the black holes with scalar hair. Thus, it is natural that the appearance of scalar hairs changes the horizon of a black hole and also influences its observable behavior. On the other hand, studying gravitational lensing effects of the black holes gives us a way to probe its existence and properties from potential astronomical observations. Einstein–Maxwell-conformally coupled scalar theory is an extension of Einstein-conformally coupled scalar theory in which the first counterexample to the no hair theorem using scalar field was constructed in spite of the non-regular scalar field, but the charged black hole constructed in Einstein–Maxwell-conformally coupled scalar theory admits a regular scalar field due to the introducing of the Maxwell field. Depending on the strength of the scalar charge, this charged black hole with conformally coupled scalar field can mimic the RN black hole and beyond, which makes it attract lots of interests. This paper focused on the gravitational lensing effects of the hairy black hole, and also various strong observables lensed by supposing this black hole as the supermassive black holes in M87* and SgrA*.

In the weak field limit, we mainly calculated the light deflection angle with the use of Gauss–Bonnet theorem. The deflection angle with the vanishing scalar hair parameter \(s=0\) reproduces the result for RN black hole further with the electric charge \(q=0\) recover that for Schwarzschild black hole. For \(s>0\), the light deflection angle has degeneracy between the hairy black hole and RN black hole, and both of them have smaller deflection angles than Schwarzschild black hole. For \(s<-q^2\), the scalar charge could make the light deflect more than that in Schwarzschild and RN black holes. As a conclusion, we found that comparing to Schwarzschild and RN black holes in GR, the weak deflection angle can be enhanced/suppressed by the conformally coupled scalar field.

In the strong field limit, we first calculated the light deflection angle by calculating the strong gravitational lensing coefficients of the black hole with scalar hair, all of which become larger as the values of electric and scalar charges increase. Then we evaluated the lensing observations by supposing the supermassive M87* and SgrA* black holes as the lens by the hairy black hole. The angular positions of the first and second relativistic images decrease as the value of the scalar hair increases, which suggests that comparing to the RN black hole, the supermassive black hole with negative conformally coupled scalar hair corresponds to larger angular positions while the one with the positive scalar hair has smaller angular position. The first order image for the hairy black hole is more magnified than the second order image, and for larger scalar hair, the magnification of each order image is larger but the relative magnification of the outermost relativistic image is smaller. In addition, two more characteristic observables, the position of the innermost image \(\theta _{\infty }\) and the angular separation S, for the supermassive black holes have also been calculated. In the allowed region of the scalar charge, \(\theta _{\infty }\) decreases and S increases as the value of scalar hair increases, and their deviations from those in GR are both more significant for positive scalar charge. Moreover, our results shew that all the lensing observables for the hairy black hole and their deviations from GR for SgrA* are larger than those for M87*, which may imply it is easier to detect the strong gravitational lensing in SgrA* than M87*. Finally, we examined the time delay between the first image and the second image. It was found that the electric charge and the positive scalar charge suppress the time delay, while the negative scalar charge extends it. Additionally, due to the farther distance of M87* than SgrA* from us, M87* supermassive black hole lensing corresponds much longer time delay than SgrA* one.

In conclusion, our theoretical study suggests that the light deflection angle in both weak field and strong field regimes have degeneracy between the charged black hole with positive scalar hair in Einstein–Maxwell-conformally coupled scalar theory and RN black hole in GR, but the degeneracy would be broken by the negative scalar hair. Assuming the charged hairy black hole as the candidate of supermassive M87* and SgrA* black holes, we found that various lensing observables in strong gravity regime can differentiate the theoretical predictions from Einstein–Maxwell-conformally coupled scalar theory and GR. Thus, we could expect that the strong gravitational effects could serve as a potential probe to test this theory with negative scalar hair in the near future. It is noted that the data for the supermassive black holes we used here are from the observations of the EHT Collaboration, the shadow data of which has also been employed to set constraints on the scalar charge in [28]. However, the GRAVITY Collaboration also survey the properties of central object in SgrA*, and its observations of several stars give strict bounds on the extended mass of the central black hole [84, 85]. Thus, one possible interesting direction is to mimic the time-like orbits of various stars around the supermassive SgrA* black hole supposed as the current hairy black hole, and then further use the observations from GRAVITY to constrain the scalar charge.