1 Introduction

Since the end of the last century, standard cosmology is facing a great challenge, to explain the observational evidences which indicate that our Universe is going through an accelerated phase. To accommodate this fact in cosmological context, the cosmologist are sharing two possible modifications of standard cosmology. One of the groups introduced an extra term in Einstein–Hilbert action [1] (i.e., modification of gravity theory) while the other group prefers an exotic matter within the framework of Einstein gravity. This exotic matter is known as dark energy having large negative pressure. A hypothetical scalar field (known as inflaton [2,3,4,5]) is responsible for the early accelerated era of evolution i.e. inflationary era. In analogy, the scalar fields describing the late time acceleration (known as dark energy [6,7,8,9,10,11,12]) must have large −ve pressure.

Multiscalar field cosmology has a significant role in studying hybrid inflation, double inflation, \(\alpha \)-attractors. Quintom model [13], Chiral model are two well known examples of multiscalar field cosmological models. The quintom model (where one is a quintessence field while the other one is a phantom field) is a DE model while the Chiral model leads to hyperbolic inflation [14]. For introducing a multiscalar field model, one can consider the existence of a complex scalar field [15,16,17,18,19,20,21,22] whose real part and imaginary part give the equivalent of a two scalar-field theory [23, 24]. In this paper, scalar–tensor theory is studied with a complex scalar field [25]. The scalar field in scalar tensor theory is minimally coupled to gravity and it interacts with the gravitational action integral of Einstein’s general relativity. The scalar tensor theory is usually defined in Jordan frame [26] with Mach Principle [27]. The scalar tensor theory with teleparallel gravity describes the scalar torsion theory.

Since the last century, symmetry analysis has an important role in studying the internal symmetries of the space-time, global continuous symmetries and permutation symmetries in quantum field theory [28, 29]. In particular, Noether symmetry has a great role to identify the conserved quantities associated with a physical system. Also Noether integral can simplify a system of differential equations to a great extent [30,31,32,33,34,35]. In addition, using Noether symmetry, any arbitrary function associated in the action integral of a physical system can be obtained uniquely.

This paper is an example of using Noether symmetry analysis to a cosmological model having scalar–tensor theory with a complex scalar field. Classical cosmological solutions for this model are obtained using Noether symmetry analysis. Conserved quantities associated to this system are also obtained. In the context of quantum cosmology, formulating the Wheeler DeWitt (WD) equation, the wave function of the Universe is obtained by identifying the periodic part of the solution from the quantum version of the conserved charge. The plan of the paper is as follows: Sect. 2 presents the basic equations of scalar–tensor cosmological model while in Sect. 3 Noether symmetry approach has been used for finding the analytic solutions of the present model. In Sect. 4, the formation of WD equation in the present cosmological model and its possible solution using Noether symmetry approach have been discussed and the paper ends with a brief review in Sect. 5.

In Noether’s theorem, the invariance of the functional of the calculus of variations or in mechanics the invariance of the action integral is examined under an infinitesimal transformation. In general such transformations are generated by a differential operator termed as Noether symmetry vector. However, in the present work we are confined ourselves only to point transformation. For a complete classification one may refer to [36].

2 Basic equations of scalar–tensor cosmology

The scalar tensor and the scalar torsion theories are considered in this work where the scalar field is complex in nature and minimally coupled to gravity. Considering \(\xi \) as the complex scalar field in scalar–tensor theory, the action integral takes the form [37]

$$\begin{aligned} A=\int d^4x\sqrt{-g}\left[ F(|\xi |)R+\frac{1}{2}g^{mn}\xi _{,m}\xi ^*_{,n}-V(|\xi |)\right] . \end{aligned}$$
(1)

Here R is the usual Ricci scalar which is related to the Levi-Civita connection for the metric tensor \(g_{mn}\). Also \(\xi \) is the complex scalar field and \(|\xi |\) determines its norm i.e, \(|\xi |^2=\xi \xi ^*\). \(F(|\xi |)\) denotes the coupling function between the gravitational and the scalar field and the potential function \(V(|\xi |)\) drives the dynamics.

If the coupling function \(F(|\xi |)\) takes the value \(F_0|\xi |^2\) where \(F_0\) is a constant, then one can get the Brans–Dicke theory with a complex scalar field and the action integral (1) transforms as [37]

$$\begin{aligned} A_{BD}= & {} \int d^4x\sqrt{-g}\left[ F_0|\xi |^2R +\frac{1}{2}g^{mn}\xi _{,m}\xi ^*_{,n}-V(|\xi |)\right] .\nonumber \\ \end{aligned}$$
(2)

The line element for a spatially flat FLRW universe can be written as

$$\begin{aligned} ds^2=-N^2(t)dt^2+a^2(t)\left( dx^2+dy^2+dz^2\right) , \end{aligned}$$
(3)

where a(t) is the scale factor and N(t) denotes the lapse function.

Also the Ricci scalar takes the expression as

$$\begin{aligned} R=6\left( \frac{1}{N}{\dot{H}}+2H^2\right) , \end{aligned}$$
(4)

where H denotes the usual Hubble parameter defined by \(H=\dfrac{1}{N}\dfrac{{\dot{a}}}{a}\) and the overdot indicates the differentiation with respect to the cosmic time t.

Integrating Eq. (1) by parts after using the expression of Ricci scalar (from Eq. (4)) one gets the point-like Lagrangian as

$$\begin{aligned} L(N,a,{\dot{a}},\xi ,{\dot{\xi }})= & {} \frac{1}{N}\Bigg [6F(|\xi |)a{\dot{a}}^2+6{\dot{F}}(|\xi |)a^2{\dot{a}}\nonumber \\{} & {} +\frac{1}{2}a^3 \left( {\dot{\xi }}\dot{\xi ^*}\right) \Bigg ]-a^3NV(|\xi |). \end{aligned}$$
(5)

Similarly, integrating Eq. (2) by parts and using the expression (4) one can get the point-like Lagrangian for Brans–Dicke theory as

$$\begin{aligned} L_{\text{ BD }}(N,a,{\dot{a}},\xi ,{\dot{\xi }})= & {} \frac{1}{N}\left[ 6F_0|\xi |^2a{\dot{a}}^2+6F_0(|\xi |^2)a^2{\dot{a}}\right. \nonumber \\{} & {} \left. +\frac{1}{2}a^3\left( {\dot{\xi }}\dot{\xi ^*}\right) \right] -a^3NV(|\xi |). \end{aligned}$$
(6)

Using the polar form, the complex scalar field \(\xi \) can be written as

$$\begin{aligned} \xi (t)=\phi (t)e^{i\theta (t)} \end{aligned}$$
(7)

Using Eq. (7), the Lagrangian (6) transforms as [37]

$$\begin{aligned}{} & {} L_{\text{ BD }}(N,a,{\dot{a}},\phi ,{\dot{\phi }},\theta ,{\dot{\theta }})\nonumber \\{} & {} \qquad =\frac{1}{N}\bigg [6F_0a\phi ^2{\dot{a}}^2+12F_0a^2\phi {\dot{a}}{\dot{\phi }}\nonumber \\{} & {} \qquad +\frac{1}{2}a^3\left( {\dot{\phi }}^2+\phi ^2{\dot{\theta }}^2\right) \bigg ]-a^3NV(\phi ) \end{aligned}$$
(8)

Clearly, the above Lagrangian represents a multiscalar field cosmological model where \(\phi \) is the Brans–Dicke field and the second scalar field \(\theta \) is minimally coupled to gravity and also it is minimally coupled to \(\phi \). Further, the present cosmological model with \({V(\phi )=\phi ^{-\frac{3\alpha _0+\delta _0}{\beta _0}}}\) represents the usual Brans–Dicke field in FLRW model with a cosmological constant and an uncoupled scalar field \({\theta .}\) Such cosmological model has been widely used in the literature [38, 39].

The field equations for Brans Dicke cosmological model corresponding to the Lagrangian (8) can be written as

$$\begin{aligned}{} & {} \frac{1}{N}\left( 6F_0\phi ^2H^2+12F_0\phi H{\dot{\phi }}\right. \nonumber \\{} & {} \left. \quad +\frac{1}{2}\left( {\dot{\phi }}^2+\phi ^2{\dot{\theta }}^2\right) \right) +NV(\phi )=0 \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \frac{1}{N}\left( 2F_0\phi ^2\left( 2{\dot{H}}+3H^2\right) +8F_0H\phi {\dot{\phi }} -\frac{1}{2}{\dot{\phi }}^2\right. \nonumber \\{} & {} \left. \quad +4F_0{\dot{\phi }}^2-\frac{1}{2}{\dot{\phi }}^2{\dot{\theta }}^2+4F_0\phi \ddot{\phi }\right) +NV(\phi )=0 \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{1}{N}\left( \ddot{\phi }+\phi \left( 12F_0{\dot{H}}-{\dot{\theta }}^2\right) \right. \nonumber \\{} & {} \left. \quad +3{\dot{\phi }}{\dot{H}}+12F_0\phi H^2\right) +NV_{,\phi }=0 \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \frac{1}{N}\left( \phi \ddot{\theta }+\left( 2{\dot{\phi }}+3H\phi \right) {\dot{\theta }}\right) =0 \end{aligned}$$
(12)

3 Analytic solution using Noether symmetry approach

If the Lagrangian of a physical system remains invariant with respect to the Lie derivative [40] along an appropriate vector field then the corresponding physical system is associated with some conserved quantities (Noether’s first theorem [41]).

If \(L(q^\alpha (x^i),{\dot{q}}^\alpha (x^i))\) is the point-like canonical Lagrangian then,

$$\begin{aligned} \partial _j\left( \frac{\partial L}{\partial \partial _jq^\alpha }\right) =\frac{\partial L}{\partial q^\alpha } \end{aligned}$$
(13)

are the corresponding Euler–Lagrange equations.

After contracting the Eq. (13) with \(\mu ^\alpha \left( q^\beta \right) \) (some unknown functions), one get the following result

$$\begin{aligned} \mu ^\alpha \frac{\partial L}{\partial q^\alpha }+\left( \partial _j\mu ^\alpha \right) \left( \frac{\partial L}{\partial \partial _jq^\alpha }\right) =\partial _j\left( \mu ^\alpha \frac{\partial L}{\partial \partial _jq^\alpha }\right) . \end{aligned}$$
(14)

Thus, the Lie derivative of the Lagrangian takes the form

$$\begin{aligned} {\mathcal {L}}_{\overrightarrow{X}}L= & {} \mu ^\alpha \frac{\partial L}{\partial q^\alpha }+\left( \partial _j\mu ^\alpha \right) \left( \frac{\partial L}{\partial \partial _jq^\alpha }\right) \nonumber \\= & {} \partial _j\left( \mu ^\alpha \frac{\partial L}{\partial \partial _jq^\alpha }\right) \end{aligned}$$
(15)

This vector field \(\overrightarrow{X}\) defined by [42, 43]

$$\begin{aligned} \overrightarrow{X}=\mu ^\alpha \frac{\partial }{\partial q^\alpha }+\left( \partial _j\mu ^\alpha \right) \frac{\partial }{\partial \left( \partial _jq^\alpha \right) }. \end{aligned}$$
(16)

is known as infinitesimal generator of the symmetry. Now, according to Noether’s first theorem if \({\mathcal {L}}_{\overrightarrow{X}}L=0\) then the physical system will be invariant with respect to the vector field \(\overrightarrow{X}\).

Noether symmetry approach is very much useful to identify the conserved quantities of a physical system. The symmetry condition is associated with a constant of motion for the Lagrangian having conserved phase flux along the infinitesimal generator \(\overrightarrow{X}\). Furthermore, from Eq. (15) one can conclude that associated to this symmetry criteria there is a constant of motion of the system which is known as Noether current or conserved current \(Q^i\). It is defined by [30, 44, 45]

$$\begin{aligned} Q^i=\mu ^\alpha \frac{\partial L}{\partial \left( \partial _iq^\alpha \right) }. \end{aligned}$$
(17)

Also \(Q^i\) satisfy the condition

$$\begin{aligned} \partial _iQ^i=0. \end{aligned}$$
(18)

The energy function associated to this system can be written as [33, 46]

$$\begin{aligned} E={\dot{q}}^\alpha \frac{\partial L}{\partial {\dot{q}}^\alpha }-L. \end{aligned}$$
(19)

If the Lagrangian does not contain time explicitly, then this energy function which is also known as the Hamiltonian of the system, is a constant of motion. Using these Symmetry constraints, the evolution equations of a physical system can either be solvable or simplified to a great extent.

For the present model the configuration space is a 3D space \(\left( a,\phi ,\theta \right) \). Also from the Lagrangian (8), one can see that \(\theta \) is a cyclic variable and the infinitesimal generator takes the form

$$\begin{aligned} \overrightarrow{X}={\alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial \phi }+\delta \frac{\partial }{\partial {N}}+{\dot{\alpha }}\frac{\partial }{\partial {\dot{a}}}+{\dot{\beta }}\frac{\partial }{\partial {\dot{\phi }}}+{\dot{\gamma }}\frac{\partial }{\partial {\dot{\theta }}}}. \end{aligned}$$
(20)

Here, \(\alpha =\alpha (a,\phi )\), \(\beta =\beta (a,\phi )\), \(\gamma =\gamma (\theta )\) and \({\delta =\delta (N)}\) are the coefficients of the infinitesimal generator and

$$\begin{aligned} {\dot{\alpha }}= & {} \dfrac{\partial \alpha }{\partial a}{\dot{a}}+\dfrac{\partial \alpha }{\partial \phi }{\dot{\phi }}\nonumber \\ {\dot{\beta }}= & {} \dfrac{\partial \beta }{\partial a}{\dot{a}}+\dfrac{\partial \beta }{\partial \phi }{\dot{\phi }}\nonumber \\ {\dot{\gamma }}= & {} \dfrac{\partial \gamma }{\partial \theta }{\dot{\theta }}. \end{aligned}$$
(21)

Now, imposing the Noether’s first theorem to the Lagrangian (8) one gets

$$\begin{aligned} {\mathcal {L}}_{\overrightarrow{X}}L_{\text{ BD }}=0 \end{aligned}$$
(22)

The explicit form of the Eq. (22) gives a system of partial differential equations as follows:

$$\begin{aligned}{} & {} \phi \alpha +2a\beta +2a\phi \frac{\partial \alpha }{\partial a}+2a^2\frac{\partial \beta }{\partial a}{-\frac{a\phi }{N}\delta }=0 \end{aligned}$$
(23)
$$\begin{aligned}{} & {} 3\alpha +24F_0\phi \frac{\partial \alpha }{\partial \phi }+2a\frac{\partial \beta }{\partial \phi }{-\frac{a}{N}\delta }=0 \end{aligned}$$
(24)
$$\begin{aligned}{} & {} 3\phi \alpha +2a\beta +2a\phi \frac{\partial \gamma }{\partial \theta }{-\frac{a\phi }{N}\delta }=0 \end{aligned}$$
(25)
$$\begin{aligned}{} & {} 24F_0\phi \alpha +12F_0a\beta +12F_0\phi ^2\frac{\partial \alpha }{\partial \phi }+12F_0a\phi \frac{\partial \alpha }{\partial a}\nonumber \\{} & {} \quad +a^2\frac{\partial \beta }{\partial a} +12F_0a\phi \frac{\partial \beta }{\partial \phi }{-12F_0a\phi \frac{\delta }{N}}=0 \end{aligned}$$
(26)
$$\begin{aligned}{} & {} 3\alpha V(\phi )+a\beta V'(\phi ){+aV(\phi )\frac{\delta }{N}}=0 \end{aligned}$$
(27)

For solving the above set of partial differential equations one can use the method of separation of variable i.e, \(\alpha (a,\phi )=\alpha _1(a)\alpha _2(\phi )\), \(\beta (a,\phi )=\beta _1(a)\beta _2(\phi )\), \(\gamma =\gamma (\theta )\) and \({\delta =\delta (N)}\).

Solving the Eqs. (23–26) one can get

$$\begin{aligned} \alpha= & {} \alpha _0a\nonumber \\ {\beta }= & {} {\beta _0\phi }\nonumber \\ \gamma= & {} \gamma _0\nonumber \\ {\delta }= & {} {\delta _0N} \end{aligned}$$
(28)

where \(\alpha _0\), \({\beta _0}\), \(\gamma _0\) and \({\delta _0}\) are integration constants with the relation \({3\alpha _0+2\beta _0-\delta _0=0}\).

Putting the values of \(\alpha \), \(\beta \) and \({\delta }\) from (28) into Eq. (27) one gets on integration

$$\begin{aligned} {V(\phi )=V_0\phi ^{-\frac{3\alpha _0+\delta _0}{\beta _0}}} \end{aligned}$$
(29)

where \(V_0\), an integration constant is strictly positive.

Thus imposing the symmetry condition on the Lagrangian one can find out the infinitesimal generator of Noether symmetry. Also the potential function \(V(\phi )\) is determined using the symmetry criteria rather than choosing phenomenologically.

Another important feature of Noether Symmetry is that there are some conserved quantities associated with it. There is no well defined notion of energy for a field theory in a curved space. But when there exists a time like killing vector in the system, then an associated conserved energy exists. It is well known that there is no time like killing vector in FLRW space-time. But the Lagrangian density is explicit time independent. Hence, for a point-like Lagrangian, one can define a conserved energy. So associated to this symmetry criteria there are two conserved quantities, namely, conserved charge (defined in Eq. (17)) and conserved energy (defined in Eq. (19)) which have the explicit form as follows:

$$\begin{aligned} Q= & {} \frac{1}{N}\left( 12F_0(\alpha _0+\beta _0)a^2\phi ^2{\dot{a}}\right. \nonumber \\{} & {} \left. +(12F_0\alpha _0+\beta _0)a^3\phi {\dot{\phi }}+\gamma _0a^3\phi ^2{\dot{\theta }}\right) \end{aligned}$$
(30)
$$\begin{aligned} E= & {} \frac{1}{N}\left( 6F_0a\phi ^2{\dot{a}}^2+12F_0a^2\phi {\dot{a}}{\dot{\phi }}\right. \nonumber \\{} & {} \left. +\frac{1}{2}a^3\left( {\dot{\phi }}^2+a^2{\dot{\theta }}^2\right) \right) +NV_0a^3\phi ^{-\frac{3\alpha _0+\delta _0}{\beta _0}} \end{aligned}$$
(31)

Usually Eq. (17) gives the conserved current associated to this symmetry criteria. Integrating the time component of the conserved current over the spatial volume one can get conserved charge. But all the variables in the present model are time dependent. So Eq. (30) gives the conserved charge associated to this symmetry. Moreover, this conserved charge also can be expressed as the inner product of the infinitesimal generator with Cartan one form as [47]

$$\begin{aligned} Q=i_{\overrightarrow{X}}\Theta _L \end{aligned}$$
(32)

where Cartan one form \(\Theta _L\) is defined as

$$\begin{aligned} \Theta _L=\frac{\partial L}{\partial {\dot{a}}}da+\frac{\partial L}{\partial {\dot{\phi }}}d\phi +\frac{\partial L}{\partial {\dot{\theta }}}d\theta \end{aligned}$$
(33)

and \(i_{\overrightarrow{X}}\) denotes the inner product with the vector field \(\overrightarrow{X}\).

Now, we want to make a point transformation \((a,\phi ,\theta ,N)\rightarrow (u,v,\theta ,w)\) in such a way that u becomes cyclic because cyclic variable is very much useful for solving non-linear coupled evolution equations. For the above transformation, the transformed infinitesimal generator takes the form as

$$\begin{aligned} \overrightarrow{X_T}= & {} \left( i_{\overrightarrow{X}}du\right) \frac{\partial }{\partial u}+\left( i_{\overrightarrow{X}}dv\right) \frac{\partial }{\partial v} +\left( i_{\overrightarrow{X}}d\theta \right) \frac{\partial }{\partial \theta }\nonumber \\{} & {} +\left( i_{\overrightarrow{X}}dw\right) \frac{\partial }{\partial w}+\left\{ \frac{d}{dt}\left( i_{\overrightarrow{X}}du\right) \right\} \frac{d}{d{\dot{u}}}\nonumber \\{} & {} +\left\{ \frac{d}{dt}\left( i_{\overrightarrow{X}}dv\right) \right\} \frac{d}{d{\dot{v}}}+\left\{ \frac{d}{dt}\left( i_{\overrightarrow{X}}d\theta \right) \right\} \frac{d}{d{\dot{\theta }}} \end{aligned}$$
(34)

For making u cyclic, one can restrict the transformation as

$$\begin{aligned} i_{\overrightarrow{X}}du=1,~i_{\overrightarrow{X}}dv=0~{\text{ and }~~}{i_{\overrightarrow{X}}dw=0}. \end{aligned}$$
(35)

The explicit form of Eq. (35) can be written as

$$\begin{aligned} u= & {} \frac{1}{\alpha _0}\ln a\nonumber \\ v= & {} {\ln \left( \frac{a^{\beta _0}}{\phi ^{\alpha _0}}\right) }\nonumber \\ {w}= & {} {\ln \left( \frac{a^3\phi ^2}{N}\right) } \end{aligned}$$
(36)

Equation (36) actually describes the relation between the old co-ordinates and new co-ordinates. Then using Eq. (36), the Lagrangian (8) transforms as

$$\begin{aligned} {L_T=e^w\left\{ A{\dot{u}}^2+C{\dot{v}}^2-B{\dot{u}}{\dot{v}}+\frac{1}{2}{\dot{\theta }}^2-V_0e^{-2w}e^{\frac{6v}{\beta _0}}\right\} } \end{aligned}$$
(37)

Here A, B and C are arbitrary constants.

Now, Euler–Lagrange equations for the transformed Lagrangian can be written as

$$\begin{aligned}{} & {} {2A{\dot{u}}-B{\dot{v}}=R~~(\text{ constant})}\nonumber \\{} & {} {{\dot{\theta }}=c_1~~(\text{ constant})}\nonumber \\{} & {} {e^w(-B\ddot{u}+2C\ddot{v})+\frac{6V_0}{\beta _0}e^{-w}e^{\frac{6v}{\beta _0}}=0}\nonumber \\{} & {} {e^w\left( A{\dot{u}}^2+C{\dot{v}}^2-B{\dot{u}}{\dot{v}}+\frac{1}{2}{\dot{\theta }}^2+V_0e^{-2w}e^{\frac{6v}{\beta _0}}\right) =0} \end{aligned}$$
(38)

Solving the set of equations (38) one can write the new variables as

$$\begin{aligned} {u(t)}= & {} \frac{B\beta _0}{12A}\ln \left[ \frac{c_1}{2N_1}\left\{ \tanh ^2\left( \frac{1}{2M}\sqrt{\frac{6Mc_1}{\beta _0}}(t+c_2)\right) -1\right\} \right] \nonumber \\{} & {} +\frac{Rt}{2A}+\frac{l}{2A} \end{aligned}$$
(39)
$$\begin{aligned} {v(t)}= & {} \frac{\beta _0}{6}\ln \left[ \frac{c_1}{2N_1}\left\{ \tanh ^2\left( \frac{1}{2M}\sqrt{\frac{6Mc_1}{\beta _0}}(t+c_2)\right) -1\right\} \right] \end{aligned}$$
(40)
$$\begin{aligned} {\theta (t)}= & {} c_1t+c_3 \end{aligned}$$
(41)

Here, \({c_1,~c_2,~c_3,~M,~N_1,~R,~l}\) are arbitrary constants. Also we may get \({``w''}\) by using the relation (38). The consequence of this value we may determine the Lapse function.

Using the relation (36) and the solutions (39)–(41) one can find out the solutions of the evolution equations of Brans–Dicke cosmological model for the old variables as:

$$\begin{aligned} {a(t)}= & {} {Ee^{\frac{\alpha _0Rt}{12A}}\left\{ \tanh ^2\left( \frac{1}{2M}\sqrt{\frac{6Mc_1}{\beta _0}}(t+c_2)\right) -1\right\} ^{\frac{\alpha _0\beta _0B}{12A}}} \end{aligned}$$
(42)
$$\begin{aligned} {\phi (t)}= & {} {Fe^{\frac{\beta _0Rt}{12A}}\left\{ \tanh ^2\left( \frac{1}{2M}\sqrt{\frac{6Mc_1}{\beta _0}}(t+c_2)\right) -1\right\} ^{\frac{B\beta _0^2}{12A}-\frac{\beta _0}{6\alpha _0}}} \end{aligned}$$
(43)
$$\begin{aligned} {\theta (t)}= & {} {c_1t+c_3} \end{aligned}$$
(44)

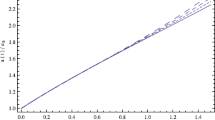
The variation of the dimensionless scale factor \(\frac{a(t)}{a_0}\) has been presented with respect to the dimensionless cosmic time \(\frac{t}{t_0}\) in Fig. 1 (here \(a_0\) is the value of the scale factor and \(H_0\) is the value of the Hubble parameter at the present cosmic time \(t_0\)). Similarly the dimensionless hubble parameter \(\frac{H}{H_0}\) and the deceleration parameter q(t) has been presented graphically with the variation of the dimensionless scale factor \(\frac{a(t)}{a_0}\) in Figs. 2 and 3. Figure 1 shows that in the present model the Universe is an expanding model with rate of expansion gradually diminishes as reflected in Fig. 2. The graphical representation of the deceleration parameter shows that initially the Universe was in an accelerating phase, subsequently there was an era of deceleration and then again at present the Universe has entered an acceleration epoch (from Fig. 3). Lastly it is to be mentioned that for proper choice of the parametric symbol the present value of the deceleration parameter for the model with the observed value \(``-0.55615''\) [48].

Fig. 1
figure 1

Graphical representation of the scale factor with respect to cosmic time t for different values of \((E,M,c_1, \beta _0, \alpha _0,B,A,R)\) parameter spaces

Full size image
Fig. 2
figure 2

Graphical representation of the dimensionless Hubble parameter with respect to scale factor a(t)

Full size image
Fig. 3
figure 3

Graphical representation of deceleration parameter q(t) with respect to scale factor a(t)

Full size image

4 Formation of WD equation and wave function of the Universe: a description of quantum cosmology

In the context of quantum cosmology, the Noether symmetry condition can be rewritten as

$$\begin{aligned} {\mathcal {L}}_{\overrightarrow{X}_H}H=0 \end{aligned}$$
(45)

Here H is the Hamiltonian of the system which is very much useful to derive the Wheeler Dewitt (WD) equation and \({\overrightarrow{X}_H}\) is defined by

$$\begin{aligned} {\overrightarrow{X}_H}={\dot{q}}\frac{\partial }{\partial q}+\ddot{q}\frac{\partial }{\partial {\dot{q}}}, \end{aligned}$$
(46)

the symmetry vector in phase space.

In minisuperspace models of quantum cosmology, symmetry analysis can appropriately interpret the wave function of the Universe as follows:

The conserved canonically conjugate momenta can be written as

$$\begin{aligned} p_l=\frac{\partial L}{\partial {\dot{q}}^l}=\Sigma _l,\quad l=1,2,\ldots ,m \end{aligned}$$
(47)

where m is the number of symmetries.

The operator version of Eq. (47) can be written as

$$\begin{aligned} -i\partial _{q^l}\vert \psi \rangle =\Sigma _l\vert \psi \rangle \end{aligned}$$
(48)

The above Eq. (48) gives an oscillatory solution which is given by

$$\begin{aligned} \vert \psi \rangle =\sum _{l=1}^{m}e^{i\Sigma _lq^l}\vert \phi (q^k)\rangle ,\qquad \qquad k<n \end{aligned}$$
(49)

Here k stands for the direction along which there is no symmetry. Thus the oscillatory part of the wave function indicates the existence of Noether symmetry.

In 3D configuration space \(\{a,\phi ,\theta \}\), the canonically conjugate momenta associated to this model can be written as

$$\begin{aligned} p_a= & {} {\frac{1}{N}(12F_0a\phi ^2{\dot{a}}+12F_0a^2\phi {\dot{\phi }})} \end{aligned}$$
(50)
$$\begin{aligned} p_{\phi }= & {} {\frac{1}{N}(12F_0a^2\phi {\dot{a}}+a^3{\dot{\phi }})} \end{aligned}$$
(51)
$$\begin{aligned} p_{\theta }= & {} {\frac{1}{N}a^3\phi ^2{\dot{\theta }}} \end{aligned}$$
(52)

Then the Hamiltonian of the system takes the form

$$\begin{aligned} H= & {} N\left[ \left( \frac{l_{11}}{a\phi ^2}-\frac{l_{22}}{a\phi }\right) p_a^2 +\left( \frac{l_{33}}{a^3}-\frac{l_{22}\phi }{a^3}\right) p_{\phi }^2\right. \nonumber \\{} & {} \left. +\left( \frac{l_{44}}{a^2}-\frac{l_{55}}{a^2\phi }\right) p_ap_{\phi } +\frac{p_{\theta }^2}{2a^3\phi ^2}+V_0a^3\phi ^{-\frac{3\alpha _0+\delta _0}{\beta _0}}\right] \nonumber \\ \end{aligned}$$
(53)

where \({l_{11},l_{22},l_{33},l_{44},l_{55}}\) are arbitrary constants. In quantum cosmology, the wave function of the Universe is a solution of the Wheeler DeWitt (WD) equation. WD equation is a second order hyperbolic partial differential equation. Actually it is the operator version of the Hamiltonian constraint. WD equation can be written as \({\hat{H}}\psi (a,\phi ,\theta )=0\), where \({\hat{H}}\) is the operator version of the Hamiltonian and \(\psi (a,\phi ,\theta )\) is the wave function of the Universe. But in course of conversion to the operator version we have encountered a problem which is known as operator ordering problem. Here \(p_a\rightarrow -i\frac{\partial }{\partial a}\), \(p_\phi \rightarrow -i\frac{\partial }{\partial \phi }\) and \(p_\theta \rightarrow -i\frac{\partial }{\partial \theta }\). Then WD equation corresponding the Hamiltonian (53) takes the form as

$$\begin{aligned}{} & {} \bigg [-\left( \frac{l_{11}}{a\phi ^2}-\frac{l_{22}}{a\phi }\right) \frac{\partial ^2}{\partial a^2}-\left( \frac{l_{33}}{a^3}-\frac{l_{22}\phi }{a^3}\right) \frac{\partial ^2}{\partial \phi ^2}\nonumber \\{} & {} \quad -\left( \frac{l_{44}}{a^2}-\frac{l_{55}}{a^2\phi }\right) \frac{\partial ^2}{\partial a\partial \phi }\nonumber \\{} & {} \quad -\frac{1}{2a^3\phi ^2}\frac{\partial ^2}{\partial \theta ^2}+V_0a^3\phi ^{-\frac{3\alpha _0+\delta _0}{\beta _0}}\bigg ]\psi (a,\phi ,\theta )=0 \end{aligned}$$
(54)

The solution of this equation can be obtained by separation of eigen functions of the WD operator as follows: [49]

$$\begin{aligned} \psi (a,\phi ,\theta )=\int W(Q)\psi (a,\phi ,\theta ,Q)dQ \end{aligned}$$
(55)

Here \(\psi \) is treated as the eigen function of the WD operator, Q is the conserved charge and W(Q) is a weight function. But we can’t get any explicit solution from the above WD equation (54) using separation of variables because the minisuperspace variables are highly coupled in WD operator. Thus one may analyze this model using the new variables \((u,v,\theta )\). So associated to the point-like Lagrangian (37), the canonically conjugate momenta can be written as [50]

$$\begin{aligned} p_u= & {} \frac{\partial {L}}{\partial {{\dot{u}}}}={e^w(2A{\dot{u}}-B{\dot{v}})}=\sigma ~~(\text{ conserved}) \end{aligned}$$
(56)
$$\begin{aligned} p_v= & {} \frac{\partial {L}}{\partial {{\dot{v}}}}={e^w\left( 2C{\dot{v}}-B{\dot{u}}\right) } \end{aligned}$$
(57)
$$\begin{aligned} p_{\theta }= & {} \frac{\partial {L}}{\partial {{\dot{\theta }}}}={e^{w}{\dot{\theta }}}=\Sigma ~~(\text{ conserved}) \end{aligned}$$
(58)

Since u and \(\theta \) are cyclic in the Lagrangian (37), \(p_u\) and \(p_\theta \) will be conserved in nature.

Then the Hamiltonian of the system takes the form as follows:

$$\begin{aligned} H={A'p_u^2+B'p_v^2+C'p_up_v+D'p_{\theta }^2+V_0e^{-w}e^{\frac{6v}{\beta _0}}} \end{aligned}$$
(59)

Here, \(A'\), \(B'\), \(C'\) and \({D'}\) are arbitrary constants.

As mentioned earlier the issue of factor ordering in the quantization scheme is nothing but the ordering of a variable and its conjugate momentum. So with the usual operator conversion: \(f{p_u\rightarrow -i\frac{\partial }{\partial {u}},~p_v\rightarrow -i\frac{\partial }{\partial {v}}}\) and \({p_{\theta }\rightarrow -i\frac{\partial }{\partial {\theta }}}\) one gets a six parameter family of Wheeler–DeWitt(WD) equation

$$\begin{aligned}{} & {} \left[ A'e^{-\frac{6v}{\beta _0}}\frac{\partial ^2}{\partial {u}^2}+B'e^{-l_1\frac{6v}{\beta _0}}\frac{\partial }{\partial {v}} e^{-l_2\frac{6v}{\beta _0}}\frac{\partial }{\partial {v}}e^{-l_3\frac{6v}{\beta _0}}\right. \\{} & {} \left. \quad +C'\frac{\partial }{\partial {u}}\left( e^{-m_1\frac{6v}{\beta _0}}\frac{\partial ^2}{\partial {v}}e^{-m_2\frac{6v}{\beta _0}}\right) +D'\frac{\partial ^2}{\partial {\theta }^2}-V_0e^{-w}\right] \\{} & {} \quad \times \psi (u,v,\theta )=0 \end{aligned}$$

with the restriction \({l_1+l_2+l_3=1}\) and \({m_1+m_2=1.}\) As there are infinite number of possibilities for the choice of the triplet \({(l_1,l_2,l_3)}\) and the dublet \({(m_1,m_2)}\) so it is possible to have infinite possible ordering. In the literature, there are some preferred choices for the above triplet and dublet as follows:

  1. (i)

    Vilenkin operator ordering: \(l_1=l_3=0,~l_2=1;~m_1=0,~m_2=1.\)

  2. (ii)

    D’Alembert operator ordering: \(l_1=2,~l_2=-1,~l_3=0;~m_1=2,~m_2=-1.\)

  3. (iii)

    no ordering: \({l_1=1,~l_2=0=l_3;~m_1=1,~m_2=0.}\)

Through the nature of the wave function depends on the choice of operator ordering, yet the semi-classical description remain unaltered [50, 51]. For simplicity we shall confine ourselves to the above 3rd choice (i.e., no ordering) and the WD equation takes the form

$$\begin{aligned}{} & {} \left[ A'\frac{\partial ^2}{\partial {u}^2}+B'\frac{\partial ^2}{\partial {v}^2}+C'\frac{\partial ^2}{\partial {u}\partial {v}}\right. \nonumber \\{} & {} \left. \quad +D'\frac{\partial ^2}{\partial {\theta }^2}-V_0e^{-w}e^{\frac{6v}{\beta _0}}\right] \psi (u,v,\theta )=0 \end{aligned}$$
(60)

For solving Eq. (60) one can use the method of separation of variable as

$$\begin{aligned} \psi (u,v,\theta )=\psi _1(u)\psi _2(v)\psi _3(\theta ) \end{aligned}$$
(61)

The operator version of (56) and (58) can be written as

$$\begin{aligned} -i\frac{\partial {\psi }}{\partial {u}}= & {} \sigma \psi \end{aligned}$$
(62)
$$\begin{aligned} -i\frac{\partial {\psi }}{\partial {\theta }}= & {} \Sigma \psi \end{aligned}$$
(63)

Solving (62) and (63) using (61) one can get

$$\begin{aligned} \psi _1(u)= & {} \sigma _0e^{i\sigma {u}} \end{aligned}$$
(64)
$$\begin{aligned} \psi _3(\theta )= & {} \Sigma _0e^{i\Sigma {\theta }} \end{aligned}$$
(65)

where \(\sigma _0\) and \(\Sigma _0\) are integration constants. Actually Eqs. (64) and (65) describes the oscillatory part of the wave function.

Putting the value of \(\psi _1(u)\) and \(\psi _3(\theta )\) in WD equation (60) one gets a second order differential equation as

$$\begin{aligned}{} & {} B'\frac{d^2\psi _2(v)}{dv^2}+i\sigma {C'}\frac{d\psi _2(v)}{dv}-V_0e^{-w}\psi _2(v)\nonumber \\{} & {} \quad -\left( A'\sigma ^2+D'\Sigma ^2\right) \psi _2(v)=0 \end{aligned}$$
(66)

The solution of Eq. (66) describes the non-oscillatory part of the wave function and is given by

$$\begin{aligned} \psi _2(v)= & {} e^{-iv\mu +\frac{A_3\pi }{2}}\left[ \Gamma (1-A_3)I_{-A_3}\left( A_4e^{\frac{3v}{\beta _0}}\right) \right. \nonumber \\{} & {} \left. +(-1)^{A_3}\Gamma (1+A_3)I_{A_3}\left( A_4e^{\frac{3v}{\beta _0}}\right) \right] \end{aligned}$$
(67)

Here, I is the modified Bessel function of first kind and gamma function is denoted by \(\Gamma \). \(A_2\), \(A_3\) and \(A_4\) are arbitrary constants. So the wave function of the Universe becomes

$$\begin{aligned} \psi (u,v,\theta )= & {} {\Sigma _0\sigma _0e^{\frac{A_3\pi }{2}}e^{i(-v\mu +\sigma {u}+\Sigma {\theta })}}\nonumber \\{} & {} \cdot \left[ \Gamma (1-A_3)I_{-A_3}\left( A_4e^{\frac{3v}{\beta _0}}\right) \right. \nonumber \\{} & {} \left. +(-1)^{A_3}\Gamma (1+A_3)I_{A_3} \left( A_4e^{\frac{3v}{\beta _0}}\right) \right] \nonumber \\ \text{ i.e., } \psi (a,\phi ,\theta )= & {} {\Sigma _0\sigma _0e^{\frac{A_3\pi }{2}}e^{i(-\mu \ln \left( \frac{a^{\beta _0}}{\phi ^{\alpha _0}}\right) +\frac{\sigma }{\alpha _0}\ln {a}+\Sigma {\theta })}}\nonumber \\{} & {} \cdot \left[ \Gamma (1-A_3)I_{_{-A_3}}\left( \frac{A_4a^3}{\phi ^{\frac{\alpha _0}{\beta _0}}}\right) \right. \nonumber \\{} & {} \left. +(-1)^{A_3}\Gamma (1+A_3)I_{_{A_3}}\left( \frac{A_4a^3}{\phi ^{\frac{\alpha _0}{\beta _0}}}\right) \right] \end{aligned}$$
(68)

It is to be noted that \(|\psi |^2\) gives the probability measure on the minisuperspace.

The Figs. 4 and 5 shows that the measure of probability depends on the sign of the constant \(A_3\). There is finite non-zero probability at zero volume for \(A_3=0\) while the probability at zero volume will be zero if \(A_3>0\) or \(A_3\) is a \(-ve\) integer. However, the probability can not be defined for negative non-integral values of \(A_3\). Thus quantum description allow the big-bang singularity for \(A_3=0\) while quantum formulation overcomes the initial singularity for \(A_3>0\) or a \(-ve\) integer.

For WKB approximation in the semi classical limit one may write

$$\begin{aligned} {\psi =\exp \left( \frac{i}{\hbar }S\right) } \end{aligned}$$
(69)

where the classical HJ function S can be expanded as power series in \({\hbar }\) as

$$\begin{aligned} {S=S_0+\hbar {S_1}+\hbar ^2S_2+\cdots } \end{aligned}$$
(70)

Thus the wave packet

$$\begin{aligned} {\psi }={\int {S(\overrightarrow{k})}\exp {\left( \frac{i}{\hbar }S_0\right) d\overrightarrow{k}}} \end{aligned}$$
(71)

Characterizes the classical solution with \({\overrightarrow{k}=(k_1,~k_2,~k_3)}\) as arbitrary parameters (i.e., separation constants). The above semiclassical limit in the WD equation gives the HJ equation (in zeroth order) for so as

$$\begin{aligned}{} & {} \left[ A'e^{-\frac{6v}{\beta _0}}\left( \frac{\partial {S_0}}{\partial {u}}\right) ^2+B'e^{-\frac{6v}{\beta _0}} \left( \frac{\partial {S_0}}{\partial {v}}\right) ^2\right. \nonumber \\{} & {} \left. \quad +C'e^{-\frac{6v}{\beta _0}}\frac{\partial ^2S_0}{\partial {u}\partial {v}}+D'e^{-\frac{6v}{\beta _0}}\left( \frac{\partial {S_0}}{\partial {\theta }}\right) ^2-V_0e^{-w}\right] =0\nonumber \\ \end{aligned}$$
(72)

For an explicit solution for \({S_0}\) the following separation form is suitable

$$\begin{aligned} {S_0(u,v,\theta )=S_u(u)+S_v(v)+S_{\theta }(\theta )} \end{aligned}$$
(73)

with

$$\begin{aligned} {S_u}= & {} {\frac{1}{4}\left( \frac{l_0}{\sqrt{A'}}u+c_0\right) ^2} \end{aligned}$$
(74)
$$\begin{aligned} {S_{\theta }}= & {} {\frac{1}{4}\left( \frac{m_0}{\sqrt{D'}}\theta +d_0\right) ^2} \end{aligned}$$
(75)

and

$$\begin{aligned} {S_v}={\beta _1^2\left[ \left( v'-k^2e^{-\frac{6v}{\beta _0}}\right) ^{\frac{3}{2}}+V_0\right] ^2} \end{aligned}$$
(76)

Here \({l_0,~m_0}\) are separation constants and \({c_0,~d_0}\) and \({V_0}\) are constants of integration.

Thus the wave packet (71) has the explicit form as

$$\begin{aligned} \psi (u,v,\theta )= & {} \int \int \int \mu (l_0,m_0)\exp \Bigg [\frac{i}{\hbar }\nonumber \\{} & {} \times S_u(u,l_0)S_v(v,l_0,m_0)S_{\theta }(\theta ,m_0)\Bigg ]dl_0dm_0\nonumber \\ \end{aligned}$$
(77)

where \({\mu }\) has the bivariate Gaussian distribution having means \({\bar{l_0}>0,~\bar{m_0}>0.}\) For \({{l_0},~{m_0}>0}\), the wave function will oscillate rapidly if \({u,\theta \rightarrow -\infty }\) i.e., \({a\rightarrow {0}.}\) Thus constructive interference is possible provided

$$\begin{aligned} {\left( \frac{\partial {S_0}}{\partial {l_0}}\Big |_{l_0={\bar{l}}_0}\right) ^2+\left( \frac{\partial {S_0}}{\partial {m_0}}\Big |_{m_0={\bar{m}}_0}\right) ^2=0.} \end{aligned}$$
(78)

This is supported by the classical solutions. Thus as usual the classical limit will be obtained when \({a\rightarrow {0}.}\)

Fig. 4
figure 4

The graphical representation of \({|\psi |^2}\) when \((\alpha _0,\beta _0,A_3,A_4)=(1.07,-1.4,.035,.01)\)

Full size image
Fig. 5
figure 5

The graphical representation of \({|\psi |^2}\) when \((\alpha _0,\beta _0,A_3,A_4)=(1.07,-1.4,0,0)\)

Full size image

In metric formulation of Einstein gravity, there are four constraints of which the super momentum constrain (a group of three) or the vector constraint vanish identically for minisuperspaces homogeneous in nature. The only non-trivial constraint equation is known as Hamiltonian constraint or scalar constraint having operator form in quantum version is nothing but the WD equation

$$\begin{aligned} {{\hat{H}}\left( {\hat{q}}_{\alpha }(t),~{\hat{p}}^{\alpha }(t)\right) \psi (q_{\alpha })=0} \end{aligned}$$
(79)

The homogeneous degrees of freedom \({q_{\alpha }(t)}\) and \({p^{\alpha }(t)}\) can be deduced from the three metric \({h_{ij}}\) and the conjugate momenta \({\pi ^{ij}}.\) Now analogous to WKB approximation if the wave function \({\psi }\) can be written as

$$\begin{aligned} {\psi =A(q)\exp \left[ \frac{i}{\hbar }B(q)\right] } \end{aligned}$$
(80)

then from the WD equation one gets the quantum modified Hamilton–Jacobi equation as

$$\begin{aligned} {\frac{1}{2}l_{\mu \nu }(q_{\alpha })\frac{\partial {S}}{\partial {q_{\mu }}}\frac{\partial {S}}{\partial {q_{\nu }}}+\phi (q_{\mu })+\xi (q_{\mu })=0} \end{aligned}$$
(81)

where \({l_{\mu \nu }}\) is the reduced supermetric to the given minisuperspace [52], \({\phi }\) is the particularization of the scalar curvature density \({\left( -h^{\frac{1}{2}}{^{(3)}R}\right) }\) of the spacelike hypersurfaces and

$$\begin{aligned} {\xi (q_{\mu })=-\frac{1}{R}l_{\mu \nu }\frac{\partial ^2R}{\partial {q_{\mu }}\partial {q_{\nu }}}} \end{aligned}$$
(82)

is termed as quantum potential.

Now, due to causal interpretation in quantum cosmology the trajectories \({q_{\alpha }(t)}\) should be real and independent of any observations. Such trajectories are identified by the corresponding HJ equation. By identifying

$$\begin{aligned} {p^{\alpha }=\frac{\partial {S}}{\partial {q_{\alpha }}}} \end{aligned}$$
(83)

with the usual momentum–velocity relation

$$\begin{aligned} {p^{\alpha }=l^{\alpha \beta }\frac{1}{N}\frac{\partial {q_{\beta }}}{\partial {t}},} \end{aligned}$$
(84)

the first order trajectories namely

$$\begin{aligned} {\frac{\partial {S}}{\partial {q_{\alpha }}}=l^{\alpha \beta }\frac{1}{N}\frac{\partial {q_{\beta }}}{\partial {t}}} \end{aligned}$$
(85)

are termed as Bohmian trajectories (i.e., quantum trajectories). One may note that these quantum trajectories are invariant under time reparametrization [52].

In the present context the Bohmian trajectories are characterized by (choosing \({\omega =0)}\)

$$\begin{aligned} {\frac{\partial {S}}{\partial {u}}=2A{\dot{u}}-B{\dot{v}},~\frac{\partial {S}}{\partial {v}}=2C{\dot{v}}-B{\dot{u}},~\frac{\partial {S}}{\partial {\theta }}={\dot{\theta }}} \end{aligned}$$
(86)

Also the quantum corrected HJ equation takes the form

$$\begin{aligned}{} & {} A'\left( \frac{\partial {S}}{\partial {u}}\right) ^2+B'\left( \frac{\partial {S}}{\partial {v}}\right) ^2 +C'\frac{\partial ^2{S_0}}{\partial {u}\partial {v}}\nonumber \\{} & {} \quad +D'\left( \frac{\partial {S}}{\partial {\theta }}\right) ^2-V_0e^{\frac{6v}{\beta _0}}+\xi =0 \end{aligned}$$
(87)

with

$$\begin{aligned} {\xi =\frac{1}{A}\left[ A'\frac{\partial ^2A}{\partial {u^2}}+B'\frac{\partial ^2A}{\partial {v^2}}+C'\frac{\partial ^2A}{\partial {u}\partial {v}}+D'\frac{\partial ^2A}{\partial {\theta ^2}}\right] } \end{aligned}$$
(88)

as the explicit form of the quantum potential.

5 A brief summary

The present work deals with a multiscalar field cosmological model where one scalar field is non-minimally coupled to both gravity and the other scalar field while the second scalar field is minimally coupled to gravity. Due to highly coupled and non-linear field equations the present model cannot be studied cosmologically in the usual way. However, here it is shown how the symmetry analysis specifically the Noether symmetry helps us to analyze the present cosmological model both classically and quantum mechanically. The identification of a cyclic variable through the symmetry vector simplifies the Lagrangian to a great extend so that the field equations become solvable. From the classical solution, the relevant cosmological parameters are plotted in Figs. 1, 2 and 3. Most specifically Fig. 1 shows that the Universe is expanding through out the evolution. The graph of the dimensionless Hubble parameter in Fig. 2 indicates that though the universe is expanding but the rate of expansion gradually diminishes with the evolution. Figure 3 indicates that the present model describes all the three phases of evolution (initially accelerating era, subsequently decelerating phase and lastly the present accelerated expansion) after the big-bang. Also with proper choice of the parameter involved the present theoretical prediction of the deceleration parameter matches the observed value. So one may say that the present model agrees with observation at least qualitatively. The Noether symmetry takes a crucial role in analyzing quantum cosmology with canonical quantization. The fundamental equation in quantum cosmology namely the WD equation is a 2nd order hyperbolic type p.d.e. The operator version of the conserved charge not only identifies the periodic part of the wave function but also helps to solve the WD equation. As a result, one may examine whether the big-bang singularity may be eliminated by quantum description or not. Here it is found that with proper choice of the parameter \(A_3\), the singularity may be avoided by quantum formulation. Therefore, Noether symmetry analysis plays a crucial role to study any cosmological model.