Unified cosmology with scalar–tensor theory of gravity

Abstract

Unlike the Noether symmetry, a metric independent general conserved current exists for non-minimally coupled scalar–tensor theory of gravity if the trace of the energy-momentum tensor vanishes. Thus, in the context of cosmology, a symmetry exists both in the early vacuum and radiation dominated era. For slow roll, symmetry is sacrificed, but at the end of early inflation, such a symmetry leads to a Friedmann-like radiation era. Late-time cosmic acceleration in the matter dominated era is realized in the absence of symmetry, in view of the same decayed and redshifted scalar field. Thus, unification of early inflation with late-time cosmic acceleration with a single scalar field may be realized.

1 Introduction

A smooth luminosity-distance versus redshift curve of the distant SN1a supernovae results in apparent dimming of the supernovae than usual [1,2,3]. These observations require the present accelerated expansion of the universe. A host of dark energy models and their alternatives, viz., modified theories of gravity, exist in the literature, which explain the above phenomena. It is important to mention that after initial cosmic inflation, the universe should enter a radiation dominated era. At this epoch, the cosmic scale factor must behave like the Friedmann–Lemaitre standard model solution ($a\propto \sqrt{t}$). Again, after decoupling of the CMBR photons and at the advent of the pure matter dominated era ($z_{\mathrm{dec}}\approx 1100$), the scale factor should behave like a Friedmann–Lemaitre standard model solution, viz. ($a \propto t^{2\over 3}$). These are required to match other observational constraints like standard big-bang-nucleosynthesis (BBN), the formation of cosmic microwave background radiation (CMBR), the epoch of matter–radiation equality ($z_{\mathrm{eq}} \approx 3200$), the observed epoch of decoupling ($z_{\mathrm{dec}} \approx 1100$) and the beginning of the matter dominated era, structure formation etc [4]. An analysis based on observational data also suggests that only recently, around redshift $z \approx 1$, the universe has entered an accelerating phase, and the present value of the state parameter is $-0.5 \le \omega _0\le -1.5$. A viable cosmological model must accommodate all these features. Although the F(R) theory of gravity and its extended versions claim to have unified early inflation with late-time cosmic acceleration, this requires scalar–tensor equivalence at both ends [5,6,7], which might be misleading, since physical equivalence has been questioned over decades [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. An attempt of unification has been made with a non-minimally coupled dark energy model for the first time by Faraoni [23]. This motivates us to explore the essence of non-minimally coupled models in further detail, in the context of such a unification.

Over the decades, Noether symmetry has been found to play important roles in explaining the cosmic evolution [24,25,26,27,28,29,30,31,32]. However, for a non-minimally coupled scalar–tensor theory of gravity, a metric independent conserved current is admissible directly from the field equations in general, which is not realized from Noether symmetry [33,34,35,36]. Such a conserved current has been found to play a very important role in generating solutions, even for a higher order theory of gravity [34,35,36]. In view of such a symmetry, here we show that the same non-minimally coupled scalar field can possibly drive the inflation at the very early stage of cosmic evolution, and although it decays (slowly) in the process, it explains a late-time cosmological behaviour with extremely good precision as well.

2 The model and the symmetry

Non-minimal coupling is unavoidable in a quantum theory of the scalar field $\phi$. Since such coupling is generated by quantum corrections, even if it is primarily absent in the classical action. Particularly, it is required by the renormalization properties of the theory in curved space-time background. Further, chaotic inflation with self interaction quartic potential ($V_0\phi ^4$) proposed by Linde [37] is disfavoured, since the spectral index of density perturbation ($n_\mathrm{s}$) and the scalar to tensor ratio (r) do not agree with the constraints, viz. $0.96< n_\mathrm{s} < 0.984$ and $r < 0.14$ implicated by recent Planck data [38]. However, long before arrival of these data, Fakir and Unruh proposed an improvement of cosmological chaotic inflation taking a non-minimal coupling into account [39]. We therefore start with the following action corresponding to a non-minimally coupled scalar–tensor theory of gravity:

$$\begin{aligned} A = \displaystyle \int \Big [f(\phi ) R - {\omega (\phi )\over \phi }\phi _{,\mu }\phi ^{,\mu } - V(\phi )- {\mathcal L_m} \Big ]\sqrt{-g} \mathrm{d}^4x\nonumber \\ \end{aligned}$$

(1)

where $\phi$ is a real scalar field having potential $V(\phi )$, $f(\phi )$ and $\omega (\phi )$ are the non-minimal coupling parameter and the Brans–Dicke coupling parameter, respectively, and ${\mathcal L_\mathrm{m}}$ stands for the matter Lagrangian density. The above action is a straightforward generalization of the one considered long ago to study late-time cosmic acceleration [40, 41]. The corresponding field equations are

$$\begin{aligned}&f(R_{\mu \nu } - {1\over 2} g_{\mu \nu } R) + \Box f g_{\mu \nu } - f_{;\mu ;\nu }\nonumber \\&\quad -{\omega \over \phi }\phi _{,\mu }\phi _{,\nu }+{1\over 2}g_{\mu \nu } \left( {\omega \over \phi }\phi _{,\mu }\phi _{,\nu }+V(\phi )\right) = {1\over 2}T_{\mu \nu } \end{aligned}$$

(2)

$$\begin{aligned} Rf' +2{\omega \over \phi }\Box \phi +\left( {\omega '\over \phi }-{\omega \over \phi ^2}\right) \phi ^{,\mu }\phi _{,\mu }-V'(\phi ) = 0. \end{aligned}$$

(3)

In the above, a prime denotes a derivative with respect to $\phi$, $\Box$ stands for the D’Alembertian operator, and $T_{\mu \nu }$ is the energy-momentum tensor for the matter action. Now the trace of Eq. (2) reads

$$\begin{aligned} R f -3\Box f-{\omega \over \phi }\phi ^{,\mu }\phi _{,\mu } -2 V +{T\over 2} = 0. \end{aligned}$$

(4)

Now multiplying Eq. (3) by f and (4) by $f'$ and taking the difference of the two, the above field equations may be cast in the form [33,34,35]

$$\begin{aligned}&\left( 3f'^2 + {2\omega f\over \phi }\right) ^{1/2} \left[ \left( 3f'^2 + {2\omega f\over \phi }\right) ^{1/2}\phi ^{;\mu }\right] _{;\mu }\nonumber \\&\quad - f^3 \left( {V\over f^2}\right) '= {f'\over 2}T \end{aligned}$$

(5)

In view of Eq. (5), a conserved current $J^\mu$ therefore exists where

$$\begin{aligned} J^\mu _{;\mu } = \left[ \left( 3f'^2 + {2\omega f\over \phi }\right) ^{1/2}\phi ^{~;\mu }\right] _{;\mu } = 0 \end{aligned}$$

(6)

for a trace-less matter field, provided (for non-vanishing potential)

$$\begin{aligned} V(\phi ) \propto f(\phi )^2. \end{aligned}$$

(7)

It is important to mention that the Noether symmetry has been applied extensively in different theories of gravity to find the forms of the potential, coupling parameters and even a form of F(R) in higher order theory of gravity. However, such application of Noether symmetry is possible and performed only in minisuperspace models. On the contrary, here the conserved current (6) is realized due to the presence of a general in-built symmetry of non-minimally coupled scalar–tensor theory of gravity. It is therefore also important to study the behaviour of such a conserved current (6) in different contexts. Here, we are particularly interested in the study of its behaviour in a cosmological context. The motivation is to check how far it can accommodate present cosmological observations. In the spatially homogeneous and isotropic Robertson–Walker line element,

$$\begin{aligned} \mathrm{d}s^2 = - \mathrm{d}t^2 + a^2(t) \left[ \frac{\mathrm{d}r^2}{1-kr^2} + r^2 (\mathrm{d}\theta ^2 + \mathrm{sin}^2 \theta \mathrm{d}\phi ^2)\right] , \end{aligned}$$

(8)

we have two independent field equations among (2) and (3) and a third in view of the conserved current (6), which now reads

$$\begin{aligned} \sqrt{\left( 3f'^2 + {2\omega f\over \phi }\right) }a^3\dot{\phi }= C_1 \end{aligned}$$

(9)

under the condition presented in Eq. (7). In the above, $C_1$ is the integration constant. It is important to note that the energy-momentum tensor of the matter field is trace-less ($T = \rho -3p = 0$) both in the vacuum dominated ($\rho = p = 0$), and in the radiation dominated ($p = {1\over 3}\rho$) era. Thus, the conserved current (9) exists in these regime under the condition (7). However, in a matter dominated era, the content of the universe behaves as pressure-less dust, $p = 0$, and so the trace of the energy-momentum tensor does not vanish. Hence, symmetry is broken in the matter dominated era. Here, $\rho$ and p are the matter energy density and the pressure of the barotropic fluid under consideration, respectively. Now, to obtain an exact solution of the field equations, we need two additional assumptions. Let us therefore make the following choice on $f(\phi )$, which automatically fixes the form of $V(\phi )$:

$$\begin{aligned} f(\phi ) = \phi ^2 \Longrightarrow V(\phi ) = V_0\phi ^4. \end{aligned}$$

(10)

Such a form of coupling parameter and the potential were chosen earlier [42] to study the cosmological dynamics of the scalar–tensor theory of gravity, since the low energy effective action of several effective quantum field theories admits such couplings and self-interacting potentials [43, 44]. Additionally, we need to fix $\omega$ too. This should be done in such a manner that it leads to interesting consequences. Under the choice

$$\begin{aligned} 3f'^2 + {2\omega f\over \phi }=\omega _0^2 \end{aligned}$$

(11)

where $\omega _0$ is a constant, the conserved current (9) reduces to

$$\begin{aligned} a^3\dot{\phi }= {C_1\over \omega _0}=C, \end{aligned}$$

(12)

C being yet another constant, and the form of $\omega (\phi )$ is fixed as

$$\begin{aligned} \omega (\phi ) = {\omega _0^2 - 12\phi ^2\over 2\phi }. \end{aligned}$$

(13)

It is important to note that the choice (11) leads to a very interesting consequence by admitting the conserved current (12). In minimally coupled theories, $a^3\dot{\phi }$ is a Noether conserved current, provided $\phi$ is cyclic, as in the case of pure Brans–Dicke theory [45]. However, here, despite the presence of tight coupling of gravity with the scalar field $\phi$ through the coupling parameter $f(\phi )$, the non-trivial Brans–Dicke parameter $\omega (\phi )$ and the quartic potential $V(\phi )$, the same conserved current has been found to exist. Thus, the symmetry under consideration cannot be found by a Noether symmetry analysis, and of course it is more general. At this stage, the functions $f(\phi )$, $V(\phi )$ and $\omega (\phi )$ have been expressed explicitly as a function of $\phi$, and the field equations therefore read

$$\begin{aligned}&\left( 2{\ddot{a}\over a}+{\dot{a}^2\over a^2}+{k\over a^2}\right) +2\left( {\ddot{\phi }\over \phi }+{\dot{\phi }^2\over \phi ^2}+2{\dot{a}\over a}{\dot{\phi }\over \phi }\right) \nonumber \\&\quad +\left( \omega _0^2-12\phi ^2\over 4\phi ^2\right) {\dot{\phi }^2\over \phi ^2}-{1\over 2}V_0\phi ^2 = -{p\over 2\phi ^2}, \end{aligned}$$

(14)

$$\begin{aligned}&6\left( {\ddot{a}\over a}+{\dot{a}^2\over a^2}+{k\over a^2}\right) -{\omega _0^2-12\phi ^2\over 2\phi ^2}\left( {\ddot{\phi }\over \phi }+3{\dot{a}\over a}{\dot{\phi }\over \phi }\right) \nonumber \\&\quad +{\omega _0^2\over 2\phi ^2} {\dot{\phi }^2\over \phi ^2} - 2 V_0\phi ^2 = 0, \end{aligned}$$

(15)

$$\begin{aligned} 3\left( {\dot{a}^2\over a^2}+{k\over a^2}\right) + 6{\dot{a}\over a}{\dot{\phi }\over \phi } - {\omega _0^2-12\phi ^2\over 4\phi ^2}{\dot{\phi }^2\over \phi ^2} - {1\over 2}V_0\phi ^2 = {\rho \over 2\phi ^2}.\nonumber \\ \end{aligned}$$

(16)

Equations (14) and (15) are the $a~\mathrm {and} ~\phi$ variation equations, respectively, while Eq. (16) is the $(^0_0)$ equation of Einstein; it is also known as the Hamilton constraint equation, when expressed in terms of phase-space variables. Note that we have kept both p and $\rho$ in the field equations above. In this connection, let us explain the motivation clearly. We have chosen the forms of the coupling parameters $f(\phi ), ~\omega (\phi )$ and the potential $V(\phi )$ in view of the general symmetry. However, the conserved current (12) exists only if $T=0$, which is realized in the vacuum dominated era ($p = 0 = \rho$) and in the radiation dominated era ($p = {1\over 3}\rho$). On the other hand, in the matter dominated era $p= 0$, $T \ne 0$ and the conserved current (12) ceases to exist. Nevertheless, the forms of the parameters and the potential remain unaltered throughout the cosmic evolution, while, in the matter dominated era, one is required to study the evolution without considering the conserved current (12). With this clarification, we now turn our attention to a study of the evolution at different epochs.

3 Three stages of cosmic evolution

3.1 Early universe

In the vacuum dominated era $p = 0= \rho$, so the action (1) may be expressed in the form

$$\begin{aligned} A = \int \Big [f(\phi ) R - {K(\phi )\over 2}\phi _{,\mu }\phi ^{,\mu } - V(\phi )\Big ]\sqrt{-g} \mathrm{d}^4x. \end{aligned}$$

(17)

Inflation with such a non-minimal coupling has been undergoing serious investigation over the decades [23, 46,47,48,49,50,51,52,53,54,55]. In the Einstein frame (under a conformal transformation $g_{\mu \nu }^E = f(\phi ) g_{\mu \nu }$), the above action may be cast in the form [56]

$$\begin{aligned} A = \int \Big [R_\mathrm{E} - {1\over 2}(\partial _E \sigma )^2 - V_\mathrm{E}(\sigma (\phi ))\Big ]\sqrt{-g_E} \mathrm{d}^4x, \end{aligned}$$

(18)

where

$$\begin{aligned} V_\mathrm{E} = {V(\phi )\over f(\phi )^2},\quad \left( {\mathrm{d}\sigma \over \mathrm{d}\phi }\right) ^{2} = {K(\phi )\over f(\phi )} + 3 {f'(\phi )^2\over f(\phi )^2}. \end{aligned}$$

(19)

In the non-minimal theory, the flat section of the potential $V(\phi )$, responsible for slow rollover, is usually distorted. Generalizing the form of non-minimal coupling by an arbitrary function $f(\phi )$, Park and Yamaguchi [57] could show that the flat potential is still obtainable when $V_E$ is asymptotically constant. Let us therefore relax the symmetry and choose the potential in the form

$$\begin{aligned} V = V_0\phi ^4 - B\phi ^2,\;\mathrm {so}\;\mathrm {that},\;V_\mathrm{E} = V_0 - {B\over \phi ^2}. \end{aligned}$$

(20)

It is important to mention that the same form of potential was used earlier to study late-time cosmic acceleration [40]. Therefore, initially when $\phi \gg \sqrt{B\over V_0}$, the second term may be neglected, so that $V_\mathrm{E} = V_0$, and the potential becomes flat, admitting slow roll. Now the slow-roll parameters are

$$\begin{aligned} \epsilon = \left( {V_\mathrm{E}'\over V_\mathrm{E}}\right) ^{2}\left( \mathrm{d}\sigma \over \mathrm{d}\phi \right) ^{-2} = {4B^2\phi ^2\over \omega _0^2(V_0\phi ^2-B)^2} \end{aligned}$$

(21)

$$\begin{aligned} \eta= & {} 2\left[ {V_\mathrm{E}''\over V_\mathrm{E}}\left( \mathrm{d}\sigma \over \mathrm{d}\phi \right) ^{-2}-{V_\mathrm{E}'\over V_E}\left( \mathrm{d}\sigma \over \mathrm{d}\phi \right) ^{-3}{\mathrm{d}^2\sigma \over \mathrm{d}\phi ^2}\right] \nonumber \\= & {} {4B\phi ^2\over \omega _0^2(V_0\phi ^2 -B)}. \end{aligned}$$

(22)

The number of e-foldings of slow-roll inflation is given by an integral over $\phi$,

$$\begin{aligned} N_\mathrm{e}(\phi ) = {1\over 2}\int _{\phi _{e}}^{\phi _{b}} {\mathrm{d}\phi \over \sqrt{\epsilon (\phi )}}{\mathrm{d}\sigma \over \mathrm{d}\phi } = {\omega _0^2\over 4 B}\left( {B\over 2\phi ^2}+V_0\ln \phi \right) _{\phi _e}^{\phi _b} \end{aligned}$$

(23)

where $\phi _\mathrm{b}$ is the initial value $\phi$ when inflation starts, and $\phi _\mathrm{e}$ is its final value, when inflation ends, i.e. at $\epsilon \approx 1$. Now, under the choice, $V_0 = 1.0\times 10^{-13}$, $\omega _0 = 3.26\times 10^{-3}$, $B = 0.79\times 10^{-21}$ and $\phi _\mathrm{b} = 1.26\times 10^{-4}$, we obtain $\epsilon = 0.0059,~ \eta = 0.059$. Therefore, the spectral index ($n_s$) and the scalar to tensor ratio (r) take the following values:

$$\begin{aligned} n_\mathrm{s} = 1 -6\epsilon + 2\eta = 0.976;\quad r = 16\epsilon = 0.094, \end{aligned}$$

(24)

which agree fairly well with recently released Planck TT + low P + lensing data, which puts even tighter constraints on these parameters viz., $n_\mathrm{s} < 0.984$ and $r < 0.14$ [38], as already mentioned. The end of inflation $\epsilon =1$, occurs at the value of the scalar $\phi _e = 0.9134 \times 10^{-4}$. This results in $N_\mathrm{e} = 33$ e-foldings, which, however, appears to be a little less than usual, viz. $50< N < 60$. But it does not matter, since the precise number of e-foldings at which the present Hubble scale $k = a_0H_0$ is equal to the Hubble scale during inflation is model dependent and the objective is to get enough e-foldings such that inflation ends, leading to a flat universe. The same above set of data with a slightly different value of $V_0 = 1.1\times 10^{-13}$ yields $\epsilon = 0.0041$, $\eta = 0.0049$, $n_s = 0.984$ and $r = 0.065$. Inflation in this case ends at $\phi _e = 0.86 \times 10^{-4}$, which gives $N_\mathrm{e} = 45$ e-folding. This appears to be even better, although $n_\mathrm{s}$ is at its limit. It might appear that $\phi _\mathrm{b}$ is small enough, but it again does not matter, since the results are consistent. However, it is to be mentioned that the value of $\phi _\mathrm{b}$ has been chosen in accordance with the values of $V_0$ and $\omega _0$, which give an excellent fit with the observed data at late-time cosmological evolution, as we shall see later.

3.2 Radiation era

The most compelling feature of non-minimally coupled scalar–tensor theory of gravity is that the scalar field $\phi$ decays via gravitational effects. This is possible because the coupling between the scalar and matter fields arises spontaneously when $\phi$ settles down to its vacuum expectation value $<\phi>$ and oscillates, ensuring reheating of the universe [58,59,60,61,62,63]. In particular, it has been shown that reheating occurs in a broad class of $f(\phi )R$ models [59]. We therefore presently just assume that it may also be possible for the present model, and we attempt to show the same in the future. Now after the graceful exit from the inflationary regime, the universe enters a radiation dominated era. But, in the pure radiation era if the scale factor $a \propto \sqrt{t}$, i.e. if the universe evolves like a standard Friedmann solution, then only standard nucleosynthesis and structure formation are realized. This is possible if somehow the second term in the potential vanishes at the end of inflation, which we demonstrate below. But, actually following the decay of the scalar field $\phi$, $V_0\phi ^4$ and $B\phi ^2$ are now of the same order of magnitude. So if one ignores the second term¹ or associates it with the first (since both are small and of the order of $10^{-29}$), then one can restore symmetry in the radiation era. In view of Eqs. (14) and (16), one can construct yet another equation, viz.,

$$\begin{aligned}&6\left( {\ddot{a}\over a}+{\dot{a}^2\over a^2}+{k\over a^2}\right) +6\left( {\ddot{\phi }\over \phi }+{\dot{\phi }^2\over \phi ^2}+3{\dot{a}\over a}{\dot{\phi }\over \phi }\right) \nonumber \\&\quad +\left( {\omega _0^2-12\phi ^2\over 2\phi ^2}\right) {\dot{\phi }^2\over \phi ^2} - 2 V_0\phi ^2 = {1\over 2\phi ^2}(\rho - 3p) = 0.\nonumber \\ \end{aligned}$$

(25)

Further, differentiating the conserved current (12) twice and doing a little algebraic manipulation, one obtains

$$\begin{aligned} 3\left( {\ddot{a}\over a}+{\dot{a}^2\over a^2} +{k\over a^2}\right) = -{\mathop {\phi }\limits ^{...}\over \dot{\phi }} + {5\over 3}{\ddot{\phi }^2\over \dot{\phi }^2}+3k\left( {\dot{\phi }\over C}\right) ^{2\over 3}. \end{aligned}$$

(26)

The last couple of Eqs. (25) and (26) may be combined to eliminate the scale factor, resulting in

$$\begin{aligned} \dot{\phi }\mathop {\phi }\limits ^{...}- {5\over 3}\ddot{\phi }^2 -{\omega _0^2\over 4}{\dot{\phi }^4\over \phi ^4} - 3k\left( {\dot{\phi }^4\over C}\right) ^{2\over 3} + V_0\phi ^2\dot{\phi }^2 = 0. \end{aligned}$$

(27)

Equation (27) admits a solution for the scalar field in the form

$$\begin{aligned} \phi = {\phi _0\over \sqrt{At -t_0}} \end{aligned}$$

(28)

where A and $\phi _0$ are constants of integration and the third constant has been absorbed. The scale factor therefore evolves as

$$\begin{aligned} a = a_0 \sqrt{At - t_0}. \end{aligned}$$

(29)

Note that, in view of the above solutions, $a(t) \phi (t) = \mathrm {const}$. The interesting fact is that, despite a tight coupling with the scalar field, the radiation era admits a Friedmann-like solution. Thus, nucleosynthesis, the era of matter–radiation equality, structure formation and the decoupling epoch remain unaffected.

3.3 Matter dominated era

As already noticed, during the matter dominated era, the matter content of the universe behaves like pressure-less dust, $p = 0$, and therefore, the trace of the energy-momentum tensor does not vanish ($T \ne 0$); as a result, the cherished symmetry fails to exist. Hence, there is no conserved current (9). It is therefore impossible to solve the set of field Eqs. (14) through (16) analytically. Nevertheless, we try for a numerical solution in the flat space, $k = 0$. First of all note that in the matter dominated era, the Bianchi identity $\dot{\rho }+ 3H(\rho +3p)$, where H is the Hubble parameter, leads to $\rho a^3 = \rho _0$, where the constant $\rho _0$ is the matter content of the universe at present. Now using the expression for the matter density and the chosen form (11) one can reduce Eq. (5) to the following form:

$$\begin{aligned} \omega _0^2 {\mathrm{d}\over \mathrm{d}t}(a^3\dot{\phi }) = -{\rho _0\over a^3} = -\rho . \end{aligned}$$

(30)

We plug the form of $\rho$ so obtained into the right hand side of the $(^0_0)$ component of Einstein’s Eq. (16) and solve the set of Eqs. (14) and (16) in a fourth-order Runge–Kutta approach. Since, after decoupling of the CMBR photons ($z = 1100$), a pure matter dominated era started, in the present approach, we set the initial values of $a, \dot{a}, \phi , \dot{\phi }$ at $z = 1100$, according to Table 1, for which we have chosen $t = 490{,}000$ years.

Table 1 The range of parametric values which fits late-time cosmological evolution

Fig. 1

Qualitative behaviour of the scale factor $a \propto \sinh ^{2\over 3}{t}$ is apparent in a versus t plot. Therefore at early epoch, the scale factor evolves as $t^{2\over 3}$, confirming early deceleration and late-time acceleration

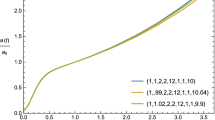
Note that we have kept $V_0$ and $\omega _0$ to be the same as required to drive inflation. Also, we remember that the scalar field at the end of inflation was $\phi _\mathrm{e} = 0.79 \times 10^{-4}$. But, at the advent of the matter dominated era, we have chosen it to be a few orders of magnitude less. This is because, at the end of inflation, the scalar field oscillates and decays via a gravitational effect and finally the rest has been redshifted according to the solution (31) almost for $10^5$ years, till the photons decoupled. Other initial data have been chosen under trial and error, so that these might lead to late-time acceleration having an excellent fit with the presently available cosmological observations. We present several plots to demonstrate the results obtained in the present scheme. The plot of scale factor versus proper time (Fig. 1) gives the following qualitative behaviour of the scale factor:

$$\begin{aligned} a \propto \sinh {t}^{2\over 3}. \end{aligned}$$

(31)

Fig. 2

Scale factor a versus redshift z plot confirms that the present value of the scale factor $a_0 = 1$

Fig. 3

The Hubble parameter H versus redshift z plot gives the present value of the Hubble parameter $H_0 = 7.15 \times 10^{-11} \mathrm {year^{-1}}$. This value corresponds to $H_0 = 69.96 ~\mathrm {Km~s^{-1} Mpc^{-1}}$

So at the early stage of the matter dominated era, the universe had undergone Friedmann-like decelerated expansion ($a \propto t^{2\over 3}$), and accelerated expansion started at the late stage of cosmic evolution. The scale factor versus redshift plot (Fig. 2) confirms that the present value of the scale factor is exactly 1. The evolution of the Hubble parameter is shown in the Hubble parameter versus redshift graph (Fig. 3), which gives its present value, $H_0 = 7.15 \times 10^{-11} \mathrm {year^{-1}}$. The age versus redshift plot (not presented) indicates that the present age of the universe is $t_0 = 13.86~ \mathrm {Gyr}$. Therefore $H_0 t_0 = 0.991$, which fits the observational data with high precision, and has been demonstrated in Fig. 4. Figure 5 represents the deceleration parameter versus redshift plot. The top inset plot demonstrates that $q = 0.5$ till $z = 200$. It then falls very slowly and at around $z = 4$, it takes the value $q \approx 0.48$. Afterwards, it falls sharply and acceleration starts at $z = 0.75$, as depicted in the inset plot below. The present value of deceleration parameter is $q = -0.59$. The present value of the effective state parameter is therefore, $w_{\mathrm{eff}0} = -0.73$. As usual, ignoring a small variation of the prefactor, we consider the CMBR temperature to fall as $a^{-1}$. If we consider the CMBR temperature at decoupling to be $T_{\mathrm{dec}} \approx 3000~\mathrm {K}$ [64], then the present value of it is $T_0 = 2.7255 ~\mathrm {K}$. In Fig. 6, we have presented the time–temperature graph. In a nutshell, our findings are as follows.

Fig. 4

The Ht versus z plot shows present value $H_0\times t_0 = 0.99$

Fig. 5

Deceleration parameter q versus redshift z plot indicates a long matter dominated era till $z \approx 4$. Accelerated expansion starts at $z = 0.75$. The present value of the deceleration parameter $q_0 = -0.59$

• 1. Age of the universe $t_0 = 13.86~ \mathrm {Gyr}$.

• 2. The universe undergoes a Friedmann-like matter dominated era for quite a long time, before entering the accelerated expansion epoch. Acceleration starts at the redshift value, $z = 0.75$, which is at about half the age of the universe, $t_{\mathrm{acceleration}} = 7.20~ \mathrm {Gyr}$.

• 3. The present value of the scale factor, $a_0 = 1.00$.

• 4. The present value of the Hubble parameter, $H_0 = 7.15\times 10^{-11}~ \mathrm {year^{-1}}$, which is equivalent to $H_0 = 69.96~\mathrm {Km~s^{-1}Mpc^{-1}}$.

• 5. $H_0\times t_0 = 0.99$.

• 6. The present value of the deceleration parameter, $q _0 = - 0.59$.

• 7. The deceleration parameter, q, remains almost constant, $q \approx 0.5$, till $z = 4.0$, confirming a long Friedmann-like matter dominated era.

• 8. The present value of the state parameter $\omega _{\mathrm{eff} _0} = - 0.73$.

• 9. The present value of $\phi$ is $9.0\times 10^{-4}$.

Further, from the relations

$$\begin{aligned} \rho _{\phi } = \phi ^2\left[ -6{\dot{a}\dot{\phi }\over a\phi }+{1\over 4}{\omega _0^2 - 12\phi ^2\over \phi ^4}\dot{\phi }^2 + {1\over 2}V_0\phi ^2\right] , \end{aligned}$$

(32)

and

$$\begin{aligned} \rho _{\mathrm{c}} = 3 {\dot{a}^2 \over a^2}\phi ^2, \end{aligned}$$

(33)

we have found $\Omega _{\phi _0} = {\rho _{\phi _0}\over \rho _{c}} = 0.71 = 71\%$, and hence $\Omega _{m0} = 0.29 = 29\%$. All these results have been found to remain unaltered within the specified range presented in Table 1.

Fig. 6

The CMBR temperature T versus redshift z plot shows presently $T_0 = 2.725$

We have also studied the behaviour of the state-finder [65] using the following relations:

$$\begin{aligned} r = q+2q^2 -{{\dot{q}}\over H};\quad s = {r-1\over 3(q-1/2)}. \end{aligned}$$

(34)

Numerical analysis shows that at present $\{r, s\} \approx \{1, 0\}$, which has been presented in Fig. 7. Thus the correspondence of the present model with the standard $\Lambda \mathrm {CDM}$ universe model has also been established.

Fig. 7

The state-finder s versus r plot represents perfect correspondence of the present model with the standard $\Lambda \mathrm {CDM}$ model

It is usually argued [23] that the self-coupling constant $V_0$ of the scalar field in the chaotic inflation potential $V = V_0 \phi ^4$ is subject to the constraint $V_0 < 10^{-12}$ coming from the observational limits on the amplitude of fluctuations in the cosmic microwave background. This constraint makes the scenario uninteresting because the energy scale predicted by particle physics is much higher. We therefore relax the constraint on $V_0$ by and large and observe that for a totally different set of initial and the parametric values of $V_0,~\omega _0$, presented in Table 2, the qualitative behaviour of cosmic evolution remains almost unaltered.

Table 2 A second range of parametric values to which late-time cosmological data fits as well

In the above, we assume that, at a redshift $z=1100$, the age of the universe was $t=510{,}000 ~\mathrm {years}$. The present values obtained in the process are enlisted now.

• 1. The age of universe $t_0 = 14.26~ \mathrm {Gyr}$.

• 2. The universe is in a Friedmann-like matter dominated era for quite a long time, before entering the accelerated expansion epoch. Acceleration starts at the redshift value, $z = 0.78$, which is at about half the age of the universe, $t_{\mathrm{acceleration}} = 7.20~ \mathrm {Gyr}$.

• 3. The present value of the scale factor $a_0 = 1.00$.

• 4. The present value of the Hubble parameter $H_0 = 7.08\times 10^{-11}~ \mathrm {year^{-1}}$, which is equivalent to $H_0 = 69.24~\mathrm {Km~s^{-1}Mpc^{-1}}$.

• 5. $H_0\times t_0 = 1.01$.

• 6. The present value of the deceleration parameter $q _0 = - 0.62$.

• 7. The deceleration parameter, q, remains almost constant, $q \approx 0.5$, till $z = 5.76$, confirming a long Friedmann-like matter dominated era.

• 8. The present value of the state parameter $\omega _{\mathrm{eff}_0} = - 0.75$.

• 9. The present value of $\phi$ $1.33\times 10^{-10}$.

• 10. Taking $T_{\mathrm{dec}}=3004.41$, at a redshift $z = 1100$, the present value of the CMBR temperature $T_0 = 2.725$.

• 11. $\{r, s\} \approx \{1,0\}$.

• 12. Here again $\Omega _{\phi _0} = 71\%$ and so $\Omega _{m0} = 29\%$.

It is needless to present the plots, since as already mentioned, the qualitative behaviour remains unaltered. Thus, it is clear that the technique works fairly well, for a wide range of parametric and initial values. However, inflation has not been tested for this second set of initial values.

4 Conclusion

The same scalar, responsible for early inflation, resulting in the inflationary parametric values $r < 0.10,~ n_\mathrm{s} \approx 0.98$, (which are on a par with recent Planck data), gives way to a Friedmann-like solution ($a\propto \sqrt{t}$) in the radiation era, a Friedmann-like long matter dominated era ($q = 0.5$ till $z \approx 4$) and late-time accelerated expansion at around redshift $z \approx 0.75$. The present value of the Hubble parameter ($H_0 \approx 69.96~\mathrm {Km~s^{-1}~Mpc^{-1}}, H_0t_0 =0.99$) is also on a par with Planck’s data. These results are definitely interesting. However, the claim that a single scalar field might possibly solve the cosmological puzzle singlehandedly can only be made after one can show that the field oscillates and reheats the universe sufficiently ($t\approx 1$ MeV), since primordial nucleosynthesis requires that the universe is close to thermal equilibrium at a temperature around 1 MeV. This research we propose to attempt in the future.

Unification has been possible since a general conserved current is associated with a non-minimally coupled scalar–tensor theory of gravity. One has to give up the conserved current at the very early universe, since the potential $V = V_0 \phi ^4$ needs to be modified to $V(\phi ) = V_0 \phi ^4 - B \phi ^2$, for admitting slow roll. When $\phi$ is large, the second term may be neglected, resulting in a flat potential. Usually, the discussion with scalar field models ends up, after giving way to the radiation era. Now, to keep all the calculations (baryogenesis, nucleosynthesis, growth of perturbation etc.) based on standard model unaltered, the scale factor in the radiation era must evolve like in the Friedmann-model ($a\propto \sqrt{t}$). This may be achieved, provided one can restore the symmetry, which requires one to neglect the second term yet again. In the present situation, the parameters and $\phi _b$ have been so chosen that neglecting the second term in the potential does not create any problem. However, as we have suggested (see footnote), this may be done, if one chooses $B = k$, where k, the curvature parameter, vanishes, making the universe flat at the end of inflation. Although we cannot present any physical argument behind such choice, still this may be considered.

The results remain almost unaltered over a wide range of initial and parametric values and it appears that one can tinker with these values to obtain even better results. However, at the end, let us mention that there is a subtle but important difference in the cosmic evolutions arising out of the two sets of data presented in Tables 1 and 2 also. According to the first set of data, $\phi |_{z=1100} = 3.17\times 10^{-8}$, and its present value is $\phi |_{0} = 9.0\times 10^{-4}$. Therefore the scalar field as well as the potential increases. In the second set, $\phi |_{z=1100} = 0.1$, and its present value is $\phi |_{0} = 1.33\times 10^{-10}$. Therefore $\phi$ falls off rapidly. As a result, in the matter dominated era only, the potential is reduced by a factor of $10^{-35}$. This might solve the cosmological constant problem as well without (possibly) requiring fine tuning, since it works within a range of parametric values.