1 Introduction

Gravity and nonlinear electrodynamics theories have generated various regular black hole (BH) solutions [1, 2]. Magnetically charged black holes (BHs) is an example of a regular and extremal system. The theory of anti-de Sitter BH (AdS-BH) that take into account the so-called Power Maxwell Invariant (PMI) [3,4,5,6] field is also included in this framework. The electromagnetic action, i.e. \((F_{\mu \nu }F^{\mu \nu })\) has a power term represented by a parameter s, this leads to Maxwell field when \(s=1\). The studies of quantum electrodynamic effect loop corrections and heterotic string theory at the low energy limit have utilized nonlinear electrodynamic theory effectively [7]. The research on BH thermodynamics is a major component of theoretical physics. One of the most solid reasons to use BHs in quantum gravity research is that their thermodynamics will allow us to understand more about the microscopic structure.

The study of asymptotically AdS-BH thermodynamics is based on Maldacena’s [8] norm/gravity connection, which connects BHs on the gravity side with temperatures on the field theory. The research carried out by Hawking and Page [9] showed that BHs could be allocated entropy, making it possible to investigate thermodynamic features like phase transitions and interaction. For instance, it was discovered to have phase transitions in \(n+1\) dimensions Reissner–Nordström–AdS (RNAdS) BH [10] or cosmological constant is a new thermodynamic variable in AdS-BH [11, 12]. Unfortunately, the complete implications of the relationship between gravitation and thermodynamics are not yet clear [13, 14]. Different methods of the geometric representation of BH thermodynamic properties have been used, such as Weinhold and Ruppeiner’s thermodynamic geometry approach [15, 16] and which is known as geometrothermodynamics (GTD) [17].

When constructing an equilibrium state space for thermodynamic processes, both of these formalizations utilize the Riemannian manifold. The Ruppeiner and Weinhold are not invariant under Legendre transformation [18], which means a thermodynamic system’s properties may be based on the thermodynamic potential. In classical thermodynamics, GTD formalism is a geometric approach that takes into account Legendre invariance and characterizes the thermodynamic system regardless of its potential. Recently, Alberto described the GTD of BHs with a nonlinear source [19]. The order of homogeneity in the basic equation is not generally considered in BH thermodynamics, because it tells us whether the thermodynamic variables are sub-extensive and supra-extensive.

Recently, Barrow [20] was motivated to examine the prospect that the surface of a BH may have a complicated structure down to arbitrarily microscopic scales as a result of quantum-gravitational phenomena. He did this after being inspired by the visualizations of the Covid-19 virus. In this fractal construction, the horizon has limited volume but an infinite/finite surface area. Since thermodynamics states that BHs are infinitely complex systems, this new entropy relation will arise from the aforementioned probable impacts on the horizon area of the quantum-gravitational spacetime foam which is called Barrow entropy. A power Maxwell invariant field will be used to examine the characteristics of BHs in this paper. The impact of thermal fluctuation and the dynamics of particles around a regular BH with a nonlinear electrodynamic source are studied by Jawad et al. [21,22,23,24].

This paper is arranged in the following manner. The detailed analysis of BHs with non-linear sources and also examine the thermodynamics of such BHs are covered in Sect. 2. We have discussed the basic formalism for the geometrothermodynamics and also present its graphical representations in Sect. 3. In the end, we have presented our conclusive remarks in Sect. 4.

2 Black holes with nonlinear sources and their thermodynamics

The Einstein-PMI gravity is described by the following action [3]

$$\begin{aligned} I=-\frac{1}{16\pi }\int _M \Big [R+\frac{n(n-1)}{l^2}+\big (F_{\mu \nu }F^{\mu \nu }\big )^s\Big ]d^{n-1}x\sqrt{-g}.\nonumber \\ \end{aligned}$$
(1)

The nonlinearity parameter is denoted by s and \(F_{\mu \nu }\) is the electromagnetic field tensor. The relationship between l and the cosmological constant is given by the formula \(\Lambda =-\frac{3}{l^2}\). The action Eq. (1) is applicable for any \(n\ge 3\) dimension, but the value of the parameter s can provide different results. For example, we get Maxwell’s theory by taking \(s=1\) in PMI theory and get \((n+1)\)-dimensions conformally invariant for \(s=\frac{n+1}{4}\) [4]. After this point, we choose random values of parameter s and evaluate its role for the thermodynamic analysis of this model. The line element of spherically symmetric are as follow

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr}{f(r)}+r^2d\Omega _{d-2}^2. \end{aligned}$$
(2)

The standard element on \(S^d\) is denoted by \(d\Omega _{d-2}^2\). The variation of action in Eq. (1) yields the BH solution for PMI source [4, 5]

$$\begin{aligned} f(r)=1+\frac{r^2}{l^2}-\frac{m}{r^{n-2}}+\frac{(2s-1)^2 \Bigg [\frac{(n-1)(2s-1)^2q^2}{(n-2)(2s-1)^2} \Bigg ]^s}{(n-1)(n-2s)r^{\frac{2(ns-3s+1)}{2s-1}}}. \end{aligned}$$
(3)

Here, the ADM mass M and scalar charge Q are linked to m and q with the connection

$$\begin{aligned} m= & {} \frac{16\pi M}{(n-1)\omega _{n-1}},\end{aligned}$$
(4)
$$\begin{aligned} q= & {} \Bigg [\frac{8\pi }{\sqrt{2}\omega _{n-1}} \Bigg ]^{\frac{1}{2s-1}}\Bigg [\frac{n-2}{n-1}\Bigg ]^{\frac{1}{2}} \frac{(2s-1)^{\frac{2s-2}{2s-1}}}{n-2s}Q^{\frac{1}{2s-1}}, \end{aligned}$$
(5)

with \(\omega _{n-1}=\frac{2\pi ^{\frac{n}{2}}}{\Gamma (\frac{n}{2})}\). Using Eqs. (2) and (3), a BH with a cauchy horizon \((r_-)\) and an event horizon \((r_+)\) can be described [14]. It is possible to determine mass M of BHs in terms of \(r_+\) using \(f(r_+)=0\), which has the largest real positive root.

$$\begin{aligned} M(r_+,Q)=\frac{(n-1)\omega _{n-1}}{16\pi }\Bigg [r^{n-2}_++\frac{r^n_+}{l^2}-f_n r_+^{\frac{2s-n}{2s-1}}Q^{\frac{2s}{2s-1}}\Bigg ],\nonumber \\ \end{aligned}$$
(6)

with

$$\begin{aligned} f_n= & {} \frac{(2 s-1)^{2-2 s} (n-1)^{s-1} (2 s-n)^{2 s-1}}{(n-2)^s}\nonumber \\{} & {} \times \Bigg [\frac{8 \pi }{\sqrt{2} s \omega _{n-1} }\Bigg ]^{\frac{2 s}{2 s-1}}\Bigg [\frac{n-2}{n-1}\Bigg ]^s\frac{(2 s-1)^{\frac{2 s (2 s-2)}{2 s-1}}}{(n-2 s)^{2 s}}. \end{aligned}$$
(7)

Barrow proposed a fractal geometry for the horizon of a BH horizon, which increases its surface area. Based on Barrow’s modifications, the modified entropy relation is expressed as [20]

$$\begin{aligned} S=\Bigg (\frac{A}{A_0}\Bigg )^{1+\frac{\Delta }{2}}, \end{aligned}$$
(8)

where BH horizon area is denoted by A, \(A_0\) is the Planck’s area, and \(\Delta \) stands for the new exponent having range \(0\le \Delta \le 1\). There are some characteristic values for \(\Delta \). We get Bekenstein–Hawking entropy when \(\Delta =0\) and for \(\Delta =1\) we have maximal distortion. In this paper, we consider \(A_0=G\) with \(G=1\) and \(A=\frac{\omega _{n-1}r_+^{n-1}}{4}\) after replacing in Eq. (8), we get the relation between area and entropy

$$\begin{aligned} S=\Bigg (\frac{\omega _{n-1}r_+^{n-1}}{4}\Bigg )^{1+\frac{\Delta }{2}}. \end{aligned}$$
(9)

After substituting Eq. (9) in (7), we obtain mass in terms of entropy S

$$\begin{aligned} M(S,Q)= & {} \frac{(n-1)\omega _{n-1}^{\frac{1}{n-1}}}{4^{\frac{n}{n-1}}\pi } \Bigg [S^{\frac{2n-4}{(n-1)(2+\Delta )}}+l^{-2}\Bigg ( \frac{4}{\omega _{n-1}}\Bigg )^{\frac{2}{n-1}}\nonumber \\{} & {} \times \, S^{\frac{2n}{(n-1)(2+\Delta )}}-\digamma Q^{\frac{2s}{2s-1}}S^{\frac{4s-2n}{(n-1)(2s-1)(2+\Delta )}}\Bigg ], \end{aligned}$$
(10)

where

$$\begin{aligned} \digamma = \Bigg [\frac{4}{\omega _{n-1}}\Bigg ]^{\frac{6s-2 n s-2}{(n-1) (2 s-1)}}f_n. \end{aligned}$$
(11)
Fig. 1
figure 1

Plot of mass M versus entropy S

Full size image

In Fig. 1, we have plot equation of mass M with respect to entropy S with fix values of \(s=3, n=4, \Delta =0.4\) and \(Q=1\). Mass function shows the increasing behavior with increasing values of S. The Eq. (10) is the basic equation of BH along with the PMI source. In the BH metric, all thermodynamic variables are connected to this equation. The first law of BH thermodynamics is satisfied by the BHs physical parameters with a PMI source [22],

$$\begin{aligned} dM=TdS+\Phi dQ+L dl. \end{aligned}$$
(12)

Here, T stands for Hawking temperature, which is connected to horizon gravity, L stands for thermodynamic variable dual to l and \(\Phi \) is electric potential. To ensure that the fundamental equation depends only on extensive variables, the variable l, which is related to the cosmological constant, must be taken into account. As a result, one can managed to develop a fundamental equation with properties that are similar to those found in classical thermodynamic systems. The existence of a thermodynamic variable necessitates the expansion of the equilibrium space by one dimension. Thus, thermodynamic Variable dual L extends the space of equilibrium by one dimension. The following formulations provide the limitations imposed by thermodynamic equilibrium

$$\begin{aligned} T=\frac{\partial M}{\partial S},\quad \Phi =\frac{\partial M}{\partial Q},\quad L=\frac{\partial M}{\partial l}. \end{aligned}$$
(13)

Taking the derivative of Eq. (10) with respect to S,  Q and l then Substituting in Eq. (13), we get the following expressions

$$\begin{aligned} T= & {} \Omega _n\Bigg [\frac{2 (n-2) S^{\frac{\Delta -n\Delta -2}{(\Delta +2) (n-1)}}}{(n-1)(\Delta +2)}+\frac{2^{\frac{n+3}{n-1}} n \Bigg (\frac{1}{\omega _{n-1} }\Bigg )^{\frac{2}{n-1}} S^{\frac{2 n}{(\Delta +2) (n-1)}-1}}{(\Delta +2) l^2 (n-1)}\nonumber \\{} & {} -\,\frac{2\digamma (2 s-n) Q^{\frac{2s}{2 s-1}} S^{\frac{2 (2s-n)}{(n-1)(\Delta +2)(2 s-1)}-1}}{(n-1)(\Delta +2)(2 s-1)} \Bigg ],\end{aligned}$$
(14)
$$\begin{aligned} \Phi= & {} -\frac{2s\Omega _n }{2s-1}\digamma Q^{\frac{1}{2s-1}}S^{\frac{2(2s-n)}{(n-1)(2s-1)(2+\Delta )}},\end{aligned}$$
(15)
$$\begin{aligned} L= & {} -\frac{2^{\frac{n+3}{n-1}}\Omega _n}{l^3}S^{\frac{2n}{(n-1)(2+\Delta )}}, \end{aligned}$$
(16)
Fig. 2
figure 2

Plot of temperature T versus entropy S

Full size image
Fig. 3
figure 3

Plot of electric potential \(\Phi \) versus entropy S

Full size image

with

$$\begin{aligned} \Omega _n=\frac{(n-1)\Omega _n^{\frac{1}{n-1}}}{4^{\frac{n}{n-1}}\pi }. \end{aligned}$$
Fig. 4
figure 4

Plot of temperature T versus entropy S

Full size image
Fig. 5
figure 5

Plot of electric potential \(\Phi \) versus entropy S

Full size image

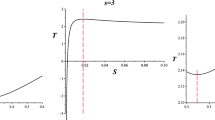
In Fig. 2, we have discussed the behavior of temperature T with respect to entropy S for fixed values of \(s=3,~n=4,\Delta =0.4,~l=1\), and \(Q=1\). The trajectory of temperature initially shows positively rising behavior and reaches its maximum point, after that it starts declining with increasing S. The red lines indicate the maximum and minimum values of temperature for different intervals of entropy S. The thermodynamic variable L and electric potential \(\Phi \) are plotted in Fig. 3 for fixed values of \(s=3,~n=4,\Delta =0.2,~l=1\), and \(Q=1\). We can see \(\Phi \) and L represent negatively decreasing behavior as increasing entropy S. The behavior of temperature for fixed values of parameters \(s=4,~n=5,\Delta =0.4,~l=1\), and \(Q=1\) is illustrated in Fig. 4. From this figure, the temperature indicates the same behavior as we discussed in Fig. 2 and red lines show the point of maximum and minimum temperature. In Fig. 5, we represent the behavior of electric potential \(\Phi \) and thermodynamic variable L for constant values of \(s=4,~n=5,\Delta =0.2,~l=1\), and \(Q=1\). We observed that \(\Phi \) and L indicate the same behavior as in Fig. 3.

The expression that is used to compute the heat capacity at specific amounts of Q and l is as follows

$$\begin{aligned} C_{Q,l}=T\Bigg (\frac{\partial S}{\partial T}\Bigg )_{Q,l}=\frac{\Bigg (\frac{\partial M}{\partial S}\Bigg )_{Q,l}}{\Bigg (\frac{\partial ^2 M}{\partial ^2 S}\Bigg )_{Q,l}}. \end{aligned}$$
(17)

Here, the subscript denotes the derivatives are computed while Q and l remain constant throughout the process. Taking the single and double derivatives of Eq. (10) with S and replacing them in Eq. (17), we obtain the equation for heat capacity by keeping Q and l constant.

Fig. 6
figure 6

Plot of heat capacity C versus entropy S

Full size image
$$\begin{aligned} C_{Q,l}= & {} (n-1) (2 s-1)(\Delta +2) \nonumber \\{} & {} \times \Big [2 \digamma l^2 (n-2 s) Q^{\frac{2s}{2 s-1}} S^{\frac{-2 (n-2 s)}{ (n-1) (2 s-1)(\Delta +2)}-1}\nonumber \\{} & {} +\,2 l^2 (n-2) (2 s-1) S^{\frac{2 (n-2)}{(\Delta +2) (n-1)}-1}+n (2 s-1)2^{\frac{n+3}{n-1}} \omega _{n-1}^{\frac{-2}{n-1}}\nonumber \\{} & {} \times \, S^{\frac{2 n-(n-1)(\Delta +2) }{ (n-1)(\Delta +2)}}\Big ]/D_1, \end{aligned}$$
(18)

where

$$\begin{aligned} D_1= & {} 2 \digamma l^2 (2 s{-}n) Q^{\frac{1}{2 s-1}+1} \{\Delta (n{-}1) (2 s{-}1){+}4 (n{-}2) s{+}2\} \nonumber \\{} & {} \times \, S^{\frac{-2 (n-2 s)}{ (n-1) (2 s-1)(\Delta +2)}-2}-2 (n-2) (2 s-1)^2 l^2(\Delta (n-1)+2)\nonumber \\{} & {} \times \, S^{\frac{2 (n-2)}{ (n-1)(\Delta +2)}-2} - n (1-2 s)^2 (\Delta (n-1)-2)2^{\frac{n+3}{n-1}} \omega _{n-1}^{-\frac{2}{n-1}} \nonumber \\{} & {} \times \, S^{\frac{2 n-(\Delta +2) (n-1)}{(n-1)(\Delta +2) }}. \end{aligned}$$
(19)

In Fig. 6, we have discussed the behavior of heat capacity \(C_{Q,l}\) versus entropy S with fixed values of \(s=3,~n=4,~\Delta =0.2,~l=1\), and \(Q=1\). A phase transition occurs when the heat capacity diverges, i.e. for \(D_1=0\), according to Ehrenfest’s [25, 26]. Consequently, equation Eq. (19) cannot be solved to determine analytically where the phase transition points exist. In order to better understand how it works, we can perform numerical analysis. Figure 6 provides an illustration of this with regard to some specific values. The heat capacity diverges at two points \(S_1\approx 0.033\), and \(S_2\approx 4.6\), which indicate phase transition points \((C\rightarrow \infty )\). The BH system is in a stable phase at \(0< S< S_1,~S> S_2\). For the range of entropy S from \(0<S<4.5\), which represents BH is in an unstable phase. The behavior of heat capacity for fixed values of \(s=4,~n=5,~\Delta =0.2,~l=1\), and \(Q=1\) is depicted in Fig. 7. The phase transitions take place at these points \(S_3\approx 0.014,~S_4\approx 16\) where the \(C_{Q,l}\) converges to infinity. At the range of \(0<S<S_3\), \(S>S_4\), the BH is in a stable phase, while the BH is in an unstable phase at \(0.015<S<16\). Figures 5 and 6 provide various examples of how the heat capacity behaves when \(s=1\) is not used. The phase transitions happen for \(s=3\) and \(s=4\) in any dimension n.

Fig. 7
figure 7

Plot of heat capacity C versus entropy S

Full size image
Fig. 8
figure 8

Plot of heat capacity C versus entropy S

Full size image

A linear source theory can be obtained by taking into account the power \(s=1\). Then, the heat capacity in Eq. (18) has the following form

$$\begin{aligned} C_{Q,l}= & {} (n-1)(\Delta +2) S \nonumber \\{} & {} \times \Bigg [2^{\frac{2 n+2}{n-1}}\pi ^2 l^2 Q^2 \omega _{n-1} ^{-\frac{2}{n-1}} S^{\frac{4-2 n}{(n-1)(\Delta +2) }}+l^2 (n-1) (4-2 n)\nonumber \\{} & {} \times \, S^{\frac{2 n-4}{(n-1)(\Delta +2) }}-n(n-1) 2^{\frac{n+3}{n-1}} \omega _{n-1} ^{-\frac{2}{n-1}} S^{\frac{2 n}{ (n-1)(\Delta +2)}}\Bigg ]/\nonumber \\{} & {} \times \,\Bigg [2 l^2 (n-1)(n-2) (\Delta n-\Delta +2) S^{\frac{2 n-4}{(n-1)(\Delta +2) }}\nonumber \\{} & {} +n (\Delta n-\Delta -2) (n-1)2^{\frac{n+3}{n-1}} \omega _{n-1} ^{-\frac{2}{n-1}} S^{\frac{2 n}{(n-1)(\Delta +2)}}\nonumber \\{} & {} \, -(3 \Delta +\Delta n-6)\pi ^2 Q^2l^22^{\frac{2 (n+1)}{n-1}}\times \omega _{n-1} ^{-\frac{2}{n-1}}S^{-\frac{2 (n-2)}{ (n-1)(\Delta +2)}}\Bigg ].\nonumber \\ \end{aligned}$$
(20)

In this case, when the following equation are satisfied then the heat capacity divergence point exist,

$$\begin{aligned}{} & {} 2 l^2 (n-1)(n-2) (\Delta n-\Delta +2) S^{\frac{2 n-4}{(n-1)(\Delta +2) }}\nonumber \\{} & {} \quad +\,n (\Delta n-\Delta -2) (n-1)2^{\frac{n+3}{n-1}} \omega _{n-1} ^{-\frac{2}{n-1}}S^{\frac{2 n}{(n-1)(\Delta +2)}}\nonumber \\{} & {} \quad -\,(3 \Delta +\Delta n-6)\pi ^2 Q^2l^22^{\frac{2 (n+1)}{n-1}} \omega _{n-1} ^{-\frac{2}{n-1}}S^{-\frac{2 (n-2)}{ (n-1)(\Delta +2)}}=0,\nonumber \\ \end{aligned}$$
(21)

which indicates phase transitions. Again, equation Eq. (21) cannot be solved analytically to determine phase transitions. There are no phase transitions when \(l=Q=1\) is used in numerical analysis. In Fig. 8, this condition is depicted. In the case of \(l=2,~Q=4\) and \(\Delta =0.4\), again phase transition does not exist. This fact is illustrated in Fig. 9. These results indicate how l and Q affect the presence of phase transitions. To study this fact, consider \(n=3\) and Eq. (20) has the form

$$\begin{aligned} C_{Q,l}=-\frac{(\Delta +2) S \Big [l^2 \Big (\omega _{n-1} S^{\frac{2}{\Delta +2}}-4 \pi ^2 Q^2\Big )+12 S^{\frac{4}{\Delta +2}}\Big ]}{l^2 \Big [\!(\Delta {+}1) \omega _{n-1} S^{\frac{2}{\Delta +2}}{-}4 \pi ^2 (\Delta {+}3) Q^2\!\Big ]{+}12 (\Delta {-}1) S^{\frac{4}{\Delta +2}}}.\nonumber \\ \end{aligned}$$
(22)

As we can see, there is a phase transition of the second order taking place at the points where

$$\begin{aligned}{} & {} l^2 \Big [(\Delta +1) \omega _{n-1} S^{\frac{2}{\Delta +2}}-4 \pi ^2 (\Delta +3) Q^2\Big ]\nonumber \\{} & {} \qquad +12 (\Delta -1) S^{\frac{4}{\Delta +2}}=0. \end{aligned}$$
(23)

This is similar to the situation that occurs with AdS-Bhs, in which transitions phase were discovered [26].

3 Geometrothermodynamics formalism

A Riemannian contact manifold \((\tau ,\Theta , G)\) with \((2n + 1)\)-dimensions is the basis of the GTD approach. Where differential manifold denoted by \(\tau \), \(\Theta \wedge (d\Theta )^n\ne 0\) is the contact form of \(\Theta \) and G stands for Riemannian metric. Darboux theorem states that, if the coordinates \(Z^A=\{\Phi ,E^a,I^a\}\) are introduced in \(\tau \) with \(a=1,\ldots n\) and \(A=0,\ldots ,2n\), then the contact form \(\Theta \) may be expressed as \(\Theta =d\Phi -\delta _{ab}I^adE^b\). However, The Legendre invariance is the most important part of GTD, which is examined using the metric G and necessitated by its invariance against Legendre transformations [26]. The invariance of three specific metrics has been established by Legendre [27]. The thermodynamics of BHs can be described using one of these equations

$$\begin{aligned} G=\Theta ^2+(\delta _{ab}E^aI^b)(\eta _{cd}dE^cdI^d). \end{aligned}$$
(24)

Here \(\eta _{ab}=\text {diag}(-1,1,\ldots ,1)\) and \(\delta _{ab}=\text {diag}(1,\ldots ,1)\). The smooth embedding map \(\varphi :\varepsilon \rightarrow \tau \) is related to pullback \(\varphi ^*(G)= g\) and meets the constraint \(\varphi ^*(\Theta )=0\). In the n-dimensional submanifold of \(\varepsilon \subset \tau \), a Legendre invariant metric g is generated. There is a basic equation \(\Phi (E^a)\) that may be found by constructing the embedding of \(\varphi :{E^a}\rightarrow \{\Phi (E^a),E^a,I^a(E^a)\}\) with \(E^a\) as the coordinate set, the resulting metric becomes

$$\begin{aligned} g^{I/II}=\beta _\Phi \Phi \eta _a^b\Phi _{,bc}dE^adE^c, \end{aligned}$$
(25)

where \(\Phi _{,a}=\frac{\partial \Phi }{\partial E^a},~\beta _\Phi \) is a constant and for generalized homogeneous function, we used Euler identity in the form \(\beta _aE^a\Phi _{,a}=\beta _a\Phi \) [27]. Applying the above formalism to the scenario of BHs with PMI sources is the next step. It is important to remember that the fundamental equation Eq. (10) is a generic homogeneous function of degree 1 that does not change the physical characteristics of a thermodynamic system [27, 28]. We are fascinated about the way the curvature behaves as it is indication of phase transitions.

Take a look at the metric \(g^{I}\) for the equilibrium space

$$\begin{aligned} g^{I/II}=\beta _\Phi \Phi \eta _a^b\Phi _{,bc}dE^adE^c,~\eta _a^b=(1,1,1) \end{aligned}$$
(26)

where we have put \(\beta _\Phi =1\) for simplification without sacrificing any generality.

The 3-dimensional thermodynamic metric from Eq. (25) reduces to

$$\begin{aligned} g^{I}= & {} g=\Theta _1\nonumber \\{} & {} \times \Bigg \{\Bigg [\frac{2 \digamma (2 s{-}n) Q^{\frac{1}{2 s-1}+1} \{\Delta (n{-}1) (2 s{-}1){+}4 (n{-}2) s{+}2\}}{(\Delta +2)^2 (n-1)^2 (1-2 s)^2S^{\frac{2 (n-2 s)}{ (n-1) (2 s-1)(\Delta +2)}+2}}\nonumber \\{} & {} -\,\frac{2^{\frac{n+3}{n-1}} n (\Delta (n-1)-2) \Bigg (\frac{1}{\omega _{n-1}}\Bigg ){}^{\frac{2}{n-1}}}{(\Delta +2)^2 l^2 (n-1)^2S^{2-\frac{2 n}{(n-1)(\Delta +2)}}}\nonumber \\{} & {} -\,\frac{2 (n-2) (\Delta n-\Delta +2)}{(\Delta +2)^2 (n-1)^2S^{2-\frac{2 (n-2)}{(n-1)(\Delta +2)}}}\Bigg ]dS^2\nonumber \\{} & {} -\,\frac{2 s\digamma Q^{\frac{2-2s}{2 s-1}}}{(1-2 s)^2S^{\frac{2 (n-2 s)}{ (n-1) (2 s-1)(\Delta +2)}}}dQ^2\nonumber \\{} & {} +\,\frac{3\Bigg (\frac{1}{\omega _{n-1}}\Bigg ){}^{\frac{2}{n-1}}2^{\frac{n+3}{n-1}} S^{\frac{2 n}{(\Delta +2) (n-1)}}}{l^4}dl^2\Bigg \}, \end{aligned}$$
(27)

where

$$\begin{aligned} \Theta _1=\frac{M(n-1)\omega _{n-1}^{\frac{1}{n-1}}}{4^{\frac{n}{n-1}}\pi }. \end{aligned}$$

The curvature scalar related to Eq. (27), as follows

$$\begin{aligned} R=\frac{\pi ^7 l^8(1-2 s)^8 (\Delta +2)^4 2^{\frac{8 n-2}{n-1}} Q^{\frac{4s-4}{2 s-1}} S^{\frac{-8 (n (s-1)+s)}{ (n-1) (2 s-1)(\Delta +2)}}N(S,Q,l)}{9 (n-1)^3 s^2\omega _{n-1}^{\frac{3}{n-1}}\digamma ^2D_2^3 D_1^2},\nonumber \\ \end{aligned}$$
(28)

where

$$\begin{aligned} D_1= & {} 2 l^2\digamma (2 s-n) Q^{\frac{2s}{2 s-1}} \{\Delta (n-1) (2 s-1)+4 (n-2) s+2\} \nonumber \\{} & {} \times S^{\frac{2 (2 s-n)}{ (n-1) (2 s-1)(\Delta +2)}-2}-2 l^2 (n-2) (\Delta n-\Delta +2)\nonumber \\{} & {} \times S^{\frac{2 (n-2)}{ (n-1)(\Delta +2)}-2} (2 s-1)^2- n (2 s-1)^2 (\Delta n-\Delta -2)2^{\frac{n+3}{n-1}}\nonumber \\{} & {} \times \omega _{n-1}^{\frac{-2}{n-1}} S^{\frac{2 n}{(n-1)(\Delta +2) }-2},\nonumber \\ D_2= & {} -\digamma Q^{\frac{2 s}{2 s-1}} S^{\frac{2 (2 s-n)}{ (n-1) (2 s-1)(\Delta +2)}}+S^{\frac{2 (n-2)}{ (n-1)(\Delta +2)}}\nonumber \\{} & {} -\frac{4^{\frac{2}{n-1}} \omega _{n-1}^{\frac{-2}{n-1}} S^{\frac{2 n}{(n-1)(\Delta +2)}}}{l^2}. \end{aligned}$$
(29)

The \(N(S, Q, l)\ne 0\) is a function that cannot be compactly described when the denominator disappears. In this situation, there are two curvature singularities. According to Eq. (10), one of these occurs when \(D_2=0\), which is equivalent to \(M=0\). Since there is no BH present because this singularity is non-physical. According to Eq. (19), one can find a second singularity at the points where \(D_1=0\). It corresponds with \(C_{Q,l}\rightarrow \infty \), which determines phase transition critical points. This finding is invariant since its based on scalar analysis, not on coordinates. Figures 10 and  11 demonstrate how the curvature scalar behaves numerically for various values of n, l and Q. The curvature singularities can be found at second-order phase transition locations, when denominators of the curvature scalar and heat capacity overlap, according to GTD [29, 30].

Now, we discuss the behavior of scalar curvature for various values of parameters n,  l,  Q, and \(\Delta \) with fix value of electromagnetic parameter \(s=1\) is illustrated in Figs. 12 and 13. From Fig. 12, we observed that there exists a singularity, for \(l=Q=1\) and \(\Delta =0.4\) with \(n=4,~n=5\). But we can see in Fig. 13 singularities are not present for \(l=Q=5\) and \(\Delta =0.6\) with \(n=4,~n=5\). Therefore, for\(l=Q=5\) GTD accurately propagates this instance as compared to \(l=Q=1\). In GTD, a nonzero curvature measures thermodynamic interaction. Our thermodynamic curvature Eq. (28) was nonzero, indicating thermodynamic interaction for this BH structure with a nonlinear source. Physically, this effect can be attributed to the BH microstructure’s connection between nearby states explains in this phenomenon by Wei et al. [31]. Another way to differentiate between attracting and repelling interactions is to examine the symmetry of the curvature [32]. In our scenario, the curvature equation cannot be compactly stated to identify its sign. Figures 10 and 11 indicate that there exists negative curvature region based on the parameter values.

Fig. 9
figure 9

Plot of heat capacity C versus entropy S

Full size image
Fig. 10
figure 10

Plot of curvature scalar R versus entropy S

Full size image
Fig. 11
figure 11

Plot of curvature scalar R versus entropy S

Full size image
Fig. 12
figure 12

Plot of curvature scalar R versus entropy S

Full size image
Fig. 13
figure 13

Plot of curvature scalar R versus entropy S

Full size image

Now, the line element for metric \(g^{II}\) obtained by doing some manipulation in Eq. (28) is given as [33]

$$\begin{aligned} g^{II}= & {} \Theta _1\Bigg \{\Bigg [\frac{2 \digamma (2 s-n) Q^{\frac{1}{2 s-1}+1} \{\Delta (n-1) (2 s-1)+4 (n-2) s+2\}}{(\Delta +2)^2 (n-1)^2 (1-2 s)^2S^{\frac{2 (n-2 s)}{ (n-1) (2 s-1)(\Delta +2)}+2}} -\,\frac{2^{\frac{n+3}{n-1}} n (\Delta (n-1)-2) \Bigg (\frac{1}{\omega _{n-1}}\Bigg ){}^{\frac{2}{n-1}}}{(\Delta +2)^2 l^2 (n-1)^2S^{2-\frac{2 n}{(n-1)(\Delta +2)}}}\nonumber \\{} & {} -\,\frac{2 (n-2) (\Delta n-\Delta +2)}{(\Delta +2)^2 (n-1)^2S^{2-\frac{2 (n-2)}{(n-1)(\Delta +2)}}}\Bigg ]dS^2 -\,\frac{2 \digamma s (4 s-2 n) Q^{\frac{2 s}{2 s-1}-1} S^{\frac{4 s-2 n}{(\Delta +2) (n-1) (2 s-1)}-1}}{(\Delta +2) (n-1) (2 s-1)^2}dSdQ\nonumber \\{} & {} -\,\frac{2^{\frac{4}{n-1}+2} n (\frac{1}{\omega })^{\frac{2}{n-1}} S^{\frac{2 n}{(\Delta +2) (n-1)}-1}}{(\Delta +2) l^3 (n-1)}dSdl -\,\frac{2 s\digamma Q^{\frac{2-2s}{2 s-1}}}{(1-2 s)^2S^{\frac{2 (n-2 s)}{ (n-1) (2 s-1)(\Delta +2)}}}dQ^2+\,\frac{3 \Bigg (\frac{1}{\omega _{n-1}}\Bigg ){}^{\frac{2}{n-1}}2^{\frac{n+3}{n-1}} S^{\frac{2 n}{(\Delta +2) (n-1)}}}{l^4}dl^2\Bigg \}. \end{aligned}$$
(30)

The curvature scalar of Eq. (30) is written as

$$\begin{aligned} R^{II}= & {} -\bigg [\pi l^2 \bigg (s-\frac{1}{2}\bigg )^2 \omega ^{\frac{1}{1-n}} Q^{\frac{4-6 s}{2 s-1}} \nonumber \\{} & {} \times \, S^{-\frac{2 (\Delta +\Delta (-n)+2 s (-\Delta +\Delta n+n-3)+2)}{(\Delta +2) (n-1) (2 s-1)}} \bigg (J_2 4^{\frac{n}{1-n}} \bigg (s-\frac{n}{2}\bigg ) \nonumber \\{} & {} \times \, Q^{\frac{2 s}{2 s-1}} (\Delta +\Delta (-n)+2 (\Delta +2) ns\nonumber \\{} & {} -\,2 (\Delta +4) s+2) S^{-\frac{2 (\Delta -(\Delta +1) n+2 s (-\Delta +(\Delta +2) n-3)+2)}{(\Delta +2) (n-1) (2 s-1)}}\nonumber \\{} & {} +\,J_1 Q\bigg )\bigg ]\bigg [6 J_3^2 (n-1)\bigg (\digamma Q^{\frac{2 s}{2 s-1}} S^{\frac{4 s-2 n}{(\Delta +2) (n-1) (2 s-1)}}\nonumber \\{} & {} +\,\frac{4^{\frac{2}{n-1}} \bigg (\frac{1}{\omega }\bigg )^{\frac{2}{n-1}} S^{\frac{2 n}{(\Delta +2) (n-1)}}}{l^2} +S^{\frac{2 (n-2)}{(\Delta +2) (n-1)}}\bigg )\bigg ]^{-1}, \end{aligned}$$
(31)

where

$$\begin{aligned} J_{1}{} & {} =\digamma l^2 2^{\frac{n+1}{1-n}} n s \big (-\Delta +(\Delta +5) n-2\big ) (n-2 s)^2 \\{} & {} \quad \times \, Q^{\frac{2}{2 s-1}+1} S^{-\frac{2 (\Delta -\Delta n+2 s (-\Delta +\Delta n+n-4)+n+2)}{(\Delta +2) (n-1) (2 s-1)}}\\{} & {} \quad +\,4^{\frac{1}{1-n}} Q^{\frac{1}{2 s-1}} S^{\frac{4 s-2 n}{(\Delta +2) (n-1) (2 s-1)}}\\{} & {} \quad \times \bigg (-\frac{1}{32} l^2 (n-2) (\Delta (n-1)+2) \bigg (4 \big (4 n^2+6 n-9\big ) s^2\\{} & {} \quad + \big (-24 n^2+8 n+12\big ) s+n (5 n-4)\bigg ) \\{} & {} \quad \times S^{-\frac{2 \Delta }{\Delta +2}}-\,2^{\frac{3-n}{n-1}} n (\Delta (n-1)-2) S^{-\frac{2 (-\Delta +\Delta n+n-2)}{(\Delta +2) (n-1)}}\\{} & {} \quad \times \,\bigg (4^{\frac{1-2 n}{n-1}} (n-2) (l-2 l s)^2 (\Delta (n-1)+2) S^{\frac{2 (n-2)}{(\Delta +2) (n-1)}}\\{} & {} \quad -\,3\ 2^{\frac{6-4 n}{n-1}} (n-2 s)^2 \big (\frac{1}{\omega }\big )^{\frac{2}{n-1}} S^{\frac{2 n}{(\Delta +2) (n-1)}}\bigg )\\{} & {} \quad +2^{\frac{5-n}{n-1}} n^2 (n-2 s)^2 \bigg (\frac{1}{\omega }\bigg )^{\frac{2}{n-1}} S^{\frac{4-2 \Delta (n-1)}{(\Delta +2) (n-1)}}\bigg )\\{} & {} \quad +16^{\frac{1}{1-n}} s \bigg (s-\frac{n}{2}\bigg ) Q^{\frac{1}{2 s-1}} S^{\frac{\frac{4 s-2 n}{(n-1) (2 s-1)}-2 \Delta }{\Delta +2}} \\{} & {} \quad \times \,\bigg (\frac{1}{2} l^2 (n-2) (\Delta (n-1)+2) \bigg (2^{\frac{2 n}{n-1}} (n-3) s\\{} & {} \quad +\,2^{\frac{1}{n-1}} \bigg (3\ 2^{\frac{1}{n-1}} n-2^{\frac{n}{n-1}} n +\,3\ 2^{\frac{1}{n-1}}\bigg )\bigg )\\{} & {} \quad +2^{\frac{3 (n+1)}{n-1}} n^2 (n-2 s) \bigg (\frac{1}{\omega }\bigg )^{\frac{2}{n-1}} S^{\frac{4}{(\Delta +2) (n-1)}}+\,3\ 2^{\frac{6}{n-1}-1} n \\{} & {} \quad \times (\Delta (n-1)-2) (n-2 s) \bigg (\frac{1}{\omega }\bigg )^{\frac{2}{n-1}} S^{\frac{4}{(\Delta +2) (n-1)}}\bigg ), \\ J_{2}{} & {} =\digamma l^2 4^{\frac{n}{1-n}} n \bigg (\Delta 2^{\frac{2}{n-1}} n-\Delta 2^{\frac{2}{n-1}}\\{} & {} \quad +\,2^{\frac{2 n}{n-1}+1} n-3\ 2^{\frac{2}{n-1}} n-2^{\frac{n+1}{n-1}}\bigg ) Q^{\frac{2 s}{2 s-1}}S^{\frac{4 (n s-n+s)}{(\Delta +2) (n-1) (2 s-1)}}\\{} & {} \quad +\frac{1}{4} s S^{\frac{4}{\Delta +2}} \bigg (-3 l^2 (n-2) (\Delta (n-1)+2)-n \\{} & {} \quad \times \, \bigg (n \bigg (3 \Delta 2^{\frac{4}{n-1}}+2^{\frac{4 n}{n-1}}\bigg )-3 (\Delta +2) 2^{\frac{4}{n-1}}\bigg )\\{} & {} \quad \times s \bigg (\frac{1}{\omega }\bigg )^{\frac{2}{n-1}} S^{\frac{4}{(\Delta +2) (n-1)}}\bigg ),\\ J_{3}{} & {} =\digamma l^2 \bigg (-2^{\frac{n+1}{1-n}}\bigg ) s (n-2 s)^2 Q^{\frac{2}{2 s-1}}\\{} & {} \quad \times \, S^{-\frac{2 (\Delta -\Delta n+2 s (-\Delta +\Delta n+n-4)+n+2)}{(\Delta +2) (n-1) (2 s-1)}}+\digamma l^2 2^{\frac{3-5 n}{n-1}} (n-2 s)\\{} & {} \quad \times \, Q^{\frac{2}{2 s-1}} (\Delta +\Delta (-n)+2 s (-\Delta +(\Delta +2) n-4)+2) \\{} & {} \quad \times \, S^{-\frac{2 (\Delta -\Delta n+2 s (-\Delta +\Delta n+n-4)+n+2)}{(\Delta +2) (n-1) (2 s-1)}}\\{} & {} \quad +\,\frac{1}{3} 2^{\frac{3-6 n}{n-1}} (1-2 s)^2 Q^{-\frac{2 (s-1)}{2 s-1}} S^{-\frac{2 (\Delta -\Delta n+2 s (\Delta (n-1)-1)+n)}{(\Delta +2) (n-1) (2 s-1)}} \\{} & {} \quad \times \,\bigg (3 l^2 \bigg (\Delta 2^{\frac{n}{n-1}} n^2+n \bigg (2^{\frac{1}{n-1}+2}\\{} & {} \quad -3 \Delta 2^{\frac{n}{n-1}}\bigg )+(\Delta -2) 2^{\frac{1}{n-1}+2}\bigg )+2^{\frac{n}{n-1}} n \\{} & {} \quad \times \, \bigg (3 \Delta 2^{\frac{4}{n-1}} n-3 \Delta 2^{\frac{4}{n-1}}+2^{\frac{4 n}{n-1}} n-3\ 2^{\frac{n+3}{n-1}}\bigg )\\{} & {} \quad \times \bigg (\frac{1}{\omega }\bigg )^{\frac{2}{n-1}} S^{\frac{4}{(\Delta +2) (n-1)}}\bigg ). \end{aligned}$$
Fig. 14
figure 14

Plot of curvature scalar \(R^{II}\) versus entropy S

Full size image
Fig. 15
figure 15

Plot of curvature scalar \(R^{II}\) versus entropy S

Full size image
Fig. 16
figure 16

Plot of curvature scalar \(R^{II}\) versus entropy S

Full size image
Fig. 17
figure 17

Plot of curvature scalar \(R^{II}\) versus entropy S

Full size image

Figures 14 and 15 explains the conduct of curvature scalar of \(g^{II}\) for numerous values of n, l, Q and \(\Delta \). It can observe that there exist both regions negative and positive curvature depending on the values of the parameter. The region of negative curvature indicates that the interaction between the particles of the black holes are repulsive while the positive region demonstrates the interaction among the particles of the black holes is repulsive.

The behavior of scalar curvature \(R^{II}\) for various values of parameters n,  l,  Q, and \(\Delta \) with a fixed value of electromagnetic parameter \(s = 1\) is demonstrated in Figs. 16 and 17. From Figs. 16 and 17 it observed that there is no singularity present for \(l=~Q=~1,~5\) and \(\Delta =0.4,0.6\) with \(n=4,5\). According to GTD, a non-zero curvature predicts thermodynamic interaction. It is observed that the curvature scalar in Figs. 16 and 17 indicates that the interaction between the particles is repulsive.

The equilibrium space’s third metric for GTD may be expressed as

$$\begin{aligned} g^{III}=\sum ^{b=1}_{n} (\delta _{ad} E^{d}\Phi _{,a})\delta _{ab}\Phi _{,bc}dE^{a}dE^{c}. \end{aligned}$$
(32)

In order to study the all the geometrical properties we just need to find out the fundamental equation \(\Phi (E^{a})\). Now, we can derive our third metric from the Eq. (32) given as [34]

$$\begin{aligned} g^{III}= & {} S\Phi _{,S}\Phi _{,SS}dS^{2}+\big (S\Phi _{,S}+Q\Phi _{,Q}+l\Phi _{,l}\big )\nonumber \\{} & {} \times \big (\Phi _{,SQ}dSdQ +\Phi _{,Sl}dSdl\big )\nonumber \\{} & {} +Q\Phi _{,Q}\Phi _{,QQ}dQ^{2}+l\Phi _{,l}\Phi _{,ll}dl^{2}, \end{aligned}$$
(33)

where \(\Phi _{,S}=\frac{\partial \Phi }{\partial S}\) and \(\Phi _{,SS}=\frac{\partial ^{2}\Phi }{\partial S^{2}}\). The curvature scalar we obtained from Eq. (33) is quite difficult to write in compact form [34]. Also, the curvature scalar obtained by the condition from the metric \(g^{III}\) did not satisfy the fundamentalequation of Van der Waals. We come to the conclusion that the metrics \(g^{I}\) and \(g^{II}\) alone contain all the data in this case concerning the curvature singularities of the equilibrium space [34].

4 Conclusion

In this paper, we studied the thermodynamic quantities like mass, temperature, and heat capacity spherical AdS-BH along with PMI source through Barrow entropy, we examined geometrothermodynamics structure as well. We have analyzed the behavior of temperature for different values of parameters like n,  l,  Q, and \(\Delta \). We have observed that the trajectories of temperature for \(n=4\) and 5 with \(\Delta =0.4\) showed only positive behavior which indicates physical \((T>0)\) BH, also red lines represented the maximum and minimum temperature. The thermodynamic variable L and electric potential revealed only negative behavior. We also observed the stability of BH by means of heat capacity, for \(s=3,~n=4\), and \(n=5\) with Barrow entropy exponent \(\Delta =0.2\) showed phase transition points on different locations. The heat capacity does not exist in any singularity in the case of \(s=1\) with \(l=Q=1\) and \(l=2,~Q=4\).

We also investigated the geometric structure of spherical AdS-BH along with PMI source under the concept of GTD. There exists a non-zero curvature scalar that represents thermodynamic connection. We also figured out that the heat capacity transition point coincides with curvature scalar singular points. This is proven by applying GTD to a specific metric in thermodynamic dimensional space. Due to its Legendre transformation invariance, the features of our geometric thermodynamic explanation are unaffected by the selection of potential or representation used in thermodynamic theory. The curvature scalar does not exist any singularity for particular values of parameters \(s=1,~\Delta =0.6\) with \(l=Q=5\). We find that the GTD formalism appropriately describes the thermodynamic features of this type of BHs with a nonlinear source.