Lectures on SMEFT

Abstract

This document contains lectures on SMEFT, which is an effective field theory of the degrees of freedom of the Standard Model. The material is at a basic, introductory level, without assuming any prior knowledge of effective field theory techniques. The main focus is on phenomenological applications of SMEFT in collider, flavor, and low-energy physics.

1 0 Goals, notation, conventions

This is a write-up of my lectures given on several occasions (Saclay’17, Orsay’20, Les Houches’21, Bhubaneswar’22, Orsay’22, Les Houches’23) about a specific effective field theory (EFT) called the Standard Model Effective Field Theory or SMEFT in short. My intention was to prepare these lectures at a very basic, introductory level, without assuming any prior knowledge of EFT techniques. On the other hand, I assume the reader is versed in Quantum Field Theory (QFT) roughly at the Peskin–Schroeder level [1]. The focus is on phenomenological applications of SMEFT, especially in Higgs, electroweak, flavor, and low-energy physics. This document is not meant to be a SMEFT review. It leaves out or barely touches upon many important topics (running, matching, Hilbert series, collider simulations, on-shell techniques, ...), it does not try to summarize all recent developments in this field, and it does not attempt to provide references to all the important papers in the vast SMEFT literature. For a more general introduction to EFT, I recommend Refs. [2,3,4]. For a broader scope of SMEFT topics and more references see Refs. [5, 6].

Here is the layout of these lectures. Section 1 describes the place of SMEFT in the ladder of effective theories, from extremely low energies to large scales that are not directly accessible by experiment. In Sect. 2 I will discuss in some details the assumptions under which SMEFT is the relevant formalism to describe physics above the electroweak scale. Next, in Sect. 3 I explain how to systematically construct the SMEFT Lagrangian. Various equivalent representations of the SMEFT Lagrangian, the so-called bases, are discussed in Sect. 4. In Sect. 5 I will discuss how the observables, at the Large Hadron Collider (LHC) and in other experiments, depend on the Wilson coefficients of higher-dimensional SMEFT operators. Finally, Sect. 6 is devoted to the phenomenological importance of new SMEFT sources of CP violation.

I work with the mostly minus Minkowski metric $\eta _{\mu \nu } = (1,-1,-1,-1)$. The metric is used to raise and lower indices, e.g. $A^{\mu } = \eta ^{\mu \nu } A_{\nu }$. As usual, repeated Lorentz and other indices are implicitly summed over, unless otherwise noted. Since the Lorentz contractions are unambiguous, sometimes I may write contracted Lorentz indices on the same level (e.g. $A^{\mu } A^{\mu }$ instead of $A^{\mu } A_{\mu }$) if this improves the aesthetics (usually when there are many other indices). The sign convention for the totally anti-symmetric Levi-Civita tensor $\epsilon ^{\mu \nu \rho \alpha }$ is $\epsilon ^{0123} = 1$, which implies $\epsilon _{0123} = -1$. When I refer to a vector I always mean a Lorentz 4-vector. For 3-vectors I use the bold notation rather than an arrow top: ${\varvec{x}} \equiv {\vec {x}}$.

I always use the natural units, $\hbar = c = 1$. Energy, momentum, area, distance, time, etc. are expressed in appropriate powers of electronvolts (eV).

The $SU(3)_C\times SU(2)_L \times U(1)_Y$ gauge fields of the Standard Model (SM) are denoted by $G_{\mu }^a$, $W_{\mu }^k$, $B_{\mu }$, where $a = 1\dots 8$, $k=1\dots 3$. The corresponding gauge couplings are called $g_s$, $g_L$, $g_Y$, and the corresponding field strengths are defined as $G_{\mu \nu }^a = \partial _{\mu } G_{\nu }^a -\partial _{\nu } G_{\mu }^a - g_s f^{abc} G_{\mu }^b G_{\nu }^c$, $W_{\mu \nu }^k = \partial _{\mu } W_{\nu }^k -\partial _{\nu } W_{\mu }^k - g_L \epsilon ^{abc} W_{\mu }^b W_{\nu }^c$, $B_{\mu \nu } = \partial _{\mu } B_{\nu } - \partial _{\nu } B_{\mu }$. I use the plus sign covariant derivative convention: $D_{\mu } X = \partial _{\mu } X + i G_{\mu }^a T^a X + i W_{\mu }^k {\sigma ^k \over 2} X + i B_{\mu } Y_X X$. The (sine of the) weak mixing angle is related to the electroweak coupling as $\sin \theta _W = {g_Y \over \sqrt{g_L^2 +g_Y^2}}$, and the electromagnetic coupling is $e = {g_L g_Y \over \sqrt{g_L^2 +g_Y^2}}$. After electroweak symmetry breaking, the photon field is denoted by $A_{\mu }$, and its field strength by $F_{\mu \nu }$. The massive electroweak vector bosons are denoted $W_{\mu }^{\pm }$ and $Z_{\mu }$, and in this case I define $V_{\mu \nu } \equiv \partial _{\mu } V_{\nu } -\partial _{\nu } V_{\mu }$, without any non-abelian piece. The vector boson eigenstates are related to the $SU(2)_L \times U(1)_Y$ gauge fields by $W_{\mu }^1 = {W_{\mu }^+ + W_{\mu }^- \over \sqrt{2}}$, $W_{\mu }^2 = i {W_{\mu }^+ - W_{\mu }^- \over \sqrt{2}}$, $W_{\mu }^3 = {g_Y A_{\mu } + g_L Z_{\mu } \over \sqrt{g_L^2 + g_Y^2}}$, $B_{\mu } = {g_L A_{\mu } - g_Y Z_{\mu } \over \sqrt{g_L^2 + g_Y^2}}$.

I use the 2-component spinor formalism, following the conventions of Ref. [7]. A Dirac fermion is described by a pair anti-commuting fields $f_\alpha$, ${\bar{f}}^c_{{\dot{\alpha }}}$ transforming respectively under the first and the second component of the $SU(2) \otimes SU(2)$ Lorentz algebra. The spinor index can be raised and lowered by the anti-symmetric $\epsilon$ tensor, $f^\alpha = \epsilon ^{\alpha \beta } f_\beta$, $\epsilon ^{12} = - \epsilon ^{21} = 1$, and then Lorentz invariant contractions can be easily constructed by marrying the upper and lower undotted and dotted indices. For example, $f^c f \equiv f^{c \, \alpha } f_\alpha$ and ${\bar{f}}^c {\bar{f}} \equiv f^{c}_{{\dot{\alpha }}} f^{{\dot{\alpha }}}$ are Lorentz invariant, whereas $f^c_{\alpha } f_\alpha$, $f^{c}_{{\dot{\alpha }}} f_{{\dot{\alpha }}}$, or $f_\alpha {\bar{f}}_c^{{\dot{\alpha }}}$ are not Lorentz invariant. The fermion kinetic and mass terms are written as ${{\mathcal {L}}} = i {\bar{f}} {\bar{\sigma }}^{\mu } \partial _{\mu } f + i f^c \sigma ^{\mu } \partial _{\mu } {\bar{f}}^c - m f^c f - m {\bar{f}} {\bar{f}}^c$, where $\sigma ^{\mu } = (1, {\varvec{\sigma }})$, ${\bar{\sigma }}^{\mu } = (1, -{\varvec{\sigma }})$, ${\bar{f}} \equiv f^*$, ${\bar{f}} {\bar{\sigma }}^{\mu } \partial _{\mu } f \equiv {\bar{f}}_{{\dot{\alpha }}} [{\bar{\sigma }}^{\mu }]^{{\dot{\alpha }} \alpha } \partial _{\mu } f_\alpha$. $f^c \sigma ^{\mu } \partial _{\mu } {\bar{f}}^c \equiv f^{c \,\alpha } [\sigma ^{\mu }]_{\alpha {\dot{\alpha }}} \partial _{\mu } {\bar{f}}^{c {\dot{\alpha }}}$. If you’re not familiar with this notation...that’s very bad, you should learn this as soon as possible, it’s an essential part of modern education of a particle physicist. But if you don’t want to learn, you can always quickly translate to the 4-component Dirac fermion using the map

$$\begin{aligned} F = \begin{pmatrix} f \\ {\bar{f}}^c \end{pmatrix}, \quad {\bar{F}} \equiv F^{\dagger } \gamma ^0 = \begin{pmatrix} f^c&{\bar{f}} \end{pmatrix},\quad \gamma ^{\mu } = \begin{pmatrix} 0 &{} \sigma ^{\mu } \\ {\bar{\sigma }}^{\mu } &{} 0 \end{pmatrix}.\nonumber \\ \end{aligned}$$

(0.1)

For example, ${\bar{f}} {\bar{\sigma }}^{\mu } \partial _{\mu } f = {\bar{F}} \gamma ^{\mu } \partial _{\mu } P_L F$, $f^c \sigma ^{\mu } \partial _{\mu } {\bar{f}}^c = {\bar{F}} \gamma ^{\mu } \partial _{\mu } P_R F$, $f^c f = {\bar{F}} P_L F$, ${\bar{f}} {\bar{f}}^c = {\bar{F}} P_R F$, where $P_{L,R} = {1 \mp \gamma _5 \over 2}$ are the Dirac chirality projectors.

The $1\sigma$ uncertainty on theoretical or experimental quantities is often expressed either using the bracket notation, e.g. $x = 1.234(56)$ is the same as $x = 1.234 \pm 0.056$. The former notation is especially useful when precision reaches many digits.

All abbreviations are defined the first time they are introduced, but in case you forget they are all collected in Appendix A.

2 EFT ladder

In the previous century the Holy Grail of theoretical particle physics was the Theory of Everything. Physicist would imagine that internal consistency of quantum theories of matter and gravity selects essentially a unique theory, with very few or none at all free parameters. The Theory of Everything would be valid at all energies, up to the Planck scale and beyond, and it would lead to the SM as its low-energy approximation, possibly with some intermediate supersymmetric or grand-unified theories emerging between the electroweak and the Planck scales. Alas, this top-down approach has not quite delivered, and the quest for the Theory of Everything is now largely abandoned. Around the turn of century the focus shifted to the less ambitious but more practical Theories of Something. These theories are meant to be valid only in a restricted energy range, and often the degrees of freedom they describe are emergent rather than fundamental. For these reasons they are commonly referred as effective fields theories, or EFTs in short.

Fig. 1

Simple illustration of the EFT idea using the example of multipole expansion of the potential produced by electric charges

The central idea behind EFT is that things may appear simpler when viewed from a distance. For countless physical systems complexity is dramatically reduced by focusing on the large-scale behavior. Take for example a system of many static electric charges confined to a region of space of size R, see Fig. 1. A near observer positioned at a distance $L \sim R$ must trace the position of each charge to accurately determine the electric field in her vicinity. However, for a far observer at $r \gg R$ the details of the charge distribution are not essential. Instead, the electric field at large r can be described using the multipole moments of the charge distribution: the total charge, the dipole moment, the quadrupole moment, etc. The error of this approximation is controlled by the ratio $(R/r)^n$, where n is the number of multipoles taken into account. For large enough r only a first few multipoles need to be included to adequately describe the electric field, and this way the description of a possibly complex system with many degrees of freedom is reduced to a small number of discrete parameters.

This reduction of degrees of freedom with increasing distance is so pervasive in physics that is often taken for granted. Indeed, the far observer could be a humble engineer tuning his antenna, who would be shocked when told that his actions have anything to do with EFT. It is easy to evoke other familiar examples: a gas in equilibrium, where the enormous mess of gazillions of atoms bouncing against each other can be summarized by a small number of thermodynamic quantities like temperature, pressure, entropy; planets rotating around the star, all of which may be complicated objects, with a finite radius, not-exactly-spherical shapes, and non-trivial density profiles, but for the purpose of planetary dynamics they can be perfectly approximated as point particles, while tidal corrections due to their sizes are calculable in a quickly converging expansion; and then the whole universe at the scales larger than that of galaxy clusters is described by the simple Friedmann equations depending only on the density of matter, radiation, and dark energy. We could go on with similar classical examples for hours. Instead, we will now head straight to particle physics and quantum field theory (QFT).

In relativistic QFT, instead of distance scales L, it is more convenient to refer to energy scales E. The two are simply connected via the uncertainty relation, $E \sim 1/L$ (in natural units $\hbar = c = 1$), thus long distance translates low energy, or infrared (IR) in our jargon, while short distance translates to high energy, or ultraviolet (UV). As understood long ago by Wilson, Weinberg, and other giants of the past century, changes in complexity of QFT as we move towards lower energies can be nicely formalized in the language of “integrating out the UV degrees of freedom”. The concept is perhaps most succinctly summarized using the path integral formulation of QFT. Consider a QFT with low-energy degrees of freedom denoted collectively as $\phi$, and with high-energy degrees of freedom denoted as H. Here, $\phi$ and H can refer to, respectively, light and heavy particles in the theory, or to low- and high-frequency modes of the same particle. Quite generally, the full UV theory of $\phi$ and H can be defined by the Lagrangian ${{\mathcal {L}}}_{\textrm{UV}}$ from which the partition function $Z_{\textrm{UV}}$ is calculated:

$$\begin{aligned}{} & {} Z_{\textrm{UV}}[J_\phi ,J_H] = \int [D\phi ] [D H] \nonumber \\{} & {} \quad \times \exp \left[ i \int d^4x \left( {{\mathcal {L}}}_{\textrm{UV}}(\phi ,H) + J_\phi \phi + J_H H \right) \right] . \end{aligned}$$

(1.1)

All correlation functions of $\phi$’s and H’s (and thus all S-matrix elements) can be obtained by differentiating $Z_{\textrm{UV}}$ with respect to the auxiliary sources J. At low energies, such that the H modes cannot be excited, we only need the correlators of $\phi$ to calculate observables, hence we can set $J_H = 0$. From this IR perspective we can define

$$\begin{aligned} Z_{\textrm{EFT }}[J_\phi ]\equiv & {} Z_{\textrm{UV}}[J_\phi ,0] \nonumber \\= & {} \int [D\phi ] \exp \left[ i \int d^4x \left( {{\mathcal {L}}}_{\textrm{EFT}}(\phi ) + J_\phi \phi \right) \right] . \nonumber \\ \end{aligned}$$

(1.2)

The first equality is a definition of the EFT partition function $Z_{\textrm{EFT}}$. It is adequate for our purpose since $Z_{\textrm{EFT}}$, trivially, leads to the same correlation functions of $\phi$ as $Z_{\textrm{UV}}$. However, this is a tad formal as in QFT we rarely know the full partition function. The second equality is far more useful for practitioners. It defines the EFT Lagrangian ${{\mathcal {L}}}_{\textrm{EFT}}$, which captures the effective interactions of the light degrees of freedom.¹ These interactions should reproduce the correlation functions and scattering amplitudes in the full theory. An important point is that ${{\mathcal {L}}}_{\textrm{EFT}}$ can be determined algorithmically, order by order in perturbation theory, if ${{\mathcal {L}}}_{\textrm{UV}}$ is known and weakly coupled. The effective Lagrangian is sufficient to calculate all low-energy observables involving $\phi$ without ever referring to H. This often leads to conceptual and calculational simplifications compared to working with the full UV theory.

In general, $\mathcal {L}_{\textrm{EFT}}$ defined by Eq. (1.2) is a very complicated non-local object.² Indeed, even though it depends only on $\phi$, it must somehow contain information about the scattering amplitudes in the full UV theory, including the effects of propagating virtual H degrees of freedom at all loop levels. However, a dramatic simplification occurs in the presence of scale separation, when the mass M (or the characteristic frequency) of H is parametrically larger than the relevant energy scale, $E \ll M$. In such a case, $\mathcal {L}_{\textrm{EFT}}$ can be approximated by a local Lagrangian, that is by polynomial of $\phi$ and its derivatives. Mathematically speaking, the full $\mathcal {L}_{\textrm{EFT}}$ will contain non-local expressions such as e.g. $(\Box + M^2)^{-1}$, which for $E \ll M$ can be Taylor-expanded into local ones, $(\Box + M^2)^{-1} \approx M^{-2} - M^{-4} \Box + \cdots$. This is where the power of EFT shows up: the possibly very complicated short-distance physics mediated by H is summarized by a discrete set of local interactions of $\phi$ suppressed by increasing powers of M, in close analogy with the multipole expansion in electrodynamics. The expansion can be truncated at some fixed order n in 1/M, depending on the precision required.

The philosophy sketched above has been applied over and over again in many areas of particle physics. One important example is the SM below the electroweak scale. At energies $E \lesssim m_W \simeq 80$ GeV (giga-electronvolt, that is $10^9$ eV), one can integrate out the W and Z bosons, together with the Higgs boson and the top quark. The resulting EFT, which I will call Weak Effective Field Theory (WEFT, also known as WET or LEFT in the literature), has the photon, the gluon octet, the 3 generations of SM leptons, and the 5 lightest flavors of SM quarks as the degrees of freedom, and is valid in the range $2~\textrm{GeV}\lesssim E \lesssim m_W$. In this case the UV theory is known and weakly coupled, therefore the effective Lagrangian defined by Eq. (1.2) can be calculated and all Wilson coefficients can be determined as functions of the SM parameters. Because the massive electroweak gauge bosons are absent, the WEFT Lagrangian is invariant only under the $SU(3)_C \times U(1)_{\textrm{em}}$ subgroup of the SM $SU(3)_C \times \times SU(2)_W \times U(1)_{Y}$ gauge symmetry. The memory of the larger gauge symmetry survives only in the specific pattern of the WEFT interactions and corresponding Wilson coefficients. In particular, the weak interactions, which in the SM are mediated by the exchange of W and Z, emerge in WEFT as 4-fermion effective interactions between the quarks and leptons. Many of these effective operators violate the (approximate) flavor symmetry and thus can mediate transitions between different quark flavors. WEFT is thus the theory underlying the vast phenomenology of flavor physics, that is the studies of transitions between mesons and baryons made of different quarks. Another well-known example is the so-called Chiral Perturbation Theory (ChPT) describing the physics of light mesons (pions, kaons, eta) at energies below the $\rho$ resonance mass, $E \lesssim m_{\rho } \simeq 775$ MeV (mega-electronvolt = $10^6$ eV). In this case the UV theory is known, but because the SM $SU(3)_C$ interactions become strongly coupled at $E \sim 2$ GeV, the effective Lagrangian cannot be calculated analytically. Nevertheless, the approximate chiral symmetry of Quantum Chromodynamics (QCD) with light quarks, which resurfaces in another form in ChPT, allows one to systematically construct $\mathcal {L}_{\textrm{EFT}}$ as a derivative expansion in $\partial /(4 \pi F)$, where $F \sim 100$ MeV is called the pion decay constant. A less familiar example is the so-called General Relativity EFT (GREFT), which is an EFT extension of the Einstein theory of general relativity. Here the quantum field encoding the gravitational degrees of freedom is the spacetime metric $g_{\mu \nu }$, which describes, in the limit of the flat Minkowski background, a massless spin-2 particle called the graviton. The Lagrangian is invariant under general coordinate transformations, which is necessary to decouple the unphysical degrees of freedom in the metric. The lowest order term is the Einstein-Hilbert Lagrangian, ${{\mathcal {L}}}_{\textrm{GREFT}} \supset {1 \over 2 } M_{\textrm{Pl}}^2 R$, corresponding in the classical limit to the usual Einsteinian general relativity. Higher order corrections are constructed from powers of the Riemann tensor $R_{\mu \nu \alpha \beta }$ (more precisely, from its Weyl tensor part), with the EFT expansion organized in powers of $R_{\mu \nu }/\Lambda$, where $\Lambda$ may or may not be equal to the Planck scale. The validity regime of this EFT is $0 \lesssim E \lesssim {\textrm{min}} (M_{\textrm{Pl}},\Lambda )$.³ Unlike in the two previous examples, we only have vague speculations about the UV completion of GREFT: it may be some form of string theory, or something completely different. For this reason, we do not know the coupling constants multiplying the higher-derivative interactions terms in the GREFT Lagrangian; they have to be treated as free parameters to be determined one day from experiment.

Yet another important example is SMEFT, which is the main topic of these lectures. The SMEFT philosophy has been employed in high-energy physics since more than 40 years [8], but only quite recently, around the year 2010, the theory gained large prominence. SMEFT is an EFT of the SM degrees of freedom: the photon, the gluon octet, the W and Z bosons, the Higgs boson, and the 3 generations of quarks and leptons. Much as in the SM, the action is exactly invariant under the local (gauge) $SU(3)\times SU(2) \times U(1)$ symmetry. The SMEFT Lagrangian contains the SM one, but also an infinite set of higher-dimensional gauge-invariant interaction terms,⁴ The latter interactions, which are non-renormalizable in the old parlance, describe the effects of heavy particles from beyond the SM. Under very broad assumptions, which will be spelled out in Sect. 2, SMEFT is the theory of fundamental interactions in the energy range $100~\textrm{GeV}\lesssim E \lesssim \Lambda$, where $\Lambda \gg m_W$ is the scale at which non-SM particles appear. The Lagrangian is organized in a systematic expansion based on the canonical dimensions of the interaction terms, with the operators of canonical dimension D suppressed by $\Lambda ^{D-4}$. The operators with $D=5$ and $D=6$ are expected to provide the leading deformations of the SM Lagrangian. Most often, the expansion is truncated at $D=6$, with the $D > 6$ operators deemed as irrelevant at the currently available energies.

Fig. 2

The ladder of EFTs describing nature, assuming SMEFT is a valid description of nature in the regime $100~\textrm{GeV}\lesssim E \lesssim \Lambda$, with $\Lambda \gg 100~\textrm{GeV}$

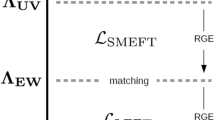
Let us discuss the place of SMEFT in the larger scheme of things. The ladder of effective theories is sketched in Fig. 2. On top of the ladder, for $E \gtrsim \Lambda$, we have a hypothetical theory that UV completes SMEFT (which itself may be an EFT of another, more fundamental theory). At the time of writing, we have no clue what it is, what its degrees of freedom are, or what its mass scale $\Lambda$ is. Nevertheless, given the lack of discovery of non-SM particles at the LHC, it is a reasonable assumption that $\Lambda \gg 1$ TeV (tera-electronvolt $=10^{12}$ eV). The validity domain of SMEFT is $100~\textrm{GeV}\lesssim E \lesssim \Lambda$, and our assumption about $\Lambda$ implies in particular that SMEFT is the relevant theory to describe processes at the LHC collider. Since the UV completion of SMEFT is unknown, much as for GREFT, the Wilson coefficients in the SMEFT Lagrangian should be treated as free parameters to be determined from experiment. Below the electroweak scale, for $1~\textrm{GeV}\lesssim E \lesssim 100~\textrm{GeV}$, SMEFT reduces to WEFT mentioned earlier, but now due to more general assumptions regarding the UV completion the WEFT Wilson coefficients should be treated as free parameters. Moving to lower energies, something dramatic happens around 1 GeV. The number of degrees of freedom and complexity explodes due to the onset of strong QCD coupling and emergence of baryons and hadrons as bound states of quarks. When the smoke clears, for $100~\textrm{MeV}\lesssim E \lesssim m_{\rho }$, we are left with ChPT describing the lightest mesons coupled to electrons, muons, photons, and neutrinos. The local symmetry is reduced to $U(1)_{\textrm{em}}$, while the color $SU(3)_C$ and the associate gluons are no longer relevant degrees of freedom at these energies. Below $100~\textrm{MeV}$ we have a series of EFTs with less and less degrees of freedom and complexity. First we have an EFT extension of QED coupled to neutrinos. Then electrons can be decoupled, and we are left with massless photons, and almost massless neutrinos, interacting with the former via highly suppressed dipole interactions. Finally, below the mass of the lightest neutrinos (which is also unknown, but I’m assuming here it is non-zero) we have the EFT of pure light. As far as we know, photons are exactly massless, therefore the theory preserves the $U(1)_{\textrm{em}}$ local symmetry, and its validity extends down to the scales of the order of the inverse size of the universe. In this ultimate EFT, photons still interact with each other, albeit very weakly, via dimension-8 and higher operators in the so-called Euler–Heisenberg (EH) Lagrangian.

Each rung of this ladder deserves a series of lectures on its own, but in the following I will focus almost exclusively on SMEFT.

3 Assumptions behind SMEFT

In theory, SMEFT is a perfectly consistent EFT of the SM degrees of freedom. However, it is not guaranteed that there is any energy range where SMEFT is the relevant EFT to describe physical processes. For this to happen, several broad assumptions have to be satisfied. Let me first list these assumption, and then we will discuss them in some detail.

#1:

QFT. Physics above the electroweak scale is described by a manifestly Poincaré-invariant local quantum theory.

#2:

Mass Gap. The mass scale $\Lambda$ of the non-SM particles is much larger than the electroweak scale, $\Lambda \gg m_W$.

#3:

Gauge Symmetry. The Lagrangian describing interactions above the electroweak scale is invariant under the SM gauge symmetry $SU(3)_C \times SU(2)_W \times U(1)_Y$.

In Assumption #1, Poincaré-invariant entails Lorentz and translational invariance in four spacetime dimensions. This is often taken for granted. QFT is a surprisingly rigid structure, and there are very few ways to modify it without wrecking some fundamental principles, such as unitarity and causality for example. Within QFT, one consistent departure from Assumption #1 would be to introduce extra space-time dimensions, but these are very unlikely to be relevant anywhere near the electroweak scale. Consistent non-QFT quantum frameworks are rare and far between; one such example is string theory, but, again, it is unlikely to be relevant anywhere near the electroweak scale. At the same time, there is no single hint from experiment that the standard QFT techniques may break down at the energy scales available in the foreseeable future. All in all, the first assumption seems a very safe one. Even though we do not know until which energy scale QFT can be used, we will assume it works at all the scales relevant for these lectures.

Assumption #2 is more tricky because, strictly speaking, it is false. Indeed, the degrees of freedom at the electroweak scale include not only the SM spectrum, but also a massless spin-2 particle called the graviton, which mediates the gravitational interactions. Thus, in order to describe all known physics at that scale we should also include the graviton in our EFT, which leads to the construction called GRSMEFT [9]. Nevertheless, gravity is expected to be very weak around the electroweak scale. Consistency of the theory requires the leading order coupling of matter to gravitons to be universal and controlled by the scale $M_{\textrm{Pl}} \simeq 10^{18}$ GeV, leading to the suppression factor of $\textrm{TeV}/M_{\textrm{Pl}} \sim 10^{-15}$ at the LHC energies. Subleading graviton couplings are controlled by the GRSMEFT expansion scale $\Lambda$, which is unknown, but the (rather safe) assumption here is that $\Lambda \gg m_W$, perhaps even $\Lambda \sim M_{\textrm{Pl}}$. If that is satisfied, graviton emission is totally irrelevant at the LHC and in other experiments that focus on non-gravitational interactions. For those experiments, SMEFT provides an adequate description. On the other hand, for observables where gravity plays a central role, for example for gravitational wave emission and detection, GREFT or GRSMEFT should be used.

Are there any other light non-SM degrees of freedom except for the graviton? This is an open question at present. Theorist have hypothesized countless light particles, some of which are even well motivated, and sometimes even hinted at by some experiments. As examples one could mention the sterile neutrinos, the axion, and a light dark matter particle. An affirmative answer to our question will be provided if we are very lucky and such a particle is discovered in some ongoing or future experiment. However a negative answer may never be established, because in many scenarios the coupling of the new particle to the SM matter is a free parameter that can be adjusted to arbitrary small values. From our point of view, a more immediate question is whether the non-SM degrees of freedom are relevant at the LHC energies. Again, this is an open question that may be difficult to settle in the near future. For all we know, a new light particle could for example couple to the Higgs boson, and could lead to an invisible Higgs branching fraction up to $\mathcal {O}(10)\%$. Using the SMEFT framework one misses such a possibility. All in all, it is reasonable to assume that the graviton is the only non-SM light degree of freedom, however it certainly requires a certain leap of faith. SMEFT practitioners should always keep their eyes and minds open and follow experimental developments in collider physics and elsewhere. In case the existence of a new light particle is established, the SMEFT approach may have to be abandoned.

We arrive at Assumption #3, which is the most mysterious one. In the SM, the action is exactly invariant under the $SU(3)_C \times SU(2)_W \times U(1)_Y$ local symmetry, which in the global limit acts as a linear transformation on the fields in the Lagrangian. At the level of the spectrum this symmetry is not visible, because it is spontaneously broken by a vacuum expectation value (VEV) of the Higgs field. With some experimental input about the quantum numbers of SM matter, the gauge principle has led to highly non-trivial and successful predictions. For example, the interactions strength of all left-handed fermions with the W boson are predicted to be universal (in the tree-level approximation) and controlled by the $SU(2)_L$ gauge coupling $g_L$, while the interactions with the Z boson are predicted non-universal but controlled only by the fermion’s quantum numbers and one universal parameter called the weak mixing angle $\sin \theta _W$.

All in all, gauge symmetry has proved to be one of the deepest foundational ideas in QFT, and the SM gauge symmetry has time and again proved to be extremely successful phenomenologically. That’s all very impressive, but why should SMEFT respect the same gauge symmetry as the SM? In the end, the goal of SMEFT is to provide a model independent description of heavy new physics beyond the SM. The discussion is further complicated by the fact that, in the modern view, gauge symmetry is not a real symmetry of the physical system, but merely a redundancy of ifs description. Why do we insist on imposing that particular redundancy on SMEFT?

First, let us recall what is the true purpose of gauge symmetry, or gauge redundancy [10]. The point is that a consistent, unitary QFT that is manifestly Lorentz invariant and contains massless spin-1 particles must be equipped with gauge redundancy, one generator for each massless spin-1 particle. Heuristically, this is because a spin-1 particle is described in QFT by a 4-component vector field $A_{\mu }$, $\mu = 0 \dots 3$, or equivalently by the associated polarization wave function $\epsilon _{\mu }(p)$. Since, an on-shell massless spin-1 particle has 2 degrees of freedom, corresponding to the two helicities, two of the four components must be somehow projected from $\epsilon _{\mu }(p)$. One can be taken care of in a Lorentz invariant way by the transversality condition $p_{\mu } \epsilon ^{\mu }(p) = 0$. It turns out that the only Lorentz invariant way to project out the other spurious degree of freedom is to identify the states described by the polarization wave functions $\epsilon ^{\mu }(p)$ and $\epsilon ^{\mu }(p) + p^{\mu }$, that is by imposing gauge redundancy on the theory.

In the SMEFT we have two kinds of massless spin-1 particles: a photon and a gluon octet. Accordingly, we need 9 generators of local symmetry to have a consistent and manifestly Lorentz-invariant theory. An input from phenomenology is needed to identify that $SU(3)_C\times U(1)_{\textrm{em}}$ provides a correct description of these degrees of freedom, because the gluons all self-interact with each other, thus they are described by the non-abelian SU(3) factor, while the photons do not have self-interactions, thus they are described by the abelian U(1) factor. But this raises another question: why do we insist on the larger $SU(3)_C \times SU(2)_W \times U(1)_Y$ local symmetry if the smaller $SU(3)_C\times U(1)_{\textrm{em}}$ is enough to satisfy the consistency principles of QFT?

In fact, an EFT for the SM degrees of freedom, where only the $SU(3)_C\times U(1)_{\textrm{em}}$ gauge symmetry is realized linearly, does exist and is most often referred to as HEFT (as in Higgs EFT). In HEFT, the generators of the larger $SU(3)_C \times SU(2)_W \times U(1)_Y$ gauge symmetry that do not belong to $SU(3)_C\times U(1)_{\textrm{em}}$ are realized as a non-linear transformation of the scalar Goldstone bosons eaten by W and Z, akin to the realization of the $SU(2)_L \times SU(2)_R/SU(2)_V$ in ChPT. While the formal difference between HEFT and SMEFT is clear, the physical difference between the two EFTs is more subtle and was elucidated only recently [11, 12]. The long story short: HEFT is an effective theory for non-decoupling UV physics, that is for theories where the masses of non-SM particles are dominated by contributions from electroweak symmetry breaking. A simple toy model for such a UV completion is a real scalar field S without a mass term but with the quartic interaction with the Higgs field: ${{\mathcal {L}}} \supset - \lambda |H|^2\,S^2$. After electroweak symmetry breaking S acquires mass $m_S^2 = 2 \lambda |H|^2$, which can be large if the quartic coupling $\lambda$ is $\mathcal {O}(1)$ or larger. Integrating out S will lead to an EFT described by the HEFT framework rather than SMEFT. Another less artificial example is the SM with 4 generations of chiral fermions, in which case all fermions are massless in the limit of the Higgs VEV going to zero. Integrating out the 4th generation will again lead to HEFT rather than SMEFT. On the other hand, integrating out the 4th generation of vector-like fermions, where the masses of the non-SM fermions are dominated by a vector-like mass term $M \gg v$, will lead to SMEFT rather than HEFT.

In the end, the gauge symmetry Assumption #3 turns out to be closely related to the mass gap Assumption #2. Indeed, in non-decoupling theories masses of non-SM particles are of the form $m_i \sim g_i v$, where $g_i$ is some gauge or Yukawa coupling. Since couplings are restricted by perturbativity to be $|g_i| \lesssim 4\pi$, the masses are $m_i \lesssim 4 \pi v$. This means the new particles in non-decoupling theories are within the reach of the LHC or just around the corner. Conversely, if new physics enters at the scale $\Lambda \gtrsim 4 \pi v \sim 3$ TeV, then the physics below $\Lambda$ is necessarily described by SMEFT and not HEFT. By imposing Assumption #3 we make an implicit decision to neglect the possibility of non-decoupling UV completions. Note that large swathes of non-decoupling theories have already been experimentally excluded; for example, the chiral 4th generation was definitely excluded by the Higgs production rate measurements at the LHC. Even though, at present, one cannot formally exclude the existence of non-decoupling new physics, and some wiggle room remains for certain constructions, it is a very unlikely possibility in my opinion. Focusing on decoupling new physics, and thus restricting our scope to SMEFT, seems a very reasonable assumption.

Note that assumptions #1– #3 do not restrict the SMEFT Lagrangian to be renormalizable. There was a time in the history of particle physics when renormalizability was hailed as a sacred principle that every successful quantum theory should obey. Now the pendulum has swung in the opposite direction, and we think that every QFT description of a real-life physical system corresponds to a non-renormalizable EFT. Now, in some case that EFT may be well approximated by a renormalizable QFT, as is the case for physics at the electroweak scale. We think of this as an accident due to a large separation between the electroweak scale and the scale suppressing the non-renormalizable interactions. However we expect that these non-renormalizable interactions are present in the Lagrangian, and that they will become apparent when enough experimental precision is achieved.

4 Constructing SMEFT

This section reviews a systematic prescription to construct the SMEFT Lagrangian. The fields corresponding to the SM particles and their representations under the gauge symmetry are summarized in Table 1. Using these fields as building blocks, we will write down the most general Lagrangian consistent with the assumptions spelled out in Sect. 2.

Table 1 Transformation properties of the SM fields under the SM gauge group. We also display the spin of the associated particle and the canonical dimension of the field. The matter fields (rows 4–8) are 3-vectors in the generation space: $Q =(q_1,q_2,q_3)$, $U^c = (u_1^c,u_2^c,u_3^c )\equiv (u^c,c^c,t^c)$, $D^c = (d_1^c,d_2^c,d_3^c )\equiv (d^c,s^c,b^c)$, $L =(l_1,l_2,l_3) = \bigg ( \begin{pmatrix} \nu _e \\ e \end{pmatrix}, \begin{pmatrix} \nu _{\mu } \\ \mu \end{pmatrix}, \begin{pmatrix} \nu _{\tau } \\ \tau \end{pmatrix} \bigg )$, $E^c = (e_1^c,e_2^c,e_3^c) \equiv (e^c,\mu ^c,\tau ^c)$. I work in the basis where $q_1 = \begin{pmatrix} u_J V_{Jd}^* \\ d_1 \end{pmatrix}$, $q_2 = \begin{pmatrix} u_J V_{Js}^* \\ d_2 \end{pmatrix}$, $q_3 = \begin{pmatrix} u_J V_{Jb}^* \\ d_3 \end{pmatrix}$, where $d_1 \equiv d$, $d_2 \equiv s$, $d_3 \equiv b$, and $u_J$, $u_J^c$, $d_J$, $d_J^c$, $\nu _J$, $e_J$, $e_J^c$ are mass eigenstates. The generation indices will be often suppressed to reduce the clutter

4.1 Power counting

Because the SMEFT Lagrangian is non-renormalizable, it contains an infinite number of interaction terms. Even if we wanted to arbitrarily restrict to a finite number of interactions, loop corrections would force us to introduce an infinite number of counterterms to cancel the UV divergences. In order to make the theory usable in practice we need power counting, which is the EFT jargon for an organizing principle that allows us to establish a relative importance of different interaction terms. In SMEFT, a natural power counting is based on the canonical dimension of an interaction. We organize the SMEFT Lagrangian as

$$\begin{aligned} \mathcal {L}_{\textrm{SMEFT}} = \sum _{D=2}^\infty \mathcal {L}_D, \end{aligned}$$

(3.1)

where each term $\mathcal {L}_D$ in this series contains operators $O_{i,D}$ of canonical dimension D:

$$\begin{aligned} \mathcal {L}_D = \sum _i C_{i,D} O_{i,D}. \end{aligned}$$

(3.2)

Above, i indexes all independent gauge-invariant operators constructed out of the SM fields at a given dimension (more about it in Sect. 4), and $C_{i,D}$ are field-independent coupling constants called the Wilson coefficients. By definition, the dimension of $O_{i,D}$ is D, which we write as $[O_{i,D}] = D$. Since the Lagrangian has dimension four, $[{{\mathcal {L}}}] = 4$, it follows that $[C_{i,D}] = 4-D$. We can write down the Wilson coefficients in the form

$$\begin{aligned} C_{i,D} = {c_{i,D} \over \Lambda ^{D-4}}, \end{aligned}$$

(3.3)

where $c_{i,D}$ are dimensionless, and $\Lambda$ is a common mass scale entering all Wilson coefficients. At this point Eq. (3.3) is completely general. The scale $\Lambda$ can be identified with the mass scale of new particles in the UV completion of SMEFT. Then the dimensionless coefficients $c_{i,D}$ are functions of the couplings and mass ratios in the UV completion of SMEFT, as well as of the SM couplings. Now, the standard SMEFT power counting relies on the assumption that $|c_{i,D}| \sim 1$, that is to say

$$\begin{aligned} C_{i,D} \sim {1 \over \Lambda ^{D-4}}, \end{aligned}$$

(3.4)

which is basically dimensional analysis. In such a case we have a simple estimate of the relative relevance of different Wilson coefficients. Matching the dimensions in tree-level scattering amplitudes (which are dimensionless) one finds that, for the relevant scattering energy E much larger than the particles’ mass, a Wilson coefficient at a given D will enter as

$$\begin{aligned} {\mathcal {M}}\sim C_{i,D} E^{D-4} \sim \bigg ( {E \over \Lambda } \bigg )^{D-4}. \end{aligned}$$

(3.5)

For example, the effects of dimension-4 operators are unsuppressed, the effects of dimension-5 operators are suppressed by $E/\Lambda$, the effects of dimension-6 operators are suppressed by $(E/\Lambda )^2$, and so on. The higher the dimension of the operator, the larger is the suppression. Thus, operators with lower dimensions will have a larger impact on phenomenology, assuming $E \ll \Lambda$, that is when SMEFT is used at the energy scale well below the mass scale of the UV completion. We can thus truncate the SMEFT Lagrangian at some particular D, ignoring the contributions of all but a finite number of operators. Conversely, for $E \sim \Lambda$ the suppression of higher-dimensional operators is no more, and one should take into account the whole infinite series of operators in the Lagrangian to correctly evaluate the amplitude. Obviously, in this regime SMEFT in unusable, and thus $\Lambda$ is the cutoff scale of SMEFT, beyond which it should be replaced by a more fundamental theory.

One important consequence of the standard power counting is that it allows one to define SMEFT at the quantum level. Recall that SMEFT is non-renormalizable, thus in principle an infinite number of unknown counterterms has to be introduced to properly define loop corrections to amplitudes of physical processes. However, working at $E \ll \Lambda$, we can declare that we drop from the amplitudes all the contributions that are $\mathcal {O}(\Lambda ^{4-D_{\textrm{max}} -1})$ or smaller. By dimensional analysis it is easy to see that the counterterms corresponding to operators of dimension $D_{\textrm{max}} + 1$ are moot and we can neglect them in our analysis. This leaves a finite number of operators of dimension $D \le D_{\textrm{max}}$, together with the associated counterterms. Thus, SMEFT with the standard power counting and truncated at a finite $D_{\textrm{max}}$ is as renormalizable as the renormalizable theories in the standard sense $(D_{\textrm{max}} = 4).$ From the SM it differs only by a larger number of counterterms (if $D_{\textrm{max}}>4$), thus a larger number of free parameters that have to be fixed by experiments.

The standard power counting sketched above has the advantage of being simple and self-consistent. One should remember however that it is not the only option, and it may not be the most sound one from the physics point of view. A run-of-the-mill UV completion will not generate all Wilson coefficients universally; typically it will generate a handful of operators at tree level, while others will be suppressed by loop factors, leading to hierarchies not captured by Eq. (3.5). Moreover, certain types of operators can never be generated at tree level, independently of the UV completion. Next, flavor or other symmetries in the UV completion may lead to special patterns in SMEFT, leading to additional suppression of Wilson coefficients. For example, Eq. (3.5) suggests that Wilson coefficients corresponding to analogous operators involving say, up and top quarks scale in the same way, however if the UV completion incorporates something akin to SM flavor hierarchies (which is very likely) one expects the former will be suppressed compared to the latter by a small factor $(m_u/m_t)^n$. Finally, Eq. (3.5) ignores the dependence of the Wilson coefficients on the coupling strength in the UV theory. Consider a UV theory with a single coupling $g_*$. Very often, Wilson coefficients of dimension-6 and -8 operators will scale $C_{i,6} \sim {g_*^2 \over \Lambda ^2}$ and $C_{i,8} \sim {g_*^2 \over \Lambda ^4}$. In the standard power counting, $C_{i,6}^2$ is always of the same order as $C_{i,8}$, which is indeed the case for $g_* \sim 1$. But for $g_* \ll 1$ we have $C_{i,8} \gg C_{i,6}^2$, whereas for $1 \ll g_* \lesssim 4\pi$ we have $C_{i,8} \ll C_{i,6}^2$, in both case the parametric hierarchy being missed in the standard power counting.

Nevertheless, let us brush aside these caveats for the time being and proceed under the assumption that the canonical dimension of an operator is the central determinant of its relevance for the low-energy phenomenology at $E \ll \Lambda$. Consequently, we will build the SMEFT Lagrangian starting from the operators of lowest dimensions, and working up towards higher D.

4.2 $D \le 4$

The sum in Eq. (3.1) starts at $D=2$ because there is nothing at lower dimensions: $D=0$ would be a field-independent constant, which has no physical consequences in non-gravitational theories, while there is no gauge invariant $D=1$ operators because there are no singlet scalars in the spectrum in Table 1. At $D=2$ there is a single gauge invariant operator, the Higgs mass squared:

$$\begin{aligned} {{\mathcal {L}}}_{D=2} = \mu _H^2 H^{\dagger } H. \end{aligned}$$

(3.6)

The Wilson coefficient in this case has mass dimension 2 and is denoted as $\mu _H^2$. According to our power counting in Eq. (3.4), we should have $\mu _H \sim \Lambda \gg v$. In reality we expect $\mu _H \lesssim v$ because the Higgs mass term triggers electroweak symmetry breaking by the Higgs VEV. In the SM, where there are no free unknown parameters anymore, we know precisely the tree level value $\mu _H \simeq 88$ GeV. In SMEFT I cannot give you a number for $\mu _H$ because unknown higher dimensional operators also affect the Higgs VEV. Nevertheless, $\mu _H \gg v$ would be unnatural as it would require large cancelations between $\mu _H$ and higher-dimensional operators to arrive at the correct value of v. We thus have a puzzle. On one hand, power counting predicts $\mu _H \sim \Lambda \gg v$. On the other hand, phenomenological and naturalness arguments imply $\mu _H \lesssim v$. This clash is nothing else but the hierarchy problem.⁵ Not so long ago, the hierarchy problem was considered an almost certain indication that there are new degrees of freedom at the electroweak scale, for example the supersymmetric partners or the Kaluza–Klein modes of the SM particles. If that were the case, SMEFT would not be a useful theory in any energy range. However, the results from the LHC strongly suggest that the SM degrees of freedom are all there is near the electroweak scale, and that SMEFT is the correct description of physics, at least in the energy range from 100 GeV up to a few TeV. That’s good for SMEFT and fortunate for my lectures, however the hierarchy problem remains puzzling. Have we somehow missed the degrees of freedom responsible for stabilizing the electroweak scale? Can the hierarchy problem be addressed with no new degrees of freedom at the electroweak scale? Do we misunderstand something about how QFT works? Is the SM more fundamental than we think? It is fair to say that no one has presented a convincing solution so far.

So, we start with high ideals: everything is EFT, physics is basically dimensional analysis, etc., but at the first opportunity reality slaps us in the face...Nevertheless let us press on and apply the standard power counting to SMEFT operators of dimensions higher than two. At $D=3$ again there are no gauge invariant operators because there are no singlet fermions in the spectrum in Table 1.⁶ At $D=4$ there are multiple gauge-invariant operators. Here is the complete list⁷

$$\begin{aligned} {{\mathcal {L}}}_{D=4}&= -{1 \over 4}\sum _{V \in B,W^i,G^a} V_{\mu \nu } V^{\mu \nu } \nonumber \\&\quad + \sum _{f \in Q,L} i {\bar{f}} {\bar{\sigma }}^{\mu } D_{\mu } f + \sum _{f \in U,D,E} i f^c \sigma ^{\mu } D_{\mu } {\bar{f}}^c \nonumber \\&\quad - \left( {\bar{Q}} {\tilde{H}} Y_u {\bar{U}}^c + {\bar{Q}} H Y_d {\bar{D}}^c + {\bar{L}} H Y_e {\bar{E}}^c + {{\mathrm{h.c.}}} \right) \nonumber \\&\quad + D_{\mu } H^{\dagger } D^{\mu } H - \lambda (H^{\dagger } H)^2 \nonumber \\&\quad + {\tilde{\theta }} G_{\mu \nu }^a {\tilde{G}}_{\mu \nu }^a, \end{aligned}$$

(3.7)

where $V_{\mu \nu }^a = \partial _{\mu } V_{\nu }^a -\partial _{\nu } V_{\mu }^a - g f^{abc} V_{\mu }^b V_{\nu }^c$, $D_{\mu } X = \partial _{\mu } X + i g_s G_{\mu }^a T^a X + i g_L W_{\mu }^i {\sigma ^i \over 2} X + i g_Y B_{\mu } Y X$, ${\tilde{H}}_a = \epsilon ^{ab} H_b^*$, ${\tilde{G}}_{\mu \nu }^a \equiv {1 \over 2} \epsilon _{\mu \nu \alpha \beta }G^{\alpha \beta \ }{}^a$, and $Y_f$ are $3 \times 3$ matrices in the generation space. Dimensional analysis dictates that all the couplings in the dimension-4 Lagrangian: the gauge couplings $g_X$, the Yukawa couplings $Y_f$, and the quartic coupling $\lambda$, are dimensionless. The standard power counting in Eq. (3.4) treats them all as $\mathcal {O}(\Lambda ^0)$ couplings. In reality, this is reasonably well borne out for the gauge and quartic couplings, but not for most of the elements of $Y_f$. Clearly Eq. (3.4) does not know about flavor hierarchies. Some of the $D=4$ Wilson coefficients are extremely suppressed, e.g. $[Y_e]_{11} \simeq 3 \times 10^{-6}$ (in a convenient basis). It is conceivable that contributions of some $D>4$ operators to certain scattering amplitudes will be larger than the effects proportional to the electron Yukawa coupling, which would represent another break down of the standard power counting. But, overall, the standard power counting is a very successful principle at $D=4$: all but the last term in Eq. (3.7) have been experimentally shown to exist (again assuming that hey are not somehow mimicked by higher-dimensional operators). Of course, ${{\mathcal {L}}}_{D=2}+ {{\mathcal {L}}}_{D=4}$ is nothing else than the SM Lagrangian, so the success of SMEFT with the standard power counting is to reproduce the SM as the leading terms in its EFT expansion. Concerning the last term in Eq. (3.7), the current constraints are $|{\tilde{\theta }}| \lesssim 10^{-12}$. The lack of experimental evidence for the $\theta$ term, which is referred to as the strong CP problem, is as much puzzling from the EFT perspective as it is within the SM. Fortunately, unlike for the hierarchy problem, we have some reasonable ideas about the solution. The smallness of ${\tilde{\theta }}$ likely means that there is a new particle called the QCD axion, which effectively makes ${\tilde{\theta }}$ a dynamical quantity settled in a minimum where ${\tilde{\theta }} \sim 0$. But at this point one cannot completely exclude the possibility that we misunderstand something fundamental about QCD, and in reality the ${\tilde{\theta }}$ term has no physical effects.⁸ Or that the parameter ${\tilde{\theta }}$ is very small by pure accident.

4.3 $D = 5$

We move to $D=5$, that is beyond the SM. At this order in the SMEFT expansion we have the following gauge-invariant interactions [8]:

$$\begin{aligned} {{\mathcal {L}}}_{D= 5} = - ({\bar{L}} H^{\dagger }) C_5 ({\bar{L}} H^{\dagger }) + {{\mathrm{h.c.}}} \end{aligned}$$

(3.8)

The Wilson coefficients $C_5$ form a $3 \times 3$ matrix in the generation space. Here and in most of the following, the generation indices are implicitly contracted, so that one should read Eq. (3.8) as ${{\mathcal {L}}}_{D= 5} = - \sum _{J,K=1}^3 ({\bar{l}}_J H^{\dagger } ) [C_5]_{JK} ({\bar{l}}_K H^{\dagger }) + {\mathrm{h.c.}}$. Dimensional analysis dictates that $[C_5] = {\textrm{mass}}^{-1}$, and standard power counting treats them as $\mathcal {O}(\Lambda ^{-1})$ parameters. The $SU(2)_W$ indices of the lepton and Higgs doublets are contracted via the epsilon tensor: $l H \equiv \epsilon ^{ab} l^a H^b$. After electroweak symmetry breaking, Eq. (3.8) gives rise to Majorana neutrino masses:

$$\begin{aligned} {{\mathcal {L}}}_{D= 5} \rightarrow - {v^2 \over 2} {\bar{\nu }}_J [C_5]_{JK} \, {\bar{\nu }}_K + {\mathrm{h.c.}} \end{aligned}$$

(3.9)

Incidentally, neutrinos are known to be massive particles.⁹ While we do not know the absolute values of the masses, we know the mass differences (squared) with a good accuracy, see e.g. [15]. Given this, one can estimate $C_5 v^2 \sim 10^{-1}$ eV, that is to say $C_5 \sim {1 \over 10^{15} \textrm{GeV}}$.

One cannot emphasize enough what an enormous success of the SMEFT paradigm this is. In SMEFT, the most relevant phenomenological effects at $E \ll \Lambda$ are expected from the $D=2$ and $D=4$ operators, which are those of the SM, and which are indeed seen in nature. Furthermore, the standard power counting predicts that the most relevant deviations from the SM should be due to $D=5$ operators. This prediction was spectacularly confirmed by the discovery of neutrino masses in the Super-Kamiokande detector in 1998 [16], almost 20 years after Weinberg’s paper [8].

At the same time, this very success carries a premonition of doom. The neutrino masses turn out to be quite small, leading to the appearance of a very large scale in the denominator of $C_5$. Since in the standard power counting $C_5 \sim \Lambda ^{-1}$, it would be most natural to conclude that the SMEFT expansion parameter $\Lambda = 10^{15}$ GeV. This would not be a problem for SMEFT – on the contrary, it would mean that the expansion is very quickly convergent, and thus the operators up to $D=5$, maybe plus a handful of operators at $D=6$ are enough to describe all physics at available energy scales. But this would be a problem for you and for me. It would mean that the gap between the electroweak scale and the new physics scale is enormous, which would make the options for fundamental research very limited. The directions worth pursuing would be neutrino physics, and perhaps proton decay. Otherwise one could switch to astrophysics, cosmology, quantum computing, nuclear fusion, climate science, or banking. Not much point for future colliders, flavor physics, charged lepton flavor violation, which would only serve to confirm ad nauseam the SM predictions.

This may be the future, but it does not have to be. Even within the SMEFT paradigm (no new light degrees of freedom), it is quite possible that the expansion parameter $\Lambda$ is much smaller than $10^{15}$ GeV. New physics responsible for the operators in Eq. (3.8) may be much lighter, perhaps even near the TeV scale, but coupled very weakly to the SM fermions. A sharper argument can be formulated by noticing that the operators is Eq. (3.8) are very special, as they violate the lepton number symmetry acting as $L \rightarrow e^{i \alpha } L$, $E^c \rightarrow e^{-i \alpha } E^c$. This is an accidental symmetry at the $D \le 4$ level, as one simply cannot construct a gauge invariant operators with $D \le 4$ that violates it, and thus $D=5$ is the lowest dimension where lepton-number-violating operators can appear. One can modify the standard power counting by assuming that there are two scales governing the SMEFT expansion. One, call it $\Lambda _L$, corresponds to the mass scale of $B-L$-violating new physics, and it happens to be very high, $\Lambda _L \sim 10^{15}$ GeV. Another, let’s keep calling it $\Lambda$ without a sub-index, corresponds to the mass scale of $B-L$-conserving new physics. It is then perfectly natural to have a huge gap between these two scales, $\Lambda \ll \Lambda _L$. Symmetry consideration forbid new physics at the scale $\Lambda$ to generate $D=5$ operators, and the lowest dimension it can show up is $D=6$. This assumption of the two-scale expansion gives us a rationale for exploring the SMEFT Lagrangian at $D=6$ and higher, and we will tacitly adopt this point of view in all of the following.

4.4 $D = 6$

We have arrived at dimension-6 operators, which is the nexus of the SMEFT research. At $D=2$ there is a single operator; the $D=4$ Lagrangian can fit a t-shirt; at $D=5$ there is basically a single operator but, taking into account the generation structure, it counts as 12 operators.¹⁰ At $D=6$, all hell breaks loose: we have...wait for it...3045 independent operators. They contribute to phenomenology in virtually all areas of particle physics, such as Higgs physics, electroweak precision observables, flavor physics, nuclear physics, electric dipole moments, and much more. Below I will present a quick survey of dimension-6 operators using the set proposed in Ref. [17] and known under the name of the Warsaw basis. To organize the presentation, let me divide them into several classes:

$$\begin{aligned} {{\mathcal {L}}}_{D=6} = {{\mathcal {L}}}_{D=6}^{\textrm{bosonic}} + {{\mathcal {L}}}_{D=6}^{\textrm{Yukawa}} + {{\mathcal {L}}}_{D=6}^{\textrm{current}} + {{\mathcal {L}}}_{D=6}^{\textrm{dipole}} + {{\mathcal {L}}}_{D=6}^{4\text {-}{\textrm{fermion}}}.\nonumber \\ \end{aligned}$$

(3.10)

The bosonic operators, as the name suggest, are constructed out of the SM gauge and Higgs fields, without involving any fermionic fields. In the Warsaw basis there are 15 bosonic operators:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{\textrm{bosonic}}&= C_H (H^{\dagger } H)^3 + C_{H\Box } (H^{\dagger } H) \Box (H^{\dagger } H) \nonumber \\&\quad + C_{HD} | H^{\dagger } D_{\mu } H |^2 +C_{HWB} H^{\dagger } \sigma ^k H \, W^k_{\mu \nu } B_{\mu \nu } \nonumber \\&\quad + C_{HG} H^{\dagger } H\, G^a_{\mu \nu } G^a_{\mu \nu } +C_{HW} H^{\dagger } H\, W^k_{\mu \nu } W^k_{\mu \nu } \nonumber \\&\quad +C_{HB} H^{\dagger } H\, B_{\mu \nu } B_{\mu \nu } \nonumber \\&\quad +C_{W} \epsilon ^{klm} W_{\mu \nu }^k W_{\nu \rho }^l W_{\rho \mu }^m +C_{G} f^{abc} G_{\mu \nu }^{a} G_{\nu \rho }^b G_{\rho \mu }^c \nonumber \\&\quad +C_{H {\widetilde{G}}} H^{\dagger } H\, {\widetilde{G}}^a_{\mu \nu } G^a_{\mu \nu } +C_{H {\widetilde{W}}} H^{\dagger } H\, {\widetilde{W}}^k_{\mu \nu } W^k_{\mu \nu } \nonumber \\&\quad +C_{H {\widetilde{B}}} H^{\dagger } H\, {\widetilde{B}}_{\mu \nu } B_{\mu \nu } + C_{H {\widetilde{W}}B} H^{\dagger } \sigma ^k H \, {\widetilde{W}}^k_{\mu \nu } B_{\mu \nu } \nonumber \\&\quad + C_{ {\widetilde{W}}} \epsilon ^{klm} {\widetilde{W}}_{\mu \nu }^k W_{\nu \rho }^l W_{\rho \mu }^m +C_{ {\widetilde{G}}} f^{abc} {\widetilde{G}}_{\mu \nu }^{a} G_{\nu \rho }^b G_{\rho \mu }^c , \end{aligned}$$

(3.11)

where $\Box \equiv \partial _{\mu } \partial ^{\mu }$ and $\sigma ^k$ are the three Pauli matrices. Already this relatively small subset of dimension-6 operators contains rich phenomenology. $C_H$ changes the shape of the Higgs potential, in particular it affects the cubic Higgs boson self-coupling – perhaps the last landmark measurement to be delivered by the LHC. $C_{H \Box }$ contributes to the Higgs boson kinetic term and thus, indirectly, affects universally all Higgs boson production and decay rates. The following two operators contribute to electroweak precision observables measured long ago by the LEP collider. $C_{HD}$ contributes to the Z boson mass, while $C_{HWB}$ contributes to the kinetic mixing between the photon and the Z boson. Through these intermediaries, they affect the whole lot of electroweak precision observables. In fact, these two are just the famous oblique S and T parameters of Peskin and Takeuchi [18] in another (more modern) guise. Furthermore, $C_{HWB}$ as well as the Wilson coefficients $C_{HG}$, $C_{HW}$, $C_{HB}$ in the second line contribute to the ever important Higgs boson interaction strengths with gluons, W, Z, and photons, which are measured at the LHC. In the third line, $C_{W}$ and $C_{G}$ induce 3-derivative anomalous cubic interactions of electroweak gauge bosons and gluons, respectively. The final two lines contain CP violating interactions. They can be searched for in colliders, but more easily discernible effects appear via their loop contributions to electric dipole moments of the electron or the neutron.

The next class of dimension-6 operators we discuss are Yukawa-like interactions:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{\textrm{Yukawa}}&= H^{\dagger } H ({\bar{L}} H C _{eH} {\bar{E}}^c) +H^{\dagger } H ({\bar{Q}} {\tilde{H}} C _{uH} {\bar{U}}^c) \nonumber \\&\quad + H^{\dagger } H ({\bar{Q}} H C _{dH} {\bar{D}}^c) + {\mathrm{h.c.}}\end{aligned}$$

(3.12)

Each $C_{fH}$ is a $3 \times 3$ complex matrix in the generation space, thus each comes with 18 free parameters, which makes 54 parameters overall. These operators contribute to the fermion masses, but that is unobservable because it merely renormalizes the unknown Yukawa matrices in Eq. (3.7). The observables effect is the modification of the Higgs boson Yukawa couplings to the fermions. In the SM, the Yukawa coupling is not a free parameter but it is uniquely fixed by the fermion’s mass. In the presence of the operator is Eq. (3.12) that relation no longer holds, and the Higgs boson couplings to fermions become free parameters independent of fermion masses. Moreover, a qualitatively new effect of flavor violation in Higgs interactions may appear. That is to say, the Higgs boson can couple to two fermions from different generations, e.g. ${{\mathcal {L}}}_{\textrm{SMEFT}} \supset h {\bar{e}} {\bar{\mu }}^c$, which does not occur in the SM.

Next, we have what I call the current operators:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{\textrm{current}}&= i H^{\dagger } \overleftrightarrow {D}_{\mu } H ({\bar{L}} C_{Hl}^{(1)} {\bar{\sigma }}^{\mu } L) \nonumber \\&\quad + i H^{\dagger } \sigma ^k \overleftrightarrow {D}_{\mu } H ({\bar{L}} C_{Hl}^{(3)} {\bar{\sigma }}^{\mu } \sigma ^k L) \nonumber \\&\quad + i H^{\dagger } \overleftrightarrow {D}_{\mu } H (E^c C_{He} \sigma ^{\mu } {\bar{E}}^c) \nonumber \\&\quad + i H^{\dagger } \overleftrightarrow {D}_{\mu } H ({\bar{Q}} C_{Hq}^{(1)} {\bar{\sigma }}^{\mu } Q) \nonumber \\&\quad + i H^{\dagger } \sigma ^k \overleftrightarrow {D}_{\mu } H ({\bar{Q}} C_{Hq}^{(3)} {\bar{\sigma }}^{\mu } \sigma ^k Q) \nonumber \\&\quad + i H^{\dagger } \overleftrightarrow {D}_{\mu } H (U^c C_{Hu} \sigma ^{\mu } {\bar{U}}^c) \nonumber \\&\quad + i H^{\dagger } \overleftrightarrow {D}_{\mu } H (D^c C_{Hd} \sigma ^{\mu } {\bar{D}}^c)\nonumber \\&\quad + \bigg \{ i {\tilde{H}}^{\dagger } {D}_{\mu } H (U^c C_{Hud} \sigma ^{\mu } {\bar{D}}^c) + {\mathrm{h.c.}}\bigg \} , \end{aligned}$$

(3.13)

where $H^{\dagger } \overleftrightarrow {D}_{\mu } H \equiv H^{\dagger }{D}_{\mu } H - {D}_{\mu } H^{\dagger } H$. The Wilson coefficient $C_{Hf}$ are matrices in the generation space, but now only $C_{Hud}$ is a general complex matrix, while the remaining ones are Hermitian matrices (thus with 9 free parameters each). This adds up to 81 free parameters in Eq. (3.13). These operators contribute to the W and Z bosons interactions with fermions, which have been precisely measured in the LEP, Tevatron, and LHC colliders. Several qualitatively new effects are introduced by Eq. (3.13). One is the W boson couplings to right-handed quarks, e.g. ${{\mathcal {L}}}_{\textrm{SMEFT}} \supset W_{\mu } (t^c \sigma ^{\mu } {\bar{b}}^c)$, whereas in the SM W couples only to left-handed quarks. Another is tree-level flavor-changing neutral currents, that is Z boson couplings to quarks or leptons of different generations, e.g. ${{\mathcal {L}}}_{\textrm{SMEFT}} \supset Z_{\mu } ({\bar{b}} {\bar{\sigma }}^{\mu } s)$.

Next, we have the dipole operators

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{\textrm{dipole}}&= ({\bar{Q}} \sigma ^k {\tilde{H}} C _{uW} {\bar{\sigma }}^{\mu \nu } {\bar{U}}^c) W_{\mu \nu }^k + ({\bar{Q}} {\tilde{H}} C _{uB} {\bar{\sigma }}^{\mu \nu } {\bar{U}}^c) B_{\mu \nu } \nonumber \\&\quad + ({\bar{Q}} {\tilde{H}} C _{uG} T^a {\bar{\sigma }}^{\mu \nu } {\bar{U}}^c) G_{\mu \nu }^a \nonumber \\&\quad + ({\bar{Q}} \sigma ^k H C _{dW} {\bar{\sigma }}^{\mu \nu } {\bar{D}}^c) W_{\mu \nu }^k + ({\bar{Q}} H C _{dB} {\bar{\sigma }}^{\mu \nu } {\bar{D}}^c) B_{\mu \nu } \nonumber \\&\quad + ({\bar{Q}} H C _{dG} T^a {\bar{\sigma }}^{\mu \nu } {\bar{D}}^c) G_{\mu \nu }^a \nonumber \\&\quad + ({\bar{L}} \sigma ^k H C _{eW} {\bar{\sigma }}^{\mu \nu } {\bar{E}}^c) W_{\mu \nu }^k \nonumber \\&\quad + ({\bar{L}} H C _{eB} {\bar{\sigma }}^{\mu \nu } {\bar{E}}^c) B_{\mu \nu } + {\mathrm{h.c.}}\end{aligned}$$

(3.14)

Given that $C_{fV}$ are $3\times 3$ complex matrices in the generation space, the above introduces 144 free parameters. An important effect of the operators in Eq. (3.13) is their contribution to the anomalous magnetic dipole moments of fundamental particles. In particular, the Wilson coefficients $[C _{eW}]_{22}$ and $[C _{eB}]_{22}$ contribute to the muon $g-2$ which, at the time of writing, may or may not deviate from the SM prediction. The imaginary parts of these Wilson coefficients contribute to electric dipole moments. Moreover, the operators in Eq. (3.13) can mediate certain processes that are forbidden in the SM, e.g. the $\mu \rightarrow e \gamma$ decay.

The dimension-6 operators introduced so far come with $15+54+81+144=294$ free parameters. It follows that a large majority of dimension-6 operators are hiding in the last term in Eq. (3.10), which contains 4-fermion operators. For the sake of this discussion let me split them further into four sub-classes:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{\mathrm{4-fermion}} = {{\mathcal {L}}}_{D=6}^{4L} + {{\mathcal {L}}}_{D=6}^{2L2Q} + {{\mathcal {L}}}_{D=6}^{4Q} + {{\mathcal {L}}}_{D=6}^{3Q1L}, \end{aligned}$$

(3.15)

defined by the number of lepton and of quark fields. The first sub-class in Eq. (3.15) is the 4-lepton operators:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{4L}&= {1 \over 2} ({\bar{L}} {\bar{\sigma }}^{\mu } L) C_{ll} ({\bar{L}} {\bar{\sigma }}_{\mu } L) + {1 \over 2} (E^c \sigma _{\mu } {\bar{E}}^c) C_{ee}\nonumber \\&\quad \times (E^c \sigma _{\mu } {\bar{E}}^c) + ({\bar{L}} {\bar{\sigma }}^{\mu } L) C_{le} (E^c \sigma _{\mu } {\bar{E}}^c). \end{aligned}$$

(3.16)

This time and for all 4-fermion operators in the following, the Wilson coefficients are 4-index tensors $[C_X]_{JKLM}$ in the generation space. The indices are implicitly contracted with the generation indices of the fermions on the left and on the right; for example, the first term in Eq. (3.16) should be read as ${1 \over 2} \sum _{J,K,L,M=1}^3 ({\bar{l}}_J {\bar{\sigma }}^{\mu } l_K) [C_{ll}]_{JKLM} ({\bar{l}}_L {\bar{\sigma }}_{\mu } l_M)$. Hermiticity of the Lagrangian implies that the Wilson coefficients in Eq. (3.16) are Hermitian in the first two and the last two indices: $[C_{XY}]_{JKLM} = [C_{XY}]_{KJML}^*$. For $C_{ll}$ and $C_{ee}$ there is an additional complication stemming from the fact that $({\bar{l}}_J {\bar{\sigma }}^{\mu } l_K) ({\bar{l}}_K {\bar{\sigma }}_{\mu } l_L)$ and $({\bar{l}}_K {\bar{\sigma }}^{\mu } l_J) ({\bar{l}}_J {\bar{\sigma }}_{\mu } l_K)$ are the same. Thus, for example, Eq. (3.16) contains

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{4L}&\supset {1 \over 2} [C_{ll}]_{1221} ({\bar{l}}_1 {\bar{\sigma }}^{\mu } l_2) ({\bar{l}}_2 {\bar{\sigma }}_{\mu } l_1) \nonumber \\&\quad + {1 \over 2} [C_{ll}]_{2112} ({\bar{l}}_2 {\bar{\sigma }}^{\mu } l_1) ({\bar{l}}_1 {\bar{\sigma }}_{\mu } l_2) \nonumber \\&= {1 \over 2} ([ C_{ll}]_{1221} + [C_{ll}]_{2112}) ({\bar{l}}_1 {\bar{\sigma }}^{\mu } l_2) ({\bar{l}}_2 {\bar{\sigma }}_{\mu } l_1) \nonumber \\&= {\textrm{Re}} \,[ C_{ll}]_{1221} ({\bar{l}}_1 {\bar{\sigma }}^{\mu } l_2) ({\bar{l}}_2 {\bar{\sigma }}_{\mu } l_1). \end{aligned}$$

(3.17)

Therefore the components $[C_{ll}]_{JKKJ}$ and $[C_{ee}]_{JKKJ}$ can be declared real, as their imaginary parts do not enter the Lagrangian.¹¹ Four-lepton operators containing electron fields are relevant for physics at LEP-2, where $e^+e^-$ pair were collided with the center-of-mass energy above the Z pole. A subset of interactions in Eq. (3.16) mediate tree-level charge-lepton-flavor violating processed, where the overall lepton number is conserved, but the separate electron, muon, or tau numbers are not. Such processes are forbidden in the SM, while they are mediated at loop level via the $D=5$ intermediaries but with very suppressed rates due to the smallness of the neutrino masses. For example, $[C_{ee}]_{1112}$ mediates the $\mu ^- \rightarrow e^- e^- e^+$ decay, which is subject to current experimental searches [20]. Finally, it is worth mentioning that $[C_{ll}]_{1221}$ contributes to the usual muon decay $\mu ^- \rightarrow e^- {\bar{\nu }}_e \nu _{\mu }$, which in the SM is a standard candle to determine the Fermi constant. By disrupting this standard candle, $[C_{ll}]_{1221}$ indirectly affects SM predictions for countless precision measurements.

The next sub-class in Eq. (3.15) are semi-leptonic operators, that is 4-fermion operators containing two quark and two lepton fields:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{2L2Q}&= ({\bar{L}} {\bar{\sigma }}^{\mu } L ) C_{lq}^{(1)} ({\bar{Q}} {\bar{\sigma }}_{\mu } Q ) + ({\bar{L}} {\bar{\sigma }}^{\mu } \sigma ^k L )C_{lq}^{(3)} ({\bar{Q}} {\bar{\sigma }}_{\mu } \sigma ^k Q ) \nonumber \\&\quad + (E^c \sigma _{\mu } {\bar{E}}^c) C_{eu} (U^c \sigma _{\mu } {\bar{U}}^c) + (E^c \sigma _{\mu } {\bar{E}}^c) C_{ed} (D^c \sigma _{\mu } {\bar{D}}^c) \nonumber \\&\quad + ({\bar{L}} {\bar{\sigma }}^{\mu } L ) C_{lu} (U^c \sigma _{\mu } {\bar{U}}^c) +({\bar{L}} {\bar{\sigma }}^{\mu } L ) C_{ld} (D^c \sigma _{\mu } {\bar{D}}^c)\nonumber \\&\quad + (E^c \sigma _{\mu } {\bar{E}}^c) C_{eq} (Q {\bar{\sigma }}_{\mu } Q) \nonumber \\&\quad + \bigg \{ ({\bar{L}} {\bar{E}}^c) C_{ledq} (D^c Q) +\epsilon ^{kl} ({\bar{L}}^k {\bar{E}}^c) C_{lequ}^{(1)}({\bar{Q}}^l {\bar{U}}^c) \nonumber \\&\quad + \epsilon ^{kl} ({\bar{L}}^k {\bar{\sigma }}^{\mu \nu } {\bar{E}}^c) C_{lequ}^{(3)} ({\bar{Q}}^l {\bar{\sigma }}^{\mu \nu } {\bar{U}}^c) + {\mathrm{h.c.}}\bigg \} . \end{aligned}$$

(3.18)

The semi-leptonic operators affect myriads of important precision observables: hadronic cross sections at LEP-2, Drell–Yan production of leptons in hadron colliders, electric dipole moments, beta decays, and so on. They also play a major role in flavor physics, where they contribute to semileptonic flavor transitions. These are often under reasonable theoretical control, such that reliable SM predictions can be established, and thus stringent constraints on the dimension-6 operators can de derived. Moreover, the importance of the operators contributing to flavor-changing neutral currents is amplified by the suppression of these processes in the SM. One of many relevant examples of this kind is the $B_s \rightarrow \mu ^+ \mu ^-$ decay, whose branching fraction is currently measured with 10% precision, and the SM prediction is know with a similar accuracy. That decay rate is affected, among others, by the Wilson coefficient $[C_{lq}^{(1)}]_{2232}$.

The third sub-class singled out in Eq. (3.15) are four-quark operators:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{4Q}&= {1 \over 2} ({\bar{Q}} {\bar{\sigma }}^{\mu } Q) C_{qq}^{(1)} ({\bar{Q}} {\bar{\sigma }}_{\mu } Q) \nonumber \\&\quad + {1 \over 2} ({\bar{Q}} {\bar{\sigma }}^{\mu } \sigma ^k Q )C_{qq}^{(3)} ({\bar{Q}} {\bar{\sigma }}_{\mu } \sigma ^k Q) \nonumber \\&\quad + {1 \over 2} (U^c \sigma _{\mu } {\bar{U}}^c) C_{uu} (U^c \sigma _{\mu } {\bar{U}}^c) \nonumber \\&\quad + {1 \over 2} (D^c \sigma _{\mu } {\bar{D}}^c) C_{dd} (D^c \sigma _{\mu } {\bar{D}}^c) \nonumber \\&\quad + (U^c \sigma _{\mu } {\bar{U}}^c) C_{ud}^{(1)} (D^c \sigma _{\mu } {\bar{D}}^c) \nonumber \\&\quad + (U^c \sigma _{\mu } T^a {\bar{U}}^c) C_{ud}^{(8)} (D^c \sigma _{\mu } T^a {\bar{D}}^c) \nonumber \\&\quad + (Q^c \sigma _{\mu } {\bar{Q}}^c) C_{qu}^{(1)} (U^c \sigma _{\mu } {\bar{U}}^c) \nonumber \\&\quad + (Q^c \sigma _{\mu } T^a {\bar{Q}}^c) C_{qu}^{(8)} (U^c \sigma _{\mu } T^a {\bar{U}}^c)] \nonumber \\&\quad + (Q^c \sigma _{\mu } {\bar{Q}}^c) C_{qd}^{(1)} (D^c \sigma _{\mu } {\bar{D}}^c)\nonumber \\&\quad + (Q^c \sigma _{\mu } T^a {\bar{Q}}^c) C_{qd}^{(8)} (D^c \sigma _{\mu } T^a {\bar{D}}^c) \nonumber \\&\quad + \bigg \{ \epsilon ^{kl} ({\bar{Q}}^k {\bar{U}}^c) C_{quqd}^{(1)}({\bar{Q}}^l {\bar{D}}^c) \nonumber \\&\quad + \epsilon ^{kl} ({\bar{Q}}^k T^a {\bar{U}}^c) C_{quqd}^{(1)}({\bar{Q}}^l T^a {\bar{D}}^c) + {\mathrm{h.c.}}\bigg \} . \end{aligned}$$

(3.19)

These play arguably a lesser role in phenomenology. The reason is that their effects have to compete with QCD processes, which are typically abundant and poorly controlled theoretically, especially at hadron colliders. Nevertheless, some of the operators in Eq. (3.19) will appear later in our story in the context of precision observables.

The final sub-class in Eq. (3.15) is perhaps the most exciting one, as it consists of operators violating the baryon and lepton numbers:

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{3Q1L}&= (D^c U^c) C_{duq} ({\bar{Q}} {\bar{L}}) + (QQ) C_{qqu} ({\bar{U}}^c {\bar{E}}^c) \nonumber \\&\quad + (QQ) C_{qqq} (Q L) + (D^c U^c) C_{duu} (U^c E^c) + {\mathrm{h.c.}} \end{aligned}$$

(3.20)

Above, the quark color indices are implicitly contracted by epsilon tensors, e.g. $q q q \equiv \epsilon ^{abc} q^a q^b q^c$. These operators violate the baryon number B defined as the global symmetry transformation $Q \rightarrow e^{i \beta /3 } Q$, $U^c \rightarrow e^{-i \beta /3 }U^c$, $D^c \rightarrow e^{-i \beta /3 }D^c$. Baryon number is a symmetry for all operators with $D \le 5$.¹² They also violate the lepton number defined as the global symmetry transformation $L \rightarrow e^{i \alpha } L$, $E^c \rightarrow e^{- i \alpha } E^c$. The violation of baryon and lepton number implies that these operators can mediate proton decay, in particular the $p \rightarrow \pi ^0 e^+$ process can be mediated at tree level by the operators involving the first generation fermions. Since experimental bounds on proton decay are extremely stringent, some of the Wilson coefficients in Eq. (3.20) must be suppressed by a very high scale. To my knowledge, among all processes mediated by higher dimensional operators, proton decay probes the highest scale, not too far from the mythical Planck scale. Comparison of different scales probed by different precision experiments is shown in Fig. 3.

Fig. 3

The scale suppressing higher-dimensional SMEFT operators probed by selected observables. From left to right: proton decay, neutrino oscillations, electron EDM, $\mu \rightarrow e \gamma$, kaon mixing, neutron EDM, B-meson mixing, electron anomalous magnetic moment, beta decay, Higgs decay to tau leptons

4.5 Beyond $D = 6$

The sum in Eq. (3.1) extends to $D= \infty$, and one could press on, but, more often than not, the discussion in SMEFT stops at dimension six. What lies beyond? At $D=7$ we have 1542 independent operators, at $D=8$ the number is 44807, at $D=9$ it grows to 90456, and at $D=10$ we have a whopping 2092441 operators (two million!) [21]. There is a good chance, however, that in your research you won’t ever deal with this cornucopia of higher-dimension operators. The exponential growth of the number of operators with increasing D is one reason, as it quickly makes any systematic analysis difficult. But that practical difficulty is not the only reason. The philosophy of SMEFT with the standard power counting is that, the higher the dimension of the operator, the more suppressed its effect is. Since at present we do not have any observational evidence of dimension-6 operators, it is hard to believe that $D>6$ operators might show up in any experiment in a foreseeable future. This general conclusion should hold for other reasonable power counting beyond the standard one. There are a few exceptions, however, that one should be aware of. First of all, if new physics is close to the electroweak scale, the effect of higher-dimensional operators may be non-negligible, especially for observables probing the high-energy tail of differential distributions at the LHC, such as for example the Drell–Yan production of leptons, $pp \rightarrow \ell ^+ \ell ^-$. But that is of course also the situation where the SMEFT itself is least useful, since the central assumption of the mass gap is not quite satisfied. A more relevant case is when a qualitatively new phenomenon, which cannot be induced by $D \le 6$ operators, appears at $D>6$. For example, tree-level contributions to light-by-light scattering enter at $D=8$ from operators such as $(B_{\mu \nu } B^{\mu \nu })^2$; another $D=8$ operator $({\bar{l}}_1 H {\bar{\sigma }}^{\mu } {\tilde{H}} l_1)(u^c \sigma _{\mu } {\bar{d}}^c)$ might play an important role in CP violation in nuclear beta decay [22]; neutron-antineutron oscillations arise at $D=9$ from operators such as $({\bar{u}}^c {\bar{d}}^c)^3$ [23]. When analyzing this kind of observables, one should however pay attention whether new physics generating these higher-dimensional operators might not show up in other observables via $D \le 6$ operators.

All in all, while every particle physicist should have at least a rudimentary knowledge of the dimension-6 SMEFT operators, excursions beyond that are necessary and justified only in rare circumstances. You should be aware of the existence of higher-dimensional operators, and you should be able to use power counting to estimate their effects relative to the ones coming from lower-dimensional operators. But it is quite unlikely that the higher-dimensional operators can play a useful role in discovering or constraining new physics. The situation will of course change if dimension-6 operators are observed in nature. In such a case, going to higher dimensions will sharpen our low-energy description of new physics, and may help to pinpoint the scale of new physics [24].

4.6 Summary of the SMEFT Lagrangian

To summarize this section, SMEFT is a QFT with the spectrum given in Table 1 and the Lagrangian of the form

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} = {{\mathcal {L}}}_{D=2} + {{\mathcal {L}}}_{D=4} + {{\mathcal {L}}}_{D=5} + {{\mathcal {L}}}_{D=6} + \cdots \end{aligned}$$

(3.21)

where the consecutive terms are given in Eqs. (3.6) to (3.8) and (3.10) and the dots stand for higher dimensional interactions. The interactions in ${{\mathcal {L}}}_{D=5}$ and ${{\mathcal {L}}}_{D=6}$ describe various effects of the virtual exchange of exotic particles not included in Table 1, and the scale $\Lambda$ inherent in their Wilson coefficients is related to the mass scale M of these exotic particles. Almost any BSM model you will encounter will induce some $D=5$ and $D=6$ interactions.¹³ The Wilson coefficients of the $D \ge 7$ interactions are suppressed by higher powers of M, and they are rarely of phenomenological relevance as long as $M \gg v$. SMEFT is an effective theory, implying a finite validity range $m_Z \lesssim E \lesssim M$. At the energy scale $E \sim M$ it should be replaced with its UV completion, which contains new weakly coupled particles and interactions, or maybe a strong dynamics from which some of the particles in Table 1 emerge. At the energy scale $E \sim m_Z$ it is convenient to integrate out the electroweak bosons, top quark, and Higgs, to derive another effective theory called WEFT with a smaller spectrum and a smaller gauge symmetry.

Since we do not know what is the UV completion of SMEFT, the usual philosophy is to include all possible independent interactions in Eq. (3.21) with completely arbitrary Wilson coefficients. This is a sane approach, up to small caveats. First, we should pay attention that the validity range is not null. This could happen if the Wilson coefficients are too large, as then the SMEFT amplitudes may violate perturbative unitarity already at $E \sim v$. Second, the existing experimental results already put important bounds on some combinations of Wilson coefficients; more about it in Sect. 5. Third, several interaction terms in Eq. (3.21), such as e.g. $\epsilon ^{klm}W_{\mu \nu }^k W_{\nu \rho }^l W_{\rho \mu }^m$ or ${\bar{L}} H {\bar{\sigma }}^{\mu \nu } {\bar{E}}^c B_{\mu \nu }$ arise from integrating out new particles at one loop level. Therefore we should not expect their Wilson coefficients to be very small, e.g. $C_W \sim {1 \over v^2}$ would imply BSM particles below the electroweak scale, in contradiction with the assumptions behind SMEFT. Finally, there exist more subtle constraints on EFT Wilson coefficient arising from the mere assumption that the UV completion is local, unitary, and Poincaré invariant [26]. These typically imply a definite sign of a Wilson coefficient or a combination thereof, therefore they are referred to as the positivity constraints. With completely general assumptions about the high-energy behavior of the amplitudes in the UV completion, the positivity bounds are relevant for dimension-8 operators and higher. Therefore their application to SMEFT is limited to very specific cases, for example to the study of quartic gauge boson interactions [27, 28]. In order to apply the positivity constraints to dimension-6 operators, additional assumptions about the UV completion are necessary [29].

5 Bases of SMEFT

A basis is a complete, non-redundant set of operators in the Lagrangian at a given order in the EFT expansion. Complete means that the full parameter space of the EFT is accounted for at that order. Non-redundant means that none of the operators in that set can be expressed as a linear combination of the remaining ones. In the previous section we introduced the dimension-6 SMEFT operators using one particular representation called the Warsaw basis. In this section we take a more general view, and discuss the technical side of establishing equivalence classes of higher-dimensional operator. The issue is non-trivial because there is a huge redundancy at the core of the Lagrangian formulation of QFT. We are so used to working with Lagrangians that we unconsciously assign a physical meaning to its interactions terms. However Lagrangians are merely tools – very useful, but also very crude ones. Seemingly distinct sets of interaction terms can lead to the same on-shell scattering amplitudes, and thus to exactly the same observable consequences.

One can distinguish three main ways we can reshuffle the interaction terms in the Lagrangian:

• 1. Integration by parts,

• 2. Fierz transformations,

• 3. Field redefinitions.

These operations do not change on-shell scattering amplitudes, which define the physical content of the theory,¹⁴ Below I discuss them in more detail.

Starting with integration by parts, a simple example is

$$\begin{aligned} C_{H\Box } (H^{\dagger } H) \Box (H^{\dagger } H) \rightarrow -C_{H\Box } \partial ^{\mu } (H^{\dagger } H) \partial _{\mu } (H^{\dagger } H). \end{aligned}$$

(4.1)

This transformation, which consist in reshuffling how the derivatives act on the fields, changes the apparent form of the interaction term. However, both interaction terms above lead to the same Feynman rules once momentum conservation is taken into account. At a more mathematical level, integration by parts does not change physics because it shifts the Lagrangian by a total derivative $\partial _{\mu } F$, which shifts the action $S = \int d^4 x {{\mathcal {L}}}$ by a boundary term, which does not affect scattering amplitudes.¹⁵

Moving to the second point, Fierz transformations are rearrangements of the way the spinor or gauge indices are contracted. Let us illustrate them in a simple example, which is relevant for constructing a set of independent dimension-6 operators. Naively, it seems one could supplement the four-lepton operators in Eq. (3.16) by another one:

$$\begin{aligned} \Delta {{\mathcal {L}}}_{D=6}^{4L} = ({\bar{L}} {\bar{\sigma }}^{\mu } \sigma ^k L) C_{ll}^{(3)} ({\bar{L}} {\bar{\sigma }}_{\mu } \sigma ^k L) , \end{aligned}$$

(4.2)

where the $\sigma ^k$ matrices act on the $SU(2)_W$ indices of the lepton fields (unlike ${\bar{\sigma }}^{\mu }$, which act on the Lorentz group spinor indices). This is a legitimate interaction term, in particular it is gauge invariant. However, one can show that it is redundant, in the sense it is already contained in the term proportional to $C_{ll}$ in Eq. (3.16). In order to show this, we first use the Fierz identity for the Pauli matrices, $[\sigma ^k]_{ab} [\sigma ^k]_{cd} = 2 \delta _{ad} \delta _{bc} - \delta _{ab} \delta _{cd}$. This allows us to rewrite

$$\begin{aligned}&\Delta {{\mathcal {L}}}_{D=6}^{4L} = [C_{ll}^{(3)}]_{JKLM} \nonumber \\&\quad \times \bigg \{ 2 ({\bar{l}}_{J,a} {\bar{\sigma }}^{\mu } l_{K,b}) ({\bar{l}}_{L,b} {\bar{\sigma }}_{\mu } l_{M,a}) - ({\bar{l}}_J {\bar{\sigma }}^{\mu } l_K) ({\bar{l}}_L {\bar{\sigma }}_{\mu } l_M) \bigg \} , \end{aligned}$$

(4.3)

I only display the $SU(2)_W$ indices in the first term in the bracket, where they contracted in an unobvious way. The second term in the bracket has already the same form as the $L^4$ term in Eq. (3.16), but we still need to work on the first term. To this end, we need another Fierz identity to rearrange the spinor indices. For anti-commuting spinors $\psi _i$ one can prove $({\bar{\psi }}_1 {\bar{\sigma }}_{\mu } \psi _2) ({\bar{\psi }}_3 {\bar{\sigma }}_{\mu } \psi _4) = ({\bar{\psi }}_1 {\bar{\sigma }}_{\mu } \psi _4) ({\bar{\psi }}_3 {\bar{\sigma }}_{\mu } \psi _2)$. Using this we rewrite

$$\begin{aligned} \Delta {{\mathcal {L}}}_{D=6}^{4L}&= [C_{ll}^{(3)}]_{JKLM} \nonumber \\&\quad \times \bigg \{ 2 ({\bar{l}}_J {\bar{\sigma }}^{\mu } l_M) ({\bar{l}}_L {\bar{\sigma }}_{\mu } l_K) - ({\bar{l}}_J {\bar{\sigma }}^{\mu } l_K) ({\bar{l}}_L {\bar{\sigma }}_{\mu } l_M) \bigg \} \nonumber \\&= \big ( 2 [C_{ll}^{(3)}]_{JMLK}- [C_{ll}^{(3)}]_{JKLM} \big ) ({\bar{l}}_J {\bar{\sigma }}^{\mu } l_K) ({\bar{l}}_L {\bar{\sigma }}_{\mu } l_M). \end{aligned}$$

(4.4)

This completes the proof that the operator in Eq. (4.2) is equivalent to the $L^4$ term in Eq. (3.16), and we also found the mapping between the two tensor Wilson coefficients: $[C_{ll}]_{JKLM} = 2 [C_{ll}^{(3)}]_{JMLK} - [C_{ll}^{(3)}]_{JKLM}$; in particular $[C_{ll}]_{1111} = [C_{ll}^{(3)}]_{1111}$, and $[C_{ll}]_{1221} = 2 [C_{ll}^{(3)}]_{1122} - [C_{ll}^{(3)}]_{1221}$.

Finally, we discuss the last point, which is the least trivial one. In QFT, the so-called equivalence theorem [32, 33] stipulates that physics is invariant under arbitrary non-linear redefinitions of bosonic and fermionic fields of the form

$$\begin{aligned} \Phi _X \rightarrow \Phi _X + {1 \over \Lambda } F_X^{(1)}(\Phi ) + {1 \over \Lambda ^2} F_X^{(2)}(\Phi ) + \cdots , \end{aligned}$$

(4.5)

where $F_X^{(i)}(\Phi )$ are function of all fields $\Phi$ in the theory with the same Lorentz and gauge transformation properties as $\Phi _X$. The expansion in some scale $\Lambda$ is to ensure that one can apply this transformation perturbatively, such that kinetic terms in the Lagrangian do not change, but only the interaction terms do. In SMEFT, $\Lambda$ can be naturally identified with the cutoff scale controlling the dimensional expansion of the Lagrangian. If we once again evoke the path integral formulation, invariance under field redefinitions seems obvious, as Eq. (4.5) amounts to a change of variables under the integral. In the context of effective theories the invariance of on-shell Green’s functions under field redefinitions, also at the loop level, was formally proven in Ref. [34]. However, at the Lagrangian level this invariance seems far from obvious and often counter-intuitive. Indeed, field redefinitions can produce new interaction terms that were not present in the original Lagrangian. Let as consider an extreme example of a free scalar theory,

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{free}} = {1 \over 2} \partial _{\mu } \phi ' \partial ^{\mu } \phi ', \end{aligned}$$

(4.6)

and make a field redefinition $\phi ' \rightarrow \phi + {1 \over \Lambda } \phi ^2$. The shifted Lagrangian reads

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{free}} = {1 \over 2} \partial _{\mu } \phi \partial ^{\mu } \phi + {2 \over \Lambda } \phi \partial _{\mu } \phi \partial ^{\mu } \phi + {2 \over \Lambda ^2} \phi ^2 \partial _{\mu } \phi \partial ^{\mu } \phi . \end{aligned}$$

(4.7)

This naively looks like a Lagrangian of an interacting theory, with derivative cubic and quartic scalar self-interactions. However we know it is a free theory in disguise, as it was constructed via a field redefinition from the free Lagrangian in Eq. (4.6). And indeed, if you derive Feynman rules from Eq. (4.7) and calculate scattering amplitudes, you will always obtain zero, whatever the number of loops or external legs. It would be however difficult to search whether there exists a field redefinition to a free theory, each time somebody hands you a new Lagrangian, Fortunately, there is a simple hack to quickly see that Eq. (4.7) is a free Lagrangian in disguise. Using integration by parts we can rewrite the cubic interaction term as

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{free}} \supset - {1 \over \Lambda } \phi ^2 \Box \phi . \end{aligned}$$

(4.8)

At the same time, the equation of motion for the field $\phi$ following from Eq. (4.7) is $\Box \phi = \mathcal {O}(\Lambda ^{-1})$. Inserting this equation of motion back into Eq. (4.8) makes the cubic terms vanish, leaving only an $\mathcal {O}(\Lambda ^{-2})$ residue (which contains quartic and higher interactions). This exercise demonstrates the truth that, at least at the leading order in the $1/\Lambda$ expansion, applying field redefinitions is equivalent to using equations of motions at a lower order in $1/\Lambda$. In fact, in the literature this kind of equivalent Lagrangians are commonly referred to as related via equations of motions, rather than via field redefinitions. The two formulations are largely equivalent¹⁶ but the former may be puzzling for some non-practitioners: why should quantum fields be constrained to obey the equations of motions, also in the context of loop calculations when they are off-shell? The formulation via field redefinitions appears much more intuitive.

All in all, QFT Lagrangians have this huge redundancy due to field redefinitions. The redundancy exists also in the SM but it is rarely discussed in this context, as there exists a canonical choice of field variables where the SM Lagrangian appears renormalizable, that is without higher-dimensional operators. However in SMEFT, as in any garden-variety EFT, the redundancy is very relevant, because there is no canonical choice of field variables. As a consequence, Lagrangians with apparently distinct interaction terms may belong to the same equivalence classes, that is to say, they lead to the same scattering amplitudes. The equivalence classes can be confusing at times; for example a purely bosonic operator can be equivalent to a linear combination of operators containing fermions! Let us see in a concrete example how field redefinitions relate different dimension-6 SMEFT operators. The bosonic operator in the Warsaw basis, cf. Eq. (3.11), contains two quartic two-derivative self-interaction terms: $(H^{\dagger } H) \Box (H^{\dagger } H)$, and $|H^{\dagger } D_{\mu } H |^2$. There is another interaction term of this type:

$$\begin{aligned} \Delta {{\mathcal {L}}}_{D=6}^{\textrm{bosonic}} = C_{HD}' (H^{\dagger } H) (D^{\mu } H^{\dagger } D_{\mu } H) , \end{aligned}$$

(4.9)

which is perfectly legal and gauge invariant. However, using integration by parts and field redefinitions one can show its effects are already accounted for by other dimension-6 operators in the Warsaw basis. First we rewrite the operator multiplying $C_{HD}'$ as

$$\begin{aligned} \Delta {{\mathcal {L}}}_{D=6}^{\textrm{bosonic}}&= C_{HD}' \bigg \{ -\partial ^{\mu } (H^{\dagger } H) (H^{\dagger } D_{\mu } H) \nonumber \\&\quad - (H^{\dagger } H) ( H^{\dagger } D^2 H) \bigg \} \nonumber \\&= C_{HD}' \bigg \{ - \partial _{\mu } (H^{\dagger } H) (D^{\mu } H^{\dagger } H) \nonumber \\&\qquad - (H^{\dagger } H) ( D^2 H^{\dagger } H) \bigg \} \nonumber \\&= C_{HD}' \bigg \{ - {1\over 2} \partial _{\mu } (H^{\dagger } H) \partial ^{\mu } (H^{\dagger } H)\nonumber \\&\quad - {1 \over 2} H^{\dagger } H \big [ H^{\dagger } D^2 H + D^2 H^{\dagger } H \big ] \bigg \} \nonumber \\&= { C_{HD}' \over 2} (H^{\dagger } H) \Box (H^{\dagger } H)\nonumber \\&\quad - { C_{HD}' \over 2} H^{\dagger } H \big [ H^{\dagger } D^2 H + D^2 H^{\dagger } H \big ] . \end{aligned}$$

(4.10)

In the first two lines we integrated by parts in two different fashions, and in the third line we summed the first two lines with weight 1/2 each. We also used a generalized version of the Leibnitz rule: $\partial _{\mu } (H^{\dagger } H) = (D^{\mu } H^{\dagger } H) + (H^{\dagger } D_{\mu } H)$. The first term above can be absorbed into the $C_{H\Box }$ Wilson coefficient in Eq. (3.11), but the second term requires more work. To get rid of it we can redefine the Higgs field as¹⁷

$$\begin{aligned} H \rightarrow H' - {C_{HD}' \over 2} (H'{}^{\dagger } H') H', \end{aligned}$$

(4.11)

where I put the prime on the right-hand side to mark that it is a redefined field, but in the following I will omit it to reduce clutter. Then the last term in Eq. (4.10) is canceled by the shift of the Higgs kinetic term

$$\begin{aligned} D_{\mu } H^{\dagger } D^{\mu } H&\rightarrow D_{\mu } H^{\dagger } D^{\mu } H \nonumber \\&\quad + {C_{HD}' \over 2} (H^{\dagger } H) D^2 H^{\dagger } H \nonumber \\&\quad + {C_{HD}' \over 2} (H^{\dagger } H) H^{\dagger } D^2 H + \mathcal {O}(\Lambda ^{-4}). \end{aligned}$$

(4.12)

However, the field redefinition in Eq. (4.11) also shifts other $D=2$ and $D=4$ terms (it also shift $D=5$ and higher operators, but that does not affect dimension-6 operators, which we are focused on here). One finds

$$\begin{aligned}&\mu _H^2 (H^{\dagger } H) - \lambda (H^{\dagger } H)^2\nonumber \\&\qquad - \left( U^c Y_u^{\dagger } {\tilde{H}}^{\dagger } Q + D^c Y_d^{\dagger } H^{\dagger } Q + E^c Y_e^{\dagger } H^{\dagger } L + {\mathrm{h.c.}} \right) \nonumber \\&\quad \rightarrow C_{HD}' \bigg \{ - \mu _H^2 (H^{\dagger } H)^2 + 2 \lambda (H^{\dagger } H)^3 + {1\over 2} (H^{\dagger } H)\nonumber \\&\qquad \times \left( U^c Y_u^{\dagger } {\tilde{H}}^{\dagger } Q + D^c Y_d^{\dagger } H^{\dagger } Q + E^c Y_e^{\dagger } H^{\dagger } L + {\mathrm{h.c.}} \right) \bigg \} . \end{aligned}$$

(4.13)

Fortunately, all the terms that appear above are already in the Warsaw basis. At the end of the day, the effects of the dimension-6 operator in Eq. (4.9) can be simulated by concerted efforts of several dimension-4 and -6 operators in the Warsaw basis with the Wilson coefficients

$$\begin{aligned} \lambda&= - \mu _H^2 C_{HD}', \nonumber \\ C_H&= 2 \lambda C_{HD}', \nonumber \\ C_{H\Box }&= { 1 \over 2}C_{HD}' ,\nonumber \\ C_{uH}&= {1\over 2} Y_u C_{HD}',\nonumber \\ C_{dH}&= {1\over 2} Y_d C_{HD}',\nonumber \\ C_{eH}&= {1\over 2} Y_e C_{HD}'. \end{aligned}$$

(4.14)

Note that multiple bosonic and fermionic operators are needed to simulate a single bosonic operator. This may be counter-intuitive, but again can be confirmed by an explicit calculation of scattering amplitudes.

By the sort of exercises as the ones above, one can show that every dimension-6 operator can be expressed by the ones already present in the Warsaw basis. A proof seems like a non-trivial task, and indeed it took a long time to complete. While dimension-6 operators have been frequently used in the literature since the influential work of Buchmüller and Wyler in 1986 [36], a complete basis of dimension-6 operators appeared only in 2010 [17]. A more systematic road to constructing a basis is offered by the Hilbert series techniques [21, 37].

The Warsaw basis is by no means a unique representation of the parameter space of dimension-6 SMEFT operators. For example, one could drop from the Warsaw basis the operator proportional to $C_{ll}$ in Eq. (3.16) and replace it by the one proportional to $C_{ll}'$ defined in Eq. (4.2). Or one could drop the operator proportional to $C_{H\Box }$ in Eq. (3.11) and replace it with the one proportional to $C_{HD}'$ defined in Eq. (4.9). Or keep an arbitrary linear combination of the two. And so on. This way, there are infinite ways to write a basis of dimension-6 SMEFT operators. Any such basis will have 3045 operators, and will lead to completely equivalent predictions of physical observables.

The Warsaw basis is widely used in the literature, and it is nowadays an indispensable reference point for all phenomenological studies of dimension-6 operators. Nevertheless, different bases may be more convenient for specific applications. Another popular choice of operators is the so-called SILH basis [38].¹⁸ In this basis, the bosonic operators are

$$\begin{aligned} {{\mathcal {L}}}_{D=6}^{\textrm{bosonic}}&= S_6 (H^{\dagger } H)^3 + S_{H} \partial _{\mu }(H^{\dagger } H) \partial ^{\mu } (H^{\dagger } H) \nonumber \\&\quad + S_{T} ( H^{\dagger } \overleftrightarrow {D}_{\mu } H )^2 + S_W (H^{\dagger } \sigma ^k \overleftrightarrow {D}^{\mu } H) D^\nu W_{\mu \nu }^k \nonumber \\&\quad + S_B (H^{\dagger } \overleftrightarrow {D}^{\mu } H) D^\nu B_{\mu \nu } + S_{HW} (D^{\mu } H^{\dagger } \sigma ^k D^\nu H) W_{\mu \nu }^k \nonumber \\&\quad + S_{HB} (D^{\mu } H^{\dagger } D^\nu H) B_{\mu \nu } \nonumber \\&\quad + S_{g} H^{\dagger } H\, G^a_{\mu \nu } G^a_{\mu \nu } +S_{\gamma } H^{\dagger } H\, B_{\mu \nu } B_{\mu \nu } \nonumber \\&\quad + S_{2W} D^{\mu } W_{\mu \nu }^k D_{\rho } W^{\rho \nu \, k} + S_{2B} D^{\mu } B_{\mu \nu } D_{\rho } B^{\rho \nu } \nonumber \\&\quad + S_{2G} D^{\mu } G_{\mu \nu }^a D_{\rho } G^{\rho \nu \, a} +S_{3W} \epsilon ^{klm} W_{\mu \nu }^k W_{\nu \rho }^l W_{\rho \mu }^m \nonumber \\&\quad +S_{3G} f^{abc} G_{\mu \nu }^{a} G_{\nu \rho }^b G_{\rho \mu }^c \nonumber \\&\quad + {\widetilde{S}}_{HW} (D^{\mu } H^{\dagger } \sigma ^k D^\nu H) W_{\mu \nu }^k + {\widetilde{S}}_{HB} (D^{\mu } H^{\dagger } D^\nu H) B_{\mu \nu }\nonumber \\&\quad +{\widetilde{S}}_{G} H^{\dagger } H\, {\widetilde{G}}^a_{\mu \nu } G^a_{\mu \nu }+ {\widetilde{S}}_{ \gamma } H^{\dagger } H\, {\widetilde{B}}_{\mu \nu } B_{\mu \nu }\nonumber \\&\quad + {\widetilde{S}}_{ 3 W} \epsilon ^{klm} {\widetilde{W}}_{\mu \nu }^k W_{\nu \rho }^l W_{\rho \mu }^m+{\widetilde{S}}_{ 3{\widetilde{G}}} f^{abc} {\widetilde{G}}_{\mu \nu }^{a} G_{\nu \rho }^b G_{\rho \mu }^c . \end{aligned}$$

(4.15)

In this case I denote the Wilson coefficients by the letter S, to distinguish them from the Warsaw basis Wilson coefficients. Some operators from the Warsaw basis – the ones proportional to $C_{H\Box }$, $C_{HW}$, $C_{HWB}$, $C_{H{\widetilde{W}}}$, and $C_{H {\widetilde{W}} B }$ – are missing in Eq. (4.15) and their role is played by other operators. A more striking fact is that there are 20 bosonic operators in the SILH basis, compared to 15 bosonic operators in the Warsaw basis. This is possible because, as discussed above, field redefinitions relate bosonic operators to those containing fermions. The corollary is that some fermionic operators present in the Warsaw basis must be absent in the SILH basis. A possible choice [40] is to remove the operators multiplying $[C_{Hl}^{(1)}]_{11}$ and $[C_{Hl}^{(3)}]_{11}$ in Eq. (3.13), the four-lepton operators multiplying $[C_{ll}]_{1221}$ and $[C_{ll}]_{1122}$ in Eq. (3.16), and the four-quark operator multiplying $[C_{uu}]_{3333}$, while keeping all other two- and four-fermions operators the same as in the Warsaw basis. From this discussion you can gather that the SILH basis may be a bit awkward for the sake of describing new physics with a non-trivial flavor structure. On the other hand, it is convenient to describe the so-called oblique new physics, that is the one where the leading non-SM effects enter via corrections to gauge boson propagators. Indeed, the SILH basis connects in a simple manner to the oblique S, T, W, and Y parameters defined in Refs. [18, 41]: the S parameter corresponds to a linear combination of the $S_W$ and $S_B$ Wilson coefficients, while T, W, and Y translated directly into $S_T$, $S_{2W}$, and $S_{2B}$, respectively.

A somewhat different approach to parametrizing the space of dimension-6 SMEFT operators was proposed in Ref. [42]. The connection between the Wilson coefficients in the Warsaw or SILH basis and observables can be quite complicated (see later in Sect. 5). For phenomenological applications it is often easier to work with the SMEFT Lagrangian expressed in terms of the fields that are mass eigenstates after electroweak symmetry breaking: the photon, the W and Z bosons, the Higgs boson. The idea is to pick a set of independent couplings in the Lagrangian – the so-called BSM primaries, which, at least at tree level, are simply related to experimentally observable quantities. Typically, such a set would include the Higgs boson couplings to matter (related to the Higgs signal strength measured at the LHC) and the W an Z boson couplings to fermions (related to cross sections, branching fractions, and forward–backward asymmetries precisely measured at LEP). With a judicious choice of this set (see for example the Higgs basis [43]), there exists an invertible map between the BSM primaries and the Wilson coefficients of the Warsaw or SILH basis, Then one can translate the theoretical predictions from the Wilson coefficient language to the BSM primaries language, and vice-versa. While the two are completely equivalent, the latter can be more convenient for certain applications. In global SMEFT fits to electroweak precision observables, the BSM primaries allow one to easily separate strongly constrained directions in the parameter space (typically, coming from the LEP measurements at the Z pole) from the weakly constrained direction (for example, coming from the Higgs measurements at the LHC), which improves stability of the fit.

Bases of SMEFT operators are also known beyond $D=6$. For $D=7$ operators (which are $B-L$-violating, much as those at $D=5$ and at any other odd dimension) a basis was constructed in Ref. [44]. More recently, bases at $D=8,9,10,11,12$ were constructed in Refs. [45,46,47]. A code to generate a SMEFT basis at any dimension is now available [48]. As I discussed in the previous section, operators of dimension higher than six currently have limited phenomenological applications, and no one even dreams of using a complete set of independent operators beyond $D=6$. Nevertheless, these constructions serve as proof-of-principle demonstrations and useful look-up tables for specific applications.

Let me close this section by a couple of loosely related comments. The first concerns the choice of basis in the flavor space. Even when a specific operator basis is chosen, for example the Warsaw basis as in Sect. 3, there still remains freedom of making U(3) rotations separately for each fermionic 3-vector in the generation space: Q, $U^c$, $D^c$, L, $E^c$. The power of these $U(3)^5$ rotations can be used for good. The most convenient choice is to make the fermion mass terms as diagonal as possible. This last clause is due to the fact that we cannot simultaneously make the up and down quark masses diagonal by these rotations without destroying the manifest $SU(2)_L$ symmetry of the SMEFT Lagrangian, that is without rotating differently the left-handed U and D fields sitting in Q. One convenient choice, which is adopted in these lectures, is the so-called down-type basis. In this basis, the fields $U^c$, $D^c$, L, $E^c$ are rotated such that their components are mass eigenstates, for example $U^c = (u^c, c^c, t^c)$ contains the right-handed up, charm, and top quark fields that do not have any flavor-off-diagonal mass terms. Concerning the quark doublet field Q, in the down-type basis it takes the form

$$\begin{aligned} Q = \begin{pmatrix} V^{\dagger } U \\ D \end{pmatrix} \end{aligned}$$

(4.16)

where $U= (u,c,t)$ and $D=(d,s,b)$ contain the left-handed quark mass eigenstates, and V is the unitary $3 \times 3$ CKM matrix. The latter must appear here so that, after electroweak symmetry breaking, the kinetic term $i Q {\bar{\sigma }}^{\mu } D_{\mu } Q$ yields the usual quark-mixing interactions with the W boson: ${{\mathcal {L}}}_{\textrm{SMEFT}} \supset - {g_L \over \sqrt{2}} W_{\mu }^+ {\bar{U}}{\bar{\sigma }}^{\mu } V D + {\mathrm{h.c.}}$. Another logical and equally good choice is the so-called up-type basis, where $Q = \begin{pmatrix} U \\ V D \end{pmatrix}$. The down-type basis is slightly more popular in the literature, probably because more flavor physics is done with the bottom and strange quarks than with the charm and top quarks.

Another comment concerns on-shell amplitude methods. As discussed earlier in this section, the freedom of field reparametrization adds a lot of complications to constructing an EFT basis. It turns out that this excess baggage can be dropped: one can practice QFT without referring to fields, Lagrangians, gauge invariance, or other off-shell concepts. Instead, the theory can be formulated at the level of scattering amplitudes with all involved particles being on the mass shell (that is to say, with their respective momenta p constrained by $p^2 = m^2$). See Ref. [49] for a nice introduction. Unsurprisingly, the on-shell approach greatly simplifies the task of constructing an EFT basis, see e.g. [50, 51]. It has been applied specifically to SMEFT [52], allowing one to swap a basis of higher-dimensional operators for a more tractable basis of independent amplitudes. This has lead to a more transparent derivation of some known results, as well as to several novel results. The advantages appear particularly clear in relation to renormalization group running, see e.g. [53,54,55], facilitating extension of the program beyond one loop.

6 From operators to observables

Currently, the SM is the reference point for any physical theory at the electroweak scale. It enjoys huge success, correctly accounting for a host of phenomena measured in colliders and low-energy precision experiments. SMEFT differs from the SM by the presence of interactions originating from operators with dimension $D=5,6$, and higher. In this section we discuss, in more precise and quantitative terms, the observable effects of these operators.

There are many ways in which higher-dimensional operators can affect observables. To organize the following discussion, it is convenient to divide them into three broad classes:

• 1. New vertices: interaction vertices in the SMEFT Lagrangian that do not occur in the SM Lagrangian, due to symmetries or accidental reasons.

• 2. New Lorentz structures: interaction vertices that do occur in the SM Lagrangian, but which appear in the SMEFT with a different number of derivatives, different contractions of Lorentz or spinor indices, etc.

• 3. Modified couplings: corrections to the coupling strengths of the interaction terms present in the SM Lagrangian.

In this following I will discuss each of these classes in turn.

6.1 New vertices

The most spectacular effects of SMEFT occur when higher-dimensional operators violate an exact global symmetry of the SM. One important example of this kind is baryon and lepton number violation¹⁹ by the dimension-6 operators in Eq. (3.20). Let us take one of these operators at random, say

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset C_{duu} (d^c u^c)(u^c e^c) + C_{duu}^* ( {\bar{u}}^c {\bar{d}}^c)({\bar{e}}^c {\bar{u}}^c), \end{aligned}$$

(5.1)

where I abbreviated $C_{duu} \equiv [C_{duu}]_{1111}$ and explicitly displayed both the operator and its Hermitian conjugate. The latter mediates the quark-level process $u u \rightarrow {\bar{d}} e^+$. In a bit hand-waving but intuitive way, one can think of this process as transforming two up quarks from the proton (uud) into a down antiquark, leading to a $d {\bar{d}}$ meson state. Consequently, the operator can mediate proton decay into meson states. One important example is $p \rightarrow e^+ \pi ^0$ - the decay to a positron and a neutral pion (who is a combination of $d {\bar{d}}$ and $u {\bar{u}}$ quark states, the latter pair you can think of as being pulled from the vacuum sea during the decay). To calculate the rate for this process, one needs to take the on-shell matrix elements of the operator in Eq. (5.1) between the initial and final states:

$$\begin{aligned} {{\mathcal {T}}}(p \rightarrow e^+ \pi ^0)= & {} C_{duu}^* \langle e^+ (k_3) \pi ^0(k_2)| \int d^4 x ({\bar{u}}^c(x) {\bar{d}}^c(x))\nonumber \\{} & {} \times ({\bar{e}}^c(x) {\bar{u}}^c(x)) |p (p_1)\rangle , \end{aligned}$$

(5.2)

where ${{\mathcal {T}}}$ is the non-trivial part of the S matrix, $S = 1 + i {{\mathcal {T}}}$, $p_1$ is the incoming momentum of the proton, $k_2$, $k_3$ are the outgoing momenta of the pion and positron, and we also define $q = p_1 - k_2$. The electron field acts on the annihilation operator of the positron final state, leaving the spinor wave function ${\bar{x}}_3$ corresponding to the momentum $k_3$. We get

$$\begin{aligned} {{\mathcal {T}}}(p \rightarrow e^+ \pi ^0){} & {} = C_{duu}^* {\bar{x}}_3 \int d^4 x e^{i k_3 x } \langle \pi ^0(k_2)|\nonumber \\{} & {} \quad \times ({\bar{u}}^c(x) {\bar{d}}^c(x)) {\bar{u}}^c(x) |p (p_1)\rangle . \end{aligned}$$

(5.3)

The remaining matrix element between the proton and pion states is non-perturbative, and we cannot calculate it using the familiar textbook methods. Nevertheless, the Poincaré and little group covariance of the S-matrix tell us that it has to be proportional to a linear combination of the spinor wave functions of the incoming proton (pion is a scalar particle): We can thus parametrize

$$\begin{aligned}{} & {} \langle \pi ^0(k_2)| ({\bar{u}}^c(x) {\bar{d}}^c(x)) {\bar{u}}^c(x) |p (p_1)\rangle \nonumber \\{} & {} \quad = { 1 \over \sqrt{2} } \big ( W_0 {\bar{y}}_1 + W_1 {q^{\mu } \over m_p} {\bar{\sigma }}_{\mu } x_1 \big ) e^{i (k_3 - p_1) x}, \end{aligned}$$

(5.4)

where $W_0$ and $W_1$ encode the information about the non-perturbative brown muck. To know its value you have to ask your lattice friends, and they may reply $W_0 \approx 0.15~\textrm{GeV}^2$, $W_1 \approx -0.13~\textrm{GeV}^2$, with roughly a $20\%$ error [56]. Thus

$$\begin{aligned} {{\mathcal {T}}}(p \rightarrow e^+ \pi ^0)&= {C_{duu}^* \over \sqrt{2} } \big ( W_0 ({\bar{x}}_3 {\bar{y}}_1) \nonumber \\&\quad + W_1 {q^{\mu } \over m_p} ({\bar{x}}_3 {\bar{\sigma }}_{\mu } x_1) \big )\int d^4 x e^{i (k_3 + k_2 - p_1) x } \nonumber \\&= {C_{duu}^* \over \sqrt{2} } \big ( W_0 ({\bar{x}}_3 {\bar{y}}_1)+ W_1 {q^{\mu } \over m_p} ({\bar{x}}_3 {\bar{\sigma }}_{\mu } x_1) \big )\nonumber \\&\quad (2\pi )^4 \delta ^4 (k_3 + k_2 - p_1), \end{aligned}$$

(5.5)

or trading the matrix element for the more familiar amplitude via ${{\mathcal {T}}} = (2\pi )^4 \delta ^4(\sum _i p_i - \sum _j k_j) {{\mathcal {M}}}$:

$$\begin{aligned} {{\mathcal {M}}}(p \rightarrow e^+ \pi ^0) = {C_{duu}^* \over \sqrt{2} } \big ( W_0 ({\bar{x}}_3 {\bar{y}}_1) + W_1 q^{\mu } ({\bar{x}}_3 {\bar{\sigma }}_{\mu } x_1) \big ) . \end{aligned}$$

(5.6)

The rest is standard QFT manipulations. Taking the square of the amplitude, summing/averaging over the positron/proton spins, and plugging the result into the formula for the decay width one gets

$$\begin{aligned} \Gamma (p \rightarrow e^+ \pi ^0) = {|C_{duu}|^2 m_p W_0^2 \over 32 \pi } \bigg ( 1 - {m_{\pi _0}^2 \over m_p^2} \bigg )^2 . \end{aligned}$$

(5.7)

Above I approximated the electron mass by zero, which is perfectly legitimate given the uncertainty on $W_0$ (actually, even approximating the much larger $m_{\pi _0}$ as zero would be fine). In this limit the contribution of the $W_1$ form factor drops out. I presented this calculation here so that you can get familiar with hadronic matrix element, but as long as you are not interested in precision calculation you could easily obtain the order of magnitude of the result via dimensional analysis: $\Gamma (p \rightarrow e^+ \pi ^0) \sim m_p^5 |C_{duu}|^2/16 \pi$.

Now, a sneak peak into the Particle Data Group booklet [57] reveals that the limit on this proton decay channel is $\Gamma (p \rightarrow e^+ \pi ^0) \le 1.3 \times 10^{-66}$ GeV at 90% confidence level (CL), which translates into the limit on the Wilson coefficient

$$\begin{aligned} |C_{duu}| \le \bigg ( {1 \over 3.5 \times 10^{15}~\textrm{GeV}} \bigg )^2. \end{aligned}$$

(5.8)

This limit is valid assuming only a single baryon-number violating operator is present in the Lagrangian; otherwise proton decay constrains a linear combination of various baryon-number violating Wilson coefficients.

It is mind-blowing that low-energy experiments searching for proton decay allow us to probe new physics up to scales not so far from the Planck scale! To my knowledge, this is the highest scale we can indirectly access via low-energy experiments within a sane theoretical framework (unitary, causal, local, Lorentz-symmetric). The reason for this extreme sensitivity is that it is feasible to amass astronomical number of protons for a long period of time in a controlled setting, for example in a tank filled with water and surrounded by photo-detectors [58]. Moreover, the detection capabilities are impressive and would allow us to see the signal even if a handful of the protons in the tank decayed. Thanks to this combination of favorable circumstances, the limit on the proton lifetime can be orders of magnitude larger than the age of the universe! The final fact making the limit so strong is that we search for an effect that is predicted to be zero in the SM, so we do not have to face the uncertainty due to imprecise theory predictions.

Baryon and lepton number violation is certainly the most spectacular prediction of SMEFT. Nevertheless, higher-dimensional operators can also break other exact or approximate global symmetries of the SM, with quite interesting consequences. A nice example is the decay $\mu \rightarrow e \gamma$. In the SM, not only the overall lepton number L is conserved, but also the individual lepton numbers $L_\alpha$ for each generation, $\alpha = e,\mu ,\tau$. The process $\mu \rightarrow e \gamma$ preserves L, but breaks $L_{\mu }$ and $L_e$, that is to say, these quantum numbers are different for the initial and final states. Therefore in the SM $\mu \rightarrow e \gamma$ is forbidden, and the predicted branching ratio is exactly zero. In the SMEFT, dimension-5 operators break L and consequently each $L_\alpha$, but the smallness of the neutrino masses (translating to the large scale suppressing the dimension-5 Wilson coefficients) suppresses their contribution to $\mu \rightarrow e \gamma$ to an unobservable level. On the other hand, there are many dimension-6 operators that break $L_e$ and $L_{\mu }$, and their contributions may be more significant. In particular, one of the dipole operators in Eq. (3.14) reads

$$\begin{aligned} {{\mathcal {L}}}_{D=6} \supset [C _{eB}]_{12} ({\bar{l}}_1 H {\bar{\sigma }}^{\alpha \beta } {\bar{\mu }}^c) B_{\alpha \beta } + {\mathrm{h.c.}}, \end{aligned}$$

(5.9)

where $l_1 = (\nu _e, e)$ is the doublet of left-handed first generation leptons. After electroweak symmetry breaking, this operator leads to the interaction term

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset {\cos \theta _W \over \sqrt{2}} [C _{eB}]_{12} v ({\bar{e}} {\bar{\sigma }}^{\alpha \beta } {\bar{\mu }}^c) F_{\alpha \beta } + {\mathrm{h.c.}}\end{aligned}$$

(5.10)

mediating $\mu \rightarrow e \gamma$ at tree level, with $\cos \theta _W \approx 0.89$ being the cosine of the Weinberg angle. In the presence of this interaction, the branching ratio for the $\mu \rightarrow e \gamma$ can be calculated to be

$$\begin{aligned} \textrm{Br}(\mu \rightarrow e \gamma ) = {\cos ^2 \theta _W \big |[C _{eB}]_{12} \big |^2 v^2 m_{\mu }^3 \over 8 \pi \Gamma _{\mu }}, \end{aligned}$$

(5.11)

where $\Gamma _{\mu } \approx 3 \times 10^{-19}$ GeV is the total muon decay width.²⁰ We again peek into Particle Data Group, and find the 90% CL experimental constraint $\textrm{Br}(\mu \rightarrow e \gamma ) \le 4.2 \times 10^{-13}$ coming from the MEG experiment [59]. This translates into the constraint on the Wilson coefficient

$$\begin{aligned} \big |[C _{eB}]_{12} \big | \le {1 \over \big ( 6.5 \times 10^7~\textrm{GeV}\big )^2} . \end{aligned}$$

(5.12)

The scale probed by $\mu \rightarrow e \gamma$ is less impressive than that probed by proton decay, but it is nevertheless several orders of magnitude above the direct reach of the LHC. Again, it helps that we consider a process forbidden in the SM, so we avoid dealing with theoretical errors on the SM prediction. Moreover, muons are relatively long-lived ($\Gamma _{\mu }$ in the denominator of Eq. (5.11) is small), and that we can easily produce and handle large amounts of them.

There is one caveat concerning the scale probed by $\mu \rightarrow e \gamma$. In typical BSM models, the mass of the new particles that can be excluded by this constraint will be much smaller. One reason is that in perturbative models the operator in Eq. (5.9) cannot be generated at tree level, thus it will appear with at least one loop suppression factor. Furthermore, the BSM model is likely to have some form of the chiral symmetry, with some small parameters suppressing the transitions between left- and right-handed fermions. If that symmetry is akin to the one in the SM (for example, if chirality is violated only by the SM Yukawa interactions), the operator in Eq. (5.9) will be generated with the $y_{\mu } \sim 10^{-3}$ suppression factor. But even if $[C _{eB}]_{12} = {y_{\mu } e \over 16 \pi ^2 \Lambda ^2}$, with $\Lambda$ identified as the scale of BSM particles, $\mu \rightarrow e \gamma$ still probes $\Lambda \sim 10^{5}$ GeV, comfortably above the LHC reach.

Fig. 4

Feynman diagrams for Higgs production via gluon fusion. Left: Via a fermion loop, as in the SM. Right: Via a contact interaction due to the dimension-6 operator in Eq. (5.13)

New SMEFT vertices violating established SM symmetries may be our best path to new physics at high energy scales. Nevertheless, not all new SMEFT vertices are of this type. There are many examples of SMEFT interactions that preserve all SM symmetries but do not appear in the SM Lagrangian, usually due to renormalizability of the latter. As an example, consider this dimension-6 operator:

$$\begin{aligned} {{\mathcal {L}}}_{D=6} \supset C_{HG} H^{\dagger } H \, G^a_{\mu \nu } G^a_{\mu \nu } . \end{aligned}$$

(5.13)

Its effect is to induce the Higgs boson couplings to gluons:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset v^2 C_{HG} {h \over v} G^a_{\mu \nu } G^a_{\mu \nu } , \end{aligned}$$

(5.14)

which permits the Higgs boson to mutate into two gluons or vice-versa. Such a contact interaction term between the Higgs and gluons is absent in the SM. However, the process where two gluons collide to produce a Higgs boson does appear in the SM at the one-loop level, see Fig. 4. This is in fact the most common way the Higgs is created at the LHC. The SM loops and the contact interaction in Eq. (5.14) are in principle distinguishable experimentally, in particular they lead to a different $p_T$ distribution of the Higgs production in hadron colliders. In practice, we can best distinguish them indirectly via global fits to Higgs data, as the SM process and the Eq. (5.14) are differently correlated with the associated tth production rate. The resulting bounds are in the ballpark of $|C_{HG}| \lesssim {1 \over (10~\textrm{TeV})^2 }$, see e.g. Ref. [60]. This is visibly less spectacular than the bounds discussed previously in this subsection. The sensitivity to $\mathcal {O}(10)$ TeV scale is rather typical for new SMEFT vertices not violating any exact or approximate symmetries of the SM.

6.2 New Lorentz structures

We turn to another class of effects of higher-dimensional operators, which are related to interaction terms with different Lorentz structures compared to those in the SM. Perhaps the most iconic example in this class are the interactions contributing to the anomalous magnetic and electric moments of elementary particles. The dimension-6 SMEFT Lagrangian contains

$$\begin{aligned} {{\mathcal {L}}}_{D=6} \supset [C _{eB}]_{11} ({\bar{l}}_1 H {\bar{\sigma }}^{\mu \nu } {\bar{e}}^c) B_{\mu \nu } . \end{aligned}$$

(5.15)

In the presence of this operator, the Lagrangian after electroweak symmetry breaking contains

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}&\supset i {\bar{e}} {\bar{\sigma }}^{\mu } \partial _{\mu } e + i e^c \sigma ^{\mu } \partial _{\mu } {\bar{e}}^c - \big [ m_e e^c e + {\mathrm{h.c.}}\big ] \nonumber \\&\quad - q_e e A_{\mu } ({\bar{e}} {\bar{\sigma }}^{\mu } e) - q_e e A_{\mu } (e^c \sigma ^{\mu } {\bar{e}}^c)\nonumber \\&\quad - \bigg \{ {\Delta \mu _e - i d_e \over 4 } F_{\mu \nu } (e^c \sigma ^{\mu \nu } e) + {\mathrm{h.c.}}\bigg \} \end{aligned}$$

(5.16)

where $q_e = -1$ for the electron and

$$\begin{aligned} \Delta \mu _e&= - 2 \sqrt{2} v \cos \theta _W {\textrm{Re}} \,[C _{eB}]_{11} , \nonumber \\ d_e&= - 2 \sqrt{2} v \cos \theta _W {{\textrm{Im}}} \,[C _{eB}]_{11} \end{aligned}$$

(5.17)

The first line in Eq. (5.16) contains the usual kinetic and mass terms for the electron. In the second line we have electron’s interaction with the electromagnetic field. The minimal coupling proportional to $q_e$ is, of course, already present in the SM. The effect of the operator in Eq. (5.15) is to introduce another vertex with two electrons and one photon, but with a different Lorentz structure, in particular with the photon entering via the field strength $F_{\mu \nu }$.

As the name suggests, $d_e$ in Eq. (5.16) is the electric dipole moment of the electron, while $\Delta \mu _e$ is its anomalous magnetic dipole moment. It is worth pausing here to justify this identification. The notion of dipole moments stems from non-relativistic physics, therefore it is convenient to match Eq. (5.16) to the non-relativistic EFT for the electron. This can be achieved by this change of variables:

$$\begin{aligned} e_\alpha&= {1 \over \sqrt{2}} \bigg \{ e^{- i m_e t} \bigg ( \psi + { i \over 2 m_e} {\varvec{\sigma }} \cdot {\varvec{\nabla }} \psi \bigg )_\alpha \nonumber \\&\quad - e^{i m_e t} \bigg ( \psi _c^{\dagger } - { i \over 2 m_e} {\varvec{\sigma }} \cdot {\varvec{\nabla }} \psi _c^{\dagger } \bigg )_\alpha \bigg \} + \mathcal {O}(\nabla ^2) , \nonumber \\ {\bar{e}}_c^{{\dot{\alpha }}}&= {1 \over \sqrt{2}} \bigg \{ e^{- i m_e t} \bigg ( \psi - {i \over 2 m_e} {\varvec{\sigma }} \cdot {\varvec{\nabla }} \psi \bigg )_\alpha \nonumber \\&\quad + e^{i m_e t} \bigg ( \psi _c^{\dagger } + {i \over 2 m_e} {\varvec{\sigma }} \cdot {\varvec{\nabla }} \psi _c^{\dagger } \bigg )_\alpha \bigg \} + \mathcal {O}(\nabla ^2) . \end{aligned}$$

(5.18)

Here, $\psi$ and $\psi _c$ are non-relativistic fermionic fields describing a spin-1/2 particle (electron) and a spin 1/2 antiparticle (positron), respectively The spinor index $\alpha = 1,2$ counts the two polarizations. The mismatch between the up and down positions of the spinor indices in Eq. (5.18) is not a typo: this transformation breaks manifest Lorentz symmetry. The point of this change of variables is that it separates the electron and positron degrees of freedom. Indeed, plugging in Eq. (5.18) in the first line of Eq. (5.16) we get

$$\begin{aligned}{} & {} i {\bar{e}} {\bar{\sigma }}^{\mu } \partial _{\mu } e + i e^c \sigma ^{\mu } \partial _{\mu } {\bar{e}}^c - \big [ m_e e^c e + {\mathrm{h.c.}}\big ] \nonumber \\{} & {} \quad = i \psi ^{\dagger } \partial _t \psi + {1 \over 2 m_e} \psi ^{\dagger } {\varvec{\nabla }}^2 \psi + i \psi _c^{\dagger } \partial _t \psi _c \nonumber \\{} & {} \qquad + {1 \over 2 m_e} \psi _c^{\dagger } {\varvec{\nabla }}^2 \psi _c + \mathcal {O}(\nabla ^3). \end{aligned}$$

(5.19)

In other words, $\psi$ and $\psi ^c$ do not mix at the quadratic level, and they both satisfy the Schrödinger equation in the non-relativistic limit ${\varvec{\nabla }}/m_e \ll 1$.

Consider now the electromagnetic couplings in the second line of Eq. (5.16) Plugging the change of variables Eq. (5.18) and ignoring the couplings of the positron field $\psi _c$ one obtains

$$\begin{aligned}&-q_e e A_{\mu } ({\bar{e}} {\bar{\sigma }}^{\mu } e) -q_e e A_{\mu } (e_c \sigma ^{\mu } {\bar{e}}_c) \nonumber \\&\qquad - \bigg \{ {\Delta \mu _e - i d_e \over 4 } F_{\mu \nu } (e_c \sigma ^{\mu \nu } e) + {\mathrm{h.c.}}\bigg \} \nonumber \\&\quad = - q_e e V \psi ^{\dagger } \psi - {i q_e e \over 2 m} A^k \psi ^{\dagger } \overleftrightarrow {\nabla }_k \psi \nonumber \\&\qquad + \bigg ( { q_e e \over m_e} + \Delta \mu _e \bigg ) B^k (\psi ^{\dagger } {\sigma ^k \over 2} \psi ) + d_e E^k \left( \psi ^{\dagger } {\sigma ^k \over 2} \psi \right) , \end{aligned}$$

(5.20)

where $V \equiv A^0$ is the Coulomb potential, ${\varvec{E}} \equiv - {\varvec{\nabla }} V - \partial _t {\varvec{A}}$ is the electric field, and ${\varvec{B}} \equiv {\varvec{\nabla }} \times {\varvec{A}}$ is the magnetic field. The first two terms describe the interaction of electron’s charge with the Coulomb and vector potentials. The remaining two terms describes the interaction of its dipole moments with the external electric and magnetic fields. We can compare them with the textbook expressions for the dipole Hamiltonian: $H_{\textrm{int}} \supset - {\varvec{B}}\cdot {\varvec{\mu }} - {\varvec{E}}\cdot {\varvec{d}}$. We can thus identify²¹ the magnetic and electric moments of the electron at tree level:

$$\begin{aligned} {\varvec{\mu }}_e = \bigg ( { q_e e \over m_e} + \Delta \mu _e \bigg ) {\varvec{s}}, \quad {\varvec{d}}_e = d_e {\varvec{s}} , \end{aligned}$$

(5.21)

where the spin vector is defined as $s^k = \psi ^{\dagger } {\sigma ^k \over 2} \psi$. Furthermore, defining the g-factor for a charged particle via the relation ${\varvec{\mu }} = g { q e \over 2\,m} {\varvec{s}}$, we have

$$\begin{aligned} {g_e - 2 \over 2} = {g_e^{\textrm{SM}} - 2 \over 2} + \Delta \mu _e {m_e \over q_e e}, \end{aligned}$$

(5.22)

where $g_e^{\textrm{SM}} - 2$ encodes the SM loop effects, and the contributions from higher-dimensional operators are contained in $\Delta \mu _e$.

In the following let us assume that $[C _{eB}]_{11}$ is real (the imaginary part will be discussed later in Sect. 6), so that $d_e = 0$ while $\Delta \mu _e$ is allowed to linger. We want to determine the constraint on $[C_{eB}]_{11}$ from the measurement of the anomalous magnetic moment of the electron. These days, $g_e$ is predicted and measured with the incredible $10^{-13}$ accuracy, which is often hailed as a triumph of both experimental and theoretical prowess and a powerful demonstration of the robustness of the QFT framework. The most recent experimental result comes from Ref. [61]: ${g_e - 2 \over 2} = 0.00115965218059(13)$. To constrain new physics we also need the SM prediction $g_e^{\textrm{SM}}$. This can be calculated perturbatively, mainly in function of the fine structure constant $\alpha$. Unfortunately, at this point in time there is some confusion about $\alpha$. Measurements using rubidium atoms in Ref. [62] lead to $1/\alpha (0) = 137.035999206(11)$, while those using cesium atoms in Ref. [63] find $1/\alpha (0) = 137.035999046(27)$, the two disagreeing at more than 5 sigma. Clearly, one or both experiments underestimated their systematic errors. To deal with this kind of situations, Particle Data Group developed a completely ad-hoc but nevertheless very useful procedure. The idea is to punish both groups indiscriminately by inflating the error bars to the point where the two measurements become consistent with each other at 1 sigma. Using this procedure, I find the combined value $1/\alpha (0) = 137.035999183(56)$, where the errors are inflated by $S=5.5$. This is a loss of precision by a factor of 5(2) compared to the more (less) precise input, but, undeniably, this combination better reflects our current knowledge of $\alpha$ than the two individual results with the smaller errors. With this value of $\alpha$ one can obtain the prediction $g_e^{\textrm{SM}}/2 = 1.00115965218045(48)$. Note that the theoretical error is now almost 4 times larger than the experimental one.²²

At this point we have all the ingredients to constrain the Wilson coefficient $[C_{eB}]_{11}$. Using Eq. (5.22) and replacing $\Delta \mu _e$ using Eq. (5.17) we get $[C_{eB}]_{11} = 1.4(5.0)\times 10^{-13}~\textrm{GeV}^{-2}$ or

$$\begin{aligned} \big |[C_{eB}]_{11} \big | \lesssim {1 \over (940~\textrm{TeV})^2} \end{aligned}$$

(5.23)

at $95\%$ CL. We can see that the anomalous magnetic moment of the electron probes very high scales, although not as high as, say, $\mu \rightarrow e \gamma$. Moreover, similar caveat as the one discussed below Eq. (5.12) applies: in natural BSM models the chiral symmetry will typically be implemented, leading to $[C_{eB}]_{11} \sim {y_e \over 16 \pi ^2 \Lambda ^2}$. The same scaling is true when $[C_{eB}]_{11}$ is induced by other dimension-6 operators via renormalization group running. If that is the case, measurements of $g_e$ currently probe the very unimpressive new physics scale $\Lambda \sim 100$ GeV, such that the validity range of SMEFT would be null in this scenario. The most accurate precision experiment in physics may not be accurate enough to reach new physics above a TeV!

Let me also discuss a less spectacular but more typical example of new Lorentz structures in the SMEFT Lagrangian. Consider one of the bosonic dimension-6 operators in Eq. (3.11):

$$\begin{aligned} {{\mathcal {L}}}_{D=6} \supset C_{W} \epsilon ^{klm} W_{\mu \nu }^k W_{\nu \rho }^l W_{\rho \mu }^m . \end{aligned}$$

(5.24)

It contributes to self-interactions of the electroweak gauge bosons, in particular, it affects the WWZ vertex. Cubic self-interactions between electroweak gauge bosons are predicted as a consequence of the non-abelian structure of the electroweak gauge group, and the existence of the WWZ vertex was spectacularly confirmed at the turn of century by the LEP-2 experiment [64]. However, the SM predicts WWZ interactions with a single derivative acting on one of the fields, whereas Eq. (5.24) yields one derivative acting on each field.

Let us put this in a wider context. The CP-conserving triple interactions of electroweak gauge bosons are traditionally parametrized as [65]

$$\begin{aligned} \mathcal {L}_{\textrm{TGC}}&= i e \bigg \{ \left( W_{\mu }^+ W_{\mu \nu }^- - W_{\mu }^- W_{\mu \nu }^+ \right) A_{\nu }\nonumber \\&\quad + g_1^Z {g_L \over g_Y} \left( W_{\mu }^+ W_{\mu \nu }^- - W_{\mu }^- W_{\mu \nu }^+ \right) Z_{\nu } \nonumber \\&\quad - \kappa _{\gamma } W_{\mu }^+W_{\nu }^- F_{\mu \nu } - \kappa _Z {g_L \over g_Y} W_{\mu }^+W_{\nu }^- Z_{\mu \nu } \nonumber \\&\quad - \lambda _{\gamma } {1 \over m_W^2 } W_{\mu \nu }^+W_{\nu \rho }^- F_{\rho \mu } - \lambda _Z {g_L \over g_Y m_W^2} W_{\mu \nu }^+W_{\nu \rho }^- Z_{\rho \mu } \bigg \} , \end{aligned}$$

(5.25)

where $g_{1,Z}$, $\kappa _V$ and $\lambda _V$ are real and referred to as the triple gauge couplings. It is worth knowing this parametrization because experimental collaboration more often than not present their results in this language. One physical interpretation of $\kappa _{\gamma }$ and $\lambda _{\gamma }$ is that they parametrize the dipole and quadrupole moments of the W boson: ${\varvec{\mu }} = {e \over 2 m_W}(\kappa _{\gamma } - \lambda _{\gamma }) {\varvec{s}}$, $Q^{ij} = -{3 e \over 2m_W^2} (\kappa _{\gamma } + \lambda _{\gamma }) s^i s^j$. In the SM, $g_1^Z = \kappa _{\gamma } = \kappa _Z = 1$, and $\lambda _{\gamma } = \lambda _Z = 0$, which corresponds to the W boson g-factor being equal to two at tree level, and a particular non-zero value of the quadrupole moment. In SMEFT, dimension-6 operators may lead to deviations from these predictions, while respecting the pattern $\kappa _{\gamma } = \kappa _Z$ and $\lambda _{\gamma } = \lambda _Z$. For this reason, let us define $g_1^Z = 1 + \delta g_1^Z$, $\kappa _{\gamma } = \kappa _Z = 1 + \delta \kappa$, $\lambda _{\gamma } = \lambda _Z = \lambda$, and we will treat $\delta g_1^Z$, $\delta \kappa$ and $\lambda$ as $\mathcal {O}(\Lambda ^{-2})$ parameters in the SMEFT power counting. In particular, in the presence of just the single dimension-6 operator in Eq. (5.24) one has $\delta g_1^Z = \delta \kappa = 0$ and

$$\begin{aligned} \lambda = {3 g_L \over 2 } v^2 C_W. \end{aligned}$$

(5.26)

How can one constrain the parameters $\delta g_{1,Z}$, $\delta \kappa$ and $\lambda$ in Eq. (5.25)? Unlike for the electron or muon, measuring electromagnetic moments for such a short-lived particle as the W boson is not feasible. Instead, one good handle is the energy dependence of the $f {\bar{f}} \rightarrow W^+ W^-$ and $f {\bar{f}}' \rightarrow W^{\pm } Z$ amplitudes. In SMEFT with dimension-6 operators for $E \gg m_W$ one expects ${\mathcal {M}}= {\mathcal {M}}_{\textrm{SM}} [1 +(c_1 \delta g_1^Z + c_2 \delta \kappa + c_3 \lambda ) E^2/\Lambda ^2 ]$, with $c_i \sim \mathcal {O}(1)$ and ${\mathcal {M}}_{\textrm{SM}}$ asymptoting to a constant at large energies. Therefore, the effects of the non-SM triple gauge couplings should increase with the collision energy, which provides a way to distinguish them from the SM pieces. It is fortunate that the LEP-2 phase of the CERN’s $e^+ e^-$ collider was operating at several different center-of-mass energies. The measured $e^- e^+ \rightarrow W^- W^+$ production cross section is tabulated in 10 different energy bins in the 161–207 GeV energy range [64]. Moreover, the triple gauge couplings affect differently the polarization of the produced W bosons, which is reflected in the distribution of the W production angle. All in all, there is enough information to disentangle all the three triple gauge couplings. It is a straightforward if tedious to calculate the differential $e^- e^+ \rightarrow W^-W^+$ cross sections using the Lagrangian in Eq. (5.25) and then to compare them with the data in Ref. [64]. Once the dust settles one finds the result

$$\begin{aligned} \begin{pmatrix} \delta g_1^Z \\ \delta \kappa \\ \lambda \end{pmatrix}&= \begin{pmatrix} -0.96 \pm 0.50 \\ -0.09 \pm 0.14 \\ 0.48 \pm 0.37 \end{pmatrix} ,\nonumber \\ \rho&= \left( \begin{array}{ccc} 1 &{} 0.773 &{} -0.955 \\ 0.773 &{} 1 &{} -0.921 \\ -0.955 &{} -0.921 &{} 1 \\ \end{array} \right) . \end{aligned}$$

(5.27)

Above I show the $1\sigma$ confidence intervals in the simultaneous fit to the three triple gauge couplings in the Gaussian approximation where $\mathcal {O}(\Lambda ^{-4})$ effects in the WW cross section are ignored. I also show the correlation matrix, which is an important part of the result. From this result, using Eq. (5.26), one can obtain the LEP-2 constraint on $C_W$ independently of other contributions to triple gauge couplings: $|C_W| \lesssim {1 \over (220~\textrm{GeV})^2}$ at 95% CL. This is rather disappointing, and also surprising, given that the typical precision of the LEP-2 experiment is $\mathcal {O}(1\%)$, suggesting the reach up to $\Lambda \sim 3$ TeV. The reason for this loose constraint is that LEP-2 alone, for certain accidental reasons, cannot efficiently disentangle all the three triple gauge couplings. The final likelihood has an approximately flat direction, as witnessed by the large off-diagonal entries in the correlation matrix (more precisely, the determinant of the correlation matrix is very close to zero).

We can nevertheless obtain stronger constraints on $C_{3W}$ assuming that this is the only Wilson coefficient affecting WW production. All the necessary information for this purpose is already encoded in Eq. (5.27). First, from that equation we can reconstruct the complete likelihood: $\chi ^2 = ({\varvec{x}}-{\varvec{x}}_0) \cdot \sigma ^{-2} \cdot ({\varvec{x}}-{\varvec{x}}_0)$, where ${\varvec{x}} = (\delta g_1^Z,\delta \kappa , \lambda )$, ${\varvec{x}}_0$ are the central values in Eq. (5.27), $[\sigma ^2]_{ij} = \Delta {\varvec{x}}_i \rho _{ij} \Delta {\varvec{x}}_j$ is the error matrix built from the $1\sigma$ uncertainties $\Delta {\varvec{x}}$ and the correlation matrix $\rho$ in Eq. (5.27), and $\sigma ^{-2}$ is the inverse of the error matrix. In this 3-dimensional likelihood function we set to zero $\delta g_1^Z$ and $\delta \kappa$, to obtain 1-dimensional likelihood for $\lambda$. Minimizing that likelihood one finds $\lambda = -0.049(27)$, a much stronger constraint than in Eq. (5.27), although still weaker than naively expected, which has to do with the suppressed interference terms between the SM and $\lambda$ contributions [66]. This translates to

$$\begin{aligned} |C_W| \lesssim {1 \over (760~\textrm{GeV})^2} \end{aligned}$$

(5.28)

at 95% CL. The LHC also probes this Wilson coefficient. There the relevant processes at the parton level are $q {\bar{q}} \rightarrow W^+ W^-$ and $q {\bar{q}}' \rightarrow W^{\pm } Z$, while the scanning of the center-of-mass energy is automatically delivered via to the parton distribution functions of the colliding protons. The recent analysis by ATLAS quotes $|C_W| \lesssim {1 \over (1.6~\textrm{TeV})^2}$ at 95% CL, a factor of four better than the LEP-2 bound in Eq. (5.28).

6.3 Modified couplings

We turn to yet another important class of effects of higher-dimensional operators. The SM has merely 18 free parameters (not counting the theta term), and in terms of those it predicts countless interaction strengths between particles in the SM Lagrangian. For example, all interactions of the Higgs boson are uniquely predicted in terms of the Higgs VEV v and the SM particles masses:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SM}}&\supset {h \over v} \bigg \{ 2 m_W^2 W_{\mu }^+ W_{\mu }^- + m_Z^2 Z_{\mu } Z^{\mu } \nonumber \\&\quad - \sum _{f=d,u,s,c,b,t} m_f \big [ f^c f + {\bar{f}} {\bar{f}}^c ] \bigg \}- {m_h^2 \over 2 v} h^3 - {m_h^2 \over 8 v^2} h^4. \end{aligned}$$

(5.29)

All of the parameters above are well known. The experimental precision varies (e.g. $m_Z$ is measured with a relative $10^{-4}$ error, while for the up and down quark the accuracy is closer to $10\%$) but is invariably better than what is needed to adequately predict the LHC rates of Higgs production and decay. Staying within the SM paradigm, the LHC measurements of Higgs cross sections and branching ratios teach us next to nothing about fundamental interactions. Things are completely different in SMEFT, where literally every interaction strength in Eq. (5.29) can be altered by higher-dimensional operators. As an example, consider the dimension-6 operator in Eq. (3.11) that modifies the Higgs boson coupling to tau leptons:

$$\begin{aligned} {{\mathcal {L}}}_{D=6} \supset [C_{eH}]_{33} H^{\dagger } H ({\bar{l}}_3 H {\bar{\tau }}^c) + {\mathrm{h.c.}}\end{aligned}$$

(5.30)

After electroweak symmetry breaking this becomes

$$\begin{aligned} \Delta {{\mathcal {L}}}_{\textrm{SM}}&= [C_{eH}]_{33} {(v + h)^3 \over 2 \sqrt{2}} ({\bar{\tau }} {\bar{\tau }}^c) + {\mathrm{h.c.}}\nonumber \\&= [C_{eH}]_{33} {v^3 + 3 v^2 h + 3 v h^2 + h^3 \over 2 \sqrt{2}} ({\bar{\tau }} {\bar{\tau }}^c) + {\mathrm{h.c.}}\end{aligned}$$

(5.31)

The $h^2$ and $h^3$ are new vertices in the nomenclature of this section. They have currently very limited phenomenological relevance, so let us leave them aside. The first two terms shift the $\tau$ mass term and the Higgs Yukawa coupling to $\tau$:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}&\supset {v \over \sqrt{2}} \bigg ( [Y_e]_{33} + {v^2 \over 2} [C_{eH}]_{33} \bigg ) \big [ \tau ^c \tau + {\bar{\tau }} {\bar{\tau }}^c \big ] \nonumber \\&\quad +{h \over \sqrt{2}} \bigg ( [Y_e]_{33} + {3 v^2 \over 2} [C_{eH}]_{33} \bigg ) \big [ \tau ^c \tau + {\bar{\tau }} {\bar{\tau }}^c \big ] , \end{aligned}$$

(5.32)

where, to simplify this discussion, I assume that $[C_{eH}]_{33}$ does not have an imaginary part. By convention, I always work in a basis where $Y_e +(v^2/2) C_{eH}$ is diagonal and real, see the comment at the end of Sect. 4. Therefore we can identify the $\tau$ mass as $m_{\tau } = {v \over \sqrt{2}} \big ( [Y_e]_{33} + {v^2 \over 2} [C_{eH}]_{33} \big )$, and rewrite the Yukawa

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}&\supset {h \over \sqrt{2}} \bigg ( [Y_e]_{33} + {v^2 \over 2} [C_{eH}]_{33} \bigg ) \nonumber \\&\quad \times \bigg ( 1 + {v^2 \over [Y_e]_{33}} [C_{eH}]_{33} \bigg ) \big [ \tau ^c \tau + {\bar{\tau }} {\bar{\tau }}^c \big ] \nonumber \\&= m_{\tau } \big ( 1 + \delta y_{\tau } \big ) h \big [ \tau ^c \tau + {\bar{\tau }} {\bar{\tau }}^c \big ] , \nonumber \\ \delta y_{\tau }&= {v^3 \over \sqrt{2} m_{\tau }} [C_{eH}]_{33} , \end{aligned}$$

(5.33)

where I’m neglecting $\mathcal {O}([C_{eH}]_{33}^2) \sim \mathcal {O}(\Lambda ^{-4})$ effects. Thus, $[C_{eH}]_{33}$ destroys the correlation between the Higgs boson Yukawa coupling to the $\tau$ lepton and the $\tau$ lepton mass. In other words, that coupling is modified, deviating from the SM prediction. This is in fact the best way to constrain $[C_{eH}]_{33}$. Particle Data Group performs an average of the ATLAS and CMS bounds on the $h \rightarrow \tau \tau$ signal strength, finding $\Gamma (h \rightarrow \tau \tau )/\Gamma (h \rightarrow \tau \tau )_{\textrm{SM}} = 1.15 \pm 0.15$ [57]. This translates to $\delta y_{\tau } = 0.08 \pm 0.08$, or

$$\begin{aligned} \big |[C_{eH}]_{33} \big | \lesssim {1 \over (5~\textrm{TeV})^2} \end{aligned}$$

(5.34)

at 95% CL. The reach up to a few TeV is representative to what one can currently squeeze out of Higgs physics.

There are two main lessons from this simple example. One is the importance of precision measurements. $C_{eH}$ is just one of many dimension-6 operators that shift interaction strengths away from the SM value. Searching for such effects relies not only on improving experimental accuracy, but also on a good control of the theoretical predictions. This is often challenging, but the payoff is important: increasing precision of the measurements directly translates into increased scale of higher-dimensional operators (thus, increased scale of new physics) that we can probe. The second lesson concerns the importance of properly identifying the input parameters in SMEFT. In the above example, one had to take into account that $[C_{eH}]_{33}$ contributes not only to the $h \tau \tau$ Yukawa, but also to the $\tau$ mass term. Had we forgotten about it, and just naively looked at the Yukawa term in Eq. (5.32), we would have obtained a wrong answer for $\delta y_{\tau }$. In this case the error committed would be of order one, but it can be much more dramatic. Consider another example, where we switch on the four-fermion operator

$$\begin{aligned} {{\mathcal {L}}}_{D=6} \supset [C_{ll}]_{1221} ({\bar{l}}_1 {\bar{\sigma }}^\rho l_2) ({\bar{l}}_2 {\bar{\sigma }}_{\rho } l_1) , \end{aligned}$$

(5.35)

where $[C_{ll}]_{1221}$ is real in our conventions (see the comment below Eq. (3.16)). This operator contains the interaction terms ${{\mathcal {L}}}_{\textrm{SMEFT}} \supset [C_{ll}]_{1221} ({\bar{e}} {\bar{\sigma }}^\rho \mu ) ({\bar{\nu }}_{\mu } {\bar{\sigma }}_{\rho } \nu _e) + {\mathrm{h.c.}}$, which contributes to muon decay, $\Gamma (\mu ^- \rightarrow e^- {\bar{\nu }}_e \nu _{\mu })/\Gamma (\mu ^- \rightarrow e^- {\bar{\nu }}_e \nu _{\mu })_{\textrm{SM}} = 1 - v^2 [C_{ll}]_{1221}$. Now, muon decay is measured with impressive precision, with the relative error of order $10^{-6}$. One might naively jump to the conclusion that $[C_{ll}]_{1221}$ is stringently constrained, $v^2 | [C_{ll}]_{1221} | \lesssim 10^{-6}$, that is to say $| [C_{ll}]_{1221} | \lesssim {1 \over (300~\textrm{TeV})^2}$. This would be terribly wrong. The reason is that, in the usual approach to SM precision tests, muon decay is the standard candle that determines one of the unknown parameters of the SM - the Higgs VEV v. Indeed, the tree-level formula²³$\Gamma _{\mu \rightarrow e \nu \nu }^{\textrm{SM}} = m_{\mu }^5/(384 \pi ^3 v^4)$ allows one to precisely fix v, given that $m_{\mu }$ is known with an even better accuracy. On the other hand, in SMEFT in the presence of $[C_{ll}]_{1221}$ one has $\Gamma _{\mu \rightarrow e \nu \nu }^{\textrm{SMEFT}} = m_{\mu }^5(1 - v^2 [C_{ll}]_{1221})/(384 \pi ^3 v^4)$. Since both v and $[C_{ll}]_{1221}$ are a-priori unknown parameters, muon decay does not fix either, but just one combination of the two. Let us repeat it loudly and clearly: muon decay alone leads to no constraint at all on $C_{ll}$!

Nevertheless, the effects of $[C_{ll}]_{1221}$ do not jus disappear, when regarded from a more global perspective. To understand how $[C_{ll}]_{1221}$ re-emerges we need to do a small detour first, and discuss the input parameters for electroweak precision tests. The latter can be defined as a set of observables that, in the SM at tree level, depend on the parameters $g_L$, $g_Y$ and v in the electroweak sector. The numerical values of these parameters are traditionally fixed by three precisely known input observables:

• 1. The Fermi constant $G_F$, extracted from the measured muon lifetime using the formula $\Gamma _{\mu \rightarrow e \nu \nu }^{\textrm{SM}} = G_F^2 m_{\mu }^5/(192 \pi ^3)$ plus radiative corrections [67].

• 2. The electromagnetic structure constant $\alpha$, currently best extracted from the spectroscopy of rubidium [62] and cesium [63] atoms.

• 3. The Z boson mass $m_Z$, extracted from the position of the corresponding resonance in $e^+ e^-$ scattering in the LEP-1 collider [68].

In SMEFT, in the presence of $[C_{ll}]_{1221}$, working at $\mathcal {O}(\Lambda ^{-2})$ and at tree²⁴ level, these input observables are connected to the SMEFT parameters as

$$\begin{aligned} G_F= & {} {1 \over \sqrt{2} v_0^2} \bigg ( 1 - {v^2 \over 2} [C_{ll}]_{1221} \bigg ), \quad \alpha ={g_{L0}^2 g_{Y0}^2 \over 4 \pi (g_{L0}^2 + g_{Y0}^2)}, \nonumber \\ m_Z= & {} { \sqrt{g_{L0}^2 + g_{Y0}^2} v_0 \over 2}, \end{aligned}$$

(5.36)

where I re-labeled the parameters from the SM Lagrangian using the subscript zero to distinguish them from the $g_L$, $g_Y$ and v parameters in the following, which will differ by $\mathcal {O}(\Lambda ^{-2})$, and which will be assigned definite numerical values. Note at, at $\mathcal {O}(\Lambda ^{-2})$, it does not matter whether I write $v^2 C_{ll}$ or $v_0^2 C_{ll}$. If $[C_{ll}]_{1221} = 0$ then, as in the SM, Eq. (5.36) relates 3 parameters to 3 observables and we can readily solve for $v_0$, $g_{L0}$, and $g_{Y0}$. However when $[C_{ll}]_{1221} \ne 0$ we have 3 equations for 4 parameters. In this case it is convenient to use a trick: we can get rid of $[C_{ll}]_{1221}$ from Eq. (5.36) by absorbing it into the other parameters. These can be achieved by defining

$$\begin{aligned} v_0= & {} v (1 + \delta v), \qquad g_{L,0} = g_L (1 + \delta g_L), \nonumber \\ g_{Y,0}= & {} g_Y (1 + \delta g_Y), \end{aligned}$$

(5.37)

where

$$\begin{aligned} \delta v&= - {v^2 \over 4} [C_{ll}]_{1221} , \quad \delta g_L = {g_L^2 v^2 \over 4 (g_L^2 - g_Y^2) } [C_{ll}]_{1221} ,\nonumber \\ \delta g_Y&= - {g_Y^2 v^2 \over 4 (g_L^2 - g_Y^2) } [C_{ll}]_{1221} . \end{aligned}$$

(5.38)

The shift $\delta v$ removes the $[C_{ll}]_{1221}$ pollution from $G_F$ at $\mathcal {O}(\Lambda ^{-2})$. The other two shifts are then needed to prevent $[C_{ll}]_{1221}$ from popping up in $m_Z$ and $\alpha$. After the shift Eq. (5.36) becomes

$$\begin{aligned} G_F = {1 \over \sqrt{2} v^2}, \quad \alpha ={g_{L}^2 g_{Y}^2 \over 4 \pi (g_{L}^2 + g_{Y}^2)}, \quad m_Z= { \sqrt{g_{L}^2 + g_{Y}^2} v \over 2}, \nonumber \\ \end{aligned}$$

(5.39)

which means that $g_L$, $g_Y$, and v are related to observables in exactly the same way as the corresponding SM parameters, and therefore they can be assigned exactly the same numerical values. Plugging in the numbers into Eq. (5.39), $G_F = 1.1663787(6) \times 10^{-5}~\textrm{GeV}^{-2}$, $\alpha (m_Z) = 7.81549(55) \times 10^{-3}$, $m_Z = 91.1876(21)$ GeV [57], one finds²⁵

$$\begin{aligned} v= & {} 246.219651(63)~\textrm{GeV}, \quad g_L = 0.648457(10), \nonumber \\ g_Y= & {} 0.357968(18). \end{aligned}$$

(5.40)

OK, we managed to assign numerical values to electroweak couplings in SMEFT, but where is $[C_{ll}]_{1221}$ now? The point is that, due to the shift in Eq. (5.37), that Wilson coefficient will pop in practically every other electroweak precision observable. Let us focus on just one of them - the W boson mass. Starting from the tree-level formula $m_W = g_{L0} v_0/2$ and applying the shift in Eq. (5.37) one finds that the correction to the W boson mass in the presence of $[C_{ll}]_{1221}$ is given by

$$\begin{aligned} {\Delta m_W\over m_W} = {g_Y^2 v^2 \over 4(g_L^2-g_Y^2) } [C_{ll}]_{1221}. \end{aligned}$$

(5.41)

Now we are ready to constrain $[C_{ll}]_{1221}$. Using the average of experimental measurements from Particle Data Group, $m_W = 80.377(12)$ [57], as well as their SM prediction $m_W^{\textrm{SM}} = 80.361(6)$ [57], one obtains $v^2 [C_{ll}]_{1221} = 1.8(1.5) \times 10^{-3}$. This translates to

$$\begin{aligned} \big |[C_{ll}]_{1221} \big | \lesssim {1 \over (3.5~\textrm{TeV})^2} \end{aligned}$$

(5.42)

at $95\%$ CL. $[C_{ll}]_{1221}$ contributes to many other electroweak precision observables via the shift in Eq. (5.37), therefore the true bound is somewhat stronger than what one obtains based on the W mass alone. Using the global likelihood from Ref. [69] I obtain $\big | [C_{ll}]_{1221} \big | \lesssim {1 \over (5.7~\textrm{TeV})^2}$ at $95\%$ CL.

6.4 One more thing

In this section, for the sake of simplicity, the discussion of phenomenological effects of higher-dimensional operators is divided into “new vertices”, “new Lorentz structures”, and “modified couplings” parts. It is however important to mention that sometimes there is no invariant way to make this distinction. Consider the following example of self-interactions of the Higgs boson h:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}{} & {} \supset {1 \over 2} (\partial _{\mu } h)^2 - {m_h^2 \over 2} h^2 - {m_h^2 \over 2 v} \left( 1 + \delta _1 \right) h^3\nonumber \\{} & {} \quad - {\delta _2 \over v} h \partial _{\mu } h \partial _{\mu } h + \cdots \end{aligned}$$

(5.43)

where the dots denote terms with 4 and more Higgs bosons. Two possible effects of higher-dimensional operators appear above. The one proportional to $\delta _1$ changes the magnitude of the triple Higgs self-coupling, which is already present in the SM Lagrangian but with the magnitude strictly fixed by the Higgs boson mass. This is a modified coupling in our nomenclature. The other effect proportional to $\delta _2$ is a two-derivative Higgs self-interaction term which does not appear in the SM Lagrangian in its canonical form. This is a new Lorentz structure in our nomenclature. Both $\delta _i$ can be generated by dimension-6 operators, therefore we will treat $\delta _i$ as $\mathcal {O}(\Lambda ^{-2})$. For example, switching on the Wilson coefficients $C_H$ and $C_{H\Box }$ in Eq. (3.11), one gets $\delta _1 = 3 v^2 C_{H\Box } -5 {v^4 \over m_h^2} C_H$, $\delta _2 = 2 v^2 C_{H\Box }$. Both $\delta _i$ contribute in a non-trivial way to the Higgs scattering amplitudes, for example to $h h \rightarrow h h$, or to double Higgs production at the LHC once interactions of h with the rest of the SM are taken into account. Nevertheless, we can equivalently work with an effective Lagrangian where the 2-derivative $h (\partial _{\mu } h)^2$ interaction is completely eliminated via field redefinitions. To this end we redefine the Higgs boson field as

$$\begin{aligned} h \rightarrow h + {\delta _2 \over 2 v} h^2. \end{aligned}$$

(5.44)

After this redefinition the effective Lagrangian of Eq. (5.43) takes the form

$$\begin{aligned} {{\mathcal {L}}} = {1 \over 2} (\partial _{\mu } h)^2 - {m_h^2 \over 2} h^2 - {m_h^2 \over 2 v} \left( 1 +\delta _1 + \delta _2 \right) h^3 + \cdots , \nonumber \\ \end{aligned}$$

(5.45)

where I ignored $\delta _i^2 \sim \mathcal {O}(\Lambda ^{-4})$ terms resulting from the redefinition. Seemingly, the Lagrangians in Eqs. (5.43) and (5.45) are different, as they contain different interaction terms. However, the equivalence theorem ensures that field redefinitions cannot change the physical content of the theory, as was discussed in Sect. 4 in the context of SMEFT bases. Therefore, the two Lagrangians give exactly the same predictions for physical observables, at any order in the perturbation theory, which can be verified by explicit calculations. This demonstrates that we can get rid of some of the new Lorentz structures generated by higher-dimensional operators and absorb them into modified couplings. Conversely, a shift $h \rightarrow h - {\delta _1 \over 2 v} h^2$ applied to Eq. (5.43) would erase the modified coupling in favor of the new Lorentz structure. Once the fermions are included in the discussion, the above shift of the Higgs boson field produces Yukawa-like interactions between two powers of the Higgs boson and the SM fermions. Such interactions are absent in the SM Lagrangian, thus they are “new vertices” in our nomenclature. Therefore the boundaries between new vertices and modified couplings or new Lorentz structures are also blurred by field redefinitions. The sharp boundary persists only for the new vertices violating the SM symmetries, as those can never be redefined away into modified couplings or new Lorentz structures.

6.5 On the importance of global fits

In this section I have presented several examples of experimental constraints on Wilson coefficients of dimension-6 operators. Most of the time, in the derivation I was assuming that just a single Wilson coefficient was present at a time. This was for the sake of simplicity and clarity. My main goal was to sketch the path between the SMEFT Lagrangian and observable quantities. One should be aware, however, that such one-at-a-time results are rarely useful in practice. The higher-dimensional SMEFT operators are meant to describe effects of heavy BSM particles. But BSM models will never produce a single operator. Typical ones will produce dozens already at tree level. Even if not, renormalization group running and other loop effects will make sure to generate additional operators. Note also that one-operator-at-a-time is inherently a basis-dependent statement: what is a single operator in one basis may map to several operators with correlated Wilson coefficients in another basis.

For the practical purposes what you need is a global likelihood function. This should be derived without assuming that any particular Wilson coefficient in the SMEFT Lagrangian vanishes. A single observable typically depends on several Wilson coefficients but, at least at tree level and truncating the analysis at $\mathcal {O}(\Lambda ^{-2})$, the relevant linear combination of Wilson coefficient can be determined by the similar techniques as discussed in this section. Beyond tree level it may be more challenging to proceed in full generality, but the more and more widespread availability of automatization tools should help to overcome the difficulties. The real power of this approach is highlighted when multiple observables are combined. More often than not, different observables will depend on different linear combinations of Wilson coefficients, therefore they are complementary. If a large enough number of observables is included in the global fit, multiple Wilson coefficients can be independently constrained without any simplifying assumptions. The taste of this procedure was given around Eq. (5.27), where constraints from the LEP-2 WW cross section measured in different angular and energy bins were combined to simultaneously determine three triple gauge couplings of electroweak gauge bosons.

The likelihood function obtained in such global fits can be easily shared in a numerical form. If the likelihood is approximately Gaussian, the full information can be succinctly encoded by giving the central values, uncertainties, and the correlation matrix for the constrained Wilson coefficients. This likelihood can then be used by other researchers to constrain their preferred BSM models. There are many groups extracting such likelihoods from different classes of observables: Higgs physics, electroweak precision tests, flavor physics, etc. Each such work can be regarded as a lego block to create an even larger likelihood function covering more aspects of physics beyond the SM. Combining different likelihoods often brings forward important synergies. For example, within the SMEFT framework there is an important complementarity between measuring the triple gauge couplings and the Higgs coupling. Combining the two sets of observables allows one to lift approximate flat directions that occur in each standalone set. An advanced example of such brinkmanship is Ref. [69], where a wide selection of electroweak precisions tests at low and high energies is used to simultaneously constrain 73 linear combinations of dimension-6 Wilson coefficients. This is still a bit less than the complete set of 3045 dimension-6 Wilson coefficients in the SMEFT Lagrangian, but we’re getting there:)

7 CP violation in SMEFT

Charge conjugation (C) and parity (P) are badly violated in the SM. Their combination, ${\varvec{C}}{\varvec{P}}$, is not a symmetry of the Lagrangian either, however, due to certain accidents of nature, the observable effects of the SM sources of CP violation are feeble. This leaves ample room for CP-violating higher-dimensional operators to leave an imprint.

7.1 Formalism of CP violation

Let us begin by discussing how CP acts on the quantum fields in SMEFT. The Higgs field H is scalar²⁶ and the transformation is quite simple:

$$\begin{aligned} (CP) H (t,{\varvec{x}}) (CP)^{-1} = H^* (t,-{\varvec{x}}) . \end{aligned}$$

(6.1)

The action of P is responsible for ${\varvec{x}} \rightarrow -{\varvec{x}}$, and the action of C is responsible for the complex conjugation on the right-hand side. This in particular implies that the Higgs boson, which lives in the real part of H, is CP even: $(CP) h(t,{\varvec{x}}) (CP)^{-1} = h (t,-{\varvec{x}})$.

For the gauge fields, P and C act as

$$\begin{aligned} P V^0(t,{\varvec{x}}) P^{-1}&= V^0 (t,-{\varvec{x}}) , \nonumber \\ P V^k(t,{\varvec{x}}) P^{-1}&= - V^k (t,-{\varvec{x}}) , \nonumber \\ C V^{\mu }(t,{\varvec{x}}) C^{-1}&= - V^{\mu } (t,{\varvec{x}}) . \end{aligned}$$

(6.2)

The action of parity is the usual one for vectors. For electromagnetic fields it implies the well known fact that the electric field ${\varvec{E}}$ is P-odd, while the magnetic field ${\varvec{B}}$ is P-even. The minus in the action of C is intuitive: changing a particle into its anti-particle flips the electric charge and thus the sign of the potential. It follows that CP acts as

$$\begin{aligned} (CP) V^0(t,{\varvec{x}}) (CP)^{-1}&= -V^0 (t,-{\varvec{x}}) , \nonumber \\ (CP) V^k(t,{\varvec{x}}) (CP)^{-1}&= V^k (t,-{\varvec{x}}) . \end{aligned}$$

(6.3)

It is easy to show that the kinetic term $V_{\mu \nu } V^{\mu \nu }$ is CP even. On the other hand $V_{\mu \nu } {\tilde{V}}^{\mu \nu }$ is CP odd:

$$\begin{aligned}&(CP) \int d^4 x V_{\mu \nu } {\tilde{V}}^{\mu \nu }(x) (CP)^{-1}\nonumber \\&\quad \equiv {1 \over 2 } \epsilon ^{\mu \nu \alpha \beta }(CP) \int d^4 x V_{\mu \nu } V_{\alpha \beta }(x) (CP)^{-1} \nonumber \\&\quad = 2 \epsilon ^{ijk}(CP) \int d^4 x V_{0i} V_{jk}(x) (CP)^{-1}\nonumber \\&\quad = 2 \epsilon ^{ijk} (CP) \int d^4 x [\partial _0 V_i - \partial _i V_0 ] [\partial _j V_k - \partial _k V_j ] (x) (CP)^{-1} \nonumber \\&\quad = 2 \epsilon ^{ijk} \int d^4 x [\partial _0 V_i + \partial _i V_0 ] [\partial _j V_k - \partial _k V_j ] (t,-{\varvec{x}}) \nonumber \\&\quad = - 2 \epsilon ^{ijk} \int d^4 x [\partial _0 V_i (t,{\varvec{x}}) - \partial _i V_0 (t,{\varvec{x}}) ] [\partial _j V_k (t,{\varvec{x}}) - \partial _k V_j (t,{\varvec{x}}) ]\nonumber \\&\quad = - \int d^4 x V_{\mu \nu }(x) {\tilde{V}}^{\mu \nu }(x) . \end{aligned}$$

(6.4)

In the next-to-last step we changed the integration variables ${\varvec{x}} \rightarrow - {\varvec{x}}$. This shows that the $\theta$ term in the $D=4$ Lagrangian Eq. (3.7) violates CP. Likewise, the bosonic interactions proportional to the Wilson coefficients $C_{H{\widetilde{G}}}$, $C_{H{\widetilde{W}}}$, $C_{H{\widetilde{B}}}$, and $C_{H {\widetilde{W}} B}$ in Eq. (3.11) are CP odd. By an analogous calculation one can show that also the ones proportional to $C_{{\widetilde{W}}}$ and $C_{{\widetilde{G}}}$ are CP violating. Note that in these cases CP violation is not associate with complex couplings in the Lagrangian.

Let us move to the fermionic fields. One can show that parity and charge conjugation act on two-component fermion fields as

$$\begin{aligned} P \psi _\alpha (t,{\varvec{x}}) P^{-1}&= {\bar{\psi }}^{c \, {\dot{\alpha }}}(t,-{\varvec{x}}), \nonumber \\ P \psi ^\alpha (t,{\varvec{x}}) P^{-1}&= - {\bar{\psi }}^c_{{\dot{\alpha }}}(t,-{\varvec{x}}), \nonumber \\ P \psi ^c_{ \alpha }(t,{\varvec{x}}) P^{-1}&= - {\bar{\psi }}^{{\dot{\alpha }}}(t,-{\varvec{x}}) , \nonumber \\ P \psi ^{c\, \alpha }(t,{\varvec{x}}) P^{-1}&= {\bar{\psi }}_{{\dot{\alpha }}}(t,-{\varvec{x}}) , \end{aligned}$$

(6.5)

$$\begin{aligned} C \psi (t,{\varvec{x}}) C^{-1}&= \psi ^c(t,{\varvec{x}}), \nonumber \\ C \psi ^c(t,{\varvec{x}}) C^{-1}&= \psi (t,{\varvec{x}}) . \end{aligned}$$

(6.6)

Parity, intuitively, exchanges left- and right-handed fermions. The action of C provides the rationale for the $\cdot ^c$ notation. It follows that CP acts as

$$\begin{aligned} (CP) \psi _\alpha (t,{\varvec{x}}) (CP)^{-1}&= {\bar{\psi }}^{{\dot{\alpha }}}(t,-{\varvec{x}}), \nonumber \\ (CP) \psi ^\alpha (t,{\varvec{x}}) (CP)^{-1}&= - {\bar{\psi }}_{{\dot{\alpha }}}(t,-{\varvec{x}}), \nonumber \\ (CP) \psi ^c_{ \alpha }(t,{\varvec{x}}) (CP)^{-1}&= - {\bar{\psi }}^{c \, {\dot{\alpha }}}(t,-{\varvec{x}}) ,\nonumber \\ (CP) \psi ^{c\, \alpha }(t,{\varvec{x}}) (CP)^{-1}&= {\bar{\psi }}^c_{{\dot{\alpha }}}(t,-{\varvec{x}}) . \end{aligned}$$

(6.7)

Now we are ready to investigate how CP acts on a fermionic mass term in the action:

$$\begin{aligned}&(CP) \int d^4 x \big [ m \psi ^c\psi + m^* {\bar{\psi }} {\bar{\psi }}^c \big ](t,{\varvec{x}}) (CP)^{-1}\nonumber \\&\quad \equiv (CP) \int d^4 x h \big [ m \psi ^{c\,\alpha } \psi _\alpha + m^* {\bar{\psi }}_{{\dot{\alpha }}} {\bar{\psi }}^{c \, {\dot{\alpha }} } \big ](t,{\varvec{x}}) (CP)^{-1} \nonumber \\&\quad = \int d^4 x \big [ m {\bar{\psi }}^c_{{\dot{\alpha }}}{\bar{\psi }}^{{\dot{\alpha }}} + m^* \psi ^{\alpha } \psi ^c_{\alpha } \big ](t,- {\varvec{x}}) \nonumber \\&\quad = \int d^4 x \big [ m {\bar{\psi }}_{{\dot{\alpha }}} {\bar{\psi }}^{c\, {\dot{\alpha }}} + m^* \psi ^{c\, \alpha } \psi _{\alpha } \big ](t, {\varvec{x}}) \nonumber \\&\quad \equiv \int d^4 x \big [m^* \psi ^c \psi + m {\bar{\psi }} {\bar{\psi }}^c \big ](t, {\varvec{x}}) . \end{aligned}$$

(6.8)

In the last step we changed the integration variables ${\varvec{x}} \rightarrow - {\varvec{x}}$, and used that for anti-commuting fermion fields we have $\psi ^{\alpha } \psi ^c_{\alpha } = - \psi ^c_{\alpha } \psi ^{\alpha } = \psi ^{c \, \alpha } \psi _{\alpha }$. It follows that complex mass terms violate CP. This is however not the whole story. The chiral transformation:

$$\begin{aligned} \psi&\rightarrow e^{-i {\textrm{Arg}}[m]/2 + i \eta } \psi , \nonumber \\ \psi ^c&\rightarrow e^{-i {\textrm{Arg}}[m]/2 - i \eta } \psi ^c, \end{aligned}$$

(6.9)

with an arbitrary phase $\eta$, removes the complex phase of the mass term and restores CP conservation at the level of the kinetics terms. Thus CP violation can only arise due to unremovable relative phases between fermionic mass and interaction terms. For example, by exactly the same calculation as in Eq. (6.8), CP transformation of a Yukawa interaction of the fermion with a real scalar field h is given by

$$\begin{aligned}&(CP) \int d^4 x h \big [ y \psi ^c\psi + y^* {\bar{\psi }} {\bar{\psi }}^c \big ](t,{\varvec{x}}) (CP)^{-1}\nonumber \\&\quad \rightarrow \int d^4 x h \big [y^* \psi ^c \psi + y {\bar{\psi }} {\bar{\psi }}^c \big ](t, {\varvec{x}}) . \end{aligned}$$

(6.10)

If ${\textrm{Arg}}[m] \ne {\textrm{Arg}}[y]$ then the relative phase cannot be removed and CP violation is physical. This simple example illustrates the fact that CP is a collective endeavour. Phases in a single interaction are not physical, as they can always be transferred elsewhere by a phase redefinition of fermionic fields. For this reason, the mathematically proper language to discuss CP involves invariants under phase and other unitary transformations. In the SM there is only one such object: the famous Jarlskog invariant. SMEFT proliferates the number of physical phases and invariants; at the level of dimension-6 operators they were recently classified in Ref. [70].

7.2 CP violation at $D=4$

To set the stage, I will now briefly discuss CP violation at the level of $D=4$ operators in SMEFT, which is the same as CP violation in the SM. This will be the springboard to describe observable CP-violating effects of selected higher-dimensional SMEFT operators in the following subsections.

The $D=4$ SMEFT Lagrangian in Eq. (3.7) contains the so-called theta term:

$$\begin{aligned} {{\mathcal {L}}}_{D=4} \supset {\tilde{\theta }} G_{\mu \nu }^a {\tilde{G}}_{\mu \nu }^a . \end{aligned}$$

(6.11)

This is a total derivative, which does not affect any perturbative amplitudes. However, at the non-perturbative level this term does contribute to CP-violating hadronic observables, in particular to the neutron EDM. The most recent lattice evaluation in Ref. [14] estimates

$$\begin{aligned} d_n = 0.158(36) {\tilde{\theta }} \, e \, {\textrm{fm}}. \end{aligned}$$

(6.12)

The current experimental limit is $d_n = (0.0 \pm 1.1) \times 10^{-13 }\, e \, {\textrm{fm}}$ [71], which leads to the 95% CL limit

$$\begin{aligned} |{\tilde{\theta }}| \lesssim 1.4 \times 10^{-12} . \end{aligned}$$

(6.13)

The smallness of CP violation due the theta term is one of the biggest mysteries of contemporary particle physics.

The $D=4$ SMEFT Lagrangian also contains the Yukawa interactions:

$$\begin{aligned} {{\mathcal {L}}}_{D=4} \supset {\bar{Q}} {\tilde{H}} Y_u {\bar{U}}^c + {\bar{Q}} H Y_d {\bar{D}}^c + {\bar{L}} H Y_e {\bar{E}}^c + {\mathrm{h.c.}} \end{aligned}$$

(6.14)

As discussed around Eq. (6.10), Yukawa terms transform under CP as $Y_f \rightarrow Y_f^*$, therefore complex Yukawa phases may lead to CP violation. However, phases in standalone Yukawa terms are removable, therefore they have to be discussed in conjunction with other interactions in the SMEFT Lagrangian. The leptonic part will be discussed later in the context of $D=5$ operators, and we focus on the quark Yukawas for now. The usual way to isolate the physical phases is to first write down the quark mass term after electroweak symmetry breaking: ${{\mathcal {L}}}_{\textrm{SMEFT }} \supset {v \over \sqrt{2}} \bigg ( {\bar{U}} Y_u {\bar{U}}^c + {\bar{D}}^c Y_d {\bar{D}}^c + {\mathrm{h.c.}} \bigg )$, where $Q = (U,D)$. In full generality, one can decompose any matrix as $Y_f = L_f M_f R_f^{\dagger }$, where $L_f$ and $R_f$ are unitary, and $M_f$ is diagonal with real entries. Then we can rotate the quark fields $U \rightarrow L_u U$, $D \rightarrow L_d D$, $U^c \rightarrow U^c R_u^{\dagger }$, $D^c \rightarrow D^c R_d^{\dagger }$.²⁷ This transformation leaves invariant most of the terms originating from the $D=4$ Lagrangian, in particular $R_f$ cancel out completely. The only place where $L_f$ emerge is in the charged current interactions between the W boson and left-handed quarks:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset - {g_L \over \sqrt{2}} W_{\mu }^+ {\bar{U}} {\bar{\sigma }}^{\mu } V D + {\mathrm{h.c.}}, \end{aligned}$$

(6.15)

where the CKM matrix V is related to the left rotations as $V = L_u^{\dagger } L_d$ and therefore it is unitary, $V^{\dagger } V = \textbf{1}$. By an analogous calculation as the one in Eq. (6.8) one can show that the CP transformation effectively takes $V \rightarrow V^*$, thus phases of the CKM matrix may lead to CP violation. A general unitary matrix has 9 free parameters: 3 angles and 6 phases, however most of the phases are removable. Indeed, we can make the transformations $u_J \rightarrow e^{i \phi _J} u_J$, $u_J^c \rightarrow e^{i \phi _J} u_J^c$, $d_J \rightarrow e^{i \eta _J} d_J$, $d_J^c \rightarrow e^{i \eta _J} d_J^c$, which maintain real quark masses, and transform the CKM matrix elements as $[V]_{JK} \rightarrow e^{i (\phi _J + \eta _K)} [V]_{JK}$. Physics does not depend on conventions, therefore CP-violating observables must depend on invariants of V under such phase redefinitions. The non-trivial invariant that can be constructed is $J_{IJKL} = {{\textrm{Im}}} \,[V_{IK} V_{JL}V_{IL}^* V_{JK}^*]$ (no summation of repeated indices). It may seem that there are several invariants for different values of $I,J,K,L= 1 \ldots 3$. However, it is easy to see that $J_{IJKL}$ is antisymmetric in IJ and in KL indices, and it is symmetric under $IJ \leftrightarrow KL$. Furthermore, using the unitarity of V, one can show that $J_{IJJK} = - J_{IJIK} = - J_{IJJI}$ for $I \ne J \ne K$. All in all, for 3 generations there remains a single order parameter for CP violation via the CKM matrix, the so-called Jarlskog invariant:

$$\begin{aligned} {{\mathcal {J}}} \equiv J_{1223} = {{\textrm{Im}}} \,[V_{us} V_{cb} V_{ub}^* V_{cs}^*] , \end{aligned}$$

(6.16)

while the other components of J are given by the formula $J_{IJKL} = {{\mathcal {J}}} \sum _{M,N} \epsilon _{IKM}\epsilon _{JLN}$. In the SM, this single invariant controls CP violation observed in multiple processes with mesons containing strange, charm, and bottom quarks. From these observations, assuming negligible contributions from higher-dimensional operators, one can extract ${{\mathcal {J}}} = 3.08(14) \times 10^{-5}$ [57]. This is a small number but, actually, the phase itself in the CKM matrix is large, order one. In particular, in the widely used Wolfenstein parametrization of the CKM matrix, where the phase is located mostly in the $V_{ub}$ and $V_{td}$ elements, one gets ${\textrm{Arg}}[V_{ub}] \simeq -1.1$, ${\textrm{Arg}}[V_{td}] \simeq -0.4$. However the Jarlskog invariant is suppressed by the smallness of the absolute values of the off-diagonal CKM elements: $|V_{us}| \sim \lambda$, $|V_{cb}| \sim \lambda ^2$, $|V_{ub}| \sim \lambda ^3$, where $\lambda \sim 0.2$ is the Cabibbo angle. Due to this hierarchical structure, ${{\mathcal {J}}} \sim \lambda ^6$, leading to a severe suppression of observable signals of CP violation. Although CP violation was first discovered some 60 years ago [72], to this day experimental detections of CP-violating quantities are few and far between, and each new detection is announced with fanfare.

The partly mysterious and partly accidental suppression of CP violation at the level of the $D=4$ Lagrangian opens the playground for higher-dimensional CP-violating operators. $D=5$ operators introduce three more CP invariants, including the so-called PMNS phase, which is a subject of an intense ongoing experimental program in neutrino physics. At the level of $D=6$ operators all hell breaks loose, and there are literally hundreds of new CP invariants [70]. Dimension-6 operators can provide tree-level contributions to basically any CP-violating observable, including the EDMs of elementary (electron) and composite (neutron, nuclei, molecules) particles, and the neutral meson mixing ($K{\bar{K}}$, $D {\bar{D}}$, $B {\bar{B}}$). In the rest of this section we discuss selected CP-violating observables and their dependence on higher-dimensional SMEFT operators.

7.3 CP violation at $D=5$

The dimension-5 operator in Eq. (3.8) after electroweak symmetry breaking yields the neutrino mass terms. Together with the charged lepton masses from the $D=4$ Yukawa interactions, the lepton masses are given by

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset - {v \over \sqrt{2}} {\bar{E}} Y_e {\bar{E}}^c - {v^2 \over 2} {\bar{\nu }} C_5 {\bar{\nu }} + {\mathrm{h.c.}} \end{aligned}$$

(6.17)

An analogous calculation as in Eq. (6.8) shows that CP takes $Y_e \rightarrow Y_e^*$, $C_5 \rightarrow C_5^*$, therefore the phases in $C_5$ and $Y_e$ are potentially CP-violating. As in the quark case earlier, in order to identify the physical phases it is convenient to make the masses diagonal and real. One can decompose $Y_e = L_e M_e R_e^{\dagger }$, $C_5 = L_{\nu }^T M_{\nu } L_{\nu }$ (recall that $C_5$ is symmetric), where $L_e$, $R_e$ and $L_{\nu }$ are unitary, while $M_e$ and $M_{\nu }$ are diagonal, real, and positive. Rotating the fields as $\nu \rightarrow L_{\nu } \nu$, $E \rightarrow L_e E$, $E^c \rightarrow E^c R_e^{\dagger }$, the phases then re-emerge in the W boson interactions with left-handed leptons:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset {g_L \over \sqrt{2}} W_{\mu }^- {\bar{E}} {\bar{\sigma }}^{\mu } U \nu + {\mathrm{h.c.}}, \end{aligned}$$

(6.18)

where the PMNS matrix $U = L_e^{\dagger } L_{\nu }$ is unitary.

In general, a unitary matrix has 6 phases. We can remove 3 phases from U by redefining $e_J \rightarrow e^{i \phi _J} e_J$, $e_J^c \rightarrow e^{i \phi _J} e_J^c$. Contrary to the CKM case, we cannot remove further two phases, because the transformations $\nu _n \rightarrow e^{i \eta _n}\nu _n$ would feed the complex phases back into the neutrino mass terms. Thus, there are three physical phases in U. One corresponds to the usual Jarlskog invariant,

$$\begin{aligned} {\hat{J}}_{JKmn} = {{\textrm{Im}}} \,[U_{Jm} U_{Kn} U_{Jn}^* U_{Km}^*] = \hat{{\mathcal {J}}} \sum _{L,p} \epsilon _{JKL}\epsilon _{mnp}. \end{aligned}$$

(6.19)

The phase controlling $\hat{{\mathcal {J}}}$ is called the Dirac phase, and it remains physical in the limit of vanishing neutrino masses. It is measurable in oscillation experiments as it affects the oscillation probabilities. Ignoring contributions from higher-dimensional operators, these can be written as

$$\begin{aligned} P(\nu _J \rightarrow \nu _K)&= \sum _{m,n=1}^3 e^{i {\Delta _{mn}^2 \over 2 E_{\nu } }}U_{J m} U_{K n} U_{J n}^* U_{K m}^* , \nonumber \\ P({\bar{\nu }}_J \rightarrow {\bar{\nu }}_K)&= \sum _{m,n=1}^3 e^{-i {\Delta _{mn}^2 \over 2 E_{\nu } }}U_{J m} U_{K n} U_{J n}^* U_{K m}^* , \end{aligned}$$

(6.20)

where $\Delta _{kl}^2 \equiv m_{\nu _k}^2 - m_{\nu _l}^2$ are the differences of the squared masses of neutrino eigenstates. The CP-violating observable is the difference between oscillation probabilities of neutrinos and anti-neutrinos of a given flavor:

$$\begin{aligned}&P(\nu _J \rightarrow \nu _K) - P({\bar{\nu }}_J \rightarrow {\bar{\nu }}_K) \nonumber \\&\quad = - 2 \sum _{m,n=1}^3 \sin \bigg ( {\Delta _{mn}^2 \over 2 E_{\nu } } \bigg ) {{\textrm{Im}}} \,[ U_{J m} U_{K n} U_{J n}^* U_{K m}^*] \nonumber \\&\quad = -2 \hat{{\mathcal {J}}} \sum _L \epsilon _{JKL} \sum _{m,n,p=1}^3 \epsilon _{mnp} \sin \bigg ( {\Delta _{mn}^2 \over 2 E_{\nu } } \bigg ) . \end{aligned}$$

(6.21)

This explicitly shows that CP violation in neutrino oscillations at the $D=5$ level is controlled by the single Jarlskog invariant $\hat{{\mathcal {J}}}$ defined in Eq. (6.19). Determining whether $\hat{{\mathcal {J}}}$ is non-zero is subject to an intensive experimental program, with several ongoing experiments (T2K, NO$\nu$A, Super-K) placing non-trivial limits. Some of these even provide preliminary hints that $\hat{{\mathcal {J}}} \ne 0$, and that the phase in the PMNS matrix, much like in the CKM matrix, is large [73]. The matter should be ultimately resolved in the coming years, or at latest in the next decade, when the future DUNE and Hyper-K experiments collect enough data. The importance of these measurements go beyond measuring yet another parameter in the PMNS matrix. If $\hat{{\mathcal {J}}} \ne 0$, it will be another (after the CKM phase) demonstration that phases are present in the fundamental Lagrangians. Philosophically, it will be a strong hint that phases are generic, that is to say, they arise whenever they are allowed to, and there is no physical principles suppressing them. Adopting this point of view would have tremendous consequences for BSM model building.²⁸

The other two physical phases in the PMNS matrix can be isolated by rewriting $U_{Jn} = {\hat{U}}_{Jn} e^{i \gamma _n}$, where ${\hat{U}}_{Jn}$ contains only the Dirac phase. The $\gamma _n$ phases cancel out in ${\hat{J}}_{JKmn}$ but the two relative phases (the differences $\gamma _n- \gamma _m$) are physical. They are called the Majorana phases and they enter into predictions for physical observables, such as neutrino oscillations into anti-neutrinos, or neutrinoless double beta decay. However they become unphysical in the limit of vanishing neutrino masses, as in this limit one is free to use phase redefinitions of the neutrino fields to get rid of these phases. Therefore, their effects on physical observables must always be proportional to the neutrino masses, and therefore extremely suppressed. For the moment, there is little hope of ever measuring them in low-energy experiments.

7.4 Electric dipole moments

Electric dipole moments, abbreviated as EDMs, are mundane in classical electrodynamics. Take two opposite charges $\pm Q$, put them very close together at a distance R, and what you get from a sufficiently large distance $r \gg R$ looks like a particle without an electric charge but with the electric dipole moment $|d| = Q R$. On the other hand, EDMs of elementary particles are dramatic because they signal CP violation. To date, no such EDMs have been detected, in spite of the existence of CP violation in the SM - the contributions proportional to the CKM phase are still many orders of magnitude below the experimental sensitivity. The same remains true concerning the EDMs of sufficiently simple composite particles: protons, neutrons, atoms in ground state in vacuum...To observe permanent EDMs one has to go up to the molecule level, the prime example being the water molecule with $d_{H_2 O} \simeq 2 \times 10^{-5}~{\textrm{eV}}^{-1}$.

Let us begin the discussion with the simple case of the electron. The SMEFT Lagrangian contains the dimension-6 operators

$$\begin{aligned} {{\mathcal {L}}}_{D=6}&\supset [C _{eW} ]_{11} ({\bar{l}}_1 \sigma ^k H {\bar{\sigma }}^{\mu \nu } {\bar{e}}^c) W_{\mu \nu }^k \nonumber \\&\quad + [C _{eB}]_{11} ({\bar{l}}_1 H {\bar{\sigma }}^{\mu \nu } {\bar{e}}^c) B_{\mu \nu } + {\mathrm{h.c.}} \end{aligned}$$

(6.22)

where $l_1 = (\nu _e,e)$ is the first generation left-handed lepton doublet. Once the Higgs gets a VEV this leads to

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}} \supset - \bigg \{ {\Delta \mu _e - i d_e \over 4 } F_{\mu \nu } (e^c \sigma ^{\mu \nu } e) + {\mathrm{h.c.}}\bigg \} , \end{aligned}$$

(6.23)

where

$$\begin{aligned} \Delta \mu _e&= - 2 \sqrt{2} v {\textrm{Re}} \,\bigg [ \cos \theta _W [C _{eB}]_{11} - \sin \theta _W [C _{eW} ]_{11} \bigg ] , \nonumber \\ d_e&= - 2 \sqrt{2} v {{\textrm{Im}}} \,\bigg [ \cos \theta _W [C _{eB}]_{11} - \sin \theta _W [C _{eW} ]_{11} \bigg ] . \end{aligned}$$

(6.24)

As the notation suggests, $\Delta \mu _e$ is the anomalous magnetic dipole moment of the electron, and $d_e$ is its electric dipole moment. Therefore, $d_e \ne 0$ in the presence of imaginary Wilson coefficients in Eq. (6.22). See the derivation of Eq. (5.20) to understand the precise connection between the coefficients of the $F_{\mu \nu } f^c \sigma ^{\mu \nu } f$ interaction, and the dipole moments of spin-1/2 particles.

The current experimental constraint on the electric dipole moment of the electron is $d_e = (4.3 \pm 4.0) \times 10^{-30} e \, {\textrm{cm}}$ [74], which is $d_e = (6.6 \pm 6.2) \times 10^{-17}~{\textrm{GeV}}^{-1}$ in natural units. Assuming $C_{eW}=0$, using Eq. (6.24) we can translate the experimental constraint into a bound on the SMEFT Wilson coefficient $C_{eB}$:

$$\begin{aligned} \big | {{\textrm{Im}}} \,[C_{eB}]_{11} \big | \lesssim {1 \over (1.8~{\textrm{EeV}} )^2 } \end{aligned}$$

(6.25)

at 95% CL. A similar constraint holds for ${{\textrm{Im}}} \,[C_{eW}]_{11}$. At face value this is absolutely amazing, allowing us to probe physics at the enormous scales of exa-electronvolt (EeV), that is $10^{6}$ TeV. In practice the sensitivity may be more modest. First of all, for perturbative UV completions the $C_{eB}$ Wilson coefficient is always generated at one loop level, thus $C_{eB} \sim g_Y/16\pi ^2$. Moreover, most UV completions will implement some sort of chiral symmetry, leading to $[C_{eB}]_{11}$ suppressed by the small Yukawa coupling of the electron (otherwise there will be large contributions to the electron mass, leading to a new hierarchy problem). All in all, one typically has ${{\textrm{Im}}} \,[C_{eB}]_{11}\sim {g_Y m_e \over 16 \pi ^2 v \Lambda ^2}$, where $\Lambda$ is the scale of new physics generating the electron’s EDM. But even under this conservative hypothesis one probes $\Lambda \sim 100$ TeV, far above the LHC reach.

It is worth stressing that the good sensitivity of $d_e$ to new physics is not restricted to the $[C_{eB}]_{11}$ operator. Indeed, by renormalization group equations, certain other operators generated at a high scale can flow into $[C_{eB}]$ at lower energies, and thus get constrained. For example, the evolution of $C_{eB}$ contains the contribution [75]

$$\begin{aligned} {d C_{eB} \over d \log \mu } = - {g_Y \over 8 \pi ^2} \bigg ( C_{H B} + i C_{H {\widetilde{B}} } \bigg ) Y_e + \cdots \end{aligned}$$

(6.26)

Thus, the bosonic operator $C_{H {\widetilde{B}} }$ defined in Eq. (3.11) renormalizes ${{\textrm{Im}}} \,C_{eB}$. This leads to the constraint

$$\begin{aligned} | C_{H {\widetilde{B}} } (\Lambda )| \lesssim { 1 \over (200~{\textrm{TeV}})^2 \times \log \big (\Lambda /m_Z \big ) } . \end{aligned}$$

(6.27)

Similar constraints can be obtained for $C_{H {\widetilde{W}} }$, and some components of $C_{lequ}$ are also strongly constrained by the electron’s EDM. The power of the electron EDM is such that even operators contributing via two-loop effects are subject to relevant constraints [76].

We move to discussing another important EDM. This time it is about a composite particle – the neutron. Because of the strong interactions involved, connecting the neutron’s EDM to SMEFT Wilson coefficients is a complicated business, involving difficult calculations in Chiral Perturbation Theory, lattice determination of nuclear matrix elements, phenomenological extraction of nuclear parameters, etc. I am not daring enough to review the necessary technology here. Instead, I will just quote the result from Ref. [77]:

$$\begin{aligned} d_n&= \bigg [ (43 \pm 27) {{\textrm{Im}}} \,C^{us \, us}_{1\, LR} + (210 \pm 130) {{\textrm{Im}}} \,C^{us \, us}_{2\, LR} \nonumber \\&\quad + (22 \pm 14) {{\textrm{Im}}} \,C^{ud \, ud}_{1\, LR} + (110 \pm 70) {{\textrm{Im}}} \,C^{ud \, ud}_{2\, LR} \nonumber \\&\quad - (0.93 \pm 0.05) {{\textrm{Im}}} \,C_{\gamma u}^{uu}- (4.0 \pm 0.2) {{\textrm{Im}}} \,C_{\gamma d}^{dd}\nonumber \\&\quad - (0.8 \pm 0.9) {{\textrm{Im}}} \,C_{\gamma d}^{ss} - (3.9 \pm 2.0) {{\textrm{Im}}} \,C_{g u}^{uu}\nonumber \\&\quad - (16.8 \pm 8.4) {{\textrm{Im}}} \,C_{g d}^{dd} + (320 \pm 260) C_{{\tilde{G}}} \bigg ] v^2\nonumber \\&\quad \times 10^{-9} e \, \textrm{fm} , \end{aligned}$$

(6.28)

where the Wilson coefficients above are defined by the following Lagrangian below the electroweak scale,

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{WEFT}}&\supset \bigg \{ - C_{1 \, LR}^{ij \, lm} ({\bar{d}}_m {\bar{\sigma }}_{\mu } u_l) (u^c_i \sigma ^{\mu } d^c_j ) \nonumber \\&\quad - C_{2 \, LR}^{ij \, lm} ({\bar{d}}_{m \, a} {\bar{\sigma }}_{\mu } u_{l\, b}) (u^c_{i \, b} \sigma ^{\mu } d^c_{j\, a} ) \nonumber \\&\quad - {g_s \over 2 }\sum _{i,j=u,c} m_{u_j }C_{gu}^{ij} {\bar{u}}_i \sigma ^{\mu \nu } T^a {\bar{u}}^c_j G^a_{\mu \nu } \nonumber \\&\quad - {g_s \over 2 }\sum _{i,j=u,c} m_{d_j } C_{gd}^{ij} {\bar{d}}_i \sigma ^{\mu \nu } T^a {\bar{d}}^c_j G^a_{\mu \nu } \nonumber \\&\quad - {e q_u \over 2 }\sum _{i,j=u,c} m_{u_j }C_{\gamma u}^{ij} {\bar{u}}_i \sigma ^{\mu \nu } {\bar{u}}^c_j F_{\mu \nu } \nonumber \\&\quad - {e q_d \over 2 }\sum _{i,j=u,c} m_{d_j } C_{\gamma d}^{ij} {\bar{d}}_i \sigma ^{\mu \nu } {\bar{d}}^c_j F_{\mu \nu } + {\mathrm{h.c.}}\bigg \} \nonumber \\&\quad + {g_s \over 3 }f^{abc} C_{{\widetilde{G}}} {\tilde{G}}_{\mu \nu }^a G_{\mu \rho }^b G_{\nu \rho }^c. \end{aligned}$$

(6.29)

Note that the operators multiplied by $C_{1 \, LR}$ and $C_{2 \, LR}$ differ by how the color indices are contracted. It is remarkable that $d_n$ is sensitive to such a diverse selections of interaction terms: electric and chromo-electric dipole interactions of quarks, 4-quark terms, and anomalous triple gluon couplings. This way the neutron EDM acts as a lightning rod attractor to many kinds of new physics. For this reason, it is an absolutely essential observable, in spite of the difficulties due to strong interactions.

Let us study some examples to see how strongly neutron EDM constrains SMEFT Wilson coefficients. Beginning with $[C_{uB}]_{11}$ in Eq. (3.14), this Wilson coefficient is related to the up-quark EDM coupling in Eq. (6.29) by $C_{\gamma u}^{uu} = - {3 \cos \theta _W v \over \sqrt{2} e m_u }[C_{uB}]_{11}$. Applying Eq. (6.28) and using the current best measurement $d_n = (0.0 \pm 1.1) \times 10^{-26} e \, {\textrm{cm}}$ [71], we get the following $95\%$ CL constraint

$$\begin{aligned} | {{\textrm{Im}}} \,[C_{uB}]_{11} | \lesssim {1 \over (13~{\textrm{PeV}})^2 }. \end{aligned}$$

(6.30)

Thus, in sheer numbers, the scale of the SMEFT operators probed by the neutron EDM is some two orders of magnitude below the scale probed by the electron EDM, cf. Eq. (6.25).

Let us also study another problem: what are the neutron EDM constraints on the $C_{Hud}$ Wilson coefficient in Eq. (3.13) ? This may be a surprising question, since that operator multiplied by $C_{Hud}$, which is ${\tilde{H}}^{\dagger } D_{\mu } H (u^c \sigma ^{\mu } {\bar{d}}^c)$, couples the Higgs field to right-handed quarks, and at first sight it has little to do with EDMs. It turns out that the effect on the neutron EDM originates from the fact that this operator induces a coupling of the W boson to the right-handed up and down quarks:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}{} & {} \supset - {g_L \over \sqrt{2}} W_{\mu }^+ \Bigg [ {\bar{\nu }}_e {\bar{\sigma }}^{\mu } e + V_{ud} {\bar{u}} {\bar{\sigma }}^{\mu } d \nonumber \\{} & {} \quad + {v^2 \over 2} [C_{H u d}]_{11} u^c \sigma ^{\mu } {\bar{d}}^c \Bigg ] + {\mathrm{h.c.}}\end{aligned}$$

(6.31)

Integrating out the W boson induces the 4-fermion operator $- V_{ud} [C_{H u d}]_{11} ({\bar{d}} {\bar{\sigma }}_{\mu } u ) (u^c \sigma ^{\mu } {\bar{d}}^c) + {\mathrm{h.c.}}$. Matching that to Eq. (6.29), we have $C_{1 \, LR}^{ud \, ud} = V_{ud} [C_{H u d}]_{11}$. Applying again Eq. (6.28), ignoring the theoretical error for the sake of simplicity, and comparing with the experimental constraint we find

$$\begin{aligned} | {{\textrm{Im}}} \,[C_{Hud}]_{11} | \lesssim {1 \over (100~{\textrm{TeV}})^2 } \end{aligned}$$

(6.32)

at 95% CL. This is again an impressive sensitivity. As remarked above, the result may be somewhat unexpected, because the connection between $C_{Hud}$ and EDMs is not obvious.

Finally, we also discuss another class of observables, namely EDM of diamagnetic atoms (such as ${}^{199}$Hg) and paramagnetic molecules (such as ThO). These are in fact the same observables from which the electron EDM is extracted. However, they are sensitive to other interactions beside the electron-photon ones. In particular, they are instrumental to probing the following SMEFT operators:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}{} & {} \supset [C_{lequ}^{(1)}]_{1111} \epsilon ^{ab} ({\bar{l}}_a {\bar{e}}^c)({\bar{q}}_{b} {\bar{u}}^c) \nonumber \\{} & {} \quad + [C_{lequ}^{(3)}]_{1111} \epsilon ^{ab} ({\bar{l}}_a {\bar{\sigma }}^{\mu \nu } {\bar{e}}^c)({\bar{q}}_{b} {\bar{\sigma }}_{\mu \nu } {\bar{u}}^c)\nonumber \\{} & {} \quad +[C_{ledq}]_{1111} ({\bar{l}}_a {\bar{e}}^c)(d^c q_a ) + {\mathrm{h.c.}}\end{aligned}$$

(6.33)

Above q and l are the 1st generation quark and lepton doublet fields. These operators simultaneously generate charged current interactions (relevant e.g. for nuclear beta decay, and for $pp \rightarrow \ell \nu$ signals at colliders) and the neutral current ones:

$$\begin{aligned} {{\mathcal {L}}}_{\nu \mathrm WEFT}{} & {} \supset -[C_{lequ}^{(1)}]_{1111} V_{ud} ({\bar{e}} {\bar{e}}^c) ({\bar{u}} {\bar{u}}^c) \nonumber \\{} & {} \quad - [C_{lequ}^{(3)}]_{1111} V_{ud} ({\bar{e}} {\bar{\sigma }}^{\mu \nu } {\bar{e}}^c)({\bar{u}} {\bar{\sigma }}_{\mu \nu } {\bar{u}}^c) \nonumber \\{} & {} \quad +[C_{ledq}]_{1111} ({\bar{e}} {\bar{e}}^c)(d^c d ) + {\mathrm{h.c.}}\end{aligned}$$

(6.34)

If the Wilson coefficients of these interactions have imaginary parts, at even lower energies they match to the nucleon-electron contact interactions $i ({\bar{N}} N) ({\bar{e}} \gamma _5 e)$, which in turn contributes to the EDM of diamagnetic atoms and paramagnetic molecules. Using the theoretical expressions from Ref. [78] and the EDM measurement using the ThO molecule [74] we find the $95\%$ CL constraints

$$\begin{aligned}{} & {} |{\textrm{Im}} [C_{lequ}^{(1)} ]_{1111} | \lesssim {1 \over (20~{\textrm{PeV}})^2}, \nonumber \\{} & {} |{\textrm{Im}}[C_{lequ}^{(3)}]_{1111} | \lesssim {1 \over (40~{\textrm{PeV}})^2},\nonumber \\{} & {} |{\textrm{Im}}[C_{ledq}]_{1111} | \lesssim {1 \over (20~{\textrm{PeV}})^2}. \end{aligned}$$

(6.35)

Once again we are sensitive to scales 4 orders of magnitude above the LHC reach. Assuming the operators in Eq. (6.33) have generic phases, the CP constraints exclude the possibility that they have any visible effects of in nuclear beta decay or at the LHC,

7.5 Meson mixing

Mesons are bound states of a quark and an anti-quark. Of particular interest in this section are neutral kaons, who are spin-zero mesons made of down (d) and strange (s) (anti-)quarks. One can construct two neutral kaon states: $|K^0\rangle \equiv {\bar{s}} d$ and its antiparticle $|{\bar{K}}^0\rangle \equiv s {\bar{d}}$. From these two one can construct the CP eigenstates $|K^0_\pm \rangle = {1 \over \sqrt{2}} \big (|K^0\rangle \pm |{\bar{K}}^0\rangle \big )$, such that $CP |K^0_\pm \rangle = \pm |K^0_\pm \rangle$. Now, due to CP violating interactions, the observed mass eigenstates $K_S$ and $K_L$ are not CP eigenstates, but instead

$$\begin{aligned} |K_S\rangle \simeq&|K^0_+\rangle + \epsilon _K |K^0_-\rangle , \nonumber \\ |K_L\rangle \simeq&|K^0_-\rangle + \epsilon _K |K^0_+\rangle . \end{aligned}$$

(6.36)

The “short” eigenstate $K_S$ decays mostly to two pions with a lifetime of about $10^{-10}$ second, whereas the “long” eigenstate $K_L$ decays mostly to three pions and lives about 1000 times longer due to the phase space suppression. However, due to CP violation parametrized by $\epsilon _K$, one in a thousand of the long eigenstates decays to two pions as well, as observed in the Cronin and Fitch experiment in 1964. From the existing $K_L\rightarrow \pi \pi$ data one can extract $|\epsilon _K| = 2.228(11)\times 10^{-3}$ [57]. The decay $K_S \rightarrow 3\pi$ has not been observed to date.

In the EFT below the electroweak scale, obtained from the SM by integrating out the W bosons at one loop, one generates the four-fermion operator

$$\begin{aligned} {{\mathcal {L}} }_{\textrm{WEFT}}&\supset c (V_{ts}^* V_{td})^2 {m_W^2 \over 32 \pi ^2 v^4} ({\bar{s}} {\bar{\sigma }}_{\mu } d) ({\bar{s}} {\bar{\sigma }}^{\mu } d) + {\mathrm{h.c.}}\nonumber \\&\approx \bigg ( {1 \over (31~\mathrm PeV)^2 } - {i \over (28~{\textrm{PeV}})^2 } \bigg ) ({\bar{s}} {\bar{\sigma }}_{\mu } d) ({\bar{s}} {\bar{\sigma }}^{\mu } d) + {\mathrm{h.c.}}\end{aligned}$$

(6.37)

with the numerical coefficient in front $c \sim 2.3$. This operator violates the strangeness quantum number by two units, therefore it has good quantum numbers to contribute to K–${\bar{K}}$ mixing. Furthermore, the Wilson coefficient in Eq. (6.37) inherits the complex phase from the CKM matrix, therefore it violates CP. Consequently, $\epsilon _K$ is predicted to be non-zero in the SM: $|\epsilon _K^{\textrm{SM}}| = 2.027(195)\times 10^{-3}$ [79].²⁹ While there is quite some lattice hocus-pocus involved to translate Eq. (6.37) into $\epsilon _K$, the error of the SM prediction is largely due to the uncertainty on the CKM elements. Note that the theoretical error dominates the experimental one by an order of magnitude. All in all $|\epsilon _K|/|\epsilon _K^{\textrm{SM}}| = 1.099(97)$, that is the ratio is known with a 10% error.

The suppression scale of the effective operator in Eq. (6.37) is by the whopping $\mathcal {O}(10)$ PeV, rather than by 100 GeV characteristic of the particles being integrated out. The additional suppression, apart from the one-loop factor, is due to the so-called GIM mechanism [81]. This forces the main contribution to involve a top quark, and the effect is suppressed by the small CKM mixing between the first two generations and the third. The suppression of the SM contribution opens the playing field for new physics. In SMEFT there are several dimension-6 four-fermion operators changing strangeness by two units [17]:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}&\supset [C_{qq}^{(1)}]_{2121} ({\bar{q}}_2 {\bar{\sigma }}_{\mu } q_1) ({\bar{q}}_2 {\bar{\sigma }}^{\mu } q_1) \nonumber \\&\quad +[C_{qq}^{(3)}]_{2121} ({\bar{q}}_2 {\bar{\sigma }}_{\mu } \sigma ^k q_1) ({\bar{q}}_2 {\bar{\sigma }}^{\mu } \sigma ^k q_1) \nonumber \\&\quad + [C_{qd}^{(1)}]_{2121} ({\bar{q}}_2 {\bar{\sigma }}_{\mu } q_1) (s^c \sigma ^{\mu } {\bar{d}}^c)\nonumber \\&\quad + [C_{qd}^{(8)}]_{2121} ({\bar{q}}_2 {\bar{\sigma }}_{\mu } T^a q_1) (s^c \sigma ^{\mu } T^a {\bar{d}}^c) \nonumber \\&\quad + [C_{dd}]_{2121} (s^c \sigma _{\mu } {\bar{d}}^c) (s^c \sigma ^{\mu } {\bar{d}}^c) , \end{aligned}$$

(6.38)

where the quark doublets above are $q_1 = (u_k V_{kd}^*, d)$, $q_2 = ( u_k V_{ks}^*, s)$ (that is, we use the down-type basis). The operators in the first line directly correct the Wilson coefficient of the WEFT operator Eq. (6.37). The remaining operators yield different chirality and/or color structures, but they also contribute to $\epsilon _K$ at tree level. Reference [82] estimates the contributions of the SMEFT Wilson coefficients in Eq. (6.38) to $\epsilon _K$ as

$$\begin{aligned} {|\epsilon _K| \over |\epsilon _K^{\textrm{SM}}| }&= 1 + {{\textrm{Im}}} \,\bigg \{ - (13.3~{\textrm{PeV}})^2 [C_{qq}^{(1)}+ C_{qq}^{(3)}+C_{dd}]_{2121} \nonumber \\&\quad +(105~{\textrm{PeV}})^2[C_{qd}^{(1)}]_{2121} + (127~{\textrm{PeV}})^2[C_{qd}^{(8)}]_{2121} \bigg \} . \end{aligned}$$

(6.39)

Assuming only one Wilson coefficient is switched on at a time, one finds the following $95\%$ CL bounds

$$\begin{aligned}&- {1 \over (25~{\textrm{PeV}})^2 } \lesssim {{\textrm{Im}}} \,[C_{qq}^{(1)}, C_{qq}^{(3)}, C_{dd}]_{2121} \lesssim {1 \over (44~{\textrm{PeV}})^2 }, \nonumber \\&\quad - {1 \over (350~{\textrm{PeV}})^2 } \lesssim {{\textrm{Im}}} \,[C_{qd}^{(1)}]_{2121} \lesssim {1 \over (200~{\textrm{PeV}})^2 }, \nonumber \\&\quad - {1 \over (420~{\textrm{PeV}})^2 } \lesssim {{\textrm{Im}}} \,[C_{qd}^{(8)}]_{2121} \lesssim {1 \over (240~{\textrm{PeV}})^2 }, \end{aligned}$$

(6.40)

where the Wilson coefficients are defined at the electroweak scale. These quantitative results again rely on some lattice inputs, but their order of magnitude could have been guessed without calculations. $C_{qq}^{(1)}$ leads to the same form of the interaction below the electroweak scale as the SM loop, and the bound is similar as the magnitude of the operator in Eq. (6.37) given the SM prediction is known only at the 10% level. Idem for $C_{qq}^{(3)}$. For $C_{dd}$, the low-energy operator differs from the one in Eq. (6.37) by trading left-handed quarks for right-handed, and the bound is again the same as for $C_{qq}^{(1)}$ because QCD is vector-like and cannot tell left from right. It is a bit less trivial to understand why the bounds on $C_{qd}^{(1)}$ and $C_{qd}^{(8)}$ are an order of magnitude stronger. This is because these operators marry left- and right-handed quarks, and gain in the course of low-energy running thanks to not having to rely on quark masses for chirality violation.

All in all, CP violation in kaon mixing impressively probes the scales up to almost EeV, five orders of magnitude above the direct reach of the LHC. New physics at the TeV scale typically requires some elaborate mechanism to suppress the operators in Eq. (6.38), causing much headache for pre-LHC model building. In supersymmetry it has motivated for example the baroque edifices around gauge mediated supersymmetry breaking. The situation was not much better in the Randall–Sundrum family of models, even in spite of the natural mechanism of suppressing flavor-changing neutral currents that these models offered.

In a similar fashion, one can constrain the SMEFT operators affecting the mixing of neutral $B_d$ and $B_s$ mesons. The analogous loop diagram to the one generating Eq. (6.37) yields the 4-fermion WEFT operators violating the b number:

$$\begin{aligned} {{\mathcal {L}} }_{\textrm{WEFT}}&\supset c {m_W^2 \over 32 \pi ^2 v^4} \bigg \{ (V_{tb}^* V_{td})^2 ({\bar{b}} {\bar{\sigma }}_{\mu } d) ({\bar{b}} {\bar{\sigma }}^{\mu } d) \nonumber \\&\quad + (V_{tb}^* V_{ts})^2 ({\bar{b}} {\bar{\sigma }}_{\mu } s) ({\bar{b}} {\bar{\sigma }}^{\mu } s) + {\mathrm{h.c.}}\bigg \} \nonumber \\&\rightarrow \sim - {i \over (1.2~{\textrm{PeV}})^2} ({\bar{b}} {\bar{\sigma }}_{\mu } d) ({\bar{b}} {\bar{\sigma }}^{\mu } d) \nonumber \\&\quad + {i \over (1.1~{\textrm{PeV}})^2} ({\bar{b}} {\bar{\sigma }}_{\mu } s) ({\bar{b}} {\bar{\sigma }}^{\mu } s) + {\mathrm{h.c.}}\end{aligned}$$

(6.41)

From this one can guess that CP violation in the neutral B-meson mixing probes dimension-6 SMEFT operators suppressed by 1 PeV, only a tad lower than the kaon mixing. This is indeed borne out by more careful calculations [83]. Furthermore, one also generates the flavor-changing neutral current operator $({\bar{c}} {\bar{\sigma }}_{\mu } u)^2$, with the suppression scale similar to the one Eq. (6.37). Thus, CP violation in $D {\bar{D}}$ mixing also probes $\mathcal {O}(10)$ PeV scale [82]. The sensitivity of neutral meson mixing to new physics is visualized in Fig. 5.

Fig. 5

Illustration of the sensitivity of CP violation in neutral meson mixing to the scale of the SM-like dimension-6 SMEFT operator $[O_{qq}^{(1)}]_{KLKL} \equiv ({\bar{q}}_K {\bar{\sigma }}^{\mu } q_L)^2$. This is compared to the direct reach of the LHC of about 5 TeV

7.6 Nuclear beta decay

A less frequented path to CP violation leads through nuclear beta decay. We will see it is a less promising place to find CP violating new physics. Nevertheless, the discussion is useful to highlight correlations and interdependencies between different probes of CP violation in the context of SMEFT.

Consider the process ${{\mathcal {N}}} \rightarrow {{\mathcal {N}}'} e^- {\bar{\nu }}_e$ ($\beta ^-$ decay) or ${{\mathcal {N}}} \rightarrow {{\mathcal {N}}'} e^+ \nu _e$ ($\beta ^+$ decay). Here ${{\mathcal {N}}}$ and ${{\mathcal {N}}}'$ are called the parent and daughter nuclei respectively, the electron and the positron are jointly referred to as the beta particle, and both neutrino and anti-neutrino are referred to simply as neutrino in the following. The simplest example is the neutron decay, where ${{\mathcal {N}}}$ is the neutron and ${{\mathcal {N}}}'$ is the proton, but many more processes where ${{\mathcal {N}}}$ and ${{\mathcal {N}}}'$ are heavier nuclei are studied in laboratories. We are dealing with a 3-body decay process, thus there is a lot of kinematics and differential distributions to play with. For the so-called allowed beta decays, at the leading (zero-th) order in expansion in $1/m_{{\mathcal {N}}}$, after summing over beta particle and daughter nucleus polarizations, the differential distribution of the decay products takes the most general form [84]

$$\begin{aligned}&{ d \Gamma \over d E_e d \Omega _e d \Omega _{\nu } } \sim 1 + b {m_e \over E_e} + a { {\varvec{k}}_e \cdot {\varvec{k}}_{\nu } \over E_e E_{\nu }} + A {{\varvec{J}} \cdot {\varvec{k}}_e \over J E_e } + B {{\varvec{J}} \cdot {\varvec{k}}_{\nu } \over J E_{\nu } } \nonumber \\&\quad + {\hat{c}} {J(J+1) - 3 ({\varvec{J}} \cdot \varvec{j})^2 \over J (J+1)} {({\varvec{k}}_e \cdot {\varvec{k}}_{\nu }) - 3 ({\varvec{k}}_e \cdot \varvec{j}) ({\varvec{k}}_{\nu } \cdot \varvec{j}) \over 3 E_e E_{\nu } } \nonumber \\&\quad + {D} {{\varvec{J}} \cdot ({\varvec{k}}_e \times {\varvec{k}}_{\nu }) \over J E_e E_{\nu }} , \end{aligned}$$

(6.42)

where $m_e$ is the electron mass, ${\varvec{J}}$ is the polarization vector of the parent nucleus and J is its spin, $\varvec{j}$ is the unit vector in the polarization direction, and ${\varvec{k}}_e$, ${\varvec{k}}_{\nu }$, $E_e$, $E_{\nu }$ are the 3-momenta and the energies of the beta particle and of the neutrino.

The correlation coefficients in Eq. (6.42) are denoted somewhat inaptly as b, a, A, B, ${\hat{c}}$, and D. All of these coefficients except for ${\hat{c}}$ have been measured experimentally for many transitions, sometimes with an accuracy better than per-mille. Historically, these measurements have played a crucial role in the development of the theory of fundamental interactions. Since momenta are parity odd, whereas angular momenta (hence ${\varvec{J}}$) are parity even, non-zero values of A and B signal parity violation. The famous Wu experiment [85], which demonstrated parity violation in weak interaction, was in fact a measurement of the A coefficient in the beta decay of ${}^{60}{\textrm{Co}}$.

For the sake of this section we will focus on the D coefficient. It quantifies the triple correlation between the polarization of the parent nucleus and the momenta of the beta particle and the neutrino. Since both momenta and angular momenta flip signs under T, a non-zero D signals violation of time reversal invariance. Due to CPT conservation in QFT, CP violation implies T violation, therefore CP violating interactions can contribute to the D parameter. Within the SM, D is very suppressed and has not been observed in any transition yet.³⁰ This is just as good, as it leaves a lot of room to spot the possible contributions to D from non-SM CP violation, in particular from complex phases of dimension-6 operators in SMEFT.

There are several SMEFT operators that contribute to the D parameter at tree level. Below we only discuss a couple of them, but the lesson we will draw is more general. Consider first the dimension-6 operator

$$\begin{aligned} {{\mathcal {L}} }_{\textrm{SMEFT}} \supset i [C_{H u d}]_{11} {\tilde{H}}^{\dagger } D_{\mu } H (u^c \sigma ^{\mu } {\bar{d}}^c) + {\mathrm{h.c.}}\end{aligned}$$

(6.43)

This operator induces a coupling of the W boson to the right-handed up and down quarks:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{SMEFT}}{} & {} \supset - {g_L \over \sqrt{2}} W_{\mu }^+ \Bigg [ {\bar{\nu }}_e {\bar{\sigma }}^{\mu } e + V_{ud} {\bar{u}} {\bar{\sigma }}^{\mu } d \nonumber \\{} & {} \quad + {v^2 \over 2} [C_{H u d}]_{11} u^c \sigma ^{\mu } {\bar{d}}^c \Bigg ] + {\mathrm{h.c.}}\end{aligned}$$

(6.44)

in addition to the couplings to left-handed leptons and quarks present in the SM. To understand the consequences for beta decay we need to descend a few steps in the EFT ladder. Integrating out the W boson at tree level, in the EFT below the electroweak scale one obtains the quark-level charged-current interactions mediating beta decay:

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{WEFT}}{} & {} \supset - \frac{2 V_{ud}}{v^2} \Big \{ (\bar{e} {\bar{\sigma }}_{\mu } \nu )({\bar{u}} {\bar{\sigma }}^{\mu } d ) + \epsilon _R (\bar{e} {\bar{\sigma }}_{\mu } \nu _e) (u^c \sigma ^{\mu } {\bar{d}}^c) \Big \} \nonumber \\{} & {} \quad + {\mathrm{h.c.}}, \end{aligned}$$

(6.45)

$$\begin{aligned} \epsilon _R = {v^2 \over 2 V_{ud}} [C_{H u d}]_{11}. \end{aligned}$$

(6.46)

Beta decays occurs at the level of nucleons or nuclei, thus we need to descend further. The nucleon-level Lagrangian relevant for beta decay matching to Eq. (6.45) is

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{nucleon}}{} & {} \supset - \frac{V_{ud}}{v^2} \Big \{ g_V (\bar{e} {\bar{\sigma }}_{\mu } \nu _e)({\bar{p}} \gamma ^{\mu } n )\nonumber \\{} & {} \quad - g_A \epsilon _R (\bar{e} {\bar{\sigma }}_{\mu } \nu _e) ({\bar{p}} \gamma ^{\mu } \gamma _5 n ) \Big \} + {\mathrm{h.c.}}, \end{aligned}$$

(6.47)

where for nucleon we use the Dirac fermion notation. Our ignorance of the non-perturbative aspects of the matching has been swiped under the carpet of the $g_V$ and $g_A$ parameters. Now, one can show that $g_V = 1$ in the limit of unbroken isospin symmetry, and moreover $g_V \approx 1$ up to $\mathcal {O}(10^{-4})$ corrections quadratic in isospin breaking [87]. On the other hand, $g_A$ is not protected by isospin symmetry, and we have to resort to lattice determinations, $g_A = 1.246(28)$ [88]. From Eq. (6.47), using standard techniques to calculate amplitudes and distributions, a tedious but not impossible calculation yields

$$\begin{aligned} D_n= & {} {4 g_V g_A \over g_V^2 + 3 g_A^2} {{\textrm{Im}}} \,\epsilon _R \nonumber \\= & {} {2 g_V g_A \over V_{ud} (g_V^2 + 3 g_A^2)} v^2{{\textrm{Im}}} \,[C_{H u d}]_{11} \approx 0.4 v^2{{\textrm{Im}}} \,[C_{H u d}]_{11}.\nonumber \\ \end{aligned}$$

(6.48)

The current limit on the D parameter in neutron decay is $D_n = -1.2(2.0)\times 10^{-4}$ [57], while the SM contribution predicts $D_n^{\textrm{SM}} \sim 10^{-5}$. It appears that neutron decay is sensitive to non-standard CP violation, probing the scales of ${{\textrm{Im}}} \,[C_{H u d}]_{11}$ on the order of 10 TeV. There is an issue however: the same operator is better probed by EDMs [22]. We discussed this in the context of the neutron EDM, finding $| v^2 {{\textrm{Im}}} \,[C_{Hud}]_{11} | \lesssim 6 \times 10^{-6}$ at 95% CL, see Eq. (6.32). We can rewrite Eq. (6.48) in the form

$$\begin{aligned} |D_n| \approx 2 \times 10^{-6} {v^2 |{{\textrm{Im}}} \,[C_{H u d}]_{11}| \over 6 \times 10^{-6}}, \end{aligned}$$

(6.49)

which demonstrates that $|D_n| \lesssim 2 \times 10^{-6}$. This is two orders of magnitude below the current experimental sensitivity, and unlikely to be reached in the near future. One should not expect a discovery of CP violation in nuclear beta decay, at least in the scenario sketched above.

Can we avoid this negative conclusion? One way is to ask for help our good old friend the fine-tuning. A larger D parameter can be achieved if one allows for some fine-tuning between different contributions to the neutron EDM. For example, one can arrange for a partial cancellation between the contributions proportional to ${{\textrm{Im}}} \,[C_{H u d}]_{11}$ and those proportional to the QCD $\theta$ parameter [89]. Another way is to resort to a more baroque model building.

7.7 Closing comments

In this section we have studied a couple of examples illustrating sensitivity of CP-violating observables to new physics. These observables probe $D=6$ operators suppressed by scales much higher than the reach of current colliders – sometimes as large as EeV! Indeed, CP violation is the most sensitive probe of generic new physics that does not violate the SM symmetries.³¹ The non-discovery of non-SM CP violation foreshadowed the non-discovery of new physics at the LHC. It has been known for decades that new particles with TeV scale masses and order one couplings to the SM can easily be at odds with the EDM constraints. This is especially true for frameworks addressing the hierarchy problem (supersymmetry, composite Higgs, extra dimensions, etc.) as they invariably come with many new interactions, which potentially contain many new CP-violating phases. The past expectations of dozens new particles popping out at the LHC were always relying on the belief that new physics, in stark contrast to the SM, is non-generic, that is to say, that the new CP invariants associated to the new particle interactions vanish. Well...now we are older and wiser. While new physics can still be around the corner, and be discovered tomorrow at the LHC, in my opinion a more probable scenario is that the new particles are very heavy, perhaps 100 TeV, perhaps more. At the same time, my expectation is that new physics, much like the SM, comes with generic CP-violating phases. If these expectations are correct, it is very likely that new physics will first be discovered via CP-violating observables, in particular via the electron or neutron EDM.

One more comment is in order. We have seen that distinct CP-violating observables may probe the same operator, but the sensitivity may be different. For example, both the neutron EDM and neutron beta decay constrain the $C_{Hud}$ Wilson coefficient, with the former having $\mathcal {O}(100)$ better sensitivity. The gap is even larger, $\mathcal {O}(10^5)$, concerning the sensitivity to $C_{H{\widetilde{B}}}$ from the electron EDM and from Higgs physics. The logical conclusion is that some experiments are more destined to discover new physics. Indeed, if CP violation was detected in, say, Higgs decays to Z bosons, my theorist bias would strongly suspect an unfortunate fluctuation or an experimental error. One should however not jump to the conclusion that only EDMs are worth pursuing. Less sensitive experiments also play an important role. The SMEFT parameter space is multi-dimensional, and one needs many different probes to disentangle the different relevant parameters. For example, the neutron EDM is sensitive (among others) to a linear combination of $C_{Hud}$ and the theta term ${\tilde{\theta }}$, while the D parameter measured in nuclear beta decay is sensitive only to the former. We cannot exclude the possibility of large cancellations (accidental or implied by the structure of the BSM theory) between $C_{Hud}$ and ${\tilde{\theta }}$, and the flat direction in this 2-parameter fit is only lifted by the D parameter measurement. The less sensitive experiments will become even more vital if non-SM CP violation is finally observed in an EDM experiment, as they will play the crucial role in the task of identifying the UV completion of SMEFT.

Appendix: Abbreviations

• BSM: Beyond the Standard Model. In these lectures I define it as any theory with new particles in addition to the ones present in the SM.

• ChPT: Chiral Perturbation Theory. The effective theory of pions and sometimes kaons and eta mesons, valid below the QCD resonance scale $m_{\rho } \simeq 770$ MeV.

• CL: Confidence level. This refers to the size of the confidence intervals in the standard Gaussian statistics. In particular, 68% CL is roughly one sigma, while 95% CL translates roughly to 1.96 sigma.

• eV: Electronvolt. It cannot be logically explained why this is the basic unit in particle physics.

• EeV: Exa-electronvolt = $10^{18}$ eV. The scale probed by EDMs.

• EFT: Effective field theory. The theoretical framework on which SMEFT and many other theories are based.

• GeV: Giga-electronvolt = $10^9$ eV. Roughly the mass of the proton.

• GREFT: General Relativity Effective Field Theory. The EFT of a single massless spin-2 particle.

• GRSMEFT: General Relativity Standard Model Effective Field Theory. The EFT of a single massless spin-2 particle coupled to the SM particles.

• IR: Infrared. In the particle physics literature this is a posh way to say low-energy.

• MeV: Mega-electronvolt = $10^{6}$ eV. Roughly the electron mass.

• LHC: Large Hadron Collider. The proton-proton collider currently operating at CERN.

• PeV: Peta-electronvolt = $10^{15}$ eV. The scale probed by many flavor observables.

• QCD: Quantum Chromodynamics. The theory of strong interactions mediated by the $SU(3)_C$ gauge bosons of the SM.

• QFT: Quantum Field Theory. Our fundamental framework for relativistic quantum mechanics.

• SM: Standard Model. From the modern point of view, it can be defined as SMEFT truncated at the level of $D \le 4$ operators.

• SMEFT: Standard Model Effective Field Theory. The main focus of these lectures.

• TeV: Tera-electronvolt = $10^{12}$ eV. The energy scale probed by the LHC.

• UV: Ultraviolet. In the particle physics literature this is a posh way to say high-energy.

• VEV: Vacuum Expectation Value. A tool to describe a ground state violating some of the symmetries of the theory at the Lagrangian level.

• WEFT: Weak Effective Field Theory. The effective theory of the SM degrees of freedom below the electroweak scale, where W, Z, top, and Higgs are integrated out.