1 Introduction

The full phase diagram of nuclear matter, represented with temperature and net-baryon density, turns out to contain several structures that await further understanding and investigation via both theoretical and experimental approaches [1]. In the high-temperature, high-density region, the Quark-Gluon Plasma (QGP) phase of matter has been predicted by Quantum Chromodynamics (QCD), and also experimental results increasingly point to its existence [2,3,4]. It is believed that a smooth cross-over between the nucleon phase and the QGP occurs at low density and a first-order phase boundary occurs at high density. Exotic phases like color superconductivity, which may exist in neutron stars, are suspected at low temperature and extremely high baryon density [5]. An ideal method for investigating the QCD phase structure on Earth is to construct and operate heavy-ion collision facilities [6]. With the elaborate design of the collision systems and energy, nuclear matter can be compressed to the region of specific interest.

The heavy-ion experiments that currently take data include RHIC-STAR [7], LHC-ALICE [8], sPHENIX [9], and so on. There are also scheduled ones such as NICA-MPD [10] and FAIR-CBM [11]. The particularity of the Cooler storage ring External-target Experiment (CEE) is the focus on the phase transition from the low energy up, making use of the beam from the Heavy-Ion Research Facility in Lanzhou (HIRFL) [12] for collisions with a fixed target. The incident beam energy is between 0.5 and 1.2 GeV/u, and the heaviest collision system can reach U–U. CEE aims to study the phase diagram in the low-temperature and high-density regions and to explore the critical point at the end of the transition line. It can also provide a supplementary constraint for the asymmetry energy in the Equation of State (EoS) [13] for nuclear matter, especially with a polarized deuteron beam [14]. Other goals of studying the production of the exotic particles, hyper-nucleus, are also proposed for CEE [15].

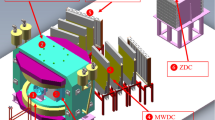
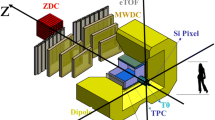
CEE as an advanced spectrometer employs a time-of-flight (TOF) method [16] for the identification of the secondary charged particles which are produced from collisions and deflected by a large dipole magnet. The spectrometer is designed to operate with a \(10^4~\textrm{Hz}\) level event rate, which is reached from a \(10^6~\textrm{Hz}\) beam flux and 1% interaction ratio. The majority of the charged particles in the CEE energy region are baryons, which are easier to identify than mesons. Because of the low energies for CEE, Kaon production shall be suppressed [17]. A requirement of 3-\(\sigma \) separation between \(\pi /\textrm{p}\) up to 1.5 GeV/c is set to the detectors according to the simulated momentum distribution [18]. As a fixed target experiment, the momentum of the particles differs significantly with respect to polar angles, which leads to the design of two sets of tracking and timing detectors: a Time Projection Chamber (TPC) [19, 20] and an inner TOF (iTOF) system [21] are placed inside the magnet for the identification in intermediate rapidity region, while a Multi-Wire Drift Chamber (MWDC) array of three layers and an external TOF (eTOF) wall are installed downstream of the magnet, covering the forward angle for high momentum particle identification. Figure 1 shows the layout of the CEE spectrometer. In addition to the subsystems mentioned above, a T0 [18] counter and a Zero Degree Calorimeter (ZDC) [22] are marked.

The relative momentum resolution should be within 5% for both TPC and MWDC. Performance requirements for the timing detectors are defined according to their distance from the collision center. For iTOF detectors to be positioned inside the magnet, a higher time precision of 30 ps is required. The time resolution should be 60 ps for eTOF detectors placed at 2.6 m downstream from the collision center, outside the magnet. Extending the distance of the eTOF wall leads to a looser requirement of time resolution, but the accordingly larger coverage area will increase the cost. T0 is a scintillation detector in front of the target. It measures the time of the incident beam ions with 32 independent readout channels and has an improved time precision of 30 ps.

Fig. 1
figure 1

Upper: the schematic layout for CEE. Subsequent descriptions will also follow the Cartesian coordinate established in this figure. The coordinate origin is in the center of the TPC. The target is placed at \(z=-35~\textrm{m}\). Lower: the X–Z transversal view, modified and generated from [23]. The detectors are shown as their active volumes

Full size image

The iTOF and eTOF systems are both constructed with Multigap Resistive Plate Chambers (MRPC) [24], which can reach a time resolution of tens of picoseconds and have been extensively employed in many High Energy Physics experiments [25,26,27]. At STAR, MRPCs have been operating stably with a 60 ps level resolution since their initial installation in 2003. Thanks to the timing detectors, the particle identification capability improved significantly which contributed to a number of observations, such as the detection of \(\overline{^{4}\text {He}}\) [28]. Despite the success of scientific discoveries, the operation of the MRPC gaseous detector has recently raised concerns due to the emission of gas with a severe greenhouse effect [29,30,31]. The ‘standard’ working gas mixture for MRPCs in CEE-eTOF and many other experiments is composed of Freon-134a, \(\mathrm {iC_{4}H_{10}}\) (isobutane), and \(\mathrm {SF_6}\) with a fraction of around 90/5/5. The global warming potential values for Freon and \(\mathrm {SF_6}\) are 1300 and 22,800 respectively. The regulations of reducing the production, usage, and emission of HFC gases have directly raised the cost of Freon. To address the environmental issues and the budget risk, a novel structure named the Sealed MRPC [32] is adopted to form the eTOF wall at CEE. The main advancement that the sealed MRPC brings, is the enclosing structure for each stack of the glass electrodes and gas gaps, as demonstrated in Fig. 7. In the sealed chamber, the outermost glass electrodes act as panels with their edge sections affixed with a 3D-printed sealing frame. The total gas volume for the sealed MRPC has drastically dropped to the level of the sensitive volume compared with the earlier MRPCs housed in gas-tight boxes, which results in the operation with a low flow rate. Moreover, the sealed MRPC shows stability in high counting rates thanks to the promoted gas exchange in the sensitive volume by the inlet gas pressure. Tests with an initial prototype have validated this new concept, reaching performances similar to the traditional MRPCs [32, 33].

To give a detailed description of the CEE-eTOF wall, in terms of simulation, system design, and development status, this work will be organized as follows: in Sect. 2, a FairRoot [34] based simulation was carried out to give Monte-Carlo estimations of the key parameters, and to assess how eTOF will contribute to CEE’s trigger and Data Acquisition (DAQ); Sect. 3 shows the design of the eTOF wall including the detector array, readout chain, and mechanical considerations; Sect. 4 discusses the status of the detector development, showing the cosmic and in-beam test results. The work is then summarized and concluded in Sect. 5.

2 The eTOF wall simulation

2.1 Data and framework

The simulation in this work is conducted under CeeRoot [23], which is a competent framework empowered by FairRoot for not only Monte-Carlo simulation but future works in experimental data analysis and event visualization. A simplified geometry has been implemented containing envelopes of each subsystem. Primary particles, which in the context of this work refer to the ones produced directly through a collision, are generated by experimental data or theoretical models, e.p., the Quantum Molecular Dynamics (QMD) models. A magnetic field map based on the actual situation is registered to the framework. When executing a simulation, the Virtual Monte Carlo (VMC) [35] concept in FairRoot calls the Geant4 [36] engine for particle transport calculations. The information on the interaction between primary particles and detectors will be organized and stored in ROOT files.

Table 1 Simulation data description
Full size table

Two particular data sets of collision products are prepared for the study, the details of which are listed in Table 1. To evaluate the rate condition and event selection, the IQMD [37] model is used for its good description of heavy-ion collisions. However, the production of mesons is not considered. In order to evaluate the identification power for typical charged particles, a data set from the UrQMD [38] model is used, and an extreme system of Au–Au collision at 1.23 GeV/u is chosen to demonstrate the \(\pi /\textrm{K}/\textrm{p}\) separation of the forward detectors.

2.2 Coverage and particle identification

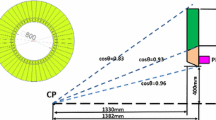
The central task of the eTOF wall is to provide high-precision time measurement for incident charged particles, especially the ones whose track can be reconstructed from the MWDC array. In this cooperation, the proper coverage for forward detectors is 30\(^{\circ }\) of half flare angle at the X direction and 20\(^{\circ }\) at the Y direction, and areas beyond this range will be covered by TPC and iTOF. The active areas of the forward detectors are shown in Table 2. Figure 2 shows the simulation result of the x–y distribution of the charged particles at \(z=225~\textrm{cm}\) which penetrates MWDC as well. The envelope with a \(3.2 \times 1.6~\textrm{m}^2\) size covers most of the detection.

Table 2 Envelopes and z positions for forward detectors
Full size table
Fig. 2
figure 2

Hit distribution of charged particles at eTOF location \(z=225~\textrm{cm}\). The Red square encloses the active area of the eTOF wall. This simulation run contains 10k events generated in the IQMD model

Full size image

The particle identification is carried out with a simplified treatment on the resolution from MWDC, T0, and eTOF. The momentum and flight time of the particles, obtained from simulation, are smeared with 5% relative resolution and 80 ps respectively. Figure 3 shows the identification result with eTOF placed at \(z=225~\textrm{cm}\). The separation of \(\pi /\textrm{K}/\textrm{p}\) are visible in the plot. Furthermore, a 3-\(\sigma \) separation of \((\pi +\textrm{K})/\textrm{p}\) up to 2 GeV/c is validated in Fig. 4. It completely fulfills the requirement for eTOF. The 3-\(\sigma \) identification of Kaons at 1.4 GeV/c momentum is also shown in the result.

Fig. 3
figure 3

Particle identification of eTOF, with UrQMD data

Full size image
Fig. 4
figure 4

Upper: the \(\pi /\textrm{K}/\textrm{p}\) separation at momentum range from 1.2 to 1.4 GeV/c. Lower: the \((\pi +\textrm{K})/\textrm{p}\) separation at momentum range from 1.8 to 2.0 GeV/c. The kaon production is minimal in the latter momentum range, so the result represents the \(\pi /\textrm{p}\) separation as well. The areas with color depict the 3-\(\sigma \) boundaries for the corresponding particles

Full size image

2.3 Triggering and counting rate

It is natural to notice that the MRPC, as a timing detector, is featured with a signal shaping in nanoseconds via the principle of electron avalanche in gas gaps. Therefore, it is able to execute an online summation of the number of fired electronic channels within a given time window with the aid of fast readout chains. The summation, called as the channel multiplicity, can then be treated as an effective probe for triggering the collision because it provides a good description of the secondary particle multiplicity at the forward angle.

The typical time evolution of a collision is around tens of \(\textrm{fm}/\textrm{c}\). Compared with the precision of the time measurement, it is reasonable to assume a simultaneous emission for primary particles. Yet, the stop time of hitting eTOF varies due to the velocity difference. According to the simulation, the flight time distributes within a 20 ns width, which is much lower compared with the \(10^4~\textrm{Hz}\) event rate. The time characteristics above lead to the ability for trigger generation and a 3–4 times width of the flight time is assumed as the time window for multiplicity.

A trigger circuit will gather the signal counts, and make trigger decisions with a proper criterion. In the case of CEE, it can be formulated as the coincidence of the signal from T0 and that from TOF with the channel multiplicity beyond a certain threshold. One of the primary purposes of triggering is to depress fake events caused by noise. The accidental coincidence ratio with T0 is around 7.5% given the \(10^6\) Hz peak beam intensity and the 75 ns coincidence window. So controlling the noise trigger ratio from the stop time side is crucial. It can be seen from Fig. 5 that the eTOF covered multiplicity is about 30 on average, while for a TOF system constructed with MRPC the typical noise level is \(0.5~\textrm{Hz}/\textrm{cm}^2\). With a 75 ns time window, the estimated noisy count for the eTOF wall shall be far less than 1. Generally speaking, the coverage of eTOF provides a sufficient signal-to-noise ratio to set trigger conditions.

Although the DAQ function works in trigger mode, the readout chains work continuously with Fast-End Electronics (FEE) and Time-to-Digital Modules (TDM) included, so the counting rate condition must be understood. The result in Fig. 5 is obtained from 10k collisions, which equals the data amount of 1-second operation time. Taking the pad size (shown in Sect. 3.1) into account, the maximum counting rate of the readout channels is 4 kHz.

2.4 Event selection

The centrality or impact parameter fully determines a collision during a beam time since it defines the number of nucleon participants in the fireball. Thus, its reconstruction is very important for selecting data with interest. Events with a central and medium bias are of interest for research on fluctuations in the particle multiplicity ratio and collective matter flow [39, 40], while events with a minimal bias might be of interest for research on asymmetry energy [41]. Former practices [42, 43] have confirmed that not only the full-space particle multiplicity but that at the forward angle is a good observable in centrality determination. Figure 5 shows the IQMD simulation of forward multiplicity distribution in different impact parameters. The ambiguity of the dependence will affect the result of the reconstructed centrality. Two methods are suggested for improvement: one uses eTOF+iTOF hit multiplicity to expand the input phase space, and the other adds high dimensions of data input for reconstruction.

With regard to the latter, Fig. 6 gives an example of two-dimensional input. With eTOF hit multiplicity divided into zonal statistics, the recognition is expected to get improved because a clear dependency as a curve is observed.

Feature recognition models may show power when the data dimensions grow up. Machine learning has been used in earlier works to determine impact parameters from simulation data. Some works use the extracted physics observable as input features, such as the charged particle multiplicity, the total transverse energy, the charge of the largest fragment, etc. [44], while others handle the hit-level variables like sub-regional counts, position, charge-to-momentum ratio [45, 46]. These models show the impressive ability of feature extraction with either type of data. However, it is also crucial to research the compatibility of the data-driven models with experimental uses, the processing speed, and so on.

Fig. 5
figure 5

The distribution of eTOF hit multiplicity with respect to impact parameters from 1 to 10 fm. Note that the event amounts for each centrality are prepared approximately according to the differential cross-section \(b\textrm{d}b\) of the collision

Full size image
Fig. 6
figure 6

The sub-regional features of eTOF hit multiplicity. Each set of point and error bars represents the statistics for data grouped by impact parameters from 1 to 10 fm. The inner and outer wall are defined in Sect. 3.3

Full size image

3 Structural design

3.1 Detectors

We designed 2 kinds of the sealed MRPC detectors for CEE-eTOF. The only difference of the two types is the number of readout strips (and of course the resulting sizes). The larger MRPC contains 32 readout strips while the smaller has 16. Both types have the same double-stack geometry with 10 0.25 mm thick gas gaps. The readout strips are 1.5 cm in width and 48 cm in length, arranged with 0.2 cm pitch. The upper left of the Fig. 7 shows the arrangement of the readout strips for the 16-strip MRPC.

As Fig. 7 shows, the working gas flows directly through the active volume which is much more efficient than using a gas box. The sealed chambers can be assembled independently and installed thereafter with other components. To assemble a sealed chamber, the 3D-printed sealing frame is first glued with one of the outermost glass electrodes. Then, the fishline spacers and glass plates are placed layer-by-layer in the chamber. In the end, the other outermost glass electrode is glued as the end panel.

A 32-strip and a 16-strip real-size prototype have been assembled for the tests described in Sect. 4.

Fig. 7
figure 7

Top: readout strip view (left) and picture (right) of the 16-strip MRPC prototype. Bottom: schematic transversal view of the sealed MRPC

Full size image

3.2 Readout electronics

A block diagram of the eTOF readout chain is shown in Fig. 8, in which the FEE and TDM as crucial electronics components are depicted [47]. In the FEE an Application Specific Integrated Circuit (ASIC) chip called NINO [48] is used, which is integrated with pre-amplification and Time-over-Threshold (ToT) discrimination. External resistors are employed and combined with the internal circuit of the NINO chip for impedance matching with the detector. The output of FEE carries the leading and trailing time of the signal and is recorded by the downstream TDM with Field Programmable Gate Array (FPGA) based Time-to-Digital Converters (TDCs) on it. The FEEs are plugged into the double ends of the detectors. FEE and TDM are physically connected by two micro coaxial flat cables, with one for signal transmission and the other for powering the FEE.

The in-channel dead time of this readout chain is less than 100 ns, which satisfies the 4 kHz counting rate condition mentioned above. A prototype of the FEE and TDM pair has been designed and tested in the laboratory with a signal source. Other components that contribute to the time precision in real practices, e.p., the clock, are also included in the test. The result in Fig. 10 indicates that the time resolution of the readout electronics is better than 10 ps.

Figure 9 exhibits the picture of the FEE and TDM prototype. Each pair of FEE and TDM offers 16 readout channels. For the tests in Sect. 4, the performances of detectors and electronics will be evaluated jointly (Fig. 10).

Fig. 8
figure 8

Block diagram of the readout chain of eTOF

Full size image
Fig. 9
figure 9

Pictures of the FEE (left) and TDM (right) prototypes for the eTOF wall. The FEE boards will be plugged directly on the detectors through 2.54 mm pin headers

Full size image
Fig. 10
figure 10

Time precision of the readout electronics with different input charges generated by the signal source. The result is taken from [47]

Full size image

3.3 Detector layout

The detector layout of the eTOF wall is shown in Fig. 11. The design, composed of 24 MRPCs in 7 columns, fulfills the coverage requirement in Sect. 2.2. From Fig. 2, the off-centered distribution reveals the deviation of charged particles amid magnetic fields, and the latter may differ in values and polarity among runs. For the above reason, the entire eTOF wall is movable by a slideway in the X direction.

The 6 smaller detectors in the inner part of the wall are the 16-strip MRPCs, while the others are the 32-strip MRPCs that forms the outer wall. The 16-strip MRPCs are designed vertically movable from the mid-line for beam avoidance because neither the detectors nor the FEEs can tolerate the direct penetration by the beam flux. Such a transmission mechanism, achieved by the pulley system, is visible in Fig. 12e.

Fig. 11
figure 11

The detector layout of the eTOF wall, constructed with 24 sealed MRPCs

Full size image

3.4 Mechanical design

Fig. 12
figure 12

a Full view and b left view of the eTOF wall. c View of the bilateral module which shows how the FEEs are connected to 2 of the MRPCs. d View of the centered eTOF module. e Pulley mechanism which drives the 16-strip detector for the centered module

Full size image

The mechanic design of the eTOF wall, shown in Fig. 12a, is carried out following the simulation in Sect. 2. The size of the entire wall is \(3869~\textrm{mm}\times 500\,\textrm{mm} \times 2383 ~\textrm{mm}\). Figure 12a, b show the structures of the eTOF wall. The eTOF is composed of 7 modules of 2 types. Each of the centered 3 modules contains two 32-strip detectors and two 16-strip detectors. The 16-strip detectors can be shifted vertically for beam avoidance through the pulley transmission mechanism. The other 4 bilateral modules are composed of three 32-strip detectors. Thanks to the application of the sealed MRPC, the detector no longer needs an aluminum box to contain the chamber fill gas. The module boxes are lightweight designs for electromagnetic shielding and radiation protection from beam-ionized electrons. Finally, overlap areas are designed between adjacent detectors and modules not only to mitigate edge effects but also to prevent coverage loss in case of oblique incidence.

4 Development and tests

4.1 Signal characteristics

Good knowledge of the features of MRPC signals is important in order to optimize the design for FEE. Before the readout chain shown above, we used a fast preamplifier [49] and a Tektronics digital oscilloscope to study the signal of the MRPC prototype. The preamplifier has a voltage gain factor of 20 and a bandwidth of 650 MHz, so it can well retain the nanosecond width waveform of the MRPC. For a typical signal, the rise time amounts to a few hundreds of picoseconds and the full width comes to about 2 ns.

A 32-strip eTOF prototype has been operated with a 6.9 kV working voltage, which translates to an electric field of  110 kV/cm in the gas gaps. A fast preamplifier and a Tektronix oscilloscope were used for waveform readout and acquisition. Figure 13 shows a typical waveform of the MRPC prototype. The signal keeps a fast leading edge which is essential for high-precision discrimination, whereas after the peak a long noisy tail appears, most likely due to reflections. As observed in the tests, those noise patterns are not discriminated by the readout electronics for their low amplitudes.

The dynamic range is then studied to determine a proper threshold for the NINO chip. The coincidence of two scintillation detectors provides a triggering area of \(5\times 20~\textrm{cm}^2\), covering 3 readout strips on MRPC. 7 strips including the 3 were read out and for each event we recorded the maximum amplitude of the MRPC signals as a representative of the avalanche, as shown in Fig. 14. The data was used to derive the MRPC efficiency as a function of the signal threshold. We can set a proper threshold range of 150–200 mV to guarantee a good efficiency of over 95%.

4.2 Performance tests in cosmic rays

With the development of the readout chain, a cosmic test stand has been set up in order to evaluate the overall performance. Figure 15 shows the scheme of the setup. It includes a 32-strip MRPC prototype, a 16-strip MRPC prototype, 32 channels of readout electronics, and two scintillating detectors with related modules for discrimination and coincidence. With the above components, 8 strips of each MRPC prototype can be tested in an operation. The data taken from the tests is processed also in CeeRoot, where the related methods, e.p., position correction along the readout strips, ToT gain correction, and time-slewing correction, have been implemented [50]. MRPC prototypes are in serial gas connection and supplied with a standard gas flow of 10 ml/min. During the High Voltage (HV) scan, the FEE thresholds were set to 150 mV, which is shown to be within the optimal range in the following test. The performances of the two detectors agree well within the measurement uncertainties during the HV scan and also the following tests, so we show the results of the 16-strip prototype as a representative. As shown in Figs. 16 and 17, the HV scan reveals a 97% efficiency for detectors at a working point of 6.9 kV, and correspondingly the cluster size is 1.5 and the time resolution is 56 ps. Cluster size is defined as the average number of fired strips for each cosmic ray hit, where 1.5 readout strips is a reasonable value related to the size of the charge avalanche in the gas gaps. Time resolution results are obtained assuming the same timing precision for both MRPCs, as shown in Fig. 18. It is a reasonable assumption since they are the same in gas gap thickness and readout method. Figure 18 shows the flight time distribution determined by the difference of the independently measured time between two prototypes. The q-Gaussian fit is carried out since the distribution does not seem to follow a pure Gaussian distribution, and such an effect has been reported as well in [51]. The q-Gaussian distribution is described as [52]:

$$\begin{aligned} p(t) = A_{q}e_{q}^{-B_{q}(t-\mu )^{2}}, q<3 \end{aligned}$$
(1)

where \(A_q\) is a normalization constant, \(e_q\) is the q-exponential given by:

$$\begin{aligned} e_{q}^{t} ={\left\{ \begin{array}{ll} [1+(1-q)t]^{\frac{1}{1-q}}, &{} 1+(1-q)t\ge 0 \\ 0, &{} \text {else} \\ \end{array}\right. } \end{aligned}$$
(2)

and the width of the distribution is characterized by

$$\begin{aligned} B_q = [(3-q)\sigma ^{2}]^{-1}, q<3. \end{aligned}$$
(3)

In Fig. 18, an effort is made to explain the slow tail in the flight time distribution. To exclude events with large incident angles and hits whose positions are imprecisely reconstructed due to possible noises, a cut on the position x along the readout strip of \(|x|<9~\textrm{cm}\) was imposed, which removes 20% of the events. The resulting time resolution is then \(84.38/\sqrt{2}=59.67\) ps. However, the q-Gaussian fit seems to well interpret the complete data, and gives a sigma of 80 ps, 56 ps overall resolution for a single detector.

The dependency of time resolution with HV in Fig. 17 seems to show different slope factors before and after 6.2 kV, which corresponds with a simulation result [53]. Moreover, discontinuity points are observed at 6.2 and 6.6 kV. The phenomena might be explained by a study [54] which indicates that the number of gas gaps with avalanches developed in an event is the main source of time uncertainty at low HV, and it rises rapidly before the working point. Figures 19 and 20 show the threshold scan results for a constant HV of 6.9 kV. From the results, the optimal threshold lies between 150 and 200 mV, corresponding with the study of the dynamic range.

Fig. 13
figure 13

A typical MRPC signal displayed by the oscilloscope

Full size image
Fig. 14
figure 14

The dynamic range of MRPC signals with a voltage gain of 20 and a differential impedance of 100 \( \Omega \). Such parameters are close to those of the NINO chips. The red curve shows the efficiency-threshold correlation generated using the measured data in the histogram

Full size image
Fig. 15
figure 15

The test setup. S1 &2: scintillating detectors. Disc.: CAEN N844 signal discriminator. CLK: 40 MHz global clock based on EMXO EX-380. &: CAEN N455 coincidence module

Full size image
Fig. 16
figure 16

The efficiency and cluster size of the 16-strip prototype with respect to high voltages

Full size image
Fig. 17
figure 17

The time resolution of the prototypes with respect to high voltages

Full size image
Fig. 18
figure 18

The flight time distribution of the test system at 6.9 kV. Red line is the Gaussian fit to data with position cut (gray histogram). Blue line is the q-Gaussian fit to all the data whose parameters are shown in the statistic box. The time resolution is \(79.87 / \sqrt{2} = 56.49~\textrm{ps}\)

Full size image
Fig. 19
figure 19

The efficiency and cluster size of the 16-strip prototype with respect to NINO thresholds

Full size image
Fig. 20
figure 20

The time resolution of the prototypes with respect to NINO thresholds

Full size image

It is necessary to give further discussions on the contributions to the measured time resolutions. Although the time precision of the electronics is measured independently, a simple subtraction from the overall resolution is inappropriate because the signals from the detector are in dynamic amplitudes which can lead to dispersion in leading-edge discrimination of the FEE. The time-slewing relationship with ToT can give a partial correction to the time walk. However, for signals with low amplitudes, the discrimination of FEE with a relatively high threshold results in a leading time after the exponential growth of the signal, which introduces an irremediable uncertainty. Another contribution to the measured resolution shall be the ones from the angular and momentum distributions of the cosmic rays, but the related corrections are not included in this work. We prevent selections based on the reconstructed incident angles because they will affect the correct estimation of efficiency. As a result, in terms of the intrinsic time resolution of the MRPC, we can only estimate that it is better than 50 ps. Nevertheless, the overall time resolution obtained in this work guarantees a qualified timing performance of the system in real operations.

For the examination of operational stability, the test condition was kept to 6.9 kV, 150 mV for successive 7 days. Figure 21 shows the efficiency and time resolution measured each day, with at least 6k events. The result indicates that the system of both detector and readout electronics is capable of working continuously with excellent performance.

Fig. 21
figure 21

Stability test results for the 16-strip prototype with a 10 ml/min gas flow

Full size image

5 Conclusion

The CEE-eTOF wall detects the arrival time of charged particles in the forward region with a resolution better than 60 ps. According to the simulation studies, the subsystem can reach adequate \(\pi /\textrm{K}/\textrm{p}\) identification, i.e. the maximum momentum of 3-\(\sigma \) separation up to 1.4 GeV/c for \(\pi /\textrm{K}\) and 2.0 GeV/c for \((\pi +\textrm{K})/\textrm{p}\). With the fast readout, large coverage, and high granularity, eTOF plays an important role in triggering and event selection. In particular, the special features of hits on the eTOF wall may benefit the prediction of collision centrality. Besides the simulation and discussion, the technical design of eTOF is described in this paper, including detectors, readout chains, and mechanics. Tests with cosmic rays have been carried out to evaluate the performance of the prototypes. The real-size prototypes, with detectors and readout chains included, have a 97% efficiency and an overall time resolution within 60 ps. The test system operated stably for the tested 7 days with a 10 ml/min low gas flow. The results mark a readiness for further in-beam tests and mass production which have been scheduled for the near future. The operation of eTOF will not only contribute to the studies of the EoS of nuclear matter but also take a step toward the eco-friendly running of RPC-type detectors in future experiments.