Topologically nontrivial black holes of Lovelock gravity sourced by logarithmic electrodynamics

Abstract

I investigate the topologically nontrivial black holes of Lovelock gravity sourced by logarithmic electrodynamics. To calculate the solution describing these black holes, additional constraints are also imposed on the base manifold of the higher dimensional spacetime. Relying on the selection of geometric mass, electric charge, and the nonlinearity parameter, this solution can be portrayed as a black hole with a single horizon, two horizons, or naked singularity. I also look into how the thermodynamical and conserved quantities of this solution are affected by the logarithmic electromagnetic field. Additionally, it is demonstrated that these quantities correspond to the first law of thermodynamics. At last, the local and global thermodynamic stabilities of the accomplished black hole are studied as well.

1 Introduction

Higher order curvature theories of gravity have received a lot of interest and are actively investigated these days. As expected, the simple extension of Einstein’s theory of gravity (EG) can effectively give rise to a wide range of modified gravities whose actions incorporate higher order curvature terms. Although EG is a non-renormalizable theory, a renormalizable one [1] can be developed provided these terms are considered in the action. Due to the inclusion of these terms, additional couplings between the operators of the dual CFT are created in the case of AdS/CFT correspondence, and a more comprehensive class of dual CFTs is formed [2,3,4]. The Lovelock gravity [5] is the most intriguing modified theory that encompasses higher curvature corrections. It can offer the general covariance requirements and is the most extensive theory in higher dimensions. Furthermore, the Lovelock action is also compatible with the modifications proposed by string theory to the model of EG [6,7,8]. The most rigorous study of the gravitational fields has been carried out in the Gauss–Bonnet (GB) gravity [9,10,11,12,13]. Even though the field equations that arise in third order Lovelock gravity seem complicated, different black hole solutions of this gravity theory are derived [13,14,15,16,17,18,19]. The GB gravity is known to guarantee supersymmetric extension [20, 21], whereas all higher order Lovelock gravities merely allow the demand of supersymmetric extension [22, 23]. Certain investigations have also been broadened to generic Lovelock gravity to explore new black holes and their properties [24,25,26,27,28].

Although the majority of the established solutions of Lovelock gravity are characterizing black holes with maximally symmetric horizons, the existence of black holes with nonconstant curvature horizons could also be debatable. As an example, Page discovered the first explicit inhomogeneous compact Einstein metric in four dimensions [29]. Likewise, the generalized version of this metric in higher dimensions was presented in Ref. [30]. Bohm also discovered a vast class of inhomogeneous solutions that had positive curvature on product of spheres [31]. The physical aspects of Bohm and Einstein metrics were addressed in Ref. [32]. The even dimensional nontrivial black hole solution of Lovelock-BI gravity was derived by selecting the non-Einstein base manifold [33]. If the horizons of the Lovelock black holes are supposed to be nonconstant curvature spaces, the higher curvature terms have also an influence on the geometry of the boundary due to the restrictions on its Weyl tensor. [34]. Consequently, the new charge-like parameters appeared in the solution. The black hole solution of GB gravity under these restrictions has been obtained in Ref. [34], while its physical properties were extensively studied in Refs. [35,36,37,38,39,40,41]. In third order Lovelock gravity, the spacetimes with Einstein manifold were also explored. For these geometries, the Weyl curvature is adhered to two different sorts of algebraic restrictions [42]. The general tensorial conditions required for the topologically nontrivial black holes of an arbitrary order Lovelock theory were established in Ref. [43]. Additionally, the Birkhoff’s theorem has also been generalized under these conditions [43]. The physical properties of these vacuum black holes were discussed in Ref. [44]. Similarly, the Lovelock black holes sourced by Maxwell’s electrodynamics under these conditions were investigated in Ref. [45].

The objective of this work is to investigate charged Lovelock black holes with nonconstant curvature horizons sourced by nonlinear electrodynamics (NED). In the subject of black holes, numerous frameworks for NED have been put out, each with a distinct motivation [46,47,48,49,50,51,52,53]. In contrast to Maxwell’s electrodynamics, these formulations provide predictions concerning the finite nature of electromagnetic energy and potentials [54,55,56,57,58]. Among these models, the Born–Infeld (BI) NED [46] was developed to figure out a well-behaved self-energy of electrons. The first solution of EG sourced by BI electrodynamics was derived in Ref. [59]. Following that, different nonlinearly charged black holes of EG were extensively investigated in Refs. [60,61,62,63,64,65,66,67,68,69,70,71,72,73,74]. Additionally, the nonlinearly charged black hole solutions of GB and Lovelock theories have also been derived [75,76,77,78,79,80,81,82,83,84,85,86]. Recently, the effects of the BI electromagnetic field on the Lovelock black holes with nonconstant curvature horizon have also been investigated [87]. Presently, I want to calculate the new solution characterizing the topologically nontrivial black holes of the third order Lovelock gravity sourced by logarithmic electrodynamics.

I make the outline of this paper as follows: In Sect. 2, I briefly review the field equations of Lovelock gravity and logarithmic electrodynamics. Then, the family of static solutions describing nonlinear electrically charged black holes with nonconstant curvature horizon is deduced. Section 3 is devoted to the thermodynamic properties of these topologically nontrivial black holes. Finally, I present the concluding remarks in Sect. 4.

2 Black hole solution

The action of Lovelock gravity coupled with logarithmic electrodynamics can be defined as

$$\begin{aligned} {\mathcal {I}}= & {} \int d^dx\sqrt{-g}\nonumber \\{} & {} \quad \times \left[ \sum _{k=0}^{k_{max}}\frac{\alpha _k}{2^k}\delta ^{\mu _1\cdots \mu _{k}\rho _1\cdots \rho _k}_{\nu _1\cdots \nu _{k}\sigma _1\cdots \sigma _k} R^{\nu _1\sigma _1}_{\mu _1\rho _1}\cdots R^{\nu _{k}\sigma _{k}}_{\mu _{k}\rho _{k}}+{\mathcal {L}}(\Upsilon )\right] ,\nonumber \\ \end{aligned}$$

(2.1)

where ${\mathcal {L}}$ stands for the Lagrangian density of logarithmic electrodynamics and is specified as

$$\begin{aligned} {\mathcal {L}}(\Upsilon )=-8\beta ^2\ln {\Bigg (1+\frac{\Upsilon }{8\beta ^2}\Bigg )}, \end{aligned}$$

(2.2)

in which $\beta$ is the nonlinearity parameter, $\Upsilon =F_{\lambda \rho }F^{\lambda \rho }$, $F_{\lambda \rho }=\partial _{\lambda }A_{\rho }-\partial _{\rho }A_{\lambda }$, and $A_{\lambda }$ is the gauge potential. Furthermore, $\Lambda$ is the cosmological constant, and $\alpha _k$’s are the arbitrary coupling parameters. Variation of Eq. (2.1) with respect to the metric tensor, $g_{\mu \nu }$, gives

$$\begin{aligned}{} & {} \sum _{k=0}^{k_{max}}\frac{\alpha _k}{2^{k+1}}\delta ^{\nu \lambda _1\sigma _1\cdots \lambda _{k}\sigma _k}_{\mu \rho _1\beta _1\cdots \rho _{k}\beta _{k}} R^{\rho _1\beta _1}_{\lambda _1\sigma _1}\cdots R^{\rho _{k}\beta _{k}}_{\lambda _{k}\sigma _{k}}\nonumber \\{} & {} \quad =-\frac{1}{2}\delta ^{\nu }_{\mu }{\mathcal {L}}(\Upsilon )+2F^{\nu }_{\rho }F^{\rho }_{\mu }\frac{\partial {\mathcal {L}}}{\partial \Upsilon }. \end{aligned}$$

(2.3)

Likewise, the nonlinear Maxwell’s equations would be obtained if one take variation of Eq. (2.1) with respect to the gauge potentials $A^{\lambda }$. Hence, one can find

$$\begin{aligned} \partial _{\rho }\Bigg (\sqrt{-g}\frac{\partial {\mathcal {L}}}{\partial \Upsilon }F^{\rho \lambda }\Bigg )=0. \end{aligned}$$

(2.4)

Consider the general line element in the form as

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2h_{ij}(z)dz^idz^j. \end{aligned}$$

(2.5)

This line element represents the d-dimensional manifold ${\mathcal {M}}^d$ as the wraped product of a two dimensional Riemannian submanifold ${\mathcal {M}}^2$ and a $(d-2)$-dimensional submanifold ${\mathcal {K}}^{d-2}$. We define the submanifold ${\mathcal {K}}^{d-2}$ as an Einstein manifold of nonconstant curvature, and has unit metric $h_{ij}$. Subsequently, tilde will be used for denoting the tensor quantities defined on the submanifold ${\mathcal {K}}^{d-2}$. Accordingly, the Ricci scalar, Ricci tensor, and Riemann tensor of this submanifold can be stated as

$$\begin{aligned} \begin{aligned}&{\tilde{R}}=\kappa (d-2)(d-3),\\ {}&{\tilde{R}}_{ij}=\kappa (d-3)h_{ij},\\ {}&{\tilde{R}}_{ij}^{kl}={\tilde{W}}_{ij}^{kl}+\kappa (\delta _i^k\delta _j^l-\delta _i^l\delta _j^k), \end{aligned} \end{aligned}$$

(2.6)

where $i,j=2,3,...,d-1$ and ${\tilde{W}}_{ij}^{kl}$ are the components of Weyl tensor defined on the submanifold ${\mathcal {K}}^{d-2}$. The vanishing of Weyl tensor in four dimensions guarantees the satisfaction of the third relation in Eqs. (2.6) for the manifolds with constant curvature. Nevertheless, manifolds of constant curvatures are the particular cases of Einstein manifolds in dimensions higher than four. It is shown that the constraints [43]

$$\begin{aligned}{} & {} \frac{1}{2^{n+1}}\delta ^{ls_1m_1\cdots s_nm_n}_{jr_1q_1\cdots r_nq_n}{\tilde{W}}_{s_1m_1}^{r_1q_1}\cdots \nonumber \\{} & {} {\tilde{W}}_{s_nm_n}^{r_nq_n}=\frac{(d-3)!\delta ^l_j}{2(d-2k-3)!}\sum _{n=0}^{k}\left( \begin{array}{c} k \\ n \end{array} \right) (-\xi _1)^n\xi _{k-n}, \end{aligned}$$

(2.7)

should be imposed on the ${\tilde{W}}_{ij}^{kl}$ when the Einstein manifolds are satisfying Eqs. (2.6). Moreover, $n=d-1$ and the $\xi _k$’s are dependent on the geometry of the submanifold.

Using the ansatz (2.5) in Eq. (2.4), one can find the potential $A_{\lambda }$ as

$$\begin{aligned} A_{\lambda }= & {} \frac{2\beta ^2r^{d-1}}{(d-1)q}\left( F_1\left( \Bigg [\frac{-1}{2},\frac{-(d-1)}{2d-4}\Bigg ],\Bigg [\frac{d-3}{2d-4}\Bigg ],\right. \right. \nonumber \\{} & {} \left. \left. -\frac{q^2}{\beta ^2r^{2d-4}}\right) -1\right) \delta ^0_{\lambda }, \end{aligned}$$

(2.8)

where $F_1$ denotes the Gaussian hypergeometric function and q is the integration constant related to electric charge. One can see that in the limit $\beta \rightarrow \infty$, $A_{\lambda }$ corresponds to that of the Maxwell’s theory. In order to construct the family of nonlinearly charged black hole solutions with nonmaximally symmetric horizon, one need to express Eq. (2.7) for $k=2$ and $k=3$ as

$$\begin{aligned} {\tilde{W}}_{li}^{ms}{\tilde{W}}_{ms}^{lj}=\frac{1}{d}\delta ^{j}_{i}{\tilde{W}}_{nm}^{kl}{\tilde{W}}_{kl}^{nm}\equiv \zeta _2\delta ^{j}_{i}, \end{aligned}$$

(2.9)

and

$$\begin{aligned}{} & {} 2(4{\tilde{W}}_{pk}^{nm}{\tilde{W}}_{ni}^{kl}{\tilde{W}}_{ml}^{pj}+{\tilde{W}}_{in}^{pm}{\tilde{W}}^{jnkl}{\tilde{W}}_{klpm})=\frac{2}{d}\delta ^j_i\nonumber \\{} & {} \times (4{\tilde{W}}_{pk}^{qm}{\tilde{W}}_{qr}^{kl}{\tilde{W}}_{ml}^{pr}+{\tilde{W}}_{qr}^{pm}{\tilde{W}}^{qrkl}{\tilde{W}}_{klpm})\equiv \zeta _3\delta ^{j}_{i}, \end{aligned}$$

(2.10)

respectively. These two conditions were first derived in Refs. [34, 42]. Now, by substituting Eqs. (2.8)–(2.10), and metric ansatz (2.5) in Eq. (2.3) with $k_{max}=3$, one can obtain the following cubic equation

$$\begin{aligned} \begin{aligned}&{\overline{\alpha }}_3\Phi ^3+{\overline{\alpha }}_2\Phi ^2+\Bigg (1+\frac{3{\overline{\alpha }}_3{\tilde{\zeta }}_2}{r^4}\Bigg )\Phi +{\overline{\alpha }}_0+\frac{{\overline{\alpha }}_2{\tilde{\zeta }}_2}{r^4}\\&\quad +\frac{{\overline{\alpha }}_3{\tilde{\zeta }}_3}{r^6}=\frac{m}{r^{d_1}}-\frac{8(2d-3)\beta ^2}{d_1^2d_2}\\&\quad \times \Bigg (1-\sqrt{1+\frac{q^2}{\beta ^2r^{2d_2}}}\Bigg )\\&\quad +\frac{8\beta ^2}{d_1d_2}\ln {\Bigg (\frac{2\sqrt{1+\frac{q^2}{\beta ^2r^{2d_2}}}-2}{q^2\beta ^{-2}r^{-2d_2}}\Bigg )}\\&\quad -\frac{8d_2q^2}{d_1^2d_3r^{2d_2}}F_1\Bigg (\Bigg [\frac{1}{2},\frac{d_3}{2d_2}\Bigg ],\Bigg [\frac{3d-7}{2d_2}\Bigg ],-\frac{q^2}{\beta ^2r^{2d_2}}\Bigg ), \end{aligned}\nonumber \\ \end{aligned}$$

(2.11)

where $\Phi (r)=(\kappa -f(r))/r^2$, $d_i=d-i$, and the coupling parameters ${\overline{\alpha }}_k$’s and ${\tilde{\zeta }}_k$’s are defined as

$$\begin{aligned} \begin{aligned}&{\overline{\alpha }}_0=-\frac{2\Lambda }{d_1d_2},\\ {}&{\overline{\alpha }}_k=\frac{d_3!\alpha _k}{(d_1-2k)!}, \\ {}&{\tilde{\zeta }}_k=\frac{(d_2-2k)!\zeta _k}{d_2!}. \end{aligned} \end{aligned}$$

(2.12)

It should be emphasized that the integration constant m denotes the object’s geometric mass. The real solution of Eq. (2.11) can be found as

$$\begin{aligned} f(r)&=\kappa +\frac{{\overline{\alpha }}_2r^2}{3{\overline{\alpha }}_3}\nonumber \\&\quad \left[ 1+\Bigg (\psi (r)\pm \sqrt{{\mathcal {Y}}(r)+\psi ^2(r)}\Bigg )^{1/3}\right. \nonumber \\&\quad \left. -{\mathcal {Y}}^{1/3}(r)\Bigg (\psi (r)\pm \sqrt{{\mathcal {Y}}+\psi ^2(r)}\Bigg )^{-1/3}\right] ,\nonumber \\ \end{aligned}$$

(2.13)

in which

$$\begin{aligned} {\mathcal {Y}}=\Bigg (-1+\frac{3{\overline{\alpha }}_3}{{\overline{\alpha }}_2^2}+\frac{9{\overline{\alpha }}_3^2{\tilde{\zeta }}_2}{{\overline{\alpha }}_2^2r^4}\Bigg )^3, \end{aligned}$$

(2.14)

and

$$\begin{aligned} \psi (r){} & {} =1-\frac{9{\overline{\alpha }}_3}{2{\overline{\alpha }}_2^2}+\frac{27{\overline{\alpha }}_3^2}{2{\overline{\alpha }}_2^3}\left[ -\frac{2\Lambda }{d_1d_2}-\frac{m}{r^{d_1}}+\frac{{\overline{\alpha }}_3{\tilde{\zeta }}_3}{r^6}\right. \nonumber \\{} & {} \left. \quad +\frac{8(2d-3)\beta ^2}{d_1^2d_2}\left( 1-\sqrt{1+\frac{q^2}{\beta ^2r^{2d_2}}}\right) \right. \nonumber \\{} & {} \left. \quad +\frac{8d_2q^2}{d_1^2d_3r^{2d_2}}F_1\left( \Bigg [\frac{1}{2},\frac{d_3}{2d_2}\Bigg ],\Bigg [\frac{3d-7}{2d_2}\Bigg ],-\frac{q^2}{\beta ^2r^{2d_2}}\right) \right. \nonumber \\{} & {} \left. \quad -\frac{8\beta ^2}{d_1d_2}\ln {\left( \frac{2\sqrt{1+\frac{q^2}{\beta ^2r^{2d_2}}}-2}{q^2\beta ^{-2}r^{-2d_2}}\right) }\right] .\nonumber \\ \end{aligned}$$

(2.15)

One can verify that the topologically nontrivial solution corresponding to the Maxwell’s electromagnetic source [45] will be obtained from Eq. (2.13) if one imposes the limit $\beta \rightarrow \infty$ or when $r\rightarrow \infty$. In addition, when the charge and nonlinearity parameter are vanishing, the solution describing uncharged black hole with nonmaximally symmetric horizon is recovered [42]. Furthermore, the Kretschmann scalar related to Eqs. (2.5) and (2.13) is irregular at $r=0$. It follows that $r=0$ is a true curvature singularity. By looking at the roots of $f(r)=0$, one may be able to recognize the horizons of a black hole. Therefore, it is trivial to figure out the geometric mass in terms of event horizon $r_+$ as

$$\begin{aligned} m&={\overline{\alpha }}_3\kappa ^3r_+^{d_7}+{\overline{\alpha }}_2k^2r_+^{d_5}+\kappa r_+^{d_7}(r_+^4+3{\overline{\alpha }}_3{\tilde{\zeta }}_2)\nonumber \\&\quad +{\overline{\alpha }}_2{\tilde{\zeta }}_2r_+^{d_5}+{\overline{\alpha }}_3{\tilde{\zeta }}_3r_+^{d_7}-\frac{2\Lambda r_+^{d_1}}{d_1d_2}\nonumber \\&\quad +\frac{8(2d-3)\beta ^2r_+^{d_1}}{d_1^2d_2}\Bigg (1-\sqrt{1+\frac{q^2}{\beta ^2r_+^{2d_2}}}\Bigg )\nonumber \\&\quad -\frac{8\beta ^2r_+^{d_1}}{d_1d_2}\ln {\Bigg (\frac{2\sqrt{1+\frac{q^2}{\beta ^2r_+^{2d_2}}}-2}{q^2\beta ^{-2}r_+^{-2d_2}}\Bigg )}\nonumber \\&\quad +\frac{8d_2q^2}{d_1^2d_3r_+^{d_3}}F_1\Bigg (\Bigg [\frac{1}{2},\frac{d_3}{2d_2}\Bigg ],\Bigg [\frac{3d-7}{2d_2}\Bigg ],-\frac{q^2}{\beta ^2r_+^{2d_2}}\Bigg ). \end{aligned}$$

(2.16)

Fig. 1

Geometric mass m (Eq. (2.16)) versus $r_+$ for $d=10$, $\Lambda =-1$, $q=10$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Fig. 2

Geometric mass m (Eq. (2.16)) versus $r_+$ for $d=10$, $\Lambda =-1$, $\beta =0.005$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

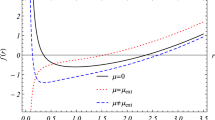
Figure 1 shows the plot of the geometric mass $m(r_+)$ for various values of $\beta$. It turns out that the topologically nontrivial black holes have two horizons for greater values of $\beta$. However, when the value of this parameter falls the two horizons collide and the black hole becomes extremal. Likewise, the impact of the electric charge on the behaviour of geometric mass is depicted in Fig. 2. It is recognized that there exists a critical value of charge parameter q for which Eq. (2.13) represents the extremal black hole. Despite this, the solution (2.13) predicts black hole with two horizons when the charge magnitude rises over this value. Remember that the radius of the event horizon $r_+$ can be described by the largest root of

$$\begin{aligned} g(r)&=\frac{m}{r^{d_1}}-\frac{{\overline{\alpha }}_3\kappa ^3}{r^{6}}-\frac{{\overline{\alpha }}_2k^2}{r^4}-\frac{\kappa }{r^2}\big (1+3{\overline{\alpha }}_3{\tilde{\zeta }}_2r^{-4}\big )\nonumber \\&\quad -\frac{{\overline{\alpha }}_2{\tilde{\zeta }}_2}{r^4}-\frac{{\overline{\alpha }}_3{\tilde{\zeta }}_3}{r^6}+\frac{2\Lambda }{d_1d_2}\nonumber \\&\quad -\frac{8(2d-3)\beta ^2}{d_1^2d_2}\Bigg (1-\sqrt{1+\frac{q^2}{\beta ^2r^{2d_2}}}\Bigg )\nonumber \\&\quad +\frac{8\beta ^2}{d_1d_2}\ln {\Bigg (\frac{2\sqrt{1+\frac{q^2}{\beta ^2r^{2d_2}}}-2}{q^2\beta ^{-2}r^{-2d_2}}\Bigg )}\nonumber \\&\quad -\frac{8d_2q^2}{d_1^2d_3r^{2d_2}}F_1\Bigg (\Bigg [\frac{1}{2},\frac{d_3}{2d_2}\Bigg ],\Bigg [\frac{3d-7}{2d_2}\Bigg ],-\frac{q^2}{\beta ^2r^{2d_2}}\Bigg )=0. \end{aligned}$$

(2.17)

Fig. 3

g(r) given by Eq. (2.16) versus r for $d=10$, $\Lambda =-1$, $\beta =0.5$, $q=1$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

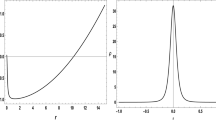
Figure 3 shows the behaviour of g(r) for various values of geometric mass m. The position of the event horizon corresponds to the largest value of the radial coordinate at which the function g(r) crosses the horizontal axis. Additionally, the mass of the extremal black hole can be determined from the condition $f(r_e)=0$ and $(df/dr)|_{r=r_e}=0$ as follows:

$$\begin{aligned} \begin{aligned} m_e&=\frac{r_e^{d_1}}{2}\left[ \frac{{\overline{\alpha }}_3}{d_1r_e^6}\big ((\kappa ^3+{\tilde{\zeta }}_3+3\kappa {\tilde{\zeta }}_2)d_1\right. \\&\left. \quad +(6\kappa ^3+6\kappa +1){\tilde{\zeta }}_3+12\kappa ^3\big )+\frac{{\overline{\alpha }}_2(d+3)(\kappa ^2+{\tilde{\zeta }}_2)}{d_1r_e^4}\right. \\&\left. \quad +\frac{\kappa (d+1)}{d_1r_e^2}-\frac{2\Lambda }{d_1d_2}+\frac{8(2d-3)\beta ^2}{d_1^2d_2}\right. \\&\left. \quad \times \left( 1-\sqrt{1+\frac{q^2}{\beta ^2r_e^{2d_2}}}\right) -\frac{16q^2\beta }{d_1^2r_e^{d_2}\sqrt{\beta ^2r_e^{2d_2}+q^2}}+\frac{8\beta ^2}{d_1^2}\right. \\&\left. \quad +\frac{8d_2q^2}{d_1^2d_3r_e^{2d_2}}F_1\left( \Bigg [\frac{1}{2},\frac{d_3}{2d_2}\Bigg ],\Bigg [\frac{3d-7}{2d_2}\Bigg ],-\frac{q^2}{\beta ^2r_e^{2d_2}}\right) \right. \\&\left. \quad -\frac{8\beta ^2}{d_1d_2}\ln {\left( \frac{2\sqrt{1+\frac{q^2}{\beta ^2r_e^{2d_2}}}-2}{q^2\beta ^{-2}r_e^{-2d_2}}\right) }-\frac{8\beta ^3r_e^{d_2}}{d_1^2\sqrt{\beta ^2r_e^{2d_2}+q^2}}\right] , \end{aligned}\nonumber \\ \end{aligned}$$

(2.18)

with $r_e$ refers to the extremal black hole’s horizon satisfying

$$\begin{aligned} \begin{aligned}&\frac{{\overline{\alpha }}_3\big ((\kappa ^3+{\tilde{\zeta }}_3)d_7-18\kappa {\tilde{\zeta }}_3\big )}{d_1r_e^6}+\frac{{\overline{\alpha }}_2d_5(\kappa ^2+{\tilde{\zeta }}_2)}{d_1r_e^4}\\&\quad +\frac{d_3\kappa }{d_1r_e^2}+\frac{3{\overline{\alpha }}_3{\tilde{\zeta }}_2\kappa }{r_e^6}-\frac{2\Lambda }{d_1d_2}\\&\quad +\frac{8(2d-3)\beta ^2}{d_1^2d_2}\left( 1-\sqrt{1+\frac{q^2}{\beta ^2r_e^{2d_2}}}\right) \\&\quad -\frac{8\beta ^2}{d_1d_2}\ln {\left( \frac{2\sqrt{1+\frac{q^2}{\beta ^2r_e^{2d_2}}}-2}{q^2\beta ^{-2}r_e^{-2d_2}}\right) }\\&\quad +\frac{8q^2\beta }{d_1^2r_e^{d_2}\sqrt{\beta ^2r_e^{2d_2}+q^2}}+\frac{8\beta ^3r_e^{d_2}}{d_1^2\sqrt{\beta ^2r_e^{2d_2}+q^2}}-\frac{8\beta ^2}{d_1^2}=0. \end{aligned}\nonumber \\ \end{aligned}$$

(2.19)

It should be reported that for ${\overline{\alpha }}_3={\overline{\alpha }}_2^2/3$ and ${\tilde{\zeta }}_2={\tilde{\zeta }}_3=0$, Eq. (2.13) leads to the black hole solution of Lovelock gravity coupled to logarithmic electrodynamics [81]. It is also crucial to remember that the solution (2.13) with $m=0$ can still possess horizon as opposed to the maximally symmetric solutions of Lovelock gravity which possess no horizons under this substitution.

3 Thermodynamics

In this section, I wish to figure out the thermodynamic quantities of the accomplished solution (2.13). Firstly, the Hawking temperature can be determined from the notion of surface gravity [88] as

$$\begin{aligned} \begin{aligned} T&=\frac{1}{4\pi }\left[ -\frac{2\kappa }{r_+}+\frac{1}{{\mathcal {Z}}_1(r_+)}\times \left( \frac{{\overline{\alpha }}_3}{r_+}(d_1\kappa ^3-6{\tilde{\zeta }}^3(2\kappa +1)\right. \right. \\&\left. \left. \quad +d_1{\tilde{\zeta }}_3)+{\overline{\alpha }}_2(d_1(\kappa ^2+{\tilde{\zeta }}_2)-4{\tilde{\zeta }}_2)r_+\right. \right. \\&\left. \left. \quad +\frac{d_1\kappa }{r_+}(r_+^4+3{\overline{\alpha }}_2{\tilde{\zeta }}_2)-\frac{2\Lambda r_+^5}{d_2}\right. \right. \\&\left. \left. \quad +\frac{8\beta ^2(2d-3)}{d_1d_2r_+^{d_7}}\left( \beta r_+^{d_2}-\sqrt{\beta ^2r_+^{2d_2}+q^2}\right) -\frac{8\beta ^2r_+^5}{d_1}\right. \right. \\&\left. \left. \quad -\frac{8\beta ^2r_+^{d_5}}{d_2}\ln {\left( \frac{2\sqrt{\beta ^2r_+^{2d_2}+q^2}-2\beta r_+^{d_2}}{q^2\beta ^{-1}r_+^{-d_2}}\right) }\right. \right. \\&\left. \left. \quad +\frac{8q^2\beta }{d_1r_+^{d_7}\sqrt{\beta ^2r_+^{2d_2}+q^2}}+\frac{8\beta ^3r_+^{d+3}}{d_1\sqrt{\beta ^2r_+^{2d_2}+q^2}}\right) \right] , \end{aligned}\nonumber \\ \end{aligned}$$

(3.1)

with

$$\begin{aligned} {\mathcal {Z}}_1(r_+)=r_+^4+2{\overline{\alpha }}_2\kappa r_+^2+3{\overline{\alpha }}_3(\kappa ^2+{\tilde{\zeta }}_2). \end{aligned}$$

(3.2)

Fig. 4

Temperature versus $r_+$ for $d=10$, $\Lambda =-1$, $q=10$, ${\tilde{\zeta }}_2=1$, ${\tilde{\zeta }}_3=5$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Fig. 5

Temperature versus $r_+$ for $d=10$, $\Lambda =-1$, $\beta =1.5$, ${\tilde{\zeta }}_2=1$, ${\tilde{\zeta }}_3=5$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

The implications of the nonlinearity parameter and electric charge on the black hole’s temperature are investigated in Figs. 4 and 5, respectively. The radii with positive temperature values encode the horizons of the physical black holes. The area law, which stipulates that the entropy is equal to one quarter of the horizon area, is invalid in Lovelock gravity. Because of this, it is helpful to utilize the Wald’s prescription for figuring out the entropy [89, 90]. This formulation can be applied to any black hole whose event horizon is the Killing horizon. Hence, by using this technique we have

$$\begin{aligned} S=-2\pi \oint d^{d_2}x\sqrt{{\overline{\gamma }}}\frac{\partial {\mathcal {L}}}{\partial R_{\alpha \beta \gamma \delta }}{\tilde{b}}_{\alpha \beta }{\tilde{b}}_{\gamma \delta }, \end{aligned}$$

(3.3)

where ${\mathcal {L}}$ refers to the Lagrangian density, while ${\tilde{b}}_{\alpha \beta }$ denotes the binormal to the Killing horizon. Thus, the entropy associated with solution (2.13) is given by

$$\begin{aligned} \begin{aligned} S=\frac{\Sigma _{\kappa }d_2r_+^{d_2}}{4}\Bigg [\frac{1}{d_2}+\frac{2\kappa {\overline{\alpha }}_2}{d_4r_+^2}+\frac{3{\overline{\alpha }}_3(\kappa ^2+{\tilde{\zeta }}_2)}{d_6r_+^4}\Bigg ], \end{aligned} \end{aligned}$$

(3.4)

where $\Sigma _{\kappa }$ designates the volume of a hypersurface with nonconstant curvature. Note that the first term corresponds to the horizon’s area. Additionally, topological invariants can be seen to contribute to the overall entropy of the solution (2.13). Likewise, the terms containing parameters ${\overline{\alpha }}_2$ and ${\overline{\alpha }}_3$ represent contributions from the maximally symmetric horizons, and term containing ${\tilde{\zeta }}_2$ is present due to the contribution of Einstein horizon.

The finite mass of the black hole is computed as

$$\begin{aligned} \begin{aligned} M&=\frac{\Sigma _{\kappa }d_2m}{16\pi }=\frac{\Sigma _{\kappa }d_2}{16\pi }\left[ {\overline{\alpha }}_3\kappa ^3r_+^{d_7}\right. \\&\left. \quad +{\overline{\alpha }}_2k^2r_+^{d_5}+\kappa r_+^{d_7}(r_+^4+3{\overline{\alpha }}_3{\tilde{\zeta }}_2)+{\overline{\alpha }}_2{\tilde{\zeta }}_2r_+^{d_5} +{\overline{\alpha }}_3{\tilde{\zeta }}_3r_+^{d_7}\right. \\&\left. \quad -\frac{2\Lambda r_+^{d_1}}{d_1d_2}+\frac{8(2d-3)\beta ^2r_+^{d_1}}{d_1^2d_2}\left( 1-\sqrt{1+\frac{q^2}{\beta ^2r_+^{2d_2}}}\right) \right. \\&\left. \quad -\frac{8\beta ^2r_+^{d_1}}{d_1d_2}\ln {\left( \frac{2\sqrt{1+\frac{q^2}{\beta ^2r_+^{2d_2}}}-2}{q^2\beta ^{-2}r_+^{-2d_2}}\right) }\right. \\&\left. \quad +\frac{8d_2q^2}{d_1^2d_3r_+^{d_3}}F_1\left( \left[ \frac{1}{2},\frac{d_3}{2d_2}\right] ,\left[ \frac{3d-7}{2d_2}\right] ,-\frac{q^2}{\beta ^2r_+^{2d_2}}\right) \right] . \end{aligned}\nonumber \\ \end{aligned}$$

(3.5)

Fig. 6

Finite mass given by Eq. (3.5) versus $r_+$ for $d=10$, $\Lambda =-1$, $\Sigma _{\kappa }=1$, $q=10$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Fig. 7

Finite mass given by Eq. (3.5) versus $r_+$ for $d=10$, $\Lambda =-1$, $\Sigma _{\kappa }=1$, $\beta =5.5$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

The unavoidable effects of the parameters $\beta$ and q on the black hole’s finite mass M can be respectively analyzed from Figs. 6 and 7. Furthermore, calculating the electromagnetic flux at infinity will yield the thermodynamic electric charge Q of the black hole. Hence, one might discover

$$\begin{aligned} Q=\frac{\Sigma _{\kappa }q}{4\pi }\sqrt{\frac{d_2d_3}{2}}. \end{aligned}$$

(3.6)

One can see that the above formula of electric charge is independent of the parameter $\beta$. In order to work out the expression for electric potential of the black hole [91, 92], one need to take nonzero component of the gauge potential $A_{\lambda }$. It can be verified that the electric potential vanishes when r tends to infinity. Consequently, the black hole’s electric potential can be claimed as

$$\begin{aligned} \Psi (r_+)= & {} A_{\lambda }X^{\lambda }\big |_{r\rightarrow \infty }-A_{\lambda }X^{\lambda }\big |_{r=r_+} \nonumber \\= & {} \frac{-2\beta ^2r_+^{d_1}}{d_1q}\Bigg [F_1\Bigg (\Bigg [\frac{-1}{2},\frac{-d_1}{2d_2}\Bigg ],\nonumber \\{} & {} \Bigg [\frac{d_3}{2d_2}\Bigg ],-\frac{q^2}{\beta ^2r_+^{2d_2}}\Bigg )-1\Bigg ]. \end{aligned}$$

(3.7)

Here $X^{\lambda }$ denotes the temporal Killing vector. Consider that the temperature T and electric potential $\Psi$, respectively, are the intensive parameters conjugate to entropy and electric charge Q. Hence, one may write

$$\begin{aligned} T=\frac{\partial M}{\partial S}\Bigg |_{Q}=\Bigg (\frac{\partial M}{\partial r_+}\Bigg )\Bigg |_{Q}\Bigg (\frac{\partial S}{\partial r_+}\Bigg )^{-1}\Bigg |_Q,\nonumber \\ \end{aligned}$$

(3.8)

and

$$\begin{aligned} \Psi =\frac{\partial M}{\partial Q}\Bigg |_{S}=\Bigg (\frac{\partial M}{\partial q}\Bigg )\Bigg |_{r_+}\Bigg (\frac{\partial Q}{\partial q}\Bigg )^{-1}\Bigg |_{r_+}. \end{aligned}$$

(3.9)

It can be easily shown that the Eqs. (3.8)–(3.9) are in the same forms as Eq. (3.1) and (3.7), respectively. Hence, the first law

$$\begin{aligned} \begin{aligned} dM&=TdS+\Psi dQ. \end{aligned} \end{aligned}$$

(3.10)

is satisfied by the above quantities.

The local thermodynamic stability of the black hole can be demonstrated from the positivity of specific heat capacity [93]. This condition determines local stability in the canonical ensemble. Since M depends on the horizon radius and charge, the heat capacity can be stated as

$$\begin{aligned} C_H=T\frac{dS}{dT}\Bigg |_{q}. \end{aligned}$$

(3.11)

Substitution of Eqs. (3.1) and (3.4) yields

$$\begin{aligned} C_H&=\frac{\Sigma _{\kappa }d_2{\mathcal {H}}_2\big (r_+^2{\mathcal {Z}}_1{\mathcal {H}}_1-2\kappa r_+{\mathcal {Z}}_1^2\big )}{4d_5\big (r_+^2{\mathcal {Z}}_1{\mathcal {H}}_1'(r_+)-(4r_+^5+4{\overline{\alpha }}_2\kappa r_+^3){\mathcal {H}}_1-2\kappa {\mathcal {Z}}_1^2\big )}, \end{aligned}$$

(3.12)

where

$$\begin{aligned} {\mathcal {H}}_1(r_+)&=\frac{{\overline{\alpha }}_3}{r_+}\big (d_1\kappa ^3-6{\tilde{\zeta }}_3(2\kappa +1)+d_1{\tilde{\zeta }}_3\big ) \nonumber \\&\quad +{\overline{\alpha }}_2(d_1\kappa ^2+{\tilde{\zeta }}_2d_5)r_++\frac{d_1\kappa }{r_+} \nonumber \\&\quad \times (r_+^4+3{\overline{\alpha }}_3{\tilde{\zeta }}_2)-\frac{2\Lambda r_+^5}{d_2}+\frac{8\beta ^2(2d-3)}{d_1d_2r_+^{d_7}} \nonumber \\&\quad \times \Bigg (\beta r_+^{d_2}-\sqrt{\beta ^2r_+^{2d_2}+q^2}\Bigg ) \nonumber \\&\quad -\frac{8\beta ^2r_+^{d_5}}{d_2}\ln {\Bigg [\frac{2\sqrt{\beta ^2r_+^{2d_2}+q^2}-2\beta r_+^{d_2}}{q^2\beta ^{-1}r_+^{-d_2}}\Bigg ]} \nonumber \\&\quad +\frac{8q^2\beta }{d_1r_+^{d_7}\sqrt{\beta ^2r_+^{2d_2}+q^2}} \nonumber \\&\quad -\frac{8\beta ^2r_+^{d_5}}{d_1}+\frac{8\beta ^3r_+^{d_+3}}{d_1\sqrt{\beta ^2r_+^{2d_2}+q^2}}, \end{aligned}$$

(3.13)

$$\begin{aligned} {\mathcal {H}}_1'(r_+)&=\frac{{\overline{\alpha }}_3}{r_+^2}\big (-d_1\kappa ^3+6{\tilde{\zeta }}_3(2\kappa +1)-d_1{\tilde{\zeta }}_3\big ) \nonumber \\&\quad +{\overline{\alpha }}_2(d_1\kappa ^2+{\tilde{\zeta }}_2d_5)+\frac{3d_1\kappa (r_+^4-{\overline{\alpha }}_3{\tilde{\zeta }}_2)}{r_+^2} -\frac{10\Lambda r_+^4}{d_2} \nonumber \\&\quad -\frac{8\beta ^2(2d-3)\Bigg (\beta r_+^{d_2}-\sqrt{\beta ^2r_+^{2d_2}+q^2}\Bigg )}{d_1d_2r_+^{d_6}\sqrt{\beta ^2r_+^{2d_2}+q^2}\Bigg (d_2\beta r_+^{d_2}+\sqrt{\beta ^2r_+^{2d_2}+q^2}\Bigg )^{-1}} \nonumber \\&\quad -\frac{8\beta ^2d_5r_+^{d_6}}{d_2} \ln {\Bigg [\frac{2\sqrt{\beta ^2r_+^{2d_2}+q^2}-2\beta r_+^{d_2}}{q^2\beta ^{-1}r_+^{-d_2}}\Bigg ]} \nonumber \\&\quad +\frac{8\beta ^2r_+^{d_6}\Bigg (\beta r_+^{d_2}-\sqrt{\beta ^2r_+^{2d_2}+q^2}\Bigg )}{\sqrt{\beta ^2r_+^{2d_2}+q^2}} \nonumber \\&\quad -\frac{40\beta ^2r_+^4}{d_1}+\frac{(8q^2d_7\beta -8(d+3)\beta ^3r_+^{2d_2})}{d_1r_+^{d_6}\sqrt{\beta ^2r_+^{2d_2}+q^2}} \nonumber \\&\quad -\frac{8q^2\beta ^3d_2r_+^{d+2}+8\beta ^5d_2r_+^{3d-5}}{d_1\big (\sqrt{\beta ^2r_+^{2d_2}+q^2}\big )^{3/2}}, \end{aligned}$$

(3.14)

and

$$\begin{aligned} {\mathcal {H}}_2=d_5r_+^{d_3}+2\kappa d_5{\overline{\alpha }}_2r_+^{d_5}+3{\overline{\alpha }}_3(\kappa ^2+{\tilde{\zeta }}_2)d_6r_+^{d_7}. \end{aligned}$$

(3.15)

Fig. 8

Heat capacity $C_H$ (Eq. (3.12)) versus $r_+$ for $d=10$, $\Lambda =-1$, $q=10$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Fig. 9

Heat capacity $C_H$ (Eq. (3.12)) versus $r_+$ for $d=10$, $\Lambda =-1$, $\beta =30$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Figure 8 demonstrates the effect of parameter $\beta$ on the behaviour of heat capacity (3.12) as a function of the outer horizon. It is observed that $C_H$ vanishes at $r_+=r_e$ and infinite at $r_+=r_i$ with $i=1,2,3,\ldots$, and $r_1<r_2<\ldots$. Hence, the black hole possesses phase transition at these points. It can also be seen that the smaller black holes having $r_e<r_+<r_1$ are locally stable while the larger objects for $r_+>r_i$ could be unstable as well. One can examine that these phase transition points are shifting to the right when the parameter $\beta$ increases in magnitude. Furthermore, the effect of electric charge on the behaviour of $C_H$ can be observed in Fig. 9. One can see that the horizon radii associated with the phase transitions and extreme black holes ($T=0$) are increasing when the electric charge increases.

In the grand canonical ensemble, the local thermodynamic stability of black hole requires the positivity of the determinant of Hessian matrix. This determinant is given by

$$\begin{aligned} \begin{aligned} H(r_+)&=\Bigg (\frac{\partial ^2M}{\partial {\mathcal {S}}^2}\Bigg )\Bigg (\frac{\partial ^2M}{\partial Q^2}\Bigg )-\Bigg (\frac{\partial ^2M}{\partial {\mathcal {S}}\partial Q}\Bigg )^2. \end{aligned} \end{aligned}$$

(3.16)

Thus by using Eqs. (3.4) and (3.5) we have

$$\begin{aligned} \begin{aligned} H(r_+)&=\frac{d_5{\mathcal {H}}_3\big (r_+^2{\mathcal {Z}}_1{\mathcal {H}}_1'-(4r_+^5+4{\overline{\alpha }}_2\kappa r_+^3){\mathcal {H}}_1-2\kappa {\mathcal {Z}}_1^2\big )}{\pi d_2r_+^2\Sigma _{\kappa }{\mathcal {Z}}_1^2{\mathcal {H}}_2}\\&\quad -\frac{2d_5^2}{\pi ^2d_2^2Q^2\Sigma _{\kappa }^2{\mathcal {H}}_2^2}\\&\quad \times \Bigg (\sqrt{d_2d_3}\beta r_+^{d_2}-\sqrt{\beta ^2r_+^{2d_2}\Sigma _{\kappa }^2d_2d_3+32\pi ^2Q^2}\Bigg )^2, \end{aligned}\nonumber \\ \end{aligned}$$

(3.17)

with

$$\begin{aligned} {\mathcal {H}}_3(r_+)= & {} \frac{\sqrt{2}\beta r_+}{4\pi Q^2d_2}\sqrt{\beta ^2r_+^{2d_2}\Sigma _{\kappa }^2d_2d_3+32\pi ^2Q^2} \nonumber \\{} & {} -\frac{\sqrt{2d_2d_3}\beta ^2\Sigma _{\kappa }r_+^{d_1}}{4\pi Q^2d_1} -\frac{\sqrt{2d_2d_3}\beta ^2\Sigma _{\kappa }r_+^{d_1}}{4\pi Q^2d_1d_2}F_1 \nonumber \\{} & {} \times \Bigg (\Bigg [\frac{-1}{2},\frac{-d_1}{2d_2}\Bigg ],\Bigg [\frac{d_3}{2d_2}\Bigg ],\nonumber \\{} & {} \frac{-32\pi ^2Q^2}{d_2d_3\Sigma _{\kappa }^2\beta ^2r_+^{2d_2}}\Bigg ). \end{aligned}$$

(3.18)

Fig. 10

Determinant of the Hessian matrix $H(r_+)$ (Eq. (3.17)) versus $r_+$ for $d=10$, $\Lambda =-1$, $Q=10$, $\Sigma _{\kappa }=1$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Fig. 11

Determinant of the Hessian matrix $H(r_+)$ (Eq. (3.17)) versus $r_+$ for $d=10$, $\Lambda =-1$, $\beta =1$, $\Sigma _{\kappa }=1$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

In Figs. 10 and 11, the consequences of the parameter $\beta$ and thermodynamical charge on the determinant of the Hessian matrix (3.17) are explored, respectively. It is concluded that there exist horizon radii $r_a$ and $r_b$ such that $H(r_+)$ remains positive in the domain $r_a<r_+<r_b$. Thus the black hole is stable in this domain and remains unstable outside of it. It is also noted that both the radii $r_a$ and $r_b$ grow in their magnitudes when the parameter $\beta$ increases. Additionally, Fig. 11 suggests that the regions of local stability in the grand canonical ensemble are getting larger when the magnitude of the electric charge rises. The expression of Gibbs free energy density [93] can be written as

$$\begin{aligned} \begin{aligned} G&=M-T S, \end{aligned} \end{aligned}$$

(3.19)

where T, S, and M are respectively calculated in Eqs. (3.1), (3.4), and (3.5).

Fig. 12

Gibbs energy (Eq. (3.19)) versus $r_+$ for $d=10$, $\Lambda =-1$, $q=10$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

Fig. 13

Gibbs energy (Eq. (3.19)) versus $r_+$ for $d=10$, $\Lambda =-1$, $\beta =0.005$, ${\tilde{\zeta }}_2=0.5$, ${\tilde{\zeta }}_3=0.006$, $\kappa =1$, ${\overline{\alpha }}_2=2$, and ${\overline{\alpha }}_3=5$

The negativity of the Gibbs energy density can be used to estimate the black hole’s global stability. The response of this quantity in terms of $r_+$ with various values of $\beta$ and q is respectively illustrated in Figs. 12 and 13. One can conclude that the topologically nontrivial black holes described by Eq. (2.13) are globally unstable.

4 Summary and conclusion

In this paper, I used the model of logarithmic electrodynamics and found the new topologically nontrivial black hole solution of the third order Lovelock gravity. The relevant horizon space for this solution can be inferred to be an Einstein space with nonzero Weyl curvature. Due to the emergence of charge-like parameters ${\tilde{\zeta }}_k$’s in the metric function, the extra constraints on the Weyl tensor resulted in a considerable alteration to the solution and its physical properties. I further demonstrated that, based on the selection of parameters q, $\beta$, ${\tilde{\zeta }}_2$, and ${\tilde{\zeta }}_3$, the resultant solution (2.13) either characterizes nonlinearly charged black holes with single or two horizons or represents naked singularities. Additionally, I calculated thermodynamic and conserved quantities of the resultant gravitating object and showed that they adhere to the first law of thermodynamics.

Using the expressions of thermodynamic quantities in terms of $r_+$, I also investigated the local stability of the resultant black hole in both canonical and grand canonical ensembles. It is concluded that there exists $r_+=r_e$ at which both temperature and specific heat are equal to zero. This value of the event horizon corresponds to the first order phase transition and coincides with the horizon radius of the extremal black hole. The specific heat exhibits singularities at $r_+=r_i$’s that are analogous to the second order phase transition of the black hole. It is shown that the horizon radius of the extremal black hole grows in size when the electric charge and nonlinearity parameter $\beta$ rise in magnitude. According to the plots of the determinant of the Hessian matrix, the object would be stable if its horizon radius $r_+$ falls in the range $r_a<r_+<r_b$, otherwise unstable. I have also observed that the values of $r_a$ and $r_b$ grow with the increase in $\beta$. Additionally, when the thermodynamic electric charge Q increases, the interval of $r_+$ corresponding to the stability in the grand canonical ensemble grows. Finally, I have also studied the behaviour of Gibbs free energy density as a function of the event horizon and showed that for any value of q and $\beta$, black holes described by (2.13) are globally unstable.

It may be very important to explore the impacts of dark energy, dark fluid, and the cloud of strings on black holes with nonmaximally symmetric horizons. Similarly, it could also be highly fascinating to investigate the quasitopological black holes with nonconstant curvature horizons and their physical characteristics. These issues are reserved for my next solo work.