Self-supporting wormholes in four dimensions with scalar field

Abstract

In this paper, we investigated the space-time obtained by quotients of the $AdS_4$ space-time. Further quotient with specific ${\mathbb {Z}}_2$ is considered. Taking up the first-order perturbation in metric, we estimated the backreaction of the matter field on space-time geometry. We can calculate the expectation value of the stress-energy tensor by pulling it back onto the covering space. The average null energy becomes negative when the suitable boundary condition is chosen, resulting in a traversable wormhole.

1 Introduction

Wormholes have been a topic of interest for both scientists [1, 2], and the general public as they provide a way for rapid transit between two distant points in space or also for communication over long distances. Wormholes are Einstein equation solutions that use a throat to connect two otherwise different space-times or two widely separated areas of the same space-time. Several studies showed that wormholes also present themselves as exact solutions in the context of modified gravity [3,4,5,6,7,8]. Classically, wormholes are not traversable, meaning that a causal curve cannot pass through the wormhole’s throat, connecting the two different regions. A traversable wormhole is possible only if the geodesics entering the wormhole on one side (and thus converging as they approach the throat) will emerge on the other side, diverging from each other. Raychaudhuri’s equation showed that it can only happen if certain energy conditions are violated – the null energy condition (NEC) and the averaged null energy conditions (ANEC). The ANEC asserts that, there must be an infinite number of null geodesics with a tangent vector $k^\mu$ and affine parameter $\lambda$ passing through the wormhole to satisfy the condition

$$\begin{aligned} \int _{-\infty }^\infty T_{\alpha \beta } k^\alpha k^\beta d \lambda < 0 . \end{aligned}$$

(1.1)

The ER = EPR conjecture [9] states that whenever two particles are entangled, they must be connected through a wormhole. Reference [10] originally addressed the issue of wormhole traversability for static, spherically symmetric wormholes, and it has been shown that wormholes must have exotic matter for traversability. References [2, 11, 12] further investigated this issue and established the violation of the average null energy condition (ANEC) as an essential requirement for wormhole traversability. The ANEC has been demonstrated to hold for achronal null geodesics [13,14,15]. As a result, space-times with only achronal null geodesics do not allow for traversable wormholes. The topological censor theorem [16] and its generalization to asymptotically localized anti-de Sitter spaces [17] declare that any causal curve whose endpoints reside in the boundary at infinity $({\mathcal {I}})$ can be transformed to a causal curve that wholly lies in $({\mathcal {I}})$.

Gao, Jafferis, and Wall [18] recently made a significant advance in this direction. By adding a time-dependent coupling between the two asymptotic regions of an eternal BTZ black hole, they were able to create a traversable wormhole. Using the point-splitting method, they calculated the one-loop stress-energy tensor. By correctly choosing the sign of the coupling, the vacuum expectation value of the double null component of the stress-energy tensor may be made negative, allowing the wormhole to be traversable. These findings were then generalized in [19] to investigate the effect of rotation on wormhole size. In [20], a connection between the two boundaries were used to create an eternally traversable wormhole in nearly-$AdS_2$ space-time.

In the presence of massless fermions, [21] constructed a four-dimensional traversable wormhole by connecting the throats of two charged extremal black hole geometries. This construction did not rely on any non-local external coupling between the two boundaries, and the result was what is known as self-supporting wormholes, which form purely from the local dynamics of the fermion fields existing in the bulk of space-time. In [22], authors have constructed eternal AdS$_4$ traversable wormhole by coupling CFT$_3$ boundary theories. In [23], authors have constructed the traversable wormhole without adding any coupling between its asymptotic regions. They have presented an alternative analysis to ascertain traversable wormholes from bulk dynamics by considering a free scalar field in quotients of $AdS_3$ and $AdS_3\times S^1$ by discrete symmetries. The authors calculated the gravitational backreaction and demonstrated that causal curves that cannot be deformed to the boundary exist in space-time. Taking the quotient by a discrete symmetry is essential in that it destroys the globally specified Killing field, which is crucial for attaining the average null energy condition. This finding was later extended [24] to include fermions in bulk and [25] to include massive spin one, resulting in traversable wormholes.

In this paper, we generalize the aforementioned conclusions to the four dimensions. In the case of $AdS_4$, an exact analytic equation for the propagator in closed form is not possible. We computed the expectation value of the stress tensor by fixing different values of mass m and show that this leads to traversable wormholes when sufficient boundary conditions are imposed. The preliminaries for developing self-supporting wormholes from free scalar fields are summarised in the following section. By quotienting out the $AdS_4$, we get the space-time in Sect. 3. The expectation value of the stress tensor for the scalar field is then computed using the images approach. The choice of co-ordinate is discussed in appendix A, and the linearized Einstein’s equation up to first order is discussed in appendix B.

2 Preliminaries

The AdS$_3$ metric in Kruskal-like coordinates $(U,V,\phi )$ is

$$\begin{aligned} dS^2= & {} g_{\alpha \beta }dx^\alpha dx^\beta \nonumber \\= & {} \frac{1}{(1+UV)^2}\Big (-4 l^2 dU dV + r_+(1-UV)^2 d\phi ^2\Big ),\nonumber \\ \end{aligned}$$

(2.1)

where $\phi$ is the azimuthal angle. By identifying $\phi \thicksim \phi +2\pi$, it gives rise to a non-rotating BTZ black hole with horizon radius $r_+$. $U=0$ and $V=0$ are the horizons of black hole and $1+UV=0$ indicates the boundary of black hole. The $\mathbb{R}\mathbb{P}^2$-geon [26] is generated by multiplying this geometry by the ${\mathbb {Z}}_2$ isometry J, which has the following effect on the co-ordinates: $J: (V, U, \phi ) \rightarrow (V, U, \phi +\pi )$. The above solution was constructed and discussed in [27]. From the gauge-gravity perspective, the solution has been discussed in [28]. In the case of wormhole discussed in [29]. This is the first solution in which the authors of [18] have discussed the traversability issue of the wormhole by taking an appropriate double trace deformation coupled to two boundaries. The appropriate double trace deformation in boundary CFT amounts to adding a stress tensor in bulk, resulting in a perturbation of the space-time geometry

We’ll start with the fact that is discussed in [18]. By using the fact that the background metric (2.1) has constant $g_{UV}$ along the horizon $(V = 0)$, which implies that the geodesic equation at linear order implies a null ray starting from the right boundary in the far past to have

$$\begin{aligned} V(U)= & {} -(2g_{UV}(V=0))^{-1} \int _{-\infty }^U dU h_{UU} , \end{aligned}$$

(2.2)

$$\begin{aligned}= & {} \frac{1}{2 l^2} \int _{-\infty }^U dU h_{UU} , \end{aligned}$$

(2.3)

where $h_{kk}$ is the norm of $k^a$ after first-order back-reaction from the quantum stress tensor. By taking one of the horizons into account, let’s take $V=0$ horizon with the horizon generator $k^\lambda$ such that $k^\lambda \partial _\lambda = \partial _U$. The null geodesics tangent to this horizon can be parametrized by choosing U as the affine parameter. For the metric perturbation on the chosen horizon ($V=0$), the linearized Einstein’s equation for $h_{\mu \nu }=\delta g_{\mu \nu } \thicksim {\mathcal {O}}(\epsilon )$ is written as¹

$$\begin{aligned} \frac{1}{2} \Big [\frac{1}{l^2}(h_{UU}+\partial _U(Uh_{UU}))-\frac{1}{r_+^2}\partial _U^2h_{\phi \phi }\Big ]= 8 \pi G_N T_{UU} , \end{aligned}$$

(2.4)

By integrating the Eq. (2.4) overall U to get the shifts in the ray from far past to far future. While integrating and using the asymptotically AdS boundary conditions, the equation reduces to

$$\begin{aligned} 8\pi G_N \int dU {\langle }{T_{kk}}{\rangle } = \frac{1}{2l^2} \int dU h_{kk} , \end{aligned}$$

(2.5)

the shift at the far future is

$$\begin{aligned} \Delta V(+\infty )= & {} -\frac{8 \pi G_N l^2}{g_{UV}(0)} \int _{-\infty }^\infty dU {\langle }{T_{kk}}{\rangle } \nonumber \\= & {} 4 \pi G_N \int _{-\infty }^\infty dU {\langle }{T_{kk}}{\rangle } . \end{aligned}$$

(2.6)

The time delay of the null geodesics starting from $U = -\infty$ and ending at $U=\infty$ can be measured using the quantity $\Delta V(\infty )$. This quantity also provides a measure for the size of the wormhole’s opening. The wormhole becomes traversable iff the ANEC is violated or, equivalently, $\Delta V(\infty ) < 0$. By choosing an appropriate non-local coupling between the boundaries, it has been shown in [18] that taking a one-loop stress tensor can violate the ANEC and result in wormhole traversability.

The above construction relies on the addition of any non-local boundary interaction. Another method has been proposed in [23] to give rise to a traversable wormhole without adding non-local coupling. This method relies on choosing a suitable ${\mathbb {Z}}_2$ quotient of BTZ black hole space-time${\tilde{M}}$; it results in a smooth, globally hyperbolic manifold, called as $\mathbb{R}\mathbb{P}^2$-geon [26], M. The manifold ${\tilde{M}}$ is also called the covering space. A new homotopy cycle in manifold M arises due to the introduction of the ${\mathbb {Z}}_2$ quotient and, it allows to take the scalar field in M to be either periodic or anti-periodic around this circle. By using the method of images, one can relate the state on M and ${\tilde{M}}$. The points ${\tilde{x}} \in {\tilde{M}}$ can be projected into M by taking an isometry, let’s say J, i.e., the pairs $({\tilde{x}}, J{\tilde{x}})$ project on point $x \in M$. By using the Method of images, the scalar quantum fields ${\tilde{\phi }}(x)$ in ${\tilde{M}}$ are used to construct the quantum fields in M as

$$\begin{aligned} \phi _\pm (x) = \frac{1}{\sqrt{2}} \left( {\tilde{\phi }}({\tilde{x}}) \pm {\tilde{\phi }}(J{\tilde{x}})\right) , \end{aligned}$$

(2.7)

where ± corresponds to the periodic and anti-periodic boundary conditions. The points ${\tilde{x}}$ and $J{\tilde{x}}$ can’t coincide as M is smooth. Thus they are spacelike separated and the quantum fields at these points commute.

The action for free scalar field $\phi _\pm (x)$ in M is

$$\begin{aligned} S=\int d^4x \sqrt{-g}\left( -\frac{1}{2}g^{\alpha \beta }\partial _\alpha \phi _\pm (x) \partial _\beta \phi _\pm (x) -\frac{1}{2}m^2 \phi _\pm ^2(x) \right) . \end{aligned}$$

(2.8)

The stress-energy tensor by varying the action with respect to $g^{\alpha \beta }$,

$$\begin{aligned} T_{\alpha \beta } = \partial _\alpha \phi \partial _\beta \phi -\left[ \frac{1}{2}g_{\alpha \beta } g^{\gamma \delta } \partial _\gamma \phi \partial _\delta \phi + \frac{1}{2} g_{\alpha \beta }m^2 \phi ^2\right] . \end{aligned}$$

(2.9)

To compute the expectation value of the double null component of the stress tensor in the Hartle–Hawking state. Hartle–Hawking state in M is represented as ${\left| {HH,M}\right\rangle }$ and in ${\tilde{M}}$ as ${\left| {HH,{\tilde{M}}}\right\rangle }$. As the quantity of interest is $k^\alpha k^\beta T_{\alpha \beta }$, the term inside the parenthesis in Eq. (2.9) vanishes because of $T_{\alpha \beta }k^\alpha k^\beta =0$. Finally we have [25]

$$\begin{aligned}{} & {} {\left\langle {HH,M}\right| }k^\alpha k^\beta T_{\alpha \beta \pm } {\left| {HH,M}\right\rangle } \nonumber \\{} & {} \quad = \pm {\left\langle {HH,{\tilde{M}}}\right| }k^\alpha \partial _\alpha {\tilde{\phi }}({\tilde{x}}) k^\beta \partial _\beta {\tilde{\phi }}(J{\tilde{x}}) {\left| {HH,{\tilde{M}}}\right\rangle }\nonumber \\{} & {} \quad = \pm {\left\langle {HH,{\tilde{M}}}\right| }\partial _U {\tilde{\phi }}({\tilde{x}}) \partial _U {\tilde{\phi }}(J{\tilde{x}}) {\left| {HH,{\tilde{M}}}\right\rangle } . \end{aligned}$$

(2.10)

This result emphasizes the main idea. Unless the integral of the right-hand side disappears, it will be negative for some boundary conditions $(\pm )$. Backreaction will then make the wormhole traversable with that decision. It is thus only necessary to investigate this integral in certain circumstances, demonstrating that it is non-zero and quantifying the degree to which the wormhole becomes traversable. This has been calculated for several smooth, globally hyperbolic, ${\mathbb {Z}}_2$ quotients of $\mathrm BTZ$ and $BT Z \times S^1$ space-times [23,24,25]. The results have been subsequently utilized to demonstrate the ANEC violation.

3 BTZ black hole in 3+1 dimensions

A BTZ black hole is a space-time obtained by identifying points in AdS-space. The BTZ black hole could be reviewed as the quotient space $[AdS]/\textrm{G}_T$. $\textrm{G}_T$ is a group generated by $\Gamma$: $\textrm{G}_T=\{\Gamma ^n; n \epsilon {\mathbb {Z}}\}$, $\Gamma =e^{\alpha \xi }$ for some fixed $\alpha$, $\Gamma$ represents the discrete symmetry of AdS space and $\xi$ is the killing field. If $\xi$ is timelike in some regions of AdS-space then the point identified by $e^{\alpha \xi }$ results in the closed timelike curve (CTC). So, an observer avoids entering the region where $\xi$ is timelike. When $\xi$ is lightlike i.e., $\xi _\mu \xi ^\mu =0$ hypersurface is known as singularity and interpreted as the horizon.

Let’s start with defining $3+1$ AdS space as hyperboloid

$$\begin{aligned} -T_1^2-T_2^2+X_1^2+X_2^2+X_3^2 = -l^2 , \end{aligned}$$

(3.1)

embedded in the flat $5-$dimensional space with metric

$$\begin{aligned} ds^2=-dT_1^2-dT_2^2+dX_1^2+dX_2^2+dX_3^2 . \end{aligned}$$

(3.2)

This surface given by the above equation, in particular, has a Killing vector $\xi ^\alpha \partial _\alpha = \frac{r_+}{l}(T_1 \partial _{X_1}+ X_1 \partial _{T_1})$, which is a boost in the $(T_1, X_1)$ plane with a norm of $\xi ^2=r_+^2(T_1^2-X_1^2)$, where $r_+$ is an arbitrary real constant. From now without loss of generality, we can fix $l=1$. The Norm can be positive, negative, or zero. That defines the existence of a Black hole. Locating points along the orbits of $\xi ^\alpha$ is necessary to build a black hole. The orbits are timelike in the region $\xi ^2 < 0$. They will, however, be closed (i.e., they contain closed timelike coordinates) after the identification has been made. As a result, the region $\xi ^2 < 0$ is not physical in this sense and no longer physical and its boundary $\xi ^2 = 0$ is singular. As a result, three regions in spacetime are of interest: $I:= r_+< \xi ^2 < \infty$, $II:=0< \xi ^2 < r_+$ and $III:= -\infty < \xi ^2 \le 0$. The causal structure has been discussed in [30,31,32].

From [33], for non-rotating BTZ black hole is obtained by restricting to the region $T_1^2>X_1^2$ (i.e.,$\xi ^2>0)$, where the Killing vector is space-like, and quotienting by the discrete isometry group results in black hole solution. By introducing local coordinates of AdS space in the region $\xi ^2 > 0$ to write down the identification along the orbits of $\xi ^\alpha$ explicitly as

$$\begin{aligned} T_1= & {} \frac{ r}{r_+} \cosh \left( r_+ \phi \right) \nonumber \\ X_1= & {} \frac{ r}{r_+} \sinh \left( r_+ \phi \right) \nonumber \\ X_i= & {} \frac{2 y_i}{1-y^2} , \end{aligned}$$

(3.3)

with

$$\begin{aligned} r=r_+\frac{1+y^2}{1-y^2}, \quad y^2=-y_0^2+y_2^2+y_3^2 \end{aligned}$$

(3.4)

where $X_i's$ are $T_2$, $X_2$ and $X_3$ for $y_0$, $y_2$ and $y_3$ respectively. Here $-\infty< y_i <\infty$ and $-\infty< \phi <\infty$ with restriction $-1< y^2 <1$. The boundaries, i.e., $r \rightarrow \infty$, represent a hyperbolic “ball” $y^2=1$. The induced metric can be written as

$$\begin{aligned} ds^2 = \frac{(r^2+r_+^2)^2}{r_+^2} \left( -dy_0^2+dy_2^2 +dy_3^2 \right) + r^2 d\phi ^2 . \end{aligned}$$

(3.5)

The killing field is $\xi =\partial _\phi$ and $\xi ^2=r^2$. Quotient space can be identified by $\phi \equiv \phi + 2 n \pi$. The topology of space-time is ${\mathbb {R}}^3 \times S^1$.

By introducing the coordinates on hyperplane $\{y_0, y_2, y_3\}$ as

$$\begin{aligned} y_0= & {} f(r) \; \sinh \left( r_+t\right) \nonumber \\ y_2= & {} f(r) \; \cosh \left( r_+t\right) \; \cos \left( r_+\theta \right) \nonumber \\ y_2= & {} f(r) \; \cosh \left( r_+t\right) \; \sin \left( r_+\theta \right) , \end{aligned}$$

(3.6)

with $f(r)=\sqrt{\frac{r^2}{r_+^2}-1}$. Using this, the metric can be written as²

$$\begin{aligned} ds^2= & {} - \left( r^2-r_+^2\right) dt^2 + \frac{dr^2}{r^2-r_+^2}\nonumber \\{} & {} + \frac{r^2-r_+^2}{r_+^2} \cosh ^2\left( r_+ t\right) d \theta ^2+ r^2 d\phi ^2 . \end{aligned}$$

(3.7)

One can notice that the metric is non-static. The space-time has topology ${\mathbb {R}}^2 \times {\mathbb {T}}^2$. Thus it describes a growing toroidal black hole. By defining $u^2=r^2-r_+^2$ one can easily verify that throat lies at $u=0$. By calculating the Kretschmann scalar $K=R_{\alpha \beta \gamma \delta } R^{\alpha \beta \gamma \delta }$, there is a symmetry of both sides of the throat. At $u=0$ we have minimum area $4 \pi r_+^2$.

Using embedding in A we can find the metric in Kruskal like $(U,V,\theta , \phi )$ co-ordinate is

$$\begin{aligned} ds^2= & {} \frac{1 }{(1+UV)^2}\Bigg ( -4 dUdV + (U-V)^2 d \theta ^2 \nonumber \\{} & {} \quad + r_+^2(-1+UV)^2d\phi ^2 \Bigg ) . \end{aligned}$$

(3.8)

The further quotient of ${\mathbb {Z}}_2$ will give rise to an isometry J with identification $J: (U, V, \phi , \theta ) \rightarrow (V,U, \phi , \theta +\pi )$. Using the linearized equation at $V=0$, integrating over all U with appropriate AdS boundary conditions reduces to³

$$\begin{aligned} \int dU h_{UU} = \frac{32 \pi G_N }{5} \int dU T_{UU} . \end{aligned}$$

(3.9)

To find the shift $\Delta V$ at $U=\infty$ we have

$$\begin{aligned} \Delta V (+\infty )= & {} -\frac{32 \pi G_N }{5 g_{UV}(0)} \int _{-\infty }^{\infty } dU {\langle }{T_{kk}}{\rangle } \nonumber \\= & {} \frac{16 \pi G_N }{5 } \int _{-\infty }^{\infty } dU {\langle }{T_{kk}}{\rangle } . \end{aligned}$$

(3.10)

For the traversability of the wormhole, ANEC has to violate, i.e., $\Delta V < 0$.

4 The scalar field

From the above discussion, to examine the ANEC, we have to compute the expectation value of the stress-energy tensor. As the expectation value is evaluated in covering space ${\tilde{M}}$, but due to the property that it is the quotient of AdS$_4$ with identification $\phi \thicksim \phi +2n \pi$. From Eq. (2.10), using the two-point function, one can compute the expectation value of the stress-energy tensor. The scalar two-point function in arbitrary dimension d has been discussed in [34]. We will quickly summarise the aspects of their results that are relevant to our goal in this section.

The scalar two-point function can be written as

$$\begin{aligned} G(x, x') = {\left\langle {\psi }\right| }\phi (x)\phi (x'){\left| {\psi }\right\rangle } . \end{aligned}$$

(4.1)

Here the state $\psi$ is maximally symmetric, $G(x, x')$ solely depends on the geodesic distance $\mu (x, x')$ for spacelike separated points $x, x'$. Since $\mu (x, x')$ is the proper distance along a geodesic, the vectors $n_\alpha (x,x')=\nabla _{\alpha } \mu (x,x')$ and $n_{\alpha '}(x,x')=\nabla _{\alpha '} \mu (x,x')$ have unit length. Because they are pointing away from one another by the relation . The parallel propagator $g_{\alpha \beta '}(x, x' )$ along the geodesic joining x to $x'$ is unique for maximally symmetric spaces. It possesses the following properties:

(4.2)

(4.3)

(4.4)

The derivatives of $n_\alpha$ and $g_{\alpha \beta }$ may thus be represented in terms of our fundamental set:

$$\begin{aligned} \nabla _\alpha n_\beta= & {} A(\mu ) \left[ g_{\alpha \beta } (x) - n_\alpha (x, x') n_\beta (x, x') \right] \end{aligned}$$

(4.5)

$$\begin{aligned} \nabla _\alpha n_{\beta '}= & {} C(\mu ) \left[ g_{\alpha {\beta '}} (x, x') + n_\alpha (x, x') n_{\beta '}(x, x') \right] \end{aligned}$$

(4.6)

$$\begin{aligned} \nabla _\alpha g_{\beta \gamma '}= & {} -\left[ A(\mu ) + C(\mu )\right] \{ g_{\alpha \beta }(x) n_{\gamma '}(x, x')\nonumber \\{} & {} + g_{\alpha \gamma '} (x, x') n_\beta (x, x') \} . \end{aligned}$$

(4.7)

and the similar expression for the derivatives with respect to $\nabla _{\alpha '}$. The functions $A(\mu )$ and $C(\mu )$ are

$$\begin{aligned} A(\mu ) = \coth \left( \mu \right) \quad C(\mu ) = -\text {csch}\left( \mu \right) . \end{aligned}$$

(4.8)

By using $G' = \frac{dG}{d\mu }$, we obtain

$$\begin{aligned} \Box G(\mu )= & {} \nabla ^\alpha \nabla _\alpha G (\mu ) \nonumber \\= & {} \nabla ^\alpha (G'(\mu ) n_\alpha ) \quad \nonumber \\= & {} G''(\mu ) + 3 G'(\mu ) A(\mu ) . \end{aligned}$$

(4.9)

In the second line we have used $\nabla _\alpha \mu = n_\alpha$ and in last and $n^\alpha n_\alpha =1$. The equation of motion $(\Box -m^2)\phi (x)=0$ can be written as (if $x \ne x')$,

$$\begin{aligned} G''(\mu ) + 3 G'(\mu ) A(\mu ) -m^2 G=0 . \end{aligned}$$

(4.10)

By changing variables as

$$\begin{aligned} z= \text {Cosh}^2 \left( \frac{\mu }{2}\right) , \end{aligned}$$

(4.11)

then the Eq. (4.10) reduces to

$$\begin{aligned}{} & {} \left[ z(1-z) \frac{d^2}{dz^2}+\{c-(a_++a_-+1)\} \frac{d}{dz} - a_+a_-\right] \nonumber \\{} & {} \quad G(z) = 0 , \end{aligned}$$

(4.12)

with the parameters $2a_\pm = \left[ 3\pm \sqrt{9 + 4 m^2 }\right]$ and $c=2$. The two-point function G(z) as the solution of (4.12) in terms of hypergeometric functions can be written as

$$\begin{aligned} G(z) = p z^{-a_+} F(a_+, a_+-c+1; a_+-a_-+1; z^{-1}), \nonumber \\ \end{aligned}$$

(4.13)

with normalization constant p is given by

$$\begin{aligned} p = \frac{\Gamma (a_+) \Gamma (a_+-c+1)}{16 \pi ^2 \Gamma (a_+-a_-+1)} . \end{aligned}$$

(4.14)

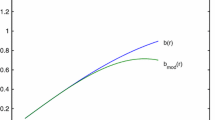
In the case of AdS$_3$, the hypergeometric function is summed up to an exact analytic expression. But in the case of AdS$_4$, we don’t have the exact analytic form (Figs. 1, 2). In the terms of the conformal weight $\Delta =\sqrt{9+4 m^2 }$, the above parameters reduces to $2a_\pm = 3 \pm \Delta$ and $c=2$.

A standard calculation using the embedding in Eq. (A.5) the geodesics distance is

$$\begin{aligned} \mu= & {} \frac{1}{(1+UV)(1+U'V')} \\{} & {} \times \Bigg [ (U+V)(U'+V')- (U-V)\\{} & {} \times (U'-V') \; \cos \; \left( r_+(\theta -\theta ')\right) \\{} & {} + (-1+U'V')(-1+UV)\; \cosh \; \left( r_+(\phi -\phi ')\right) \Bigg ]. \end{aligned}$$

By defining ${\mathcal {C}}=\cos \left( r_+[\theta -\theta ']\right)$ and ${\mathcal {K}}=\cosh \left( r_+[\phi -\phi ']\right)$ the above expression can be written as

$$\begin{aligned} \mu= & {} \frac{1}{(1+UV)(1+U'V')} \\{} & {} \times \Bigg [ (U+V)(U'+V')- (U-V)(U'-V'){\mathcal {C}} \\{} & {} + (-1+U'V')(-1+UV){\mathcal {K}} \Bigg ] . \end{aligned}$$

Working on the horizon $V=0$, we define

$$\begin{aligned} f({\mathcal {K}},U,{\mathcal {C}},\Delta ) = \langle 0 |\partial _U \phi (x) \partial _U \phi (x') |0\rangle , \end{aligned}$$

(4.15)

with $x=(U, V, \theta , \phi )$ and $x'=(U', V', \theta ', \phi ')$ points in AdS$_4$

4.1 Calculations of stress energy tensor

As we claimed above, we don’t have a closed form for the two-point function in the case of AdS$_4$. We will compute a two-point function for different values of $m^2$. From Eq. (4.13) for different values of $m^2$ we will have two point function. For $(m^2=0)$

$$\begin{aligned} G(z)= & {} \frac{\Gamma (3) \Gamma (2)}{\Gamma (4) 16 \pi ^2} z^{-3} F\left( 3, 2, 4, \frac{1}{z} \right) = \frac{1}{16 \pi ^2 z(z-1)}\nonumber \\{} & {} \quad \left[ -1+2z+(2z^2-2z)\text {log}\left( \frac{z-1}{z}\right) \right] . \end{aligned}$$

(4.16)

Fig. 1

Some of the functions Left: ${\mathcal {K}}=1, {\mathcal {C}}=0$, for $\Delta =3$ (red), $\Delta =5$ (yellow), $\Delta =7$ (green). Right: ${\mathcal {K}}=1, {\mathcal {C}}=0$, for $\Delta =3$ (red), $\Delta =5$ (yellow), $\Delta =7$ (green)

Fig. 2

Some of the functions Left: ${\mathcal {K}}=1.5, {\mathcal {C}}=0$, for $\Delta =3$ (red), $\Delta =5$ (yellow), $\Delta =7$ (green). Right: ${\mathcal {K}}=1.5, {\mathcal {C}}=0$, for $\Delta =3$ (red), $\Delta =5$ (yellow), $\Delta =7$ (green)

The graphs are identical as [23] for BTZ in the $2+1$ case. Now computation of f for $m^2=0$ we have

$$\begin{aligned}{} & {} f({\mathcal {C}},U,{\mathcal {K}}) \\{} & {} \quad = \frac{(1+{\mathcal {C}})\left[ {\mathcal {K}}-{\mathcal {K}}^2l^2+(1+{\mathcal {C}})(-1+2{\mathcal {K}}l^2)U^2+3(1+{\mathcal {C}})^2l^2U^4\right] }{16 l^2 \pi ^2\left( {\mathcal {K}}+(1+{\mathcal {C}})U^2\right) ^3 \left( -1+l^2({\mathcal {K}}+(1+{\mathcal {C}})U^2\right) ^3} . \end{aligned}$$

By fixing ${\mathcal {C}}=1$ the above expression reduces to

$$\begin{aligned} f(U,{\mathcal {K}}) = \frac{{\mathcal {K}}-{\mathcal {K}}^2+(-1+2{\mathcal {K}})U^2+3U^4}{16 \pi ^2 (-1+{\mathcal {K}}+U^2)^3({\mathcal {K}}+U^2)^3} . \end{aligned}$$

By integrating the above equation, i.e.,

$$\begin{aligned}{} & {} \int _0^\infty f(U,{\mathcal {K}}) dU \nonumber \\{} & {} \quad = - \frac{\sqrt{1-{\mathcal {K}}}+3{\mathcal {K}}\sqrt{1-{\mathcal {K}}}-4{\mathcal {K}}^2\sqrt{1-{\mathcal {K}}}}{128 \pi ({\mathcal {K}}(1-{\mathcal {K}})){3/2}} < 0 .\nonumber \\ \end{aligned}$$

(4.17)

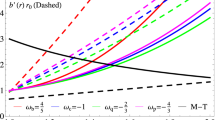
This shows the violation of ANEC. By plotting $\int _{0}^{\infty } f({\mathcal {K}}, U, {\mathcal {C}}, \Delta )$ for fixed value of ${\mathcal {C}}$ (e.g 0, 1) with respect to ${\mathcal {K}}$ one can also verify the same (Fig. 3).

Fig. 3

Left: $\int _{0}^{\infty } f({\mathcal {K}}, U, {\mathcal {C}}, \Delta )$ for $\Delta =3$ (red), $\Delta =5$ (yellow), $\Delta =7$ (green). Right: $\int _{0}^{\infty } f({\mathcal {K}}, U, {\mathcal {C}}, \Delta )$ for $\Delta =3$ (red), $\Delta =5$ (yellow), $\Delta =7$ (green)

5 Results and discussion

In this paper, we posed the issue of wormhole traversability in a quotient of the space-time obtained from quotients of $AdS_4$ space with specific ${\mathbb {Z}}_2$ symmetry in the presence of scalar fields. Back-reaction from quantum scalar fields in Hartle–Hawking states is explored on simple explicit examples of ${\mathbb {Z}}_2$ wormholes asymptotic to $\mathrm AdS_4$. These examples are often traversable when the scalar satisfies periodic boundary condition (chosen from Eq. (2.7)) around the ${\mathbb {Z}}_2$ cycle. In $AdS_4$, we found the expression for the scalar fields’ two-point function. We calculated the average null energy using this and discovered that it becomes negative when the periodic boundary conditions on the scalar fields are chosen. The wormholes can then be traversable due to the back reaction on the geometry. It’s also interesting extrapolating this to investigate wormhole traversability in the context of higher spin fields. Recent research has revealed that Euclidean wormholes serve an important role in providing a new viewpoint on the information loss paradox. It would be fascinating to see if the problem of traversability in Lorentzian wormholes like the ones investigated in this paper sheds any light on this topic. For static space-time, Hartle–Hawking Vacua has been discussed in [35]. We’re using Hartle–Hawking vacua to calculate expectation values, but their forms aren’t essential. It would be fascinating to learn the form of the Hartle–Hawking state for non-static space times, particularly for the above metric.

Appendices

Appendices

Appendix A: Co-ordinate choice and their Kruskal extension

The choice of co-ordinate is

$$\begin{aligned} T_1= & {} \frac{r }{r_+} \cosh \left( r_+ \phi \right) \nonumber \\ T_2= & {} f(r) \sinh \left( r_+ t \right) \nonumber \\ X_1= & {} \frac{r }{r_+} \sinh \left( r_+ \phi \right) \nonumber \\ X_2= & {} f(r) \cosh \left( r_+ t \right) \; \cos \left( r_+ \theta \right) \nonumber \\ X_3= & {} f(r) \cosh \left( r_+ t \right) \; \sin \left( r_+ \theta \right) . \end{aligned}$$

(A.1)

Again by using Eq. (3.1) one can find $f(r)= \sqrt{\frac{r^2}{r_+^2}-1}$. For the Kruskal extension, one can start with

$$\begin{aligned} ds^2= & {} -\left( r^2-r_+^2 \right) dt^2 + \frac{dr^2}{r^2-r_+^2} \nonumber \\= & {} \left( r^2-r_+^2\right) \left[ -dt^2+dr_*^2\right] . \end{aligned}$$

(A.2)

One can find $r_* = \frac{1}{2r_+}\text {ln} \frac{|r-r_+|}{r+r_+}$. Lets define the co-ordinate $u=t-r_*$ and $v=t+r_*$ then the metric (A.2) can be written as

$$\begin{aligned} ds^2 = \left( r^2-r_+^2\right) \left[ -du dv \right] . \end{aligned}$$

(A.3)

As we have $t=\frac{u+v}{2}$ and $r_*=\frac{v-u}{2}$ then

$$\begin{aligned} r^2-r_+^2= & {} \left( r+r_+\right) ^2 \; e^{r_+(v-u)} . \end{aligned}$$

(A.4)

Let’s define again $U=-e^{-r_+u}$ and $V=e^{r_+ v}$, using this $t=- \frac{1}{2r_+} \text {ln} \left( - \frac{U}{V}\right)$ and $r=r_+ \frac{1-UV}{1+UV}$, and finally our co-ordinate becomes

$$\begin{aligned} T_1= & {} \frac{1-UV}{1+UV} \cosh \; \left( r_+ \phi \right) \nonumber \\ T_2= & {} \frac{V+U}{1+UV} \nonumber \\ X_1= & {} \frac{1-UV}{1+UV} \sinh \; \left( r_+ \phi \right) \nonumber \\ X_2= & {} \frac{V-U}{1+UV} \cos \; \left( r_+ \theta \right) \nonumber \\ X_3= & {} \frac{V-U}{1+UV} \sin \; \left( r_+ \theta \right) . \end{aligned}$$

(A.5)

By using the formula

$$\begin{aligned}{} & {} \mu (U,V,\phi ,\theta ,U',V',\phi ',\theta ') = T_1 T_1' + T_2 T_2' - X_1 X_1'\nonumber \\ {}{} & {} \quad - X_2 X_2' - X_3 X_3' , \end{aligned}$$

(A.6)

one can get the form of geodesics distance same as (2.2).

Appendix B: Linearized equation

In this section, we derive the Linearized Einstein in both cases e.g., AdS$_3$ and AdS$_4$ case.

1.1 B.1 AdS$_3$ case

The Einstein equation in the $\mathrm AdS_3$ case can be written as

$$\begin{aligned} R_{\alpha \beta } - \frac{1}{2}g_{\alpha \beta }\left( R+\frac{2}{l^2} \right) = 8 \pi G_N T_{\alpha \beta } . \end{aligned}$$

(B.1)

With the small perturbation in the metric i.e., $g_{\alpha \beta }=g_{\alpha \beta }+\delta g_{\alpha \beta }=g_{\alpha \beta }+\epsilon h_{\alpha \beta } + {\mathcal {O}}(\epsilon ^2)$. We are perturbing the metric in Kruskal co-ordinate. By putting this in Einstein’s equation and putting $V=0$ as we are working on $V=0$ horizon. Only taking the terms independent of $\frac{1}{U}$ as we are interested in $U \rightarrow \pm \infty$

$$\begin{aligned}{} & {} \frac{1}{2l^2} \left[ 2 h_{UU}+U \partial _U h_{UU} - \frac{1}{2r_+^2} \partial _U ^2 h_{\phi \phi }\right] = 8 \pi G_N T_{UU} \nonumber \\{} & {} \frac{1}{2l^2} \left[ 2 h_{UU}+ \partial _U (U h_{UU}) - h_{UU} - \frac{1}{2r_+^2} \partial _U ^2 h_{\phi \phi }\right] \nonumber \\{} & {} \quad = 8 \pi G_N T_{UU} \nonumber \\{} & {} \frac{1}{2l^2} \left[ h_{UU}+ \partial _U (U h_{UU}) - \frac{1}{2r^2} \partial _U ^2 h_{\phi \phi }\right] = 8 \pi G_N T_{UU} .\nonumber \\ \end{aligned}$$

(B.2)

By integrating overall U and dropping the boundary terms as the requirements of boundary stress tensor be unchanged at this order. Finally, we have

$$\begin{aligned} \int dU h_{UU} = 16\pi G_N l^2 \int dU T_{UU}. \end{aligned}$$

(B.3)

1.2 B.2 AdS$_4$ case

The Einstein equation in the $\mathrm AdS_4$

$$\begin{aligned} R_{\alpha \beta } - \frac{1}{2}g_{\alpha \beta }\left( R+\frac{6}{l^2} \right) = 8 \pi G_N T_{\alpha \beta } . \end{aligned}$$

(B.4)

Again perturbing the metric and taking the limits as above it is easy to verify that we have

$$\begin{aligned}{} & {} \frac{1}{2l^2}\left[ 4 h_{UU}+ \frac{3}{2} U\partial _U h_{UU} - \frac{1}{2r_+^2} \partial _U ^2 h_{\phi \phi }\right] = 8 \pi G_N T_{UU} \nonumber \\{} & {} \frac{1}{2l^2}\left[ 4 h_{UU}+ \frac{3}{2} \left\{ \partial _U (U h_{UU})-h_{UU} \right\} - \frac{1}{2r_+^2} \partial _U ^2 h_{\phi \phi }\right] \nonumber \\{} & {} \quad = 8 \pi G_N T_{UU} \nonumber \\{} & {} \frac{1}{2l^2} \left[ \frac{5}{2} h_{UU}+ \frac{3}{2}\partial _U (U h_{UU}) - \frac{1}{2r^2} \partial _U ^2 h_{\phi \phi }\right] \nonumber \\{} & {} \quad = 8 \pi G_N T_{UU} . \end{aligned}$$

(B.5)

By integrating overall U and dropping the boundary terms as the requirements of boundary stress tensor be unchanged at this order. Finally, we have

$$\begin{aligned} \int dU h_{UU} = \frac{32 \pi G_N l^2}{5} \int dU T_{UU} \end{aligned}$$

(B.6)

This is the same as Eq. (3.9).