1 Introduction

Classical gravitational theory enables us to predict the evolution of the universe by specifying physically reasonable initial data on a spacelike hypersurface, also known as a Cauchy hypersurface. However, the predictability of gravitational theory is lost when the Cauchy horizon appears. Events beyond the Cauchy horizon cannot be uniquely predicted by the evolution of the initial data. The presence of parameters other than mass of black holes, such as electric charge for the Reissner–Nordström black hole or rotation for the Kerr black hole, always leads to the appearance of a Cauchy horizon [1, 2]. To address this issue, Roger Penrose proposed the Strong Cosmic Censorship (SCC) Conjecture, which aims to restore the predictability of Einstein’s equations [3]. The SCC demands that the spacetime is globally hyperbolic. For an asymptotically flat spacetime, the Cauchy horizon has a blueshift instability that causes disturbances to propagate towards it, ultimately making it singular [4,5,6,7].

However, recent research has raised questions about the validity of the SCC in the context of asymptotic de Sitter spacetime, where the cosmological constant \(\Lambda \) is included. Specifically, the inclusion of the cosmological constant changes the perturbation attenuation of \(\Lambda > 0\) from power law to exponential, altering the relationship between the exponential blueshift at the Cauchy horizon and the power-law decay of perturbations at late times [8]. Many researchers have demonstrated the dynamical behaviors of perturbation fields with different spins (i.e., scalar, electromagnetic, and gravitational perturbations) in the presence of a positive cosmological constant [9,10,11,12,13,14]. The faster exponential decay of the quasinormal mode (QNM) of perturbation outside the event horizon results in the redshift effect suppressing the corresponding blueshift effect [9,10,11], which implies that the disturbance may decay fast enough to violate the SCC. This violation was observed in a massless neutral scalar field in the Reissner–Nordström–de-Sitter (RNdS) black hole in the nearly extremal region at the linear perturbation level [15]. Subsequently, various violations of the SCC have been discovered on the RNdS background by different types of perturbations, such as the massless charged scalar field, the massless Dirac field, gravitational perturbations, and non-minimally coupled scalar field, among others [16,17,18,19,20,21,22,23,24,25]. Furthermore, the validity of the SCC has also been investigated in various black hole geometries [26,27,28,29,30,31,32,33], and the influence of initial data, nonlinear effects, and quantum effects have been studied in Refs. [34,35,36]. Overall, these findings challenge the long-standing assumption of the SCC and suggest the need for further investigation.

The standard model of cosmology suggests that our universe is composed of dark matter (DM), dark energy, and baryonic matter. The existence of dark matter and dark energy has been demonstrated by a number of experiments and observations [41]. Studying DM is crucial for testing some basic assumptions of the standard model of cosmology and for better understanding the evolution and structure of the universe. Because DM influences different aspects of the singularity, from the characteristics of the horizon to the energetic properties of the surrounding matter, various evaluations of DM effects and parameter constraints on models describing the presence of DM around black holes have been proposed. The influence of dark matter and the surrounding environment of black holes on various aspects of spacetime has been investigated in several studies [37,38,39,40, 42]. Recent research has focused on studying the superradiative instability and accretion phenomena of DM clouds of axions around black holes, which can be manifested in gravitational wave signals induced by a small dense object in the black hole central field [43,44,45]. Perfect fluid dark matter (PFDM) is considered one of the candidates for DM [46, 47]. Astrophysical observations indicate the existence of a supermassive black hole surrounded by a dark matter halo [48], and many spherically symmetric black hole solutions surrounded by PFDM have been obtained [47, 49,50,51]. However, many important aspects of such black holes have not been thoroughly studied, including their potential impact on the SCC.

Fig. 1
figure 1

The parameter regions with three horizons for \(\Lambda M^2=0.03\), \(\Lambda M^2=0.06\) and \(\Lambda M^2=0.09\) are showed by the shaded part in \(b/M-Q/M\) diagram. The red dashed line presents the extremal black hole solutions and the red dotted line shows the Nariai black hole solutions

Full size image

This paper aims to investigate the effects of dark matter on SCC. Specifically, we focus on a charged de-Sitter spacetime surrounded by DM. The paper is organized as follows: in Sect. 2, we present the geometry of black holes in perfect fluid dark matter. In Sect. 3, we analyze the field equation of the massless scalar field in the black hole geometry and provide a commentary on the status of the SCC analytically. In Sect. 4, we use a detailed numerical method to evaluate the QNM frequency and study the regions where the SCC may be violated. Finally, we conclude with a discussion of the results obtained in this study.

2 Black hole in perfect fluid dark matter

In this paper, we investigate a charged black hole surrounded by perfect fluid dark matter and study the SCC in this context. The corresponding action is given by

$$\begin{aligned} S=\frac{1}{16\pi }\int d^4 x\sqrt{-g}\left[ R-2\Lambda -F_{ab}F^{ab}+\mathcal {L}_{\text {DM}}\right] , \end{aligned}$$
(1)

where R is the Ricci scalar, \(\Lambda \) is the positive cosmological constant, \(F_{ab}=\nabla _a A_b-\nabla _b A_a\) is the electromagnetic tensor and \(\mathcal {L}_{\text {DM}}\) gives the Lagrangian density of PFDM. The field equations,

$$\begin{aligned} G_{ab}+\Lambda g_{ab}=T_{ab}^{\text {DM}}+T_{ab}^{\text {EM}},\quad \nabla _a F^{ab}=0 \end{aligned}$$
(2)

are obtained by varying the action, where \(G_{ab}=R_{ab}-(1/2)R g_{ab}\) is the Einstein tensor, \(T^{\text {DM}}_{ab}\) and

$$\begin{aligned} T_{ab}^{\text {EM}}=2F_a{}^{c}F_{bc}-\frac{1}{2}F_{cd}F^{cd}g_{ab} \end{aligned}$$
(3)

are the stress–energy–momentum tensors of the PFDM and electromagnetic field, respectively.

As is considered in the previous papers, we would like to consider a charged and static solution with spherical symmetry. Using the field equations, the line element of this spacetime and the vector potential of the electromagnetic field are given by [50,51,52]

$$\begin{aligned} ds^2= & {} -f(r)dt^2+\frac{1}{f(r)}dr^2+r^2 d\Omega ^2,\nonumber \\ A_a= & {} -\frac{Q}{r}(dt)_a \end{aligned}$$
(4)

with the blackening factor

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{Q^2}{r^2}+\frac{b}{r}\text { ln} \left( \frac{r}{|b|}\right) -\frac{\Lambda r^2}{3}. \end{aligned}$$
(5)

The stress energy–momentum tenor of the perfect fluid dark matter distribution is given by

$$\begin{aligned} T^{\mu }_{\nu }=\text { diag} (\rho , -p_r, -p_\theta , -p_\phi ) \end{aligned}$$
(6)

with

$$\begin{aligned} \rho =-p_r=\frac{b}{r^3},\quad p_\theta =p_\phi =\frac{b}{2r^3}, \end{aligned}$$
(7)

where \(\rho \) is the energy density of the dark matter and b is a parameter related to the PFDM density and pressure. We impose the weak energy condition, i.e., the energy density of dark matter must be positive \(\rho \ge 0\), which implies \(b \ge 0\). Here, M and Q represent the mass and electric charge of the black hole, respectively.

Next, we investigate a charged black hole surrounded by dark matter with cauchy horizon, event horizon, and cosmological horizon. The radius of each horizon is denoted by \(r_-\), \(r_+\), and \(r_c\) respectively, and they satisfy \(r_-<r_+<r_c\) and \(f(r_i)=0\) with \(i\in {-,+,c}\). We define the surface gravity of each horizon as

$$\begin{aligned} \kappa _i=\frac{1}{2}|f'(r_i)| \end{aligned}$$
(8)

with \(i\in \{-,+,c\}\). In Fig. 1, we present the parameter region of such solutions in \(b/M-Q/M\) diagram for different values of \(\Lambda M^2\) and show that the allowed parameter region of the solution with three horizons is bounded by the extremal solutions with \(r_+=r_-\) and Nariai solutions with \(r_+=r_c\). We also find that there exists a maximal value of b/M, and the allowed region in \(b/M-Q/M\) diagram gets larger as the reduced cosmological constant increases.

3 Quasinormal modes and strong cosmic censorship

Now, we consider a minimally coupled massless scalar field perturbation in the above background. The equation of the motion is given by the Klein–Gordon equation,

$$\begin{aligned} \nabla _a\nabla ^a\Psi = 0. \end{aligned}$$
(9)

After considering the scalar field, the Einstein equation can be written as:

$$\begin{aligned} G_{ab} + \Lambda g_{ab} = T_{ab} \end{aligned}$$
(10)

where the total stress–energy–momentum tensor \(T_{ab}\) is composed of contributions from the scalar field, electromagnetic field, and dark matter, i.e.,

$$\begin{aligned} T_{ab} = T_{ab}^{\text {SC}} + T_{ab}^\text {EM}+T_{ab}^{\text {DM}}. \end{aligned}$$
(11)

The stress–energy–momentum tensor \(T^{\text {SC}}_{ab}\) of the scalar field is given by

$$\begin{aligned} T^{\text {SC}}_{ab} = 2 \nabla _a \Psi \nabla _b \Psi - g_{ab} \nabla _c\Psi \nabla ^c\Psi . \end{aligned}$$
(12)

Considering the symmetries of the spacetime, we can expand the scalar field as

$$\begin{aligned} \Psi (t,r,\theta ,\phi )=\sum _{l,m}e^{-i \omega t}Y_{lm}(\theta ,\phi )\frac{\psi (r)}{r} \end{aligned}$$
(13)

with the spherical harmonics \(Y_{lm}(\theta ,\phi )\). Using this expansion, the field equation of the scalar perturbation can be expressed as

$$\begin{aligned} \frac{d^2 \psi (r)}{d r_*^2}+[\omega ^2-V(r)] \psi (r)=0 \end{aligned}$$
(14)

with

$$\begin{aligned} V(r)=\frac{f(r)}{r^2}\left[ l(l+1)+r f'(r)\right] . \end{aligned}$$
(15)

Here we used the tortoise coordinate defined by

$$\begin{aligned} d r_*=\frac{dr}{f(r)}. \end{aligned}$$
(16)

If we consider the physical region between \(r_+\) and \(r_c\), we have

$$\begin{aligned} r_*=\int _{r_0}^r\frac{d r}{f(r)} \end{aligned}$$
(17)

with \(r_+<r_0<r_c\). This means that \(r_* \rightarrow \pm \infty \) when \(r\rightarrow r_{c,+}\). With some physical considerations [56], we need to impose the boundary conditions such that there is only ingoing wave near the event horizon \(r_+\) \((r_*\rightarrow -\infty )\) and only outgoing wave near the cosmological horizon \(r_c\) \((r_*\rightarrow \infty )\), i.e., we have

$$\begin{aligned}{} & {} \psi \sim e^{-i\omega r_{*}},\quad r\rightarrow r_+,\nonumber \\{} & {} \psi \sim e^{i\omega r_{*}},\quad \,\,\,\, r\rightarrow r_c. \end{aligned}$$
(18)

Then, the QNM frequencies can be evaluated by solving the field equation (14) with the above boundary conditions.

We can make sense of Eq. (10) even when \(\Psi \) and \(g_{\mu \nu }\) are not twice continuously differentiable, by multiplying both sides with a smooth, compactly supported, test function \(\Phi \) and integrating over a small neighborhood \({\mathcal {V}}\subset {\mathcal {M}}\). If the outcome of the integral is bounded, we obtain a weak solution to the field equation (10). Thus, for a weak solution at the Cauchy horizon, we require finiteness of [15, 24, 25, 31]

$$\begin{aligned} \int _{\mathcal {V}}d^4x\sqrt{-g}(G_{\mu \nu }+\Lambda g_{\mu \nu }-8\pi T_{\mu \nu })\Phi =0. \end{aligned}$$
(19)

The terms in (19) consist of the usual first two terms, which lead to the requirement of square integrability of the Christoffel symbols [24]. This is expressed as:

$$\begin{aligned}{} & {} \int _{\mathcal {V}}d^4x\sqrt{-g}(G_{\mu \nu }+\Lambda g_{\mu \nu })\Phi \sim \int _{\mathcal {V}}d^4x\sqrt{-g}(\partial \Phi )\Gamma \nonumber \\{} & {} \quad +\int _{\mathcal {V}}d^4x\sqrt{-g} \Gamma ^2\Phi +\Lambda \int _{\mathcal {V}}d^4x\sqrt{-g} g_{\mu \nu }\Phi , \end{aligned}$$
(20)

where \(G_{\mu \nu }\sim \Gamma ^2+\partial \Gamma \) and \(\Gamma \) represents the Christoffel symbols, and we have suppressed most of the indices for brevity. Therefore, to ensure that (20) is bounded, we require \(\Gamma \in L^2_{\text {loc}}\), where \(L^2_{\text {loc}}\) is the space of locally square integrable functions in \({\mathcal {V}}\).

Table 1 The lowest-lying QNMs \(\beta =-{\text {Im}(\omega )}/{\kappa _-}\) with different l calculated by different numerical methods for \(\Lambda M^2 = 0.06, b/M = 1\) and \(Q/Q_{\text {ext}} = 0.99\)
Full size table
Table 2 The lowest-lying QNMs \(\beta =-{\text {Im}(\omega )}/{\kappa _-}\) with different l calculated by different numerical methods for \(\Lambda M^2 = 0.06, b/M = 1\) and \(Q/Q_{\text {ext}} = 0.999\)
Full size table

The contribution from the stress energy–momentum tensor of the scalar field, \(T^{\text {SC}}_{\mu \nu }\), is given by:

$$\begin{aligned} \int _{\mathcal {V}} d^4x\sqrt{-g}T^{\text {SC}}_{\mu \nu }\Phi \sim \int _{\mathcal {V}}d^4x\sqrt{-g} (\partial \Psi )^2\Phi . \end{aligned}$$
(21)

Thus, the requirement for a weak solution is that the scalar field \(\Psi \) is locally square integrable derivative, i.e., \(\Psi \in H^1_{\text {loc}}\), where \(H^p_{\text {loc}}\) is the Sobolev space of functions in \(L^2_{\text {loc}}\) whose derivatives up to order p in a weak sense are also in \(L^2_{\text {loc}}\).

The electrostatic potential \(A_{\mu }=-\delta ^0_{~\mu } Q/r\) with the electric charge Q of the black holes, and the stress energy–momentum tensor \(T_{\mu \nu }^{\text {DM}}=\text {diag} (\rho , -p_r, -p_\theta , -p_\phi )\) of the perfect fluid dark matter distribution with Eq. (7), are both regular at the Cauchy horizon. Thus, both of them do not impose any additional requirements for regularity [24].

The asymptotic solution near the Cauchy horizon from the field equation (9) is given by

$$\begin{aligned} \Psi \sim A_1 e^{-i\omega (t-r_{*})}+A_2e^{-i\omega (t+r_{*})}. \end{aligned}$$
(22)

The only part that matters for the regularity requirements, as discussed in Refs. [24, 25], is

$$\begin{aligned} \Psi \sim e^{i\frac{\omega }{\kappa _-}\ln |r-r_-|}\propto |r-r_-|^\beta \end{aligned}$$
(23)

with

$$\begin{aligned} \beta \equiv -\frac{\text {Im} (\omega )}{\kappa _-}. \end{aligned}$$
(24)

The weak solution can be extended beyond the Cauchy horizon if the scalar field is locally square integrable derivative (i.e., \(\Psi \in H^1_{\text {loc}}\)), which requires

$$\begin{aligned} \beta \ge 1/2, \end{aligned}$$
(25)

which means that the weak solution can be extended beyond the Cauchy horizon. That is to say, as long as there exits one quasinormal mode with \(\beta < 1/2\), the Cauchy horizon will become unextendable and thus the SCC is respected. Therefore, to check the validity of the SCC, we can only focus on the lowest-lying quasinormal mode.

Fig. 2
figure 2

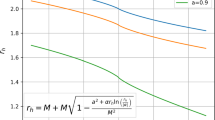
For a given value of l, the lowest-lying QNMs \(\beta =-{\text {Im}(\omega )}/{\kappa _-}\) are plotted as a function of the black hole charge ratio \(Q/Q_{\text {ext}}\) for different b/M, when \(\Lambda M^2 = 0.06\). The horizontal dashed line represents \(\beta =1/2\), which shows the critical value of the charge ratio of the SCC

Full size image

4 Numerical methods and results

In this section, we will utilize two numerical methods to accurately calculate the QNM frequency and present the corresponding results.

Numerous numerical methods have been developed for calculating QNM frequencies with high precision [53,54,55,56]. In this study, we will employ the pseudospectral method [57, 58] to evaluate the QNM frequencies and validate our results using the direct integration method [59, 60]. Additionally, we will utilize the WKB approximation [61] to obtain the photo-sphere modes, which correspond to the QNMs in the large-l limit.

Based on the boundary conditions in Eq. (18), we observe that the scalar field \(\psi (r)\) oscillates significantly near the two horizons, i.e.,

$$\begin{aligned} \psi (r)\propto & {} \left( r/r_+-1\right) ^{\frac{i \omega }{2\kappa _+}},\quad \quad \, r\rightarrow r_+,\nonumber \\ \psi (r)\propto & {} \left( 1-r/r_c\right) ^{-\frac{i\omega }{2\kappa _c}},\quad \quad r\rightarrow r_c, \end{aligned}$$
(26)

To apply the pseudospectral method to the field equation in Eq. (14), we introduce a new variable y(r) as

$$\begin{aligned} \psi (r)=\left( x+1\right) ^{\frac{i \omega }{2\kappa _+}}\left( x-1\right) ^{-\frac{i\omega }{2\kappa _c}}y(x). \end{aligned}$$
(27)

with

$$\begin{aligned} r=\frac{r_c-r_+}{2}x+\frac{r_c+r_+}{2}, \end{aligned}$$
(28)

which transforms the field equation into a regular form in the interval \([-1,1]\). With the above setup, the field equation (14) reduces to

$$\begin{aligned} a_0(\omega ,x)y(x)+a_1(\omega ,x)y'(x)+a_2(\omega ,x)y''(x)=0. \end{aligned}$$
(29)

After expanding the field equation and variable y(x) by the cardinal function \(C_i(x)\) satisfied \(C_i(x_j)=\delta _{ij}\), Eq. (29) can be transformed into a matrix equation \((M_0+\omega M_1) Y=0\) (see details in Refs. [57, 58]). Then, the QNM frequency can be obtained by solving the eigenvalue of the matrix \((-M_1^{-1}M_0)\).

As a demonstration, we present some relevant results in Tables 1 and 2, which includes the QNM frequencies obtained from the direct integration method in the lower lines. To calculate these frequencies, we utilized the field equation (29). For a given \(\omega \), we used the series expansion of y(x) at \(x=\pm 1\) as the boundary condition of y(x) near \(x=\pm 1\) and solved Eq. (29) in the interval \((-1, 0]\) and [0, 1) individually using Mathematica. To ensure that the two solutions are smooth at \(x=0\), we can obtain the acceptable frequency \(\omega \).

We have calculated the lowest-lying QNMs \(\beta = -\text {Im} (\omega )/\kappa _-\) for different l and various black hole parameters using both the pseudospectral method and direct integration method, as shown in Tables 1 and 2. These results demonstrate the reliability of our numerical calculations. Additionally, we have used the WKB approximation to evaluate the large-l lowest-lying modes, and our results are consistent with other methods. Thus, the lowest-lying modes for large l are calculated by the WKB approximation in our paper. The numerical results reveal that the frequency of the lowest-lying modes is always small, and consequently, the lowest-lying \(\beta \) is always less than 1/2 when the black hole is far from extremal. This implies that the SCC can only be violated when the black hole is close to extremal.

To study the effects of DM on the SCC, we generated a plot of the lowest-lying modes \(\beta \) as a function of the black hole charge ratio, as shown in Fig. 2. With \(\Lambda M^2\) fixed at 0.06 and b/M varying, we observed that the SCC is only violated when the charge ratio surpasses a certain critical value, as expected. This critical value can be determined by identifying the point of intersection between the curve of \(\beta =1/2\) and the curve of all lowest-lying modes encompassing every conceivable value of l. We can easily observe from these figures that the lowest-lying modes in the \(Q/Q_{\text {ext}}-\beta \) diagram are primarily governed by the mode with \(l=0\) and the mode with large l when b/M is very small or equal to zero (as in the case of \(b/M=0\)), i.e., the lowest-lying modes for non-nearly extremal black holes are given by the modes with large l, while for nearly extremal solutions, the lowest-lying mode is determined by the mode with \(l=0\). However, as b/M increases, the lowest-lying modes in the \(Q/Q_{\text {ext}}-\beta \) diagram transition to being determined by the modes with \(l=0\) and \(l=1\) (as in the case of \(b/M=3\)), before eventually returning to being determined by the mode with \(l=0\) and the mode with large l (as in the cases of \(b/M=6,9,10,11\)). Furthermore, the results for the case of \(\Lambda M^2 =0.06\) indicate that the presence of dark matter can reduce the violation interval of SCC compared to RNdS, thereby mitigating the failure of SCC in these scenarios. In other words, it indicates that dark matter can alleviate the problem of SCC violation at a certain level. However, it should be noted that for black holes approaching extremality, i.e., when the surface gravity of the Cauchy horizon tends to zero, a violation of the SCC will always occur regardless of the value of b/M, since the lowest-lying modes always tend to 1 in the extremal limit. Additionally, it is worth noting that the \(l=0\) family always satisfies \(\beta < 1\), preventing a non-weak violation of the SCC, where \(T^{\text {SC}}_{\mu \nu }\propto |r-r_-|^{2(\beta -1)}\) would be singular on the Cauchy horizon.

Fig. 3
figure 3

The red shaded region in the \(b/M-Q/Q_{\text {ext}}\) diagram represents the violation region of the SCC for \(\Lambda M^2=0.03\), \(\Lambda M^2=0.06\), and \(\Lambda M^2=0.09\). The red line indicates the critical value of the charge ratio of the SCC, while the blue dashed line represents the extremal black hole solutions. Additionally, the blue dotted line shows the Nariai black hole solutions

Full size image

Finally, to investigate the impact of the equation of state parameter b/M on the validity of the SCC, we plot the violation region of the SCC in the \(b/M-Q/Q_{\text {ext}}\) diagram (see Fig. 3) for three different values of \(\Lambda M^2\): 0.03, 0.06, and 0.09. The critical line of the SCC can be obtained as described in the previous paragraph. The figures show that, regardless of the value of b/M, the SCC will always be violated if the black hole approaches the extremal limit. For the cases presented in these figures, the critical value \(Q_{\text {crit}}/Q_{\text {ext}}\) of the charge ratio \(Q/Q_{\text {ext}}\) is larger when dark matter exists in the spacetime compared to the RNdS cases. This indicates that dark matter can alleviate the violation problem of SCC to a certain degree. However, it is important to note that the violation region \((Q_{\text {crit}}/Q_{\text {ext}}, 1)\) as a function of the parameter b/M does not monotonically decrease. Specifically, in the interval where b/M is relatively small, the violation region decreases rapidly with the increase of b/M, but it then increases for a certain interval before decreasing again. Discontinuities are present in the critical line, which may be caused by the transition of the mode curve that provides the lowest-lying mode. Overall, our findings suggest that dark matter may have a rescuing effect on the violation of SCC, particularly in the parameter range where b/M and \(\Lambda M^2\) are both small with the considerations of observations.

5 Conclusion

Considering that PFDM may be a candidate for dark matter, we calculated the QNMs of a massless neutral scalar field in a charged de-Sitter black hole background surrounded by PFDM and explored the influence of the state parameter b/M of PFDM on SCC. Our findings indicate that SCC is violated when the black hole approaches extremal one, regardless of the value of b/M. However, the presence of dark matter can alleviate the violation of SCC to some degree, particularly in the parameter range where both b/M and \(\Lambda M^2\) are small with observational consideration. It is worth noting that the violation region as a function of b/M does not exhibit a monotonic decrease, suggesting that the commonly held belief that the larger the parameter b/M, the smaller the violation region, is not always true.

There are several avenues for future research that can build on the findings of this study. Firstly, it would be interesting to investigate the effects of different types of dark matter on SCC, and explore how the properties of dark matter affect the behavior of black hole spacetime. Moreover, it is essential to investigate the influence of dark matter as a perturbation on SCC in spacetime, given that dark matter is a dynamical field. Additionally, it would be valuable to extend this study to include rotating black holes and investigate whether the presence of dark matter has a similar rescuing effect on the SCC in these cases.