Semileptonic baryonic B decays

Abstract

We study the semileptonic $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ decays with $\textbf{B}{\bar{\textbf{B}}'}$ ($L{\bar{L}}'$) representing a baryon (lepton) pair. Using the new determination of the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition form factors, we obtain $\mathcal{B}(B^-\rightarrow p{\bar{p}} \mu ^-{\bar{\nu }}_\mu ) =(5.4\pm 2.0)\times 10^{-6}$ agreeing with the current data. Besides, $\mathcal{B}(B^-\rightarrow \Lambda {\bar{p}} \nu {\bar{\nu }})=(3.5\pm 1.0)\times 10^{-8}$ is calculated to be 20 times smaller than the previous prediction. In particular, we predict $\mathcal{B}({\bar{B}}^0_s\rightarrow p{\bar{\Lambda }} e^- {\bar{\nu }}_e,p{\bar{\Lambda }} \mu ^- {\bar{\nu }}_\mu ,p{\bar{\Lambda }} \tau ^- {\bar{\nu }}_\tau ) =(2.1\pm 0.6,2.1\pm 0.6,1.7\pm 1.0)\times 10^{-6}$ and $\mathcal{B}({\bar{B}}^0_s\rightarrow \Lambda {\bar{\Lambda }} \nu {\bar{\nu }})=(0.8\pm 0.2)\times 10^{-8}$, which can be accessible to the LHCb experiment.

1 introduction

In the non-leptonic baryonic B decays, the observation of $B\rightarrow p{\bar{p}} (\pi ,K^{(*)},D^{(*)})$ and $B^-\rightarrow \Lambda {\bar{p}} (J/\psi ,\gamma )$ suggests the unique existence of the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition [1,2,3], with which the CP asymmetries of $B^-\rightarrow p{\bar{p}} (\pi ^-,K^{(*)-})$ [4, 5] and the branching fractions of $B^-\rightarrow \Lambda {\bar{p}} D^{(*)0}$, ${\bar{B}}^0\rightarrow \Sigma ^0{\bar{\Lambda }} D^0$ [6] have been predicted, and verified by the later measurements [7].

The semileptonic B decays of $B^-\rightarrow p{\bar{p}} \ell ^-{\bar{\nu }}_\ell$ and $B^-\rightarrow \Lambda {\bar{p}}\nu _\ell {\bar{\nu }}_\ell$ with $\ell$ denoting e, $\mu$ or $\tau$ can provide another evidence for the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition [8, 9]. Like the studies of the semileptonic $B^-\rightarrow \pi ^+\pi ^-\ell ^-\bar{\nu }_\ell$ decays [10, 11], the full dibaryon invariant mass spectrum can be used to test the possible co-existence of the resonant and non-resonant contributions. Therefore, we have predicted $\mathcal{B}(B^-\rightarrow p{\bar{p}} e^- \bar{\nu }_e) =(1.04\pm 0.26\pm 0.12)\times 10^{-4}$ [8] and $\mathcal{B}(B^-\rightarrow \Lambda {\bar{p}} \nu {\bar{\nu }}) =(7.9\pm 1.9)\times 10^{-7}$ [9]. We have also predicted $\mathcal{R}_{e/\mu }\equiv$ $\mathcal{B}(B^-\rightarrow p{\bar{p}} e^- {\bar{\nu }}_e)/\mathcal{B}(B^-\rightarrow p{\bar{p}} \mu ^- {\bar{\nu }}_\mu )\simeq 1$ [8]. By contrast, the pole model argument leads to the evaluation of $\mathcal{B}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}\ell \bar{\nu }_\ell )=10^{-5}-10^{-6}$ [12].

Experimentally, it has been measured that [13,14,15,16]

$$\begin{aligned}{} & {} \mathcal{B}_{ex}(B^- \rightarrow p{\bar{p}} e^-{\bar{\nu }}_e) =(5.8\pm 3.7\pm 3.6)\nonumber \\ {}{} & {} \quad \times 10^{-4}\; (<1.2\times 10^{-3})\;[\text {Cleo}]\,\nonumber \\{} & {} \mathcal{B}_{ex}(B^- \rightarrow p{\bar{p}} e^-{\bar{\nu }}_e)= (8.2^{+3.7}_{-3.2}\pm 0.6)\nonumber \\ {}{} & {} \quad \times 10^{-6}\;[\text {Belle}]\,\nonumber \\{} & {} \mathcal{B}_{ex}(B^- \rightarrow p{\bar{p}} \mu ^-{\bar{\nu }}_\mu )= (3.1^{+3.1}_{-2.4}\pm 0.7)\nonumber \\ {}{} & {} \quad \times 10^{-6}\;[\text {Belle}]\,\nonumber \\{} & {} \mathcal{B}_{ex}(B^- \rightarrow p{\bar{p}} \mu ^-{\bar{\nu }}_\mu )= (5.27^{+0.23}_{-0.24}\pm 0.21\pm 0.15)\nonumber \\ {}{} & {} \quad \times 10^{-6}\;[\text {LHCb}]\,\nonumber \\{} & {} \mathcal{B}_{ex}(B^- \rightarrow \Lambda {\bar{p}} \nu {\bar{\nu }})= (0.4\pm 1.1\pm 0.6)\nonumber \\ {}{} & {} \quad \times 10^{-5}\;(<3.0\times 10^{-5})\;[\text {Babar}]. \end{aligned}$$

(1)

The threshold effect commonly observed in $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M$ is also observed in $B^- \rightarrow p{\bar{p}} \mu ^-\bar{\nu }_e$ [15], which is drawn as a peak around the threshold area of $m_{\textbf{B}{\bar{\mathbf{B'}}}} \simeq m_\textbf{B}+m_{\bar{{ B'}}}$ in the ${\textbf{B}{\bar{\mathbf{B'}}}}$ invariant mass spectrum. There is no sign that the B to ${\textbf{B}{\bar{\mathbf{B'}}}}$ transition receives a resonant contribution. Nonetheless, it is clearly seen that $\mathcal{B}_{ex}(B^- \rightarrow p{\bar{p}} \mu ^-{\bar{\nu }}_\mu )$ is 20 times smaller than the prediction [8]. This has been pointed out as the theoretical challenge to alleviate the discrepancy [17]. On the other hand, the ratio $\mathcal{R}_{e/\mu }\simeq 1$ as a test of the lepton universality is not conclusive, and the prediction of $\mathcal{B}(B^- \rightarrow \Lambda \bar{p} \nu {\bar{\nu }})$ is within the experimental upper bound.

In Ref. [6], the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition form factors ($F_{\textbf{B}{\bar{\mathbf{B'}}}}$) are extracted with the data from $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M$, which cause the overestimation of $\mathcal{B}(B\rightarrow p{\bar{p}}\ell {\bar{\nu }})$. With the same theoretical inputs, $\mathcal{B}(B^- \rightarrow \Lambda {\bar{p}} \nu {\bar{\nu }})$ might be overestimated as well [9]. A question is hence raised: whether there exist the universal $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition form factors to explain the nonleptonic and semileptonic baryonic B decays.

Fig. 1

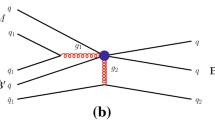
Feynman diagrams for the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L\bar{L}'$ decays, where (a) depicts $B^-\rightarrow p{\bar{p}}\ell ^-{\bar{\nu }}_\ell$ and ${\bar{B}}^0_s\rightarrow p{\bar{\Lambda }}\ell ^-{\bar{\nu }}_\ell$, while (b, c) $B^-\rightarrow \Lambda {\bar{p}}\nu _\ell {\bar{\nu }}_\ell$ and $\bar{B}^0_s\rightarrow \Lambda {\bar{\Lambda }}\nu _\ell {\bar{\nu }}_\ell$

In this paper, we propose to perform a new global fit, in order to accommodate the current data of $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ with $L{\bar{L}}'$ denoting a lepton pair and $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M$. With $F_{\textbf{B}{\bar{\mathbf{B'}}}}$ determined from the new global fit, we will re-investigate $B^- \rightarrow \Lambda {\bar{p}} \nu {\bar{\nu }}$. Since LHCb has been able to accumulate more events for the ${\bar{B}}_s^0$ decays, we will study ${\bar{B}}_s^0\rightarrow p{\bar{\Lambda }} \ell ^- {\bar{\nu }}$ and $\bar{B}_s^0\rightarrow \Lambda {\bar{\Lambda }} \nu {\bar{\nu }}$ decays for future measurements.

2 Formalism

The semileptonic baryonic B decays come from the quark-level $b\rightarrow u\ell {\bar{\nu }}_\ell$ and $b\rightarrow s\nu _\ell {\bar{\nu }}_\ell$ processes. In Fig. 1a, $b\rightarrow u\ell {\bar{\nu }}_\ell$ appear as the tree-level $b\rightarrow uW,W\rightarrow \ell {\bar{\nu }}_\ell$ decays. Due to the loop contributions from the penguin-level $b\rightarrow sZ,Z\rightarrow \nu _\ell {\bar{\nu }}_\ell$ and box diagrams in Fig. 1b,c, respectively [18], $b\rightarrow s\nu _\ell {\bar{\nu }}_\ell$ can be rarer than $b\rightarrow u\ell {\bar{\nu }}_\ell$. The effective Hamiltonians for the above semileptonic b decays are given by [18, 19]

$$\begin{aligned}{} & {} \mathcal{H}(b\rightarrow u \ell {\bar{\nu }}_\ell )= \frac{G_F V_{ub}}{\sqrt{2}}\;{\bar{u}}\gamma _\mu (1-\gamma _5)b\; {\bar{\ell }}\gamma ^\mu (1-\gamma _5)\nu _\ell \,\nonumber \\{} & {} \mathcal{H}(b\rightarrow s \nu _\ell {\bar{\nu }}_\ell )\nonumber \\{} & {} \quad = \frac{G_F}{\sqrt{2}}\frac{\alpha _{em}}{2\pi \text {sin}^2\theta _W } \lambda _t D(x_t) {\bar{s}}\gamma _\mu (1-\gamma _5)b\bar{\nu }_\ell \gamma ^\mu (1-\gamma _5)\nu _\ell \,\nonumber \\ \end{aligned}$$

(2)

where $G_F$ is the Fermi constant, $V_{ub}$ and $\lambda _t\equiv V_{ts}^* V_{tb}$ are the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, and $D(x_t)$ with $x_t\equiv m_t^2/m_W^2$ is the top-quark loop function [18,19,20,21]. According to $\mathcal{H}(b\rightarrow u \ell {\bar{\nu }}_\ell ,s \nu _\ell \bar{\nu }_\ell )$, the amplitudes of $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ with $L{\bar{L}}'=(\ell {\bar{\nu }}_\ell ,\nu _\ell {\bar{\nu }}_\ell )$ can be derived as [8, 9]

$$\begin{aligned}{} & {} \mathcal{M}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} \ell ^- {\bar{\nu }}_\ell )\nonumber \\{} & {} \quad =\frac{G_F V_{ub}}{\sqrt{2}} \langle {\textbf{B}{\bar{\mathbf{B'}}}}|{\bar{u}}\gamma _\mu (1-\gamma _5)b|B \rangle \;{\bar{\ell }}\gamma ^\mu (1-\gamma _5) \nu _\ell ,\nonumber \\{} & {} \mathcal{M}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} \nu _\ell {\bar{\nu }}_\ell )\nonumber \\{} & {} \quad = \frac{G_F}{\sqrt{2}}\frac{\alpha _{\text {em}}}{2\pi \text {sin}^2\theta _W }\lambda _t D(x_t) \langle {\textbf{B}{\bar{\mathbf{B'}}}}|\bar{s}\gamma _\mu (1-\gamma _5)b|B\rangle \nonumber \\{} & {} \qquad \times \;{\bar{\nu }}_\ell \gamma ^\mu (1-\gamma _5) \nu _\ell , \end{aligned}$$

(3)

with $\langle {\textbf{B}{\bar{\mathbf{B'}}}}|({\bar{q}}b)|B\rangle$ representing the matrix elements of the B meson to ${\textbf{B}{\bar{\mathbf{B'}}}}$ transition. In Fig. 1a–c, $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ occur as $B^-\rightarrow p{\bar{p}}\ell {\bar{\nu }}_\ell ,\Lambda {\bar{p}}\nu _\ell {\bar{\nu }}_\ell$ and ${\bar{B}}_s^0\rightarrow p{\bar{\Lambda }}\ell {\bar{\nu }}_\ell ,\Lambda \bar{\Lambda }\nu _\ell {\bar{\nu }}_\ell$ for our study.

Fig. 2

Feynman diagrams for the three-body baryonic B decays, where (a, b) and (c) depict $B\rightarrow p{\bar{p}} M(V)$ and $\bar{B}^0\rightarrow p{\bar{p}} D^{0(*)}$, respectively

The amplitudes of the non-leptonic $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M$ decays have two forms [1, 22, 23]: $\mathcal{M}_C\propto \langle {\textbf{B}{\bar{\mathbf{B'}}}}|({\bar{q}} q')|0\rangle$ $\times \langle M|({\bar{q}} b)|B\rangle$ and $\mathcal{M}_T\propto \langle M|({\bar{q}} q')|0\rangle \langle {\textbf{B}{\bar{\mathbf{B'}}}}|({\bar{q}} b)|B\rangle$, where $\mathcal{M}_C$ denotes the current amplitude with ${\textbf{B}{\bar{B'}}}$ produced from the quark current [22,23,24,25,26], and $\mathcal{M}_T$ the transition amplitude with ${\textbf{B}{\bar{B'}}}$ from the B meson transition [1,2,3]. Clearly, $\mathcal{M}_T(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M)$ and $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ can be related by $\langle {\textbf{B}{\bar{\mathbf{B'}}}}|({\bar{q}} b)|B\rangle$ [8, 9]. As seen in Fig. 2, $B\rightarrow p{\bar{p}} M$ with $M=(\pi ,K)$, $B\rightarrow p{\bar{p}} V$ with $V=(\rho ,K^{*})$, and ${\bar{B}}^0\rightarrow p{\bar{p}} D^{0(*)}$ involve the transition amplitudes, given by [1, 27,28,29]

$$\begin{aligned}{} & {} \mathcal{M}(B\rightarrow p{\bar{p}} M)=\frac{G_F}{\sqrt{2}}(\hat{\mathcal{M}}_1+\hat{\mathcal{M}}_6)\,\nonumber \\{} & {} \hat{\mathcal{M}}_1=\alpha _1^{qq'}\langle M|\bar{q}'\gamma _\mu (1-\gamma _5)u|0\rangle \langle p{\bar{p}}|{\bar{q}}\gamma ^\mu (1-\gamma _5)b|B\rangle \,\nonumber \\{} & {} \hat{\mathcal{M}}_6=\alpha _6^{qq'}\langle M|{\bar{q}}'(1+\gamma _5)u|0\rangle \langle p{\bar{p}}|{\bar{q}}(1-\gamma _5)b|B\rangle \, \nonumber \\{} & {} \mathcal{M}(B\rightarrow p{\bar{p}} V) =\frac{G_F}{\sqrt{2}}\alpha _1^{qq'}\langle V|{\bar{q}}'\gamma _\mu (1-\gamma _5)u|0\rangle \nonumber \\ {}{} & {} \quad \times \langle p{\bar{p}}|\bar{q}\gamma ^\mu (1-\gamma _5)b|B\rangle \, \nonumber \\{} & {} \mathcal{M}({\bar{B}}^0\rightarrow p{\bar{p}} D^{0(*)})=\frac{G_F}{\sqrt{2}}V_{cb}V_{ud}^*a_2 \langle D^{0(*)}|{\bar{c}}\gamma _\mu \nonumber \\{} & {} \quad \times (1-\gamma _5) u|0\rangle \langle p{\bar{p}}|{\bar{d}}\gamma ^\mu (1-\gamma _5) b|\bar{B}^0\rangle \, \end{aligned}$$

(4)

with $(q,q')=(u,d)$ for $B^-\rightarrow p{\bar{p}} \pi ^-$ and $B^-\rightarrow p\bar{p}\rho ^-$, $(q,q')=(u,s)$ for $B^-\rightarrow p{\bar{p}} K^{-}$ and $B^-\rightarrow p{\bar{p}} K^{*-}$, and $(q,q')=(d,s)$ for ${\bar{B}}^0\rightarrow p{\bar{p}} \bar{K}^0$ and ${\bar{B}}^0\rightarrow p{\bar{p}} {\bar{K}}^{*0}$. The parameters in Eq. (4) result from the factorization approach [30], written as

$$\begin{aligned}{} & {} \alpha _1^{uq'}=V_{ub}V_{uq'}^* a_1-V_{tb}V_{tq'}^*a_4\,\nonumber \\{} & {} \alpha _1^{ds}=-V_{tb}V_{ts}^*a_4\,\nonumber \\{} & {} \alpha _6^{uq'}=\alpha _6^{dq'}=V_{tb}V_{tq'}^*2a_6\, \end{aligned}$$

(5)

with $a_i=c^{eff}_i+c^{eff}_{i\pm 1}/N_c$ for $i=$odd (even), where $c_i^{eff}$ are the effective Wilson coefficients, and $N_c$ the color number [30].

The matrix elements of the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition in Eqs. (3) and (4) can be presented as [1, 3, 6, 17, 27,28,29]

(6)

with $V^b_\mu (A^b_\mu )\equiv {\bar{q}}\gamma _\mu (\gamma _5) b$, $S^b(P^b)\equiv {\bar{q}} b$, and $p_\mu \equiv (p_B-p_\textbf{B}-p_{\bar{\textbf{B}'}})_\mu$. $F_{\textbf{B}{\bar{\mathbf{B'}}}}\equiv (g_i,f_i,{\bar{g}}_j,{\bar{f}}_j)$ with $i=1,2,\ldots ,5$ and $j=1,2, 3$ are the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition form factors.

$F_{\textbf{B}{\bar{\mathbf{B'}}}}$ are momentum dependent. In terms of perturbative QCD (pQCD) counting rules [1, 3, 6, 28, 31,32,33], one parameterizes that

$$\begin{aligned}{} & {} f_i=\frac{D_{f_i}}{t^3}\,\,g_i=\frac{D_{g_i}}{t^3}\,\,\nonumber \\{} & {} {\bar{f}}_j=\frac{D_{{\bar{f}}_j}}{t^3}\,\,{\bar{g}}_j=\frac{D_{\bar{g}_j}}{t^3}\, \end{aligned}$$

(7)

with $t\equiv (p_\textbf{B}+p_{\bar{\textbf{B}'}})^2$. For $F_{\textbf{B}{\bar{\mathbf{B'}}}}\propto 1/t^n$, $n=3$ corresponds to the three gluon propagators, which are drawn in Figs. 1a–c and 2a–c. Since $V_\mu ^b$ and $A_\mu ^b$ can be combined as the right-handed chiral current $R_\mu =(V_\mu ^b+A_\mu ^b)/2$, and the baryon decomposed of the right and left-handed states, that is, , it leads to [6, 17]

(8)

where $|B_q\rangle \sim {\bar{b}}\gamma _5 q|0\rangle$ has been used. As the chiral charge, $Q\equiv R_{\mu =0}$ annihilates the b quark, and creates a valence quark in $\textbf{B}$, while the spectator quark in the B meson is transformed as a valence quark (${\bar{q}}_i$) in ${\bar{\textbf{B}}}'$. We hence obtain $G_{R,L}^{(k)}$ as the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition form factors in the chiral representation. When the chirality states of a spinor (R, L) are taken as the helicity states $(\uparrow ,\downarrow )$, one can see ${\bar{q}}_i$ with the helicity to be (anti-)parallel $[||(\overline{||})]$ to the helicity of ${\bar{\textbf{B}'}}$, such that the chiral charge acting on ${\bar{q}}_i$ can be more explicitly defined as $Q_{||(\overline{||})}(i)$ ($i=1,2,3$). We thus derive that

$$\begin{aligned} G_{R(L)}\propto & {} e_{||}^{R(L)} G_{||}+e_{\overline{||}}^{R(L)} G_{\overline{||}}\, \nonumber \\ G^k_{R(L)}\propto & {} {\bar{e}}_{||}^{R(L)}G^k_{||}+\bar{e}_{\overline{||}}^{R(L)}G^k_{\overline{||}}\, \end{aligned}$$

(9)

where $e_{||}^{R(L)}$ and $e_{\overline{||}}^{R(L)}$ sum over the weight factors of $\textbf{B}_{R(L)}{\bar{\textbf{B}'}}_{R(L)}$, and $\bar{e}_{||}^{R(L)}$ and ${\bar{e}}_{\overline{||}}^{R(L)}$ those of $\textbf{B}_{L(R)}{\bar{\textbf{B}'}}_{R(L)}$. By defining $G_{||(\overline{||})}^{(k)}\equiv D_{||(\overline{||})}^{(k)}/t^3$ $(k=2,3,\ldots ,5)$, we relate the two sorts of the form factors as [1, 3, 28]

$$\begin{aligned} D_{g_1}= & {} \frac{5}{3}D_{||} -\frac{1}{3}D_{\overline{||}} D_{f_1}=\frac{5}{3}D_{||}+\frac{1}{3}D_{\overline{||}} D_{g_k}\nonumber \\= & {} \frac{4}{3}D_{||}^k=-D_{f_k}\nonumber \\ D_{g_1}= & {} \frac{1}{3}D_{||}-\frac{2}{3}D_{\overline{||}} D_{f_1}=\frac{1}{3}D_{||}+\frac{2}{3}D_{\overline{||}} D_{g_k}\nonumber \\= & {} \frac{-1}{3}D_{||}^k=-D_{f_k}\nonumber \\ D_{g_1}= & {} D_{f_1}= -\sqrt{\frac{3}{2}}D_{||} D_{g_k}=-D_{f_k}= -\sqrt{\frac{3}{2}}D_{||}^k\nonumber \\ D_{g_1}= & {} D_{f_1}=\sqrt{\frac{3}{2}}D_{||} D_{g_k}=-D_{f_k}=\sqrt{\frac{3}{2}}D_{||}^{k}\nonumber \\ D_{g_1}= & {} D_{f_1}=D_{||}\,\,D_{g_k}=-D_{f_k}=-D_{||}^k \end{aligned}$$

(10)

for $\langle p{\bar{p}}|({\bar{u}} b)|B^-\rangle$, $\langle p{\bar{p}}|(\bar{d} b)|{\bar{B}}^0\rangle$, $\langle \Lambda {\bar{p}}|({\bar{s}} b)|B^-\rangle$, $\langle p{\bar{\Lambda }}|({\bar{u}} b)|\bar{B}^0_s\rangle$, and $\langle \Lambda {\bar{\Lambda }}|({\bar{s}} b)|\bar{B}^0_s\rangle$, respectively. Likewise, we perform a derivation for ${\bar{g}}_j$ (${\bar{f}}_j$) through the (pseudo-)scalar current, which leads to [28, 29]

$$\begin{aligned} D_{{\bar{g}}_1}= & {} \frac{5}{3}{\bar{D}}_{||}-\frac{1}{3}\bar{D}_{\overline{||}}\,\, D_{{\bar{f}}_1}=\frac{5}{3}\bar{D}_{||}+\frac{1}{3}{\bar{D}}_{\overline{||}}\,\, D_{{\bar{g}}_{2,3}}\nonumber \\= & {} \frac{4}{3}{\bar{D}}_{||}^{2,3}=-D_{{\bar{f}}_{2,3}}\,\nonumber \\ D_{{\bar{g}}_1}= & {} \frac{1}{3}{\bar{D}}_{||}-\frac{2}{3}\bar{D}_{\overline{||}}\,\, D_{{\bar{f}}_1}=\frac{1}{3}\bar{D}_{||}+\frac{2}{3}{\bar{D}}_{\overline{||}}\,\, D_{\bar{g}_{2,3}}\nonumber \\= & {} \frac{-1}{3}{\bar{D}}_{||}^{2,3}=-D_{{\bar{f}}_{2,3}}\, \end{aligned}$$

(11)

for $\langle p{\bar{p}}|({\bar{u}} b)|B^-\rangle$ and $\langle p\bar{p}|({\bar{d}} b)|{\bar{B}}^0\rangle$, respectively. Note that $R(L)\sim \uparrow (\downarrow )$ is based on the approximation with the large energy transfer, which is conveniently presented as $t\rightarrow \infty$. It is also derived that the correction term is of order $m_q/\sqrt{t}$ [31,32,33]. In fact, $\sqrt{t}$ of a few GeV has been large enough to suppress the correction term [33]. Consequently, the relations with the chirality (helicity) symmetry are shown to be able to describe the scattering processes [33]. For the baryonic B decays, $\sqrt{t} >2$ GeV is also sufficient for the holding of the relations in Eqs. (10) and (11).

Fig. 3

The angular variables $\theta _\textbf{B}$, $\theta _L$ and $\phi$ depicted for the four-body $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ decays

Table 1 The effective Wilson coefficients $c_i^{eff}$ ($i=1,2,\ldots ,6$) for b and ${\bar{b}}$ decays

The four-body $B(p_B)\rightarrow \textbf{B}(p_\textbf{B}) {\bar{\textbf{B}'}}(p_{\bar{\textbf{B}'}})L(p_L){\bar{L}}' (p_{{\bar{L}}'})$ decay involves five kinematic variables in the phase space, that is, $s\equiv (p_{L}+p_{\bar{L}'})^2\equiv m_{L{\bar{L}}'}^2$, t, and $(\theta _\textbf{B},\theta _\textbf{L},\phi )$ [34,35,36]. As depicted in Fig. 3, the angle $\theta _\mathbf{B(L)}$ is between $\vec {p}_\textbf{B}$ ($\vec {p}_{L}$) in the ${\textbf{B}{\bar{B'}}}$ ($L\bar{L}'$) rest frame and the line of flight of the ${\textbf{B}{\bar{B'}}}$ ($L\bar{L}'$) system in the B meson rest frame. The angle $\phi$ is from the ${\textbf{B}{\bar{B'}}}$ plane to the $L{\bar{L}}'$ plane defined by the momenta of the ${\textbf{B}{\bar{B'}}}$ pair and $L{\bar{L}}'$ pair in the B meson rest frame, respectively. The partial decay width then reads [8, 9]

$$\begin{aligned} d\Gamma =\frac{|\bar{\mathcal{M}}|^2}{4(4\pi )^6 m_B^3}X \alpha _\textbf{B}\alpha _\textbf{L}\, ds\, dt\, d\text {cos}\,\theta _\textbf{B}\, d\text {cos}\,\theta _\textbf{L}\, d\phi \, \end{aligned}$$

(12)

where $X=[(m_B^2-s-t)^2/4-st]^{1/2}$, $\alpha _\textbf{B}=\lambda ^{1/2}(t,m_\textbf{B}^2,m_{\bar{\textbf{B}'}}^2)/t$, and $\alpha _\textbf{L}=\lambda ^{1/2}(s,m_{L}^2,m_{{\bar{L}}'}^2)/s$, with $\lambda (a,b,c)=a^2+b^2+c^2-2ab-2bc-2ca$. For integration, the allowed ranges of the five variables are $(m_L+m_{{\bar{L}}'})^2\le s\le (m_{B}-\sqrt{t})^2$, $(m_\textbf{B}+m_{\bar{\textbf{B}'}})^2\le t\le (m_{B}-m_L-m_{{\bar{L}}'})^2$, $0\le \theta _\textbf{B,L}\le \pi$, and $0\le \phi \le 2\pi$. The partial decay width of $B(p_B)\rightarrow \textbf{B}(p_\textbf{B}){\bar{\textbf{B}'}}(p_{\bar{\textbf{B}'}})M(p_M)$ involves two variables in the phase space, given by [3, 28]

$$\begin{aligned} d\Gamma = \frac{\beta _\textbf{B}^{1/2}\beta ^{1/2}_t}{(8\pi m_B)^3} |\bar{\mathcal{M}}|^2\;dt\;d\text {cos}\theta \, \end{aligned}$$

(13)

where $\beta _\textbf{B}=[1-(m_\textbf{B}+m_{\bar{\textbf{B}'}})^2/t][1-(m_\textbf{B}-m_{\bar{\textbf{B}'}})^2/t]$, $\beta _t=[(m_B+m_M)^2-t][(m_B-m_M)^2-t]$, and $\theta$ is the angle between the meson and baryon moving directions in the ${\textbf{B}{\bar{B'}}}$ rest frame. The allowed regions of the variables are $-1<\cos \theta <1$ and $(m_\textbf{B}+m_{\bar{\textbf{B}'}})^2<t<(m_B-m_M)^2$. For the global fit in the next section, we define the CP asymmetry [4, 37], and angular asymmetries of $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M$ [3, 26, 28] and $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ [8, 9], written as

$$\begin{aligned} \mathcal{A}_{CP}\equiv & {} \frac{\Gamma (B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} M)-\Gamma ({\bar{B}}\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} {\bar{M}})}{\Gamma (B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} M)+\Gamma ({\bar{B}}\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} {\bar{M}})}\, \nonumber \\ \mathcal{A}_{FB,\theta _i}\equiv & {} \frac{\Gamma (\cos \theta _i>0)-\Gamma (\cos \theta _i<0)}{\Gamma (\cos \theta _i>0)+\Gamma (\cos \theta _i<0)}\, \end{aligned}$$

(14)

where ${\bar{B}}\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} {\bar{M}}$ represents the anti-particle decay.

3 Numerical results and discussions

In the numerical analysis, the CKM matrix elements in the Wolfenstein parameterization read [7]

$$\begin{aligned} V_{ub}= & {} A\lambda ^3(\rho -i\eta ),\, V_{ud}=1-\lambda ^2/2,\, V_{us}=\lambda ,\,\nonumber \\ V_{cb}= & {} A\lambda ^2,\, V_{tb}=1,\, V_{td}=A\lambda ^3,\, V_{ts}=-A\lambda ^2\, \end{aligned}$$

(15)

with $(\lambda ,A,\rho ,\eta )=(0.225,0.826,0.163\pm 0.010,0.357\pm 0.010)$.

From Refs. [18,19,20,21], we adopt D(x) as

$$\begin{aligned} D(x)= & {} D_0(x)+\frac{\alpha _s}{4\pi }D_1(x),\nonumber \\ D_0(x)= & {} \frac{x}{8}\bigg [-\frac{2+x}{1-x}+\frac{3x-6}{(1-x)^2}ln(x)\bigg ],\nonumber \\ D_1(x)= & {} -\frac{23x+5x^2-4x^3}{3(1-x)^2} +\frac{x-11x^2+x^3 +x^4}{(1-x)^3}ln(x)\nonumber \\{} & {} +\frac{8x+4x^2 +x^3-x^4}{2(1-x)^3}ln^2(x)\nonumber \\{} & {} -\frac{4x-x^3}{(1-x)^2}L_2(1-x) +8x\frac{\partial D_0(x)}{\partial x}ln(\mu ^2/m_W^2),\nonumber \\ \end{aligned}$$

(16)

where $L_2(1-x)\equiv \int ^x_1 ln(t)/(1-t) dt$ and $\mu =m_b$. For $B\rightarrow p{\bar{p}} M(V)$ and ${\bar{B}}^0\rightarrow p{\bar{p}} D^{0(*)}$, we present $c_i^{eff}$ in Table 1, where b and ${\bar{b}}$ decays are both considered, together with the decay constants $(f_\pi ,f_K,f_\rho ,f_{K^*})= (130.2\pm 1.2,155.7\pm 0.3,210.6\pm 0.4,204.7\pm 6.1)$ MeV [7, 38] and $(f_D,f_{D^*})=(208.9\pm 6.5,252.2\pm 22.7)$ MeV [28, 39]. In the generalized edition of the factorization [30, 37], $N_c$ is taken as the effective color number with $N_c^{(eff)}=(2,3,\infty )$, in order that the non-factorizable QCD corrections can be estimated.

Table 2 Experimental data for the $B^-\rightarrow p\bar{p}\ell ^-\nu _\ell$ and $B\rightarrow p{\bar{p}} M_{(c)}$ decays, where the notation $\dagger$ for $\mathcal{A}_{FB}$ denotes the contribution from $m_{p{\bar{p}}}<2.85$ GeV, and $\mathcal{B}(B^-\rightarrow p{\bar{p}} \mu ^- \bar{\nu }_\mu )$ has combined the Belle and LHCb data in Eq. (1)

Table 3 Our calculations for the semileptonic $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ decays. For $\mathcal{B}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}\ell {\bar{\nu }}_\ell )$, the values in the parentheses correspond to $\ell =(e,\mu ,\tau )$, where the first and second errors come from $|V_{ub}|$ and the form factors in Eq. (18), respectively. For $\mathcal{B}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}\nu \bar{\nu })=\Sigma _\ell \mathcal{B}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}\nu _\ell \bar{\nu }_\ell )$ and $\mathcal{A}_{FB}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}')$, the errors take into account the uncertainties of the form factors in Eq. (18)

Using the minimum $\chi ^2$-fit of

$$\begin{aligned} \chi ^2= & {} \sum \bigg (\frac{\mathcal{O}_{th}^i-\mathcal{O}_{ex}^i}{\sigma _{ex}^i}\bigg )^2+ \bigg (\frac{{|V_{ub}|}_{th}-{|V_{ub}|}_{ex}}{\sigma _{{|V_{ub}|}_{ex}}}\bigg )^2\, \end{aligned}$$

(17)

we test if the observables of non-leptonic and semileptonic baryonic B decays can both be interpreted, where $\mathcal{O}_{th}^i$ stand for the theoretical calculations of $\mathcal{B}$, $\mathcal{A}_{CP}$ and $\mathcal{A}_{FB}$, while $\mathcal{O}_{ex}^i$ the experimental inputs in Table 2, together with $\sigma _{ex}^i$ the experimental errors. Since the $V_{ub}$ in Eq. (3) is for the exclusive baryonic $B_{(s)}$ decays, which can be different from that in the inclusive ones [40,41,42], we choose $|V_{ub}|_{ex}=(3.43\pm 0.32)\times 10^{-3}$ determined from the ${\bar{B}}_s^0$ and baryonic $\Lambda _b$ decays [7] as our experimental input in Eq. (17).

With 16 experimental inputs from Table 2 and $|V_{ub}|_{ex}$, we fit $(D_{||},D_{\overline{||}},D_{2,3,4,5})$ and $({\bar{D}}_{||},{\bar{D}}_{\overline{||}},{\bar{D}}_{2,3})$ in Eqs. (10) and (11), respectively, and $|V_{ub}|_{th}$, which amount to 11 parameters, such that the number of degrees of freedom denoted by d.n.f is counted as $d.n.f=16-11=5$. As a result, we obtain $\chi ^2/n.d.f=1.86$ as a measure of the global fit, and extract that

$$\begin{aligned}{} & {} (D_{||},D_{\overline{||}})=(11.2\pm 43.5,332.3\pm 17.2)\;\textrm{GeV}^{5}\,\nonumber \\{} & {} (D_{||}^2,D_{||}^3,D_{||}^4,D_{||}^5)=(47.7\pm 10.1,442.2\pm 103.4,{-}38.7\nonumber \\{} & {} \qquad \pm 9.6, 80.7\pm 27.2)\;\textrm{GeV}^{4}\,\nonumber \\{} & {} ({\bar{D}}_{||},{\bar{D}}_{\overline{||}},{\bar{D}}_{||}^2,{\bar{D}}_{||}^3)\nonumber \\{} & {} \quad =({-}59.9\pm 12.9,23.8\pm 6.8, 90.9\pm 11.1, 131.7\nonumber \\{} & {} \qquad \pm 330.7)\;\textrm{GeV}^{4}\, \end{aligned}$$

(18)

with $N_c^{eff}=2$ and $\infty$ for $B\rightarrow p{\bar{p}} M(V)$ and $B\rightarrow p{\bar{p}} D^{0(*)}$, respectively. Using the parameters in Eq. (18), we calculate the branching fractions and angular asymmetries of $B^-\rightarrow p{\bar{p}}\ell {\bar{\nu }},\Lambda \bar{p}\nu {\bar{\nu }}$ and ${\bar{B}}_s^0\rightarrow p{\bar{\Lambda }}\ell \bar{\nu },\Lambda {\bar{\Lambda }}\nu {\bar{\nu }}$, of which the results are compared with the experimental data in Table 3. We also draw the ${p{\bar{p}}}$ invariant mass spectrum for $B^-\rightarrow p\bar{p}\mu ^-{\bar{\nu }}_\mu$ in Fig. 4.

4 Discussions and conclusions

Since $\chi ^2/n.d.f=1.86$ presents a reasonable fit, it indicates that the most recent data in Table 2 can be explained. It is interesting to note that $\mathcal{B}(B^-\rightarrow p{\bar{p}} \pi ^-,p\bar{p}\rho ^-)$ [3, 4] were once overestimated [7, 43, 44], and the relation of $\mathcal{A}_{FB}(B^-\rightarrow p{\bar{p}}\pi ^-)\simeq \mathcal{A}_{FB}(B^-\rightarrow p{\bar{p}} K^-)$ [3] was not verified by the measurements [43, 44]. This is due to $F_{\textbf{B}{\bar{\mathbf{B'}}}}$ determined by the $B\rightarrow p{\bar{p}} K$ data [3], while $B\rightarrow p{\bar{p}} K$ are in fact the penguin dominated decays with $\hat{\mathcal{M}}_6\propto \langle p\bar{p}|(S-P)^b|B\rangle$ to give the main contribution. To avoid the inconsistency unable to be solved at that time, one performed the extraction of Ref. [6] that excluded $\mathcal{B}(B^-\rightarrow p{\bar{p}} K^-)$, $\mathcal{B}({\bar{B}}^0\rightarrow p{\bar{p}} {\bar{K}}^0)$, and $\mathcal{A}_{FB}(B^-\rightarrow p{\bar{p}} K^-)$, in order that the more associated tree dominated decays of $B\rightarrow p{\bar{p}}(\pi ,\rho )$, ${\bar{B}}^0\rightarrow p{\bar{p}} D^{0(*)}$, and $B\rightarrow {\textbf{B}{\bar{\textbf{B}}}}L{\bar{L}}'$ can be studied. However, it resulted in an unsatisfactory global fit not to accommodate the all data.

As $F_{\textbf{B}{\bar{\mathbf{B'}}}}$ determined in this work can be universal for the non-leptonic and semileptonic decay channels, we calculate $\mathcal{B}(B^-\rightarrow p{\bar{p}} e^-{\bar{\nu }}_e)=(5.3\pm 2.0)\times 10^{-6}$ and $\mathcal{B}(B^-\rightarrow p{\bar{p}}\mu ^-{\bar{\nu }}_\mu )=(5.4\pm 2.0)\times 10^{-6}$ agreeing with the experimental values. Moreover, we revisit $B^-\rightarrow \Lambda {\bar{p}}\nu {\bar{\nu }}$, and obtain $\mathcal{B}(B^-\rightarrow \Lambda {\bar{p}}\nu {\bar{\nu }})=(3.5\pm 1.0)\times 10^{-8}$ 20 times smaller than the number of Ref. [9].

Like the theoretical illustration in $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ and $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}M$ [29, 46], the gluon propagators of Fig. 1a–c play the key role in the ${\textbf{B}{\bar{\mathbf{B'}}}}$ formation of $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$, where two of them provide the valence quarks in ${\textbf{B}{\bar{B'}}}$, while the another one speeds up the spectator quark in B. Accordingly, the approach of pQCD counting rules derives that $F_{\textbf{B}{\bar{\mathbf{B'}}}}\propto 1/t^3$.

One can test the momentum dependence of $B^-\rightarrow p{\bar{p}}\mu ^-\bar{\nu }_\mu$, which is by scanning the partial branching fraction as a function of $\sqrt{t}=m_{p{\bar{p}}}$. In Fig. 4, as we draw the line to agree with the five data points [15]; particularly, those around the area of $\sqrt{t}\sim m_\textbf{B}+m_{\bar{\textbf{B}'}}$ for the threshold effect, it is shown that $F_{\textbf{B}{\bar{\mathbf{B'}}}}$ as a function of 1/t can describe $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$.

Fig. 4

The $p{\bar{p}}$ invariant mass spectrum of $B^-\rightarrow p{\bar{p}}\mu ^-{\bar{\nu }}_\mu$, where the data points are from LHCb [15]

By normalizing the prediction of the pQCD model [8], LHCb draws the $m_{p{\bar{p}}}$ spectrum of $B^-\rightarrow p{\bar{p}}\mu {\bar{\nu }}$ in Fig. 4 of Ref. [15], where the line is higher and narrower than our result. The difference is caused by the fact that the line of of Ref. [15] is chosen to more agree with the two data points around $m_{p{\bar{p}}}\sim 2.5$ GeV. Subsequently, the peak should reach $17\times 10^{-6}$ to be above the data point around $m_{p{\bar{p}}}\sim 2$ GeV for integrating over the partial branching fraction as large as $\mathcal{B}\simeq 5\times 10^{-6}$. In comparison, our result prefers to agree with the threshold data points; however, requiring some broadening to give a sufficient branching fraction.

The decay channel ${\bar{B}}^0_s\rightarrow \Lambda {\bar{p}} K^+({\bar{\Lambda }} p K^-)$ is the first observation of a baryonic ${\bar{B}}_s^0$ decay [47], whose branching fraction $\mathcal{B}(\bar{B}^0_s\rightarrow \Lambda {\bar{p}} K^+ +{\bar{\Lambda }} p K^-)=5.46\times 10^{-6}$ is as large as those of the three-body baryonic $B^-$ (${\bar{B}}^0$) decays. Hence, the semileptonic baryonic ${\bar{B}}^0_s$ decay is supposed to be compatible with $B^-\rightarrow p{\bar{p}}\ell {\bar{\nu }}_\ell$. In our prediction, we present

$$\begin{aligned}{} & {} \mathcal{B}({\bar{B}}^0_s{\rightarrow } p{\bar{\Lambda }} e^- {\bar{\nu }}_e,p{\bar{\Lambda }} \mu ^{-} {\bar{\nu }}_\mu ) =(2.1{\pm } 0.6,2.1{\pm } 0.6){\times } 10^{{-}6}\,\nonumber \\ \end{aligned}$$

(19)

which are accessible to the LHCb experiment, whereas $\mathcal{B}(\bar{B}^0_s\rightarrow \Lambda {\bar{\Lambda }} \nu {\bar{\nu }})=(0.8\pm 0.2)\times 10^{-8}$ is relatively small.

Because of $m_\tau \gg m_{e,\mu }$ that strongly shrinks the phase space, it is anticipated that $\mathcal{B}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}\tau {\bar{\nu }})\ll \mathcal{B}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}e{\bar{\nu }},{\textbf{B}{\bar{\mathbf{B'}}}}\mu {\bar{\nu }})$. Nonetheless, the amplitude of Eq. (3) and the matrix elements of Eq. (6) result in

$$\begin{aligned}{} & {} i{\bar{u}}(g_3\gamma _5-f_3)v\; m_\ell {\bar{u}}_\ell \gamma _\mu (1+\gamma _5) v_{{\bar{\nu }}}\, \end{aligned}$$

(20)

in $\mathcal{M}(B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}} \ell {\bar{\nu }})$, where $m_\tau$ is able to enhance the decay. We thus obtain

$$\begin{aligned}{} & {} \mathcal{B}(B^-\rightarrow p{\bar{p}} \tau ^- {\bar{\nu }}_\tau ) =(7.6\pm 4.2)\times 10^{-6}\,\,\nonumber \\{} & {} \mathcal{B}({\bar{B}}^0_s\rightarrow p{\bar{\Lambda }} \tau ^- {\bar{\nu }}_\tau ) =(1.7\pm 1.0)\times 10^{-6}\, \end{aligned}$$

(21)

as large as their counterparts. Likewise, the mass effect can be found in $\mathcal{M}(B\rightarrow \tau {\bar{\nu }})\propto m_\tau \bar{u}_\tau (1+\gamma _5)v_{{\bar{\nu }}}$ [48, 49] and $\mathcal{M}(B\rightarrow \textbf{B}_c\bar{\textbf{B}}')\propto m_c \langle \textbf{B}_c\bar{\textbf{B}}'|\bar{c}(1+\gamma _5)q|0\rangle$ [50], where $m_\tau$ and $m_c$ alleviate the decays from helicity suppression.

We study the angular asymmetries of the semileptonic $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ decays. While $\mathcal{A}_{FB,\theta _\textbf{B}}(B^-\rightarrow p{\bar{p}} \ell ^- {\bar{\nu }}_\ell )$ are around several percents, $\mathcal{A}_{FB,\theta _\textbf{B}}({\bar{B}}^0_s\rightarrow p{\bar{\Lambda }} e^- {\bar{\nu }}_e, p{\bar{\Lambda }} \mu ^- {\bar{\nu }}_\mu )$ and $\mathcal{A}_{FB,\theta _\textbf{B}}({\bar{B}}^0_s\rightarrow \Lambda {\bar{\Lambda }} \nu \bar{\nu })$ can be around 25%. Like the three-body baryonic B decays [3, 26, 28], this implies a theoretical sensitivity for $F_{\textbf{B}{\bar{\mathbf{B'}}}}$ to be confirmed by future measurements.

In summary, we have investigated the semiletonic $B^-(\bar{B}_s^0)\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}L{\bar{L}}'$ decays with $L\bar{L}'=(\ell {\bar{\nu }}_\ell ,\nu {\bar{\nu }})$. We have newly extracted the $B\rightarrow {\textbf{B}{\bar{\mathbf{B'}}}}$ transition form factors with the global fit that includes the data of $B\rightarrow p{\bar{p}} M(V)$, $\bar{B}^0\rightarrow p{\bar{p}} D^{0(*)}$ and $B\rightarrow p{\bar{p}} e^-{\bar{\nu }}_e,p\bar{p}\mu ^-{\bar{\nu }}_\mu$ decays. In our demonstration, $\mathcal{B}(B^-\rightarrow p{\bar{p}} e^-{\bar{\nu }}_e,p{\bar{p}}\mu ^-{\bar{\nu }}_\mu )$ once overestimated to be as large as $10^{-4}$ has been reduced to be around $5\times 10^{-6}$, in agreement with the current data. We have also presented $\mathcal{B}(B^-\rightarrow \Lambda {\bar{p}}\nu {\bar{\nu }})=(3.5\pm 1.0)\times 10^{-8}$. It has been found that $\mathcal{B}({\bar{B}}^0_s\rightarrow p\bar{\Lambda }e^- {\bar{\nu }}_e,p{\bar{\Lambda }} \mu ^- {\bar{\nu }}_\mu , p\bar{\Lambda }\tau ^- {\bar{\nu }}_\tau ) =(2.1\pm 0.6,2.1\pm 0.6,1.7\pm 1.0)\times 10^{-6}$ and $\mathcal{B}({\bar{B}}^0_s\rightarrow \Lambda {\bar{\Lambda }} \nu {\bar{\nu }})=(0.8\pm 0.2)\times 10^{-8}$ can be promising for future measurements.