1 Introduction

Gravitational lensing under a weak-field approximation is used to find massive and dark objects [1, 2]. From the leading term of the deflection angle of a ray reflected by a mass lens in the weak-field approximation, we can estimate the mass of the lensing object if a distance to the lensing object is known. We would reveal details of the lensing object if we detect the phenomena in a strong gravitational field by the lensing object.Footnote 1

Recently, gravitational waves from black holes have been reported by LIGO Scientific Collaboration and Virgo Collaboration [6] and the shadows of the candidates of supermassive black holes in the centers of a galaxy M87 and milky way have been reported by Event Horizon Telescope Collaboration [7, 8]. Investigation on phenomena in strong gravitational fields is important to understand compact objects.

In 1931, Hagihara pointed out that the image of a star at any position can be observed in a Schwarzschild spacetime [9] because the spacetime has a photon sphere [10,11,12,13,14,15,16,17,18,19,20] which is a sphere filled with unstable circular light orbits. The image due to the rays deflected by the photon sphere around a black hole and other compact objects has been revisited often [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. In 1959, Darwin investigated the deflection angle of the ray deflected by the photon sphere in the Schwarzschild spacetime [21].

Bozza has investigated gravitational lensing in a strong deflection limit \(b\rightarrow b_\textrm{m}+0\), where b is the impact parameter of the ray and \(b_\textrm{m}\) is a critical impact parameter, in a general asymptotically-flat, spherical symmetric spacetime with the photon sphere [29]. Bozza has expressed the deflection angle \(\alpha \) of a ray reflected by the photon sphere as

$$\begin{aligned} \alpha =-\bar{a}\log \left( \frac{b}{b_\textrm{m}}-1 \right) +\bar{b}, \end{aligned}$$
(1.1)

where \(\bar{a}\) and \(\bar{b}\) can be calculated by using the metric of the spacetime.Footnote 2 In many spacetimes, \(\bar{a}\) is obtained as analytical forms while \(\bar{b}\) usually is calculated numerically. Analytic forms of \(\bar{a}\) and \(\bar{b}\) have been obtained only in simple spacetimes such as the Schwarzschild spacetime [28, 29], higher dimensional black hole spacetimes [42, 43], charged black hole spacetimes [39, 44, 45], rotating black hole spacetimes [46], and wormhole spacetimes [38, 47]. The analysis in the strong deflection limit has been extended and applied to various astrophysical situations [35, 38,39,40, 44, 46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70].

Iyer and Petters have investigated affine perturbation series of the deflection angle near the photon sphere in the Schwarzschild spacetime in the following form:

$$\begin{aligned} \alpha= & {} ( \sigma _0 +\sigma _1 b_\textrm{p}+\sigma _2 b_\textrm{p}^2 +\sigma _3 b_\textrm{p}^3 +\cdots ) \log \left( \frac{\lambda _0}{b_\textrm{p}} \right) \nonumber \\{} & {} +\rho _0+\rho _1 b_\textrm{p}+\rho _2 b_\textrm{p}^2 +\rho _3 b_\textrm{p}^3 +\cdots , \end{aligned}$$
(1.2)

where \(b_\textrm{p}\) is defined by

$$\begin{aligned} b_\textrm{p} \equiv 1-\frac{b_\textrm{m}}{b}, \end{aligned}$$
(1.3)

and \(\lambda _0\), \(\sigma _0\), \(\sigma _1\), \(\sigma _2\), \(\sigma _3\), \(\rho _0\), \(\rho _1\), \(\rho _2\), and \(\rho _3\) are constant, and they have found the 0th order of the affine perturbation series

$$\begin{aligned} \alpha =\sigma _0 \log \left( \frac{\lambda _0}{b_\textrm{p}} \right) +\rho _0 \end{aligned}$$
(1.4)

is more accurate than the deflection angle by Darwin [40]. Tsukamoto has investigated the affine perturbation series of the deflection angle in the Reissner–Nordström black hole spacetime and has confirmed the 0th order of affine perturbation series (1.4) is more accurate than the form of Eq. (1.1).

How much does the difference of the deflection angles (1.1) and (1.4) affect observables in gravitational lensing? To answer this question, we investigate gravitational lensing in a general asymptotically-flat, static, and spherical symmetric spacetime with the photon sphere by using deflection angle in a form

$$\begin{aligned} \alpha =-\bar{a}\log \left( 1-\frac{b_\textrm{m}}{b} \right) +\bar{b}, \end{aligned}$$
(1.5)

which is the same as the 0th order of affine perturbation series (1.4) with the relations

$$\begin{aligned} \bar{a}= \sigma _0 \end{aligned}$$
(1.6)

and

$$\begin{aligned} \bar{b}= \sigma _0 \log \lambda _0 + \rho _0 \end{aligned}$$
(1.7)

in a usual lens configuration and a retro lensing configuration.

This paper is organized as follows. We investigate the 0th order of affine perturbation series of the deflection angle (1.5) in Sect. 2 and we consider the Schwarzschild black hole, Reissner-Nordström black hole, and the Ellis–Bronnikov wormhole spacetimes in Sect. 3. We investigate gravitational lensing by the photon sphere in a usual lens configuration in Sect. 4 and in a retro lens configuration in Sect. 5. We conclude and discuss Sect. 6. We review gravitational lensing under weak-field approximations in the usual lens configuration in Appendix A. We use the units in which the light speed and Newton’s constant are unity.

2 0th order of affine perturbation series of the deflection angle (1.5)

In this section, we investigate the 0th order of affine perturbation series of the deflection angle (1.5) in a general, asymptotically flat, static, and spherically symmetric spacetime with a metric

$$\begin{aligned} ds^2=-A(r)dt^2+B(r)dr^2+C(r)(d\vartheta ^2+\sin ^2 \vartheta d\varphi ^2) \end{aligned}$$
(2.1)

and with time translational and axial Killing vectors \(t^\mu \partial _\mu =\partial _t\) and \(\varphi ^\mu \partial _\mu =\partial _\varphi \), respectively.

We assume a photon sphere at \(r=r_\textrm{m}\) which is the largest positive solution of \(D(r)=0\), where D(r) is defined by

$$\begin{aligned} D(r)\equiv \frac{C^\prime (r)}{C(r)}-\frac{A^\prime (r)}{A(r)}, \end{aligned}$$
(2.2)

where the prime denotes a differentiation with respect to r. We also assume that A(r), B(r), and C(r) satisfy an asymptotically-flat condition

$$\begin{aligned} \lim _{r\rightarrow \infty } A(r)=\lim _{r\rightarrow \infty } B(r)= \lim _{r\rightarrow \infty } \frac{C(r)}{r^2}=1, \end{aligned}$$
(2.3)

and that A(r), B(r), and C(r) are positive and finite for \(r>r_\textrm{m}\). We assume \(\vartheta =\pi /2\) without loss of generality because of spherical symmetry.

The trajectory of the ray is expressed by

$$\begin{aligned} -A(r)\dot{t}^2+B(r)\dot{r}^2+C(r)\dot{\varphi }^2=0, \end{aligned}$$
(2.4)

where the dot denotes a differentiation with respect to an affine parameter along the trajectory. Conserved energy \(E\equiv -g_{\mu \nu }t^\mu \dot{x}^\nu =A(r)\dot{t}\) and angular momentum \(L\equiv g_{\mu \nu }\varphi ^\mu \dot{x}^\nu =C(r)\dot{\varphi }\) of the ray are constant along the trajectory and the impact parameter of the ray is defined by \(b\equiv L/E\). For simplicity, we assume that the impact parameter is positive in this section. The trajectory can be rewritten as

$$\begin{aligned} \dot{r}^2+V(r)=0, \end{aligned}$$
(2.5)

where V(r) is an effective potential defined by

$$\begin{aligned} V(r)\equiv \frac{L^2 R(r)}{B(r)C(r)}, \end{aligned}$$
(2.6)

where R(r) is defined by

$$\begin{aligned} R(r)\equiv \frac{C(r)}{A(r)b^2}-1. \end{aligned}$$
(2.7)

We assume that the effective potential is negative \(V(r)<0\) for \(r_\textrm{m}<r<\infty \) so that the ray reaches to the photon sphere from spatial infinity.

We concentrate on a scatter case since we are interested in gravitational lensing. In this case, the ray is scattered at a closest distance \(r=r_0>r_\textrm{m}\). Equation (2.4) gives

$$\begin{aligned} A_0\dot{t}_0^2=C_0\dot{\varphi }_0^2 \end{aligned}$$
(2.8)

at the closest distance \(r=r_0\). Here and hereafter, quantities with the subscript 0 denotes the quantities at \(r=r_0\). From Eq. (2.8), the positive impact parameter is expressed by

$$\begin{aligned} b=b(r_0)=\frac{L}{E}=\frac{C_0\dot{\varphi }_0}{A_0\dot{t}_0}=\sqrt{\frac{C_0}{A_0}} \end{aligned}$$
(2.9)

and R can be rewritten as

$$\begin{aligned} R=R(r,r_0)=\frac{A_0C(r)}{A(r)C_0}-1. \end{aligned}$$
(2.10)

At the closest distance, we obtain

$$\begin{aligned} R_0=V_0=0 \end{aligned}$$
(2.11)

and

$$\begin{aligned} R^\prime _0= & {} \frac{D_0}{C_0^2}, \end{aligned}$$
(2.12)
$$\begin{aligned} V^\prime _0= & {} \frac{L^2}{B_0 C_0} R^\prime _0, \end{aligned}$$
(2.13)
$$\begin{aligned} V^{\prime \prime }_0= & {} \left( 2\frac{L^2}{B_0 C_0} \right) ^\prime R^\prime _0+\frac{L^2 }{B_0 C_0} R^{\prime \prime }_0. \end{aligned}$$
(2.14)

In a strong deflection limit \(r_0 \rightarrow r_\textrm{m}+0\) or \(b \rightarrow b_\textrm{m}+0\), where the critical impact parameter \(b_\textrm{m}\) is defined by

$$\begin{aligned} b_\textrm{m}\equiv \lim _{r_0 \rightarrow r_\textrm{m}+0} \sqrt{\frac{C_0}{A_0}}, \end{aligned}$$
(2.15)

we obtain

$$\begin{aligned} D_\textrm{m}\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} D_0=\lim _{r \rightarrow r_\textrm{m}+0} D(r)=0, \end{aligned}$$
(2.16)
$$\begin{aligned} R^\prime _\textrm{m}\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} R^\prime _0=0, \end{aligned}$$
(2.17)
$$\begin{aligned} V^\prime _\textrm{m}\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} V^\prime _0=0. \end{aligned}$$
(2.18)

We can rewrite Eq. (2.4) as

$$\begin{aligned} \left( \frac{dr}{d\varphi } \right) ^2 =\frac{R(r,r_0)C(r)}{B(r)} \end{aligned}$$
(2.19)

and we obtain the deflection angle \(\alpha (r_0)\) of the ray as

$$\begin{aligned} \alpha (r_0)=I(r_0)-\pi , \end{aligned}$$
(2.20)

where \(I(r_0)\) is defined by

$$\begin{aligned} I(r_0)\equiv 2\int ^\infty _{r_0} \frac{dr}{\sqrt{\frac{R(r,r_0)C(r)}{B(r)}}}. \end{aligned}$$
(2.21)

We change the radial coordinate r to a variable z defined by

$$\begin{aligned} z\equiv 1-\frac{r_0}{r} \end{aligned}$$
(2.22)

and we obtain \(I(r_0)\) as

$$\begin{aligned} I(r_0)=\int ^1_0 f(z,r_0) dz, \end{aligned}$$
(2.23)

where \(f(z,r_0)\) is defined by

$$\begin{aligned} f(z,r_0) \equiv \frac{2r_0}{\sqrt{G(z,r_0)}}, \end{aligned}$$
(2.24)

where \(G(z,r_0)\) is defined as

$$\begin{aligned} G(z,r_0) \equiv R(r(z),r_0)\frac{C(r(z))}{B(r(z))}(1-z)^4. \end{aligned}$$
(2.25)

By using the expansions of a function F(r(z)) and its inverse 1/F(r(z)) in the power of z, which are expressed by

$$\begin{aligned} F=F_0+F^\prime _0 r_0 z + \left( \frac{1}{2}F^{\prime \prime }_0 r^2_0+F^\prime _0 r_0 \right) z^2+O\left( z^3 \right) \end{aligned}$$
(2.26)

and

$$\begin{aligned} \frac{1}{F}= & {} \frac{1}{F_0}-\frac{F_0^\prime r_0}{F_0^2} z \nonumber \\{} & {} +\left( \frac{r_0^2 F_0^{\prime 2}}{F_0^3}-\frac{r_0 F_0^\prime }{F_0^2}-\frac{r_0^2 F_0^{\prime \prime }}{2F_0^2} \right) z^2 +O\left( z^3 \right) , \end{aligned}$$
(2.27)

respectively, we obtain the expansion of \(R(r(z),r_0)\) in the power of z as

$$\begin{aligned} R= & {} D_0 r_0 z+ \left[ \frac{r_0}{2} \left( \frac{C_0^{\prime \prime }}{C_0}-\frac{A_0^{\prime \prime }}{A_0} \right) \right. \nonumber \\{} & {} + \left. \left( 1-\frac{A_0^\prime r_0}{A_0}\right) D_0 \right] r_0 z^2+ O\left( z^3 \right) . \end{aligned}$$
(2.28)

From Eqs. (2.25)–(2.28), \(G(z,r_0)\) can be expanded in the power of z as

$$\begin{aligned} G(z,r_0) =c_1(r_0) z+ c_2(r_0) z^2 +O\left( z^3 \right) , \end{aligned}$$
(2.29)

where \(c_1(r_0)\) and \(c_2(r_0)\) are obtained as

$$\begin{aligned} c_1(r_0)= \frac{C_0 D_0 r_0}{B_0} \end{aligned}$$
(2.30)

and

$$\begin{aligned} c_2(r_0)= & {} \frac{C_0 r_0}{B_0} \left\{ D_0 \left[ \left( D_0-\frac{B_0^\prime }{B_0} \right) r_0-3 \right] \right. \nonumber \\{} & {} \left. +\frac{r_0}{2} \left( \frac{C_0^{\prime \prime }}{C_0}-\frac{A_0^{\prime \prime }}{A_0} \right) \right\} , \end{aligned}$$
(2.31)

respectively. In the strong deflection limit \(r_0 \rightarrow r_\textrm{m}+0\), we obtain

$$\begin{aligned} c_1(r_\textrm{m})=0 \end{aligned}$$
(2.32)

and

$$\begin{aligned} c_2(r_\textrm{m})=\frac{C_\textrm{m} r_\textrm{m}^2}{2 B_\textrm{m}} D_\textrm{m}^\prime , \end{aligned}$$
(2.33)

where we define

$$\begin{aligned} A_\textrm{m}\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} A_0=\lim _{r \rightarrow r_\textrm{m}+0} A, \end{aligned}$$
(2.34)
$$\begin{aligned} B_\textrm{m}\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} B_0=\lim _{r \rightarrow r_\textrm{m}+0} B, \end{aligned}$$
(2.35)
$$\begin{aligned} C_\textrm{m}\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} C_0=\lim _{r \rightarrow r_\textrm{m}+0} C, \end{aligned}$$
(2.36)
$$\begin{aligned} D_\textrm{m}^\prime\equiv & {} \lim _{r_0 \rightarrow r_\textrm{m}+0} D_0^\prime =\lim _{r \rightarrow r_\textrm{m}+0} D^\prime =\frac{C_\textrm{m}^{\prime \prime }}{C_\textrm{m}}-\frac{A_\textrm{m}^{\prime \prime }}{A_\textrm{m}} \end{aligned}$$
(2.37)

and then we get

$$\begin{aligned} G(z,r_\textrm{m})=c_2(r_\textrm{m})z^2+O(z^3). \end{aligned}$$
(2.38)

We assume that \(D_\textrm{m}^\prime \) does not vanish. Under the assumption, the term \(I(r_0)\) diverges logarithmically in the strong deflection limit \(r_0 \rightarrow r_\textrm{m}+0\).Footnote 3 We define the divergent part \(I_\textrm{D}(r_0)\) of the term \(I(r_0)\) as

$$\begin{aligned} I_\textrm{D}(r_0)\equiv & {} \int ^1_0 f_\textrm{D} (z,r_0) dz \nonumber \\= & {} \frac{4r_0}{\sqrt{c_2(r_0)}} \log \frac{\sqrt{c_2(r_0)}+\sqrt{c_1(r_0)+c_2(r_0)}}{\sqrt{c_1(r_0)}}, \end{aligned}$$
(2.39)

where \(f_\textrm{D}(z,r_0)\) is defined as

$$\begin{aligned} f_\textrm{D}(z,r_0)\equiv \frac{2r_0}{\sqrt{c_1(r_0)z+c_2(r_0)z^2}}. \end{aligned}$$
(2.40)

We expand \(c_1(r_0)\) and \(b(r_0)\) in powers of \(r_0-r_\textrm{m}\) as

$$\begin{aligned} c_1(r_0)=\frac{C_\textrm{m} r_\textrm{m} D^\prime _\textrm{m}}{B_\textrm{m}} (r_0-r_\textrm{m})+O\left( (r_0-r_\textrm{m})^2\right) \end{aligned}$$
(2.41)

and

$$\begin{aligned} b(r_0)=b_\textrm{m} +\frac{1}{4}\sqrt{\frac{C_\textrm{m}}{A_\textrm{m}}}D_\textrm{m}^\prime (r_0-r_\textrm{m})^2 +O\left( (r_0-r_\textrm{m})^3\right) , \end{aligned}$$
(2.42)

respectively. Therefore, we obtain the relation, in the strong deflection limit \(r_0 \rightarrow r_\textrm{m}+0\) or \(b \rightarrow b_\textrm{m}+0\),

$$\begin{aligned}{} & {} \lim _{r_0 \rightarrow r_\textrm{m} +0} c_1(r_0) \nonumber \\{} & {} \quad =\lim _{b \rightarrow b_\textrm{m} +0} \frac{2C_\textrm{m}r_\textrm{m}\sqrt{D_\textrm{m}^\prime }}{B_\textrm{m}} \left( \frac{b}{b_\textrm{m}}-1 \right) ^\frac{1}{2} \nonumber \\{} & {} \quad =\lim _{b \rightarrow b_\textrm{m} +0} \frac{2C_\textrm{m}r_\textrm{m}\sqrt{D_\textrm{m}^\prime }}{B_\textrm{m}} \left( 1-\frac{b_\textrm{m}}{b} \right) ^\frac{1}{2}. \end{aligned}$$
(2.43)

By using the relation, we express the divergent part \(I_\textrm{D}(b)\) in the strong deflection limit \(b \rightarrow b_\textrm{m}+0\) as

$$\begin{aligned} I_\textrm{D}(b)= & {} -\frac{r_\textrm{m}}{\sqrt{c_2(r_\textrm{m})}} \log \left( 1-\frac{b_\textrm{m}}{b} \right) +\frac{r_\textrm{m}}{\sqrt{c_2(r_\textrm{m})}} \log r_\textrm{m}^2 D_\textrm{m}^\prime \nonumber \\{} & {} +O\left( \left( 1-\frac{b_\textrm{m}}{b} \right) \log \left( 1-\frac{b_\textrm{m}}{b} \right) \right) . \end{aligned}$$
(2.44)

We define the regular part \(I_\textrm{R}(r_0)\) of the term \(I(r_0)\) as

$$\begin{aligned} I_\textrm{R}(r_0) \equiv \int ^1_0 f_\textrm{R} (z,r_0) dz, \end{aligned}$$
(2.45)

where \(f_\textrm{R} (z,r_0)\) is defined as

$$\begin{aligned} f_\textrm{R} (z,r_0) \equiv f(z,r_0)-f_\textrm{D}(z,r_0), \end{aligned}$$
(2.46)

and expand it in power of \(r_0 -r_\textrm{m}\) and we only consider the first term in which we are interested. Then, we get

$$\begin{aligned} I_\textrm{R}(r_0)= & {} \int ^1_0 f_\textrm{R} (z,r_\textrm{m}) dz, \nonumber \\{} & {} +O\left( \left( 1-\frac{r_\textrm{m}}{r_0} \right) \log \left( 1-\frac{r_\textrm{m}}{r_0} \right) \right) \end{aligned}$$
(2.47)

or

$$\begin{aligned} I_\textrm{R}(b)= & {} \int ^1_0 f_\textrm{R} (z,b_\textrm{m}) dz, \nonumber \\{} & {} +O\left( \left( 1-\frac{b_\textrm{m}}{b} \right) \log \left( 1-\frac{b_\textrm{m}}{b} \right) \right) . \end{aligned}$$
(2.48)

From \(I=I_\textrm{D}+I_\textrm{R}\), we obtain the deflection angle in the strong deflection limit \(b\rightarrow b_\textrm{m}+0\) as

$$\begin{aligned} \alpha (b)= & {} -\bar{a} \log \left( 1-\frac{b_\textrm{m}}{b} \right) +\bar{b} \nonumber \\{} & {} +O\left( \left( 1-\frac{b_\textrm{m}}{b} \right) \log \left( 1-\frac{b_\textrm{m}}{b} \right) \right) , \end{aligned}$$
(2.49)

where \(\bar{a}\) and \(\bar{b}\) are given by

$$\begin{aligned} \bar{a}=\sqrt{\frac{2B_\textrm{m} A_\textrm{m}}{C^{\prime \prime }_\textrm{m} A_\textrm{m}- C_\textrm{m} A^{\prime \prime }_\textrm{m}}} \end{aligned}$$
(2.50)

and

$$\begin{aligned} \bar{b}=\bar{a} \log \left[ r^2_\textrm{m} \left( \frac{C^{\prime \prime }_\textrm{m}}{C_\textrm{m}}- \frac{A^{\prime \prime }_\textrm{m}}{A_\textrm{m}} \right) \right] +I_\textrm{R} (b_\textrm{m}) -\pi , \end{aligned}$$
(2.51)

respectively.

3 Examples of deflection angles

In this section, we apply the formulas in the previous section to the Schwarzschild black hole, Reissner–Nordström black hole and Ellis–Bronnikov wormhole spacetimes. We obtain \(\bar{a}\) and \(\bar{b}\) in the deflection angles (1.1) and (1.5) and we show the percent errors of the deflection angles (1.1) and (1.5) defined by

$$\begin{aligned} \frac{\alpha \, \textrm{of}\, \textrm{Eq}.\,(2.20)-\alpha \, \textrm{of}\, \textrm{Eq}.\, (1.1)}{\alpha \, \textrm{of} \, \textrm{Eq}.\,(2.20)} \times 100 \end{aligned}$$
(3.1)

and

$$\begin{aligned} \frac{\alpha \, \textrm{of}\, \textrm{Eq}.\,(2.20)-\alpha \, \textrm{of}\, \textrm{Eq}.\, (1.5)}{\alpha \, \textrm{of} \, \textrm{Eq}.\,(2.20)} \times 100, \end{aligned}$$
(3.2)

respectively.

3.1 Schwarzschild black hole

In the Schwarzschild spacetime with a mass M, the functions A(r), B(r), and C(r) are given by

$$\begin{aligned} A(r)=1-\frac{2M}{r}, \end{aligned}$$
(3.3)
$$\begin{aligned} B(r)=\frac{1}{1-\frac{2M}{r}}, \end{aligned}$$
(3.4)

and

$$\begin{aligned} C(r)=r^2, \end{aligned}$$
(3.5)

respectively.

The critical impact parameter is given by \(b_\textrm{m}= 3\sqrt{3}M\) and the photon sphere is at \(r=r_\textrm{m}=3M\). As obtained in Refs. [28, 29], coefficients \(\bar{a}\) and \(\bar{b}\) of the deflection angles in the strong deflection limit are obtained as

$$\begin{aligned} \bar{a}=1 \end{aligned}$$
(3.6)

and

$$\begin{aligned} \bar{b}=\log 216(7-4\sqrt{3}) -\pi , \end{aligned}$$
(3.7)

respectively. The percent errors of the deflection angles (1.1) and (1.5) are shown in Fig. 1.

Fig. 1
figure 1

The percent errors of deflection angles in the Schwarzschild and Reissner–Nordström black hole spacetimes. The percent errors of the deflection angles in Eqs. (1.1) and (1.5) against the deflection angle in Eq. (2.20) are shown in the upper and lower panels, respectively. Wide solid (red), wide dashed (green), narrow solid (blue), and narrow dashed (black) curves show the percent errors in the cases of \(Q/M=0\), 0.6, 0.8, and 1, respectively

Full size image

3.2 Reissner–Nordström black hole

A Reissner–Nordström black hole is often considered as the simplest extension of the Schwarzschild black hole. Gravitational lensing [29, 39, 44, 53, 56, 72, 73], shadow [7, 74,75,76,77,78], and time delay [79] by the Reissner-Nordström black hole have been investigated.

Eiroa has considered gravitational lensing by the Reissner–Nordström black hole in the strong deflection limit \(b \rightarrow b_\textrm{m}+0\) in numerical [53]. Coefficients \(\bar{a}\) in an analytical form and \(\bar{b}\) in numerical have been obtained by Bozza [29]. The analytical forms of \(\bar{a}\) and \(\bar{b}\) have been obtained in Refs. [39, 44].

In the Reissner-Nordström black hole spacetime for \(0\le Q^2/M^2\le 1\), where Q is an electrical charge,Footnote 4 the functions A(r), B(r), and C(r) are given by

$$\begin{aligned} A(r)= & {} 1-\frac{2M}{r}+\frac{Q^2}{r^2}, \end{aligned}$$
(3.8)
$$\begin{aligned} B(r)= & {} \frac{1}{1-\frac{2M}{r}+\frac{Q^2}{r^2}}, \end{aligned}$$
(3.9)

and

$$\begin{aligned} C(r)=r^2, \end{aligned}$$
(3.10)

respectively.

We obtain \(r_\textrm{m}\) as

$$\begin{aligned} r_\textrm{m}=\frac{3M+\sqrt{9M^2-8Q^2}}{2} \end{aligned}$$
(3.11)

and \(b_\textrm{m}\) as

$$\begin{aligned} b_\textrm{m}=\frac{r_\textrm{m}^2}{\sqrt{Mr_\textrm{m}-Q^2}}. \end{aligned}$$
(3.12)

The coefficients \(\bar{a}\) and \(\bar{b}\) of the deflection angles in the strong deflection limit are given by

$$\begin{aligned} \bar{a}=\frac{r_\textrm{m}}{\sqrt{3Mr_\textrm{m}-4Q^2}} \end{aligned}$$
(3.13)

and

$$\begin{aligned} \bar{b}= & {} \bar{a} \log \left[ \frac{8(3Mr_\textrm{m}-4Q^2)^3}{M^2 r_\textrm{m}^2 (Mr_\textrm{m}-Q^2)^2} \right. \nonumber \\{} & {} \left. \times \left( 2\sqrt{Mr_\textrm{m}-Q^2}-\sqrt{3Mr_\textrm{m}-4Q^2} \right) ^2 \right] -\pi , \end{aligned}$$
(3.14)

respectively. We show the percent errors of the deflection angles (1.1) and (1.5) in Fig. 1.

3.3 An Ellis–Bronnikov wormhole

An Ellis–Bronnikov wormhole is the solution of Einstein equations with a phantom scalar field [82, 83]. The deflection angle in the Ellis–Bronnikov wormhole spacetime has investigated by Chetouani and Clément [84] and it has been revisited by several authors [63, 85,86,87,88,89,90,91]. The visual appearance of the wormhole [92] and images due to the photon sphere [31, 39, 47, 48, 63, 85, 90, 93,94,95,96,97] have been investigated.

We cannot apply directly Bozza’s method [29] to an ultrastatic spacetime with a time translational Killing vector with a constant norm such as the Ellis–Bronnikov wormhole spacetime.Footnote 5 An extended method for the ultrastatic spacetime has been investigated and the deflection angle in the strong deflection limit in the Ellis–Bronnikov wormhole spacetime has been calculated in Refs. [38, 39, 47].

A line element in the Ellis–Bronnikov wormhole spacetime is given by

$$\begin{aligned} ds^2=-dt^2+dl^2+(l^2+a^2)(d\vartheta ^2+\sin ^2 \vartheta d\varphi ^2), \end{aligned}$$
(3.15)

where a is a positive constant. We cannot apply formulas in Sect. 2 in a radial coordinate l since the photon sphere is at \(l=0\). We use a radial coordinate r defined by \(r\equiv l+p\), where p is a positive constant, so that the photon sphere is at \(r=r_\textrm{m}=p>0\). Under the radial coordinate r, we get

$$\begin{aligned} A(r)= & {} 1, \end{aligned}$$
(3.16)
$$\begin{aligned} B(r)= & {} 1, \end{aligned}$$
(3.17)

and

$$\begin{aligned} C(r)=(r-p)^2+a^2. \end{aligned}$$
(3.18)

The critical impact parameter is given by \(b_\textrm{m}=a\) and coefficients of the deflection angles in the strong deflection limit are obtained as [38]

$$\begin{aligned} \bar{a}=1 \end{aligned}$$
(3.19)

and

$$\begin{aligned} \bar{b}=3 \log 2 -\pi . \end{aligned}$$
(3.20)
Fig. 2
figure 2

The percent errors of deflection angles in the Ellis–Bronnikov wormhole spacetime. Solid (red) and dashed (green) curves denote the percent errors of the deflection angles in Eqs. (1.1) and (1.5), respectively, against the deflection angle in Eq. (2.20)

Full size image

The percent errors of the deflection angles (1.1) and (1.5) are shown in Fig. 2.

4 Gravitational lensing in usual lens configuration

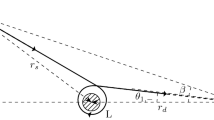
We consider that a ray with an impact parameter b, which is emitted by a source S with a source angle \(\phi \), is deflected with a deflection angle \(\alpha \) by a lens object L and its image I with an image angle \(\theta \) is observed by an observer O as shown in Fig. 3. The distances between O and S, between L and S, and between O and L are denoted by \(D_{\textrm{os}}\), \(D_{\textrm{ls}}\), and \(D_{\textrm{ol}}=D_{\textrm{os}}-D_{\textrm{ls}}\), respectively.

Fig. 3
figure 3

Configuration of gravitational lensing. A ray with an impact parameter b is emitted by a source S with a source angle \(\phi \), it is reflected with an effective deflection angle \(\bar{\alpha }\) by a lens object L, and it is observed by an observer O as an image I with an image angle \(\theta \). \(D_{\textrm{os}}\), \(D_{\textrm{ls}}\), and \(D_{\textrm{ol}}=D_{\textrm{os}}-D_{\textrm{ls}}\) denote distances between O and S, between L and S, and between O and L, respectively

Full size image

By using an effective deflection angle \(\bar{\alpha }\) defined by

$$\begin{aligned} \bar{\alpha }= \alpha \quad \textrm{mod} \quad 2\pi , \end{aligned}$$
(4.1)

a small-angle lens equation [99] is expressed by

$$\begin{aligned} D_{\textrm{ls}} \bar{\alpha }= D_{\textrm{os}}(\theta -\phi ), \end{aligned}$$
(4.2)

where we have assumed \(\left| \bar{\alpha } \right| \ll 1\), \(\left| \theta \right| = \left| b \right| /D_{\textrm{ol}} \ll 1\), and \(\left| \phi \right| \ll 1\). The deflection angle \(\alpha \) can be expressed by

$$\begin{aligned} \alpha =\bar{\alpha } + 2\pi N, \end{aligned}$$
(4.3)

where N is a winding number of the ray. We define an angle \(\theta ^0_N\) by

$$\begin{aligned} \alpha (\theta ^0_N)=2\pi N \end{aligned}$$
(4.4)

and we expand the deflection angle \(\alpha (\theta )\) around \(\theta =\theta ^0_N\) as

$$\begin{aligned} \alpha (\theta )=\alpha (\theta ^0_N)+ \left. \frac{d \alpha }{d \theta } \right| _{\theta =\theta ^0_N} (\theta -\theta ^0_N) +O\left( \left( \theta -\theta ^0_N \right) ^2 \right) . \end{aligned}$$
(4.5)
Table 1 Gravitational lensing in a usual lens configuration with the deflection angle (1.5): \(\bar{a}\), \(\bar{b}\), \(2\theta _{\infty }\), \(2\theta _{\textrm{E}1}\), \( \bar{s}\), \( \mu _{1\textrm{tot}}(\phi )\), and \(\bar{\textrm{r}}\) in the Schwarzschild and Reissner–Nordström black hole spacetimes for given Q/M and in the Ellis–Bronnikov wormhole spacetime are shown. We set the mass \(M=6.5\times 10^9 M_{\odot }\), distances \(D_{\textrm{os}}=33.6\) Mpc and \(D_{\textrm{ol}}=D_{\textrm{ls}}=16.8\) Mpc, and the source angle \(\phi =1\) arcsecond. The parameter \(a=4 \sqrt{2/\pi } \left( D_{\textrm{ls}}D_{\textrm{ol}}/D_{\textrm{os}} \right) ^\frac{1}{4} M^\frac{3}{4}\) is set so that \(2\theta _{\textrm{E}0}\) of the Ellis–Bronnikov wormhole is the same value as \(2\theta _{\textrm{E}0}=2.52\)arcsecond of the Schwarzschild and Reissner–Nordström black holes
Full size table

4.1 By using the deflection angle (1.5)

We express the 0th order of affine perturbation series of the deflection angle (1.5) as

$$\begin{aligned} \alpha (\theta )= & {} -\bar{a} \log \left( 1-\frac{\theta _\infty }{\theta } \right) +\bar{b} \nonumber \\{} & {} +O\left( \left( 1-\frac{\theta _\infty }{\theta } \right) \log \left( 1-\frac{\theta _\infty }{\theta } \right) \right) , \end{aligned}$$
(4.6)

where \(\theta _\infty \equiv b_\textrm{m}/D_{\textrm{ol}}\) is the image angle of the photon sphere. From Eqs. (4.4) and (4.6), we get

$$\begin{aligned} \theta ^0_N=\frac{\theta _\infty }{1-e^\frac{\bar{b}-2\pi N}{\bar{a}}}. \end{aligned}$$
(4.7)

From

$$\begin{aligned} \left. \frac{d \alpha }{d \theta } \right| _{\theta =\theta ^0_N}=\frac{\bar{a}\theta _\infty }{\theta ^0_N(\theta _\infty -\theta ^0_N)}, \end{aligned}$$
(4.8)

and Eqs. (4.3)–(4.5) and (4.7), the effective deflection angle \(\bar{\alpha }(\theta _N)\), where \(\theta =\theta _N\) is the positive solution of the lens equation for a positive winding number N, is obtained as

$$\begin{aligned} \bar{\alpha }(\theta _N)=-\frac{\bar{a}\theta _\infty (\theta _N-\theta _N^0)}{\left( \theta _N^0 \right) ^2 e^\frac{\bar{b}-2\pi N}{\bar{a}}}. \end{aligned}$$
(4.9)

By substituting the effective deflection angle (4.9) to the lens Eq. (4.2), we obtain the image angle as

$$\begin{aligned} \theta _N (\phi ) \sim \theta _N^0 +\frac{\left( \theta _N^0 \right) ^2 e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}}}{\bar{a}\theta _\infty D_{\textrm{ls}}} \left( \phi -\theta _N^0 \right) \end{aligned}$$
(4.10)

and the image angle of an Einstein ring with the winding number N as

$$\begin{aligned} \theta _{EN} \equiv \theta _N (0) \sim \theta _N^0 \left( 1- \frac{\left( \theta _N^0 \right) ^2 e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}}}{\bar{a}\theta _\infty D_{\textrm{ls}}} \right) . \end{aligned}$$
(4.11)

The difference of image angles between the outermost image and the photon sphere is given by

$$\begin{aligned} \bar{s}\equiv \theta _1 -\theta _\infty \sim \theta _1^0-\theta _\infty ^0 =\frac{\theta _\infty e^\frac{\bar{b}-2\pi }{\bar{a}}}{1-e^\frac{\bar{b}-2\pi }{\bar{a}}}. \end{aligned}$$
(4.12)

The magnification of the image is given by

$$\begin{aligned} \mu _N(\phi ) \equiv \frac{\theta _N}{\phi } \frac{d \theta _N}{d \phi } \sim \frac{ \theta _\infty ^2 e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}}}{\phi \bar{a} D_{\textrm{ls}} \left( 1-e^\frac{\bar{b}-2\pi N}{\bar{a}} \right) ^3 }. \end{aligned}$$
(4.13)

The ratio of the magnifications of the outermost image to the sum of the other images is obtained by

$$\begin{aligned} \bar{r}\equiv \frac{\mu _1}{\sum ^\infty _{N=2} \mu _N} \sim \frac{e^\frac{\bar{b}-2\pi }{\bar{a}}}{\left( 1-e^\frac{\bar{b}-2\pi }{\bar{a}} \right) ^3\sum ^\infty _{N=2} \frac{e^\frac{\bar{b}-2\pi N}{\bar{a}}}{\left( 1-e^\frac{\bar{b}-2\pi N}{\bar{a}} \right) ^3}}.\nonumber \\ \end{aligned}$$
(4.14)

Notice that we can get a negative solution \(\theta =\theta _{-N}(\phi )\sim -\theta _N(\phi )\) of the lens equation for each winding number N while we have concentrated on the positive solution \(\theta =\theta _N(\phi )\). The separation of the positive and negative image angles for each N is given by \(\theta _N(\phi )-\theta _{-N}(\phi )\sim 2\theta _N(\phi )\). The magnification of the negative image angle \(\theta _{-N}(\phi )\) is given by \(\mu _{-N}(\phi )\sim -\mu _{N}(\phi )\). The total magnification \(\mu _{N\textrm{tot}}(\phi )\) of the positive and negative image angles for each N is given by

$$\begin{aligned} \mu _{N\textrm{tot}}(\phi ) \equiv \left| \mu _{N}(\phi ) \right| {+} \left| \mu _{{-}N}(\phi ) \right| \sim \frac{2 \theta _\infty ^2 e^\frac{\bar{b}{-}2\pi N}{\bar{a}}D_{\textrm{os}}}{\phi \bar{a} D_{\textrm{ls}} \left( 1{-}e^\frac{\bar{b}{-}2\pi N}{\bar{a}} \right) ^3 }.\nonumber \\ \end{aligned}$$
(4.15)

Table 1 shows the observables with the deflection angle (1.5).

4.2 By using the deflection angle (1.1)

As a reference, we consider the deflection angle (1.1) in the strong deflection limit. It is rewritten in

$$\begin{aligned} \alpha (\theta )= & {} -\bar{a} \log \left( \frac{\theta }{\theta _\infty }-1 \right) +\bar{b}. \end{aligned}$$
(4.16)

By using Eqs. (4.4) and (4.16), we obtain

$$\begin{aligned} \theta ^0_N= \theta _\infty \left( 1+e^\frac{\bar{b}-2\pi N}{\bar{a}} \right) . \end{aligned}$$
(4.17)

From

$$\begin{aligned} \left. \frac{d \alpha }{d \theta } \right| _{\theta =\theta ^0_N}=\frac{\bar{a}}{\theta _\infty -\theta ^0_N}, \end{aligned}$$
(4.18)

and Eqs. (4.3)–(4.5) and (4.17), we obtain the effective deflection angle \(\bar{\alpha }(\theta _N)\) as

$$\begin{aligned} \bar{\alpha }(\theta _N)=-\frac{\bar{a}(\theta _N-\theta _N^0)}{\theta _\infty e^\frac{\bar{b}-2\pi N}{\bar{a}}}. \end{aligned}$$
(4.19)

From Eqs. (4.2) and (4.19), we get the image angle

$$\begin{aligned} \theta _N (\phi ) \sim \theta _N^0 +\frac{\theta _\infty e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}}}{\bar{a} D_{\textrm{ls}}} \left( \phi -\theta _N^0 \right) , \end{aligned}$$
(4.20)

the image angle of an Einstein ring for each N

$$\begin{aligned} \theta _{EN} \sim \theta _N^0 \left( 1- \frac{\theta _\infty e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}}}{\bar{a} D_{\textrm{ls}}} \right) , \end{aligned}$$
(4.21)

and the difference of image angles between the outermost image and the photon sphere

$$\begin{aligned} \bar{s} \sim \theta _1^0-\theta _\infty ^0 =\theta _\infty e^\frac{\bar{b}-2\pi }{\bar{a}}. \end{aligned}$$
(4.22)

The magnification of the image is obtained as

$$\begin{aligned} \mu _N(\phi ) \sim \frac{ \theta _\infty ^2 e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}} \left( 1+e^\frac{\bar{b}-2\pi N}{\bar{a}} \right) }{\phi \bar{a} D_{\textrm{ls}} } \end{aligned}$$
(4.23)

and the ratio of the magnifications of the outermost image to the sum of the other images is given by

$$\begin{aligned} \bar{r} \sim \frac{\left( e^\frac{4\pi }{\bar{a}} -1\right) \left( e^\frac{2\pi }{\bar{a}} +e^\frac{\bar{b}}{\bar{a}}\right) }{e^\frac{4\pi }{\bar{a}}+e^\frac{2\pi }{\bar{a}}+e^\frac{\bar{b}}{\bar{a}}}. \end{aligned}$$
(4.24)

The separation of two images are obtained as \(2\theta _N(\phi )\) and their total magnification for each N is given by

$$\begin{aligned} \mu _{N\textrm{tot}}(\phi ) \sim \frac{ 2 \theta _\infty ^2 e^\frac{\bar{b}-2\pi N}{\bar{a}}D_{\textrm{os}} \left( 1+e^\frac{\bar{b}-2\pi N}{\bar{a}} \right) }{\phi \bar{a} D_{\textrm{ls}} }. \end{aligned}$$
(4.25)

The observables with the deflection angle (1.1) are shown in Table 2.

Table 2 Gravitational lensing in the usual lens configuration with deflection angle (1.1): We set M, \(D_{\textrm{os}}\), \(D_{\textrm{ol}}\), \(D_{\textrm{ls}}\), \(\phi \), and a to be the same values as the ones in Table 1. We do not show \(\bar{a}\), \(\bar{b}\), and \(2\theta _{\infty }\) because they give the same values as the ones in Table 1
Full size table

5 Retro lensing

Gravitational lensing with the deflection angle \(\alpha \sim \pi \) is called retro lensing. Retro lensing in black hole spacetimes [44, 56, 57, 100,101,102,103], wormhole spacetimes [47, 63], naked singularity spacetimes [81, 104], and black bounce spacetimes [105, 106] were investigated. In this section, we investigate retro lensing with a configuration that a lens object L with a photon sphere, an observer O, and a source S are almost aligned in the order as shown in Fig. 4.

Fig. 4
figure 4

Configuration of retro lensing. A ray emitted by a source S is reflected with an effective deflection angle \(\bar{\alpha }\) by the photon sphere of a lens object L and it reaches to an observer O. We introduce an source angle \(\beta \equiv \angle \)OLS and an angle \(\bar{\theta }\) defined by an angle between a line LS and the ray at S

Full size image

A light ray emitted by the source is reflected by the photon sphere of the lens object and it is observed by the observer as an image I. The Ohanian lens equation [24, 99] is expressed as

$$\begin{aligned} \beta =\pi -\bar{\alpha }(\theta )+\theta +\bar{\theta }, \end{aligned}$$
(5.1)

where \(\beta \sim 0\) is a source angle defined by \(\angle \)OLS and \(\bar{\theta }\) is an angle between a line LS and the light ray at S. We also assume that the terms \(\theta =b/D_{\textrm{ol}}\) and \(\bar{\theta }=b/D_{\textrm{ls}}\) are small and that they can be neglected in the lens equation. We obtain a positive solution \(\theta =\theta _N\) for every winding number N and its magnification is obtained as [44, 56, 57]

$$\begin{aligned} \mu _N (\beta )=- \frac{D^2_{\textrm{os}}}{D^2_{\textrm{ls}}} s(\beta ) \theta _N \frac{d\theta _N}{d \beta }, \end{aligned}$$
(5.2)

where \(s(\beta )\) for a point source is given by

$$\begin{aligned} s(\beta )=\frac{1}{\beta } \end{aligned}$$
(5.3)

and for an uniform-luminous disk with a size \(\beta _\textrm{s} \equiv R_\textrm{s}/D_{\textrm{ls}}\), where \(R_\textrm{s}\) is the radius of the source, on a source plane,

$$\begin{aligned} s(\beta )=\frac{1}{\pi \beta _\textrm{s}^2} \int _\textrm{Disk} d\beta ^\prime d \Phi , \end{aligned}$$
(5.4)

where \(\beta ^\prime \) is a radial coordinate divided by \(D_{\textrm{ls}}\) on the source plane, \(\Phi \) is an azimuthal coordinate around the origin of the coordinates on the source plane. By fixing the point of an intersection between an axis \(\beta =0\) and the source plane as the origin of the coordinates, \(s(\beta )\) is given by

Table 3 Retro lensing with deflection angle (1.5): The total magnification \(\mu _{0\textrm{tot}}(0)\) and apparent magnitude of the sun lensed by a photon sphere at \(D_{\textrm{ol}}=0.01\)pc We have assumed \(M=60 M_{\odot }\) for the Schwarzschild and Reissner–Nordström black hole and \(a=4 \sqrt{2/\pi } \left( D_{\textrm{ls}}D_{\textrm{ol}}/D_{\textrm{os}} \right) ^\frac{1}{4} M^\frac{3}{4}\) for the Ellis–Bronnikov wormhole
Full size table
Table 4 Retro lensing with deflection angle (1.1): We have assumed the same parameters as Table 3
Full size table
$$\begin{aligned} s(\beta )= & {} \frac{2}{\pi \beta _\textrm{s}^2} \left[ \pi \left( \beta _\textrm{s}-\beta \right) \right. \nonumber \\{} & {} \left. + \int ^{\beta +\beta _\textrm{s}}_{-\beta +\beta _\textrm{s}} \arccos \frac{\beta ^2+\beta ^{\prime 2}-\beta _\textrm{s}^2}{2 \beta \beta ^\prime } d\beta ^\prime \right] \end{aligned}$$
(5.5)

for \(\beta \le \beta _\textrm{s}\) and

$$\begin{aligned} s(\beta )=\frac{2}{\pi \beta _\textrm{s}^2} \int ^{\beta +\beta _\textrm{s}}_{\beta -\beta _\textrm{s}} \arccos \frac{\beta ^2+\beta ^{\prime 2}-\beta _\textrm{s}^2}{2 \beta \beta ^\prime } d\beta ^\prime \end{aligned}$$
(5.6)

for \(\beta >\beta _\textrm{s}\). A perfectly-aligned case \(\beta =0\) for the uniform-luminous disk with the finite size, we obtain

$$\begin{aligned} s(0)=\frac{2}{\beta _\textrm{s}}. \end{aligned}$$
(5.7)

5.1 By using the deflection angle (1.5)

We investigate retro lensing by using the deflection angle (1.5) or (4.6). From Eqs. (4.3), (4.6), and (5.1), we obtain the image angle \(\theta _{N}\) with the winding number N as

$$\begin{aligned} \theta _N (\beta )=\frac{\theta _\infty }{1-e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}}} \end{aligned}$$
(5.8)

and its magnification as

$$\begin{aligned} \mu _N (\beta ) =- \frac{D_{\textrm{os}}^2}{D_{\textrm{ls}}^2} \frac{\theta _\infty ^2 e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}} }{ \bar{a} \left( 1-e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}}\right) ^3} s(\beta ). \end{aligned}$$
(5.9)

We also get a negative image angle as \(\theta _{-N} (\beta )\sim -\theta _N (\beta )\) and their total magnification as

$$\begin{aligned} \mu _{N\textrm{tot}}(\beta ) \sim \frac{2D_{\textrm{os}}^2}{D_{\textrm{ls}}^2} \frac{\theta _\infty ^2 e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}} }{ \bar{a} \left( 1-e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}}\right) ^3} s(\beta ). \end{aligned}$$
(5.10)

Table 3 shows observables by retro lensing with the deflection angle (1.5).

5.2 By using the deflection angle (1.1)

As a reference, we consider retro lensing with the deflection angle (1.1). From Eqs. (4.3), (4.16), and (5.1), we obtain the image angle \(\theta _{N}\) with the winding number N as

$$\begin{aligned} \theta _N (\beta )=\theta _\infty \left( 1+e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}}\right) \end{aligned}$$
(5.11)

and its magnification as

$$\begin{aligned} \mu _N (\beta ) =- \frac{D_{\textrm{os}}^2}{D_{\textrm{ls}}^2} \frac{\theta _\infty ^2 e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}} \left( 1+e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}}\right) }{ \bar{a}} s(\beta ).\nonumber \\ \end{aligned}$$
(5.12)

The total magnification of the positive and negative images for the winding number N is obtained as

$$\begin{aligned} \mu _{N\textrm{tot}}(\beta ) \sim \frac{2D_{\textrm{os}}^2}{D_{\textrm{ls}}^2} \frac{\theta _\infty ^2 e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}} }{ \bar{a} \left( 1-e^\frac{\beta +\bar{b}-\pi (1+2N)}{\bar{a}}\right) ^3} s(\beta ). \end{aligned}$$
(5.13)

The observables by retro lensing with the deflection angle (1.1) are shown in Table 4.

6 Conclusion and discussion

We have shown the 0th order of affine perturbation series of the deflection angle (1.5) is more accurate than the deflection angle (1.1), which is often used in the strong deflection limit \(b\rightarrow b_\textrm{m}+0\), not only in the black hole spacetimes but also in the wormhole spacetime. We have investigated gravitational lensing by using the 0th order of affine perturbation series of the deflection angle (1.5). As shown Tables 1 and 2, under the usual lens configuration with the photon sphere, the observables obtained by using the 0th order of the affine perturbation series of the deflection angle (1.5) and by using the deflection angle (1.1) in the strong deflection limit are almost the same. Thus, we can ignore the effect of the hidden errors in the deflection angle (1.1) in the strong deflection limit on the observables in the usual lens configuration.

On the other hand, in a retro lensing configuration, the error of the deflection angle (1.1) in the strong-deflection-limit analysis increases to be several percents and the error of the 0th order of affine perturbation series of the deflection angle (1.5) reduces to be the almost half of the error of the deflection angle (1.1). We have shown that the hidden errors in the deflection angle (1.1) can affect on the magnification by a dozen percent. Thus, we conclude that we should use the 0th order of affine perturbation series of the deflection angle  (1.5) rather than the deflection angle (1.1) when we consider retro lensing. The 0th order of affine perturbation series of the deflection angle can give a brighter magnification by a dozen percent than the one by using the deflection angle (1.1) in the strong-deflection-limit analysis.

On this paper, we have investigated gravitational lensing by a photon sphere in a general, asymptotically flat, static, and spherically symmetric spacetime with a photon sphere. One might think that some numerical treatments of gravitational lensing in given spacetimes are more practical than analytical treatments and one does not need analytical studies. However, we can reveal universal property of the gravitational lensing in the general spacetime with the photon sphere by using the analytical method while we have to rely on concrete examples by numerical methods. Therefore, it is still meaningful to consider the analytical treatment even if some examples were calculated numerically.

Gravitational lensing by rotating black holes in strong deflection limit has been investigated in Refs. [46, 54, 57, 58, 58, 60, 70]. On this paper, we have concentrated on asymptotically flat, static, and spherically symmetric spacetimes and our results can be extended to the rotating black holes and alternatives. The extension to the rotating case is left as future work.