Weak radiative decay $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ using light-cone sum rules

Abstract

We calculate the decay width of the $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ using light-cone sum rules. For the initial quark radiation an effective Hamiltonian is constructed, where the internal quark line shrinks to a point. The final quark radiation is studied within the full theory. The leading twist light-cone distribution amplitudes of the $\Sigma ^+$ serve as the non-perturbative input for the sum rules calculation, and the perturbative kernel is calculated at leading order. The branching fraction we obtain is $\mathcal{B}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )=1.03\pm 0.36 \times 10^{-4}$, which is below the recent upper limits $<2.6 \times 10^{-4}$ and $<4.4 \times 10^{-4}$ given by the Belle collaboration and the BESIII collaboration, respectively.

1 Introduction

Weak radiative decays of charmed hadrons are an ideal platform for investigating the interplay of the strong and the weak interactions. Unlike the flavor-changing neutral-current transition of bottom hadrons, the penguin contribution in such charm decays is highly suppressed. As a result, the weak radiative decay of charmed hadrons are Cabibbo-favored and dominated by long-distance non-perturbative effects, where the decay is induced by internal W-exchange bremsstrahlung processes such as $cd\rightarrow us\gamma$. Studying the weak radiative decays of charmed hadrons both from the experimental and the theoretical side can help us to understand the strong dynamics inside hadrons.

Over the past few decades, there are several measurements of the weak radiative decays of charmed meson [1,2,3], and the corresponding theoretical researches [4,5,6,7,8,9,10,11,12,13,14,15,16]. However, the experimental researches in the charmed baryon sector are rare. In 2022, the Belle collaboration announced the first search for the weak radiative decays $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ and $\Xi _c^0\rightarrow \Xi ^0 \gamma$ [17], where the upper limits for their absolute branching fractions are given as:

$$\begin{aligned}&{{\mathcal {B}}}_{\textrm{Belle}}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )<2.6 \times 10^{-4},~~~~ {{\mathcal {B}}}_{\textrm{Belle}}(\Xi _c^0\rightarrow \Xi ^0 \gamma ) \nonumber \\&\quad <1.7 \times 10^{-4}. \end{aligned}$$

(1)

After that, the BESIII collaboration announced the latest measurement on the upper limits for the branching fractions of $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ decay [18]:

$$\begin{aligned} {{\mathcal {B}}}_{\textrm{BESIII}}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma ) <4.4 \times 10^{-4}. \end{aligned}$$

(2)

On the theoretical side, the corresponding branching fractions have been predicted by various theoretical approaches, which include a modified nonrelativistic quark model [19], the constituent quark model [20] and the effective Hamiltonian approach combined with the pole model [21]. The theoretical predictions of the branching fractions of $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ and $\Xi _c^0\rightarrow \Xi ^0 \gamma$ are in the range $(4.5-29.1)\times 10^{-5}$ and $(3.0-19.5)\times 10^{-5}$, respectively. Most of these predictions are consistent with the experimental constraints given above, while the one from the constituent quark model are slightly larger than the upper limits in Eq. (1).

Nowadays, except the model-based theoretical approaches mentioned above, there is no model-independent calculation for the weak radiative decays of charmed baryons. In this work, we will fill this gap and calculate the decay width of the $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ with the use of light-cone sum rules (LCSR). In terms of the initial quark radiation, following Refs. [20, 21], we construct an effective Hamiltonian to simplify the calculation. Since the radiating quark comes from the heavy baryon $\Lambda _c^+$, its velocity can be assumed to be parallel to the velocity of the $\Lambda _c^+$. This enables us to shrink the internal off-shell quark line to a point so that the decay amplitude can be effectively induced by a local Hamiltonian of $cd\rightarrow us\gamma$. In terms of the final quark radiation, since the final state $\Sigma ^+$ is a light baryon, thus we cannot make the same assumption on its composite quark velocities. Therefore we have to treat the final quark radiation in the full theory. The leading twist light-cone distribution amplitudes (LCDAs) of the $\Sigma ^+$ will serve as the non-perturbative input for the sum rules calculation. These LCDAs are taken from the latest Lattice QCD calculation with $N_f=2+1$ [22]. Furthermore, the perturbative kernel will be calculated at leading order. It should be mentioned that these LCDAs are defined according to the light-cone expansion, which are most reliable when the quark masses vanish. Therefore the LCDAs of $\Xi ^0$ are not as good as those of $\Sigma ^+$ which has less massive s quarks, and we will not consider $\Xi _c^0\rightarrow \Xi ^0 \gamma$ in this work.

This paper is organized as follows. In Sect. 2, we construct an effective Hamiltonian for the initial quark radiation in the $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ decay and express the decay amplitude by several calculable matrix elements. In Sect. 3, we define suitable correlation functions to calculate the decay amplitude at the hadron level. In Sect. 4, we perform the QCD level calculation for the correlation function defined above with the use of $\Sigma ^+$ LCDAs. Section 5 contains the numerical results on the decay amplitudes and branching fraction. We will also compare them with those from literature. Section 6 is a brief summary of this work.

2 Decay amplitudes for initial and final radiation

The weak effective Hamiltonian contributing to the $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ decay reads

$$\begin{aligned} {{\mathcal {H}}}_{\textrm{eff}}&=\frac{G_F}{\sqrt{2}}V_{cd}V^{*}_{ud}\left( C_1 {{\mathcal {O}}}_1+C_2 {{\mathcal {O}}}_2\right) ,\nonumber \\ {{\mathcal {O}}}_1&={\bar{s}} \gamma ^{\mu } (1-\gamma _5)c\ {\bar{u}} \gamma _{\mu } (1-\gamma _5)d,\nonumber \\ {{\mathcal {O}}}_2&={\bar{u}} \gamma ^{\mu } (1-\gamma _5)c\ {\bar{s}} \gamma _{\mu } (1-\gamma _5)d, \end{aligned}$$

(3)

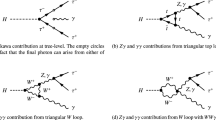
where the $C_{1,2}$ are the Wilson coefficients. Figure 1 shows the W-exchange bremsstrahlung processes $cd\rightarrow us\gamma$. In the case of initial radiation where the photon is emitted by the c or d quark as shown in Fig. 1, following the approach given in Ref. [21] we can construct an effective Hamiltonian to simplify the calculation. Here, we take the c quark radiation in the ${{\mathcal {O}}}_1$ contribution, namely Fig. 1a as an example to illustrate the procedure.

Fig. 1

W-exchange bremsstrahlung processes $cd\rightarrow us\gamma$ induced by ${{\mathcal {O}}}_1$, where the double crossed dots denote ${{\mathcal {O}}}_{1,2}$. The diagrams for ${{\mathcal {O}}}_2$ are similar, just exchanging u and s

The amplitude of Fig. 1a reads

(4)

where $p_{c,s,u,d}$ are the on-shell quark momenta, ${\bar{m}}_{c,d}$ are the constituent quark masses in the $\Lambda _{c}$ and k satisfies $k^2=0$ and $k\cdot \varepsilon =0$. Since the initial $c,\ d$ quarks are confined in the heavy baryon $\Lambda _{c}$, we can assume that c, d and $\Lambda _{c}$ have the same velocity, in other words $p_{c,d}=({\bar{m}}_{c,d}/m_{\Lambda _c}) p_{\Lambda _c}$. Thus the denominator of Eq. (4) becomes

$$\begin{aligned} (p_{c}-k)^{2}-m_{c}^{2}=\frac{\bar{m}_c}{m_{\Lambda _c}}(m_{\Sigma }^2-m_{\Lambda _c}^2), \end{aligned}$$

(5)

which implies that effectively the internal off-shell quark line shrinks to a point. Further, the numerator of Eq. (4) can be simplified by using the equation of motion of the c quark. For the case of d quark radiation the derivation is almost the same. Finally, the amplitude in Eq. (4) can be effectively generated by the following Hamiltonian

$$\begin{aligned} {{\mathcal {H}}}_{\textrm{eff}}^{{{\mathcal {O}}}_{1}}&=\frac{G_{F}}{\sqrt{2}}V_{cs}V_{ud}^{*} \ C_1 \sum _q \left[ A_{\mu }J_{{{\mathcal {O}}}_{1},q}^{\mu }-\frac{i}{2}F_{\mu \nu }K_{\mathcal{O}_{1},q}^{\mu \nu }\right] , \end{aligned}$$

(6)

where $q=c, d$ and $J_{{{\mathcal {O}}}_{1},q}, K_{{{\mathcal {O}}}_{1},q}$ are the effective four-quark currents

$$\begin{aligned} J_{{{\mathcal {O}}}_{1},c}^{\mu }&=2i\ Q_c \lambda _c\ \bar{s}\gamma ^{\nu }(1-\gamma _{5})\partial ^{\mu }c\ \bar{u}\gamma _{\nu }(1-\gamma _{5})d,\nonumber \\ K_{{{\mathcal {O}}}_{1},c}^{\mu \nu }&=i\ Q_c \lambda _c\ \bar{s}\gamma ^{\alpha }(1-\gamma _{5})\sigma ^{\mu \nu }c\ \bar{u}\gamma _{\alpha }(1-\gamma _{5})d,\nonumber \\ J_{{{\mathcal {O}}}_{1},d}^{\mu }&=2i\ Q_d \lambda _d\ \bar{s}\gamma ^{\nu }(1-\gamma _{5})c\ \bar{u}\gamma _{\nu }(1-\gamma _{5})\partial ^{\mu }d,\nonumber \\ K_{{{\mathcal {O}}}_{1},d}^{\mu \nu }&=i\ Q_d \lambda _d\ \bar{s}\gamma ^{\alpha }(1-\gamma _{5})c\ \bar{u}\gamma _{\alpha }(1-\gamma _{5})\sigma ^{\mu \nu }d~. \end{aligned}$$

(7)

Here, $Q_q$ is the electric charge and $\lambda _q=\frac{m_{\Lambda _{c}}}{{\bar{m}}_{q}(m_{\Lambda _{c}}^{2}- m_{\Sigma }^{2})}$. For the case of ${{\mathcal {O}}}_2$ the corresponding operators can be obtained by just exchanging the u, s fields. Now the initial radiation amplitude induced by ${{\mathcal {O}}}_{1,2}$ can be expressed as:

$$\begin{aligned} {{\mathcal {A}}}_{\textrm{Initial}}^{{{\mathcal {O}}}_{i}}&= -i \frac{G_{F}}{\sqrt{2}}V_{cs}V_{ud}^{*}\ C_i\ \varepsilon _{\mu }^{*}(k)\Bigg [\langle \Sigma (p)|J_{\mathcal{O}_{i}}^{\mu }(0)|\Lambda _{c}(q)\rangle \nonumber \\&\quad +\langle \Sigma (p)|k_{\alpha } K_{{{\mathcal {O}}}_{i}}^{\alpha \mu }(0)|\Lambda _{c}(q)\rangle \Bigg ], \end{aligned}$$

(8)

where $i=1,2$, $J_{{{\mathcal {O}}}_{i}}^{\mu }=J_{\mathcal{O}_{i,c}}^{\mu }+J_{{{\mathcal {O}}}_{d}}^{\mu }$ and $K_{\mathcal{O}_{i}}^{\mu \nu }=K_{{{\mathcal {O}}}_{i,c}}^{\mu \nu }+K_{\mathcal{O}_{d}}^{\mu \nu }$. $k=q-p$ is the on-shell photon momentum. It should be mentioned that in principle, the heavy quark expansion used in charm baryon decays is not as accurate as the beauty baryon decays. In a charm baryon the velocities of the three constituent quarks are not parallel with each other. The relative motion between them are described by the Fermi momentum which is of order $\Lambda _{\textrm{QCD}}$. Thus the off-shellness of the intermediate quark is also of order $\Lambda _{\textrm{QCD}}$ [21]. However, this off-shellness can be effectively described by using the constituent quark mass instead of the current quark mass when constructing the effective Hamiltonian. Here we have used the constituent mass for the initial charm and down quarks, which can reduce the uncertainty from the heavy quark expansion of charm quark.

For the final quark radiation this effective Hamiltonian approach is not suitable. The reason is that in our case the final baryon $\Sigma ^+$ contains no heavy quark, and thus we cannot equate its velocity with its constituent quarks, namely the momentum relation $p_{u,s}=({\bar{m}}_{u,s}/m_{\Sigma })p_{\Sigma }$ cannot be used any more. The amplitude for the final quark radiation is calculated in the full theory. It can be written as

$$\begin{aligned} {{\mathcal {A}}}_{\textrm{Final}}^{{{\mathcal {O}}}_i}&= -i \frac{G_{F}}{\sqrt{2}}V_{cs}^{}V_{ud}^{*}\ C_i\ \varepsilon _{\mu }^{*}(k)\nonumber \\&\quad \times \int d^4 x\ \langle \Sigma (p)|T\{ j^{\mu }(0){{\mathcal {O}}}_i(x)\}|\Lambda _{c}(q)\rangle , \end{aligned}$$

(9)

where $j^{\mu }=i Q_{u}{\bar{u}} \gamma ^{\mu }u+i Q_{s}{\bar{s}} \gamma ^{\mu }s$ is the quark electromagnetic current. According to the Ward-identity, the matrix elements appearing in Eqs. (8) and  (9) can be parameterized as

$$\begin{aligned}&\langle \Sigma (p)|{{\mathcal {J}}}_{\mathcal{O}_{i}}^{\mu }(0)|\Lambda _{c}(q)\rangle = i\ \varepsilon ^{*\mu }(k){\bar{u}}_{\Sigma } \nonumber \\&\quad \times \left( a_{i, {{\mathcal {J}}}}^{+}+b_{i, {{\mathcal {J}}}}^{+} \gamma _5\right) \, \sigma ^{\mu \nu }\frac{k_{\nu }}{m_{\Lambda _c}}u_{\Lambda _c}(q), \end{aligned}$$

(10)

where ${{\mathcal {J}}}_{{{\mathcal {O}}}_{i}}^{\mu }=J_{{{\mathcal {O}}}_{i}}^{\mu }+ k_{\alpha }K_{{{\mathcal {O}}}_{i}}^{\alpha \mu }$ for the initial radiation and ${{\mathcal {J}}}_{{{\mathcal {O}}}_{i}}^{\mu }=\int d^4 x T\{ j^{\mu }\mathcal{O}_i(x)\}$ for the final radiation. The amplitudes $a^+_{i, {\mathcal {J}}}, b^+_{i, {\mathcal {J}}}$ will be calculated using LCSR in the next section.

3 Hadron level calculation in LCSR

Now we present the calculation of $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ decay width within the LCSR approach. To obtain the matrix elements given in Eq. (10), one has to define a suitable correlation function and calculate it both at the hadron and the QCD level. Matching these two levels by the quark–hadron duality enables us to extract the decay amplitudes. Here we define a two-point correlation function as:

$$\begin{aligned} \Pi _{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}(p,q)= p^{\mu }\int d^{4}x\ e^{-iq\cdot x}\langle \Sigma (p)|T\{{{{\mathcal {J}}}_{\mu }^{{{\mathcal {O}}}_{i}}(0) \bar{J}_{\Lambda _{c}}(x)}\}|0\rangle , \end{aligned}$$

(11)

where $\bar{J}_{\Lambda _{c}}$ is a current creating the $\Lambda _c$ baryon and its explicit form will be given later. Here, we have contracted the correlation function with a momentum vector $p^{\mu }$. Without this contraction, the correlation function will have 12 independent structures , and . However, in Eq. (10) there are only two independent amplitudes. Thus it will become ambiguous which two of the 12 structures should be chosen to extract the two amplitudes. Contracting the momentum vector $p^{\mu }$ reduces the number of independent structures to four, namely , which is still too much. This mismatch can be solved by doubling the number of amplitudes, as will be explained next.

At the hadron level, this correlation function is calculated by inserting a complete set of states between the two currents. The lowest single particle state should be explicitly kept while the higher excited states will be attributed to the continuous spectrum. To match the four independent structures of the correlation function with the number of decay amplitudes, we have to introduce two extra amplitudes from the decay of the negative parity state $\Lambda _c({1/2}^-)$. Similarly to Eq. (10), the corresponding amplitudes are

$$\begin{aligned} i\ \varepsilon ^{*\mu }(k){\bar{u}}_{\Sigma } \left( a_{i, \mathcal{J}}^{-}+b_{i, {{\mathcal {J}}}}^{-} \gamma _5\right) \sigma _{\mu \nu }\frac{k^{\nu }}{m_{\Lambda _c}}(i\gamma _5)u_{\Lambda _c}(q). \end{aligned}$$

(12)

Now we have four amplitudes $a_{i, {{\mathcal {J}}}}^{\pm }, b_{i, \mathcal{J}}^{\pm }$ mapping to the four structures . Keeping both the two lowest states $\Lambda _c({1/2}^\pm )$ and attributing higher excited states to the continuous spectrum, we express the hadron level correlation function of Eq. (11) as

(13)

The last term is the continuous spectrum contribution including all the states above the $\Lambda _c({1/2}^-)$. $s_{\textrm{th}}$ is the threshold parameter of this continuous spectrum and should be larger than $m_{\Lambda _c -}^2$. $\lambda _{\pm }$ are the decay constants of the $\Lambda _c({1/2}^{\pm })$ which are defined as

$$\begin{aligned}&\langle \Lambda _c({1/2}^+)(q)|\bar{J}_{\Lambda _{c}}(0)|0\rangle ={\bar{u}}_{\Lambda _c}(q)\lambda _{+},\nonumber \\&\langle \Lambda _c({1/2}^-)(q)|\bar{J}_{\Lambda _{c}}(0)|0\rangle =\bar{u}_{\Lambda _c}(q)(i\gamma _5)\lambda _{-}. \end{aligned}$$

(14)

The same correlation function should also be calculated at the QCD level, which can be expressed as a dispersion integral:

$$\begin{aligned} \Pi _{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}(p,q)_{\textrm{QCD}} =\frac{1}{2\pi i}\int _{m_c^2}^{\infty } ds \frac{\textrm{Disc}\ \Pi _{{{\mathcal {O}}}_{i},\mathcal{J}}(p,s)_{\textrm{QCD}}}{s-q^2}. \end{aligned}$$

(15)

The discontinuity part can be parameterized as:

(16)

In principle, the correlation function calculated at the hadron and the QCD level should be equivalent. According to the quark-hadron duality, the continuous spectrum contribution in Eq. (13) is canceled by the corresponding QCD level dispersion integral in the region $s_{\textrm{th}}<s<\infty$. Furthermore, since the QCD level calculation can only be explicitly performed using a light-cone expansion (LCE), one has to perform a Borel transformation of the correlation function at both levels to improve the LCE convergence. Finally one can extract the amplitudes as

$$\begin{aligned} a_{i,{{\mathcal {J}}}}^{+}&=\frac{1}{\pi }\int _{m_{c}^{2}}^{s_{\textrm{th}}}ds\ e^{\frac{m_{\Lambda _{c}+}^{2}-s}{T_{2}}}\frac{m_{\Lambda _{c}+}\big [m_{\Lambda _{c}-}F_{\mathcal{O}_{i},{{\mathcal {J}}}}^{(2)}+F_{{{\mathcal {O}}}_{i},\mathcal{J}}^{(4)}\big ]}{\lambda _{+}(m_{\Lambda _{c}+}+m_{\Lambda _{c}-})(m_{\Lambda _{c}+}-m_{\Sigma })^{2}},\nonumber \\ b_{i,{{\mathcal {J}}}}^{+}&=\frac{1}{\pi }\int _{m_{c}^{2}}^{s_{\textrm{th}}}ds\ e^{\frac{m_{\Lambda _{c}+}^{2}-s}{T_{2}}}\frac{m_{\Lambda _{c}+}\big [F_{\mathcal{O}_{i},{{\mathcal {J}}}}^{(3)}-m_{\Lambda _{c}-}F_{{{\mathcal {O}}}_{i},\mathcal{J}}^{(1)}\big ]}{\lambda _{+}(m_{\Lambda _{c}+}+m_{\Lambda _{c}-})(m_{\Lambda _{c}+}+m_{\Sigma })^{2}}, \end{aligned}$$

(17)

where $T_2$ is the Borel parameter which will be determined during the numerical calculation. Here, $a_{i,{{\mathcal {J}}}}^{-}, b_{i,\mathcal{J}}^{-}$ are not shown since we only care about the decay amplitudes of the $\Lambda _c({1/2}^{+})$. The coefficients $F_{\mathcal{O}_{i},{{\mathcal {J}}}}^{(n)}$ will be explicitly calculated by the LCE at the QCD level.

4 QCD level calculation in LCSR

In this section, we will use light-cone expansion to calculate the correlation function defined in Eq. (11), and extract the coefficients $F_{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}^{(n)}$. Now the correlation function reads

$$\begin{aligned}&\Pi _{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}(p,q)_{\textrm{QCD}} = p^{\mu }\int d^{4}x\ e^{-iq\cdot x}\langle \Sigma (p)| T\{{{{\mathcal {J}}}_{\mu }^{{{\mathcal {O}}}_{i}}(0)\bar{J}_{\Lambda _{c}}(x)}\}|0\rangle ,\nonumber \\&\textrm{with}~~~~\bar{J}_{\Lambda _{Q}} =-\epsilon _{abc}\bar{Q}_{c}(\bar{d}_{b}C\gamma _{5}\bar{u}_{a}^{T}), \end{aligned}$$

(18)

where a, b, c are color indices. Here, $q^2\ll 0$ is taken in the deep Euclidean region to realize the light-cone expansion. Let us take $i=1$ and ${{\mathcal {J}}}=J$ as an example to illustrate the detailed calculation for the c quark radiation.

At leading order the corresponding correlation function becomes

$$\begin{aligned}&\Pi _{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}^{c}(p,q)_{\textrm{QCD}} = -2i\ Q_c \lambda _c \epsilon _{abc}\ p_{\mu }\nonumber \\&\qquad \times \int d^{4}x\ e^{-iq\cdot x}[\gamma ^{\nu }(1-\gamma _{5})\partial _{w}^{\mu }S_{c}(w,x)]_{ig}\nonumber \\&\qquad \times [\gamma _{\nu }(1-\gamma _{5})S_{d}(0,x)C\gamma _{5}]_{kn}\langle \Sigma (p)|\bar{s}_{c}^{i}(0) \bar{u}_{b}^{k}(0)\bar{u}_{a}^{n}(x)|0\rangle , \end{aligned}$$

(19)

where $S_q(x,y)$ is the free propagator of the quark q. Figure 2a shows the corresponding Feynman diagram, where the black dot at coordinate x denotes the $\Lambda _c$ current and the white crossed dot at coordinate 0 denotes the effective current $J_{{{\mathcal {O}}}_{1},c}^{\mu }$.

Fig. 2

Diagrams for the QCD level correlation function in Eq. (18). a Is the initial quark radiation where the white crossed dot denotes the effective four-quark currents in Eq. (7). b is the final s quark radiation where the white crossed dot denotes the current $j^{\mu }$. The black dot denotes the $\Lambda _c$ current. The grey ellipse represents the LCDAs of the $\Sigma ^+$

The last matrix element in Eq. (19) is represented by the grey ellipse in Fig. 2, which can be parameterized by the LCDAs of the $\Sigma ^+$. The three leading twist LCDAs are defined as [22,23,24,25,26]

(20)

where $g_{\mu \nu }^{\perp }=g_{\mu \nu }-(\tilde{n}_{\mu } n_{\nu }+\tilde{n}_{\nu } n_{\mu })/(\tilde{n} \cdot n)$ with $\tilde{n}_{\mu }=p_{\mu }-(m_{\Sigma }^{2}/2p \cdot n) n_{\mu }$ and n is a light-cone vector. with $u_{\Sigma }$ the Dirac spinor of the $\Sigma ^+$ baryon. The coordinate x of the quark field is parallel to n, $x=(x\cdot p/m_{\Sigma })n$, where we have used $p=m_{\Sigma } v$, $v=(n+{\bar{n}})/2$ and $n\cdot {\bar{n}}=2$. In the chiral limit $m_u=m_d=0$ the contribution of $V^B$ and $A^B$ to the correlation function vanishes. The explicit form of $T^B$ of the $\Sigma ^+$ baryon now reads

$$\begin{aligned} T^B(u_{1},u_{2},u_{3})=120 u_{1} u_{2} u_{3}\left( \pi _{00}^{B} \mathcal {P}_{00} + \pi _{11}^{B} \mathcal {P}_{11}+\ldots \right) ,\nonumber \\ \end{aligned}$$

(21)

where the $\mathcal {P}_{ij}$ are polynomials, $\mathcal {P}_{00}=1,~~ \mathcal {P}_{11}=7\left( u_{1}-2 u_{3}+u_{2} \right)$ [22]. $\pi _{00}^B$ and $\pi _{11}^B$ are the shape parameters which encode all non-perturbative information of the baryon. The numerical value of these parameters will be taken from the Lattice calculation [22]. The ellipsis denotes terms of higher power polynomials, which are suppressed and omitted here. Nowadays the Lattice calculation has only provided the leading twist LCDAs for the octet baryons. Thus in this work we will only perform the calculation up to the leading twist.

Using the $\Sigma ^+$ LCDAs given above, we can express the correlation function in Fig. 2a as

(22)

Here, we have defined $\tilde{T}^{B}(u_{1},u_{2})=T^{B}(u_{1},u_{2},1-u_{1}-u_{2})$. Note that since $n=(m_{\Sigma }/x\cdot p)x$, we can use the following trick to remove the x in the denominator:

$$\begin{aligned}&\int du_{1}du_{2}\int d^{4}x\ e^{-i(q-k_{1}-k_{2}-u_{1}p)\cdot x}\ \tilde{T}^{B}(u_{1},u_{2})n_{\kappa }\ \cdots \nonumber \\&=\ m_{\Sigma }\frac{\partial }{\partial q^{\kappa }}\int du_{1}du_{2}\int d^{4}x\ e^{-i(q-k_{1}-k_{2}-u_{1}p)\cdot x}\ \tilde{T}_{(1)}^{B}(u_{1},u_{2})\ \cdots , \end{aligned}$$

(23)

where the ellipses represents all the terms independent of $u_1, u_2$, and

$$\begin{aligned}&\tilde{T}_{(i)}^{B}(u_{1},u_{2})=\int _{0}^{u_{1}}dt\ \tilde{T}_{(i-1)}^{B}(t,u_{2})\nonumber \\~~~~~&\textrm{with}~~~\tilde{T}_{(0)}^{B}(t,u_{2})=\tilde{T}^{B}(t,u_{2}). \end{aligned}$$

(24)

From Eq. (23), it follows that for each $n_{\kappa }$ one can equivalently replace it with an operator ${\hat{n}}_{\kappa }=m_{\Sigma }\ \partial /\partial q^{\kappa }$ and simultaneously replace $\tilde{T}^{B}$ with $\tilde{T}_{(1)}^{B}$. Therefore, the correlation function takes the form

(25)

where the operator ${\mathcal {N}}$ is defined as

$$\begin{aligned}&{{\mathcal {N}}}[{{\hat{n}}}, T_{(i)}^B]^{\alpha \beta \rho \kappa } =\ {\hat{n}}^{\kappa }\left[ p^{\alpha }g^{\rho \beta }\tilde{T}_{(1)}^{B}(u_{1},u_{2})\right. \nonumber \\&\qquad \left. +\left( \frac{1}{2}m_{\Sigma }g^{\rho \alpha }-\frac{1}{m_{\Sigma }}p^{\rho }p^{\alpha }\right) {\hat{n}}^{\beta }\tilde{T}_{(2)}^{B}(u_{1},u_{2})\right. \nonumber \\&\qquad \left. +\frac{1}{2}p^{\alpha }{\hat{n}}^{\beta }{\hat{n}}^{\rho }\tilde{T}_{(3)}^{B}(u_{1},u_{2})\right] . \end{aligned}$$

(26)

Now we have to express the QCD level correlation function as a dispersive integral. The discontinuity part can be extracted from the cutting rules:

(27)

where

$$\begin{aligned}&d\Phi _2[(q-u_1 p)^2]\nonumber \\&\quad =\int \frac{d^{3}k_{1}}{(2\pi )^{3}}\frac{1}{2E_{k_{1}}}\frac{d^{3}k_{1}}{(2\pi )^{3}}\frac{1}{2E_{k_{1}}}\delta ^{4}(q-u_1 p-k_{1}-k_{2}) \end{aligned}$$

(28)

is the two-body phase space integration, which corresponds to cutting off the c, d quark loop in Fig. 2a. Further, $\Pi _{\mathcal{O}_{2},{{\mathcal {J}}}}^{c}(p,q)_{\textrm{QCD}}= -\Pi _{{{\mathcal {O}}}_{1},\mathcal{J}}^{c}(p,q)_{\textrm{QCD}}$ so that we only have to calculate the amplitudes induced by ${{\mathcal {O}}}_1$. The integration in Eq. (27) is involved but straightforward, so we will not present further calculational details here.

For the case of the final quark radiation, the corresponding diagram is shown in Fig. 2b, where we take the s quark radiation as an example. The calculation for this diagram is similar to Fig. 2a and the only difference is that now we have an extra s quark propagator:

$$\begin{aligned} \frac{1}{(q-(u_{1}+u_{2})p)^{2}}=\frac{1}{u_{3}(s-(u_{1}+u_{2})m_{\Sigma }^{2})}. \end{aligned}$$

(29)

It should be mentioned that for the final quark radiation $\mathcal{J}_{\mu }^{{{\mathcal {O}}}_{i}}(0)$ is an composite operator of $j_{q^{\prime }\mu }$ and ${{\mathcal {O}}}_i$, so that the hadron level correlation function in Eq. (11) is actually induced by three operators. However, since we only insert a complete set of states between ${{\mathcal {J}}}_{\mu }^{{{\mathcal {O}}}_{i}}(0)$ and $\bar{J}_{\Lambda _{c}}(x)$, the composite operator $\mathcal{J}_{\mu }^{{{\mathcal {O}}}_{i}}(0)$ is not disconnected. Therefore, at the QCD level when extracting the discontinuity part, we only have to cut off the c, d quark loop in Fig. 2b and keep the s quark propagator unchanged.

5 Numerical results

We first give the input parameters. We use the $\overline{\textrm{MS}}$ masses for the quarks, $m_c(\mu )=1.27$ GeV and $m_s(\mu )=0.103$ GeV with $\mu = 1.27$ GeV [27]. The masses of u, d quarks are omitted. The composite masses of the c, d quarks are taken as ${\bar{m}}_c=1.6$ GeV and ${\bar{m}}_d=0.32$ GeV [21]. The masses of the baryons are $m_{\Sigma }=1.19$ GeV, $m_{\Lambda _c+}=2.286$ GeV and $m_{\Lambda _c-}=2.6$ GeV [27]. The decay constant of the $\Lambda _c({1/2}^+)$ is taken as $\lambda _+=0.01\pm 0.001$ [28]. From Eq. (17), it can be seen that the amplitudes are proportional to the inverse of $\lambda _+$ so that its uncertainty may affect the result a lot. Therefore, we will include the uncertainty of $\lambda _+$ when evaluating the uncertainty of the decay amplitudes. The shape parameters of the $\Sigma ^+$ LCDAs are taken from a lattice calculation with $N_f=2+1$ and vanishing lattice spacing limit $a\rightarrow 0$: $\pi _{00}^B=5.14\times 10^{-3}$ GeV$^2$ and $\pi _{11}^B=-0.09\times 10^{-3}$ GeV$^2$ [22].

Further, the LCSR contains two kinds of extra parameters, namely the threshold parameter $s_{\textrm{th}}$ and the Borel parameter $T_2$. The threshold parameter should in principle be process independent and only related to the corresponding hadron state. Here, $s_{\textrm{th}}$ is taken from a QCD sum rules study on the decay constant of the $\Lambda _c$ [28]: $s_{\textrm{th}}=2.85^2$ GeV$^2$. Generally, the sum rules results are sensitive to the threshold parameter, thus here we consider a small uncertainty $\pm 0.5$ GeV$^2$ near this value to evaluate the uncertainty from the threshold parameter on the decay amplitudes.

Fig. 3

Decay amplitudes $a_{{\mathcal {J}}}^+$ and $b_{{\mathcal {J}}}^+$ (in unit $10^{-3}$ GeV$^2$) as functions of the Borel parameter $T^2$. In each diagram, the blue band denotes the error from the uncertainty of the threshold $s_{\textrm{th}}=2.85^2\pm 0.5$ GeV$^2$. The upper and lower red bands denote the error from the uncertainty of $\lambda _+$

Generally, the Borel parameter $T_2$ is chosen to satisfy three requirements. First, $T_2$ cannot be too large so that the continuous spectrum contribution is suppressed. Second, $T_2$ must be large enough to ensure the light-cone expansion to convergence. Finally, the result must be stable in a window of $T_2$. The first and the second requirement can determine the upper and lower bound of the $T_2$ window, respectively. Figure 3 shows the amplitudes $a_{i, {{\mathcal {J}}}}^{+}$ and $b_{i, {{\mathcal {J}}}}^{+}$ as functions of $T_2$. To determine the upper bound, we require that the pole contribution must be larger than the continuous spectrum contribution, namely:

$$\begin{aligned} \displaystyle \frac{\displaystyle \int _{m_{c}^{2}}^{s_{\textrm{th}}}ds\ e^{-s/T^{2}}\textrm{Disc}\ \Pi _{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}(p,s)_{\textrm{QCD}}}{\displaystyle \int _{m_{c}^{2}}^{\infty }ds\ e^{-s/T^{2}}\textrm{Disc}\ \Pi _{{{\mathcal {O}}}_{i},{{\mathcal {J}}}}(p,s)_{\textrm{QCD}}}>0.5. \end{aligned}$$

(30)

The numerator is the pole contribution, which represents the integral on the right-hand side of Eq. (17). The denominator is the same integral but the upper limit of s is extended to infinity, which contains both pole and continuous spectrum contributions. Note that although the value for this fraction is derived from experience, as long as the third requirement for stability is satisfied, the result will be insensitive to this fraction, and its uncertainty can be attributed to choosing the window of $T_2$.

On the other hand, in principle, the lower bound of the $T_2$ is determined by the ratio between the contribution from the leading order and next-to-leading order QCD corrections to the perturbative kernel. However, in this work only the leading order contribution is considered so that this method cannot be used. Following our previous work [29], to get the window of $T_2$, we can set the center value of $T_2$ as its upper bound, and find a range $\pm 1$ GeV$^2$ around this center value. The amplitudes and the corresponding errors from the uncertainties of $s_{\textrm{th}}$, $T_2$ and $\lambda _+$ are listed in Table 1. Note that the center value of the $T_2$ is already in a relatively stable region as shown in Fig. 3, thus the procedure given above is sufficient for determining the errors of the amplitudes. Generally, the Borel parameters are close to the corresponding mass square of hadrons. From Table 1, the $T_2$ s for initial-state radiation are close to $m_{\Lambda _c}^2$ which is as expected. However, the $T_2$ s for final-state radiation are much smaller. The reason is that in Fig. 2b the extra propagator as shown in Eq. (29) provides a lighter mass scale $m_{\Sigma }$. Now the s dominates around $m_{\Sigma }^2$, which reduces the optimal value of $T_2$.

Table 1 Decay amplitudes $a_{{\mathcal {J}}}^+$ and $b_{{\mathcal {J}}}^+$ (in unit $10^{-3}$ GeV$^2$) and the corresponding Borel parameters (GeV$^2$) for the initial- and the final-state radiation

Using the amplitudes given in Table 1, we can obtain the decay width of the $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ from the formula

$$\begin{aligned}&\Gamma \left( \Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma \right) =\frac{1}{8 \pi \ m_{\Lambda _{c}+}^{2}}\left( \frac{m_{\Lambda _{c}+}^{2}-m_{\Sigma }^{2}}{m_{\Lambda _{c}+}}\right) ^{3}\nonumber \\&\quad \times \frac{G_F^2}{2} |V_{cs}V_{ud}|^2 (C_1-C_2)^2 \left( |a|^{2}+|b|^{2}\right) \end{aligned}$$

(31)

with $a=a_{\textrm{Ini}}^{+}+a_{\textrm{Fin}}^{+}$ and $b=b_{\textrm{Ini}}^{+}+b_{\textrm{Fin}}^{+}$. The Wilson coefficients are taken as $C_1=1.22$ and $C_2=-0.43$ at $\mu =m_c$ [30]. The CKM matrix elements are $|V_{cs}|=0.975$ and $|V_{ud}|=0.973$ [27]. Using the $\Lambda _c^+$ lifetime $\tau (\Lambda _c^+)=2.01\times 10^{-13}$ s [27], we can obtain the branching fraction

$$\begin{aligned} {{\mathcal {B}}}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )=1.03\pm 0.36 \times 10^{-4}, \end{aligned}$$

(32)

which is below the experimental upper limits given recently by the Belle and BESIII Collaborations [17, 18]:

$$\begin{aligned}&{{\mathcal {B}}}_{\textrm{Belle}}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )<2.6 \times 10^{-4},\nonumber \\&{{\mathcal {B}}}_{\textrm{BESIII}}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )<4.4 \times 10^{-4}. \end{aligned}$$

(33)

Table 2 gives a comparison of the $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ branching fraction from this work, the result from the Belle Collaboration, the modified nonrelativistic quark model (NRQM) [19], the constituent quark model (CQM) [20] and the effective Hamiltonian approach (EHA) [21]. The branching fraction from the CQM is slightly larger than the experimental upper limit, while the branching fractions from other theoretical methods are nearly one order smaller than the upper limit. Our result is between these theoretical predictions and the experimental upper limit. Due to the limitation on the data sample and resolution, an extremely small branching fraction is difficult to be measured. However, the relatively larger branching fraction predicted in this work is more likely to be tested by future experiments.

Table 2 Comparison of the branching fraction $\mathcal{B}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )$ from this work with those from the literature and the experiments

6 Conclusion

We have calculated the decay width of $\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma$ using light-cone sum rules. For the initial quark radiation we constructed an effective Hamiltonian to simplify the calculation, where the internal quark line shrinks to a point. The final quark radiation is studied utilizing the full theory. The leading twist light-cone distribution amplitudes of the $\Sigma ^+$ serve as the non-perturbative input for the sum rule calculation, and the perturbative kernel is calculated at leading order. The branching fraction we obtain is $\mathcal{B}(\Lambda _{c}^{+}\rightarrow \Sigma ^{+}\gamma )=1.03\pm 0.36 \times 10^{-4}$, which is between previous theoretical predictions and the experimental upper limits. Considering the data sample and resolution of the experiment, we believe that our prediction can be tested in the near future.