1 Introduction

Einstein’s general theory of relativity predicts that an adequately compact mass, bends the spacetime such that nothing can escape from a critical surface named as the event horizon. This paved the way of modern foundation of the concept of black holes (BHs). The BH can be designated by mass, angular momentum and charge as stated by the so called no hair theorem. All the information regarding the matter that formed the BH is lost beyond the event horizon and remains obscure for the external observers. Black holes do not emit any light, but the regions in their vicinity could become very luminous due to emission of radiations as the accreting matter spirals around and vanish while reaching the event horizon. The Strong gravitational field of the BH bends the light rays, known as gravitational lensing, which is the well known application of general relativity. The circular photon orbits play a vital role in the study of the geometrical structure of BH as well as probing the various features of strong gravity. The strong gravitational lensing corresponds to the shadow of BH embedded in luminous background. The shadow of a BH can be perceived as a dark zone surrounded by a photon ring as the BH is situated between a bright source and far away observer.

The study of non-rotating, spherically symmetric BH shadow was initiated by Synge [1] and Luminet [2]. Synge [1] provided the technique of calculating the angular radius of the capture region of the photon, in the vicinity of Schwarzschild BH while Luminet [2] shed light on the optical appearance of Schwarzschild BH surrounded by an emitting, thin accretion disc. Bardeen [3] pioneered in providing the study of a rotating BH shadow. He showed that the shape of the rotating BH shadow is no longer a perfect circle as compared to non-rotating BH, but slightly flattened due to the frame dragging. Cunningham and Bardeen [4] explored the optical appearance of a star orbiting in the equatorial plane of extreme Kerr BH. The further deformation in the shape of the shadow was observed for the charged rotating BH [5]. Hioki and Maeda [6], by defining the observables (characterizing the radius as well as distortion parameter), found that the spin and the inclination angle of Kerr BH can be deduced by the observation. Since then, the topic of shadows has been extensively studied [7,8,9,10,11].

It is believed that the central region of many galaxies as well as Milky Way contains a supermassive BH. The shadows formed due to gravitational lensing, serve as a great tool to explore the nature of such compact object. Although, the idea of BH shadows dates back to 70’s, but the concept of its representation in the centre of galaxy using very long baseline interferometry (VLBI) was first demonstrated by Falcke et al. [12]. Recently, the central compact region with radio emission in the elliptical galaxy M87 at the wavelength of 1.3 mm with the Event Horizon Telescope (EHT) collaborations. The observation of flux near the horizon as well as the emission from this region provided the direct evidence of the BH shadow. The observed shadow is consistent with the existence of central BH, that is predicted by general relativity [13,14,15,16,17,18].

It has commonly been assumed that the BHs as well as other compact objects are surrounded by plasma medium. The propagation of light of a curved spacetime through isotropic, dispersed medium was discussed by Synge in his remarkable book [19], where he discussed the geometrical optics in a dispersive medium by considering the relativistic Hamiltonian approach. Bisnovatyi-Kogan and Tsupko [20, 21] investigated the influence of plasma on the gravitational lensing using different approaches. Perlick [22] explored the effect of spherically symmetric, time independent plasma density on the deflection of light in Schwarzschild spacetime.

The curvature singularities in GR are best demonstrated by the BH. As the classical illustration of gravitational field in GR breaks down near the singularities, quantum theory of gravity provides a reliable framework to resolve such problem. Noncommutative (NC) geometry is a mathematical concept, compatible with quantum mechanics and contemplated as a promising candidate in removing the singularities. The noncommutativity can be postulated in a commutation relation [23]

$$\begin{aligned}{}[x^{\kappa },x^{\lambda }]=\iota \vartheta ^{\kappa \lambda }, \end{aligned}$$

where \(\vartheta \) is the antisymmetric tensor (constant) having dimension \((length)^2\) as well as possesses real value. The point like mass is replace by the smeared mass in NC geometry

$$\begin{aligned} \rho _{\vartheta }(r)=\frac{M}{(4\pi \vartheta )^{2/3}}e^{\frac{-r^2}{4\vartheta }}, \end{aligned}$$

where M denotes the point mass.

During the past few years, the interest in NC BHs has been raised and several important aspects concerning such BHs have been taken into consideration. In the framework of NC geometry, many BH have been obtained, for instance, neutral [24], charged [25], rotating [26] and higher dimensional [27, 28]. Subsequently, diverse properties of NC BHs have been discussed, such as quantum tunneling [29], gravitational lensing [30], shadows [31, 32], red/blue shifts [33] etc.

A vigorously studied class of BHs, related to the non-linear electrodynamics is the regular BHs. Bardeen [34] was the first one who provided the idea of regular spherically symmetric BH which satisfy the weak energy condition. Motivated by Bardeen’s model, several regular BHs were obtained in the background of NED theory. Ayon-Beato and Garcia introduced regular BH solutions with physically reasonable sources. They also discussed that GR coupled with NED having correct weak field corresponds to regular BHs solutions [35,36,37,38]. Hayward [39] studied the formation as well as evaporation of new regular solution. The regular rotating BHs have also been obtained and explored extensively [40,41,42,43,44,45,46].

In this article, we discuss the shadow of a NC rotating Hayward BH. The plan of the paper is as follows. The following section provides the analysis of the null geodesics for the rotating NC Hayward BH. In Sect. 3, we study the apparent shape of the shadows as well as the properties of observables quantities. Section 4 explores the shadows as well as observables quantities in the plasma background. Finally, in the last section, we summed up the main results with concluding remarks.

2 Analysis of the geodesics for NC rotating Hayward BH

In this section, we discuss the geodesics of NC rotating Hayward BH. The regular BHs are considered as the alternating to classical BHs and have been extensively studied. Such BHs solutions are obtained by coupling of GR with NED and their central region behaves like de Sitter spacetime. The Hayward BH is considered as the most popular among the class of regular BHs. The massive scalar quasinormal modes for the Hayward BH has been studied which distinguished the Schwarzschild BH with regular BHs [47]. The geodesic structure [48] as well as accretion onto modified Hayward BH has been investigated [49]. The Hayward BH remains stable after thermal fluctuation if the event horizon has the larger value then the critical value [50]. The final stages of evaporation of Hayward BH has been explored by Mehdipour and Ahmadi [51]. They found that the free parameter (g), the noncommutativity as well as the rotation may increase the minimum value of energy for the possible formation of BHs in Tera electron volt (TeV)-scale collisions. It is shown that the rotational motion of rotating modified Hayward BH has an infinite centre of mass energy near the horizon [52].

The metric of the NC rotating Hayward BH in Boyer–Lindquist coordinates read as [51]

$$\begin{aligned} ds^{2}= & {} f(r,\theta )dt^2 -\frac{\Xi }{\Delta _{\vartheta }}dr^2-\Xi d\theta ^2\nonumber \\{} & {} +2a\sin \theta (1-f(r,\theta ))dt d\varphi \nonumber \\{} & {} -\sin ^2\theta (\Xi +a^2\sin ^2\theta (2-f(r,\theta )))d\varphi ^2, \end{aligned}$$
(1)

where

$$\begin{aligned}{} & {} f(r,\theta )=\frac{\Delta -a^2\sin ^2\theta }{\Xi },\\{} & {} \Delta _{\vartheta }=r^2-2m(r)r+a^2,\quad \Xi =r^2+\cos ^2\theta +a^2, \end{aligned}$$

with a being the rotation parameter, M denotes the mass, g represents the Hayward’s free parameter and \(m(r)=M_{\vartheta }(\frac{r^3}{r^3+g^3})\), is given in terms of the smeared mass, \(M_{\vartheta }=\frac{2\,M\gamma (\frac{3}{2}; \frac{r^2}{4\vartheta })}{\sqrt{\pi }}\), where \(\vartheta \) is the NC parameter.

The horizon radius of metric (1) is given by the largest root of the following equation

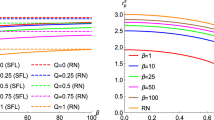
$$\begin{aligned} r^2-2m(r)r+a^2=0. \end{aligned}$$

The maximum values for spin and the non-commutative parameter corresponding to different values of the free parameter have been found by solving \(\Delta _{\vartheta }(r)=0\) as well as \(\frac{d\Delta _{\vartheta }(r)}{dr}=0\) and its numerical solution is presented in Fig. 1.

Fig. 1
figure 1

The plots demonstrating the parameter space for the NC rotating Hayward BH. The upper panel corresponding to \(g=1\) (left), \(g=1.1\) (right) while the lower panel represents \(g=1.3\) (left), \(g=1.4\) (right). The dotted blue line is the borderline separating the BH region from non-BH

Full size image

The motion of the particle can be determined by the Lagrangian, given as

$$\begin{aligned} {\mathfrak {L}}=\frac{1}{2}g_{\sigma \varrho }\dot{x}^{\sigma }\dot{x}^{\varrho }, \end{aligned}$$
(2)

where \(\dot{x}^{\varrho }=u^{\varrho }=dx^{\varrho }/d\tau \), denotes four velocity of the particle and \(\tau \) is the proper time. The specific energy (\({\mathcal {E}}\)) as well as angular momentum (\({\mathcal {L}}_{z}\)) are given by

$$\begin{aligned} {\mathcal {E}}= & {} p_{t}=\frac{\partial {\mathfrak {L}}}{\partial \dot{t}}=g_{tt}\dot{t}+g_{\varphi t}\dot{\varphi }, \nonumber \\ {\mathcal {L}}_{z}= & {} -p_{\varphi }=\frac{\partial {\mathfrak {L}}}{\partial \dot{\varphi }}=-g_{\varphi t}\dot{t}+g_{\varphi \varphi }\dot{\varphi }. \end{aligned}$$
(3)

We observe that the Lagrangian do not depend on t as well as \(\varphi \) which shows that both \(p_{t}\) and \(p_{\varphi }\) are the conserved quantities describing the stationary as well as axisymmetric attributes of NC rotating Hayward BH.

The light rays can be discussed by defining the impact parameter as

$$\begin{aligned} b=\frac{{\mathcal {L}}_{z}}{{\mathcal {E}}}=\frac{g_{\varphi \varphi } \frac{d\varphi }{dt}-g_{t\varphi }}{g_{t\phi }\frac{d\varphi }{dt}+g_{tt}}. \end{aligned}$$
(4)

Next, we introduce a new variable \(u=\frac{1}{r}\) and derive an important relation

$$\begin{aligned} \frac{dr}{d\varphi }=\frac{\dot{r}}{\dot{\varphi }}=\frac{-1}{u^2}\frac{du}{d\varphi }, \end{aligned}$$
(5)

and the equation of the light ray is given as

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) ^2=\frac{(g_{\varphi \varphi }-2g_{t\varphi }b-g_{tt}b^2) (g_{tt}g_{t\varphi }+g^2_{\varphi \varphi })u^4}{(g_{t\varphi }-g_{tt}b^2)g_{rr}}. \end{aligned}$$
(6)

We analyze the photon trajectories by taking into account \(\frac{du}{d\phi }\) and \(\frac{d^2u}{d\phi ^2}\). Figure 2, shows that the null particle is orbiting close to the event horizon with the increase in g but never crosses it.

The Hamilton–Jacobi equation reads as

$$\begin{aligned} \frac{\partial {\mathcal {S}}}{\partial \tau }=\frac{1}{2}g^{\sigma \varrho }\frac{\partial {\mathcal {S}}}{\partial x^{\sigma }}\frac{\partial {\mathcal {S}}}{\partial x^{\varrho }}. \end{aligned}$$
(7)

Equation (7) takes the following form

$$\begin{aligned} {\mathcal {S}}=\frac{1}{2}m^2_{0}\tau -{\mathcal {E}}t+ {\mathcal {L}}_{z}\varphi +{\mathcal {S}}_{r}(r)+{\mathcal {S}}_{\theta }(\theta ). \end{aligned}$$
(8)

Using (7) and (8), the equations of motion of the test particle, for Eq. (1) are obtained as

$$\begin{aligned} \Sigma \frac{\partial t}{\partial \tau }= & {} \frac{r^2+a^2}{\Delta }[{\mathcal {E}}(r^2+a^2) -a{\mathcal {L}}_{z}]-a(a{\mathcal {E}}\sin ^2\theta -{\mathcal {L}}_{z}),\nonumber \\ \end{aligned}$$
(9)
$$\begin{aligned} \Sigma \frac{\partial \phi }{\partial \tau }= & {} \frac{a}{\Delta }[{\mathcal {E}}(r^2+a^2) -a{\mathcal {L}}_{z}]-(a{\mathcal {E}}-{\mathcal {L}}_{z}\csc ^2\theta ), \end{aligned}$$
(10)
$$\begin{aligned} \Sigma \frac{\partial r}{\partial \tau }= & {} \pm \sqrt{\mathcal {R_{\vartheta }}}, \end{aligned}$$
(11)
$$\begin{aligned} \Sigma \frac{\partial r}{\partial \tau }= & {} \pm \sqrt{\Theta _{\vartheta }}, \end{aligned}$$
(12)

where

$$\begin{aligned} {\mathcal {R}}_{\vartheta }= & {} [{\mathcal {E}}(r^2+a^2)-a{\mathcal {L}}_{z}]^2 -\Delta [{\mathcal {C}}+({\mathcal {L}}_{z}-a{\mathcal {E}})^2],\end{aligned}$$
(13)
$$\begin{aligned} \Theta _{\vartheta }= & {} {\mathcal {C}}+\cos ^2\theta (a^2{\mathcal {E}}^2 -{\mathcal {L}}_{z}^2\csc ^2\theta ), \end{aligned}$$
(14)

here \({\mathcal {C}}\) is the Carter’s constant.

Equation (11) can be written as

$$\begin{aligned} (\Sigma \frac{\partial r}{\partial \lambda })^2+{\mathcal {U}}_{eff}=0, \end{aligned}$$
(15)

where

$$\begin{aligned} {\mathcal {U}}_{eff}=[{\mathcal {E}}(r^2+a^2)-a{\mathcal {L}}_{z}]^2 -\Delta [{\mathcal {C}}+({\mathcal {L}}_{z}-a{\mathcal {E}})^2]. \end{aligned}$$

Radial motion of the particles can be described by the above equation. The behavior of the effective potential of the photons is depicted in Fig. 3. Here, we observe that the photon orbits are unstable with respect to the increasing value of g as well as r.

Fig. 2
figure 2

Particle trajectories corresponding to \(g=1\) (upper panel, left), \(g=1.1\) (upper panel, right), \(g=1.2\) (bottom panel) and \(\vartheta =0.2\)

Full size image

Using the conditions for unstable circular orbit (\({\mathcal {R}}_{\vartheta }(r)=0\) as well as \(\frac{d{\mathcal {R}}_{\vartheta }(r)}{dr}=0\) [5]), we get

$$\begin{aligned}{} & {} r^4+(a^2-\eta -\xi ^2)r^2\nonumber \\{} & {} \qquad \quad +2((\xi -a)^2+\eta )m(r)r-a^2\eta =0, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} 4r^3+2(a^2-\eta -\xi ^2)r\nonumber \\{} & {} \quad \qquad +((\xi -a)^2+\eta )(2rm'(r)+2m(r))=0, \end{aligned}$$
(17)

where

$$\begin{aligned} m'(r)=-\frac{Mr^2e^{-\frac{r^2}{4 \vartheta }}(r^3+g^3)(\frac{r^2}{\vartheta })^{3/2} +12g^3\gamma (\frac{3}{2},\frac{r^2}{4\vartheta })}{ 2\sqrt{\pi }(r^3+g^3)^2}.\nonumber \\ \end{aligned}$$
(18)

Solving the above equations, we have

$$\begin{aligned} \xi= & {} \Bigg [(a^2 + r^2)(g^3 + r^3)\Bigg (M r^4 \sqrt{\frac{r^2}{\vartheta }}-2e^{\frac{r^2}{4 \vartheta }}\vartheta \sqrt{\pi }(g^3 + r^3)-4e^{\frac{r^2}{4 \vartheta }} \nonumber \\{} & {} \times M r^2 (-3 r^5 + a^2 (4 g^3 + r^3))\vartheta \gamma \Bigg (\frac{3}{2},\frac{r^2}{4\vartheta }\Bigg )\Bigg ] \Bigg [a\Bigg ((g^3 + r^3)\Bigg (Mr^4\sqrt{\frac{r^2}{\vartheta }} \end{aligned}$$
(19)
$$\begin{aligned}{} & {} +2e^{\frac{r^2}{4 \vartheta }}\vartheta \sqrt{\pi }(g^3 + r^3)\Bigg )-4e^{\frac{r^2}{4 \vartheta }}M r^2 \vartheta (4 g^3 + r^3)\gamma \Bigg (\frac{3}{2},\frac{r^2}{4\vartheta }\Bigg )\Bigg )\Bigg ]^{-1}, \nonumber \\ \eta= & {} \Bigg [\pi (g^3 + r^3)^4\Bigg [16 a^2 r^2\Bigg (a^2 + r^2-\frac{4Mr^4\gamma \Bigg (\frac{3}{2},\frac{r^2}{4\vartheta }\Bigg )}{\sqrt{\pi }(g^3 + r^3)}\Bigg )\nonumber \\{} & {} -\frac{e^{-\frac{r^2}{2 \vartheta }}(r(g^3 + r^3)\Bigg (-Mr^6\sqrt{\frac{r^2}{\vartheta }}+2\vartheta \sqrt{\pi }e^{\frac{r^2}{4 \vartheta }}(2 a^2 + r^2) (g^3 + r^3)\Bigg )-12e^{\frac{r^2}{4 \vartheta }}Mr^8\vartheta \gamma \Bigg (\frac{3}{2},\frac{r^2}{4\vartheta }\Bigg )\Bigg )^2}{\pi \vartheta ^{2}(g^3 + r^3)^4}\Bigg ]\Bigg ] \nonumber \\{} & {} \times \Bigg [a^2r^2\Bigg (\frac{e^{-\frac{r^2}{4 \vartheta }}(g^3 + r^3)\Bigg (M r^4\sqrt{\frac{r^2}{\vartheta }}+2e^{\frac{r^2}{4 \vartheta }}\sqrt{\pi }\vartheta (g^3 + r^3)\Bigg )}{\vartheta } \end{aligned}$$
(20)
$$\begin{aligned}{} & {} -4Mr^2(4 g^3 + r^3)\gamma \Bigg (\frac{3}{2},\frac{r^2}{4\vartheta }\Bigg )\Bigg )^2\Bigg ]^{-1}. \end{aligned}$$
(21)

Equations (13)–(19) provides the expressions of the critical impact parameters, \(\xi \) and \(\eta \) which describe the shadow’s contour (will be discussed in the next section) for the NC Hayward BH.

Fig. 3
figure 3

Plot of the effective potential with respect to r for \(\vartheta =0.2\)

Full size image

3 Some features of rotating NC Hayward black hole

In this section, we discuss some optical properties of NC rotating Hayward BH, such as shadows, observable quantities as well as the rate of energy emission.

3.1 Black hole shadow

The gravitational field near the event horizon of BHs is so strong that it allows nothing to escape not even light. Therefore, photons emitted from a light source or from the radiation from the accretion disk, will undergo deflection due strong gravitational field. Such photons could be captured by the BH or sent off to the far away observer. Accordingly, the observer will see a dark region around the BH having a greater radius as compared to the event horizon.

The apparent silhouette of the shadow can be visualized by the following celestial coordinates [35,36,37,38]

$$\begin{aligned} \alpha= & {} \lim \limits _{r\rightarrow \infty } \left( -r^2_{0}\sin \theta _{0}\frac{d\phi }{dr}\right) =-\xi \csc \theta _{0},\\ \beta= & {} \lim \limits _{r\rightarrow \infty }\left( r^2_{0}\frac{d\theta }{dr}\right) =\pm \sqrt{\eta -\xi ^2\cot ^2\theta _{0}+a^2\cos ^2\theta _{0}}. \end{aligned}$$

where, \(r_{0}\) denotes the distance from the BH to the distant observer and \(\theta _{0}\) denotes the angle between the axis of rotation of BH as well as the observer’s line of vision. The celestial coordinates \(\alpha \) (seen from the symmetry axis) and \(\beta \) (seen from its axis of symmetry in the equatorial plane) are the apparent, orthogonal distances of the image near the BH.

Fig. 4
figure 4

Shadows of NC Hayward BH for \(\theta =\frac{\pi }{2}\)

Full size image

The analysis of shadows of NC Hayward BH is presented in Fig. 4, where we consider \(M=1\) and \(\theta =\pi /2\). Here, we observe that the shape of the shadow is deformed for highly spinning BH. Also, the high values of g caused the shadows to be smaller in size as well as a slight dent in the shadow is noted for the high value of g as compared to the smaller ones. Therefore, the shape of shadow differs from the standard circle for high values of g. The variation of \(\vartheta \) is shown in the lower panel. The shadow becomes smaller in size as with the increase in g.

3.2 Astronomical observables

For the detailed analysis of the shape of the shadow, we discuss the astronomical observables for the NC rotating Hayward BH, suggested by Hioki and Meada [7,8,9,10,11]: The radius, \(R_{s}\), that determines the estimated size of the BH shadow and \(\delta _{s}\) which computes the deformation of the shadow. The silhouette of the shadow passes through three points, \(A(\alpha _{t}, \beta _{t})\) (at the top), \(B(\alpha _{b}, \beta _{b})\) (at the bottom), \(D(\alpha _{r}, \beta _{0})\) (the most right). The radius of the shadow as well as the deformation parameter can be calculated as

$$\begin{aligned} R_{s}=\frac{(\alpha _{t}-\alpha _{r})^2}{2|\alpha _{r}-\alpha _{t}|},~ \delta _{s}=\frac{D_{s}}{R_{s}}=\frac{|\alpha _{p}-\tilde{\alpha }_{p}|}{R_{s}}, \end{aligned}$$
(22)

where, \(D_{s}\) represents the distance between the most left position of the shadow \(C(\alpha _{p},0)\) and the reference circle \(F(\tilde{\alpha }_{p},0)\).

The behavior of the radius of the shadow as well as the deformation parameter is observed in Fig. 5. The radius of the shadow shows the same behavior when \(\vartheta =0\), whereas for the increasing values of NC parameter, it gradually attains higher values. It is also observed that the larger the g parameter, the smaller value of shadow radius is attained. The plots of deformation parameter describe that the shadow is more deformed for the increasing values of g, which indicates that the shadow’s shape will be a circle, approximately for the small values of g.

Fig. 5
figure 5

Analysis of the observables corresponding to \(\pi /2\)

Full size image

3.3 Rate of energy emission

It is believed that the BH shadow corresponds to high energy absorption by the BH, for a far away observer at infinity. The cross section of the absorbtion of BH, oscillates near a limiting constant value \(\sigma _{lim}\), at high energy. For a spherically symmetric BH, the limiting constant value of the geometrical cross section of the photon sphere is given as [53,54,55]

$$\begin{aligned} \sigma _{lim}\approx \pi R^2_{s}, \end{aligned}$$
(23)

using this the above limiting value, one can get the rate of energy emission

$$\begin{aligned} \frac{d^2 E(w)}{d w dt}=\frac{2\pi ^{2}R^2_{s}}{e^{w/T}-1}w^3, \end{aligned}$$
(24)

where, w denotes the photon frequency and T represents the Hawking temperature can be calculated for the event horizon (\(r_{+}\)) as [51]

$$\begin{aligned} T= & {} \frac{-1}{4\sqrt{(\pi \vartheta )^3}(r^2_{+}+a^2)(r^3_{+}+g^3)}\nonumber \\{} & {} \times \Bigg [8\sqrt{\pi \vartheta ^3}Mr^3_{+} \Bigg (\frac{r^3_{+}}{4}+g^3\Bigg )\tilde{\Xi }\Bigg (\frac{r_{+}}{2\vartheta }\Bigg )\Bigg ] \nonumber \\{} & {} +(Mr^9_{+}+Mg^3r^6_{+}-2M\vartheta r^7_{+}-8Mg^3\vartheta r^4_{+})e^{-\frac{r^2_{+}}{4\vartheta }} \end{aligned}$$
(25)
$$\begin{aligned}{} & {} -2r_{+}\sqrt{\pi \vartheta ^3}(r_{+}+g)^2(r^2_{+}+gr_{+}+g^2)^2, \end{aligned}$$
(26)

here, \(\tilde{\Xi }(\frac{r_{+}}{2\vartheta })\) is Gaussian error function. The standard result \(T=\frac{1}{4\pi r_{+}}\), \(r{+}=2M\), is retrieved, when \(a=0,~g=0\). The Fig. 6, depicts the behavior of rate of energy emission. We observe that \(\frac{d^2 E(w)}{d w dt}\), attains a peak for small values of w and decreases when w increases. The energy emission gradually reduced as g takes large values, also it is higher for large \(\vartheta \).

Fig. 6
figure 6

Analysis of the rate of energy emission for \(\vartheta =0.2\) (left) and \(\vartheta =0.24\) (right)

Full size image

4 Shadow of the NC rotating Hayward BH in the presence of plasma

This section is devoted to study the effects caused by plasma on the shadow cast by NC rotating Hayward BH. The plasma refraction index is given as \(\tilde{n}=\tilde{n}(x^{i},w)\), here w represents the photon frequency, appraised by an observer having velocity \(u^{\rho }\). The photon effective energy is given as \(\hbar w=-p_{\rho }u^{\rho }\), (\(p_{\rho }\) denotes the photon’s four momentum). The expression of the plasma refraction index is given as [19]

$$\begin{aligned} \tilde{n}^2=1+\frac{p_{\rho }p^{\rho }}{(p_{\nu }u^{\nu })^2}, \end{aligned}$$
(27)

where \(\tilde{n}=1\), corresponds to the vacuum case. It is convenient to represent refraction index with a frequency of plasma \(w_{e}\) [56]

$$\begin{aligned} \tilde{n}^2=1-\frac{w^2_{e}}{w^2}. \end{aligned}$$
(28)

The Hamilton–Jacobi equation which describes the motion of the photon near the BH in plasma environment, is given as [19, 56]

$$\begin{aligned} \frac{\partial {\mathcal {S}}}{\partial \tau }=-\frac{1}{2}[g^{\nu \rho }p_{\nu }p_{\rho } -(\tilde{n}^2-1)(p_{0}\sqrt{-g^{tt}})^2]. \end{aligned}$$
(29)

This yields the set of null geodesic equations, given as

$$\begin{aligned} \Sigma \frac{\partial t}{\partial \tau }= & {} \frac{r^2+a^2}{\Delta }[\tilde{n}^2{\mathcal {E}}(r^2+a^2)-a{\mathcal {L}}_{z}]\nonumber \\{} & {} -a(a\tilde{n}^2{\mathcal {E}}\sin ^2\theta -{\mathcal {L}}_{z}), \end{aligned}$$
(30)
$$\begin{aligned} \Sigma \frac{\partial \phi }{\partial \tau }= & {} \frac{a}{\Delta }[{\mathcal {E}}(r^2+a^2)-a{\mathcal {L}}_{z}]-(a{\mathcal {E}}-{\mathcal {L}}_{z}\csc ^2\theta ), \end{aligned}$$
(31)
$$\begin{aligned} \Sigma \frac{\partial r}{\partial \tau }= & {} \pm \sqrt{{\mathcal {R}}_{\mathfrak {pl}}}, \end{aligned}$$
(32)
$$\begin{aligned} \Sigma \frac{\partial \theta }{\partial \tau }= & {} \pm \sqrt{\Theta _{\mathfrak {pl}}}, \end{aligned}$$
(33)

where

$$\begin{aligned} {\mathcal {R}}_{\mathfrak {pl}}= & {} [{\mathcal {E}}(r^2+a^2)-a{\mathcal {L}}_{z}]^2+(\tilde{n}^2-1)(r^2+a^2)^2{\mathcal {E}}^2 \nonumber \\{} & {} -\Delta [{\mathcal {C}}+({\mathcal {L}}_{z}-a{\mathcal {E}})^2],\end{aligned}$$
(34)
$$\begin{aligned} \Theta _{\mathfrak {pl}}= & {} {\mathcal {C}}+(a^2{\mathcal {E}}^2 -{\mathcal {L}}_{z}^2\csc ^2\theta )\cos ^2\theta \nonumber \\{} & {} -a^2(\tilde{n}^2-1){\mathcal {E}}^2\sin ^2\theta . \end{aligned}$$
(35)

For convenience, we consider the analytic form of \(w_{e}\), given as

$$\begin{aligned} w^2_{e}=\frac{4\pi e^2{\check{\mathcal {N}}}(r)}{m_{e}}, \end{aligned}$$

where e is the electron charge and \(m_{e}\) denotes the mass of the electron respectively, and the number density of electrons \({\check{\mathcal {N}}}(r)\) is the radial function. The variation of \({\check{\mathcal {N}}}\) with r as power law, is stated as [56]

$$\begin{aligned} {\check{\mathcal {N}}}(r)={\check{\mathcal {N}}}_{0}/r^{h},\quad h\ge 0, \end{aligned}$$

that provides \(w^2_{e}=\kappa /r^{h}\), here \(\kappa \ge 0\) is a constant. For calculations, we consider \(h=1\). Following section 2, we discuss the influence of plasma on the shadow cast by NC rotating Hayward BH. The parameters, \(\xi \) and \(\eta \) takes the form the form

$$\begin{aligned} \xi= & {} \frac{P}{Q}+\sqrt{\frac{P^2}{Q^2}-\frac{W}{Q}}, \nonumber \\ \eta= & {} \frac{(r^2-a\xi +a^2)^2+(\tilde{n}^2-1)(r^2+a^2)^2}{\Delta _{\vartheta }}-(\xi -a)^2,\nonumber \\ \end{aligned}$$
(36)

where

$$\begin{aligned} Q= & {} \frac{a^2}{\Delta _{\vartheta }}, \\ P= & {} \frac{a}{a^2+r^2-\frac{4Mr^4\gamma (\frac{3}{2},\frac{r^4}{4\vartheta }) }{\sqrt{\pi }(g^3 + r^3)}}\\{} & {} \times \Bigg [r^2+a^2-\Bigg (2(g^3 + r^3)\vartheta e^{r^2/4\vartheta }\Bigg (\sqrt{\pi }(a^2 + r^2)\\{} & {} \times (g^3 + r^3)-4Mr^4\gamma \Bigg (\frac{3}{2},\frac{r^4}{4\vartheta }\Bigg )\Bigg )\Bigg )\Bigg ((g^3 + r^3)\\{} & {} \times \Bigg (Mr^4\sqrt{\frac{r^2}{\vartheta }}+2\vartheta \sqrt{\pi }e^{r^2/4\vartheta }(g^3 + r^3)\Bigg )\\{} & {} -4e^{r^2/4\vartheta }Mr^2 (4 g^3 + r^3)\vartheta \gamma \Bigg (\frac{3}{2},\frac{r^4}{4\vartheta }\Bigg )\Bigg )^{-1}\Bigg ],\\ W= & {} \frac{\tilde{n}^2(r^2+a^2)^2}{a^2+r^2-\frac{4Mr^4\gamma \Bigg (\frac{3}{2},\frac{r^4}{4\vartheta }\Bigg ) }{\sqrt{\pi }(g^3 + r^3)}}\\{} & {} \times \Bigg [r^2+a^2-\Bigg \{(2(g^3 + r^3)\vartheta e^{r^2/4\vartheta }(\sqrt{\pi }(a^2 + r^2)\\{} & {} \times (g^3 + r^3)-4Mr^4\gamma \Bigg (\frac{3}{2},\frac{r^4}{4\vartheta }\Bigg )\Bigg ) \Bigg )(2 \tilde{n} r + \tilde{n}')\Bigg \}\\{} & {} \Bigg \{\tilde{n}\Bigg ((g^3 + r^3)\Bigg (Mr^4\sqrt{\frac{r^2}{\vartheta }}+2\vartheta \sqrt{\pi }e^{r^2/4\vartheta }(g^3 + r^3)\Bigg )\\{} & {} -4e^{r^2/4\vartheta }Mr^2 (4 g^3 +r^3)\vartheta \gamma \Bigg (\frac{3}{2},\frac{r^4}{4\vartheta }\Bigg )\Bigg )^{-1} \Bigg \}\Bigg ]. \end{aligned}$$

The celestial coordinates with the effect of plasma are given by

$$\begin{aligned} \alpha= & {} -\frac{\xi }{\tilde{n}},\\ \beta= & {} \pm \frac{\sqrt{\eta -\tilde{n}^2a^2\sin ^2\theta +a^2\cos ^2\theta _{0} -\xi ^2\cot ^2\theta _{0}}}{\tilde{n}}. \end{aligned}$$

Using Eqs. (22)–(26) with Eq. (36), we analyze the observables as well as the rate of energy emission in the existence of plasma.

Figure 7 describes the influence of plasma on the shadows of NC rotating Hayward BH for \(M=1\), \(\theta =\frac{\pi }{2}\), and varying g as well as \(w_{e}/w\). We see that the shadow becomes smaller for increasing values of plasma and possess the circle shape in its absence. The shadow gets deformed as the free parameter g increases. In Fig. 8, it is observed that the radius of the shadow as well as deformation parameter becomes smaller for the high value of plasma parameters. The Fig. 9 shows that the impact of plasma on the rate of energy emission. We see that the peak of energy emission rate decreases as the value of \(w_{e}/w\) increases. It is also noted that for the large value of \(\vartheta \), the rate of energy emission is higher as compared to the small value which is similar to the case of without plasma.

Fig. 7
figure 7

Shadow of NC rotating Hayward BH with the effect of plasma

Full size image
Fig. 8
figure 8

Observable quantities in the presence of plasma for \(g=1.3\)

Full size image
Fig. 9
figure 9

Analysis of the energy emission in the presence of plasma for \(g=1.3\), \(\vartheta =0.2\) (left) and \(g=1.3\), \(\vartheta =0.24\) (right)

Full size image

5 Final remarks

In the wake of current observation of the premier image of supermassive BH in \(M87^{*}\) [19], the shadow of BH remains the topic of interest in order to study the spacetime structure in the strong field regime. In this research work, we have explored the shadow of a static, axially symmetric NC rotating Hayward BH based on Newman–Janis algorithm. We have discussed the null geodesics with the help of Hamilton Jacobi formalism. We have then calculated the celestial coordinates \(\alpha \), \(\beta \) to study the silhouette of the shadow. We have considered both cases, the presence as well as the absence of plasma. We have investigated the observables, the shadow radius \(R_{s}\) as well as deformation parameter \(\delta _{s}\) and the rate of energy emission. The obtained results can be summarized as follows.

  • We have found the parametric range for the spin a, Hayward’s free parameter g as well as NC parameter \(\vartheta \) (Fig. 1).

  • We have observed that the light trajectory passes near to event horizon, but do not capture by the BH. Also, the light trajectory gets closer to the event horizon for the increasing values of g (Fig. 2).

  • The analysis of the effective potential shows that the particles have an unstable motion for the increasing values of the free parameter g as well as the radius r (Fig. 3) which contrast charged NC BH [57]. We have also examined the Silhouette as well as the radius of the shadow, deformation parameter and the rate of energy emission for both cases, i.e., in the absence as well in the presence of plasma. Here, we consider the angle of inclination as \(\theta =\pi /2\), motivated by the fact that the gravitational effects on the shadow that raise with the inclination angle are substantial when the observer is located in the equatorial plane of the BH. Moreover, it is believed that the angle of inclination is expected to be closed to \(\pi /2\), for the supermassive BH. In the following, we discuss the results of both cases. − For the vacuum case:

  • The analysis of shadows shows that its silhouette deviates from the shape of a perfect circle for the high values of the free parameter g which is opposite to [57] but analogous to [31, 32, 58]. The increase in the NC parameter caused the shadow to be in smaller in size, but its shape is all circle, this behavior is comparable to NC Ayón Beato García (ABG) BH [31, 32]. We have observed that shape of the shadow for the immense spinning BH is more deformed as compared to the slowly spinning BH which corresponds to [31, 32, 58,59,60] (Fig. 4).

  • The radius of the shadow increases with NC parameter while becomes smaller with the increase of g which is similar to [57, 58] where the radius tends to decrease with NC charge (Fig. 5).

  • The increase in g corresponds to more deformation unlike [57]. Hence, both g as well as \(\vartheta \) influence the size and shape of the shadow identical to [31, 32] (Fig. 5).

  • We have calculated the energy emission rate of the NC Hayward BH, assuming that the BH shadow equals to the high energy absorption cross section. We have found that the rate of energy emission is maximum when w is small. More energy is emitted for small g as compared to its larger values which is similar to the Einstein–Maxwell-Dilaton-Axion BH [59] as well as BH in perfect fluid dark matter [60], also the rate of energy emission for the large value of \(\vartheta \) is higher than the small value (Fig. 6). − For the plasma case:

  • The shadows get smaller under the influence of plasma however deformed with respect to the increasing values of g, contrasting charged NC BH [57] (Fig. 7).

  • The size of the shadow as well as the deformation parameter gets smaller with the effect of plasma unlike [31, 32] as only distortion is effected by the influence of plasma for NC ABG BH (Fig. 8).

  • The rate of energy emission decreases with the influence of plasma. We have observed that the impact of \(\vartheta \) remains the same in both cases, ie., in the absence as well as presence of plasma (Fig. 9). In the view of the above discussion, we infer that this analysis could be helpful in exploring the attributes of non commutativity of BHs.