1 Introduction

Although General Relativity (GR) is a well-established physical theory and can successfully explain a wide range of effects at an astrophysical scale, many modified gravity theories have attracted meaningful attention in recent years. Such theories represent attempts of explaining open questions such as accelerated universe expansion and dark matter. In the cosmological context, a gravity theory based on scalar curvature R is the so-called f(R) gravity [1,2,3], which is a direct extension of general relativity. Another extension that has been investigated is \(f(R,{\mathscr {T}})\) gravity [4,5,6], where \({\mathscr {T}}\) is the trace energy-momentum tensor.

Teleparallel gravity is an interesting gravity theory that considers torsion instead of curvature. Moreover, the so-called tetrad field becomes the fundamental dynamical quantity of teleparallel gravity. The formulation of teleparallel gravity results from contractions of the torsion tensor and the torsion scalar T [7,8,9,10,11]. Although the teleparallel gravity is equivalent to GR, extensions as f(T) gravity are not equivalent to f(R) gravity since f(T) gravity leads to second-order field equations, whereas f(R) gravity has fourth-order equations. Therefore, studying topics such as black holes, wormholes, and cosmology in f(T) gravity has recently become attractive.

Proposed for the first time by Kaluza [12] and Klein [13] as an attempt of unifying electromagnetism and general relativity, the existence of extra dimensions has been an attractive research field, where the braneworld scenarios have been intensively investigated since the seminal work of Lisa Randall and Raman Sundrum (RS) [14, 15], which considered the existence of extra dimensions in a warped geometry. Such work was proposed as an alternative way of solving the hierarchy problem. Despite the great success, the original RS model in the GR context presented some problems in the location of the fermion and gauge fields, which motivates the study of the braneworld scenario in other gravities than the GR.

In recent years, the braneworld models have been investigated in the context of modified gravity such as mimetic gravity [16, 17], f(R) gravity [18], f(R, T) gravity [19,20,21] and modified teleparallel gravity [22, 23, 25,26,27]. In addition to the strong agreement with recent observations of the expansion of the universe, it has been shown that it is possible to build a thick brane with internal structure generated by a single scalar field within gravity f(T) [23, 27].

Besides the localization of gravity, an interesting question is to understand how matter fields, which can be bosonic or fermionic, can be localized on a brane in the context of modified gravity. However, there are some problems that should be circumvented. For instance, the gauge vector field, which describes the photon, can not be localized on brane following the standard action for the field. Such a problem can be overcome by introducing some kind of coupling. In the String Theory, there is an antisymmetric tensor field known as Kalb Ramond (KR) field which comes from the bosonic spectrum. This field can be investigated in braneworld scenarios, but it exhibits the same problem as the gauge vector field.

The localization of field on braneworld scenarios has been analyzed in gravity based on curvature scalar [28, 30,31,32, 34,35,36,37,38]. However, it would be unprecedented an investigation of the behavior of gauge field and of KR field on branes in the context of modified teleparallel gravity. Then, the main goal of this work is to address that question. In order to study the localization of the gauge field on the brane, we will consider a coupling between the gauge field and the scalar field that generates the thick brane. We also investigate a geometrical coupling considering that the field is coupled to torsion. Both couplings proposed are introduced in the kinetic part and therefore keep gauge invariant the action that describes the dynamics of the gauge field. We followed the same steps to study the KR field.

This work is structured as follows. In Sect. 2 we review some basic concepts of braneworld in f(T) teleparallel gravity. In Sect. 3 we study the localization of the gauge field and Kalb Ramond field considering a coupling with the scalar field. In addition, we analyze the massless and massive modes as well as resonant modes. In Sect. 4, we introduce a geometrical coupling between the fields (gauge field and Kalb Ramond field) and the scalar torsion and we make the same analysis as Sect. 3. Finally, our conclusions and perspectives are outlined in Sect. 5.

2 Basic aspects of teleparallel gravity

Unlike general relativity, which is based on metric formalism, teleparallel gravity has the vielbein as a dynamic variable. The vielbein is related to metric through the following relation [39]

$$\begin{aligned} g_{MN}=\eta _{ab}h^a\ _M h^b\ _N. \end{aligned}$$
(1)

Besides, using the vielbein we define a curvature free connection \(\widetilde{\varGamma }^P\ _{MN}=h_a\ ^P\partial _N h^a\ _M\), which is known as Weitzenbock connection and leads to non vanishing torsion \(T^P\ _{MN}=\widetilde{\varGamma }^P\ _{NM}-\widetilde{\varGamma }^P\ _{MN}\). With the torsion we can define [39]

$$\begin{aligned} K^{P}\ _{MN}=\frac{1}{2}\Big (T_{M}\ ^{P}\ _{N}+T_{M}\ ^{P}\ _{N}-T^{P}\ _{MN}\Big ), \end{aligned}$$
(2)

and

$$\begin{aligned} S^{P}\ _{MN}=\frac{1}{2}\Big (K^{MN}\ _P-\delta ^N_P T^{QM}\ _Q+ \delta ^M_P T^{QN}\ _Q\Big ), \end{aligned}$$
(3)

where \(K^{P}\ _{NM}\) and \(S^{P}\ _{NM}\) are contortion and the superpotential respectively. It is also possible to define the so-called scalar torsion [39]

$$\begin{aligned} T=T_{PMN}S^{PMN}. \end{aligned}$$
(4)

For f(T) gravity, the gravitational action that describes gravity coupled to scalar field in five dimensional spacetime is given by [23]

$$\begin{aligned} S=\int d^5x h\Big [-\frac{1}{4}f(T)+{\mathscr {L}}_m\Big ], \end{aligned}$$
(5)

where \(h=\sqrt{-g}\) and \({\mathscr {L}}_m\) represent the matter Lagrangian that will be defined later. By varying the action 5 with respect to vielbein, we get the following field equation

$$\begin{aligned}{} & {} \frac{1}{h}f_T\Big [\partial _Q(hS_N\ ^{MQ})-h\widetilde{\varGamma }^R\ _{SN} S_N\ ^{MQ}\Big ]\nonumber \\{} & {} \quad +f_{TT}S_N\ ^{MQ}\partial _Q T+\frac{1}{4}f\delta _N\ ^M={\mathscr {T}}_N\ ^M, \end{aligned}$$
(6)

where \(f\equiv f(T)\), \(f_{T}\equiv \partial f(T)/\partial T\) and \({\mathscr {T}}_N\ ^M\) is a tensor given by

$$\begin{aligned} {\mathscr {T}}_N\ ^M=h^a\ _N\frac{\delta {\mathscr {L}}_m}{\delta h^a\ _M}+\delta _N\ ^M {\mathscr {L}}_m. \end{aligned}$$
(7)

2.1 Thick brane setup

The Randall–Sundrum metric reads

$$\begin{aligned} ds^2=e^{2A}\eta _{\mu \nu }dx^\mu dx^\nu + dy^2, \end{aligned}$$
(8)

where \(e^{2A}\) is known as warp factor and \(\eta _{\mu \nu }\) is the Minkowski metric. We can choose the funfbein (vielbein defined in the five-dimensional spacetime) as follows

$$\begin{aligned} h^a\ _M=\begin{pmatrix} e^{A}\delta ^\mu _\nu &{} 0\\ 0 &{} 1 \end{pmatrix}, \end{aligned}$$
(9)

which represents a good choice among all possible vielbein, as they generate gravitational field equations that do not involve any additional restrictions on the function f(T) or the scalars T [8, 9]. As a matter of fact, the vielbein (9) is proved to be a good choice for the teleparallel f(T) [10, 11, 22, 23], f(T, B) [25, 26], and \(f(T,{{\mathscr {T}}})\) [40] gravity models.

The brane is generated by a single scalar field which depends only on the extra dimension, whose Lagrangian is given by

$$\begin{aligned} {\mathscr {L}}_{m}=-\frac{1}{2}\partial _{M}\phi \partial ^{M}\phi -V(\phi ), \end{aligned}$$
(10)

which leads to the following tensor

$$\begin{aligned} {\mathscr {T}}_{MN}=\partial _M\phi \partial _N\phi -g_{MN}{\mathscr {L}}_m. \end{aligned}$$
(11)

Thus, with the vielbein ansatz given by Eq. (9), the gravitational field equations are

$$\begin{aligned}{} & {} \phi ''+4A'\phi =\frac{d V}{d\phi }, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} 6A'^2f_T+\frac{1}{4}f= \frac{1}{2}\phi ^2-V, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \frac{1}{4}f+\Bigg (\frac{3}{2}A''+6A'^2\Bigg )f_T-36A'^2A''f_{TT}= -\frac{1}{2}\phi ^2-V.\nonumber \\ \end{aligned}$$
(14)

From Lagrangian 10, we define the energy density as

$$\begin{aligned} \rho (y)=-e^{2A}{\mathscr {L}}_m. \end{aligned}$$
(15)

To simplify our analysis we can propose an ansatz warp factor of the form [41]

$$\begin{aligned} e^{2A(y)}=\cosh ^{-2p}(\lambda y), \end{aligned}$$
(16)

where p and \(\lambda \) are the parameters that determine the amplitude and the width of the source.

Allow us to propose a model of f(T) in the form \(f(T)=T+kT^{n}\), that is a model already analyzed in the braneworld scenario [22,23,24]. This model is very interesting because it represents a generalization of teleparallel gravity. The k and n parameters control the modification of the usual teleparallel theory.

Thus, the Eqs. (13) and (14) take the form

$$\begin{aligned} \phi '^2(y)= & {} \frac{3}{2}p\lambda ^2\textrm{sech}^2(\lambda y)\Big \{1+(-1)^{2(n-1)}B_nkn\nonumber \\ {}{} & {} \Big [p\lambda \tanh (\lambda y)\Big ]^{2(n-1)}\Big \}, \end{aligned}$$
(17)
$$\begin{aligned} V(\phi (y))= & {} \frac{3}{4}p\lambda ^2\textrm{sech}^2(\lambda y)-3[p\lambda \tanh (\lambda y)]^2\nonumber \\{} & {} +\frac{(-1)^{2n}3B_nk}{4p}\Bigg \{\Big [4p-n\ \textrm{csch}^2(\lambda y)\Big ]\nonumber \\{} & {} \times \Big [p\lambda \tanh (\lambda y)\Big ]^{2n}\Bigg \}. \end{aligned}$$
(18)

Through the Eq. (15), we have the energy density in the form

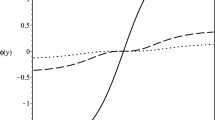
$$\begin{aligned} \rho (y)= & {} \frac{3}{2p}\Bigg \{(p\lambda )^2\Big [2p\tanh ^2(\lambda y)-\textrm{sech}^2(\lambda y)\Big ]\nonumber \\{} & {} +(-1)^{2n}B_nk\Big [2p-n\ \textrm{csch}^2(\lambda y)\Big ]\nonumber \\{} & {} \times \Big [p\lambda \tanh (\lambda y)\Big ]^{2n}\Bigg \}\cosh ^{-2p}(\lambda y). \end{aligned}$$
(19)

The differential equation (17) gives us the solutions of the scalar field. For \(n=1\) the scalar field has the form of a kink-like solution independent of the parameter k. Through Eq. (19) we obtain the form of the energy density in the brane. For \(n=1\) the energy density presents a localized profile satisfying the dominant and strong energy conditions independent of the parameter k.

Fig. 1
figure 1

Behavior of the solution of the scalar field and the energy density in the brane for \(n=2\) and \(p=\lambda =1\). a \(k=-0.005\). b \(k=-\,0.09\). c \(k=-\,0.5\)

Full size image

For \(n=2\) something interesting happens. The scalar field solution presents a behavior similar to a double-kink. The energy density has two peaks near the origin. This behavior represents a brane splitting, which is very evident in Fig. 1. In Fig. 1a, where \(k=-0.005\), we observe that the scalar field presents a kink-like behavior and the energy density is well located around the origin. When we increase the value from k to \(k=-\,0.09\) (Fig. 1b) we observe that the solution of the kink-like scalar field tends to be a solution similar to a double-kink and this behavior is influenced by the energy density that tends to split into two peaks around the origin. Finally, with the value of \(k=-\,0.5\), the emergence of a new structure that tries to split a brane becomes more evident (Fig. 1c).

3 Field localization with minimal coupling

Once we have constructed the thick braneworld in the context of f(T) teleparallel gravity, we should analyze the localization of the gauge field and Kalb Ramond field. For this purpose, we will consider that the fields are minimally coupled to the scalar field responsible for the generation of the thick brane. The localization of gravity was investigated in Ref. [22].

The braneworld scenario in a gravity f(T), as well as the other thick brane scenarios, is not capable of supporting the localization of the gauge field zero modes. Indeed, as the warp factor is factorized out of the effective action, one obtains non-normalizable solutions from the equations of motion to the gauge field. To overcome this difficulty, some models have appeared in the literature. An additional scalar field (the dilaton) has been introduced in the action of five dimensions, making possible the location of the gauge field, through the coupling between the dilaton and the kinetic term of gauge fields [30, 31]. In Ref. [42] gauge field localization is obtained via kinetic terms induced by localized fermions. It is relevant to note that there is no complete and standard mechanism for the location of the gauge field on the brane [32], therefore, leaving us free to choose a proper mechanism.

To make it possible to locate gauge fields in thick branes, we introduce a coupling with a function of the scalar field \(G(\phi )\) [32, 34, 35]. This coupling is based on same mechanism that provides the location of the fermion field in a five-dimensional space-time braneworld scenario [10, 23, 43,44,45,46, 50,51,52,53,54,55,56].

3.1 Gauge field

In order to investigate the behavior of the gauge field in the bulk, we assume the following action [31, 32]

$$\begin{aligned} S=\frac{1}{4}\int d^5x h G(\phi )F_{MN}F^{MN}, \end{aligned}$$
(20)

where \(F_{MN}=\partial _M A_N-\partial _N A_M\) and \(G(\phi )\) is a suitable function of scalar field, which yields a normalizable zero mode for gauge field after dimensional reduction. The gauge field governed by action 20 should satisfy the motion equation

$$\begin{aligned} \partial _M(h G(\phi ) F^{MN})=0. \end{aligned}$$
(21)

Now we consider the gauge \(\partial _\mu A^\mu =A_4=0\), as it was considered in Refs. [29,30,31,32]. Also, the Kaluza–Klein decomposition is \(A_\mu (x^M)=\sum \widehat{A}_\mu (x^\mu )\chi (y)\), so that the Eq. (21) becomes

$$\begin{aligned} \chi ^{\prime \prime }+\left( 2A^{\prime }+\frac{G^{\prime }}{G}\right) \chi ^{\prime }=-m^2e^{-2A}\chi . \end{aligned}$$
(22)

3.2 Kalb–Ramond field

For Kalb–Ramond field, the action is given by [31, 32]

$$\begin{aligned} S=\frac{1}{6}\int d^5x h G(\phi )H_{LMN}H^{LMN}, \end{aligned}$$
(23)

where \(H_{LMN}=\partial _L B_{MN}+\partial _M B_{NL}+\partial _N B_{LM}\). Like gauge field, we consider a function \(G(\phi )\) which produces a normalizable zero mode for Kalb–Ramond field. By varying the action 23 with respect to the field \(B_{MN}\), we arrive at

$$\begin{aligned} \partial _L(hG(\phi )H^{LMN})=0. \end{aligned}$$
(24)

By adopting the gauge choice \(\partial _\mu B^{\mu \nu }=B^{5\nu }=0\) [32, 33], and Kaluza-Klein decomposition \(B_{\mu \nu }(x^M)=\sum \widehat{B}_{\mu \nu }(x^\mu )\chi (y)\), we obtain the following equation for \(\chi \)

$$\begin{aligned} \chi ^{\prime \prime }+\frac{G^{\prime }}{G}\chi ^{\prime }=-m^2e^{-2A}\chi , \end{aligned}$$
(25)

3.3 Massless modes

We can transform Eqs. (22) and (25) into a single equation of the form

$$\begin{aligned} \chi ^{\prime \prime }+\left( qA^{\prime }+\frac{G^{\prime }}{G}\right) \chi ^{\prime }=-m^2e^{-2A}\chi , \end{aligned}$$
(26)

where q is a constant. If \(q=2\) we have the equation for the gauge field, and if \(q=0\) we have the equation for the KR field.

Let us consider the conformal coordinate \(dz=e^{-A}dx\) so that the equation becomes

$$\begin{aligned} \ddot{\chi }(z)+2H\dot{\chi }(z)=-m^2\chi (z), \end{aligned}$$
(27)

where

$$\begin{aligned} H=\frac{1}{2}\left[ (q-1)\dot{A}+\frac{\dot{G}}{G}\right] . \end{aligned}$$
(28)

Here, the dot ( \(\dot{ }\) ) denotes differentiation with respect to conformal coordinate z. We can now write Eq. (27) in Schrödinger-like form by employing the following change \(\chi (z)=e^{K}(z)\psi (z)\), being \(K=-\int H dz \). Thus, with this change, we get the following Schrödinger-like equation

$$\begin{aligned} -\ddot{\psi }+V\psi =m^2\psi , \end{aligned}$$
(29)

where we have defined the potential

$$\begin{aligned} V=\dot{H}+H^2. \end{aligned}$$
(30)

The Schrödinger-type Eq. (29) represents a supersymmetric quantum mechanical equation, which guarantees the stability of the spectrum and allows a massless modes in the form

$$\begin{aligned} \psi _0=N_0e^{\frac{1}{2}(q-1)A+\frac{1}{2}\int \frac{\dot{G}}{G}dz}, \end{aligned}$$
(31)

where \(N_0\) is a normalization constant. In order to recover the four-dimensional gravity, the zero mode should be localized on the brane.

To choose the form of \(G(\phi )\), we follow the following rules: \(G(\phi )\) should satisfy the asymptotically condition \(G(\phi (y\rightarrow \infty ))\rightarrow c\) where c is a constant, and the finity condition at the same time

$$\begin{aligned} \int ^{\infty }_{-\infty } G(\phi )dy<\infty , \end{aligned}$$
(32)

to preserve the canonical form of 4D action [31, 32].

We propose two values for \(G(\phi )\), namely

$$\begin{aligned} G_1(\phi )=b\cos \Big (\frac{\phi }{b}\Big ), \end{aligned}$$
(33)

and

$$\begin{aligned} G_2(\phi )=b-\frac{\phi ^2}{b}, \end{aligned}$$
(34)

where b is a parameter that controls the model. We make these choices based on the results found in Refs. [32, 34, 35].

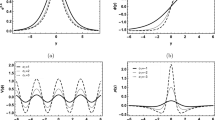
The expression for the potentials is too big to be represented here. So, let us represent the behavior of potentials graphically. When \(n=1\) the parameter k disappears, making \(G_1\) and \(G_2\) invariant over the variation of k. For \(G_1(\phi )\) with \(n=1\), the potential shows a potential well behavior for both a gauge field and for the KR field (Fig. 2a). For \(n=2\) the influence of the torsion parameter k is evident (Fig. 2b, c). Very similar to \(G_1(\phi )\), for \(G_2(\phi )\) the potential presents a potential well behavior both for a gauge field and for the KR field. With the Fig. 3a, b it is possible to see the influence of the torsion parameter k for the case of \(n=2\).

Fig. 2
figure 2

Effective potential behavior for \(G_1(\phi )\) with \(p=\lambda =1\). a \(n=1\). Being \(b=4\) and \(n=2\). b Gauge field. c KR field

Full size image
Fig. 3
figure 3

Effective potential behavior for \(G_2(\phi )\) with \(n=2\), \(b=4\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image

As was to be expected from Eq. (31) massless modes are localized for both the gauge and KR fields (Fig. 4a). The massless modes are influenced by the changes caused in the effective potential due to the torsion parameters. For \(G_1\) with \(n=2\), when we decrease the value of the parameter k, we make the massless modes more localized, both for the gauge field (Fig. 4b) and for the KR field (Fig. 4c). The same goes for \(G_2\) with \(n=2\) (Fig. 5a, b).

Fig. 4
figure 4

Behavior of massless modes for \(G_1(\phi )\) with \(p=\lambda =1\). a \(n=1\). Being \(b=4\) and \(n=2\). b Gauge field. c KR field

Full size image
Fig. 5
figure 5

Behavior of massless modes for \(G_2(\phi )\) with \(n=2\), \(b=4\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image

3.4 Massive modes

By knowing the behavior of the effective potentials, we can see that they are even functions. Then we can find the massive modes by numerically solving Eq. (29), keeping in mind that the wave functions will be even or odd. Therefore, the boundary conditions are

$$\begin{aligned} \psi _{even}(0)= & {} c,\ \ \dot{\psi }_{even}(0)=0,\nonumber \\ \psi _{odd}(0)= & {} 0, \ \ \dot{\psi }_{odd}(0)=c, \end{aligned}$$
(35)

where c is just a constant [26,27,28, 55, 56]. It is important to note that here \(\psi _{even}\) and \(\psi _{odd}\) respectively represent the even and odd parity modes of \(\psi (z)\).

The behavior of the effective potential that presents a potential well close to the brane, enables the emergence of resonate modes. The study of resonances is very relevant, as it provides important information about the massive modes [55, 56]. Although these modes are not located on the brane, some of these massive states can present a large amplitude very close to the brane [28].

Fig. 6
figure 6

The behavior of massive modes for \(G_1(\phi )\), with \(n=1\) and \(b=2\) and \(p=\lambda =1\). To the Gauge field, a \(\psi _{even}\) b \(\psi _{odd}\). KR field, c \(\psi _{even}\). d \(\psi _{odd}\)

Full size image
Fig. 7
figure 7

The behavior of the relative probability P(m) for \(G_1(\phi )\) with \(n=2\), \(b=4\) \(k=-0.3\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 8
figure 8

The behavior of massive modes for \(G_1(\phi )\), with \(n=2\), \(b=4\) and \(p=\lambda =1\). To the Gauge field, a \(\psi _{even}\) with \(m=1.001\). b \(\psi _{odd}\) with \(m=0.741\). KR field, c \(\psi _{even}\) with \(m=0.685\). d \(\psi _{odd}\) with \(m=0.580\)

Full size image
Fig. 9
figure 9

The behavior of the relative probability P(m) for \(G_2(\phi )\) with \(n=2\), \(b=4\) \(k=-0.1\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 10
figure 10

The behavior of massive modes for \(G_2(\phi )\), with \(n=2\), \(b=4\) and \(p=\lambda =1\). To the Gauge field, a \(\psi _{even}\) with \(m=0.847\). b \(\psi _{odd}\) with \(m=0.762\). KR field, c \(\psi _{even}\) with \(m=0.635\). d \(\psi _{odd}\) with \(m=0.508\)

Full size image

The resonant modes can be obtained by the analog quantum mechanical structure of massive modes, where the relative probability P(m) of finding a particle with mass m in a narrow band \(2z_b\) is [28, 55, 56]

$$\begin{aligned} P(m)=\frac{\int _{-z_b}^{z_b} |\psi (z)|^2 dz}{\int _{-z_{max}}^{z_{max}} |\psi (z)|^2 dz}, \end{aligned}$$
(36)

where \(z_{max}\) stands for the domain limits. Larger values of the parameter \(z_b\) do not change the results for the position of the resonance peaks, but small values of \(z_b\) are more efficient to identify the peaks.

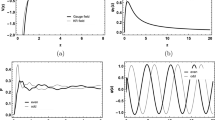
For \(G_1\) with \(n=1\), it is possible to perceive the influence of the mass eigenvalues in the field solutions (Fig. 6). In the case of the gauge field, when we increase the mass eigenvalue, we increase the number of oscillations, decreasing the amplitudes of the oscillations (Fig. 6a, b). The same happens with the KR field (Fig. 6c, d), but something interesting happens at the origin of the even solution. Indeed, it is possible to observe the formation of a division at the peak of oscillation at the origin for low mass eigenvalues (Fig. 6c).

The relative probability P(m), for \(G_1(\phi )\), with \(n=2\) is shown in Fig. 7. The odd solutions for the gauge field, show a sharp peak for \(m^2=0.41\), which indicates a massive resonate state (Fig. 7a). Something similar happens for the KR field, but the peak appears in a more discrete way at \(m^2=0.23\) (Fig. 7b). It is interesting to note that the even solutions, both for the gauge field and for KR field, do not clearly show resonance peaks.

The influence of torsion is evident when we analyze the variation of the parameter k. We do this analysis for \(n=2\) (Fig. 8). For the gauge field, when we decrease the value of k, we modify the amplitude of the oscillations that tend to move away from the origin of the brane (Fig. 8a, b). For the KR field, when we vary k, we modify the amplitudes of the oscillations, but they do not depart from the origin (Fig. 8c, d).

In Fig. 9, we show the behavior of the relative probability P(m), for \(G_2(\phi )\), with \(n=2\). The odd solutions for the gauge field show a sharp peak for \(m^2=0.45\) (Fig. 9a). On the other hand, even solutions do not show evident peaks. For the KR field, the odd solutions show a peak at \(m^2=0.19\) (Fig. 9b). Something similar happens with even solutions.

Fig. 11
figure 11

Effective potential behavior for \(G_1(T)\) with \(n=2\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 12
figure 12

Effective potential behavior for \(G_2(T)\) with \(n=2\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 13
figure 13

Behavior of massless modes for \(G_1(T)\) with \(n=2\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 14
figure 14

Behavior of massless modes for \(G_2(T)\) with \(n=2\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 15
figure 15

The behavior of the relative probability P(m) for \(G_1(T)\) with \(n=2\), \(k=-0.06\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 16
figure 16

The behavior of massive modes for \(G_1(T)\), with \(n=2\) and \(p=\lambda =1\). To the Gauge field, a \(\psi _{even}\) with \(m=0.651\). b \(\psi _{odd}\) with \(m=0.661\). KR field, c \(\psi _{even}\) with \(m=0.476\). d \(\psi _{odd}\) with \(m=0.481\)

Full size image
Fig. 17
figure 17

The behavior of the relative probability P(m) for \(G_2(T)\) with \(n=2\), \(k=-\,0.05\) and \(p=\lambda =1\). a Gauge field. b KR field

Full size image
Fig. 18
figure 18

The behavior of massive modes for \(G_2(T)\), with \(n=2\) and \(p=\lambda =1\). To the Gauge field, a \(\psi _{even}\) with \(m=0.652\). b \(\psi _{odd}\) with \(m=0.593\). KR field, c \(\psi _{even}\) with \(m=0.556\). d \(\psi _{odd}\) with \(m=0.476\)

Full size image

For \(G_2\) with \(n=2\), in the case of the gauge field, when we decrease the value of k, we modify the amplitudes of the oscillations that tend to move towards the origin (Fig. 10a, b). The same is true for the KR field (Fig. 10c, d).

4 Field localization with geometric coupling

In this section, we will use the geometric coupling in which the fields are non-minimally coupled to torsion. Therefore, this section is dedicated to studying the effects of the f(T) modified teleparallel gravity on scalar, gauge and Kalb–Ramond fields by considering geometric coupling. It is worth mentioning that this kind of coupling have been considered in the context of gravitational waves and cosmology [47,48,49].

4.1 Massless modes

Similar to the Sect. 3, we can write the gauge field and KR field equations as a single equation of the form

$$\begin{aligned} \chi ^{\prime \prime }+\left( qA^{\prime }+\frac{G^{\prime }}{G}\right) \chi ^{\prime }=-m^2e^{-2A}\chi , \end{aligned}$$
(37)

which is the same equation as (26), the only difference is that now \(G\equiv G(T)\). Therefore, the same process performed in the previous section is repeated here, where when \(q=2\) we have the equation for the gauge field, and if \(q=0\) we have the equation for the KR field.

To choose the form of G(T), we follow the following rules: G(T) should satisfy the positivity condition \(G(T)>0\) and the finity condition at the same time

$$\begin{aligned} \int ^{\infty }_{-\infty } G(T)dy<\infty , \end{aligned}$$
(38)

to preserve the canonical form of 4D action [37]. We propose two values for G(T), which are

$$\begin{aligned} G_1(T)=(12+T)+k(12+T)^n, \end{aligned}$$
(39)

and

$$\begin{aligned} G_2(T)=1-\exp [k(12+T)^n]. \end{aligned}$$
(40)

We make these choices based on the results found in Ref. [37].

Figure 11 shows the behavior of the potential for \(G_1(T)\) with \(n=2\). In the case of the gauge field, the potential presents the shape of a well, and when we vary the parameter k a new well is formed (Fig. 11a). When k takes on a very negative value, the potential becomes a potential barrier. As for the KR field, when the parameter k is varied, the potential goes from a well to a barrier (Fig. 11b).

For \(G_2(T)\) the behavior of the potential for n is shown in the Fig. 12. In the case of the gauge field, when decreasing the value of the parameter k, new wells appear (Fig. 12a). As for the KR field, when the parameter k is varied, the potential well is divided into two wells (Fig. 12b).

Massless modes are influenced by the variation of torsion parameters. For \(G_1(T)\) with \(n=2\) and \(k=-\,0.005\) the massless mode presents a single peak and when we vary the value of k it is possible to notice the emergence of a new peak (Fig. 13). This behavior happens for both a gauge field and a KR field. As for \(G_2(T)\) with \(n=2\) in the case of the gauge field, when the value of the parameter k is varied, we observe the formation of a deformed structure in the massless modes (Fig. 14a). In the case of the KR field, the massless modes are divided by varying the parameter k (Fig. 14b).

4.2 Massive modes

As the effective potentials are even functions, we can find the massive modes numerically, keeping in mind that the wave functions will be even (\(\psi _{even}\)) or odd (\(\psi _{odd}\)). Therefore, we will use the boundary conditions shown in Eq. (35).

The relative probability P(m), for \(G_1(T)\), with \(n=2\) is shown in Fig. 15. The even and odd solutions for both the gauge field (Fig. 15a) and the KR field (Fig. 15b) do not clearly show resonance peaks. However, we can clearly observe the influence of the k parameter in massive modes through Fig. 16. In the case of the gauge field, when we decrease the value of k, we decrease the amplitudes and increase the oscillations that tend to move closer to the origin (Fig. 16a, b). As for the KR field, when we decrease the value of k, we decrease the amplitudes and oscillations, which tend to move away from the origin (Fig. 16c, d). Something interesting happens in \(k=-\,0.06\), where we notice the formation of a new structure that tends to split the peak that is located at the origin of the brane (Fig. 16c).

In Fig. 17, we show the behavior of the relative probability P(m), for \(G_2(T)\), with \(n=2\). The solutions for the gauge field show sharp peaks at odd solutions for \(m^2=0.39\) and at even solutions for \(m^2=0.91\). The same happens with the case of the KR field, the odd solutions show a peak at \(m^2=0.18\) and the even solutions show a peak at \(m^2=1.02\). These sharp peaks in P(m) reveal the massive resonant modes.

For \(G_2(T)\) with \(n=2\), in the case of a gauge field, when we decrease the value of the parameter k, we decrease the amplitudes and increase the oscillations, which present a small deformation at the origin of the brane (Fig. 18a, b). The same happens for the case of the KR field (Fig. 18c, d), and when we decrease the value of k, the formation of a structure that divides the peak at the origin of the brane is very evident (Fig. 18c).

It is interesting to note that the massive modes propagate to the bulk similar to free wave solutions. This behavior may contribute in some way to gravitational waves. The massless modes are confined to the brane. Therefore, they do not contribute to gravitational waves. See for example Refs [47, 48], where the authors studied the behavior of gravitational waves in the context of f(T) and f(T, B) modified teleparallel gravity coupled to a scalar field. The authors also show that the scalar field does not propagate at the first order of perturbation.

5 Conclusion

In this work, we have investigated the mechanism of localization of gauge field and Kalb Ramond field in a thick brane generated by a single scalar field in the context of modified teleparallel gravity. We consider two types of gauge-invariant couplings. The first one is a non-minimal coupling between the gauge and KR field and scalar field responsible for generation of thick brane. The second one is a non-minimal coupling with torsion. For both proposed couplings, we observed significant results that make them possible mechanisms to locate vector fields in a braneworld scenario, and also in other scenarios such as black holes and wormholes.

Both coupling allow us to investigate the massive spectrum of fields. For such a purpose, we write the equations of motion in a Schroedinger-like equation in the structure of supersymmetric quantum mechanics. The effective potentials are modified through parameters that control the influence of torsion (k and n). Massless modes are localized and sense the change caused by torsion parameters. The same goes for massive modes.

Something interesting happens for the geometric coupling. The effective potentials present new wells and peaks when we vary the torsion parameters, also modifying the localized massless modes, which tend to splitting. Another interesting result is that in the case of the KR field, the massive even solutions present the appearance of a small structure (two peaks) near the brane when we vary the torsion parameters. Furthermore, it was possible to observe resonating modes of the massive spectrum in both couplings, being more evident for the geometric coupling.

A future perspective would investigate the effects of massive modes on gravitational waves. The massless modes does not contribute to gravitational waves since they are trapped on the brane. However, the massive modes could be relevant in such a context. Therefore, a complete analysis should be considered.