1 Introduction

Instantons are non-perturbative classical solutions of Euclidean equations of motion in non-abelian gauge theories [1]. In the semi-classical limit, instantons describe quantum tunneling between different vacuum sectors of the theory [2,3,4]. They are either directly responsible for generating or at least contributed to many key aspects of non-perturbative low-energy dynamics of strong interactions [5,6,7,8,9,10]. These include the role of instantons in the breaking of the \(U(1)_A\) symmetry and the spontaneous breakdown of the chiral symmetry, the formation of quark and gluon condensates, \(\langle 0|\bar{q}q |0\rangle \) and \(\langle 0|G^a_{\mu \nu }G^a_{\mu \nu }|0\rangle \) and so on.

Unfortunately, up to now, the QCD instanton has never been observed experimentally.Footnote 1 The problem is that the large-size instanton is very challenging to distinguish from various possible soft QCD contributions, while the cross-section of the heavy (small-size) instanton production is exponentially suppressed by the \(e^{-2S_I}\) factor, where the corresponding to instanton action \(S_I=2\pi /\alpha _s\). Nevertheless, it would be very appealing to observe the small-size instanton signal since in such a case, the uncertainties due to the soft QCD and other non-perturbative effects are better controllable.

The characteristic signature of small-size instanton is the production of a large number of isotropically distributed (mini)jets. That is, we are searching for the high multiplicity events with large (close to 1) sphericity S.

It was shown in Ref. [14] that at high multiplicities the role of the multiple parton interactions (MPI) strongly increases and the resulting sphericity of these MPI events becomes also close to one. Therefore, first of all, we have to suppress the MPI contributions. This can be done by selecting the events with large rapidity gaps (LRGs). Indeed, it was demonstrated in Ref. [15] that in this case there is a good chance to observe the instanton signal at the LHC. Recall that the kinematics considered in Ref. [15] corresponds to the LRG events, selected by observing the leading proton which carries away a very close to 1 (\(x_L\sim 0.997\)) fraction of its initial momentum in the ALFA or TOTEM detectors [16, 17]. Since the remaining energy is quite small, the mass of the instanton is not too large: \(M_{\textrm{inst}}\sim 20{-}40\) GeV.

In the present paper we discuss the possibility to observe the higher mass instantons (\(M_{\textrm{inst}}>60\) GeV) by tagging the leading protons with the dedicated forward proton detectors (FPDs): AFP [18, 19] on the ATLAS side or CT-PPS [20, 21] on the CMS side, when the remaining fraction of beam energy, \(\xi =1-x_L\sim 0.03\). They were both installed in Run 2 and first experience shows that they cover a \(0.02< \xi < 0.15\) region. They are also equipped by time-of-flight (ToF) detectors with a time resolution of 10 ps expected to be achieved in Run 4. The goal for the Run 3 data taking is 20 ps.

Due to the strong, \(e^{-2\pi /\alpha _s}\), suppression of a heavy instanton amplitude the expected cross-section becomes rather small. Thus, we have to consider the possibility to work at a large luminosity and account for the pile-up background. We study the ’one LRG’ kinematics, where only one leading proton is detected, and the central instanton production, when both leading protons are observed.

We will follow here and below the results of the previous [15, 22] papers. In Sect. 2 we recall the definition and basic formulae for the instanton-induced processes. In Sect. 3 the main details of the generation and selection of instanton events with one or two LRGs are discussed. Searching strategy and the optimal cuts are described ed in Sect. 4, while the results are presented in Sect. 5. We conclude in Sect. 6.

2 The QCD instanton

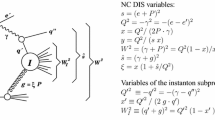
In QCD, the instanton configuration consists of the gauge field,

$$\begin{aligned} A_\mu ^{a\, \textrm{inst}}(x)= & {} \frac{2 \rho ^2}{g} \frac{\bar{\eta }^a_{\mu \nu } (x-x_0)_\nu }{(x-x_0)^2((x-x_0)^2+\rho ^2)}, \end{aligned}$$
(1)

along with the fermion components for light (\(m_f <1/\rho \)) fermions,

$$\begin{aligned} \bar{q}_{Lf} = \psi ^{(0)}(x), \quad q_{Rf} = \psi ^{(0)}(x). \end{aligned}$$
(2)

The gauge field \(A_\mu ^{a\, \textrm{inst}}\) is the Belavin–Polyakov–Schwartz–Tyupkin (BPST) instanton solution [1] of the self-duality equations in the singular gauge. Here \(\rho \) is the instanton size and \(x_0\) is the instanton position. Constant group-theoretic coefficients \(\bar{\eta }^a_{\mu \nu }\) are the ’t Hooft eta symbols defined in Ref. [2]. The fermionic components \(\psi ^{(0)}\) are the corresponding normalised solutions of the Dirac equation \(\gamma ^\mu D_\mu [A_\mu ^{a\, \textrm{inst}}] \psi ^{(0)} \,=0\). These are the fermion zero modes of the instanton. The instanton configuration is a local minimum of the Euclidean action, and the action on the instanton is given by \(S_I= \frac{8\pi ^2}{g^2} = \frac{2\pi }{\alpha _s}\).

The instanton configuration in Eq. (1) has a topological charge equal to one and thus, due to the chiral anomaly, the instanton processes violate chirality. If the instanton is produced by a two-gluon initial state, the final state of this instanton-mediated process will have \(N_f\) pairs of quarks and anti-quarks with the same chirality,

$$\begin{aligned} g+g\rightarrow n_g\times g + \sum ^{N_f}_{f=1}(q_{Rf}+\bar{q}_{Lf}), \end{aligned}$$
(3)

where \(N_f\) is the number of light flavours relative to the inverse instanton size, \(m_f <1/\rho \). The instanton contribution to the amplitude for this process comes from expanding the corresponding path integral in the instanton field background. At leading order in the instanton perturbation theory, the amplitude takes the form of an integral over the instanton collective coordinates (see e.g. Refs. [11, 12] for more detail)

$$\begin{aligned}{} & {} {{\mathcal {A}}}^\mathrm{\, L.O.}_{\, 2\rightarrow \, n_g+ 2N_f} \nonumber \\ {}{} & {} = \int d^4 x_0 \int _0^\infty d\rho \, D(\rho ) \, e^{-S_I}\, \prod _{i=1}^{n_g+2} A_{\textrm{LSZ}}^\textrm{inst}(p_i;\rho )\nonumber \\ {}{} & {} \quad \times \prod _{j=1}^{2N_f} \psi ^{(0)}_{\textrm{LSZ}}(p_j; \rho ). \end{aligned}$$
(4)

The factors of \(A_{\textrm{LSZ}}^\textrm{inst}(p_i;\rho )\) and \( \psi ^{(0)}_{\textrm{LSZ}}(p_j; \rho )\) are the standard insertions of the LSZ-reduced instanton fields in the momentum representation and \(D(\rho )\) is given by the known expression for the instanton density [2].

From the point of view of Feynman graphs the leading order instanton amplitude (Eq. (4)) reveals itself as a family of multi-particle vertices (with different numbers of emitted gluons), integrated over the instanton position and size. It describes the emission of a large number of gluons, \(n_g \propto E^2/\alpha _s\), together with a fixed number of quarks and anti-quarks, one pair for each light flavour in accordance with Eq. (3). The semi-classical suppression factor, \(\exp (-S_I)=\exp (-2\pi /\alpha _s)\), will be partially compensated by the growth with jet energy, E, of the high multiplicity cross-section for the process in Eq. (3). The fully factorised structure of the field insertions on the right-hand side of Eq. (4) implies that at leading order in instanton perturbation theory there are no correlations between the momenta of the external legs in the instanton amplitude. The momenta of individual particles in the final state are mutually independent, apart from overall momentum conservation.

Thus, to discover the QCD instanton we have to observe in the final state a multi-particle cluster or a fireball which contains in general a large number of isotropically distributed gluon (mini)jets accompanied by \(N_f\) pairs of light quark jets generated by a subprocess such as in Eq. (3).

It is quite challenging, however, to identify the instanton on top of the underlying event. Recall, that the instanton is not a particle and there will be no peak in the invariant mass, \(M_\textrm{inst}\), distribution.Footnote 2 The mean value of \(M_{\textrm{inst}}\) can at least in principle be “measured” or reconstructed as the mass of the minijet system created by the instanton fireball in each given event. Talking about the instanton we actually mean a family of objects of different sizes, \(\rho \) and different orientations in the colour and the Lorentz spaces. The mean value of \(M_{\textrm{inst}}\) depends on \(\rho \), increasing when \(\rho \) decreases. Since experimentally it is impossible to measure the instanton size, \(\rho \), below we use the mass \(M_{\textrm{inst}}\) to characterise the properties of the instanton production event.

Fig. 1
figure 1

Instanton production in a diffractive process with an LRG. The Pomeron exchange is shown by the thick doubled line. The red bar shows the range of \(\eta \) considered in this paper. Y indicates the incoming proton position in rapidity. As shown in the diagram secondaries will be produced also outside this range but they will not be used when calculating \(E_{T}\) or \(N_{ch}\)

Full size image

3 Generation of events

As discussed above, we expect a large ‘underlying event’ background. However the background caused by multi-parton interactions can be effectively suppressed by selecting events with Large Rapidity Gaps (LRGs) or the leading proton. Indeed, each additional ’parton-parton\(\rightarrow \) dijet’ scattering needs additional energy and is accompanied by the colour flow created by the parton cascade needed to form the incoming partons. This colour flow produces secondaries that fill the LRG. The LRG survival probability, \(S^2\), (i.e. the probability not to destroy the LRG) is rather small, \(S^2\le 0.1\), see e.g. Ref. [23].Footnote 3 Thus, the probability to observe n additional branches of parton-parton interactions in LRG events is suppressed by the factor \((S^2)^n\).

For the case of one leading proton, the instanton events are generated as being produced in the proton–Pomeron collision (see Fig. 1 for illustration). When the two leading protons are detected, the Pomeron–Pomeron inelastic collision is considered (see Ref. [22] for more details). The incoming Pomeron parton distribution is taken from the HERA data. In particular, we use the fit B of H1 collaboration [26]. The obtained cross-section is multiplied by the gap survival probability \(S^2=0.1 (0.05)\) for the one (two) leading proton kinematics. To diminish the possible scale uncertainty we use the \(k_T\)-factorization approach as it was described in [22]. The unintegrated PDFs are calculated based on the LO KMR prescription [27]. We account for the Mueller form factor [28], describing quantum corrections to the gluon-gluon collision, and for the incoming gluon virtuality, \(Q^2\), via the corresponding instanton form factor

$$\begin{aligned} J(\rho Q)~=~\rho QK_1(\rho Q), \end{aligned}$$
(5)

where \(\rho \) is the instanton radius and \(K_1\) is the Bessel function.

In this study we work at \(\sqrt{s} = 14\) TeV and we scrutinize two mass regions, namely \(M_{\textrm{inst}} > 60\) GeV and \(M_{\textrm{inst}} > 100\) GeV, both in the FPD acceptance \(0.02< \xi < 0.05\) and for the single-tagged (ST) configuration, the latter also for the double-tagged (DT) configuration. In total, we then work with three instanton signal event record samples. All are generated using the RAMBO algorithm [29] at \(\xi = 0.03\), with proton–Pomeron collision type for the ST approach (\(2.5\cdot 10^{6}\) events for \(M_{\textrm{inst}} > 60\) GeV and \(5\cdot 10^{5}\) events for \(M_{\textrm{inst}} > 100\) GeV) and with Pomeron–Pomeron collision type for the DT approach (\(10^{5}\) events). The respective instanton production cross-sections integrated over the \(0.02< \xi < 0.05\) region are 1004.6 pb and 39.6 pb for the proton–Pomeron sample and for \(M_{\textrm{inst}} > 60\) GeV and 100 GeV, respectively, and 500 fb for the Pomeron–Pomeron sample and \(M_{\textrm{inst}} > 100\) GeV. All samples are showered and hadronised using PYTHIA 8.2 [30] with initial-state radiation (ISR), final-state radiation (FSR) and the MPI switched on. For simplicity, in all cases the instanton signal is generated with a forward leading proton only in one hemisphere with \(p_z < 0\). For this reason, in the following all studies are done and all cuts are tailored for one hemisphere. Assuming a full symmetry in z coordinate, final numbers are then obtained by doubling those from the studied hemisphere.

For both, ST and DT approaches, we consider two backgrounds, dijet production in Single-diffractive (SD) and Non-diffractive (ND) interactions, which are by far most dominant due to resemblance of their final states to the final state of the signal and due to their huge production cross-sections with respect to that of the signal. In both, again ISR, FSR and MPI are switched on. For the SD dijet background, we use the dynamical gap survival approach with MPI between Pomeron and proton switched on [31]. Production cross-sections for \(\hat{p}_{\textrm{T,min}} > 10\) GeV are 80 \(\mu \)b for SD and 8.64 mb for ND. At truth level, we have generated roughly \(5\cdot 10^{11}\) SD events and \(8.5\cdot 10^{11}\) ND events.

Since the relatively heavy instanton produces a rather large number of jets with the energy \(E_T\sim 1/\rho \) we are looking for high multiplicity events which:

  • do not contain very high-\(E_T\) jets, and

  • still have a large density of the transverse energy, \(\sum _i dE_{Ti}/d\eta \sim M_{\textrm{inst}}/3\) (the sum is over all secondary particles in the given \(\eta \) interval).

Moreover, since each jet from the instanton cluster contains a leading hadron we can select events with a large multiplicity (say, \(N_{\textrm{ch}} >20\)) of charged particles with \(p_T>0.5\) GeV in a limited rapidity interval. Since the LHC detectors never cover the whole (\(4\pi \)) rapidity interval, there is no chance to adequately measure the value of \(M_{\textrm{inst}}\). To select the events with appropriate \(M_{\textrm{inst}}\) we introduce the cut on the total transverse energy measured within the given rapidity interval \(\sum _i E_{Ti}>M_0\).

Here we consider the instanton production in the proton–Pomeron collision (in terms of Regge theory the Pomeron exchange is responsible for the presence of the LRG) selecting events with a large multiplicity and relatively large transverse energy.Footnote 4 We expect that these events will be more or less spherically symmetric, that is, in such events there should be a large probability to observe the sphericity S close to 1. Since we can not observe the particles in the whole \(4\pi \) sphere we consider the “transverse sphericity” (or cylindricity) defined as \(S_T=2\lambda _2/(\lambda _1+\lambda _2)\) where \(\lambda _i\) are the eigenvalues of the matrix

$$\begin{aligned} S^{\alpha \beta }=\frac{\sum _i p^\alpha _i p^\beta _i}{\sum _i |\vec {p}^2_i|}, \end{aligned}$$
(6)

and \(\lambda _2<\lambda _1\). Here \(p_i^\alpha \) is the two-dimensional transverse component of the momentum of the i-the particle and we sum over all particles observed in the event within a given rapidity interval.

4 Search strategy

The search for instanton signal in the harsh environment of various backgrounds consists of two steps. In the first step, we work at generator level, examine several cut scenarios and select the one giving the best signal to background (S/B) ratio, which we then call a “golden scenario”. In the second step, a fast simulation of the detector and pile-up effects is added, and their impact on the S/B ratio for this golden scenario is investigated.

As reported in publications by ATLAS and CMS where forward proton detectors AFP and CT-PPS, respectively, were used, the lowest \(\xi \) value reachable in Run 2 was 0.02 and a similar reach is expected for Run 3. Regions of higher \(\xi \) may be contaminated by Reggeon contributions and ND events that survive the \(\xi >0.02\) cut thanks to fluctuations in the hadronization process and the large cross-section. Therefore, to suppress both these contributions, we decided to work in a rather narrow \(0.02< \xi < 0.05\) range which is used as a baseline acceptance region in all considerations below. We study two approaches, using single-tagged and double-tagged protons. While in the former, the selection efficiency is higher but background contamination is usually higher and one cannot use the ToF detector to suppress pile-up background, in the latter, all backgrounds are usually better suppressed including the pile-up by utilizing the ToF detector but we pay for that by lower selection efficiencies. Nevertheless in the end it depends on production cross-sections of signal and backgrounds and on the impact of various cut scenarios for a chosen FPD acceptance and a given luminosity scenario. Since pile-up effects can easily diminish advantages of the final state of the signal (including the presence of LRG), we concentrate on low pile-up scenarios in the case of single-tagged approach and on medium pile-up amounts in the double-tagged approach.

4.1 Combinatorial background

With the increasing average number of pile-up events per bunch crossing, \(\langle \mu \rangle \), the probability to detect a pile-up proton in the FPD acceptance increases. When overlaid with a hard-scale event (triggered by various L1 triggers) it forms a combinatorial background which is usually dangerous due to resemblance of its final state to that of the signal and due to the fact that both, the pile-up proton seen in FPD and the hard-scale event can occur much more frequently than the signal. Detailed discussions and dependences on \(\langle \mu \rangle \) of this probability to fake either single-tagged (ST) or double-tagged (DT) signal in FPDs, and how this background can be tamed by using time-of-flight (ToF) detectors installed in FPDs at LHC can be followed in Refs. [33,34,35]. Frequency of both, the fake ST and DT signal in FPD, depends on the probability to see a proton from minimum bias events in the acceptance of FPD on one side, \(P_{\textrm{ST}}\). For the acceptance considered here, namely \(0.02< \xi < 0.05\), \(P_{\textrm{ST}} = 0.0048\) as predicted by Pythia 8.2 at \(\sqrt{s} = 14\) TeV for minimum bias events with ISR, FSR and MPI switched on. For a given amount of pile-up, \(\langle \mu \rangle \), the probability per bunch crossing to have a pile-up proton in the acceptance of FPD on one side is

$$\begin{aligned} P_{\textrm{comb}} = 1 - (1 - P_{\textrm{ST}})^{\langle \mu \rangle }. \end{aligned}$$
(7)

This combinatorial factor serves to estimate the total combinatorial background for both, the ST and DT strategies. The most dangerous situation for ST occurs when one hard-scale event (for example SD or ND dijets with low jet \(p_T\)) is overlayed with another soft SD event producing a forward going proton. For the DT strategy, the danger lies in an overlay of three events: one hard-scale SD or ND dijet event and two soft SD events each giving a forward going proton on opposite sides from the IP. The total combinatorial background is then estimated as a product of the fiducial cross section for the SD or ND dijet process (i.e. after applying all cuts except the \(\xi \) acceptance) times the combinatorial factor \(P_{\textrm{comb}}\) in the ST case or \(P_{\textrm{comb}}^2\) in the DT case. We remind that the \(\xi \) acceptance cut is applied already on the one soft SD event for ST (two soft SD events for DT), so it cannot be applied anymore on the hard-scale event.

The values of the combinatorial factor are then 0.48%, 0.96% and 2.38% for \(\langle \mu \rangle \) of 1, 2 and 5, considered for ST, and 0.84% and 4.58% for \(\langle \mu \rangle \) of 20 and 50, considered for DT. The last two can be further reduced by making use of ToF detectors (we need to detect a proton on each side in one event). If we assume a resolution of 10 ps, the ToF suppression of the combinatorial background by a factor of about 18 (16) for \(\langle \mu \rangle \) of 20 and 50, respectively, can be achieved. We also note that production cross section of the ST (DT) instanton signal is roughly 100 (1000) times smaller than the corresponding instanton signal cross-section in inclusive events. The reasoning is based on the presence of \(S^2\) in the case of diffractively produced instanton and on the ratio of diffractive to inclusive PDFs being about 10.

4.2 Generator level

In addition to the FPD acceptance, the following variables based on properties of particles measured in the central detector were examined (note that we are limiting ourselves to positive pseudorapidities because the leading protons in signal samples are generated only with negative rapidities):

  • \(N_{\textrm{ch05}}\) = number of charged particles with \(p_T > 0.5\) GeV and detected in a part of the central tracker \(0.0< \eta < 2.0\)

  • \(N_{\mathrm{ch20(25,30)}}\) = number of charged particles with \(0< \eta < 2.0\) and \(p_T > 2.0, 2.5\) or 3.0 GeV

  • \(\sum E_T\) = sum of \(E_T\) of charged particles with \(p_T > 0.5\) GeV and \(0.0< \eta < 2.0\)

  • \(N_{\textrm{ch05fw}}\) = number of charged particles with \(p_T > 0.5\) GeV detected in one half of the forward calorimeter \(2.5< \eta < 4.9\)

  • \(\sum E_T^\textrm{fw}\) = sum of \(E_T\) of charged particles with \(p_T > 0.5\) GeV and \(2.5< \eta < 4.9\)

From each variable we constructed at least one cut as follows: \(N_{\textrm{ch05}} > 30(40)\), \(N_{\mathrm{ch20(25,30)}} = 0\), \(\sum E_T > 30(40)\) GeV, \(N_{\textrm{ch05fw}} < 6\) and \(\sum E_T^\textrm{fw} < 4\) GeV. While vetoing particles with a relatively high transverse momentum aims at rejecting events with high-\(E_T\) jets, the cuts on the activity in the forward calorimeter are introduced in order to suppress a fake signal caused by the MPI. In total we have examined 42 cut scenarios on the proton–Pomeron sample with \(M_{\textrm{inst}} > 100\) GeV. From comparing fiducial cross-sections of signal and background for each cut scenario using the signal sample and a very large SD sample, we conclude that the best S/B ratio of 2.1 is obtained for two cut scenarios, namely one with

$$\begin{aligned} N_{\textrm{ch05}} > 40 \mathrm{\ \ and \ \ } N_{\textrm{ch25}} = 0 \mathrm{\ \ and \ \ } \sum E_T^\textrm{fw} < 4~\textrm{GeV} \end{aligned}$$
(8)

and one with the same cuts as in Eq. (8) but with \(\sum E_T > 30\) GeV in addition. Since the ratio S/B after adding the cut \(\sum E_T > 30\) GeV remains the same, we drop this second one and call the cuts in Eq. (8) the “golden cut scenario”. For this scenario the corresponding S/B for the signal sample with \(M_{\textrm{inst}} > 60\) GeV is 2.3. When applying the same set of cuts on a large sample of ND dijet events (over 8.5\(\cdot 10^{11}\) events were generated), none survives. This translates to an estimated fiducial cross-section for ND background to be smaller than 10.2 fb. The differential cross-section as a function of transverse sphericity, \(S_T\), for the signal and SD dijet background and for the golden cut scenario is shown in Fig. 2. For both proton–Pomeron signal samples, \(M_{\textrm{inst}} > 60\) GeV and \(M_{\textrm{inst}} > 100\) GeV, the signal is clearly seen to be well-separated from the SD background and peaking at higher \(S_T\) values as expected. By comparing the left with the right plot, we can say that the cuts from the golden scenario reduce to a large extent the contribution from \(M_{\textrm{inst}} < 100\) GeV.

Fig. 2
figure 2

Differential cross-section as a function of transverse sphericity at generator level separately for the instanton signal from proton–Pomeron collisions (\(M_{\textrm{inst}} > 60\) GeV on the left and \(M_{\textrm{inst}} > 100\) GeV on the right) generated by RAMBO and SD dijet background generated by PYTHIA 8.2 for the golden cut scenario (Eq. (8)). Only statistical uncertainties are plotted

Full size image

4.3 Detector level

The detector and pile-up effects for events surviving the golden cut scenario are then studied using Delphes 3.5 fast simulation package [36] with an ATLAS input card. On both, the signal and background samples of events at generator level, we run Delphes with various amounts of pile-up, defined by an average number of pile-up events per bunch crossing, \(\langle \mu \rangle \). For each pile-up amount, we are also considering an adequate integrated luminosity, which leads us to the following working (\(\langle \mu \rangle \),\({\mathcal {L}}\) [fb\(^{-1}\)]) points: (0,0.1), (1,0.1), (2,1) and (5,10) for the ST approach and (20,60) and (50,300) for the DT approach. Given the assumed difficulties to distinguish the signal from all relevant backgrounds including pile-up, we rather concentrate on low (in ST approach) and medium (in DT approach) amounts of pile-up. At the same time, we are convinced that these are conceivable luminosity scenarios for Run 2 and Run 3.

At detector level, we work with tracks in the central tracker and with calorimeter clusters in the forward calorimeter. On the sample of signal events, we first need to tune track selection criteria and cuts that are based on tracks. Following the track selection procedure used in the analysis of charged tracks at 13 TeV by ATLAS [37], we reduce tracks from overlaid pile-up events to an acceptable minimum. Although we observe more than twice as many tracks with \(p_T > 0.5\) GeV for \(\langle \mu \rangle = 5\) than for no pile-up, after requiring \((z_{\textrm{vtx}}-z_{\textrm{trk}})\sin \theta < 1.5\) mm and \(d_0^\textrm{trk} < 1.5\) mm in addition, the number of tracks with \(p_T > 0.5\) GeV drops considerably and exceeds the one at zero pile-up by only 2.5%. Here \(z_{\textrm{vtx}}\) is the z-coordinate of the primary vertex, \(z_{\textrm{trk}}, \theta \) and \(d_0^\textrm{trk}\) are z-coordinate, polar angle and transverse impact parameter of a given track, respectively. Track reconstruction efficiencies and resolutions as functions of track \(p_T\) and \(\eta \) are accounted for via Delphes input card. A nominal track efficiency is roughly 80% on average for \(p_T > 0.5\) GeV and not close to the tracker edges (see e.g. Ref. [38, Fig. 13]) and this one is applied in all studies. As a systematic cross-check, we also examine an optimized track efficiency (see Ref. [39]) which reaches almost 90% on average for \(p_T > 0.5\) GeV. Our aim is to illustrate the situation after data taking, thus to estimate real numbers of collected events, therefore we do not correct for these track reconstruction inefficiencies but rather adapt the first cut in Eq. (8) to \(N_{\textrm{tr05}} > X\) (where \(N_{\textrm{tr05}}\) is number of tracks with \(p_T > 0.5\) GeV and \(0< \eta < 2.0\) and \(X < 40\)). The energy flow measurement from Run 1 by ATLAS [40] indicates that the third cut in Eq. (8) needs to be adapted as well. As Fig. 2 a in Ref. [40] shows, Pythia 6 predicts a steeper distribution of \(\sum E_T\) in the forward region \(4.0< |\eta |< 4.8\) than data, both at detector level. While for \(\sum E_T < \) 3–4 GeV, it overestimates the data, for \(\sum E_T > \) 3–4 GeV it underestimates them. To account for this Pythia 6 discrepancy, one would need to re-weight it by a ratio data to MC at detector level as is done in Ref. [40]. But taking into account two small caveats, namely that in our analysis we work with Pythia 8.2 and in the larger region, \(2.5< \eta < 4.9\), we decide to take rather a simplistic approach and adapt the third cut in Eq. (8) to \(\sum E_T^\textrm{fwcalo} < 5\) (or 6) GeV (where the sum runs over clusters in the forward calorimeter). At the same time, this new threshold should not be too far from the original 4 GeV threshold used at generator level. The reason is that clusters in the forward calorimeter lie outside the tracker coverage, so they cannot be linked with tracks and consequently we do not have information about which part of cluster energy comes from pile-up. Therefore, if departing too far from the 4 GeV threshold, we would be picking up an uncontrollable amount of pile-up. Furthermore, we should also take into account that detector and pile-up effects may cause migrations of events from regions below to regions above cut thresholds (for example at generator level, \(N_{\textrm{ch05}} < 40\) but pile-up events may cause \(N_{\textrm{tr05}} > 40\)). To this end, out of many generated ND and SD background events (\(2\cdot 10^{11}\) for SD, \(6\cdot 10^{11}\) for ND) we retain subsamples of events surviving cuts that are more relaxed than those in Eq. (8), namely we apply cuts \(N_{\textrm{ch05}} > 30\) and \(N_{\textrm{ch30}} = 0\) and \(\sum E_T^\textrm{fw} < 6\) GeV. Those samples (about 100 (1500) thousand of SD (ND) events) are then processed with Delphes and subsequently four samples with different amounts of pile-up events are created for each instanton mass region and analyzed in detail. For the sake of completeness, we note that to save computational power, the proton \(\xi \) cut has not been applied even for the zero pile-up scenario and its effect has been accounted for by scaling the fiducial cross section for SD (ND) dijets by \(P_{\textrm{ST}}(\mu =0)\) = 4.3% (0.015%). These \(P_{\textrm{ST}}\) values correspond to SD (ND) dijet backgrounds with \(\hat{p_{\textrm{T}}}>\) 10 GeV. On another large-statistics SD dijet sample we have applied the proton \(\xi \) acceptance cut and got very similar results as using the SD dijet sample without this preselection. This confirms the validity of this factorization of the FPD \(\xi \) acceptance cut.

As explained above, to avoid double-counting, the generator-level FPD \(\xi \)-acceptance cut obtained from the proton information cannot be applied for the hard-scale event since it is already applied on overlayed soft pile-up events. But we can make use of information from the central detector and try to restrict ourselves to a \(\xi \)-region similar to that of the applied FPD acceptance \(0.02< \xi < 0.05\) at generator level - note that a strict matching is not possible using tracker information only due to its too narrow \(\eta \)-acceptance but the \(\xi \) quantity evaluated using the calorimeter (whose coverage is \(\mid \eta \mid <4.9\)), \(\xi ^\textrm{calo}\), can bring us much closer to the generator-level \(\xi \)-range. The additional cut on \(\xi ^\textrm{calo} < 0.025\) turns out to be reasonably efficient. Following the discussion above, we adapt the golden cut scenario in Eq. (8) to these two sets of cuts at detector level:

$$\begin{aligned}{} & {} N_{\textrm{tr05}} > 25 \mathrm{\ \ and \ \ } N_{\textrm{tr20}} = 0 \mathrm{\ \ and \ \ } \nonumber \\{} & {} \quad \sum E_T^\textrm{fwcalo}< 5~\mathrm{GeV \ \ and \ \ } \xi ^\textrm{calo} < 0.025 \end{aligned}$$
(9)
$$\begin{aligned}{} & {} N_{\textrm{tr05}} > 30 \mathrm{\ \ and \ \ } N_{\textrm{tr25}} = 0 \mathrm{\ \ and \ \ } \nonumber \\{} & {} \quad \sum E_T^\textrm{fwcalo}< 5~\mathrm{GeV \ \ and \ \ } \xi ^\textrm{calo} < 0.025 \end{aligned}$$
(10)

where \(N_{\textrm{tr05}}\), \(N_{\textrm{tr25}}\) and \(N_{\textrm{tr20}}\) are numbers of tracks in the region \(0.0< \eta < 2.0\) and for \(p_T > 0.5\) GeV, \(p_T > 2.5\) GeV and \(p_T > 2.0\) GeV, respectively, and \(E_T^\textrm{fwcalo}\) is a sum of \(E_T\) of clusters in the forward calorimeter with \(p_T > 0.5\) GeV and \(2.5< \eta < 4.9\). The \(\xi ^\textrm{calo}\) quantity is calculated as a sum of \(E_{\textrm{T}}e^{-\eta }\) over calorimeter clusters with \(E_{\textrm{T}} > 0.2\) GeV. The cuts in Eq. (9) (Eq. (10)) are used as nominal for \(M_{\textrm{inst}} > 60\) GeV (\(M_{\textrm{inst}} > 100\) GeV).

5 Results

5.1 Single tag

To illustrate the situation after data taking at detector level, the expected event yields for signal generated with \(M_{\textrm{inst}} > 60\) GeV and \(M_{\textrm{inst}} > 100\) GeV together with both backgrounds, the SD dijets and ND dijets, are shown in Figs. 3 and 4 as functions of \(S_T\) for four luminosity scenarios, defined above after applying detector-level cuts defined in Eqs. (9) and (10), respectively.

Fig. 3
figure 3

Distributions of expected event yields as functions of transverse sphericity at detector level for instanton signal from proton–Pomeron collisions generated by RAMBO for \(M_{\textrm{inst}} > 60\) GeV and backgrounds from ND dijets and SD dijets generated by PYTHIA 8.2 after applying detector-level cuts in Eq. (9) for four luminosity scenarios. Only statistical uncertainties are shown, estimated using expected event numbers from Table 1

Full size image
Fig. 4
figure 4

Distributions of expected event yields as functions of transverse sphericity at detector level for instanton signal from proton–Pomeron collisions generated by RAMBO for \(M_{\textrm{inst}} > 100\) GeV and backgrounds from ND dijets and SD dijets generated by PYTHIA 8.2 after applying detector-level cuts in Eq. (10) for four luminosity scenarios. Only statistical uncertainties are shown, estimated using expected event numbers from Table 1

Full size image

To estimate the influence of detector effects, we remove the \(\xi ^\textrm{calo} < 0.025\) cut and compare the S/B ratio at zero pile-up with the generator-level S/B ratio. While the latter amounts to 2.3 (2.1) for \(M_{\textrm{inst}} > 60\) (100) GeV, the former drops to about 0.6 (0.3) which suggests that the detector effects are noticeable. To study their origin in more detail, we investigate event samples without the \(\xi ^\textrm{calo} < 0.025\) cut in the following. For the \(M_{\textrm{inst}} > 60\) GeV signal, the mean values of \(\sum E_T\) in the forward region for these two cases (9.2  GeV vs. 10.1 GeV) do not differ much hence the track reconstruction inefficiencies and resolutions seem to be responsible for the observed S/B deterioration. By adding more and more pile-up, the mean values of \(\sum E_T^\textrm{fwcalo}\) in signal increase to 17, 24 and 37 GeV for \(\langle \mu \rangle \) of 1, 2 and 5, respectively, giving rise to fewer and fewer events surviving the \(\sum E_T^\textrm{fwcalo}\) cut with increasing pile-up. But the same holds for the SD background, where corresponding values are 3.5 and 4.1 GeV for generator level and detector level without pile-up, which then rise with increasing pile-up to 11.5, 18.7 and 41 GeV. The lower mean values for the SD background are due to the pre-selection procedure applied to the SD sample. We remind that we pre-select SD events at generator level by cuts defined in Sect. 4.3 where one of cuts is \(\sum E_T^\textrm{fw} < 6\) GeV. It is also evident that the pile-up effect is slightly more pronounced for SD background than for the signal.

As demonstrated, however, on the zero pile-up case in Fig. 3 (top left), the effect of the detector-level \(\xi ^\textrm{calo} < 0.025\) cut is remarkable – it brings the S/B ratio back above 1.0. Thanks to the much bigger resemblance of the SD background to the signal, it is the SD process which dominates the total contamination. The situation dramatically changes when combinatorial effects enter the game: here the ND background dominates thanks to roughly two orders of magnitude higher cross section than the SD background and to the fact that the size of the combinatorial factor \(P_{\textrm{comb}}\) stays the same for both ND and SD backgrounds. The mean value of the \(\xi ^\textrm{calo}\) distribution rises with increasing \(\langle \mu \rangle \), but more for signal than for both backgrounds. Convoluted with the increasing combinatorial factor \(P_{\textrm{comb}}\) this leads to a decreasing S/B ratio as the level of pile-up increases.

The final event yields for signal, SD and ND dijet backgrounds are shown in Table 1. As explained above, they correspond to doubling those obtained from analyzing all generated event samples since the signal has been generated with the forward proton scattered in one hemisphere only and consequently the selection cuts have been tailored to one hemisphere as well.

For the specific cut scenarios in Eqs. (9) and (10) considered for the two mass intervals, we observe that the S/B ratio safely exceeds unity when pile-up is not considered, thanks to the efficient \(\xi ^\textrm{calo}\) cut. If we require \(\xi ^\textrm{calo} < 0.025\), the S/B stays above unity for \(\langle \mu \rangle = 1\) and \(M_{\textrm{inst}} > 60\) GeV, all other luminosity scenarios give S/B below 1.0. Its value further decreases with increasing \(\langle \mu \rangle \) and reaches minima of 0.3 (0.2) at \(\langle \mu \rangle = 5\) for \(M_{\textrm{inst}} > 60\) (100) GeV. It is therefore a clear preference to collect data at rather low amounts of pile-up, and we believe that a special run with \(\langle \mu \rangle \sim \) 1 and \({\mathcal {L}} \sim \) 0.1 fb\(^{-1}\) is realistic to consider.

5.2 Systematic studies or searching for an optimum working point

In the effort to improve S/B ratios, we investigate variations of the selection cuts or tracking efficiency. We observe very similar numbers for a loosened cut \(\sum E_T^\textrm{fwcalo} < 6\) GeV. As anticipated, we also study the effect of a more efficient tracking. This leads to an increase of the average efficiency from 80% to 90% and hence of the track multiplicity. This allows us to apply a more strict cut on the track multiplicity for \(M_{\textrm{inst}} > 60\) GeV, namely \(N_{\textrm{tr05}} > 28\), but the S/B ratios appear to be unchanged. Tightening the track multiplicity cut to \(N_{\textrm{tr05}} > 26\) and \(N_{\textrm{tr05}} > 27\) for \(M_{\textrm{inst}} > 60\) GeV and the original tracking or to \(N_{\textrm{tr05}} > 30\) for the optimal tracking does not change the S/B ratio significantly either. For \(M_{\textrm{inst}} > 100\) GeV tightening the track multiplicity to \(N_{\textrm{tr05}} > 32\) or \(N_{\textrm{tr05}} > 35\) increases the S/B ratio with respect to that achieved for the scenario in Eq. (10), however, since very few signal events survive, statistical significances would be rather small thus do not make this option viable.

The numbers in Table 1 correspond to the whole \(S_T\) spectrum shown in Fig. 3. Restricting ourselves to the region where the instanton signal is expected, namely \(S_T > 0.5\), would in general lead to an increase of S/B by roughly 30%, only for the highest pile-up point the increase is above 100%. The improvement of significances is rather modest.

Table 1 Summary of event yields after applying cuts in Eqs. (9) and (10) for the single-tag search approach for \(M_{\textrm{inst}} > 60\) GeV and \(M_{\textrm{inst}} > 100\) GeV, respectively, and for four luminosity scenarios (\(\langle \mu \rangle \), \({\mathcal {L}}\)). For each scenario, a ratio of number of signal to background events, \(N_{\textrm{S}}/(N_{\textrm{ND}}+N_{\textrm{SD}})\), is shown
Full size table

5.3 Double tag

As discussed in [22], the central instanton production processes have some promising advantages. Thus, in such a case, the Pomeron–Pomeron colliding energy is relatively low, which strongly reduces the multiplicity of the background underlying events. Moreover, in this energy range, the central detector becomes almost hermetic (close to \(4\pi \)) for the Pomeron–Pomeron secondaries, and only a small part of the finally produced hadrons will avoid detection.Footnote 5 Note also that detecting two outgoing protons would allow one to place an upper limit on the instanton mass.

For the double-tag approach, we use the signal sample generated using Pomeron–Pomeron collisions. We studied a limited set of cut scenarios which are close to the golden one (Eq. (8)) and observe selection efficiencies that are in the ballpark with those obtained on the proton–Pomeron signal sample. Given about 80 times smaller production cross-section compared to the proton–Pomeron case, that would give fiducial cross-sections of the order of fractions of femtobarns. We have to consider higher values of \(\langle \mu \rangle \) with correspondingly larger integrated luminosities, for example (\(\langle \mu \rangle \), \({\mathcal {L}}\) [fb\(^{-1}\)]) = (20, 60) and (50, 300). This would lead to increasing the event yields for all, signal and backgrounds, by a factor of 60 or 300 with respect to e.g. the (2,1) scenario considered in the ST approach.

As explained in Sect. 4.1, the combinatorial factor \(P_{\textrm{comb}}^2\) from the fake protons seen in the acceptance of FPDs due to additional pile-up collisions is not large, due, mainly, to the narrow \(\xi \) range chosen. It can then be further reduced by utilizing ToF detectors. The ToF detectors with an assumed 20 ps resolution (which is a goal of AFP ToF in Run 3 and slightly better than achieved by AFP ToF in Run 2 [42]) would be able to suppress the combinatorial background by a factor of 9 and 8 for \(\langle \mu \rangle \) of 20 and 50, respectively. Taking into account the values of \(P_{\textrm{comb}}^2\) evaluated above (0.84% and 4.58% for \(\langle \mu \rangle \) of 20 and 50, respectively), we can make a very rough extrapolation from the ST results discussed in the previous section to much higher pile-up amounts considered for the DT analysis. If we for example compare the luminosity scenarios (1,0.1) for ST and (20,60) for DT, the fiducial cross section of ND and SD backgrounds would be scaled by a 5 times lower factor (0.84%/9 vs. 0.48%) for DT but the ratio of signal cross sections is 1/80. This leads to a reduction of the S/B ratio obtained for the (1,0.1) scenario for ST by a factor of about 16. For the (50,300) scenario in DT, the S/B ratio would even drop by two orders of magnitude. It should be noted that outlooks for significances may be more favourable since in both luminosity scenarios for DT we collect much more statistics than for ST but it has to be added that the expected effect of such a high level of pile-up on both, signal and backgrounds, is a considerable drop of selected events. A central instanton production either in the DT or ST approach deserves a detailed analysis including the simulation of detector and pile-up effects, and is in our plans for a future paper.

5.4 Potential improvements

Triggers were not discussed in this note and to our knowledge, there are no dedicated instanton triggers being used by the LHC experiments, so instanton signals would have to be searched in data collected by other triggers, e.g. very-low \(E_T\) jets or minimum bias triggers used to study properties of charged particles. It would, however, be extremely useful to propose and build triggers with conditions tailored to collect instanton-enhanced data samples, e.g. those in Eqs. (8, 9, 10). So far tracking information is not available at L1 and so are not vertices since vertex reconstruction is a time-consuming procedure but triggering an instanton-like signal already at L1 would make the instanton search in collected data more efficient. At HLT, a full-scan tracking (collecting information about track multiplicities, \(\eta \), \(p_T\) or \(\sum E_T\)) can be obtained in special low pile-up runs. In standard runs other approaches should be taken, for example to run the full-scan online tracking in coordination with very low-\(E_T\) jet or other-soft scale triggers, getting possibly also the full information about primary vertices. Tracking in a limited region-of-interest (similar to that in Eq. (9) or Eq. (10)) should be possible at HLT too.

As we have discussed in Sect. 4.3, pile-up increases enormously \(\sum E_T\) in the forward region (\(2.5< |\eta |< 4.9\)), according to Delphes with the ATLAS input card, from 9 GeV at zero pile-up up to 37 GeV at \(\langle \mu \rangle \) of 5 for signal. This is because the tracking information is missing there so we do not have control over what fraction of energy comes from pile-up. One can of course require just one primary vertex which would greatly suppress pile-up effects but would drastically reduce available statistics which is not affordable. Alternatively, adding time information of individual calorimeter cells, if possible already in Run 2 and Run 3, should help to identify those coming from pile-up vertices distant from the primary one. This should be much improved in Run 4 where both, trackers in ATLAS as well as CMS will be upgraded to cover a region \(|\eta |< 4.9\) and time information of tracks should be available as well [43, 44]. This time information about tracks in the central detector, whether alone or together with the ToF information about the leading forward proton on one side from the interaction point will not only help in searches for the proton–Pomeron signal but could also potentially allow us to use single-tagged events to separate the Pomeron–Pomeron-induced instanton signal from all backgrounds (in this case the undetected proton will often have \(\xi < 0.02\), below the current FPD acceptance). Indeed this combined time information and the increased selection efficiency expected for single-tagged events promises to significantly increase the S/B ratio compared to double-tagged approach for the search for instantons produced in the Pomeron–Pomeron collisions.

Next, we can exploit the fact that the density of secondary particles \(\textrm{d}N_{\textrm{ch}}/\textrm{d}\eta \) reaches its maximum at the rapidity \(\eta =\eta _{\textrm{inst}}\) equal to the instanton rapidity. Indeed, in terms of \(\eta \) the spherical distribution caused by the instanton decay reads

$$\begin{aligned} \textrm{d}N_{\textrm{ch}}/\textrm{d}\eta \propto 1/\cosh ^2(\eta -\eta _{\textrm{inst}}). \end{aligned}$$

In the present study we chose the interval \(0<\eta <2\) which, on average, corresponds to this maximum, however, the statistical significance of the result may be improved if the \(N_{\textrm{ch}}\) and \(\sum E_T\) cuts are imposed in the central detector within the \(\eta _0<\eta <\eta _0+2\) interval, where the particle density is maximal in each particular event. We are planning to implement this idea in future studies.

Finally we remind that the decay of the instanton produces one additional pair of each flavour of light (\(m_f<1/\rho \)) quark [11, 13, 15]. So in the case of the signal, we expect to observe a larger number of strange and charm particles than in background events. While this fact has not been examined in this study, we believe it has potential to improve the S/B ratio.

6 Conclusions

In Ref. [15, 22] it was proposed to search for QCD instantons at the LHC in events with Large Rapidity Gaps. Here we investigate the search strategy for the case of heavy instanton by tagging leading protons with dedicated AFP or CT-PPS forward proton detectors at \(\sqrt{s} = 14\) TeV. Since the expected cross-sections are quite small we consider scenarios with relatively large integrated luminosities and, thus, we have to account for effects of pile-up. In addition, we include fast simulation of central detector response. For instanton signal, we use a dedicated MC event generator RAMBO, while the dominant backgrounds, Single-diffractive and Non-diffractive dijets are estimated using PYTHIA 8.2, all including full underlying event simulation. The small size (heavy) instanton produces a large number of mini-jets and large transverse energy in a limited rapidity interval, therefore we are selecting events with a large multiplicity. To suppress the main background caused by multiple parton interactions and pile-up events, we introduce an additional cut, transverse energy in the forward (\(2.5<\eta <4.9\)) calorimeter should be less than 5–6 GeV. The combinatorial background, caused by fake protons from pile-up interactions seen in the acceptance of FPD, is greatly reduced if we limit the acceptance interval to \(0.02< \xi < 0.05\). We investigate two proton tagging strategies, the single-tag and double-tag with appropriate initial collisions, namely proton–Pomeron and Pomeron–Pomeron, respectively, both simulated by RAMBO. By concentrating on instanton masses larger than 60 GeV, we show that by applying appropriate cuts and requiring one leading proton, we could expect the signal-to-background ratio S/B \(> 2.3\) at generator level. To keep the pile-up effects in both, the central and forward parts of the main detector at a tolerable level, we choose to work at a relatively low pile-up rate, with \(\langle \mu \rangle < 5\). We show that the detector and pile-up effects are kept under control and consequently the S/B ratio kept well above unity if \(\langle \mu \rangle \lesssim 1\) and integrated luminosity is around 0.1 fb\(^{-1}\).

The kinematics with two tagged leading protons have some advantages. In this case, the central detector becomes almost hermetic for the Pomeron–Pomeron collision. Unfortunately, the expected cross-section becomes about 80 times smaller compared to proton–Pomeron collisions. That is, we have to consider a larger \(\langle \mu \rangle =\) 20–50. In such a case, even with a good forward proton timing resolution the combinatorial background caused by the non-diffractive events, accompanied by leading protons from two other soft events turns out to be too large to reach advantageous S/B ratios, although a detailed analysis including detector and pile-up effects is necessary to make firm conclusions.

For any instanton searches in both, the proton–Pomeron and Pomeron–Pomeron collisions, the additional time information about tracks in the central and forward rapidities seems to be beneficial.