1 Introduction

The Standard Model of particle physics contains certain anomalous processes induced by instantons which violate the conservation of baryon and lepton number (\(B + L\)) in the case of electroweak interactions and chirality in the case of strong interactions [1–3]. In quantum chromodynamics (QCD), the theory of strong interactions, instantons are non-perturbative fluctuations of the gluon field. They can be interpreted as tunnelling transitions between topologically different vacua. Deep-inelastic scattering (DIS) offers a unique opportunity [4] to discover a class of hard processes induced by QCD instantons. The corresponding cross section will be referred to as the instanton cross section. It is calculable within “instanton-perturbation theory” and is expected to be sizable [5–8]. Moreover, the instanton-induced final state exhibits a characteristic signature [4, 9–12]. Detailed reviews are given elsewhere [13, 14]. The theory overview given here follows closely the one in the previous H1 publication [15].

Fig. 1
figure 1

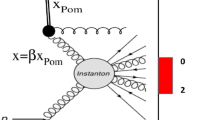
Kinematic variables of the dominant instanton-induced process in DIS. The virtual photon ( \(\gamma =e-e'\), virtuality \(Q^2\)), emitted by the incoming electron e, fuses with a gluon (g) radiated from the proton (P). The gluon carries a fraction \(\xi \) of the longitudinal proton momentum. The virtual quark \((q')\) is viewed as entering the instanton subprocess and the outgoing quark \(q''\) from the photon splitting process is viewed as the current quark. The invariant mass of the quark gluon (\(q'g\)) system is \(W_I\), W denotes the invariant mass of the total hadronic system (the \(\gamma P\) system) and \(\hat{s}\) refers to the invariant mass squared of the \(\gamma g\) system

Full size image

An experimental observation of instanton-induced processes would constitute a discovery of a basic and yet novel non-perturbative QCD effect at high energies. The theory and phenomenology for the production of instanton-induced processes at HERA in neutral current (NC) electronFootnote 1-proton collisions has been worked out by Ringwald and Schrempp [4, 6–10]. The size of the predicted cross section is large enough to make an experimental observation possible. The expected signal rate is, however, still small compared to that from the standard NC DIS (sDIS) process. The suppression of the sDIS background is therefore the key issue. QCD instanton-induced processes can be discriminated from sDIS by their characteristic hadronic final state signature, consisting of a large number of hadrons at high transverse energy emerging from a “fire-ball”-like topology in the instanton rest system [4, 9, 10]. Discriminating observables, derived from simulation studies, are exploited to identify a phase space region where a difference between data and sDIS expectations would indicate a contribution from instanton-induced processes.

Upper cross section limits on instanton-induced processes have been reported by the H1 [15] and ZEUS [16] collaborations. This analysis is a continuation of the previous H1 search for QCD instanton-induced events using a seventeen times larger data sample. The search is carried out at significantly higher virtualities of the exchanged photons as suggested by theoretical considerations [11].

2 Phenomenology of QCD instanton-induced processes in NC DIS

Instanton processes predominantly occur in photon gluon (\(\gamma g\)) fusion processes as sketched in Fig. 1. The characteristic instanton event signatures result from the following basic chirality violating reaction:

$$\begin{aligned} \gamma ^* + g \mathop {\rightarrow }\limits ^{(I)} \sum _{q=d,u,s,...} (q_R + \bar{q}_R) + \, n_g \, g, \; \; \; ( I \rightarrow \bar{I}, R \rightarrow L), \end{aligned}$$
(1)

where g, \(q_R\) (\(\bar{q}_R\)) denotes gluons, right-handed quarks (anti-quarks), and \(n_g\) is the number of gluons produced. The chirality violationFootnote 2 is induced for each flavour, in accord with the corresponding axial anomaly [2, 3]. In consequence, in every instanton event, quark anti-quark pairs of each of the \(n_f\) flavours occur precisely once. Right-handed quarks are produced in instanton-induced processes (I), left-handed quarks are produced in anti-instanton \((\bar{I}\)) processes. The final state induced by instantons or anti-instantons can be distinguished only by the chirality of the quarks. Experimental signatures sensitive to instanton-induced chirality violation are, however, not exploited in this analysis. Both instanton and anti-instanton processes enter likewise in the calculation of the total cross section.

In photon-gluon fusion processes, a photon splits into a quark anti-quark pair in the background of an instanton or an anti-instanton field, as shown in Fig. 1. The so-called instanton subprocess \(q' + g \mathop {\rightarrow }\limits ^{(I,\bar{I})} X\) is induced by the quark or the anti-quark fusing with a gluon g from the proton. The partonic system X contains \(2 \, n_f \) quarks and anti-quarks, where one of the quarks (anti-quarks) acts as the current quark (\(q''\)). In addition, an average number of \(\langle n_g \rangle \sim \mathcal{O}(1/\alpha _s) \sim 3\) gluons is emitted in the instanton subprocess.

The quarks and gluons emerging from the instanton subprocess are distributed isotropically in the instanton rest system defined by \(\mathbf {q'} + \mathbf {g} = 0\). Therefore one expects to find a pseudo-rapidityFootnote 3 (\(\eta \)) region with a width of typically 2 units in \(\eta \), densely populated with particles of relatively high transverse momentum and isotropically distributed in azimuth, measured in the instanton rest frame. The large number of partons emitted in the instanton process leads to a high multiplicity of charged and neutral particles. Besides this band in pseudo-rapidity, the hadronic final state also contains a current jet emerging from the outgoing current quark \(q''\).

The instanton production cross section at HERA, \(\sigma ^{(I)}_\mathrm{HERA}\), is determined by the cross section of the instanton subprocess \(q' + g \mathop {\rightarrow }\limits ^{(I,\bar{I})} X\). The subprocess cross section is calculable in instanton perturbation theory. It involves the distributions of the size \(\rho \) of instantons and of the distance R between them. By confronting instanton perturbation theory with non-perturbative lattice simulations of the QCD vacuum, limits on the validity of instanton perturbation theory have been derived [7, 8, 11]. The perturbative and lattice calculations agree for \(\rho \lesssim 0.35 \) fm and \(R/\rho \gtrsim 1.05\). At larger \(\rho \) or smaller \(R/\rho \), the instanton perturbative cross section grows, whereas the lattice calculations suggest that the cross section is limited. There is a relation between the variables \({Q'~}\) and \({x'~}\) in momentum space and the spatial variables \(\rho \) and \(R/\rho \). Large \({Q'~}\) and \({x'~}\) values correspond to small \(\rho \) and large \(R/\rho \), respectively. The aforementioned limits can be translated into regions of the kinematical variables \({x'~}\) and \({{Q}^{\prime 2}}\), in which the perturbative calculations are expected to be valid, \({{Q}^{\prime 2}}\ge {{Q'}^2_{\min }}\simeq (30.8\times \Lambda ^{n_f}_{\overline{MS}})^2\) and \({x'}\ge {x'_{\min }}\simeq 0.35\) [12]. Here \(\Lambda ^{n_f}_{\overline{MS}}\) is the QCD scale in the \(\overline{MS}\) scheme for \(n_f\) flavours. In order to assure the dominance of planar diagrams the additional restriction \(Q^2 \ge {{Q'}^2_{\min }}\) is recommended [6, 11, 12]. The cross section depends significantly on the strong couplingFootnote 4 \(\alpha _s\), or more precisely on \(\Lambda ^{n_f}_{\overline{MS}}\), but depends only weakly on the choice of the renormalisation scale.

The calculation of the instanton production cross section in instanton perturbation theory [6–8] is valid in the dilute instanton-gas approximation for approximately massless flavours, i.e. \(n_f=3\), in the HERA kinematic domain. The contribution of heavy flavours is expected to be (exponentially) suppressed [17, 18]. Thus calculations of the instanton production cross section using the QCDINS Monte Carlo generator [12] are performed for \(n_f=3\) massless flavours. It was checked that the predicted final state signature does not change significantly when heavy flavours are included in the simulation.

The analysis is performed in the kinematic region defined by \( 0.2< y < 0.7\) and \(150< Q^2< 15000~\mathrm{GeV}^2\). In this kinematic region, and additionally requiring \({{Q'}^2~}> 113\) \({\mathrm{~GeV}^2}\) and \({x'~}> 0.35\), the cross section predicted by QCDINS is \(\sigma ^{(I)}_\mathrm{HERA} = 10\pm 3 \; \mathrm{pb}\), using the QCD scale \(\Lambda _{\overline{MS}}^{(3)}= 339\pm 17 \; \mathrm{MeV}\) [19]. The quoted uncertainty of the instanton cross section \(\sigma ^{(I)}_\mathrm{HERA}\) is obtained by varying the QCD scale by one standard deviation.

The fiducial region in \({{Q}^{\prime 2}}\) and \({x'~}\) of the validity of instanton perturbation theory was derived from \(\mathrm{n}_f=0\) lattice simulations, since \(\mathrm{n}_f=3\) was not available for this purpose. The perturbative instanton calculation is made in the “dilute instanton gas” approximation, where the average distance between instantons should be large compared to the instanton size. This approximation is valid for \({x'~}\!\rightarrow \!1\), whereas the boundary \({x'~}= 0.35\) corresponds to a configuration where the distance R is similar to the instanton size \(\rho \). A further simplifying assumption is made by choosing a simple form of the fiducial region with fixed \({{Q'}^2_{\min }}\) and \({x'_{\min }}\), whereas \({{Q'}^2_{\min }}\) could be varied as a function of \({x'_{\min }}\). In summary, the kinematic region in \({{Q}^{\prime 2}}\) and \({x'~}\), where instanton perturbation theory is reliable, is, for the reasons given above, not very well defined. Thus, the theoretical uncertainty of the instanton cross section is difficult to define and could be larger than the already significant uncertainty due to the uncertainty of the QCD scale \(\Lambda _{\overline{MS}}^{(3)}\) alone. On the other hand, given that the predicted cross section is large, dedicated searches for instanton-induced processes at HERA are well motivated.

3 Experimental method

3.1 The H1 detector

A detailed description of the H1 detector can be found elsewhere [20–23]. The origin of the H1 coordinate system is given by the nominal ep interaction point at \(z=0\). The direction of the proton beam defines the positive z–axis (forward direction) and the polar angle \(\theta \) and transverse momentum \(P_T\) of every particle is defined with respect to this axis. The azimuthal angle \(\phi \) defines the particle direction in the transverse plane. The detector components most relevant to this analysis are the Liquid Argon (LAr) calorimeter, which measures the positions and energies of particles over the range \(4^\circ<\theta <154^\circ \) with full azimuthal coverage, the inner tracking detectors, which measure the angles and momenta of charged particles over the range \(7^\circ<\theta <165^\circ \), and a lead-fibre calorimeter (SpaCal) covering the range \(153^\circ<\theta <174^\circ \).

The LAr calorimeter consists of an electromagnetic section with lead absorbers and a hadronic section with steel absorbers. The electromagnetic and the hadronic sections are highly segmented in the transverse and the longitudinal directions. Electromagnetic shower energies are measured with a resolution of \(\delta E/E \simeq 0.11/\sqrt{E/\mathrm{GeV}} \oplus 0.01\) and hadronic energies with \(\delta E/E \simeq 0.50/\sqrt{E/\mathrm{GeV}} \oplus 0.03\) as determined using electron and pion test beam measurements [24, 25].

In the central region, \(15^{\circ }<\theta <165^{\circ }\), the central tracking detector (CTD) measures the trajectories of charged particles in two cylindrical drift chambers immersed in a uniform \(1.16\,\mathrm{T}\) solenoidal magnetic field. In addition, the CTD contains a drift chamber (COZ) to improve the z-coordinate reconstruction and a multi-wire proportional chamber at inner radii (CIP) mainly used for triggering [26]. The CTD measures charged particles with a transverse momentum resolution of \(\delta (p_T)/p_T\simeq 0.002 \, p_T/\mathrm{GeV} \oplus 0.015\). The forward tracking detector (FTD) is used to supplement track reconstruction in the region \(7^{\circ }<\theta <30^{\circ }\) [27]. It improves the hadronic final state reconstruction of forward going low transverse momentum particles. The CTD tracks are linked to hits in the vertex detector, the central silicon tracker (CST) [28, 29], to provide precise spatial track reconstruction.

In the backward region the SpaCal provides an energy measurement for hadronic particles, and has a hadronic energy resolution of \(\delta E/E \simeq 0.70/\sqrt{E/\mathrm{GeV}}\oplus 0.01\) and a resolution for electromagnetic energy depositions of \(\delta E/E \simeq 0.07/\sqrt{E/\mathrm{GeV}}\oplus 0.01\) measured using test beam data [30].

The ep luminosity is determined by measuring the event rate for the Bethe–Heitler process \(ep \rightarrow ep\gamma \), where the photon is detected in the photon tagger located at \(z=-103\,\mathrm{m}\). The overall normalisation is determined using a precision measurement of the QED Compton process [31] with the electron and the photon detected in the SpaCal.

3.2 Data samples

High \(Q^2\) neutral current DIS events are triggered mainly using information from the LAr calorimeter. The calorimeter has a finely segmented pointing geometry allowing the trigger to select localised energy deposits in the electromagnetic section of the calorimeter pointing to the nominal interaction vertex. For electrons with energies above 11 GeV the trigger efficiency is determined to be close to \(100\,\,\%\) [32].

This analysis is performed using the full \(e^{\pm }p\) collision data set taken in the years 2003–2007 by the H1 experiment. The data were recorded with a lepton beam of energy 27.6 GeV and a proton beam of energy 920 GeV, corresponding to a centre-of-mass energy \(\sqrt{s}=319\) GeV. The total integrated luminosity of the analysed data is 351 pb\(^{-1}\).

3.3 Simulation of standard and instanton processes

Detailed simulations of the H1 detector response to hadronic final states have been performed for two QCD models of the sDIS (background) and for QCD instanton-induced scattering processes (signal).

The background is modelled using the RAPGAP and DJANGOH Monte Carlo programs. The RAPGAP Monte Carlo program [33] incorporates the \(\mathcal{O} (\alpha _{s})\) QCD matrix elements and models higher order parton emissions to all orders in \(\alpha _s\) using the concept of parton showers [34] based on the leading-logarithm DGLAP equations [35–37], where QCD radiation can occur before and after the hard subprocess. An alternative treatment of the perturbative phase is implemented in DJANGOH [38] which uses the Colour Dipole Model [39] with QCD matrix element corrections as implemented in ARIADNE [40]. In both MC generators hadronisation is modelled with the LUND string fragmentation [41, 42] using the ALEPH tune [43]. QED radiation and electroweak effects are simulated using the HERACLES [44] program, which is interfaced to the RAPGAP and DJANGOH event generators. The parton density functions of the proton are taken from the CTEQ6L set  [45].

QCDINS [12, 46] is a Monte Carlo package to simulate QCD instanton-induced scattering processes in DIS. The hard process generator is embedded in the HERWIG [47] program and is implemented as explained in Sect. 2. The number of flavours is set to \(n_f = 3\). Outside the allowed region defined by \({{Q'}^2_{\min }}\) and \({x'_{\min }}\) the instanton cross section is set to zero. The CTEQ5L [48] parton density functions are employed.Footnote 5 Besides the hard instanton subprocess, subleading QCD emissions are simulated in the leading-logarithm approximation, using the coherent branching algorithm implemented in HERWIG. The hadronisation is performed according to the Lund string fragmentation.

The generated events are passed through a detailed GEANT3 [49] based simulation of the H1 detector and subjected to the same reconstruction and analysis chains as are used for the data.

3.4 Inclusive DIS event selection

Neutral current DIS events are triggered and selected by requiring a cluster in the electromagnetic part of the LAr calorimeter. The scattered electron is identified as the isolated cluster of highest transverse momentum. A minimal electron energy of 11  GeV is required. The remaining clusters in the calorimeters and the charged tracks are attributed to the hadronic final state (HFS), which is reconstructed using an energy flow algorithm without double counting of energy [50–52]. The default electromagnetic energy calibration and alignment of the H1 detector [53] as well as the HFS calibration [32, 54] are applied. The longitudinal momentum balance is required to be within \(45\,\mathrm{~GeV~}< \sum (E - p_z) < 65\,\mathrm{~GeV}\), where the sum runs over the scattered electron and all HFS objects. Furthermore the position of the z-coordinate of the reconstructed event vertex must be within \(\pm 35\,\text{ cm }\) of the nominal interaction point.

The photon virtuality \(Q^2\), the Bjorken scaling variable x and the inelasticity of the interaction y are reconstructed from the scattered electron and the hadronic final state particles using the electron-sigma method [55]. This method is the most precise one in the kinematic range of this analysis. The events are selected to cover the phase space region defined by \( 0.2< y < 0.7\), \(x >10^{-3}\) and \(150< Q^2< 15000~\mathrm{GeV}^2\).

The events passing the above cuts yield the NC DIS sample which forms the basis of the subsequent analysis. It consists of about 350000 events. The simulated events are subjected to the same reconstruction and analysis chains as the real data. They reproduce well the shape and the absolute normalisation of the distributions of the energy and angle of the scattered electron as well as the kinematic variables x, \(Q^2\) and y.

3.5 Definition of the observables and the search strategy

The observables used to discriminate the instanton-induced contribution from that of sDIS processes are based on the hadronic final state objects and on a selection of charged particles. Only HFS objects with \( \eta _\mathrm{Lab} < 3.2\) are considered. Charged particles are required to have transverse momenta with \(P_T^\mathrm{Lab} > 0.12\)  GeV and polar angles with \(20^\circ< \theta < 160^\circ \). Here \(\eta _\mathrm{Lab}\) and \( P_T^\mathrm{Lab}\) are measured in the laboratory frame.

Fig. 2
figure 2

Distributions of a the Bjorken-scaling variable x, b the photon virtuality \(Q^2\), c the inclusive distribution of the transverse energy of the jets \(E_{T, \mathrm jets}\), d the pseudorapidity of the jets \(\eta _\mathrm{jets}\) and e the charged particle multiplicity \(n_\mathrm{ch}\). Data (filled circles), the RAPGAP and DJANGOH sDIS background predictions (dotted and solid lines) and the QCDINS signal prediction scaled up by a factor of 50 (hatched) are shown.

Full size image

In the following, all HFS objects are boosted to the hadronic centre-of-mass frame (HCM).Footnote 6 Jets are defined by the inclusive \(k_{T}\) algorithm [56] as implemented in FastJet [57], with the massless \(P_{T}\) recombination scheme and with the distance parameter \(R_{0}= 1.35 \times R_\mathrm{cone} \). A cone radius \(R_\mathrm{cone} = 0.5\) is used. Jets are required to have transverse energy in the HCM frame \({E_{T,\mathrm jet}}\) \( > 3 \)  GeV. Additional requirements on the transverse energy and pseudorapidity of the jets in the laboratory frame are imposed, \(-1.0< \eta ^\mathrm{Lab}_\mathrm{Jet} < 2.5 \) and \(E_{T,\mathrm Jet}^\mathrm{Lab} > 2.5 \)  GeV, in order to ensure that jets are contained within the acceptance of the LAr calorimeter and are well calibrated. The events are selected by requiring at least one jet with \({E_{T,\mathrm jet}}\) \(> 4\)  GeV. The jet with the highest transverse energy is used to estimate the 4-momentum \(q''\) of the current quark (see Fig. 1). \({{Q'}^2~}\) can be reconstructed from the particles associated with the current jet and the photon 4-momentum, which is obtained using the measured momentum of the scattered electron. The \({{Q'}^2~}\) resolution is about \(40\,\,\%\). However, the distribution of the true over the reconstructed value exhibits large tails, since in about \(35\,\,\%\) of the cases the wrong jet is identified as the current jet. Due to the limited accuracy of the \({{Q'}^2~}\) reconstruction, the reconstructed \({{Q}^{\prime 2}}\), labelled \({{Q'}^2_{ \mathrm rec}}\), cannot be used to experimentally limit the analysis to the kinematically allowed region \({{Q}^{\prime 2}}\) \( \gtrsim \) \({{Q'}^2_{\min }}\). Details of the \({{Q'}^2~}\) reconstruction are described in [10, 58, 59].

The hadronic final state objects belonging to the current jet are not used in the definition of the following observables. A band in pseudo-rapidity with a width of \(\pm 1.1\) units in \(\eta \) is defined around the mean \(\bar{\eta } = \sum E_T \eta /(\sum E_T)\), where the sum includes hadronic final state objects [60]. This pseudo-rapidity band is referred to as the “instanton band”. The number of charged particles in the instanton band \({n_B~}\) and the total scalar transverse energy of all hadronic final state objects in the instanton band \({E_{T,B}~}\) are measured.

An approximate instanton rest frame, where all hadronic final state objects in the instanton band are distributed isotropically, is defined by \(\mathbf {q'} + \xi \mathbf {P} = 0\). The definition of \(\xi \) is given in Fig. 1. A numerical value of \(\xi = 0.076\) is used throughout this analysis [15]. In the instanton rest frame the sphericity \({\mathrm{Sph_B}}~\) and the first three normalised Fox-Wolfram moments are calculated [42, 61]. For spherical events \({\mathrm{Sph_B}}~\) is close to unity, while for pencil-like events \({\mathrm{Sph_B}}~\) tends to zero. Furthermore, the axes \(\mathbf {i}_\mathrm{min}\) and \(\mathbf {i}_\mathrm{max}\) are found for which in the instanton rest system the summed projections of the 3-momenta of all hadronic final state objects in the instanton band are minimal or maximal [9]. The relative difference between \(E_\mathrm{in} = {\sum _h |\mathbf {p}_h \cdot \mathbf {i}_\mathrm{max} |}\) and \(E_\mathrm{out}= {\sum _h |\mathbf {p}_h \cdot \mathbf {i}_\mathrm{min} |}\) is called \({\Delta _B}= (E_\mathrm{in}-E_\mathrm{out})/E_\mathrm{in}\). This quantity is a measure of the transverse energy weighted azimuthal isotropy of an event. For isotropic events \({\Delta _B~}\) is small while for pencil-like events \({\Delta _B~}\) is close to unity.

The reconstruction of the variable \({x'~}\) suffers from poor resolution as in the case of \({{Q'}^2_{ \mathrm rec}}\). Using two methods to calculate the invariant mass of the quark gluon system, \(W_{I}\), \(x'\) is reconstructed as \(x'_\mathrm{rec}= (x'_{1}+x'_{2})/2\), where \(x'_{i}= {{Q'}^2_{ \mathrm rec}~}/ (W^2_{I,i}+{{Q'}^2_{ \mathrm rec}~})\) with \(W^2_{I,1}=(q'_\mathrm{rec}+ \xi P)^2\) and \(W^2_{I,2}= (\sum _{h} p_{h})^2\) where the sum runs over the HFS objects in the instanton band. The \(W^2_{I,1}\) calculation is based on the scattered electron and the current jet, while the \(W^2_{I,2}\) reconstruction relies on the measurement of the hadronic final state objects in the instanton band. The \(x'_\mathrm{rec}\) resolution achieved is about \(50 \,\,\%\). As for the case of \({{Q'}^2_{ \mathrm rec}}\), the reconstructed \(x'_{rec}\) cannot be used to limit the analysis to the kinematically allowed region \({x'}\gtrsim {x'_{\min }}\). However, \(x'_\mathrm{rec}\) as well as \({{Q'}^2_{ \mathrm rec}~}\) can be used to discriminate instanton processes from the sDIS background.

Exploiting these observables, a multivariate discrimination technique is used to find the most sensitive set of observables to distinguish between signal and background [62].

3.6 Comparison of data to standard QCD predictions

Both the RAPGAP and DJANGOH simulations provide a reasonable overall description of the experimental data in the inclusive DIS and jet sample. To further improve the agreement between Monte Carlo events and data, event weights are applied to match the jet multiplicities as a function of \(Q^{2}\). The MC events are also weighted as a function of \(P_{T}\) and \(\eta \) of the most forward jet in the Breit frame [32, 54]. Furthermore, the track multiplicity distribution is weighted. The weights are obtained from the ratio of data to the reconstructed MC distributions and are applied to the events on the generator level. After these weights are applied, the simulations provide a good description of the shapes and normalisation of the data distributions. Examples of these control distributions are shown in Fig. 2: distributions of the kinematic variables x and \(Q^2\), the transverse energy of the jets \(E_{T,\mathrm jets}\), the pseudorapidity of the jets \(\eta _\mathrm{jets}\) in the hadronic centre-of-mass frame and the charged particle multiplicity \(n_\mathrm{ch}\).

The measured distributions of the five observables \({E_{T,\mathrm jet}}, {n_B}\), \(x'_\mathrm{rec}\), \({\Delta _B~}\) and \(E_\mathrm{in}\) are compared in Fig. 3 to the expectations from the standard DIS QCD models (RAPGAP, DJANGOH) and from the instanton model (QCDINS). The data are reasonably well described by the reweighted sDIS Monte Carlo simulations. The models are able to describe the data within \(5-10\,\,\%\) except at very low and/or very large values of the given observable, where differences up to \(20\,\,\%\) are observed. The expected instanton distributions differ in shape from the sDIS background. However, the magnitude of the expected signal is small and advanced discrimination methods are required to enhance the signal to background ratio.

Fig. 3
figure 3

Distributions of the observables used in the multivariate analysis: a the transverse current jet energy \({E_{T,\mathrm jet}}\), b the charged particle multiplicity in the instanton band \({n_B}\), c, d two variables measuring the azimuthal isotropy of the event, \({\Delta _B~}\) and \(E_\mathrm{in}\), respectively, and e the reconstructed instanton kinematic variable \(x'\). Data (filled circles), the RAPGAP and DJANGOH sDIS background predictions (dotted and solid lines) and the QCDINS signal prediction scaled up by a factor of 50 (hatched), are shown. The error band, shown only for DJANGOH, represents the MC statistical and systematic uncertainties added in quadrature

Full size image

4 Search for instanton-induced events

A multivariate discrimination technique is employed to increase the sensitivity to instanton processes. The PDERS (Probability Density Estimator with Range Search) method as implemented in the TMVA ROOT package [63] is used.Footnote 7

The strategy to reduce the sDIS background is based on the observables \({E_{T,\mathrm jet}}, {n_B}\), \(x'\), \({\Delta _B~}\) and \(E_\mathrm{in}\). This set of observables has been chosen since it provides the best signal to background separation [62]. Moreover, the distributions of these variables are overall well described by both Monte Carlo simulations. The distribution of the discriminator D is shown in Fig. 4. Taking into account the systematic uncertainties, the discriminator distribution is described by the sDIS Monte Carlo simulations in the background dominated region. For \(D<0.2\) predictions and data agree within systematic uncertainties. The background events are mainly concentrated at low discriminator values, while the instanton signal peaks at large values of the discriminator. At large D both data and predicted background fall off steeply.

A signal region is defined for \(D > D_{cut}=0.86\), optimised for a determination of the instanton signal from event counting. The distributions of the expected instanton signal and of the background are shown in Fig. 5. No excess of events is observed and the DJANGOH MC describes the data well, while the prediction of RAPGAP is systematically above the data.

Fig. 4
figure 4

Distribution of the discriminator D. Data (filled circles), the RAPGAP and DJANGOH sDIS background predictions (dotted and solid lines) and the QCDINS signal prediction scaled up by a factor of 50 (red line) are shown. The error band, shown only for DJANGOH, represents the MC statistical and systematic uncertainties added in quadrature

Full size image
Fig. 5
figure 5

Distribution of the discriminator D in the signal region \(D > 0.86\). Data (filled circles), the RAPGAP and DJANGOH sDIS background predictions (dotted and solid lines) and the QCDINS signal prediction (red line) are shown. The error band, shown only for DJANGOH, represents the MC statistical and systematic uncertainties added in quadrature

Full size image
Table 1 Number of events observed in data and expected from the DJANGOH and RAPGAP simulations in the signal region
Full size table

The expected and observed number of events are summarised in Table 1. In the signal region, a total of 2430 events are observed in data, while DJANGOH predicts \(2483^{+77}_{-90}\) and RAPGAP \(2966^{+~90}_{-103}\). The uncertainties on the expected number of events include experimental systematic uncertainties and small contributions from the finite sample sizes. For the expected number of instanton-induced events the dominating uncertainty is due to \(\Lambda _{\overline{MS}}^{(3)}\).

The following sources of systematic uncertainties are propagated through the full analysis chain:

  • The energy scale of the HFS is known to a precision of \(1\,\,\%\) [32, 54].

  • Depending on the electron polar angle the energy of the scattered electron is measured with a precision of \(0.5-1\,\,\%\) [64].

  • The precision of the electron polar angle measurement is 1  mrad [64].

  • Depending on the electron polar angle, the uncertainty on the electron identification efficiency ranges from 0.5 to \(2\,\,\%\) [54].

  • The uncertainty associated with the track reconstruction efficiency and the effect of the nuclear interactions in the detector material on the efficiency of track reconstruction are estimated to be \(0.5\,\,\%\) each [65].

The effect of these uncertainties on the expected signal and background distributions is determined by varying the corresponding quantities by \(\pm 1\) standard deviation in the MC samples and propagating these variations through the whole analysis. The above systematic and statistical uncertainties added in quadrature are shown in the Figures and in Table 1. The included statistical uncertainties due to the limited Monte Carlo statistics are approximately an order of magnitude smaller than the experimental systematic uncertainties.

The main contributions to the experimental systematic uncertainties arise from the energy scale calibration of the scattered electron ranging from \({\sim }4\,\,\%\) in the background dominated region to \({\sim }1\,\,\%\) in the signal region and from the energy scale of the HFS ranging from \({\sim }1\,\,\%\) in the background region to \({\sim }2.5\,\,\%\) in the signal region. Uncertainties connected with the track reconstruction and secondary interactions of the produced hadrons in the material surrounding the interaction region contribute to the systematic error in the signal region at a level of \({\sim }2\,\,\%\) each, and in the background dominated region by less than \(0.5\,\,\%\). In the full range of the discriminator, the uncertainties on the electron identification and on the precision of the electron polar angle are smaller than \(0.5\,\,\%\) each.

Given the observed and expected numbers of events, no evidence for QCD instanton-induced processes is observed. In the following, the data are used to set exclusion limits.

5 Exclusion limits for instanton-induced processes

The upper limit is determined from a CL\(_{s}\) statistical analysis [66, 67] using the method of fractional event counting [68]. A test statistic X is constructed as a fractional event count of all events using the discriminator distribution:

$$\begin{aligned} X = \sum _{i=1}^{N_\mathrm{bin}} w_i n_i\,, \end{aligned}$$
(2)

where the sum runs over all bins, and \(n_{i}\) is the number of events observed in bin i. The weights \(w_i\) are calculated from the predicted signal and background contributions and their uncertainties, using an appropriate set of linear equations [68]. They are defined in such a way as to ensure that only bins with both a large signal-to-background ratio and small systematic uncertainties enter with sizable weights into the test statistic X. In case of negligible systematic uncertainties, the weights behave as \(w_i = s_i/(s_i + 2b_i)\) where \(s_i\) and \(b_i\) are the predicted number of signal and background events in a given bin i, respectively. In the presence of bin-to-bin correlated systematic uncertainties, the weights may become negative in background-dominated regions. When calculating the test statistics X the negative weights correspond to a subtraction of background contributions, estimated from data. The distribution of the resulting weights \(w_i\) is shown in Fig. 6. Large positive weights are attributed to bins in the signal region, \(D>0.9\). Negative weights are assigned in the region \(0.4<D<0.75\). A large number of MC experiments are generated by varying the expected number of events in absence or presence of the signal within the statistical and systematic uncertainties. Systematic uncertainties are treated as Gaussian distributions and statistical fluctuations are simulated using Poisson statistics. If \(1-CL_s>0.95\), the signal hypothesis is excluded at \(95\,\,\%\) confidence level.

Fig. 6
figure 6

Distribution of the bin weights \(w_i\) as a function of the discriminator D. The bin weights are calculated using the signal and background predictions together with their systematic uncertainties and the respective bin-to-bin correlations

Full size image

Limits are calculated using the full range of the discriminator distribution as shown in Fig. 4. The following additional systematic uncertainties are included in the exclusion limit calculation:

  • The normalisation uncertainty due to the precision of the integrated luminosity measurement is \(2.3\,\,\%\) [31].

  • The difference between the prediction from DJANGOH and RAPGAP is assigned as model uncertainty of the background estimation, i.e. the difference between two background histograms in Fig. 4. This model uncertainty is large, 8–20 and 13–46 %, for small \(D<0.2\) and large \(D>0.85\) values of the discriminator, respectively. For intermediate values of D it amounts to \(0.3-8\,\,\%\).

  • The uncertainty of the background normalisation is \(1.1\,\,\%\). This uncertainty is estimated as \(\epsilon = (N_\mathrm{Dj}-N_\mathrm{Rap})/N_\mathrm{Dj}\), where \(N_\mathrm{Dj}\) and \(N_\mathrm{Rap}\) are the total number of predicted events in the full discriminator range for the DJANGOH and RAPGAP MC simulations, respectively.

  • The uncertainty of the predicted signal cross section due to the uncertainty of \(\Lambda _{\overline{MS}}^{(3)}\) (Sect. 2) varies from 20 to 50  % depending on the region in \({Q'~}\) and \({x'~}\).

Figure 7 shows the behaviour of the observed CL\(_s\) as a function of the instanton signal cross section. In this study the total instanton cross section is taken as a free parameter, whereas the signal shape is taken from the QCDINS simulation. At \(95\,\,\%\) CL, the observed limit is 2 pb, as compared to a median expected cross section limit of \(3.7^{+1.6}_{-1.1}(68\,\,\%)^{+3.8}_{-1.7}(95\,\,\%)\) pb. The first (second) set of uncertainties indicates the corresponding \(\pm 1\sigma \) (\(\pm 2\sigma \)) deviations of the median expected cross section limit. The observed \(-2\sigma \) deviation between the expected and observed limit is caused by a downward fluctuation of the observed data test statistics X. This downward fluctuation receives contributions both from regions where the weights \(w_i\) are positive and the data are below the background prediction and from regions where the \(w_i\) are negative and the data are somewhat larger than expected.

The QCD instanton model implemented in QCDINS, restricted to the kinematic region defined by \({x'_{\min }}=0.35\) and \({{Q'}^2_{\min }}=113\) \({\mathrm{~GeV}^2~}\), predicts a cross section of \(10\pm 3\) pb, and thus is excluded by the H1 data. Note that the cross section uncertainty of \(30\,\,\%\), stemming from the variation of \(\Lambda ^{(3)}_{\overline{MS}}\), is already included in the observed limit of 2 pb.

Fig. 7
figure 7

Observed CL\(_{s}\) (solid line) as a function of the instanton cross section. The \(95\,\,\%\) CL limit is indicated by a horizontal line. The dark and light bands correspond to \(\pm 1\sigma \) and \(\pm 2\sigma \) fluctuations of the expectation (dashed line)

Full size image
Fig. 8
figure 8

Instanton production exclusion limits as a function of \({x'_{\min }}\) and \({{Q'}^2_{\min }}\). The regions excluded at confidence levels of 90, 95 and 99  % are shown. The region of validity of instanton perturbation theory is indicated (dashed line)

Full size image
Fig. 9
figure 9

Upper limits on the instanton cross section at \(95\,\,\%\)  confidence level, as a function of \({x'_{\min }}\) and \({{Q'}^2_{\min }}\). Also shown are isolines of predicted fixed instanton cross section and the effects of varying the QCD scale \(\Lambda ^{(3)}_\mathrm{QCD}\) defined in the \(\overline{\mathrm{MS}}\) scheme within uncertainties. The instanton cross section extrapolated beyond the indicated region of validity of instanton perturbation theory is shown as well

Full size image

In order to assess the sensitivity of the instanton cross section on the kinematic variables \({x'_{\min }}\) and \({{Q'}^2_{\min }}\), limits are also determined as a function of the lower bounds \({x'_{\min }}\) and \({{Q'}^2_{\min }}\). As explained in Sect. 3.3, outside these bounds the instanton cross section is set to zero. The results are shown in Fig. 8, where the observed confidence levels, using the QCDINS predictions, are shown in the \(({x'_{\min }},{{Q'}^2_{\min }})\) plane. At \(95\,\,\%\) confidence level, parameter values \({x'_{\min }}<0.404\) are excluded at fixed \({{Q'}^2_{\min }}=113\) \({\mathrm{~GeV}^2~}\). For fixed \({x'_{\min }}=0.35\), values of \({{Q'}^2_{\min }}<195\) \({\mathrm{~GeV}^2~}\) are excluded. The exclusion regions depend somewhat on the choice of \(\Lambda ^{(3)}_{\overline{MS}}\) and its uncertainty. In order to assess these effects, the analysis was repeated for \(\Lambda ^{(3)}_{\overline{MS}}=340\pm 8\)  MeV [69] instead of \(\Lambda ^{(3)}_{\overline{MS}}=339\pm 17\)  MeV . For this choice, more stringent limits are obtained. For example, at fixed \({{Q'}^2_{\min }}=113\) \(\mathrm {GeV}^2\) the excluded range at \(95\,\,\%\) confidence level would change to \({x'_{\min }}<0.413\).

A less model-dependent search is presented in Fig. 9. Here, limits on the instanton cross section are determined as a function of the parameters \({x'_{\min }}\) and \({{Q'}^2_{\min }}\), using the signal shapes predicted by QCDINS. No uncertainty on the instanton cross section normalisation is included in this determination of the experimental cross section limit. The most stringent exclusion limits of order 1.5  pb are observed for large \({{Q'}^2_{\min }}\) and small \({x'_{\min }}\). For increasing \({x'_{\min }}\) the limits are getting weaker. At the nominal QCDINS setting, \({x'_{\min }}=0.35\) and \({{Q'}^2_{\min }}=113\) \({\mathrm{~GeV}^2~}\), one expects to find back an exclusion limit of 2 pb, as discussed with Fig. 7. The limit in Fig. 9, however, is observed to be somewhat better, because the theory uncertainty on the cross section normalisation is included in Fig. 7 but not in Fig. 9.

6 Conclusions

A search for QCD instanton-induced processes is presented in neutral current deep-inelastic scattering at the electron-proton collider HERA. The kinematic region is defined by the Bjorken-scaling variable \(x > 10^{-3}\), the inelasticity \(0.2< y < 0.7\) and the photon virtuality \(150< Q^2 < 15000\)  GeV\(^2\). The search is performed using H1 data corresponding to an integrated luminosity of  351 pb\(^{-1}\).

Several observables of the hadronic final state of the selected events are exploited to identify a potentially instanton-enriched sample. Two Monte Carlo models, RAPGAP and DJANGOH, are used to estimate the background from the standard NC DIS processes. The instanton-induced processes are modelled by the program QCDINS. In order to extract the expected instanton signal a multivariate data analysis technique is used. No evidence for QCD instanton-induced processes is observed. In the kinematic region defined by the theory cut-off parameters \({x'_{\min }}=0.35\) and \({{Q'}^2_{\min }}=113\) \({\mathrm{~GeV}^2~}\) an upper limit of 2 pb on the instanton cross section at \(95\,\,\%\) CL is determined, as compared to a median expected limit of \(3.7^{+1.6}_{-1.1}(68\%)^{+3.8}_{-1.7}(95\,\,\%)\) pb. Thus, the corresponding predicted instanton cross section of \(10\pm 3\) pb is excluded by the H1 data. Limits are also set in the kinematic plane defined by \({x'_{\min }}\) and \({{Q'}^2_{\min }}\). These limits may be used to assess the compatibility of theoretical assumptions such as the dilute gas approximation with H1 data, or to test theoretical predictions of instanton properties such as their size and distance distributions.

Upper cross section limits on instanton-induced processes reported previously by the H1 [15] and ZEUS [16] collaborations are above the theoretical predicted cross sections. In a domain of phase space with a lower \(Q^2\) range (\(10 \lesssim Q^2 < 100\)  GeV\(^2\)), H1 reported an upper limit of 221 pb at \(95\,\,\%\) CL, about a factor five above the corresponding theoretical prediction. At high \(Q^2\) (\(Q^2 > 120\) GeV\(^2\)), the ZEUS Collaboration obtained an upper limit of 26 pb at \(95\%\) CL in comparison to a predicted cross section of 8.9 pb. In summary, compared to earlier publications, QCD instanton exclusion limits are improved by an order of magnitude and are challenging predictions based on perturbative instanton calculations with parameters derived from lattice QCD.