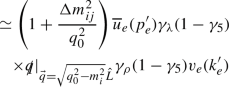Abstract
Recently, several studies of neutrino oscillations in the vacuum have not found the decoherence long expected from the separation of wave packets of neutrinos in different mass eigenstates. We show that such decoherence will, on the other hand, be present in a treatment including any mechanism which leads to a dependence of the final state on both the neutrino’s emission and absorption time. Using a simplified model in \(1+1\)d, we show that if the positions of the final state particles are measured, or equivalently entangled with the environment, then decoherence will damp neutrino oscillations. We also show that wave packet spreading can cause the decoherence to eventually saturate, without completely suppressing the oscillations. These results are not an artifact of the approximation used: we show that, considering the \(V-A\) model in \(3+1\)d, the difference would be simply a total multiplicative factor that would not affect the oscillation probability nor the decoherence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Neutrinos are described by wave packets. Lighter neutrinos in general correspond to faster wave packets which eventually are expected to pull ahead of wave packets corresponding to heavier neutrinos, ruining their coherence and thus the observed pattern of neutrino oscillations. This old expectation has been confirmed in quantum mechanics [1,2,3] and in external wave packet models [4, 5]. However, Nature is described by quantum field theory with dynamical fields. In the full, dynamical quantum field theory, in a vacuum, Refs. [6,7,8] found no such decoherence. Furthermore, Ref. [9] argued that decoherence, in a vacuum or coupled to an environment, would anyway be unobservable as it can appear only when the detector’s energy resolution is too poor to observe neutrino oscillations. This state of affairs has led some to believe that neutrino quantum decoherence cannot be observed even in principle, even when the system is coupled to an environment, despite many calculations [10, 11] in simplified models which suggest the contrary.
In the present note, we examine how the arguments in the above vacuum studies fail in the presence of an environment.Footnote 1 The decoherence is a result of the fact that the final state of the environment depends on the spacetime region in which the neutrino is created and absorbed, which in turn depend on the neutrino mass eigenstate. We will see, in Appendix B that this statement is quite independent of the details of the model and so, in a simplified model, we provide a counter example to one step in the argument of Ref. [9].
Often, in order to obtain analytical results, energies are expanded up to first order in momentum. At this order the entire wave packet moves rigidly, at a constant velocity. We have considered the second order expansion in a simplified model. We found that the dynamical evolution of the neutrino wave packet can affect the decoherence: at first the oscillation amplitude decreases, however at some point the decoherence can saturate, leading to a regime where the partially dampened oscillations are not further damped.
1.1 Three sources of decoherence
In a quantum theory, the probability of a given set of final states \(\{|i\rangle \}\) given a known initial state is calculated via two sums. First, one sums the amplitudes for all processes yielding a given final state \(|i\rangle \). This sum of complex numbers is called the coherent sum, and it results in the total amplitude for each final state. Next, one takes the norm squared of each total amplitude and sums these over the set of final states of interest \(\{|i\rangle \}\). This sum of real numbers is called the incoherent sum.
While each term in a coherent sum is an amplitude with the same final state, the intermediate states are in general different. For example, an internal neutrino line may correspond to different mass eigenstates in different terms in the sum, so long as these different mass eigenstates lead to the same final state. When this is the case, the coherent sum of different mass eigenstate processes leads to neutrino oscillations. On the other hand, oscillations will be washed out by quantum decoherence if distinct mass eigenstates at intermediate steps lead to distinct final states.Footnote 2
Do distinct neutrino mass eigenstates always lead to the same final state? If the neutrino propagates over a long baseline, then it will nearly be on shell and then the relevant kinematic constraints in many experiments of interest imply that the heavier mass eigenstates will travel more slowly. This means that the space-time point at which the neutrino is created or absorbed will, in such cases, differ for different mass eigenstates.Footnote 3 As a result, if the final state is sufficiently sensitive to the neutrino emission and absorption points, then the distinct mass eigenstates will lead to distinct final states and will be incoherently summed, leading to a damping in the oscillation amplitude.
Why might the final states depend on the space-time locations of the neutrino emission and absorption? There are three physical mechanisms for such a dependence. First, the macroscopic observables of the experiment inevitably place some constraint on the neutrino emission and absorption. For example, in a terrestrial neutrino experiment, emission is generally spatially localized at a radioactive source, at a target station or in a decay tube. Absorption is spatially localized in a detector. Emission is temporally localized as a result of the finite lifetime of the source or the beam structure. Detection is temporally localized by the time resolution of the detector. As was shown in Ref. [7], such macroscopic constraints are far too weak to lead to observable decoherence and we will not consider them further.
The second mechanism is that the processes in which the neutrino is emitted and absorbed will inevitably affect the environment, so long as they do not occur in a vacuum. The final state of the environment therefore will depend on the locations of both the neutrino emission and also its absorption.
Third, lepton number conservation together with the light mass of the neutrino implies that neutrinos are generally emitted together with charged leptons, and when they are absorbed charged leptons are generally created. These charged leptons survive to the final state in many experimental setups of interest and so these final states will generally be sensitive to the space-time locations where the charged leptons are created,Footnote 4 which are precisely the locations where the neutrino is emitted and absorbed. Thus, for each final state, one expects decoherence. If this decoherence survives when all experimentally indistinguished final states are summed, it will provide an irreducible contribution to the decoherence. This irreducible source of decoherence is present in the vacuum and can be calculated precisely using the Standard Model, or low energy approximations to it such as the \(V-A\) model.
1.2 Outline
In Sect. 2 we present a simplified model, containing only scalar fields in 1 + 1d, that will be used to compute the shape and dimension of the neutrino wave packet as a function of t. We will see that, even if the uncertainty on the momentum of the source particle leads to a spread in the neutrino momentum, their widths are not the same: the dimension of the neutrino wave packet is suppressed by a factor of \(v_I-v_F\simeq q/M\), where q is the neutrino momentum and M the source particle mass. This mismatch addresses the objection of Ref. [9]. In Sect. 3 we use this simplified model to compute the transition amplitude, showing that if the final states are localized as well, decoherence can emerge. In Sect. 4 we show that, if the time-evolution of the neutrino wave packet is taken into account, decoherence will not completely erase the oscillations.
However, one could object that neutrinos are not described by 1 + 1d scalar fields. For this reason in Appendix B, using the 3 + 1d \(V-A\) model, we will show that the details of the model affect only the normalization of the oscillation probability.
2 Neutrino wave packets
Above we have argued that decoherence occurs when the neutrino momentum and energy is determined so precisely by the final state that the mass shell condition excludes some mass eigenstates. This decoherence smears neutrino oscillations. However sometimes neutrino oscillations are anyway smeared by a poor knowledge of the neutrino’s momentum. Disentangling these two effects is essential to observing decoherence.
In Ref. [9] it was argued that such a disentangling is impossible, as decoherence only arises when oscillations are anyway washed out by the poor momentum resolution. This motivates us, in the present section, to perform a careful analysis of neutrino production, to understand how the uncertainty in the neutrino’s momentum is determined.
Neutrinos cannot be observed directly but they can be detected via their interactions with other particles. Even if we consider a two-body decay, where the energy of the daughter particles is fixed, any uncertainty on the momentum of the source or detector particle will lead to an uncertainty on the momentum of the neutrino as well. We will show, however, that in the two-body decay the uncertainty on the neutrino momentum will be considerably smaller than that on the source (or detector) particle, due to the on-shell condition, allowing a key step in the argument from Ref. [9] to be evaded.Footnote 5
2.1 The simplified model
We will show in Appendix B that the terms related to the propagator and the hadronic currents in the full 3 + 1d \(V-A\) model contribute only a constant factor to the transition amplitude. This factor does not affect the oscillations in general nor the decoherence in particular. For this reason from here thereafter we will consider a simplified model, using only scalar fields in 1 + 1d, similar to the one used in [8, 18]. In Ref. [17], it was argued that the physics of both oscillations and entanglement are well captured by a projection to one spatial dimension.
We will consider a model described by a Hamiltonian H which is the sum of the standard kinetic term \(H_0\) and an interaction term
where \(\nu _1\) and \(\nu _2\) are neutrino mass eigenstates. Here \(\phi _{H(L)}\) represent the heavy (light) source particle and the colons denote the standard normal ordering. The notation \(|H,p;0\rangle \) will indicate a state containing a heavy source particle with momentum p and no neutrino, while \(| L,k;j,q\rangle \) will contain a light source particle (i.e. after the decay) with momentum k and a neutrino in the jth mass eigenstate with momentum q.
In our simplified model, \(\nu _1\pm \nu _2\) play the role of the fields for flavor eigenstates. Our initial state contains only the heavy source particle, that will later decay via the process
and creates the neutrino in the flavor eigenstate a, which is intuitively the sum of the two mass eigenstates. More concretely, our initial state \(|I\rangle \) will be a linear combination of the \(|H,p;0\rangle \)
Here \(\sigma _I\) is the dimension of the heavy source wave packet and \(p_0\) is its initial momentum. The initial data \(p_0\) and \(\sigma _I\) is determined by the experimenter. This state, like the others we will consider later, is not normalized, since such a normalization factor will not be relevant in the following calculations. The experiment runs until time \(t_f\). Evolving in the Schrodinger picture, the final state
will be a linear combination of the \(| L,k;j,q\rangle \).
At tree-level one finds the matrix elements [18],
where \(t_1\) is the time of creation of the neutrino and
Here \(M_H\) (\(M_L\)) and \(m_j\) are the masses of the heavy (light) source particle and of the jth eigenstate of the neutrino mass matrix, respectively. \(E_I\) and \(E_{F,j}\) are the eigenvalues of the free Hamiltonian before and after emission of a neutrino in the jth mass eigenstate. Note that, since they are not the eigenvalues of the total interacting Hamiltonian H, they need not be conserved and so \(E_I\) and \(E_F\) are in general not equal, such a condition is satisfied only when the momenta are on-shell.
Usually in analytic computations these energies are expanded up to the first order in the momentum. At this order, all of the modes propagate at the same velocity and the wave packet does not spread. We will proceed as follows: first we will consider only the first-order approximation, to see how the localization in space of the final state leads to decoherence, then we will see, in one particular case, how the inclusion of the second order terms change the picture.
2.2 First-order approximation
The largest contribution comes from the peak of the initial wave packet \(p=p_0\) and an on-shell neutrino. A neutrino in mass eigenstate j is on-shell if its momentum \(q={\hat{q}}_j\) which satisfies
Taking the neutrinos to be much lighter than the source particles and expanding in m/M, one finds
We will consider only two neutrino flavors. To ensure a good convergence of our expansion, let us expand q about \(q_0\) which is defined to be the average between the two \({\hat{q}}_{j}\)
where
We define
Expanding p and q about \(p_0\) and \(q_0\) we can write (2.6) as
where \(v_{\nu ,j}\) , \(v_I\) and \(v_F\) are the group velocities of the neutrino and the heavy and light source particle, respectively and \(E_0=E_I(p_0)\) is the peak value of the on-shell energy. It will be useful to point out that
2.3 Neutrino wave packet
All the information about the neutrino creation is contained in the time-evolution operator \(U=e^{-iHt_f}\). What is then the size and the shape of the wave packets of the neutrino and the light source particle, after a time \(t_f\) is passed? The state at time \(t_f\), \(e^{-iHt_f}|I\rangle \) contains both the neutrino and the light source particle.
The wave packet of the system in momentum space, at time \(t_f\), is defined as
Expanding the energy at first order, the distribution of the neutrino momentum can be computed (up to an unimportant multiplicative factor) to be
where (assuming that the neutrino is ultrarelativistic and the source particle, both before and after the decay, is non-relativistic)
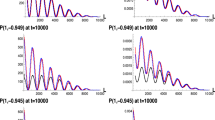
The neutrino wave packet in momentum space after a time t. The red curve corresponds to our analytical approximation (2.15), while the black curve is obtained computing Eq. (2.14) via numerical integration. We considered \(\sigma _I=0.01\), \(M=10\), \(\Delta M=1\), \(m_1=0\) and neglected the term proportional to \(\Delta m_{ji}^2=0.01\). We can see that when \(t\gg t_w\simeq 10^3\) the dimension of the wave packet reaches the asymptotic value, given by the blue curve
In the last step, we performed the change of variables \(\{t_1,t_2\}\rightarrow \{T_+,T_-\}\), \(T_\pm =t_1\pm t_2\); the factor \((t_f-|T_-|)\) comes from the integration over \(T_+\). While it is possible to solve the integral analytically, its solution is lengthy and does not give us interesting information, so we will not write down it explicitly. It is sufficient to point out that \(I_j(\delta q,t_f)\) represents the contribution of the off-shell momenta: when \(t_f\) is large (\(t_f\gg t_w=1/\sigma _\nu \)), the q-dependence of \(I_j\) can be neglected, and that term is just a multiplicative constant.Footnote 6 For large \(t_f\), the wave packet is a Gaussian with \(\sigma =\sigma _{\nu }\); for small \(t_f\), as long as \(\sigma _I\) is sufficiently small, our approximation is still valid and in Fig. 1 we can see that there is a good agreement between our approximate expression from Eq. (2.15) and the numerical estimation.
Following the same procedure, we can find the same expression for the wave packet of the light source particle, after the emission of the neutrino. In particular we have
Equation (2.17) tells us that the wave packet of the final state of the source particle will have more or less the same dimension as the initial one, while the expression for \(\sigma _{\nu ,j}\) in (2.16) shows that the distribution of the neutrino momentum will be much more peaked. The reason for this is that the dimension of these wave packets is determined by imposing energy conservation. If the mass of the source particle, both before and after the decay, is much larger than the neutrino mass, a change in the initial momentum of the source particle will translate into a much smaller change of the neutrino momentum, hence the spread will be significantly reduced.
A more intuitive way of obtaining the same result could be the following: let us consider the on-shell condition, which is satisfied for \(p=p_0\) and \(q=q_0\) (we will ignore, for simplicity, the additional term proportional to \(m_j^2\), which is equivalent to assuming that the difference between \(q_{s,1}\) and \(q_{s,2}\) is very small). After a slight shift of the momenta we have
This resolves the problem suggested in Ref. [9], where the uncertainties in the momenta of the source particle and the neutrino were identified. We see that the neutrino momentum is more strongly peaked than that of the source particle by a factor of \((v_I-v_F)/(v_{\nu ,i}-v_F)\) which is of order the velocity of the nonrelativistic source particle.
2.4 Coordinate space wave packet
Let us assumeFootnote 7 that \(v_{\nu ,j}>v_I\) and that \(v_I>0\). This will allow us to simplify the calculations that will follow.
We start by considering the wave packet of the system in coordinate space. Let x be the position of the neutrino at time \(t_f\) and, for reasons that will be clear in a moment, let \(x-y\) be the position of the light source particle:
Due to the delta function, the integral over \(t_1\) is trivial and the result is different from 0 as long as
This is not surprising, since y is the distance between the neutrino and the light source particle (and we assumed the neutrino to be ultrarelativistic, while the source particle is non relativistic, which means that the former will be considerably faster). Neglecting again the total normalization factors we have
The distribution of the neutrino position in coordinate space at time \(t_f\) is given by
Please notice that, due to condition 2.20, the integral is not from \(-\infty \) to \(+\infty \). \(\psi _{x,j}(x-y, x)\) is proportional to a Gaussian, which is peaked at
As long as \(\tilde{y}\) is within the boundaries of the integration region,Footnote 8 the integral will be constant and does not depend on x. Such a condition is fulfilled when
which, given our assumptions, is the region where a classical neutrino could be found if the decay happens at some point between times \(t=0\) and \(t=t_f\). This means that the dimension of the wave packet in coordinate space will grow linearly in \(t_f\), while in momentum space it will reach an asymptote. Thus, even if the neutrino wave packet in momentum space is described by a Gaussian, its dimension in coordinate space could be significantly larger than \(1/\sigma _q\).
This growth of the wave packet is not in contradiction with the uncertainty principle, which provides only a lower bound on the product of these uncertainties. Note that it is not to be confused with the spreading of the wave packet, studied below, which results from the spread in the velocity of the neutrinos. Rather this growth is caused by the continuous neutrino production.
3 Transition amplitude
3.1 Gaussian wave packets
References [8, 18] considered neutrinos created by a nonrelativistic source in a 2-body decay, which also produced a nonrelativistic remnant. The neutrino production, and a similar detection, occurred in a vacuum. As a result, there was no environment to record the creation and absorption times \(t_1\) and \(t_2\) of the neutrinos. Also, the nonrelativistic approximation led to very little dependence of the final state on \(t_1\) and \(t_2\). The result was that there was no decoherence due to the separation of the wave packets.
In the present paper, we would like to begin our investigation of just how this situation changes in the presence of an environment. We expect, as a result of the general arguments above, that if the environment is sufficiently sensitive to both \(t_1\) and \(t_2\), then there will be decoherence. There are two approaches to testing this expectation. First, one may perform a complete calculation in the context of the full 3+1d \(V-A\) model, including neutrino production and detection and an incoherent sum over different intervals for \(t_1\) and \(t_2\). This is reliable, but somewhat complicated and so the cause of the decoherence is somewhat obscured by details which in the end are irrelevant to the final results. Thus we relegate that calculation to Appendix B.
The second approach is to use the simplified model of the previous section of a 1 + 1d scalar field with neutrino production, but no measurement. Due to its simplicity, it allows to mechanism responsible for decoherence to be displayed clearly. Here measurement is replaced with the choice of a final state \(|F\rangle \). This state can in principle be taken to be a sum or difference of mass eigenstates, to serve as a proxy for a measurement in the disappearance or appearance channel.
Furthermore, one may choose its distribution in physical and momentum space. For example, if a plane wave is used, it does not contain any information on the position of the particles at \(t_f\), there are no constraints on \(t_1\) and \(t_2\) and so one does not expect decoherence. We therefore use a spatially localized \(|F\rangle \), as a proxy for environmental interactions.Footnote 9 This will allow only a certain range of \(t_1\) to give a non-negligible contribution to the transition probability, and, as we will see, decoherence will emerge.
We want to compute the transition amplitude
where \(\sigma _{\nu (F)}\) and \(L_{\nu (F)}\) are, respectively, the dimension of the wave packet and the position at time t of the neutrino (light source particle). It should be noticed that the conservation of momentum will impose \(k=p-q\), so the integral over k will be trivial. This amplitude plays the role of the survival amplitude in our crude model, whereas \(\langle F_1|-\langle F_2|\) would have led to the appearance amplitude for the other flavor.
It is convenient to write the product of the Gaussians as
where
Following the same procedure used in the previous section, the linear approximation allows us to write the transition amplitude as
where
Completing the square, and integrating first over p and then over q, we can write the transition amplitude
where \(\theta \) is a global phase, that can be neglected since it does not depend on the mass eigenstate j and
The dependence of \(I_j\) on the mass eigenstate j becomes negligible at large times. The terms \(\rho _{T,j}\) and \(\delta _j^2\) are defined as
where
\(L_\nu \) and \(L_F\) are parameters that can be arbitrarily chosen and correspond to the position of the neutrino and the light source particle at time \(t_f\). Note that, at \(t=0\), the heavy source particle is located in the origin of our reference system.
These quantities are intrinsically related to the localization of the neutrino production: classically, if we know all the masses and the momenta involved, the position of the light source particle at time t would determine the moment when the neutrino was created. However, in QFT, particles do not occupy a precise position in space, so instead of “position”, \(L_F\) would only determine the “region” where the neutrino was created, let’s call it \(\mathcal {R}_F\). Similarly \(L_\nu \) determines a different creation region for each mass eigenstate, \(\mathcal {R}_{\nu ,j}\). If all the \(\mathcal {R}_{\nu ,j}\)’s have a significant overlap with \(\mathcal {R}_F\), no mass eigenstate is suppressed and we would see the oscillations, otherwise we would have decoherence.
Let us write
where \(\delta L\), \(\tilde{t}_1\), \(v_{\nu ,0}\) and \(L_{F,0}\) are parameters. The final state depends only on two parameters, \(L_\nu \) and \(L_F\). The three equations in (3.10) provide three relations between these six parameters, and so only three are independent. We take \(\delta L\), \(\tilde{t}_1\) and \(v_{\nu ,0}\) to be the independent parameters. Since the final state depends only on \(L_\nu \), \(L_F\), there will be a degeneracy, i.e. different values of \(\delta L\), \(\tilde{t}_1\) and \(v_{\nu ,0}\) will correspond to the same final state.
The motivation for this parametrization is as follows. If you consider a classical two-body decay, the final position of the daughter particles depends only on the velocities of the particles and the decay time. If we identify \(\tilde{t}_1\) with the neutrino creation time and \(v_{\nu ,0}\) with the neutrino velocity, we can see that for \(\delta L=0\) the peaks of the wave packets of \(\phi _L\) and the neutrino are exactly in the position expected in the classical case. The main problem is that, while for \(\phi _{H}\) and \(\phi _{L}\) it is easy to identify the group velocity as the particle’s velocity in the classical limit, the neutrino is the superposition of two mass eigenstates, with different group velocities. The choice of \(v_{\nu ,0}\) is equivalent to choosing where we look for the neutrino at time \(t_f\) when \(\delta _L=0\): if we choose \(v_{\nu ,0}=v_{\nu ,1}\), this means that at \(t_f\) we are looking for the neutrino in the position where the mass eigenstate 1 will be. With this choice of the parameters (or a similar one, for example where \(v_{\nu ,0}=v_{\nu ,2}\)) it is easier to see how the decoherence emerges. First of all, we will be in a setting where, like in the classical case, the final state depends only on one parameter, \(\tilde{t}_1\), which is related to the baseline (with an ultrarelativistic neutrino, \(L\simeq t_f-\tilde{t}_1\)). Moreover it will be easier to see that, while \(\delta _1^2\) will be zero, if the separation between the wave packet will be non-negligible, \(\delta _2^2\) will grow, leading to a suppression of \({\mathcal {A}}_2\) and the emergence of decoherence. Of course, due to the degeneracy between \(\delta L\), \(\tilde{t}_1\) and \(v_{\nu ,0}\), even if \(v_{\nu ,0}=v_{\nu ,1}\) there will always be a value of \(\delta L\) for which \(\delta _2^2=0\), but it would be less straightforward to identify the case where only one of the two eigenstates is suppressed.
The transition probability \(P(t_f)\) (neglecting the multiplicative factor \(I_j\) which, as we pointed out, can be considered constant and independent of j) reads
The terms \(\delta ^2_j\) and \(\rho _{T,j}\), however, do not have a simple form and it would be difficult to compare Eq. (3.11) with other results available in literature. It is possible to simplify these expressions, however we must be careful. For example, one may be tempted to consider \(v_F\simeq v_I\simeq 0\), since usually the source particle is very heavy and non-relativistic. However in this case, assuming \(\delta L=0\), one obtains \(\delta ^2_j=0\). This is not surprising, since we have seen previously that we expect the dimension of the neutrino wave packet to be proportional to \(\sigma _I(v_I-v_F)\). If we consider \(v_F\simeq v_I\simeq 0\), this is equivalent to considering the neutrino to be completely delocalized, so the only suppression to the transition probability would come from the displacement of the final state of the source particle and not from the different velocities of the neutrino mass eigenstates.
For this reason, we will consider \(\sigma _\nu \simeq \sigma _I(v_I-v_F)\) and \(\sigma _F\simeq \sigma _I\). Assuming \(v_I, v_F\ll 1\) and considering only the leading order, Eq. (3.3) now reads
It is easy now to compute the denominator that appears in \(\delta _j^2\) and \(\rho _{T,j}\) at leading order
It should be noticed that there should be some additional terms, proportional to \(v_{\nu ,j}-1\). However, since we already know that the \(\delta _j^2\)’s depend on the difference between the velocities of the mass eigenstates, and \(\rho _{T,j}\) is proportional to \(\Delta m^2\), these terms would only contribute at the next-to-leading order, and they can be safely neglected.
Let us take a look at \(\delta _j^2\). We can safely neglect the term proportional to \(e_j^2\), since it goes like \((\Delta m^2)^2\). Taking into account Eq. (3.10), we have
where \(v_{\nu ,0}\) is the parameter introduced in Eq. (3.10) as the classical velocity of the neutrino. This term is the one that controls the decoherence. The term proportional to \(t_f-\tilde{t}_1\) is the one related to decoherence itself, i.e. the dampening of the oscillations due to the separation of the wave packets. As expected, it depends on the dimension of the neutrino wave packet (which is considerably smaller, in momentum space, with respect to the one of the source particle). We can also see that, if \(v_{\nu ,j}\ne v_{\nu ,0}\), for each \(\tilde{t}_1\) there is a specific value of \(\delta L\) that makes \(\delta _j^2\) vanish. This corresponds to the case where the shift due to the difference between the velocities and the shift with respect the classical position compensate each other.
Considering only the leading order, \(\rho _{T,j}\) is
3.1.1 \(\delta L_W=0\)
In order to simplify the calculations, let us choose \(v_{\nu ,0}=v_{\nu ,1}\). If \(\delta L_{W}=0\), then we have
where \(E=|q_0|\) is the neutrino energy, \(L\simeq t_f-\tilde{t}_1\) is the baseline for neutrino oscillations, \(\sigma _{x,\nu }=1/\sigma _{\nu }\) and, in the last step, we have used the approximation
We define \(L_{coh}\) as
Neglecting the multiplicative factor of 4, that contributes to the total rate but not to the oscillation probability, (3.11) can be written as
If the final state is localized, then, we will have decoherence, which would not be present if our final state \(|F\rangle \) were a momentum eigenstate as in Ref. [8]. In other words, decoherence occurs because the environment has constrained the position of \(\phi _L\). The reason for this can be found in Eq. (3.7), from which we can see that the localization of the final state implies a localization of the production time of the neutrino as well, similarly to the direct environmental constraint on the production time used in Sec. B.1 or in Ref. [7], where the time constraints are introduced directly in the Hamiltonian, by turning on the interactions only during a given time window.
We can see that the limit \(\tau \rightarrow \infty \), considered in [7], is equivalent to the limit
which would eliminate decoherence in the simple model we considered as well. Decoherence could still emerge, however, if the time of creation of the neutrino is determined more precisely: this is equivalent to the localization in space of the final state of the source particle \(\phi _L\) by environmental interactions.
3.1.2 \(\delta L \ne 0\)
Let us return to the case of an experiment in a vacuum. Imagine that the final state of \(\phi _L\) is not entangled to the environment. Then one needs integrate over all the possible values of its position \(\delta L\). We have
The transition probability as a function of \(\delta L\) reads
All the possible positions of the final state of the source particle should be summed incoherently, since they all correspond to a different final state. We have
where \(\sigma _{\nu ,x}=1/\sigma _q\). By integrating over \(\delta L\) we are taking into account all the possible production regions which would allow the neutrino to be detected in a certain point. This in equivalent to an uncertainty on the baseline, related to the finite dimension of the wave packets, as is found, for example in Refs. [19, 20]. In principle this would depend on the dimensions of all the wave packet involved. However, since \(\sigma _\nu \ll \sigma _I, \sigma _F\), the spatial dimension of the neutrino wave packet is considerably larger that the ones of the source particle (before and after the neutrino emission), so this term is dominated by \(\sigma _{\nu ,x}\).
There is still some decoherence when only the neutrino’s position is measured. This is to be expected as the neutrino position also contains information regarding the production time. We suspect that, including a detector as in Appendix B, the sensitivity of the final state position to the production time would be reduced. However, we will leave a methodical study of the irreducible decoherence expected in this case to a companion paper.
4 Second order expansion
Intuitively, decoherence emerges because different mass eigenstates travel at different velocities, and when the separation between the wave packets, which goes like \(\Delta v_{\nu ,ij}t\) becomes larger than the dimension of the wave packet, they no longer interfere. However, it is well known that the size of a Gaussian wave packet increases with time, since different p-components of the state will travel at different velocities as well. If we do not consider the time evolution, a Gaussian wave packet of dimension \(\sigma _p\) in momentum space will correspond, in momentum space, to a Gaussian wave packet of dimension \(\sigma _x=1/\sigma _p\). However, after a time t, each p-component of the wave packet will have acquired a different phase proportional to \(\mathcal {E}(p)\), which will affect the Fourier transform. Unfortunately, for massive particles it is not possible to obtain a closed-form expression for the time-evolved wave packet in coordinate space without using some approximations, namely expanding the energy as a Taylor series around \(p_0\) (peak of the wave packet in momentum space). If we consider only the first order expansion, like the one used in Eq. (2.12), we have
which means that all the p-components of the wave packet will travel at the same velocity. Using this approximation, the wave packet in coordinate space will simply be a Gaussian of dimension \(\sigma _x\) and centered around \(x_0=vt\).
If we consider the second order of the Taylor series, however, we have
The Fourier transform can be calculated explicitly, and we notice that now the dimension of the wave packet is no longer constant: \(\sigma _{x,t}=\sqrt{\sigma _x^2+(\sigma _p v't)^2}\). For simplicity, let us assume that \(v'\) will be roughly the same for all the mass eigenstates, the intuitive condition for decoherence we wrote before will now read
We can see now that, depending on the values of \(\Delta v_{\nu ,ij}\), \(\sigma _x\) and \(v'\) we have three regimes
-
If \(\Delta v_{\nu ,ij}\ll \sigma _p v'\), decoherence can never be dominant, since condition (4.3) can never be satisfied, indeed
$$\begin{aligned} \sqrt{\sigma _x^2+(\sigma _p v't)^2}> \sigma _p v't\gg \Delta v_{\nu ,ij}t \end{aligned}$$(4.4) -
If the opposite is true, \(\Delta v_{\nu ,ij}\gg \sigma _p v'\), then there is some value of \(t={t_f}\), such that for every \(t>{t_f}\), Eq. (4.3) is satisfied and the oscillations will be suppressed.
-
If \(\Delta v_{\nu ,ij}\simeq \sigma _p v'\), the separation of the wave packets will be partially canceled by their spread: the oscillations will be damped, but they will not disappear completely
Using our model, we will now confirm the conclusions of this intuitive argument. We will consider only the expansion of the neutrino energy up to the second order, while keeping only the terms up to the first order for the source particles (light and heavy). While \(E_0(p)\) remains the same, \(E_{1,i}(p-q,q)\) from Eq. (2.12) now reads
where
Since the additional term is proportional to \(\delta q^2\), we can incorporate it in \(G(\delta q, \sqrt{2}\sigma _q)\). This is equivalent to replacing \(\sigma _\nu \) with \(\tilde{\sigma }_\nu \)
If we assume again \(\sigma _F\simeq \sigma _I\) and \(\sigma _\nu \simeq \sigma _I(v_I-v_F)\), \(\sigma _p\) and \(\sigma _q\), as defined as in Eq. (3.3), now reads
Please notice that, in order to obtain this expression in the previous section, we assumed that \(\sigma _\nu \ll \sigma _I\simeq \sigma _F\). This assumption is not affected by the inclusion of the second order terms, since \(\text {Re}\Sigma ^2(t_1)<1\). We can now follow the same procedure used in the previous section, taking care to substitute \(\tilde{\sigma }_q\) for \(\sigma _q\) . The integration over \(t_1\) is not trivial, however, since now \(\tilde{\sigma }_q\) depends on \(t_1\) as well. If we ignore \(\Sigma (t_1)\) and if the wave packets are sufficiently peaked, the Gaussian over \(t_1\) can be approximated by \(\delta (t_1-\tilde{t}_1)\). Moreover if \(t_f-t_1\) is large, \(\Sigma (t_1)\rightarrow 0\), which does not affect the validity of such an approximation. We obtain then an expression similar to Eq. (3.11), where however now we have
where \(\Sigma _p=\Sigma (\tilde{t}_1)\). To simply the notation, let us define
where \(L=t_f-\tilde{t}_1\) is the baseline, assuming the neutrino is ultrarelativistic.
Please notice that the transition probability is always given by Eq. (3.11), regardless of the functional forms of \(\delta ^2_{s,j}\) and \(\rho _{Ts,j}\), as long as they are real. It should also be noticed, however, that since \(\Sigma _p^2\) is complex, now \(\delta _j^2\) will have an imaginary part as well, that will contribute to the oscillatory behavior. It is convenient then to define
Now the phase of each wave packet will change. This is not surprising, since it is proportional to the energy, and we are considering an additional term in the Taylor series. However this term can (and should, in order to be consistent with the approximations done so far) be neglected, since it is of the next-to-leading order in \(\Delta m^2\), and we have considered only the leading order in our calculation. Indeed, if we consider \(\delta L=0\), we have
since \(L_{coh}\propto 1/\Delta m^2\), \(\text {Im}(\delta _{s,2}^2)\propto (\Delta m^2)^2\) and is subdominant with respect to \(\rho _{Ts,2}\propto \Delta m^2\), which means that it can be neglected in the computation of the phase.Footnote 10 As a result, \(\rho _{Ts,2}-\rho _{Ts,1}\) has the usual expression, equal to that found in the previous section:
The transition probability now reads
When \(L_{sp}\rightarrow \infty \), we obtain exactly Eq. (3.19). If \(L\gg L_{sp}\), instead, the effect of the spreading of the wave packet cannot be neglected anymore: while \(\Sigma _p\rightarrow 0\), however \(\text {Re}(\Sigma _p^2 )L^2\rightarrow \text {const}\). \(\delta _{s,2}^2\) asymptotically takes the value
which means that, when \(L\ge L_{sp}\), the decoherence “saturates” and the oscillations are not damped further. Eq. (4.13) now reads
The three cases described at the beginning of this section correspond to \(L_{sp}\ll L_{coh}\), \(L_{sp}\gg L_{coh}\) and \(L_{sp}\sim L_{coh}\), respectively.
5 Remarks
Using a simplified model in 1+1d and containing only scalar fields we have shown that, if the initial and final states are localized, then the neutrino production time is limited and decoherence will emerge. This can be used to approximate the environmental interactions that in Nature would localize in space and time the position of the neutrino production and detection. In Appendix B, it can be seen that, even if we consider the full \(V-A\) 3+1d model, the difference would simply be a multiplicative factor that would not affect decoherence.
If the source particle is not in a momentum eigenstate, there will be an uncertainty on the neutrino momentum as well. However the spread of the neutrino wave packet will be considerably smaller than that of the source particle: it will be rescaled by a factor \(v_I-v_F\). If the source is non-relativistic (which would be the case, for example, for reactor neutrinos), this factor is very small. This provides a counterexample to one step in the argument of Ref. [9], where it was argued that decoherence can never be observed as it appears only when the detector’s energy resolution is too poor to see the oscillations.
Often in analytical calculations the energies of the particles are expanded only up to the first order in the momenta. A consequence of such an approximation is that each momentum component of the wave packet would travel at the same velocity. We have shown that, if the second order of the expansion is taken into account as well, the spread of the wave packet will prevent decoherence from completely canceling the oscillations, which would be damped but still present. It should be pointed out that such an exact compensation (namely, the fact that the spread of the wave packet, asymptotically, has the same t-dependence as the separation of the wave packets) is, most likely, an artifact of our approximation, i.e. considering only up to the second order of the expansion. If higher orders are taken into account as well, there could be regimes where the spreading is even faster than the separation of the wave packets, and the oscillation amplitude, after being suppressed, starts to grow again. This does not change the fact that, as we have shown, there are regimes where the spreading of the wave packets can qualitatively affect the decoherence.
The arguments here have been rather formal. How can they be converted into a quantitative estimate of neutrino decoherence?
In Appendix B we computed the decoherence resulting from a given time window. This can straightforwardly be generalized to a given space-time window for the production, and for the detection. One simply adds an environmental quantum number for each dimension and introduces an amplitude similar to (B.3) and (B.4) for each quantum number. Thus, if there is no preferred spatial direction, one expects an oscillated spectrum which depends on four decoherence parameters, the temporal and spatial window size at the production and the absorption point. Next, for any given environmental coupling, one can calculate these four parameters by calculating the corresponding amplitude. For this purpose, the production process and absorption processes may be considered separately, each yielding the corresponding two parameters.
In the literature, similar windows have been constructed. In the external wave packet approach [5], the allowed space-time window is constructed as the intersection of a set of rigid wave packets. The shape of this window is entirely determined by the kinematics of the particles directly involved in neutrino production and absorption and is independent of the kinematics of the particles in the environment. The presence of the environment is only encoded in the overall sizes of the wave packets. In some studies [21], on the other hand, a time window is used with no spatial constraint. These two approaches lead to specific constraints on the four parameters above, relating the temporal and spatial size of each window. However, we claim that the four parameters above are instead determined by the microphysics of the environmental interactions which need not obey such constraints. Thus we expect that such a full, microscopic approach will lead to a quantitative disagreement with previous studies.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This a theoretical calculation, there is no data].
Notes
Our notion of the environment, as described in Appendix A, is very general. It includes components of the source and detector.
This is not to be confused with classical decoherence, which was observed more than 20 years ago and arises from incoherent sums, as a result of distinct final states which cannot be distinguished due to limited energy resolution or a poor identification of the source location. For a recent review, see Ref. [12]. We also do not consider dissipative effects caused by new physics [13, 14].
The wave packet description of neutrinos arises from the same mechanism. The neutrino trajectories which lead to the same final state sum coherently and so can be treated as a coherent wave packet. A concrete connection between the finiteness of the spacetime production region and the neutrino wave packet in quantum field theory was provided in Refs. [15, 16].
The entanglement of these charged leptons with the neutrinos has been stressed in Ref. [17].
This does not necessarily imply that decoherence is observable when the momentum resolution is sufficient to observe oscillations, but rather it means that the question is still open.
It will increase linearly with \(t_f\), due to our tree-level approximation: indeed, the probability of the decay will increase linearly with \(t_f\), as long as \(t_f\ll \tau \), \(\tau \) being the lifetime of the source particle.
This is equivalent to assuming that the neutrino travels in the same direction as the source particle, after having chosen, by definition, such a direction to be the positive one.
To be precise, it should be far away from the boundaries, but as long as \(t_f\) is large, the difference will be negligible.
Intuitively this choice follows from the observation of Ref. [19] that environmental interactions have the effect of measuring the position of the final state of the unobserved particle \(\phi _L\).
It should be underlined that, on the other hand, terms proportional to \((\Delta m^2)^2\) are dominant in \(\delta _{s,j}^2\) and cannot be ignored there.
References
S. Nussinov, Solar neutrinos and neutrino mixing. Phys. Lett. 63B, 201 (1976). https://doi.org/10.1016/0370-2693(76)90648-1
B. Kayser, On the quantum mechanics of neutrino oscillation. Phys. Rev. D 24, 110 (1981). https://doi.org/10.1103/PhysRevD.24.110
J. Rich, The quantum mechanics of neutrino oscillations. Phys. Rev. D 48, 4318–4325 (1993). https://doi.org/10.1103/PhysRevD.48.4318
C. Giunti, C.W. Kim, J.A. Lee, U.W. Lee, On the treatment of neutrino oscillations without resort to weak eigenstates. Phys. Rev. D 48, 4310 (1993). https://doi.org/10.1103/PhysRevD.48.4310. arXiv:hep-ph/9305276
M. Beuthe, Oscillations of neutrinos and mesons in quantum field theory. Phys. Rep. 375, 105 (2003). https://doi.org/10.1016/S0370-1573(02)00538-0. arXiv:hep-ph/0109119
A. Kobach, A.V. Manohar, J. McGreevy, Neutrino oscillation measurements computed in quantum field theory. Phys. Lett. B 783, 59 (2018). https://doi.org/10.1016/j.physletb.2018.06.021. arXiv:1711.07491 [hep-ph]
W. Grimus, Revisiting the quantum field theory of neutrino oscillations in vacuum. J. Phys. G 47(8), 085004 (2020). https://doi.org/10.1088/1361-6471/ab716f. arXiv:1910.13776 [hep-ph]
E. Ciuffoli, J. Evslin, H. Mohammed, Approximate neutrino oscillations in the vacuum. Eur. Phys. J. C 81(4), 325 (2021). https://doi.org/10.1140/epjc/s10052-021-09110-y. arXiv:2001.03287 [hep-ph]
Oscillations and decoherence, K.T. McDonald, Talk at NuFact 2013, August 23, 2013, Beijing, China. Based on: http://puhep1.princeton.edu/~mcdonald/examples/neutrino_osc.pdf
J.A.B. Coelho, W.A. Mann, Decoherence, matter effect, and neutrino hierarchy signature in long baseline experiments. Phys. Rev. D 96(9), 093009 (2017). https://doi.org/10.1103/PhysRevD.96.093009. arXiv:1708.05495 [hep-ph]
A.L.G. Gomes, R.A. Gomes, O.L.G. Peres, Quantum decoherence and relaxation in neutrinos using long-baseline data. arXiv:2001.09250 [hep-ph]
T. Cheng, M. Lindner, W. Rodejohann, Microscopic and macroscopic effects in the decoherence of neutrino oscillations. JHEP 08, 111 (2022). https://doi.org/10.1007/JHEP08(2022)111. arXiv:2204.10696 [hep-ph]
E. Lisi, A. Marrone, D. Montanino, Probing possible decoherence effects in atmospheric neutrino oscillations. Phys. Rev. Lett. 85, 1166–1169 (2000). https://doi.org/10.1103/PhysRevLett.85.1166. arXiv:hep-ph/0002053
F. Benatti, R. Floreanini, Open system approach to neutrino oscillations. JHEP 02, 032 (2000). https://doi.org/10.1088/1126-6708/2000/02/032. arXiv:hep-ph/0002221
E.K. Akhmedov, J. Kopp, Neutrino oscillations: quantum mechanics vs. quantum field theory. JHEP 04, 008 (2010). https://doi.org/10.1007/JHEP04(2010)008. arXiv:1001.4815 [hep-ph]. [Erratum: JHEP 10, 052 (2013)]
E.K. Akhmedov, A.Y. Smirnov, Neutrino oscillations: entanglement, energy–momentum conservation and QFT. Found. Phys. 41, 1279–1306 (2011). https://doi.org/10.1007/s10701-011-9545-4. arXiv:1008.2077 [hep-ph]
A.G. Cohen, S.L. Glashow, Z. Ligeti, Disentangling neutrino oscillations. Phys. Lett. B 678, 191–196 (2009). https://doi.org/10.1016/j.physletb.2009.06.020. arXiv:0810.4602 [hep-ph]
J. Evslin, H. Mohammed, E. Ciuffoli , Y. Zhou, Eur. Phys. J. C 79(6), 491 (2019). https://doi.org/10.1140/epjc/s10052-019-7009-8. arXiv:1902.03934 [hep-ph]. [Erratum: Eur. Phys. J. C 80(3), 253 (2020)]
C. Giunti, JHEP 11, 017 (2002). https://doi.org/10.1088/1126-6708/2002/11/017. arXiv:hep-ph/0205014
C. Giunti, C.W. Kim, U.W. Lee, Phys. Lett. B 421, 237–244 (1998). https://doi.org/10.1016/S0370-2693(98)00014-8. arXiv:hep-ph/9709494
K. Kiers, N. Weiss, Neutrino oscillations in a model with a source and detector. Phys. Rev. D 57, 3091–3105 (1998). https://doi.org/10.1103/PhysRevD.57.3091. arXiv:hep-ph/9710289
W. Grimus, P. Stockinger, Real oscillations of virtual neutrinos. Phys. Rev. D 54, 3414–3419 (1996). https://doi.org/10.1103/PhysRevD.54.3414. arXiv:hep-ph/9603430
Acknowledgements
JE is supported by the CAS Key Research Program of Frontier Sciences grant QYZDY-SSW-SLH006 and the NSFC MianShang grants 11875296 and 11675223. EC is supported by the Chinese Academy of Sciences Presidents International Fellowship Initiative Grant No. 2020FYM002. JE and EC also thank the Recruitment Program of High-end Foreign Experts for support.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: What is the environment?
In this paper we consider various models of neutrino production and, in Appendix B, also detection. These models contain the following elements. First there is a particle which emits the neutrino, and in Appendix B also a particle which absorbs the neutrino. The emission and absorption are accompanied by the creation of one or two particles in each setup. There is also the neutrino itself. These particles are always present and we assume that they are always in their ground states. If these are the only particles present, then we say that the experiment is performed in a vacuum. If there is decoherence in the neutrino oscillations in this setup, we call this decoherence intrinsic decoherence. This can be calculated within the Standard Model. However, it is not the subject of the present paper.
The present paper is instead concerned with any other particles which may be present. All such particles are referred to as the environment. As explained in the Introduction, one expects such particles to be important because the probability of any outcome consists of an incoherent sum over all orthogonal final states, whereas histories which lead to the same final state are summed coherently. These final states include the quantum numbers associated with the environment. Therefore, if the two neutrino mass eigenstates lead to differing final states for the environment, they will be summed incoherently and decoherence will result.
The most obvious mechanism by which the final state of the environment may depend on the neutrino mass eigenstate is as follows. Distinct mass eigenstates have distinct masses, and so distinct velocity distributions. As the baseline traveled is essentially independent of the mass eigenstate, the travel time \(t_2-t_1\) will depend on the mass eigenstate. At the times \(t_1\) and \(t_2\) the particles associated with neutrino emission and absorption change radically, for example in general they change their charge. This will necessarily affect the environmental particles, and the effect will depend on \(t_1\) and \(t_2\). Thus each final state of the environmental particles will correspond to some window of \(t_1\) and \(t_2\). In Appendix B the final states corresponding to given windows will be labeled by integral quantum numbers I and J.
Appendix B: \(V-A\) 3+1 model
1.1 B.1 Defining the amplitude in the \(V-A\) model
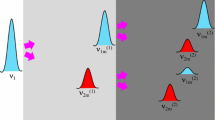
In this section, we will consider a setup similar to that of Ref. [7]. It is an initial value problem in quantum field theory, beginning at time \(t=0\) and ending at time \(t={t_f}\). The initial state is fixed at time \({0}\) and we will calculate the probability of various final states at time \({t_f}\). We describe the emission of an antineutrino in the \(\beta \)-decay process
at time \(t_1\) followed by its absorption via inverse \(\beta \)-decay
at time \(t_2\), all in the \(V-A\) model. The total process is drawn in Fig. 2.
While Ref. [7] considers this process in a vacuum, we do not. Instead, we consider the system coupled to an environment in the following approximation. The environment does not affect the system, however the final state of the environment depends on \(t_1\) and \(t_2\). More precisely, the final state of the environment is described by two integer quantum numbers \(|IJ\rangle \). If the neutrino is emitted at time \(t_1\) then the amplitude for the first quantum number to have a fixed value I is
where \(\sigma \) is a real parameter, the only parameter in our model. Similarly, if the neutrino is absorbed at time \(t_2\) then the amplitude for a fixed second quantum number J is
In other words, the final state of the environment will be \(|IJ\rangle \) if the times \(t_1\) and \(t_2\) are close to \(\tau _{S,I}\) and \(\tau _{D,J}\) respectively, where close means a distance of order \(\sigma \). In particular, the neutrino travel time \(t_2-t_1\) will be close to \(t_f+(J-I)\sigma \). This means that the neutrino velocity for a given final state depends on \(J-I\). For a given neutrino momentum distribution, and a given mass eigenstate, this velocity may or may not be consistent with the on-shell condition. If it is not, this value of \(J-I\) leads to a suppression in the corresponding contribution to the amplitude. If the suppression depends strongly on the mass eigenstate, it will lead to decoherence.
The initial value problem is then completely determined by the initial condition. The initial condition is that the heavy source and light detector particles are described by the wave functions \(\psi _S\) and \(\psi _D\), so that the initial state is
In signature (+, −, −, −), we may then write the amplitude for the final state with momenta \(p^\prime ,\ p^\prime _e,\ k^\prime \) and \(k^\prime _e\) and environmental final state \(|IJ\rangle \). It is

where J is the usual hadronic form factor [7]
Here \(m_j\) is the mass of the jth neutrino mass eigenstate, which is related to the electron via the element \(U_{ej}\) of the PMNS matrix.
Unlike Ref. [7], we consider neither the finite lifetime of the source nor the data taking time, as the author of that paper showed that neither has a significant effect on decoherence. Our scale \(\sigma \), in order to be phenomenologically relevant, must be much shorter than both of these scales.
1.2 B.2 Evaluating the amplitude
Integrate over \(\vec {x}_1\) and \(\vec {x}_2\)

Define
and then integrate over p and k

Now integrate over \(t_1\) and \(t_2\)

We define
where \({\hat{L}}\) is a unit vector. At large L, using the Grimus–Stockinger Theorem [22]
Let us try the \(\vec {q}\) integral directly on (B.11)

where it is understood that \(E^j_S\) and \(E^j_D\) are evaluated at \(\vec {q}=\sqrt{q_0^2-m_j^2}{\hat{L}}\)
In particular at \(I=J=0\), we find

Let us ignore the flavor dependence of the recoil (since the difference between two mass eigenstates would be proportional to \(\Delta m_{ij}^2/(m_Pq_0)\ll 1\)), by removing the j superscripts from \(E_S\) and \(E_D\) and fixing
where m is of order \(m_j\). Now assume that the Gaussians on the third line have a much steeper dependence on \(q_0\) then the other terms. By completing the squares, it is possible to rewrite the two Gaussian as one. Let us expand around a certain value of \(q_0\), \({\hat{q}}_0\), which will be chosen in a moment:
Let us also define
The exponents of the two Gaussian can be written as
and \({\hat{q}}_0\) can be determined by imposing
Defining
we can write
for some functions \(c_j\) which depend only weakly on j. Indeed, the dependence of \(c_j\) on the mass eigenstate arises from the following terms
-
\(\psi _S\left( \sqrt{q_0^2-m_j^2}{\hat{L}}+\vec {p}^\prime +\vec {p}^\prime _e\right) \) and \(\psi _D\left( -\sqrt{q_0^2-m_j^2}{\hat{L}}+\vec {k}^\prime +\vec {k}^\prime _e\right) \). However, in order to see the oscillations the energy width of the source and the energy resolution of the detector should not allow us to discriminate between two different mass eigenstates directly. Moreover, the fractional dependence is of order \(\Delta m^2/q_0^2\), which is of order \(10^{-15}\) or less. So these terms can be neglected.
-
The hadronic currents, \(J_{S}^\lambda \left( \vec {p}^\prime ,\sqrt{q_0^2-m_j^2}{\hat{L}}+\vec {p}^\prime +\vec {p}^\prime _e\right) \) and \(J_{D}^\rho \left( \vec {k}^\prime ,-\sqrt{q_0^2-m_j^2}{\hat{L}}+\vec {k}^\prime +\vec {k}^\prime _e\right) \). These are related to the cross section for the neutrino production and absorption. The different mass eigenstates would change the on-shell momenta, but such a difference would be extremely small (for example, in reactor neutrino experiment it would be of the order of \(10^{-9}-10^{-10}\) eV), so it would not significantly change the amplitude, and these terms can be considered independent of j.
-
The neutrino propagator, i.e.
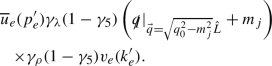 (B.24)
(B.24)Here it should be noticed that the term proportional to the mass eigenstate is identically zero, only the term proportional to
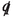 will remains. Since the direction of the momentum is fixed, the expansion in \(m_j\) can be written as
will remains. Since the direction of the momentum is fixed, the expansion in \(m_j\) can be written as 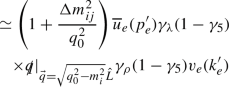 (B.25)
(B.25)where \(m_i\) is one of the neutrino mass eigenvalues that can be chosen arbitrarily. The fractional j dependence in the first term is again of order \(\Delta m^2/q_0^2\).
Moreover, all these microscopic terms are not multiplied by any macroscopic quantity, such as the baseline L, unlike the phase, so they can be safely ignored.
We can complete the square and, after performing the last integral and absorbing the complex Gaussian factor in the \(c_j\)’s, we have
or more generally
Note that the Gaussian resulting from the \(\delta q_0\) integration in Eq. (B.23) is complex and contains the oscillation phases.
We see that the Gaussian for each flavor j is suppressed if the corresponding flavor of neutrino, at velocity \(v_j\), did not travel a distance \(L/v_j\) in a time within \(\sigma \) of \({t_f}+(J-I)\sigma \). For each flavor there will be some expected arrival time, and so some \(J-I\) which is not suppressed, but the value of the unsuppressed \(J-I\) will depend on the flavor j. In particular, the unsuppressed \(J-I\) will be
1.3 The probability
Now the probability is
The cross terms between different flavors \(j_1\) and \(j_2\) will be suppressed by Gaussians if the corresponding \((J-I)_j\) differ, which occurs if
In the absence of cross terms, there will be no oscillations. Therefore we find decoherence in neutrino oscillations when the coherence windows \(\sigma \) are sufficiently small or the baseline L is sufficiently large.
In Ref. [7], the decoherence was lost above Eq. (61) when the Gamma term was dropped, making the time interval of creation infinite. In Ref. [6], the effect here is present in their Eq. (27): Notice that the norm of the amplitude is maximized when the creation occurs at time 0, and the detection occurs at a time corresponding to the neutrino propagation time for a given mass eigenstate. However this time will not agree for different eigenstates, and so the cross terms will be suppressed by the exponential factors in (27). Similarly in Ref. [8] no oscillations were present as there was no constraint on either the creation or the detection times.
In the ultrarelativistic limit, Eq. (B.30) is very familiar. The left hand side becomes the velocity difference and L is the propagation time. Interpreting \(\sigma \) as the spatial size of the neutrino wave packets, this is just the old statement that decoherence appears when the wave packets have separated. Another interpretation, whose consistency with the uncertainty principle merits investigation, is that decoherence occurs when \(\sigma \) is less than the inverse of the energy resolution required to observe neutrino oscillations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Ciuffoli, E., Evslin, J. Where neutrino decoherence lies. Eur. Phys. J. C 82, 1097 (2022). https://doi.org/10.1140/epjc/s10052-022-11090-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-11090-6





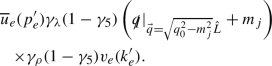
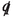 will remains. Since the direction of the momentum is fixed, the expansion in
will remains. Since the direction of the momentum is fixed, the expansion in