1 Introduction

The precise determination of the electromagnetic form factors (EMFFs) of the nucleon has become an urgent task since the emergence of notable “proton radius puzzle” in 2010, namely the tension between the muonic determination of proton charge radius and previous measurements based on the electron-proton scattering and hydrogen spectroscopy [1,2,3], though it must be said that the dispersion theoretical analysis of the scattering data always led to a value consistent with the one from muonic hydrogen, see the discussion in Ref. [4]. The nucleon EMFFs are accessed experimentally through elastic electron-proton scattering \(e^-p\rightarrow e^-p\) as well as electron scattering on light nuclei (as no neutron target exists) for the space-like region, and the \({\bar{p}}p\) annihilation process \({\bar{p}}p\rightarrow e^+e^-\) and likewise the reactions \(e^+e^-\rightarrow {\bar{p}}p\) and \(e^+e^-\rightarrow {\bar{n}}n\) for the time-like region (see, e.g., Refs. [5,6,7] for recent reviews). In this context, some impressive experimental results have been reported over the last decade. The PRad collaboration measured the differential cross sections of \(e^- p\) scattering down to an unprecedented momentum transfer of \(Q^2=2.1\times 10^{-4}\) GeV\(^2\) [8] while the BaBar [9] and BESIII [10,11,12,13] collaborations measured the total cross sections for \(e^+e^-\rightarrow {\bar{p}}p\) over a large range of center-of-mass energies. And still many experimental and theoretical efforts continue. On the theoretical side, we mention in particular a high-precision dispersion-theoretical analysis of the world data of the nucleon EMFFs in the space- and time-like regions that was reported in Ref. [14] last year. The statistical uncertainties of the extracted form factors were estimated using the bootstrap method, while systematic errors were determined from variations of the spectral functions. This work further solidified the earlier findings of a small proton charge radius \(r_p = 0.84\,\)fm with subpercent accuracy.

There has also been increasing interest in the electromagnetic structure of hyperons in the past two decades, both from the experimental [15,16,17,18,19,20,21,22,23,24,25] and theoretical [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41] side. Compared to the nucleon, the development of experiments exploring the hyperon EMFFs is somewhat lagging behind since the hyperons are unstable. Therefore hyperon targets for elastic electron scattering experiments that access the EMFFs of hyperons in the spacelike region are not available. The main source of information are measurements of the reaction \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \) that depends on the EMFFs in the time-like region. For a recent review of the current experimental status on \(\Lambda \) EMFFs see Ref. [42]. A recent improvement of the data base is provided by the cross section for \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \) around 4 GeV reported by the BESIII Collaboration last year [25]. It enriches the data base of the \(\Lambda \) EMFFs, which previously only covered the near-threshold region, to a great extent.

To date, only a subset of these \({\bar{\Lambda }}\Lambda \) data has been studied theoretically [29, 30, 32, 39,40,41]. In particular, the previous near-threshold data were analyzed in Refs. [29, 39], which used phenomenological \({\bar{Y}}Y\) potential models, that are constrained by final-state interaction (FSI) effects in reactions like \({\bar{p}}p\rightarrow {\bar{Y}}Y\), to calculate the EMFFs of hyperons. Moreover, Ref. [30] utilized Fano-type form factors, that include the interference between several resonances and one continuum background constructed based on perturbative QCD (pQCD) predictions, to fit those data near threshold. This analysis found that the excited \(\phi \) meson \(\phi (2170)\) is required to reproduce the close-to-threshold enhancement observed in the \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \) reactions. Similar interpretations were also investigated in Refs. [32, 40] using the vector meson dominance (VMD) parameterization for the EMFFs of the \(\Lambda \) hyperon. In contrast, the work of Ref. [41] only focused on the newest measurements around 4 GeV by the BESIII group. It was found that the dip near the mass of \(\psi (3770)\) in the cross sections of \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \) gets contributions from both D-meson loops and the three gluon charmonium annihilation mechanism.

The present work seeks to obtain a fit to the full data basis of \({\bar{\Lambda }}\Lambda \) production data collected so far based on dispersion theory [43,44,45,46]. The spectral function of the EMFFs is parametrized in terms of narrow and broad vector meson poles and includes the constraints from unitarity, analyticity and crossing symmetry. Moreover, it is consistent with the strictures from pQCD at very large momentum transfer [47]. The uncertainties in the extracted form factors are estimated by means of the bootstrap sampling method. We already note here that for an estimation of the systematic uncertainty, which can be accessed by varying the number of poles in the spectral function [4, 45], the data base is simply too sparse. A recent review of the dispersion-theoretical formalism is given in Ref. [4]. Here we extend this dispersive strategy to the hyperon cases in a straightforward way.

The paper is organized as follows: in Sect. 2 the total cross section of the process \(e^+e^- \rightarrow \Lambda {\bar{\Lambda }}\) in Born approximation is presented and the details of the dispersion-theoretical parameterization of the electromagnetic form factors of \(\Lambda \) hyperon as well as the fit strategy are illustrated. Section 3 contains the numerical results for the EMFFs of the \(\Lambda \) hyperon and their discussion. A summary and conclusion is given in Sect. 4.

2 Formalism

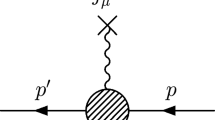
We briefly introduce the basic formulae for the analysis of the EMFFs of the \(\Lambda \) hyperon in the dispersion-theoretical framework. When assuming one-photon exchange as the sole contribution, the so-called Born approximation, the total cross section of the annihilation reaction \(e^+e^-\rightarrow {\bar{Y}}Y\) can be written as [39],

$$\begin{aligned}{} & {} \sigma _{e^+e^-\rightarrow {\bar{Y}}Y}\nonumber \\{} & {} \quad =\frac{4\pi \alpha ^2\beta }{3s}C(s) \left[ |G_M(s)|^2+\frac{2m_Y^2}{s}|G_E(s)|^2\right] , \end{aligned}$$
(1)

where \(Y=\Lambda \), \(\Sigma \), \(\Xi \) denotes the hyperons with \({\bar{Y}}\) the corresponding anti-hyperons. Moreover, \(\alpha \approx 1/137.036\) is the fine-structure constant and \(\beta =k_Y/k_e\) denotes a phase-space factor. Here, \(k_Y\) and \(k_e\) are the moduli of the center-of-mass three-momenta in the outgoing \({\bar{Y}}Y\) and incoming \(e^+e^-\) systems, satisfying \(s=4(m_Y^2+k_Y^2)=4(m_e^2+k_e^2)\), with \(\sqrt{s}\) the total energy and \(m_Y\) (\(m_e\)) the hyperon (electron) masses. C(s) represents the S-wave Sommerfeld–Gamow factor defined by \(C=y/(1-e^{-y})\) with \(y=\pi \alpha m_Y/k_Y\). Note that \(C(s)\equiv 1\) for the neutral hyperons (\(\Lambda \), \(\Sigma ^0\), \(\Xi ^0\)). The complex functions \(G_E(s)\) and \(G_M(s)\) are the Sachs electric and magnetic form factors of the hyperons in the time-like region. They are accessible in this reaction for \(s\ge 4m_Y^2\). When the functions are analytically continued to negative values of s, i.e. to the space-like region, they are real and describe the elastic scattering of electrons of the hyperons. The variable \(-s\equiv Q^2\) then specifies the four-momentum transfer \(Q^2\) in the elastic scattering process.

Since the separation of \(G_E\) and \(G_M\) requires angular distributions, the time-like experimental data is often given in the form of the effective form factor \(G_\textrm{eff}\), which is defined by

$$\begin{aligned} |G_\textrm{eff}(s)|=\sqrt{\frac{\sigma _{e^+e^-\rightarrow {\bar{Y}}Y}(s)}{\frac{4\pi \alpha ^2\beta }{3s}C(s)\left( 1+\frac{2m_Y^2}{s}\right) }}. \end{aligned}$$
(2)

When employing the dispersion-theoretical analysis, it is convenient to express the Sachs form factors in terms of the Dirac (\(F_1\)) and Pauli (\(F_2\)) form factors,

$$\begin{aligned} G_M=F_1+F_2,\quad G_E=F_1+\frac{s}{4m_Y^2}F_2, \end{aligned}$$
(3)

with the normalization at zero momentum transfer given by \(F_1(0)=G_E(0)=0\) and \(F_2(0)=G_M(0)=\mu _{\Lambda }\) for the electrically neutral \(\Lambda \) hyperon. Here \(\mu _\Lambda =-0.613{\hat{\mu }}_N=-0.723{\hat{\mu }}_\Lambda \) is the magnetic moment of the \(\Lambda \) hyperon [49] with \({\hat{\mu }}_N\equiv e/(2m_N)\) and \({\hat{\mu }}_\Lambda \equiv e/(2m_\Lambda )\).

The strategy of the dispersion-theoretical analysis for the EMFFs of the \(\Lambda \) hyperon is quite similar to the nucleon case which is explained comprehensively in the review [4]. The dispersion relation for a generic form factor F(s) is written as

$$\begin{aligned} F(s)=\lim _{\epsilon \rightarrow 0^+}\frac{1}{\pi }\int _{s_0}^\infty d s^\prime \frac{\textrm{Im}~F(s^\prime )}{s^\prime -s-i\epsilon }, \end{aligned}$$
(4)

where \(\textrm{Im}~F\) in the time-like region, also called the spectral function, is required as input. Furthermore, \(s_0\) denotes the threshold of the lowest cut of the form factor F(s). In the nucleon case, \(s_0=4M_\pi ^2~(9M_\pi ^2)\) for the isovector (isoscalar) form factors. For the \(\Lambda \) hyperon, there is only an isoscalar contribution, i.e., \(F^\Lambda _i=F_i^s\) with \(i=1,2\) and \(s_0=9M_\pi ^2\), since the \(\Lambda \) is a isospin singlet. The contribution of the three-pion cut is expected to be small except for the \(\omega \) contribution. See Ref. [48] for an explicit calculation in the nucleon case, which shows that the anomalous threshold in the three-pion channel is effectively masked by the phase space behavior.

Therefore, the spectral functions for the \(\Lambda \) isoscalar FFs are parameterized as a sum of effective vector meson poles, narrow delta function poles on the real axis and broad delta function poles in the complex plane, without any explicit continuum contributions. This leads to the following representation of the FFs:

$$\begin{aligned} F_i^s(s)&=\sum _{V=\omega ,\phi ,s_1,\cdots }\frac{a_i^{V\Lambda \Lambda }}{M_V^2-s-i\epsilon }\nonumber \\&\quad +\sum _{V=\phi _{2170},\psi _{3770},S_1,\cdots }\frac{a_i^{V\Lambda \Lambda }}{M_V^2-s-iM_V\Gamma _V},i=1,2. \end{aligned}$$
(5)

The residues \(a_i^{V\Lambda \Lambda }\) must be real in order to ensure a real spectral function. Here, the broad vector meson poles are introduced to generate the non-zero imaginary part of the EMFFs of the \(\Lambda \) in the timelike region. In the narrow sector, two physical states, the \(\omega \) and \(\phi \) mesons, are included as in our previous analyses to the nucleon EMFFs [4, 14]. Following the previous studies on the \({\bar{\Lambda }}\Lambda \) data in the near-threshold region [30, 32, 40] and works on the newest BESIII data set around 4 GeV [25, 41], the \(\phi (2170)\) and \(\psi (3770)\) states are included in the broad sector. The PDG values [49] for the masses and widths of those physical vector states are used as input in our analysis. The fit parameters are therefore the various meson residua \(a_i^{V\Lambda \Lambda }\) and the masses and widths of the additional vector mesons \(s_i\), \(S_i\). Since these parametrize continuum contributions, we require the widths of the \(S_i\) to be larger than the width of the physical \(\psi (3770)\). Finally, several physical constraints are included in the parametrizations of Eq. (5). First, two normalization conditions for the values of FFs at zero momentum transfer must be fulfilled. Second, three constraints from the superconvergence relations inferred from the pQCD predictions for the asymptotic behavior of the EMFFs are taken into account. They are given by

$$\begin{aligned} \int _{s_0}^\infty \textrm{Im}~F_i^s(s) s^n ds=0, \quad i=1,2, \end{aligned}$$
(6)

with \(n=0\) for \(F_1^s\) and \(n=0,1\) for \(F_2^s\). These relations ensure the correct fall-off with inverse powers of s at large space-like momentum transfer s as predicted by pQCD [47], i.e., \(F_1^s\sim 1/s^2\) and \(F_2^s\sim 1/s^3\). Small logarithmic corrections to the power law behavior are neglected. Third, the electric charge radius of the \(\Lambda \) hyperon is fixed to the value \(\langle r_E^2\rangle =0.11\pm 0.02~\textrm{fm}^2\) that was calculated in chiral perturbation theory [50]. This constraint is useful since the energy region covered by the time-like data starts at \(s=4m_\Lambda ^2\) and thus the slope at \(s=0\) can not be constrained well by them. In principle, one could also introduce the corresponding magnetic radius \(\langle r_M^2\rangle \) as a constraint. However, \(\langle r_M^2\rangle \) has a significantly larger absolute uncertainty since the rather poorly known LECs \(b_9\), \(b_{10}\), and \(b_{11}\) contribute [50]. Therefore, it is less useful as a constraint and we make a prediction from the fit instead.

Fig. 1
figure 1

Results of the fit to the full data sets for the total cross sections of the reaction \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \) that taken from Refs. [15, 16, 18, 20, 21, 25]. Left panel: comparison between Fit-I (dashed line) and Fit-II (solid line). Right panel: Fit-II with the error band given by the bootstrap method. The \({\bar{\Lambda }}\Lambda \) threshold is represented by the vertical dash-dotted lines

Full size image

Our previous work on the nucleon form factors [4, 14] emphasized that the two-pion continuum plays an important role to describe the nucleon isovector radii [51]. However, in the timelike region above the two nucleon threshold, these effects are small and the form factors are mainly determined by the effective vector meson poles [4, 14]. In the present work, we only analyzed the \(\Lambda \) form factor data in the time-like region and above the \(\Lambda {\bar{\Lambda }}\) threshold. Therefore one can safely assume that the effective vector poles located above 1 GeV contribute dominantly. Whether the continuum contributions play a similar role for the radii as in the nucleon case is an open question that is beyond the scope of this work. These contributions are not well known for the \(\Lambda \) form factors. Once more experimental information becomes available, the explicit inclusion of continuum contributions obtained from other processes would be desirable.

Table 1 Comparison between the Fit-I and Fit-II. Fit-II is our preferred fit. The \(\ddagger \) represents an input quantity that was fixed to the physical state from PDG [49] (mass and width are constant in the fit)
Full size table

3 Fit strategy and results

The first step is to find the best configuration for the EMFFs of the \(\Lambda \) hyperon, i.e., the numbers of the narrow poles \(s_i\) and the broad poles \(S_i\) in Eq. (5). We start by including only the narrow physical poles (\(\omega \) and \(\phi \) mesons) with fixed masses while the \(\phi (2170)\) and \(\psi (3770)\) states are not included a priori. In the second step, we increase the numbers of narrow poles \(s_i\) and broad poles \(S_i\) one by one. All pole masses except those of the \(\omega \) and \(\phi \) poles and all residua are fit parameters. Using this procedure, the database for the \({\bar{\Lambda }}\Lambda \) production composed of the measurements by the DM2 [15], BaBar [16], CLEO [18] and BESIII [20, 21, 25] collaborations is fitted with 7 constraints: 2 normalization conditions, 3 superconvergence relations, and 1 radius condition for \(\langle r_E^2\rangle \).

We find that at least one additional narrow and three broad poles are required for an acceptable \(\chi ^2\) in the fit. The reduced \(\chi ^2\) for the best fit is 1.531. In this fit the EMFFs of the \(\Lambda \) hyperon get contributions from 6 pole terms: \(\omega \), \(\phi \) and \(s_1(2014)\) in the narrow part and \(S_1(2232)\), \(S_2(3760)\) and \(S_3(4170)\) in the broad part. We refer to this fit as Fit-I. It is displayed as the dashed line in the left panel of Fig. 1. Comparing the pole masses to the mass spectra for the light vector mesons and charmonia (\(c{\bar{c}}\)) listed in PDG [49], the effective narrow pole \(s_1(2014)\) and the broad pole \(S_1(2232)\) obtained in the fit are close to the physical \(\phi (2170)\) state (\(M=2162\pm 7\) MeV and \(\Gamma =100^{+31}_{-23}\) MeV). Moreover, the \(S_2(3760)\) and \(S_3(4170)\) poles are quite close to the charmonium states \(\psi (3770)\) (\(M=3773.7\pm 0.4\) MeV and \(\Gamma =27.2\pm 1.0\) MeV) and \(\psi (4160)\) (\(M=4191\pm 5\) MeV and \(\Gamma =70\pm 10\) MeV), respectively. When the \(\phi (2170)\), \(\psi (3770)\) and \(\psi (4160)\) states are included as broad poles with fixed masses in the spectral function, one gets a relatively large reduced \(\chi ^2\) of 3.877. The main contribution to the \(\chi ^2\) comes from the data set reported in Ref. [25] (labeled as BESIII(2021) in the following). Our analysis suggests that the contribution to the \(\chi ^2\) of the data set BESIII(2021) is quite sensitive to the parameters of the effective poles located in the energy region of the data. This is because there are large statistical fluctuations in this data set, especially in the region above 4 GeV, which was also noticed in Ref. [52].

Because of these observations, we focus in the following on the choice of the \(\Lambda \) spectral function where the two physical mesons (\(\omega \) and \(\phi \)) and one floating effective pole \(s_1\) are contained in the narrow sector and the \(\phi (2170)\) and \(\psi (3770)\) states with fixed masses together with one additional floating pole \(S_1\) make up the broad sector (the best solution for this choice of spectral function is labeled as Fit-II).

Table 2 The parameters corresponding to our best fit (Fit-II) together with the bootstrap errors. Masses \(M_V\) and widths \(\Gamma _V\) are given in units of GeV and residua \(a_i^V\) in \(\mathrm GeV^2\). The \(\ddagger \) indicates that the corresponding parameter was taken as input and is not fitted
Full size table

A comparison between the pole content and results of Fit-I and Fit-II is given in Table 1 and Fig. 1, respectively. The reduced \(\chi ^2\) of Fit-II is 2.596 which is compatible with the “Fit I” implemented by the BESIII Collaboration in their experimental announcement [25]. The uncertainties are estimated by using the bootstrap sampling method. As one can see from the right panel of Fig. 1, all measurements for the reaction \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \) can be described well by Fit-II. Note that the oscillation in the near-threshold region generated by the interference of \(s_1(2011)\) and \(S_1(2232)\) in Fit-I is gone. In Fit-I, the data point in BESIII(2018) [20] close to threshold is reproduced by that oscillation in agreement with the finding of Ref. [40].

We replace this feature with the simpler single-pole contribution from the physical state \(\phi (2170)\) in Fit-II since such an oscillation can not be confirmed definitely by the current experiments. This is in conjunction with the general strategy to use as few poles as possible to stabilize the ill-posed problem of reconstructing the spectral function from experimental data [53, 54]. However, a further experimental investigation of this issue is required in the future. Furthermore, a pole located around 4.163 GeV is suggested by Fit-II which could be identified with the physical state \(\psi (4160)\). Its mass is, however, outside the mass range for the \(\psi (4160)\) quoted in PDG [49]. The physical information regarding this pole will be more clear if the statistical fluctuations in BESIII(2021) data can be reduced. In this fit, we use the electric radius of the \(\Lambda \) hyperon as input, \(r_E=\sqrt{\langle r_E^2\rangle }={0.332}~\textrm{fm}\) from Ref. [50] to have some constraint from the space-like region. The magnetic radius of the \(\Lambda \) hyperon derived from Fit-II is then given by

$$\begin{aligned} r_M=0.681\pm 0.002~\textrm{fm}~. \end{aligned}$$
(7)

The obtained magnetic radius is a bit larger than the value in Ref. [32], \(r_M=0.42\) fm but also the electric radius given there is smaller than the CHPT determination, \(r_E=0.11\) fm. The fit parameters of Fit-II are presented in Table 2 together with the bootstrap error bars. For convenience, we also show the effective form factor \(|G_\textrm{eff}|\) defined in Eq. (2) for Fit-II in Fig. 2.

Fig. 2
figure 2

The effective form factor of the \(\Lambda \) hyperon defined by Eq. (2) from Fit-II. The error band was obtained by the bootstrap method. The \({\bar{\Lambda }}\Lambda \) threshold is indicated by the vertical dash-dotted lines

Full size image

Here, we only focus on the residua of the \(\omega \) and \(\phi \) mesons. Translating into the \(\omega \Lambda \Lambda \) and \(\phi \Lambda \Lambda \) couplings [4], one has

$$\begin{aligned} g_i^{V\Lambda \Lambda }&= \frac{f_V}{M_V^2} \, a_i^{V\Lambda \Lambda }~,~~i=1,2,\nonumber \\&\text {with }f_\omega =16.5,\, f_\phi =13.4, \end{aligned}$$
(8)

and therefore

$$\begin{aligned} g_1^{\omega \Lambda \Lambda }&=18.04_{-0.11}^{+0.13},\quad g_2^{\omega \Lambda \Lambda }=-34.45_{-0.24}^{+0.20}, \quad g_1^{\phi \Lambda \Lambda }\nonumber \\&=-16.81_{-0.24}^{+0.19},\quad g_2^{\phi \Lambda \Lambda }=18.99_{-0.20}^{+0.25}, \end{aligned}$$
(9)

corresponding to a tensor-to-vector coupling ratio (\(\kappa _{V\Lambda \Lambda }=g_2^{V\Lambda \Lambda }/g_1^{V\Lambda \Lambda }\)) of about \(-2\) for the \(\omega \Lambda \Lambda \) and \(-1\) for \(\phi \Lambda \Lambda \) case. The corresponding \(\omega \) couplings to the nucleon derived from the residua in the dispersion analysis of nucleon form factors [4] including the statistical (first error) and systematic (second error) uncertainties are \(g_1^{\omega NN}=18.6\pm 2.0\pm 3.8\) and \(g_2^{\omega NN}=8.4\pm 3.2\pm 5.8\) such that the tensor-to-vector coupling ratio, \(\kappa _{\omega NN}= 0.42^{+0.44}_{-1.24}\) [14]. It thus has a large uncertainty, but is still compatible with zero. Also, the statistical and systematic errors are added in quadrature when calculating the ratio. Note that for the nucleon no \(\phi \) couplings were given since the separation of the \(\phi \) from the \(K{\bar{K}}\) continuum is ambiguous.

Next we investigate the role of SU(3) flavor symmetry for the vector couplings. The ratios between the nucleon and \(\Lambda \) hyperon vector couplings are given by \(g_1^{\omega \Lambda \Lambda }/g_1^{\omega NN}=1.00_{-0.39}^{+0.65}\) and \(g_1^{\phi \Lambda \Lambda }/g_1^{\omega NN}=-0.94_{-1.09}^{+0.38}\) which are expressed as \((2/3)\times (5\alpha _\textrm{BBV}-2)/(4\alpha _\textrm{BBV}-1)\) and \((-\sqrt{2}/3)\times (2\alpha _\textrm{BBV}+1)/(4\alpha _\textrm{BBV}-1)\), respectively, with the SU(3) relationsFootnote 1 [55]. The ratio \(g_1^{\omega \Lambda \Lambda }/g_1^{\omega NN}\) follows the SU(3) expectation when \(\alpha _\textrm{BBV}\ge 0.82\), while the matching condition for \(g_1^{\phi \Lambda \Lambda }/g_1^{\omega NN}\) is \(\alpha _\textrm{BBV}\le 0.8\). Only the former case can be compatible with the SU(3) symmetry expectation that \(\alpha _\textrm{BBV}\approx 1.0\). For the tensor coupling, \(g_2^{\omega NN}\) is expected to be zero in SU(3) symmetry and \(g_2^{\omega \Lambda \Lambda }\) can be expressed in terms of \(g_2^{\omega NN}\) and \(g_2^{\rho NN}\). However, the latter quantity is not available in the previous dispersion-theoretical analysis of NFFs as the \(\rho \) is part of the two-pion continuum. Further, we can extract the couplings for the \(\psi (3770)\). We find \(g_1^{\psi (3770)\Lambda \Lambda }=-0.0040\pm 0.0008\) and \(g_2^{\psi (3770)\Lambda \Lambda }=0.0012\pm 0.0004\). A similar extraction of the \(\phi (2170)\) couplings is not possible since there is no experimental data for the partial width of \(\phi (2170)\rightarrow e^+e^-\).

4 Summary

In this work, we have analyzed the full set of cross section full data for the reaction \(e^+e^-\rightarrow {\bar{\Lambda }}\Lambda \), including the recent measurements around \(s=4\) GeV by BESIII in dispersion theory. The extracted EM form factors of the \(\Lambda \) hyperon from our best fit (Fit-II, see Table 2, right panel of Figs. 1, 2) can describe the world data base with a reduced \(\chi ^2\) of 2.596. The \(\Lambda \) spectral function of the best fit contains two physical mesons, \(\omega (782)\) and \(\phi (1020)\), and one floating effective pole \(s_1\) in the narrow sector and the \(\phi (2170)\) and \(\psi (3770)\) states with fixed masses together with one additional floating pole \(S_1\) in the broad sector. A slightly better \(\chi ^2\) of 1.531 was obtained in Fit-I at the expense of a double pole structure close to threshold whose experimental status is unclear. The uncertainties in the extracted form factors are given by means of the bootstrap approach. An estimate of the systematic errors from a variation of the number of effective poles is precluded by the sparse data set. The form factors in the space-like region are only weakly constrained by the data in the time-like region. Including the value for electric radius from the chiral perturbation theory calculation of Ref. [50] as a constraint, however, a magnetic radius \(\langle r_M^2 \rangle ^{1/2}= 0.681\pm 0.002~\textrm{fm}\) was extracted. From the fit, we could determine the vector and tensor couplings of the \(\omega \) and the \(\phi \) to the \(\Lambda \) hyperon, see Eq. (9). We have further extracted the \(\omega NN\) couplings and confirm that the tensor coupling is suppressed and compatible with zero. It is also small for the \(\psi (3770)\Lambda \Lambda \) coupling, where the tensor-to-vector coupling ratio is \(\kappa ^{\psi (3770)\Lambda \Lambda } = -0.3\pm 0.5\).