Abstract
We study four-dimensional Einstein–Maxwell fields for which any higher-order corrections to the field equations effectively reduces to just a rescaling of the gravitational and the cosmological constant. These configurations are thus simultaneous solutions of (virtually) any modified theory of gravity coupled (possibly non-minimally) to any electrodynamics. In the case of non-null electromagnetic fields we provide a full characterization of such universal solutions, which correspond to a family of gravitational waves propagating in universes of the Levi-Civita–Bertotti–Robinson type. For null fields we first obtain a set of general necessary conditions, and then a full characterization for a special subfamily, which turns out to represent electromagnetic waves accompanied by pure radiation in the (anti-)Nariai background. The results are exemplified for the case of Born–Infeld, ModMax and Horndeski electrodynamics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background and definition of universal and almost universal solutions
Attempts to cure the divergent electron’s self-energy motivated early proposals for modified classical theories of electrodynamics [1,2,3]. Nonlinear deviations from Maxwell’s theory also arise in effective theories derived from quantum electrodynamics [4,5,6,7] or from string theory [8]. While finding exact solutions of nonlinear electrodynamics (NLE) is in general much more difficult than in Maxwell’s theory, Schrödinger observed [9, 10] that all null fields (defined by \(F_{ab}F^{ab}=0={}^{*}\!F_{ab}F^{ab}\)) which solve Maxwell’s equations automatically solve also a large set of NLE and are, in this sense, “universal” solutions. It was subsequently pointed out that plane waves (a special case of null fields) solve not only NLE but also higher-derivative theories [11]. Extensions beyond the case of plane waves and to allow for certain curved backgrounds, p-forms of higher ranks and higher dimensions have been obtained in recent years in the case of electromagnetic test fields [12,13,14]. However, it is clearly also desirable to understand how such universal electromagnetic fields backreact on the spacetime geometry, i.e., to study universal solutions of modified theories of gravity coupled to modified electrodynamics. In that direction, Kuchynka and the present author have obtained a characterization of Einstein–Maxwell solutions for which all higher-order correction vanish identically [15]. In this work we will go beyond the results of [15] by relaxing some of the assumptions made there, as we explain in the following.
In the absence of matter sources, an Einstein–Maxwell solution consists of a pair \(({\varvec{g}},{\varvec{F}})\) in which \({\varvec{g}}\) is a Lorentzian metric and \({\varvec{F}}=\textrm{d}{\varvec{A}}\) a 2-form field, such that the Einstein–Maxwell field equations are satisfied, i.e.,
where \(\Lambda _0\) and \(\kappa _0\) are constants (\(\kappa _0\) is dimensionless in geometrized units), \(G_{ab}\) is the Einstein tensor and
We will be interested in modified theories of gravity coupled to an electromagnetic field, for which the field equations (1), (2) are replaced by a more general system
where \(\Lambda \) and \(\kappa \) are again constants (possibly different from \(\Lambda _0\) and \(\kappa _0\)), while \({\varvec{E}}\) is a symmetric, divergencefree 2-tensor and \({\varvec{H}}\) a 2-form, both constructed in terms of \({\varvec{F}}\), the Riemann tensor \({\varvec{R}}\) associated with \({\varvec{g}}\), and their covariant derivatives of arbitrary order (and contractions with \({\varvec{g}}\)). In particular, if one considers theories defined by a Lagrangian density of the form \(\mathcal{L}=\frac{1}{\kappa }(R-2\Lambda )+L({\varvec{R}},\nabla {\varvec{R}},\ldots ,{\varvec{F}},\nabla {\varvec{F}},\ldots )\), then \(E_{ab}\) and \(\nabla _b{H}^{ab}\) will be determined by the variations \(\frac{1}{\sqrt{-g}}\frac{\delta S_L}{\delta g^{ab}}\) and \(\frac{1}{\sqrt{-g}}\frac{\delta S_L}{\delta A_a}\), respectively, where \(S_L=\int \textrm{d}^4x\sqrt{-g}L\) (some explicit examples will be given in Sects. 5 and 6).
The purpose of the present paper is to identify a class of four-dimensional Einstein–Maxwell fields \(({\varvec{g}},{\varvec{F}})\) solutions of (1), (2) for which all possible tensors \({\varvec{E}}\) and \({\varvec{H}}\) that one can construct (as described above) are such that:
-
1.
\({\varvec{E}}\) takes the form
$$\begin{aligned} E_{ab}=b_1T_{ab}+b_2 g_{ab}, \end{aligned}$$(6)where \(b_1\) and \(b_2\) are spacetime constants (but may depend on the particular \({\varvec{E}}\) being considered and on the specific solution \(({\varvec{g}},{\varvec{F}})\) chosen withing the given class) and \(T_{ab}\) is as in (3).
-
2.
\(\nabla _b{H}^{ab}=0\) identically.
Pairs \(({\varvec{g}},{\varvec{F}})\) satisfying conditions 1 and 2 will be referred to as universal solutions.
The reason for condition 2 is obvious – the modified Maxwell equation (5) will be automatically satisfied by the pair \(({\varvec{g}},{\varvec{F}})\). On the other hand, condition 1 ensures that the modified Einstein equation (4) is also satisfied for values of the coupling constants determined by
In other words, a universal Einstein–Maxwell solution \(({\varvec{g}},{\varvec{F}})\) does not only solve the Einstein–Maxwell theory (1), (2) but also any modified theory admitting field equations of the form (4) and (5), provided the algebraic conditions (7) are satisfied.Footnote 1 In the vacuum limit \(T_{ab}=0\), condition (6) reduces to \(E_{ab}=b_2 g_{ab}\), which defines universal spacetimes in the sens of [16], i.e., those which solve (virtually) any purely gravitational modified theory.
As we shall discuss in Sect. 3, in the case of null fields it will ultimately be necessary to relax condition 1 and allow \(b_1\) in (6) to be a spacetime function. This effectively means that, from the viewpoint of the original Einstein–Maxwell theory, one needs to pick a pair \(({\varvec{g}},{\varvec{F}})\) that solves an Einstein equation also containing an additional term that can be interpreted as pure radiation (aligned with the null Maxwell field) – i.e., one should add the quantity \((\kappa b_1-\kappa _0)T_{ab}\) to the RHS of (1) (ultimately affecting only one component of the Einstein equation since \({\varvec{F}}\) is null). Nevertheless, it should be emphasized no pure radiation will be present in the modified theory (4), (5), which thus remains electrovac. A similar approach in the case of modified gravities in vacuum was considered in [17,18,19,20] and for certain electrovac solutions in [21, 22]. Similarly as in [19], solutions of this type can be referred to as almost universal. That is, an almost universal Einstein–Maxwell solution containing a null \({\varvec{F}}\) and aligned pure radiation solves any modified theory admitting field equations of the form (4) and (5), provided the first of (7) is satisfied. Such solutions are thus only “almost” universal because \(b_1\) may be a different function in different theories, which means that the pure radiation term on the Einstein–Maxwell side can be specified only once a particular modified electrovac theory has been chosen. This will be illustrated more explicitly in Sect. 3 and, by an example, in Sect. 6.2
For Lagrangian theories that can be seen (in a sense specified in [15]) as higher-order modifications of the Einstein–Maxwell theory, the special configurations \(({\varvec{g}},{\varvec{F}})\) for which \(b_1=1\) and \(b_2=0\) have been fully characterized in [15] (in arbitrary dimension). These can be regarded as strongly universal solutions (using a terminology similar to [16]) since \(\Lambda =\Lambda _0\) and \(\kappa =\kappa _0\), and corrections to the field equations vanish identically (rather than just being of the special form allowed by (6)). However, this leads to a rather restricted class of solutions, namely a specific \(\Lambda _0=0\) subset of Kundt spacetimes of Petrov type III (or more special) coupled to a null \({\varvec{F}}\) and admitting a recurrent null vector field (see [15] for more details). The present paper will thus extend the analysis of [15] in various directions, in particular to include non-null electromagnetic fields, and also null fields in spacetimes of Petrov type II and D, neither of which were covered by [15].
1.2 Preliminaries
First, it is easy to see that (6) in condition 1 implies the two electromagnetic invariants
are constant. This follows, for example, by considering the form of \(E_{ab}\) which arises in NLE (given below in (75)) for \(L=I^q\) and \(L=I+J^q\) (\(q\ne 0,1\)).Footnote 2
Next, since the energy–momentum tensor (3) is traceless, it follows from the assumption (6) that all possible tensors \(E_{ab}\) have constant trace (vanishing iff \(b_2=0\)). This applies, in particular, to tensors \(E_{ab}\) constructed out of just the curvature tensor and its covariant derivatives. Thanks to theorem 3.2 of [23], one can thus conclude that metrics satisfying condition 1 must belong to the class of spacetimes for which all curvature invariants are constant (i.e., CSI spacetimes) [24, 25].
Furthermore, four-dimensional CSI spacetimes consist of a (proper) subset of degenerate Kundt metricsFootnote 3 and of (locally) homogeneous spacetimes (theorem 2.1 of [25]). Taking advantage of this simplification, in the rest of the paper we can thus restrict our analysis to these two subclasses, without losing generality. In fact, for degenerate Kundt metrics it will be convenient to consider non-null and null electromagnetic fields separately. Furthermore, since a large amount of results for null fields in degenerate Kundt spacetimes of Petrov type III, N and O has been already obtained [15] (see also [22]), in the null case we shall focus on metrics of type II (and D), leaving the complete analysis of the types III/N/O for future work. On the other hand, no restriction on the Petrov types will be a priori assumed neither in the non-null degenerate Kundt nor in the homogeneous case. The plan and main results of the paper are thus as follows:
-
(i)
Section 2: we show that the metric (30) with the 2-form (31) represents the most general universal solution \(({\varvec{g}},{\varvec{F}})\) for which \({\varvec{F}}\) is non-null and \({\varvec{g}}\) degenerate Kundt
-
(ii)
Section 3: when \({\varvec{F}}\) is null and \({\varvec{g}}\) degenerate Kundt, we first obtain a set of general necessary conditions for \(({\varvec{g}},{\varvec{F}})\) to be (almost) universal (Sect. 3.1) and of Petrov type II (D), and then a complete characterization of the special subfamily of almost universal solutions defined by the assumption \(D\Psi _4=0\) (Sect. 3.2) – this is represented by the metric (55) with the 2-form (47), and \(H^{(0)}\) determined by (65) with (64)
-
(iii)
Section 4: both in the non-null and null cases, universal and almost universal solutions with a homogeneous \({\varvec{g}}\) are shown to fall into the already investigated degenerate Kundt class, which also implies that spacetimes of Petrov type I cannot occur (recall footnote 3).
In Sects. 5 and 6 we exemplify the previous results for the specific cases of NLE (in particular Born–Infeld and ModMax theories) and Horndeski’s theory, respectively. Finally, in the appendices we prove some technicalities needed in the main body of the paper. To that end, we employ the formalism of Geroch–Held–Penrose [30], which is briefly summarized in Appendix A. Then we analyze separately the case of non-null and null fields in Appendices B and C, respectively. Some of the results obtained there go beyond the purposes of the present paper and can be useful also for future applications.
Notation \({\varvec{R}}\), \({\varvec{C}}\), \({\varvec{S}}\) denote the Riemann and Weyl tensors and the tracefree part of the Ricci tensor, respectively. A real 2-form is denoted by \({\varvec{F}}\) or \({\varvec{H}}\), while a generic spinor (possibly complex) by \(\varvec{\mathcal{S}}\). We will use the abbreviations “b.w.” and “s.w.” for boost and spin weight, respectively – these are the standard notions of the Newman–Penrose (NP) [31] and Geroch–Held–Penrose (GHP) [30] formalisms (cf. also [29, 32] and Appendix A). An asterisk will denote Hodge duality. A tensor is called a VSI (vanishing scalar invariants) tensor if all its scalar polynomial invariants (obtained by contracting polynomials in the metric, the tensor itself and its covariant derivatives of arbitrary order) vanish. A similar terminology is employed for tensors possessing only constant scalar invariants, referred to as CSI tensors. When a metric or a spacetime is called VSI [CSI], it is actually meant that its Riemann tensor is VSI [CSI].
To express the Maxwell field, it will be often convenient to use the self-dual 2-form [29, 32]
Its algebraic complex invariant will be hereafter assumed (by the comments in the paragraph following (8)) to be constant, i.e.,
In terms of \({\varvec{\mathcal{F}}}\), the energy–momentum tensor (3) takes the compact form
We will be using the complex NP formalism [31], with the conventions of [29]. In a complex frame \((\varvec{\ell },{\varvec{n}},{\varvec{m}},{\varvec{{\bar{m}}}})\), the metric reads
while the form of \({\varvec{\mathcal{F}}}\) and of the Maxwell equation (2) will be given in Sects. 2 and 3 in the non-null and null case, respectively. In the above frame, the tracefree part of the Einstein equation (1) reads \(\Phi _{ij}=\kappa _0\Phi _{i}{\bar{\Phi }}_{j}\) (\(i,j=0,1,2\)), while its trace gives \(R=4\Lambda _0\).
2 Degenerate Kundt: non-null fields
2.1 Necessary conditions
In a frame adapted to the two null PNDs of \(\mathcal{F}\), one has [29]
so that \(\varvec{\ell }\) and \({\varvec{n}}\) are repeated PNDs of the energy–momentum tensor
and the only non-zero component of the traceless Ricci tensor is \(\Phi _{11}=\kappa _0\Phi _1{\bar{\Phi }}_1\). Since \({\mathcal {F}}_{ab}{\mathcal {F}}^{ab}=-16\Phi _1^2\), by (10) one gets
At least one of the PNDs of \({\varvec{\mathcal{F}}}\) is Kundt (footnote 3) – for definiteness, let’s say it is \(\varvec{\ell }\). We thus have
where the last equality can be ensured by exploiting a freedom of boosts and spins, without loss of generality.
With the above conditions, Maxwell’s equation reduce to (cf., e.g., [29])
This implies that \(\varvec{\ell }\) is recurrent and that the frame in use is parallelly transported along it. A further rescaling enables one to set also (without affecting the previous conditions)
such that \(\varvec{\ell }\) becomes a gradient.
By condition (6) with (14), the following symmetric 2-tensorFootnote 4
must vanish in order for \(\mathcal{F}\) to be universal, so that
We further note that the Ricci and Bianchi identities give [29]
We have now enough information to introduce adapted coordinates and arrive at the explicit form of the line element. We already observed that \(\varvec{\ell }\) is a gradient, while Eqs. (16), (17), (20) and (18) further ensure \({\varvec{m}}\wedge \textrm{d}{\varvec{m}}=0\), \(\varvec{\ell }\wedge \textrm{d}{\varvec{n}}=0\), \(\varvec{\ell }\wedge \textrm{d}{\varvec{m}}=-2\beta \varvec{\ell }\wedge {\varvec{m}}\wedge \varvec{{\bar{m}}}\). We can thus define coordinates \((u,r,\zeta ,{\bar{\zeta }})\) such that
An r-independent spin can be used to make P real (without affecting the previously obtained conditions), while imposing \(\mu =0\) (cf. (17)) additionally gives
The latter condition also ensures that Maxwell’s equation is satisfied. Thanks to the last of (23), a coordinate transformation \(r\mapsto r+g(u,\zeta ,{\bar{\zeta }})\) can be used to set
We have thus arrived at a special subcase of the canonical Kundt line-element (cf. [29] for more details). The component \((\zeta {\bar{\zeta }})\) of Einstein’s equations gives
The component (ur) reads \(\bigtriangleup \ln P=\Lambda _0+2\kappa _0\Phi _1{\bar{\Phi }}_1\) (where \(\bigtriangleup =2P^2\partial _{{\bar{\zeta }}}\partial _\zeta \) is the Laplace operator in the transverse 2-space spanned by \((\zeta ,{\bar{\zeta }})\)), which enables one to redefine the coordinates \((\zeta {\bar{\zeta }})\) such that
The equation \((u\zeta )\) gives \(H^{(1)}=H^{(1)}(u)\), which guarantees that we can redefine \(u\mapsto U(u)\), \(r\mapsto r/\dot{U}\) to achieve
Lastly, the equation (uu) requires \(\bigtriangleup H^{(0)}=0\) and therefore
The line-element thus finally reads
and the Maxwell field (13) becomes
together with (15) and (from (26), (27)), \(k_1=\Lambda _0-2\kappa _0\Phi _1{\bar{\Phi }}_1\), \(k_2=\Lambda _0+2\kappa _0\Phi _1{\bar{\Phi }}_1\). The relative signs of \(k_1\), \(k_2\) and \(\Lambda _0\) must be such that \(\Phi _1{\bar{\Phi }}_1>0\) [33, 34].
2.2 Sufficiency of the conditions
In the above section we have obtained a set of necessary conditions for an Einstein–Maxwell solution to be universal, which led to the solution (30), (31). Let us now show that those conditions are also sufficient, i.e., that the solution (30), (31) is indeed universal.
First, we observe that the curvature tensor contains only components of b.w. 0 (the Weyl \(\Psi _2\) and the Ricci \(R=4\Lambda _0\) and \(\Phi _{11}=\kappa _0\Phi _1{\bar{\Phi }}_1\)) and \(-2\) (i.e., \(\Psi _4\)), while \({\varvec{\mathcal{F}}}\) only components of b.w. 0 (i.e., \(\Phi _1\)) – in both cases, those of b.w. 0 are constant. Furthermore, the covariant derivatives of \({\varvec{\mathcal{F}}}\) and of the energy–momentum tensor (which is proportional to the tracefree part of the Ricci tensor) are of the form
Together with (15) and (21), this means that both tensors (32) are 1-balanced tensors (as defined in [23], cf. also Appendix B). One can similarly show that also the covariant derivative of the Weyl tensor is 1-balanced (a proof of this statement can be found in section 4.1 of [35]), therefore the covariant derivative of the full Riemann tensor is 1-balanced as well. This implies that covariant derivatives of arbitrary order of both \({\varvec{R}}\) and \({\varvec{\mathcal{F}}}\) possess only components of b.w. \(\le -2\) (see lemma A.7 of [14] and the proof of proposition 2.9 in the same reference, and [12, 23, 35,36,37,38] for several related earlier results). Therefore, any possible \(E_{ab}\) can only contain terms of b.w. 0 and \(-2\), while possible \(H_{ab}\) can only be of b.w. 0 (since a 2-form cannot have components of b.w. \(\le -2\)).
All the components of b.w. 0 are the same as those of the “background” direct-product spacetime defined by setting \(h=0\) in (30) (cf. [14, 39]) and therefore are invariant under the symmetries of the latter (cf. [14] for related comments). This means that components of b.w. 0 of any possible tensor that can be constructed out of \({\varvec{R}}\) and \({\varvec{\mathcal{F}}}\) (their covariant derivatives cannot contribute since have b.w. \(\le -2\)) will still admit the same symmetries – in particular, both their boost and spin weights will be zero. Therefore, the b.w. 0 part of any possible symmetric 2-tensor \(E_{ab}\) will be given by a linear combination, with constant coefficients, of \(g_{ab}\) and \(T_{ab}\) (in agreement with (6)), while any possible 2-form (necessarily of b.w. 0, as observed above) will consist of a linear combination of the 2-volume elements of the two factor spaces. It is easy to check that any such 2-form is necessarily closed and co-closed [14], therefore the generalized Maxwell equation (5) is also automatically satisfied.
We can thus hereafter focus only on the possible b.w. \(-2\) components of \(E_{ab}\). These are proportional to \(\ell _a\ell _b\) and thus have s.w. 0. Let us first note that the b.w. \(-2\) part of \({\varvec{R}}\) cannot contribute to those, since it is traceless and has s.w. \({\mp }2\) (thus any symmetric 2-tensor obtained by contractions of the b.w. \(-2\) part of \({\varvec{R}}\) with the b.w. 0 parts of \({\varvec{R}}\) and \({\varvec{\mathcal{F}}}\) is necessarily zero – cf. [16] for related comments). Thanks to this and to the previous observations, b.w. \(-2\) components of \(E_{ab}\) must thus contain terms linear in the covariant derivatives of either \({\varvec{R}}\) or \({\varvec{\mathcal{F}}}\), suitably contracted with certain tensor components of b.w. 0 and s.w. 0. Therefore, only terms of the covariant derivatives of \({\varvec{R}}\) and \({\varvec{\mathcal{F}}}\) possessing b.w. \(-2\) and s.w. 0 can give rise to b.w. \(-2\) components of \(E_{ab}\). However, one can show iteratively that such terms vanish for covariant derivatives of arbitrary order, and thus the b.w. \(-2\) components of \(E_{ab}\) are identically zero. Such a proof can be found in Appendix B.2.
To summarize, we have shown that the family of Einstein–Maxwell solutions \(({\varvec{g}},{\varvec{F}})\) given by (30) and (31) are universal in the sense defined in Sect. 1.1. It also follows from the above derivation that they are the unique universal solutions when \({\varvec{\mathcal{F}}}\) is non-null.
Let us recall that in the Einstein–Maxwell theory solutions (30), (31) represent non-expanding gravitational waves propagating in the Levi-Civita–Bertotti–Robinson, charged (anti-)Nariai and Plebański–Hacyan direct product universes [33, 40,41,42,43,44], to which they reduce for \(h=0\). They were first found in [45, 46] and further studied in [34, 47, 48] (see also [49, 50] in the vacuum limit \(\Phi _1=0\)). They are of Petrov type II(D) iff \(\Lambda _0\ne 0\) (i.e., iff \(k_1\ne -k_2\)) and of type N(O) otherwise. Since for these solutions the covariant derivatives of \({\varvec{\mathcal{F}}}\) and \({\varvec{R}}\) are both 1-balanced (as noticed above), they cannot be used to construct any invariants. Furthermore, the frame components of b.w. 0 of both \({\varvec{R}}\) and \({\varvec{\mathcal{F}}}\) are constant (\(R=4\Lambda _0\) and (15) with the first of (21)), which enables one to conclude that no non-constant invariants can be constructed, neither from \({\varvec{R}}\) nor from \({\varvec{\mathcal{F}}}\) (not even mixed ones) – in particular demonstrating that the metric is CSI (cf. Sect. 1.2).
3 Degenerate Kundt (Petrov type II): null fields
3.1 On the general class
In this case in an adapted frame one has [29]
giving
where the unique PND \(\varvec{\ell }\) of \({\varvec{\mathcal{F}}}\) is necessarily Kundt and a multiple PND of the Weyl tensor (cf. footnote 3), i.e.,
In a parallelly transported frame adapted to \(\varvec{\ell }\), one has
Maxwell’s equation thus takes the form [29]
It follows that \({\varvec{\mathcal{F}}}\) is a balanced tensor (as defined in [36, 37], cf. also Appendix C) together with its covariant derivatives of arbitrary order, and therefore it is VSI [12].
Moreover, by the assumptions (cf. Sect. 1.2), the metric is VSI iff \(\Lambda _0=0=\Psi _2\) [36], CSI otherwise – in both cases, \(\Psi _2=\)const. From now on we will restrict ourselves to spacetimes of Petrov type II and D, i.e., \(\Psi _2\ne 0\) will be assumed hereafter. Partial results for the types III, N and O can be found in [15, 22].
In a Kundt CSI spacetime of Weyl type II and traceless-Ricci type N, a subset of the Ricci and Bianchi identities gives [29] (using (35), (36))
The latter equation suffices to show that \({\varvec{S}}\) and its covariant derivatives of arbitrary order are 1-balanced (cf. also lemma B.4 of [15] for a more general result). Using also the commutator \([\delta ,D]=({\bar{\alpha }}+\beta )D\) [29], from the second of (40) one finds
Since for type II one has \(\Psi _2\ne 0\), the first of (40) implies
which means that \(\varvec{\ell }\) is recurrent.
the first of which also reads alternatively \(\Psi _2=-\Lambda _0/3\ne 0\).
Following the same steps as in [35] one can therefore argue that \(\nabla ^k{\varvec{C}}\) is balanced for any \(k\ge 1\) (while \({\varvec{C}}\) is not, since of type II). Furthermore, we note that for any \(k\ge 1\) \(\nabla ^k{\varvec{C}}\) is 1-balanced (and thus \(\nabla ^k{\varvec{R}}\) is 1-balanced since \({\varvec{S}}\) also is, see above) iff \(D\Psi _4=0\), which thus characterizes a geometrically privileged subcase (to be analyzed in Sect. 3.2).
Recalling that the spacetime in question must be recurrent Kundt and solve the Einstein–Maxwell equations sourced by (33) (and thus necessarily be aligned with \(\varvec{\ell }\) [29]), the metric can be written as [29, 51, 52]
with [52]Footnote 5
and the Maxwell field (33) is given by
where the complex functions g and f are arbitrary. In a null tetrad [29]
equation (47) corresponds to (33) with
We also note that the form (45) of W implies
Equations (44)–(47) ensure that all components of the Einstein equation (1) are satisfied, except for the one along \(\ell _a\ell _b\), i.e., the component \(\Phi _{22}=\kappa _0\Phi _2{\bar{\Phi }}_2\) in NP notation – hence at this stage also pure radiation aligned with \({\varvec{\mathcal{F}}}\) is present. If one imposes also \(\Phi _{22}=\kappa _0\Phi _2{\bar{\Phi }}_2\), then the real function \(H^{(0)}=H^{(0)}(u,\zeta ,{\bar{\zeta }})\) must obey a second order linear PDE that in GHP notation can be written compactly as (using (36), (42), (50))Footnote 6

However, in the following we will not impose (51) and thus \(H^{(0)}\) will remain, for now, unconstrained. The reason for this is related to the comments about almost universal solution given in Sect. 1.1, as will be made more explicit in Sect. 3.2.
By setting \(g=f=H^{(2)}=0\) in (44)–(47) one obtains the (anti)-Nariai vacuum “background” [41], which is a direct product of two 2-dimensional spaces with identical Gaussian curvature and therefore [38] a universal spacetime. The b.w. 0 part of the curvature tensor (with components \(\Psi _2\) and R) of the full metric (44) is the same as the one of the (anti)-Nariai background (since it does not contain the functions W, \(H^{(1)}\) and \(H^{(2)}\), as noted in [39]). By the result of [38] just mentioned, this means that components of \(E_{ab}\) of b.w. 0 reduce to terms proportional to the metric and are thus harmless. It also follows that no components of \(H_{ab}\) of b.w. 0 (which could only come from the curvature tensor, since \({\varvec{\mathcal{F}}}\) is balanced) are possible – otherwise the “square” of such terms would produce a symmetric 2-tensor not proportional to the metric, contradicting [38]. One can thus focus on components of \(E_{ab}\) and \(H_{ab}\) of negative b.w.. For simplicity, in the rest of this section we will restrict ourselves to the special subcase (identified above) with \(D\Psi _4=0\). We recall that even in the vacuum case a conclusive answer for the generic case \(D\Psi _4\ne 0\) has not been obtained yet [35] – this will thus deserve a separate investigation.
3.2 Special subclass \(D\Psi _4=0\)
3.2.1 Necessary conditions
From now on we thus assume the additional condition \(D\Psi _4=0\). It is not difficult to see [52] that for the metric (44)–(46) one has \(D\Psi _4=0\Leftrightarrow g_{,\zeta \zeta \zeta }=0\), so that here we can take
With (45) this gives
Next, a transformation of the formFootnote 7
under which \(\left( 1+\frac{\Lambda _0}{2}\zeta {\bar{\zeta }}\right) ^{-2}\textrm{d}\zeta \textrm{d}{\bar{\zeta }}=\left( 1+\frac{\Lambda _0}{2}\zeta '{\bar{\zeta }}'\right) ^{-2}\textrm{d}\zeta '\textrm{d}{\bar{\zeta }}'\), can be used to set \({\bar{a}}_1'-a_1'=0\) and \(2{\bar{a}}_2'+\Lambda _0 a_0'=0\). In the new coordinates one thus has (after dropping the primes) \(W=\varphi _{,\zeta }\), where \(\varphi =\left( 1+\frac{\Lambda _0}{2}\zeta {\bar{\zeta }}\right) ^{-1}(\bar{a}_0\zeta +a_0{\bar{\zeta }}+a_1\zeta {\bar{\zeta }})\) is a real function. This enables one to make a further transformation \(r'=r+\varphi \) to set \(W'=0\), i.e., \(g'=0\) [29, 52]. This also gives \(H'^{(1)}=0\) (recall (46)) and the final form of the metric is thus (dropping again the primes)
with (47) unchanged (up to suitably redefining f after (54)).
Let us also note that one now has
which will be useful in the following (these conditions can be obtained from the general expressions given in [29]).
As mentioned in the paragraph below (50), an Einstein–Maxwell solution without pure radiation would correspond to determining \(H^{(0)}\) from (51). For \(W=0=H^{(1)}\) the latter simply becomes \(\bigtriangleup H^{(0)}=2\kappa _0\Phi _2{\bar{\Phi }}_2\), whose solution reads [47]
with \(h(u,\zeta )\) arbitrary. We will, however, allow for arbitrary aligned pure radiation in the Einstein–Maxwell theory and thus will not assume (57) but rather keep \(H^{(0)}\) unspecified at this stage (it will be fixed in a theory-dependent way by (65), see the comments following it). In passing, let us note that for the metric (55), apart from \(\Psi _2=-\Lambda _0/3\), the only other Weyl component is given by \(\Psi _4=P(PH^{(0)})_{,{\bar{\zeta }}{\bar{\zeta }}}\).
3.2.2 Sufficiency of the conditions
We have obtained above a set of necessary conditions for an Einstein–Maxwell solution with a null field and \(D\Psi _4=0\) to be universal or almost universal, which led to the solution (55), (47). To be precise, the latter is an Einstein–Maxwell solution only once \(H^{(0)}\) is taken as in (57) – for a generic \(H^{(0)}\), an additional term representing aligned pure radiation is also present (as already mentioned in Sect. 1.1). We shall now argue that the necessary conditions obtained in Sect. 3.2.1 are also sufficient for (55), (47) to describe an almost universal solution. We emphasize again that a difference with respect to the universal solutions of Sect. 2 is that here the function \(H^{(0)}\) cannot be be fixed a priori in the Einstein–Maxwell theory (i.e., as in (57)) but can be specified only once a particular theory has been chosen (whereby the solution (55), (47) is only “almost” universal – cf. [17,18,19, 21, 22] for a similar approach in other contexts).
As noticed at the end of Sect. 3.1, we only need study components of negative b.w.. Since here \(\nabla ^k{\varvec{R}}\) is 1-balanced (for \(k\ge 1\)) and \({\varvec{\mathcal{F}}}\) is balanced (cf. Sect. 3.1), components of \({\varvec{H}}\) can only be constructed linearly in terms of \({\varvec{\mathcal{F}}}\) and its covariant derivatives (and the complex conjugates of those). As it turns out, however, any such term necessarily has \(s\ne 0\) if \(b=-1\) (this is proven in Appendix C.2), which means that the divergence of such terms in necessarily zero (since a vector with \(b=-1\) can only have \(s=0\)) and therefore \(\nabla _b{H}^{ab}=0\) identically, as we needed to ensure.
Concerning possible components of \(E_{ab}\) of negative b.w., one has to consider separately those of b.w. \(-1\) (which may admit \(s=\pm 1\)) and \(-2\) (with \(s=0\)). The former can only consist of terms linear in \({\varvec{\mathcal{F}}}\), its covariant derivatives and their complex conjugates (appropriately contracted with the metric and/or the Weyl tensor – only the b.w. 0 part of the latter giving a non-zero contribution). The latter may be constructed out of terms quadratic in \({\varvec{\mathcal{F}}}\) and its covariant derivatives (namely, products of two terms of b.w. \(-1\))Footnote 8 or terms linear in \({\varvec{S}}\) or linear in the covariant derivatives of \({\varvec{\mathcal{F}}}\) or of \({\varvec{R}}\) (both in general contain also terms of b.w. \(-2\)). We note that terms linear in the Weyl tensor cannot contribute here, since those with \(b=-2\) have necessarily \(s=\pm 2\ne 0\).
Let us first show that components of \(E_{ab}\) of b.w. \(-1\) are identically zero. These consist of terms linear in (covariant derivatives of) \({\varvec{\mathcal{F}}}\) contracted with arbitrary powers of the b.w. 0 part of the curvature tensor, resulting in a term with weights \((-1,-1)\) which is, in addition, invariant under the Sachs symmetry [30, 32] \(\varvec{\ell }\mapsto {\varvec{m}}\), \({\varvec{m}}\mapsto -\varvec{\ell }\), \({\bar{{\varvec{m}}}}\mapsto {\varvec{n}}\), \({\varvec{n}}\mapsto -{\bar{{\varvec{m}}}}\) (as follows from the discussion in Appendix C.2). The only 2-tensor with such properties is (up to an overall factor) \({\varvec{\mathcal{F}}}\) itself, which is antisymmetric and cannot thus contribute to components of \(E_{ab}\) of b.w. \(-1\), as we wanted to prove. A similar discussion applies to terms with weights \((-1,+1)\) constructed out of \({\bar{{\varvec{\mathcal{F}}}}}\) (cf. again Appendix C.2 and, in particular, footnote 24).
As for components of \(E_{ab}\) of b.w. \(-2\), they must necessarily have \(s=0\), since they can only be terms proportional to \(\ell _a\ell _b\). It follows from the discussion in Appendix C.2 that terms linear in the covariant derivatives of \({\varvec{\mathcal{F}}}\) cannot contribute, since those do not possess components with \((b,s)=(-2,0\)). Terms quadratic in \({\varvec{\mathcal{F}}}\) and its covariant derivatives do instead contribute, as we now detail. Obviously the only possible term quadratic in \({\varvec{\mathcal{F}}}\) is \({\mathcal {F}}_{ac}\mathcal {{\bar{F}}}_b^{\ c}=4\Phi _2{\bar{\Phi }}_2\ell _a \ell _b\). When considering terms quadratic in \(\nabla ^k{\varvec{\mathcal{F}}}\) it is useful to first note thatFootnote 9

From Appendix C.2 it follows that, in the product of a term linear in \(\nabla ^k{\varvec{\mathcal{F}}}\) with a term linear in \(\nabla ^h{\bar{{\varvec{\mathcal{F}}}}}\), products of components with weights, respectively, \((-1,-1)\) and \((-1,+1)\) (possible only if k and h are both even) will be either zero or again proportional (via a power of \(\Lambda _0\)) to \(\Phi _2{\bar{\Phi }}_2\ell _a \ell _b\). For example, using (58) one finds
However, \(\nabla ^k{\varvec{\mathcal{F}}}\) may also contain components with \((-1,s)\) and \(s<-1\), which are of the form (C14) and thus give rise also to components \((-2,0)\) proportional to \(\eth '^j\Phi _2\eth ^j{\bar{\Phi }}_2\) in products \(\nabla ^k{\varvec{\mathcal{F}}}\nabla ^h{\bar{{\varvec{\mathcal{F}}}}}\) (with \(0\le j\le \text{ min }\{k,h\}\) and j, k, h having the same parity). One has, for example (cf. Lemma D.3 of [15]),
and
Finally, theorem C.3 in Appendix C.2 implies that terms linear in the traceless Ricci tensor or in the covariant derivatives of the Riemann tensor can only contribute to \(E_{ab}\) with a linear combination of terms of the form \(\bigtriangleup ^k\Phi _{22}\) for \(k\ge 0\) (or, equivalently, \(\eth '^k\eth ^{k}\Phi _{22}\)). For example one finds
Combining the results obtained above, we have shown that, in the spacetime (55) with (47), any rank-2 tensor constructed from \({\varvec{F}}\), \({\varvec{R}}\) and their covariant derivatives of arbitrary order takes the form
where \(N_1,N_2\in {\mathbb {N}}\), \(\lambda _0\), \(a_k\) and \(c_j\) are constants, and \(\Phi _{22}=\frac{1}{2}\bigtriangleup H^{(0)}\). This is clearly of the required form (6) (recall (34)), as we wanted to prove.
However, the coefficient \(b_1\), given by
will in general be a spacetime function. This means that (1) will not, as it stands, be compatible with (4) – namely, one should add \(2\Phi _2{\bar{\Phi }}_2(\kappa b_1-\kappa _0)\ell _a\ell _b\) to the RHS of (1) (which is precisely the additional pure radiation term already mentioned in Sects. 1.1 and 3.1). This affects only one component of the latter, which thus reads
and can be solved (at least in principle) to determine \(H^{(0)}\) and thus to fully characterize the spacetime metric (55). We note that while the result (63)–(65) is theory-independent, once a particular theory has been specified, the corresponding Einstein equation (4) will dictate the specific form of the tensor \(E_{ab}\) and thus the precise values of the constants appearing in (63)–(65). The obtained solution of (65) will thus be specific to the considered theory. This should be contrasted with the class of (strongly) universal solutions with \(\Lambda _0=0\) obtained in [15], which can be fully specified as solutions of the Einstein–Maxwell theory (i.e., also fixing the function \(H^{(0)}\), with no need to include additional pure radiation) and then automatically solve also higher-order theories (in other words, there one has \(E_{ab}=T_{ab}\) identically for any of the possible theories specified in [15]).
We finally observe that the solutions (55), (47) with (65) represent in the Einstein–Maxwell theory electromagnetic waves accompanied by aligned gravitational waves and pure radiation in the (anti)-Nariai universe [46, 47, 50]. On the other hand, they are also solutions of any modified field equations (4), (5), in which case the pure radiation term is absent. The spacetime is generically of Petrov type II and becomes of type D iff \((PH^{(0)})_{,\zeta \zeta }=0\).Footnote 10 For these solutions, no non-zero invariants can be constructed using \({\varvec{\mathcal{F}}}\), while all curvature invariants are constant (in other words, \({\varvec{\mathcal{F}}}\) is VSI and the metric is CSI).
4 Locally homogeneous spacetimes
By definition, a homogeneous spacetime admits a transitive group of motions. It follows from the discussion in section 12.1 of [29] (see also, e.g., [55]) that in the case of a multiply-transitive group of motions, either: (i) the spacetime is Kundt (after excluding certain metrics not compatible with a Maxwell field); or (ii) there exists a simply-transitive subgroup \(G_4\). In case (i), imposing the Einstein equation (1) implies that the spacetime is degenerate Kundt (see also footnote 3), and one is thus reduced to the analysis of Sects. 2 and 3. We can therefore restrict ourselves here to the case when the group is (or contains) a simply-transitive \(G_4\). Using a complex null tetrad of invariant vectors, the spin coefficients and the curvature components are constant (cf., e.g., [29, 56,57,58]). Therefore, a Lorentz transformation with constant parameters enables one to align the (invariant) frame to the energy–momentum tensor of the Maxwell field, and thus to \({\varvec{\mathcal{F}}}\) itself (recall \(\Phi _{ij}=\kappa _0\Phi _{i}{\bar{\Phi }}_{j}\)).
4.1 Non-null fields
Using the frame described above, the Maxwell field is given by (13) and its energy–momentum tensor by (14), where \(\Phi _1\) is a constant by (10) (this means that \({\varvec{\mathcal{F}}}\) shares the symmetries of the metric, i.e., it is inheriting). From Maxwell’s equation [29] one readily obtains
using which one can computeFootnote 11
The above quantity must vanish in order to fulfill the assumption (6), thus giving
Therefore either \(\kappa =0\) or \(\nu =0\), meaning (with (66)) that either \(\varvec{\ell }\) or \({\varvec{n}}\) is a Kundt vector field.Footnote 12 This case is thus already contained in Sect. 2.
In passing, let us note that Ozsváth [57] obtained an Einstein–Maxwell solution with a homogeneous metric (of Petrov type I) admitting a simply-transitive \(G_4\) and an inheriting, non-null Maxwell field (recently shown to be the unique such solution [59]). One can verify that it is not a universal solution, precisely because the above tensor (67) is non-zero.
4.2 Null fields
Using the invariant frame mentioned above, the Maxwell field is given by (33). The Maxwell equation (or the Mariot–Robinson theorem [29]) then gives
i.e., \(\varvec{\ell }\) is geodesic and shearfree. Thanks to \(\Phi _{00}=\Phi _{01}=\Phi _{02}=0\), the Goldberg-Sachs theorem [60] (cf. also theorem 7.1 of [29]) further gives
while the Sachs equation (cf. the NP equation (7.21a) of [29]) reduces to
With the previous results and \(\Phi _{11}=\Phi _{12}=0\), the Bianchi equation (7.32k) of [29] takes the form
which thus requires \(\rho +{\bar{\rho }}-2\epsilon -2{\bar{\epsilon }}=0\). However, compatibility of the latter with (71) gives
so that \(\varvec{\ell }\) is Kundt. This case therefore belongs to the discussion of Sect. 3, as far as spacetimes of Petrov type II and D are concerned. Let us only mention here that certain homogeneous Kundt (plane wave) metrics of type N and O in the presence of a null Maxwell fields and \(\Lambda _0=0\) (cf. theorem 12.1 of [29]) are known to describe universal solutions [15].
5 Example I: nonlinear electrodynamics (NLE)
Nonlinear modifications of Maxwell’s theory were originally proposed in order to cure the divergent electron’s self-energy, most famously by Born and Infeld [2, 3]. An overview of more general NLE can be found, e.g., in [61]. For simplicity, here we mostly restrict ourselves to NLE minimally coupled to Einstein’s gravity (but some comments on Einstein–Weyl gravity are also given in Sect. 5.2.1). The theory is thus given by
where L is a (in principle arbitrary) function of the two algebraic invariants (8). In (4) and (5) one thus has (see, e.g., [61, 62])
with \(T_{ab}\) as in (3).
On a solution of the Maxwell equation, by (2) and \({\varvec{F}}=\textrm{d}{\varvec{A}}\) one has \(\nabla _b F^{ab}=0=\nabla _b {}^{*}\!F^{ab}\). Recalling also that for the fields considered in this paper the invariants I and J are constant (cf. (10)), it is obvious that (5) is satisfied identically, while the tensor (75) is precisely of the required form (6), with both \(b_1\) and \(b_2\) (which can be read off from (75)) being constants.Footnote 13 In other words, the field equations (4), (5) of any theory (74) are satisfied identically by the pairs \(({\varvec{g}},{\varvec{F}})\) identified in Sects. 2 and 3 (namely (30), (31) and (55), (47) with (57)), provided the algebraic constraints (7) admit a real solution. Violations of the latter occur, e.g., in special theories such that, for a given solution \(({\varvec{g}},{\varvec{F}})\), one of the quantities L, \(L_{,I}\) or \(L_{,J}\) becomes singular, thus giving rise to ill-defined terms in (75) or in (76) – see Sect. 5.2 below for an example. Another exception arises when (on a given solution) \(L_{,I}=0\), so that \(b_1=0\) in (6) (as happens, e.g., for stealth fields [63]). In the following Sects. 5.1 and 5.2 the general results just described will be exemplified in the case of two specific theories of NLE that are of particular interest.
It should be observed that, in the case of null fields, it was already known to Schröedinger [9, 10] that any (76) solves (5), while the validity of condition (6) was subsequently pointed out in [62, 64, 65].Footnote 14 Our results extends also to non-null fields and to theories of gravity other than Einstein’s (although in this section we have exemplified only the latter).
We further note that the simple structure of the field equations of NLE enables one to easily identify other Einstein–Maxwell solutions that also solve NLE (but are not universal), in addition to those of Sects. 2 and 3. An example with a non-null field and a non-Kundt metric is given by the homogenous solution obtained by Ozsváth mentioned in Sect. 4 [57, 59]. Examples with a null field are contained, e.g., in the Robinson–Trautman family [29].
5.1 Born–Infeld theory
The celebrated NLE of Born and Infeld [3] is given by
where b is a constant parameter with the dimension of an inverse length (such that Maxwell’s theory is recovered for \(b\rightarrow \infty \)). Then (75) takes the form (6) with
5.1.1 Non-null fields
For the Einstein–Maxwell solution (30), (31) one has (cf. (10), (13)) \(I=-4(\Phi _1^2+{\bar{\Phi }}_1^2)\) and \(J=4i(\Phi _1^2-{\bar{\Phi }}_1^2)\), where \(\Phi _1\) is a complex constant. Reparametrizing the latter as
constraints (7) become
where the parameter \(\theta _0\) reflects the consequences of a duality rotation. Type D and O solutions of this type (i.e., (30) with \(h=0\)) in the Born–Infeld electrodynamics were already obtained in [66] (see also [67] for more general NLE).Footnote 15
5.1.2 Null fields
When \(I=0=J\) one has (on-shell) \(L_0=1\), so that \(b_1=1\), \(b_2=0\) and (7) reduces to
i.e. any Einstein–Maxwell solution with a null field (and in particular the one given by (55), (47), (57)) also solves Einstein’s gravity coupled to the electrodynamics of Born and Infeld, with no need to redefine \(\Lambda _0\) and \(\kappa _0\). This fact was already known [62, 64, 65].
5.2 ModMax theory
The recently proposed [68] ModMax electrodynamics is of particular interest in that it preservers both SO(2) duality and conformal invariance (see also [69]). It is described by
where \(\gamma \) is a dimensionless parameterFootnote 16 (see [68] for physical reasons to restrict to \(\gamma \ge 0\), with \(\gamma =0\) corresponding to Maxwell’s theory). Here (75) takes the form (6) with
Since here neither \(E_{ab}\) nor \(H^{ab}\) in Eqs. (75), (76) are well-defined for null fields (i.e., for \(I=0=J\)) [68],Footnote 17 we will consider only the non-null case, i.e., the solution (30), (31). Then (7) gives
where \(\theta _0\) is defined as in (79). Here one should exclude special fine-tuned configurations with \(\cosh \gamma +\sinh \gamma \cos \theta _0\), which correspond to \(b_1=0\) and thus \(E_{ab}=0\), i.e., to stealth configurations of the theory (82), for which the spacetime metric is Einstein.
Solutions of this type (in the case with \(k_2=0\) in (30)) were considered in [70].
5.2.1 Extension to Einstein–Weyl gravity
The results given above refer to Einstein’s gravity coupled to ModMax electrodynamics (i.e., (74) with (82)). Given the conformal invariance of the latter, it may be now instructive to consider an example where also gravity is modified by the addition of a conformal invariant term. A well-known theory with such a property is given by Einstein–Weyl gravity, corresponding to the action
with (82), where \(\alpha _0\) is a coupling constant with the dimension of a length squared (Weyl conformal gravity is obtained for \(\kappa ^{-1}=0\)). Here (76) is unchanged, while (75) becomes [71, 72]
where \(B_{ab}\) is the (symmetric, traceless, conserved) Bach tensor
As above, it makes sense here to consider only the non-null field solution (30), (31). For the latter one easily finds (in agreement with the results of Sect. 2)
which with (6), (7), (86), (87) and (79) gives
Similarly as in the case of Einstein gravity discussed above, special configurations with \(\cosh \gamma +\sinh \gamma \cos \theta _0+\frac{8}{3}\alpha _0 \kappa _0 \Lambda _0=0\) describe stealth fields (i.e., \(E_{ab}=0\)) and should be considered separately.
6 Example II: Horndeski’s electrodynamics
Horndeski [73] obtained the unique theory (constructed from a Lagrangian depending on the metric, the vector potential and their derivatives) such that: (i) the corresponding field equations are of second order; (ii) in the presence of sources they are compatible with charge conservation; (iii) the equation for the electromagnetic field reduces to Maxwell’s equation in flat space. The theory of [73] is given by
where \(\beta _0\) and \(\gamma _0\) are coupling constants (dimensionless and with the dimension of a length squared, respectively), and the standard Einstein–Maxwell theory is recovered for \(\gamma _0=0\). In (4) and (5) this gives rise to [73,74,75]
with \(T_{ab}\) as in (3).
6.1 Non-null fields
For the Einstein–Maxwell solution (30), (31), the term \(F_{df}\,{}^{*}\!R^{*abdf}\) in (92) becomes a linear combination with constant coefficients of \(F^{ab}\) and \({}^{*}\!F^{ab}\), so that (5) is satisfied identically, in agreement with the results of Sect. 2. In (91) one has \(\nabla _d{}^{*}\!F_{ac}\,\nabla ^c{}^{*}\!{F_{b}}^{d}=0\) (see Sect. 2), while one can compute
Using (91), (93), (6) and again the parametrization (79), constraints (7) become
Here one should exclude special fine-tuned configurations such that \(\beta _0-\gamma _0(\Lambda _0+\kappa _0\rho _0^2\cos \theta _0)=0\), which correspond to \(b_1=0\) and thus to stealth configurations in the theory (90), for which the spacetime metric is Einstein (more precisely, these configurations are “almost stealth”, since in general \(b_2\ne 0\)).
Solutions of the form (30), (31) were also constructed in [76] in the case \(h=0\) with \(k_2>0\).
6.2 Null fields
For the fields \(({\varvec{g}},{\varvec{F}})\) given by (55), (47), in (92) one finds \(F_{df}\,{}^{*}\!R^{*abdf}=0\), therefore (5) is satisfied trivially, in agreement with the results of Sect. 3. The terms in (91) take the form (recall (58) and footnotes 4, 6, and 9)
Hence (91), (6) give \(b_2=0\) and thus, by (7),
However, \(b_1\) as determined from (91) (with (34), (95), (96)) is not a constant, so that the field equation (65) (i.e., the only remaining component of (4) to be solved) reduces to the following partial differential equation
This can be solved (at least in principle) to determine the metric function \(H^{(0)}\) of (55). We emphasize once again that here \(H^{(0)}\) is not of the form (57) as in the electrovac Einstein–Maxwell theory – i.e., a solution of (98) corresponds on the Einstein–Maxwell side to a null electromagnetic field accompanied by aligned pure radiation, as discussed in more generality in Sects. 1.1 and 3.2. In the limit \(\Lambda _0=0\) one recovers the pp -waves obtained in [77, 78].
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This work is purely theoretical ]
Notes
The spacetime constants \(b_1\) and \(b_2\) may be functions of \(\Lambda _0\) and possible coupling constants of the modified theory, as well as of other parameters which characterize a specific pair \(({\varvec{g}},{\varvec{F}})\) – see Sects. 5 and 6 for some explicit examples (cf. also [16,17,18,19] in the vacuum case). It should be noted that in certain cases the algebraic equations (7) may not admit a real solution for \((\Lambda _0,\kappa _0)\) in terms of \((\Lambda ,\kappa )\). Moreover, there may be particular degenerate cases for which \(b_1\) or \(b_2\) become singular, or \(b_1=0\), in which case the “seed” solution \(({\varvec{g}},{\varvec{F}})\) cannot be used to obtain a solution of the modified theory (4), (5) with the method described above (cf. again the examples in Sects. 5 and 6).
A related result was obtained with a different method in theorem 3.2 of [14].
Degenerate Kundt metrics [26, 27] are defined as a subset of Kundt metrics for which the Riemann tensor and its covariant derivatives of arbitrary order are of algebraic type II (or more special) aligned with the Kundt vector field \(\varvec{\ell }\) (cf. also the review [28]). As it turns out, a Kundt spacetime is degenerate if it is of aligned Riemann type II and \(\ell ^a R_{,a}=0\) [12]. In the following we will also bear in mind the known fact that for Einstein–Maxwell fields in the Kundt class, \(\varvec{\ell }\) is automatically a principal null direction (PND) of \({\varvec{F}}\) and a double PND of the Weyl tensor (see, e.g., chapter 31 of [29]). This implies that in the Einstein–Maxwell case a Kundt space is necessarily degenerate and the Petrov type is II or more special.
A tensor of this form appears, for example, in the Einstein equation of Horndeski’s electrodynamics, cf. (91) below, as can be seen using the identity (recall (9)) \(\nabla _d\,{}^{*}\!F_{ac}\nabla ^c\,{}^{*}\!F_{b}^{\ d}=\frac{1}{4}(\nabla _d{\mathcal {F}}_{ac}\nabla ^c\mathcal {\bar{F}}_{b}^{\ d}-\nabla _d{\mathcal {F}}_{ac}\nabla ^c{\mathcal {F}}_{b}^{\ d}+\text{ c.c.})\). We note that here \(\nabla _d{\mathcal {F}}_{ac}\nabla ^c{\mathcal {F}}_{b}^{\ d}=0\) (thanks to (13), (16), (17)), and the additional term \(F^{ce}{F^{d}}_{e}\,{}^{*}\!R^*_{acbd}\) contained in (91) does not affect the present discussion since it does not possess a component proportional to \(\ell _a \ell _b\), as can be seen using (13), the fact that the traceless Ricci tensor must obey \(\Phi _{11}=\kappa _0\Phi _1{\bar{\Phi }}_1\) (thus possessing only components of b.w. 0) and \({}^{*}\!R^*_{acbd}=-C_{acbd}+\ldots \), where the dots denote terms constructed from the Ricci tensor and the metric.
Hereafter the symbols
 ,
,  , \(\eth \) and \(\eth '\) denote the standard derivative operators defined in the compact GHP formalism [30], which is reviewed in Appendix A. The explicit form of (51) in terms of ordinary partial derivatives, which will not be needed in the rest of the paper, can be found in [29, 52]. For the sake of definiteness, let us only mention here that, in the spacetime (44)–(46), the function \(H^{(0)}\) appears in (51) only through the term \(\eth \nu =\frac{1}{2}\bigtriangleup H^{(0)}+\ldots \), where where \(\bigtriangleup =2P^2\partial _{{\bar{\zeta }}}\partial _\zeta \) is the Laplace operator in the transverse 2-space spanned by \((\zeta ,{\bar{\zeta }})\), and the ellipsis denotes quantities which vanish when \(g=0\) (as will be relevant in Sect. 3.2).
, \(\eth \) and \(\eth '\) denote the standard derivative operators defined in the compact GHP formalism [30], which is reviewed in Appendix A. The explicit form of (51) in terms of ordinary partial derivatives, which will not be needed in the rest of the paper, can be found in [29, 52]. For the sake of definiteness, let us only mention here that, in the spacetime (44)–(46), the function \(H^{(0)}\) appears in (51) only through the term \(\eth \nu =\frac{1}{2}\bigtriangleup H^{(0)}+\ldots \), where where \(\bigtriangleup =2P^2\partial _{{\bar{\zeta }}}\partial _\zeta \) is the Laplace operator in the transverse 2-space spanned by \((\zeta ,{\bar{\zeta }})\), and the ellipsis denotes quantities which vanish when \(g=0\) (as will be relevant in Sect. 3.2).To be precise, by a term quadratic in \({\varvec{\mathcal{F}}}\) we actually mean a product \({\varvec{\mathcal{F}}}{\bar{{\varvec{\mathcal{F}}}}}\), which indeed has \((-2,0)\) if \({\varvec{\mathcal{F}}}\) has \((-1,-1)\) (and similarly for terms quadratic in the covariant derivatives).
Cf. footnote 6 and Appendix A for details on the GHP notation. Let us only mention here that in the spacetime (55) one has \(\eth '\Phi _2=(P\Phi _2)_{,{\bar{\zeta }}}=(P^2{\bar{f}})_{,{\bar{\zeta }}}\) (which is necessarily non-zero since \(\Lambda _0\ne 0\ne f\)), and higher-order derivatives can be expressed as \(\eth '^{k+1}\Phi _2=P^{-k}(P^{k+1}\eth '^k\Phi _2)_{,{\bar{\zeta }}}\).
A result of [54] states that Einstein–Maxwell solutions of type D with a null Maxwell field do not exist in the Kundt class, when the only contribution to the energy–momentum tensor comes from the Maxwell field. However, this does not apply here precisely because we have allowed also for pure radiation.
This is the same tensor computed for the degenerate Kundt case in (19) and, mutatis mutandis, comments similar to those given in footnote 4 apply also here.
Further analysis reveals that in fact both \(\kappa =0\) and \(\nu =0\) (cf. [57] for related computations) – this is however not relevant to the present discussion.
We emphasize this is a very special situation for which \(b_1=\)const also in the null case (i.e., Eq. (75) with (34) means that in (63) one has \(a_k=0\) for \(k\ge 0\) and \(c_j=0\) for \(j\ge 1\)) so that \(({\varvec{g}},{\varvec{F}})\) can be taken to be an Einstein–Maxwell solution also there – without the additional pure radiation that needs to be included in the general discussion of Sects. 1.1 and 3.2.
According to [66], earlier unpublished results were obtained by Jan Slavík: “It should be noticed that Slavík, looking for some solutions in nonlinear electrodynamics (NLE), mentions already that, in the conformally flat subcase, it is possible to assign the BR metric the role of a carrier of a solution to nonlinear dynamics (J. Slavík: Doctoral Thesis, 1976, Institute of Theoretical Physics of the University of Warszawa, Poland)”.
The field equations for the electromagnetic field, however, remain well-behaved in the Hamiltonian formalism [68]. Thanks to Dmitri Sorokin for useful comments on this point.
We warn the reader that in the appendices we use for spinors the more traditional signature convention of [30, 32], i.e., the basis (A2) with (A1) corresponds to minus the metric (12) used in the main body of the paper. Furthermore, to make the contact with the NP formalism easier, in the GHP notation we make the standard substitutions [29, 30, 32] \(\tau '=-\pi \), \(\sigma '=-\lambda \), \(\rho '=-\mu \), \(\kappa '=-\nu \), \(\gamma '=-\epsilon \), \(\beta '=-\alpha \).
The Maxwell equation is satisfied identically here as a consequence of () and (A13).
More precisely, such components are 2-balanced, as defined in [19] (see also Lemma 1 therein).
Although \({\bar{\phi }}_{AB}\) (and thus \({\bar{{\varvec{\mathcal{F}}}}}\)) is not invariant under the Sachs symmetry (as opposed to \(\phi _{AB}\), cf. (C5)), it is invariant under a “dual” Sachs symmetry \(o_A\mapsto -\iota _A\), \(\iota _A\mapsto o_A\), \({\bar{o}}_{A'}\mapsto {\bar{o}}_{A'}\), \({\bar{\iota }}_{A'}\mapsto {\bar{\iota }}_{A'}\).
For completeness, it should be observed that if \(\eta \) is a component of a certain covariant derivative of \(\Psi _{ABCD}\), one additional differentiation also produces terms of the form \(\nu \eta \) and \({\bar{\nu }}\eta \) (via (B4), cf. (B8)). However, since \(\eta \) is 1-balanced and
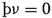 (recall (B2)), all such terms are automatically 3-balanced (as defined in [19], see also Lemma 1 therein), which implies they possess b.w. not greater than \(-4\) and can thus be neglected for the purposes of the present discussion.
(recall (B2)), all such terms are automatically 3-balanced (as defined in [19], see also Lemma 1 therein), which implies they possess b.w. not greater than \(-4\) and can thus be neglected for the purposes of the present discussion.
References
G. Mie, Grundlagen einer Theorie der Materie. Ann. Phys. 342, 511–534 (1912)
M. Born, Modified field equations with a finite radius of the electron. Nature 132, 282 (1933)
M. Born, L. Infeld, Foundations of the new field theory. Proc. R. Soc. A 144, 425–451 (1934)
W. Heisenberg, H. Euler, Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 98, 714–732 (1936)
V. Weisskopf, Über die Elektrodynamik des Vakuums auf Grund der Quantentheorie des Elektrons. Kong. Dan. Vid. Sel. Mat. Fys. Med. 14(6), 1–39 (1936)
H. Euler, Über die Streuung von Licht an Licht nach der Diracschen Theorie. Ann. Phys. 418, 398–448 (1936)
J.S. Schwinger, On gauge invariance and vacuum polarization. Phys. Rev. 82, 664–679 (1951)
E.S. Fradkin, A.A. Tseytlin, Non-linear electrodynamics from quantized strings. Phys. Lett. B 163, 123–130 (1985)
E. Schrödinger, Contributions to Born’s new theory of the electromagnetic field. Proc. R. Soc. Lond. Ser. A 150, 465–477 (1935)
E. Schrödinger, A new exact solution in non-linear optics (two-wave-system). Proc. R. Irish Acad. A 49, 59–66 (1943)
S. Deser, Plane waves do not polarize the vacuum. J. Phys. A 8, 1972–1974 (1975)
M. Ortaggio, V. Pravda, Electromagnetic fields with vanishing scalar invariants. Class. Quantum Gravity 33, 115010 (2016)
M. Ortaggio, V. Pravda, Electromagnetic fields with vanishing quantum corrections. Phys. Lett. B 779, 393–395 (2018)
S. Hervik, M. Ortaggio, V. Pravda, Universal electromagnetic fields. Class. Quantum Gravity 35, 175017 (2018)
M. Kuchynka, M. Ortaggio, Einstein–Maxwell fields with vanishing higher-order corrections. Phys. Rev. D 99, 044048 (2019)
A.A. Coley, G.W. Gibbons, S. Hervik, C.N. Pope, Metrics with vanishing quantum corrections. Class. Quantum Gravity 25, 145017 (2008)
İ Güllü, M. Gürses, T.C. Şişman, B. Tekin, AdS waves as exact solutions to quadratic gravity. Phys. Rev. D 83, 084015 (2011)
T. Málek, V. Pravda, Type III and N solutions to quadratic gravity. Phys. Rev. D 84, 024047 (2011)
M. Kuchynka, T. Málek, V. Pravda, A. Pravdová, Almost universal spacetimes in higher-order gravity theories. Phys. Rev. D 99, 044048 (2019)
M. Gürses, S. Hervik, T.C. Şişman, B. Tekin, Anti-de Sitter-wave solutions of higher derivative theories. Phys. Rev. Lett. 111, 101101 (2013)
M. Gürses, Y. Heydarzade, Ç. Şentürk, Kerr–Schild–Kundt metrics in generic gravity theories with modified Horndeski couplings. Eur. Phys. J. C 81, 1147 (2021)
M. Gürses, Y. Heydarzade, Ç. Şentürk, Kerr–Schild–Kundt metrics in generic Einstein–Maxwell theories. Phys. Rev. D 105, 044004 (2022)
S. Hervik, V. Pravda, A. Pravdová, Type III and N universal spacetimes. Class. Quantum Gravity 31, 215005 (2014)
A. Coley, S. Hervik, N. Pelavas, On spacetimes with constant scalar invariants. Class. Quantum Gravity 23, 3053–3074 (2006)
A. Coley, S. Hervik, N. Pelavas, Lorentzian spacetimes with constant curvature invariants in four dimensions. Class. Quantum Gravity 26, 125011 (2009)
A. Coley, S. Hervik, N. Pelavas, Spacetimes characterized by their scalar curvature invariants. Class. Quantum Gravity 26, 025013 (2009)
A. Coley, S. Hervik, G.O. Papadopoulos, N. Pelavas, Kundt spacetimes. Class. Quantum Gravity 26, 105016 (2009)
M. Ortaggio, V. Pravda, A. Pravdová, Algebraic classification of higher dimensional spacetimes based on null alignment. Class. Quantum Gravity 30, 013001 (2013)
H. Stephani, D. Kramer, M. MacCallum, C. Hoenselaers, E. Herlt, Exact Solutions of Einstein’s Field Equations, 2nd edn. (Cambridge University Press, Cambridge, 2003)
R. Geroch, A. Held, R. Penrose, A space-time calculus based on pairs of null directions. J. Math. Phys. 14, 874–881 (1973)
E.T. Newman, R. Penrose, An approach to gravitational radiation by a method of spin coefficients. J. Math. Phys. 3, 566–578 (1962) [See also E. Newman and R. Penrose, Errata. J. Math. Phys. 4, 998 (1963)]
R. Penrose, W. Rindler, Spinors and Space-Time, vol. 1 (Cambridge University Press, Cambridge, 1984)
B. Bertotti, Uniform electromagnetic field in the theory of general relativity. Phys. Rev. 116, 1331–1333 (1959)
M. Ortaggio, J. Podolský, Impulsive waves in electrovac direct product spacetimes with \(\Lambda \). Class. Quantum Gravity 19, 5221–5227 (2002)
S. Hervik, V. Pravda, A. Pravdová, Universal spacetimes in four dimensions. JHEP 10, 028 (2017)
V. Pravda, A. Pravdová, A. Coley, R. Milson, All spacetimes with vanishing curvature invariants. Class. Quantum Gravity 19, 6213–6236 (2002)
A. Coley, R. Milson, V. Pravda, A. Pravdová, Vanishing scalar invariant spacetimes in higher dimensions. Class. Quantum Gravity 21, 5519–5542 (2004)
S. Hervik, T. Málek, V. Pravda, A. Pravdová, Type II universal spacetimes. Class. Quantum Gravity 32, 245012 (2015)
A. Coley, S. Hervik, N. Pelavas, Lorentzian manifolds and scalar curvature invariants. Class. Quantum Gravity 27, 102001 (2010)
T. Levi-Civita, Realtà fisica di alcuni spazi normali del Bianchi. Rend. Acc. Lincei 26, 519–531 (1917)
H. Nariai, On a new cosmological solution of Einstein’s field equations of gravitation. Sci. Rep. Tôhoku Univ. 35, 62–67 (1951)
I. Robinson, A solution of the Maxwell–Einstein equations. Bull. Acad. Polon. 7, 351–352 (1959)
M. Cahen, L. Defrise, Lorentzian 4 dimensional manifolds with “local isotropy’’. Commun. Math. Phys. 11, 56–76 (1968)
J.F. Plebański, S. Hacyan, Some exceptional electrovac type \(D\) metrics with cosmological constant. J. Math. Phys. 20, 1004–1010 (1979)
D.A. García, C.M. Alvarez, Shear-free special electrovac type-II solutions with cosmological constant. Nuovo Cimento B 79, 266–270 (1984)
V.I. Khlebnikov, Gravitational radiation in electromagnetic universes. Class. Quantum Gravity 3, 169–173 (1986)
J. Podolský, M. Ortaggio, Explicit Kundt type \(II\) and \(N\) solutions as gravitational waves in various type \(D\) and \(O\) universes. Class. Quantum Gravity 20, 1685–1701 (2003)
M. Ortaggio, M. Astorino, Ultrarelativistic boost of a black hole in the magnetic universe of Levi–Civita–Bertotti–Robinson. Phys. Rev. D 97, 104052 (2018)
J. Lewandowski, Reduced holonomy group and Einstein equations with a cosmological constant. Class. Quantum Gravity 9, L147–L151 (1992)
M. Ortaggio, Impulsive waves in the Nariai universe. Phys. Rev. D 65, 084046 (2002)
A.G. Walker, Canonical form for a Riemannian space with a parallel field of null planes. Q. J. Math. Oxf. 1, 69–79 (1950)
J. Leroy, R.G. McLenaghan, Sur les espace-temps contenant un champ de vecteurs isotropes récurrents. Bull. Acad. R. Belg. Cl. Sci. 59, 584–610 (1973)
H. Kadlecová, A. Zelnikov, P. Krtouš, J. Podolský, Gyratons on direct-product spacetimes. Phys. Rev. D 80, 024004 (2009)
N. Van den Bergh, Einstein–Maxwell null fields of Petrov type D. Class. Quantum Gravity 6, 1871–1878 (1989)
A.Z. Petrov, Einstein Spaces (Pergamon Press, Oxford, 1969) [translation of the 1961 Russian ed.]
I. Ozsváth, New homogeneous solutions of Einstein’s field equations with incoherent matter obtained by a spinor technique. J. Math. Phys. 6, 590–610 (1965)
I. Ozsváth, Homogeneous solutions of the Einstein–Maxwell equations. J. Math. Phys. 6, 1255–1265 (1965)
M.P. Ryan, L.C. Shepley, Homogeneous Relativistic Cosmologies (Princeton University Press, Princeton, 1975)
I. Anderson, C. Torre, Spacetime groups. J. Math. Phys. 61, 072501 (2020)
J.N. Goldberg, R.K. Sachs, A theorem on Petrov types. Acta Phys. Polon. Suppl. 22, 13–23 (1962)
J. Plebański, Lectures on Non-linear Electrodynamics (Nordita, Copenhagen, 1970)
A. Peres, Nonlinear electrodynamics in general relativity. Phys. Rev. 122, 273–274 (1961)
I. Smolić, Spacetimes dressed with stealth electromagnetic fields. Phys. Rev. D 97, 084041 (2018)
S. Kichenassamy, Sur le champ électromagnétique singulier en théorie de Born–Infeld. C. R. Hebd. Seanc. Acad. Sci. 248, 3690–3692 (1959)
H. Kremer, S. Kichenassamy, Sur le champ électromagnétique singulier dans une théorie du type Born–Infeld. C. R. Hebd. Seanc. Acad. Sci. 250, 1192–1194 (1960)
L.E. Morales, The Bertotti–Robinson solutions as interpreted in terms of nonlinear electrodynamics. Nuovo Cimento B 68, 55–72 (1982)
J. Plebański, L.E. Morales, Exceptional \(D\)-type solutions to Einstein’s equations with nonlinear electromagnetic sources and \(\lambda \). Nuovo Cimento B 92, 61–77 (1986)
I. Bandos, K. Lechner, D. Sorokin, P.K. Townsend, Nonlinear duality-invariant conformal extension of Maxwell’s equations. Phys. Rev. D 102, 121703(R) (2020)
B.P. Kosyakov, Nonlinear electrodynamics with the maximum allowable symmetries. Phys. Lett. B 810, 135840 (2020)
D. Flores-Alfonso, B.A. González-Morales, R. Linares, M. Maceda, Black holes and gravitational waves sourced by non-linear duality rotation-invariant conformal electromagnetic matter. Phys. Lett. B 812, 136011 (2021)
R. Bach, Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungsbegriffs. Math. Z. 9, 110–135 (1921)
H.A. Buchdahl, On a set of conform-invariant equations of the gravitational field. Proc. Edinb. Math. Soc. 10, 16–20 (1953)
G.W. Horndeski, Conservation of charge and the Einstein–Maxwell field equations. J. Math. Phys. 17, 1980–1987 (1976)
G.W. Horndeski, A theorem on second-order vector-tensor field theories (1976) (unpublished)
G.W. Horndeski, J. Wainwright, Energy–momentum tensor of the electromagnetic field. Phys. Rev. D 16, 1691–1701 (1977)
G.W. Horndeski, Birkhoff’s theorem and magnetic monopole solutions for a system of generalized Einstein–Maxwell field equations. J. Math. Phys. 19, 668–674 (1978)
M. Gürses, M. Halil, PP-waves in the generalized Einstein theories. Phys. Lett. A 68, 182–184 (1978)
G.W. Horndeski, Null electromagnetic fields in the generalized Einstein–Maxwell field theory. J. Math. Phys. 20, 726–732 (1979)
Acknowledgements
I am grateful Sigbjørn Hervik for useful comments. This work has been supported by research plan RVO: 67985840 and research grant GAČR 19-09659S.
Author information
Authors and Affiliations
Corresponding author
Appendices
Basics of the GHP formalism
In this appendix we summarize the basic equations of the GHP formalism needed for the purposes of the present paper. Some familiarity with the formalism will, however, be assumed – see [30, 32] for more details.
1.1 Preliminaries
Let us introduce a normalized spinor dyad \((o^A,\iota ^A)\), such that
out of which one can define a standard null tetrad [30, 32]
as used in the main text of the present paper.Footnote 18 In this basis one has
A boost-spin transformation of the dyad is defined by
where \(\chi \) is a complex scalar field.
A quantity (a scalar, a spinor or a tensor) \(\eta \) is called a weighted quantity of type \(\{p,q\}\) if under (A4) it transforms as
In particular, \(o^A\) and \(\iota ^A\) can be regarded themselves as spinors of type \(\{1,0\}\) and \(\{-1,0\}\), respectively. Recall also that complex conjugation interchanges the values of p and q.
Equivalently, one can also say that \(\eta \) possesses boost and spin weights (b, s) given by
which will be useful in the following. Under complex conjugation b is thus invariant whereas s changes sign.
The GHP derivative operators are defined by their action on a quantity of type \(\{p,q\}\), namely


where \((D,D'=\bigtriangleup ,\delta ,\delta '={\bar{\delta }})\) are the standard directional derivatives of the Newman–Penrose formalism [29,30,31,32].
For later use it is useful to display how the derivative operators act on the basis spinors, i.e.,




the RHS of each of the above equations defining one of the weighted spin coefficients.
The types of the weighted spin coefficients, of the Maxwell, traceless Ricci and Weyl spinor components and of the derivative operators are given by

1.2 Type II Kundt spacetimes with an aligned electromagnetic field
From now on we assume that the spacetime is Kundt of Riemann type II, the electromagnetic field is aligned, and the basis dyad is parallelly transported, i.e.,
The commutators thus take the simplified form




along with the complex conjugates of the last two equations.
If one also assumes that the energy–momentum tensor originates from the electromagnetic field, i.e., \(\Phi _{\alpha \beta }=\kappa _0\Phi _\alpha {\bar{\Phi }}_\beta \) (with \(\alpha ,\beta =0,1,2\)), then one also has
Proof for non-null fields (Sect. 2)
In addition to (A13) and (A18), for the solutions of Sect. 2 we have
so that also \(\Phi _{12}=\Phi _{22}=0\), and the spin-coefficient equations and Bianchi identities needed in the following readFootnote 19


The only non-zero derivatives of basis spinors (A8A9A10)–(A11) are given by

1.1 1-balanced s-balanced spinors
Let us consider a spinor (or tensor)Footnote 20 field \(\varvec{\mathcal{S}}\). By a refinement of the notion of 1-balanced tensors introduced in [23] (see also [12, 14, 35,36,37,38]) it is useful to give the following
Definition B.1
(1-balanced s-balanced spinors) A scalar \(\eta \) of boost and spin weights (b, s) is a “1-balanced s-balanced scalar” if it satisfies the following two conditions


A spinor \(\varvec{\mathcal{S}}\) whose components are all 1-balanced s-balanced scalars is a “1-balanced s-balanced spinor”.
Condition (B5) defines 1-balanced scalars [23], therefore a 1-balanced s-balanced spinor is, in particular, a 1-balanced spinor. We will consider only 1-balanced s-balanced spinors with an integer b, which means that \(b\le -2\) for all non-zero components of \(\varvec{\mathcal{S}}\). Furthermore, by (B6), components with \(b=-2\) can only have \(s<0\) (with \(\eth ^{-s}\eta =0\)).
We will need the following
Theorem B.2
(Derivatives of 1-balanced s-balanced spinors) In the spacetime (30) the covariant derivative of a 1-balanced s-balanced spinor \(\varvec{\mathcal{S}}\) is again a 1-balanced s-balanced spinor.
Proof
By assumption, the components of \(\varvec{\mathcal{S}}\) satisfy (B5) and (B6). Since the spacetime is degenerate Kundt, it follows from [14, 23] that \(\nabla \varvec{\mathcal{S}}\) is automatically 1-balanced, i.e., Eq. (B5) is satisfied also by the components of \(\nabla \varvec{\mathcal{S}}\). It remains to be shown that the same is true for Eq. (B6). To this end, we note that the possible non-zero components of \(\nabla \varvec{\mathcal{S}}\) and their respective boost and spin weights are given in terms of those of \(\varvec{\mathcal{S}}\) (the latter being indicated generically as \(\eta \)) by


where we have used (A12), (B4) and (A5), and the components of \(\nabla \varvec{\mathcal{S}}\) are meant up to numerical factors. Recalling (B5), (B6) and the fact that \(b\le -2\) for components of \(\varvec{\mathcal{S}}\) (being 1-balanced), it is easy to see that among the components (B7), (B8), those of b.w. \(-2\) (if any) can only have s.w.\(<0\). Using (A14)–(A17), ()–(B3) and (B5), (B6), one can also see that the property (B6) holds also when \(\eta \) is replaced by any of the components (B7), (B8) (and their respective weights), as we wanted to prove. \(\square \)
Iteratively, it is obvious that the same property holds for any covariant derivative of \(\varvec{\mathcal{S}}\) of arbitrary order, i.e., any components of such covariant derivatives necessarily have b.w. not greater than \(-2\), and those of b.w. \(-2\) can only have negative s.w..
1.2 Application to Sect. 2.2
Let us now employ the above general results for the purposes of the present paper. As discussed in Sect. 2 (and references therein), the covariant derivative of the self-dual Maxwell tensor \({\varvec{\mathcal{F}}}\), of the energy–momentum tensor and of the Weyl tensor are all 1-balanced tensors. It is also easy to see that the covariant derivatives of both the self-dual Maxwell tensor and the self-dual part of the Weyl tensor (or spinor) additionally satisfy condition (B6) and are therefore 1-balanced s-balanced tensors (spinors) – by theorem B.2 this will be true also for their covariant derivatives of any order. The covariant derivative of the energy–momentum tensor (32) is a sum of two terms, the first of which is again a 1-balanced s-balanced tensor. The second term in \(\nabla _c T_{ab}\) is simply the complex conjugate of the first one, and instead of (B6) it satisfies its complex conjugate version, namely  for \(s>0\), and
for \(s>0\), and  for \(s\le 0\) (with \(b=-2\), \(s=1\)). Theorem B.2 ensures that the first covariant derivative of the first term of \(\nabla _c T_{ab}\) is also a 1-balanced s-balanced tensor, while an equivalent (up to complex conjugation) result for the second term is obvious. Iteratively, one can argue similarly for covariant derivatives of \(T_{ab}\) of any order.
for \(s\le 0\) (with \(b=-2\), \(s=1\)). Theorem B.2 ensures that the first covariant derivative of the first term of \(\nabla _c T_{ab}\) is also a 1-balanced s-balanced tensor, while an equivalent (up to complex conjugation) result for the second term is obvious. Iteratively, one can argue similarly for covariant derivatives of \(T_{ab}\) of any order.
As a conclusion, terms of b.w. \(-2\) (i.e., those of highest b.w.) in the covariant derivatives of arbitrary order of the (anti-)self-dual Maxwell tensor, the energy–momentum tensor or the (anti-)self-dual Weyl tensor can only have either \(s<0\) or \(s>0\), but not \(s=0\) – which is indeed the result used in Sect. 2.2.
Proof for null fields with \(D\Psi _4=0\) (Sect. 3.2)
In addition to (A13) and (A18), for the solutions of Sect. 3.2 we have
so that also \(\Phi _{11}=\Phi _{12}=0\), and the spin-coefficient equations, the Bianchi identities and the Maxwell equations needed in the following read



The only non-zero derivatives of basis spinors (A8A9A10)–(A11) are as in (B4).
Before proceeding, it is useful to recall that the spinor equivalent of the null field (33) reads [29, 30, 32]
As discussed in Sects. 1.1 and 3, we do not impose the last component of the Einstein equation in the Einstein–Maxwell theory \(\Phi _{22}=\kappa _0\Phi _2{\bar{\Phi }}_2\).
1.1 Balanced s-balanced spinors
We can now conveniently adapt the approach of Sect. B and refine the notion of balanced spinors given in [36] (cf. also [12, 14, 35, 37]) by defining
Definition C.1
(Balanced s-balanced spinors) A scalar \(\eta \) of boost and spin weights (b, s) is a “balanced s-balanced scalar” if it satisfies the following two conditions


A spinor \(\varvec{\mathcal{S}}\) whose components are all balanced s-balanced scalars is a “balanced s-balanced spinor”.
Condition (C6) defines balanced scalars [36, 37], therefore a balanced s-balanced spinor is, in particular, a balanced spinor. We will consider only spinors with an integer b, which means that \(b\le -1\) for all non-zero components of \(\varvec{\mathcal{S}}\). The above definition also means, in particular, that components of \(\varvec{\mathcal{S}}\) with \(b=-1\) can only have \(s<0\) (with \(\eth ^{-s}\eta =0\)). Recalling also definition B.1, we further note that one has the following series of implications for a spinor: \(\varvec{\mathcal{S}}\) is 1-balanced s-balanced \(\Rightarrow \) \(\varvec{\mathcal{S}}\) is balanced s-balanced \(\Rightarrow \) \(\varvec{\mathcal{S}}\) is balanced.
One has the following useful
Theorem C.2
(Derivatives of balanced s-balanced spinors) In the spacetime (55) the covariant derivative of a balanced s-balanced spinor \(\varvec{\mathcal{S}}\) is again a balanced s-balanced spinor.
Proof
Since the spacetime is degenerate Kundt, \(\nabla \varvec{\mathcal{S}}\) is a balance spinor as well [12, 23, 36, 37], i.e., (C6) holds true for any of its components, so that it remains to prove that (C7) is also obeyed by all components of \(\nabla \varvec{\mathcal{S}}\).
The possible non-zero components of the covariant derivative of \(\varvec{\mathcal{S}}\) and their respective boost and spin weights are again given (up to numerical factors) by (B7), (B8). Those of b.w. \(-1\) (if any) can only have a negative s.w., as can be easily seen using (C6), (C7) and the fact that \(b\le -1\) for components of \(\varvec{\mathcal{S}}\) (being balanced). Furthermore, using (A14)–(A17), (C1)–(C4) and (C6), (C7), it follows that the property (C7) holds also when \(\eta \) is replaced by any of the components (B7), (B8) (and their respective weights). This means that the covariant derivative of \(\varvec{\mathcal{S}}\) is also a balanced s-balanced spinor, as we wanted to prove. \(\square \)
Clearly the above theorem can be applied iteratively, such that covariant derivative of arbitrary order of a balanced s-balanced spinor \(\varvec{\mathcal{S}}\) are also balanced s-balanced spinors. It follows, in particular, that any components of such covariant derivatives with b.w. \(-1\) can only have a negative s.w..
Let us now consider a spinor \(\varvec{\mathcal{S}}\) possessing components that, in addition to (C6) and (C7), further obey

(Note that (C8) is stronger than (C7) but only applies to components with \(b\le -2\).) This implies, in particular, that components of \(\varvec{\mathcal{S}}\) with \(b=-2\) can only have \(s<0\), with \(\eth ^{-s}\eta =0\). Similarly as above, it is easy to see iteratively that this property is inherited by covariant derivatives of \(\varvec{\mathcal{S}}\) of any order. It follows that, for all of those, terms with \((b,s)=(-2,0)\) vanish identically.
1.2 Application to Sect. 3.2.2
1.2.1 Components of \(\nabla ^k{\varvec{F}}\)
The null electromagnetic field (33) (or its spinor equivalent (C5)) has \((b,s)=(-1,-1)\). Its only component \(\Phi _2\) satisfies (C4), which means that \({\varvec{\mathcal{F}}}\) is balanced s-balanced (as defined by (C6), (C7)). By theorem C.2, covariant derivatives of \({\varvec{\mathcal{F}}}\) of arbitrary order are also balanced s-balanced, which implies that their components with \(b=-1\) necessarily have \(s<0\). For the complex conjugate \({\bar{{\varvec{\mathcal{F}}}}}\) and its covariant derivatives, a similar argument shows that components with \(b=-1\) necessarily have \(s>0\). Therefore, in neither case are components with \(b=-1\) and \(s=0\) possible. Notice that this conclusion also applies to arbitrary contractions of covariant derivatives \({\varvec{\mathcal{F}}}\) or \({\bar{{\varvec{\mathcal{F}}}}}\) with the metric or with the Weyl tensor. This result is used in Sect. 3.2.2 to prove that \(\nabla _b{H}^{ab}=0\) identically, in the context of the Einstein–Maxwell solutions considered there.
Let us now discuss the form of components with \((b,s)=(-1,-1)\) contained in the covariant derivatives (of arbitrary order) of \({\varvec{\mathcal{F}}}\). First, let us notice that after each differentiation, the produced components which are proportional to \(\nu \) or \({\bar{\nu }}\) (cf. (B8)) will always have \(b\le -3\), which follows from \({\varvec{\mathcal{F}}}\) being balanced and from the first of (C2).Footnote 21 For the purposes of our discussion these components can thus be neglected, i.e., when considering derivatives \(\nabla ^k\phi _{AB}\) it suffices to focus on components of the form \(\nabla ^k\Phi _2\). It follows that components of \(\nabla ^k\phi _{AB}\) with \((b,s)=(-1,-1)\) can only be produced by applying on \(\Phi _2\) an equal number of  and
and  operators, and/or an equal number of \(\eth \) and \(\eth '\) (in any order) – in particular this implies that they can appear only in derivatives of even order. Now, because of (C4), it suffices to consider components of the form
operators, and/or an equal number of \(\eth \) and \(\eth '\) (in any order) – in particular this implies that they can appear only in derivatives of even order. Now, because of (C4), it suffices to consider components of the form  and \((\ldots )\eth '^k\Phi _2\), where the dots represent an arbitrary sequence of derivative operators such that (because of what we have just remarked) the total number of operators
and \((\ldots )\eth '^k\Phi _2\), where the dots represent an arbitrary sequence of derivative operators such that (because of what we have just remarked) the total number of operators  acting on \(\Phi _2\) equals that of
acting on \(\Phi _2\) equals that of  , and similarly for \(\eth \) and \(\eth '\). Thanks to (A14) and (A16), all operators
, and similarly for \(\eth \) and \(\eth '\). Thanks to (A14) and (A16), all operators  can be shifted to the right until they act on \(\Phi _2\) – up to bearing in mind that every time that
can be shifted to the right until they act on \(\Phi _2\) – up to bearing in mind that every time that  is swapped with
is swapped with  , also an additional term of lower order of differentiation will be produced. Therefore, terms containing
, also an additional term of lower order of differentiation will be produced. Therefore, terms containing  can be iteratively reduced to either zero or to terms of the form
can be iteratively reduced to either zero or to terms of the form  , which can be further simplified by noticing that
, which can be further simplified by noticing that

which follows from (A14). This can be repeated until all operators  and
and  have disappeared. There thus remain to consider terms which contain only an equal number of operators \(\eth \) and \(\eth '\), but no operators
have disappeared. There thus remain to consider terms which contain only an equal number of operators \(\eth \) and \(\eth '\), but no operators  and
and  . Here one can use (A14) to shift \(\eth \) to the right, up to producing a term of lower order of differentiation every time that \(\eth \) is swapped with \(\eth '\), and thus iteratively arrive at either zero or at a term proportional to (using (A15))
. Here one can use (A14) to shift \(\eth \) to the right, up to producing a term of lower order of differentiation every time that \(\eth \) is swapped with \(\eth '\), and thus iteratively arrive at either zero or at a term proportional to (using (A15))
To summarize, the components of the covariant derivatives of \({\varvec{\mathcal{F}}}\) possessing \((b,s)=(-1,-1)\) are either zero or proportional (via a numerical factor) to
in the latter case k being an even positive integer corresponding to the order of differentiation of the particular covariant derivative being considered.Footnote 22 From the previous comments it also follows that k-th covariant derivative of (C5) takes the form
where \(\Upsilon _{C_1C'_1\ldots C_kC'_k}\) is a spinor with weights (0, 0) and the dots denote terms with weights different from \((-1,-1)\) (see (C16) below for an explicit example). For certain applications it is also useful to observe that, irrespective of its precise form, the spinor \(\Upsilon _{C_1C'_1\ldots C_kC'_k}\) (and thus the full first term on the RHS of (C13)) is invariant under the “Sachs symmetry”Footnote 23\(o_A\mapsto o_A\), \(\iota _A\mapsto \iota _A\), \({\bar{o}}_{A'}\mapsto {\bar{\iota }}_{A'}\), \({\bar{\iota }}_{A'}\mapsto -{\bar{o}}_{A'}\). By complex conjugation, similar conclusions hold for the components of the covariant derivatives of \({\bar{{\varvec{\mathcal{F}}}}}\) possessing \((b,s)=(-1,+1)\).Footnote 24
More generally, a similar reasoning reveals that, for \(s\le -1\), components with \((b,s)=(-1,s)\) contained in the covariant derivatives of \({\varvec{\mathcal{F}}}\) will be linear combinations of terms of the form
where k is the order of the covariant derivative in question, k and s have opposite parity and \(-k-1\le s\le -1\).
Finally, \(\phi _{AB}\) does not possess components of b.w. \(-2\), and the components of \(\nabla _{CC'}\phi _{AB}\) satisfy (C8) (in addition to (C6) and (C7)), therefore (as follows from the comments following (C8)) no non-zero components with \((b,s)=(-2,0)\) are possible in covariant derivatives of \({\varvec{\mathcal{F}}}\) or \({\bar{{\varvec{\mathcal{F}}}}}\) of any order.
For the sake of definiteness, let us demonstrate explicitly the above results for the first two covariant derivatives of (C5). The first derivative reads, thanks to (C4),

while the second derivative is

where we have used again (C4) along with the commutators (A14)–(A17). Below each term we have indicated the weights (b, s) of the component it gives rise to (after acting on \(\Phi _2\)). Equations (C15) and (C16) show that no components with \((b,s)=(-2,0)\) are present, as proven more in general above, and that components with \((b,s)=(-1,s)\) are in agreement with the general results (C11) and (C14).
1.2.2 Components of \(\nabla ^k{\varvec{C}}\) and \(\nabla ^k{\varvec{S}}\)
Let us now discuss the form of components of covariant derivatives of the Weyl tensor possessing \((b,s)=(-2,0)\) (as noticed in Sect. 3, here \(\nabla ^k{\varvec{C}}\) is 1-balanced for \(k\ge 1\), therefore it cannot contain terms with \(b>-2\)). In spinorial terms, the first covariant derivative reads (cf. also [35])

No components with weights \((-2,0)\) are present here, but such terms can be produced by taking further derivatives, as we now explain. Recalling (C1) and (C2), one can observe that all components of (C17) are expressed only (up to multiplicative constants) in terms of \(\nu \) and some of its (second) GHP derivatives. Since \(\nu \) has weights \((-2,-1)\), in order to produce (by differentiation) a term with \((-2,0)\) one needs to act on \(\nu \) with an equal number of  and
and  operators, and with a number of \(\eth \) which exceeds precisely by 1 the number of \(\eth '\), in any order – for example one such term is given by (up to reordering of the derivatives)
operators, and with a number of \(\eth \) which exceeds precisely by 1 the number of \(\eth '\), in any order – for example one such term is given by (up to reordering of the derivatives)  .Footnote 25 First, this means that non-zero components with \((-2,0)\) can arise only in covariant derivatives of \(\Psi _{ABCD}\) of even order. Second, using (A14)–(A17) one can argue that any such component can be rewritten as a linear combination of terms of the form (for various values of k)
.Footnote 25 First, this means that non-zero components with \((-2,0)\) can arise only in covariant derivatives of \(\Psi _{ABCD}\) of even order. Second, using (A14)–(A17) one can argue that any such component can be rewritten as a linear combination of terms of the form (for various values of k)
where we have used (C2). Noticing that \((\eth '\eth +\eth \eth ')\Phi _{22}=\bigtriangleup \Phi _{22}\), where \(\bigtriangleup =2P^2\partial _{{\bar{\zeta }}}\partial _\zeta \) is the Laplace operator in the transverse 2-space with metric \(2P^{-2}\textrm{d}\zeta \textrm{d}{\bar{\zeta }}\) (recall (44), (45)), and using (A15), a linear combination of terms (C18) can also be expressed equivalently as a linear combination of terms
For example, one has \(\bigtriangleup ^2\Phi _{22}=4(\eth '^2\eth ^2-\Lambda _0 \eth '\eth )\Phi _{22}\), \(\bigtriangleup ^3\Phi _{22}=8(\eth '^3\eth ^3-4\Lambda _0 \eth '^2\eth ^2+\Lambda _0^2\eth '\eth )\Phi _{22}\), etc..
Since here the Ricci tensor has the form \(R_{ab}=\Lambda _0 g_{ab}+2\Phi _{22}\ell _a\ell _b\), the argument given above for the covariant derivatives of the Weyl tensor can easily be adapted to the covariant derivatives of the Ricci tensor, so their components \((-2,0)\) can also only be a linear combination of terms (C19) (and no components with b.w. greater than \(-2\) are possible).
From the fact that the Weyl and Ricci tensor only possess components of b.w. 0 (cf. the comments in the last paragraph of Sect. 3.1) and \(-2\) and their covariant derivatives are 1-balanced, it follows that any rank-2 tensor constructed from the Riemann tensor and its covariant derivatives of arbitrary order is necessarily symmetric and its component are either proportional to the metric tensor (b.w. 0) or a linear combination of terms (C19) (b.w. \(-2\)). Thus we have the the followingFootnote 26
Theorem C.3
(Rank-2 tensors) In the family of spacetimes (55), any rank-2 tensor constructed from the Riemann tensor and its covariant derivatives of arbitrary order takes one of the two following equivalent forms
where \(N\in {\mathbb {N}}\), \(\lambda _0\), \(a_k\) and \({\hat{a}}_k\) are constants, and \(\Phi _{22}=\frac{1}{2}\bigtriangleup H\).
Remark C.4
From the previous discussion it follows that the term of b.w. \(-2\) in (C20) (i.e., the one proportional to \(\ell _a\ell _b\)) can only be constructed linearly in the traceless Ricci tensor and the covariant derivatives of arbitrary order of the Riemann tensor.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Ortaggio, M. Einstein–Maxwell fields as solutions of higher-order theories. Eur. Phys. J. C 82, 1056 (2022). https://doi.org/10.1140/epjc/s10052-022-10966-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10966-x



 ,
,  ,
, 
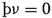 (recall (
(recall (