EKO: evolution kernel operators

Abstract

We present a new QCD evolution library for unpolarized parton distribution functions: EKO. The program solves DGLAP equations up to next-to-next-to-leading order. The unique feature of EKO is the computation of solution operators, which are independent of the boundary condition, can be stored and quickly applied to evolve several initial PDFs. The EKO approach combines the power of N-space solutions with the flexibility of a x-space delivery, that allows for an easy interface with existing codes. The code is fully open source and written in Python, with a modular structure in order to facilitate usage, readability and possible extensions. We provide a set of benchmarks with similar available tools, finding good agreement.

1 Introduction

As we are entering the era of high-energy precision physics, theorists strive to keep up with the experimental precision [1]. The determination of parton distribution functions (PDFs) is becoming a major limiting factor and theory groups come up with more and more involved procedures to improve the extraction [2,3,4] eventually aiming for a one percent accuracy [5]. In order to achieve this goal a thorough treatment of theoretical uncertainties is required [6], that so far was challenging with the current state-of-the-art codes. In this paper, we present EKO a new QCD evolution library that matches the requirements and desiderata of this new era.

EKO solves the evolution equations [7,8,9] in Mellin space (see Sect. 2.1) to allow for simpler solution algorithms (both iterative and approximated). Yet, it provides result in momentum fraction space (see Sect. 2.2) to allow an easy interface with existing codes.

EKO computes evolution kernel operators (EKO) which are independent of the initial boundary conditions but only depend on the given theory settings. The operators can thus be computed once, stored on disk and then reused in the actual application. This method can lead to a significant speed-up when PDFs are repeatedly being evolved, as it is customary in PDF fits. This approach has been introduced by FastKernel [10,11,12] and it is further developed here.

EKO is open-source, allowing easy interaction with users and developers. The project comes with a clean, modular, and maintainable codebase that guarantees easy inspection and ensures it is future-proof. We provide both a user and a developer documentation. So, not only a user manual, but even the internal documentation is published, with an effort to make it as clear as possible.

EKO currently implements the leading order (LO), next-to-leading order (NLO) and next-to-next-to-leading order (NNLO) solutions [13,14,15]. However, it is organized in such a way that the addition of higher order corrections, such as the next-to-next-to-next-to-leading order (N$^{3}$LO) [16], can be achieved with relative ease. This accuracy is needed to match the precision in the determination of the matrix elements for several processes at LHC (see e.g. [17] and references therein). We also expose the associated variations of the various scales.

EKO correctly treats intrinsic heavy quark distributions, required for studies of the heavy quark content of the nucleon [18]. While the treatment of intrinsic distributions in the evolution equations is mathematically simple, as they decouple in a specific basis, their integration into the full solution, including matching conditions, is non-trivial. We also implement backward evolution, again including the non-trivial handling of matching conditions.

EKO is another corner stone in a suite of tools that aims to provide new handles to the theory predictions in the PDF fitting procedure. To obtain the theory predictions in a typical fitting procedure, first, one needs to evolve a candidate PDF up to the process scale, and then convolute it with the respective coefficient function. The process specific coefficient function can be stored in the PineAPPL format [19, 20]. EKO is interfaced with PineAPPL to produce interpolation grids that can be directly used in a PDF fit, avoiding to do the evolution on the fly, but beforehand. EKO is also powering yadism [21] a new DIS coefficient function library.

EKO adopts Python as a programming language opting for a high-level language which is easy to understand for newcomers. In particular, with the advent of Data Science and Machine Learning, Python has become the language of choice for many scientific applications, mainly driven by the large availability of packages and frameworks. We decided to write a code that can be used by everyone who needs QCD evolution, and to make it possible for applications that are not supported yet to be built on top of the provided tools and ingredients. For this reason the code is developed mainly as a library, that contains physics, math, and algorithmic tools, such as those needed for managing or storing the computed operators. As an example we also expose a runner, making use of the built library to deliver an actual evolution application. We apply modern best practices for software development, such as automated tests, Continuous Integration (CI), and Continuous Deployment (CD), to ensure a high quality of coding standard and a routinely checked code basis.

References The open-source repository is available at: https://github.com/N3PDF/eko

In the following we do not attempt to give a complete overview over all provided features and options, but limit ourselves to a brief review. The full documentation instead can be accessed at: https://eko.readthedocs.io/en/latest/

This document is also regularly updated and extended upon the implementation of new features.

2 Theory overview

We do not attempt to give a full review of the underlying theory here as it is known since a long time and discussed extensive elsewhere (see e.g. [22, 23] and references therein). We refer the interested reader to the specific references given in the following and to the accompanying online documentation where instead we give a detailed overview. All sections in the following have an equivalent section in the online documentation. Also the respective code implementations of the various ingredients contain relevant information and are also accessible in the documentation via the API section.

The central equations that EKO is solving are the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution equations [7,8,9] given by

(1)

where ${\textbf {f}}(x,\mu _F^2)$ is a vector of PDFs over flavor space with x the momentum fraction and $\mu _F^2$ the factorization scale. The main ingredients to Eq. (1) are the Altarelli-Parisi splitting functions ${\textbf {P}}(a_s(\mu _R^2),x,\mu _F^2)$ [13, 14], which are matrices over the flavor space. Finally, $\otimes$ denotes the multiplicative (or Mellin) convolution.

The splitting functions ${\textbf {P}}(a_s(\mu _R^2),x,\mu _F^2)$ expose a perturbative expansion in the strong coupling $a_s(\mu _R^2)$:

(2)

which is currently known at NNLO [13,14,15] and is under investigation for N$^{3}$LO [16]. In a first step, the renormalization scale $\mu _R$ and the factorization scale $\mu _F$ can be assumed to be equal $\mu _R= \mu _F$ and the renormalization scale dependence can be restored later on. The variation of the ratio $\mu _R/\mu _F$ can be considered as an estimated to missing higher order uncertainties (MHOU) [6].

In order to solve Eq. (1) a series of steps has to be taken, and we highlight these steps in the following sections.

2.1 Mellin space

The presence of the derivative on the left-hand-side and the convolution on the right-hand-side turns Eq. (1) into a set of coupled integro-differential equations which are non-trivial to solve.

A possible strategy in solving Eq. (1) is by tackling the problem head-on and iteratively solve the integrals and the derivative by taking small steps: we refer to this as “x-space solution”, as the solution uses directly momentum space and this approach is adopted, e.g., by APFEL [24], HOPPET [25], and QCDNUM [26]. However, this approach becomes quite cumbersome when dealing with higher-order corrections, as the solutions becomes more and more involved.

We follow a different strategy and apply the Mellin transformation $\mathcal {M}$

(3)

where, as well here as in the following, we denote objects in Mellin space by a tilde. This approach is also adopted by PEGASUS [27] and FastKernel [10,11,12]. The numerically challenging step is then shifted to the treatment of the Mellin inverse $\mathcal {M}^{-1}$, as we eventually seek for results in x-space (see Sect. 2.2).

2.2 Interpolation

Mellin space has the theoretical advantage that the analytical solution of the equations becomes simpler, but the practical disadvantage that it requires PDFs in Mellin space. This constraint is in practice a serious limitation since most matrix element generators [28] as well as the various generated coefficient function grids (e.g. PineAPPL [19, 20], APPLgrid [29] and FastNLO [30]) are not using Mellin space, but rather x-space.

This is bypassed in PEGASUS by parametrizing the initial boundary condition with up to six parameters in terms of the Euler beta function. However, this is not sufficiently flexible to accommodate more complex analytic forms, or even parametrizations in form of neural networks.

We are bypassing this limitation by introducing a Lagrange-interpolation [31, 32] of the PDFs in x-space on arbitrarily user-chosen grids $\mathbb G$:

$$\begin{aligned} f(x) \sim \bar{f}(x) = \sum _{j} f(x_j) p_j(x), \quad \text {with}\,x_j\in \mathbb G \end{aligned}$$

(4)

For the usage inside the library we do an analytic Mellin transformation of the polynomials . For the interpolation polynomials $p_j$ we are choosing a subset with $N_{degree} + 1$ points of the interpolation grid $\mathbb G$ to avoid Runge’s phenomenon [32, 33] and to avoid large cancellation in the Mellin transform.

2.3 Strong coupling

The evolution of the strong coupling $a_s(\mu _R^2) = \alpha _s(\mu _R^2)/(4\pi )$ is given by its renormalization group equation (RGE):

(5)

and is currently known at 5-loop ($\beta _4$) accuracy [34,35,36,37,38].

This is crucial for DGLAP solution, indeed, since the strong coupling $a_s$ is a monotonic function of the renormalization scale in the perturbative regime, we can actually consider a transformation of Eq. (1)

$$\begin{aligned} \frac{\hbox {d}{\tilde{{\textbf {f}}}}}{\hbox {d}a_s}{}(N,a_s) = - \frac{{\varvec{\gamma }}(N,a_s)}{\beta (a_s)} {\tilde{{\textbf {f}}}}(N, a_s) \end{aligned}$$

(6)

with ${\varvec{\gamma }} = - {\tilde{{\textbf {P}}}}$ the anomalous dimension and $\beta (a_s)$ the QCD beta function, where the multiplicative convolution is reduced to an ordinary product.

2.4 Flavor space

Next, we address the separation in flavor space: formally we can define the flavor space $\mathcal {F}$ as the linear span over all partons (which we consider to be the canonical one):

(7)

The splitting functions ${\textbf {P}}$ become block-diagonal in the “Evolution Basis”, a suitable decomposition of the flavor space: the singlet sector ${\textbf {P}}_S$ remains the only coupled sector over , while the full valence combination $P_{ns,v}$ decouples completely (i.e. it is only coupling to V), and the non-singlet singlet-like sector $P_{ns,+}$ is diagonal over , and the non-singlet valence-like sector $P_{ns,-}$ is diagonal over . The respective distributions are given by their usual definition.

This Evolution Basis is isomorphic to our canonical choice

$$\begin{aligned}&\mathcal {F}\sim \mathcal {F}_{ev} = \text {span}(g, \Sigma , V, T_{3}, T_{8}, T_{15}, T_{24},\nonumber \\&\quad T_{35}, V_{3}, V_{8}, V_{15}, V_{24}, V_{35}) \end{aligned}$$

(8)

but, it is not a normalized basis. When dealing with intrinsic evolution, i.e. the evolution of PDFs below their respective mass scale, the Evolution Basis is not sufficient. In fact, for example, $T_{15} = u^{+} + d^{+} + s^{+} - 3c^{+}$ below the charm threshold $\mu _c^2$ contains both running and static distributions which need to be further disentangled.

We are thus considering a set of “Intrinsic Evolution Bases” $\mathcal {F}_{iev, n_f}$, where we retain the intrinsic flavor distributions as basis vectors. The basis definition depends on the number of light flavors $n_f$ and, e.g. for $n_f=4$, we find

$$\begin{aligned}&\mathcal {F}\sim \mathcal {F}_{iev,4} = \text {span}(g, \Sigma _{(4)}, V_{(4)}, T_{3}, T_{8}, T_{15}, V_{3}, \nonumber \\&\quad V_{8}, V_{15}, b^+, b^-, t^+, t^-) \end{aligned}$$

(9)

with $\Sigma _{(4)} = \sum \nolimits _{j=1}^4 q_j^+$ and $V_{(4)} = \sum \nolimits _{j=1}^4 q_j^-$.

2.5 Solution strategies

The formal solution of Eq. (6) in terms of evolution kernel operators ${\tilde{{{{\textbf {E}}}}}}$ is given by

(10)

with $\mathcal {P}$ the path-ordering operator. If the anomalous dimension ${\varvec{\gamma }}$ is diagonal in flavor space, i.e. it is in the non-singlet sector, it is always possible to find an analytical solution to Eq. (10). In the singlet sector sector, however, this is only true at LO and to obtain a solution beyond, we need to apply different approximations and solution strategies, on which EKO offers currently eight implementations. For an actual comparison of selected strategies, see Sect. 3.2.

2.6 Matching at thresholds

EKO can perform calculation in a fixed flavor number scheme (FFNS) where the number of active or light flavors $n_f$ is constant. This means that both the beta function $\beta ^{(n_f)}(a_s)$ and the anomalous dimension ${\varvec{\gamma }}^{(n_f)}(a_s)$ in Eq. (6) are constant with respect to $n_f$. However, this approximation is likely to fail either in the high energy region $\mu _F^2 \rightarrow \infty$ for a small number of active flavors, or to fail in the low energy region $\mu _F^2 \rightarrow \Lambda _{\text {QCD}}^2$ for a large number of active flavors.

This can be overcome by using a variable flavor number scheme (VFNS) that changes the number of active flavors when the scale $\mu _F^2$ crosses a threshold $\mu _h^2$. This then requires a matching procedure when changing the number of active flavors, and for the PDFs we find

$$\begin{aligned} \tilde{\mathbf {f}}^{(n_f+1)}(\mu _{F,1}^2)&= \tilde{\mathbf {E}}^{(n_f+1)}(\mu _{F,1}^2\leftarrow \mu _{h}^2) {\mathbf {R}^{(n_f)}} \tilde{\mathbf {A}}^{(n_f)}(\mu _{h}^2)\nonumber \\&\quad \times {{\tilde{{\textbf {E}}}}}^{(n_f)}(\mu _{h}^2\leftarrow \mu _{F,0}^2) \tilde{\mathbf {f}}^{(n_f)}(\mu _{F,0}^2) \end{aligned}$$

(11)

where the superscript refers to the number of active flavors and we split the matching into two parts: the perturbative operator matrix elements (OME) $\tilde{\mathbf {A}}^{(n_f)}(\mu _{h}^2)$, currently implemented at NNLO [39], and an algebraic rotation ${\mathbf {R}^{(n_f)}}$ acting only in the flavor space $\mathcal {F}$.

For backward evolution this matching has to be applied in the reversed order. The inversion of the basis rotation matrices $\mathbf {R}^{(n_f)}$ is simple, whereas this is not true for the OME $\varvec{\tilde{A}}^{(n_f)}$ especially in case of NNLO or higher order evolution. In EKO we have implemented two different strategies to perform the inverse matching: the first one is a numerical inversion, where the OMEs are inverted exactly in Mellin space, while in the second method, called expanded, the matching matrices are inverted through a perturbative expansion in $a_s$, given by:

(12)

with $\mathbf {I}$ the identity matrix in flavor space.

2.7 Running quark masses

In the context of PDF evolution, the most used treatment of heavy quarks masses are the pole masses, where the physical values are specified as input and do not depend on any scale. However for specific applications, such as the determination of MHOU due to heavy quarks contribution inside the proton [40], $\overline{\mathrm{MS}}$ masses can also be used. In particular, in [41] it is found that higher order corrections on heavy quark production in DIS are more stable upon scale variation when using the $\overline{\mathrm{MS}}$ scheme. EKO allows for this option as it is discussed briefly in the following paragraphs.

Whenever the initial condition for the mass is not given at a scale coinciding with the mass itself (i.e. $\mu _{h,0} \ne m_{h,0}$, being $m_{h,0}$ the given initial condition at the scale $\mu _{h,0}$), EKO computes the scale at which the running mass $m_{h}(\mu _h^2)$ intersects the identity function. Thus for each heavy quark h we solve:

$$\begin{aligned} m_{\overline{MS},h}(m_h^2) = m_h \end{aligned}$$

(13)

The value $m_h(m_h)$ is then used as a reference to define the evolution thresholds.

The evolution of the $\overline{\mathrm{MS}}$ mass is given by:

(14)

with $\gamma _m(a_s)$ the QCD anomalous mass dimension available up to N$^{3}$LO [42,43,44].

Note that to solve Eq. (14) $a_s(\mu _R^2)$ must be evaluated in a FFNS until the threshold scales are known. Thus it is important to start computing the $\overline{\mathrm{MS}}$ masses of the quarks which are closer to the the scale $\mu _{R,0}$ at which the initial reference value $a_s(\mu _{R,0}^2)$ is given.

Furthermore, to find consistent solutions the boundary condition of the $\overline{\mathrm{MS}}$ masses must satisfy $m_h(\mu _h) \ge \mu _h$ for heavy quarks involving a number of active flavors greater than the number of quark flavors $n_{f,0}$ at $\mu _{R,0}$, implying that we find the intercept between the RGE and the identity in the forward direction ($m_{\overline{MS},h} \ge \mu _h$). The opposite holds for scales related to fewer active flavors.

3 Benchmarking and validation

Although EKO is totally PDF independent, for the sake of plotting we choose NNPDF4.0 [5] as a default choice for our plots, but for Sect. 3.1 where we choose the toy PDF of the Les Houches Benchmarks [45, 46]. We show the gluon distribution g(x) as a representative member of the singlet sector and the valence distribution V(x) as a representative member of the non-singlet sector. Note that PDFs in the same sector have mostly the same behavior, apart from some specific regions (e.g. the $T_{15}$ distribution right after charm matching).

3.1 Benchmarks

In this section we present the outcome of the benchmarks between EKO and similar available tools assuming different theoretical settings.

3.1.1 Les Houches benchmarks

EKO has been compared with the benchmark tables given in [45, 46]. We find a good match except for a list of typos which we list here:

• in table head in [45] should be $2xL_+ = 2x(\bar{u} + \bar{d})$

• in the head of table 1: the value for $\alpha _s$ in FFNS is wrong (as pointed out and corrected in [46])

• in table 3, part 3 of [45]: $xL_-(x=10^{-4}, \mu _F^2 = 10^{4}\,\,\hbox {GeV}^{2})=1.0121\cdot 10^{-4}$ (wrong exponent) and $xL_-(x=0.1, \mu _F^2 = 10^{4}\,\,\hbox {GeV}^{2})=9.8435\cdot 10^{-3}$ (wrong exponent)

• in table 15, part 1 of [46]: $xd_v(x=10^{-4}, \mu _F^2 = 10^{4}\,\,\hbox {GeV}^{2}) = 1.0699\cdot 10^{-4}$ (wrong exponent) and $xg(x=10^{-4}, \mu _F^2 = 10^{4}\,\,\hbox {GeV}^{2}) = 9.9694\cdot 10^{2}$ (wrong exponent)

Some of these typos have been already reported in [47].

Fig. 1

Relative differences between the outcome of NNLO QCD evolution as implemented in EKO and the corresponding results from [46], APFEL [24] and PEGASUS [27]. We adopt the settings of the Les Houches PDF evolution benchmarks [45, 46]

In Fig. 1 we present the results of the VFNS benchmark at NNLO, where a toy PDF is evolved from $\mu _{F,0}^2={2}\,\,\hbox {GeV}^{2}$ up to $\mu _{F}^2=10^{4}\,\,\hbox {GeV}^{2}$ with equal values of the factorization and renormalization scales $\mu _F=\mu _R$. For completeness, we display the singlet S(x) and gluon g(x) distribution (top), the singlet-like $T_{3,8,15,24}(x)$ (middle) and the valence V(x), valence-like $V_{3}(x)$ (bottom) along with the results from APFEL and PEGASUS. We find an overall agreement at the level of $O(10^{-3})$.

3.1.2 APFEL

APFEL [24] is one of the most extensive tool aimed to PDF evolution and DIS observables’ calculation. It is provided as a Fortran library, and it has been used by the NNPDF collaboration up to NNPDF4.0 [5].

APFEL solves DGLAP numerically in x-space, sampling the evolution kernels on a grid of points up to NNLO in QCD, with QED evolution also available at LO. By construction this method is PDF dependent and the code is automatically interfaced with LHAPDF [48]. For specific application, the code offers also the possibility to retrieve the evolution operators with a dedicated function.

The program supplies three different solution strategies, with various theory setups, including scale variations and $\overline{\mathrm{MS}}$ masses.

The stability of our benchmark at different perturbative orders is presented in Fig. 2, using the settings of the Les Houches PDF evolution benchmarks [45, 46]. The accuracy of our comparison is not affected by the increasing complexity of the calculation.

Fig. 2

Relative differences between the outcome of evolution as implemented in EKO and the corresponding results from APFEL at different perturbative orders. We adopt the same settings of Fig. 1

3.1.3 PEGASUS

PEGASUS [27] is a Fortran program aimed for PDF evolution. The program solves DGLAP numerically in N-space up to NNLO. PEGASUS can only deal with PDFs given as a fixed functional form and is not interfaced with LHAPDF.

As shown in Fig. 1, the agreement of EKO with this tool is better than with APFEL, especially for valence-like quantities, for which an exact solution is possible, where we reach $\mathcal {O}(10^{-6})$ relative accuracy. This is expected and can be traced back to the same DGLAP solution strategy in Mellin space.

Similarly to the APFEL benchmark, we assert that the precision of our benchmark with PEGASUS is not affected by the different QCD perturbative orders, as visible in Fig. 3. As both, APFEL and PEGASUS, have been benchmarked against HOPPET [25] and QCDNUM [26] we conclude to agree also with these programs.

Fig. 3

Same of Fig. 2, now comparing to PEGASUS [27]

3.2 Solution strategies

As already mentioned in Sect. 2.5, due to the coupled integro-differential structure of Eq. (1), solving the equations requires in practice some approximations to which we refer as different solution strategies. EKO currently implements 8 different strategies, corresponding to different approximations. Note that they may differ only by the strategy in a specific sector, such as the singlet or non-singlet sector. All provided strategies agree at fixed order, but differ by higher order terms.

In Fig. 4 we show a comparison of a selected list of solution strategies¹:

• iterate-exact: In the non-singlet sector we take the analytical solution of Eq. (6) up to the order specified. In the singlet sector we split the evolution path into segments and linearize the exponential in each segment [49]. This provides effectively a straight numerical solution of Eq. (6). In Fig. 4 we adopt this strategy as a reference.

• perturbative-exact: In the non-singlet sector it coincides with iterate-exact. In the singlet sector we make an ansatz to determine the solution as a transformation ${\textbf {U}}(a_s)$ of the LO solution [27]. We then iteratively determine the perturbative coefficients of ${\textbf {U}}$.

• iterate-expanded: In the singlet sector we follow the strategy of iterate-exact. In the non-singlet sector we expand Eq. (6) first to the order specified, before solving the equations.

• truncated: In both sectors, singlet and non-singlet, we make an ansatz to determine the solution as a transformation ${\textbf {U}}(a_s)$ of the LO solution and then expand the transformation ${\textbf {U}}$ up to the order specified. Note that for programs using x-space this strategy is difficult to pursue as the LO solution is kept exact and only the transformation ${\textbf {U}}$ is expanded.

The strategies differ most in the small-x region where the PDF evolution is enhanced and the treatment of sub-leading corrections become relevant. This feature is seen most prominently in the singlet sector between iterate-exact (the reference strategy) and truncated. In the non-singlet sector the distributions also vanish for small-x and so the difference gets artificially enhanced. This is eventually the source of the spread for the valence distribution V(x) making it more sensitive to the initial PDF.

Fig. 4

Compare selected solutions strategies, with respect to the iterated-exact (called exa in label) one. In particular: perturbative-exact (pexa) (matching the reference in the non-singlet sector), iterated-expanded (exp), and truncated (trn). The distributions are evolved in $\mu _F^2=1.65^2\rightarrow 10^4\,\,\hbox {GeV}^{2}$

Fig. 5

Relative differences between the outcome of NNLO QCD evolution as implemented in EKO with 20, 30, and 60 points to 120 interpolation points respectively

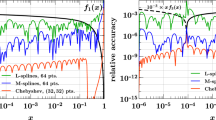
PDF plots The PDF plot shown in Fig. 4 contains multiple elements, and its layout is in common with Figs. 5 and 7.

All the different entries corresponds to different theory settings, and they are normalized with respect to a reference theory setup (e.g. in Fig. 4 the iterative-exact strategy) and the lines correspond to the relative difference.

Furthermore, an envelope and dashed lines are displayed. To obtain them, the full PDF set is evolved, replica by replica, for each configuration (corresponding to a single evolution operator, that is applied to each replica in turn). Then ratios are taken between corresponding evolved replicas, to highlight the PDF independence of EKO rather then any specific set-related features. The upper and lower borders of the envelope correspond respectively to the 0.16 and 0.84 quantiles of the replicas set, while the dashed lines correspond to one standard deviation.

3.3 Interpolation

To bridge between the desired x-space input/output and the internal Mellin representation, we do a Lagrange-Interpolation as sketched in Sect. 2.2 (and detailed in the online documentation). We recommend a grid of at least 50 points with linear scaling in the large-x region ($x > rapprox 0.1$) and with logarithmic scaling in the small-x region and an interpolation of degree four. Also the grids determined by aMCfast [50] perform sufficiently well for specific processes.

Fig. 6

Strong coupling evolution $a_s(\mu _R^2)$ at LO, NLO and NNLO respectively with the bottom matching $\mu _b^2$ at 1/2, 1,  and 2 times the bottom mass $m_b^2$ indicated by the band. In the left panel we show the absolute value, while on the right we show the ratio towards the central scale choice

For a first qualitative study we show in Fig. 5 a comparison between an increasing number of interpolation points distributed according to [19, Eq. 2.12]. The separate configurations are converging to the solution with the largest number of points. Using 60 interpolation points is almost indistinguishable from using 120 points (the reference configuration in the plot). In the singlet sector (gluon) the convergence is significantly slower due to the more involved solution strategies and, specifically, the oscillating behavior is caused due to these difficulties. The spikes for $x\rightarrow 1$ are not relevant since the PDFs are intrinsically small in this region (${\textbf {f}}\rightarrow 0$) and thus small numerical differences are enhanced.

Also note that the results of Sect. 3.1 (i.e. Figs. 1, 2 and 3) confirm that the interpolation error can be kept below the benchmark accuracy.

3.4 Matching

We refer to the specific value of the factorization scale at which the number of active flavors is changing from $n_f$ to $n_f+1$ (or vice-versa) as the threshold $\mu _h$. Although this value usually coincides with the respective quark mass $m_h$, EKO implements the explicit expressions when the two scales do not match. This variation can be used to estimate MHOU [6].

In Fig. 6 we show the strong coupling evolution $a_s(\mu _R^2)$ around the bottom mass with the bottom threshold $\mu _b^2$ eventually not coinciding with the respective bottom quark mass $m_b^2$. The dependency on the LO evolution is only due to the change of active flavor in the beta function ($\beta _0 = \beta _0(n_f)$), which can be seen in the ratio plot by the continuous connections of the lines. At NLO evolution the matching condition already becomes discontinuous for $\mu _h^2 \ne m_h^2$, represented in the ratio plot by the offset for the matched evolution. The matching for the NNLO evolution [43, 44] is intrinsically discontinuous, which is indicated in the ratio plot by the discrete jump at the central scale $\mu _R^2 = m_b^2$. For $\mu _R^2 > 2m_b^2$ the evolution is only determined by the reference value $a_s(m_Z^2)$ and the perturbative evolution order. For $\mu _R^2 < m_b^2/2$ we can observe the perturbative convergence as the relative difference shrinks with increasing orders. Since it is converging, the effect of the matching condition should cancel more and more exactly with the difference in running, but the magnitude of both is increasing with the order, since the perturbative expansion of the beta function $\beta (a_s)$ is a same sign series.

Fig. 7

Difference of PDF evolution with the bottom matching $\mu _b^2$ at 1/2, 2,  and 5 times the bottom mass $m_b^2$ relative to $\mu _b^2 = m_b^2$. Note the different scale for the two distributions. All evolved in $\mu _F^2=1.65^2\rightarrow 10^4\,\,\hbox {GeV}^{2}$

Fig. 8

Relative distance of the product of two opposite NNLO EKOs and the identity matrix, in case of exact inverse and expanded matching (see Eq. (12)) when crossing the bottom threshold scale $\mu _{b}^2=4.92^2\,\,\hbox {GeV}^{2}$. In particular the lower scale is chosen $\mu _F^2={4.90^2}\,\,\hbox {GeV}^{2}$, while the upper is equal to $\mu _F^2={4.94^2}\,\,\hbox {GeV}^{2}$,

In Fig. 7 we show the relative difference for the PDF evolution with threshold values $\mu _h^2$ that do not coincide with the respective heavy quark masses $m_h^2$. When matching at a lower scale the difference is significantly more pronounced as the evolution includes a region where the strong coupling varies faster. When dealing with $\mu _h^2 \ne m_h^2$ the PDF matching conditions become discontinuous already at NLO [39]. These contributions are also available in APFEL [24], but not in PEGASUS [27] and although they are present in the code of QCDNUM [26] they can not be accessed there. For the study in [18] we also implemented the PDF matching at N$^{3}$LO [51,52,53,54,55,56,57,58,59].

3.5 Backward

As a consistency check we have performed a closure test verifying that after applying two opposite EKOs to a custom initial condition we are able to recover the initial PDF. Specifically, the product of the two kernels is an identity both in flavor and momentum space up to the numerical precision. The results are shown in Fig. 8 in case of NNLO evolution crossing the bottom threshold scale $\mu _{F}=m_{b}$. The differences between the two inversion methods are more visible for singlet-like quantities, because of the non-commutativity of the matching matrix $\tilde{\mathbf {A}}_{S}^{(n_f)}$.

Fig. 9

(left) The NNPDF4.0 perturbative charm distribution $T_{15}(x)$ [5] with $\overline{\mathrm{MS}}$ and pole masses NNLO evolution when running on $\mu _F^2=1\rightarrow 10^4\,\,\hbox {GeV}^{2}$. (right) Relative difference to EKO for the same run with APFEL [24]

Fig. 10

Running of the bottom quark mass $m_b(\mu _m^2)$ for different threshold ratios, similar to Fig. 6. The plot shows how the different choices of matching scales affect the running in the matching region (and slightly beyond) at LO, NLO, and NNLO. The border condition for the running has been chosen at $m_b(m_b) = {4.92}\,\,\hbox {GeV}$, as it is clear from the plot, since it is the intersection point of all the curves shown

Special attention must be given to the heavy quark distributions which are always treated as intrinsic, when performing backward evolution. In fact, if the initial PDF (above the mass threshold) contains an intrinsic contribution, this has to be evolved below the threshold otherwise momentum sum rules can be violated. This intrinsic component is then scale independent and fully decoupled from the evolving (light) PDFs. On the other hand, if the initial PDF is purely perturbative, it vanishes naturally below the mass threshold scale after having applied the inverse matching. In this context, EKO has been used in a recent study to determine, for the first time, the intrinsic charm content of the proton [18].

3.6 $\overline{\mathrm{MS}}$ masses

In Fig. 9 we investigate the effect of adopting a running mass scheme onto the respective PDF sets. The left panel shows the $T_{15}(x)$ distribution obtained from the NNPDF4.0 perturbative charm determination [5] using the pole mass scheme and the $\overline{\mathrm{MS}}$ scheme, respectively. The distributions have been evolved on $\mu _F^2={1\rightarrow 10^4}\,\,\hbox {GeV}^{2}$. The mass reference values are taken from [60], with the $\overline{\mathrm{MS}}$ boundary condition on the charm mass given as $m_c(\mu _m={3}\,\,\hbox {GeV}) = {0.986}\,\,\hbox {GeV}$, leading to $m_c(m_c) = {1.265}\,\,\hbox {GeV}$, while the charm pole mass is $m^\mathrm{pole}_{c}\approxeq {1.51}\,\,\hbox {GeV}$ [5]. The major differences are visible in the low-x region where the DGLAP evolution is faster and the differences between the charm mass treatment are enhanced: an higher value of the charm mass increases the singlet like distribution $T_{15}(x)$. For the sake of comparison, in the right panel, we plot the relative distance to our result when comparing with the APFEL [24] implementation. As expected the pole mass results are closer due to the same value of the charm mass, while the $\overline{\mathrm{MS}}$ results have a slightly bigger discrepancy which remains in all the x-range around $1\permille$ accuracy.

Table 1 Comparison between several evolution programs. The upper part of refers to some physical features: by x we mean the momentum fraction, N the Mellin variables, $x^{*}$ denotes that PEGASUS is able to deal with x-space input, but only for fixed PDF parametrization (see [27]). ${\textbf {E}}$ and ${\textbf {f}}$ stands for evolution operators and PDFs respectively. The lower part refers to program aspects, such as program language and interface with LHAPDF

In Fig. 10 we show the evolution of the $\overline{\mathrm{MS}}$ bottom mass $m_b(\mu _m^2)$ using different matching scales $\mu _b^2$ equal to 1/2, 1 and 2 times the mass $m_b^2$, for each perturbative order (LO, NLO, and NNLO). The curve for $\mu _b^2 = m_b^2$ has been plotted as the central one (bold), while the other two are used as the upper and lower borders of the shaded area (according to their value, point by point). The reference value $m_b(\mu _{b,0}^2)$, has been chosen equal for the three curves, and it has been chosen at $m_b(m_b) = {4.92}\,\,\hbox {GeV}$. For this reason, above the central matching point $\mu _m^2 \ge m_b^2$ two curves coincide ($\mu _b^2 = m_b^2$ and $\mu _b^2 = m_b^2/2$) since they are both running with the same number of flavors ($n_f=5$) and they have the same border condition. The curve using $\mu _b^2 = 2m_b^2$, however, still runs with a smaller number of flavors ($n_f=4$) and so does not match the former two. In the lower region $\mu _m^2 < m_b^2$ this is not happening, because even if the number of flavors is now the same, the border condition is specified above matching for $\mu _b^2 = m_b^2$ (in $n_f=5$). So, starting from $m_b^2$ and going downward, the central choice $\mu _b^2 = m_b^2$ is matched first and then evolved, while the higher scale choice $\mu _b^2 = 2m_b^2$ immediately runs with four light flavors at $m_b^2$. Thus the difference consists just in the matching.

4 Conclusions

In this paper we presented a new QCD tool to perform perturbative DGLAP evolution. In Sect. 2 we reviewed some theory aspects that are relevant for this paper. In Sect. 3 we presented a few applications of the implemented EKO features.

Most of the work done to develop EKO has been devoted to reproduce known results from other programs (and slightly extending or amending them to have a consistent behavior), in order to have a more flexible framework where to implement new essential features for physics study (more on this in the Outlook at the end of this section). Benchmarks with already existing and widely used codes are shown in Sect. 3.1, and demonstrated to be successful. Further, the multiple options and configurations available are presented in subsequent sections and discussed, all leading to known and understood behaviors.

This does not mean that the current status of EKO does not expose any novelty. Table 1 summarizes a general comparison on specific features between several evolution programs; we list only tools targeting the same scope of EKO, that is unpolarized PDF fitting. It is exactly for this target (PDF fitting) that EKO is optimized, and among the others three specific features are outstanding: the solution in N-space, the backward VFNS evolution, and the operator-oriented nature.

EKO is the first code to solve DGLAP in Mellin space that has been explicitly designed to be used for PDF fitting, and while this may seem irrelevant, it has been explicitly picked as an improvement for EKO over the similar codes. There are multiple solutions that are only available in x-space by applying numerical approximated procedures, making the exact solution the most reliable one. In N-space this is not required, and the choice of the solution is left completely up to the user, with no numerical deterioration among the alternatives (as it was already for PEGASUS), and thus it can be based on theory considerations. Moreover, the perturbative QCD ingredients used in the evolution (like anomalous dimensions) are often first computed in N-space, making them available for EKO immediately, while a further complex transformation is needed for usage in the other codes.

All the programs listed are able to preform backward evolution in FFNS, that consists in swapping the integral evolution bounds, but the VFNS backward evolution is a unique feature of EKO, which involves the non-trivial inversion of the matching matrix, as outlined in Sect. 2.6.

The reason why EKO is an operator-first framework is discussed in detail in Appendix A.1, but essentially it makes EKO particularly suited for our target: repeated evaluation of evolution for PDF fitting. Producing only operators makes EKO less competitive for single one-shot applications, but the optimal scaling with the size of the task (practically constant, since the time consumed is dominated by the operator calculation) makes it extremely good for massive evolution (and already good when evolving elements).

It should be observed that while the choice of Python as programming language particularly stands out among the other programs (all written in Fortran, either 77 or 95), this is only a benefit from the point of view of project management (being Python much expressive) and third parties contributions (since its syntax is familiar to many). Indeed, we make sure not to experience Python infamous performances, when it comes to the most demanding tasks (like complex kernels evaluation, or Mellin inverse integration) as they either use compiled extensions (e.g. those available in scipy [61]) or they are compiled Just In Time (JIT), using the numba [62] package.

While the main purpose of EKO is to evolve PDFs, other QCD ingredients are required to perform the main task, like evolving the strong coupling $\alpha _s$, running quark masses, or dealing with different flavor bases: they are all provided to the end user, and for this reason actual results are shown in this paper.

We remark that EKO is an open and living framework, providing all ingredients as a public library, and accepting community contributions, bug reports and feature requests, available through the public EKO repository.

Outlook As outlined above EKO implements mostly well-known physics, but we expect a series of upcoming project to build on the provided framework that will extend the current knowledge on PDFs. Several features are already scheduled to be implemented, and a few of them are already at an advanced stage: the N$^{3}$LO solution will be included as soon as it becomes available [16], while N$^{3}$LO matching conditions and strong coupling are already implemented and used in the recent determination of the intrinsic charm content of the proton [18].

Another main goal of EKO is to provide a backbone in the determination of MHOU, in the first place by allowing the variation of the various scales used in the determination of evolved PDFs, that can be considered as an approximation to higher orders, implementing the strategies described in [6]. The variation of matching scales involved in VFNS is already implemented and available.

Other planned features include: polarized evolution [63,64,65], evolution of fragmentation functions [66,67,68], and the QED$\otimes$QCD evolution of the photon-in-hadron distribution [69,70,71], to estimate the impact of electro-weak corrections onto precision predictions.

Appendices

A Technical overview

An EKO is effectively a rank 5 tensor $E_{\mu ,i \alpha j \beta }$, that evolves a PDF set from one given scale to a user specified list of final scales $\mu$:

$$\begin{aligned} f_{\mu ,i\alpha } = E_{\mu ,i \alpha j \beta } f^{(0)}_{j \beta } \end{aligned}$$

(A.1)

where i and j are indices on flavor, and $\alpha$ and $\beta$ are indices on the x-grid.

The computation of each rank 4 tensor is almost independent: In a FFNS for each target $\mu _F^2$ an operator ${\tilde{{\textbf {E}}}}(\mu _{F,0}^2 \rightarrow \mu _F^2)$ is computed separately. Instead, in a VFNS first a set of operators is computed, to evolve from the initial scale to any matching scales (we call these threshold operators). Then, for each target $\mu _F^2$, an operator is computed from the last intermediate matching scale to $\mu _F^2$; finally they are composed together.

1.1 A.1 Performance motivations and operator specificity

Before diving into the details of EKO performances there is a fundamental point that has to be taken into account: EKO is somehow unique as an evolution program, because its main and only output consists in evolution operators.

For this reason, a close comparison on performances with other evolution codes (whose main purpose is the evolution of individual PDFs) would be rather unfair: evolving a single PDF is comparable to the generation of the transformation of a single direction in the PDF space, while the operator acts on the whole function space.

The motivation to primarily look for the operator itself relies on the specific needs of a PDF fit itself. Indeed, a fit requires repeated usage of evolution for the $\chi ^2$ evaluation for each fit candidate, and a final evolution step for the generation of the PDF grids to deliver, as those used by LHAPDF [48]. The first step has been automated long ago, by the generation of the FastKernel tables (formerly done with APFEL evolution, through APFELcomb, inspired to [72]), that store PDF evolution into the grids for predictions, while the second was repeated at any fit, since for each fit is a one-time operation (even though it is actually repeated for the number of Monte Carlo replicas, or Hessian eigenvectors, whose typical sizes are reported in Table 2).

Table 2 Selected PDF sets with their respective number of members

Actually, both the operations of including evolution in theory grids and PDF grids generation can be further optimized, considering that the evolution only depends on a small number of theory parameters, and so the operator does, such that it can be generated only once, and then used over and over.

On top of replicas generation, the search towards an optimal fitting methodology is an iterative process, that involves a large number number of fits. Moreover, whatever program supports the generation of FastKernel tables has to create some kind of evolution operator on its own (since the goal of FastKernel tables is exactly to be PDF agnostic).

So, the EKO work-flow is not a complete novelty, since it was preceded by APFEL in-memory operator generation, but it is a further and strong improvement in that direction: being operator-oriented from the beginning, optimizations have been performed for this specific task², and maintaining an actual operator format, the operators reuse is possible even across the boundary of FastKernel tables generation, and applied with benefit, e.g., for the massive replicas set evolution (consider NNPDF40_nnlo_as_01180_1000, that is a single set consisting of 1000 replicas, that can be evolved with a single operator instead of running 1000 times an evolution program, like all the other similar sets), but even repeated fits.

While the benefit is limited for other use cases, any other highly iterative phenomenological study, in which PDF evolution is repeatedly evaluated from different border conditions, would benefit from being backed by EKO, since the cost of DGLAP evaluation is paid only once (even though we are conscious that this is mainly beneficial for PDF fitting).

1.2 A.2 Computation time

As we said above the computation almost happens independently for each target $\mu _F^2$ and the amount of time required scales almost linearly with the number of requested $\mu _F^2$, except for the thresholds operators in VFNS that are computed only once.

We call computing an operator with a fixed number of flavors “evolving in a single patch”, since in a VFNS the evolution might span multiple patches. When more than a single patch is involved, operators have to be joined at matching scales $\mu _h$ with a non-trivial matching, that has to be computed separately (these are part of the threshold operators).

Typical times required for these calculations in EKO are presented in Table 3. As expected the complexity of the calculation grows with perturbative order, and so even the time taken increases. At LO no matching conditions are needed, while for NLO and NNLO they are computed once for each matching scale.

Table 3 Rough estimates of times taken by EKO, with an average sized x-grid of 50 points and single core

We consider these time performances satisfactory, even though it is not straightforward to compare EKO with the other evolution codes, as mentioned in Appendix A.1. As an example, NNLO evolution in $\mu _F^2 = {1.65^2}\,\,\hbox {Gev}^{2} \rightarrow {100}\,\,\hbox {GeV}^{2}$ crossing the bottom matching at ${4.92^2}\,\,\hbox {Gev}^{2}$ takes $\sim {60}\,\,\hbox {s} + {135}\,\,\hbox {s}$ in EKO (${135}\,\,\hbox {s}$ for the thresholds operators initialization, ${60}\hbox {s}$ for the last patch). APFEL takes $\sim {25}\,\,\hbox {s}$ on the same custom interpolation x-grid (APFEL is able to perform significantly better on a pre-defined, built-in grid).

This comparison shows that on the evolution of a single PDF EKO is not really competitive, but the ratio is limited to $\sim 7.5$. However, we already pointed out that the two programs perform a rather different task: computing a whole operator against a single PDF evolution (on which the benchmarking is done, only because both programs are able to perform this simple task, but it is a worthless task for EKO usage).

The comparison is technically possible, but we do not encourage this kind of benchmarks, because the typical task is actually different, and this motivates the different performances. EKO perform bad in the case of the single task, but with a perfect scaling (negligible work needed for repeated evolution, practically constant), while any other program would perform better for the atomic task, but with a linear scaling in the number of objects to be evolved.

Each program should be selected having in mind the specific usage. EKO is recommended for PDF fitting, and repeated evolution in general.

The time measures in Table 3 and the rest of this section have been obtained on a regular consumer laptop:

None one of them is a careful benchmark, i.e. repeated multiple times, but is mainly meant to show an order of magnitudes comparison.

1.3 A.3 Memory footprint

Memory usage is dominated by the size of the final object produced, since a much smaller internal representation is used during the computation. The final object holds information about the rank 5 operator, so it is strictly dependent on the size of the interpolation x-grid and the amount of target $\mu _F^2$ values.

For an average sized x-grid of 50 points, and a single target $\mu _F^2$ the size of the object in memory is of $\sim {7.5}\hbox {MB}$, which scales linearly with the amount of $\mu _F^2$ requested. The dependency on the size of the x-grid is roughly quadratic.

1.4 A.4 Storage

For permanent storage similar considerations applies with respect to the memory object. The main difference is that the object dumped by the EKO functions is always compressed, leading to a size of $\sim {500}\hbox {kB}$ for a single $\mu _F^2$, which does not necessarily scales linearly with the amount $\mu _F^2$ since the full rank 5 tensor is compressed all-together (a linear scaling is just the worst case). Similar considerations applies to the dependency on the size of the x-grid.

1.5 A.5 Possible improvements

There are a few easy directions to boost the current performances of EKO, leveraging the $\mu _F^2$ splitting.

Jobs To improve the speed of the computation, all the ingredients of the final tensor (patches & matching) can be computed by separate jobs, and dispatched to different processors. They just need to be joined at the very end in a simple linear algebra step.

Notice that the time measures presented in Appendix A.2 are obtained with a fully sequential computation on a single processor, the only one available at present time.

Memory Since both the computation and the consumption of an EKO can be done one $\mu _F^2$ at a time, it is possible to store each rank 4 tensor on disk as soon as it is computed, and to load them in memory only while applying them.

Both of these improvements are in the process of being implemented in EKO.

B User manual

In this section we provide an extremely brief manual about EKO usage. We give here the instruction for the release version associated to this paper. A more expanded and updated manual for the current version can be found in the on-line documentation: https://eko.readthedocs.io/en/latest/overview/tutorials/index.html.

1.1 B.1 Installation

The installation provided to the user of the package is very simple.

We require only:

• a working installation of Python 3³ and

• the official Python package manager pip, usually bundled together any distribution of Python itself.

You can check their availability on your system with:

(for a non sh based environment, e.g. Windows, check the official Python documentation).

The actual installation of the package can be obtained with the following command:

1.2 B.2 Usage

Using EKO as an evolution application is pretty simple, involving the call of a single function to produce an evolution operator.

Nevertheless, it has been intentionally left up to the user the definition of all the settings required for a run. This might be confusing for a newcomer, but it is the best approach since the actual settings might be different for any given application, and there is no one that can be recommended as a best practice; in order to not suggest such an interpretation, we decided to not provide any defaults, and to require the user to be aware of the whole set of settings.

We present now a minimal example, in which the settings are taken from the official benchmarking setup in [45] (which is not worse nor better than any other choice). To be able to access the toy PDF established in [45] you need to install in addition our benchmarking package:

Then you are set to run the following snippet:

For more information about the settings, please refer to the online documentation.

Note, that the reference values for the gluon and the strong coupling are taken from [45, Table 2].

Also note, that the example may not work with newer version of the code, for which, instead, we recommend to follow the online tutorials.