Geodesic congruences in modified Schwarzschild black holes

Abstract

We investigate two different kinds of modified Schwarzschild black holes: A regularized Schwarzschild black hole and a quantum deformed Schwarzschild black hole. We study the geodesics and geodesic congruences in these two modified Schwarzschild black holes. In particular, we calculate the expansion of radial timelike and null geodesic congruences. Based on these results, we discuss some similarities and differences between these two kinds of modified Schwarzschild black holes.

1 Introduction

Black holes are of great interest as being elegant solutions of Einstein’s gravitational field equation. The simplest black hole can be described by the Schwarzschild solution [1] with gravitational mass M. The Schwarzschild solution has been well tested by many experimental tests, such as the deflection of light and the gravitational redshift [2]. However, this solution has a spacetime singularity at $r=0$ [3] with divergent curvature scalar. Also, it possesses incomplete geodesics according to the Penrose and Hawking-Penrose singularity theorems [4, 5].

Among many attempts to avoid the black hole singularity, regular black holes [6, 7] without introducing dramatic deviations from standard physics are of great interests. In 1993, based on spherically symmetric quantum fluctuations of the metric, Kazakov and Solodukhin [8] proposed a deformation of the Schwarzschild solution in general relativity. This quantum deformed Schwarzschild (QDS) metric was originally derived in a reduction of the four-dimensional Einstein action, namely the two-dimensional dilaton theory of gravity. Even though the metric components are regular, the curvature scalars are still singular for the original QDS spacetime. Recently, the author of Ref. [9] proposed a generalized two-parameter class of QDS black holes which have better regularities.

On the other hand, Klinkhamer [10] found an exact solution of the Einstein field equations over a nonsimply-connected manifold [11], which can be viewed as a regularized version of the singular Schwarzschild solution. This particular regularization removes the Schwarzschild curvature singularity at the price of introducing a spacetime defect with a vanishing determinant of the metric. Recently, this regularization has been applied to the singular Friedmann solution in cosmology [12]. The resulting nonsingular bouncing cosmology is studied by Klinkhamer and the present author [13, 14]. The expansions of geodesic congruences in the nonsingular bouncing cosmology are found to be finite at the cosmic time $t=0$ [15].

The aim of the present paper is to study the geodesic congruences in the backgrounds of the above two modified Schwarzschild spacetime: The Schwarzschild–Klinkhamer (SK) solution and the quantum deformed Schwarzschild solution. In particular, we focus on the expansion of geodesic congruence, which is divergent at the Schwarzschild singularity. We will see that there are actually some similarities between these two modified Schwarzschild black holes.

The outline of this paper is as follows. In Sect. 2, by introducing a non-simply connected manifold, we review the Schwarzschild–Klinkhamer solution of the Einstein equation. In Sect. 3, we study the geodesic congruences of the Schwarzschild–Klinkhamer black hole. Subsequently, in Sect. 4, we first briefly review the original quantum deformed black hole and then study the geodesic congruences of this black hole. A brief summary is given in Sect. 5. In Appendix A, we study the geodesics of the modified Schwarzschild black holes systematically. The Eddington–Frinkelstein coordinates of the modified Schwarzschild black holes are presented in Appendix B. In Appendix C, we study the geodesic congruences of the generalized QDS black holes.

2 The Schwarzschild–Klinkhamer black-hole solution

In this section, we will introduce a new type of vacuum solution to the Einstein equation over nonsimply-connected manifold, which could be regarded as a possible regularization of the Schwarzschild solution [10, 11].

Instead of the manifold ${\mathbb {R}}^4$, we will consider a noncompact, orientable, non-simply connected manifold ${\mathcal {M}} = {\mathbb {R}}\times {\mathcal {M}}_3$ in this section. To construct ${\mathcal {M}}_3$, we consider first a three-dimensional Euclidean space, remove the interior of a ball with radius b, then identify antipodal points on the defect surface (two-dimensional sphere with radius b) of the ball. The first step is to remove the potential singular point in the final manifold, and the second step is to remove the boundary (Fig. 1).

Actually, ${\mathcal {M}}_3$ has the topology:

$$\begin{aligned} {\mathcal {M}}_3 \simeq {\mathbb {R}}P^3 - {\text {point}}, \end{aligned}$$

(1)

with ${\mathbb {R}}P^3$ the three-dimensional real projective plane.¹ Also, the defect surface has the topology $S^2/{\mathbb {Z}} \sim {\mathbb {R}}P^2$.

Fig. 1

The sketch of the three-dimensional space manifold ${\mathcal {M}}_3$ (as indicated by the shaded area), which is obtained by the following surgery on ${\mathbb {R}}^3$: the interior of the ball with radius b is removed and antipodal points on the boundary of the ball are identified (as indicated by open and filled circles)

Because of the nontrivial spatial topology, it is impossible to cover the manifold by using only one chart. As suggested in Refs. [10, 11], a relatively simple coordinate system is to use three overlapping charts. In this paper, we will focus on the chart-2 coordinates. The results and discussions based on the chart-2 coordinates are general and also hold in the other two coordinate systems. Next, we will show a solution to the Einstein equation over the manifold ${\mathcal {M}}$.

The general spherically symmetric Ansatz for the metric over manifold ${\mathcal {M}}$ is given by the following line element [10, 11, 16]:

$$\begin{aligned} ds^2\,\Big | _{\text {chart-2}}&=-M(W)\,dt^2+N(W)\,dY^2 \nonumber \\&\quad +W\, \Big ( dZ^2+\sin ^2Z\,dX^2 \Big ), \end{aligned}$$

(2a)

$$\begin{aligned} W&\equiv b ^2 + Y^2, \end{aligned}$$

(2b)

$$\begin{aligned} M(W)&\equiv \big [\mu (W) \big ]^2, \end{aligned}$$

(2c)

$$\begin{aligned} N(W)&\equiv (1- b^2/W) \big [\sigma (W) \big ]^2, \end{aligned}$$

(2d)

where $b >0$ corresponds to the defect length scale and $Y=0$ gives the position of the defect surface. The functions $\mu (M)$ and $\sigma (W)$ are determined by the field equations and the boundary conditions. Note that we only show the chart-2 coordinates. The chart-2 spatial coordinates have the following ranges:

$$\begin{aligned} X&\in (0,\pi ), \end{aligned}$$

(3a)

$$\begin{aligned} Y&\in (-\infty ,\infty ), \end{aligned}$$

(3b)

$$\begin{aligned} Z&\in (0,\pi ), \end{aligned}$$

(3c)

where X and Z are angular coordinates and Y is a quasi-radial coordinate. Note that the coordinates Eq. (2) automatically implements the antipodal identification on the boundary of the defect. In other words, the nontrivial manifold ${\mathcal {M}}_3$ is completely determined by the spatial part of the metric Eq. (2) without further need of introducing additional boundary conditions.

The coordinates (X, Y, Z) is related to the standard spherical coordinates $(r,\vartheta , \varphi )$ via the following transformation

$$\begin{aligned}&{\left\{ \begin{array}{ll} r=\sqrt{Y^2+b^2}\\ \vartheta =Z\\ \varphi =X \end{array}\right. } \;\text {for} \;Y>0, \nonumber \\&{\left\{ \begin{array}{ll} r=\sqrt{Y^2+b^2}\\ \vartheta =\pi -Z\\ \varphi =X+\pi \end{array}\right. } \;\text {for} \;Y<0. \end{aligned}$$

(4)

Considering the vacuum Einstein equation and the metric Ansatz (2), the regular black hole solution has been obtained in Ref. [10] and can be written as follows:

$$\begin{aligned} \begin{aligned} ds^2 \Big | ^{\text {SK}} _{\text {chart-2}}&=-\left( 1-\frac{2M}{\sqrt{b^2+Y^2}} \right) dt^2 \\&\quad +\left( 1- \frac{2M}{\sqrt{b^2+Y^2}}\right) ^{-1}\frac{Y^2}{b^2+Y^2} dY^2 \\&\quad +(b^2+Y^2)\left( dZ^2+\sin ^2 Z dX^2 \right) , \end{aligned} \end{aligned}$$

(5)

with parameters

$$\begin{aligned} 2M>b >0. \end{aligned}$$

(6)

Several remarks are in order. First, by using relation Eq. (4), we can write the metric Eq. (5) as the following standard Schwarzschild metric form:

$$\begin{aligned} ds^2 \Big | ^{\text {Schwarzschild}}&=-\left( 1-\frac{2M}{r} \right) dt^2 +\left( 1- \frac{2M}{r}\right) ^{-1} dr^2 \nonumber \\&\quad +r^2\left( d \vartheta ^2+\sin ^2 \vartheta d\varphi ^2 \right) , \end{aligned}$$

(7)

$$\begin{aligned} r&\in [b,\infty ). \end{aligned}$$

(8)

However, note that the transformation Eq. (4) is not a one-to-one map at the defect surface, for example, $(b,\pi /2 , \pi /2)$ and $(b,\pi /2 , 3\pi /2)$ in $(r,\vartheta ,\varphi )$ coordinates correspond to the same point, i.e., $(0,\pi /2 , \pi /2)$ in (Y, X, Z) coordinates. This observation reflects that the differential structure of the metric (5) is different from the one of the metric (7). (This is not a surprise since these two manifolds have different topology.)

Second, note that $g\equiv \text {det}\, g_{\mu \nu } =0$ at $Y=0$, hence the metric from Eq. (5) is degenerate at the defect surface, which corresponds to an ${\mathbb {R}}P^2$ submanifold. A possible understanding of the degeneracy could be as follows [17]: The projective plane ${\mathbb {R}}P^2$ cannot be embedded in ${\mathbb {R}}^3$ without intersections (see, for example, page 40 in Ref. [18]). This observation then suggests that the third extra dimension (coordinate Y) emerging from the two-dimensional defect surface (with local coordinates X and Z) must have a vanishing metric component $g_{YY}$ at $Y = 0$, which is precisely the structure of the metric Ansatz (2). See Refs. [10, 13, 15, 17] for further discussion on spacetime defects and Ref. [19] for a discussion on mathematical aspects of degenerate metrics.

Third, the metric (5) is singular at the event horizon $Y_{H}=\pm \sqrt{4M^2-b^2}$ (For the light cones of the regularized black hole Eq. (5), see Appendix B2. In a similar way as for the Schwarzschild solution, this coordinate singularity can be removed by introducing Eddington–Frinkelstein-type or Kruskal–Szekeres-type coordinates [10]. In the main text of this paper, we will be interested in the expansion $\theta$ of a geodesic congruence, which is a scalar field and does not depend on coordinates choices. Hence, the coordinate (t, X, Y, Z) is enough for our purposes. Still, for completeness, a discussion on Eddington–Frinkelstein-type coordinates for the metric (5) will be given in Appendix B2.

Fourth, in the calculation of this paper, we will only consider the case $Y>0$ (Originally, $Y \in {\mathbb {R}}$.) This simplification is viable for two reasons. First, we will restrict our study on radial geodesics in this paper. These geodesics cannot go from $Y>0$ region to $Y<0$ region, and vice versa. (In fact, based on the light cones of SK spacetime given in Appendix B2, all ingoing radial geodesics will terminate at the defect surface at $Y=0$.) Second, the metric (5) is spherically symmetric and conclusions obtained in the case $Y>0$ can be straightforwardly generalized to the case $Y<0$.

Fifth, as already mentioned in Ref. [10], the coordinate Y of metric (5) becomes timelike inside the event horizon and ranges from $-\sqrt{4M^2-b^2}<Y <\sqrt{4M^2-b^2}$. This might give rise to the presence of “closed time-like curves” (CTCs). These CTCs could be avoided if one consider the regularized Reissner–Nordström solution [10]. For the present work, we don’t need to worry about the potential CTCs problem as we will consider only radial geodesics (there is no CTC for radial curves).

Sixth, the Kretschmann scalar for the metric(5) is given by²

$$\begin{aligned} K \equiv R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma } = 48 \frac{M^2}{(b^2+Y^2) ^3}. \end{aligned}$$

(9)

For a nonvanishing b, it is clear that the Kretschmann scalar remains finite at $Y=0$. The black hole curvature singularity that appears in the Schwarzschild metric no longer exists in the metric (5). The degenerate metric with nontrivial topology is the key to evade the curvature singularity.

3 Geodesic congruences of the Schwarzschild–Klinkhamer black hole

In this section, congruences of timelike and null geodesics of the SK spacetime will be studied. We first start with some definition.

For a spacetime manifold (${\mathcal {M}}, g_{\mu \nu }$ ) and an open subset $O \in {\mathcal {M}}$, a geodesic congruence in the subset O is a family of curves such that through each point in O there lies on one and only one geodesic from this family [2]. The evolution of the congruence can be described by the expansion $\theta$, the shear $\sigma _{\mu \nu }$ and the twist $\omega _{\mu \nu }$.

Now, consider a timelike geodesic congruence with its tangent vector field $\xi ^{\mu }$. Then, the expansion $\theta$, the shear $\sigma _{\mu \nu }$ and the twist $\omega _{\mu \nu }$ of the timelike geodesic congruence are given by [2]

$$\begin{aligned} \theta&\equiv B^{\mu \nu } h_{\mu \nu }, \end{aligned}$$

(10a)

$$\begin{aligned} \sigma _{\mu \nu }&\equiv \frac{1}{2}(B_{\mu \nu }+B_{\nu \mu })-\frac{1}{3} \theta \, h_{\mu \nu },\end{aligned}$$

(10b)

$$\begin{aligned} \omega _{\mu \nu }&\equiv \frac{1}{2} (B_{\mu \nu }-B_{\nu \mu }), \end{aligned}$$

(10c)

where

$$\begin{aligned} B_{\mu \nu }&\equiv \nabla _{\nu } \xi _{\mu },\end{aligned}$$

(11a)

$$\begin{aligned} h_{\mu \nu }&\equiv g_{\mu \nu } +\xi _{\mu } \xi _{\nu }. \end{aligned}$$

(11b)

Since $B_{\mu \nu }$ is “spatial”, i.e.,

$$\begin{aligned} B_{\mu \nu } \xi ^{\mu } = B_{\mu \nu } \xi ^{\nu } =0, \end{aligned}$$

(12)

we have

$$\begin{aligned} \theta = B^{\mu \nu } g_{\mu \nu } = \nabla _{\mu } \xi ^{\mu }. \end{aligned}$$

(13)

In a geodesic congruence, $\theta$ measures the expansion of nearby geodesics, i.e., $\theta >0$ means that the geodesics are diverging and $\theta <0$ means the geodesics are converging. $\sigma _{\mu \nu }$ measures the shear and $\omega _{\mu \nu }$ measures the rotation of nearby geodesics. We will focus on the expansion $\theta$ as it is of great importance in discussing the black hole singularity. Moreover, the black hole singularity is related to the future-directed geodesic congruences (Notice that the past-directed geodesic congruences are relevant for the big bang singularity.)

For a future-directed geodesic congruence, $\xi ^{\mu }$ is actually a four-velocity vector (field), which satisfies the geodesic equation

$$\begin{aligned} \frac{d \xi _{\rho }}{d \uplambda } - \frac{1}{2} \, \frac{\partial g_{\nu \beta }}{\partial x^{\rho }} \xi ^{\nu } \xi ^{\beta }=0, \end{aligned}$$

(14)

with $\uplambda$ being the proper time for massive particle or the affine parameter for massless particle.

3.1 Congruence of radial timelike geodesics

We consider a congruence of radial timelike geodesics of the nonsingular black-hole spacetime (5). In this case, we have $\xi ^{Z} =\xi ^{X} =0$. Since the metric (5) is time independent, we obtain from Eq. (14) that

$$\begin{aligned} \frac{d \xi _{t}}{d \uplambda } = 0 \end{aligned}$$

(15)

along geodesics. From (15), we have

$$\begin{aligned} E&\equiv -\xi _{t},\end{aligned}$$

(16)

$$\begin{aligned} \xi ^{t}&= E\,\left( 1-\frac{2M}{\sqrt{b^2+Y^2}}\right) ^{-1}, \end{aligned}$$

(17)

where E is a real constant along the geodesic.

Then, by the normalization condition $g_{\mu \nu }\xi ^{\mu } \xi ^{\nu }=-1$, we get

$$\begin{aligned} \xi ^{Y} ={\left\{ \begin{array}{ll} \pm \sqrt{\left( E^2-1+\frac{2M}{\sqrt{b^2+Y^2}} \right) \,\frac{b^2+Y^2}{Y^2}}, &{} \quad Y>Y_{H} \\ -\sqrt{\left( E^2-1+\frac{2M}{\sqrt{b^2+Y^2}} \right) \,\frac{b^2+Y^2}{Y^2}}, &{} \quad 0<Y<Y_{H}. \end{array}\right. } \nonumber \\ \end{aligned}$$

(18)

For geodesics outside the black hole ($Y>Y_{H}$), the upper sign in the first line of Eq. (18) applies to the outgoing radial geodesic and the lower sign applies to the ingoing radial geodesic. Meanwhile, inside the black hole ($Y<Y_{H}$), we only have minus sign in the second line of Eq. (18) since Y decreases for both ingoing and “outgoing” geodesics. A systematic study on the geodesics of the SK spacetime will be given in Appendix A.

In the main text of this paper, we will focus on the ingoing geodesics since they are relevant for discussing the black hole singularity.

The expansion for the congruence of ingoing radial timelike geodesics is calculated as

$$\begin{aligned} \theta (Y)&=\frac{1}{\sqrt{-g}}\, \partial _{\mu } (\sqrt{-g} \xi ^{\mu })\nonumber \\&= \theta _{1} (Y)+\theta _{2} (Y), \end{aligned}$$

(19a)

where

$$\begin{aligned} \theta _{1} (Y)&=-\frac{2 \left( E^2-1\right) }{\sqrt{b^2+Y^2} \sqrt{\frac{2 M}{\sqrt{b^2+Y^2}}+E^2-1}}, \end{aligned}$$

(19b)

$$\begin{aligned} \theta _{2} (Y)&=-\frac{3M}{(b^2+Y^2) \sqrt{\frac{2 M}{ \sqrt{b^2+Y^2}}+E^2-1}}. \end{aligned}$$

(19c)

To understand how the regular black hole solution Eq. (5) removes the singularity in the expansion scalar $\theta$, we shall discuss Eq. (19) in the following cases.

3.1.1 Case one. $M=0$ and $b=0$

In this case, Eq. (5) represents the Minkowski spacetime, and the expansion of the congruence for the ingoing radial geodesics is given by

$$\begin{aligned} \theta (Y) =\theta _1 (Y) = -\frac{2\sqrt{E^2-1}}{Y}, \end{aligned}$$

(20)

where $E\ge 1$ is the total energy per unit (rest) mass of a particle. If $E>1$, the expansion scalar is divergent at the origin of the spherical coordinates ($Y=0$). This singularity of the congruence is, of course, not a singularity of the spacetime but an intrinsic nature of the congruence for ingoing radial geodesics.

Note that we have a vanishing expansion scalar if $E=1$. This is easy to understand since the particles are at rest $(Y=\text {constant})$ for $E=1$ and the geodesics of these particles will not have any intersection.

3.1.2 Case two. $M\ne 0$ and $b = 0$

In this case, Eq. (5) represents the standard Schwarzschild spacetime, and the expansion of the congruence for the ingoing radial geodesics is given by

$$\begin{aligned} \theta (Y) =\theta _1 (Y) +\theta _{2} (Y), \end{aligned}$$

(21a)

with

$$\begin{aligned} \theta _{1} (Y)&=-\frac{2 \left( E^2-1\right) }{Y \sqrt{\frac{2 M}{Y}+E^2-1}}, \end{aligned}$$

(21b)

$$\begin{aligned} \theta _{2} (Y)&=-\frac{3M}{(Y^2) \sqrt{\frac{2 M}{Y}+E^2-1}}. \end{aligned}$$

(21c)

For $E>1$, both $\theta _{1}$ and $\theta _{2}$ are singular at the origin of the spherical coordinates ($Y=0$). However, they have different divergent behavior at $Y=0$: $\theta _{1} \propto Y^{-1/2}$ and $\theta _{2} \propto Y^{-3/2}$.

Note that $\theta _{1}$ vanishes for $E=1$, which is similar to $Case \; one$. $\theta _2 (Y)$ for $E=1$ is given by

$$\begin{aligned} \theta (Y) = -\frac{3}{2}\sqrt{\frac{2M}{Y^{3}}}, \end{aligned}$$

(22)

which agrees with result in Ref. [20]. The divergence in $\theta _{2}$ depends only on the mass M and this divergence always exists provided $M\ne 0$. This observation strongly suggests that the divergence in $\theta _{2}$ indicates the existence of the spacetime singularity. It is well-known that the Schwarzschild spacetime indeed has a physical singularity at $Y=0$ [for example, the Kretschmann scalar is divergent at $Y=0$ for Schwarzschild metric, see Eq. (9) with $b=0$.]

3.1.3 Case three. $M= 0$ and $b \ne 0$

In this case, Eq. (5) represents a flat spacetime with a nontrivial topology ${\mathbb {R}}\times {\mathcal {M}}_3$ (by “flat”, we mean the Riemann curvature tensor $R_{\mu \nu \rho } ^{\sigma }=0$ outside the defect surface), and the expansion of the congruence for the ingoing radial geodesics is given by

$$\begin{aligned} \theta (Y) =\theta _1 (Y) = -\frac{2\sqrt{E^2-1}}{\sqrt{b^2+Y^2}}, \end{aligned}$$

(23)

where $E\ge 1$ is the total energy per unit (rest) mass of a particle. If $E=1$, the expansion scalar vanishes since the particles are at rest. Note that the expansion scalar is no longer singular at $Y=0$, which is different from that in $Case \; one$. The nontrivial topology, i.e., ${\mathbb {R}}\times ({\mathbb {R}}P^3 - {\text {point}})$, is responsible for the nonsingular behavior of the geodesic congruence at $Y=0$. We emphasize that the corresponding spacetime is geodesic complete, particles can safely cross the defect surface (see Ref. [21] for a detailed discussion.)

3.1.4 Case four. $M\ne 0$ and $b \ne 0$

In this case, we return to the regular black hole solution. The expansion of the congruence for the ingoing radial geodesics is given by Eq. (19)

$$\begin{aligned} \theta (Y) = \theta _{1} (Y)+\theta _{2} (Y), \end{aligned}$$

(24a)

with

$$\begin{aligned} \theta _{1} (Y)&=-\frac{2 \left( E^2-1\right) }{\sqrt{b^2+Y^2} \sqrt{\frac{2 M}{\sqrt{b^2+Y^2}}+E^2-1}}, \end{aligned}$$

(24b)

$$\begin{aligned} \theta _{2} (Y)&=-\frac{3M}{(b^2+Y^2) \sqrt{\frac{2 M}{ \sqrt{b^2+Y^2}}+E^2-1}}. \end{aligned}$$

(24c)

Both $\theta _{1}$ and $\theta _{2}$ are regular at $Y\rightarrow 0$.

In particular, we have

$$\begin{aligned} \lim _{Y=0^+} \theta (Y)&= -\frac{2 \left( E^2-1\right) }{ \sqrt{2 M b+(E^2-1)b^2}}\nonumber \\&\quad -\frac{3 M}{b \sqrt{2 M b+(E^2-1)b^2}}. \end{aligned}$$

(25)

Again, $\theta _{1} (Y)$ vanishes for $E=1$. The divergence of $\theta _2 (Y)$ in $Case\; two$ has now been removed by a nonvanishing regulator b. The physical singularity in Schwarzschild spacetime is replaced by a spacetime defect with topology ${\mathbb {R}} P^2$.

The rate of change of the expansion $\theta$ along the geodesic congruence is also well-behaved at $Y=0$. For example, we have for $E=1$

$$\begin{aligned} \frac{d \theta }{d \uplambda } = \frac{d \theta }{d Y} \xi ^{Y} = -\frac{9 M}{2 \left( b^2+Y^2\right) ^{3/2}}. \end{aligned}$$

(26)

3.2 Congruence of radial null geodesics

For a timelike geodesic congruence, $h_{\mu \nu }$ is unique once the tangent vector is determined. However, for a given null geodesic congruence, $h_{\mu \nu }$ is not unique. See Chapter 2.4 of Ref. [20] for more discussion on null geodesic congruence. Still, it can be proved that the expansion scalar is still unique and given by [20]:

$$\begin{aligned} \theta = \nabla _{\mu } k^{\mu }, \end{aligned}$$

(27)

where $k^{\mu }$ is the tangent null vector field.

Focusing on the ingoing radial geodesic, we have

$$\begin{aligned} E&\equiv - k_{t}, \end{aligned}$$

(28)

$$\begin{aligned} k^Y&= -\sqrt{\frac{E^2 \left( b^2+Y^2\right) }{Y^2}}, \end{aligned}$$

(29)

where E is a real positive constant along the geodesic.

The expansion for the congruence of ingoing radial null geodesics is easily calculated:

$$\begin{aligned} \theta (Y)= -\frac{2 E}{\sqrt{b^2+Y^2}}, \end{aligned}$$

(30)

which is independent of M. The singularity in the congruence of ingoing radial null geodesics may not imply the existence of spacetime singularity (even though the expansion is regular at $Y= 0$ for a nonvanishing regulator b.) For the congruence of ingoing radial null geodesics in Minkowski spacetime, the expansion scalar is given by Eq. (30) with $b=0$, which is singular at $Y=0$. As we mentioned before, this singularity of the congruence is not a singularity of the spacetime but an intrinsic nature of the congruence for ingoing radial geodesics. The absence of the singularity in the ingoing radial geodesics of the SK spacetime actually reflects the nontrivial topology of the manifold.

Note that the rate of change of the expansion $\theta$ along the geodesic congruence is given by

$$\begin{aligned} \frac{d \theta }{d \uplambda } = \frac{d \theta }{d Y} k ^{Y} = -\frac{2 E^2}{b^2+Y^2}, \end{aligned}$$

(31)

which is well-behaved at $Y=0$.

4 Geodesic congruences in a quantum deformed black hole

The original quantum deformed Schwarzschild black hole proposed by Kazakov and Solodukhin [8] has the following line element

$$\begin{aligned} ds^2 \Big | ^{\text {QDS}}&=-\left( -\frac{2M}{r}+\frac{\sqrt{r^2-a^2}}{r}\right) dt^2 + \frac{ dr^2}{-\frac{2M}{r}+\frac{\sqrt{r^2-a^2}}{r}}\nonumber \\&\quad +r^2\left( d \vartheta ^2+\sin ^2 \vartheta d\varphi ^2 \right) , \end{aligned}$$

(32)

$$\begin{aligned} r&\in [a,\infty ). \end{aligned}$$

(33)

Even though Eqs. (33) and (8) take the same form, i.e., the radial coordinate r can not take all value from ${\mathbb {R}}^+$, they have different origin. For the QDS metric, Eq. (33) is required to keep components of the metric (32) real. While for the KS metric, Eq. (8) is a manifestation of the nontrivial topology.

The QDS metric (32) returns to the standard Schwarzschild metric if $a=0$. The original Schwarzschild singularity at $r=0$ is now been “smeared out” to finite r [9]. Note that all components of the metric (32) are regular at $r=a$. The event horizon for the QDS black hole (32) is located at

$$\begin{aligned} r_{H} = \sqrt{4M^2+a^2}. \end{aligned}$$

(34)

The coordinate singularity at $r=r_H$ could be removed by introducing Eddington–Frinkelstein-type coordinates (see Appendix B1.) However, the singularity in the curvature tensor still remains. For example, the Ricci scalar is given by

$$\begin{aligned} R= \frac{a^2 \left( 3 r-2 \sqrt{r^2-a^2}\right) +2 {r^2} \left( \sqrt{r^2-a^2}-{r}\right) }{r^2 \left( r^2-a^2\right) ^{3/2}}, \end{aligned}$$

(35)

which is divergent at $r=a$. For completeness, we also have the result for the Kretschmann scalar at $r\rightarrow a$³:

$$\begin{aligned} K\Big |_{r \rightarrow a }&= \frac{1}{8a(r-a)^3}+\frac{9}{16 a^2(r-a)^2}\nonumber \\&\quad +\frac{2\sqrt{2}M}{a^{7/2}(r-a)^{3/2}}+{\mathcal {O}}\left( \frac{1}{r-a}\right) , \end{aligned}$$

(36)

which is also divergent at $r=a$. This curvature singularity can be removed if one consider more general QDS black holes [9]. In Appendix C, we will briefly discuss this general class of QDS black holes and study their geodesic congruences.

At large r, we have

$$\begin{aligned} -\frac{2M}{r}+\frac{\sqrt{r^2-a^2}}{r}=1-\frac{2M}{r}-\frac{a^2}{2r^2}+{\mathcal {O}} \left( \frac{a^4}{r^4} \right) , \end{aligned}$$

(37)

which indicates that the QDS metric is asymptotically flat.

4.1 Congruence of radial timelike geodesics

For ingoing radial geodesic congruence of the QDS spacetime (32), we have

$$\begin{aligned} \xi _{t}&=-E, \end{aligned}$$

(38)

$$\begin{aligned} \xi ^{r}&=-\sqrt{E^2+\frac{2M}{r}-\frac{\sqrt{r^2-a^2}}{r}}, \end{aligned}$$

(39)

from which we obtain

$$\begin{aligned} \theta (r) =\nabla _{\mu } \xi ^{\mu }=\theta _1 (r) + \theta _2 (r) \end{aligned}$$

(40a)

with

$$\begin{aligned} \theta _1(r)&=\frac{4 r \left( r-E^2 \sqrt{r^2-a^2}\right) -3 a^2}{2 \sqrt{r^3 \left( r^2-a^2\right) \left( -\sqrt{r^2-a^2}+E^2 r+2 M\right) }}, \end{aligned}$$

(40b)

$$\begin{aligned} \theta _2(r)&= -\frac{3 M}{\sqrt{r^3 \left( -\sqrt{r^2-a^2}+E^2 r+2 M\right) }}. \end{aligned}$$

(40c)

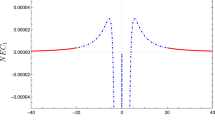
For $a=0$ and $r=Y$, Eqs. (40b) and (40c) reduce to Eqs. (21b) and (21c), respectively. A plot of the expansion scalar as the function of r is shown in Fig. 2. Notice that $\theta _2$ vanishes for $M=0$. In the limit $r \rightarrow a$ and for $a\ne 0$, we have

$$\begin{aligned} \theta _1(r)&=\frac{1}{2 \sqrt{2} \sqrt{ a E^2+2 M}} \frac{1}{\sqrt{r-a} }+{\mathcal {O}} \left( \frac{1}{a}\right) , \end{aligned}$$

(41)

$$\begin{aligned} \theta _2(a)&= -\frac{3 M}{\sqrt{a^3 \left( E^2 a+2 M\right) }}. \end{aligned}$$

(42)

We see explicitly that $\theta _1 (r)$ is divergent at $r=a$ (this divergence no longer exists for a more general QDS black hole, see Appendix C). The rate of change of the expansion $\theta$ along the geodesic congruence is calculated

$$\begin{aligned} \frac{d \theta }{d \uplambda }&= \frac{1}{4 r^3 \left( r^2-a^2\right) ^2 \left( -\sqrt{r^2-a^2}+E^2 r+2 M\right) }\cdot \nonumber \\&\quad \times \Bigg \{9 a^6+2 a^2 r^2 \Big [36 M^2 \,\nonumber \\&\quad -32 M \left( \sqrt{r^2-a^2}-E^2 r\right) \nonumber \\&\quad +r \left( -15 E^2 \sqrt{r^2-a^2}+8 E^4 r+11 r\right) \Big ] \nonumber \\&\quad -4 r^4 \left[ -8 M \left( \sqrt{r^2-a^2}-E^2 r\right) \right. \nonumber \\&\quad \left. +2 r \left( -2 E^2 \sqrt{r^2-a^2}+E^4 r+r\right) +9 M^2\right] \nonumber \\&\quad +a^4 \left[ 4 M \left( 9 \sqrt{r^2-a^2}-8 E^2 r\right) \right. \nonumber \\&\quad \left. +r \left( 16 E^2 \sqrt{r^2-a^2}-8 E^4 r-23 r\right) -36 M^2\right] \Bigg \}. \end{aligned}$$

(43)

In the limit $r \rightarrow a$, we have

$$\begin{aligned} \frac{d \theta }{d \uplambda }=\frac{a}{2 (r^2-a^2)^{3/2}}+{\mathcal {O}}\left( \frac{1}{r^2-a^2}\right) . \end{aligned}$$

(44)

To understand why $\theta _1 (r) \rightarrow +\infty$ for $r\rightarrow a$, we could use the following Raychaudhuri’s equation for a congruence of timelike geodesics:

$$\begin{aligned} \frac{d \theta }{d \uplambda } =-\frac{1}{3}\theta ^2 -\sigma _{\mu \nu } \sigma ^{\mu \nu } +\omega _{\mu \nu } \omega ^{\mu \nu } - R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }. \end{aligned}$$

(45)

For the congruence of radial timelike geodesics considered in this paper, we have⁴

$$\begin{aligned} \omega _{\mu \nu }=0. \end{aligned}$$

(46)

Meanwhile, the shear tensor $\sigma _{\mu \nu }$ is purely spatial, $\sigma _{\mu \nu } \sigma ^{\mu \nu }\ge 0$.

By using the Christoffel symbols in Appendix A and Eq. (38), we could obtain

$$\begin{aligned} -R_{\mu \nu } \xi ^{\mu } \xi ^{\nu } =\frac{a^2}{2 r \left( r^2-a^2\right) ^{3/2}}, \end{aligned}$$

(47)

which is independent of M and E. We find that $R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }$ is always negative (for a nonvanishing a) along radial geodesics of the QDS black hole (32). Moreover, it goes to $-\infty$ when $r \rightarrow a$.

If we remain within the domain of general relativity, we have

$$\begin{aligned} R_{\mu \nu } \xi ^{\mu } \xi ^{\nu } = 8 \pi \left( T_{\mu \nu } \xi ^{\mu } \xi ^{\nu }+\frac{1}{2}T \right) , \end{aligned}$$

(48)

where $T_{\mu \nu }$ is the energy-momentum tensor and $T=g^{\mu \nu } T_{\mu \nu }$. Then, a negative $R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }$ implies the violation of the strong energy condition⁵ (SEC) along the radial timelike geodesic. The closer the geodesics approach to the two-sphere at $r=a$ the stronger the SEC is violated.

In the limit $r\rightarrow a$, the right-hand side (RHS) of Eq (47) is coincident with the first term on the RHS of Eq. (44). This observation indicates that, for $r \rightarrow a$, the rate of the change of the expansion scalar is dominated by the quantity $R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }$.

Fig. 2

The expansion scalar of the ingoing radial geodesic congruence in the quantum deformed black hole (32). The dashed curve is given by Eq. (40) with $M=0$ and $E=1$, while the solid curve is given by Eq. (40) with $M=a\ne 0$ and $E=1$

4.2 Congruence of radial null geodesics

For the ingoing radial geodesic of the QDS spacetime (32), we have

$$\begin{aligned} E&\equiv - k_{t}, \end{aligned}$$

(50)

$$\begin{aligned} k^r&= -E, \end{aligned}$$

(51)

where E is a real positive constant along the geodesic.

Equation (51) implies that we could take $-r$ as an affine parameter for ingoing radial null geodesic. Then, the expansion for the congruence of ingoing radial null geodesics is as follows:

$$\begin{aligned} \theta (r)= -\frac{2 }{r}, \end{aligned}$$

(52)

which is regular for $r\rightarrow a$ provided $a \ne 0$.

The rate of change of the expansion $\theta$ along the geodesic congruence is given by

$$\begin{aligned} \frac{d \theta }{d \uplambda } = -\frac{2}{r^2}, \end{aligned}$$

(53)

which is also well-behaved at $r=a$ for $a\ne 0$.

The quantity $R_{\mu \nu } k ^{\mu } k ^{\nu }$ vanishes identically for ingoing radial null geodesics, which is quite different from that for ingoing radial timelike geodesics [see Eq. (47).]

5 Conclusions and discussion

In this paper, we investigated two different kinds of modified Schwarzschild black holes, namely the Schwarzschild–Klinkhamer black hole [10] and the quantum deformed Schwarzschild black hole [8, 9]. These two kinds of black holes could return to the standard Schwarzschild black hole by setting a vanishing regulator: $b=0$ for the Schwarzschild–Klinkhamer black hole and $a=0$ for the quantum deformed Schwarzschild black hole. We studied radial geodesics of these black holes in the main text while nonradial geodesics were briefly discussed in Appendix A.

Far way from the origin of the spherical coordinates, i.e., $Y\gg b$ for the SK black hole and $r\gg a$ for the QDS black hole, the evolution for the geodesic congruence of modified Schwarzschild black holes are identical to that of the Schwarzschild black hole. However, the situation is different for a small r or Y. For the original QDS black hole [8], as $r\rightarrow a$ the expansion scalar for a radial timelike geodesic congruence goes to $+\infty$ (the expansion scalar goes to $-\infty$ as $r\rightarrow 0$ in the Schwarzschild case.) The violation of strong energy condition along radial timelike geodesic is responsible for this divergent behavior. For a more general QDS black hole [9], the strong energy condition is not globally violated and the expansion scalar for a radial geodesic congruence could remain finite at $r=a$ (see Appendix C for the calculation details.) For the SK black hole, the expansion scalar for a radial timelike geodesic congruence remains finite as $Y\rightarrow 0$ due to the nontrivial topology of the manifold and there is no violation of the strong energy condition.

There is another issue we would like to address here. The procedure of the spacetime-defect regularization of the Schwarzschild solution can actually be applied to the singular Friedmann solution in cosmology [12, 13, 22]. The expansion of geodesic congruence could remain finite at cosmic time $t=0$ for this regularized FLRW universe [15], while it is divergent at the big bang singularity for the standard FLRW universe. This conclusion, together with the result obtained in the present paper, strongly suggests that finite expansions of geodesic congruences (without violation of the strong energy condition) are key manifestations of the spacetime defects.

Even though the conjugate points⁶ appearing in the Schwarzschild black hole no longer exists in the modified Schwarzschild black holes, ingoing radial geodesics still seem to be incomplete [at least for the spacetime from metric (5) or (32)]. All particles inside the event horizon will eventually reach a surface with finite area (see Fig. 3 in Appendix B for light cones of the modified Schwarzschild black holes). For the SK black hole, the surface is $S^2/{\mathbb {Z}} \sim {\mathbb {R}}P^2$. While for the QDS black hole, the surface is a two-sphere with area $4\pi a^2$. One interesting point is that, if the conformal anomaly is taken into account [8], the extended QDS spacetime appears to be geodesically complete. Whether the SK spacetime can be extended to be geodesically complete by a similar procedure remains an open question.

The other open question is physical origin of the regulator in the modified Schwarzschild black holes. For the QDS spacetime, the parameter a comes from the effective potential of the two-dimensional dilaton gravity. Then, a deep understanding and the physical explanation of this potential is required to reveal the nature of the length scale a. For SK spacetime, the parameter b is the length scale of the spacetime defect, which may trace back to the underlying (unknown) theory of quantum spacetime [23].

Appendices

Appendix A: Geodesics of modified Schwarzschild black holes

In general, a static spherically symmetric metric can be written as the following diagonal form:

$$\begin{aligned} ds^2 = -B(r)dt^2 + A(r) dr^2 + w(r)(d\vartheta ^2 + \sin ^2 \vartheta d \varphi ^2).\quad \end{aligned}$$

(A1)

Then, the nonvanishing Christoffel symbols are as follows:

$$\begin{aligned} \Gamma ^{t}_{tr}&=\Gamma ^{t}_{rt}=\frac{B'}{2B}, \end{aligned}$$

(A2a)

$$\begin{aligned} \Gamma ^{r}_{tt}&=\frac{B'}{2A},\end{aligned}$$

(A2b)

$$\begin{aligned} \Gamma ^{r}_{rr}&=\frac{A'}{2A},\end{aligned}$$

(A2c)

$$\begin{aligned} \Gamma ^{r}_{\vartheta \vartheta }&=-\frac{w'}{2A},\end{aligned}$$

(A2d)

$$\begin{aligned} \Gamma ^{r}_{\varphi \varphi }&=-\frac{\sin ^2 \vartheta \,w'}{2A},\end{aligned}$$

(A2e)

$$\begin{aligned} \Gamma ^{\vartheta }_{r\vartheta }&=\Gamma ^{\vartheta }_{\vartheta r}=\frac{w'}{2w},\end{aligned}$$

(A2f)

$$\begin{aligned} \Gamma ^{\vartheta }_{\varphi \varphi }&=-\sin \vartheta \,\cos \vartheta ,\end{aligned}$$

(A2g)

$$\begin{aligned} \Gamma ^{\varphi }_{r\varphi }&=\Gamma ^{\varphi }_{\varphi r}=\frac{w'}{2w},\end{aligned}$$

(A2h)

$$\begin{aligned} \Gamma ^{\varphi }_{\varphi \vartheta }&=\Gamma ^{\varphi }_{\vartheta \varphi }=\cot \vartheta , \end{aligned}$$

(A2i)

where the prime denotes d/dr. Using the nonvanishing Christoffel symbols given by (A2), we find from the geodesic equation that

$$\begin{aligned} 0&=\frac{d^2 t}{d \uplambda ^2}+ \frac{B'}{B}\,\frac{dt}{d\uplambda }\frac{dr}{d\uplambda },\end{aligned}$$

(A3a)

$$\begin{aligned} 0&=\frac{d^2 r}{d \uplambda ^2}+\frac{B'}{2A}\,\left( \frac{dt}{d\uplambda }\right) ^2+\frac{A'}{2A}\,\left( \frac{dr}{d\uplambda }\right) ^2-\frac{w'}{2A}\,\left( \frac{d\vartheta }{d\uplambda }\right) ^2\nonumber \\&\quad -\frac{w'\,\sin ^2 \vartheta }{2A}\,\left( \frac{d\varphi }{d\uplambda }\right) ^2,\end{aligned}$$

(A3b)

$$\begin{aligned} 0&=\frac{d^2 \vartheta }{d \uplambda ^2}+ \frac{w'}{w}\,\frac{d\vartheta }{d\uplambda }\,\frac{dr}{d\uplambda }-\sin \vartheta \cos \vartheta \,\left( \frac{d\varphi }{d\uplambda }\right) ^2,\end{aligned}$$

(A3c)

$$\begin{aligned} 0&=\frac{d^2 \varphi }{d \uplambda ^2}+\frac{w'}{w}\,\frac{dr}{d\uplambda }\,\frac{d\varphi }{d\uplambda }+2\cot \vartheta \,\frac{d\varphi }{d\uplambda }\,\frac{d\vartheta }{d\uplambda }. \end{aligned}$$

(A3d)

where $\uplambda$ is the proper time for massive particle or the affine parameter for massless particle. We now solve above equations by looking for constants of the motion. First, dividing (A3a) by $dt/d\uplambda$, we have

$$\begin{aligned} 0= \frac{d}{d\uplambda }\left( \ln \frac{dt}{d\uplambda }+\ln B \right) , \end{aligned}$$

(A4)

which leads to a constant of motion

$$\begin{aligned} E\equiv B\,\frac{dt}{d\uplambda }. \end{aligned}$$

(A5)

Since the metric is spherically symmetric, we need only consider the case $\vartheta = \pi /2$, i.e., particles are confined to the equatorial plane. In this case. we can forget about $\vartheta$ as a dynamical variable. Now, dividing (A3d) by $d\varphi /d\uplambda$, we can find a constant of motion

$$\begin{aligned} J=w \,\frac{d\varphi }{d\uplambda }, \end{aligned}$$

(A6)

which is actually the angular momentum parameter. With (A5), (A6), and multiplying (A3b) by $2A dr/d\uplambda$, we find

$$\begin{aligned} 0=\frac{d}{d\uplambda }\left[ A\left( \frac{dr}{d\uplambda }\right) ^2+\frac{J^2}{w}-\frac{E^2}{B} \right] , \end{aligned}$$

(A7)

which leads to the following constant of motion

$$\begin{aligned} -N\equiv A\left( \frac{dr}{d\uplambda }\right) ^2+\frac{J^2}{w}-\frac{E^2}{B}. \end{aligned}$$

(A8)

Now, the metric (A1) along the geodesic can be written as

$$\begin{aligned} ds^2 = -N\,d\uplambda ^2. \end{aligned}$$

(A9)

From (A8), we observe that

$$\begin{aligned} N&=0, \;\; \text {for a massless particle},\end{aligned}$$

(A10)

$$\begin{aligned} N&=1, \;\; \text {for a massive particle}. \end{aligned}$$

(A11)

Also remark from (A9) that, a free particle can reach radius r only if

$$\begin{aligned} \frac{1}{A(r)}\left( \frac{E^2}{B(r)}-\frac{J^2}{w(r)}-N\right) \ge 0. \end{aligned}$$

(A12)

We emphasize that the inequality (A12) holds not only outside a black hole but also inside a black hole.

Moreover, (A8) can be written as

$$\begin{aligned} \frac{1}{2} (AB)\left( \frac{dr}{d\uplambda }\right) ^2+\frac{J^2\,B}{w}+\frac{NB}{2}=\frac{E^2}{2}, \end{aligned}$$

(A13)

which has the same form of the equation for a particle with effective mass AB and energy $E^2/(2)$ moving in a one-dimensional effective potential⁷

$$\begin{aligned} V(r)=\frac{J^2\,B}{2w}+\frac{NB}{2}. \end{aligned}$$

(A14)

Consider first the Schwarzschild black hole (SBH)

$$\begin{aligned} B(r)=\frac{1}{A(r)}=1-\frac{2M}{r},\;\;w=r^2, \end{aligned}$$

(A15)

the effective potential is given by

$$\begin{aligned} V_{\text {SBH}}(r)=\frac{J^2}{2r^2}\left( 1-\frac{2M}{r}\right) +\frac{N}{2}\left( 1-\frac{2M}{r}\right) . \end{aligned}$$

(A16)

Observe that the effective potential goes to $-\infty$ as $r\rightarrow 0$ for Schwarzschild spacetime (except for massless particles with vanishing angular momentum).

For the SK black hole from metric (5), we have

$$\begin{aligned} B (Y)&= 1-\frac{2M}{\sqrt{b^2+Y^2}},\end{aligned}$$

(A17a)

$$\begin{aligned} A (Y)&= \left( 1- \frac{2M}{\sqrt{b^2+Y^2}}\right) ^{-1}\frac{Y^2}{b^2+Y^2},\end{aligned}$$

(A17b)

$$\begin{aligned} w&= b^2+Y^2, \end{aligned}$$

(A17c)

the effective potential is calculated⁸

$$\begin{aligned}&V_{\text {SKBH}}(Y) =\frac{J^2}{2(Y^2+b^2)}\nonumber \\&\quad \left( 1-\frac{2M}{\sqrt{b^2+Y^2}}\right) +\frac{N}{2}\left( 1-\frac{2M}{\sqrt{b^2+Y^2}}\right) , \end{aligned}$$

(A18)

which remains finite at $Y=0$.

For a QDS black hole, we have

$$\begin{aligned} B(r)=\frac{1}{A(r)}=-\frac{2M}{r}+\frac{\sqrt{r^2-a^2}}{r},\;\;w=r^2, \end{aligned}$$

(A19)

the effective potential is given by

$$\begin{aligned} V_{\text {QDSBH}}(r)&=\frac{J^2}{2r^3}\left( \sqrt{r^2-a^2}-2M\right) \nonumber \\&\quad +\frac{N}{2r}\left( \sqrt{r^2-a^2}-2M\right) , \end{aligned}$$

(A20)

which remains finite at $r=a$.

Fig. 3

Light cones of the quantum deformed Schwarzschild spacetime in the Eddington–Frinkelstein coordinates (v, r). Ingoing radial null geodesics are characterized by $v=\text {const.}$ (indicated by full curves). Outgoing radial null geodesics are indicated by dashed curves. The event horizon is located at $r_{H} = \sqrt{4M^2+a^2}$. For $r<r_H$ all (future-directed) radial geodesics are in the direction of decreasing r and finally reach a two-sphere of area $4\pi a^2$. The light cones for the SK spacetime are also given by this figure if r is replaced by $\sqrt{b^2+Y^2}$ and a is replaced by b

We conclude that the divergent behavior for the effective potential of the Schwarzschild has been removed in the modified Schwarzschild spacetime.

Appendix B: Eddington–Frinkelstein coordinates

In this appendix, we derive the Eddington–Frinkelstein coordinates for the modified Schwarzschild black holes. We consider first the quantum deformed Schwarzschild spacetime.

1.1 1. Eddington–Frinkelstein coordinates for the quantum deformed Schwarzschild spacetime.

To remove the coordinate singularity at $r=r_H$, we could first define the following “Regge–Wheeler tortoise coordinate” $r_{*}$⁹:

$$\begin{aligned} r_{*} =\sqrt{r^2-a^2}+2M \ln \Big |\frac{\sqrt{r^2-a^2}}{2M}-1 \Big |. \end{aligned}$$

(B2)

Then, by defining Eddington–Frinkelstein coordinate

$$\begin{aligned} v=t+r_*, \end{aligned}$$

(B3)

the QDS metric could be written as

$$\begin{aligned} ds^2 \Big | ^{\text {QDS}}&=-\left( -\frac{2M}{r}+\frac{\sqrt{r^2-a^2}}{r}\right) dv^2+2dvdr \nonumber \\&\quad +r^2\left( d \vartheta ^2+\sin ^2 \vartheta d\varphi ^2 \right) . \end{aligned}$$

(B4)

Even though the metric $g_{vv}$ vanishes at the event horizon, the determinant of the metric is

$$\begin{aligned} g=-r^4 \sin ^2 \vartheta , \end{aligned}$$

(B5)

which is nonvanishing at $r=r_H$. Therefore, the metric (B4) is well-behaved at the event horizon and the coordinate singularity in the QDS metric is removed.

In the Eddington–Frinkelstein coordinates, the condition for radial null geodesics is given by

$$\begin{aligned} \frac{d v}{d r} ={\left\{ \begin{array}{ll} 0 \\ 2\,\left( -\frac{2M}{r}+\frac{\sqrt{r^2-a^2}}{r}\right) ^{-1}, \end{array}\right. } \end{aligned}$$

(B6)

where the first line on the RHS corresponds to the ingoing radial null geodesic and the the second line on the RHS corresponds to the outgoing radial null geodesic.

The light cones of the QDS black hole in the Eddington–Frinkelstein coordinates (v, r) are plotted in Fig. 3. Note that all radial geodesic inside the QDS black hole will finally reach a two-sphere of area $4\pi a^2$.

1.2 2. Eddington–Frinkelstein coordinates for Schwarzschild–Klinkhamer spacetime.

First, we could define the following Regge–Wheeler-type tortoise coordinate $Y_{*}$:

$$\begin{aligned} Y_{*} = \mathrm {sgn}(Y) \left( \sqrt{Y^2+b^2}+2M\ln \Big |\frac{\sqrt{Y^2+b^2}}{2M}-1 \Big |\right) . \end{aligned}$$

(B7)

Then, by defining Eddington–Frinkelstein coordinate

$$\begin{aligned} v=t+Y_*, \end{aligned}$$

(B8)

the SK metric could be written as

$$\begin{aligned} ds^2 \Big | ^{\text {SK}}&=-\left( 1-\frac{2M}{\sqrt{b^2+Y^2}}\right) dv^2+2\sqrt{\frac{Y^2}{Y^2+b^2}}dvdY \nonumber \\&\quad +(b^2+Y^2)\left( d \vartheta ^2+\sin ^2 \vartheta d\varphi ^2 \right) . \end{aligned}$$

(B9)

The metric (B9) is well-behaved at the event horizon $Y=Y_H$ and the coordinate singularity in the SK metric is removed. With replacements $r \rightarrow \sqrt{b^2+Y^2}$ and $a \rightarrow b$, the light cones for the SK spacetime is coincident with Fig. 3.

Appendix C: Radial geodesic congruences in a general class of QDS black holes

Recently, a general class of quantum deformed spacetimes is proposed in Ref. [9] and the metrics are given by

$$\begin{aligned} ds^2 \Big | ^{\text {general QDS}} _n&=-\left[ -\frac{2M}{r}+\left( 1-\frac{a^2}{r^2} \right) ^{\frac{n}{2}}\right] dt^2\nonumber \\&\quad +\left[ -\frac{2M}{r}+\left( 1-\frac{a^2}{r^2} \right) ^{\frac{n}{2}}\right] ^{-1} dr^2 \nonumber \\&\quad +r^2\left( d \vartheta ^2+\sin ^2 \vartheta d\varphi ^2 \right) , \end{aligned}$$

(C1)

$$\begin{aligned} r&\in [a,\infty ), \end{aligned}$$

(C2)

where

$$\begin{aligned} n\in \{ 0\} \cup \{1,3,5\ldots \}. \end{aligned}$$

(C3)

Fig. 4

The expansion scalar of the ingoing radial timelike geodesic congruences in a general class of quantum deformed black hole (C1). The black curve is given by Eq. (C6) with $n=1$, the dashed curve is given by Eq. (C6) with $n=3$ and the gray curve is given by Eq. (C6) with $n=5$. We have specified $M=a$ and $E=1$ in all curves

The general QDS metric (C1) reduces to the standard Schwarzschild metric and the original QDS metric with $n=0$ and $n=1$, respectively. As stated in Ref. [9], the metrics (C1) are metric-regular for $n\ge 1$, Christoffel-symbol-regular for $n\ge 3$ and curvature-regular for $n\ge 5$. For example, the Ricci scalar for $n=5$ is given by

$$\begin{aligned} R= -\frac{a^2 r^2 \sqrt{r^2-a^2}+2 r^4 \sqrt{r^2-a^2}+12 a^4 \sqrt{r^2-a^2}-2 r^5}{r^7}, \end{aligned}$$

(C4)

which is finite at $r=a$. For completeness, we also have the result for the Kretschmann scalar at $r=a$:

$$\begin{aligned} K\Big |_{r = a } = \frac{4 \left( a^2+4 a M+12 M^2\right) }{a^6}, \end{aligned}$$

(C5)

which is also finite.¹⁰

The expansion scalar for ingoing radial timelike geodesic congruences of the general QDS black holes are given by

$$\begin{aligned} \theta = \theta _1 + \theta _2, \end{aligned}$$

(C6)

with

$$\begin{aligned} \theta _1 (r)&= \frac{\left( 1-\frac{a^2}{r^2}\right) ^{n/2} \left( \frac{n\,a^2}{1-\frac{a^2}{r^2}}+4 r^2\right) -4 E^2 r^2}{2 r^3 \sqrt{-\left( 1-\frac{a^2}{r^2}\right) ^{n/2}+E^2+\frac{2 M}{r}}}, \end{aligned}$$

(C7)

$$\begin{aligned} \theta _2 (r)&= -\frac{3 M}{r^2 \sqrt{-\left( 1-\frac{a^2}{r^2}\right) ^{n/2}+E^2+\frac{2 M}{r}}}, \end{aligned}$$

(C8)

where E is a real positive constant along the geodesics. A plot of the expansion scalar as the function of r is shown in Fig. 4. For $n\ge 3$, we have

$$\begin{aligned} \theta _1(a)&=-\frac{2E^2}{\sqrt{a^2 E^2+2M a}}, \end{aligned}$$

(C9)

$$\begin{aligned} \theta _2(a)&= -\frac{3 M}{\sqrt{a^3 \left( E^2 a+2 M\right) }}, \end{aligned}$$

(C10)

from which we see explicitly that the divergence in $\theta _1$ at $r=a$ no longer exists for $n\ge 3$.

The quantity $R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }$ is calculated

$$\begin{aligned} -R_{\mu \nu } \xi ^{\mu } \xi ^{\nu } = {\left\{ \begin{array}{ll} \frac{3a^2 \left( r^2-2 a^2\right) }{2 r^5 \sqrt{r^2-a^2}} &{}\quad \text {for} \quad n=3,\\ \frac{5 a^2 \left( r^2-4 a^2\right) \sqrt{r^2-a^2}}{2 r^7} &{}\quad \text {for} \quad n=5. \end{array}\right. } \end{aligned}$$

(C11)

We find that $R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }$ is not always negative (for a nonvanishing a) along radial timelike geodesics of a general QDS black hole with $n\ge 3$. More precisely, it can be found that $R_{\mu \nu } \xi ^{\mu } \xi ^{\nu }$ is negative only in the region $r>a \sqrt{n-1}$ along radial geodesics.

The expansion scalar for ingoing radial null geodesic congruence of a general QDS black hole is independent of n and given exactly by Eq. (52).