Higgs-mass prediction in the NMSSM with heavy BSM particles

Abstract

We address the prediction for the mass of the SM-like Higgs boson in NMSSM scenarios where all BSM particles, including the singlets, have masses at the TeV scale. We provide a full one-loop computation of the matching condition for the quartic Higgs coupling in the NMSSM, supplemented with the two-loop contributions that involve the strong gauge coupling. We discuss the impact of the one- and two-loop corrections that are specific to the NMSSM on the prediction for the Higgs mass, and propose a method to estimate of the uncertainty associated with the uncomputed higher-order terms. Finally, we illustrate how the measured value of the Higgs mass can be used to constrain some yet-unmeasured parameters of the NMSSM.

1 Introduction

The discovery of a Higgs boson with mass around 125 GeV and properties compatible with the predictions of the Standard Model (SM) [1,2,3,4], combined with the negative (so far) results of the searches for additional new particles at the LHC, point to scenarios with at least a mild hierarchy between the electroweak (EW) scale and the scale of beyond-the-SM (BSM) physics. In this case, the SM plays the role of an effective field theory (EFT) valid between the two scales. The requirement that a given BSM model include a state that can be identified with the observed Higgs boson can translate into important constraints on the model’s parameter space.

One of the prime candidates for BSM physics is supersymmetry (SUSY), which predicts scalar partners for all SM fermions, as well as fermionic partners for all bosons. A remarkable feature of SUSY extensions of the SM is the requirement of an extended Higgs sector, with additional neutral and charged bosons. In contrast to the case of the SM, the masses of the Higgs bosons are not free parameters, as SUSY requires all quartic scalar couplings to be related to the gauge and Yukawa couplings. Moreover, radiative corrections to the tree-level predictions for the quartic scalar couplings introduce a dependence on all of the SUSY-particle masses and couplings. In a hierarchical scenario such as the one described above, the lightest scalar of the SUSY model plays the role of the SM Higgs boson, and the prediction for its quartic self-coupling at the SUSY scale must coincide with the SM coupling extracted at the EW scale from the measured value of the Higgs mass and evolved up to the SUSY scale with appropriate renormalization group equations (RGEs). This “matching” condition can be used to constrain some yet-unmeasured parameters of the SUSY model, such as, e.g., the masses of the scalar partners of the top quarks, the stops.

In the next-to-minimal SUSY extension of the SM, or NMSSM, the Higgs sector includes two SU(2) doublets $H_1$ and $H_2$ – as in the case of the minimal extension, the MSSM – plus a complex scalar S, singlet with respect to the SM gauge group.¹ The vacuum expectation value (vev) of the singlet, induced by the mass and interaction terms in the soft SUSY-breaking Lagrangian, generates a superpotential mass term for the doublets. This provides a solution to the so-called “$\mu$ problem” of the MSSM, i.e., the question of why the supersymmetric Higgs-mass parameter $\mu$ should be at the same scale as the soft SUSY-breaking parameters. The doublet–singlet interactions of the NMSSM also induce new contributions to the prediction for the quartic self-coupling of the SM-like Higgs boson. Depending on the considered region of the NMSSM parameter space, these additional contributions can either increase or decrease the prediction for the quartic Higgs coupling (and hence the Higgs mass) with respect to the case of the MSSM.

The fixed-order (FO) calculation of the NMSSM Higgs boson masses – in which the Higgs self-energies are computed up to a given order in the perturbative expansion, considering the full content of heavy and light fields of the theory – is quite advanced by now, albeit not yet at the level of the corresponding calculation in the MSSM.² After early studies of the NMSSM Higgs sector at the tree level [9, 10] and partial calculations of the dominant one-loop corrections [11,12,13,14,15,16,17,18,19,20], full calculations of the one-loop corrections – for increasingly general versions of the NMSSM and using a variety of renormalization schemes for the NMSSM parameters – were made available in Refs. [21,22,23,24,25,26,27,28,29]. At the two-loop level, the corrections involving the strong gauge coupling were computed in Refs. [21, 30,31,32], those involving only the top Yukawa coupling were computed in Ref. [33], and those involving also the remaining superpotential couplings of the NMSSM were computed in Refs. [31, 34,35,36]. It is worth pointing out that, in all of the two-loop calculations listed above, the two-loop part of the Higgs self-energies was computed under the approximation of vanishing external momentum and in the so-called “gaugeless limit” of vanishing EW gauge couplings. These full one-loop and partial two-loop calculations of the NMSSM Higgs masses were implemented in various public codes, such as NMSSMTools [37, 38], SARAH/SPheno [39,40,41,42,43,44,45], NMSSMCALC [46], SOFTSUSY [47, 48], FlexibleSUSY [49, 50] and FeynHiggs [51,52,53].³ Detailed comparisons among the predictions of these codes for the NMSSM Higgs masses were also presented in Refs. [54, 55].

Compared with the case of the FO calculation, much less attention has been devoted so far to the calculation of the NMSSM Higgs boson masses in the EFT approach, in which the heavy fields are “integrated out” of the theory at a scale comparable to their mass, leaving behind matching conditions for the couplings of the low-energy theory. This approach is the most appropriate to scenarios characterized by a hierarchy between the SUSY scale and the EW scale, where the FO calculation is plagued by large logarithms of the ratio of the two scales. In Ref. [56] a method was proposed to numerically obtain the boundary condition for the quartic Higgs coupling at the SUSY scale, by matching the FO calculation of the pole mass of the lightest Higgs boson in the NMSSM, as implemented in FlexibleSUSY, with the corresponding calculation in the SM. A similar method was later implemented in SARAH/SPheno in Ref. [57]. The “hybrid” approach to the Higgs-mass calculation in Refs. [56, 57] accounts for terms suppressed by powers of $v^2/M_S^2$ – where v stands for the EW scale and $M_S$ for the SUSY scale – that would be neglected in a pure EFT calculation. However, this approach required successive adjustments [50, 58] to avoid the introduction of spurious large-logarithmic effects at higher orders, and it does not provide explicit analytic results for the matching conditions. The latter would come in useful, e.g., to assess the relevance of the various contributions, to check and compare existing calculations, or as building blocks for further calculations.

A sensible approach to obtain explicit analytic results for the matching conditions consists in adapting to the NMSSM the formulas that were computed independently in Refs. [59, 60] for the one-loop matching of a general high-energy theory (without heavy gauge bosons) on a general renormalizable EFT. Indeed, in Ref. [60] analytic results for the one-loop matching condition for the quartic Higgs coupling were obtained in an extremely constrained NMSSM scenario in which all of the BSM-particle masses depend on just one parameter. Subsequently, the general formulas of Ref. [60] were employed in Ref. [61] to study a “Split-SUSY” scenario in which the NMSSM is matched to an EFT that, beyond the SM fields, includes also the complex singlet as well as the gauginos, the higgsinos and the singlino (i.e., the SUSY partners of the gauge bosons, the Higgs doublets and the singlet, respectively).

In this paper we aim to improve the accuracy of the EFT calculation of the SM-like Higgs mass in the NMSSM, and to illustrate how the measured value of the Higgs mass can constrain the parameter space of the model even in scenarios where all of the BSM particles are heavy. In Sect. 2 we adapt to the NMSSM the general formulas of Ref. [59], and obtain the full one-loop matching condition for the quartic Higgs coupling, for arbitrary values of all of the relevant parameters, in the EFT setup in which the NMSSM is matched directly to the SM. We compare our results with those of Ref. [60], in the constrained scenario considered in that paper, and find a discrepancy. We also compute directly the full two-loop-QCD contribution to the matching condition, i.e., the contribution of all two-loop terms that involve the strong gauge coupling. In Sect. 3 we discuss the effect of the corrections computed in Sect. 2 on the prediction for the mass of the SM-like Higgs boson, including an estimate of the uncertainty associated with uncomputed higher-order terms. We also discuss the constraints on the NMSSM parameters that arise from the requirement that the theory prediction for the Higgs mass correspond to the measured value. Finally, Sect. 4 contains our conclusions.

2 Matching condition for the quartic Higgs coupling

In this section we describe our calculation of the full one-loop and two-loop-QCD contributions to the matching condition for the quartic Higgs coupling in the NMSSM. To fix our notation, which follows the SLHA2 conventions [62], we list here the terms in the superpotential W and in the soft SUSY-breaking Lagrangian $\mathcal{L}_\mathrm{soft}$ that determine the Higgs potential:

(1)

(2)

where the hats denote superfields, and the SU(2) indices of the Higgs doublets are contracted by the antisymmetric tensor $\epsilon _{ab}$, with $\epsilon _{12} =1$. For simplicity, we take the parameters in Eqs. (1) and (2) to be all real, and we enforce the $Z_3$ symmetry that forbids tadpole and mass terms in W and the corresponding SUSY-breaking terms in $\mathcal{L}_\mathrm{soft}$. We assume that the singlet develops a vev $v_s \equiv \langle S \rangle$, providing effective $\mu$ and $B_\mu$ terms for the Higgs doublets. It is also convenient to rotate the two doublets to the so-called Higgs basis, in which they have the same hypercharge and only one of them develops a vev

$$\begin{aligned} \left( \!\begin{array}{c} H \\ A \end{array}\!\right) = \left( \!\begin{array}{rr} \cos \beta &{}\!\sin \beta \\ sin\beta &{}\!\cos \beta \end{array}\!\right) \left( \!\!\!\begin{array}{c} -\epsilon H_1^* \\ ~~\,H_2 \end{array}\!\right) ~, \end{aligned}$$

(3)

where the rotation angle is defined by $\tan \beta \equiv v_2/v_1$, with $v_i \equiv \langle H_i^0 \rangle$. In this basis the neutral component of H has the vev $v = (v_1^2 + v_2^2)^{1/2}$, while A has no vev.

We consider the hierarchical scenario in which all of the SUSY particles, as well as the Higgs doublet A and the scalar and pseudoscalar components of the singlet, are significantly heavier than the EW scale. We then adopt an EFT setup in which all of the heavy particles of the NMSSM are integrated out at a common renormalization scale $Q\approx M_S$, below which the field content of the theory is just the one of the SM, and in particular the Higgs doublet H plays the role of the SM Higgs. In the matching of the NMSSM to the SM we work in the limit of unbroken EW symmetry, $v\rightarrow 0$. This amounts to neglecting corrections suppressed by powers of $v^2/M_S^2$, which can be mapped to the effect of non-renormalizable, higher-dimensional operators in the EFT Lagrangian. In this limit we can neglect the mixing among gauginos, higgsinos and singlino, as well as the mixing between the “left” and “right” sfermions (i.e., the SUSY partners of the left- and right-handed fermions of the SM).

2.1 Tree-level masses and couplings

We now discuss the tree-level masses and couplings in the Higgs/higgsino sector. As mentioned above, we work in the limit $v\rightarrow 0$, as appropriate to the calculation of the matching conditions in the EFT approach. The masses of the scalar and pseudoscalar components of the singlet, which we decompose as $S = v_s + (s + i\,a)/\sqrt{2}$, are

$$\begin{aligned} m_s^2 ~=~\kappa \,v_s\,(A_\kappa + 4\,\kappa \,v_s)~,~~~~~~~ m_a^2 ~=~-3\,\kappa \,v_s\,A_\kappa ~, \end{aligned}$$

(4)

where one of the minimum conditions of the tree-level scalar potential has been used to replace the soft SUSY-breaking mass for the singlet with a combination of the other parameters,

$$\begin{aligned} m_S^2 ~=~ - \kappa \,v_s\,(A_k + 2\,\kappa \,v_s), \end{aligned}$$

(5)

and the requirement that $\langle S\rangle = v_s$ be a deeper minimum than $\langle S\rangle = 0$ implies $3\,\kappa \,v_s/A_\kappa < - 1$. The mass of the heavy Higgs doublet A is

$$\begin{aligned} m_A^2 = \frac{\lambda \,v_s\,(A_\lambda + \kappa \,v_s)}{\sin \beta \cos \beta }~, \end{aligned}$$

(6)

where again the minimum conditions have been used to remove the dependence on $m^2_{H_1}$ and $m^2_{H_2}$. Finally, the higgsinos $\tilde{h}_1$ and $\tilde{h}_2$ combine into a Dirac fermion with mass $\mu = \lambda \, v_s$, and the singlino acquires a mass $m_{\tilde{s}} = 2\,\kappa \,v_s$.

In the EFT approach, the calculation of the mass of the SM-like Higgs boson H – or, alternatively, the determination of the constraints on the NMSSM parameters that arise from the measured value of the Higgs mass – require the calculation of the NMSSM prediction for the quartic Higgs coupling at the matching scale.⁴ At the tree level, the latter reads

$$\begin{aligned} \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}} =\frac{1}{4}(g^2 + g^{\prime \,2}) \cos ^22\beta + \frac{1}{2}\,\lambda ^2 \sin ^22\beta -\frac{a_{hhs}^2}{m_s^2},\quad \end{aligned}$$

(7)

where the first term on the r.h.s. is the D-term contribution analogous to the one in the MSSM, the second term is the F-term contribution specific to the NMSSM, and the third term originates from the decoupling of the singlet scalar. The trilinear coupling $a_{hhs}$ enters the NMSSM Lagrangian as $\mathcal{L} ~\supset -(a_{hhs}/2)\,h^2 s$, where h is the neutral scalar component of H, and at the tree level it reads

$$\begin{aligned} a_{hhs} ~=~ \frac{\lambda }{\sqrt{2}}\, \left[ 2\,\lambda \,v_s - (A_\lambda + 2\,\kappa \,v_s)\,\sin 2\beta \right] . \end{aligned}$$

(8)

Combining Eqs. (4), (7) and (8), we remark that the contribution to $\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}$ that arises from the decoupling of the singlet is always negative, and contains a piece that does not depend on $\tan \beta$.

2.2 One-loop matching

We now describe our calculation of the full one-loop contribution to the matching condition for the quartic Higgs coupling. This contribution can be decomposed as:

$$\begin{aligned} \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }= & {} \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,{\scriptscriptstyle \mathrm{1PI}}} +\,2\,\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\,\Delta Z_h^{1\ell } -\,2\,\frac{a_{hhs}}{m_s^2}\,\Delta a_{hhs}^{1\ell } \nonumber \\&+\, \frac{a^2_{hhs}}{m_s^4}\, \Delta m_s^{2\,,\,1\ell } +\,\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,{\scriptscriptstyle \mathrm{RS}}} ~. \end{aligned}$$

(9)

The first term on the r.h.s. of Eq. (9) originates from one-particle-irreducible (1PI) diagrams with heavy particles in the loop and four external Higgs legs. The second term arises from diagrams with a wave-function renormalization (WFR) insertion on one of the external legs, and it involves the derivative with respect to the external momentum of the heavy-particle (HP) contribution to the renormalized self-energy of the Higgs field:

$$\begin{aligned} \Delta Z_h^{1\ell } ~=~ -\left. \frac{d\hat{\Pi }_{hh}^{\scriptscriptstyle \mathrm{1\ell ,\, HP}}}{dp^2}\, \right| _{p^2=0}~. \end{aligned}$$

(10)

The third term on the r.h.s. of Eq. (9) arises from singlet-exchange diagrams with a HP loop insertion on one of the trilinear Higgs–singlet vertices, while the fourth term arises from singlet-exchange diagrams with a HP loop insertion on the singlet propagator. The exact form of the latter term depends on the choices made for the definitions of the singlet vev $v_s$ and of the singlet mass $m_s^2$ entering the tree-level part of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$, see Eq. (7). Assuming that $v_s$ corresponds to the minimum of the loop-corrected scalar potential, and using the expression in Eq. (4) for the singlet mass, we get

$$\begin{aligned} \Delta m_s^{2\,,\,1\ell }~=~ -\left. \hat{\Pi }_{ss}^{\scriptscriptstyle \mathrm{1\ell ,\, HP}} \right| _{p^2=0} +\, \frac{~~ \hat{T}_s^{\scriptscriptstyle \mathrm{1\ell ,\, HP}}}{\sqrt{2}\,v_s}~, \end{aligned}$$

(11)

involving the HP contributions to the renormalized self-energy and tadpole of the singlet. We remark that the tadpole term in Eq. (11) originates from the fact that, with our choice for $v_s$, the minimum condition of the scalar potential used to remove the explicit dependence of the singlet mass on the soft SUSY-breaking parameter $m_S^2$ includes a loop correction,

$$\begin{aligned} m_S^2 ~=~ - \kappa \,v_s\,(A_k + 2\,\kappa \,v_s) \,+\, \frac{~~ \hat{T}_s^{\scriptscriptstyle \mathrm{1\ell ,\, HP}}}{\sqrt{2}\,v_s}~. \end{aligned}$$

(12)

By expressing the singlet mass as in Eq. (4), we are effectively moving the tadpole term from the singlet mass to the one-loop part of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}\,$. If we were instead to express the singlet mass entering the tree-level part of the matching condition as $\,m_s^2 \,=\, m_S^2 \,+\, 2\, \kappa \,v_s\,(A_\kappa + 3\,\kappa \,v_s)$, while still considering $v_s$ as the minimum of the loop-corrected potential, there would be no tadpole term in Eq. (11). If, on the other hand, we were to consider $v_s$ as the minimum of the tree-level potential, there would still be no tadpole term in Eq. (11), and the two expressions for the singlet mass discussed above would be equivalent to each other, i.e. $m_s^2 = \kappa \,v_s\,(A_\kappa + 4\,\kappa \,v_s)= m_S^2 \,+\, 2\, \kappa \,v_s\,(A_\kappa + 3\,\kappa \,v_s)$. However, the one-loop contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ in Eq. (9) would receive direct contributions from non-1PI diagrams with tadpole insertions (see Ref. [63] for a related discussion)

$$\begin{aligned}&\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\mathrm{tad}} ~=~ \left[ \sqrt{2} \,\kappa \, (A_k + 6\,\kappa \,v_s)\,\frac{a_{hhs}^2}{m_s^6} \right. \nonumber \\&\quad \left. - 2\,\lambda \,(\lambda -\kappa \,\sin 2\beta )\,\frac{a_{hhs}}{m_s^4}\right] \,\hat{T}_s^{\scriptscriptstyle \mathrm{1\ell ,\, HP}}, \end{aligned}$$

(13)

where the first term within square brackets arises from a diagram with a tadpole insertion on the singlet propagator, and the second from diagrams with tadpole insertions on the singlet-doublet vertices.

Finally, the last term on the r.h.s. of Eq. (9) includes contributions arising from differences in the renormalization scheme (RS) used for the couplings of the NMSSM and for those of the EFT valid below the matching scale (i.e., the SM). In particular, the calculation of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ is performed in the ${ \overline{\mathrm{DR}}}$ scheme assuming the field content of the NMSSM, whereas in the EFT $\lambda _{\scriptscriptstyle \mathrm{SM}}$ is interpreted as an $\overline{\mathrm{MS}}$ parameter, and we also choose to interpret the EW gauge couplings entering Eq. (7) as $\overline{\mathrm{MS}}$ parameters of the SM. We remark, however, that the presence of the singlet superfield does not affect these contributions at one loop, thus they can be taken directly from the MSSM calculation of Refs. [64, 65].

To obtain the quartic- and trilinear-vertex corrections and the self-energies entering the various contributions to Eq. (9) we use the formulas in appendix B of Ref. [59], which discusses the one-loop matching of a general high-energy theory (without heavy gauge bosons) on a general renormalizable EFT. To obtain the singlet tadpole we use analogous formulas from Ref. [66]. This saves us the trouble of actually calculating one-loop Feynman diagrams, but requires that we adapt to the case of the NMSSM the notation of Refs. [59, 66] for masses and interactions of scalars and fermions in a general renormalizable theory.⁵ We find that, once the higgsino mass and the Higgs–sfermion interaction parameters are expressed in terms of $\mu =\lambda \,v_s$, the threshold correction $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }$ splits neatly into a part that does not depend explicitly on $\lambda$ and coincides with the corresponding correction in the MSSM, see Refs. [64, 65], plus an NMSSM-specific, $\lambda$-dependent part that vanishes in the limit $\lambda \rightarrow 0$.

Our full formulas for $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }$, valid for generic values of all of the relevant NMSSM parameters, are lengthy and not particularly illuminating, therefore we make them available on request in electronic form. For later convenience, we provide here the contribution to the NMSSM-specific part of $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }$ from diagrams involving stop squarks. The sfermion contribution to $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,{\scriptscriptstyle \mathrm{1PI}}}$ is the same as in the MSSM once we set $\mu =\lambda \,v_s$, and in the limit $v\rightarrow 0$ there are no one-loop sfermion contributions to the self-energy and tadpole of the singlet. The NMSSM-specific stop contribution to the one-loop matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ thus reduces to

$$\begin{aligned} \left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\,\tilde{t}}\,\right) _\lambda ~=~ 2\,(\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}})_\lambda \,\Delta Z_h^{1\ell ,\,\tilde{t}} -\,2\,\frac{a_{hhs}}{m_s^2}\,\Delta a_{hhs}^{1\ell ,\,\tilde{t}}~. \end{aligned}$$

(14)

In the first term on the r.h.s. of Eq. (14) above, $\left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda = \lambda ^2 \sin ^22\beta /2 - a_{hhs}^2/m_s^2$ is the $\lambda$-dependent part of the tree-level matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$, see Eq. (7), and $\Delta Z_h^{1\ell ,\,\tilde{t}}$ is the stop contribution to the Higgs WFR:

$$\begin{aligned} \Delta Z_h^{1\ell ,\,\tilde{t}} ~=~ -\frac{g_t^2N_c}{(4\pi )^2} \,\frac{X_t^2}{6\,m_{Q_3}m_{U_3}}\,\widetilde{F}_5\left( \frac{m_{Q_3}}{m_{U_3}}\right) ~, \end{aligned}$$

(15)

where $N_c=3$ is a color factor, $X_t = A_t - \mu \cot \beta$ is the trilinear Higgs-stop interaction parameter (with $A_t$ being the corresponding soft SUSY-breaking coupling), $m_{Q_3}$ and $m_{U_3}$ are the soft SUSY-breaking masses for the left and right stop, respectively, and the loop function $\widetilde{F}_5(x)$ is defined in the appendix A of Ref. [64]. In the second term on the r.h.s. of Eq. (14) above, the tree-level quantities $m_s^2$ and $a_{hhs}$ are given in Eqs. (4) and (8), respectively, while $\Delta a_{hhs}^{1\ell ,\,\tilde{t}}$ is the one-loop stop contribution to the Higgs–singlet coupling in the limit $v\rightarrow 0$,

$$\begin{aligned} \Delta a_{hhs}^{1\ell ,\tilde{t}} ~= & {} ~ \sqrt{2}\,N_c\,\frac{\lambda \,g_t^2}{(4\pi )^2}\, \frac{X_t\,\cot \beta }{m_{Q_3}^2-m_{U_3}^2}\,\nonumber \\&\quad \left[ \,m_{Q_3}^2\left( 1 - \ln \frac{m_{Q_3}^2}{Q^2}\right) - m_{U_3}^2\left( 1 - \ln \frac{m_{U_3}^2}{Q^2}\right) \right] .\nonumber \\ \end{aligned}$$

(16)

The NMSSM-specific sbottom contribution $\left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\,\tilde{b}}\,\right) _\lambda$ can be obtained from Eqs. (14)–(16) with the replacements $g_t\rightarrow g_b$, $X_t\rightarrow X_b$, $\cot \beta \rightarrow \tan \beta$ and $m_{U_3} \rightarrow m_{D_3}$, where $g_b$ is the bottom Yukawa coupling, $X_b = A_b - \mu \tan \beta \,$, and $m_{D_3}$ is the soft SUSY-breaking mass for the right sbottom. Analogous replacements (with $N_c=1$) yield also the stau contribution. For simplicity, we set the tiny Yukawa couplings of the first two generations to zero, hence there are no NMSSM-specific contributions to $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }$ from the corresponding sfermions.

As a non-trivial check of our full one-loop calculation, we verified that by taking the derivative of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ with respect to $\ln Q^2$ we recover the corresponding one-loop RGE of the SM, i.e.,

$$\begin{aligned}&(4\pi )^2\,\frac{d}{d\ln Q^2}\, \left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}+\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }\right) \nonumber \\&\quad =\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\left( 6\,\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}+\, 6\,g_t^2\,+\,6\,g_b^2\,+\,2\,g_\tau ^2\,-\,\frac{9}{2}\,g^2 \,-\,\frac{3}{2} g^{\prime \,2}\right) \nonumber \\&\qquad -\, 6\,g_t^4\,-\,6\,g_b^4\,-\,6\,g_\tau ^4 \,+\,\frac{9}{8}\,g^4 \,+\, \frac{3}{8}\,g^{\prime \,4} + \frac{3}{4} \, g^2 g^{\prime \,2}~. \end{aligned}$$

(17)

To this effect, we must combine the explicit scale dependence of our result for $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }$ with the implicit scale dependence of all of the parameters entering $\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}$. For the latter we use the RGEs of the NMSSM as listed in Ref. [7], with the exception of the EW gauge couplings for which our definitions require that we use the RGEs of the SM.

As mentioned in Sect. 1, the authors of Ref. [60] obtained the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ in an extremely constrained NMSSM scenario in which all of the masses and couplings in the singlet/singlino sector depend only on $\lambda$, $\tan \beta$ and a lone mass parameter $m_0$. After adapting our formulas for $\Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell }$ to this constrained scenario, we compared them with those of Ref. [60],⁶ but we found a discrepancy. Indeed, it appears that in Ref. [60] the one-loop matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ misses a tadpole contribution analogous to the one in our Eq. (11). This is inconsistent with the fact that the authors of Ref. [60] appear to have defined the singlet mass entering $\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}$ as in our Eq. (4) – thus obtaining $m_s^2 = 2/3\,m_0^2\,$ in the constrained scenario – and $v_s$ as the vev of the loop-corrected potential, as can be inferred from the absence of direct contributions from tadpole-insertion diagrams in their results.

2.3 Two-loop-QCD matching

As mentioned earlier, the one-loop squark contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ splits into a $\lambda$-independent part that coincides with the analogous MSSM result and a $\lambda$-dependent part that is specific to the NMSSM. This structure allows for a relatively economical calculation of the two-loop contribution that involves the strong gauge coupling. Indeed, once we identify $\mu = \lambda \,v_s$, the contribution from two-loop 1PI diagrams that involve the strong interactions of the squarks is the same as in the MSSM, and has already been computed in Refs. [64, 67]. Furthermore, the fact that there are no squark contributions to the singlet self-energy and tadpole at one loop implies that there are no two-loop contributions involving the strong interactions either. In analogy with Eqs. (9) and (14), the NMSSM-specific, $\lambda$-dependent two-loop-QCD contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ can thus be decomposed as

$$\begin{aligned} \left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}\right) _\lambda= & {} 2\,\left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda \,\Delta Z_h^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}\nonumber \\&-2\,\frac{a_{hhs}}{m_s^2}\, \Delta a_{hhs}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}} \,+~\left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{2\ell ,{\scriptscriptstyle \mathrm{RS}}}\right) _\lambda ~.\nonumber \\ \end{aligned}$$

(18)

The quantity denoted as $\Delta Z_h^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}$ in the first term on the r.h.s. of Eq. (18) above is the two-loop contribution to the Higgs WFR from diagrams that involve the strong interactions of the squarks. Again, once we identify $\mu = \lambda \,v_s$, this contribution is the same as in the MSSM and has already been computed in Ref. [67]. Explicit formulas for $\Delta Z_h^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}$ in the limit of degenerate squark and gluino masses can be gleaned from Eqs. (13)–(17) in Sect. 2.2 of that paper, and the formulas with full dependence on all of the relevant parameters are available on request in electronic form. It is worth noting that, in the EFT calculation of the SM-like Higgs mass, the WFR contribution in Eq. (18) accounts for effects that, in the corresponding FO calculation, arise from the external-momentum dependence of the two-loop self-energies; in particular, it is related to the first-order term in the $p^2$-expansion of $\hat{\Pi }_{hh}^{2\ell , \tilde{q}}$, the contribution to the renormalized Higgs-boson self-energy from two-loop diagrams involving the strong interactions of the squarks. Higher-order terms in the $p^2$-expansion of $\hat{\Pi }_{hh}^{2\ell , \tilde{q}}$ are suppressed by powers of $v^2/M_S^2$ and can be neglected in our hierarchic scenario, while the momentum dependence of the two-loop quark–gluon contribution to the self-energy is fully accounted for in the calculation of the relation between $\lambda _{\scriptscriptstyle \mathrm{SM}}$ and $M_h$ at the EW scale, see Sect. 3. Hence, the EFT approach allows for a straightforward inclusion of external-momentum effects that are of the same order in the relevant couplings as the other two-loop contributions computed in this section. In contrast, these effects are missed by the FO calculations of the NMSSM Higgs masses in Refs. [21, 30,31,32], where the two-loop part of the self-energies is computed – whether “diagrammatically” or in the effective-potential approach – under the approximation of vanishing external momentum.

The quantity denoted as $\Delta a_{hhs}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}$ in the second term on the r.h.s. of Eq. (18) is the contribution to the trilinear Higgs–singlet coupling from two-loop, 1PI diagrams that involve the strong interactions of the squarks. This contribution is not available in the literature, but can be straightforwardly computed with the same effective-potential techniques adopted in Refs. [64, 67] for the calculation of the two-loop-QCD contributions to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$. In particular, we can write

$$\begin{aligned} \Delta a_{hhs}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}} ~=~ \left. \frac{\partial ^3 \Delta V^{2\ell ,\,\tilde{q}}}{\partial ^2 h\,\partial s } \right| _{v=0}~, \end{aligned}$$

(19)

where $\Delta V^{2\ell ,\,\tilde{q}}$ is the contribution to the NMSSM scalar potential from two-loop diagrams involving the strong interactions of the stop and sbottom squarks (the first two generations of squarks do not contribute in the limit in which we neglect the corresponding Yukawa couplings). The stop contribution to $\Delta V^{2\ell ,\,\tilde{q}}$ can be found, e.g., in Eq. (28) of Ref. [64], and the sbottom contribution can be obtained from the stop one with trivial replacements. The squark masses and mixing angles in $\Delta V^{2\ell ,\,\tilde{q}}$ are then expressed as function of field-dependent quark masses, and Eq. (19) becomes

$$\begin{aligned}&\Delta a_{hhs}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}} \nonumber \\&\quad = -\,\frac{\lambda \,g_t^2}{\sqrt{2}}\,\cot \beta \,\frac{d}{dX_t} \left[ \left( \mathcal{D}^{t b}_1 +\, m_t^2\,\mathcal{D}^t_2 \right) \Delta V^{2\ell ,\,\tilde{t}}\,\right] _{m_t\rightarrow 0}\nonumber \\&\qquad -\, \frac{\lambda \,g_b^2}{\sqrt{2}}\,\tan \beta \,\frac{d}{dX_b} \left[ \left( \mathcal{D}^b_1 \,+\, m_b^2\,\mathcal{D}^b_2 \right) \Delta V^{2\ell ,\,\tilde{b}}\,\right] _{m_b\rightarrow 0}~,\nonumber \\ \end{aligned}$$

(20)

where we define the operators

$$\begin{aligned} \mathcal{D}^q_i ~\equiv ~\left( \frac{d}{dm_q^2}\right) ^i. \end{aligned}$$

(21)

We use relations such as those in Eq. (32) of Ref. [64] for the derivatives of the field-dependent parameters with respect to the quark masses, then we obtain the limits of vanishing quark masses as described in that paper (note that in this calculation we do not encounter terms that diverge for $m_q\rightarrow 0$). Finally, the derivatives with respect to the parameters $X_t$ and $X_b$ in Eq. (20) account for the derivative with respect to the singlet field in Eq. (19). In units of $g_s^2\,C_F\,N_c/(4\pi )^4$, where $g_s$ is the strong gauge coupling and $C_F=4/3$ and $N_c=3$ are color factors, we obtain for the stop contribution

$$\begin{aligned}&\left( \Delta a_{hhs}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}\right) ^{\tilde{t}} =\! - 2\sqrt{2}\,\lambda \,g_t^2\,\cot \beta \,\Biggr \{ X_t\left[ -2\right. \nonumber \\&\quad \left. +\left( 2 -\frac{2\,(1+x_Q)\ln x_Q}{x_Q-x_U}\right) \ln \frac{m_{\tilde{g}}^2}{Q^2} -\frac{1}{2} \ln ^2\frac{m_{\tilde{g}}^2}{Q^2} \right. \nonumber \\&\quad +\frac{2 \,(1+2\,x_Q)\,\ln x_Q}{x_Q-x_U} -\frac{(x_Q^2 +x_Q-x_U)\,\ln ^2 x_Q}{(x_Q-x_U)^2}\nonumber \\&\quad \left. + \frac{x_Q\,x_U\,\ln x_Q\,\ln x_U}{(x_Q-x_U)^2} - \frac{2\,(1-x_Q)}{x_Q-x_U}\,\mathrm{Li}_2\left( 1-\frac{1}{x_Q}\right) \right] \nonumber \\&\quad + m_{\tilde{g}}\left[ \,\frac{5}{2} -\left( 2-\frac{2\,x_Q\,\ln x_Q}{x_Q-x_U}\right) \ln \frac{m_{\tilde{g}}^2}{Q^2} + \frac{1}{2} \ln ^2\frac{m_{\tilde{g}}^2}{Q^2}\right. \nonumber \\&\quad \left. -\frac{4\,x_Q\,\ln x_Q}{x_Q-x_U} \right. \nonumber \\&\quad \left. -\frac{(1-x_Q)\,\ln ^2 x_Q}{x_Q-x_U} - \frac{2\,(1-x_Q)}{x_Q-x_U}\,\mathrm{Li}_2\left( 1-\frac{1}{x_Q}\right) \right] \nonumber \\&\quad + ~(x_Q \,\longleftrightarrow \, x_U)\Biggr \}, \end{aligned}$$

(22)

where $m_{\tilde{g}}$ is the gluino mass, and we defined the ratios $x_Q = m_{Q_3}^2/m_{\tilde{g}}^2\,$ and $x_U = m_{U_3}^2/m_{\tilde{g}}^2\,$. Again, the sbottom contribution can be obtained from the stop contribution in Eq. (22) with the replacements $g_t\rightarrow g_b$, $X_t\rightarrow X_b$, $\cot \beta \rightarrow \tan \beta$ and $m_{U_3} \rightarrow m_{D_3}$.

The third term on the r.h.s. of Eq. (18) contains in fact two separate contributions that arise from choices of renormalization scheme for the couplings involved in the matching condition:

$$\begin{aligned} \left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{2\ell ,{\scriptscriptstyle \mathrm{RS}}}\right) _\lambda= & {} \frac{g_s^2\,C_FN_c}{(4\pi )^4}\,(g_t^2+g_b^2)\, \left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda \nonumber \\&+ 2\,\Delta g_t \left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\,\tilde{t}}\,\right) _\lambda . \end{aligned}$$

(23)

The first term on the r.h.s. of Eq. (23) above is the NMSSM-specific completion of the contribution in Eq. (21) of Ref. [67], and stems from the fact that SUSY provides a prediction for the ${ \overline{\mathrm{DR}}}$-renormalized quartic Higgs coupling, whereas we interpret the parameter $\lambda _{\scriptscriptstyle \mathrm{SM}}$ in the EFT as $\overline{\mathrm{MS}}$. The second term stems from the fact that we choose to express the one-loop part of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ in terms of the $\overline{\mathrm{MS}}$-renormalized top Yukawa coupling of the SM rather than the corresponding ${ \overline{\mathrm{DR}}}$-renormalized coupling of the NMSSM.⁷ The quantity $\left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\,\tilde{t}}\,\right) _\lambda$ is given in Eqs. (14)–(16), while $\Delta g_t$ denotes the one-loop, $\mathcal{O}(g_s^2)$ part of the difference between the $\overline{\mathrm{MS}}$ coupling of the SM and the ${ \overline{\mathrm{DR}}}$ coupling of the NMSSM,

$$\begin{aligned} \Delta g_t= & {} - \frac{g_s^2\,C_F}{(4\pi )^2}\,\left[ 1+ \ln \frac{m_{\tilde{g}}^2}{Q^2} \,+\, \widetilde{F}_6\left( \frac{m_{Q_3}}{m_{\tilde{g}}}\right) \right. \nonumber \\&\left. \,+\, \widetilde{F}_6\left( \frac{m_{U_3}}{m_{\tilde{g}}}\right) \,-\, \frac{X_t}{m_{\tilde{g}}}\, \widetilde{F}_9\left( \frac{m_{Q_3}}{m_{\tilde{g}}},\frac{m_{U_3}}{m_{\tilde{g}}}\right) \right] , \end{aligned}$$

(24)

where the loop functions $\widetilde{F}_6(x)$ and $\widetilde{F}_9(x,y)$ are defined in the appendix A of Ref. [64].

Finally, we verified that, by taking the derivative with respect to $\ln Q^2$ of the NMSSM-specific part of the two-loop-QCD matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$, we do recover the terms involving $g_s^2$ that we should expect from the RGE of the quartic Higgs coupling of the SM:

$$\begin{aligned}&(4\pi )^4\,\frac{d}{d\ln Q^2}\, \left[ (\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}})_\lambda + \left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\,\tilde{q}}\right) _\lambda + \left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}\right) _\lambda \right] \nonumber \\&\quad ~\supset ~ 40\,g_s^2\,(g_t^2+g_b^2)\,(\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}})_\lambda ~. \end{aligned}$$

(25)

To this effect, we must combine the explicit scale dependence of our result for $\left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{2\ell ,{\scriptscriptstyle \mathrm{QCD}}}\right) _\lambda$ with the implicit scale dependence of the parameters in $(\lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}})_\lambda$ whose RGEs have QCD contributions at two loops (namely $\lambda$, $A_\lambda$ and $\tan \beta$), and of the parameters in the one-loop stop and sbottom contributions $\left( \Delta \lambda _{\scriptscriptstyle \mathrm{SM}}^{1\ell ,\,\tilde{q}}\right) _\lambda$ whose RGEs have QCD contributions at one loop (namely the soft SUSY-breaking masses and trilinear couplings of the squarks, and the top and bottom Yukawa couplings).

3 Higgs-mass prediction and constraints on the NMSSM parameters

In this section we analyze the impact of the one- and two-loop corrections to the quartic Higgs coupling computed in Sects. 2.2 and 2.3, respectively, on the prediction for the mass of the lightest Higgs scalar of the NMSSM, focusing on the scenario in which all of the SUSY particles, the heavier SU(2) doublet, and the scalar and pseudoscalar components of the singlet are all significantly heavier than the EW scale. We also propose a method to estimate the so-called “theory uncertainty” of our calculation, i.e., the uncertainty associated with uncomputed higher-order corrections. Finally, we discuss how the prediction for the mass of the SM-like Higgs boson can constrain the parameter space of the NMSSM even in scenarios in which all of the BSM particles are heavy.

Our numerical calculations rely on an EFT setup analogous to the one developed in Ref. [67]. We use the public code mr [68] to extract – at full two-loop accuracy – the $\overline{\mathrm{MS}}$-renormalized parameters of the SM Lagrangian from a set of physical observables, and to evolve them up to the SUSY scale using the three-loop RGEs of the SM. For the physical observables other than the Higgs mass, we use as input for the code the PDG values $G_F= 1.1663787 \times 10^{-5}$ GeV$^{-2}$, $M_Z = 91.1876$ GeV, $M_W = 80.379$ GeV, $M_t= 172.76$ GeV, $M_b = 4.78$ GeV and $\alpha _s(m_{\scriptscriptstyle Z})=0.1179$ [69]. In order to obtain a prediction for the Higgs mass from a full set of SUSY parameters, we vary the value of the pole mass $M_h$ that we give as input to mr until the value of the $\overline{\mathrm{MS}}$-renormalized SM parameter $\lambda _{\scriptscriptstyle \mathrm{SM}}(Q)$ returned by the code at the SUSY scale $Q=M_S$ coincides with the NMSSM prediction for the quartic coupling of the lightest scalar. In alternative, we can treat the measured value of the Higgs mass, $M_h = 125.25$ GeV [69], as an additional input parameter, and use the matching condition on the quartic Higgs coupling at the SUSY scale to constrain the NMSSM parameter space. In this case we vary one of the SUSY parameters until the NMSSM prediction for the quartic Higgs coupling coincides with the value of $\lambda _{\scriptscriptstyle \mathrm{SM}}(M_S)$ returned by mr.

To obtain the NMSSM prediction for the quartic coupling of the SM-like Higgs boson at the SUSY scale, we combine the tree-level prediction in Eq. (7) with the full one-loop contribution computed in Sect. 2.2, the NMSSM-specific, $\lambda$-dependent two-loop-QCD contribution computed in Sect. 2.3, and the $\lambda$-independent two-loop contributions that are in common with the MSSM, given in Refs. [64, 65, 67]. As a result, our determination of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ includes all of the two-loop contributions that involve the strong gauge coupling, whereas the remaining two-loop contributions are included only under the approximations of vanishing EW gauge couplings and of vanishing $\lambda$. While the first approximation is generally good in view of the relative sizes of g, $g^\prime$, $g_t$ and $g_s$, the goodness of the second approximation obviously depends on the considered values of $\lambda$. In particular – similarly to what was found in Refs. [31, 34,35,36] in the context of the FO calculation of the NMSSM Higgs masses – when $\lambda$ is of $\mathcal{O}(1)$ the two-loop, NMSSM-specific contributions that are omitted in our prediction for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ can become as large as the dominant MSSM-like contributions that are included, i.e., those of $\mathcal{O}(g_t^4 g_s^2)$ and $\mathcal{O}(g_t^6)$. We recall that, in the EFT approach, the (next-to)$^n$-leading-logarithmic (N$^n$LL) resummation of the large logarithmic corrections requires the combination of ($n\!+\!1$)-loop RGEs with n-loop matching conditions at the boundary scales. Our calculation thus provides a full NLL resummation of the large logarithmic corrections, but, in view of the incomplete determination of the two-loop boundary condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ at the SUSY scale, only a partial NNLL resummation. An estimate of the impact of the omitted contributions seems desirable.

As was discussed already in Ref. [64], the EFT calculation of the Higgs mass in scenarios where all heavy particles are integrated out at a common scale $M_S$ is subject to three distinct sources of theory uncertainty: (i) a “SM uncertainty” stemming from uncomputed higher-order corrections in the relations between the physical observables taken as input for the calculation and the $\overline{\mathrm{MS}}$-renormalized parameters of the SM Lagrangian; (ii) a “SUSY uncertainty” stemming from uncomputed higher-order corrections in the matching conditions for the couplings of the SM Lagrangian at the scale $M_S$; (iii) an “EFT uncertainty” associated to the corrections suppressed by powers of $v^2/M_S^2$ that are omitted when the EFT Lagrangian is identified with the renormalizable Lagrangian of the SM in the unbroken phase of the EW symmetry. We neglect the third source of uncertainty in the following, because we consider scenarios in which all BSM particles are heavy enough to make the $\mathcal{O}(v^2/M_S^2)$ effects fully negligible. In contrast, we aim to simulate the effects of uncomputed higher-order corrections in the matching conditions at both the EW scale and the SUSY scale.

To obtain an estimate of the SM uncertainty, we change the accuracy of the determination of the top Yukawa coupling in mr, removing corrections of $\mathcal{O}(g_s^6)$ and higher that are implemented by default in the code. This simulates the effect of uncomputed N$^3$LL corrections that involve the highest powers of the strong gauge coupling, which are expected to be the largest among those neglected in the “SM” part of the calculation (see, e.g., the discussion in Sect. 6.3.1 of Ref. [8]).

For what concerns the SUSY uncertainty, we combine two estimates of different classes of higher-order effects. To obtain our first estimate, which targets the uncomputed two-loop and higher-order corrections that involve the top Yukawa coupling, we change the definition of the coupling $g_t$ entering the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ from the $\overline{\mathrm{MS}}$-renormalized parameter of the SM to the ${ \overline{\mathrm{DR}}}$-renormalized parameter of the NMSSM. The two definitions are related by

$$\begin{aligned} g_t^{\mathrm{{\scriptscriptstyle NMSSM}}}(M_S) ~=~ \frac{g_t^{\mathrm{{\scriptscriptstyle SM}}}(M_S)}{1- \Delta g_t^{\mathrm{{\scriptscriptstyle MSSM}}} - (\Delta g_t)_{\lambda }}~, \end{aligned}$$

(26)

where $\Delta g_t^{\mathrm{{\scriptscriptstyle MSSM}}}$ is the threshold correction given for the MSSM in Refs. [64, 65], and $(\Delta g_t)_{\lambda }$ is the $\lambda$-dependent contribution that turns the MSSM coupling into the NMSSM coupling. This contribution is related to the $\lambda$-dependent part of the Higgs WFR by $(\Delta g_t)_{\lambda } = - (\Delta Z_h)_\lambda /2$. For the latter we find:

$$\begin{aligned}&(4\pi )^2\,(\Delta Z_h)_\lambda \nonumber \\&\quad \,= -\frac{a_{hhs}^2}{2\,m_s^2} \,-\,\frac{a_{hHs}^2}{6\,m_A\,m_s}\,\widetilde{F}_5\left( \frac{m_s}{m_A}\right) -\,\frac{a_{hAa}^2}{6\,m_A\,m_a}\,\widetilde{F}_5\left( \frac{m_a}{m_A}\right) \nonumber \\&\qquad + \,\frac{\lambda ^2}{3}\,\left[ \, 3\,\ln \frac{\mu ^2}{Q^2} \,-\,\sin 2\beta \,f\left( \frac{m_{\tilde{s}}}{\mu }\right) +\,g\left( \frac{m_{\tilde{s}}}{\mu }\right) \,\right] , \end{aligned}$$

(27)

where the terms in the first line are the contributions of diagrams involving scalars or pseudoscalars, while those in the second line are the contributions of diagrams involving higgsinos and singlino. The loop functions $\widetilde{F}_5(x)$, f(x) and g(x) are defined in the appendix A of Ref. [64]. The coupling $a_{hhs}$ is given in Eq. (8), and the remaining trilinear couplings are

$$\begin{aligned} a_{hHs}= & {} -\frac{\lambda }{\sqrt{2}}\,(A_\lambda + 2\,\kappa \,v_s)\,\cos 2\beta ~,\nonumber \\ a_{hAa}= & {} \frac{\lambda }{\sqrt{2}}\,(A_\lambda - 2\,\kappa \,v_s)~. \end{aligned}$$

(28)

The inclusion of this $\lambda$-dependent contribution in the redefinition of $g_t$, see Eq. (26), simulates the effect of two-loop contributions of $\mathcal{O}(g_t^4\lambda ^2)$ to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$. As mentioned above, these can in principle compete with the known $\mathcal{O}(g_t^4 g_s^2)$ and $\mathcal{O}(g_t^6)$ contributions when $\lambda$ is large enough. We remark that, to avoid the inclusion in our uncertainty estimate of effects that are in fact accounted for by our calculation, the redefinition of $g_t$ must be accompanied by shifts in the known two-loop contributions to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$. In particular, in the NMSSM-specific, $\lambda$-dependent two-loop-QCD contribution computed in Sect. 2.3 we must remove the second term on the r.h.s. of Eq. (23). The analogous shifts for the MSSM-like two-loop contributions can be trivially obtained from Refs. [64, 65, 67].

Our second estimate of the SUSY uncertainty targets the uncomputed two-loop and higher-order corrections that involve the highest powers of the doublet–singlet coupling $\lambda$. We replace the definitions in Eq. (4) for the scalar and pseudoscalar singlet masses with $\,m_s^2 \,=\, m_S^2 \,+\, 2\, \kappa \,v_s\,(A_\kappa + 3\,\kappa \,v_s)$ and $\,m_a^2 \,=\, m_S^2 \,+\, 2\, \kappa \,v_s\,(-A_\kappa + \kappa \,v_s)$, respectively. The two sets of mass definitions are equivalent at the tree level, but they differ at one loop, because the soft SUSY-breaking singlet mass $m_S$ is related to the other parameters as in Eq. (12) when $v_s$ is defined as the vev of the loop-corrected potential. As discussed in Sect. 2.2, the change in the definition of the scalar singlet mass entering the tree-level part of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ must be compensated for at the one-loop level by removing the tadpole term in Eq. (11). On the other hand, the change in the definition of both scalar and pseudoscalar singlet masses entering the one-loop part of the matching condition simulates the effect of two-loop $\lambda$-dependent corrections that do not involve the strong gauge coupling, and the change in the definition of the scalar singlet mass entering the two-loop-QCD part simulates the effect of three-loop $\lambda$-dependent corrections that do involve the strong gauge coupling.

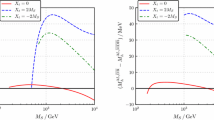
To assess the impact of the different contributions to the matching condition for the quartic Higgs coupling computed in Sect. 2, we plot in Fig. 1 the prediction for the mass of the SM-like Higgs boson as a function of $\lambda$. We consider an NMSSM scenario in which all sfermions of the first and second generations have degenerate masses of 2 TeV, while those of the third generation (namely stops, sbottoms and staus) have degenerate masses $M_S= 5$ TeV. The trilinear Higgs-stop interaction parameter is fixed as $X_t = \sqrt{6}\,M_S$ , which maximizes the one-loop stop contribution to $\lambda _{\scriptscriptstyle \mathrm{SM}}$. For given values of $\mu$ and $\tan \beta$ this determines the soft SUSY-breaking coupling $A_t$, and the corresponding sbottom and stau couplings are fixed as $A_b=A_\tau =A_t$. For consistency with our calculation of the two-loop contributions to $\lambda _{\scriptscriptstyle \mathrm{SM}}$, all sfermion masses and trilinear couplings are interpreted as $\overline{\mathrm{DR}}$-renormalized parameters, at a scale that we choose as $Q=M_S$. The soft SUSY-breaking masses of bino, wino and gluino are fixed as $M_1=1$ TeV, $M_2=2$ TeV and $M_3=2.5$ TeV, respectively.

In contrast to the case of the MSSM, in which the tree-level masses of the heavy Higgs bosons and of the higgsinos in the limit of unbroken EW symmetry are determined by the three parameters $\mu$, $B_\mu$ and $\tan \beta$ (with $m_A^2 = 2\,B_\mu /\sin 2\beta$), the Higgs/higgsino sector of the NMSSM depends on the six parameters $\lambda$, $\kappa$, $v_s$, $A_\lambda$, $A_\kappa$ and $\tan \beta$. In the plots of Fig. 1 we choose to vary the doublet–singlet coupling $\lambda$, because that parameter determines the size of the NMSSM-specific contributions to the quartic Higgs coupling, and in the limit $\lambda \rightarrow 0$ we recover the MSSM prediction. For the remaining parameters, we choose: $\kappa = \lambda$; a tree-level higgsino mass $\mu = \lambda \,v_s = 1.5$ TeV, which determines $v_s$ for a given value of $\lambda$; a tree-level heavy-Higgs-doublet mass $m_A = 3$ TeV, which determines $A_\lambda$ via Eq. (6) for a given value of $\tan \beta$; and $A_\kappa = -2$ TeV. Finally, we fix $\tan \beta =3$ in the left plot of Fig. 1 and $\tan \beta =5$ in the right plot. For consistency with our calculation of the one-loop contributions to $\lambda _{\scriptscriptstyle \mathrm{SM}}$, all of these six parameters – which enter the boundary condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ already at the tree level – are interpreted as $\overline{\mathrm{DR}}$-renormalized parameters, also at the scale $Q=M_S$. Our choices of parameters correspond to a tree-level mass of 3 TeV for the singlino, and to tree-level masses of about $2.45$ TeV and $3$ TeV for the scalar and pseudoscalar components of the singlet, respectively.

Fig. 1

Higgs-mass prediction as a function of $\lambda$, for $\tan \beta =3$ (left) or $\tan \beta =5$ (right), in the NMSSM scenario described in the text. The three lines in each plot correspond to different accuracies of the NMSSM-specific contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$. The band around the red, solid line is our estimate of the theory uncertainty

In all of the lines in the plots of Fig. 1, the Higgs-mass prediction includes all of the contributions to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ that are in common with the MSSM, so that the left edge of the plot where $\lambda = 0$ corresponds to our best prediction for $M_h$ in the so-called “MSSM limit”. The three lines in each plot correspond to different accuracies for the inclusion of the NMSSM-specific contributions. The green, dot-dashed line corresponds to the inclusion of the tree-level contribution $\left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda = \lambda ^2 \sin ^22\beta /2 - a_{hhs}^2/m_s^2\,$ alone; the blue, dashed line corresponds to the inclusion of the full one-loop, $\lambda$-dependent contribution computed in Sect. 2.2; the red, solid line corresponds to the additional inclusion of the two-loop-QCD, $\lambda$-dependent contribution computed in Sect. 2.2. The band around the red, solid line corresponds to our total estimate of the theory uncertainty of the Higgs-mass prediction, obtained by summing linearly the absolute values of the three estimates described above. Comparing the different contributions, we find that the SM uncertainty estimate alone is generally larger than the combination of the two SUSY uncertainty estimates.

The comparison between the left and right plots in Fig. 1 shows that, in our scenario, the $\lambda$-dependent contributions increase the prediction for $M_h$ for lower values of $\tan \beta$, and decrease it for higher values of $\tan \beta$. This behavior is driven already at the tree level by the $\tan \beta$ dependence of $\left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda$, whose first, positive-definite term is suppressed at larger $\tan \beta$, whereas the second, negative-definite term contains a $\tan \beta$-independent piece, as remarked after Eq. (8). The comparison between the dot-dashed and dashed lines in each plot shows that the full one-loop, $\lambda$-dependent contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ can become substantial when $\lambda \gtrsim 0.5$, changing the prediction for $M_h$ by several GeV. Finally, the comparison between the dashed and solid lines shows that the effect on the Higgs-mass prediction of the two-loop-QCD, $\lambda$-dependent contribution is quite modest, and it is much smaller than our estimate of the uncomputed higher-order effects. This is likely related to the fact that, with our choices of parameters, the $\lambda$-dependent stop contribution is suppressed already at the one-loop level. In particular, the second term in Eq. (14) vanishes for degenerate stop masses and $Q=M_S$, and the first term only amounts to a $2\%$ shift of the tree-level contribution.

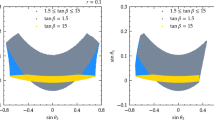
The knowledge of the mass of the SM-like Higgs boson can be used to constrain the parameters of the yet-undiscovered SUSY sector. For example, Fig. 3 of Ref. [67] showed the values of $M_S$ and $X_t$ – i.e., the two parameters that most affect the stop contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ – that are selected by the requirement that the prediction for $M_h$ coincide with its measured value in an MSSM scenario with moderately large $\tan \beta$. Here we keep the parameters in the stop sector fixed, and exploit the Higgs-mass prediction to constrain two of the parameters that determine the NMSSM-specific contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ already at the tree level. In Fig. 2 we show the values of $\tan \beta$ and $\lambda$ that yield the required prediction $M_h=125.25$ GeV in a representative NMSSM scenario with heavy BSM particles. We adopt the same choices of SUSY parameters as in Fig. 1, except that i) we set $M_S$ to 3 TeV (red lines), 5 TeV (blue lines) or 10 TeV (green lines), and ii) we set either $\kappa =\lambda$ (left plot) or $\kappa = 2\,\lambda$ (right plot).⁸ Each of the lines in Fig. 2 is obtained with our full one-loop and partial two-loop calculation of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$, and is accompanied by an uncertainty estimate obtained as described earlier.⁹

The behavior of the different lines in the plots of Fig. 2 can be qualitatively understood by considering the dependence on $\tan \beta$ and $\lambda$ of the three terms entering the tree-level matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$, see Eq. (7). The first term, which is in common with the MSSM, vanishes for $\tan \beta =1$ and increases for increasing $\tan \beta$, reaching a constant positive value at large $\tan \beta$. With our choices for the parameters that determine $a_{hhs}$ and $m_s$, the remaining, NMSSM-specific contribution $\left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda = \lambda ^2 \sin ^22\beta /2 - a_{hhs}^2/m_s^2\,$ scales as $\lambda ^2$, with a coefficient that is positive at low values of $\tan \beta$, decreases for increasing $\tan \beta$, eventually turns negative, and finally reaches a constant negative value at large $\tan \beta$. In each of the plots of Fig. 2, the line corresponding to a given value of $M_S$ is split into a left branch at lower $\tan \beta$, where the NMSSM-specific contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ is positive, and a right branch at higher $\tan \beta$, where the NMSSM-specific contribution is negative. The point where each line meets the x axis corresponds to a value of $\tan \beta$ that we denote as $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$, for which the required prediction for $M_h$ is obtained in the “MSSM limit” $\lambda \rightarrow 0$. This depends on the value of $M_S$, because heavier stops induce a larger positive contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ and thus allow for lower $\tan \beta$ in the MSSM limit.

Fig. 2

Regions of the $\tan \beta$–$\lambda$ plane that yield $M_h=125.25$ GeV, for $\kappa =\lambda$ (left) or $\kappa =2\,\lambda$ (right), in the NMSSM scenario described in the text. The three sets of lines in each plot correspond to different values of the common mass term for the third-generation sfermions. The band around each line is our estimate of the theory uncertainty

In the left plot of Fig. 2, where we set $\kappa =\lambda$, the NMSSM-specific contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ turns negative for a value of $\tan \beta$ that is lower than $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$. At the left edge of the plot, where $\tan \beta =1$, the MSSM prediction for the Higgs mass is too low, and the required prediction $M_h=125.25$ GeV is obtained thanks to the positive NMSSM-specific contribution. Moving to higher values of $\tan \beta$, the value of $\lambda$ that yields the required prediction for $M_h$ decreases at first, as the tree-level, MSSM-like contribution to $\lambda _{\scriptscriptstyle \mathrm{SM}}$ increases. However, the coefficient of $\lambda ^2$ in the tree-level,¹⁰ NMSSM-specific contribution decreases for increasing $\tan \beta$, and as it approaches zero the value of $\lambda$ that yields $M_h=125.25$ GeV shoots up. In the gap between the value of $\tan \beta$ for which the NMSSM-specific contribution turns negative and $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$ there is no value of $\lambda$ that yields the required Higgs-mass prediction. Finally, when $\tan \beta$ is larger than $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$ the MSSM prediction for $M_h$ is too high, and the required prediction is obtained thanks to the negative NMSSM-specific contribution. As both the coefficient of $\lambda ^2$ in $\left( \lambda _{\scriptscriptstyle \mathrm{SM}}^{\scriptscriptstyle \mathrm{tree}}\right) _\lambda$ and the MSSM prediction for $M_h$ reach a plateau at large $\tan \beta$, so does the value of $\lambda$ that brings the Higgs mass down to 125.25 GeV.

In the right plot of Fig. 2, where we set $\kappa =2\,\lambda$, the qualitative behavior of the red line corresponding to $M_S=3$ TeV is the same as in the left plot. However, the blue and green lines corresponding to higher values of $M_S$ behave differently. In this case, the value of $\tan \beta$ for which the NMSSM-specific contribution to the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$ turns negative is higher than $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$. Consequently, as $\tan \beta$ approaches $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$ from the left, the requirement that $M_h=125.25$ GeV drives $\lambda$ to zero. On the right of $(\tan \beta )_\mathrm{{\scriptscriptstyle MSSM}}$ there is a gap in which the MSSM prediction for $M_h$ is too high but the NMSSM-specific contribution remains positive, so there is no value of $\lambda$ that yields the required Higgs-mass prediction. Finally, when the NMSSM-specific contribution does turn negative, the value of $\lambda$ that brings the prediction for $M_h$ down to 125.25 GeV decreases with increasing $\tan \beta$, and eventually reaches a plateau as in the left plot.

4 Conclusions

If SUSY is realized in nature, there appears to be at least a mild hierarchy between the scale of the superparticle masses and the EW scale. In this kind of hierarchical scenario the prediction for the mass of the SM-like Higgs boson is best obtained in the EFT approach, which allows for the all-orders resummation of potentially large corrections enhanced by powers of the logarithm of the two scales. The EFT calculation of the Higgs masses in the MSSM is by now quite advanced, with full one-loop and partial two-loop results for the matching conditions for the Higgs self-couplings under a variety of mass hierarchies (see Ref. [8] for a review). In contrast, in the case of the NMSSM analytic calculations of the matching conditions have been performed so far only at the one-loop level, in an extremely constrained scenario where all BSM particles are heavy and their masses depend on just one parameter [60], and in a Split-SUSY scenario where the low-energy EFT includes also the scalar and pseudoscalar components of the singlet plus all of the SUSY fermions [61].

In this paper we obtained a full one-loop result, valid for arbitrary values of all relevant parameters, for the matching condition for the quartic coupling of the Higgs boson, in the NMSSM scenario where all BSM particles are heavy and the EFT valid below the SUSY scale is just the SM. To this purpose, we adapted to the NMSSM the results of Ref. [59], which provides the one-loop matching of a general high-energy theory (without heavy gauge bosons) on a general renormalizable EFT. We compared our results with those of Ref. [60] – in the constrained scenario discussed in that paper – and found a discrepancy related to the definition of the singlet mass entering the tree-level part of the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$. In addition to the full one-loop calculation of the matching condition, we directly computed the two-loop contributions that involve the strong gauge coupling. Our result includes also terms associated with the external-momentum dependence of the two-loop Higgs self-energy that are missed by the FO calculations of the corresponding corrections in Refs. [21, 30,31,32]. Finally, we proposed a way to extend to the NMSSM the estimates of the theory uncertainty associated with uncomputed higher-order effects that had previously been developed for the MSSM.

We found that, in the NMSSM scenario with heavy BSM particles, the matching condition for the quartic Higgs coupling splits neatly into a part that is in common with the MSSM, and an NMSSM-specific part which vanishes for $\lambda \rightarrow 0$. We studied the numerical impact on the Higgs-mass prediction of the different contributions to the NMSSM-specific part of the matching condition, and found that the one-loop and two-loop-QCD contributions modify only moderately, and only for quite large values of $\lambda$, the leading behavior driven by the tree-level contribution. We stress that the smallness of these effects is in fact a desirable feature of the EFT calculation of the Higgs mass, in which the logarithmically enhanced corrections are accounted for by the evolution of the parameters between the SUSY scale and the EW scale, and high-precision calculations at the EW scale can be borrowed from the SM.

Turning to the modern approach of treating the Higgs mass as an input rather than an output of the calculation, we illustrated how the requirement of a correct prediction for $M_h$ can be used to constrain some of the yet-unmeasured parameters of the NMSSM. Focusing on the $\tan \beta$–$\lambda$ plane, we noticed how the shape of the allowed regions can change drastically depending on the choice of the remaining parameters. This is a well-known aspect of the NMSSM, in which the Higgs sector depends on a relatively large number of parameters already at the tree level. However, a systematic phenomenological study of the constraints that the Higgs-mass prediction imposes on the parameter space of the NMSSM goes beyond the scope of this paper. What we provide here is a set of fully analytic formulas for the matching condition for $\lambda _{\scriptscriptstyle \mathrm{SM}}$, available on request in electronic form. Our results can be used to implement the resummation of the large logarithmic corrections in the existing public codes for the Higgs-mass calculation in the NMSSM [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53], bringing the accuracy of those codes closer to what has already been attained for the MSSM.