Decays of the neutral Higgs bosons into SM fermions and gauge bosons in the $\mathcal{CP}$-violating NMSSM

Abstract

The Next-to-Minimal Supersymmetric Standard Model (NMSSM) offers a rich framework embedding physics beyond the Standard Model as well as consistent interpretations of the results about the Higgs signal detected at the LHC. We investigate the decays of neutral Higgs states into Standard Model (SM) fermions and gauge bosons. We perform full one-loop calculations of the decay widths and include leading higher-order QCD corrections. We first discuss the technical aspects of our approach, before confronting our predictions to those of existing public tools, performing a numerical analysis and discussing the remaining theoretical uncertainties. In particular, we find that the decay widths of doublet-dominated heavy Higgs bosons into electroweak gauge bosons are dominated by the radiative corrections, so that the tree-level approximations that are often employed in phenomenological analyses fail. Finally, we focus on the phenomenological properties of a mostly singlet-like state with a mass below the one at 125 GeV, a scenario that appears commonly within the NMSSM. In fact, the possible existence of a singlet-dominated state in the mass range around or just below 100 GeV would have interesting phenomenological implications. Such a scenario could provide an interpretation for both the $2.3\,\sigma$ local excess observed at LEP in the $e^+e^-\rightarrow Z(H\rightarrow b\bar{b})$ searches at $\mathord {\sim }\,98$ GeV and for the local excess in the diphoton searches recently reported by CMS in this mass range, while at the same time it would reduce the “Little Hierarchy” problem.

1 Introduction

The signal that was discovered in the Higgs searches at ATLAS and CMS at a mass of $\mathord {\sim }\,125$ GeV [1,2,3] is, within the current theoretical and experimental uncertainties, compatible with the properties of the Higgs boson predicted within Standard-Model (SM) of particle physics. No conclusive signs of physics beyond the SM have been reported so far. However, the measurements of Higgs signal strengths for the various channels leave considerable room for Beyond Standard Model (BSM) interpretations. Consequently, the investigation of the precise properties of the discovered Higgs boson will be one of the prime goals at the LHC and beyond. While the mass of the observed particle is already known with excellent accuracy [4, 5], significant improvements of the information about the couplings of the observed state are expected from the upcoming runs of the LHC [3, 6,7,8,9] and even more so from the high-precision measurements at a future $e^+e^-$ collider [10,11,12,13].

Motivated by the “Hierarchy Problem”, Supersymmetry (SUSY)-inspired extensions of the SM play a prominent role in the investigations of possible new physics. As such, the Minimal Supersymmetric Standard Model (MSSM) [14, 15] or its singlet extension, the Next-to-MSSM (NMSSM) [16, 17], have been the object of many studies in the last decades. Despite this attention, these models are not yet prepared for an era of precision tests as the uncertainties at the level of the Higgs-mass calculation [18,19,20] are about one order of magnitude larger than the experimental uncertainty. At the level of the decays, the theoretical uncertainty arising from unknown higher-order corrections has been estimated for the case of the Higgs boson of the SM (where the Higgs mass is treated as a free input parameter) in Refs. [21, 22] and updated in Ref. [23]: depending on the channel and the Higgs mass, it typically falls in the range of $\mathord {\sim }\,0.5$–$5\%$. To our knowledge, no similar analysis has been performed in SUSY-inspired models, but one can expect the uncertainties from missing higher-order corrections to be larger in general – with many nuances depending on the characteristics of the Higgs state and the considered point in parameter space: we provide some discussion of this issue at the end of this paper. In addition, parametric uncertainties that are induced by the experimental errors of the input parameters should be taken into account as well. For the case of the SM decays those parametric uncertainties have been discussed in the references above. In the SUSY case the parametric uncertainties induced by the (known) SM input parameters can be determined in the same way as for the SM, while the dependence on unknown SUSY parameters can be utilized for setting constraints on those parameters. While still competitive today, the level of accuracy of the theoretical predictions of Higgs-boson decays in SUSY models should soon become outclassed by the achieved experimental precision on the decays of the observed Higgs signal. Without comparable accuracy of the theoretical predictions, the impact of the exploitation of the precision data will be diminished – either in terms of further constraining the parameter space or of interpreting deviations from the SM results. Further efforts towards improving the theoretical accuracy are therefore necessary in order to enable a thorough investigation of the phenomenology of these models. Besides the decays of the SM-like state at 125 GeV of a SUSY model – where the goal is clearly to reach an accuracy that is comparable to the case of the SM – it is also of interest to obtain reliable and accurate predictions for the decays of the other Higgs bosons in the spectrum. The decays of the non-SM-like Higgs bosons can be affected by large higher-order corrections as a consequence of either large enhancement factors or a suppression of the lowest-order contribution. Confronting accurate predictions with the available search limits yields important constraints on the parameter space.

In this paper we present an evaluation of the decays of the neutral Higgs bosons of the $\mathbb {Z}_3$-conserving NMSSM into SM particles. The extension of the MSSM by a gauge-singlet superfield was originally motivated by the ‘$\mu$ problem’ [24], but also leads to a richer phenomenology in the Higgs sector (see e.g. the introduction of Ref. [25] for a recent summary of related activities). Several public tools provide an implementation of Higgs decays in the NMSSM: HDECAY [26,27,28], focusing on the SM and MSSM, was the object of various extensions to the $\mathcal{CP}$-conserving or -violating NMSSM for NMSSMTools [29,30,31,32] and NMSSMCALC [33, 34]; SOFTSUSY [35, 36] recently released its own set of routines [37], which generally are confined to the leading order or leading QCD corrections; a one-loop evaluation of two-body decays in the $\overline{\mathrm {DR}}$ $\left( \overline{\mathrm {MS}}\right)$ scheme for generic models [38] has been recently presented for SPHENO [39,40,41,42], which employs SARAH [43,44,45,46]. Moreover, the non-public code SloopS [47] has been extended to the NMSSM [48, 49] and applied to the calculation of Higgs decays [49, 50].

The current work focusing on NMSSM Higgs decays is part of the effort for developing a version of FeynHiggs [18, 51,52,53,54,55,56,57] dedicated to the NMSSM [25, 58]. The general methodology relies on a Feynman-diagrammatic calculation of radiative corrections, which employs FeynArts [59, 60], FormCalc [61] and LoopTools [61]. The implementation of the renormalization scheme within the NMSSM [25] has been done in such a way that the result in the MSSM limit of the NMSSM exactly coincides with the MSSM result obtained from FeynHiggs without any further adjustments of parameters (cases where the NMSSM result is more complete than the current implementation of the MSSM result will be discussed below). Concerning the Higgs decays, our routines, in their current status, contain an evaluation of all the two-body decays of neutral and charged Higgs bosons. In the present paper, we wish to focus on decays of the neutral Higgs bosons into SM final states, where we have obtained results including higher-order contributions as detailed below as well as further refinements. The channels of the type Higgs-to-Higgs and Higgs-to-SUSY are currently only implemented at leading order.¹

For the evaluation of the decays of the neutral Higgs bosons of the NMSSM into SM final states we have followed the same general approach as for the implementation of the MSSM Higgs decays in FeynHiggs, which have been described in Refs. [63, 67]. At the level of the external Higgs fields, mixing effects are consistently taken into account as explained in Refs. [25, 68]. Full one-loop contributions are considered in the fermionic decay channels, supplemented by QCD higher-order corrections. For the bosonic decay modes generated at the radiative order, leading QCD corrections are taken into account. For decays into massive electroweak gauge bosons, the implementation in the MSSM is such that FeynHiggs first extracts the loop-corrected width that Prophecy4f [69,70,71] calculates in the SM for a Higgs boson at a given mass, and then rescales this result by the squared coupling of the MSSM Higgs boson to WW and ZZ, normalized to the SM value. We go beyond this approach and include full one-loop on-shell results for these decay widths – however, the on-shell kinematical factor of the tree-level contribution is replaced by its off-shell counterpart, leading to a tree-level estimate below threshold.² More generally, the refinements that we implement, e.g. the inclusion of higher-order corrections, often surpass the assumptions made in public codes dedicated to the NMSSM. However, we stress that we strictly confine ourselves to the free-particle approximation for the final states. Accordingly, dedicated analyses would be needed for a proper treatment of decays close to threshold, since finite-width effects need to be taken into account in this region, and effects of the interactions among the final states can be very large [72,73,74,75,76].

The case where the Higgs spectrum contains a singlet-dominated Higgs state with a mass below the one of the signal detected at 125 GeV is a particularly interesting scenario that commonly emerges in the NMSSM. Among the appealing features of this class of scenarios it should be mentioned that the somewhat high mass (in an MSSM context) of the SM-like Higgs state observed at the LHC could be understood more naturally as the result of the mixing with a lighter singlet state – see e.g. Ref. [77] for a list of references and an estimate of the possible uplift in mass. Furthermore, the existence of a mostly singlet-like state in the range of $\mathord {\lesssim }\,100$ GeV has been suggested [78, 79] as a possible explanation of the $2.3\,\sigma$ local excess observed at LEP in the $e^+e^-\rightarrow Z(H\rightarrow b\bar{b})$ searches [80]. More recently, the CMS collaboration has reported a local excess in its diphoton Higgs searches for a mass in the vicinity of $\mathord {\sim }\,96$ GeV [81]. This excess reaches the (local) $2.9\,\sigma$ level in the Run II data and has already received attention from the particle-physics community [82,83,84,85]. A similar excess ($2.0\,\sigma$) was already present in the Run I data in the same mass range. In an NMSSM context, the possibility of large diphoton signals is well-known [86,87,88]. Here we show that it is in fact possible to describe simultaneously the LEP and the CMS excesses within the NMSSM. However, it should be kept in mind that the excesses that were observed at LEP and CMS at $\mathord {\lesssim }\,100$ GeV could of course just be statistical fluctuations of the background and that their possible explanation in terms of an NMSSM Higgs state remains somewhat speculative. In particular, the diphoton excess observed at CMS would of course require confirmation from the ATLAS data as well [89].

In the following section, we discuss the technical aspects of our calculation, describing the conventions, assumptions and higher-order corrections that we address. Section 3 illustrates the workings of our decay routines in several scenarios of the NMSSM, and we perform comparisons with existing public tools. We also investigate the NMSSM scenario with a mostly singlet-like state with mass close to 100 GeV. Furthermore we discuss the possible size of the remaining theoretical uncertainties from unknown higher-order corrections. The conclusions are summarized in Sect. 4.

2 Higgs decays to SM particles in the $\mathcal{CP}$-violating NMSSM

In this section, we describe the technical aspects of our calculation of the Higgs decays. Our notation and the renormalization scheme that we employ for the $\mathbb {Z}_3$-conserving NMSSM in the general case of complex parameters were presented in Sect. 2 of Ref. [25], and we refer the reader to this article for further details.

2.1 Decay amplitudes for a physical (on-shell) Higgs state – Generalities

On-shell external Higgs leg In this article, we consider the decays of a physical Higgs state, i.e. an eigenstate of the inverse propagator matrix for the Higgs fields evaluated at the corresponding pole eigenvalue. The connection between such a physical state and the tree-level Higgs fields entering the Feynman diagrams is non-trivial in general since the higher-order contributions induce mixing among the Higgs states and between the Higgs states and the gauge bosons (as well as the associated Goldstone bosons). The LSZ reduction fully determines the (non-unitary) transition matrix $\mathbf {Z}^{\hbox { mix}}$ between the loop-corrected mass eigenstates and the lowest-order states. Then, the amplitude describing the decay of the physical state $h_i^{{ \mathrm{phys}}}$ (we shall omit the superscript ‘phys’ later on), into e.g. a fermion pair $f\bar{f}$, relates to the amplitudes in terms of the tree-level states $h_j^0$ according to (see below for the mixing with gauge bosons and Goldstone bosons):

(2.1)

Here, we characterize the physical Higgs states according to the procedure outlined in Ref. [25] (see also Refs. [53, 63, 68]):

• the Higgs self-energies include full one-loop and leading $\mathcal {O}{(\alpha _t\alpha _s,\alpha _t^2)}$ two-loop corrections (with two-loop effects obtained in the MSSM approximation via the public code FeynHiggs³);

• the pole masses correspond to the zeroes of the determinant of the inverse-propagator matrix;

• the $(5 \times 5)$ matrix $\mathbf {Z}^{ \text{ mix }}$ is obtained in terms of the solutions of the eigenvector equation for the effective mass matrix evaluated at the poles, and satisfying the appropriate normalization conditions (see Sect. 2.6 of Ref. [25]).

In correcting the external Higgs legs by the full matrix $\mathbf {Z}^{ \text{ mix }}$ – instead of employing a simple diagrammatic expansion – we resum contributions to the transition amplitudes that are formally of higher loop order. This resummation is convenient for taking into account numerically relevant leading higher-order contributions. It can in fact be crucial for the frequent case where radiative corrections mix states that are almost mass-degenerate in order to properly describe the resonance-type effects that are induced by the mixing. On the other hand, care needs to be taken to avoid the occurrence of non-decoupling terms when Higgs states are well-separated in mass, since higher-order effects can spoil the order-by-order cancellations with vertex corrections.

We stress that all public tools, with the exception of FeynHiggs, neglect the full effect of the transition to the physical Higgs states encoded within $\mathbf {Z}^{ \text{ mix }}$, and instead employ the unitary approximation $\mathbf {U}^0$ neglecting external momenta (which is in accordance with leading-order or QCD-improved leading-order predictions). We refer the reader to Refs. [25, 53, 68] for the details of the definition of $\mathbf {U}^0$ or $\mathbf {U}^m$ (another unitary approximation) as well as a discussion of their impact at the level of Higgs decay widths.

Higgs–electroweak mixing For the mass determination, we do not take into account contributions arising from the mixing of the Higgs fields with the neutral Goldstone or Z bosons since these corrections enter at the sub-dominant two-loop level (contributions of this kind can also be compensated by appropriate field-renormalization conditions [92]). We note that, in the $\mathcal{CP}$-conserving case, only external $\mathcal{CP}$-odd Higgs components are affected by such a mixing. Yet, at the level of the decay amplitudes, the Higgs mixing with the Goldstone and Z bosons enters already at the one-loop order (even if the corresponding self-energies are canceled by an appropriate field-renormalization condition, this procedure would still provide a contribution to the $h_if\bar{f}$ counterterm). Therefore, for a complete one-loop result of the decay amplitudes it is in general necessary to incorporate Higgs–Goldstone and Higgs–Z self-energy transition diagrams [62, 63, 66]. In the following, we evaluate such contributions to the decay amplitudes in the usual diagrammatic fashion (as prescribed by the LSZ reduction) with the help of the FeynArts model file for the $\mathcal{CP}$-violating NMSSM [25]. The corresponding one-loop amplitudes (including the associated counterterms) will be symbolically denoted as . These amplitudes can be written in terms of the self-energies $\Sigma _{h_iG/Z}$ with Higgs and Goldstone / Z bosons in the external legs. In turn, these self-energies are connected by a Slavnov–Taylor identity (see e.g. App. A of Ref. [93]):⁴

$$\begin{aligned}&0 = M_Z\,\Sigma _{h_iG}{\left( p^2\right) } \nonumber \\&\qquad +\, \imath \,p^2\,\Sigma _{h_iZ}{\left( p^2\right) } + M_Z\left( p^2-m_{h_i}^2\right) f{\left( p^2\right) }\nonumber \\&\qquad -\,\frac{e}{2\,s_{\text {w}}\,c_{\text {w}}}\sum _j\left[ {\left( U_n\right) }_{i1}{\left( U_n\right) }_{j4}-{\left( U_n\right) }_{i2}{\left( U_n\right) }_{j5}\nonumber \right. \\&\qquad \left. -\,{\left( U_n\right) }_{j1}{\left( U_n\right) }_{i4}+{\left( U_n\right) }_{j2}{\left( U_n\right) }_{i5} \right] T_{h_j}\,, \end{aligned}$$

(2.2a)

$$\begin{aligned}&f{\left( p^2\right) } \equiv -\frac{\alpha }{16\,\pi \,s_{\text {w}}\,c_{\text {w}}}\sum _j \left[ {\left( U_n\right) }_{i1}{\left( U_n\right) }_{j4}\nonumber \right. \\&\quad \left. -\,{\left( U_n\right) }_{i2}{\left( U_n\right) }_{j5}-{\left( U_n\right) }_{j1}{\left( U_n\right) }_{i4}+{\left( U_n\right) }_{j2}{\left( U_n\right) }_{i5}\right] \nonumber \\&\quad \times \left[ c_\beta \,{\left( U_n\right) }_{j1} + s_\beta \,{\left( U_n\right) }_{j2}\right] B_{0}{\left( p^2,m_{h_j}^2,M_Z^2\right) }, \end{aligned}$$

(2.2b)

where the $T_{h_i}$ correspond to the tadpole terms of the Higgs potential, and ${\left( U_n\right) }_{ij}$ are the elements of the transition matrix between the gauge- and tree-level mass-eigenstate bases of the Higgs bosons – the notation is introduced in Sect. 2.1 of Ref. [25]. Similar relations in the MSSM are also provided in Eqs. (127) of Ref. [63]. We checked this identity at the numerical level.

Inclusion of one-loop contributions The wave function normalization factors contained in $\mathbf {Z}^{ \text{ mix }}$ together with the described treatment of the mixing with the Goldstone and Z bosons ensure the correct on-shell properties of the external Higgs leg in the decay amplitude, so that no further diagrams correcting this external leg are needed. Moreover, the SM fermions and gauge bosons are also treated as on-shell particles in our renormalization scheme. Beyond the transition to the loop-corrected states incorporated by $\mathbf {Z}^{ \text{ mix }}$, we thus compute the decay amplitudes at the one-loop order as the sum of the tree-level contribution  (possibly equal to zero), the Higgs–electroweak one-loop mixing  and the (renormalized) one-loop vertex corrections  (including counterterm contributions) – we note that each of these pieces of the full amplitude is separately ultraviolet-finite. In the example of the $f\bar{f}$ decay, the amplitudes with a tree-level external Higgs field $h_j^0$ – on the right-hand side of Eq. (2.1) – thus symbolically read:

(2.3)

All the pieces on the right-hand side of this equation are computed with the help of FeynArts [59, 60], FormCalc [61] and LoopTools [61], according to the prescriptions that are encoded in the model file for the $\mathcal{CP}$-violating NMSSM. However, we use a specific treatment for some of the contributions, such as QED and QCD one-loop corrections to Higgs decays into final state particles that are electrically and/or color charged, or include certain higher-order corrections. We describe these channel-specific modifications in the following subsections.

Goldstone-boson couplings The cubic Higgs–Goldstone-boson vertices can be expressed as

$$\begin{aligned}&\mathcal {L}\ni -\frac{1}{\sqrt{2}\,v}\left\{ \sum _j m^2_{h_j}\left[ \cos \beta \,{\left( U_n\right) }_{j1}\nonumber \right. \right. \\&\quad \left. \left. +\sin \beta \,{\left( U_n\right) }_{j2}\right] h_j^0\left[ G^+G^-+\tfrac{1}{2}\left( G^{0}\right) ^2\right] \right. \nonumber \\&\quad +\Big [\sum _j\left( m^2_{H^{\pm }}-m^2_{h_j}\right) \left( \sin \beta \left[ {\left( U_n\right) }_{j1}+\imath \,{\left( U_n\right) }_{j4}\right] \nonumber \right. \\&\quad \left. -\cos \beta \left[ {\left( U_n\right) }_{j2}-\imath \,{\left( U_n\right) }_{j5}\right] \right) h_j^0H^+G^-+\text {h. c.}\Big ]\nonumber \\&\quad \left. +\frac{1}{2}\sum _{j,\,k}\left( m^2_{h_k}-m^2_{h_j}\right) \left[ {\left( U_n\right) }_{j1}{\left( U_n\right) }_{k4}\nonumber \right. \right. \\&\quad \left. \left. -{\left( U_n\right) }_{j2}{\left( U_n\right) }_{k5}-\left( j\leftrightarrow k\right) \right] h_j^0h_k^0G^0\right\} . \end{aligned}$$

(2.4)

The doublet vacuum expectation value (vev), $v=\,M_W\,s_{\text {w}}/\sqrt{2\,\pi \,\alpha }$, is expressed in terms of the gauge-boson masses $M_W$ and $M_Z$ $\big (s_{\text {w}}=\sqrt{1-M_W^2/M_Z^2}\big )$, as well as the electromagnetic coupling $\alpha$. The symbol $m_{h_j}^2$, ($j=1,\ldots ,5$), represents the tree-level mass squared of the neutral Higgs state $h_j^0$, and $m^2_{H^{\pm }}$ the mass squared of the charged Higgs state.

The use of the tree-level couplings of Eq. (2.4) together with a physical (loop-corrected) external Higgs leg $h_i=\sum _jZ^{ \text{ mix }}_{ij}\,h^0_j$ is potentially problematic regarding the gauge properties of the matrix elements. The structure of the gauge theory and its renormalization indeed guarantee that the gauge identities are observed at the order of the calculation (one loop). However, the evaluation of Feynman amplitudes is not protected against a violation of the gauge identities at the (incomplete) two-loop order. We detected such gauge-violating effects of two-loop order at several points in our calculation of the neutral-Higgs decays, e.g.:

• the Ward identity in $h_i\rightarrow \gamma \gamma$ is not satisfied (see also Ref. [87]);

• infrared (IR) divergences of the virtual corrections in $h_i\rightarrow W^+W^-$ do not cancel their counterparts in the bremsstrahlung process $h_i\rightarrow W^+W^-\gamma$ (see also Ref. [94]);

• computing $h_i\rightarrow f\bar{f}$ in an $R_{\xi }$ gauge entails non-vanishing dependence of the amplitudes on the electroweak gauge-fixing parameters $\xi _Z$ and $\xi _W$.

As these gauge-breaking effects could intervene with sizable and uncontrolled numerical impact, it is desirable to add two-loop order terms restoring the gauge identities at the level of the matrix elements. Technically, there are different possible procedures to achieve this: one would amount to replace the kinematic Higgs masses that appear in Higgs–gauge-boson couplings by tree-level Higgs masses; we prefer the alternative procedure consisting in changing the Higgs–Goldstone-boson couplings of Eq. (2.4): for the Higgs mass associated to the external Higgs leg the loop-corrected Higgs mass $M_{h_i}$ is used instead of the tree-level one. This is actually the form of the Higgs–Goldstone-boson couplings that would be expected in an effective field theory of the physical Higgs boson $h_i$. Using the definition of the i-th row of $Z^{ \text{ mix }}_{ij}$ as an eigenvector of the loop-corrected mass matrix for the eigenvalue $M^2_{h_i}$ – see Sect. 2.6 of Ref. [25] – one can verify that the effective Higgs–Goldstone-boson vertices employing the physical Higgs mass differ from their tree-level counterparts by a term of one-loop order (proportional to the Higgs self-energies) so that the alteration of the one-loop amplitudes is indeed of two-loop order. Employing this shift of the Higgs–Goldstone couplings cures the gauge-related issues that we mentioned earlier.

Another issue with gauge invariance appears in connection with the amplitudes . The Goldstone and Z-boson propagators generate denominators with pole $M_Z^2$ (or $\xi _Z\,M_Z^2$ in an $R_{\xi }$ gauge): in virtue of the Slavnov–Taylor identity of Eq. (2.2a) these terms should cancel one another in the total amplitude at the one-loop order – we refer the reader to Sect. 4.3 of Ref. [63] for a detailed discussion. However, the term $\left( p^2-M_Z^2\right) ^{-1}$ multiplying $f{\left( p^2\right) }$ of Eq. (2.2a) only vanishes if $p^2=m^2_{h_i}$: if we employ $p^2=M^2_{h_i}$ (the loop-corrected Higgs mass), the cancellation is spoiled by a term of two-loop order. In order to address this problem, we re-define  by adding a two-loop term:

(2.5)

where $\Gamma ^{\text {tree}}_{Gf\bar{f}}$ represents the tree-level vertex of the neutral Goldstone boson with the fermion f (in the particular example of a Higgs decay into $f\bar{f}$). Then, it is straightforward to check that  is gauge-invariant. The transformation of Eq. (2.5) can also be interpreted as a two-loop shift re-defining $\Sigma _{h_iZ}$, so that it satisfies a generalized Slavnov–Taylor identity of the form of Eq. (2.2a), but applying to a physical (loop-corrected) Higgs field, with the term $\left( p^2-m^2_{h_i}\right) f{\left( p^2\right) }$ of Eq. (2.2a) replaced by $\left( p^2-M^2_{h_i}\right) f{\left( p^2\right) }$.

Numerical input in the one-loop corrections As usual, the numerical values of the input parameters need to reflect the adopted renormalization scheme, and the input parameters corresponding to different schemes differ from each other by shifts of the appropriate loop order (at the loop level there exists some freedom to use a numerical value of an input parameter that differs from the tree-level value by a one-loop shift, since the difference induced in this way is of higher order). Concerning the input values of the relevant light quark masses, we follow in our evaluation the choice of FeynHiggs and employ $\overline{\text{ MS }}$ quark masses with three-loop QCD corrections evaluated at the scale of the mass of the decaying Higgs, $m_q^{\overline{ \text{ MS }}}(M_{h_i})$, in the loop functions and the definition of the Yukawa couplings. In addition, the input value for the pole top mass is converted to $m_t^{\overline{ \text{ MS }}}(m_t)$ using up to two-loop QCD and one-loop top Yukawa/electroweak corrections (corresponding to the higher-order corrections included in the Higgs-boson mass calculation). Furthermore, the $\tan \beta$-enhanced contributions are always included in the defining relation between the bottom Yukawa coupling and the bottom mass (and similarly for all other down-type quarks). Concerning the Higgs vev appearing in the relation between the Yukawa couplings and the fermion masses, we parametrize it in terms of $\alpha (M_Z)$. Finally, the strong coupling constant employed in SUSY-QCD diagrams is set to the scale of the supersymmetric particles entering the loop. We will comment on deviations from these settings if needed.

2.2 Higgs decays into SM fermions

Our calculation of the Higgs decay amplitudes into SM fermions closely follows the procedure outlined in the previous subsection. However, we include the QCD and QED corrections separately, making use of analytical formulae that are well-documented in the literature [95, 96]. We also employ an effective description of the Higgs–$b\bar{b}$ interactions in order to resum potentially large effects for large values of $\tan \beta$. Below, we comment on these two issues and discuss further the derivation of the decay widths for this class of channels.

Tree-level amplitude At the tree level, the decay $h^0_j\rightarrow f\bar{f}$ is determined by the Yukawa coupling $Y_f$ and the decomposition of the tree-level state $h^0_j$ in terms of the Higgs-doublet components:

(2.6)

The $\delta$-s are Kronecker symbols selecting the appropriate Higgs matrix element for the fermionic final state, $u_k=u,c,t$, $d_k=d,s,b$ or $e_k=e,\mu ,\tau$. We have written the amplitude in the Dirac-fermion convention, separating the scalar piece $g_{h_jff}^S$ (first two terms between curly brackets in the first line) from the pseudoscalar one $g_{h_jff}^P$ (last two terms). The fermion and antifermion spinors are denoted as $\bar{u}_f(p_f)$ and $v_f(p_{\bar{f}})$, respectively.

Case of the ${b}\bar{{b}}$final state: $\tan \beta$-enhanced corrections In the case of a decay to $b\bar{b}$ (and analogously for down-type quarks of first and second generation, but with smaller numerical impact), the loop contributions that receive a $\tan \beta$ enhancement may have a sizable impact, thus justifying an effective description of the Higgs–$b\bar{b}$ vertex that provides a resummation of large contributions [33, 63, 97,98,99,100,101,102]. We denote the neutral components of $\mathcal {H}_1$ and $\mathcal {H}_2$ from Eq. (2.2) of Ref. [25] by $H_d^0$ and $H_u^0$, respectively. The large $\tan \beta$-enhanced effects arise from contributions to the $\left( H_u^{0}\right) ^*\,\bar{b}\,P_L\,{b}$ operator – $P_{L,R}$ are the left- and right-handed projectors in the Dirac description of the b spinors – and can be parametrized in the following fashion:

$$\begin{aligned} \mathcal {L}^{\text {eff}}&= -Y_b\,\bar{b}\left[ H_d^0 + \frac{\Delta _b}{\tan \beta }\left( \frac{\lambda }{\mu _{\text {eff}}}\,S\,H_u^0\right) ^* \right] P_L\,b + \text {h.c.} \nonumber \\&\equiv -\sum _j g_{h_jbb}^{L\,\text {eff}}\,h^0_j\,\bar{b}\,P_L\,b + \text {h. c.} \end{aligned}$$

(2.7)

Here, $\Delta _b$ is a coefficient that is determined via the calculation of the relevant ($\tan \beta$-enhanced) one-loop diagrams to the Higgs–$b\bar{b}$ vertex, involving gluino–sbottom, chargino–stop and neutralino–sbottom loops.⁵ The symbol $\mu _{\text {eff}}$ represents the effective $\mu$ term that is generated when the singlet field acquires a vev. The specific form of the operator, $\left( S\,H_u^0\right) ^*\,\bar{b}\,P_L\,b$, is designed so as to preserve the $\mathbb {Z}_3$ symmetry, and it can be shown that this operator is the one that gives rise to leading contributions to the $\tan \beta$-enhanced effects. We evaluate $\Delta _b$ at a scale corresponding to the arithmetic mean of the masses of the contributing SUSY particles: this choice is consistent with the definition of $\Delta _b$ employed for the Higgs-mass calculation.

From the parametrization of Eq. (2.7), one can derive the non-trivial relation between the ‘genuine’ Yukawa coupling $Y_b$ and the effective bottom mass $m_b$: $Y_b=\frac{m_b}{v_1\left( 1 + \Delta _b\right) }$ . Then, the effective couplings of the neutral Higgs fields to $b\bar{b}$ read:

$$\begin{aligned} g_{h_jbb}^{L\,\text {eff}}&= \frac{m_b}{\sqrt{2}\,v_1\left( 1 + \Delta _b\right) }\left\{ {\left( U_n\right) }_{j1} + \imath \,{\left( U_n\right) }_{j4} \nonumber \right. \\&\quad \left. +\frac{\Delta _b}{\tan \beta }\left( {\left( U_n\right) }_{j2} - \imath \,{\left( U_n\right) }_{j5}\nonumber \right. \right. \\&\quad \left. \left. + \tfrac{\lambda ^*\,v_2}{\mu _{\text {eff}}^*}\left[ {\left( U_n\right) }_{j3} - \imath \,{\left( U_n\right) }_{j6}\right] \right) \right\} . \end{aligned}$$

(2.8)

This can be used to substitute  in Eq. (2.3) by:

(2.9)

where this expression resums the effect of $\tan \beta$-enhanced corrections to the $h^0_jb\bar{b}$ vertex. However, if one now adds the one-loop amplitude , the one-loop effects associated with the $\tan \beta$-enhanced contributions would be included twice. To avoid this double counting, the terms that are linear in $\Delta _b$ in Eq. (2.8) need to be subtracted. Employing the ‘subtraction’ couplings

$$\begin{aligned} g_{h_jbb}^{L\,\text {sub}}&= \frac{m_b\,\Delta _b}{\sqrt{2}\,v_1}\left\{ {\left( U_n\right) }_{j1} + \imath \,{\left( U_n\right) }_{j4} \nonumber \right. \\&\quad \left. -\frac{1}{\tan \beta }\left( {\left( U_n\right) }_{j2} - \imath \,{\left( U_n\right) }_{j5} + \frac{\lambda ^*\,v_u}{\mu _{\text {eff}}^*}\left[ {\left( U_n\right) }_{j3} - \imath \,{\left( U_n\right) }_{j6}\right] \right) \right\} \end{aligned}$$

(2.10)

we define the following ‘tree-level’ amplitude for the Higgs decays into bottom quarks:

(2.11a)

(2.11b)

QCD and QED corrections The inclusion of QCD and QED corrections requires a proper treatment of IR effects in the decay amplitudes. The IR-divergent parts of the virtual contributions by gluons or photons in  are canceled by their counterparts in processes with radiated photons or gluons. We employ directly the QCD and QED correction factors that are well-known analytically (see below) and therefore omit the Feynman diagrams involving a photon or gluon propagator when computing with FeynArts and FormCalc the one-loop corrections to the $h^0_jf\bar{f}$ vertex and to the fermion-mass and wave-function counterterms. The QCD- and QED-correction factors applying to the fermionic decays of a $\mathcal{CP}$-even Higgs state were derived in Ref. [95]. The $\mathcal{CP}$-odd case was addressed later in Ref. [96]. In the $\mathcal{CP}$-violating case, it is useful to observe that the $h_jf\bar{f}$ scalar and pseudoscalar operators do not interfere, so that the $\mathcal{CP}$-even and $\mathcal{CP}$-odd correction factors can be applied directly at the level of the amplitudes – although they were obtained at the level of the squared amplitudes:

(2.12a)

(2.12b)

(2.12c)

(2.12d)

Here, $Q_f$ is the electric charge of the fermion f, $C_2(f)$ is equal to 4 / 3 for quarks and equal to 0 for leptons, $M_{h_i}$ corresponds to the kinematic (pole) mass in the Higgs decay under consideration and the functions $\Delta _{S,P}$ are explicated in e.g. Sect. 4 of Ref. [105]. In the limit of $M_{h_i}\gg m_f$, both $\Delta _{S,P}$ reduce to yy$\left[ -3\log {\left( M_{h_i}/m_f\right) }+\frac{9}{4}\right]$. As noticed already in Ref. [95], the leading logarithm in the QCD-correction factor can be absorbed by the introduction of a running $\overline{\mathrm {MS}}$ fermion mass in the definition of the Yukawa coupling $Y_f$. Therefore, it is motivated to factorize $m_f^{\overline{ \text{ MS }}}(M_{h_i})$, with higher orders included in the definition of the QCD beta function.

The QCD (and QED) correction factors generally induce a sizable shift of the tree-level width of as much as $\mathord {\sim }\,50\%$. While these effects were formally derived at the one-loop order, we apply them over the full amplitudes (without the QCD and QED corrections), i.e. we include the one-loop vertex amplitude without QCD / QED corrections  and  in the definitions of the couplings $g_{h_jff}^{S,P}$ that are employed in Eq. (2.12) – we will use the notation $g_{h_jff}^{S,P\,\text {1L}}$ below. The adopted factorization corresponds to a particular choice of the higher-order contributions beyond the ones that have been explicitly calculated.

Decay width Putting together the various pieces discussed before, we can express the decay amplitude at the one-loop order as:

(2.13a)

(2.13b)

Summing over spinor and color degrees of freedom, the decay width is then obtained as:

(2.14)

At the considered order, we could dismiss the one-loop squared terms in . However, in order to tackle the case where the contributions from irreducible one-loop diagrams are numerically larger than the tree-level amplitude, we keep the corresponding squared terms in the expression above (it should be noted that the QCD and QED corrections have been stripped off from the one-loop amplitude that gets squared). The approach of incorporating the squared terms should give a reliable result in a situation where the tree-level result is significantly suppressed, since the other missing contribution at this order consisting of the tree-level amplitude times the two-loop amplitude would be suppressed due to the small tree-level result. In such a case, however, the higher-order uncertainties are expected to be comparatively larger than in the case where one-loop effects are subdominant to the tree level.

The kinematic masses of the fermions are easily identified in the leptonic case. For decays into top quarks the ‘pole’ mass $m_t$ is used, while for all other decays into quarks we employ the $\overline{\text{ MS }}$ masses evaluated at the scale of the Higgs mass $m_q^{\overline{ \text{ MS }}}(M_{h_i})$. We note that these kinematic masses have little impact on the decay widths, as long as the Higgs state is much heavier. In the NMSSM, however, singlet-like Higgs states can be very light, in which case the choice of an $\overline{\text{ MS }}$ mass is problematic. Yet, in this case the Higgs state is typically near threshold so that the free-parton approximation in the final state is not expected to be reliable. Our current code is not properly equipped to address decays directly at threshold independently of the issue of running kinematic masses. Improved descriptions of the hadronic decays of Higgs states close to the $b\bar{b}$ threshold or in the chiral limit have been presented in e.g. Refs. [74,75,76, 106,107,108].

2.3 Decays into SM gauge bosons

Now we consider Higgs decays into the gauge bosons of the SM. Almost each of these channels requires a specific processing in order to include higher-order corrections consistently or to deal with off-shell effects.

Decays into electroweak gauge bosons Higgs decays into on-shell W-s and Z-s can be easily included at the one-loop order in comparable fashion to the fermionic decays. However, the notion of WW or ZZ final states usually includes contributions from off-shell gauge bosons as well, encompassing a wide range of four-fermion final states. Such off-shell effects mostly impact the decays of Higgs bosons with a mass below the WW or ZZ thresholds. Instead of a full processing of the off-shell decays at one-loop order, we pursue two distinct evaluations of the decay widths in these channels.

Our first approach is that already employed in FeynHiggs for the corresponding decays in the MSSM. It consists in exploiting the precise one-loop results of Prophecy4f for the SM-Higgs decays into four fermions [69,70,71]. For an (N)MSSM Higgs boson $h_i$, the SM decay width is thus evaluated at the mass $M_{h_i}$ and then rescaled by the squared ratio of the tree-level couplings to gauge bosons for $h_i$ and an SM Higgs boson $H_{ \text{ SM }}$ ($V=W,Z$):

$$\begin{aligned}&\Gamma {\left[ h_i\rightarrow VV\right] } = \Gamma ^{ \text{ SM }}{\left[ H_{ \text{ SM }}(M_{h_i})\rightarrow VV\right] } \left| \mathcal {R}_{ij}\cdot \frac{g_{h_jVV}^{ \text{ NMSSM }}}{g_{HVV}^{ \text{ SM }}}\right| ^2, \end{aligned}$$

(2.15a)

$$\begin{aligned}&\frac{g_{h_jVV}^{ \text{ NMSSM }}}{g_{HVV}^{ \text{ SM }}} \equiv \cos \beta \,{\left( U_n\right) }_{j1}+\sin \beta \,{\left( U_n\right) }_{j2}\,, \end{aligned}$$

(2.15b)

where yy$\Gamma {\left[ h_i\rightarrow VV\right] }$ represents the decay width of the physical Higgs state $h_i$ in the NMSSM, while $\Gamma ^{ \text{ SM }}\Big [H_{ \text{ SM }}{\left( M_{h_i}\right) }\rightarrow VV\Big ]$ denotes the decay width of an SM-Higgs boson with the mass $M_{h_i}$. The matrix elements $\mathcal {R}_{ij}$ reflect the connection between the tree-level Higgs states and the physical states. This role is similar to $\mathbf {Z}^{ \text{ mix }}$. However, decoupling in the SM limit of the model yields the additional condition that the ratio in Eq. (2.15a) reduces to 1 in this limit for the SM-like Higgs boson of the NMSSM. For this reason, FeynHiggs employs the matrix $\mathbf {U}^m$ (or $\mathbf {U}^0$) as a unitary approximation of $\mathbf {Z}^{ \text{ mix }}$ – see Sect. 2.6 of Ref. [25]. An alternative choice consists in using $X_{ij}\equiv \left. Z^{ \text{ mix }}_{ij}\big /\sqrt{\sum _k |Z^{ \text{ mix }}_{ik}|^2}\right.$. However, the difference of the widths when employing $\mathbf {U}^0$, $\mathbf {U}^m$, $\mathbf {Z}^{ \text{ mix }}$ or $\mathbf {X} \equiv \left( X_{ij}\right)$ corresponds to effects of higher order, which should be regarded as part of the higher-order uncertainty. The rescaling of the one-loop SM width should only be applied for the SM-like Higgs of the NMSSM, where this implementation of the $h_i\rightarrow VV$ widths is expected to provide an approximation that is relatively close to a full one-loop result incorporating all NMSSM contributions. However, for the other Higgs states of the NMSSM one-loop contributions beyond the SM may well be dominant. Actually, the farther the quantity $[\mathcal {R}_{ij}\cdot {\left( U_n\right) }_{j2}]\big /[\mathcal {R}_{ij}\cdot {\left( U_n\right) }_{j1}]$ departs from $\tan \beta$, the more inaccurate the prediction based on SM-like radiative corrections becomes.

Our second approach consists in a one-loop calculation of the Higgs decay widths into on-shell gauge bosons (see Ref. [94] for the MSSM case), including tree-level off-shell effects. This evaluation is meant to address the case of heavy Higgs bosons at the full one-loop order. The restriction to on-shell kinematics is justified above the threshold for electroweak gauge-boson production (off-shell effects at the one-loop level could be included via a numerical integration over the squared momenta of the gauge bosons in the final state – see Refs. [109, 110] for a discussion in the MSSM). Our implementation largely follows the lines described in Sect. 2.1, with the noteworthy feature that contributions from Higgs–electroweak mixing  vanish. In the case of the $W^+W^-$ final state, the QED IR-divergences are regularized with a photon mass and cancel with bremsstrahlung corrections: soft and hard bremsstrahlung are included according to Refs. [111, 112] (see also [94]). We stress that the exact cancellation of the IR-divergences is only achieved through the replacement of the $h_iG^+G^-$ coupling by the expression in terms of the kinematical Higgs mass, as discussed in Sect. 2.1. This fact had already been observed by Ref. [94]. In order to extend the validity of the calculation below threshold, we process the Born-order term separately, applying an off-shell kinematic integration over the squared external momentum of the gauge bosons – see e.g. Eq. (37) in Ref. [113]. Thus, this evaluation is performed at tree level below threshold and at full one-loop order (for the on-shell case) above threshold. The vanishing on-shell kinematical factor multiplying the contributions of one-loop order ensures the continuity of the prediction at threshold. Finally, we include the one-loop squared term in the calculation. Indeed, as we will discuss later on, the tree-level contribution vanishes for a decoupling doublet, meaning that the Higgs decays to WW / ZZ can be dominated by one-loop effects. To this end, the infrared divergences of two-loop order are regularized in an ad-hoc fashion – which appears compulsory as long as the two-loop order is incomplete – making use of the one-loop real radiation and estimating the logarithmic term in the imaginary part of the one-loop amplitude.

Radiative decays into gauge bosons Higgs decays into photon pairs, gluon pairs or $\gamma Z$ appear at the one-loop level – i.e.  for all these channels. We compute the one-loop order using the FeynArts model file, although the results are well-known analytically in the literature – see e.g. Ref. [87] or Sect. III of Ref. [50] ([113] for the MSSM). The electromagnetic coupling in these channels is set to the value $\alpha (0)$ corresponding to the Thomson limit.

The use of tree-level Higgs–Goldstone couplings together with loop-corrected kinematic Higgs masses $M_{h_i}$ in our calculation would induce an effective violation of Ward identities by two-loop order terms in the amplitude: as explained in Sect. 2.1, we choose to restore the proper gauge structure by re-defining the Higgs–Goldstone couplings in terms of the kinematic Higgs mass $M_{h_i}$. Since our calculation is restricted to the leading – here, one-loop – order, the transition of the amplitude from tree-level to physical Higgs states is performed via $\mathbf {U}^m$ or $\mathbf {X}$ instead of $\mathbf {Z}^{ \text{ mix }}$ in order to ensure the appropriate behavior in the decoupling limit.

Leading QCD corrections to the diphoton Higgs decays have received substantial attention in the literature. A frequently used approximation for this channel consists in multiplying the amplitudes driven by quark and squark loops by the factors $\left[ 1-\alpha _s(M_{h_i})/\pi \right]$ and $\left[ 1+8\,\alpha _s(M_{h_i})/(3\,\pi )\right]$, respectively – see e.g. Ref. [114]. However, these simple factors are only valid in the limit of heavy quarks and squarks (compared to the mass of the decaying Higgs boson). More general analytical expressions can be found in e.g. Ref. [115]. In our calculation, we apply the correction factors $\left[ 1+C^S{(\tau _q)}\,\alpha _s(M_{h_i})/\pi \right]$ and $\left[ 1+C^P{(\tau _q)}\,\alpha _s(M_{h_i})/\pi \right]$ to the contributions of the quark q to the $\mathcal{CP}$-even and the $\mathcal{CP}$-odd $h_i\gamma \gamma$ operators, respectively, and $\Big [1+C{(\tau _{\tilde{Q}})}\,\alpha _s(M_{h_i})/\pi \Big ]$ to the contributions of the squark $\tilde{Q}$ (to the $\mathcal{CP}$-even operator). Here, $\tau _X$ denotes the ratio $\left[ 4\,m^2_X\right. \left. {(M_{h_i}/2)}/M^2_{h_i}\right]$. The coefficients $C^{S,P}$ and C are extracted from Ref. [116] and Ref. [117]. In order to obtain a consistent inclusion of the $\mathcal {O}{(\alpha _s)}$ corrections, the quark and squark masses $m_X$ entering the one-loop amplitudes or the correction factors are chosen as defined in Eq. (5) of Ref. [116] and in Eq. (12) of Ref. [117] (rather than $\overline{\mathrm {MS}}$ running masses).

The QCD corrections to the digluon decays include virtual corrections but also gluon and light-quark radiation. They are thus technically defined at the level of the squared amplitudes. In the limit of heavy quarks and squarks, the corrections are known beyond NLO – see the discussion in Ref. [113] for a list of references. The full dependence in mass was derived at NLO in Refs. [116, 117], for both quark and squark loops. In our implementation, we follow the prescriptions of Eqs. (51), (63) and (67) of Ref. [113] in the limit of light radiated quarks and heavy particles in the loop. For consistency, the masses of the particles in the one-loop amplitude are taken as pole masses. Effects beyond this approximation can be sizable, as evidenced by Fig. 20 of Ref. [116] and Fig. 12 of Ref. [117]. As the $\mathcal{CP}$-even and $\mathcal{CP}$-odd Higgs–gg operators do not interfere, it is straightforward to include both correction factors in the $\mathcal{CP}$-violating case. Finally, we note that parts of the leading QCD corrections to $h_i\rightarrow gg$ are induced by the real radiation of quark–antiquark pairs. In the case of the heavier quark flavors (top, bottom and possibly charm), the channels are experimentally well-distinguishable from gluonic decays. Therefore, the partial widths related to these corrections could be attached to the Higgs decays into quarks instead [118]. The resolution of this ambiguity would involve a dedicated experimental analysis of the kinematics of the gluon radiation in $h_i\rightarrow gq\bar{q}$ (collinear or back-to-back emission). In the following section, we choose to present our results for the $h_i\rightarrow gg$ decay in the three-radiated-flavor approach, while the contributions from the heavier quark flavors are distributed among the $h_i\rightarrow c\bar{c}$, $b\bar{b}$, and $t\bar{t}$ widths (provided the Higgs state is above threshold). These contributions to the fermionic Higgs decays are of $\mathcal {O}{(\alpha _s^2)}$.

The QCD corrections to the quark loops of an SM-Higgs decay into $\gamma Z$ have been studied in Refs. [119,120,121], but we do not consider them here.

3 Numerical analysis

In this section, we present our results for the decay widths of the neutral Higgs bosons into SM particles in several scenarios and compare them with the predictions of existing codes. While a detailed estimate of the uncertainty associated to missing higher-order corrections goes beyond the scope of our analysis, we will provide some discussion at the end of this section, based on our observations and comparisons.

Throughout this section, the pole mass of the top-quark is chosen as $m_t = 173.2$ GeV. Moreover, all $\overline{\mathrm {DR}}$ parameters are defined at the scale $m_t$, and all stop parameters are treated as on-shell parameters. Concerning the Higgs phenomenology, we test the scenarios presented in this section with the full set of experimental constraints and signals implemented in the public tools HiggsBounds -4.3.1 (and -5.1.1beta) [122,123,124,125,126,127] and HiggsSignals-1.3.1 (and -2.1.0beta) [127,128,129]. We refer the reader to the corresponding publications for a detailed list of experimental references. The input parameters employed in our scenarios are summarized in Table 1.

Table 1 Input parameters for the scenarios considered in Sect. 3. The bilinear soft SUSY-breaking parameter of all the squarks of the third generation is denoted by $m_{\tilde{Q}}$. Moreover, $2\,M_1=M_2=M_3/5=500$ GeV and $m_{\tilde{F}}=1.5$ TeV, where $\tilde{F}$ represents any sfermion of the first two generations or sleptons of the third generation. Furthermore, $A_t=|A_t|\exp {\left( \imath \,\phi _{A_t}\right) }$ and $\kappa =|\kappa |\exp {\left( \imath \,\phi _\kappa \right) }$ in the conventions of Ref. [25]. We vary x in the interval [0, 1]

3.1 Comparison with FeynHiggs in the MSSM-limit

The MSSM limit of the NMSSM is obtained at vanishingly small values of $\lambda$ and $\kappa$: the singlet superfield then decouples from the MSSM sector but the $\mu _{\text {eff}}$ term remains relevant as long as $\kappa \sim \lambda$. It is then possible to compare our results for the Higgs decays to the corresponding predictions of FeynHiggs -2.13.0. The settings of FeynHiggs are thus adjusted in order to match the level of higher-order contributions and renormalization conditions of our NMSSM mass calculation: the corresponding FeynHiggs input flags read FHSetFlags[4,0,0,3,0,2,0,0,1,1]. We will denote the MSSM(-like) Higgs bosons as h and H for the $\mathcal{CP}$-even states, and A for the $\mathcal{CP}$-odd one.

First, we consider the Higgs decays into SM fermions. We turn to a region of the parameter space of the $\mathcal{CP}$-conserving NMSSM characterized by the input provided in the column ‘Fig. 1’ of Table 1, where we vary the masses and trilinear couplings associated with the squarks of the third generation. In this setup, the lightest Higgs state is SM-like, with a mass in the range [124, 126.5] GeV, while the heavy doublet states both have masses of about 997 GeV in this scenario. The full range under study is found to be in agreement with constraints in the Higgs sector as implemented in HiggsBounds and HiggsSignals.

Fig. 1

Comparison with FeynHiggs of the decay widths of the doublet Higgs states into $b\bar{b}$ and $t\bar{t}$ in the MSSM-limit of the NMSSM. The input parameters are provided in Table 1. The black line shows the pure tree-level result (with $\overline{\mathrm {MS}}$ Yukawa couplings); for the blue line, QCD and QED corrections are included, and the loop-corrected Higgs mass eigenstate is obtained using $\mathbf {Z}^{ \text{ mix }}$; for the solid green line furthermore the SUSY corrections to the Higgs–$b\bar{b}$ couplings (in the case of the $b\bar{b}$ final state) are included; the dashed green line shows the corresponding result where $\mathbf {U}^m$ has been used instead of $\mathbf {Z}^{ \text{ mix }}$; the red curve corresponds to our prediction at the full one-loop level (with higher-order improvements). The contribution from $h_i\rightarrow g(g^*\rightarrow q\bar{q})$ is included within the results in the solid red curves. The purple diamonds mark the corresponding evaluation by FeynHiggs. We also consider the widths without the contribution from $gg^*$, as well as using $\mathcal{CP}$-even QCD/QED-correction factors in the case of the A decays (in order to match FeynHiggs) as a dashed red line (which is not visible in the case $H\rightarrow t\bar{t}$)

In Fig. 1, we show the variations of the Higgs decay widths into $b\bar{b}$ and $t\bar{t}$ for the doublet states (when kinematically allowed). The solid lines correspond to our predictions in several approximations: at the ‘tree level’ with Yukawa couplings defined in terms of running $\overline{\mathrm {MS}}$ quark masses at the scale of the physical Higgs mass (black); including QCD and QED corrections (but without SQCD contributions) as well as the transition to the physical Higgs state via $\mathbf {Z}^{ \text{ mix }}$ (blue); replacing also the Higgs couplings to the down-type quarks by their effective form as expressed in Eq. (2.9) (green); at full one loop, with higher-order improvements as described above (red). The green dotted line is similar to the solid green line, up to the replacement of $\mathbf {Z}^{ \text{ mix }}$ by its unitary approximation $\mathbf {U}^m$. The purple diamonds are obtained with FeynHiggs. As the Higgs masses vary little over the range of the scan, the modification of the decay widths is essentially driven by radiative effects: this explains the relatively flat behavior of the tree-level results – at least in the case of the heavy states; for the light state, the mass and decay widths vary somewhat more. The same remark applies to the QCD/QED-corrected widths with $\mathbf {Z}^{ \text{ mix }}$, although the $H\rightarrow t\bar{t}$ decay width displays a more pronounced variation due to the $h^0$–$H^0$ mixing at the loop level. The one-loop corrections to the $b\bar{b}$ decay width of the SM-like state shift this quantity upwards by $\mathord {\sim }\,20\%$. The bulk of this effect, beyond the QCD corrections included in the running b quark mass, is already contained within the QCD/QED-corrected width. For the heavy doublet states, however, QCD and QED corrections (beyond the effect encoded within the running Yukawa coupling) do not lead to a significant improvement of the prediction of the decay widths, as the ‘tree-level’ result often appears closer to the full one-loop widths than the blue curve – for the $b\bar{b}$ final state, this deviation is only partially explained by the radiative corrections that can be resummed within the effective Higgs couplings to the bottom quark (solid green curve).

In the case of the $t\bar{t}$ final state, the solid green curve and the blue curve are essentially identical as the effective couplings to the down-type quarks only play a secondary part. The difference between the solid and dotted green lines originates from the treatment regarding the transition matrix employed for the description of the external Higgs leg – $\mathbf {Z}^{ \text{ mix }}$ or the approximation $\mathbf {U}^m$: the consequences for the predicted width reach $\mathcal {O}(5\%)$. We note that, with the exception of FeynHiggs, public tools usually neglect the effects associated with the momentum dependence of the Higgs self-energies (only properly encoded within $\mathbf {Z}^{ \text{ mix }}$). On the other hand, the estimate using $\mathbf {U}^m$ is somewhat closer to the full one-loop result (using $\mathbf {Z}^{ \text{ mix }}$), which means that, as long as one restricts to an ‘improved tree-level approximation’, the choice of a unitary transition matrix might provide slightly more reliable results than the same level of approximation with $\mathbf {Z}^{ \text{ mix }}$. As we mentioned earlier, the $\mathord {\sim }\,10\%$ difference between the red and green curves in the case of the heavy doublets hints at sizable electroweak effects of one-loop order. This can be understood in terms of large electroweak Sudakov logarithms for the heavy Higgs bosons. The impact of the sfermion spectrum on the decay widths into SM fermions consists in a suppression in the presence of light stops and sbottoms. This effect is of order $10\%$ over the considered range of squark masses. Concerning the comparison with FeynHiggs, we observe a very good agreement of the predicted one-loop widths for the $\mathcal{CP}$-even states: this is expected since we essentially apply the same processing of the parameters. However, a small discrepancy in the $h\rightarrow b\bar{b}$ width is noticeable: it is related to our inclusion of the contribution from $h\rightarrow g(g^*\rightarrow b\bar{b})$ to the decay width. Subtracting this contribution (dashed red curve), we recover the FeynHiggs prediction. This effect is negligible for the other Higgs states.⁶ Furthermore, for the $\mathcal{CP}$-odd state, we find a deviation of a few percent in the $t\bar{t}$ channel: this difference is due to FeynHiggs employing $\mathcal{CP}$-even QCD/QED-correction factors instead of the $\mathcal{CP}$-odd ones. The agreement is restored if we adopt the same approximation (dashed red curve). No such discrepancy appears for the $b\bar{b}$ final state, as the $\mathcal{CP}$-even and $\mathcal{CP}$-odd QCD/QED-correction factors converge in the limit of very light fermions (as compared to the mass of the Higgs state). Furthermore, the processing of the effective Higgs couplings to down-type quarks differs between FeynHiggs and our implementation, leading to small numerical effects (below $1\%$) for light SUSY spectra: we evaluate $\Delta _b$ at the scale defined by the arithmetic mean of the SUSY masses involved, while FeynHiggs employs a geometric mean (‘modified $Y_b^{\text {eff}}$’). Another (numerically minor) difference with FeynHiggs is the slightly different treatment of the Goldstone–Higgs couplings regarding the restoration of gauge invariance of the result – see Sect. 2.1.

Then, we consider the Higgs decays into electroweak gauge bosons in the MSSM-limit. To this end, we perform a scan over the charged-Higgs mass in the range [150, 2000] GeV; the rest of the parameters is set as in Fig. 1, but the stop and sbottom soft masses and trilinear couplings are frozen to 1.5 TeV and 2.3 TeV, respectively. Correspondingly, the lightest $\mathcal{CP}$-even Higgs is SM-like with a mass of $\mathord {\simeq }\,124$–125 GeV as soon as $m_{H^{\pm }}\gtrsim 350$ GeV. The mass of the heavy doublet states varies over the scan and is comparable to $m_{H^{\pm }}$. For clarity, the masses are shown in Fig. 2. Except for $m_{H^{\pm }}\lesssim 300$ GeV, where the SM-like Higgs is not in the desired experimental window, this scenario is consistent with experimental bounds implemented in HiggsBounds and HiggsSignals.

Fig. 2

Higgs masses in the scenario of Fig. 3

Fig. 3

Comparison with FeynHiggs of the decay widths of the doublet Higgs states into WW and ZZ in the MSSM-limit of the NMSSM. The input parameters are provided in Table  1. The black lines correspond to the widths estimated by rescaling the SM result of Prophecy4f by the relative tree-level coupling of the Higgs state in a unitary approximation. The blue line corresponds to a tree-level off-shell evaluation, including a transformation of the Higgs states by $\mathbf {Z}^{ \text{ mix }}$. The red curve depicts our prediction for the full one-loop on-shell decay width (with higher-order improvements), including tree-level off-shell effects. The purple diamonds mark the corresponding evaluation by FeynHiggs

In Fig. 3, we show our results for the decay widths of the neutral Higgs states into WW and ZZ. The black curves correspond to the prediction obtained by rescaling the SM width of Prophecy4f by the tree-level Higgs–WW / ZZ couplings (relative to the SM). The rotation to the loop-corrected Higgs state is then described in the unitary approximation $\mathbf {U}^m$. This is the approach employed by FeynHiggs (purple diamonds), leading to a good agreement. In the case of the SM-like state (upper plots), the decays are off-shell and both the (superposed) blue and red curves correspond to the tree-level results with off-shell kinematics but with $\mathbf {Z}^{ \text{ mix }}$ applied to the external Higgs leg. Thus, the difference between the red and black lines must be interpreted as the magnitude of the SM radiative corrections implemented in Prophecy4f (which are not included in our result displayed by the red curve) and amounts to somewhat less than $10\%$. For the heavy $\mathcal{CP}$-even Higgs (plots in the middle), the red and blue curves are differentiated by the inclusion of on-shell one-loop contributions to the widths (red curves). While the results essentially agree with the ‘Prophecy4f approach’ at low mass (where the tree-level Higgs–WW / ZZ coupling remains sizable due to a substantial mixing of the heavy $\mathcal{CP}$-even Higgs with the SM-like state), large deviations are observed for $m_{H^{\pm }}\gtrsim 500$ GeV. Indeed, for this state the tree-level Higgs coupling to electroweak gauge bosons is very small (as a consequence of the decoupling limit), so that the decay width is largely dominated by one-loop effects arising both from the contributions to the external Higgs leg (via $\mathbf {Z}^{ \text{ mix }}$) and in the vertex corrections. The dip of the ‘Prophecy4f prediction’ (black line) at $m_{H^{\pm }}\simeq 1.1$ TeV is due to an exactly vanishing Higgs–gauge coupling (tree level, unitarily rotated) at this point in parameter space. This does not happen when the couplings are transformed to the physical Higgs state via $\mathbf {Z}^{ \text{ mix }}$, due to the imaginary part of this transition matrix. On the other hand, the ‘$\text {tree-level}\cdot \mathbf {Z}^{ \text{ mix }}$’ approach (blue line) does not offer an accurate estimate of the $\text {Higgs}\rightarrow WW/ZZ$ decay widths either, due to sizable vertex corrections. The ‘sudden drop’ of the H decay widths for low values of $m_{H^{\pm }}$ (for all the curves) is associated to the off-shell regime (the Higgs state has a mass below threshold). Finally, the $\mathcal{CP}$-odd Higgs decays into WW and ZZ (lower plots) are generated at the radiative level. In this case, all the approximations based on tree-level predictions (‘Prophecy4f’, ‘$\mathbf {Z}^{ \text{ mix }}$’, FeynHiggs) vanish, and therefore only our one-loop on-shell description (red curve) is displayed in the plots. The peculiar shape of the predicted decay widths – in particular the peak at $m_{H^{\pm }}\simeq 1$ TeV – is associated to various thresholds – in particular the two-wino threshold at $\mathord {\simeq }\,1$ TeV. We stress that one-loop effects dominate the decays of the heavy doublet Higgs states into WW / ZZ, which means that our results, albeit formally of next-to-leading order, come with a large uncertainty due to QCD (two-loop) corrections: in particular, we observed that the use of pole instead of $\overline{\mathrm {MS}}$ quark masses within the loop could shift the widths by $\mathord {\sim }\,50\%$.

Fig. 4

Comparison with FeynHiggs of the decay widths of the doublet Higgs states into gg and $\gamma \gamma$ in the MSSM-limit of the NMSSM. The input parameters are provided in Table 1. The black, blue and red curves correspond to a rotation to the physical Higgs states via $\mathbf {U}^0$, $\mathbf {U}^m$ and $\mathbf {X}$ respectively. In the case of the gg final state, these lines are obtained for three radiated quark flavors in the QCD corrections. The green curves are obtained for five radiated quark flavors, employing universal QCD corrections at NLO (dashed) or beyond (solid). Furthermore the dotted green line shows the widths for NLO QCD-correction factors and $\overline{\mathrm {MS}}$ quark masses, which is the current approach of FeynHiggs (purple diamonds). In the case of the diphoton final state, the dashed lines are obtained with QCD corrections in the approximation of heavy quarks/squarks and $\overline{\mathrm {MS}}$ masses like in the current version of FeynHiggs

We choose to discuss the diphoton and digluon decay widths in the MSSM-limit in a scenario where $\tan \beta$ scans the range [1, 40] – $m_{H^{\pm }}$ is set to 1 TeV again; the details of the input are available in Table 1. The mass of the SM-like Higgs state is of order 100 GeV at $\tan \beta =1$, but settles in the interval [123.5, 126.5] when $\tan \beta \gtrsim 7$. Correspondingly, the low-$\tan \beta$ limit is disfavored by HiggsSignals in this scenario. The heavy doublet states have a mass of about 996–997 GeV. The endpoints at large $\tan \beta \sim 40$ are excluded by HiggsBounds due to constraints on heavy-Higgs searches in the $\tau \tau$ channel [130].

We display the Higgs decay widths into gg and $\gamma \gamma$ in Fig. 4. The transition to the physical Higgs states is performed using various approximations: $\mathbf {U}^0$ (black curves), $\mathbf {U}^m$ (blue curves) and $\mathbf {X}$ (red curves). These three descriptions agree rather well. The predictions for the digluon final state employ the QCD corrections for three radiated quark flavors – as radiated $c\bar{c}$, $b\bar{b}$ or $t\bar{t}$ are regarded as contributions to the fermionic Higgs decays. Nevertheless, in order to compare with FeynHiggs, we also show the results in the five-radiated-flavor approach (solid green curves) and cutting off universal QCD corrections beyond NLO (dashed green curves). The resulting deviation from the predictions of FeynHiggs (purple diamonds) is resolved when replacing the pole quark masses by $\overline{\mathrm {MS}}$ masses in the one-loop amplitude (dotted green curves). The appropriate choice for the considered QCD-correction factor is that of pole masses in the loop, however. The difference between the widths depicted by the black/blue/red lines and by the solid green lines is of order $20\%$: this enhancement is due to the larger number of radiated flavors. Universal QCD corrections beyond NLO (difference between the solid and the dashed green curves) represent almost $15\%$ of the width. In the case of the diphoton widths, the results of FeynHiggs (purple diamonds) should be compared to our predictions employing $\mathbf {U}^m$ (blue curves): a deviation of somewhat less than $10\%$ is noticeable for the heavy states. We checked that this discrepancy can be interpreted in terms of the heavy-quark/squark approximation that FeynHiggs employs for the NLO QCD corrections as well as the use of $\overline{\mathrm {MS}}$ running masses (instead of the running masses defined in Eq. (5) of Ref. [116]): simplifying our processing of the widths to this approximation (dashed blue curves) yields a very good agreement with the results of FeynHiggs.

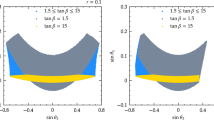
Finally, we consider a $\mathcal{CP}$-violating scenario in Fig. 5: the parameters are set as indicated in the column ‘Fig. 5’ of Table 1. We perform a scan over $\phi _{A_t}\in [-\pi ,\pi ]$. The doublet Higgs states have masses of about 125 GeV, 493 GeV and 494 GeV. This scenario is phenomenologically consistent with the limits on the Higgs sector as implemented in HiggsBounds and HiggsSignals. Ideally, limits from the measured electric dipole moments (EDMs) should be considered as well: in particular, Barr–Zee contributions involving squark loops are sensitive to variations of $\phi _{A_t}$. On the other hand, such effects are relatively suppressed given the high mass of the stops ($\mathord {\sim }\,1.5$ TeV). In any case, we mainly consider this scenario for the sake of comparison.

Fig. 5

Comparison with FeynHiggs of the decay widths of the doublet Higgs states into $b\bar{b}$ and WW in the $\mathcal{CP}$-violating MSSM-limit of the NMSSM. The input parameters are provided in Table 1. For the $b\bar{b}$ final state, the widths shown in black include only tree-level effects; these are rescaled by the QCD/QED corrections and transformed into physical states for the blue curves; for the green curve, leading corrections to the bottom Yukawa couplings are added; the red curves correspond to the full one-loop results (with higher-order improvements). In the case of the WW final state, the black curves correspond to the approach where the SM widths of Prophecy4f are rescaled; the blue curves depict tree-level off-shell widths where $\mathbf {Z}^{ \text{ mix }}$ is applied; the red curves include on-shell one-loop corrections. The purple diamonds mark the predictions of FeynHiggs

Figure 5 displays the Higgs decay widths into $b\bar{b}$ and WW. For the $b\bar{b}$ final state, we consider the tree-level widths (corresponding to an $\overline{\mathrm {MS}}$ running Yukawa coupling; black lines), incorporate QCD/QED corrections and transform to the physical Higgs state using $\mathbf {Z}^{ \text{ mix }}$ (blue), subtract and redistribute the SUSY corrections to the bottom-quark mass in the definition of the Higgs-bottom couplings (green) and finally evaluate the widths at full one-loop order (red, including two-loop pieces as described in Sect. 2). The predictions of FeynHiggs (purple diamonds) are in good agreement with our full one-loop results. While the inclusion of the corrections associated to QED/QCD effects and the definition of effective Higgs couplings to $b\bar{b}$ notably improve the tree-level width of the SM-like state, as compared to the one-loop results – from a discrepancy of $\mathord {\sim }\,20\%$ to less than $\mathord {\sim }\,4\%$ – the performance of these ‘leading’ corrections is less convincing in the case of the heavy doublet states: the deviations with respect to the full one-loop results remain of order 5–$10\%$.

Turning to the WW final state, we expectedly recover the results of FeynHiggs in the approximation with the rescaled SM widths of Prophecy4f (black lines). The impact of the one-loop corrections (red curves) on the width of the mostly $\mathcal{CP}$-even heavy doublet state $h_2$ are rather mild, which we should put in perspective with the fact that this state is comparatively light. However, for the mostly $\mathcal{CP}$-odd state $h_3$, the tree-level approximations sizably underestimate the one-loop widths.

To summarize, in this comparison with FeynHiggs in the MSSM limit of the NMSSM, we were able to quantitatively recover the widths predicted by FeynHiggs and interpret the origin of the differences with our results. In the case of the Higgs decays into electroweak gauge bosons, our one-loop approach goes beyond the current approach of FeynHiggs and shows that the tree-level approximation for the SUSY contributions – even though rescaled from the Prophecy4f SM widths – leads to significant deviations for the heavy doublet states. In the case of the digluon decay, universal QCD corrections beyond NLO as well as the number of radiated quark flavors have a sizable impact on the widths. Finally, we observed that accounting for the mass dependence in the QCD corrections to the diphoton widths has a mild effect on the decay of the heavy states. It is planned to include all the refinements that go beyond the current status of FeynHiggs and that we have employed here into the predictions of the MSSM Higgs decays of a future update of FeynHiggs.

3.2 Comparison with NMSSMCALC

We now depart from the MSSM-limit of the NMSSM. We first investigate the Higgs decays in scenarios that are similar to those that we considered in the MSSM-limit.

Fig. 6

Comparison with NMSSMCALC of the decay widths of the Higgs states into $b\bar{b}$ and $t\bar{t}$. The input parameters are provided in Table 1. The black lines are pure tree-level results; for the blue lines, QCD and QED corrections are included and the Higgs states are transformed to the loop-corrected eigenstates using $\mathbf {Z}^{ \text{ mix }}$; the green curves employ $\mathbf {U}^m$, QCD/QED corrections and an effective bottom Yukawa coupling; the red curve corresponds to our prediction at the one-loop level. The purple diamonds mark the corresponding evaluation by NMSSMCALC

We will compare our estimates for the Higgs decay widths to the predictions of NMSSMCALC -2.1 [33, 34]. In order to minimize the impact of the Higgs-mass calculation, we bypass the mass-evaluation routines of NMSSMCALC– we refer the reader to Refs. [20, 25] for a comparison of the Higgs-mass predictions – and directly inject our Higgs spectrum (two-loop masses and $\mathbf {U}^m$ mixing matrix) in the SLHA [131, 132] file serving as an interface between the mass-evaluation and the decay-evaluation routines. We proceed similarly with the squark masses and mixing angles. The subroutine of NMSSMCALC that evaluates the Higgs decays is based on a generalization of HDECAY-6.1 [26, 27]. The corresponding widths include leading NLO effects (e.g. QCD/QED corrections, effective Higgs couplings to the bottom quark, etc.) but do not represent a complete one-loop order evaluation. Furthermore, internal parameters, renormalization scales or RGE runnings are not strictly identical to our choices. For instance, the decay widths predicted by NMSSMCALC are systematically normalized to $G_F$, while we employ other parametrizations in terms of $M_W$, $M_Z$ and e.g. $\alpha (M_Z)$: the corresponding tree-level contributions numerically differ by a few percents. In the case of NMSSMCALC, such effects are of one-loop electroweak order, hence beyond the considered approximation. In our calculation, the one-loop electroweak order is consistently implemented with respect to our renormalization scheme. Other small numerical differences appear at the level of e.g. running quark masses. Therefore, the numerical comparison between the two sets of results is expected to show a certain level of deviations.

We set $\kappa =0.4$, $\lambda =0.3$ and $A_{\kappa }=-100$ GeV. In Fig. 6, we consider the Higgs decay widths into $b\bar{b}$ and $t\bar{t}$ in a scenario where the squark masses of third generation vary between 0.7 and 2 TeV while the trilinear couplings are in the interval [1.4, 4] TeV (see Table 1 for details). Correspondingly, the lightest $\mathcal{CP}$-even Higgs state is SM-like with a mass of $\mathord {\sim }\,120$–126 GeV (the lowest range in $m_{Q}$ is in tension with the measured Higgs data); the second-lightest $\mathcal{CP}$-even and the lightest $\mathcal{CP}$-odd Higgs states are singlet-like, with masses of $\mathord {\sim }\,643$ GeV and $\mathord {\sim }\,319$ GeV respectively; the heavy doublet states have masses of $\mathord {\sim }\,999$ GeV. This scenario satisfies the tests of HiggsBounds and HiggsSignals in most of the $m_{\tilde{Q}}$ range. The decay widths are shown at the tree level (with $\overline{\mathrm {MS}}$ Yukawa couplings; black curves), in the approximation of QCD/QED corrections and including the transition by $\mathbf {Z}^{ \text{ mix }}$ (blue curves), including the leading SUSY corrections to the relation between the bottom-quark mass and the bottom Yukawa coupling, and furthermore substituting $\mathbf {Z}^{ \text{ mix }}$ by $\mathbf {U}^m$ (green curves), and finally for our full one-loop calculation (red curves). These various approximations perform in the same fashion as what we observed in the MSSM-limit: while the inclusion of QCD/QED- and Yukawa-driven leading corrections improve the tree-level-based predictions for the width of the SM-like state $h_1$, the improvement is less obvious for the other Higgs states, pointing at sizable electroweak effects. The purple diamonds represent the predictions of NMSSMCALC/HDECAY: they should correspond to the approximation of our results shown in green. These results qualitatively agree at the level of a few percent (as expected, given e.g. the differing parametrizations at the tree level). These ‘improved tree-level’ predictions of the decay widths typically remain 5–$10\%$ away from our full one-loop implementation.

Fig. 7

Higgs masses in the scenario of Fig. 8

Fig. 8

Comparison with NMSSMCALC of the decay widths of the Higgs states into WW and ZZ. The input parameters are provided in Table 1. The black lines correspond to the widths estimated by rescaling the SM result of Prophecy4f by the relative tree-level coupling of the Higgs states in a unitary approximation. The blue lines correspond to a tree-level off-shell evaluation, including $\mathbf {Z}^{ \text{ mix }}$. The red curves depict our prediction for the full one-loop on-shell decay widths, including tree-level off-shell effects. The purple diamonds mark the corresponding evaluation by NMSSMCALC

Fig. 9

Comparison with NMSSMCALC of the decay widths of the Higgs states into gg and $\gamma \gamma$. The input parameters are provided in Table 1. The black, blue and red curves correspond to a transition to the physical Higgs state via $\mathbf {U}^0$, $\mathbf {U}^m$ and $\mathbf {X}$ respectively. In the case of the gg final state, the black/blue/red lines are obtained for three radiated quark flavors in the QCD corrections. The green lines are obtained for five radiated quark flavors, which agrees with the approach of NMSSMCALC (purple diamonds)

Then, we study the Higgs decays to electroweak gauge bosons as a function of the charged-Higgs mass – the squark masses and trilinear couplings of third generation are frozen to 1.5 TeV and 3 TeV respectively. The lightest $\mathcal{CP}$-even Higgs with mass $\mathord {\sim }\,122$–127 GeV is SM-like. The mostly singlet-like $\mathcal{CP}$-even and $\mathcal{CP}$-odd states have masses of order 650 GeV and 300 GeV, respectively. With growing $m_{H^{\pm }}$, the masses of the heavy doublet states increase in proportion and successively cross the singlet masses, leading to strong mixing regimes. For clarity, the Higgs masses are plotted in Fig. 7. The decay widths into WW and ZZ are displayed in Fig. 8 in the approximation where the SM widths of Prophecy4f are rescaled (black curves), in the tree-level approximation using $\mathbf {Z}^{ \text{ mix }}$ (blue curves), in our on-shell one-loop description (with off-shell tree-level contributions; red curves). The predictions of NMSSMCALC are in agreement with our result obtained by a rescaling of the Prophecy4f widths. Again, we find that this approximation is not appropriate for heavy doublet Higgs states ($h_3$ for $m_{H^{\pm }}\gtrsim 650$ GeV), in which case one-loop contributions dominate the decays into WW and ZZ. Differences may reach a factor 100 in certain mass ranges/scenarios. On the other hand, the various predictions for the width of the $\mathcal{CP}$-even singlet at $\mathord {\sim }\,650$ GeV ($h_3$ for low $m_{H^{\pm }}$, then $h_2$) are all consistent with one another: at least in the scenario under consideration, the tree-level contribution remains dominant for this state. At $m_{H^{\pm }}\sim 400$ GeV, we observe a suppression of the decay widths of the heavy doublet state $h_2$: once again, it is associated with a vanishing $h_2$–WW / ZZ coupling. One-loop effects do not lead to large deviations for this state. Furthermore, the ‘drop’ at low $m_{H^{\pm }}$ in the $h_2\rightarrow ZZ$ channel can be traced back to the crossing of the kinematical threshold for on-shell Z bosons (the width below threshold is suppressed). Finally, the decays of the $\mathcal{CP}$-odd Higgs are generated at the one-loop level: consequently, they are non-trivial only in our one-loop approach.

Fig. 10

Higgs masses in the scenario of Fig. 11

We investigate the Higgs decay widths into gluon and photon pairs as a function of $\tan \beta$. The results are displayed in Fig. 9. The Higgs masses are of order $\mathord {\sim }\,125$ GeV for the SM-like state (except for $\tan \beta \lesssim 3$, in which case the corresponding mass is too low to satisfy the observed Higgs properties), $\mathord {\sim }\,1$ TeV for the heavy-doublet states, $\mathord {\sim }\,320$ GeV and $\mathord {\sim }\,645$ GeV for the $\mathcal{CP}$-odd and $\mathcal{CP}$-even mostly singlet-like states, respectively. The points with $\tan \beta \gtrsim 35$ appear to be in tension with LHC searches for heavy Higgs bosons in the $\tau ^+\tau ^-$ decay channel. Also in this case, we consider several descriptions of the transition to the physical Higgs state (black, blue and red lines): all the predictions agree to a good accuracy. In the case of the digluon decays, we also show the widths obtained with five radiated quarks (green curves): this result is essentially in agreement with the prediction of NMSSMCALC (purple diamonds), using the same approach. For the diphoton decays, NMSSMCALC also applies full NLO QCD corrections. Again, we observe a good agreement with our results. We checked that the remaining discrepancies – at the percent level – between the predictions from NMSSMCALC for the digluon and diphoton widths and ours are largely accounted for by a relative normalization factor $\left. \left( G_F\,M_W^2\,s_{\text {w}}^2\,\sqrt{2}\right) \big /\left( \pi \,\alpha \right) \right. =\left[ 1+\mathcal {O}(\alpha )\right]$ and minor deviations in the running of $\alpha _s$ and the quark masses.

Fig. 11

Comparison with NMSSMCALC of the decay widths of the Higgs states into $b\bar{b}$ and WW in the $\mathcal{CP}$-violating NMSSM. The input parameters are provided in Table 1. For the $b\bar{b}$ final state, the widths shown in black include only tree-level effects; they are rescaled by the QCD/QED corrections, and transformed into physical states for the blue curves; for the green curves, leading corrections to the bottom Yukawa couplings are added; the red curves correspond to the full one-loop results. In the case of the WW final state, the black curves correspond to the approach where the SM widths of Prophecy4f are rescaled; the blue curves depict tree-level off-shell widths using $\mathbf {Z}^{ \text{ mix }}$; the red curves include on-shell one-loop corrections. The purple diamonds mark the predictions of NMSSMCALC

Finally, we consider a $\mathcal{CP}$-violating scenario with the parameters $\lambda =0.2$, $|\kappa |=0.6$, $\tan \beta =25$ and $A_{\kappa }=-750$ GeV. We scan over $\phi _{\kappa }\in [-\pi ,\pi ]$, which is phenomenologically realistic in the sense that EDMs in principle allow for large variations of this phase [133, 134]; however, scenarios with large $\mathcal{CP}$-violating mixing of the Higgs states – as the one we consider – tend to be constrained. The Higgs spectrum consists of an SM-like state with a mass of $\mathord {\sim }\,124.5$ GeV, a triplet of $\mathcal{CP}$-even/$\mathcal{CP}$-odd doublet and $\mathcal{CP}$-even singlet states near $\mathord {\sim }\,1$ TeV with large and fluctuating mixing depending on $\phi _{\kappa }$, as well as a mostly $\mathcal{CP}$-odd singlet at $\mathord {\sim }\,1.2$ TeV. The masses are depicted in Fig. 10. The Higgs decays into $b\bar{b}$ and WW are plotted in Fig. 11. For the $b\bar{b}$ final state we find a relatively good agreement between the predictions of NMSSMCALC (purple diamonds) and our predictions employing the same approximation (shown in green: transition via $\mathbf {U}^m$, QCD/QED corrections and effective SUSY-corrected Higgs–$b\bar{b}$ couplings). A sizable discrepancy with our full one-loop result appears for $|\phi _{\kappa }|\simeq 2.6$ in the case of $h_{2,3}$: this difference originates in large Higgs-mixing effects encoded within $\mathbf {Z}^{ \text{ mix }}$ that are not captured by the $\mathbf {U}^m$ approximation (see Sect. 3.3 and Sect. 3.4 of Ref. [25] for a detailed discussion). In the case of the WW channel, deviations can be large when the tree-level approximation fails to capture the leading contribution to the decay width (as e.g. for $h_{2,3,4}$): the predictions of NMSSMCALC are similar to our rescaled widths from Prophecy4f.

We have thus observed a qualitative agreement of our results with the decay widths predicted by NMSSMCALC, when employing the same approximations as this code. Our calculation goes beyond the approach of NMSSMCALC/HDECAY at the level of the Higgs decays into SM fermions or into WW / ZZ, since we consider the full one-loop order. Sizable differences may thus appear, e.g. in the case of the decays into electroweak gauge bosons. Concerning the decays into gluon or photon pairs, the two codes are considering the decay widths at the same order, and the results are similar.

3.3 A singlet-dominated state at $\mathord {\lesssim }\,100$ GeV and possible explanation of slight excesses in the CMS and LEP data

The possible presence of a singlet-dominated state with mass in the ballpark of $\mathord {\sim }\,100$ GeV is a long-standing phenomenological trademark of the NMSSM – see e.g. Refs. [78, 79]. One motivation for such a scenario is for instance the $2.3\,\sigma$ local excess observed in Higgs searches at LEP in the $e^+e^-\rightarrow Z(H\rightarrow b\bar{b})$ channel [80], which would be consistent with a scalar mass of $\mathord {\sim }\,98$ GeV (but with a rather coarse mass resolution). It would correspond to a signal strength with respect to the SM at the level of $\mathord {\sim }\,10\%$. A natural candidate to explain this excess consists in a mostly singlet-like Higgs with a doublet component of about $10\%$ (mixing squared). Interestingly, recent LHC Run II results [81] for CMS Higgs searches in the diphoton final state show a local excess of $\mathord {\sim }\,3\,\sigma$ in the vicinity of $\mathord {\sim }\,96$ GeV, while a similar upward fluctuation of $2\,\sigma$ had been observed in the CMS Run I data at a comparable mass. A hypothetical signal of this kind would amount to $60\% \pm 20\%$ of that of an SM Higgs boson at the same mass. In the NMSSM, relatively large Higgs branching fractions into $\gamma \gamma$ are possible due to the three-state mixing, in particular when the effective Higgs coupling to $b\bar{b}$ becomes small – see e.g. Refs. [86, 87]. However, it then appears more difficult to interpret the LEP excess simultaneously.⁷ Below, we consider the decays of a light singlet-like Higgs in this regime employing our calculation, to show that it is indeed possible to describe both ‘excesses’ simultaneously (without exploiting all possibilities within the NMSSM to describe these effects).

We first consider a region of the NMSSM parameter space characterized by the input displayed in the column ‘Fig. 13’ of Table 1: we scan over $A_{\kappa }$ with $\tan \beta =12$. In this regime, the lightest $\mathcal{CP}$-even state is singlet-like (except at the upper boundary in $A_{\kappa }$). Its mass varies within the range [50, 125] GeV. The second-lightest Higgs has SM-like properties with a mass of $\mathord {\sim }\,125$ GeV. The variations of these masses as functions of $A_{\kappa }$ are shown in Fig. 12. We do not discuss the $\mathcal{CP}$-odd singlet at $\mathord {\sim }\,700$ GeV and the heavy doublet states at $\mathord {\sim }\,1.4$ TeV in this context. The experimental constraints from Higgs searches, as summarized in HiggsBounds and HiggsSignals, are satisfied over the whole interval.

Fig. 12

Higgs masses in the scenario of Fig. 13

Fig. 13

The decay properties of the mostly singlet $\mathcal{CP}$-even Higgs state as a function of its mass are shown. The input parameters are provided in Table 1. The branching ratios into $b\bar{b}$, ZZ, gg and $\gamma \gamma$ are shown at the tree level (black), under partial one-loop approximations (blue, green) or at the full one-loop order (red). The plots at the bottom show the quantities $\xi _b$ and $\xi _{\gamma }$ of Eqs. (3.1), estimating the signals associated with $h_1$ in the $b\bar{b}$ channel at LEP and in the $\gamma \gamma$ channel at the LHC, as compared to an SM Higgs at the same mass. Explicit values at $M_{h_1}=95.4$ GeV are given in Table  2

In Fig. 13, we display the branching ratios of the lightest $\mathcal{CP}$-even Higgs state into $b\bar{b}$, ZZ, gg and $\gamma \gamma$ – the total width is calculated as the sum of the decay widths in the $b\bar{b}$, $\tau ^+\tau ^-$, $c\bar{c}$, WW, ZZ, gg and $\gamma \gamma$ channels. The tree-level results (including a tree-level evaluation of the full width, e.g. excluding the gg or $\gamma \gamma$ channels) are shown in black while the full one-loop results appear in red. Various approximations of the one-loop branching ratios are shown in blue and green: they are in good agreement with the full one-loop prediction for all the considered channels. We observe sizable deviations for the tree-level and one-loop predictions of the branching fraction into $b\bar{b}$: this is due to the existence of a region with suppressed $h_1$–$b\bar{b}$ coupling arising as a consequence of the mixing between the three neutral $\mathcal{CP}$-even Higgs states. This suppressed region occurs below the displayed range of $M_{h_1}$ at the tree level, but is shifted to $M_{h_1}\sim 90$–100 GeV at the one-loop order. At its minimum for $M_{h_1}\simeq 95$ GeV, the $h_1\rightarrow b\bar{b}$ decay is in fact dominated by its $\mathcal {O}(\alpha _s^2)$ contribution from $h_1\rightarrow g (g^*\rightarrow b\bar{b})$. Concerning the ZZ final state, the difference between tree-level and one-loop branching fractions is largely driven by the magnitude of the full width: the large $h_1\rightarrow gg$ contributions are absent at the tree level, and the large $h_1\rightarrow b\bar{b}$ contributions differ sizably. The branching fractions into gg and $\gamma \gamma$ exist only at the loop level. They show a peak at $M_{h_1}\sim 90$–100 GeV, which mostly originates from the suppression of the $h_1\rightarrow b\bar{b}$ decay in this range. In particular, the gg final state contributes about $40\%$ to the total width. Finally, we display the quantities $\xi _b$ and $\xi _{\gamma }$, defined as follows:

$$\begin{aligned}&\xi _b\equiv \frac{\Gamma [h_1\rightarrow ZZ]\cdot \text{ BR }[h_1\rightarrow b\bar{b}]}{\Gamma [H_{ \text{ SM }}(M_{h_1})\rightarrow ZZ]\cdot \text{ BR }[H_{ \text{ SM }}(M_{h_1})\rightarrow b\bar{b}]}\nonumber \\&\quad \sim \frac{\sigma [e^+e^-\rightarrow Z (h_1\rightarrow b\bar{b})]}{\sigma [e^+e^-\rightarrow Z (H_{ \text{ SM }}(M_{h_1})\rightarrow b\bar{b})]} \end{aligned}$$

(3.1a)

$$\begin{aligned}&\xi _{\gamma }\equiv \frac{\Gamma [h_1\rightarrow gg]\cdot \text{ BR }[h_1\rightarrow \gamma \gamma ]}{\Gamma [H_{ \text{ SM }}(M_{h_1})\rightarrow gg]\cdot \text{ BR }[H_{ \text{ SM }}(M_{h_1})\rightarrow \gamma \gamma ]}\nonumber \\&\quad \sim \frac{\sigma [gg\rightarrow h_1\rightarrow \gamma \gamma ]}{\sigma [gg\rightarrow H_{ \text{ SM }}(M_{h_1})\rightarrow \gamma \gamma ]}\ . \end{aligned}$$

(3.1b)

These definitions of $\xi _{b,\gamma }$ give loose estimates of the signals that $h_1$ would generate in the LEP searches for $e^+e^-\rightarrow Z (H\rightarrow b\bar{b})$ and the LHC searches for $pp\rightarrow H\rightarrow \gamma \gamma$, normalized to the SM cross-sections. The decay widths of an SM-Higgs boson are evaluated with our code, taking the SM-limit of the NMSSM. In our example, the signal in the $b\bar{b}$ searches would thus reach a few percent of an SM signal for $M_{h_1}\sim 100$–110 GeV, but would be very suppressed in the range $M_{h_1}\sim 90$–100 GeV, due to the small branching fraction into $b\bar{b}$. On the other hand, the signal in the diphoton channel would amount to $\mathord {\sim }\,20\%$ of the corresponding SM cross-section for $M_{h_1}\sim 90$–100 GeV. The Higgs properties for a specific point in this scenario are provided in the column ‘Fig. 13’ of Table 2. The production cross-sections, approximated by $\widehat{\Gamma }_{ZZ}$ for LEP and $\widehat{\Gamma }_{gg}$ for the LHC (in gluon–gluon fusion), amount to a comparable fraction – a few percent – of the corresponding SM-Higgs cross-sections. The branching ratio into $b\bar{b}$ is considerably reduced, as compared to an SM-Higgs state at the same mass, whereas the diphoton branching ratio is enhanced by up to a factor $\mathord {\sim }\,10$. This is caused by the mixing between the three neutral Higgs states, which in this parameter region gives rise to a very small $H_d^0$ component of the mostly singlet-like state implying suppressed couplings to down-type quarks (and leptons). Thus, the mechanism leading to a large diphoton signal in this scenario is purely driven by the decay properties of the light singlet state. This scenario would therefore give rise to a $\gamma \gamma$ signal at the LHC without a corresponding $b\bar{b}$ excess at LEP. In fact, the reverse is also possible: an NMSSM-Higgs singlet could cause an excess in the $e^+e^-\rightarrow Z(H\rightarrow b\bar{b})$ channel without generating a significant signal in $pp\rightarrow H\rightarrow \gamma \gamma$. A relatively large $b\bar{b}$ decay rate can naturally occur for a Higgs state in the 100 GeV mass range, in which case the diphoton branching fraction remains small.

Table 2 The Higgs properties for a few example points in Sect. 3.3 are shown. The input parameters are provided in Table 1. The Higgs width into $xx'$ is denoted by $\Gamma _{xx'}$, and the width normalized to the SM width at the same mass is represented by $\widehat{\Gamma }_{xx'}$. The symbol $\widehat{\text {BR}}_{xx'}$ represents the Higgs branching ratio into $xx'$, normalized to the SM branching ratio at the same mass. The mass values and the partial decay widths are given in GeV. The variation in the values of $M_{h_1}$ is an artifact of the scans performed for the three scenarios

Fig. 14

Higgs masses in the scenario of Fig. 15

Fig. 15

The decay properties of the mostly singlet-like $\mathcal{CP}$-even Higgs state are depicted as a function of its mass. The input parameters are provided in Table 1. The branching ratios into $b\bar{b}$, ZZ, gg and $\gamma \gamma$ are shown at the tree level (black), under partial one-loop approximations (blue, green) and at the full one-loop order (red). The plots at the bottom show the quantities $\xi _b$ and $\xi _{\gamma }$ of Eq. (3.1), estimating the signals associated with $h_1$ in the $b\bar{b}$ channel at LEP and in the $\gamma \gamma$ channel at the LHC, as compared to an SM Higgs at the same mass. Explicit values at $M_{h_1}=95.0$ GeV are given in Table 2

We now turn to another scenario in the low-$\tan \beta$ regime with large $\lambda$: the chosen input is provided in column ‘Fig. 15’ of Table 1. We vary $\mu _{ \text{ eff }}$ in a narrow interval. The masses of the two lightest Higgs states are shown in Fig. 14. In the lower range of values for $\mu _{ \text{ eff }}$, the mixing between the light singlet at $\mathord {\sim }\,101$ GeV and the SM-like state at $\mathord {\sim }\,121$ GeV almost vanishes. These points are in tension with the measured properties of the SM-like state, as tested with HiggsSignals, because of the relatively low mass of the SM-like state. However, with growing $\mu _{ \text{ eff }}$, the mixing between the two light $\mathcal{CP}$-even states increases, eventually pushing the singlet mass down to $\mathord {\sim }\,90$ GeV and the mass of the SM-like state up to $\mathord {\sim }\,128$ GeV. Consistency with the experimental results obtained on the observed state at 125 GeV is achieved for a mass of the SM-like state that is compatible with the LHC discovery within experimental and theoretical uncertainties. The $\mathcal{CP}$-odd singlet has a mass of $\mathord {\sim }\,150$ GeV, while the heavy doublet states are at $\mathord {\sim }\,1$ TeV in this scenario. The decay properties of $h_1$ are documented in Fig. 15, as well as in the column ‘Fig. 15’ of Table  2 (for a specific point). The branching ratio into $b\bar{b}$ changes very significantly between the tree-level and the one-loop approach: again, the point of vanishing $H_d^0$ component in $h_1$ is shifted in parameter space from $M_{h_1}\sim 98$ GeV to $M_{h_1}\sim 101$ GeV. On the other hand, the $H_u^0$ component in $h_1$ vanishes at $M_{h_1}\sim 101.5$ GeV, leading to a suppression of all the decay widths into gauge bosons at this mass. The magnitude of the estimated $e^+e^-\rightarrow Z(h_1\rightarrow b\bar{b})$ signal reaches $\mathord {\sim }\,13\%$ of that of an SM Higgs at $M_{h_1}\sim 95$ GeV, while $pp\rightarrow h_1\rightarrow \gamma \gamma$ corresponds to more than $40\%$ of an SM signal in the same mass range. In this example, $\text {BR}[h_1\rightarrow \gamma \gamma ]$ (or $\text {BR}[h_1\rightarrow gg]$) is only moderately enhanced with respect to the SM branching fraction due to an $H_u^0$-dominated doublet composition of $h_1$, while $\text {BR}[h_1\rightarrow b\bar{b}]$ remains dominant, albeit slightly suppressed. This scenario would thus simultaneously address the LEP and the CMS excesses in a phenomenologically consistent manner.

Finally, we consider a $\mathcal{CP}$-violating scenario, still in the large-$\lambda$, low-$\tan \beta$ regime. We scan over $\phi _{\kappa }\in \left[ -\frac{\pi }{8},\frac{\pi }{8}\right]$. The lightest Higgs state is dominantly $\mathcal{CP}$-odd, with a mass of $\mathord {\sim }\,100$ GeV in the $\mathcal{CP}$-conserving limit. The second-lightest Higgs is SM-like, with a mass of $\mathord {\sim }\,120$ GeV for $\phi _{\kappa }=0$. With increasing $|\phi _{\kappa }|$, these states mix and the masses draw apart, reaching $\mathord {\sim }\,60$ GeV and $\mathord {\sim }\,150$ GeV at $|\phi _{\kappa }|\sim \frac{\pi }{8}$, which can be seen in Fig. 16. Correspondingly, appropriate Higgs properties, as tested with HiggsBounds and HiggsSignals, are obtained for $|\phi _{\kappa }|\simeq 0.1$–0.2. The $\mathcal{CP}$-even singlet and the heavy doublet states have masses of the order of 210 GeV and 1180 GeV, respectively. In Fig. 17, we show the branching ratios of the lightest Higgs state as a function of its mass. Contrarily to the previous cases, $\text {BR}[h_1\rightarrow b\bar{b}]$ is nearly constant over the whole range; the tree-level and one-loop results agree reasonably well with each other. The branching ratios into gauge bosons show an abrupt decrease near $M_{h_1}\sim 102$ GeV: this corresponds to the $\mathcal{CP}$-conserving limit of our scenario – in which case $h_1$ is a pure $\mathcal{CP}$-odd state. The estimated signals in the $e^+e^-\rightarrow Z(h_1\rightarrow b\bar{b})$ and $pp\rightarrow h_1\rightarrow \gamma \gamma$ channels reach $\mathord {\sim }\,20$–$25\%$ of their SM counterparts at $M_{h_1}\sim 95$ GeV. As can be seen in Table 2, the decays of $h_1$ for this point ($|\phi _{\kappa }|\sim 0.14$) approximately stay in SM-like proportions. The $b\bar{b}$ and $\gamma \gamma$ signals would thus remain comparable in magnitude. In particular, a diphoton signal as large as $60\%$ of the one for an SM-Higgs boson could not be accommodated in this configuration, as the LEP limits on $h_1\rightarrow b\bar{b}$ indirectly constrain the diphoton rate. Yet, it is remarkable that a mostly $\mathcal{CP}$-odd Higgs state would trigger sizable signals at both LEP and the LHC.

To summarize this discussion, a light $\mathcal{CP}$-even – or dominantly $\mathcal{CP}$-even and even dominantly $\mathcal{CP}$-odd in the $\mathcal{CP}$-violating case – and mostly singlet-like Higgs state in the vicinity of $\mathord {\lesssim }\,100$ GeV could have interesting consequences for the phenomenology of the SM-like state. Sizable signals in the $e^+e^-\rightarrow Z(h_1\rightarrow b\bar{b})$ and/or $pp\rightarrow h_1\rightarrow \gamma \gamma$ channels are possible, independently or simultaneously. They could thus explain the corresponding ‘excesses’ reported by LEP and CMS, respectively. Further experimental effort is required to investigate this scenario.⁸

Fig. 16

Higgs masses in the scenario of Fig. 17

3.4 Discussion concerning the remaining theoretical uncertainties

Below, we provide a summary of the main sources of theoretical uncertainties from unknown higher-order corrections applying to our calculation of the NMSSM Higgs decays. We do not discuss here the parametric theoretical uncertainties arising from the experimental errors of the input parameters. For the experimentally known SM-type parameters the induced uncertainties can be determined in the same way as for the SM case (see e.g. Ref. [21]). The dependence on the unknown SUSY parameters, on the other hand, is usually not treated as a theoretical uncertainty but rather exploited for setting indirect constraints on those parameters.

Higgs decays into quarks ($\mathbf h _\mathbf i \rightarrow \mathbf q \bar{\mathbf{q }}$, $\mathbf q =\mathbf c, b, t$) In our evaluation, these decays have been implemented at full one-loop order, i.e. at QCD, electroweak and SUSY next-to-leading order (NLO). In addition, leading QCD logarithmic effects have been resummed within the parametrization of the Yukawa couplings in terms of a running quark mass at the scale of the Higgs mass. The Higgs propagator-type corrections determining the mass of the considered Higgs particle as well as the wave function normalization at the external Higgs leg of the process contain full one-loop and dominant two-loop contributions.

For an estimate of the remaining theoretical uncertainties, several higher-order effects should be taken into account:

• First, we should assess the magnitude of the missing QCD NNLO (two-loop) effects. We stress that there should be no large logarithms associated to these corrections, since these are already resummed through the choice of running parameters and the renormalization scale. For the remaining QCD pieces, we can directly consider the situation in the SM. In the case of the light quarks, the QCD contributions of higher order have been evaluated and amount to $\mathord {\sim }\,4\%$ at $m_{H}=120$ GeV (see e.g. Refs. [136, 137]). For the top quark, the uncertainty due to missing QCD NNLO effects was estimated to $5\%$ [21].

• Concerning the electroweak corrections, Fig. 1 suggests that the one-loop contribution is small – at the percent level – for an SM-like Higgs, which is consistent with earlier estimates in the SM [21]. For the heavy Higgs states, Fig. 1 indicates a larger impact of such effects – at the level of $\mathord {\sim }\,10\%$ in the considered scenario. Assuming that the electroweak NNLO corrections are comparable to the squared one-loop effects, our estimate for pure electroweak higher orders in decays of heavy Higgs states reaches the percent level. In fact, for multi-TeV Higgs bosons, the electroweak Sudakov logarithms may require a resummation. Furthermore, mixed electroweak–QCD contributions are expected to be larger than the pure electroweak NNLO corrections, adding a few more percent to the uncertainty budget. For light Higgs states, the electroweak effects are much smaller since the Sudakov logarithms remain of comparatively modest size.

• Finally, the variations with the squark masses in Fig. 1 for the heavy doublet states show that the one-loop SUSY effects could amount to 5–$10\%$ for a sub-TeV stop/sbottom spectrum. In such a case, the two-loop SUSY and the mixed QCD/electroweak–SUSY corrections may reach the percent level. On the other hand, for very heavy squark spectra, we expect to recover an effective singlet-extended Two-Higgs-Doublet model (an effective SM if the heavy doublet and singlet states also decouple) at low energy. However, all the parameters of this low-energy effective field theory implicitly depend on the SUSY radiative effects, since unsuppressed logarithms of SUSY origin generate terms of dimension $\mathord {\le }\,4$ – e.g. in the Higgs potential or the Higgs couplings to SM fermions. On the other hand, the explicit dependence of the Higgs decay widths on SUSY higher-order corrections is suppressed for a large SUSY scale. In this case, the uncertainty from SUSY corrections reduces to a parametric effect, that of the matching between the NMSSM and the low-energy Lagrangian – e.g. in the SM-limit, the uncertainty on the mass prediction for the SM-like Higgs continues to depend on SUSY logarithms and would indirectly impact the uncertainty on the decay widths.

Considering all these higher-order effects together, we conclude that the decay widths of the SM-like Higgs should be relatively well controlled (up to $\mathord {\sim }\,5\%$), while those of a heavy Higgs state could receive sizable higher-order contributions, possibly adding up to the level of $\mathord {\sim }\,10\%$.

Fig. 17

The decay properties of the mostly singlet-like $\mathcal{CP}$-even Higgs state are depicted as a function of its mass. The input parameters are provided in Table 1. The branching ratios into $b\bar{b}$, ZZ, gg and $\gamma \gamma$ are shown at the tree level (black), under partial one-loop approximations (blue, green) and at the full one-loop order (red). The plots at the bottom show the quantities $\xi _b$ and $\xi _{\gamma }$ of Eq. (3.1), estimating the signals associated with $h_1$ in the $b\bar{b}$ channel at LEP and in the $\gamma \gamma$ channel at the LHC, as compared to an SM Higgs at the same mass. Explicit values at $M_{h_1}=95.1$ GeV are given in Table 2

Higgs decays into leptons Here, QCD corrections appear only at two-loop order in the Higgs propagator-type corrections as well as in the counterterms of the electroweak parameters and only from three-loop order onwards in the genuine vertex corrections. Thus, the theory uncertainty is expected to be substantially smaller than in the case of quark final states. For an SM-like Higgs, associated uncertainties were estimated to be below the percent level [23]. For heavy Higgs states, however, electroweak one-loop corrections are enhanced by Sudakov logarithms and reach the $\mathord {\sim }\,10\%$ level for Higgs masses of the order of 1 TeV, so that the two-loop effects could amount to a few percent. In addition, light staus may generate a sizable contribution of SUSY origin, where the unknown corrections are of two-loop electroweak order.

Higgs decays into ${{\varvec{WW/ZZ}}}$ The complexity of these channels is illustrated by our presentation of two separate estimates, expected to perform differently in various regimes.

• In the SM, the uncertainty of Prophecy4f in the evaluation of these channels was assessed at the sub-percent level below 500 GeV, but up to $\mathord {\sim }\,15\%$ at 1 TeV [21]. For an SM-like Higgs, our Fig. 3 shows that the one-loop electroweak corrections are somewhat below $10\%$, making plausible a sub-percent uncertainty on the results employing Prophecy4f. On the other hand, the assumption that the decay widths for an NMSSM Higgs boson can be obtained through a simple rescaling of the result for the width in the SM by tree-level couplings, is in itself a source of uncertainties. We expect this approximation to be accurate only in the limit of a decoupling SM-like composition of the NMSSM Higgs boson. If these SM-like characteristics are altered through radiative corrections of SUSY origins or NMSSM-Higgs mixing effects – both of which may still reach the level of several percent in a phenomenologically realistic setup – the uncertainty on the rescaling procedure for the decay widths should be of corresponding magnitude.

• In the case of heavier states, Fig. 3 and Fig. 8 indicate that the previous procedure is unreliable in the mass range $\mathord {\gtrsim }\,500$ GeV. In particular, for heavy doublets in the decoupling limit, radiative corrections dominate over the – then vanishing – tree-level amplitude, shifting the widths by orders of magnitude. In such a case, our one-loop calculation captures only the leading order and one can expect sizable contributions at the two-loop level: as we already mentioned in discussing Fig. 3, shifting the quark masses between pole and $\overline{\mathrm {MS}}$ values – two legitimate choices at the one-loop order that differ in the treatment of QCD two-loop contributions – results in modifications of the widths of order $\mathord {\sim }\,50\%$. On the other hand, one expects the decays of a decoupling heavy doublet into electroweak gauge bosons to remain a subdominant channel, so that a less accurate prediction may be tolerable. It should be noted, however, that the magnitude of the corresponding widths is sizably enhanced by the effects of one-loop order, which may be of interest regarding their phenomenological impact.

Radiative decays into gauge bosons As these channels appear at the one-loop order, our (QCD-corrected) results represent (only) an improved leading-order evaluation. Yet the situation is contrasted:

• In the SM, the uncertainty on a Higgs decay into $\gamma \gamma$ was estimated at the level of $1\%$ in Ref. [21]: however, the corresponding calculation includes both QCD NLO and electroweak NLO corrections. In our case, only QCD NLO corrections (with full mass dependence) are taken into account. The comparison with NMSSMCALC in Fig. 9 provides us with a lower bound on the magnitude of electroweak NLO and QCD NNLO effects: both evaluations are at the same order but differ by a few percent. The uncertainty on the SUSY contribution should be considered separately, as light charginos or sfermions could have a sizable impact. In any case, we expect the accuracy of our calculation to perform at the level of $\mathord {\gtrsim }\,4\%$ (the typical size of the deviations in Fig. 9).

• In the case of the Higgs decays into gluons, for the SM prediction – including QCD corrections with full mass dependence and electroweak two-loop effects – an uncertainty of $3\%$ from QCD effects and $1\%$ from electroweak effects was estimated in Ref. [21]. In our case, the QCD corrections are only included in the heavy-loop approximation, and NLO electroweak contributions have not been considered. Consequently, the uncertainty budget should settle above the corresponding estimate for the SM quoted above. In the case of heavy Higgs bosons, the squark spectrum could have a significant impact on the QCD two-loop corrections, as exemplified in Fig. 5 of Ref. [117].

• For $h_i\rightarrow \gamma Z$, QCD corrections are not available so far, so that the uncertainty should be above the $\mathord {\sim }\,5\%$ estimated in the SM [21].

Additional sources of uncertainty from higher orders For an uncertainty estimate, the following effects apply to essentially all channels and should be considered as well:

• The mixing in the Higgs sector plays a central role in the determination of the decay widths. Following the treatment in FeynHiggs, we have considered $\mathbf {Z}^{ \text{ mix }}$ in all our one-loop evaluations, as prescribed by the LSZ reduction. Most public codes consider a unitary approximation in the limit of the effective scalar potential ($\mathbf {U}^0$ in our notation). The analysis of Ref. [25] and our discussion on Fig. 1 – employing $\mathbf {U}^m$, a more reliable unitary approximation than $\mathbf {U}^0$ – indicate that the different choices of mixing matrices may affect the Higgs decays by a few percent (and far more in contrived cases). However, even the use of $\mathbf {Z}^{ \text{ mix }}$ is of course subject to uncertainties from unknown higher-order corrections. While the Higgs propagator-type corrections determining the mass of the considered Higgs boson and the wave function normalization contain corrections up to the two-loop order, the corresponding prediction for the mass of the SM-like Higgs still has an uncertainty at the level of about $2\%$, depending on the SUSY spectrum.

• In this paper, we confined ourselves to the evaluation of the Higgs decay widths into SM particles and did not consider the branching ratios. For the latter an implementation at the full one-loop order of many other two-body decays, relevant in particular for the heavy Higgs states, would be desirable, which goes beyond the scope of the present analysis. Furthermore, in order to consider the Higgs branching ratios at the one-loop order, we would have to consider three-body widths at the tree level, for instance $h_i\rightarrow b\bar{b}Z$, since these are formally of the same magnitude as the one-loop effects for two-body decays. In addition, these three-body decays – typically real radiation of electroweak and Higgs bosons – exhibit Sudakov logarithms that would require resummation in the limit of heavy Higgs states.

• At decay thresholds, the approximation of free particles in the final state is not sufficient, and a more accurate treatment would require the evaluation of final-state interactions. Several cases have been discussed in e.g. Refs. [75, 76, 138].

In this discussion we did not attempt to provide a quantitative estimate of the remaining theoretical uncertainties from unknown higher-order corrections, as such an estimate would in any case sensitively depend on the considered region in parameter space. Instead, we have pointed out the various sources of higher-order uncertainties remaining at the level of our state-of-the-art evaluation of the Higgs decays into SM particles in the NMSSM. For a decoupling SM-like Higgs boson one would ideally expect that the level of accuracy of the predictions approaches the one achieved in the SM. However, even in this limit, missing NNLO pieces – that are known for the SM, but not for the NMSSM – give rise to a somewhat larger theoretical uncertainty in the NMSSM. Furthermore, uncertainties of parametric nature (for instance from the theoretical prediction of the Higgs-boson mass) need to be taken into account as well. For heavy Higgs states, the impact of electroweak Sudakov logarithms and SUSY corrections add to the theoretical uncertainty to an extent that is strongly dependent on the details of the spectrum and the characteristics of the Higgs state. For a decoupling doublet at $\mathord {\sim }\,1$ TeV, an uncertainty of $\mathord {\sim }\,5$–$15\%$ may be used as a guideline for the fermionic and radiative decays, while the uncertainty may be as large as $\mathord {\sim }\,50\%$ in $h_i\rightarrow WW/ZZ$.

4 Conclusions

In this paper, we have presented our evaluation of neutral Higgs decay widths into SM final states in the ($\mathcal{CP}$-conserving or $\mathcal{CP}$-violating) NMSSM. Full one-loop corrections have been included for all the considered channels, as well as higher-order QCD corrections to the decays that are generated at the radiative level. The inclusion of one-loop contributions to the decays into SM fermions or electroweak gauge bosons goes beyond the usual approximation amounting to a QCD/QED-corrected tree level. In addition, QCD corrections to the digluon and diphoton decay widths have been carefully processed, including the mass dependence in the $\gamma \gamma$ case and corrections beyond NLO in the gg case. In its current form, this state-of-the-art implementation of the neutral Higgs decays into SM particles is available as a Mathematica package, but should also be integrated into the FeynHiggs code in the near future.

In order to illustrate this calculation of the Higgs decay widths, we have presented our results in several regimes of the parameter space of the NMSSM. In the MSSM limit, we were able to recover the predictions of FeynHiggs and trace the origins of deviations from our new results. In particular, we emphasized the relevance of one-loop contributions in the decays of heavy doublet states into electroweak gauge bosons, for which the usual estimates based on the tree-level Higgs–gauge couplings are not appropriate. Minor effects in the treatment of QCD and QED corrections have also been noted. Beyond the MSSM limit, we have compared our decay widths to the output of NMSSMCALC. We observed a qualitative agreement wherever this could be expected. We also gave an account of the various sources of theoretical uncertainties from higher-order corrections and discussed the achieved accuracy of our predictions.

As a phenomenological application, we investigated in particular the case of a mostly singlet-like state with mass in the vicinity of $\mathord {\lesssim }\,100$ GeV. The decays of such a state can be notably affected by suppressed couplings to down- or up-type quarks which can occur in certain parameter regions as a consequence of the mixing between the different Higgs states. In particular, an additional Higgs boson $h_i$ of this kind could manifest itself via signatures in the channels $e^+e^- \rightarrow Z(h_i\rightarrow b\bar{b})$ and/or $pp \rightarrow h_i \rightarrow \gamma \gamma$. The presence of such a light Higgs boson could thus explain the slight deviations from the SM predictions reported by LEP and CMS in those channels.