1 Introduction

General relativity (GR) is the geometric theory of gravitation presented in 1905 to provide a comprehensive approach in the study of gravitational interactions. However, ordinary matter ingredients of GR do not provide a suitable explanation to some recent cosmological and astrophysical data sets (see [1,2,3,4,5,6,7] and references therein). This theory adequately describe weak field regimes, however, it do not provide satisfactory description of strong field eras. Current image of the universe suggests refinement in the framework, that strongly recommends development of alternative theories of gravity. These theories can be classified as scalar tensor gravities, theories with extra gravitational fields, extra spatial dimension. Theory of f(R) incorporates non-linear terms of curvature as a function of Ricci scalar denoted by f(R) in its action [5, 6].

Existence of some symmetry in spacetime reduces degrees of freedom in constitutive equations that makes analysis less complicated. The gravitating systems are usually studied by considering spherical symmetry. Observational evidences suggests that deviations in spherical symmetry are very rare and incidental [8]. These deformations in spacetime are not fundamental characteristic of gravitating sources, that is why spherical symmetry is preferred [9]. Weyl tensor accounts the tidal pressure that a frame feels while shifting along a geodesic. The Riemann curvature tensor defines variation in the volume of compact object while Weyl tensor describes modifications in shape distorted by the tidal forces. Vanishing of Weyl tensor refers to conformally flat spacetime.

Likewise GR, distribution of matter within the metric induces non-flatness in the spacetime that is an origin to report the gravitational interaction in extended theories. A second rank tensor termed as energy momentum tensor is used for the description of the matter dissemination at each event in spacetime. This tensor is used to explain the relationship of curvature of spacetime with the matter distribution. The inner matter configuration of compact object may consist of different types of fluid such as perfect fluid, isotropic fluid, anisotropic fluid and many others. Perfect fluid can be completely described by rest mass density and pressure, isotropic fluid have uniform pressure distribution in all directions while anisotropic fluid contains irregular pressure distribution.

In astronomy, a polytrope refers to the solution of Lane–Emden equation (LEe) in which the pressure stresses rely on the density and the polytropic equation of state (EoS). It has been considered by many researchers by means of LEe that describes departure from the hydrostatic equilibrium composition of the compact object. Polytropic EoS has tempted scientists around the globe to explore the features of polytropic models. Tooper [10] discussed the solutions to general relativistic field equations for compressible fluid sphere assuming that system obeys polytropic EoS. The generalized polytropic equation of state (GPEoS) can be written as

$$\begin{aligned} \mathop P\nolimits _r = \mathop \alpha \nolimits _1 \mathop \rho \nolimits _0 + K\mathop \rho \nolimits _0^{1 + \frac{1}{n}}, \end{aligned}$$
(1)

where \(P_r\) denotes the radial pressure, mass density is labeled as \(\mathop \rho \nolimits _0\), K is a constant and n is polytropic index. The relation between mass density \(\mathop \rho \nolimits _0\) and the total energy density \(\rho \) is expressed as

$$\begin{aligned} \rho = \mathop \rho \nolimits _0 + n\mathop P\nolimits _r . \end{aligned}$$
(2)

Second formation of GPEoS existing in literature is in the form of total energy density \(\rho \), that turns out to be

$$\begin{aligned} \mathop P\nolimits _r = \mathop \alpha \nolimits _1 \rho + k\mathop \rho \nolimits ^{1 + \frac{1}{n}}, \end{aligned}$$
(3)

and it must satisfies the following relation

$$\begin{aligned} \rho = \frac{{\mathop \rho \nolimits _0 }}{{{{(1 - k\mathop \rho \nolimits _0^{\frac{1}{n}} )}^n}}}. \end{aligned}$$
(4)

Theory of slowly rotating polytropes was reviewed and comprehend with numerical results in [11]. In [12], the polytropes were discussed by considering generalized n-dimensional system. Herrera and Barreto [13, 14] developed general framework to study polytropes in Newtonian and general relativistic regimes. Herrera and his collaborators [15] employed conformally flat condition (vanishing value of Weyl tensor) on spherically symmetric anisotropic fluid distributions incorporating polytropic EoS. The effects of generalized polytropic EoS to discuss late and early time universe under several constraints is discussed in [16,17,18]. Impact of generalized polytropic EoS on spherically and cylindrically symmetric anisotropic polytropes was studied by Azam et al. in [19, 20]. Mardan et al. [21] developed a new class of polytropic models by using generalized polytropic EoS for charged anisotropic fluid configuration. Comprehensive study of various gravitational phenomenon through GPEoS has been worked out in [22,23,24,25,26].

Bekenstein [27] generalized the Oppenheimer Volkoff equations of hydrostatic equilibrium for spherically symmetric charged perfect fluid matter configuration. Tolman mass which is a measure of the active gravitational mass has significant impact on dynamical properties of spherically symmetric gravitating systems. It is used to establish the stability or instability levels of compact object for both Newtonian and relativistic polytropes having anisotropic inner matter configuration [28, 29].

Many researchers have worked on evolution of compact objects analytically in various alternative gravitational theories [30,31,32,33,34,35,36,37]. In the present work, we are intend to workout the conformally flat condition for spherically symmetric spacetime with the help of GPEoS in f(R) gravity. This paper is the generalization of the work on conformally flat polytropes with polytropic EoS [38]. We have assumed that physical parameters follow GPEoS and apply conformally flat condition on considered f(R) model i.e., Starobinsky model.

In the framework of f(R) gravity the Einstein-Hilbert action modifies in a way that a general function of Ricci scalar is incorporated in place of its linear term. Modified action becomes

$$\begin{aligned} \mathop S\nolimits _{f(R)} = \frac{1}{{2\kappa }}\int {{d^4}x\sqrt{ - g} f(R) + {S_M}}, \end{aligned}$$
(5)

where \(\kappa \) is the coupling constant, g denotes determinant of the metric tensor and \({{S_M}}\) is the matter field action. Variation of above action (5) by metric variation leads to the following modified field equations in f(R) framework:

$$\begin{aligned} {R_{\alpha \beta }}{f_R} - \frac{1}{2}f(R)\mathop g\nolimits _{\alpha \beta } + (\mathop g\nolimits _{\alpha \beta }\Box - {\nabla _\alpha }{\nabla _\beta }){f_R} = \kappa {T_{\alpha \beta }}. \end{aligned}$$
(6)

Here \({f_R} = \frac{{df}}{{dR}}\), the usual matter energy momentum tensor is indicated by \(\mathop T\nolimits _{\alpha \beta }\), \(\mathop {\nabla _\alpha }\) is the covariant derivative and \(\Box \equiv \nabla ^\alpha \nabla _\alpha \) is de’Alembertian operator.

The manuscript is organized as follows:

  • Section 2 constitutes the development of modified field equations in f(R) gravity for anisotropic spherically symmetric spacetime. Also, the generalized hydrostatic equilibrium equations and energy condition are discussed in this section.

  • In Sect. 3, f(R) model is implemented on constitutive equations.

  • Conformally flat condition is applied in Sect. 4.

  • Section 5 covers discussion of Tolman mass.

  • Last section incorporates concluding remarks followed by an Appendix and list of references.

2 Modified field equations

The modified field equations can be written as:

$$\begin{aligned} G_{\alpha \beta } = \frac{k}{{\mathop f\nolimits _R }}(\mathop T\nolimits _{\alpha \beta }^D + \mathop T\nolimits _{\alpha \beta }). \end{aligned}$$
(7)

\({G_{\alpha \beta }}\) indicates the Einstein tensor and \(\mathop T\nolimits _{\alpha \beta }^{(D)}\) is the effective energy momentum tensor incorporating dark source constituents, given by

$$\begin{aligned} \mathop T\nolimits _{\alpha \beta }^{(D)} = \frac{1}{k}({\nabla _\alpha }{\nabla _\beta } {f_R} - {f_R}{g_{\alpha \beta }} + \frac{{\mathop g\nolimits _{\alpha \beta } }}{2}(f - R{f_R})). \end{aligned}$$
(8)

Spherically symmetric spacetime has been considered to proceed with the analysis, written as

$$\begin{aligned} ds^2=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^2 d\theta ^{2}-r^2 \sin ^2\theta {d\phi ^2}, \end{aligned}$$
(9)

where \(\nu \) and \(\lambda \) are the metric coefficients having dependence on the radial coordinate r. The usual matter energy momentum tensor is given by

$$\begin{aligned} \mathop T\nolimits _{\alpha \beta } = (\rho + \mathop p\nolimits _ \bot ){u_\alpha }\mathop u\nolimits _\beta - \mathop p\nolimits _ \bot \mathop g\nolimits _{\alpha \beta } + ({P_r} - {P_ \bot }){s_\alpha }{s_\beta }, \end{aligned}$$
(10)

where \(P_ \bot \) is tangential pressure. The four velocity is denoted by \(u^\alpha \) while \(s^\alpha \) is the radial four vector defined as:

$$\begin{aligned} \mathop u\nolimits ^\alpha = ({e^{\frac{{ - \nu }}{2}}},0,0,0), \quad {s^\alpha }= (0,{e^{\frac{{ - \lambda }}{2}}},0,0), \end{aligned}$$

satisfying \(\mathop s\nolimits ^\alpha \mathop u\nolimits _\alpha =0\), \(\mathop s\nolimits ^\alpha \mathop s\nolimits _\alpha = - 1\). The onset of modified field equations turns out to be

$$\begin{aligned} \rho= & {} \frac{{{e^{ - \lambda }}}}{{2k\mathop r\nolimits ^2 }} (\mathop r\nolimits ^2 \lambda '{{f_R}^\prime } - f {r^2}{e^{ \lambda }} + 2{f_R}r\lambda ' + {f_R}{r^2}{e^\lambda }R \nonumber \\&+ 2{f_R}{e^\lambda } - 2{r^2}{f_R}^{\prime \prime }- 4r{f_{R}}^\prime - 2{f_R}), \end{aligned}$$
(11)
$$\begin{aligned} {P_r}= & {} - \frac{{{e^{ - \lambda }}}}{{2k\mathop r\nolimits ^2 }}( - \mathop r\nolimits ^2 \nu '{{f_R}^\prime } - f{r^2}{e^{ \lambda }} \nonumber \\&- 2{f_R}r\nu ' + {f_R}{r^2}{e^\lambda }R + 2{f_R}{e^\lambda } - 4r{f_R}^\prime - 2{f_R}),\nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned} {P_ \bot }= & {} \frac{{{e^{ - \lambda }}}}{4k\mathop r}(\mathop 2r\nu '{{f_R}^\prime } - {f_R}r\nu '\lambda ' + 2{f_R}r\nu '' - 2{f_R}r{e^\lambda }R \nonumber \\&+ 2r{f_R}{e^\lambda } + 4r{f''_R}+ 4{f_R}^\prime \nonumber \\&-2{f_R}\lambda ' + {f_R}r{{\nu '}^2} - 2{f_R}\nu ' - 2r\lambda '{f'_R}), \end{aligned}$$
(13)

here prime denotes the derivative with respect to r. The expression for Ricci scalar is given by

$$\begin{aligned} R = \frac{{{e^{ - \lambda }}}}{{2{r^2}}}(4 - 4{e^\lambda } + {{\nu '}^2}{{r'}^2} - 4r{\lambda ^\prime } + 4{v^\prime }r - \lambda '{r^2}\nu ' + 2{r^2}\nu ''). \end{aligned}$$
(14)

The schwarzschild spacetime has been considered as exterior line element, written as

$$\begin{aligned} ds^2=\left( 1-\frac{2M}{r_\Sigma }\right) dt^2- \left( 1-\frac{2M}{r_\Sigma }\right) ^{-1}dr^2-r^2 d\theta ^{2}-r^2 \sin ^2\theta {d\phi ^2},\nonumber \\ \end{aligned}$$
(15)

also at the boundary surface \(r=r_\Sigma \), the internal and external region must match smoothly so we have

$$\begin{aligned} {e^{\nu _\Sigma }} = {e^{ - \lambda _\Sigma }} = 1 - \frac{{2M}}{r_\Sigma },\quad {(k{P_r} - \mathop \tau \nolimits _{11} )_{r_\Sigma }} = 0, \end{aligned}$$
(16)

where \(r_\Sigma \) denotes the boundary surface. The hydrostatic equilibrium condition can be well interpreted by following expression

$$\begin{aligned} {{P'}_r} = - \frac{{\nu '}}{2}(\rho + {P_r}) + \frac{{2\Delta }}{r} - {\chi _1}, \end{aligned}$$
(17)

where \(\Delta = {P_ \bot } - {P_r}\) is the anisotropy factor and \({\chi _1}\) represents the contribution of dark source given in appendix as Eq. (A1). The equilibrium equation is also called the generalized Tolman Oppenheimer Volkoff (TOV) equation and

$$\begin{aligned} \frac{{\nu '}}{2} = \frac{{(k{P_r}{r^3} - {\tau _{11}}{r^3}) + 2m{f_R}}}{{r(r - 2m)2{f_R}}}. \end{aligned}$$
(18)

The mass function m(r) of spherical geometry is given by

$$\begin{aligned} {e^{ - \lambda (r) }} = 1 - \frac{{2m}}{r},\quad m(r) = \frac{k}{2}\int \limits _0^r {\frac{{{r^2}}}{{{f_R}}}\left( \rho - \frac{{{\tau _{00}}}}{k}\right) dr} , \end{aligned}$$
(19)

where

$$\begin{aligned} m'(r) = \frac{{k{r^2}}}{{2{f_R}}}\left( \rho - \frac{{{\tau _{00}}}}{k}\right) . \end{aligned}$$
(20)

The dark source terms added in the above equations by using of Eq. (18) in Eq. (17), so the generalized TOV equation becomes

$$\begin{aligned} {{P'}_r} = - \left[ \frac{{(k{P_r}{r^3} - {\tau _{11}}{r^3}) + 2m{f_R}}}{{r(r - 2m)2{f_R}}}\right] (\rho + {P_r}) + \frac{{2\Delta }}{r} - {\chi _1}. \end{aligned}$$
(21)

It is already mentioned that \(\chi _1\) is given in appendix as Eq. (A1).

2.1 Energy conditions

For any compact star model to be physical realistic, certain energy conditions must be satisfied. For our model, the energy momentum tensor given in previous Eq. (7) is considered to develop such conditions. The eigenvalues \({\ell _i}\) where \(i=0,1,2,3\) are the roots of following equation

$$\begin{aligned} |\mathop T\nolimits _{\alpha \beta }^{(D)}-{\ell _\alpha }{g_{\alpha \beta }}| = 0. \end{aligned}$$
(22)

The energy conditions are given as

$$\begin{aligned} {\ell _0} \ge 0,\quad {\ell _0} + {\ell _i} \ge 0, \end{aligned}$$
(23)

where, \(\ell _0\) denotes the eigenvalue related to the timelike eigenvector and \(\ell _i\) represents the eigenvalues that corresponds to the spacelike eigenvectors. For the anisotropic matter configuration considered in our case, the Eq. (22) can be rewritten as:

$$\begin{aligned} \left| {\begin{array}{*{20}{c}} {\rho - \frac{{{\tau _{00}}}}{k} - \ell }&{}0&{}0&{}0\\ 0&{}{{P_r} - \frac{{{\tau _{11}}}}{k} + \ell }&{}0&{}0\\ 0&{}0&{}{{P_ \bot } - \frac{{{\tau _{22}}}}{k} + \ell }&{}0\\ 0&{}0&{}0&{}{{P_ \bot } - \frac{{{\tau _{22}}}}{k} + \ell } \end{array}}\right| = 0, \end{aligned}$$

we obtain the following result

$$\begin{aligned} \left[ {(\rho - \frac{{{\tau _{00}}}}{k}-\ell )({P_r} - \frac{{{\tau _{11}}}}{k} + \ell )} \right] {\left( {{P_ \bot }-\frac{{{\tau _{22}}}}{k} + \ell } \right) ^2} = 0, \end{aligned}$$
(24)

above equation have four roots, first two are distinct and the following one is repeated

$$\begin{aligned} \left( {{P_ \bot } - \frac{{{\tau _{22}}}}{k} + \ell } \right) ^2 = 0, \end{aligned}$$
(25)

The roots of Eq. (24) are listed below:

$$\begin{aligned}&{\ell _0}=\left( \rho - \frac{{{\tau _{00}}}}{k}\right) , \quad {\ell _1}= -\left( {P_r} - \frac{{{\tau _{11}}}}{k}\right) , \end{aligned}$$
(26)
$$\begin{aligned}&{\ell _2} = - \left( {P_ \bot } - \frac{{{\tau _{22}}}}{k}\right) , \quad {\ell _3} = - \left( {P_ \bot } - \frac{{{\tau _{33}}}}{k}\right) . \end{aligned}$$
(27)

Following three energy conditions have been developed by making use of Eqs. (26) and (27) in Eq. (23)

$$\begin{aligned} k\rho - {\tau _{00}} > 0,\quad \frac{{k{P_r} - {\tau _{11}}}}{{k\rho - {\tau _{00}}}} \le 1, \quad \frac{{k{P_ \bot } - {\tau _{22}}}}{{k\rho - {\tau _{00}}}} \le 1. \end{aligned}$$
(28)

The dark source terms \(\tau _{00}, \tau _{11}\) and \(\tau _{22}\) are defined in appendix as Eqs. (A2)–(A4).

3 Implementation of Starobinsky model

The f(R) model that has been considered to study the evolution of developed model is Starobinsky model [39], having following mathematical form:

$$\begin{aligned} f(R) = R + \delta {R^2}, \end{aligned}$$
(29)

where \(\delta \) can take positive value. The model under consideration depicts that the viable candidate for the constituents of dark matter pertaining stable stellar configuration.

3.1 Case I

In this case, we consider the GPEoS given in Eq. (1) and we define dimensionless variables as

$$\begin{aligned}&\alpha =\frac{P_{rc}}{\rho _{c}}, \quad \alpha _2 = (\alpha - {\alpha _1} + n\alpha {\alpha _1}),\quad r=\frac{\xi }{A}, \quad \psi _0^n = \frac{{{\rho _0}}}{{{\rho _{0c}}}}, \nonumber \\&\alpha _3= ({\alpha _1}n(1 - n\alpha )\psi _0^{ - 1} + (1 + n){\alpha _2}),\quad A^2={4\pi \rho _{c}},\nonumber \\&{\alpha _4} = ({\alpha _1} - n\alpha {\alpha _1} + {\psi _0}{\alpha _2}),\quad v({\xi })=\frac{m(r){A^3}}{4\pi \rho _{c}}. \end{aligned}$$
(30)

TOV equation for Starobinsky model can be obtained by using Eqs. (1), (2), (30) in Eq. (21) and we obtain

$$\begin{aligned}&{\xi ^2}{\alpha _3}\frac{{d{\psi _0}}}{{d\xi }}\left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] + \frac{{{\xi ^3}}}{{8\pi {f_R}}}\left[ \kappa {\alpha _1}\psi _0^n(1 - n\alpha )\right. \nonumber \\&\quad \left. + \kappa \psi _0^{n + 1}{\alpha _2} - \frac{{{\tau _{11}}}}{{{\rho _c}}} + \frac{{8\pi v{f_R}}}{{{\xi ^3}}} \right] \nonumber \\&\quad - \frac{{2\xi \Delta \psi _0^{ - n}}}{{{\rho _c}}}\left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] \nonumber \\&\quad +{\frac{{{\chi _1}{\xi ^2}\psi _0^{ - n}}}{{{\rho _c}}}}\left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] = 0. \end{aligned}$$
(31)

The mass function m(r) of spherical geometry in the framework of f(R) gravity with the help of Eq. (20) turns out to be

$$\begin{aligned} \frac{{dv}}{{d\xi }} = \frac{{{\xi ^2}\psi _0^n\kappa }}{{8\pi {f_R}}}\left[ {1 - n{\alpha _2} + n{\alpha _2}{\psi _0} - \frac{{{\tau _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}} \right] . \end{aligned}$$
(32)

Insertion of f(R) model in above expression leads to following hydrostatic equilibrium equation

$$\begin{aligned}&{{{\xi ^2}{\alpha _3}}}\frac{{d{\psi _0}}}{{d\xi }}\Big [ {\frac{{(1 - 2v/\xi ) }}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \Big ] + \frac{{{\xi ^3}}}{{8\pi + 16\pi \delta R^*}}\nonumber \\&\quad \times \Big [ {\kappa {\alpha _1}\psi _0^n(1 - n\alpha )+ \kappa \psi _0^{n + 1}{\alpha _2} - \frac{{{{\bar{\tau }} _{11}}}}{{{\rho _c}}} + \frac{{8\pi v + 16v\pi R^*}}{{{\xi ^3}}}} \Big ]\nonumber \\&\quad +\left[ - \frac{{2\xi \Delta \psi _0^{ - n}}}{{\rho _c}} + \frac{{{\bar{\chi }_1}{\xi ^2}\psi _0^{ - n}}}{{\rho _c}}\right] \times \left[ {\frac{{(1 - 2v/\xi ) }}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] = 0.\nonumber \\ \end{aligned}$$
(33)

In this case, we have

$$\begin{aligned} \frac{{dv}}{{d\xi }} = \frac{{{\xi ^2}\psi _0^n\kappa }}{{8\pi + 16v\pi R^*}}\left[ {1 - n{\alpha _2} + n{\alpha _2}{\psi _0} - \frac{{{\bar{\tau }_{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}} \right] . \end{aligned}$$
(34)

Dark source terms using f(R) model given in appendix as Eqs. (A5)–(A7). For the physical consistency of the polytropes, the energy conditions modifies in the following form

$$\begin{aligned}&(1 - n\alpha ) > \frac{{{\tau _{00}}}}{{\kappa {\rho _c}}},\nonumber \\&\quad \frac{{\left( {{\alpha _1} - n\alpha {\alpha _1} + {\psi _0}{\alpha _2}} \right) - ({\tau _{11}}\psi _0^{ - n}/\kappa {\rho _c})}}{{(1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - ({\tau _{00}}\psi _0^{ - n}/\kappa {\rho _c})}} \le 1, \end{aligned}$$
(35)
$$\begin{aligned}&\frac{1}{{\psi _0^n(1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - ({\tau _{00}}/\kappa {\rho _c})}}\nonumber \\&\quad \left( \left( {({\alpha _1} - n\alpha {\alpha _1})\psi _0^n + \psi _0^{n + 1}{\alpha _2}} \right) + \frac{{8\pi {f_R}}}{\kappa } \right. \nonumber \\&\left[ 3v/{\xi ^3} - \frac{{\psi _0^n\kappa }}{{8\pi {f_R}}}\left( (1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - \frac{{{\tau _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\right) \right] \nonumber \\&\quad - ({\tau _{11}}/\kappa {\rho _c})) \le 1, \end{aligned}$$
(36)

and with generalized polytropic conditions

$$\begin{aligned}&(1 - n\alpha ) > \frac{{{{\bar{\tau }} _{00}}}}{{\kappa {\rho _c}}},\nonumber \\&\quad \frac{{\left( {{\alpha _1} - n\alpha {\alpha _1} + {\psi _0}{\alpha _2}} \right) - ({{\bar{\tau }} _{11}}\psi _0^{ - n}/\kappa {\rho _c})}}{{(1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - ({{\bar{\tau }} _{00}}\psi _0^{ - n}/\kappa {\rho _c})}} \le 1, \end{aligned}$$
(37)
$$\begin{aligned}&\frac{1}{{\psi _0^n(1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - ({{\bar{\tau }} _{00}}/\kappa {\rho _c})}}\Bigg [\left( {({\alpha _1} - n\alpha {\alpha _1})\psi _0^n + \psi _0^{n + 1}{\alpha _2}} \right) \nonumber \\&\quad + (8\pi + 16\delta \pi R^*)/\kappa \Bigg [3v/{\xi ^3} - \frac{{\psi _0^n\kappa }}{{(8\pi + 16\pi \delta R^*)}}\nonumber \\&\quad ((1 - n{\alpha _2} + n{\alpha _2}{\psi _0})- {{\bar{\tau }} _{00}}\psi _0^{ - n}/\kappa {\rho _c})\Bigg ] - ({{\bar{\tau }} _{11}}/\kappa {\rho _c})\Bigg ] \le 1. \end{aligned}$$
(38)

3.2 Case 2

We consider the GPEoS given in Eq. (3) and define \({\psi ^n} = \frac{\rho }{{{\rho _c}}}\) as dimensionless variable, the following similar methodology as in case I, we obtain

$$\begin{aligned}&{{{\xi ^2}((\alpha - {\alpha _1})(n+1) + n{\alpha _1}{\psi ^{ - 1}})}}\frac{{d\psi }}{{d\xi }}\left[ {\frac{{(1 - 2v/\xi )}}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \right] \nonumber \\&\quad + \frac{{{\xi ^3}}}{{8\pi {f_R}}}\times \left[ {\kappa {\alpha _1}{\psi ^n} + \kappa {\psi ^{n + 1}}(\alpha - {\alpha _1}) - \frac{{{\tau _{11}}}}{{{\rho _c}}} + \frac{{8\pi v{f_R}}}{{{\xi ^3}}}} \right] \nonumber \\&\quad +\left[ -\frac{{2\xi \Delta {\psi ^{ - n}}}}{{\rho _c}}+ \frac{{{\chi _1}{\xi ^2}{\psi ^{ - n}}}}{{{\rho _c}A}}\right] \times \left[ {\frac{{(1 - 2v/\xi )}}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \right] = 0,\nonumber \\ \end{aligned}$$
(39)

and by applying Starobinsky model, we get

$$\begin{aligned}&{{{\xi ^2}((\alpha - {\alpha _1})(n+1) + n{\alpha _1}{\psi ^{ - 1}})}}\frac{{d\psi }}{{d\xi }}\Bigg [ {\frac{{(1 - 2v/\xi ) }}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \Bigg ] \nonumber \\&\quad +\frac{{{\xi ^3}}}{{8\pi + 16\pi \delta R^*}}\Bigg [ \kappa {\alpha _1}{\psi ^n} + \kappa {\psi ^{n + 1}}(\alpha - {\alpha _1})-\frac{{{{\bar{\tau }}_{11}}}}{{{\rho _c}}}\nonumber \\&\quad + \frac{{8\pi v + 16v\pi R^*}}{{{\xi ^3}}} \Bigg ]\nonumber \\&\quad +\Bigg [- \frac{{2\xi \Delta {\psi ^{ - n}}}}{\rho _c}+ \frac{{{\bar{\chi }_1}{\xi ^2}{\psi ^{ - n}}}}{{{\rho _c}A}}\Bigg ]\times \Bigg [ {\frac{{(1 - 2v/\xi )}}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \Bigg ] = 0.\nonumber \\ \end{aligned}$$
(40)

Also by using mass function given in Eq. (20) for interior spherical geometry results the form

$$\begin{aligned} \frac{{dv}}{{d\xi }} = \frac{{{\xi ^2}k{\psi ^n}}}{{8\pi {f_R}}}\left[ {1 - \frac{{{\tau _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}} \right] , \end{aligned}$$
(41)

and we obtain

$$\begin{aligned} \frac{{dv}}{{d\xi }} = \frac{{{\xi ^2}\kappa {\psi ^n}}}{8\pi ( 1 +2 \delta R^*)}\left[ {1 - \frac{{{\bar{\tau }_{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}} \right] . \end{aligned}$$
(42)

For the physically viable model, the following conditions must be satisfied

$$\begin{aligned}&\rho > \frac{{{\tau _{00}}}}{\kappa },\quad {\alpha _1} + \psi (\alpha - {\alpha _1}) \le 1 - \left( {\frac{{{\tau _{00}} - {\tau _{11}}}}{{\kappa {\rho _c}{\psi ^n}}}} \right) , \end{aligned}$$
(43)
$$\begin{aligned}&{\alpha _1} + \psi (\alpha - {\alpha _1}) + \frac{{8\pi {f_R}}}{\kappa }\left[ {\frac{{3v}}{{{\xi ^3}{\psi ^n}}} - 1 + \frac{{{\tau _{00}} - {\tau _{11}}}}{{\kappa {\rho _c}{\psi ^n}}}} \right] \le 1.\nonumber \\ \end{aligned}$$
(44)

and by applying Starobinsky model

$$\begin{aligned}&\rho > \frac{{{{\bar{\tau }} _{00}}}}{\kappa },\quad {\alpha _1} + \psi (\alpha - {\alpha _1}) \le 1 - \left( {\frac{{{{\bar{\tau }} _{00}} - {{\bar{\tau }} _{11}}}}{{\kappa {\rho _c}{\psi ^n}}}} \right) , \end{aligned}$$
(45)
$$\begin{aligned}&{\alpha _1} + \psi (\alpha - {\alpha _1}) + \frac{{8\pi ( 1 + 2R^*)}}{{\psi ^n}{\kappa }}\nonumber \\&\quad \left[ {\frac{{3v}}{{{\xi ^3}}} - {\psi ^n} + \frac{{{{\bar{\tau }} _{00}} - {{\bar{\tau }} _{11}}}}{{8\pi {\rho _c}(1 + 2 \delta R^*)}}} \right] \le 1. \end{aligned}$$
(46)

A system of ordinary differential equation (33), (34) or (40), (42), which have three unknown functions: \(\Delta \), \(\psi \) and v that can be depending any set of parameters \(\alpha \) and n, In order to closed the system we need to evaluate one unknown and for this purpose we will apply conformally flat condition.

4 Conformally flat condition

We will use conformally flat condition to calculate \(\Delta \). The electric part Weyl tensor \(C_{232}^3\) is given by

$$\begin{aligned} W=\frac{r^3 e^{-\lambda }}{6}\Bigg (\frac{e^\lambda }{r^2} +\frac{\lambda ^\prime \nu ^\prime }{4} -\frac{1}{r^2} -\frac{\nu ^{\prime 2}}{4}- \frac{\nu ^{\prime \prime }}{2}-\frac{\lambda ^\prime -\nu ^\prime }{2 r}\Bigg ), \end{aligned}$$
(47)

by using integration of mass function it become

$$\begin{aligned} W= & {} \frac{{ - \kappa }}{6}\int \limits _0^r {\frac{{{r^3}}}{{{f_R}}}} {\left( {\rho - \frac{{{\tau _{00}}}}{k}} \right) ^\prime }dr + \frac{\kappa }{6}\int \limits _0^r {\frac{{{r^3}{{f'}_R}}}{{{f_R}^2}}\left( {\rho - \frac{{{\tau _{00}}}}{\kappa }} \right) dr}\nonumber \\&{ + \frac{{{r^3}\kappa }}{{6{f_R}}}\left[ {\left( {{P_r} - \frac{{{\tau _{11}}}}{\kappa }} \right) - \left( {{P_ \bot } - \frac{{{\tau _{22}}}}{\kappa }} \right) } \right] }. \end{aligned}$$
(48)

Integrating this factor, such that

$$\begin{aligned} {e^\nu } = {\tilde{q}}_1^2{r^2}{\cosh ^2}\left[ {\int {\frac{{{e^\lambda }}}{r}dr + {\tilde{q}}} } \right] , \end{aligned}$$
(49)

where \({{\tilde{q}}}\) is the constant of integration. Now using conformally flat condition \(W=0\), we obtain

$$\begin{aligned} \Delta = \frac{{r{f_R}}}{\kappa }{\left( {\frac{{{e^{ - \lambda }} - 1}}{{{r^2}}}} \right) ^\prime } + \left( {\frac{{{\tau _{22}} - {\tau _{11}}}}{\kappa }} \right) . \end{aligned}$$
(50)

4.1 Case 1

By making use of Eqs. (12), (13) and Eq. (20), \(\Delta \) can be written as

$$\begin{aligned} \Delta= & {} \frac{{8\pi {\rho _c}{f_R}}}{\kappa }\left[ \frac{{3v}}{{{\xi ^3}}} - \frac{{\psi _0^n\kappa }}{{8\pi {f_R}}}\Bigg ((1 - n{\alpha _2} + n{\alpha _2}{\psi _0})\right. \nonumber \\&\left. -\frac{{{\tau _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\Bigg ) + \frac{{{\tau _{22}} - {\tau _{11}}}}{{8\pi {\rho _c}{f_R}}} \right] . \end{aligned}$$
(51)

Using f(R) model for anisotropic factor

$$\begin{aligned} \Delta= & {} \frac{8\pi {\rho _c}(1 + 2\delta R^*)}{\kappa }\Big [\frac{{3v}}{{{\xi ^3}}} - \frac{{\psi _0^n\kappa }}{8\pi (1 + 2\delta R^*)}\nonumber \\&\times \left( (1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - \frac{{{{\bar{\tau }} _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\right) \nonumber \\&+\frac{{{{\bar{\tau }} _{22}} - {{\bar{\tau }} _{11}}}}{{8\pi {\rho _c} + 16\pi \delta {\rho _c}R^*}}\Big ]. \end{aligned}$$
(52)

Following condition have been developed by making use of Eqs. (2), (3), (51) and dimensionless variable in Eq. (30)

$$\begin{aligned}&{{{\xi ^2}{\alpha _3}}}\frac{{d{\psi _0}}}{{d\xi }}\left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] \nonumber \\&\quad + \frac{{{\xi ^3}}}{{8\pi {f_R}}} \Bigg [\kappa {\alpha _1}\psi _0^n(1 - n\alpha ) + \kappa \psi _0^{n + 1}{\alpha _2} - \frac{{{\tau _{11}}}}{{{\rho _c}}} \nonumber \\&\quad +\frac{8\pi v{f_R}}{\xi ^3}\Bigg ]- \frac{{16\xi \pi {f_R}}}{\psi _0^{n}{\kappa }}\left[ \frac{{3v}}{{{\xi ^3}}} - \frac{{\psi _0^n\kappa }}{{8\pi {f_R}}}\Bigg ((1 - n{\alpha _2} + n{\alpha _2}{\psi _0})\right. \nonumber \\&\quad \left. - \frac{{{\tau _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\Bigg ) + \frac{{{\tau _{22}} - {\tau _{11}}}}{{8\pi {\rho _c}{f_R}}} \right] \nonumber \\&\quad \times \left[ {\frac{{(1 - 2v/\xi ) }}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] + \frac{{{\chi _1}{\xi ^2}\psi _0^{ - n}}}{{{\rho _c}A}}\nonumber \\&\quad \times \left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha +(n + 1){\alpha _4}]}}} \right] = 0. \end{aligned}$$
(53)

also by applying Starobinsky model, we obtain

$$\begin{aligned}&{\xi ^2}{\alpha _3}\frac{{d{\psi _0}}}{{d\xi }}\left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] \nonumber \\&\quad +\frac{\xi ^3}{8\pi (1 + 2\delta R^*)}\Bigg (\kappa {\alpha _1}\psi _0^n(1 - n\alpha )\nonumber \\&\quad + \kappa \psi _0^{n + 1}{\alpha _2}- \frac{{{{\bar{\tau }} _{11}}}}{{{\rho _c}}} + \frac{8\pi v(1 + 2\delta R^*)}{{{\xi ^3}}}\Bigg )\nonumber \\&\quad + \left[ {\frac{{(1 - 2v/\xi )}}{{[1 - n\alpha + (n + 1){\alpha _4}]}}} \right] \nonumber \\&\quad \times \Bigg [\frac{{{\bar{\chi }_1}{\xi ^2}{\psi ^{ - n}}}}{{{\rho _c}A}} -\frac{16\pi \xi (1 + 2R^*\delta )}{{\kappa }\psi _0^{n}}\nonumber \\&\quad \times \Bigg [\frac{{3v}}{{{\xi ^3}}} - \frac{{\psi _0^n\kappa }}{8\pi (1+ 2\delta R^*)}\times \Bigg ((1 - n{\alpha _2} + n{\alpha _2}{\psi _0})- \frac{{{{\bar{\tau }} _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\Bigg ) \nonumber \\&\quad + \frac{{{{\bar{\tau }} _{22}} - {{\bar{\tau }} _{11}}}}{8\pi {\rho _c}(1 + 2 \delta R^*)}\Bigg ]\Bigg ] = 0. \end{aligned}$$
(54)

4.2 Case 2

Following the similar pattern as in case I and by making use of Eqs. (12), (13), (20), \(\Delta \) can be written as

$$\begin{aligned} \Delta = \frac{{8\pi {\rho _c}{f_R}}}{\kappa }\left[ \frac{{3v}}{{{\xi ^3}}} - \frac{{{\psi ^n}\kappa }}{{8\pi {f_R}}}\left( 1 - \frac{{{\tau _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}\right) + \frac{{{\tau _{22}} - {\tau _{11}}}}{{8\pi {\rho _c}{f_R}}}\right] , \end{aligned}$$
(55)

after some simplifications, we have

$$\begin{aligned} \Delta= & {} \frac{8\pi {\rho _c}(1 + 2\delta R^*)}{\kappa }\Bigg [\frac{{3v}}{{{\xi ^3}}} - \frac{{{\psi ^n}\kappa }}{8\pi (1 + 2\delta R^*)}\Bigg (1 - \frac{{{{\bar{\tau }} _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}\Bigg )\nonumber \\&+ \frac{{{{\bar{\tau }}_{22}} - {{\bar{\tau }} _{11}}}}{8\pi {\rho _c}(1 + 2\delta R^*)}\Bigg ]. \end{aligned}$$
(56)

Following condition have been developed by making use Eqs. (3), (4), (55) and dimensionless variable in Eq. (21)

$$\begin{aligned}&{{{\xi ^2}\left( ((\alpha - {\alpha _1})(n+1)) + {\alpha _1}{\psi ^{ - 1}}\right) }}\frac{{d\psi }}{{d\xi }}\nonumber \\&\quad \times \left[ {\frac{{(1 - 2v/\xi ) }}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \right] + \frac{{{\xi ^3}}}{{8\pi {f_R}}}\nonumber \\&\quad \times \left[ {\kappa {\alpha _1}{\psi ^n} + \kappa {\psi ^{n + 1}}(\alpha - {\alpha _1}) - \frac{{{\tau _{11}}}}{{{\rho _c}}} + \frac{{8\pi v{f_R}}}{{{\xi ^3}}}} \right] \nonumber \\&\quad + \left[ {\frac{{(1 - 2v/\xi ) }}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \right] \nonumber \\&\quad \times \left[ \frac{{{\chi _1}{\xi ^2}{\psi ^{ - n}}}}{{{\rho _c}A}} - \frac{{2\xi {\psi ^{ - n}}}}{{{\rho _c}}}\left( \frac{{8\pi {f_R}}}{\kappa }\left[ \frac{{3v}}{{{\xi ^3}}} - \frac{{{\psi ^n}\kappa }}{{8\pi {f_R}}}\right. \right. \right. \nonumber \\&\quad \left. \left. \left. \times \left( 1 - \frac{{{\tau _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}\right) + \frac{{{\tau _{22}} - {\tau _{11}}}}{{8\pi {\rho _c}{f_R}}}\right] \right) \right] = 0, \end{aligned}$$
(57)

the generalized TOV equation we becomes

$$\begin{aligned}&{{{\xi ^2}((\alpha - {\alpha _1})(n+1) + {\alpha _1}{\psi ^{ - 1}})}}\frac{{d\psi }}{{d\xi }}\left[ {\frac{{(1 - 2v/\xi )}}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \right] \nonumber \\&\quad + \left[ {\frac{{(1 - 2v/\xi ) }}{{1 + \alpha + \psi (\alpha - {\alpha _1})}}} \right] \nonumber \\&\quad \times \left[ \frac{{{\bar{\chi }_1}{\xi ^2}{\psi ^{ - n}}}}{{{\rho _c}A}} - \frac{{2\xi {\psi ^{ - n}}}}{{{\rho _c}}}\left( \frac{8\pi (1 + 2\delta R^*)}{\kappa }\right. \right. \nonumber \\&\quad \left. \left. \times \Bigg [\frac{{3v}}{{{\xi ^3}}} - \frac{{{\psi ^n}\kappa }}{8\pi (1 + 2 \delta R^*)}(1 - \frac{{{{\bar{\tau }} _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}) + \frac{{{{\bar{\tau }} _{22}} - {{\bar{\tau }} _{11}}}}{8\pi {\rho _c}(1 + 2\delta R^*)}\Bigg ] \right) \right] \nonumber \\&\quad + \frac{{{\xi ^3}}}{{8\pi + 16\pi \delta R^*}}\times \Bigg [ \kappa {\alpha _1}{\psi ^n} + \kappa {\psi ^{n + 1}}(\alpha - {\alpha _1}) \nonumber \\&\quad - \frac{{{{\bar{\tau }} _{11}}}}{{{\rho _c}}} + \frac{{8\pi v + 16\pi v\delta R^*}}{{{\xi ^3}}} \Bigg ]= 0. \end{aligned}$$
(58)

5 Tolman mass

Tolman mass (which is the measure of active gravitational mass) is computed for our anisotropic spherical geometry in the background of f(R) gravity as and that function is used the polytropic model to check the stability

$$\begin{aligned} {m_T}= & {} \frac{{4\pi }}{\kappa }\Bigg [ {e^{\frac{{\nu + \lambda }}{2}}}(\kappa {P_r}{r^3} - {\tau _{11}}{r^3} + 2m{f_R})\nonumber \\&+\int \limits _0^r {{r^2}{e^{(\nu + \lambda )/2}}({\tau _{00}} + {\tau _{11}} + {\tau _{22}})dr} \Bigg ]. \end{aligned}$$
(59)

The alternative explanation for Tolman mass

$$\begin{aligned} {m_T}= & {} M{\left( {\frac{r}{{r_\Sigma }}} \right) ^3} - \frac{{4\pi {r^3}}}{\kappa }\int \limits _r^{r_\Sigma }\nonumber \\&\times {\left[ {{e^{(\nu + \lambda )/2}}\left( \frac{{\kappa \Delta }}{r} - \frac{{6w{f_R}}}{{{{{\tilde{r}}}^4}}} + \frac{{\tau _1^*}}{{{\tilde{r}}}} - \frac{{3\tau _2^*}}{{{{{\tilde{r}}}^4}}}\right) } \right] d{\tilde{r}}}, \end{aligned}$$
(60)

where

$$\begin{aligned} \tau _1^* = {\tau _{00}} + 2{\tau _{11}},\quad \tau _2^* = \int \limits _0^r {{r^2}} {e^{(\nu + \lambda )/2}}({\tau _{00}} + {\tau _{11}} + {\tau _{22}})dr. \end{aligned}$$

5.1 Case 1

For case 1 by integrating w.r.t r,  we get

$$\begin{aligned} \nu = \nu _\Sigma - 2\int \limits _r^{r_\Sigma } \left( \frac{{(\kappa {P_r}{r^3} - {\tau _{11}}{r^3}) + 2m{f_R}}}{{r(r - 2m)2{f_R}}}\right) dr. \end{aligned}$$
(61)

Now we will introduce the following dimensionless variables

(62)

The explanation for the stability of Tolman mass

$$\begin{aligned} {m_T}= & {} \frac{{4\pi }}{\kappa }\Bigg [ {e^{\frac{{\nu + \lambda }}{2}}}(\kappa {P_r}{r^3} - {\bar{\bar{\tau }} _{11}}{r^3} + 2m + 4m\delta R^{**})\nonumber \\&+ \int \limits _0^r {{r^2}{e^{(\nu + \lambda )/2}}({\bar{\bar{\tau }} _{00}} + {\bar{\bar{\tau }} _{11}} + {\bar{\bar{\tau }} _{22}})dr} \Bigg ], \end{aligned}$$
(63)

we obtained the following equation

$$\begin{aligned} {m_T}= & {} M{\left( {\frac{r}{{r_\Sigma }}} \right) ^3} - \frac{{4\pi {r^3}}}{\kappa }\int \limits _r^{r_\Sigma } \left[ {e^{(\nu + \lambda )/2}}\Bigg (\frac{{\kappa \Delta }}{r} - \frac{{6w(1 + 2\delta R^{**})}}{{{{{\tilde{r}}}^4}}}\right. \nonumber \\&\left. + \frac{{\tau _1^*}}{{{\tilde{r}}}} - \frac{{3\tau _2^*}}{{{{{\tilde{r}}}^4}}}\Bigg ) \right] d{\tilde{r}}, \end{aligned}$$
(64)

similarly, from TOV equation

$$\begin{aligned} \nu = \nu _\Sigma - 2\int \limits _r^{r_\Sigma } \Bigg ( \frac{{(\kappa {P_r}{r^3} - {\bar{\bar{\tau }}_{11}}{r^3}) + 2m + 4m\delta R^{**}}}{{r(r- 2m)(2 + 4\delta R^{**})}}\Bigg )dr. \end{aligned}$$
(65)

By using Eq. (63), we introduce the following auxiliary variables

$$\begin{aligned}&\frac{{{m_T}}}{M} = {x^3} + \frac{{{x^3}{{{\tilde{A}}}^2}}}{y}\int \limits _x^1 {\frac{{\sqrt{1 - 2y} }}{{\sqrt{1 - 2v\alpha (n + 1)/x{\tilde{A}}} }}\exp } \frac{1}{{8\pi {f_R}{\tilde{A}}}}\nonumber \\&\int \limits _x^1 \frac{{\kappa {x^3}{{{\tilde{A}}}^3}{\alpha _1}\psi _0^n{1-n\alpha } + \kappa {x^3}{{{\tilde{A}}}^{^3}}\psi _0^{n + 1}{\alpha _2} - 4\pi {\bar{\bar{\tau }} _{11}}{x^3}{\tilde{A}}{r^2}_\Sigma + 8\pi v{f_R}}}{{{x^2}(1 - 2v/x{\tilde{A}})}}dx\nonumber \\&\quad \times \left( \frac{{\kappa \Omega }}{x} + \frac{{4\pi \tau _1^*{r^2}_\Sigma }}{{{{{\tilde{A}}}^2}x}} - \frac{{12\pi \tau _2^*}}{{{{{\tilde{A}}}^2}{x^4}r_\Sigma }}\right) dx. \end{aligned}$$
(66)

The contribution of dark source and Ricci scalar in terms of dimensionless variables given in appendix as Eqs. (A8)–(A10) and Eq. (A13), we calculate this equation by Tolman mass and obtain result

$$\begin{aligned} \frac{{{m_T}}}{M}= & {} {x^3} + \frac{{{x^3}{{{\tilde{A}}}^2}}}{y}\int \limits _x^1 {\Bigg [\frac{{\sqrt{1 - 2y} }}{{\sqrt{1 - 2v\alpha (n + 1)/x{\tilde{A}}} }}\exp } \Bigg (\frac{1}{{8\pi (1 + 16R^{**}\delta ){\tilde{A}}}}\nonumber \\&\times \int \limits _x^1 {\frac{{\kappa {x^3}{{{\tilde{A}}}^3}{\alpha _1}\psi _0^n(1 - n\alpha ) + \kappa {x^3}{{{\tilde{A}}}^{^3}}\psi _0^{n + 1}{\alpha _2} - 4\pi {\bar{\bar{\tau }} _{11}}{x^3}{\tilde{A}}{r^2}_\Sigma + 8\pi v(1 + 2\delta R^{**})}}{{{x^2}(1 - 2v/x{\tilde{A}})}}\Bigg )dx}\nonumber \\&\times \Bigg (\frac{{\kappa \Omega }}{x} + \frac{{4\pi \tau _1^*{r^2}_\Sigma }}{{{{{\tilde{A}}}^2}x}} - \frac{{12\pi \tau _2^*}}{{{{{\tilde{A}}}^2}{x^4}r_\Sigma }}\Bigg ) dx\Bigg ]. \end{aligned}$$
(67)

Now \(\Omega \) can be calculated from anisotropic factor as

$$\begin{aligned} \Omega= & {} \frac{\Delta }{\rho _c} =\frac{{8\pi {f_R}}}{\kappa }\left[ \frac{{3v}}{{{\xi ^3}}} - \frac{{\psi _0^n\kappa }}{{8\pi {f_R}}}\Bigg ((1 - n{\alpha _2} + n{\alpha _2}{\psi _0})\right. \nonumber \\&\left. - \frac{{{\bar{\bar{\tau }} _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\Bigg ) + \frac{{{\bar{\bar{\tau }} _{22}} - {\bar{\bar{\tau }} _{11}}}}{{8\pi {\rho _c}{f_R}}} \right] , \end{aligned}$$
(68)

we may write

$$\begin{aligned} \Omega= & {} \frac{{8\pi (1 + 2\delta R^{**})}}{\kappa }\Bigg [ \frac{{3v}}{{{\xi ^3}}} - \frac{{\psi _0^n\kappa }}{{8\pi (1 + 2\delta R^{**})}}\nonumber \\&\times \Bigg ((1 - n{\alpha _2} + n{\alpha _2}{\psi _0}) - \frac{{{\bar{\bar{\tau }} _{00}}\psi _0^{ - n}}}{{\kappa {\rho _c}}}\Bigg )+ \frac{{{\bar{\bar{\tau }} _{22}} - {\bar{\bar{\tau }} _{11}}}}{{8\pi {\rho _c}(1 + 2\delta R^{**})}} \Bigg ].\nonumber \\ \end{aligned}$$
(69)

5.2 Case 2

5.2.1 Using model \(R + \delta {R^2}\)

By using Eq. (63), we introduce the following auxiliary variables

$$\begin{aligned} \frac{{{m_T}}}{M}= & {} {x^3} + \frac{{{x^3}{{{\tilde{A}}}^2}}}{y}\int \limits _x^1 {\frac{{\sqrt{1 - 2y} }}{{\sqrt{1 - 2v\alpha (n + 1)/x{\tilde{A}}} }}\exp } \frac{1}{{8\pi {f_R}{\tilde{A}}}}\nonumber \\&\times \int \limits _x^1 \frac{{\kappa {x^3}{{{\tilde{A}}}^3}{\alpha _1}{\psi ^n} + \kappa {x^3}{{{\tilde{A}}}^{^3}}{\psi ^{n + 1}}(\alpha - {\alpha _1}) - 4\pi {\bar{\bar{\tau }}_{11}}{x^3}{\tilde{A}}{r^2}_\Sigma + 8\pi v{f_R}}}{{{x^2}(1 - 2v/x{\tilde{A}})}}dx\nonumber \\&\times \Bigg (\frac{{\kappa \Omega }}{x} + \frac{{4\pi \tau _1^*{r^2}_\Sigma }}{{{{{\tilde{A}}}^2}x}} - \frac{{12\pi \tau _2^*}}{{{{{\tilde{A}}}^2}{x^4}r_\Sigma }}\Bigg )dx. \end{aligned}$$
(70)

Using f(R) model

$$\begin{aligned} \frac{{{m_T}}}{M}= & {} {x^3} + \frac{{{x^3}{{{\tilde{A}}}^2}}}{y}\int \limits _x^1 {\Bigg [\frac{{\sqrt{1 - 2y} }}{{\sqrt{1 - 2v\alpha (n + 1)/x{\tilde{A}}} }}\exp } \Bigg (\frac{1}{{8\pi (1 + 16R^{**}\delta ){\tilde{A}}}}\nonumber \\&\times \int \limits _x^1 \frac{{\kappa {x^3}{{{\tilde{A}}}^3}{\alpha _1}{\psi ^n} + \kappa {x^3}{{{\tilde{A}}}^{^3}}{\psi ^{n + 1}}(\alpha - {\alpha _1}) - 4\pi {\bar{\bar{\tau }} _{11}}{x^3}{\tilde{A}}{r^2}_\Sigma + 8\pi v(1 + 2\delta R^{**})}}{{{x^2}(1 - 2v/x{\tilde{A}})}}\Bigg )dx\nonumber \\&\times \Bigg (\frac{{\kappa \Omega }}{x} + \frac{{4\pi \tau _1^*{r^2}_\Sigma }}{{{{{\tilde{A}}}^2}x}} - \frac{{12\pi \tau _2^*}}{{{{{\tilde{A}}}^2}{x^4}r_\Sigma }}\Bigg ) dx\Bigg ]. \end{aligned}$$
(71)

Now \(\Omega \) can be calculated from anisotropic factor as

$$\begin{aligned} \Omega = \frac{{8\pi {f_R}}}{\kappa }\Bigg [\frac{{3v}}{{{\xi ^3}}} - \frac{{{\psi ^n}\kappa }}{{8\pi {f_R}}}\Bigg (1 - \frac{{{\bar{\bar{\tau }} _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}\Bigg ) + \frac{{{\bar{\bar{\tau }} _{22}} - {\bar{\bar{\tau }} _{11}}}}{{8\pi {\rho _c}{f_R}}}\Bigg ]. \end{aligned}$$
(72)

We get

$$\begin{aligned} \Omega= & {} \frac{{8\pi (1 + 2\delta R^{**})}}{\kappa }\Bigg [\frac{{3v}}{{{\xi ^3}}} - \frac{{{\psi ^n}\kappa }}{{8\pi (1 + 2\delta R^{**})}}\nonumber \\&\times \Bigg (1 -\frac{{{\bar{\bar{\tau }} _{00}}{\psi ^{ - n}}}}{{\kappa {\rho _c}}}\Bigg ) + \frac{{{\bar{\bar{\tau }} _{22}} - {\bar{\bar{\tau }} _{11}}}}{{8\pi {\rho _c}(1 + 2\delta R^{**})}}\Bigg ]. \end{aligned}$$
(73)

These results are consistent both cases of generalized polytropes.

6 Conclusion

In this work, we have developed generalized frameworks for conformally flat generalized polytropes with anisotropic fluid in modified f(R) gravity by using spherical symmetric distribution. In order to incorporate higher order curvature invariants, we have worked out the well known Starobinsky model i.e., \(f(R) = R + \delta {R^2}\) where \(\delta \) can be a positive constant. The independent components are obtained from the generalized field equations. Herein, we have presented two cases of generalized polytropes for development of LEe: firstly by using relationship between mass density, pressure and total energy density, secondly using generalized polytropic equation relating energy density and pressure. The generalized TOV equations which describes the hydrostatic equilibrium state of the systems are constructed. The energy conditions have been developed for developed frameworks and dimensionless parameters are introduced for both cases to conveniently proceed with the analysis.

The EoS are playing an important role to describe the two very fundamental aspects of the universe, dark energy and dark matter. Babichev et al. [40] used a form of EoS, called generalized linear EoS with perfect fluid distribution to describe the different scenarios for dark energy. Mukhopadhyay et al. [41] discussed the real nature of dark energy through the parameter of polytropic EoS specially in non- dust situation. The GPEoS is used to discuss the generalized polytropes for the study of astronomical objects. Slattery [42] developed a GPEoS, called a perturbed polytropic EoS, to describe the thermodynamic process of the matter inside the astronomical objects. According to this, the logarithm of pressure has an extra term that perturbs its polytropic behavior, that is, a polynomial expansion in powers of density. The GPEoS and resulting LEe are of significant importance, physical motivation behind selection of GPEoS can be depicted through some of the applications listed below.

  • GPEoS is used in the development of quasi-normal modes for superfluid neutron stars [43].

  • In relativistic superfluid stars GPEoS plays an important role in the discussion of r-modes [44].

  • The use of GPEoS is vital to discuss non-local symmetric classification of planar gas dynamics equations [45].

  • GPEoS helped in the explorations related to identification of the symmetry between early and late time universe. In cosmological point of view, the GPEoS was used in a series of papers to study dark energy and dark matter by Chavanis. He incorporated dark source along with GPEoS to explain the early and late universe [16, 17, 46, 47].

  • It is used in the study of primordial quantum fluctuations and build a universe with constant density at the origin [18].

  • The generalized thermodynamic processes expressed as a random superposition of Gaussian polytropes with the help of GPEoS [48].

  • The GPEoS is used to develop mathematical models to describe different aspects of realistic astrophysical objects like PSR J1614-2230, PSR J1903+327, Vela X-1, Vela 4U, 4U 1820-30, 4U 1608-52 [49, 50].

  • The core-envelope models to study the interior of SAX J1808.4-3658 and 4U1608-52 was developed with the help GPEoS [51].

  • The GPEoS is used to study realistic polytropic models in Finch–Skea spacetime [52].

Fig. 1
figure 1

Graphical representation of \(\Omega \) for case 1

Full size image
Fig. 2
figure 2

Graphical representation of \(\Omega \) for case 2

Full size image

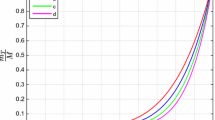
The generalized Weyl tensor is constructed for modified gravity model whose vanishing value is used to apply conformally flat condition in order to make a consistent system of differential equations. The vanishing value of this tensor establishes a specific relation between anisotropic pressure and density. The Tolman mass which is the measure of active gravitational mass is used to discuss the stability of developed frameworks. Our solutions leads to the construction of the models of highly compact spheres that are in the equilibrium mainly due to pressure anisotropy. The factor \(\Omega \) is the measure that determines stability or instability in the gravitating system and it interprets cracks or instabilities occurring in fluid distribution due to perturbations in the system. We have presented graphical representation of \(\Omega \) for three different values of k in both the frameworks as Figs. 1 and 2 by considering a unit test sphere. It is clear from figures that value of omega do not change its sign that shows no cracking for both cases.