Experimental study of the $e^+e^-\rightarrow n{\bar{n}}$ process at the VEPP-2000 $e^+e^-$ collider with the SND detector

Abstract

The process $e^+e^-\rightarrow n{\bar{n}}$ is studied in the experiment at the VEPP-2000 $e^+e^-$ collider with the SND detector. The technique of the time measurements in the multichannel NaI(Tl) electromagnetic calorimeter is used to select $n{\bar{n}}$ events. The value of the measured cross section in the center-of-mass energy range from 1.894 to 2 GeV varies from 0.5 to 0.35 nb. The effective neutron timelike form factor is derived from the measured cross section and compared with the proton form factor. The ratio of the neutron electric and magnetic form factors is obtained from the analysis of the antineutron polar angle distribution and found to be consistent with unity.

1 Introduction

Measurement of the $e^+e^-$ annihilation to nucleon-antinucleon pairs allows to study the nucleon internal structure described by the timelike electromagnetic form factors, electric $G_E$ and magnetic $G_M$. The $n{\bar{n}}$ production cross section is given by the following equation:

$$\begin{aligned} \frac{d\sigma }{d\varOmega }= & {} \frac{\alpha ^{2}\beta }{4s} \bigg [ |G_M(s)|^{2}(1+\cos ^2\theta )\nonumber \\&+\frac{1}{\gamma ^2}|G_E(s)|^{2}\sin ^2\theta \bigg ] \end{aligned}$$

(1)

where $\alpha$ is the fine structure constant, $s=4E_b^2=E^2$, $E_b$ is the beam energy, E is the center-of-mass (c.m.) energy, $\beta = \sqrt{1-4m_n^2/s}$, $m_n$ is the neutron mass, $\gamma = E_b/m_n$, and $\theta$ is the antineutron production polar angle. The $|G_E/G_M|$ ratio can be extracted from the analysis of the measured $\cos \theta$ distribution. At the threshold $|G_{E}| = |G_{M}|$. The total cross section has the following form:

$$\begin{aligned} \sigma (s) = \frac{4\pi \alpha ^{2}\beta }{3s}\left( 1+\frac{1}{2\gamma ^2}\right) |F(s)|^2, \end{aligned}$$

(2)

with

$$\begin{aligned} |F(s)|^2=\frac{2\gamma ^2|G_M(s)|^2+|G_E(s)|^2}{2\gamma ^2 +1 }. \end{aligned}$$

(3)

The function F(s) is the so-called effective form factor, which is equal to unity for pointlike particle. It is this function that is measured in most of $e^+e^-\rightarrow p{\bar{p}}$ and $n{\bar{n}}$ experiments. One can see from Eqs. (1) and (3) that the relative contribution of the $|G_E(s)|^2$ term decreases with energy as $1/E_b^2$.

The $e^+e^-\rightarrow n{\bar{n}}$ cross section near threshold was measured previously in the FENICE [1] and SND [2] experiments. Recently, BESIII results [3] on the study of the $e^+e^-\rightarrow n{\bar{n}}$ process above 2 GeV were published. In this work we present a new measurement of the $e^+e^-\rightarrow n{\bar{n}}$ cross section in the SND experiment.

Fig. 1

SND detector, section along the beams: (1) beam pipe, (2) tracking system, (3) aerogel Cherenkov counters, (4) NaI (Tl) crystals, (5) vacuum phototriodes, (6) iron absorber, (7) proportional tubes,(8) iron absorber, (9) scintillation counters, (10) VEPP-2000 focusing solenoids

2 Collider, detector, experiment

The experiment was carried out at the VEPP-2000 $e^+e^-$ collider [4] with the SND detector [5,6,7,8]. VEPP-2000 operates in the c.m. energy range from 0.3 to 2.0 GeV. The collider has two collision regions, one of which is occupied by the SND detector. The collider luminosity ranges from $10^{29}$ cm$^{-2}$s$^{-1}$ near 0.3 GeV up to $7\times 10^{31}$ cm$^{-2}$s$^{-1}$ at the maximum energy. The beam energy and its spread during data taking is measured by the laser Compton back-scattering system [9]. The accuracy of the energy measurement is 50 keV. The beam energy spread above the $n{\bar{n}}$ threshold is about 0.7 MeV.

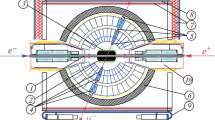
The SND (Spherical Neutral Detector) is a general-purpose non-magnetic detector for a low energy collider (Fig. 1). It consists of a tracking system, an aerogel Cherenkov detector, a three-layer spherical NaI(Tl) electromagnetic calorimeter (EMC) and a muon detector. The latter consists of layers of proportional tubes and scintillation counters with an 1 cm iron sheet between them. The EMC is the main part of SND. It is intended to measure the electromagnetic shower energy and angles, but is also suitable to detect antineutrons. At the kinetic energy of several tens of MeV the antineutron annihilation length in NaI(Tl) does not exceed 20 cm [10], which is significantly less than the EMC thickness (35 cm of NaI(Tl)) [2]. This leads to a high absorption efficiency of produced antineutrons in the SND calorimeter.

The data for this analysis were taken in the energy range from the $n{\bar{n}}$ threshold up to 2 GeV, in 7 energy points in the 2017 run and in 7 points in the 2019 run. The total integrated luminosity of these data is about 30 pb$^{-1}$. The typical collider instant luminosity in the experiment was about $2\times 10^{31}$ cm$^{-2}$s$^{-1}$. To study background, we also analyze data with an integrated luminosity of 20 pb$^{-1}$ collected below the $n{\bar{n}}$ threshold, in the range $E_b=900$–939 MeV.

3 Backgrounds and events selection

The background in this experiment is of three types: physical, beam-induced, and cosmic-ray. The physical background arises from all $e^+e^-$ annihilation processes, in particular, those with $K_L$ meson in the final state. The beam-induced background comes from interactions of off-energy beam particles with elements of the collider magnetic system and the walls of the beam pipe near the $e^+e^-$ interaction region. Beam particles can lose energy through the radiative Bhabha scattering, beam-gas scattering, and internal beam (Touschek) scattering. The total EMC energy deposition in most of beam background events does not exceed the beam energy. The EMC signals from physical and beam-induced background events are synchronized with the beam revolution frequency (12.3 MHz). In contrast, the cosmic-ray background is evenly distributed in time.

The $n{\bar{n}}$ events are very different from events of other $e^+e^-$ annihilation processes. Below 2 GeV the neutron from $n{\bar{n}}$ pair has low energy and therefore gives low energy deposition in the calorimeter. In this analysis, the signal from neutrons is not used. The antineutron annihilates inside the EMC and produces pions, protons, neutrons with the total energy up to $2m_n$. Such an annihilation “star” in the EMC is a main sign of the neutron-antineutron event. In SND, clusters in the calorimeter with energy deposition greater than 20 MeV not associated with charged tracks originated from the interaction region are reconstructed as photons.Typically, a $n{\bar{n}}$ event looks like a multiphoton event. A small part of the events contains off-center tracks in the drift chamber. In this analysis, to estimate antineutron direction we calculate the so-called event momentum $\varvec{P}_{\mathrm{EMC}}=\sum _i E_i \varvec{r}_i$, where $E_i$ is the energy deposition in EMC crystal i, and $\varvec{r}_i$ is its position unit vector. The polar angle of the event momentum ($\theta _a$) is taken as an estimate of the antineutron polar angle. Based on specific properties of signal and background events, the following criteria are chosen to select $n{\bar{n}}$ candidates.

• 1. No charged tracks in the drift chamber are found in an event ($n_{\mathrm{ch}}=0$).

• 2. The reconstructed antineutron polar angle lies in the “large-angle” region of the calorimeter $36^\circ<\theta _a<144^\circ$.

• 3. The absence of a signal in the muon system (coincidence of proportional tubes and scintillation counters) is required. This is the most efficient selection condition against the cosmic-ray background.

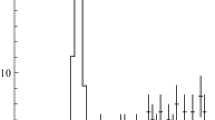
• 4. The total energy deposition in the EMC is required to be within the limits $E_b<E_{\mathrm{EMC}}<2E_b$ GeV. The $E_{\mathrm{EMC}}/(2E_b)$ distribution for data and simulated signal events is shown in Fig. 2. The sharp rise in the spectrum below $E_{\mathrm{EMC}}=E_b$ is due to the beam-induced background.

• 5. The large unbalanced total event momentum is measured in the calorimeter ($P_{\mathrm{EMC}}>0.4E_{\mathrm{EMC}}$). This condition suppresses the $e^+e^-$annihilation background.

• 6. The most energetic photon in an event has the polar angle in the range $27^\circ$–$153^\circ$. This condition suppresses $e^+e^-\rightarrow \gamma \gamma$ background.

• 7. The transverse EMC energy profile of the most energetic photon is required to be not consistent with the electromagnetic shower profile [11]. The distribution of the corresponding logarithmic likelihood function $L_\gamma$ for data and simulated signal events is shown in Fig. 3. The condition $L_\gamma >-2.5$ is used. The steep rise in the distribution at negative values is due to the $e^+e^-$ annihilation background containing real photons.

• 8. The cosmic-ray background is suppressed by the requirement that there be no cosmic-ray track in the calorimeter. The cosmic-ray track is reconstructed as a group of calorimeter crystal hits positioned along a straight line with $R_{\mathrm{min}} >10$ cm, where $R_{\mathrm{min}}$ is a distance between the track and the detector center.

• 9. For suppression of the cosmic-ray shower events, a special parameter has been developed. The moment of inertia tensor is constructed from the coordinates of the EMC crystals weighted by their energy depositions. The tensor is then diagonalized, and the ratio of the smallest to the largest eigenvalues $R_T$ is calculated. We require that $R_T<0.4$ and that the distance between the “center of mass” of the EMC crystals and the detector center be greater than 10 cm.

• 10. The energy deposition in the third layer of the EMC $E_3<0.75E_b$. This parameter is also used to suppress the cosmic-ray background.

Fig. 2

The distribution of the normalized total EMC energy deposition $E_{\mathrm{EMC}}/2E_b$ for 2019 data events with $E_b=945$, 950, 951 MeV (points with error bars) Events are satisfied the standard selection criteria except for the condition on $E_\mathrm{EMC}$. The histogram represents the same distribution for simulated signal events. The vertical lines indicate the boundaries of the condition $E_b<E_{\mathrm{EMC}}<2$ GeV

Fig. 3

The $L_\gamma$ distribution for 2019 data events with $E_b=945$, 950, 951 MeV (points with error bars). Events satisfy the standard selection criteria except for the condition on $L_\gamma$. The histogram represents the same distribution for simulated signal events. The vertical line indicates the boundary of the condition $L_\gamma >-2.5$

As a result of applying the criteria described above, we select about 200 data events per pb$^{-1}$, which corresponds to a signal-to-background ratio of about 0.5.

4 Determining the number of $n{\bar{n}}$ events for the 2019 run

Fig. 4

The $\tau _{\mathrm{EMC}}$ distribution for selected data events collected in 2019 (points with error bars) at $E_b=945$ MeV (left panel) and at $E_b=973$ MeV (right panel). The solid histogram is the result of the fit described in the text. The light-shaded (yellow) histogram shows the fitted cosmic-ray background. The medium-shaded (green) region represents the fitted beam-induced plus physical background

Due to a low antineutron velocity in the energy region under study, its signal in the EMC is delayed with respect to the typical $e^+e^-$ annihilation event, e.g. from the process $e^+e^-\rightarrow \gamma \gamma$. This delay is about 10 ns at $E_b=945$ MeV, and about 4 ns at 973 MeV.¹

In 2019, new calorimeter electronics [13] was installed on the SND detector. For each EMC crystal, the signal from the photodetector shaped with an integration time of about 1 $\upmu$s is digitized by a flash ADC with a sampling rate of 36 MHz (three times the beam revolution frequency). The measured signal shape is fitted by a function previously obtained using $e^+e^- \rightarrow e^+e^-$ events. From the fit, the signal amplitude and arrival time are determined. The event time $\tau _{\mathrm{EMC}}$ is calculated as a weighted average of EMC crystal arrival times with the energy deposition used as a weight. The averaging is done over crystals with energy deposition of more than 25 MeV. The time resolution measured using $e^+e^-\rightarrow \gamma \gamma$ events is about 0.7 ns.

The $\tau _{\mathrm{EMC}}$ distributions for selected data events at $E_B=945$ MeV and 973 MeV are shown in Fig. 4. Time zero corresponds to the average time for $e^+e^-\rightarrow \gamma \gamma$ events. The distribution consists of the nearly uniform cosmic-ray distribution, the distribution for the beam-induced and physical backgrounds, which is peaked near zero, and the wide delayed $n{\bar{n}}$ distribution. The width of the $n{\bar{n}}$ distribution is determined by the spread of the antineutron annihilation points, from the wall of the beam pipe to the rear wall of the calorimeter. The distribution is fitted by a sum of time spectra for these three components:

$$\begin{aligned} F(t)=N_{n{\bar{n}}}H_{n{\bar{n}}}(t)+N_{\mathrm{csm}}H_{\mathrm{csm}}(t)+N_\mathrm{bkg}H_{\mathrm{bkg}}(t), \end{aligned}$$

(4)

where histograms $H_{n{\bar{n}}}$, $H_{\mathrm{csm}}$ and $H_{\mathrm{bkg}}$ are the $\tau _{\mathrm{EMC}}$ distributions (normalized to unity) for signal, cosmic background, and physical + beam-induced background, respectively. $N_{n{\bar{n}}}$, $N_{\mathrm{csm}}$, and $N_{\mathrm{bkg}}$ are the number of events for these components, which are determined from the fit.

Our MC simulation reproduces the $n{\bar{n}}$ time distribution incorrectly. In particular, the time resolution is strongly underestimated in the simulation for both $e^+e^-\rightarrow \gamma \gamma$ and $e^+e^-\rightarrow n{\bar{n}}$ events. From the spread of the arrival times measured in an event in different EMC crystals, we estimate that the time resolution for $n{\bar{n}}$ events is larger than that for $\gamma \gamma$ events by a factor of 2.4. Therefore, we convolve the MC time spectrum with a Gaussian function with a standard deviation of $\sigma _{\mathrm{G}}=1.7 \pm 0.2$ ns. The quoted uncertainty is estimated from the simultaneous fit to the time spectra for $E_b=945$, 950, 951, and 956 MeV with $\sigma _{\mathrm{G}}$ floating.

Table 1 The beam energy ($E_b$), integrated luminosity (L), number of selected $n{\bar{n}}$ events ($N_{n{\bar{n}}}$), the factor taking into account radiative corrections and energy spread ($1+\delta$), detection efficiency ($\varepsilon$), measured $e^+e^-\rightarrow n{\bar{n}}$ cross section $\sigma$, and neutron effective form factor ($F_n$). The quoted errors for N, $\sigma$ are statistical and systematic. For the detection efficiency, the systematic uncertainty is quoted. For $F_n$, the combined statistical and systematic uncertainty is listed. Rows 1–7 (8–14) list data for 2017 (2019)

It is also observed that the right tails of the $\tau _{\mathrm{EMC}}$ distribution in data and simulation are different. This difference is partly explained by incorrect antineutron annihilation cross sections used in MC simulation. We study antineutron annihilation in simulation using a thin absorber of different materials, and compare the extracted cross sections with those measured in Ref. [10]. It is found that the simulation underestimates the annihilation cross section. The difference with experiment is greater for materials with higher atomic number (A). For NaI, the antineutron annihilation length calculated from the results of Ref. [10] is 7.7 (16.7) cm at $E_b=945 (990)$ MeV. In simulation, it is greater by a factor of 1.7 (1.2), respectively. For a lower-A material, such as aerogel, the same scale factor is 1.3 (1.05). Using the information about the position of the antineutron annihilation point and the scale factors defined above we reweight simulated events. It is assumed that antineutron elastic scattering, which effectively reduces the annihilation length, is simulated correctly. With the time distribution obtained using reweighed simulated events the fit is much better, but not satisfactory. To improve the fit quality, we modify the simulated distribution as follows

$$\begin{aligned} H_{n{\bar{n}}}(t)= & {} (1-\kappa )H_1^{\mathrm{MC}}(t)+\kappa H_2(t),\nonumber \\ H_2(t)= & {} H_2^{\mathrm{MC}}(t)w(t)\Big /\int H_2^\mathrm{MC}(t)w(t)dt, \end{aligned}$$

(5)

where $H_1^{\mathrm{MC}}(t)$ and $H_2^{\mathrm{MC}}(t)$ are the simulated distributions for events, in which the antineutron annihilates before and in the calorimeter, respectively, $\kappa$ is the fraction of events with the antineutron annihilation in the calorimeter. The distributions $H_1^{\mathrm{MC}}(t)$ and $H_2^\mathrm{MC}(t)$ are normalized to unity. The weight w(t) is calculated as follows

$$\begin{aligned} w(t)=\exp {(-\alpha _n\beta c t)}, \end{aligned}$$

(6)

where $\beta c$ is the antineutron velocity, and the parameter $\alpha _n$ is floating in the fit.

The shape of the physical + beam-induced background $H_{\mathrm{bkg}}$ is measured at energies below the $n{\bar{n}}$ threshold (about 10 pb$^{-1}$ collected at $E_b=935$ and 936 MeV in 2019 and 2020). The cosmic-ray distribution $H_{\mathrm{csm}}$ is measured with a special cosmic-ray selection: $E_{\mathrm{EMC}}>0.7$ GeV, a cosmic-ray track, and a signal in the muon system.

The fit results is shown in the Fig. 4. It is seen that the function (5) reproduces the shape of the $n{\bar{n}}$ distribution reasonably well.

Fig. 5

The $\tau _{\mathrm{FLT}}$ distribution for selected data events collected in 2017 (points with error bars) at $E_b=942$ MeV (left panel) and at $E_b=1003$ MeV (right panel). The solid histogram is the result of the fit described in the text. The medium-shaded (green) histogram shows the fitted cosmic-ray background. The light-shaded (yellow) region represents the fitted beam-induced plus physical background

The fitted numbers of $n{\bar{n}}$ events for 7 energy points of the 2019 run are listed in Table 1. The quoted errors are statistical and systematic. The sources of the systematic uncertainty are the uncertainty in $\sigma _{\mathrm{G}}$, uncertainty in the time shift between energy points above the $n{\bar{n}}$ threshold and below it, where $H_{\mathrm{bkg}}$ is determined, statistical fluctuations in $H_{\mathrm{bkg}}$, and dependence of $H_{\mathrm{csm}}$ on selection criteria. The time shift measured using $e^+e^-\rightarrow \gamma \gamma$ events varies from $-0.15$ ns to 0.25 ns. We conservatively estimate that the uncertainty in the shifts does not exceed 0.1 ns. The uncertainty due to the statistical fluctuations of $H_{\mathrm{bkg}}$ is estimated using toy MC study. The total systematic uncertainty listed in Table 1 grows with energy due to increasing overlap of signal and background distributions.

In total, about 1250 $n{\bar{n}}$ events are selected in the 2019 data set. The effective cross section for the beam-induced and physical background $\sigma _{\mathrm{bkg}}=N_{\mathrm{bkg}}/L$, where L is the integrated luminosity for a given energy point, is found to be independent of energy within the statistical errors. Its average value over 7 energy points $5.1\pm 1.1$ pb is consistent with the value $3.9\pm 1.0$ pb measured below the $n{\bar{n}}$ threshold. The contribution to $\sigma _{\mathrm{bkg}}$ from the physical background is estimated using MC simulation. It is dominated by the processes $e^+e^-\rightarrow K_SK_L\pi ^0$, $K_SK_L 2\pi ^0$, and $K_SK_L\eta$, and is comparable to the value obtained from the fit to data.

The parameter $\alpha _n$ does not have a clear energy dependence. It varies from 0.02 to 0.07 with a statistical error of about 0.01. Its average nonzero value $\alpha _n=0.037\pm 0.070$ cm$^{-1}$ can be explained by incorrect simulation of antineutron scattering and a noticeable fraction of events rejected by the condition $E_3<0.75E_b$, while a large nonstatistical spread arises presumably from uncertainties and shifts in time calibration.

5 Determining the number of $n{\bar{n}}$ events for the 2017 data set

In analysis of the 2017 data set, we measure the time difference $\tau _{\mathrm{FLT}}$ between the signal of the EMC first level trigger (FLT) [5] and the beam collision time with a rather poor resolution, about 8 ns for $e^+e^-\rightarrow \gamma \gamma$ events. Such a time resolution does not allow to separate $n{\bar{n}}$ events from the physical and beam-induced backgrounds, but is sufficient to measure and subtract the cosmic-ray background.

The data $\tau _{\mathrm{FLT}}$ distributions for two energy points are shown in Fig. 5. Note that the time axis is reversed so that delayed evens are located on the left side of the plot. The distributions are fitted by Eq. (4) with the parameters $N_{n{\bar{n}}}$ and $N_{\mathrm{csm}}$ floating.

Fig. 6

The $\cos \theta _a$ distributions for data $n{\bar{n}}$ events of the the 2019 run (points with error bars) with $E_b=945$, 950, and 951 MeV (left panel), with $E_b=956$, and 963 MeV (middle panel), and with $E_b=973$, and 988 MeV (right panel). The solid histogram is the result of the fit described in the text. The dashed and dotted histograms shows the fitted contributions for the magnetic and electric form factors, respectively

Our Monte Carlo simulation does not include simulation of the time distribution for the FLT signal. The $\tau _{\mathrm{FLT}}$ resolution function can be obtained using data $e^+e^-\rightarrow \gamma \gamma$ events. However, the shape of this function depends on the distribution of the energy deposition in an event over the calorimeter crystals and is different for $n{\bar{n}}$ and $\gamma \gamma$ events. This difference is studied on the 2019 data set, where both methods of time measurement can be used. From analysis of the $\tau _{\mathrm{FLT}}$ and $\tau _{\mathrm{EMC}}$ distributions for $n{\bar{n}}$ and $\gamma \gamma$ events, we extract the time shift $\Delta t=2.4\pm 0.1$ ns and the standard deviation $\sigma _G=3.7\pm 0.5$ ns of the Gaussian function, which is used to smear the $\gamma \gamma$ resolution function.

The signal distribution $H_{n{\bar{n}}}$ is obtained by convolution the time spectrum of antineutron annihilations extracted from simulation with the resolution function. The simulated events are previously reweighed to take into account difference between data and simulation in the $\tau _{\mathrm{EMC}}$ spectrum observed in Sect. 4. In addition to the procedure described in Sect. 4, Eq. (5) with $\alpha _n=0.037\pm 0.070$ cm$^{-1}$ is used for reweighing. The cosmic distribution $H_{\mathrm{csm}}$ is measured as described in Sect. 4.

From the analysis of the 2019 data set (see Sect. 4) we find that $N_{\mathrm{bkg}}\simeq L\sigma _{\mathrm{bkg}}$, and that $\sigma _{\mathrm{bkg}}$ is weakly dependent on energy. The cross section $\sigma _{\mathrm{bkg}}$ and the shape of the background distribution are measured using data with an integrated luminosity of about 10 pb$^{-1}$ collected in 2017 below the $n{\bar{n}}$ threshold ($E_b=930$–938 MeV). The shape $H_{\mathrm{bkg}}$ is described reasonably well by the $\tau _{\mathrm{FLT}}$ distribution for data $e^+e^-\rightarrow \gamma \gamma$ events. The fitted background cross section $\sigma _{\mathrm{bkg}}=12\pm 3$ pb is significantly larger than the value $5.1\pm 1.1$ pb obtained for the 2019 data set. We study predominantly background events with $0.8E_b<E_{\mathrm{EMC}}<0.9E_b$ and find that the beam-induced background in 2017 is 3-4 times greater than in 2019. Therefore, we conclude that the beam-induced background dominates in $\sigma _{\mathrm{bkg}}$ in 2017. The difference in the effective cross section for background events with $0.8E_b<E_{\mathrm{EMC}}<0.9E_b$ between energy points above and below the $n{\bar{n}}$ threshold reaches 40%. This value is taken as an estimate of the systematic uncertainty in $\sigma _{\mathrm{bkg}}$ for the standard selection.

The results of the fit is demonstrated in Fig. 5. The obtained numbers of $n{\bar{n}}$ events for 7 points of the 2017 run are listed in Table 1. The quoted errors are statistical and systematic. The sources of the systematic uncertainty are the uncertainties in the parameters $\sigma _\mathrm{G}$, $\Delta t$, $\alpha _n$, and $\sigma _{\mathrm{bkg}}$. The uncertainty of $\sigma _{\mathrm{bkg}}$ gives dominant contribution.

6 Analysis of the antineutron angular distribution

The 2019 data set is used for analysis of angular distributions. For each energy point, the range $-0.8< \cos \theta _a <0.8$ is divided into 16 intervals. Then, in each $\cos \theta _a$ interval, a fit is performed to the $\tau _{\mathrm{EMC}}$ distribution as described in Sect. 4 (but with $\alpha _n$ fixed at its average value). The obtained seven $\cos \theta _a$ distributions are combined into 3 distributions for the following groups of energy points: (945, 950, 951), (956, 963), (973,988), where the numbers in parenthesis represent the values of $E_b$ in MeV. These distributions are shown in Fig. 6. They are fitted with the function

$$\begin{aligned} F(\cos \theta _a)= A\bigg ( H_M(\cos \theta _a)+\frac{1}{\gamma ^2}\left| \frac{G_E}{G_M} \right| ^2 H_E(\cos \theta _a) \bigg ),\nonumber \\ \end{aligned}$$

(7)

where $H_M$ and $H_E$ are the $\cos \theta _a$ distributions for selected simulated $n{\bar{n}}$ events generated with the angular distributions $1+\cos ^2\theta$ and $\sin ^2\theta$ (see Eq. (1)), respectively, and A is a normalization factor. The shape $H_M$ and $H_E$ distributions differ from the generated initial distributions due to nonuniform detection efficiency (see Fig. 7) and the finite $\theta _a$ resolution, which has $\sigma =8^\circ$.

Fig. 7

The detection efficiency determined using MC simulation as a function of $\cos {\theta _{\mathrm{true}}}$, where $\theta _{\mathrm{true}}$ is the generated antineutron polar angle

Fig. 8

The neutron $|G_E/G_M|$ ratio measured using the 2019 data set. The left edge of the plot corresponds to the $n{\bar{n}}$ threshold, where $|G_E/G_M|=1$

The results of the fit are shown in Fig. 6. The fitted $|G_E/G_M|$ values for three energy groups are shown in Fig. 8 and listed in Table 2. To estimate the systematic uncertainty, we vary the parameters $\alpha _n$ and $\sigma _G$ used in the fit to the $\tau _{\mathrm{EMC}}$ distributions within their uncertainties, introduce the $\tau _{\mathrm{EMC}}$ shift ($\pm 0.1$ ns), and modify the background shape as described in Sect. 4. From MC simulation we find that most of the used selection criteria do not have a significant effect on the shape of the antineutron angular distribution. The exceptions are the conditions $n_{\mathrm{ch}}=0$ and $L_\gamma >-2.5$. We exclude the condition $L_\gamma >-2.5$ (this leads to a tenfold increase in the physical background), determine the $|G_E/G_M|$ ratios, and take the difference between the the values obtained with different selection criteria as an estimate of the systematic uncertainty. To test the effect of the condition $n_{\mathrm{ch}}=0$, we add events containing one or several off-center charged tracks (see Sect. 7), and again study a shift in the $|G_E/G_M|$ value. The systematic uncertainties from all sources are combined in quadrature.

Table 2 The measured $|G_E/G_M|$ values

Our results agree with the assumption that $|G_E/G_M|$=1, but also do not contradict larger values $|G_E/G_M|\approx 1.4$–1.5 observed in the BABAR [16] and BESIII [17] experiments for the ratio of the proton form factors near $E=2$ GeV.

Fig. 9

The energy dependence of the detection efficiency for $e^+e^-\rightarrow n{\bar{n}}$ events determined using MC simulation for the 2017 (circles) and 2019 (triangles) runs. The left edge of the plot corresponds to the $n{\bar{n}}$ threshold

7 Detection efficiency

At first approximation, the detection efficiency $\varepsilon$ is calculated using MC simulation with an angular distribution corresponding to $|G_E/G_M|=1$. The simulation includes the c.m. energy spread, which is about 1 MeV, and emission of an additional photon by initial electron and positron. It also takes into account spurious beam-generated photons and charged tracks. They are simulated by using special background events recorded during data taking with a random trigger. These events are superimposed on the simulated $n{\bar{n}}$ events. The detector response is simulated with the GEANT4 toolkit [12], release 10.5. The energy dependence of the detection efficiency obtained with our standard selection criteria (see Sect. 3) is shown in Fig. 9.

The decrease in the efficiency when approaching to the $n{\bar{n}}$ threshold is due to an increase of the fraction of antineutrons annihilating before calorimeter and producing charged tracks. The decrease of the efficiency with increasing energy is due to an increase of the probability of antineutron passing through the calorimeter without interaction.

The detection efficiency for the 2017 run is about 10% higher than for 2019. The reason is the difference in the calorimeter digitizing electronics used in these runs. This leads, in particular, to a larger numbers of fired crystals with low amplitudes in 2017. Therefore, the $E_{\mathrm{EMC}}$ and $R_T$ (see Sect. 3) distributions for the 2017 and 2019 data sets are different. Of the 10% difference in efficiency, 3% and 6% are due to the conditions on the parameters $E_{\mathrm{EMC}}$ and $R_T$, respectively.

As shown in the previous section, the measured ratio $|G_E/G_M|$ agrees with unity in the energy region under study. To take into account its possible deviation from unity and the associated change in the antineutron angular distribution, we introduce a model uncertainty in the detection efficiency of 6%. This value corresponds the $|G_E/G_M|$ variation from 0.4 to 1.7.

Fig. 10

The $\tau _{\mathrm{EMC}}$ distributions for data events with $E_b=950$, 951, 956 MeV from the 2019 data set selected with inverted conditions on the parameters $5\wedge 6\wedge 7\wedge 8$ (left), 9 (middle), and 10 (right), where the condition numbers from Sect. 3 are used. The solid histogram is the result of the fit described in the text. The light-shaded (yellow) histograms show the fitted cosmic-ray background. The medium-shaded (green) regions at the left and middle plots represent the fitted beam-induced plus physical background

Table 3 The efficiency corrections for different conditions. The condition numbers from Sect. 3 are used

The detection efficiency is corrected for the difference in detector response for $n{\bar{n}}$ events between data and MC simulation. The number of $n{\bar{n}}$ events for the 2019 data set can be determined using significantly looser selection criteria than the standard ones. We invert one of the selection conditions described in Sect. 3 and calculate the efficiency correction for the difference between data and simulation associated with this condition as follows:

$$\begin{aligned} \delta _i=\frac{n_0}{n_0+n_1}\frac{m_0+m_1}{m_0}-1, \end{aligned}$$

(8)

where $n_0$ and $n_1$ ($m_0$ and $m_1$) are the numbers of $n{\bar{n}}$ data (MC) events selected using the standard selection and the selection with the inverted condition i, respectively. The number $n_1$ is determined from the fit to the $\tau _{\mathrm{EMC}}$ spectrum as described in Sect. 4, but with $\alpha _n$ fixed at its average value. The shape of the distribution for the beam-induced and physical backgrounds is found using data recorded below the $n{\bar{n}}$ threshold.

Examples of the $\tau _{\mathrm{EMC}}$ spectra obtained with inverted conditions $5\wedge 6\wedge 7$, 8, and 9 are shown in Fig. 10. Here the condition numbers from Sect. 3 are used. It is interesting to note that the left (right) spectrum in Fig. 10 does not contain the cosmic-ray (beam-induced + physical) background component. The signal distribution in the right spectrum is delayed compared to the middle spectrum because the condition $E_3>0.75E_b$ selects events, in which antineutrons annihilate predominantly in the third calorimeter layer.

The obtained corrections averaged over seven energy points are listed in Table 3. Condition 2 ($36^\circ<\theta _a<144^\circ$) is absent in the table, since the model uncertainty associated with the antineutron angular distribution was considered above.

For selection criterion 4, the condition $0.7E_b<E_{\mathrm{EMC}}<E_b$ is used instead of full inversion. To determine the correction associated with criterion 1 ($n_{\mathrm{ch}}=0$), we select events with one or several off-center charged tracks having $D_{xy}>0.5$ cm, where $D_{xy}$ is the distance between the track and the beam collision axis. The simulation shows that about 20% of $n{\bar{n}}$ events give tracks in the SND drift chamber, most of which are off-center. At $E_b<960$ MeV antiprotons from the $e^+e^-\rightarrow p{\bar{p}}$ process annihilate in the material before the drift chamber (at a radius of about 2 cm from the beam axis) and produce events with topology similar to $n{\bar{n}}$ events. To suppress the $p{\bar{p}}$ and beam-induced backgrounds, we additionally require that the maximum over charged tracks $D_{xy}$ be greater than 2.3 cm. This condition leads to a loss about 30% of $n{\bar{n}}$ events with charged tracks. The remaining small $p{\bar{p}}$ background is subtracted using MC simulation. It should be noted that a significant fraction of $n{\bar{n}}$ events with charged tracks is rejected by the condition $L_\gamma >-2.5$. Therefore, we remove this condition when determine $n_{0,1}$ and $m_{0,1}$ for the correction associated with criterion 1.

We do not observe significant dependences of the corrections on the beam energy and, therefore, list in Table 3 the values averaged over seven energy points of the 2019 data set. The total correction is calculated as

$$\begin{aligned} \delta _{\mathrm{tot}}=\Pi (1+\delta _i)-1. \end{aligned}$$

(9)

Its energy dependence shown in Fig. 11 is well fitted by a constant value of $(-0.050\pm 0.051)$. This value is taken as an efficiency correction for data-MC simulation difference in the selection conditions for the 2019 data set.

Fig. 11

The energy dependence of the efficiency correction associated with the $n{\bar{n}}$ selection conditions. The line indicates a fit to a constant value

Fig. 12

The $E_{\mathrm{EMC}}/2E_b$ distribution for data $n{\bar{n}}$ events (points with error bars) of the 2019 run with $E_b=945$, 950, 951, 956 MeV (left panel), and with $E_b=963$, 973, 988 MeV (right panel). The solid histogram represents the same distribution for simulated $n{\bar{n}}$ events. The standard selection criteria are used, except for the condition on $E_{\mathrm{EMC}}$. The dashed histograms are the simulated distributions after the transformations $E_{\mathrm{EMC}} \rightarrow 0.93 E_{\mathrm{EMC}}$ at the left plot, and $E_{\mathrm{EMC}} \rightarrow E_{\mathrm{EMC}}-100\,\text{ MeV }$ at the right plot

In the efficiency correction study above, the $E_{\mathrm{EMC}}$ threshold was lowered to $0.7E_b$. To estimate systemic uncertainty associated with this threshold, we compare the $E_{\mathrm{EMC}}/2E_b$ spectra for $n{\bar{n}}$ events in data and simulation. The spectra for two energy intervals of the 2019 run are shown in Fig. 12. The data spectra are obtained by fitting the $\tau _{\mathrm{EMC}}$ distributions in each $E_\mathrm{EMC}/2E_b$ bin as described in Sect. 6.

It is seen that the energy deposition in data is smaller than in simulation. To match the data and MC spectra, we transform the simulation distribution either by scaling $c E_{\mathrm{EMC}}$ or by shifting $E_{\mathrm{EMC}}-b$. Then the fraction of events rejected by the condition $E_{\mathrm{EMC}}>0.7E_b$ is recalculated. The result of scaling is shown in Fig. 12 (left) by the dotted histogram, while the result of shifting is presented in Fig. 12 (right). The fraction of events below the threshold $0.7E_b$ is about 3% in the range $E_b=945$–956 MeV and about 5% in the range $E_b=963$–988 MeV. The difference in this fraction after and before the shift transformation is taken as an estimate of the efficiency correction, while the difference between the shift and scale transformations is taken as its systematic uncertainty. The correction is found to be $(-2\pm 1)\%$ below 956 MeV and $(-3\pm 2)\%$ above.

Some of the antineutrons pass through the calorimeter without interaction. Such events are not taken into account by the efficiency corrections described above. In simulation their fraction increases from 0.5% at $E_b=945$ MeV to 6.2% $E_b=973$ MeV, and then to 9.4% at $E_b=1003$ MeV. In Sect. 4 we discuss the difference in the antineutron annihilation length between data and simulation and reweight simulated $n{\bar{n}}$ events to correct for this difference. With the reweighted simulation the fraction of antineutrons passing through the calorimeter without interaction becomes 0.01% at $E_b=945$ MeV, 3.2% at $E_b=973$ MeV, and 5.5% at $E_b=1003$ MeV. The difference between the values obtained with unweighted and weighted simulation with 100% uncertainty is taken as an efficiency correction.

For the 2017 data set, the efficiency corrections for all parameters except $E_{\mathrm{EMC}}$ and $R_T$ are assumed to be the same as for 2019. The $E_{\mathrm{EMC}}$ distributions for data and simulation at $E_{\mathrm{EMC}}>0.9E_b$ are compared between each other and with the same distributions for 2019. For the parameter $R_T$, we loosen the condition on $R_T$ to $R_T>0.25$. For these both parameters we do not observe deviations from the corrections for the 2019 data set within statistical uncertainties. Therefore, the same corrections are used for these both data sets, but for 2017 data a systematic uncertainty of 7% associated with the parameters $E_{\mathrm{EMC}}$ and $R_T$ is added.

The total efficiency correction for the 2019 run is $-(6.5\pm 8.0)\%$ at $E_b=945$ MeV, $-(5.3\pm 8.5)\%$ at $E_b=963$ MeV, and $-(4.6\pm 8.7)\%$ at $E_b=988$ MeV. For the 2017 run, the total correction is $-(6.9\pm 10.6)\%$ at $E_b=942$ MeV, $-(5.1\pm 11.1)\%$ at $E_b=971$ MeV, and $-(4.3\pm 11.4)\%$ at $E_b=1003$ MeV. The values of the corrected detection efficiency and its systematic uncertainty are listed in Table 1.

8 The $e^+e^-\rightarrow n{\bar{n}}$ cross section and neutron effective form factor

The visible cross section directly measured in experiment is related to the Born cross section $\sigma$ as follows

$$\begin{aligned} \sigma _{vis}(E)= & {} \sigma (E)(1+\delta (E))\nonumber \\= & {} \int _{-\infty }^{+\infty }G(E^\prime ,E)dE^\prime \nonumber \\&\times \int _0^{x_{max}}W(s,x)\sigma (s(1-x))dx, \end{aligned}$$

(10)

where $G(E^\prime ,E)$ is a Gaussian function describing the c.m. energy spread, W(s, x) is the radiator function [14] describing emission of photons by initial electrons and positrons, x is a fraction of the beam energy carried out by these photons, and $x_{max}=1-4m_n^2/s$. When calculating the function W(s, x), the contribution of the vacuum polarization is not taken into account, so the Born cross section defined in this way is a ‘dressed” cross section. Here we define the factor $(1+\delta )$, which takes into account the combined effect of radiative corrections and beam energy spread. Equation 10 is used to fit the experimental data on the visible cross section $\sigma _{vis,i}=N_{n{\bar{n}},i}/(L_i\varepsilon _i)$, where i is the index of the energy point in Table 1. The Born cross section in the fit is given by Eq. (2), where the effective form factor is parametrized by the second-order polynomial $|F|=a_0+a_1p_n+a_2p_n^2$ (Model I), where $p_n$ is the neutron momentum, and $a_i$ are free fit parameters. After the fit, the factors $(1+\delta (E_i))$ are calculated using Eq. (10), and the experimental values of the Born cross section are obtained as $\sigma _i=\sigma _{vis,i}/(1+\delta (E_i))$. To estimate uncertainties in $(1+\delta (E_i))$, we vary the parameters $a_i$ within their errors and use the different parametrization for the Born cross section (Model II)

$$\begin{aligned} \sigma (E)= & {} b_1\left[ 1-\exp \left( -\frac{E -2m_n}{b_2}\right) \right] \left[ 1+b_3(E-2m_n)\right] .\nonumber \\ \end{aligned}$$

(11)

in the fit. Such parametrization is used to describe the energy dependence of the $e^+e^-\rightarrow p{\bar{p}}$ cross section near the threshold in Ref. [15]. The difference in $(1+\delta (E_i))$ between Models I and II is taken as an estimate of the model uncertainty. The total uncertainty in $(1+\delta (E_i))$ is 2.2% at $E_b=942$ MeV, 1.6% at $E_b=1003$ MeV, and does not exceed 1% in other energy points.

Fig. 13

The $e^+e^-\rightarrow n{\bar{n}}$ cross section measured using the 2017 (circles) and 2019 (triangles) data sets. The error bars and shaded boxes represent the statistical and systematic uncertainties, respectively. The solid and dashed curves are the fit results for Model I and II, respectively

Fig. 14

The comparison of the $e^+e^-\rightarrow n{\bar{n}}$ cross section measured in this work with the previous FENICE [1], SND [2], and BESIII [3] measurements. The combined statistical and systematic uncertainties are shown for the new SND data

The measured Born cross section is shown in Fig. 13 and listed in Table 1. The systematic uncertainty in the cross section includes uncertainties in the number of $n{\bar{n}}$ events, detection efficiency, factor $(1+\delta )$, and integrated luminosity. The comparison of the cross section measured in this work with the previous measurements is presented in Fig. 14. Our cross section is about 0.4 nb and considerably lower than the previous results of the FENICE [1] and SND [2] experiments. On the other hand, near $E=2$ GeV our result is in good agreement with the BESIII measurement [3].

The previous SND results [2] are based on data collected in 2011 and 2012. Reanalysis of the 2012 data set is performed using the selection criteria and technique described in Sects. 3 and 5, and MC simulation with GEANT4 version 10.5. Based on this reanalysis we conclude that the detection efficiency obtained from simulation and the beam-induced background were underestimated in Ref. [2]. The results on the $e^+e^-\rightarrow n{\bar{n}}$ cross section obtained in this work supersede the measurements of Ref. [2].

Fig. 15

The neutron effective form factor as a function of neutron momentum obtained in this work compared with the BESIII measurements [3], and the proton effective form factor measured by BABAR [16]. The combined statistical and systematic uncertainties are shown for all three data sets. The curves represent results of the fit to the neutron and proton form factor data with a second order polynomial

The effective neutron form factor calculated from the measured cross section using Eq. (2) is listed in Table 1. The form factor as a function of the neutron momentum is shown in Fig. 15 together with the BESIII data [3] and the proton effective form factor measured by the BABAR experiment [16]. The curve in Fig. 15 approximating the SND neutron form factor is the result of the fit with Model I described above. The second curve is the result of the fit to the proton form-factor data with a second-order polynomial. It is seen that Model I can be successfully applied both for neutron and proton data at momentum region below 0.35 GeV. In this region the ratio of the proton and neutron form factors varies from 1.3 to 1.5.

Fig. 16

The deviation of the proton and neutron effective form factor data from the dipole formula [see Eq. (13)]. The curves are the result of the simultaneous fit to the BABAR proton and BESIII neutron data described in the text

In Ref. [18] a sinusoidal modulation was observed in the proton effective form factor measured by BABAR [16, 19] when plotting the data as a function of the proton momentum in the antiproton rest frame. These oscillations are seen in Fig. 16, where the difference between the BABAR form factor data and a function smooth on the GeV/c scale are shown. The latter function [18] is obtained using a 2-parameter fit to the data in the energy range from the threshold up to 6 GeV. The same analysis was performed by the BES collaboration for their neutron form factor data. The form factor energy dependence was described as follows:

$$\begin{aligned} F(s)= & {} F_0(s)+F_{\mathrm{osc}}(s), \end{aligned}$$

(12)

$$\begin{aligned} F_0(s)= & {} \frac{{{\mathcal {A}}}_n}{\left[ 1-s/0.71(\mathrm{GeV}^{2})\right] ^2}, \end{aligned}$$

(13)

$$\begin{aligned} F_{\mathrm{osc}}(s)= & {} A\exp {(-Bp)}\cos {(Cp + D)}, \end{aligned}$$

(14)

$$\begin{aligned} p= & {} \sqrt{(s/2m_n-m_n)^2-m_n^2}. \end{aligned}$$

(15)

At first, the form factor data were fitted by Eq. (13). The difference $F(s)-F_0(s)$ is plotted in Fig. 16. Then BESIII performed the simultaneous fit to the BABAR proton and BESIII neutron data with Eq. (14). The fit parameters A, B, and D were different for the proton and neutron data sets, while C is common. The momentum p for protons was calculated with the substitution $m_n\rightarrow m_p$. The result of this fit is shown in Fig. 16. It is seen that the model with a common proton/neutron oscillation frequency C predicts a specific energy dependence of the neutron form factor in the energy region below 2 GeV. The SND results also plotted in Fig. 16 strongly contradict this prediction. The simultaneous fit to all three data sets cannot be performed with acceptable quality. We fit the SND and BES data to Eqs. (12)–(15). The result is shown in Fig. 17. We obtain a reasonable fit quality $\chi ^2/\nu =31/28$, where $\nu$ is the number of degrees of freedom. The fitted frequency $C_n=3.3\pm 1.7$ GeV$^{-1}$ is significantly lower than that obtained from the fit to the proton data $C_p=5.6\pm 1.9$ GeV$^{-1}$.

Fig. 17

The deviation of the neutron effective form factor data from the dipole formula [see Eq. (13)]. The curve is the result of the fit to the SND and BESIII neutron data described in the text

9 Summary

The experiment to measure $e^+e^-\rightarrow n{\bar{n}}$ cross section has been carried out with the SND detector at the VEPP-2000 $e^+e^-$ collider in the energy region from 1884 to 2007 MeV. The measured $e^+e^-\rightarrow n{\bar{n}}$ cross varies slowly with energy and is about 0.4 nb below 2 GeV. This value is considerably smaller than the previous measurements of the FENICE [1] and SND [2] Collaborations. Near 2 GeV our results agrees with the recent BESIII measurement [3]. The new SND measurement supersedes the result of Ref. [2].

From the measured cross section the neutron effective timelike form factor has been extracted. In the energy region under study the ratio of the proton and neutron effective form factors varies in the range 1.3–1.5. Using the measured antineutron $\cos \theta$ distribution the ratio of the electric and magnetic neutron form factors $|G_E|/|G_M|$ has been obtained. The results agree with the assumption that $|G_E/G_M|=1$, but also do not contradict larger values $|G_E/G_M|\approx 1.4$–1.5 observed in the BABAR [16] and BESIII [17] experiments for the ratio of the proton form factors near $E=2$ GeV.