Backward timelike Compton scattering to decipher the photon content of the nucleon

Abstract

The exclusive photoproduction off nucleon of a large invariant mass lepton pair in the backward region specified by the small Mandelstam variable $-u$ is discussed in the framework of collinear QCD factorization. The amplitude is factorized in terms of photon-to-nucleon Transition Distribution Amplitudes (TDAs). These new non-perturbative objects, complementary to the “photon-inside-the-nucleon PDF”, lead to a tomographic picture of the nucleon’s photon content after Fourier transforming to the impact parameter space. This allows to address the question of where in the transverse plane the nucleon emits a photon. A simplistic model-estimate of photon-to-nucleon TDAs is used to estimate the magnitude of the corresponding cross sections. The background due to the electromagnetic Bethe–Heitler process is shown to be negligible in the kinematical regime of interest.

1 Introduction

Generalized Parton Distributions (GPDs) [1] are since more than 20 years a subject of intense theoretical study and experimental effort. The process which is most profoundly studied among those where GPDs factorize from perturbatively calculable coefficient functions, is Deeply Virtual Compton Scattering (DVCS) $\gamma ^*(q) N(p_N) {\rightarrow } \gamma (q') N(p_N')$, see e.g. reviews [2, 3]. It involves a spacelike virtual photon $\gamma ^*(q)$ with $q^2{<}0$, providing a hard scale of this process with a small absolute value of t-channel invariant momentum transfer $t{=}(p'-p)^2$. The “inverse” process, $\gamma (q) N(p_N) {\rightarrow }\gamma ^*(q') N(p_N')$ with large timelike virtuality $q'^{2}>0$ of the final state photon $\gamma ^*(q')$, i.e. timelike Compton scattering (TCS) [4], shares many common features with DVCS. The hard scale in this case is the final state photon virtuality $q'^{2}$, and one still considers the kinematical region defined by small absolute value of $t=(p_N'-p_N)^2$. The studies of TCS permit to test the universality of GPDs entering both DVCS and TCS, which is one of the main consequences of the QCD collinear factorization theorem. Moreover, the crossing from a spacelike to a timelike probe provides an important test of the understanding of QCD corrections [5, 6] and of the analytic structure of the amplitude [7]. The first experimental study of TCS performed at JLab was recently reported by the CLAS collaboration [8].

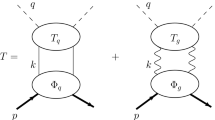
The near-backward TCS (bTCS) is a TCS process occurring in a different kinematical region, which is characterized by a small absolute value of the Mandelstam variable $u\,{=}\,(p_N'-q)^2$ and a large negative value of the variable $t\,{=}\,(p_N'-p_N)^2$. Thus bTCS involves exchanges in the $u-$channel carrying baryonic quantum number and its factorized scattering amplitude contains a new non-perturbative object, the photon-to-nucleon transition distribution amplitude (TDA), see Fig. 1. TDAs extend the concepts of GPDs and baryon DAs, see the review [9]. The ultimate goal of the study of TDAs is to uncover new facets of the understanding of the nucleon wave function. In the present case, photon-to-nucleon TDAs provide a key to decipher the photon content of the nucleon. Particularly, Fourier transforming photon-to-nucleon TDAs to the impact parameter space, we are lead to a tomographic picture of the nucleon’s electromagnetic cloud in the transverse plane, in a similar way as the nucleon to pion TDAs gave access to the meson cloud inside the nucleon.

Fig. 1

Left panel: Collinear factorization mechanism for DVCS ($\gamma ^* N \rightarrow N' \gamma$) in the near-backward kinematical regime (large $-q^2 \equiv Q^2$, $W^2 \equiv (p_N+q)^2$; fixed $x_{B}=\frac{Q^2}{2 p_N \cdot q}$; $|u| \equiv |(p_N-q')^2| \sim 0$). Right panel: Collinear factorization of TCS ($\gamma N \rightarrow \gamma ^* N'$) in the near-backward kinematical regime (large $q'^2 \equiv Q'^2$, $W^2 \equiv (p_N+q)^2$; fixed $\tau$ (2); $|u|\equiv |(q'-p_N)^2| \sim 0$); $\gamma N$ ($N\gamma$) TDA stands for the transition distribution amplitudes from a nucleon-to-a-photon (photon-to-a-nucleon); N DA stands for the nucleon distribution amplitude; CF and $CF'$ denote hard subprocess amplitudes (coefficient functions)

The case of backward DVCS was preliminary discussed in [10, 11]. It involves the much related nucleon-to-photon TDAs which we will discuss together with the photon-to-nucleon TDAs. We specialize here to the TCS process which seems to us much easier to analyze experimentally because of the large contamination of $\pi ^0 N$ final states in a backward DVCS study. After a detailed presentation of kinematics in Sect. 2, we discuss the properties of photon-to-nucleon TDAs in Sect. 3. We calculate the bTCS scattering amplitude and cross-section in Sect. 4. In Sect. 5, we calculate the Bethe–Heitler contribution to the bTCS process and show why we can safely ignore it in an experimental study. In Sect. 6, we give a simplistic estimate of near backward TCS cross-section using an oversimplified model of photon to nucleon TDAs based on vector dominance. In Sect. 7 we estimate the expected rates for a quasi-real photon experiment at an electron beam facility. Section 8 briefly presents our conclusions.

2 Kinematics of near-backward timelike Compton scattering

We consider the timelike Compton scattering

$$\begin{aligned}&\gamma (q)+N(p_N,s) \rightarrow \gamma ^*(q', \lambda _\gamma )+N(p'_N,s') \nonumber \\&\quad \rightarrow \ell ^+(k_{\ell ^+}) \ell ^-(k_{\ell ^-})+N(p'_N,s'). \end{aligned}$$

(1)

Throughout this paper we employ the usual Mandelstam variables for the hard subprocess of the reaction (1):

$$\begin{aligned}&s=(p_N+q)^2 \equiv W^2; \ \ \ t=(p'_N-p_N)^2;\\&\quad u=(q'-p_N)^2 \equiv \Delta ^2. \end{aligned}$$

The $\gamma N$ center-of-mass energy squared $s=(p_N+q)^2 \equiv W^2$ and the virtuality of the final state timelike photon $q'^2=Q'^2$ introduce the natural hard scale. We define the analogue of the Bjorken variable

$$\begin{aligned} \tau \equiv \frac{Q'^2}{2 p_N \cdot q}= \frac{Q'^2}{W^2-m_N^2}. \end{aligned}$$

(2)

In complete analogy with our analysis of the nucleon-antinucleon annihilation process [12, 13], we assume that this reaction admits a factorized description in the near-backward kinematical regime, where $Q'^2$ and $W^2$ are large; $\tau$ is fixed; and the u-channel momentum transfer squared is small compared to $Q'^2$ and $W^2$: $|u| \equiv |\Delta ^2|= |(p'_N-q)^2| \ll W^2, \, Q'^2$. Within such kinematics, the amplitude of the hard subprocess of the reaction (1) is supposed to admit a collinear factorized description in terms of photon-to-nucleon TDAs and nucleon DAs, as shown on the right panel of Fig. 1. Small |u| corresponds to the kinematics where the virtual photon is produced in the near-backward direction, in the $\gamma (q) N(p_N)$ center-of-mass system (CMS). Therefore, in what follows we refer the kinematical regime in question as the near-backward kinematics. This kinematical regime is complementary to the more familiar regime of TCS ($Q'^2$ and $W^2$ - large; $\tau$ -fixed; $|t| \ll Q'^2,\,s$), known as the near-forward kinematics. In this latter kinematical regime the conventional collinear factorization theorem leading to the description of the reaction (1) in terms of GPDs is established [1, 4] and is favored by recent experimental results [8].

We choose the z-axis along the colliding real-photon-nucleon and introduce the light-cone vectors p and n ($p^2=n^2=0$; $2 p \cdot n=1$).

We consider the following Sudakov decomposition for the momenta of the reaction (1) in the near-backward kinematical regime:

$$\begin{aligned}&q=(1+\xi ) p; \nonumber \\&p_{N}= \frac{m_N^2 (1+\xi )}{W^2- m_N^2} p + \frac{W^2-m_N^2}{1+\xi } n; \nonumber \\&\Delta \equiv \left( p'_{N}-q\right) =-2 \xi p+\left( \frac{m_{N}^{2}-\Delta _{T}^{2}}{1-\xi } \right) n+\Delta _{T}; \nonumber \\&q'=p_N-\Delta ; \quad p'_{N}=q+\Delta . \end{aligned}$$

(3)

Here $m_N$ is the nucleon mass and the skewness variable $\xi$ is defined with respect to the longitudinal momentum transfer between the initial state real photon and the final state nucleon

$$\begin{aligned} \xi \equiv -\frac{(p'_N-q) \cdot n}{(p'_N+q) \cdot n}. \end{aligned}$$

(4)

Within the collinear factorization framework we neglect both the squared nucleon mass with respect to $q'^2=Q'^2$ and $W^2$ and set $\Delta _T=0$ within the leading twist coefficient function. This results in the approximate expression for the skewness variable (4):

$$\begin{aligned} \xi \simeq \frac{Q'^2}{2 W^2-Q'^2} \simeq \frac{\tau }{2 -\tau }. \end{aligned}$$

(5)

The approximation (5) can potentially affect the definition of the physical domain of the reaction (1) determined by the requirement $\Delta _T^2 \le 0$, where

$$\begin{aligned} \Delta _T^2= \frac{1-\xi }{1+\xi } \left( u+ \frac{2\xi m_N^2}{1-\xi } \right) . \end{aligned}$$

(6)

It is also instructive to consider the exact kinematics of the reaction (1) in the $\gamma N$ CMS frame. In this frame the relevant momenta read:

$$\begin{aligned}&q= \left( \frac{W^2-m_N^2}{2W} , \, \vec {q}\right) ; \ \ \ \ \ q'= \left( \frac{W^2+Q'^2-m_N^2}{2W}, \, -\vec {p}\,'_N \right) ; \nonumber \\&p_N= \left( \frac{W^2+m_N^2}{2W} , \, -\vec {q} \right) ; \ \ \ \ \ p'_N= \left( \frac{W^2+m_N^2-Q'^2}{2W}, \, \vec {p}\,'_N \right) ,\nonumber \\ \end{aligned}$$

(7)

where

$$\begin{aligned} |\vec {q}|= \frac{W^2-m_N^2}{2W}; \ \ \ |\vec {p}\,'_N|=\frac{\Lambda (W^2,m_N^2,Q'^2)}{2W}, \end{aligned}$$

(8)

with

$$\begin{aligned} \Lambda (x,y,z)= \sqrt{x^2+y^2+z^2-2xy-2xz-2yz} \end{aligned}$$

(9)

being the Mandelstam function.

The CMS scattering angle $\theta _u^*$ is defined as the angle between $\vec {q}$ and $\vec {p}\,'_N$:

$$\begin{aligned} \cos \theta _u^*= \frac{2W^2(u-m_N^2)+(W^2-m_N^2)(W^2+m_N^2-Q'^2)}{(W^2-m_N^2)\Lambda (W^2,m_N^2,Q'^2)}.\nonumber \\ \end{aligned}$$

(10)

The transverse momentum transfer squared (6) is then given by

$$\begin{aligned} \Delta _T^2=- \frac{\Lambda ^2(W^2,Q'^2,m_N^2)}{4W^2}(1-\cos ^2 \theta _u^*), \end{aligned}$$

(11)

and the physical domain for the reaction (1) is defined from the requirement that $\Delta _T^2 \le 0$.

• In particular, the backward kinematics regime $\theta _u^*=0$ corresponds to $\vec {p}\,'_N$ along $\vec {q}$, which means that the virtual photon $\gamma ^*$ is produced along $-\vec {q}$ i.e. in the near-backward direction. In this case u reaches its maximal value

  $$\begin{aligned} u_{0}\equiv & {} \frac{2 \xi m_N^2(\xi +1)}{\xi ^2-1} \\= & {} m_N^2- \frac{(W^2-m_N^2)(W^2+m_N^2-Q'^2)}{2W^2} +2|\vec {q}||\vec {p}\,'_N|. \end{aligned}$$

  At the same time, $t=(p'_N-p_N)^2$ reaches its minimal value $t_{1}$

  $$\begin{aligned} t_{1}=2m_N^2+Q'^2-W^2-u_{0}. \end{aligned}$$

  (12)

  It is for $u \sim u_{0}$ that one may expect to satisfy the requirement $|u| \ll W^2, \, Q'^2$ that is crucial for the validity of the factorized description of (1) in terms of $\gamma \rightarrow N$ TDAs and nucleon DAs.

• The other limiting value $\theta _u^*=\pi$ corresponds to $\vec {p}\,'_N$ along $-\vec {q}$ i.e $\gamma ^*$ is produced in the near-forward direction. In this case u reaches its minimal value

  $$\begin{aligned} u_{1}=m_N^2- \frac{(W^2-m_N^2)(W^2+m_N^2-Q'^2)}{2W^2} -2|\vec {q}||\vec {p}\,'_N|.\nonumber \\ \end{aligned}$$

  (13)

  At the same time t reaches its maximal value $t_{0}$. The factorized description in terms of $\gamma \rightarrow N$ TDAs does not apply in this case as |u| turns out to be of the order of $W^2$. This is the usual domain of application of the GPD factorization.

3 The photon-to-nucleon TDAs

The collinear factorized description of the near-backward TCS involves photon-to-nucleon ($N \gamma$) TDAs defined as the Fourier transform of the $N \gamma$ matrix element of the trilocal light-cone operator¹

$$\begin{aligned}&{\widehat{O}}_{\rho \tau \chi }^{{\bar{u}} {\bar{u}} \bar{d}}(\lambda _1n,\lambda _2n,\lambda _3n)\nonumber \\&\quad =\varepsilon _{c_1 c_2 c_3} \bar{u}^{c_1}_{\rho }(\lambda _1 n) {\bar{u}}^{c_2}_{\tau }(\lambda _2 n)\bar{d}^{c_3}_{\chi }(\lambda _3 n). \end{aligned}$$

(14)

Here $c_{1,2,3}$ stand for the color group indices; and $\rho$, $\tau$, $\chi$ denote the Dirac indices.

For definiteness, we consider the case of the proton target. A study of the neutron case generally follows the same line, but it involves the $\bar{d} \bar{d} \bar{u}$ light-cone operator and leads to different rate expectations.

A crossing relation links photon-to-nucleon TDAs to the already extensively discussed nucleon-to-photon TDAs [10, 11] (see also Sec. 4.1.3 of Ref. [9]), which enter the collinear factorized description of the near-backward DVCS (see left panel of Fig. 1). This crossing relation is similar to that between nucleon-to-pion ($\pi N$) and pion-to-nucleon ($N \pi$) TDAs established in Ref. [14] in the context of the QCD-based description of near-backward production of a $J/\psi$ off nucleons with a pion beam.

To the leading twist-3 accuracy, the parametrization of photon-to-nucleon TDAs involves 16 independent $N \gamma$ TDAs $V_{\Upsilon }^{N \gamma }, \, A_{\Upsilon }^{N \gamma }, \, T_{\Upsilon }^{N \gamma }$:

$$\begin{aligned}&4 {{\mathcal {F}}} \langle N^p(p_N,s_N)| {\widehat{O}}_{\rho \tau \chi }^{{\bar{u}} {\bar{u}} \bar{d}}(\lambda _1n,\lambda _2n,\lambda _3n)|\gamma (q, \lambda _\gamma ) \rangle \nonumber \\&\quad = \delta (x_1+x_2+x_3-2\xi ) \times m_N \nonumber \\&\qquad \times \left[ \sum _{\begin{array}{c} \Upsilon = 1 {{\mathcal {E}}}, 1T, \\ 2 {{\mathcal {E}}}, 2T \end{array}} (v^{N \gamma }_\Upsilon )_{\rho \tau , \, \chi } V_{\Upsilon }^{N \gamma }(x_1,x_2,x_3, \xi , \Delta ^2; \, \mu ^2)\right. \nonumber \\&\quad \left. +\sum _{\begin{array}{c} \Upsilon = 1 {{\mathcal {E}}}, 1T, \\ 2 {{\mathcal {E}}}, 2T \end{array}} (a^{N \gamma }_\Upsilon )_{\rho \tau , \, \chi } A_{\Upsilon }^{N \gamma }(x_1,x_2,x_3, \xi , \Delta ^2; \, \mu ^2)\right. \nonumber \\&\quad \left. + \sum _{\begin{array}{c} \Upsilon = 1 {{\mathcal {E}}}, 1T, 2{{\mathcal {E}}}, 2T, \\ 3 {{\mathcal {E}}}, 3T, 4 {{\mathcal {E}}}, 4T \end{array}} (t^{N \gamma }_\Upsilon )_{\rho \tau , \, \chi } T_{\Upsilon }^{N \gamma }(x_1,x_2,x_3, \xi , \Delta ^2; \, \mu ^2) \right] ,\nonumber \\ \end{aligned}$$

(15)

with the Fourier transform operation $4 {{\mathcal {F}}} \equiv 4(p \cdot n)^{3} \int \left[ \prod _{j=1}^{3} \frac{d \lambda _{j}}{2 \pi }\right] e^{-i \sum _{k=1}^{3} x_{k} \lambda _{k}(p \cdot n)}$. Each of these 16 $N \gamma$ TDAs is a function of the light-cone momentum fractions $x_{1,2,3}$; the skewness variable $\xi$ (4), the u-channel invariant momentum transfer $\Delta ^2$; and the factorization scale $\mu ^2$.

The explicit form of the crossing relation between the $N \gamma$ and $\gamma N$ TDAs reads (see Appendix A of Ref. [14]):

$$\begin{aligned}&\left\{ V_{\Upsilon }^{N \gamma }, \, A_{\Upsilon }^{N \gamma }, \, T_{\Upsilon }^{N \gamma }\right\} \left( x_{1,2,3}, \xi , \Delta ^{2}\right) \nonumber \\&\quad = \left\{ V_{\Upsilon }^{\gamma N }, \, A_{\Upsilon }^{\gamma N }, \, T_{\Upsilon }^{\gamma N }\right\} \left( -x_{1,2,3},-\xi , \Delta ^{2}\right) . \end{aligned}$$

(16)

The set of the leading twist-3 Dirac structures $s_{\rho \tau , \chi }^{ N \gamma }= \{v^{N \gamma }_\Upsilon , \, a^{N \gamma }_\Upsilon , \, t^{N \gamma }_\Upsilon \}_{\rho \tau , \chi }$ occurring in (16) is related to $s_{\rho \tau , \chi }^{ \gamma N }= \{v^{\gamma N }_\Upsilon , \, a^{\gamma N }_\Upsilon , \, t^{\gamma N }_\Upsilon \}_{\rho \tau , \chi }$ entering the parametrization of $\gamma N$ TDAs listed in Appendix B as

$$\begin{aligned} s_{\rho \tau , \chi }^{ N \gamma } = \left( \gamma _{0}^{T}\right) _{\tau \tau ^{\prime }}\left[ s_{\rho ^{\prime } \tau ^{\prime }, \chi ^{\prime }}^{ \gamma N }\right] ^{\dagger }\left( \gamma _{0}\right) _{\rho ^{\prime } \rho }\left( \gamma _{0}\right) _{\chi ^{\prime } \chi }. \end{aligned}$$

(17)

The counting of the independent leading twist $N \gamma$ TDAs matches the number of independent helicity amplitudes $T_{h_{{\bar{u}}} h_{{\bar{u}}},h_{{\bar{d}}}}^{ h_\gamma , h_N }$ for $\gamma \, u u d \rightarrow N^p$ process, where $h_{{\bar{q}}}$, $h_\gamma$ and $h_N$ refer to the light-cone helicity of, respectively, quark, initial state photon and the final state nucleon.

In the strictly backward limit $\Delta _T=0$ only 4 $N \gamma$ TDAs $V_{1 {{\mathcal {E}}}}^{N \gamma }$, $A_{1 {{\mathcal {E}}}}^{N \gamma }$, $T_{1 {{\mathcal {E}}}}^{N \gamma }$, $T_{2 {{\mathcal {E}}}}^{N \gamma }$ are relevant. This is consistent with the number of helicity conserving processes (with obvious helicity notations: $\uparrow : h=+1 ; \downarrow : h=-1$):

$$\begin{aligned}&\gamma (\uparrow ) u(\uparrow )u(\downarrow )d(\downarrow ) \rightarrow N(\uparrow ); \nonumber \\&\gamma (\uparrow ) u(\downarrow )u(\uparrow )d(\downarrow ) \rightarrow N(\uparrow ); \nonumber \\&\gamma (\uparrow ) u(\downarrow )u(\downarrow )d(\uparrow ) \rightarrow N(\uparrow ); \nonumber \\&\gamma (\downarrow ) u(\uparrow )u(\uparrow )d(\uparrow ) \rightarrow N(\uparrow ); \end{aligned}$$

(18)

since $\Delta _T=0$ implies helicity conservation.

In this paper we mainly concentrate on the very small $\Delta _T$ region where the contribution of remaining 12 $N \gamma$ TDAs is small. The relations between the four TDAs relevant for $\Delta _T=0$ and light-front helicity amplitudes read:

$$\begin{aligned} V_{1 {{\mathcal {E}}}}^{N \gamma }&= \frac{1}{2^{1 / 4} \sqrt{1+\xi }\left( P^{+}\right) ^{3 / 2}} \frac{1}{m_N}\left[ T_{\uparrow \downarrow ,\uparrow }^{\uparrow \uparrow }+T_{\downarrow \uparrow ,\uparrow } ^{\uparrow \uparrow }\right] ; \nonumber \\ A_{1 {{\mathcal {E}}}}^{ N \gamma }&=- \frac{1}{2^{1 / 4} \sqrt{1+\xi }\left( P^{+}\right) ^{3 / 2}} \frac{1}{m_N}\left[ T_{\uparrow \downarrow ,\uparrow }^{\uparrow \uparrow }-T_{\downarrow \uparrow ,\uparrow }^{\uparrow \uparrow }\right] ;\nonumber \\ T_{1 {{\mathcal {E}}}}^{N \gamma }&=-\frac{1}{2^{1 / 4} \sqrt{1+\xi }\left( P^{+}\right) ^{3 / 2}} \frac{1}{m_{N}}\left[ T_{\downarrow \downarrow ,\uparrow }^{\uparrow \uparrow }+T_{\uparrow \uparrow ,\uparrow }^{\downarrow \uparrow }\right] ;\nonumber \\ T_{2 {{\mathcal {E}}}}^{ N \gamma }&=-\frac{1}{2^{1 / 4} \sqrt{1+\xi }\left( P^{+}\right) ^{3 / 2}} \frac{1}{m_{N}}\left[ T_{\downarrow \downarrow ,\uparrow }^{\uparrow \uparrow }-T_{\uparrow \uparrow ,\uparrow }^{\downarrow \uparrow }\right] , \end{aligned}$$

(19)

where $P\equiv \frac{q+p'_N}{2}$ is the mean momentum. Similar relations exist for the other TDAs, which do not contribute much to the cross-sections for $\Delta _T \simeq 0$ (see the discussion in Sect. 6 around Fig. 8).

Fig. 2

Impact parameter space interpretation for the $v_3$-integrated uud proton-to-photon TDA in the DGLAP-like I, DGLAP-like II and in the ERBL-like domains. Solid arrows show the direction of the positive longitudinal momentum flow

As for the nucleon-to-meson TDAs case [15], the physical contents of nucleon-to-photon TDAs can be addressed within an impact parameter picture. For that issue it is convenient to switch to the set of so-called quark–diquark coordinates, e.g. $w_3 \equiv x_3-\xi$; $v_3 \equiv \frac{x_1-x_2}{2}$ and consider the Fourier transform to the impact parameter $\Delta _T \rightarrow b_T$ of $v_3$-integrated nucleon-to-photon TDAs. This leads to a quark–diquark interpretation in the impact parameter space (see Fig. 2) that is largely analogous to the impact parameter interpretation of GPDs.

• In the DGLAP-like I region $w_3 \le -\xi$ the impact parameter specifies the location where a uu-diquark is pulled out of a proton and then replaced by an antiquark $\bar{d}$ to annihilate into the final state photon.

• In the DGLAP-like II region $w_3 \ge \xi$ the impact parameter specifies the location where a quark d is pulled out of a proton and then replaced by an antidiquark $\bar{u}\bar{u}$ which forms into the final state photon.

• In the ERBL-like region $-\xi \le w_3 \le \xi$ the impact parameter specifies the location where a three-quark cluster composed of a uu-diquark and a d-quark is pulled out of the initial nucleon in a way that the remnants form the final state photon.

By considering a different choice of quark–diquark coordinates one can obtain complementary impact parameter interpretation for $v_1 \equiv \frac{x_2-x_3}{2}$-integrated and $v_2 \equiv \frac{x_3-x_1}{2}$-integrated nucleon-to-photon TDAs with different pairs of quarks chosen to form a diquark inside nucleon. Therefore, the study of the impact parameter representation of v-integrated nucleon-to-photon TDAs allows to address the question: Where in the transverse plane does the nucleon emit a photon? This provides new information on photon contents of the nucleon complementary to that contained in “photon-inside-the-nucleon PDF” [16, 17].

4 The scattering amplitude and the backward TCS cross-section

Let us now calculate the scattering amplitude of the process

$$\begin{aligned}&\gamma (q, \lambda _\gamma ) + N(p_N,s_N) \rightarrow \gamma ^*(q', \lambda '_\gamma )+ N'(p'_N,s'_N) \nonumber \\&\rightarrow N'(p'_N,s'_N)+\ell ^+(k_{\ell ^+},s_{\ell ^+}) +\ell ^-(k_{\ell ^-},s_{\ell ^-}), \end{aligned}$$

(20)

which contains the TDAs just defined in Sect. 3.

The helicity amplitudes ${{\mathcal {M}}}^{\lambda _\gamma \lambda '_\gamma }_{s_N s'_N}$ of the hard subprocess reaction

$$\begin{aligned} \gamma (q, \lambda _\gamma ) + N(p_N,s_N) \rightarrow \gamma ^*(q', \lambda '_\gamma )+ N'(p'_N,s'_N) \end{aligned}$$

(21)

involve 4 independent tensor structures

$$\begin{aligned} {{\mathcal {M}}}_{s_N s'_N}^{\lambda _\gamma \lambda '_\gamma }= {{\mathcal {C}}} \frac{1}{Q'^4} \sum _{k=1,3,4,5} {{\mathcal {S}}}_{s_N s'_N}^{(k) \, \lambda _\gamma \lambda _V} {{\mathcal {J}}}_{\mathrm{\, bTCS}}^{(k)} (\xi , \, \Delta ^2). \end{aligned}$$

(22)

Here ${{\mathcal {J}}}_{\mathrm{\, bTCS}}^{(k)}$, $k=1,3,4,5$ stand for the integral convolutions of $N\gamma$ TDAs and nucleon DAs with hard scattering kernels. The normalization constant

$$\begin{aligned} {{\mathcal {C}}}= -i\left( \frac{\left( 4 \pi \alpha _{s}\right) ^{2} \sqrt{4 \pi \alpha _{\mathrm {em}}} f_{N} m_N}{54}\right) , \end{aligned}$$

(23)

where $\alpha _{\mathrm {em}} \simeq \frac{1}{137}$ ($\alpha _s \simeq 0.3$) is the electromagnetic (strong) coupling; and $f_N$ is the nucleon light-cone wave function normalization constant. We will use $f_N=5.0 \cdot 10^{-3} \; \mathrm{GeV}^2$ [18].

There is one tensor structure independent of $\Delta _T$:

$$\begin{aligned}&{{\mathcal {S}}}_{s_N s'_N}^{(1) \, \lambda _\gamma \lambda '_\gamma }= \bar{U}(p'_N,s'_N) \hat{{\mathcal {E}}}^*(q',\lambda '_\gamma ) \hat{\mathcal{E}}(q, \lambda _\gamma ) U(p_N,s_N),\nonumber \\ \end{aligned}$$

(24)

and three $\Delta _T$-dependent tensor structures:

$$\begin{aligned}&{{\mathcal {S}}}_{s_N s'_N}^{(3) \, \lambda _\gamma \lambda '_\gamma }= \frac{1}{m_N} ({{\mathcal {E}}}(q, \lambda _\gamma ) \cdot \Delta _T) \, \bar{U}(p'_N,s'_N)\nonumber \\&\qquad \qquad \qquad \qquad \qquad \hat{{{\mathcal {E}}}}^*(q',\lambda '_\gamma ) U(p_N,s_N); \nonumber \\&{{\mathcal {S}}}_{s_N s'_N}^{(4) \, \lambda _\gamma \lambda '_\gamma }=\frac{1}{m_N^2} ({{\mathcal {E}}}(q, \lambda _\gamma ) \cdot \Delta _T) \, \bar{U}(p'_N,s'_N)\nonumber \\&\qquad \qquad \qquad \qquad \qquad \hat{{{\mathcal {E}}}}^*(q',\lambda ') {\hat{\Delta }}_T U(p_N,s_N); \nonumber \\&{{\mathcal {S}}}_{s_N s'_N}^{(5)\,\lambda _\gamma \lambda '_\gamma }= \bar{U}(p'_N,s'_N) \hat{{{\mathcal {E}}}}^*(q',\lambda '_\gamma )\nonumber \\&\qquad \qquad \qquad \qquad \hat{\mathcal{E}}^*(q, \lambda _\gamma ) {\hat{\Delta }}_T U(p_N,s_N)\,. \end{aligned}$$

(25)

To the leading order in $\alpha _s$, the hard amplitude is calculated from the 21 Feynman diagrams analogous to those familiar from the calculation of nucleon electromagnetic form factor (see e.g. Ref. [19]) dominated by $\gamma ^*_T$. To the leading twist accuracy, the integral convolutions of $N\gamma$ TDAs and nucleon DAs ${{\mathcal {J}}}^{(k)}_{\mathrm{\, bTCS}}$, $k=1,\,3,\,4,\,5$ with hard scattering kernels $T_{\alpha }^{(k)}$ read

$$\begin{aligned}&\mathcal {J}_{\mathrm{\, bTCS}}^{(k)} (\xi ,\Delta ^2) = {\int ^{1+\xi }_{-1+\xi } }\! \! \!d_3x \; \delta \left( \sum _{j=1}^3 x_j-2\xi \right) \nonumber \\&\quad \times {\int ^{1}_{0} } \! \! \! d_3y \; \delta \left( \sum _{l=1}^3 y_l-1 \right) \; {\Bigg (2\sum _{\alpha =1}^{7} T_{\alpha }^{(k)} + \sum \limits _{\alpha =8}^{14} T_{\alpha }^{(k)} \Bigg )}, \end{aligned}$$

(26)

where the index $\alpha$ refers to the number of the diagram. The explicit expressions for $T_{\alpha }^{(k)}$ are listed in Table 1 of Appendix A.

Therefore, to the leading twist accuracy the averaged-squared amplitude (33) integrated over the lepton azimuthal angle $\varphi _\ell$ reads

$$\begin{aligned}&\int d \varphi _\ell \overline{|{{\mathcal {M}}}_{N \gamma \rightarrow N \ell ^+ \ell ^-}|^2} \Big |_{\text {Leading twist-3}}\nonumber \\&\quad = |\overline{\mathcal{M}_T}|^2 \frac{2 \pi e^2 (1+ \cos ^2 \theta _\ell )}{Q'^2}, \end{aligned}$$

(27)

where

$$\begin{aligned} |\overline{{{\mathcal {M}}}_T}|^2= & {} \frac{1}{4} \sum _{s_N s'_N {\lambda \lambda '}} {{\mathcal {M}}}^{\lambda \lambda '}_{s_N s'_N} \left( \mathcal{M}^{\lambda \lambda '}_{s_N s'_N} \right) ^* \nonumber \\= & {} \frac{1}{4} |{{\mathcal {C}}}|^2 \frac{1}{Q'^6} \frac{2(1+\xi }{\xi } \left[ 2|{{\mathcal {J}}}^{(1)}_\mathrm{\, bTCS}|^2\right. \nonumber \\&+ \frac{\Delta _T^2}{m_N^2} \left\{ -|\mathcal{J}^{(3)}_{\mathrm{\, bTCS}}|^2+ \frac{\Delta _T^2}{m_N^2} |\mathcal{J}^{(4)}_{\mathrm{\, bTCS}}|^2\right. \nonumber \\&+ \left( {{\mathcal {J}}}^{(4)}_{\mathrm{\, bTCS}} \mathcal{J}^{(1)*}_{\mathrm{\, bTCS}}+{{\mathcal {J}}}^{(4)*}_{\mathrm{\, bTCS}} \mathcal{J}^{(1)}_{\mathrm{\, bTCS}}\right) \nonumber \\&\left. -2 |\mathcal{J}^{(5)}_{\mathrm{\, bTCS}}|^2 - \left( {{\mathcal {J}}}^{(5)}_{\mathrm{\, bTCS}} {{\mathcal {J}}}^{(3)*}_{\mathrm{\, bTCS}}+{{\mathcal {J}}}^{(5)*}_{\mathrm{\, bTCS}} \mathcal{J}^{(3)}_{\mathrm{\, bTCS}}\right) \right\} \nonumber \\&\left. + {{\mathcal {O}}}(1/Q'^2) \right] ; \end{aligned}$$

(28)

and the $(1 + \cos ^2 \theta _\ell )$ dependence comes from the dominance of transversely polarized virtual photon.

The $2 \rightarrow 3$ particle scattering differential cross section of (20) reads (see e.g. [20]):

$$\begin{aligned} d \sigma= & {} \frac{(2 \pi )^4}{2 \Lambda (s,m_N^2,0)} \overline{|\mathcal{M}_{N \gamma \rightarrow N' \ell ^+ \ell ^-}|^2} \nonumber \\&\times \delta ^{(4)}(p_N+p_V-p'_N-k_{\ell ^+}-k_{\ell ^-}) \frac{d^3 p'_N}{(2 \pi )^3 2 E_{N'}} \nonumber \\&\times \frac{d^3 k_{\ell ^+}}{(2 \pi )^3 2 E_{\ell ^+}} \frac{d^3 k_{\ell ^-}}{(2 \pi )^3 2 E_{\ell ^-}}, \end{aligned}$$

(29)

where $\Lambda$ is the Mandelstam function (9).

The 3-particle Lorentz-invariant phase space (LIPS) is decomposed in the usual manner into two 2-particle LIPSs of $\gamma ^* N'$ and $\ell ^+ \ell ^-$ systems. We then get (neglecting lepton masses):

$$\begin{aligned} d \sigma= & {} \frac{1}{2 (2 \pi )^5 \Lambda (s,m_N^2,0)} \overline{|\mathcal{M}_{N \gamma \rightarrow N' \ell ^+ \ell ^-}|^2} \nonumber \\&\times \frac{d \Omega _{N'}^*}{8 s} \Lambda (s,m_N^2,Q'^2) \frac{d \Omega _\ell }{8} dQ'^2, \end{aligned}$$

(30)

where $d \Omega _{N'} \equiv d \cos \theta _{u}^* d \varphi ^*$ is the produced nucleon solid angle in the $\gamma N$ CMS (see Fig. 3); and $d \Omega _{\ell }$ is the solid angle of the produced lepton in the $\ell ^+ \ell ^-$ CMS. We express $\cos \theta _{u}^*$ through $u=(q-p'_N)^2$:

$$\begin{aligned} du= \frac{d \cos \theta _{u}^*}{2 s} (s-m_N^2) \Lambda (s,m_N^2,Q'^2). \end{aligned}$$

(31)

Then, finally,

$$\begin{aligned} \frac{d \sigma }{du d Q'^2 d \cos \theta _{\ell }}= \frac{\int d \varphi _\ell \overline{|{{\mathcal {M}}}_{N \gamma \rightarrow N' \ell ^+ \ell ^-}|^2} }{64 (s-m_N^2)^2 (2 \pi )^4}, \end{aligned}$$

(32)

where the average-squared amplitude $\overline{|{{\mathcal {M}}}_{N \gamma \rightarrow N' \ell ^+ \ell ^-}|^2}$ is expressed as

$$\begin{aligned}&\overline{|{{\mathcal {M}}}_{N \gamma \rightarrow N' \ell ^+ \ell ^-}|^2}= \frac{1}{4} \sum _{s_N s'_N {\lambda _\gamma \lambda '_\gamma }} \frac{1}{Q'^4} e^2 {{\mathcal {M}}}^{\lambda _\gamma \lambda '_\gamma }_{s_N s'_N} \mathrm{Tr}\nonumber \\&\quad \times \left\{ {\hat{k}}_{\ell ^-} {{\mathcal {E}}}(q', \lambda '_\gamma ) {\hat{k}}_{\ell ^+} {{\mathcal {E}}}^*(q', \lambda '_\gamma ) \right\} \left( {{\mathcal {M}}}^{\lambda _\gamma \lambda '_\gamma }_{s_N s'_N} \right) ^*, \end{aligned}$$

(33)

where ${{\mathcal {E}}}^*(q', \lambda '_\gamma )$ stands for the polarization vector of the outgoing virtual photon; and the factor $\frac{1}{4}$ corresponds to averaging over the polarizations of the initial nucleon and the two transverse polarizations of the initial photon.

Fig. 3

The kinematical variables and coordinate axes in the $\gamma p$ CMS. The CMS scattering angle $\theta _u^*$ (10) is defined as the angle between $\vec {q}$ and $\vec {p}\,'_N$. The boost along the $z'$ direction allows to switch to $\ell ^+ \ell ^-$-CMS frame. The azimuthal angle $\varphi ^*$ is defined as the angle between the hadronic and leptonic planes. The lepton polar angle $\theta _\ell$ is defined between $\vec {k}_{\ell ^+}$ and $\vec {p}\,'_N$ in the $\ell ^+ \ell ^-$-CMS frame. The lepton azimuthal angle $\varphi _\ell$ can be chosen to coincide with $\varphi ^*$ since a boost along $z'$ does not change the momentum components transverse with respect to $z'$

5 The Bethe–Heitler contribution

As in the forward case, the process (1) receives a contribution from the purely electromagnetic reaction, the Bethe–Heitler process (BH) where the initial photon couples directly to one of the produced leptons; see Fig. 4.

Fig. 4

The Bethe Heitler process for exclusive photoproduction of a lepton pair on a nucleon. The red disk represents the electromagnetic nucleon form factors $F_{1,2}(t)$; $-t$ is small in the near-forward kinematics but large in the near-backward kinematics studied here

The cross-section $\frac{d \sigma _{B H}}{d Q^{\prime 2} d t d\cos \theta _\ell d \varphi _\ell }$ for this subprocess is described in full details in Eq. (17) of [4]. A careful examination of this formula demonstrates how much the forward and backward cases are different. While the intrinsic order of magnitude of the BH cross section is very small, it may be enhanced in two kinematical regions where some inverse propagators become tiny. These regions are:

• the near-forward region where one photon propagator proportional to $\frac{1}{t}$ enhances the cross section when it increases up to $\frac{1}{t_{0}}$;

• one particular region of the phase space in the intermediate region where the product of the lepton inverse propagators

  $$\begin{aligned} L = \frac{(Q'^2-t)^2}{4}- \left( (k_{\ell ^+}-k_{\ell ^-})\cdot (p_N-p'_N)\right) ^2 \end{aligned}$$

  becomes small.

Fig. 5

The $-u$ dependence of the Bethe–Heitler differential cross-section at $\theta _\ell = \pi /32$ (left panel) and $\theta _\ell = \pi /8$ (right panel) for various values of $\varphi _\ell$, at $Q'^2 = 3$ $\hbox {GeV}^2$ and $s=23$ $\hbox {GeV}^2$

Fig. 6

The $-u$ dependence of the Bethe–Heitler differential cross-section at $\varphi _\ell =0$ and different values of $\theta _\ell$ (from left to the right: $\theta _\ell =0,\,\frac{\pi }{16},\,\frac{\pi }{8},\,\frac{\pi }{4}$), at $Q'^2 = 3$ $\hbox {GeV}^2$ and $s=23$ $\hbox {GeV}^2$

This is illustrated in Fig. 5 and in Fig. 6 where we plot the Bethe–Heitler differential cross section $\frac{d \sigma _{B H}}{d Q^{\prime 2} d t d\cos \theta _\ell d \varphi _\ell }$ as a function of $-u$. We employ the dipole representation for the nucleon form factors $F_{1,2}(t)$ and present the cross section for various values of the polar and azimuthal angles of the lepton pair $\theta _\ell$ and $\varphi _\ell$ angles. Apart from the peaks, the order of magnitude of the cross section is indeed tiny in the near-backward region. Analyzing the near-backward TCS cross section outside of the dangerous regions does not look like a difficult challenge.

In conclusion, easy to implement cuts on the final leptons kinematics will allow us to study the backward TCS reaction without taking into account of the BH contribution, neither of its interference with the QCD amplitude. The necessary cut-off concerns very small lepton emission angles when one stays far from the fixed angle region where $-u$ and $-t$ are of the same order. This reinforces our confidence that the pQCD-based reaction mechanism of Fig. 1 for bTCS considerably dominates over the BH contribution in the near-backward kinematics.

6 A simplistic estimate of near backward TCS cross-section

Theoretical estimates of the near-backward TCS cross section based on the QCD collinear factorization reaction mechanism require phenomenologically complete models for the photon-to-proton TDAs. These models do not exist yet and we definitely need experimental data to guide model builders. Since any experimental proposal needs an order of magnitude estimate of counting rates, hence of differential cross sections, we propose now an oversimplified model for photon to nucleon TDAs based on the quite usual vector dominance hypothesis often applied to photoproduction reactions. Needless to say, the physics of the TDAs is much richer than such a model, as shown in the previous sections, for instance in its ability to perform a tomography of the electromagnetic content of the nucleon. This VMD model should thus be taken as a strawman which we expect will trigger dedicated experiments which will help to extract in a second step realistic TDAs.

6.1 A VMD model for photon to nucleon TDAs

In this section we present a phenomenological model for $\gamma N$ TDAs based on the Vector Meson Dominance (VMD) assumption and the phenomenologically successful cross channel nucleon exchange model for nucleon-to-vector meson TDAs. Relying on the crossing relation (16) between $\gamma N$ and $N \gamma$ TDAs we then will be able to provide the theoretical estimates for the near-backward TCS cross section that can be further employed for feasibility studies at the kinematical conditions of existing and future experimental facilities.

Fig. 7

VMD-based cross channel nucleon exchange model for $N\gamma$ (left panel) and $\gamma N$ (right panel) TDAs; dashed circles contain a typical LO graph for the nucleon electromagnetic form factor in perturbative QCD; the rectangle contains the cross channel nucleon contribution into $N\gamma$ TDAs. The crossed circle depicts the $\gamma \rightarrow V_T$ vertex

Let us consider within the factorization framework involving nucleon-to-vector meson TDAs [21] the transverse amplitude of the hard production of transversely polarized vector meson off nucleon²

$$\begin{aligned} \gamma ^*(q,\lambda _\gamma )+N^p(p_N,s_N) \rightarrow V_T(p_V, \lambda _V)+N^{p'}(p'_N,s').\nonumber \\ \end{aligned}$$

(34)

Here $V_T$ is a transversely polarized vector meson ($\rho ^0$, $\omega$ or $\phi$). The VMD assumption [22, 23] allows then to connect the near-backward DVCS amplitude ${{\mathcal {M}}}(\gamma ^*N^p \rightarrow N^{p'} \gamma )$ to those of hard near-backward production of transversely polarized vector meson reactions (34):

$$\begin{aligned}&{{\mathcal {M}}}(\gamma ^*N^p \rightarrow N^{p'} \gamma ) \nonumber \\&\quad = \frac{e}{f_{\rho }} {{\mathcal {M}}}(\gamma ^*N^p \rightarrow N^{p'} \rho ^0_T) +\frac{e}{f_{\omega }} {{\mathcal {M}}}(\gamma ^*N^p \rightarrow N^{p'} \omega _T)\nonumber \\&\qquad +\frac{e}{f_{\phi }} {{\mathcal {M}}}(\gamma ^*N^p \rightarrow N^{p'} \phi _T), \end{aligned}$$

(35)

where the vector meson-to-photon couplings $f_{\rho ,\omega ,\phi }$ can be estimated from $\Gamma _{V \rightarrow e^+e^-}$ decay widths according to [24]: $\Gamma _{V \rightarrow e^+e^-}= \frac{1}{3} \alpha _{\mathrm{em}}^2 m_V \frac{4 \pi }{f_V}$.

We define the helicity amplitudes of the reaction (34) ${{\mathcal {M}}}^{\lambda _\gamma \lambda _V}_{s_N s'_N}$. Since the longitudinal $\gamma _L^*$ leads to a higher twist contribution we consider the square of the dominant transverse amplitude $\gamma ^*_T N^p \rightarrow V_T^0 N^{p'}$:

$$\begin{aligned} |\overline{{{\mathcal {M}}}_T}|^2= & {} \frac{1}{2} \sum _{s_N s'_N { \lambda _{\gamma _T} \lambda _{V_T}}} {{\mathcal {M}}}^{\lambda _\gamma \lambda _V }_{s_N s'_N} \left( {{\mathcal {M}}}^{\lambda _\gamma \lambda _V }_{s_N s'_N} \right) ^* \nonumber \\= & {} \frac{1}{2} |{{\mathcal {C}}}|^2 \frac{1}{Q^6} \frac{2(1+\xi )}{\xi } \Big [ 2|{{\mathcal {I}}}^{(1)}|^2+ \frac{\Delta _T^2}{m_N^2} \Big \{ -|{{\mathcal {I}}}^{(3)}|^2\nonumber \\&+ \frac{\Delta _T^2}{m_N^2} |{{\mathcal {I}}}^{(4)}|^2+ \left( {{\mathcal {I}}}^{(4)} {{\mathcal {I}}}^{(1)*}+{{\mathcal {I}}}^{(4)*} {{\mathcal {I}}}^{(1)}\right) \nonumber \\&-2 |{{\mathcal {I}}}^{(5)}|^2 - \left( \mathcal{I}^{(5)} \mathcal{I}^{(3)*}+\mathcal{I}^{(5)*} \mathcal{I}^{(3)}\right) \Big \} + \mathcal{O}(1/Q^2) \Big ].\nonumber \\ \end{aligned}$$

(36)

Here ${{\mathcal {C}}}$ is defined in (23) and ${{\mathcal {I}}}^{(k)}$, $k=1,3,4,5$ stand for the integral convolutions of VN TDAs and nucleon DAs with hard scattering kernels (see eq. (6.27) and Table 3 of Ref. [9]).

The summation in (36) stands over the dominant transverse polarizations of the virtual photon and over the transverse polarizations of the final state vector meson. The Eq. (36) is to be compared with eq. (7.21) of Ref. [9], that gives the transverse amplitude squared summed over both transverse and longitudinal polarizations of the final state vector meson. Note that 16 out of 24 leading-twist-3 VN TDAs contribute to the $\gamma ^*_T N \rightarrow V_T N'$ amplitude. This is consistent with the helicity counting for $\gamma N$ TDAs.

We assume the validity of the collinear leading twist factorized description for the-near backward $\gamma ^*_T N \rightarrow V_T N'$ and $\gamma ^*_T N \rightarrow \gamma N'$ in terms of VN (resp. $\gamma N$) TDAs and nucleon DAs. This results in the following VMD-based model for $\gamma N$ TDAs (see Fig. 7):

$$\begin{aligned}&\{V, \, A\}_{\Upsilon }^{\gamma N}=\frac{e}{f_{\rho }} \{V, \, A\}_{\Upsilon }^{\rho N}+\frac{e}{f_{\omega }} \{V, \, A\}_{\Upsilon }^{\omega N}+\frac{e}{f_{\phi }} \{V, \, A\}_{\Upsilon }^{\phi N}, \nonumber \\&\quad \text {with} \ \ \Upsilon = 1{{\mathcal {E}}}, \, 1T, \, 2{{\mathcal {E}}}, \, 2T; \nonumber \\&T_{\Upsilon }^{\gamma N}=\frac{e}{f_{\rho }} T_{\Upsilon }^{\rho N}+\frac{e}{f_{\omega }} T_{\Upsilon }^{\omega N}+\frac{e}{f_{\phi }} T_{\Upsilon }^{\phi _{T} N}, \nonumber \\&\quad \text {with} \ \ \Upsilon = 1{{\mathcal {E}}}, \, 1T, \, 2{{\mathcal {E}}}, \, 2T, \, 3{{\mathcal {E}}}, \, 3T, 4{{\mathcal {E}}}; \, 4T; \end{aligned}$$

(37)

6.2 Backward DVCS and TCS amplitudes in the cross-channel nucleon exchange approximation

For our phenomenological applications we employ the cross-channel nucleon exchange model for nucleon-to-vector meson TDAs described in Sec. 5.1.3 of Ref. [9]. This model has recently seen a success in the description of the near-backward $\omega$-meson electroproduction [25, 26]. The VMD-assumption (37) combined with the cross channel nucleon exchange model for VN TDAs results in great simplifications for the calculation of convolution of resulting $\gamma N$ TDAs and nucleon DAs with hard scattering kernels.

The integral convolutions $\mathcal {I}^{(k)}_{\mathrm{\, bDVCS}}$, $k=1,\,3,\,4,\,5$, within our model turn out to be linear combinations of $\mathcal {I}^{(k)}$s, $k=1,\,3,\,4,\,5$, corresponding to different vector mesons:

$$\begin{aligned}&\mathcal {I}^{(1)}_{\mathrm{\, bDVCS}}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad = \sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} {{\mathcal {I}}}_0 \frac{K_{1 {{\mathcal {E}}}}^{VN}(\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }; \nonumber \\&\mathcal {I}^{(3)}_{\mathrm{\, bDVCS}}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad = \sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} \mathcal{I}_0 \nonumber \\&\qquad \frac{K_{1 T}^{VN}(\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})+K_{2 {{\mathcal {E}}}}^{VN}(\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }; \nonumber \\&\mathcal {I}^{(4)}_{\mathrm{\, bDVCS}}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad = \sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} \mathcal{I}_0 \frac{K_{2 T}^{VN}(\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }; \nonumber \\&\mathcal {I}^{(5)}_{\mathrm{\, bDVCS}}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad = -\sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} \mathcal{I}_0 \frac{K_{2 {{\mathcal {E}}}}^{VN}(\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }\,. \end{aligned}$$

(38)

Here $G^V_{VNN}$ and $G^T_{VNN}$ stand for the vector and tensor couplings of vector mesons to nucleons (see e.g. Ref. [27] for the explicit form of the VNN effective vertices). The explicit expressions for the functions $K_{1 {{\mathcal {E}}}}^{VN}$, $K_{2 {{\mathcal {E}}}}^{VN}$, $K_{1 T}^{VN}$, $K_{2 T}^{VN}$, read [9]

$$\begin{aligned}&K_{1 {\mathcal {E}}}^{VN}( \xi , \Delta ^2)\nonumber \\&\quad = \frac{f_N}{\Delta ^2-m_N^2} \left( G^V_{VNN} \frac{2\xi (1-\xi )}{1+\xi } + G^T_{VNN}\, \xi \left( \frac{2 \xi }{1+\xi }-\frac{ \Delta ^2}{m_N^2} \right) \right) ; \nonumber \\&K_{2 {\mathcal {E}}}^{VN}( \xi , \Delta ^2)\nonumber \\&\quad =\frac{f_N}{\Delta ^2-m_N^2} \left( G^V_{VNN}(-2 \xi ) + G^T_{VNN}\xi \right) ; \nonumber \\&K_{1 T}( \xi , \Delta ^2)\nonumber \\&\quad = \frac{f_N}{\Delta ^2-m_N^2} \left( -G^V_{VNN} \frac{2 \xi (1+3 \xi )}{1-\xi } \right) ; \nonumber \\&K_{2 T}( \xi , \Delta ^2)\nonumber \\&\quad = \frac{f_N}{\Delta ^2-m_N^2} \left( G^T_{VNN} \frac{\xi (1+\xi )}{1-\xi } \right) . \end{aligned}$$

(39)

The constant ${{\mathcal {I}}}_0$ is the same constant occurring in the leading order perturbative QCD description of proton electromagnetic form factor $F_1^p(Q^2)$ [18]:

$$\begin{aligned} Q^4 F_1^p(Q^2)= \frac{(4 \pi \alpha _s)^2 f_N^2}{54}{{\mathcal {I}}}_0. \end{aligned}$$

(40)

The value of ${{\mathcal {I}}}_0$ depends on the input phenomenological solutions for nucleon DAs.³ In the $\Delta _T \rightarrow 0$ limit only the contributions of 3 TDAs $V_{1 {{{\mathcal {E}}} }}^{\gamma N}$, $A_{1 {{{\mathcal {E}}} }}^{\gamma N}$, and $T_{1 {{{\mathcal {E}}} }}^{\gamma N}+T_{2 {{{\mathcal {E}}} }}^{\gamma N}$ into the integral convolution $\mathcal {I}^{(1)}_{\mathrm{\, bDVCS}}$ turn out to be relevant.⁴

Our next step is to trace the effect of crossing from bDVCS to bTCS. It turns out that the denominators $D_\alpha$ of hard kernels read as

$$\begin{aligned} D_\alpha (x_i,\xi )=\frac{1}{2\xi } {\tilde{D}}_\alpha \left( \frac{x_i}{2 \xi } \right) ; \end{aligned}$$

(41)

and TDAs within cross channel nucleon exchange model are also functions of $\frac{x_i}{2 \xi }$ ratios times some coefficients depending on $\xi$. E.g. for the $1 {{\mathcal {E}}}$ set:

$$\begin{aligned}&\Big \{ V_{1 {{\mathcal {E}}}}^{VN}, \, A_{1 {{\mathcal {E}}}}^{VN}, \, T_{1 {{\mathcal {E}}}}^{VN}, T_{2 {{\mathcal {E}}}}^{VN} \Big \} (x_1, x_2, x_3, \xi , \Delta ^2) \Big |_{N(940)} \nonumber \\&\quad = \Theta _\mathrm{ERBL}(x_1,x_2,x_3) \frac{1}{(2 \xi )^2} K_{1 {{\mathcal {E}}}}^{VN}( \xi , \Delta ^2) \nonumber \\&\qquad \times \Big \{ V^p, \, A^p, \, -T^p,\,-T^p \Big \} \nonumber \\&\qquad \times \left( \frac{x_1}{2 \xi }, \frac{x_2}{2 \xi }, \frac{x_3}{2 \xi } \right) , \end{aligned}$$

(42)

where $\Theta _{\mathrm{ERBL}}(x_1,x_2,x_3)\equiv \prod _{k=1}^3 \theta (0 \le x_k \le 2 \xi )$ ensures that the integration with hard kernels is restricted to the ERBL-like support region. Therefore, up to an irrelevant phase factor, the effect of the crossing (16) allowing us to express the integral convolutions $\mathcal {J}^{(k)}_{\mathrm{\, bTCS}}(\xi , \Delta ^2) \Big |_{N(940)}$ of Eq. (28) through $\mathcal {I}^{(k)}_{\mathrm{\, bDVCS}}(\xi , \Delta ^2) \Big |_{N(940)}$ of Eq. (36) within our VMD-based model is reduced to a mere change of the sign of $\xi$ in the arguments of $K_{\Upsilon }^{VN}$ factors in Eq. (38):

$$\begin{aligned}&\mathcal {J}^{(1)}_{\mathrm{\, bTCS}}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad \doteq \sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} {{\mathcal {I}}}_0 \frac{K_{1 {{\mathcal {E}}}}^{VN}(-\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }; \nonumber \\&\mathcal {J}^{(3)}_\mathrm{\, bTCS}(\xi , \Delta ^2) \Big |_{N(940)} \nonumber \\&\quad \doteq \sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} {{\mathcal {I}}}_0 \nonumber \\&\qquad \frac{K_{1 T}^{VN}(-\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})+K_{2 {{\mathcal {E}}}}^{VN}(-\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }; \nonumber \\&\mathcal {J}^{(4)}_\mathrm{\, bTCS}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad \doteq \sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} {{\mathcal {I}}}_0 \frac{K_{2 T}^{VN}(-\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }; \nonumber \\&\mathcal {J}^{(5)}_\mathrm{\, bTCS}(\xi , \Delta ^2) \Big |_{N(940)}\nonumber \\&\quad \doteq -\sum _{V=\rho , \omega , \phi } \frac{e}{f_{V}} {{\mathcal {I}}}_0 \frac{K_{2 {{\mathcal {E}}}}^{VN}(-\xi , \Delta ^2, G^V_{VNN},G^T_{VNN})}{\xi }\,. \end{aligned}$$

(43)

Note, that the change of sign of the imaginary part of integral convolutions makes no effect since in our cross-channel nucleon exchange model with solely ERBL-like support, the imaginary part of the amplitude is zero.

Fig. 8

The near-backward $\gamma p \rightarrow p e^+ e^-$ scattering cross section (32) for several values of $W^2$; $Q'^2=3$ $\hbox {GeV}^2$; and lepton polar angle $\theta _\ell =\frac{\pi }{4}$ as a function of $-u$ from the minimal value $-u_0$ up to 1 $\hbox {GeV}^2$. COZ solution is employed as input phenomenological solution for nucleon DAs. Solid lines show the contribution of 4 $N \gamma$ TDAs $V_{1 {{\mathcal {E}}}}^{N \gamma }, \, A_{1 {{\mathcal {E}}}}^{N \gamma }, \, T_{1,2 {{\mathcal {E}}}}^{N \gamma }$ relevant in the strictly backward $\Delta _T=0$ limit. Dashed lines account also for the contributions of $V_{2 {{\mathcal {E}}}, 2T}^{N \gamma }, \, A_{2 {{\mathcal {E}}} 2T}^{N \gamma }, \, T_{3 {{\mathcal {E}}}, 4 {{\mathcal {E}}}, 2T,3T}^{N \gamma }$ vanishing for $\Delta _T=0$

6.3 Backward TCS cross section estimate

In Fig. 8 we show the estimates of the near-backward $\gamma p \rightarrow p e^+ e^-$ scattering cross section (32) within the reaction mechanism involving $N \gamma$ TDAs relying on the VMD assumption employing COZ input nucleon DAs. We take into account only the contribution of $\omega (782)$. Note that, as clearly can be seen from Eq. (40), the cross section of $\gamma p \rightarrow p e^+ e^-$ within our model turns to be proportional to the square of the perturbative QCD nucleon electromagnetic form factor squared since

$$\begin{aligned} \overline{|{{\mathcal {M}}}_{N \gamma \rightarrow N' \ell ^+ \ell ^-}|^2} \sim Q'^2 \left( F_1(Q'^2)\right) ^2. \end{aligned}$$

(44)

The kinematic factors occurring from Eqs. (39) bring additional dependence on $Q'^2$ and $W^2$ through the skewness variable $\xi$ (5).

Our model must be read as a very rough but plausible order of magnitude estimate⁵ since the cross channel nucleon exchange model for $\omega N$ TDAs saw some success in the description of hard exclusive backward $\omega$-production data [25]. We employ⁶ the set of $G^{V,T}_{\omega NN}$ couplings Bonn 2000 [31]. The cross section is plotted for several values of $W^2$; $Q'^2=3$ $\hbox {GeV}^2$; and lepton polar angle $\theta _\ell =\frac{\pi }{4}$ as a function of $-u$ from the minimal value $-u_0$ up to 1 $\hbox {GeV}^2$. Solid lines show the contribution of 4 $N \gamma$ TDAs $V_{1 \mathcal{E}}^{N \gamma }, \, A_{1 {{\mathcal {E}}}}^{N \gamma }, \, T_{1{{\mathcal {E}}},2 {{\mathcal {E}}}}^{N \gamma }$ relevant in the strictly backward $\Delta _T=0$ limit. Dashed lines account also for the contributions of $V_{2 {{\mathcal {E}}}, 2T}^{N \gamma }, \, A_{2 {{\mathcal {E}}}, 2T}^{N \gamma }, \, T_{3 {{\mathcal {E}}}, 4 {{\mathcal {E}}}, 2T,3T}^{N \gamma }$ vanishing for $\Delta _T=0$. The first two plots of Fig. 8 correspond to JLab@12 GeV and JLab@24 GeV kinematical conditions while subsequent plots correspond to the future EIC and EicC kinematic range.

It worth emphasizing that the signature of the onset of the partonic picture of backward TCS is thus not to be searched for in the $Q'^2$ dependence of the amplitude, which is the same as in a nucleon exchange hadronic model, provided one explains the $Q^2$ behavior of the nucleon form factor in this model. The real signature of the TDA framework is the fact that this $Q'^2$ behavior appears at fixed value of $\xi$.

The polarization signature (namely that the lepton pair comes from a transversely polarized virtual photon at leading twist) is also an important signal of this onset. Although we present our estimates at a definite value of $\theta _l$, it is easy to integrate them in a definite $\theta _l$ bin since we know, see Eq. (27), the $1+\cos ^2 \theta _l$ shape of this angular dependence.

Let us stress that the TDA picture is on no account limited to a simple cross channel nucleon exchange TDA model we employed here. Further studies with a more realistic model for $\gamma N$ and $N \gamma$ TDAs can bring more than our present very crude cross section estimates. In particular, advanced TDA models with complete domain of definition can provide predictions for polarization observables sensitive to TDAs outside the ERBL-like region. For example, a sizable $Q'^2$-independent transverse target single spin asymmetry (see Sec. 7.2.1 of [9]) for bTCS can be seen as a strong evidence in favor of validity of the factorization mechanism. Moreover, the sign of this asymmetry is predicted to be different for bTCS and bDVCS, which provides a useful additional cross check.

7 Cross sections with an electron beam

Quasi-real photoproduction generates a large fraction of the data recorded at an electron facility, such as JLab, or a future electron-ion collider [32, 33]. The cross-section is then calculated with the help of the Weizsäcker–Williams distribution [34, 35] as:

$$\begin{aligned} \sigma _{eN} = \int _{x_{\min }}^1 dx \sigma _{\mathrm{TCS}}(x) f(x), \end{aligned}$$

(45)

where x is the fraction of energy lost by the incoming electron in the target rest frame: $x= \frac{s_{\gamma N} - m_N^2}{s_{e N} - m_N^2}$ and f(x), the photon distribution in the electron, reads

$$\begin{aligned}&f(x)=\frac{\alpha _{\mathrm{em}}}{2 \pi }\nonumber \\&\left\{ 2 m_e^2 x \left( \frac{1}{Q^2_{\mathrm{max}}} -\frac{1-x}{m_e^2 x^2} \right) + \frac{\left( (1-x)^2+1\right) \ln \frac{Q^2_{\mathrm{max}}(1-x)}{m_e^2 x^2}}{x} \right\} .\nonumber \\ \end{aligned}$$

(46)

Here $m_e$ is the electron mass and $Q^2_{\mathrm{max}}$ is the typical maximal value of the virtuality of the exchanged photon, which depends on the detection system (e.g. 0.15 $\hbox {GeV}^{2}$ as in the CLAS12 experiment at JLab [8], which we use for our numerical estimates).

In Fig. 9 we present the $\frac{d\sigma _{eN}}{du dQ'^2 d \cos \theta _\ell }$ cross section integrated over the $\theta _\ell \in \left[ \frac{\pi }{8}; \, \frac{7\pi }{8}\right]$ bin:

$$\begin{aligned}&\frac{d\sigma _{eN}}{d {Q'}^2 du } \Big |_{\theta _\ell \, \mathrm{bin}} \equiv \int _{\theta _\ell \, \mathrm{bin}} d \theta _\ell \sin \theta _\ell \frac{d\sigma _{eN}}{du dQ'^2 d \cos \theta _\ell } \nonumber \\&\quad = \int _{x_{\min }}^1 dx \int _{\theta _\ell \, \mathrm{bin}} d \theta _\ell \sin \theta _\ell \frac{d \sigma _{\mathrm{TCS}}(x)}{d {Q'}^2du d \cos \theta _\ell } f(x). \end{aligned}$$

(47)

The cut in $\theta _\ell$ is intended to stay away from the narrow BH peak around $\theta _\ell =0$ (see Sect. 5) and the symmetric peak around $\theta _\ell =\pi$. We define $x_{\min }= \frac{s_{\gamma N \min } - m_N^2}{s_{e N} - m_N^2}$ and set $s_{\gamma N \min } =8$ $\hbox {GeV}^2$.

This plot clearly shows the feasibility of the experiment in an accelerator of high luminosity (say above 10 $\hbox {fb}^{-1}$ $\hbox {year}^{-1}$) and a good lepton detector system for identifying the final lepton pair against a meson pair. Let us stress that our oversimplified model for $N\gamma$ TDAs is rather conservative: one may well expect more source of electromagnetic radiation inside a nucleon when a hard probe has extracted its baryonic core than in a quite nucleon. Moreover the VMD picture of photon-nucleon interaction has not been tested in any comparable experimental setting as the backward TCS one.

Fig. 9

The electron–nucleon cross section (47) integrated over $\theta _\ell$ as a function of ${Q'}^2$ for $u=u_0$ (exactly backward TCS) at electron beam energies $E_e$ corresponding (from down to up) to kinematical conditions of JLab@12, JLab@24 and of EIC and EicC. We employ the VMD-based model for $\gamma N$ TDAs and account for the contribution of $\omega (782)$ meson. We use the set of $G^{V,T}_{\omega NN}$ couplings Bonn 2000 [31] and COZ solution for nucleon DAs as phenomenological input

8 Conclusions and outlook

In this paper, we analyzed within the collinear QCD factorization framework a never previously discussed promising reaction, namely (quasi-)real photoproduction of a lepton pair in the backward region. This reaction may be analyzed in terms of photon to nucleon TDAs the characteristic features of which we have described. Although no complete model of these non-perturbative quantities exists at the moment, we have argued that a simple-minded estimate of the cross-sections indicate that the experimental rates should be sufficient for a dedicated study at JLab to be fruitful.

Our study opens the way to a dedicated experimental program involving several steps:

• establishing the kinematical region where our description in terms of TDA factorization is relevant. This study must be centered on the two main signatures of our process: Firstly $\gamma ^*_T$ dominance and the resulting ($1+\cos ^2 \theta$) angular distribution of the final leptons. Secondly, the $1/Q^2$ scaling law of the amplitude at fixed value of $\xi$;

• measuring the magnitude of the reaction in various kinematics and compare it with model estimates as the one in Fig. 9. We must here remind the reader that our estimates are not to be taken as predictions but merely orders of magnitude;

• relying on Eq. (19), measurements with polarized beam and target would help to estimate the relative importance of various TDAs.

Although we discussed for simplicity the case of electron-positron pair production, it is clear that our results apply also to $\mu ^+ \mu ^-$ pair production (with minor corrections related to the final lepton mass effect), which may be easier to experimentally identify if the detector is instrumented with a muon detection system in the central region.

Ultra-peripheral collisions (UPCs) at high energy hadron colliders are also a fertile source of photoproduction reactions [36, 37]. It has already been noted [38, 39] that the intense quasi-real photon radiation generated by moving protons (and the even more intense one generated by nuclei) may trigger a new domain of experimental exploration of GPDs in the small skewness region through the study of near forward lepton pair production. Likewise, the near-backward TCS process that we study here may provide us with a new way to access photon-to-nucleon TDAs. All UPC processes (pp, AA or pA) are potentially good candidates for triggering backward TCS but a more detailed study is needed before a definite conclusion can be written.

Experiments on a nuclear target will enlarge the study proposed here through a search for color transparency effects [40] which may help to decide where the onset of the dominance of short distance physics hence the validity of collinear QCD factorization takes place.

In conclusion, the study of the inner content of the nucleon already benefits much from the high luminosity experiments at medium energy electron facilities through the promising first results on the extraction of GPDs and transverse momentum dependent (TMDs) distributions. More is still to come and the TDA portal – both for nucleon-to-meson and nucleon-to-photon cases [25, 26, 41,42,43] – opens completely new opportunities to access new hadronic matrix elements of quite fundamental quark trilocal operators on the light cone.

Appendices

Appendix A: Near-backward TCS amplitude

In this Appendix we present the explicit results for the near-backward TCS amplitude. The expressions for the coefficients $T_{\alpha }^{(k)}$, $k{=}1,3,4,5$ occurring in Eq. (26) result from the calculation of the familiar 21 diagrams and take the form of products of singular hard kernels $D_\alpha \equiv D_\alpha ^{(k)}(x_1,x_2,x_3,\xi ; \, y_1, y_2,y_3)$, originating from the partonic propagators, times the combinations $N_\alpha ^{(k)} \equiv N_\alpha ^{(k)}(x_1,x_2,x_3,\xi , \Delta ^2; \, y_1, y_2,y_3)$ of $N \gamma$ TDAs and nucleon DAs arising in the numerators:

$$\begin{aligned} T_{\alpha }^{(k)}\equiv D_\alpha \times N_\alpha ^{(k)}. \end{aligned}$$

(A1)

Note that no summation over the repeating index $\alpha$ is assumed in (A1).

Up to an irrelevant phase factor, the expressions for $D_\alpha$ and $N_\alpha ^{(k)}$, $k=1,3,4,5$ can be obtained from those listed⁷ in Table 3 of Ref. [9] with obvious replacement of nucleon-to-vector-meson (VN) TDAs with appropriate photon-to-nucleon ($N \gamma$) TDAs and changing the sign of i0 regularization prescription in the denominators of corresponding hard scattering kernels. This change mirrors the fact that we consider $\gamma ^*$ in the final state rather than in the initial state, as it is for backward vector meson electroproduction. We list the corresponding results below in Table 1.

Table 1 14 of the 21 diagrams contributing to the hard-scattering amplitude with their associated coefficient $T_\alpha ^{(k)} \equiv D_\alpha \times N_\alpha ^{(k)}$ (no summation over $\alpha$ assumed). The seven first ones with u-quark lines inverted are not drawn. The crosses represent the virtual-photon vertex. $Q_u$ and $Q_d$ stand for the quark charges

Appendix B: The set of Dirac structures for $\gamma N$ TDAs

The set of QED gauge invariant Dirac structures $s_{\rho \tau , \chi }^{ \gamma N}$ occurring in the definition of nucleon-to-photon TDAs are listed below in Eqs. (B1)–(B3). We adopt Dirac’s “hat” notation ${\hat{l}} \equiv l_\mu \gamma ^\mu$; $\sigma ^{\mu \nu }= \frac{1}{2} [\gamma ^\mu , \gamma ^\nu ]$; $\sigma _{p \mu } \equiv p^\lambda \sigma _{\lambda \mu }$; $\sigma _{p {\Delta }_T} \equiv p^\lambda \Delta _T^\mu \sigma _{\lambda \mu }$; C is the charge conjugation matrix; and $U^+$ stands for the large component of the nucleon spinor $U^+(p_N,s_N)= {\hat{p}} {\hat{n}} U(p_N,s_N).$

$$\begin{aligned} (v_{1 {{{\mathcal {E}}} }}^{\gamma N})_{\rho \tau , \, \chi }= & {} ({\hat{p}} C)_{\rho \tau } \left[ \left( \gamma _5 \hat{{\mathcal {E}}}^* U^{+}\right) _{\chi }-\frac{m_N}{1+\xi } ({{\mathcal {E}}}^* \cdot n)\left( \gamma _5 U^{+}\right) _{\chi }\right. \nonumber \\&\left. -\frac{2({{\mathcal {E}}}^* \cdot n)}{1-\xi }\left( \gamma _5 {\hat{\Delta }}_{T} U^{+}\right) _{\chi }\right] ; \nonumber \\ (v_{1 T}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N} \left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi } ({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times ({\hat{p}} C)_{\rho \tau }\left( \gamma _5 U^{+}\right) _{\chi }; \nonumber \\ (v_{2 {{\mathcal {E}}}}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N}({\hat{p}} C)_{\rho \tau } \left[ \left( \gamma _5 \sigma ^{\Delta _{T} {{\mathcal {E}}}^*} U^{+}\right) _{\chi }\nonumber \right. \\&\left. -\frac{m_N ({{\mathcal {E}}}^* \cdot n)}{2(1+\xi )}\left( \gamma _5 {\hat{\Delta }}_{T} U^{+}\right) _{\chi }\right] ; \nonumber \\ (v_{2 T}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N^2} \left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi } ({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times ({\hat{p}} C)_{\rho \tau }\left( \gamma _5 {\hat{\Delta }}_T U^{+}\right) _{\chi }; \nonumber \\ \end{aligned}$$

(B1)

$$\begin{aligned} (a_{1 {{{\mathcal {E}}} }}^{\gamma N})_{\rho \tau , \, \chi }= & {} \left( {\hat{p}} \gamma ^{5} C\right) _{\rho \tau }\left[ \left( \hat{\mathcal{E}}^* U^{+}\right) _{\chi }-\frac{m_N}{1+\xi }({{\mathcal {E}}}^* \cdot n)\left( U^{+}\right) _{\chi }\right. \nonumber \\&\left. -\frac{2({{\mathcal {E}}}^* \cdot n)}{1-\xi }\left( {\hat{\Delta }}_{T} U^{+}\right) _{\chi }\right] ; \nonumber \\&(a_{1 T}^{\gamma N})_{\rho \tau , \, \chi }= \frac{1}{m_N} \left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi } ({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times ({\hat{p}} \gamma ^5 C)_{\rho \tau }\left( U^{+}\right) _{\chi }; \nonumber \\ (a_{2 {{\mathcal {E}}}}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N}({\hat{p}} \gamma ^5 C)_{\rho \tau } \left[ \left( \sigma ^{\Delta _{T} {{\mathcal {E}}}^*} U^{+}\right) _{\chi }\right. \nonumber \\&\left. -\frac{m_N ({{\mathcal {E}}}^* \cdot n)}{2(1+\xi )}\left( {\hat{\Delta }}_{T} U^{+}\right) _{\chi }\right] ; \nonumber \\ (a_{2 T}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N^2} \left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi } ({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times ({\hat{p}} \gamma ^5 C)_{\rho \tau }\left( {\hat{\Delta }}_T U^{+}\right) _{\chi }; \end{aligned}$$

(B2)

$$\begin{aligned} (t_{1 {{{\mathcal {E}}} }}^{\gamma N})_{\rho \tau , \, \chi }= & {} \left( \sigma _{p \mu } C\right) _{\rho \tau } \left[ \left( \gamma _5 \sigma ^{\mu {{\mathcal {E}}}^*} U^{+}\right) _ {\chi }\right. \nonumber \\&\left. -\frac{m_N ({{\mathcal {E}}}^* \cdot n)}{2(1+\xi )}\left( \gamma ^5 \gamma ^{\mu } U^{+}\right) _{\chi }\right. \nonumber \\&\left. -\frac{2({{\mathcal {E}}}^* \cdot n)}{(1-\xi )}\left( \gamma ^5 \sigma ^{\mu \Delta _{T}} U^{+}\right) _{\chi }\right] ; \nonumber \\&(t_{1 T}^{\gamma N})_{\rho \tau , \, \chi } =\frac{1}{m_N}\left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi }({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times \left( \sigma _{p \mu } C\right) _{\rho \tau }\left( \gamma ^5 \gamma ^{\mu } U^{+}\right) _{\chi }; \nonumber \\ (t_{2 {{{\mathcal {E}}} }}^{\gamma N})_{\rho \tau , \, \chi }= & {} \left[ \left( \sigma _{p \mathcal{E}^*} C\right) _{\rho \tau }-\frac{2({{\mathcal {E}}}^* \cdot n)}{(1-\xi )}\left( \sigma _{p \Delta _{T}} C\right) _{\rho \tau }\right] \left( \gamma ^5 U^{+}\right) _{\chi }; \nonumber \\ (t_{2 T}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1)}{m_N^{2}} \left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi } ({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times \left( \sigma _{p \mu } C\right) _{\rho \tau }\left( \gamma ^5 \sigma ^{\mu \Delta _{T}} U^{+}\right) _{\chi }; \nonumber \\ (t_{3 {{{\mathcal {E}}} }}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N}\left( \sigma _{p \Delta _{T}} C\right) _{\rho \tau }\nonumber \\&\times \left[ \left( \gamma ^5 \hat{{\mathcal {E}}}^* U^{+}\right) _{\chi }-\frac{m_N ({{\mathcal {E}}}^* \cdot n)}{(1+\xi )}\left( \gamma ^5 U^{+}\right) _{\chi }\right. \nonumber \\&\left. -\frac{2({{\mathcal {E}}}^* \cdot n)}{(1-\xi )}\left( \gamma ^5 {\hat{\Delta }}_{T} U^{+}\right) _{\chi }\right] ; \nonumber \\ (t_{3 T}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N^{2}}\left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi }({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times \left( \sigma _{p \Delta _{T}} C\right) _{\rho \tau }\left( \gamma ^5 U^{+}\right) _{\chi }; \nonumber \\ (t_{4 {{{\mathcal {E}}} }}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N}\left[ \left( \sigma _{p {{\mathcal {E}}}^*} C\right) _{\rho \tau }- \frac{2({{\mathcal {E}}}^* \cdot n)}{1-\xi }\left( \sigma _{p \Delta _{T}} C\right) _{\rho \tau }\right] \nonumber \\&\times \left( \gamma ^5 {\hat{\Delta }}_{T} U^{+}\right) _{\chi }; \nonumber \\ (t_{4 T}^{\gamma N})_{\rho \tau , \, \chi }= & {} \frac{1}{m_N^{3}}\left[ \left( {{\mathcal {E}}}^* \cdot \Delta _{T}\right) -\frac{2 \Delta _{T}^{2}}{1-\xi }({{\mathcal {E}}}^* \cdot n)\right] \nonumber \\&\times \left( \sigma _{p \Delta _{T}} C\right) _{\rho \tau }\left( \gamma ^5 {\hat{\Delta }}_{T} U^{+}\right) _{\chi }. \end{aligned}$$

(B3)